1 Электрические сигналы, их классификация и параметры

Вид материала

Содержание

1.3. Распределение мощности в спектре
1.4. Спектр периодической последовательности
плотность непериодического сигнала
1.6. Спектральная плотность
1.7. Корреляционный анализ детерминированных

Подобный материал:

СИГНАЛЫ

1.1. Электрические сигналы,

их классификация и параметры

Электрические сигналы представляют собой электрические процессы, используемые для передачи, приема и преобразования информации.

Сигналы можно разделить на два больших класса: детерминированные и случайные. Детерминированными называются сигналы, мгновенные значения которых в любой момент времени можно предсказать с вероятностью, равной единице, и которые могут быть заданы в виде некоторой определенной функции времени. Приведем несколько характерных примеров: гармонический сигнал с известной амплитудой A и периодом T (рис. 1.1 а); последовательность прямоугольных импульсов с известным периодом следования T, длительностью импульса _и и его амплитудой A (рис. 1.1 б); последовательность импульсов произвольной, но не изменяющейся формы с известной длительностью _и, амплитудой A и периодом T (рис. 1.1 в). Такие детерминированные сигналы, в принципе, не содержат никакой информации.

Случайные сигналы представляют собой хаотические функции времени, значения которых в конкретный момент времени заранее неизвестны и не могут быть предсказаны с вероятностью, равной единице, например, одиночный импульс с длительностью _и и амплитудой A (рис. 1.1 г), речь или музыка, преобразованные в электрические процессы и т. д. К случайным сигналам относятся также шумы.

Детерминированные сигналы, в свою очередь, подразделяются на периодические, для которых выполняется условие S(t)=S(t+kT), где T – период, k – любое целое число, а под S(t) чаще всего понимаются изменяющиеся со временем ток, напряжение, иногда заряд (рис. 1.1 а, б, в). Очевидно, что к непериодическим сигналам относится любой детерминированный сигнал, для которого выполняется условие S(t)S(t+kT). 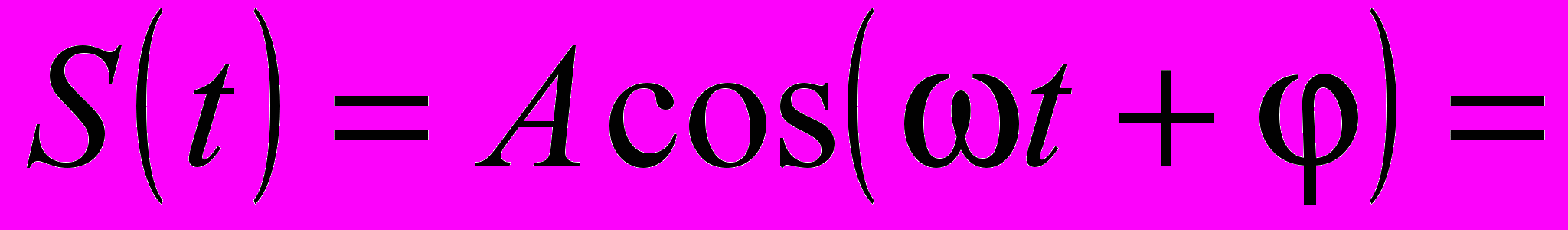Простейшим периодическим сигналом является, в частности, гармонический сигнал вида 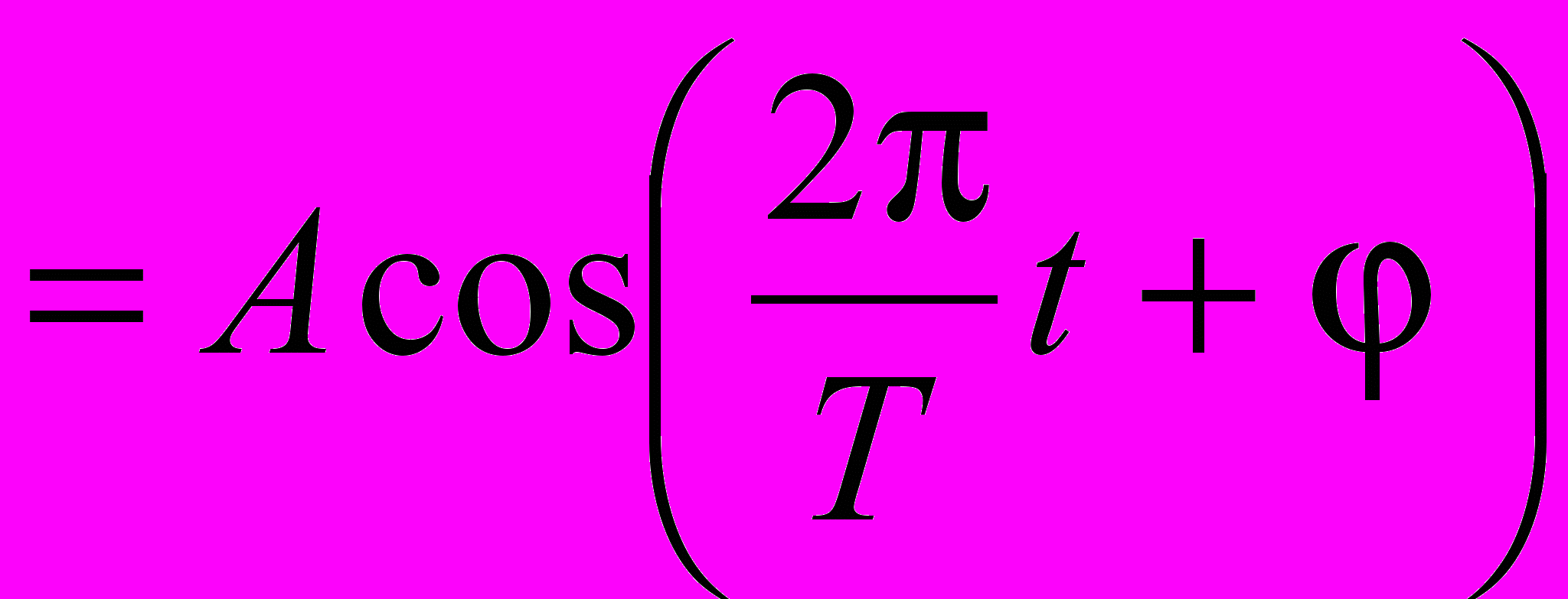, где  – круговая или циклическая частота,  – начальная фаза сигнала.

Г

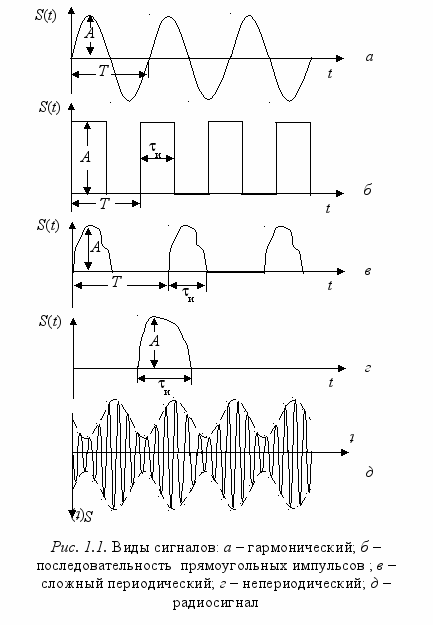
армонический сигнал высокой частоты, в котором путем модуляции, например, амплитудной, заложена информация, называется радиосигналом (рис. 1.1 д). Подробнее вопросы модуляции сигналов будут рассмотрены в п. 4.7 настоящего курса.

1.2. Периодические сигналы

Л

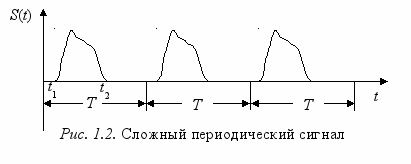
юбой сложный периодический сигнал S(t)=S(t+kT) (рис. 1.2), заданный на интервале значений времени t от – до +, может быть представлен в виде суммы элементарных гармонических сигналов. Это представление осуществляется в виде ряда Фурье, если только заданная периодическая функция удовлетворяет условиям Дирихле.

В тригонометрической форме ряд Фурье имеет вид

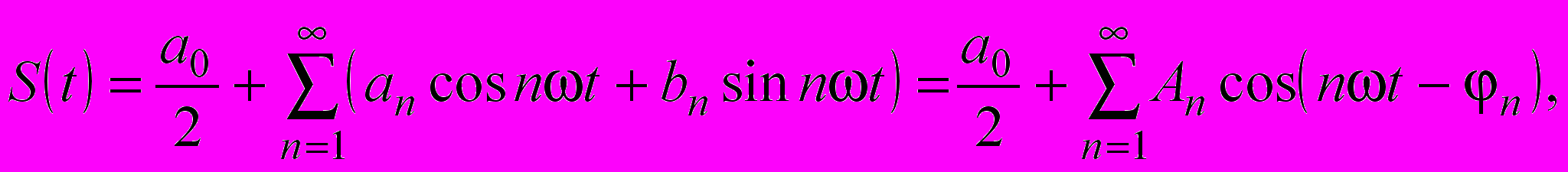(1.1)

где постоянная составляющая

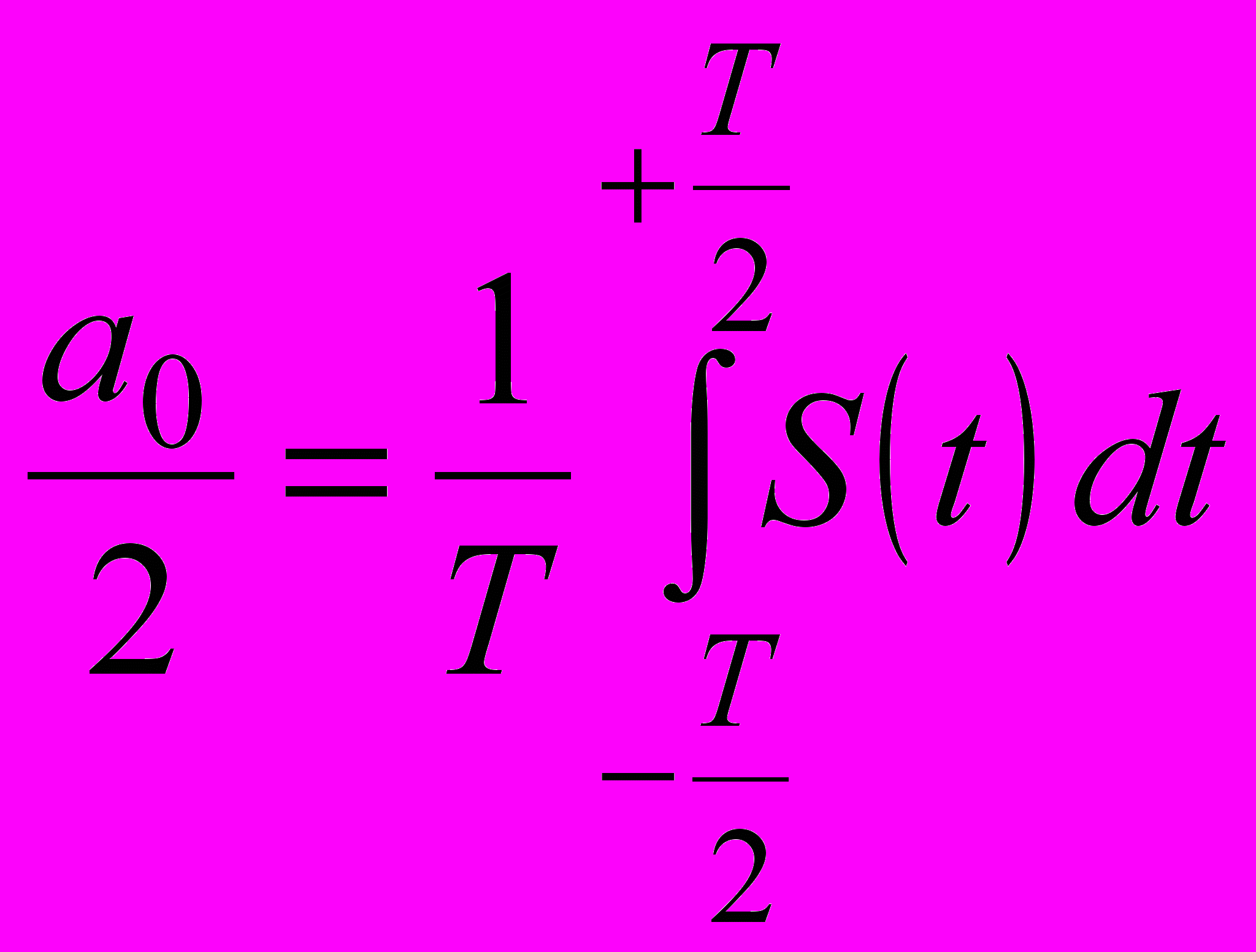(1.2)

а коэффициенты a_n, и b_n при косинусоидальных и синусоидальных членах разложения определяются выражениями

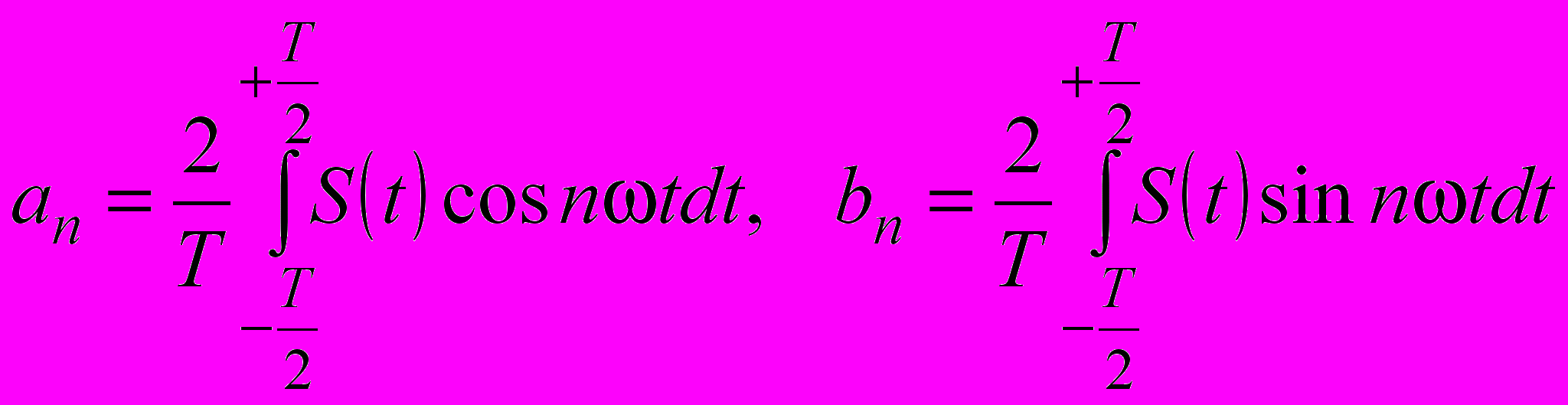(1.3)

Амплитуда (модуль) и начальная фаза (аргумент) n-й гармоники выражаются через коэффициенты a_n, и b_n следующим образом:

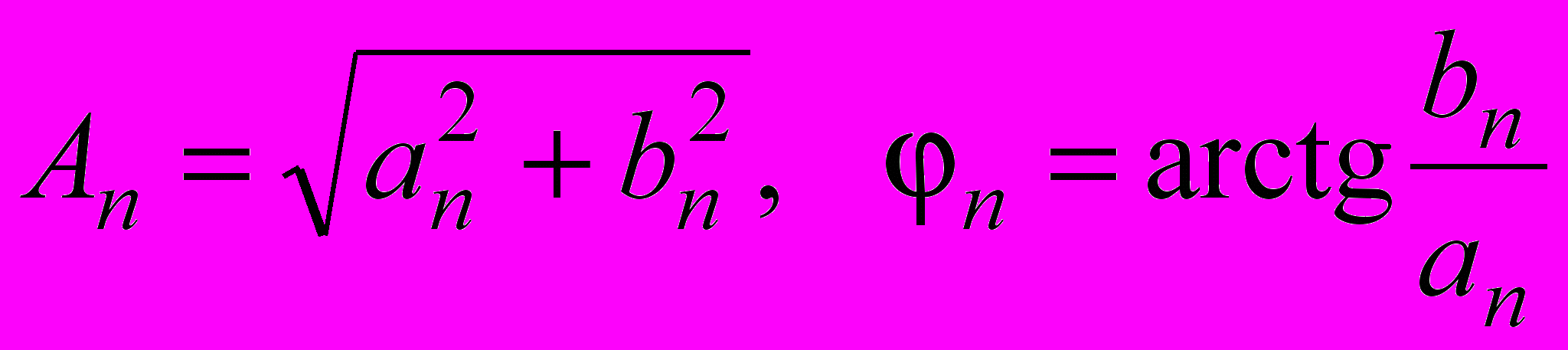(1.4)

При использовании комплексной формы записи выражение для сигнала S(t) принимает вид

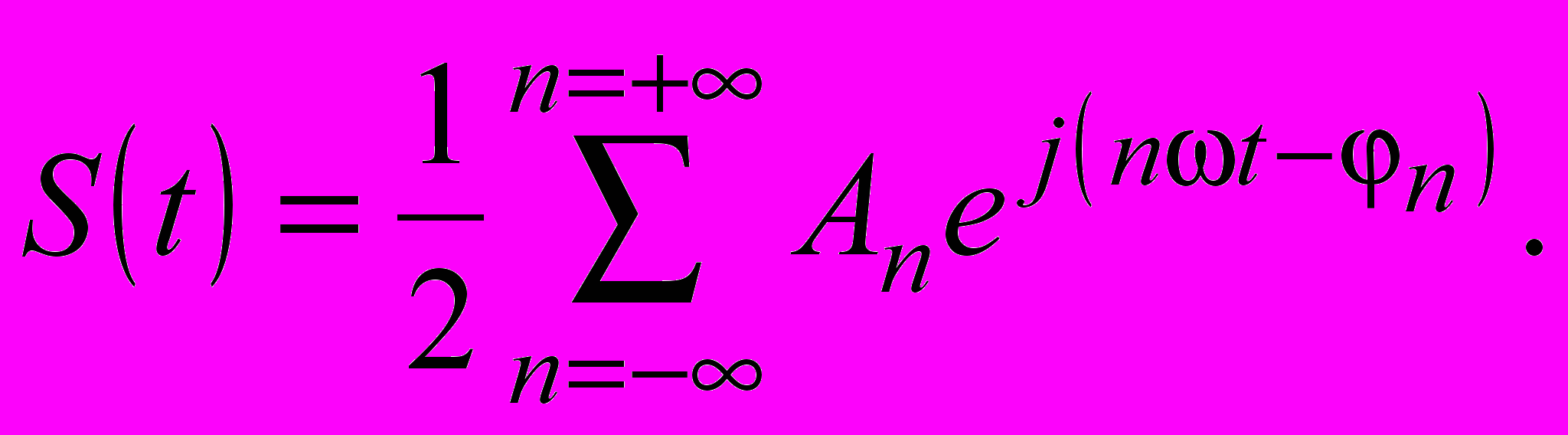Здесь коэффициенты

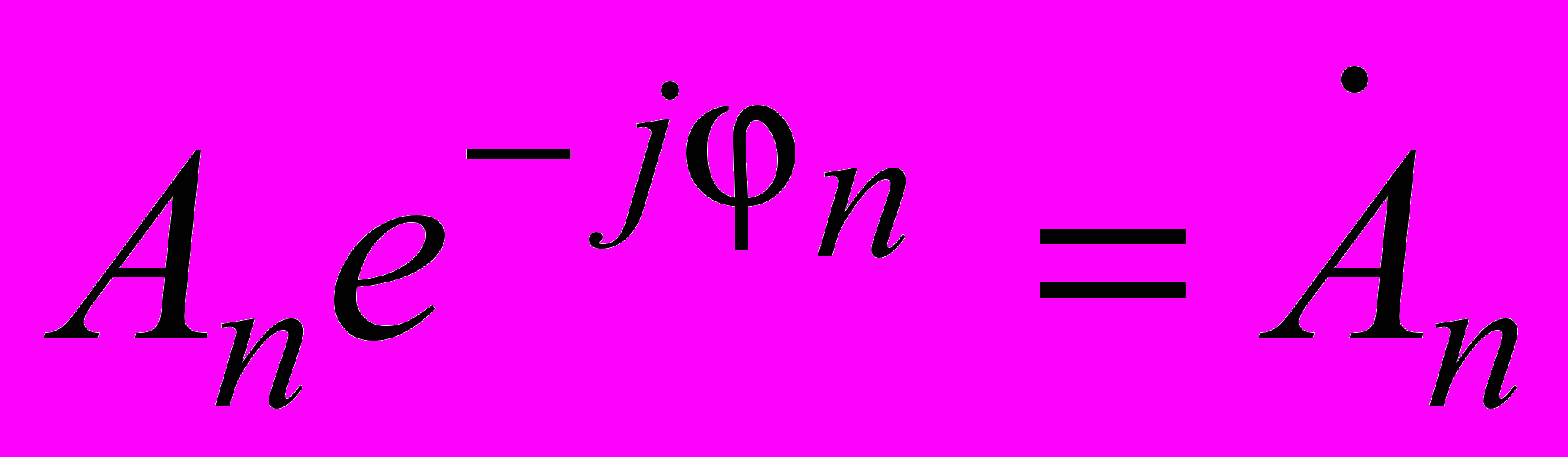, называемые комплексными амплитудами, равны

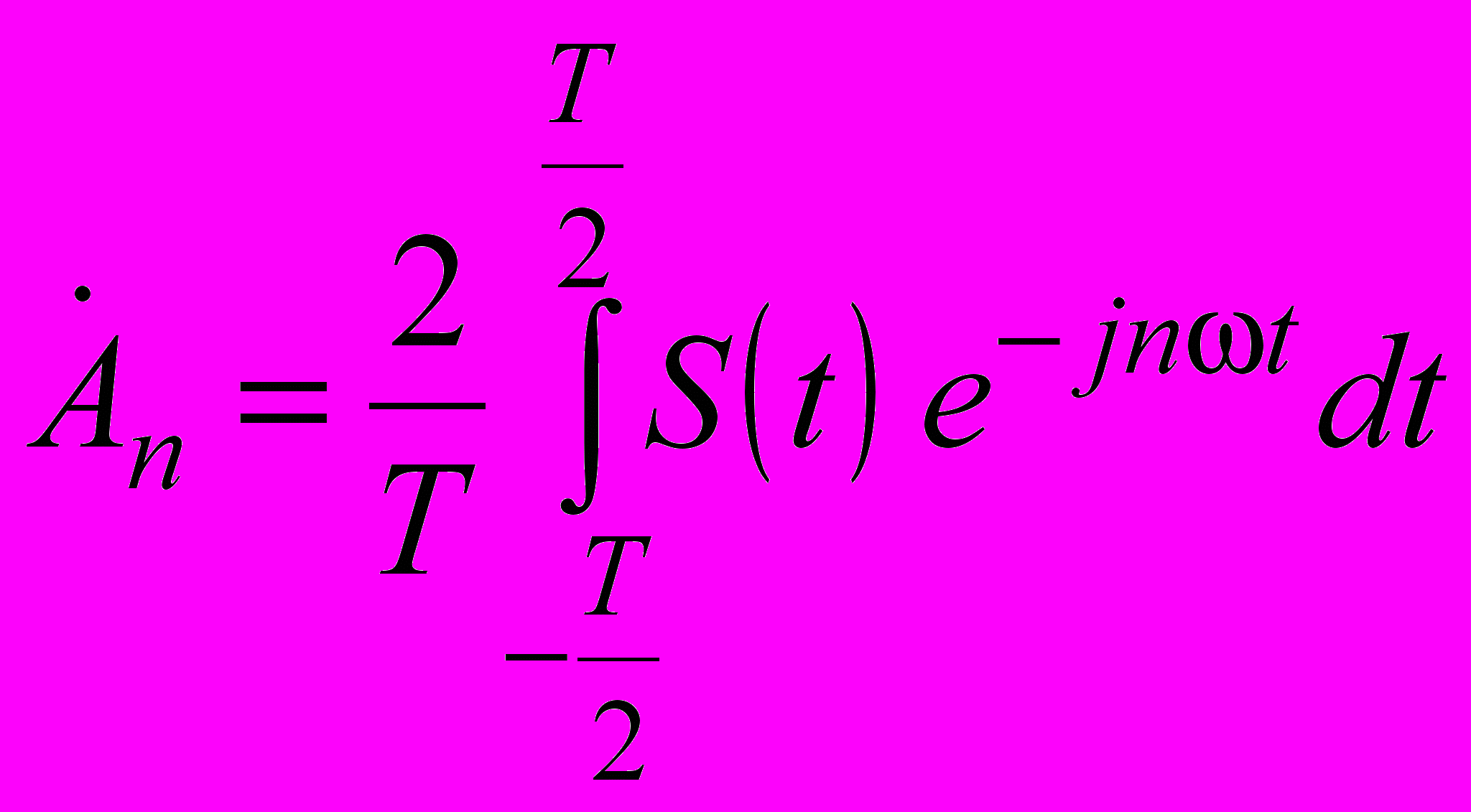и связаны с величинами a_n и b_n формулами

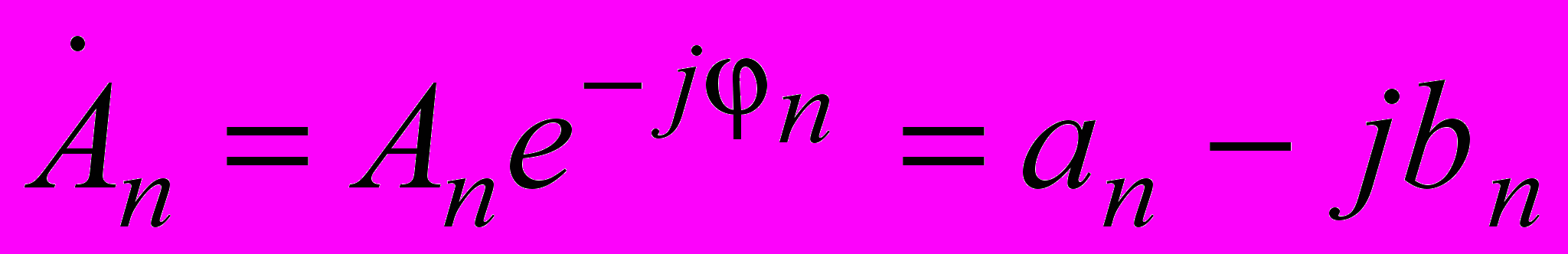при n>0 и

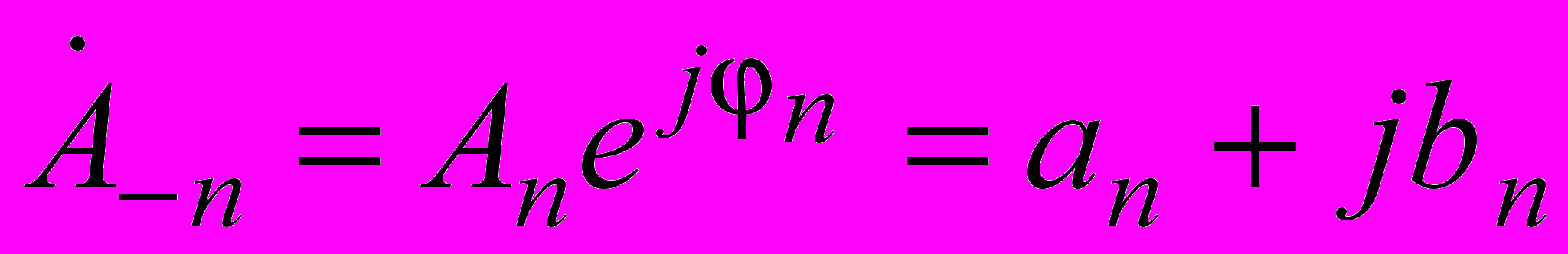при n<0. С учетом введенных обозначений сигнал в комплексном виде может быть записан как

.

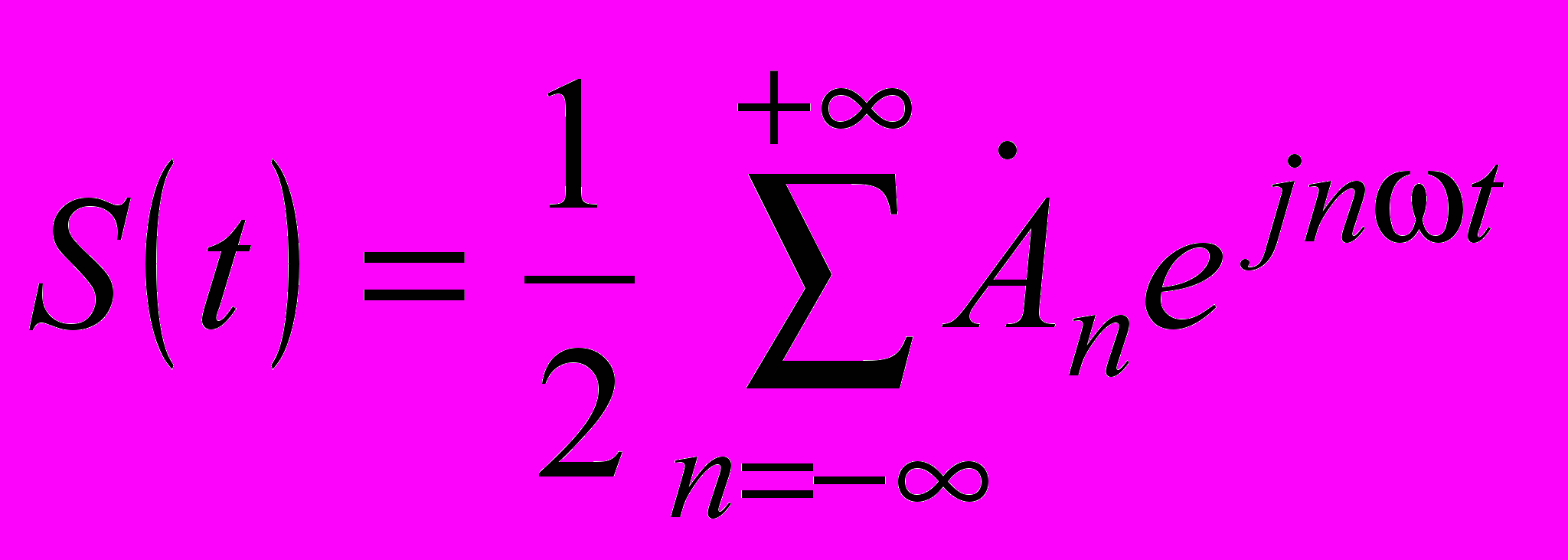С

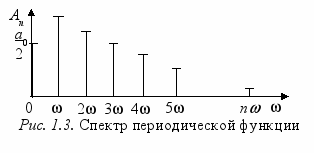пектр периодической функции состоит из отдельных линий, соответствующих дискретным частотам 0, , 2, 3, …, т. е. имеет линейчатый или дискретный характер (рис. 1.3).

При разложении периодической функции в ряд Фурье следует учитывать ее симметрию относительно начала координат, что позволяет упростить расчеты.

1.3. Распределение мощности в спектре

периодического сигнала

Рассмотрим сигнал S(t), являющийся сложной периодической функцией времени t с периодом T. По определению под средней мощностью периодического сигнала P_ср понимают среднюю мощность за один период, так что для средней мощности, выделяющейся на единичном сопротивлении, можно записать

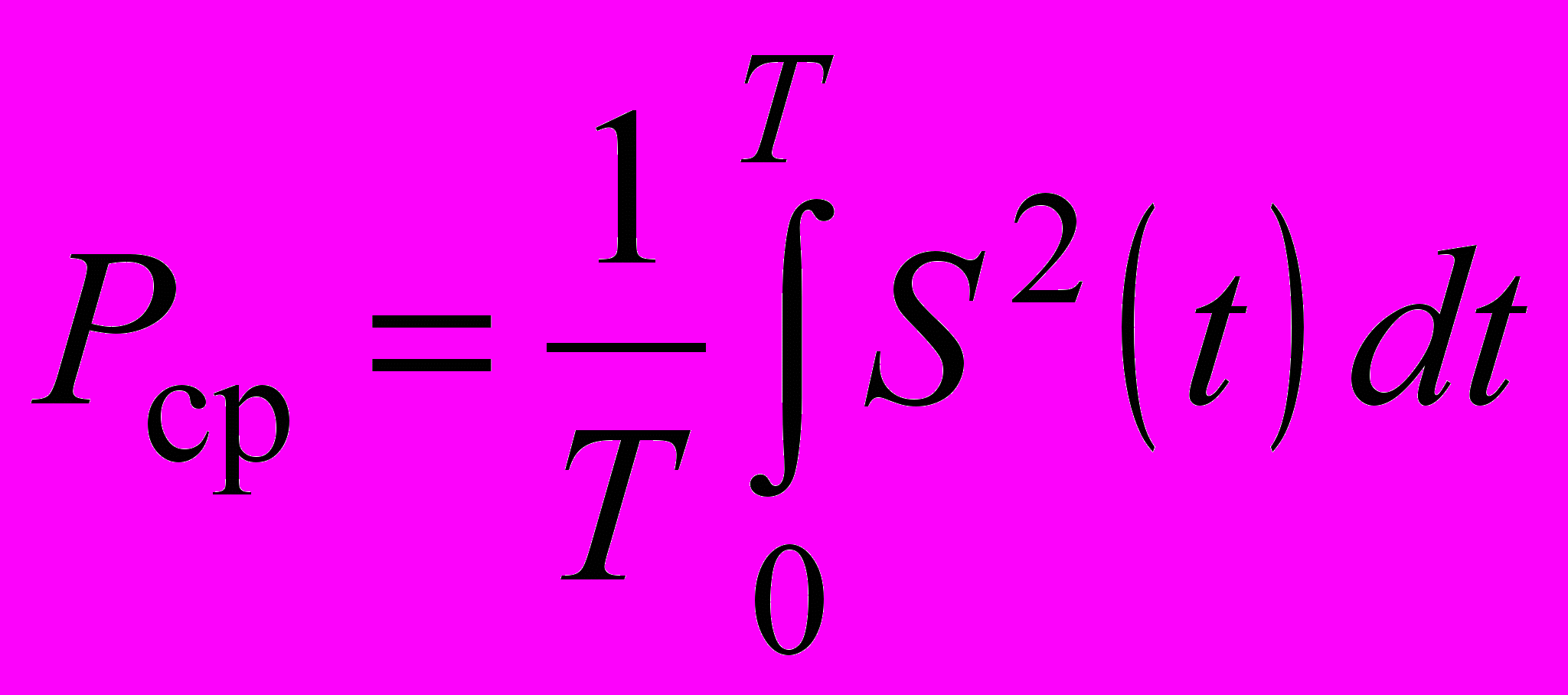(1.5)

Если разложить сигнал S(t) в ряд Фурье и воспользоваться его тригонометрической формой

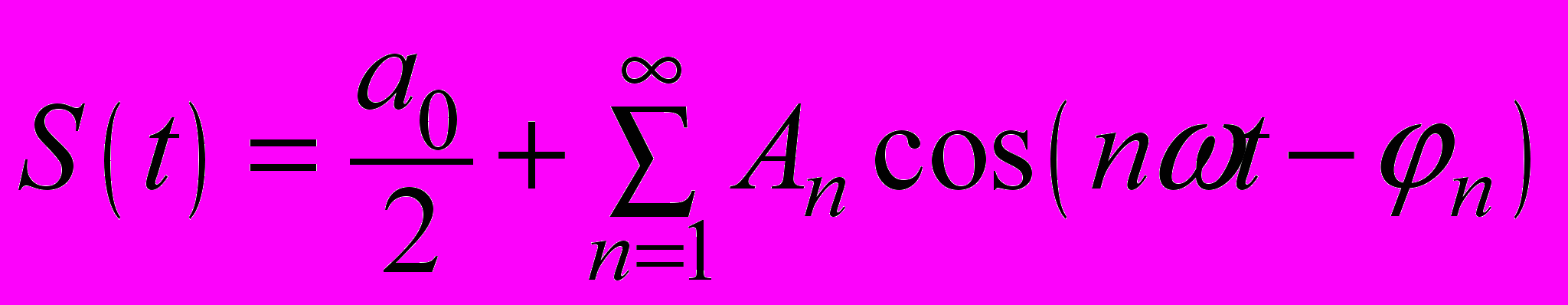, а затем возвести этот ряд в квадрат и проинтегрировать его почленно, то с учетом равенства

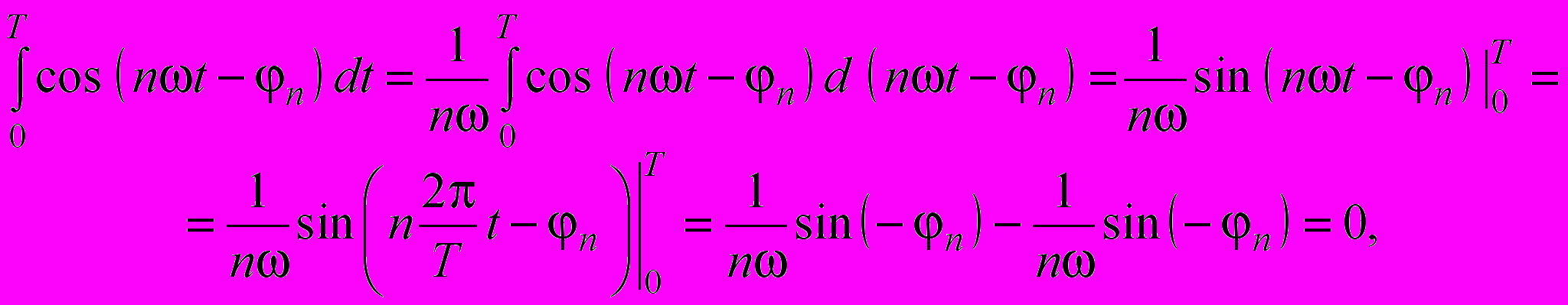а также аналогичных ему равенств

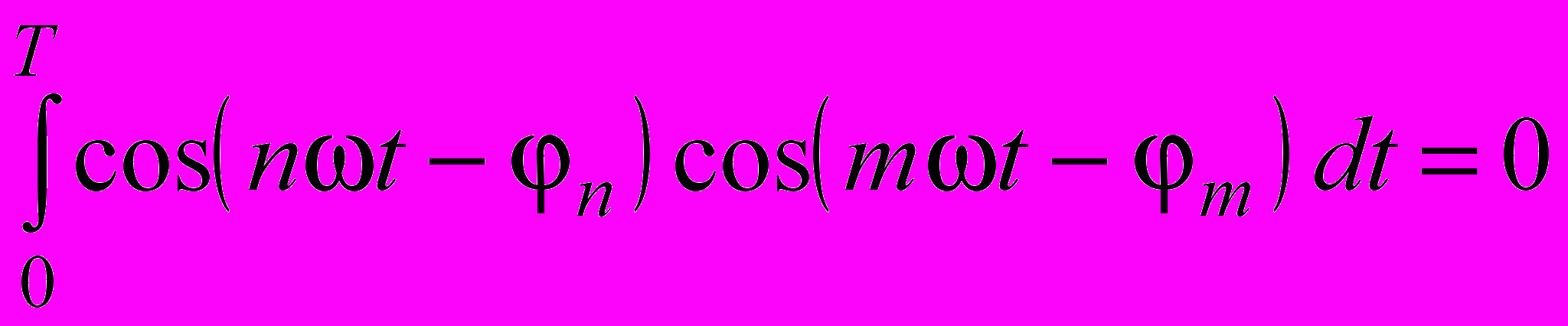при mn, и

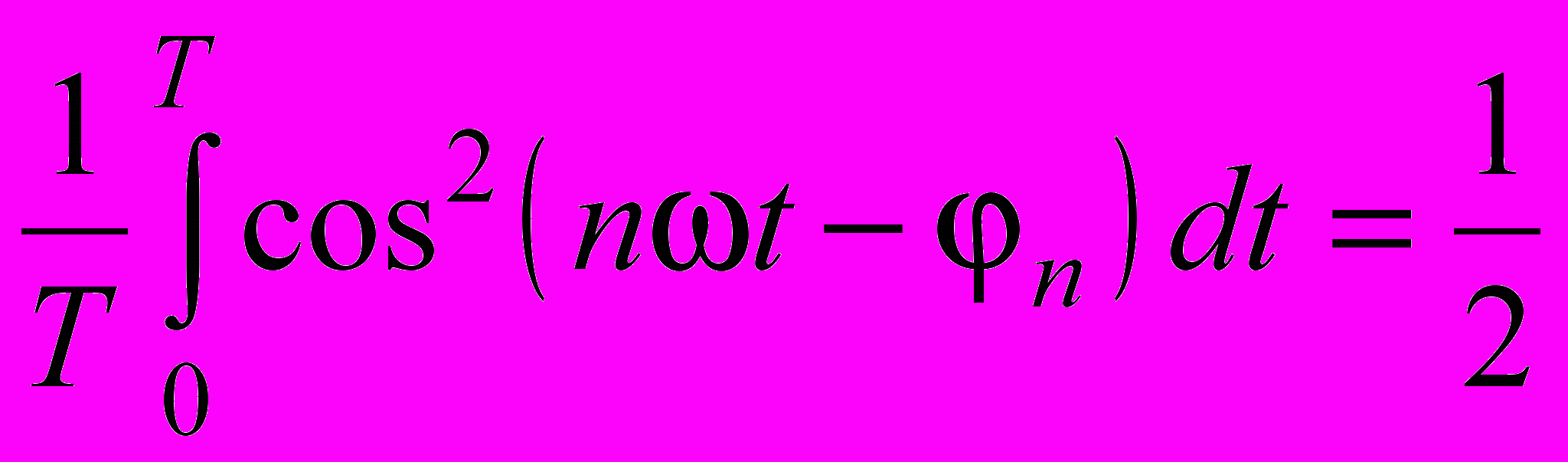, можно получить следующее выражение для мощности P_ср:

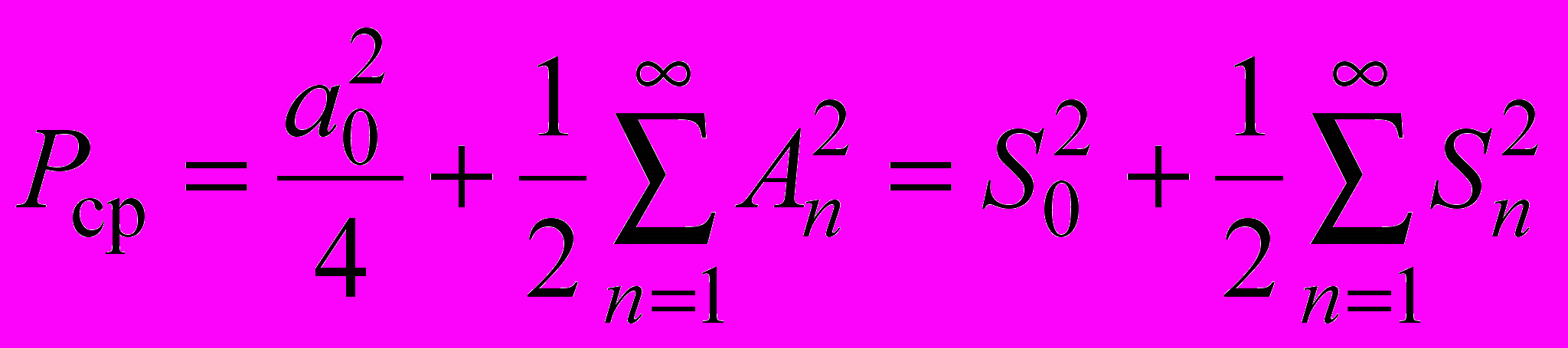(1.6)

Если взять в качестве S(t) ток i(t), то при его прохождении через сопротивление R будет выделяться средняя за период мощность

.

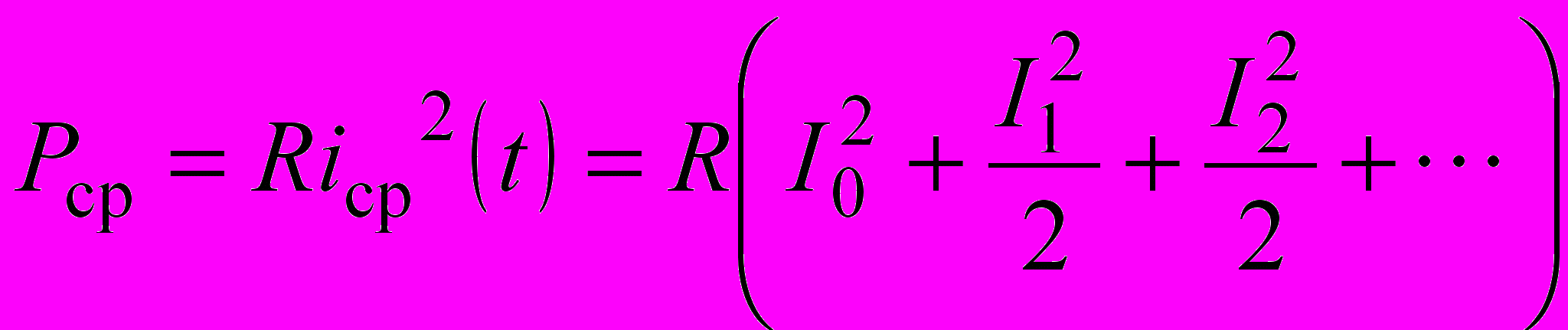Таким образом, средняя мощность периодического сигнала не зависит от фаз гармоник и является суммой средних мощностей, выделяемых по отдельности постоянной составляющей и каждой из гармоник. В силу этого, в энергетическом отношении вклад отдельных гармоник аддитивен, и суммарную мощность периодического сигнала можно представить в виде суммы мощностей всех составляющих спектра рассматриваемого сигнала.

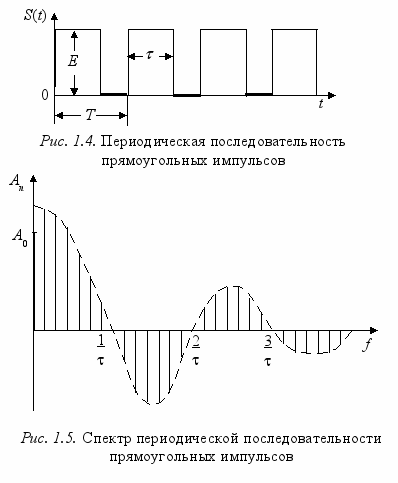
1.4. Спектр периодической последовательности

прямоугольных импульсов

Периодическая последовательность прямоугольных импульсов изображена на рис. 1.4., а ее спектр на рис. 1.5. Постоянная составляющая ряда Фурье определяется выражением (1.2) и в данном случае будет равна

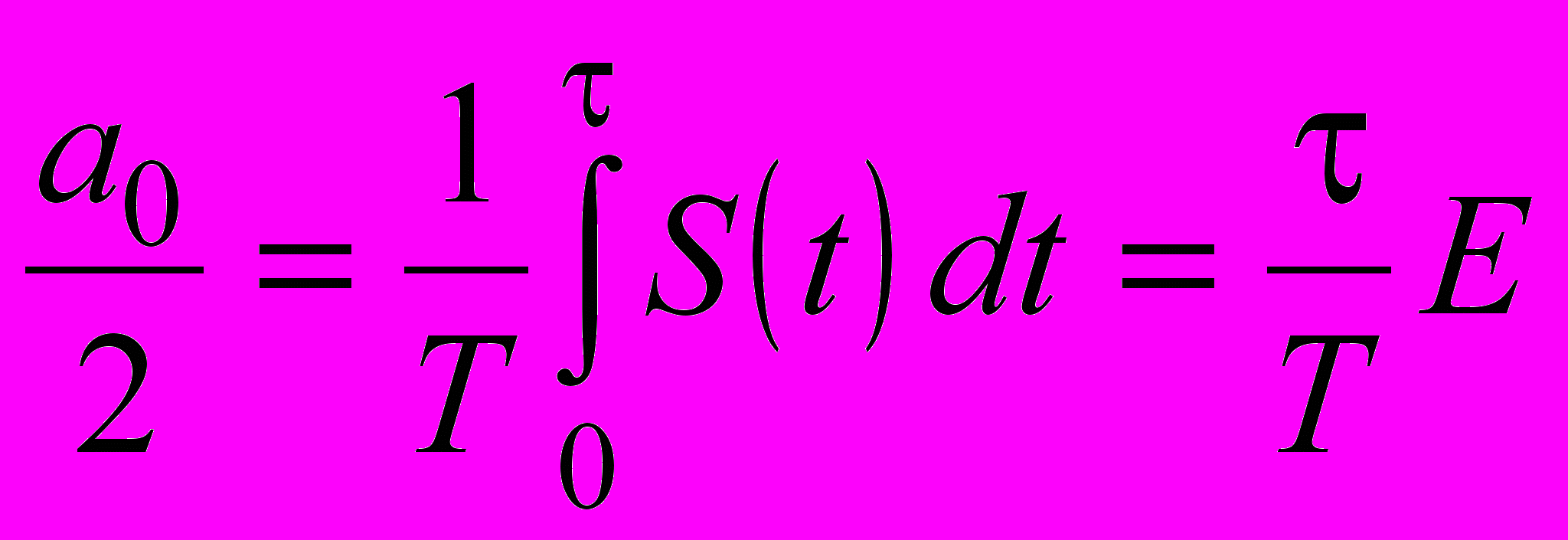. Амплитуда cos-составляющей а_n находится по первой из формул (1.3) и, соответственно, имеет вид: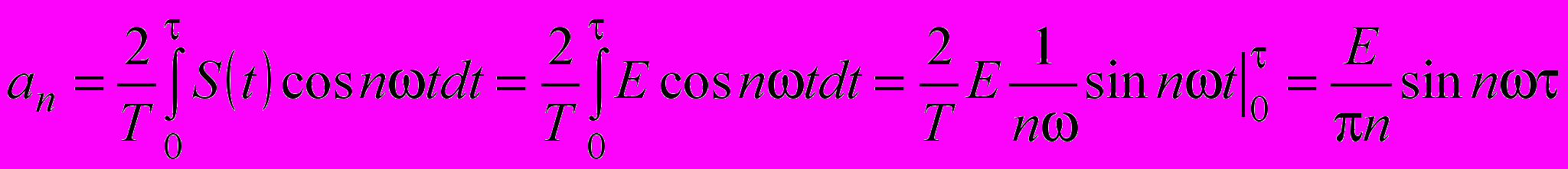

.

А амплитуда sin-составляющей b_n согласно второй формуле выражений (1.3) равна

.

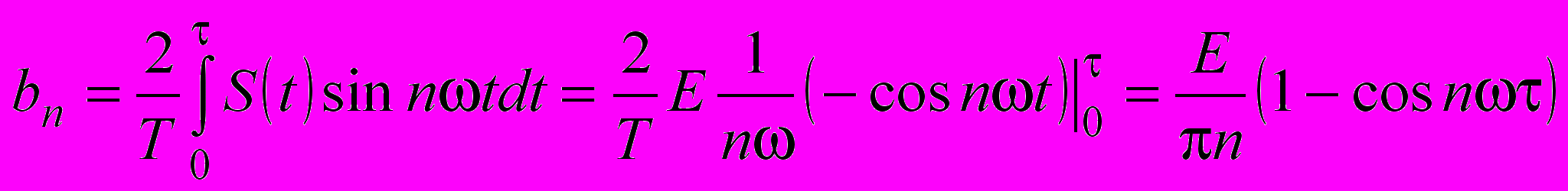Амплитуда n-й гармоники согласно (1.4)

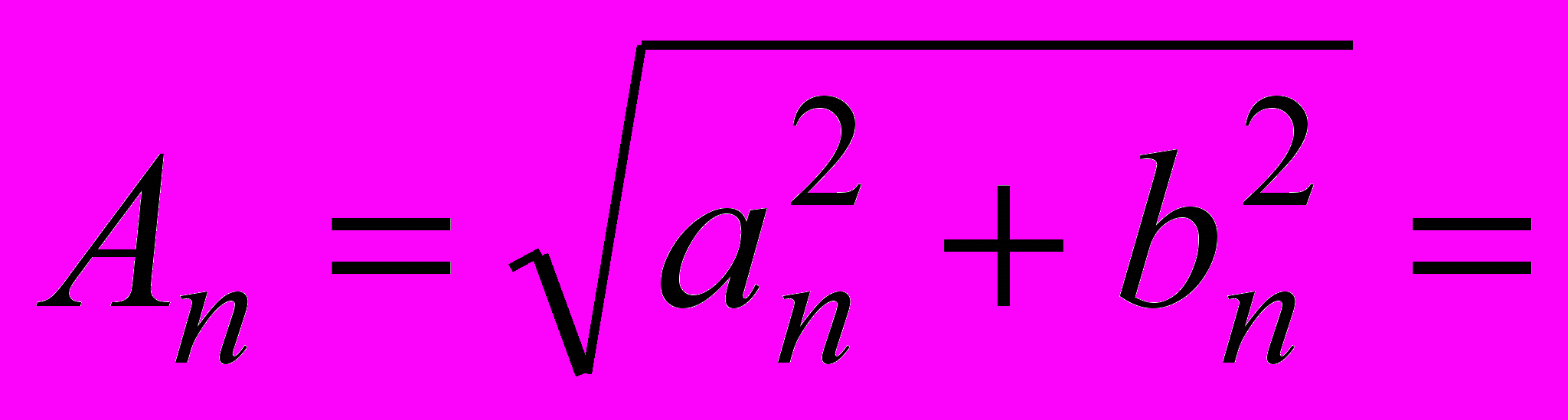
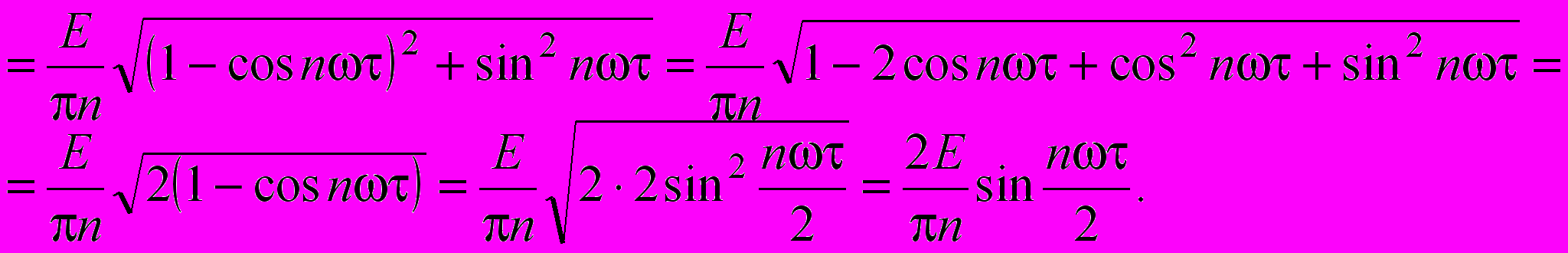
Из последнего выражения видно, что амплитуда n-й гармоники зависит от величины

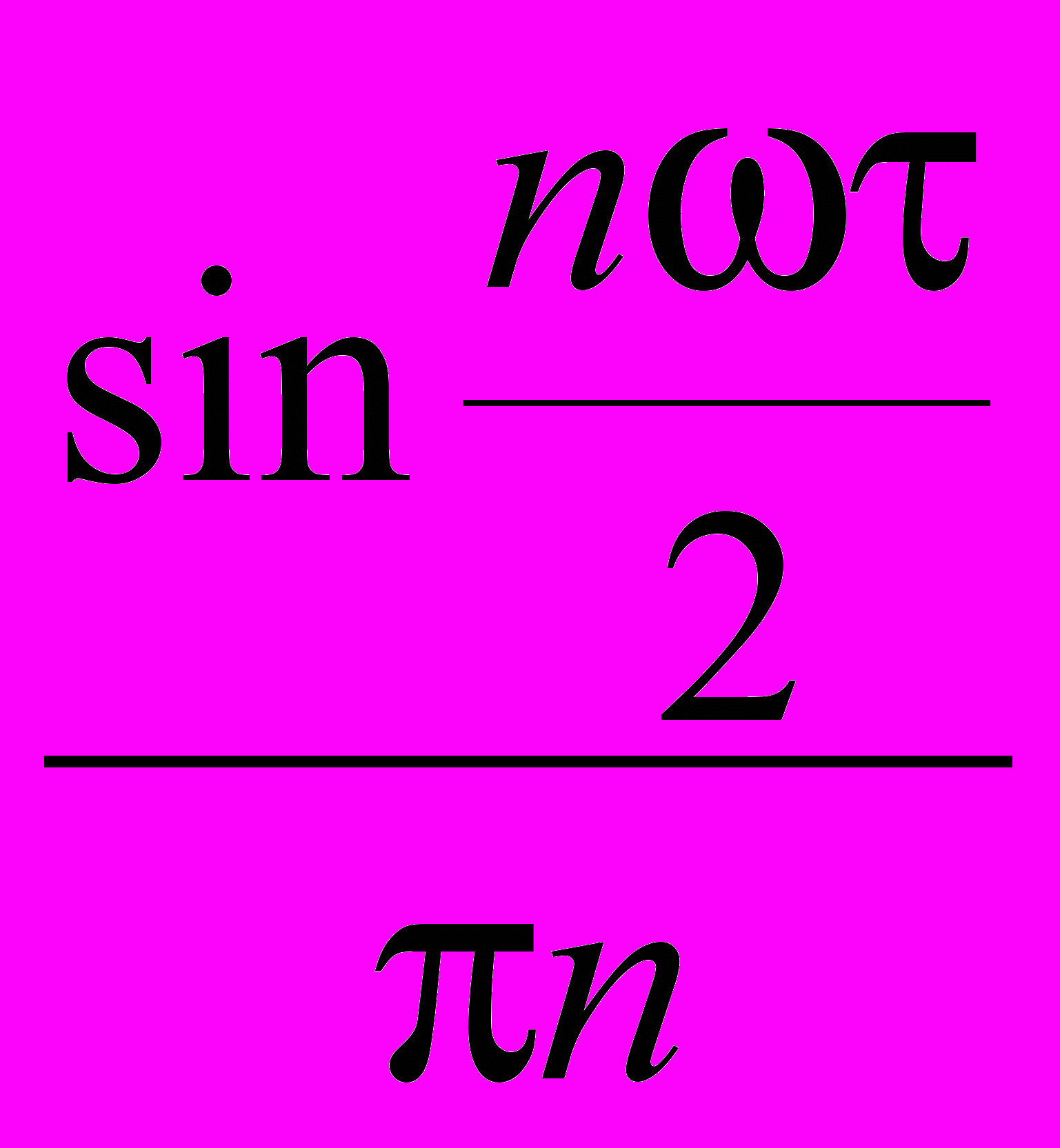, т. е. изменяется согласно этому закону.

О

пределим далее номера гармоник n₀_k, которые обращаются в нуль. Значения номеров этих гармоник находятся из условия

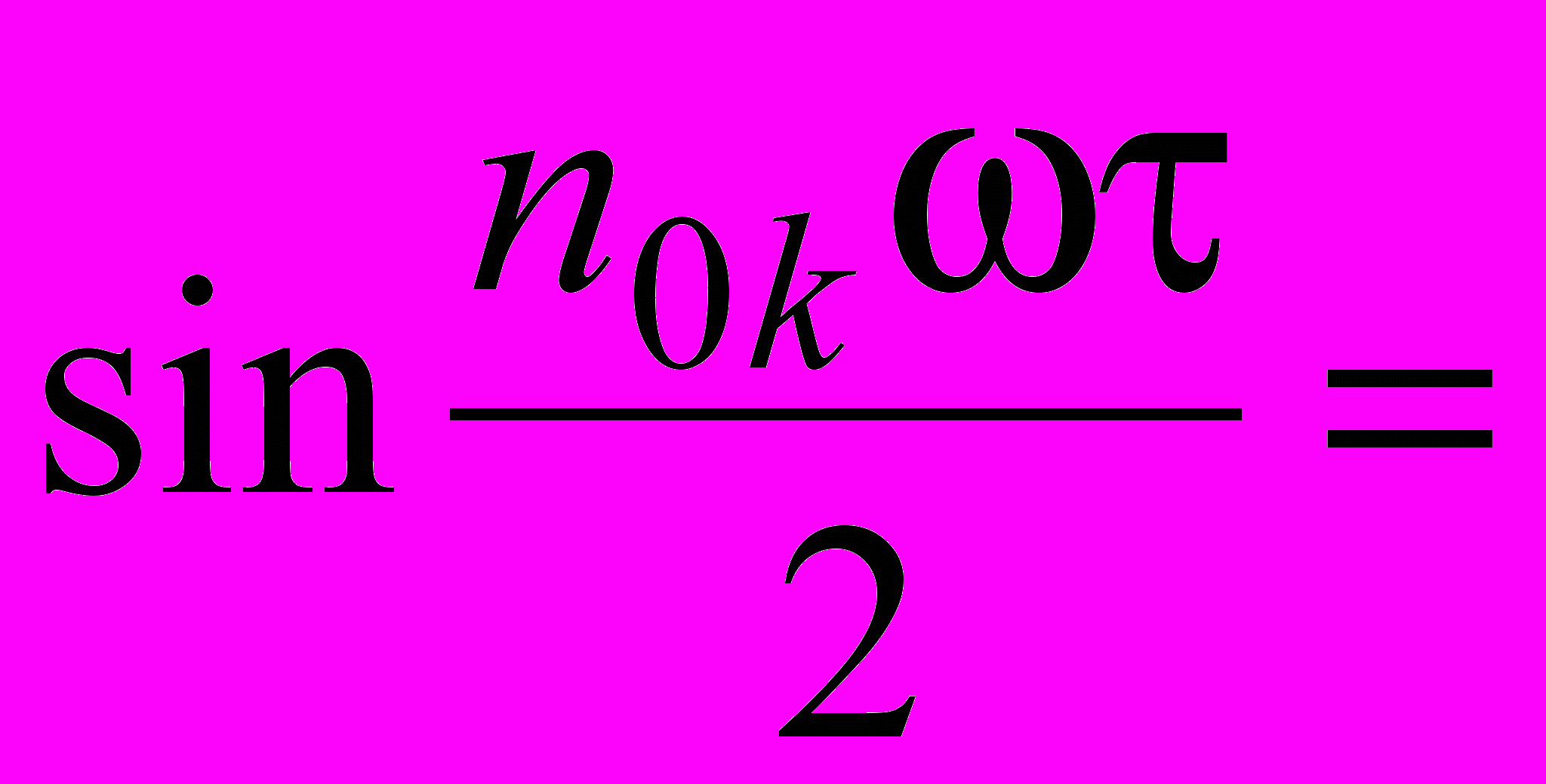
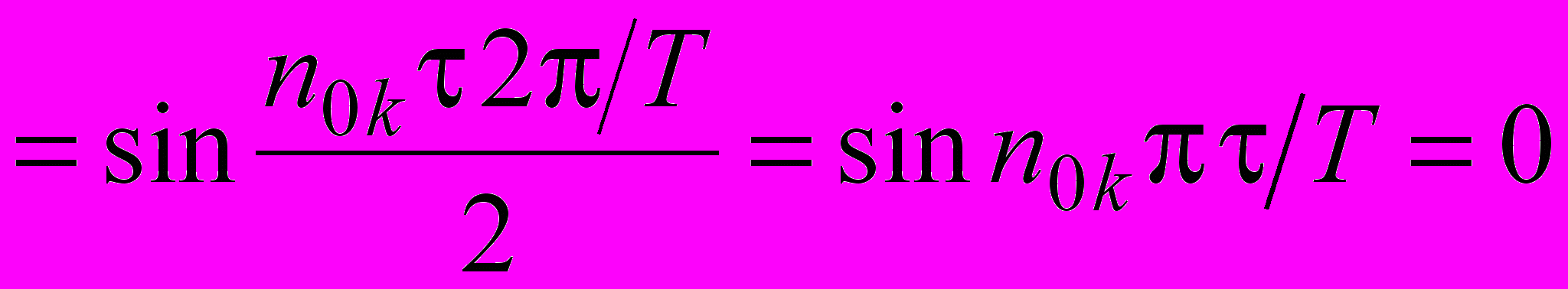, откуда

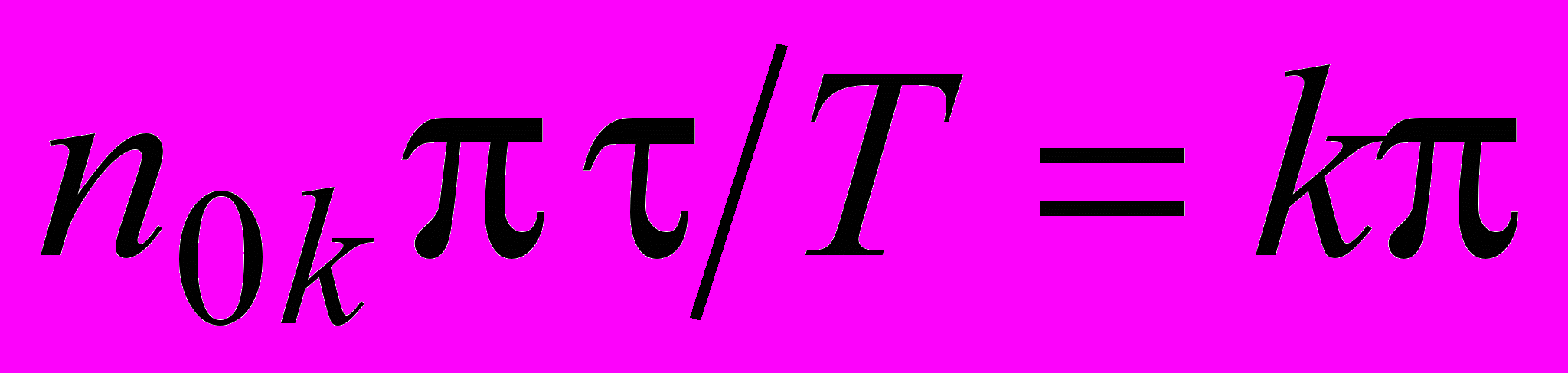, где k=1, 2, 3,…, и

.

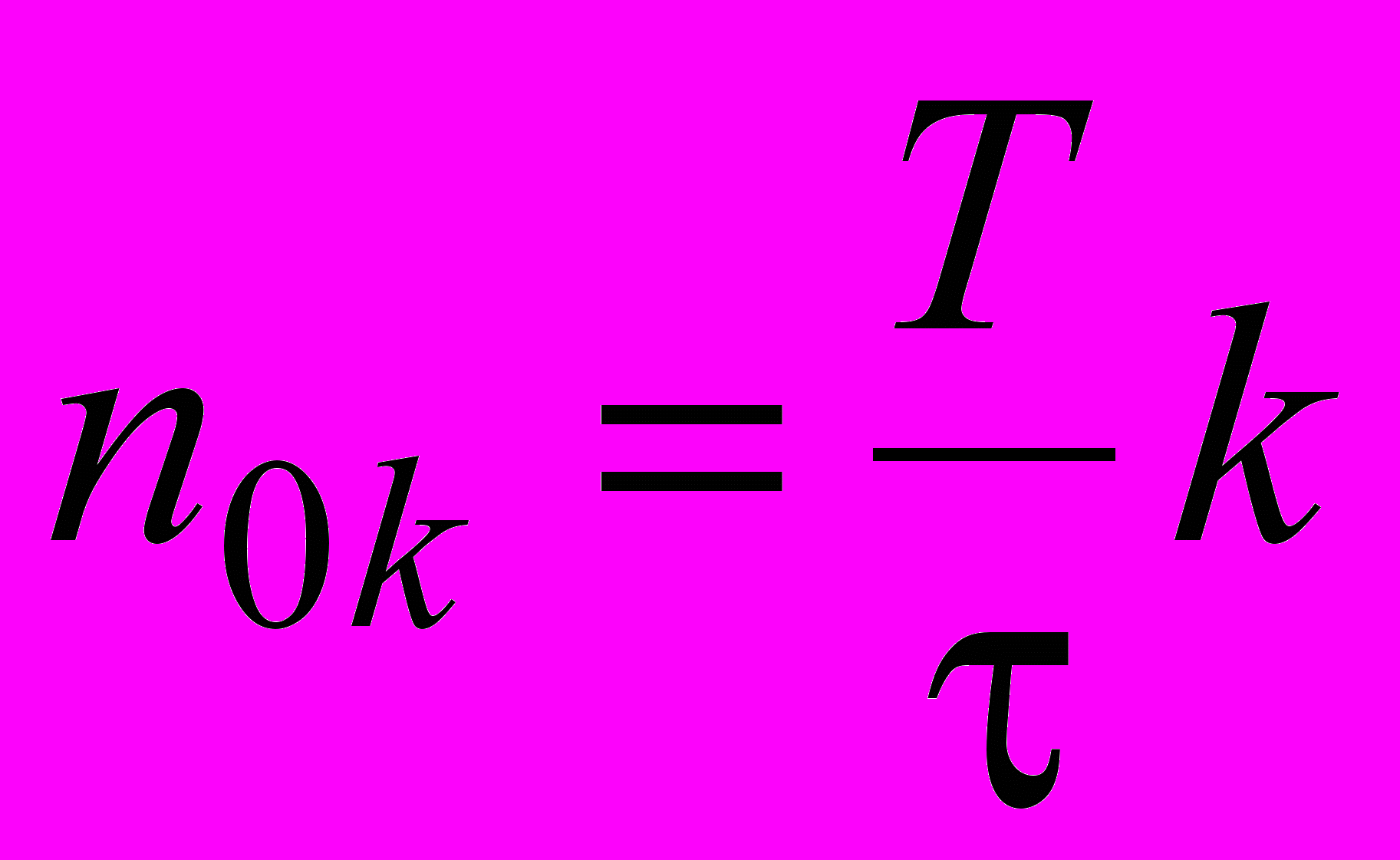Определим также соответствующие «нулевые» частоты f₀_k, т. е. те частоты, на которых амплитуда A_n равна нулю, –

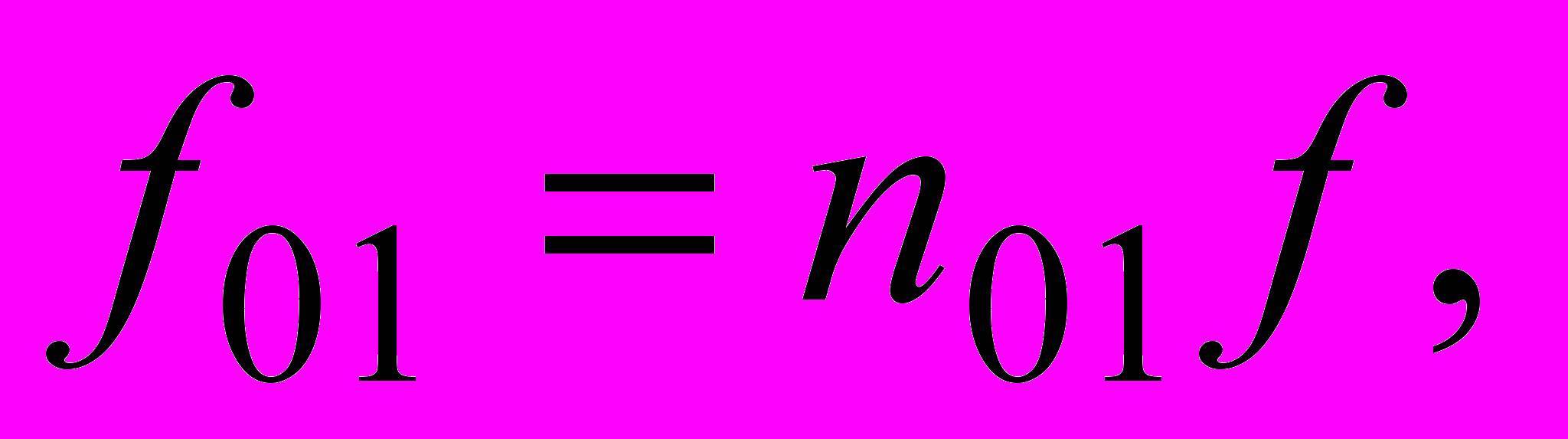
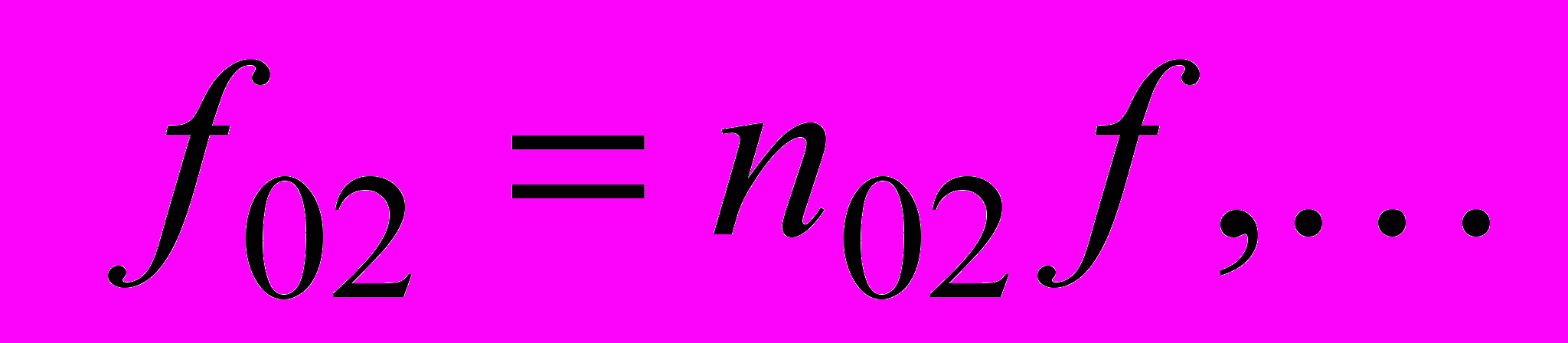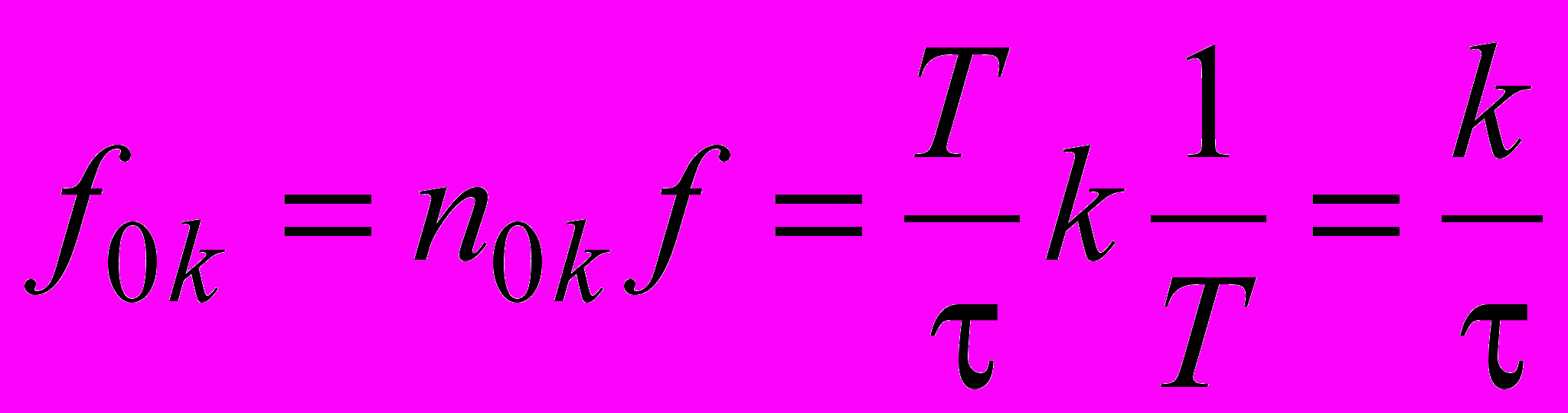и тогда

.

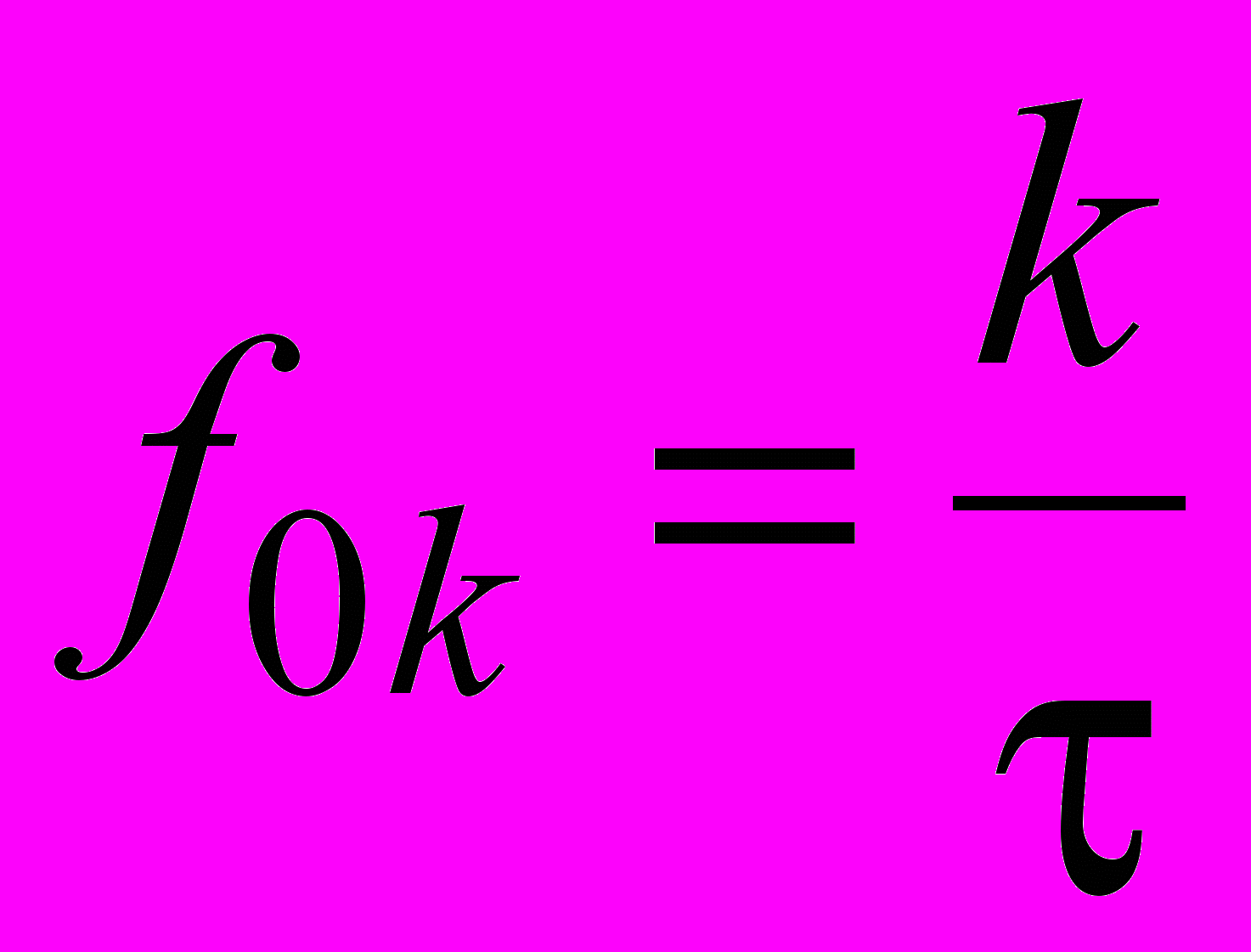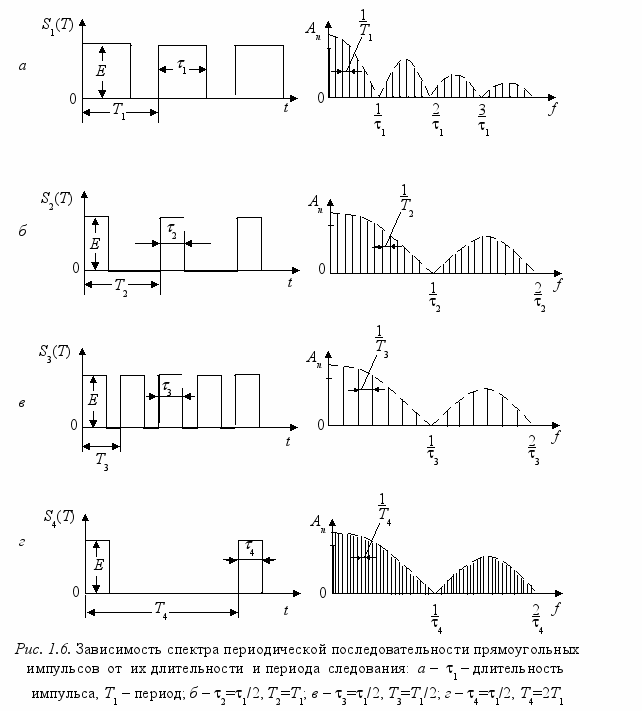
На рис. 1.6 в качестве примера изображен вид спектров (модуль амплитуд) последовательностей с различными параметрами  и Т.

1.5. Непериодические сигналы. Спектральная

плотность непериодического сигнала

От гармонического анализа периодических сигналов можно осуществить предельный переход к анализу непериодических сигналов, для которых S(t)S(t+kT). Пусть, например, непериодический сигнал S(t) задан на некотором интервале времени t₁<t<t₂. Будем считать формально эту функцию периодической, повторяющейся с периодом T>t₂–t₁. Тогда ее можно разложить в ряд Фурье и найти коэффициенты a₀/2, a_n, b_n. Устремив T , поскольку исходная функция S(t) непериодическая, получим бесконечное множество гармоник с бесконечно малыми амплитудами, составляющих сплошной спектр, (так как интервал между гармониками определяется величиной 1/T).

Воспользуемся далее комплексной формой записи разложения периодической функции в ряд Фурье (см. п. 1.2)

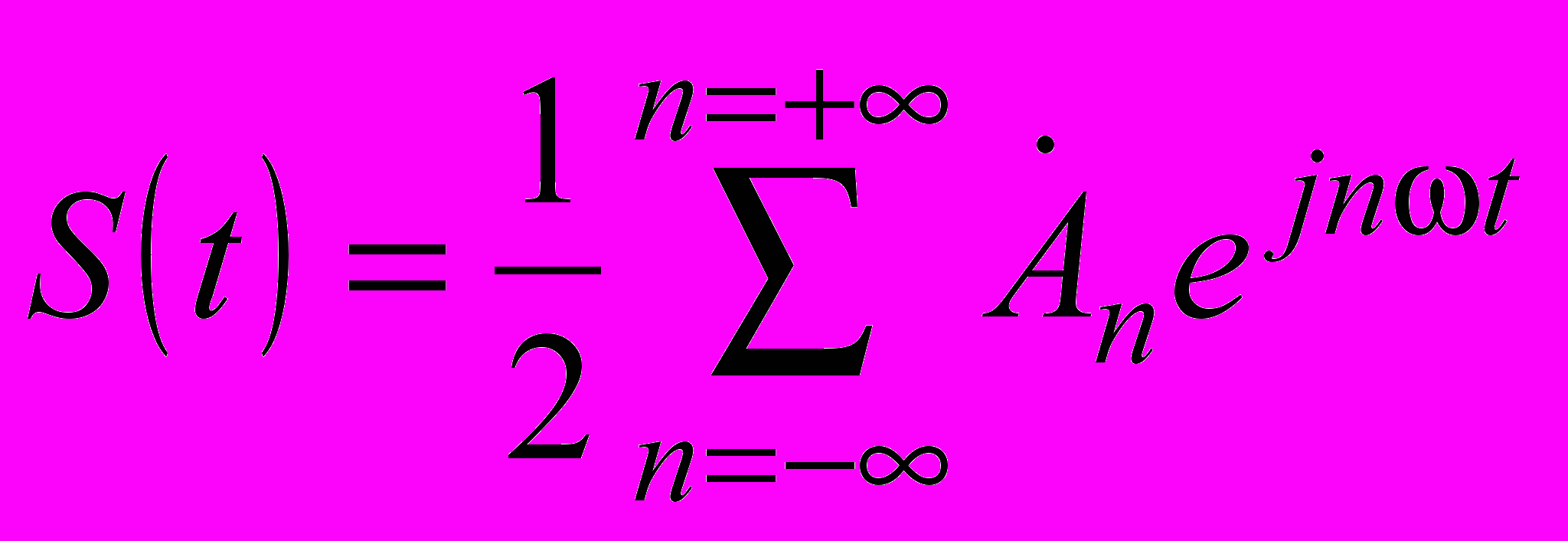(1.7)

где

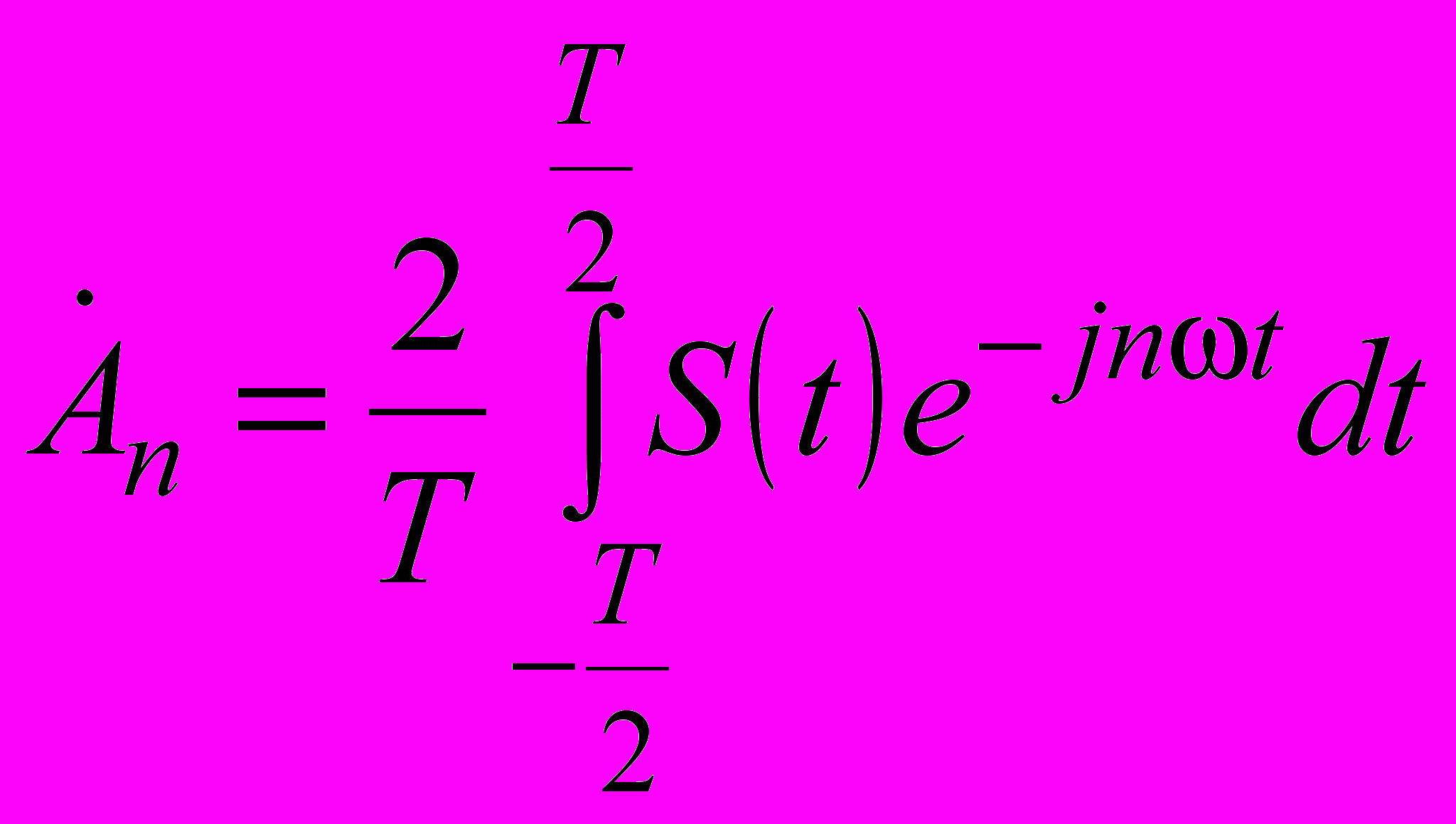(1.8)

Подставим

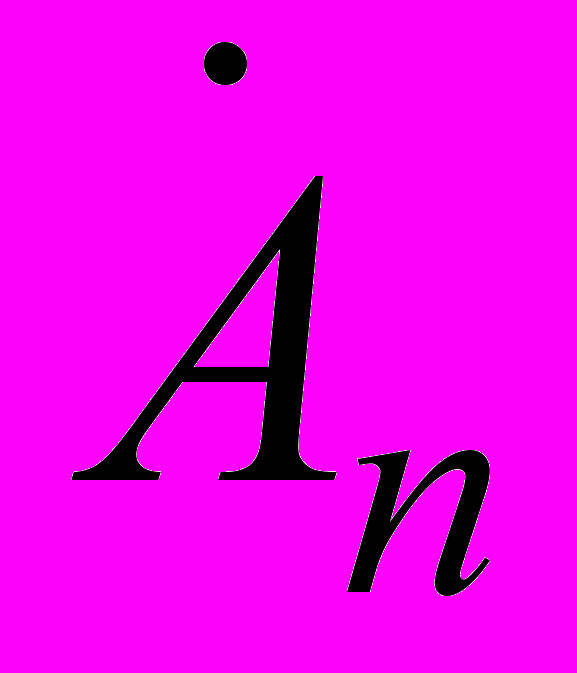из последнего равенства в формулу (1.7). Тогда получим следующее соотношение

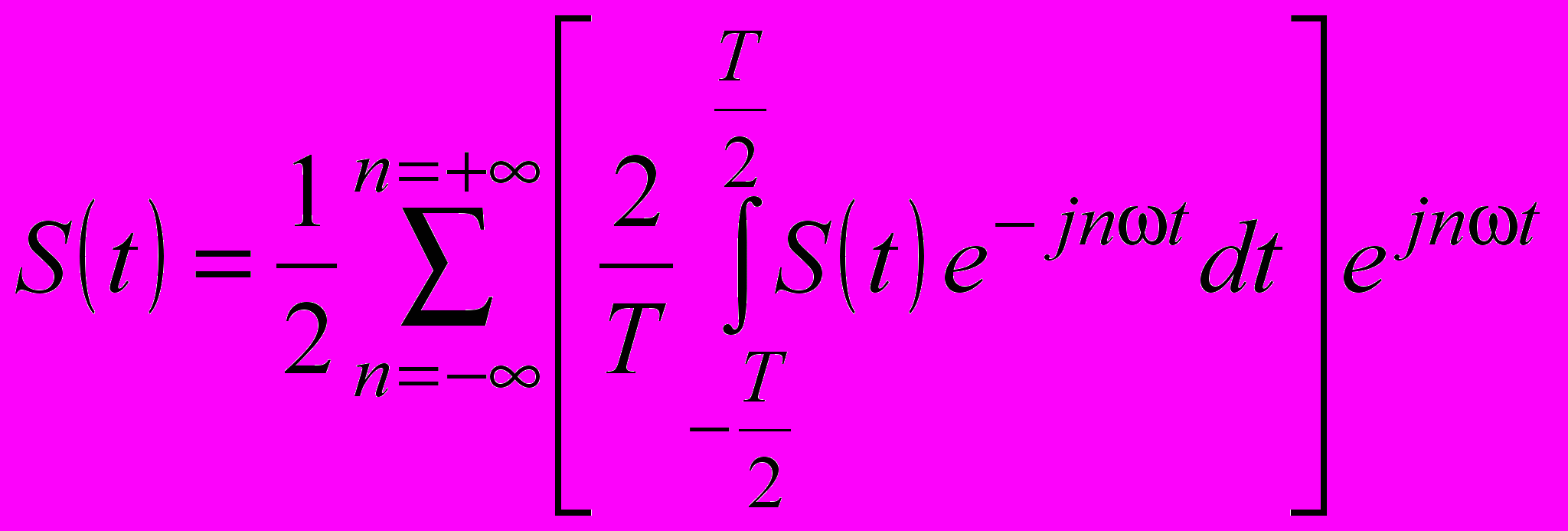(1.9)

Положим, что T  для того, чтобы периодическая функция стремилась к непериодической. При этом d, n и

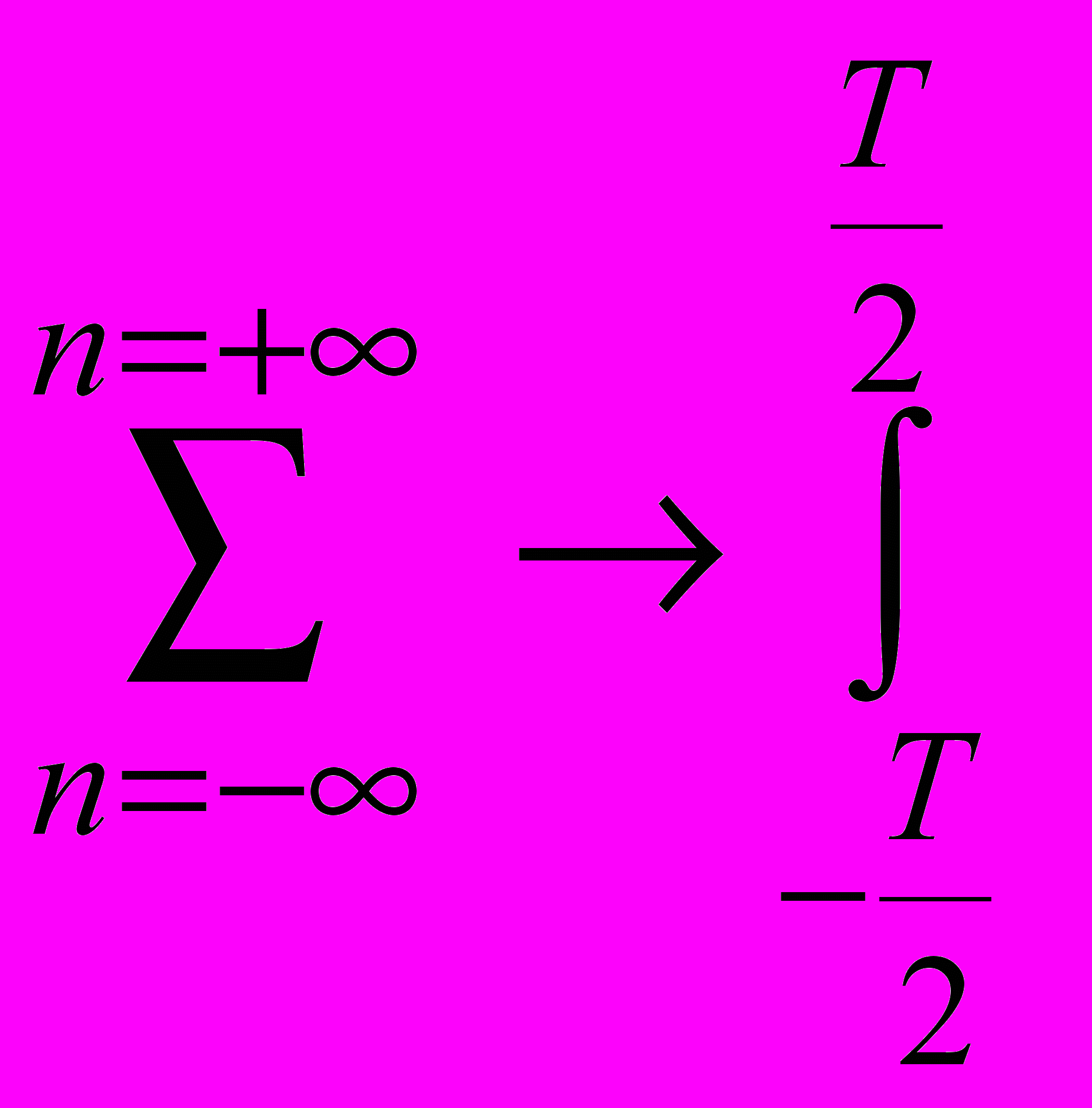. Кроме того, пределы интегрирования «от

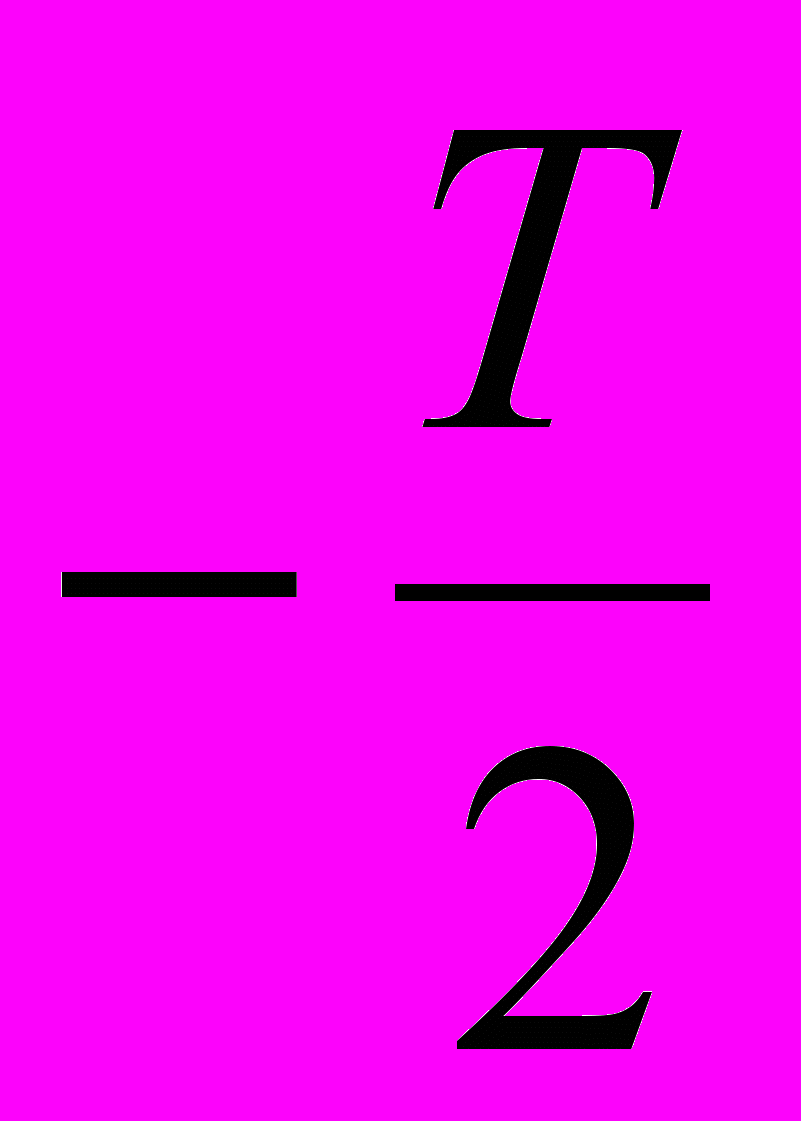до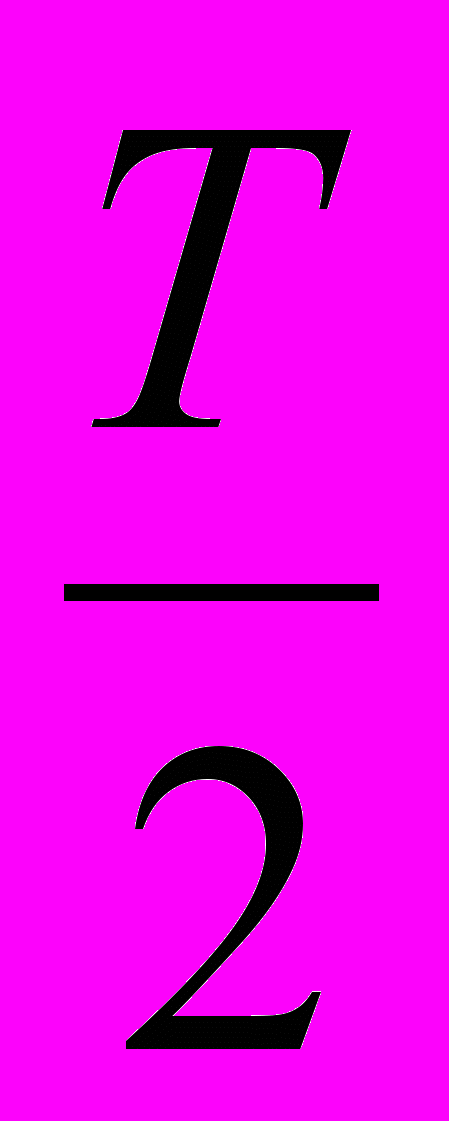

» изменяются на «от – до +». Если все эти изменения учесть в выражении (1.9), то оно примет вид

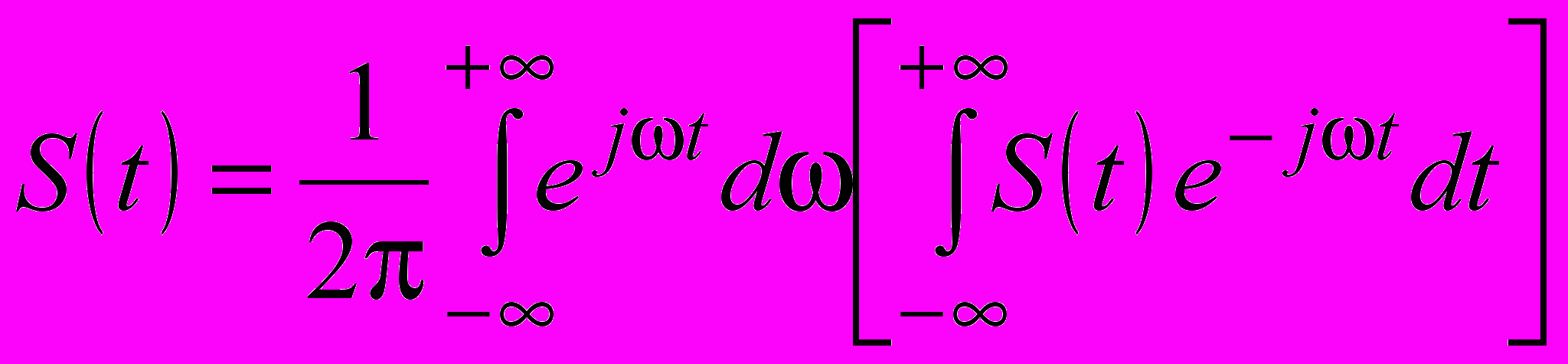(1.10)

Обозначим интеграл в квадратных скобках формулы (1.10) через

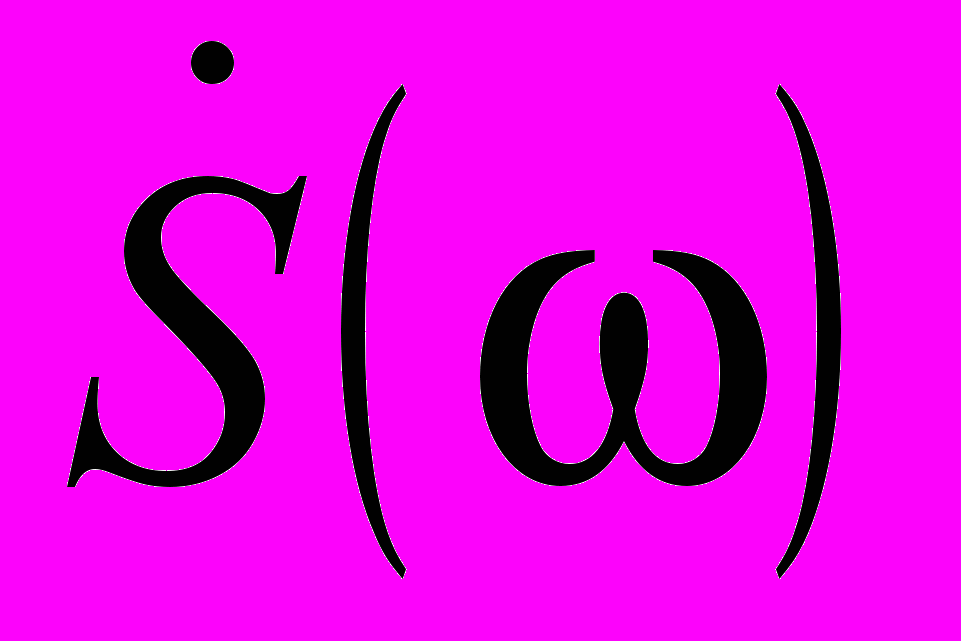
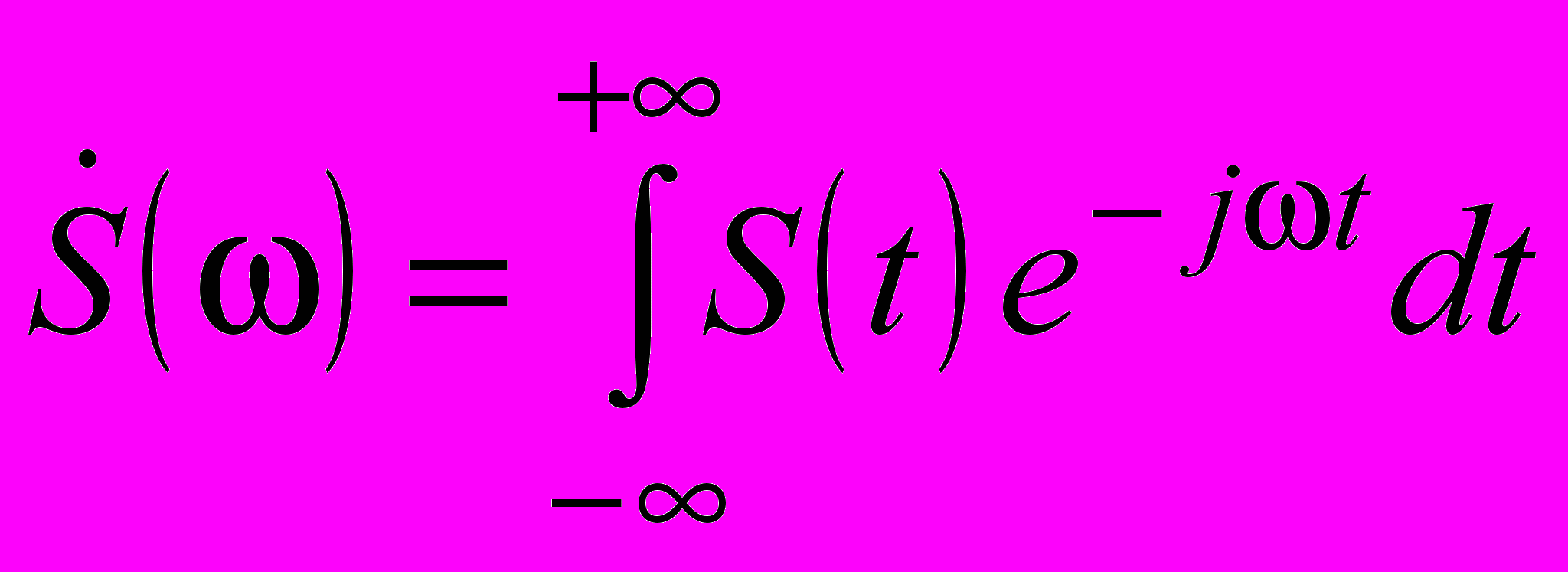(1.11)

Эта функция в теории сигналов носит название «спектральная плотность». Наконец, подставив равенство (1.11) в соотношение (1.10), получим

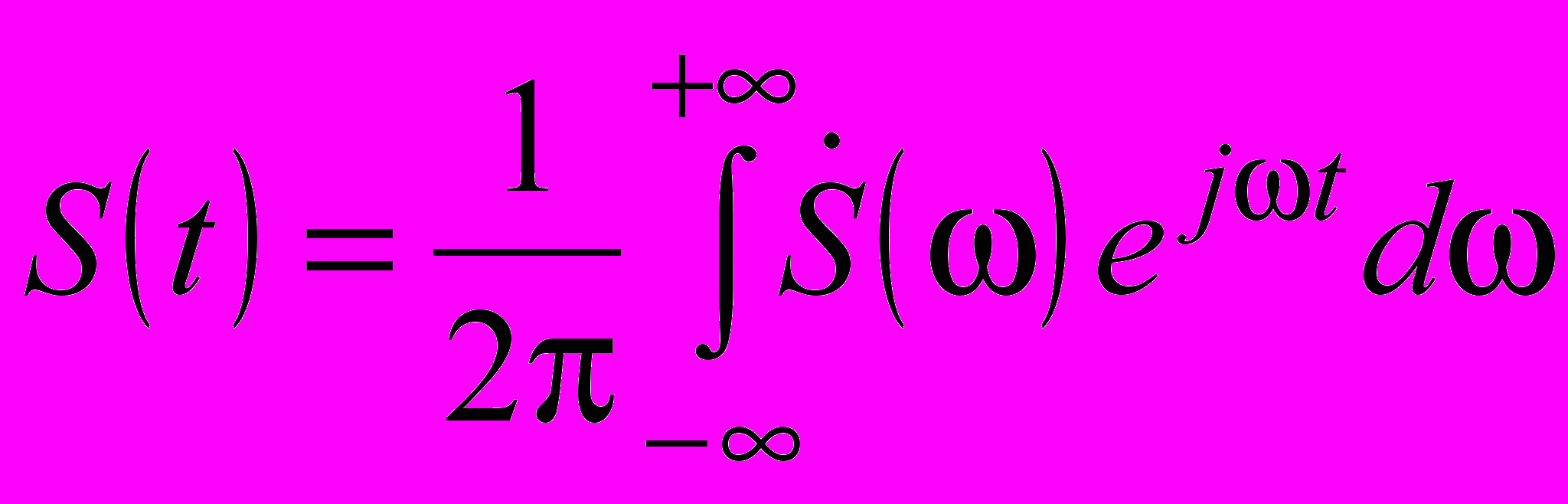(1.12)

Выражения (1.11) и (1.12) называются соответственно прямым и обратным преобразованиями Фурье. Сравнивая выражения (1.11) и (1.8), можно заключить, что в пределе выражение для комплексных амплитуд гармоник

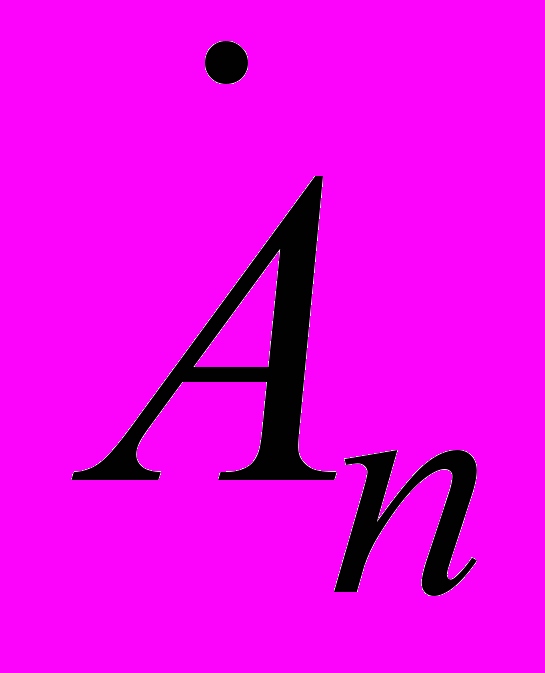периодического сигнала отличается от выражения для спектральной плотности сигнала только коэффициентом 2/Т и тогда

.

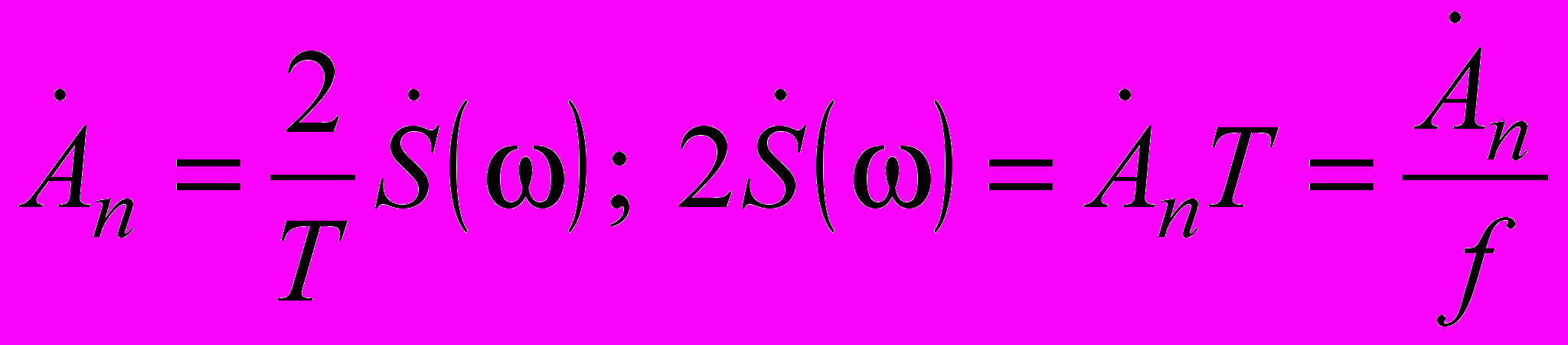Таким образом, 2

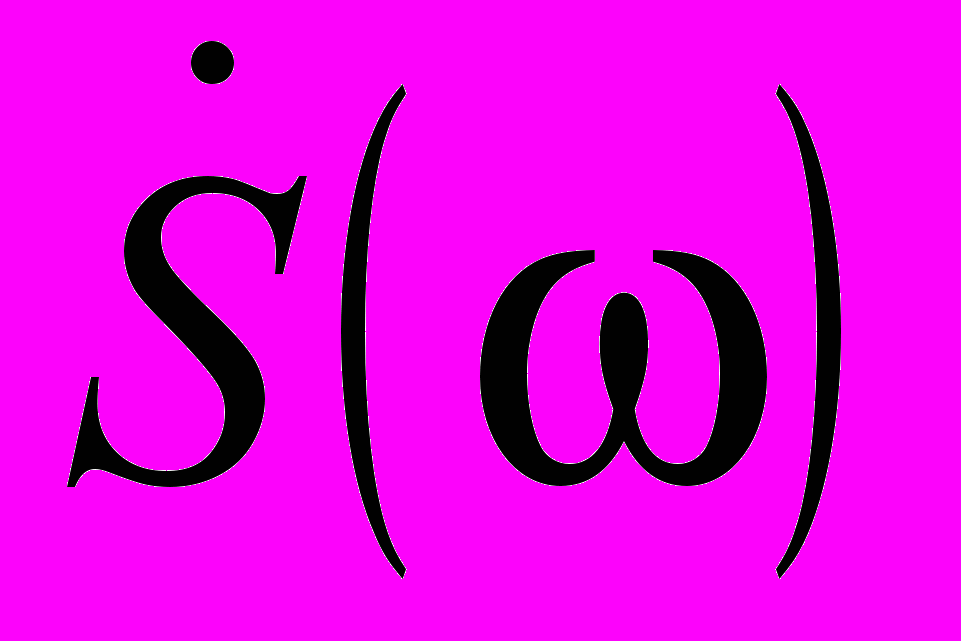получается путем деления амплитуды n-й гармоники на интервал частот между соседними гармониками, поскольку в пределе fdf. Отсюда следует, что спектральной плотности можно придать смысл плотности амплитуд.

1.6. Спектральная плотность

прямоугольного импульса

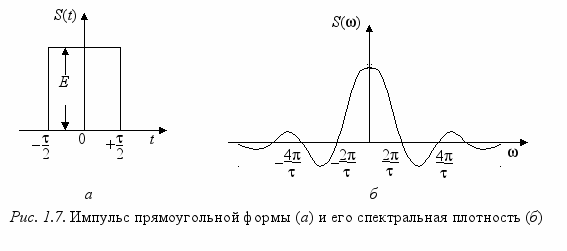
В качестве примера спектральной плотности конкретного непериодического сигнала рассмотрим спектральную плотность импульса прямоугольной формы (рис 1.7 а).

Согласно определению спектральной плотности для импульса длительности  и амплитудой E будем иметь

.

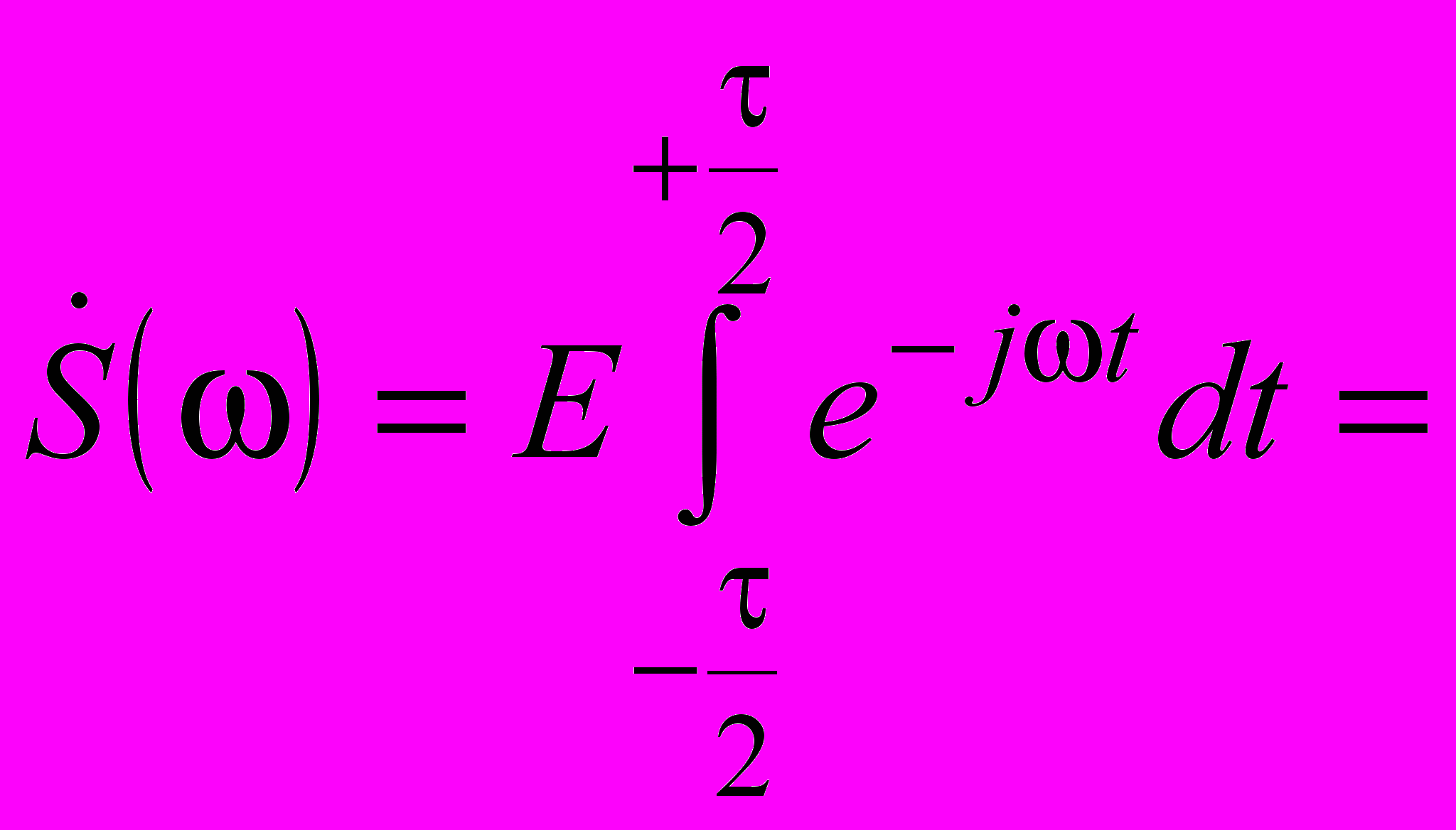
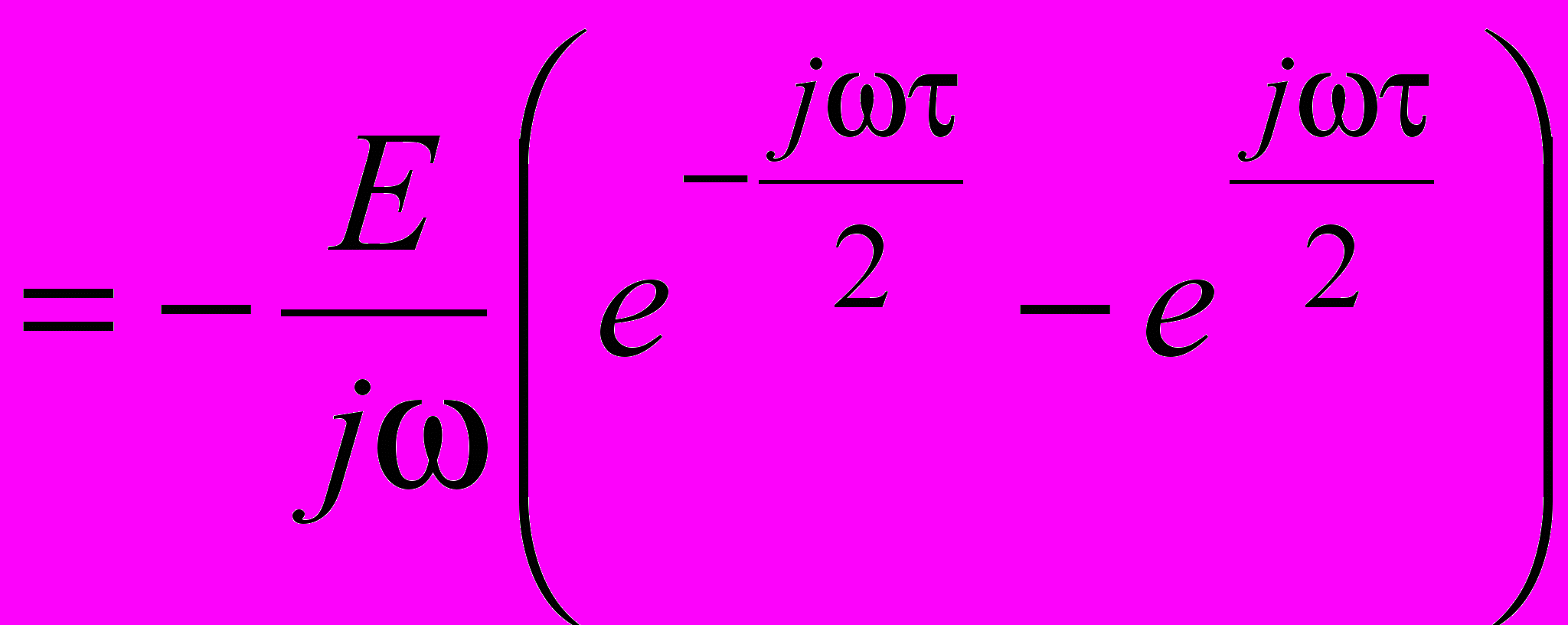Применив формулу Эйлера

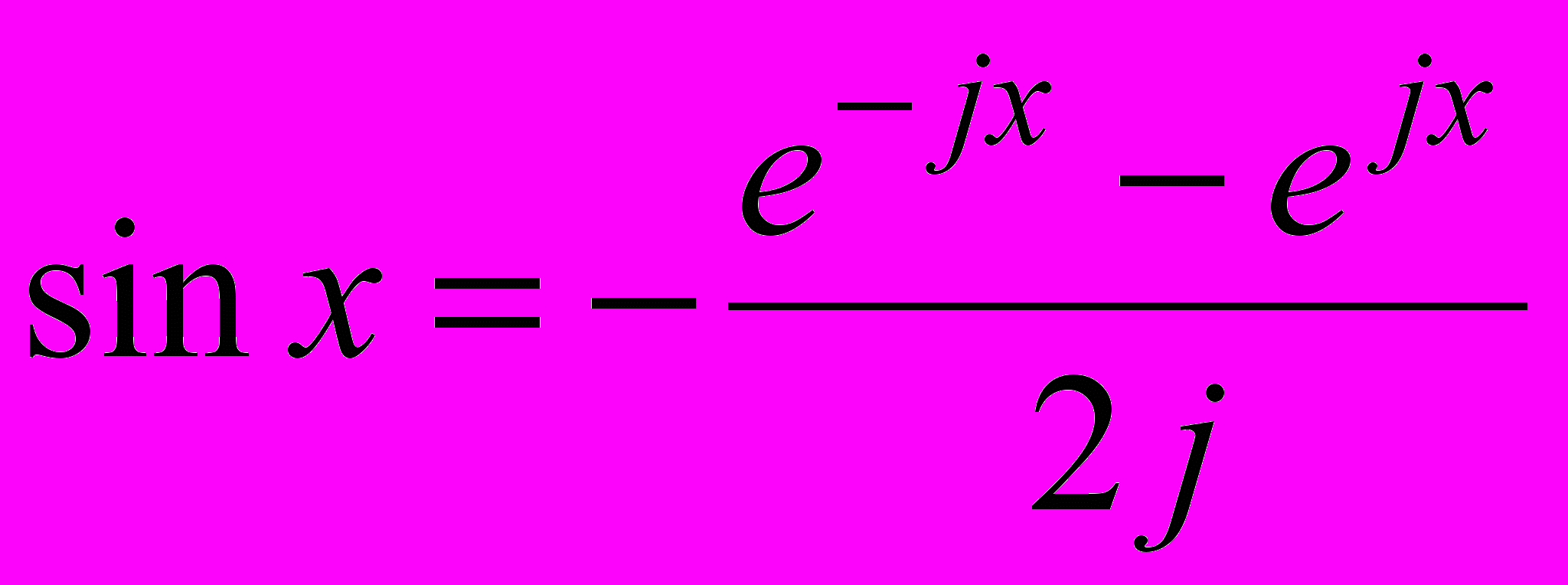, получим, что

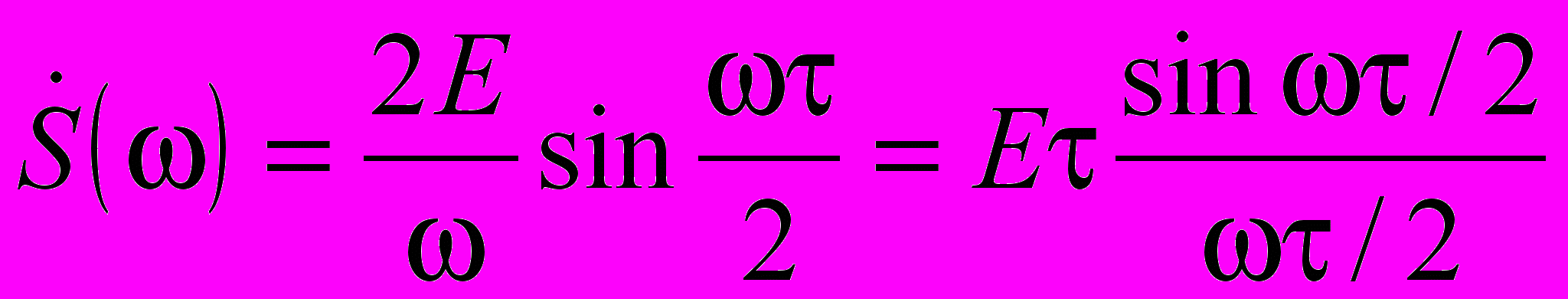. Эта функция имеет вид, показанный на рис. 1.7 б.

Спектральная плотность прямоугольного импульса

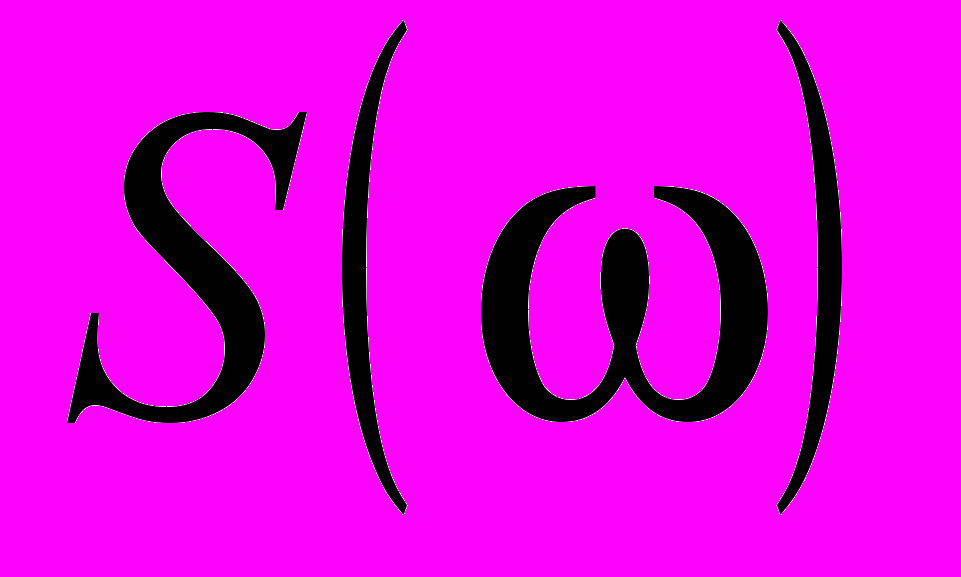обращается в нуль, когда

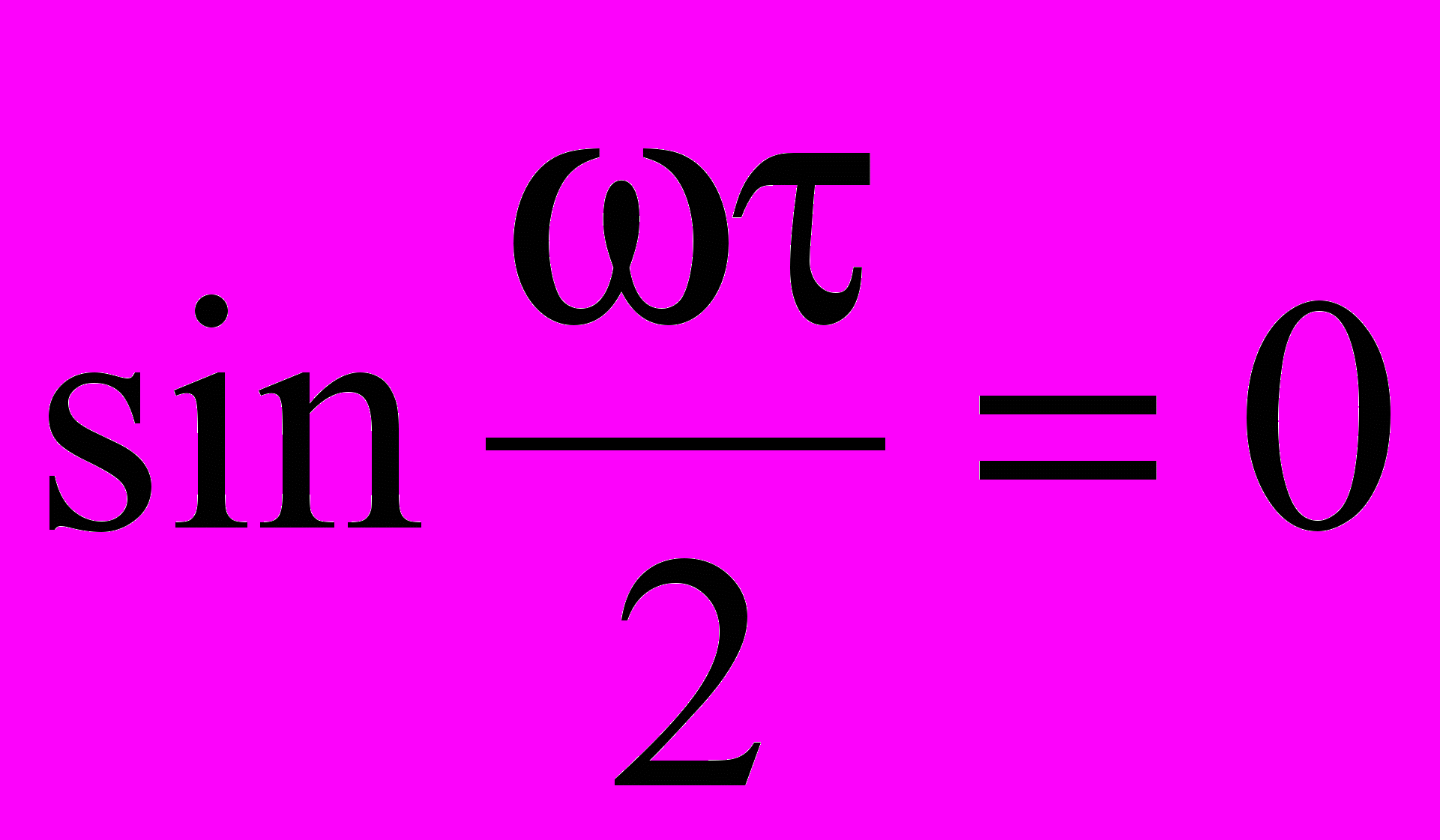, т. е. когда

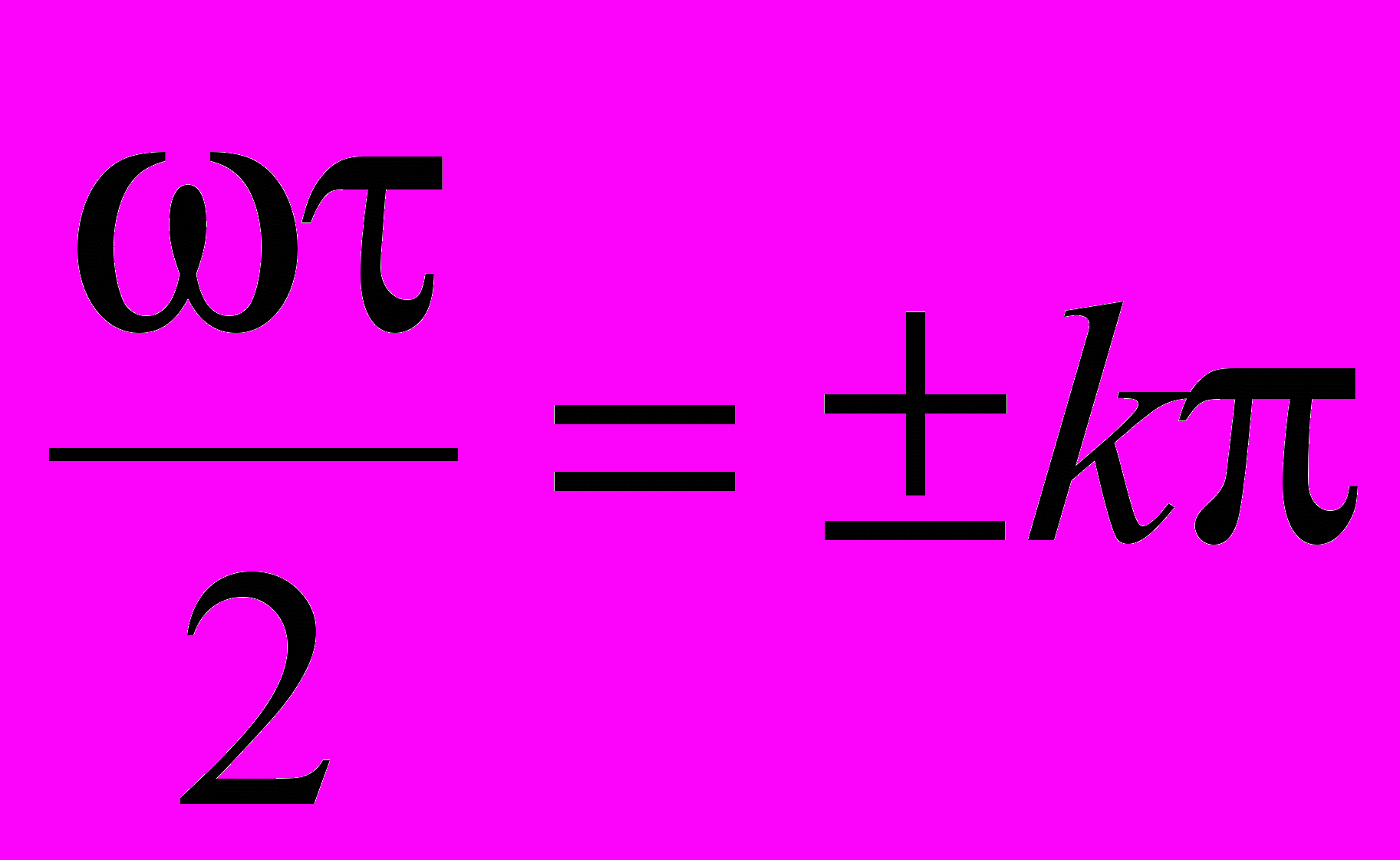, k=1, 2, 3, …. В этом случае

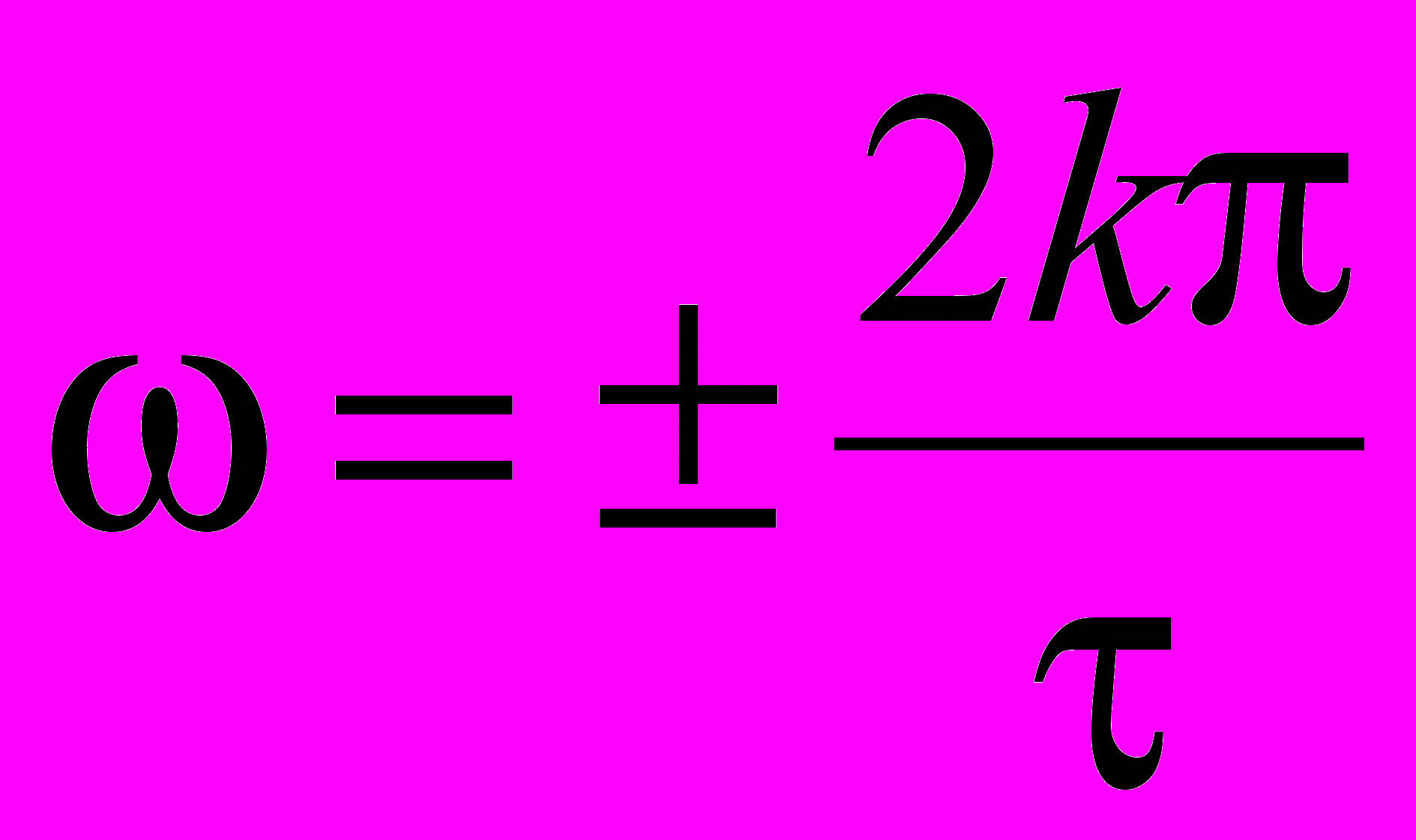, и, следовательно, точки пересечения графика спектральной плотности с осью  имеют значения

….

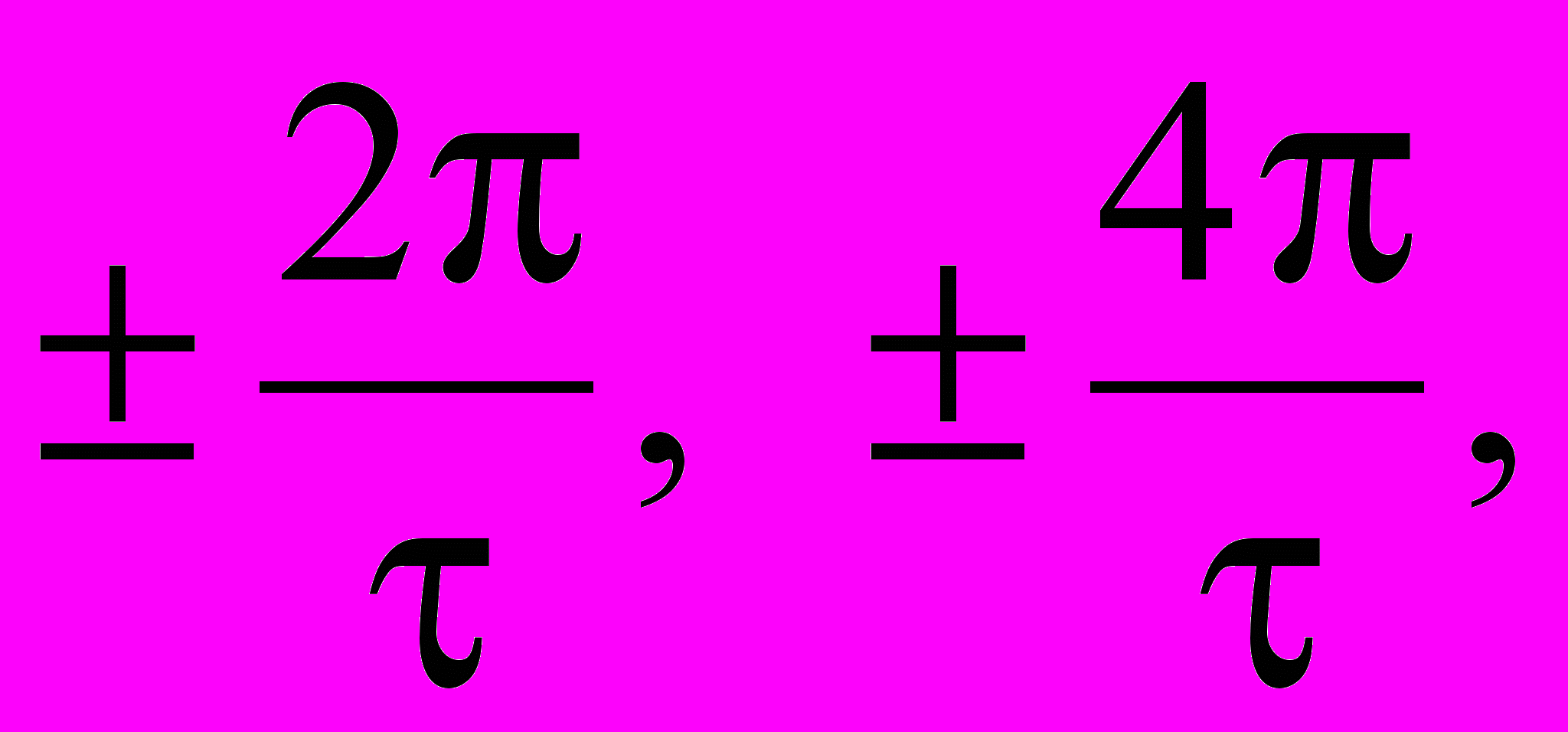1.7. Корреляционный анализ детерминированных

сигналов. Автокорреляционная

и взаимно корреляционная функции

Важным математическим инструментом, расширяющим возможность изучения детерминированных сигналов, является такое понятие, как корреляционный (или автокорреляционный) и взаимно кор-реляционный анализ функций.

Корреляционная функция сигнала S(t) определяется равенством

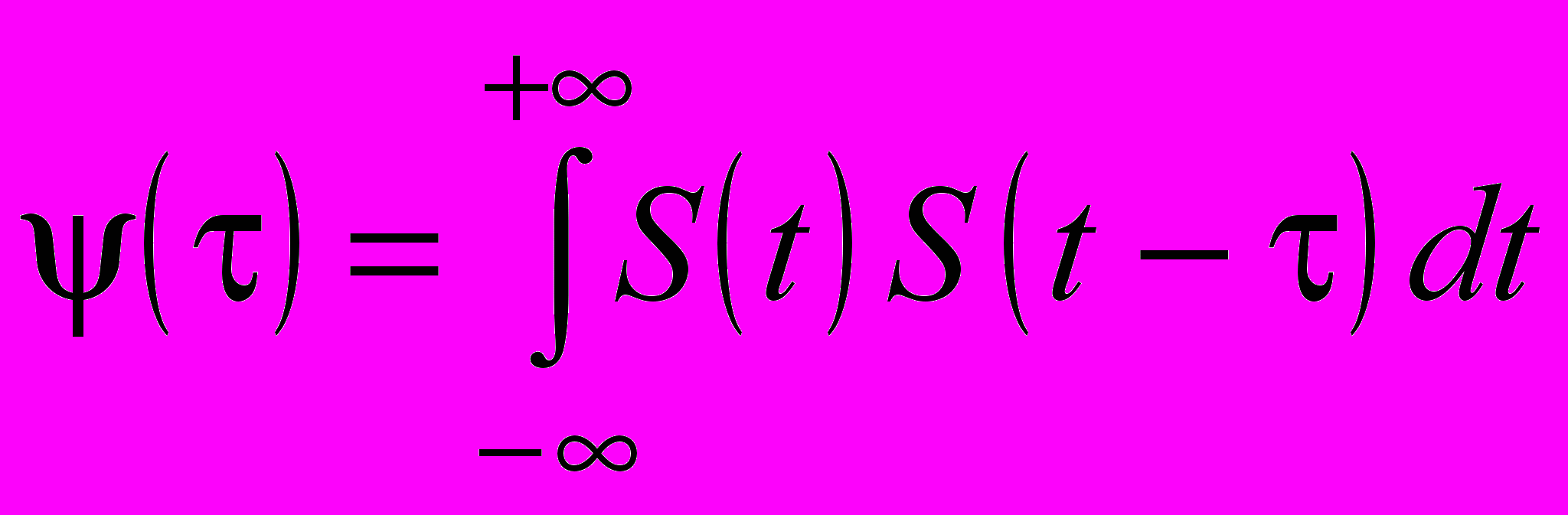(1.13)

где  – величина сдвига сигнала S(t) относительно самого себя во времени. Когда сдвиг равен нулю (=0), получим

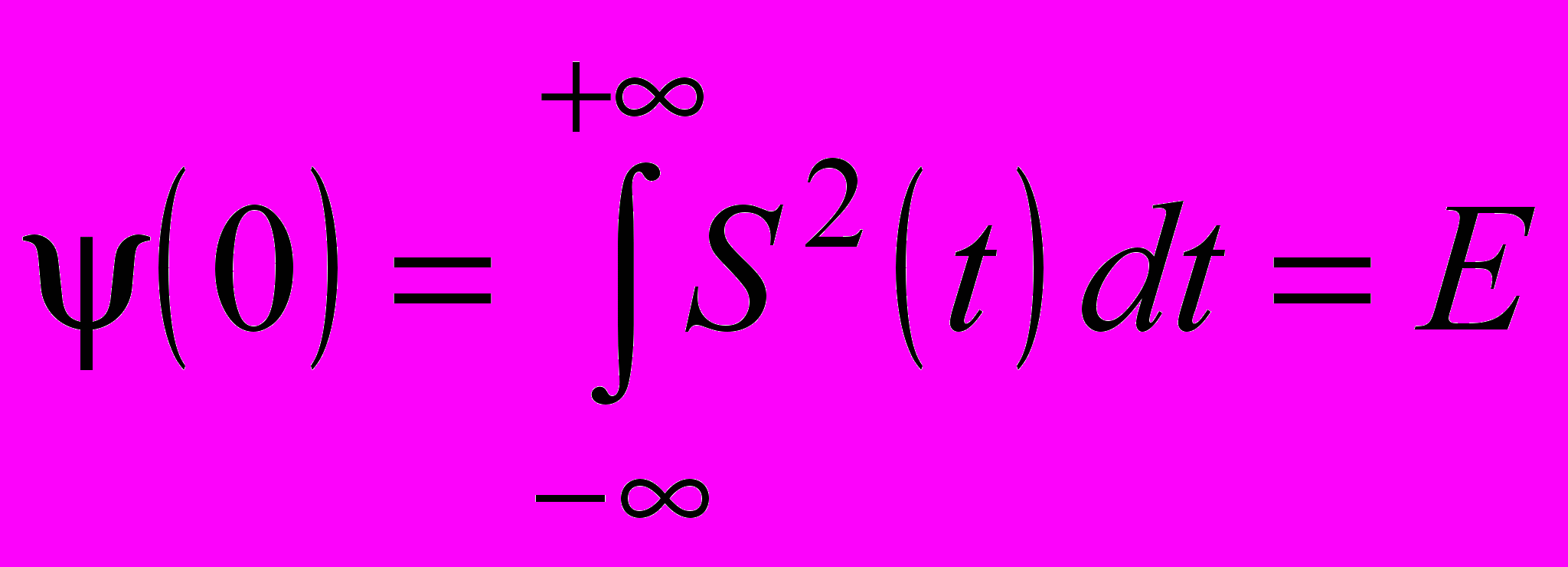(1.14)

где E – энергия сигнала, выделяющаяся на единичном сопротивлении. Следовательно, при нулевом временном сдвиге корреляционная функция численно характеризует энергию сигнала.

Отметим следующие основные свойства корреляционной функции ().

При =0 она положительна и достигает своего максимального значения, т. е. справедливо неравенство .
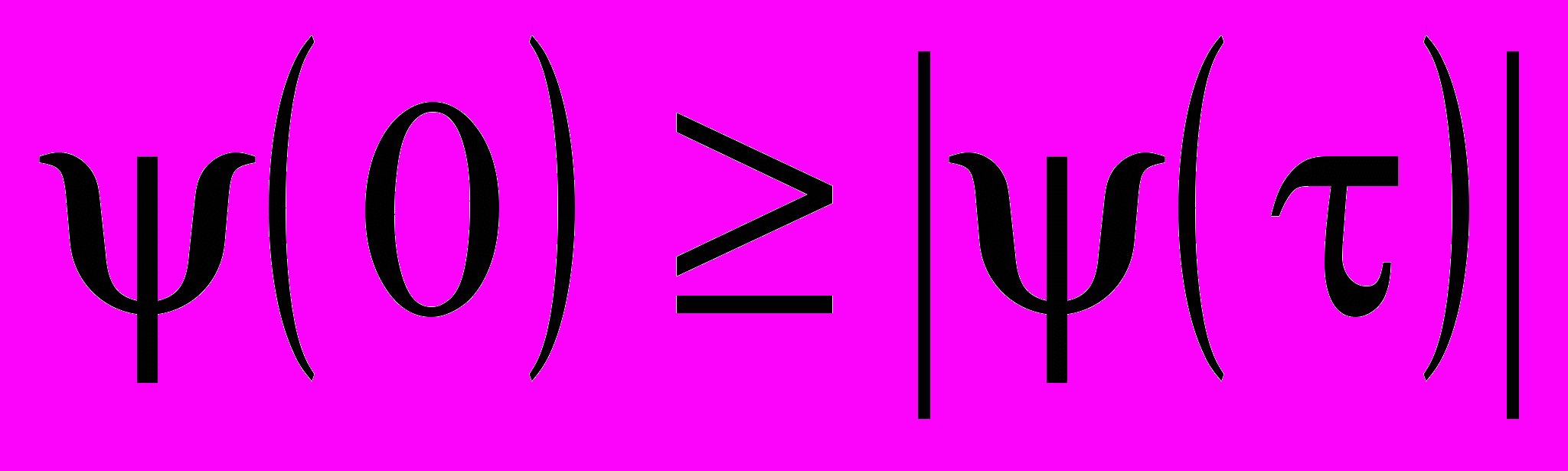Корреляционная функция представляет собой четную функцию относительно времени сдвига, т. е. (–)=(), откуда следует, что

.

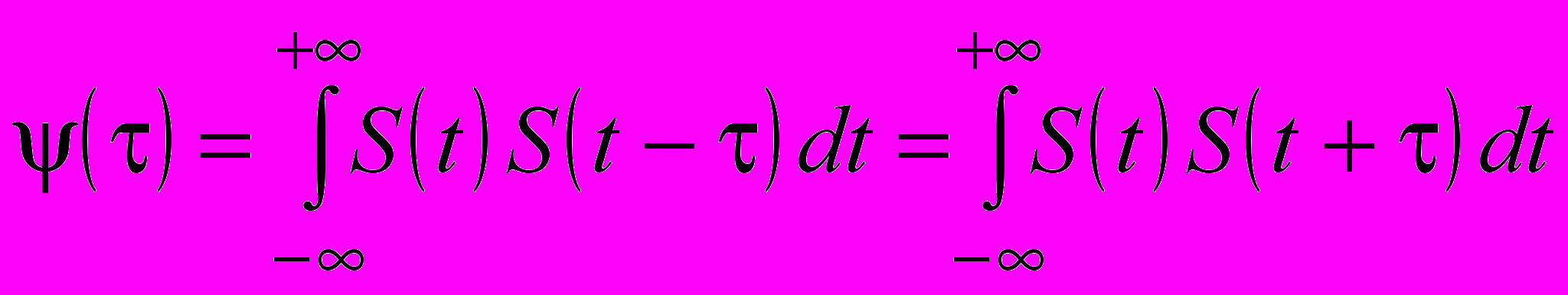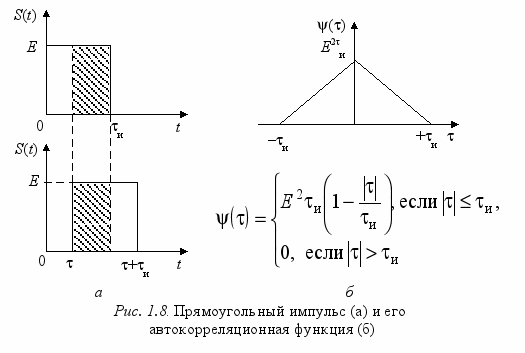
Автокорреляционная функция количественно характеризует степень сдвига сигнала S(t) и его смещенной во времени копии S(t–). Эта функция не дает возможность определить время прихода сигнала. Вид прямоугольного импульса и его автокорреляционной функции представлен на рис. 1.8. Построение () в данном случае проведено на основе графической интерпретации операции интегрирования.

Так как энергия периодического сигнала стремится к , то его энергетические свойства необходимо характеризовать отношением энергии за некоторый промежуток времени к длительности этого промежутка. Учитывая это для корреляционной функции периодического сигнала будем иметь

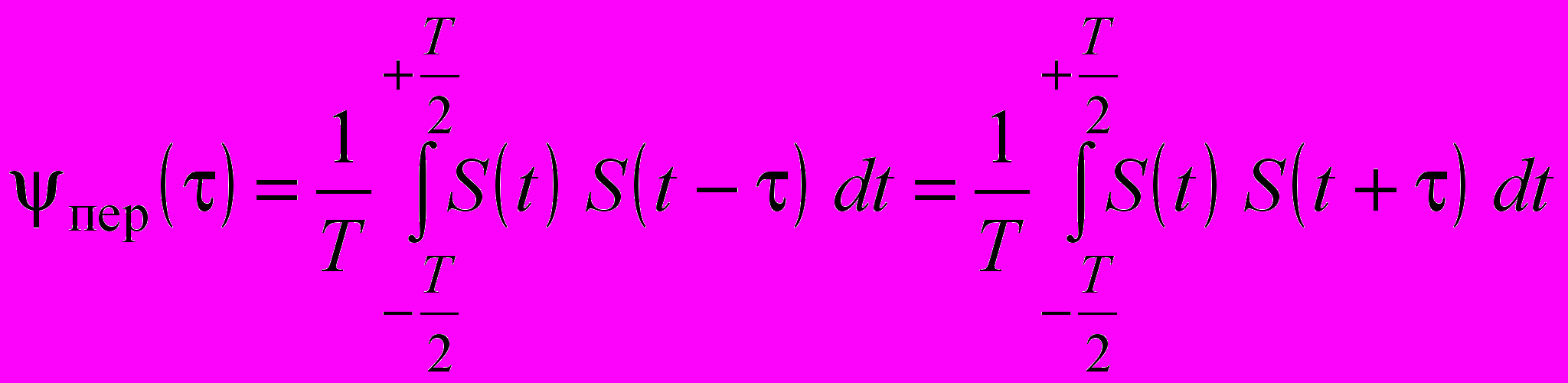(1.15)

где Т – период функции S(t). Из этого выражения следует, в частности, что автокорреляционная функция гармонического колебания есть также гармоническое колебание.

П

омимо корреляционной функции можно также ввести понятие взаимно корреляционной функции

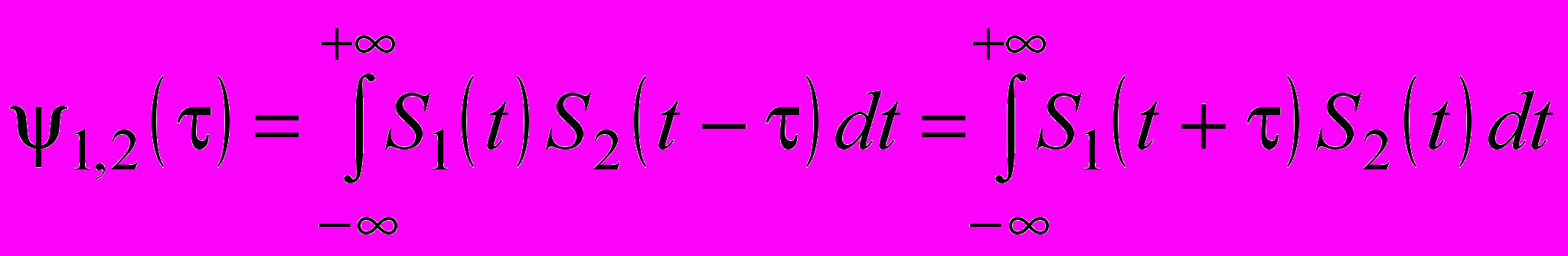(1.16)

Эта функция может и не обладать свойствами четности или нечетности относительно времени сдвига и не всегда максимальна при =0.

Автокорреляционная функция и спектральная плотность связаны следующими соотношениями:

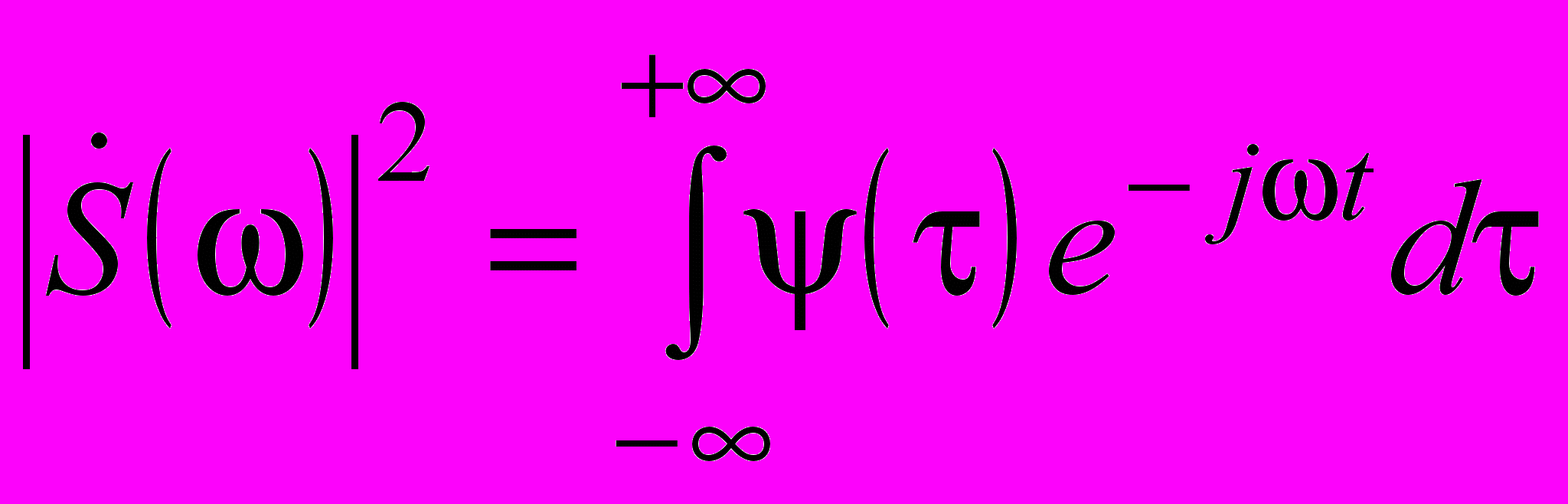	,	(1.17)
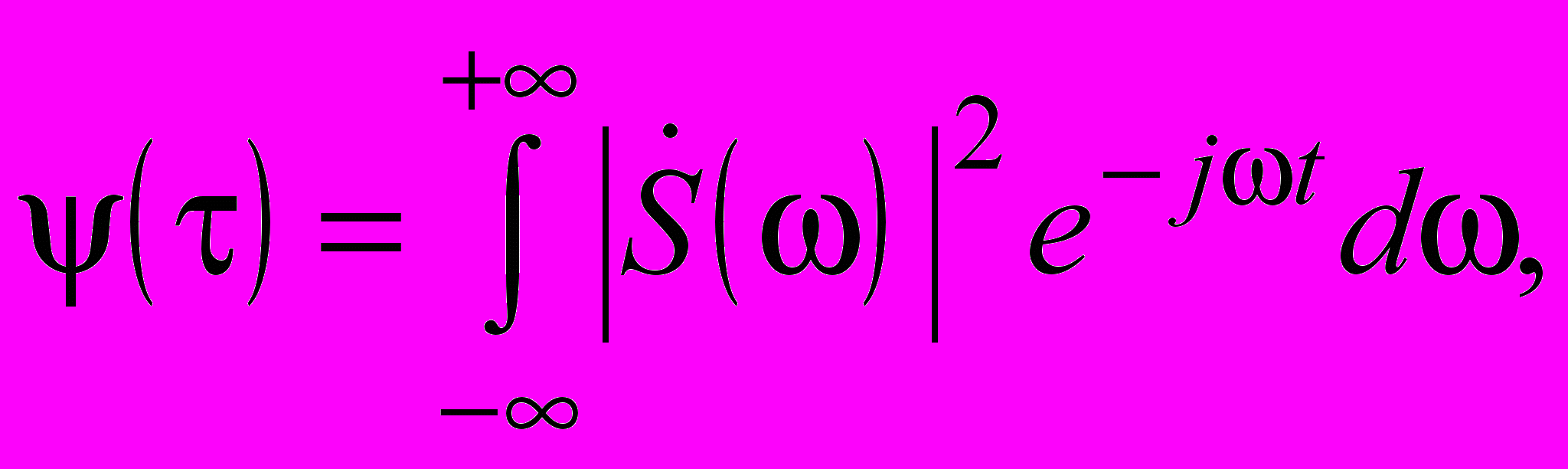		(1.18)

где формула (1.17) соответствует прямому, а формула (1.18) – обратному преобразованиям Фурье. Следовательно, прямое преобразование Фурье дает спектральную плотность энергии (энергетический спектр

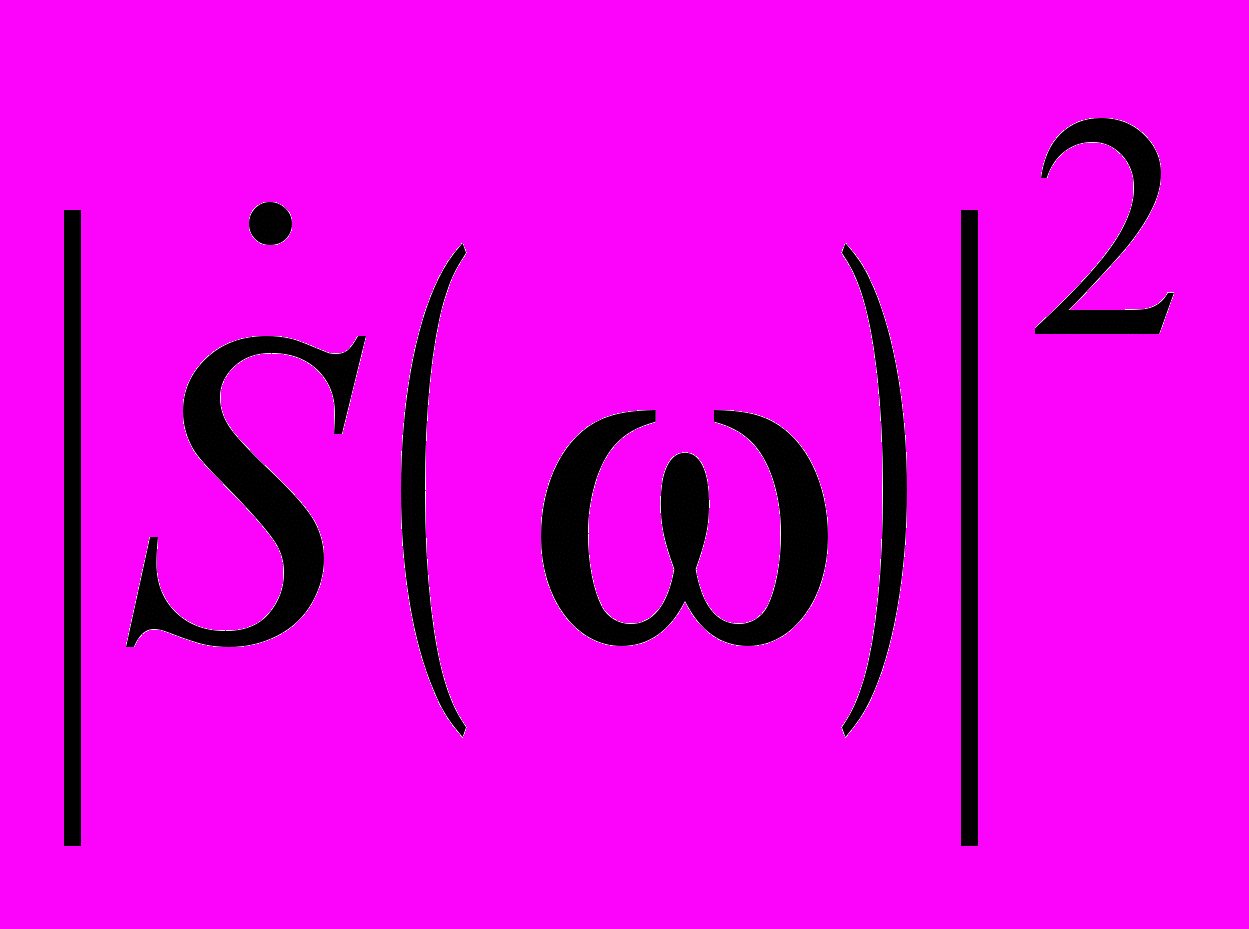), а обратное – корреляционную функцию

.

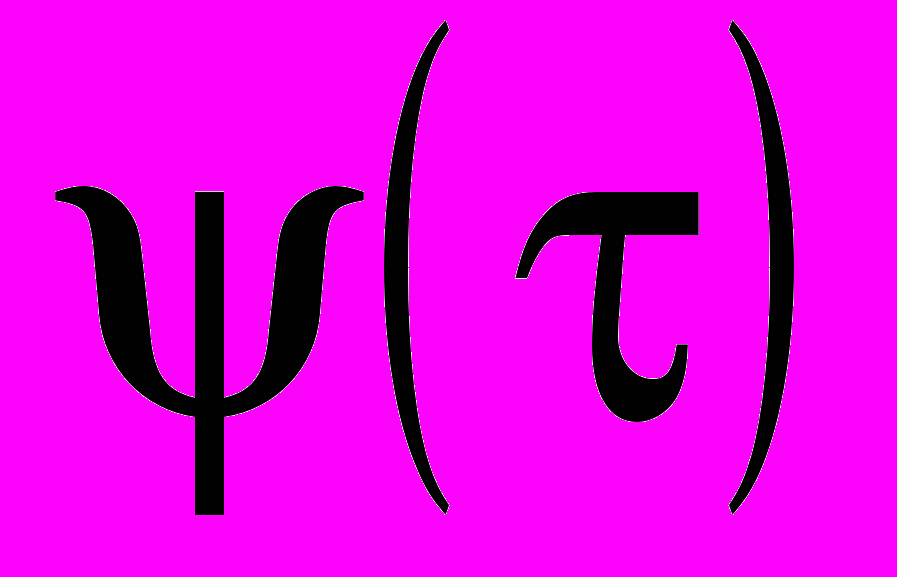Контрольные вопросы