Задачи: Дать понятие полярной системы координат. Рассмотреть некоторые кривые в этой системе

Вид материала

Документы

Содержание I. Кривые II порядка в полярной системе координат. Гиперболическая спираль определяется полярным уравнением 3) Логарифмическая спираль. 4) Спираль Архимеда. Отрезок а обозначим ОА; тогда 3. Лемниската Бернулли. Если cos 2φ отрицателен, то ρ – мнимая величина. Таким образом, между прямыми, образующими углы 45˚ и 135˚ с полярной осью, нет Улиткой Паскаля называется кривая, определяемая уравнением ρ=2r cosφ+l III. Кривые II порядка в декартовых координатах. Эпи- и гипоциклоида. IV. Использование компьютера для наглядного представления кривых II порядка. 5. Улитки Паскаля. 7. Эпициклоида. 8.Гипоциклоида. 9. Лемниската Бернулли.

Подобный материал:

• Лекция 4 аксонометрические проекции. Многогранные и кривые поверхности, 219.26kb.
• Программа курса «Общая физика. Механика», 33.84kb.
• Р. К. Шамилева, 150.98kb.
• Мониторинг 23. 01. 2011, 364.91kb.
• Моей курсовой работы "Многочлены", 398.96kb.
• Положение камеры Преобразования, определяющие положение и ориентацию объекта в мировой, 105.74kb.
• Программа: Менеджмент Данные о преподавателе: фио, 143.38kb.
• Ф. И. Щербатской центральная концепция буддизма, 6530.13kb.
• Понятие о базах и базировании, 68.36kb.
• Задачи дисциплины: Выделить основные морально-нравственные качества социального работника;, 17.27kb.

Конференция – фестиваль творчества молодежи и школьников «Наука. Творчество. Развитие.»


Использование компьютера для наглядного представления кривых второго порядка


Автор: Макарова Ирина,

ученица 10 А класса ср.шк.№12

Научный руководитель:

Кошкина Ю.Е.,

учитель информатики МОУ "Средняя общеобразовательная школа № 12" г.Новочебоксарска


г. Новочебоксарск, 2004


I . Введение.


Как часто на уроках математики нам приходится сталкиваться с ситуацией, когда, имея уравнение нестандартной функции, мы не можем построить её график только потому, что кроме прямоугольной декартовой системы координат не знакомы ни с какой другой. А ведь эта система является не единственной для построения графиков. В своей работе я рассмотрела ещё одну – полярную систему координат, которая в некоторых случаях является лучше декартовой.

Мою работу можно условно разделить на две части. В первой дано математическое описание некоторых кривых второго порядка с указанием их уравнения, способа построения и, иногда, свойств. Она группа кривых представлена в декартовой системе координат (эпи- и гипоциклоида), другая - в полярной (спирали, розы, улитки Паскаля).

Во второй части я показала, что компьютер можно использовать и для построения графиков функций. Специальные компьютерные программы позволяют увидеть, как будет выглядеть график той или иной функции на плоскости или в пространстве, исследовать некоторые его свойства, разглядеть график в различных проекциях и со всех сторон.

Цель: рассмотреть некоторые кривые второго порядка и показать, как можно использовать компьютер для их изучения.

Задачи:

1. Дать понятие полярной системы координат.
   
2. Рассмотреть некоторые кривые в этой системе.
   
3. Рассмотреть некоторые кривые в прямоугольной декартовой системе координат.
   
4. Применить компьютерную программу работы с графиками для наглядного представления кривых и изучения их свойств.
   

^ I. Кривые II порядка в полярной системе координат.


1. Полярная система координат.


Положение произвольной точки плоскости мы до сих пор определяли её декартовыми координатами x и y. Однако этот способ не является единственным: часто бывает удобнее определять положение точки М на плоскости другими величинами. Остановимся на том способе, когда положение точки М на плоскости (рис. 1) определяют расстоянием ρ=ОМ точки М от полюса О и углом φ между лучом ОМ и полярной осью ОР. Величины ρ и φ называются полярными координатами точки М. Отрезок ρ называют полярным радиусом, а угол φ – полярным углом. Заметим, что всегда ρ≥0.

Очевидно, что заданием ρ и φ положение точки М определяются однозначно: угол φ определяет направление луча ОМ, а отрезок ρ – положение точки на этом луче. Однако по точке М однозначно определяется лишь расстояние ρ, а угол φ определяется не однозначно: каждой точке М соответствует бесчисленное множество полярных углов, отличающихся друг от друга на 2πk, где k – целое число. Для устранения неоднозначности в качестве полярного угла обычно выбирают наименьший (по абсолютной величине) угол

φ, составляемый ОМ с полярной осью, т.е. выбирают φ в диапазоне от –π до +π (-π<φ≤π).

Исключение – случай, когда точка М совпадает с полюсом О и ρ=0, а полярный угол φ может быть взят каким угодно.

Установим связь между полярными (ρ и φ) и декартовыми (x и y) координатами точки М. Для этого совместим полюс с началом координат, а полярную ось – с осью абсцисс (рис. 2).

Из ∆OMN имеем

x=ρ cosφ; ρ=

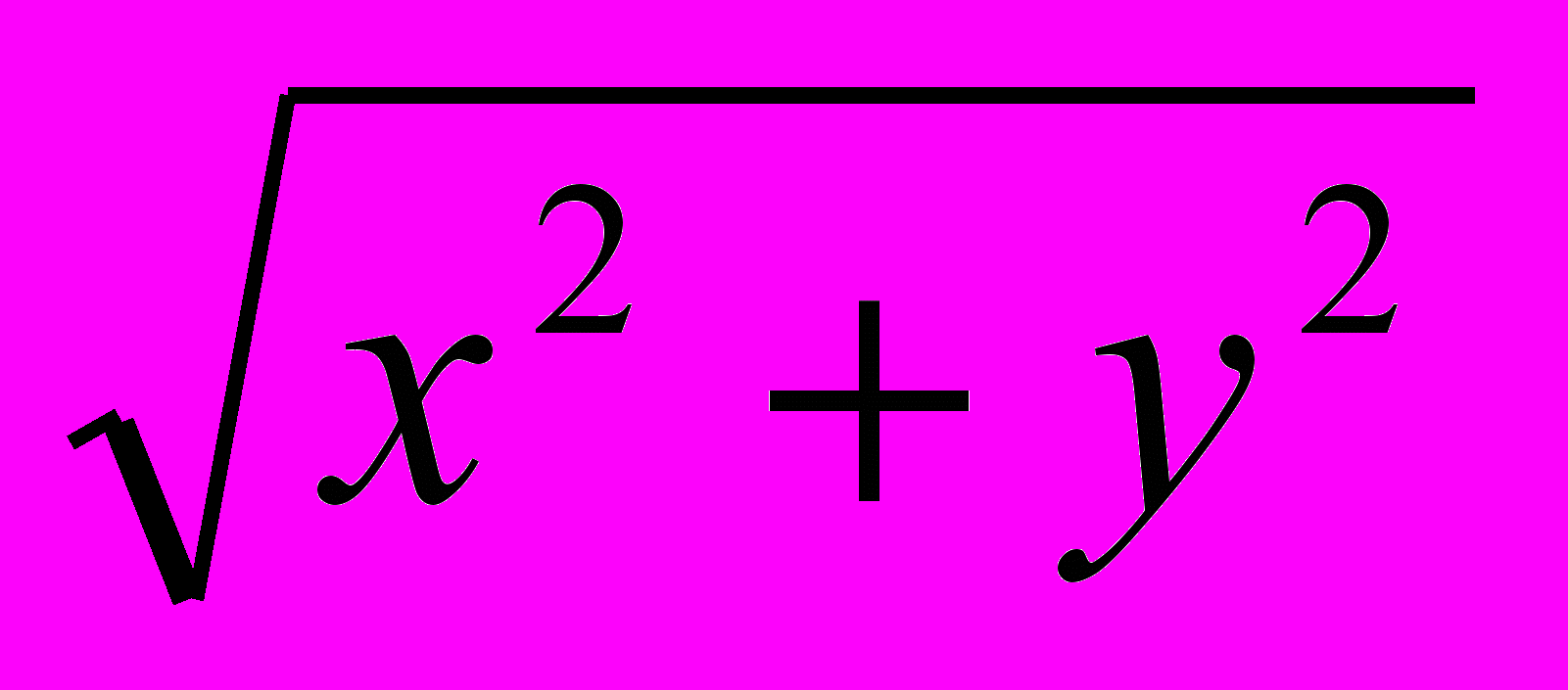
y=ρ sinφ. tg φ=.

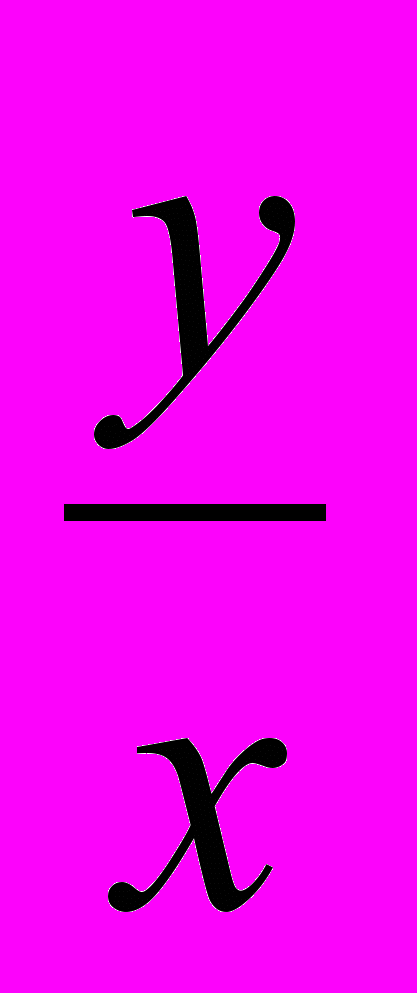Формулы (1) и (2) позволяют осуществить переход от полярной системы координат к декартовой и наоборот.

До сих пор мы строили графики функций в декартовой системе координат. Соответствующие построения можно производить и в полярной системе: если переменные ρ и φ связаны функциональной зависимостью, то, изображая значение φ полярными углами и откладывая на определяемых ими лучах отрезки, равные соответствующим значениям ρ, получим геометрическое место точек с координатами ρ и φ, образующих линию, называемую полярной диаграммой или графиком заданной функции в полярной системе координат. Особенно удобно прибегнуть к полярной диаграмме, если переменная φ фактически является ( а не только изображается) углом.


2.Спирали.


Спираль (франц. spirale, от лат. spira", греч. "σπετρα"- виток) – плоская кривая, которая обычно обходит вокруг одной (или нескольких) точки, приближаясь или удаляясь от нее.

Среди спиралей выделяют алгебраические спирали и псевдоспирали. Алгебраические спирали – спирали, уравнение которых в полярных координатах являются алгебраическими относительно переменных ρ и φ. К алгебраическим спиралям относятся: гиперболическая спираль, архимедова спираль, Галилея спираль, Ферма спираль, параболическая спираль, жезл.

Псевдоспирали – спирали, натуральные уравнения которых могут быть записаны в виде r = as^m, где r – радиус кривизны, s – длина дуги. При m = 1 псевдоспираль является логарифмической спиралью, при m = -1 – Корню спиралью, при m = ½ - эвольвентной окружностью.

Рассмотрим некоторые из них.

1. Жезл.
   

Жезл – плоская трансцендентная кривая. Уравнение в полярных координатах: ρ ==.

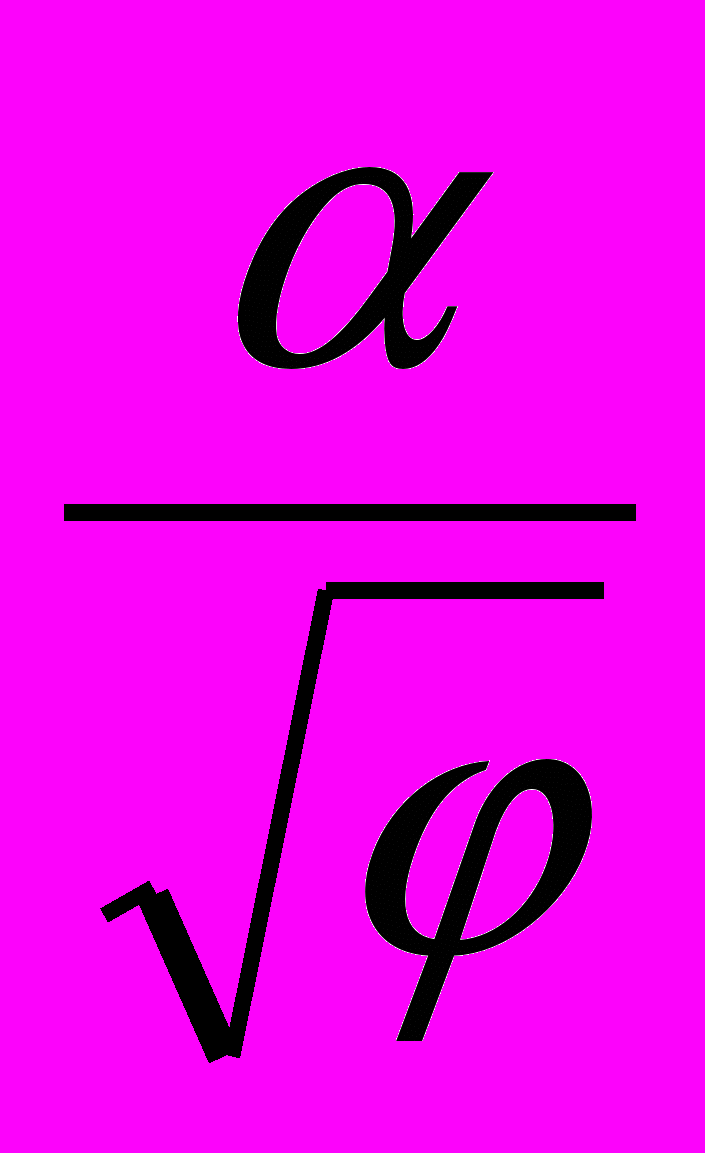Кривая состоит из двух ветвей (соответствующих положительным и отрицательным значениям ρ), каждая из которых имеет асимптоту – ось ОР, асимптотическую точку – полюс О, точки перегиба (±; ±).


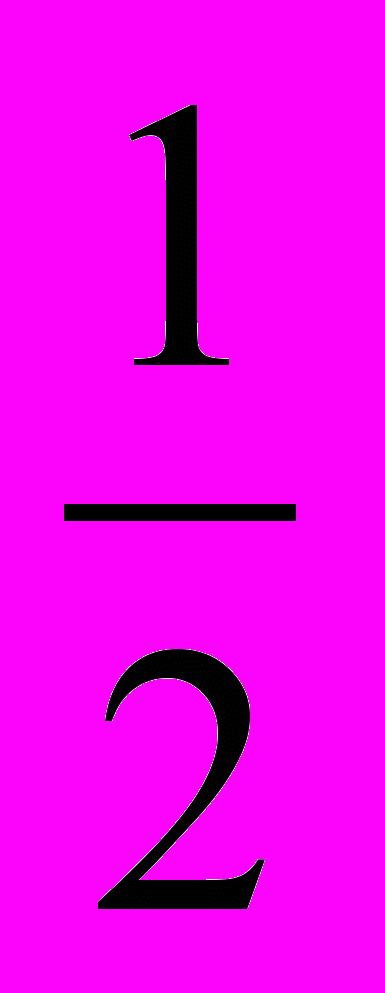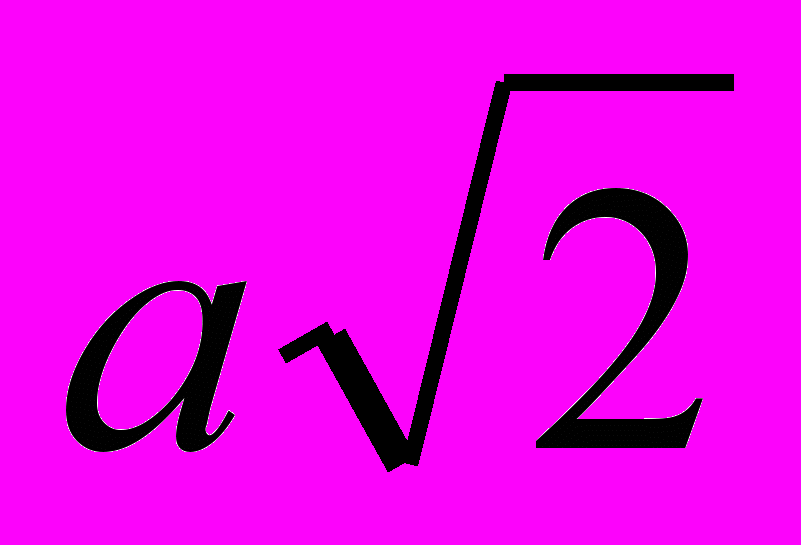2) Гиперболическая спираль.

^

Гиперболическая спираль определяется полярным уравнением

ρ=.

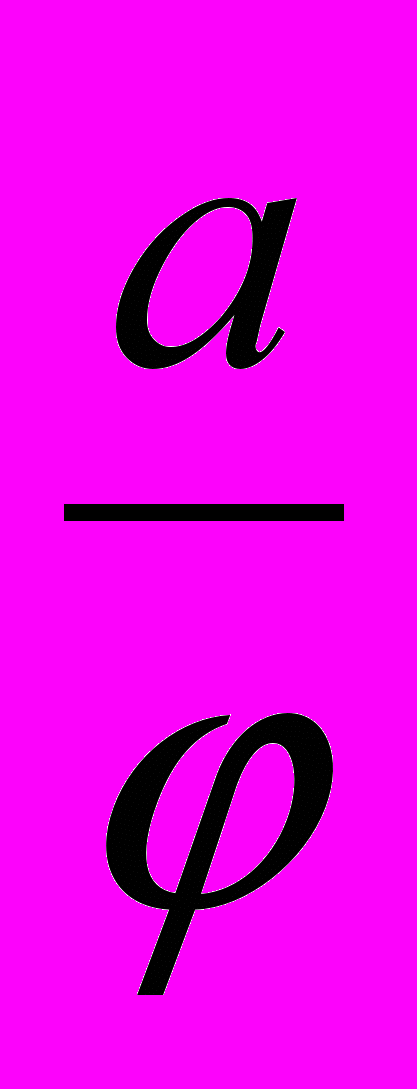При φ→∞ ρ→0, т.е. полюс является асимптотической точкой гиперболической спирали. Из ∆OMN следует, что MN=ρ sin φ, но ρ=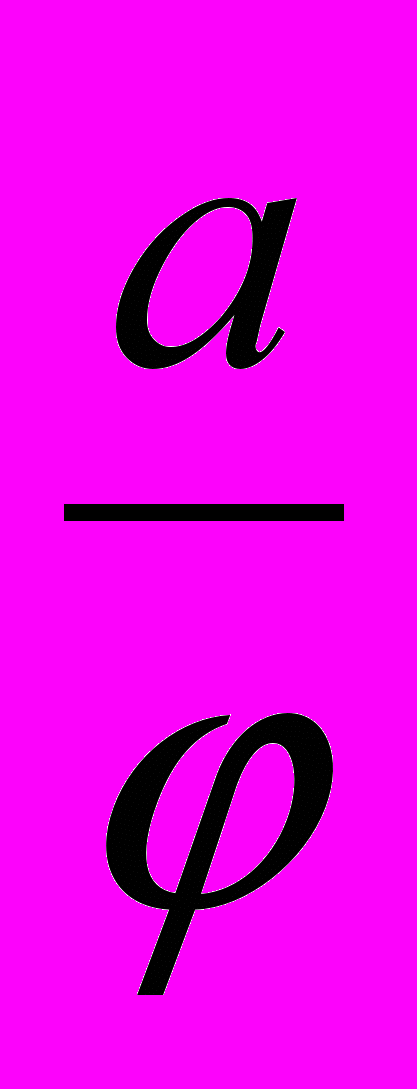, и потому MN=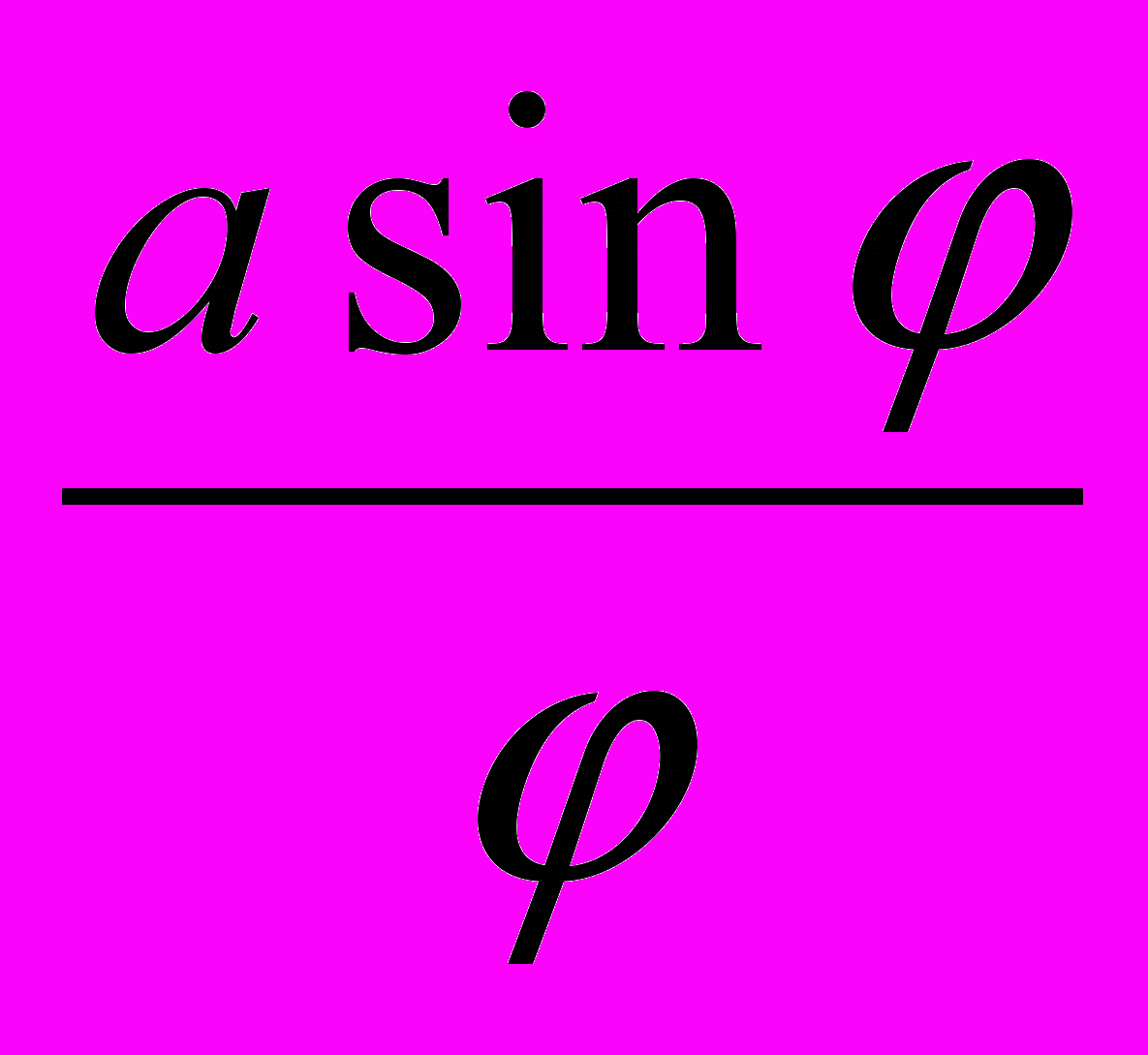. Можно доказать, что при φ→0 MN→а, т.е. прямая, параллельная полярной оси и отстающая от неё на расстоянии, равном а, является асимптотой гиперболической спирали, изображенной на рисунке.

^ 3) Логарифмическая спираль.


Так называется кривая, задаваемая в полярной системе координат уравнением

ρ=а^φ.


Если аргумент φ изменять по закону арифметической прогрессии: φ₀, φ₀+d, φ₀+2d;…, то значения φ будут:

а^φ0; а^φ0+d = a^φ0a^d; a^φ0+2d = a^φ0(a^d)²;…,

т.е. функция ρ будет возрастать в геометрической прогрессии со знаменателем q=а^d, откуда и вытекает способ построения логарифмической спирали.

Отложим на полярной оси ОА=а⁰, а на прямой перпендикулярной к ней, ОB=а². Если теперь построить прямую ломаную ABCDE…, то из подобия треугольников видно, что отрезки OA, OB, OC, … образуют геометрическую прогрессию со знаменателем а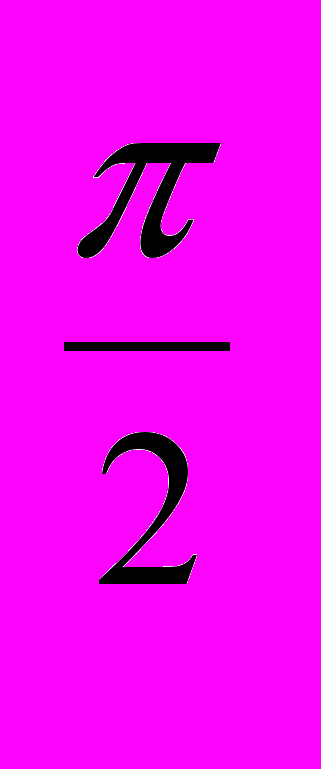^, т.е. полученные точки A,B, C, D, E, … лежат на логарифмической спирали. Когда φ возрастает от 0 до ∞, точка кривой делает бесчисленное множество оборотов вокруг полюса, неограниченно удаляясь от него (расстояния между витками уже не одинаковы!). Угол φ может принимать и отрицательные значения. Когда φ→ −∞, ρ→0 и кривая совершает бесчисленное множество оборотов вокруг полюса, безгранично к нему приближаясь, но никогда его не достигая, т.е. полюс для логарифмической спирали является асимптотической точкой.

Логарифмические спирали широко используются в технике: по логарифмической спирали выполняются профили вращающихся ножей и фриз, зубчатых передач и прочее. По логарифмической спирали очерчены некоторые раковины, по дугам, близким к данной спирали, расположены семечки в подсолнухе, чешуйки в шишках и т.д.



^ 4) Спираль Архимеда.

Рассмотрим полярную диаграмму, определяемую уравнением =а, где а - некоторая положительная постоянная (коэффициент пропорциональности). Для построения графика этой функции найдем несколько её точек, записывая расчеты в таблице.

	0		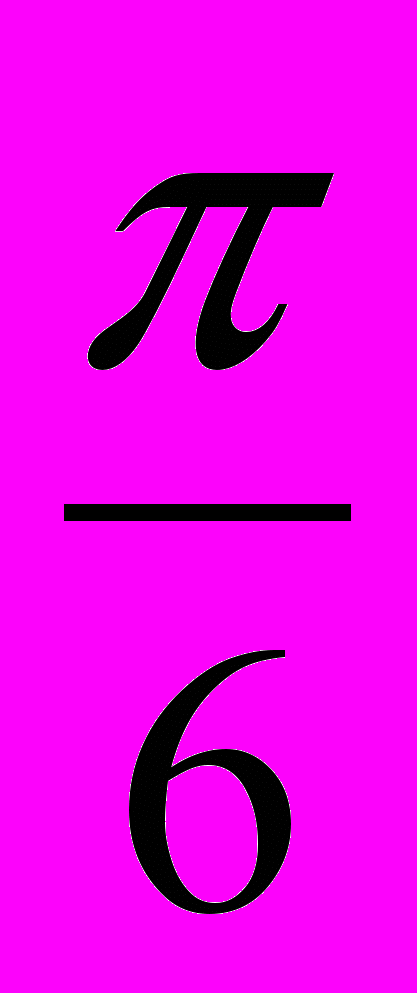		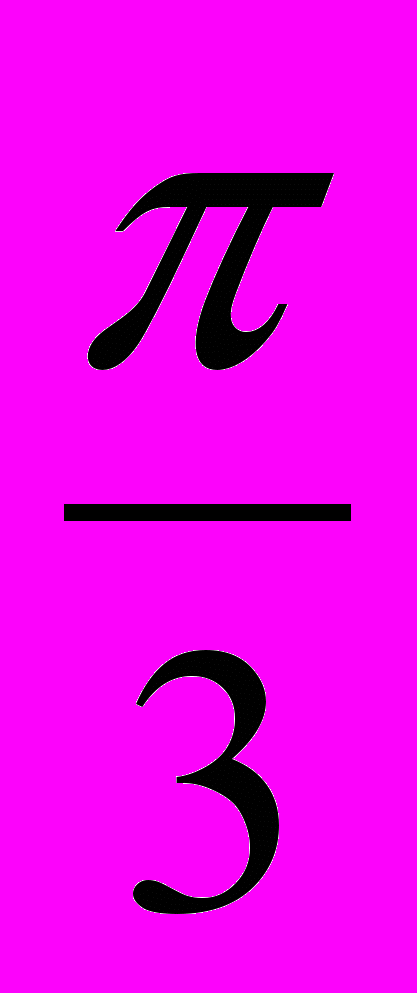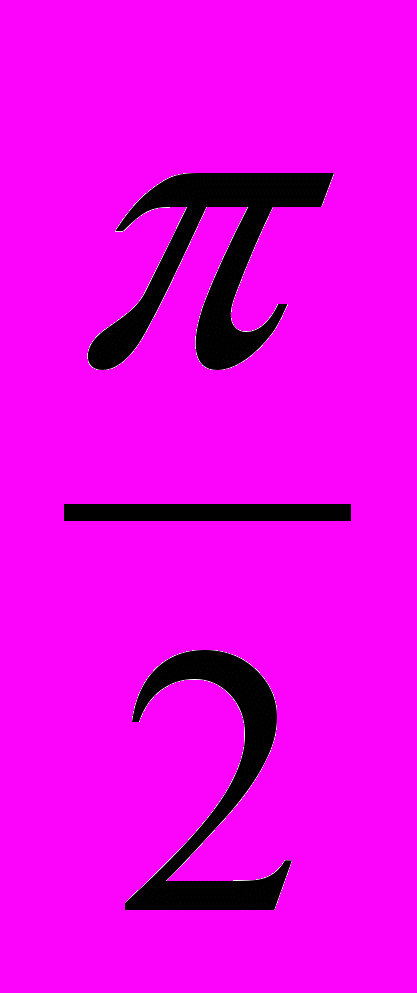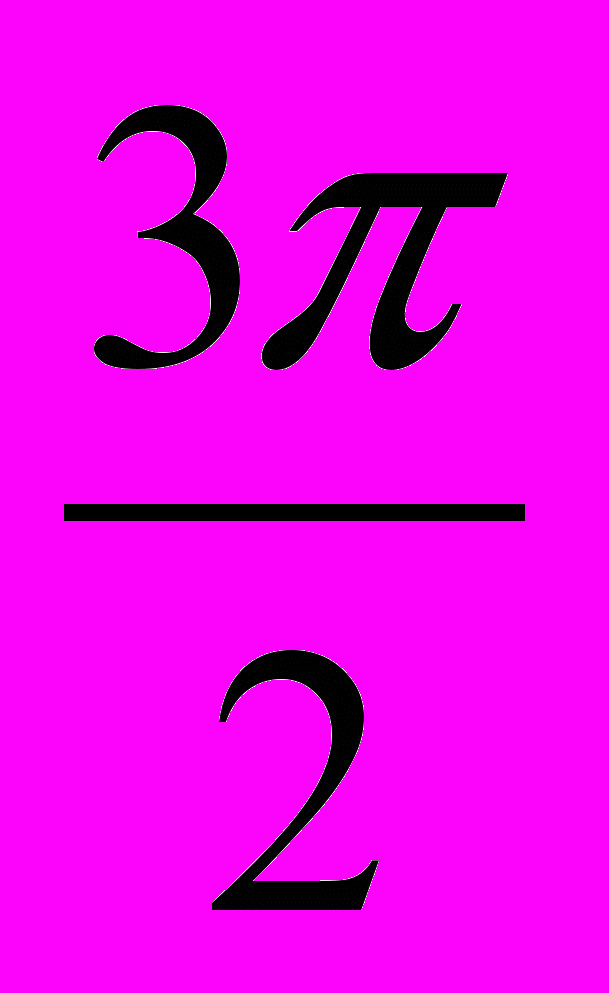		2
	0	a	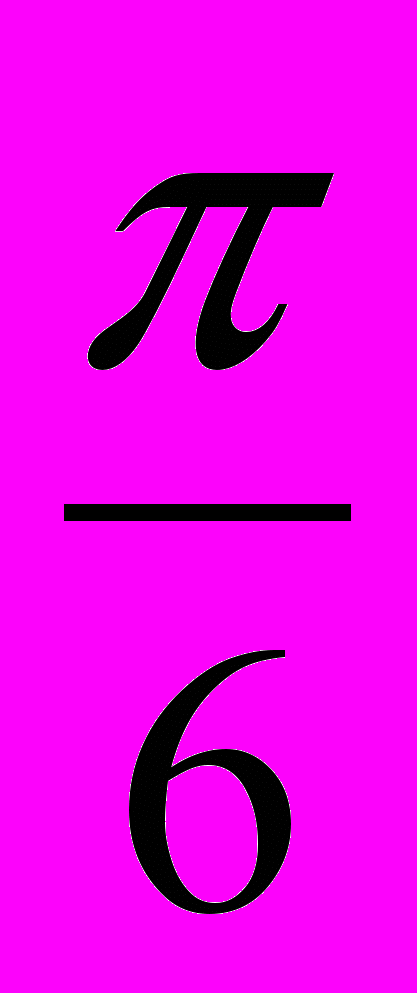a	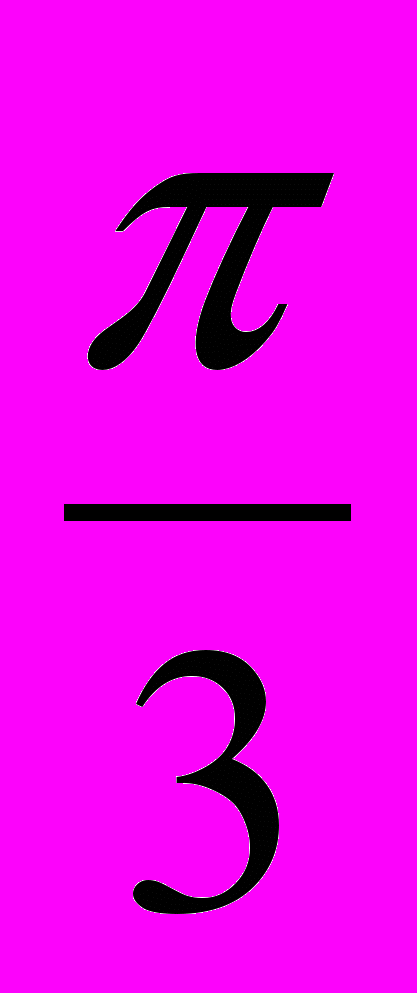a	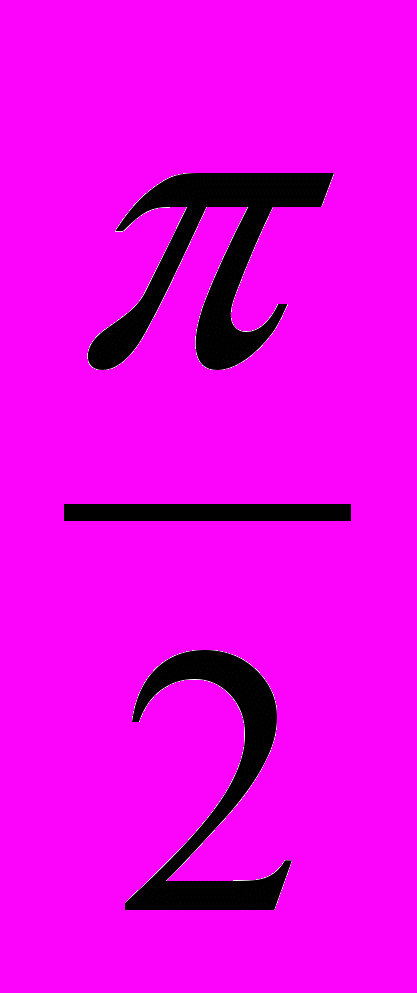a	а	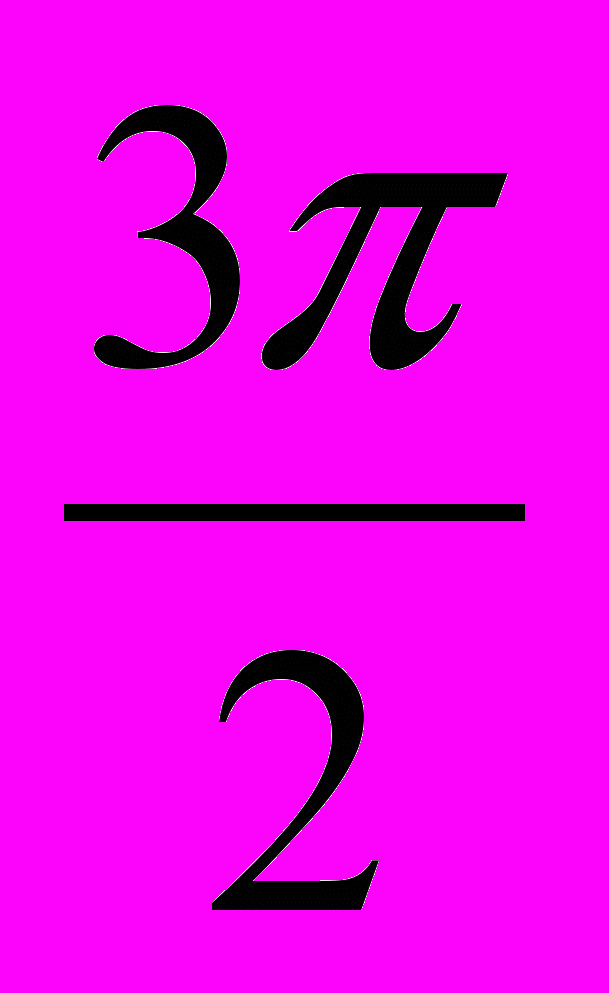a2

^

Отрезок а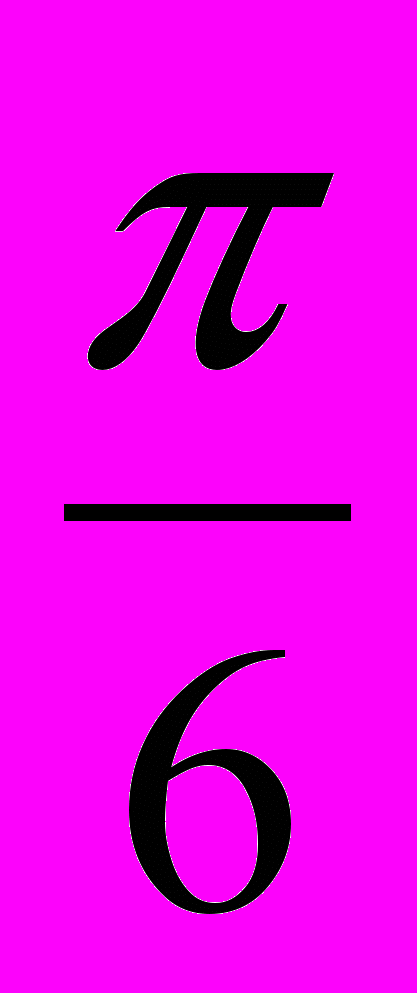 обозначим ОА; тогда

а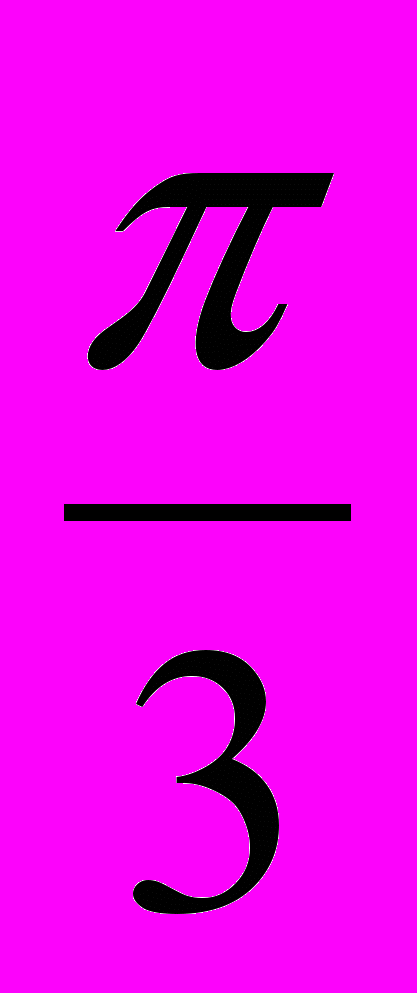=2OA, a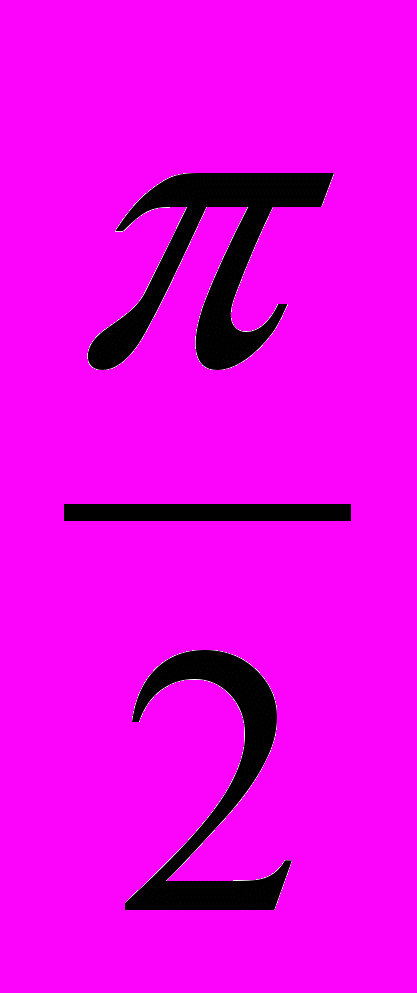=3OA, a=6OA, а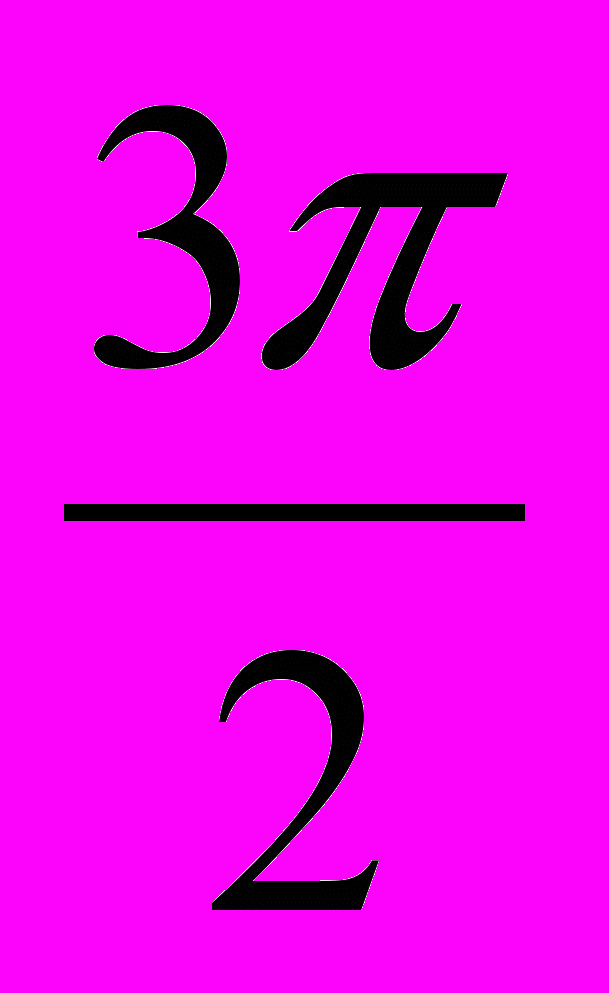=9OA, 2a=12OA.

Откладывая эти отрезки на соответствующих лучах, получим точки A,B,C,D,E,F, принадлежащие графику функции =а. Соединяя полученные точки плавной кривой, получим спираль Архимеда.

Свойства этой спирали впервые были изучены Архимедом. Одним из этих свойств является постоянство расстояний между витками. Аргумент  может расти безгранично, а поэтому кривая имеет бесконечное множество витков. Определим расстояние между двумя соседними витками MN по произвольному лучу.

OM=a;

ON=a(+2);

MN=ON-OM=a(+2)-a=2a.

Полученное выражение от  не зависит, так как MN=2a при любом .

Таким образом, в полярной системе координат Архимедова спираль имеет весьма простое уравнение: =а, и построение её графика никаких затруднений не вызывает.

Воспользуемся формулами перехода 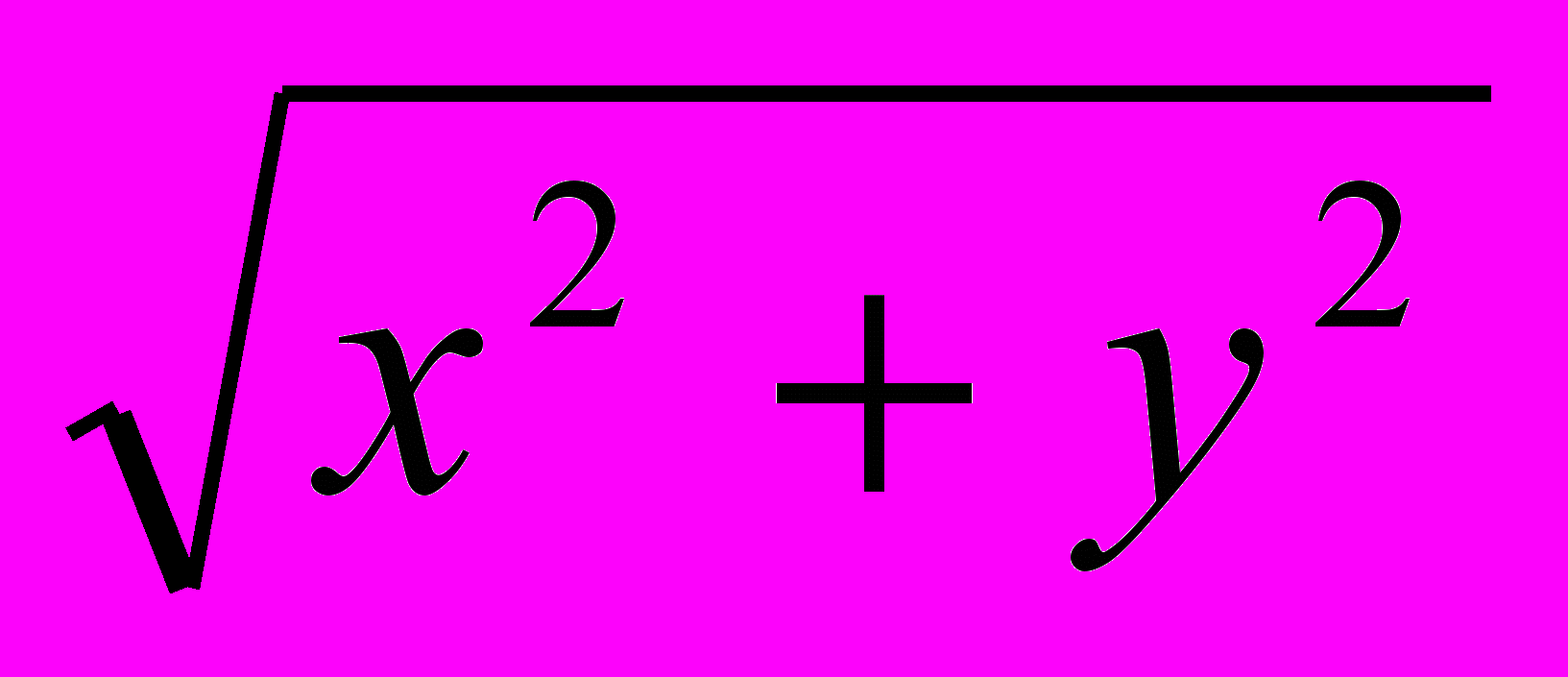=, φ=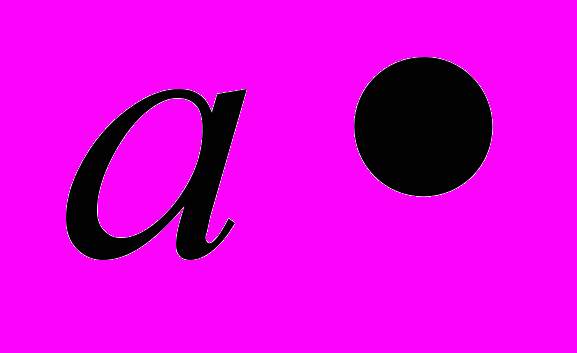arctg(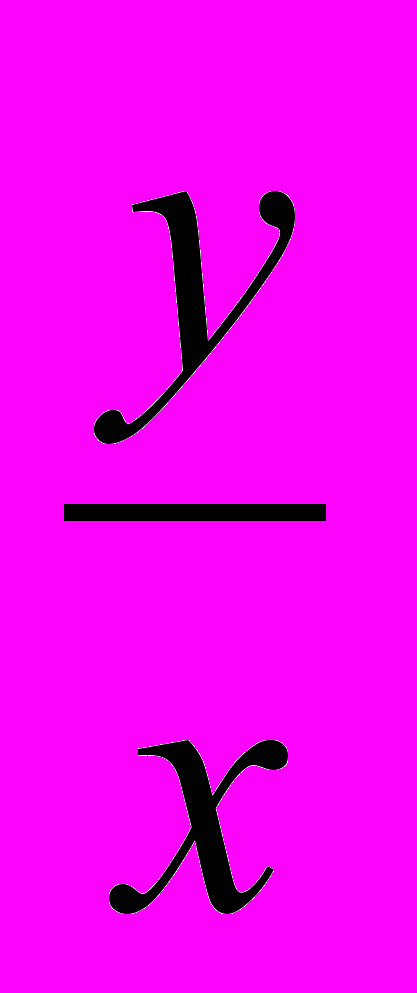) и получим вместо ρ=aφ гораздо более сложное уравнение

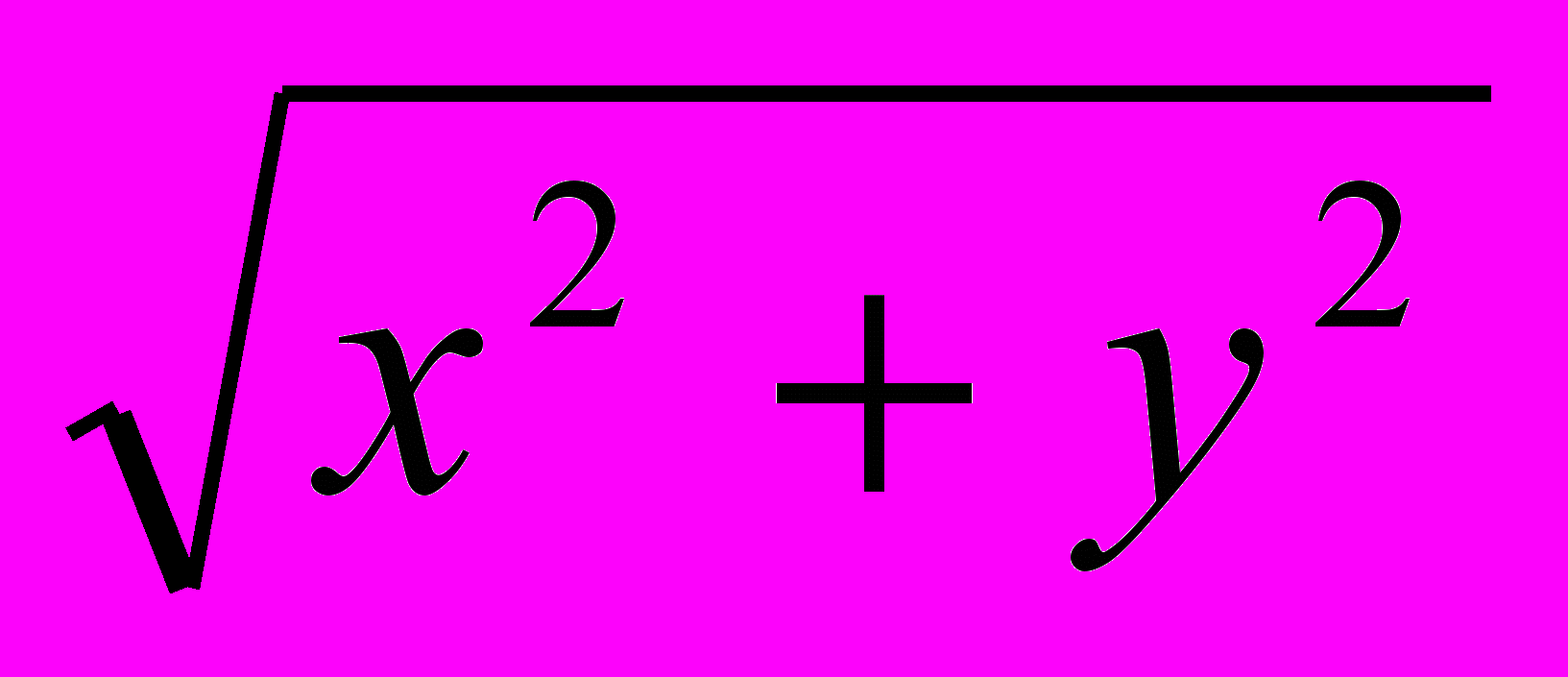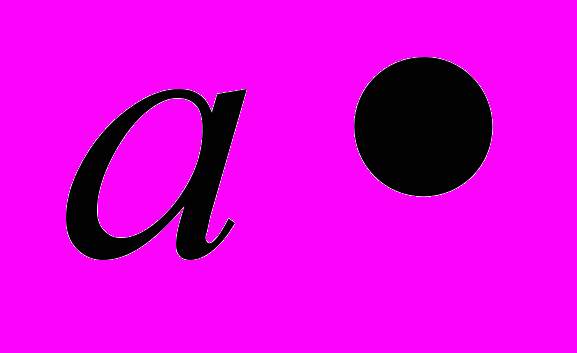= arctg()

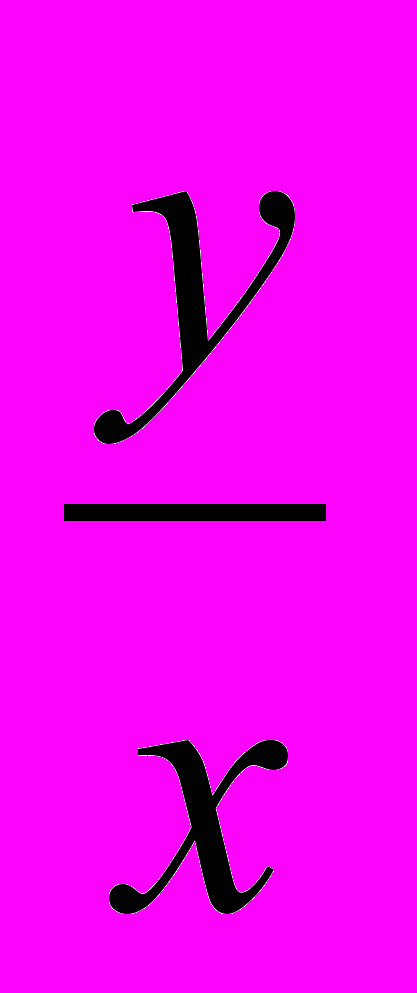Из уравнения видно, что построение графика этой функции в декартовой системе координат было бы крайне затруднительно.


^ 3. Лемниската Бернулли.

Лемнискатой называется геометрическое место точек М, произведение расстояний каждой из которых до двух фиксированных точек F₁ и F₂ есть величина постоянная.

Расположим фиксированные точки (фокусы лемнискаты) F₁ и F₂ на оси абсцисс симметрично относительно начала координат. Обозначим расстояние между ними F₁ F₂=2а. Тогда эти точки будут иметь координаты F₁ (-а,0), F₂ (а,0). Для произвольной точки лемнискаты М(x,y), по её определению должно выполняться: MF₁ ∙ MF₂=a² . Используя формулу расстояния между двумя точками d=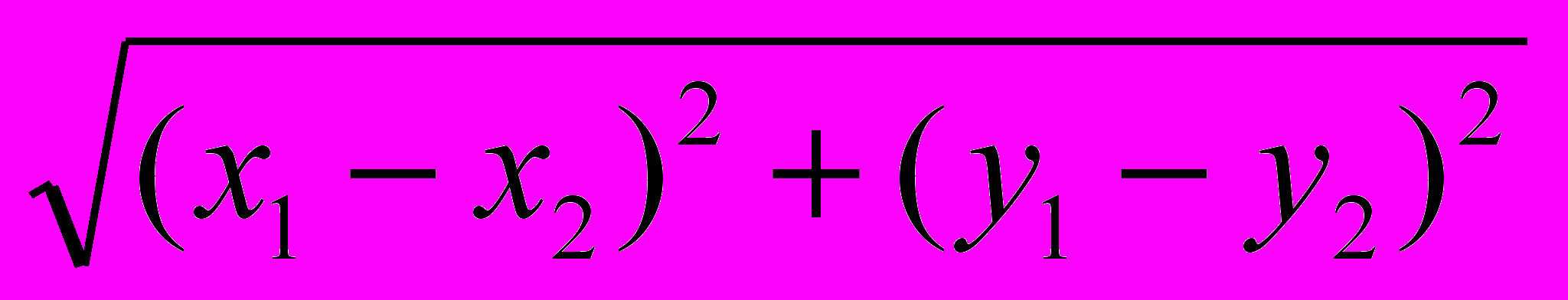, получим: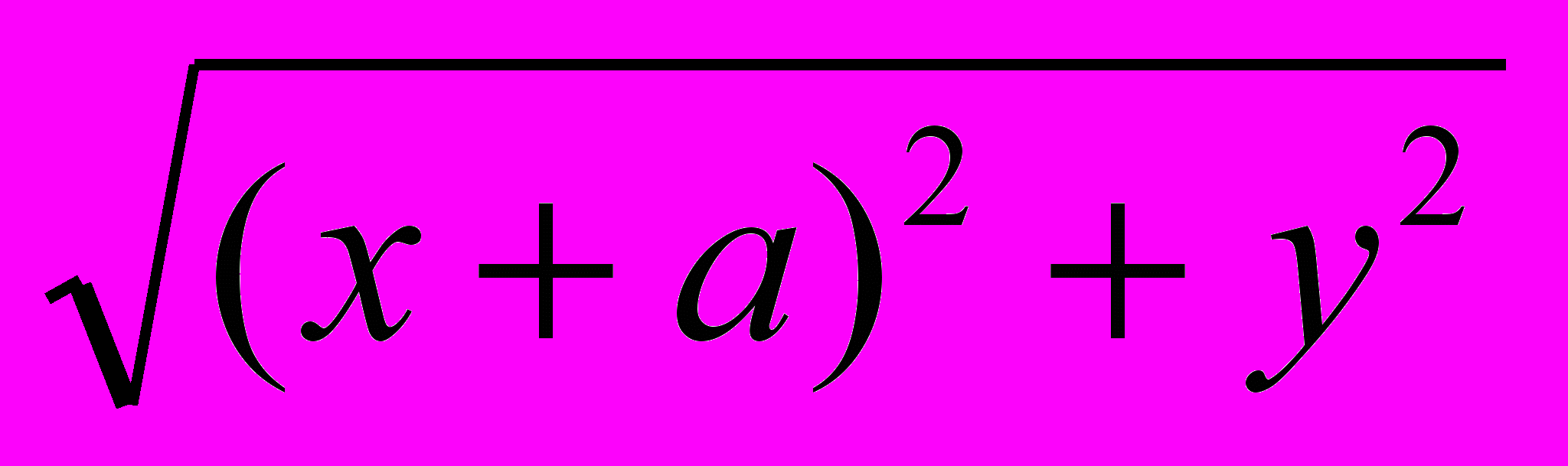

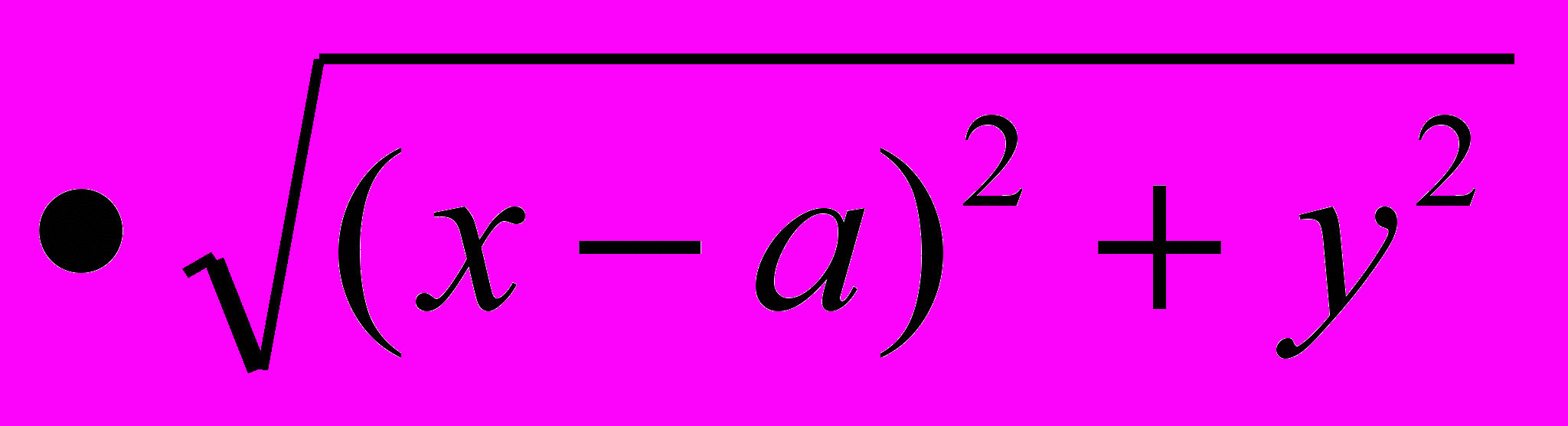
= a² .

После возведения правой и левой частей полученного уравнения в квадрат и упрощений получим:

(x²+y²)²-2a²(x²-y²)=0.












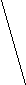
Исследовать кривую по этому уравнению в декартовой системе координат довольно сложно. Если же перейти к полярным координатам, то уравнение примет более простой вид:

(ρ²)² = 2а² (ρ² cos²φ - ρ² sin²φ) или ρ² = 2а² cos2φ.

Итак, полярное уравнение кривой имеет вид

ρ² = b² cos 2φ,

где 2а²=b² . Так как максимальное значение cos 2φ равно единице, то максимальная величина ρ есть b.
^

Если cos 2φ отрицателен, то ρ – мнимая величина. Таким образом, между прямыми, образующими углы 45˚ и 135˚ с полярной осью, нет точек кривой.

Если вместо φ подставить (-φ), то уравнение не измениться. Отсюда следует, что кривая симметрична относительно полярной оси.

Если ρ=0, то cos 2φ=0 и φ=45˚ или 135˚, следовательно, кривая проходит через полюс при этих значениях угла.

Можно также найти область существования этой функции, т.е. множество тех значений аргумента φ , при которых функция имеет вещественное значение: ρ²≥0, а потому должно быть и cos 2φ≥0, откуда

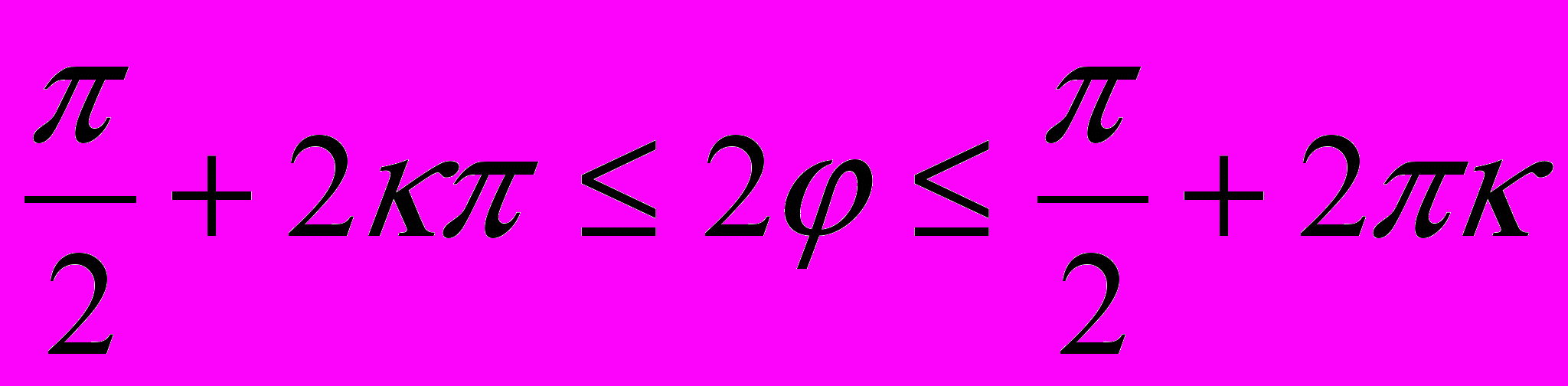
-, где к – целое число, или -.

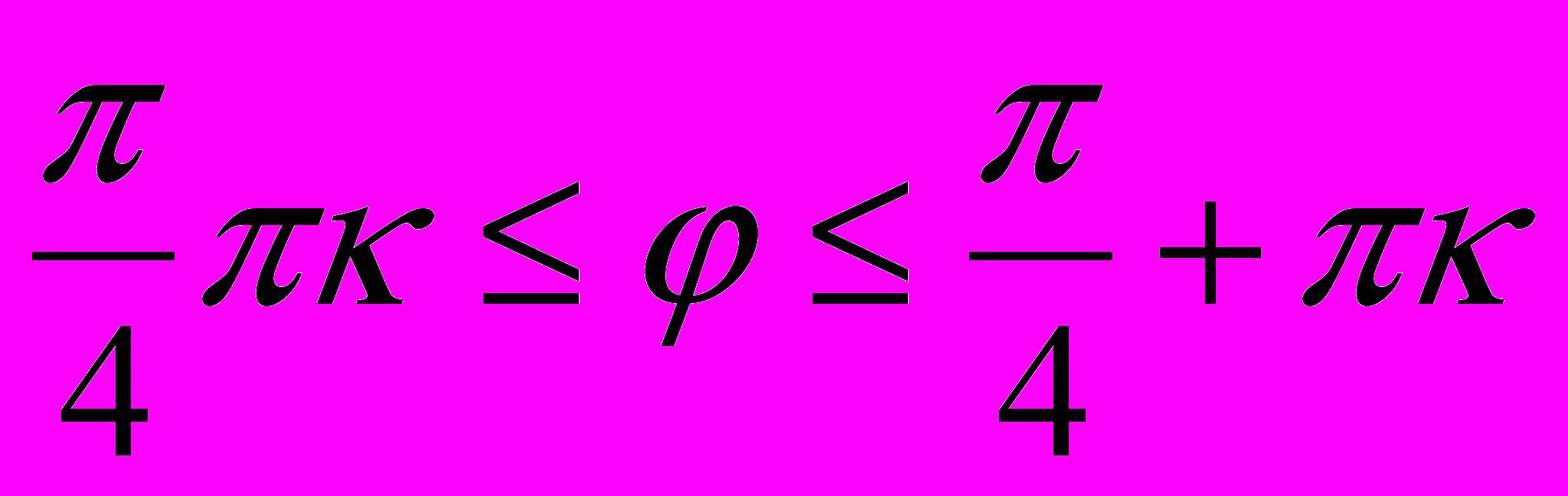Проведя биссектрисы координатных углов, выделим те секторы, в которых кривая существует. Дальнейшее построение кривой выполняется по точкам. Название этой кривой – лемниската происходит от греческого слова повязка, бант.

Лемниската Бернулли используется в качестве переходной линии на закруглениях малого радиуса ( например, на трамвайных путях).


4. Розы.

Розы – плоские кривые, уравнения которых в полярных координатах имеют вид

ρ=αsinκφ,

где α и κ – постоянные. Если κ=m/n – число рациональное, то роза - алгебраическая кривая четного порядка. Порядок этой кривой равен m + n, если m и n – нечетные числа, и равен 2(m + n), если одно из чисел m и n – нечетное. Вся кривая расположена внутри круга радиуса α, состоит из конгруэнтных лепестков. Если κ – целое, то роза состоит из κ лепестков при κ нечетном и из 2κ лепестков при κ четном. Если κ = m/n и m, n – взаимно простые, то роза состоит из m лепестков, когда m и n нечетные, и из 2m лепестков, если одно из чисел m и n является четным.

При иррациональном κ лепестков бесконечно много, розы являются гипоциклоидами, если κ>1, и эпициклоидами, если κ<1.


5. Улитка Паскаля.
^

Улиткой Паскаля называется кривая, определяемая уравнением

ρ=2r cosφ+l

(в прямоугольных координатах: (x² +y²-ax)²=l²(x²+y²)).

Для построения графика этой кривой обратим внимание на то, что при l=0 ρ=2r cosφ, а из рисунка очевидно, что ОМ=2r cosφ, а потому графиком этой кривой является окружность радиуса r ( полюс О находится в левом конце диаметра этой окружности, а полярная ось направлена по диаметру).

Теперь для построения точек, принадлежащих улитке Паскаля, надо в каждом положении полярного радиус-вектора ρ=2r cosφ достроить к нему отрезок l. На рис. 2 выполнены эти построения для трех случаев: l<2r, l=2r, l>2r.

В случае l=2r улитка Паскаля называется кардиоидой и имеет уравнение вида

ρ=2r cosφ + 2r = 2r (1+ cosφ).


^ III. Кривые II порядка в декартовых координатах.


Продолжая перечень примеров, рассмотрим ещё несколько кривых механического происхождения, полученные путем качения одних кривых по другим.


^ Эпи- и гипоциклоида.

Если один круг без скольжения катится извне по другому кругу, то кривая , описываемая произвольной точкой окружности подвижного круга, называется эпициклоидой. В случае же качения изнутри, мы имеем дело с гипоциклоидой. Остановимся на выводе уравнений первой из этих кривых.

Возьмем начало координат в центре О неподвижного круга, а ось x проведем через то положение А интересующей нас точки, в котором она является точкой касания обоих кругов. Когда подвижный круг перейдет в новое положение, указанное на чертеже, точка А перейдет в М. Геометрическое место точек М нам и надлежит определить.

Обозначим через а радиус неподвижного круга, а через mа – радиус катящегося круга. Выберем за параметр здесь угол t=
Прежде всего, посмотрим, в чем здесь проявляется отсутствие скольжения. Дуга ABпройденная точкой касания по неподвижной окружности, должна равняться дуге МВ, пройденной точкой касания по катящейся окружности:

a MCB = mat, откуда
Выразим теперь координаты x и y точки М через t. Имеем

x=OG=OE+FM=(a+ma) cos mt+ma sin
но

- mt,

так что

и sin
Окончательно

x = a[(1+m) cos mt – m cos (1+m)t]

Подобным же образом найдем

y = a[(1+m) sin mt – m sin (1+m)t].

Эти уравнения дают параметрическое представление эпициклоиды.

Когда катящейся круг снова придет в соприкосновение с неподвижным кругом в той же своей точке, что и в начале движения (т.е. при t=2π), точка М закончит одну ветвь кривой. При дальнейшем качении она будет описывать следующую ветвь, подобную первой, и т.д.

В случае же гипоциклоиды подобным же образом получаются такие параметрические уравнения:

x = a[(1-m) cos mt + m cos (1- m)t]

y = a[- (1- m) sin mt + m sin (1- m)t]

Здесь m также означает отношение радиуса катящегося круга к радиусу неподвижного. Легко заметить, что эти уравнения получаются их уравнений эпициклоиды заменой m на –m.

На рисунке изображены эпициклоиды, соответствующие m=1, 2, 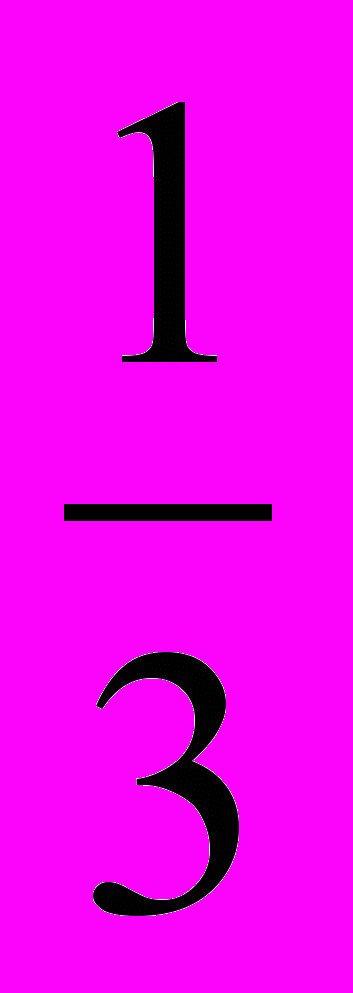, и гипоциклоиды, соответствующие m= 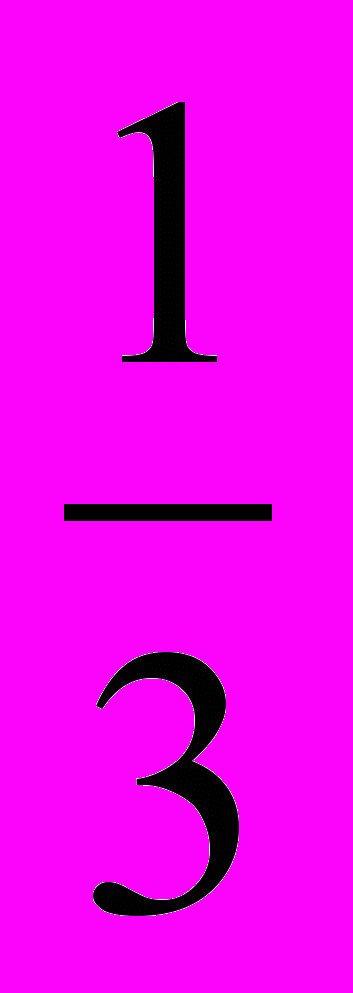и 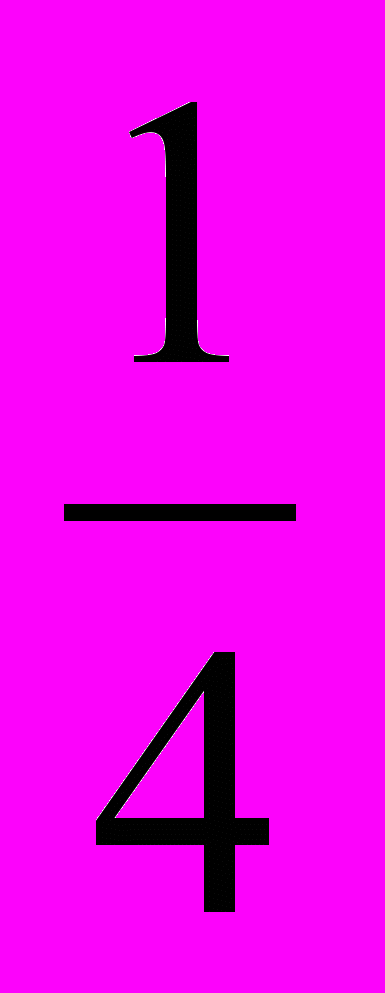. В последней можно узнать астроиду.


^ IV. Использование компьютера для наглядного представления кривых II порядка.


Программа для построения графиков является наукой, но простой в использовании. Она позволяет создавать анимированные 3D графики уравнений в табличных данных. В одной системе координат может быть неограниченное количество графиков, каждый из которых может отображаться при помощи точек, линий и поверхностей. Аналитические функции задаются в параметрическом виде и могут содержать до трех независимых переменных, включая переменную времени для анимации.

Систему координат с графиком можно вращать, перемещать и масштабировать в реальном времени. Программа позволяет отслеживать и вводить координаты курсора на плоскости или в трехмерной системе координат. Использование графической библиотеки OpenGL позволяет создавать высококачественные изображения графиков и дает возможность задействовать современные аппаратные ускорители, необходимые для достижения гладкой анимации в реальном времени.


Рассмотренные выше кривые второго порядка в компьютерной программе 3D Grapher имеют следующее изображение:

1. Жезл.
   

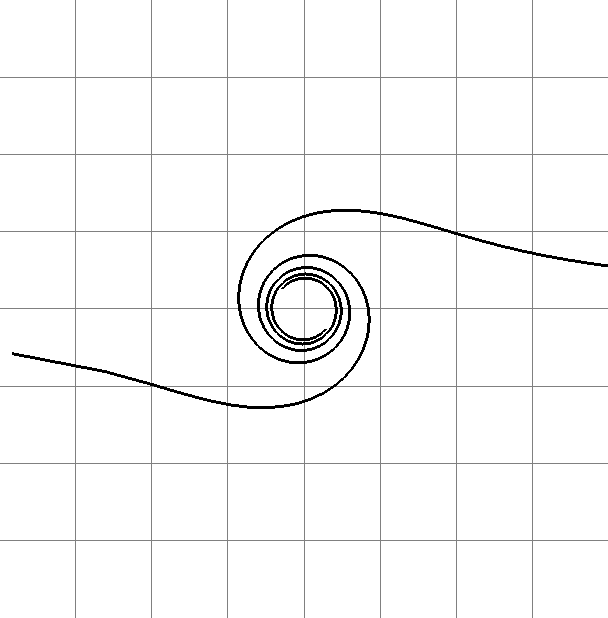
φ= U, ρ=

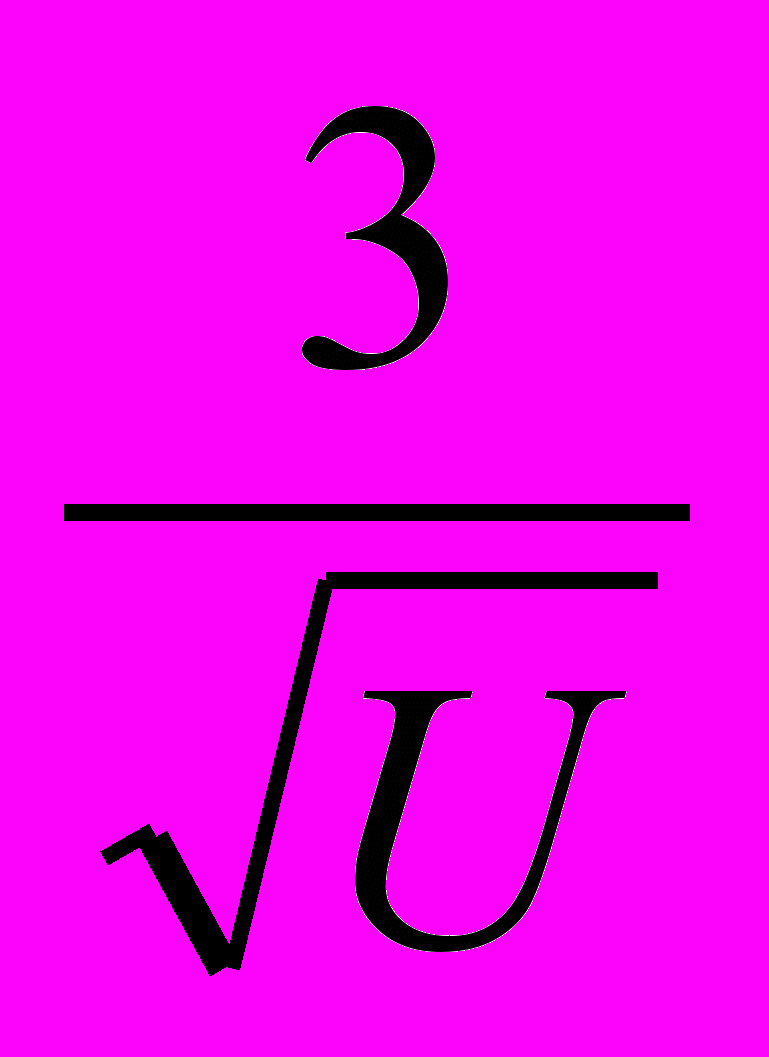
φ= U, ρ=-

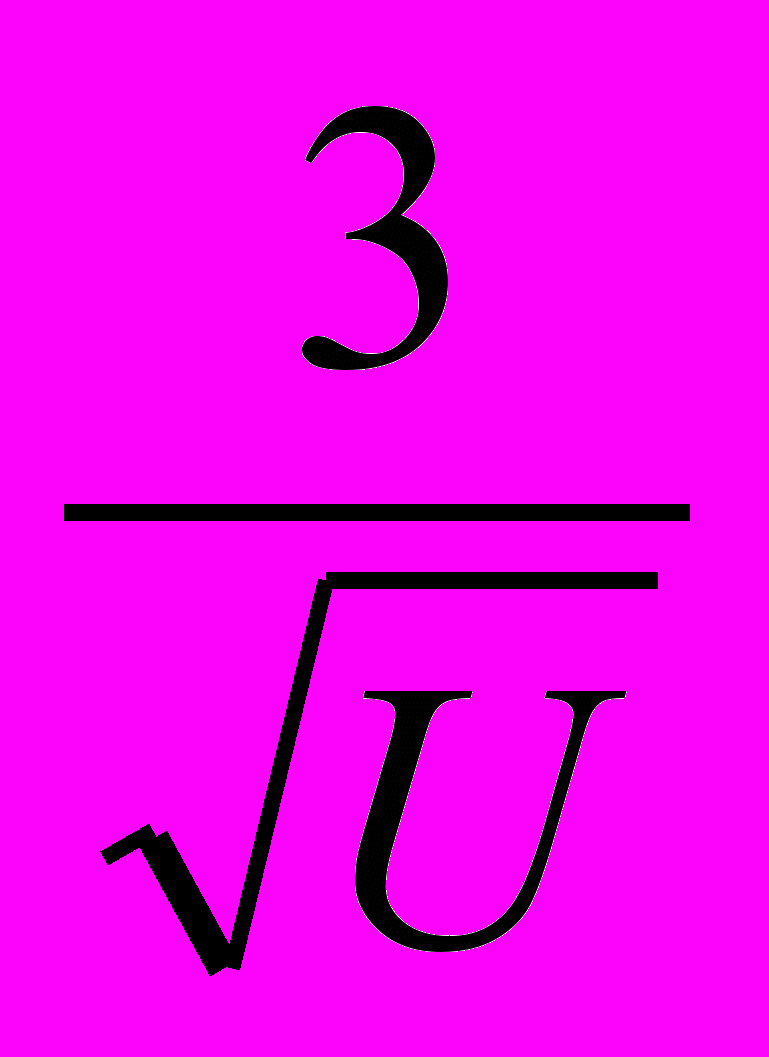
2. Гиперболическая спираль.
   

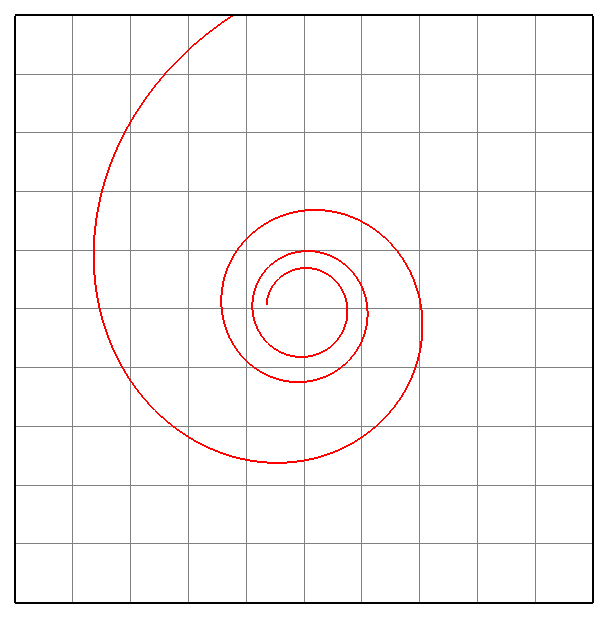
φ=u;

ρ=

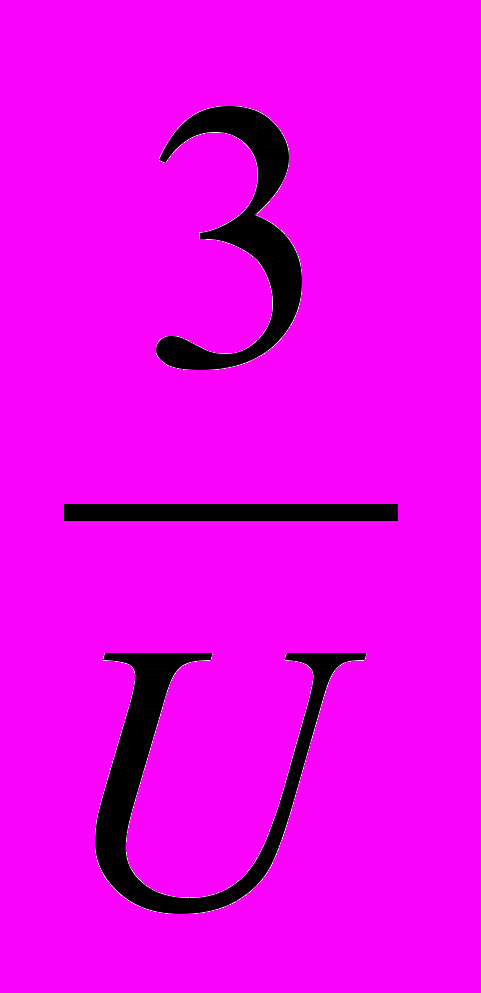
3. Логарифмическая спираль.
   

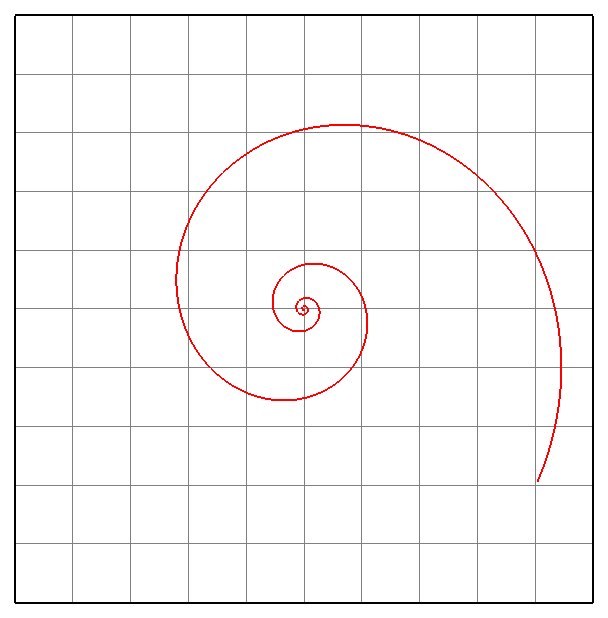
φ=u;

ρ=0.8^u

3. Спираль Архимеда.
   

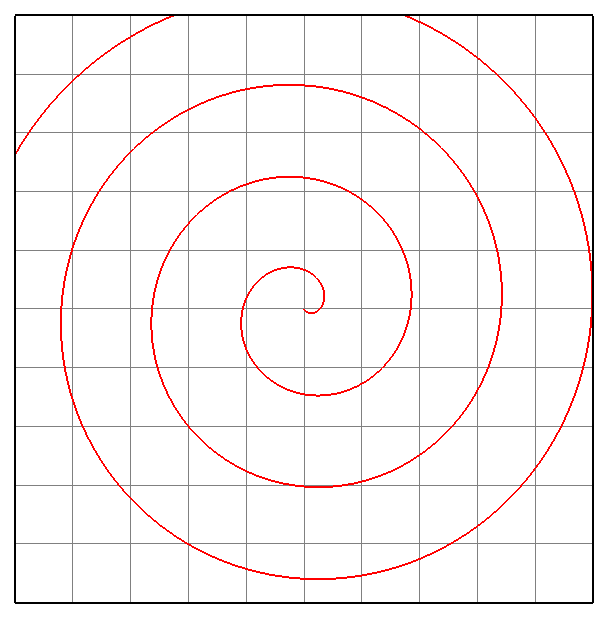
φ=u;

ρ=0.05*u

3. Улитки Паскаля.
   

^ 5. Улитки Паскаля.




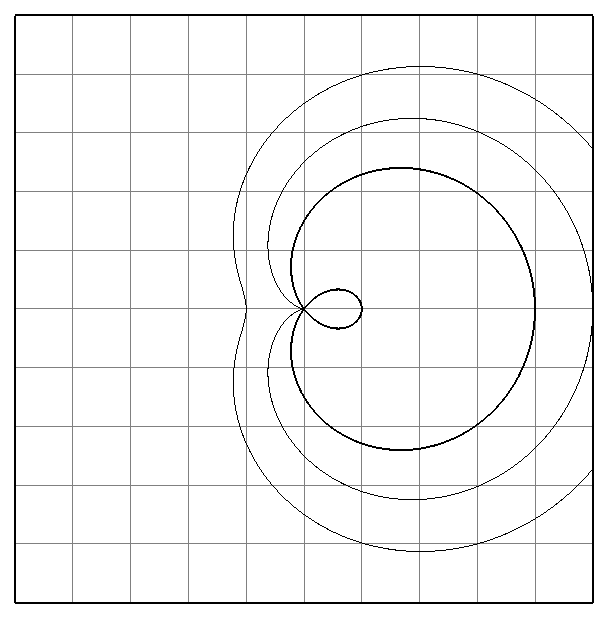
ρ=0.5*cos(u)+0.3

ρ=0.5*cos(u)+0.5

ρ=0.5*cos(u)+0.7

3. Четырёхлепестковая роза. 7. Трёхлепестковая роза.
   

ρ=7*sin(2*u) ρ=7*sin(3*u)

^ 7. Эпициклоида. 8.Гипоциклоида.




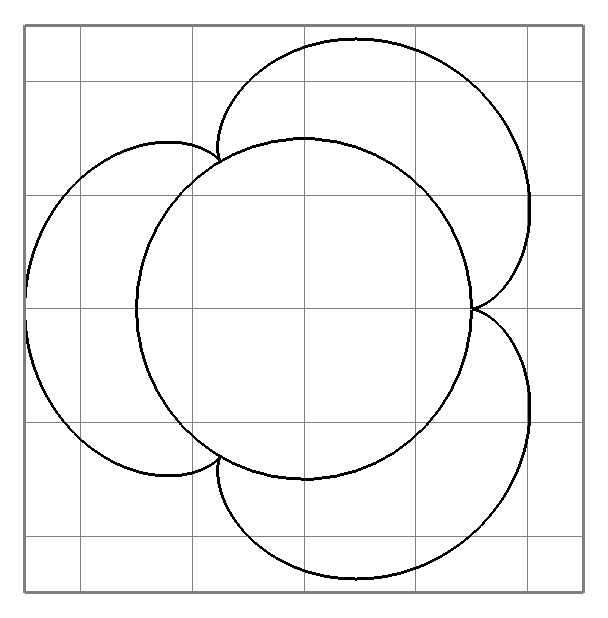
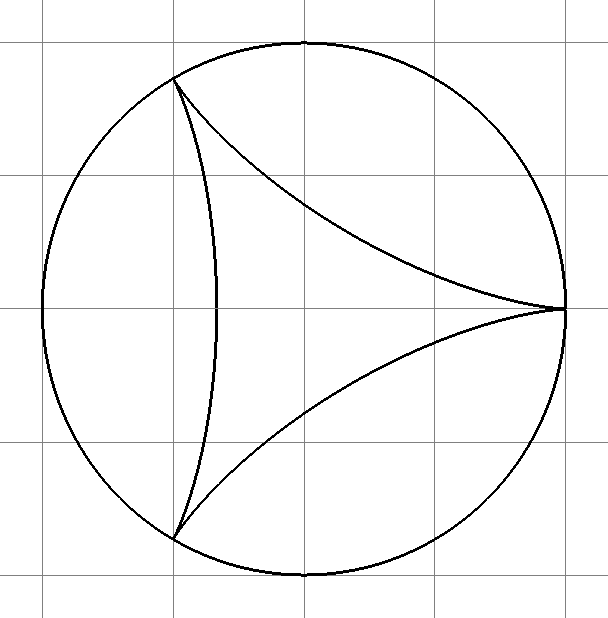
x=8 cos(u)-2 cos(4u) x=4 cos(u)+2 cos(2u);

y=8 sin(u)-2 sin(4u) y=4 sin(u)+2sin(2u)

Кривые построены при следующих значениях параметров: R=6, r=2, m=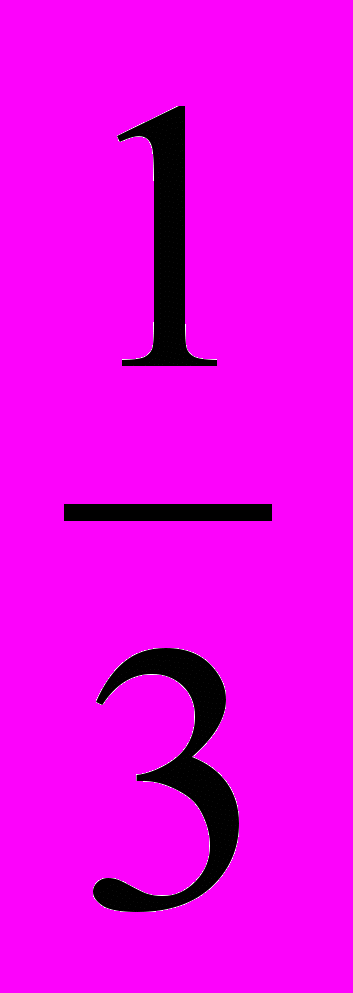, t=3.

^ 9. Лемниската Бернулли.




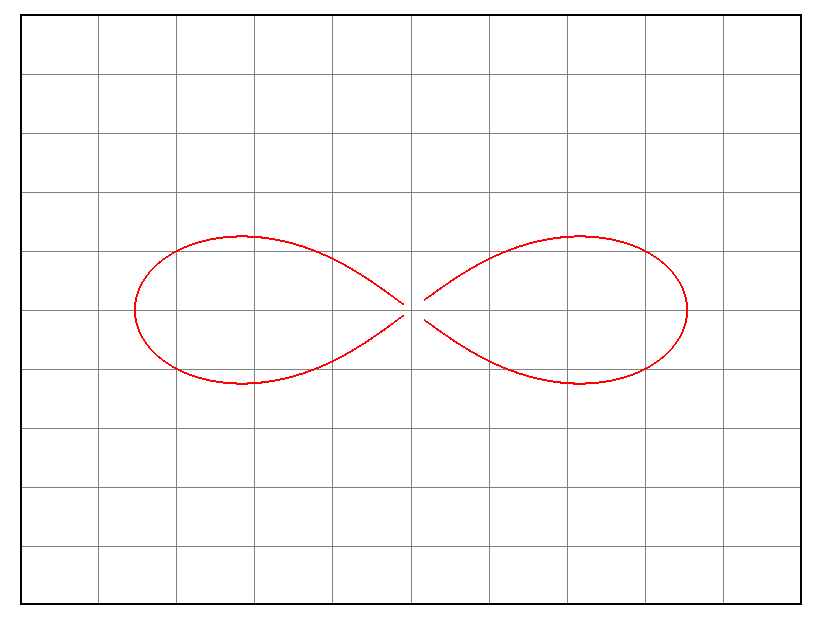
²=2а² cos(2u)


V. Заключение.


В своей работе я достигла следующих результатов:

1. Показала, что кроме прямоугольной декартовой системы координат существуют и другие, например, полярная система координат, и сделала вывод, что иногда полярная система является более удобной для построения кривых.

2. Рассмотрела построения и свойства кривых II порядка, которые не встречаются в школьном курсе математики.

3. Построила с помощью компьютерной программы 3D Grapher графики этих кривых.


VI. Список литературы.

1. Е г е р е в В. К. Методика построения графиков функций – М.: Высшая школа, 1970 – с. 137-145.
   

2. Ф и х т е н г о л ь ц Г. М. Курс дифференциального и интегрального исчисления. Том I. – М.: Наука, 1969 – с.508-516.
   

3. Математический энциклопедический словарь. – М.: Советская энциклопедия, 1988.