Учебно-методический комплекс по дисциплине опд. Ф. 015 Теоретическая физика: Квантовая теория индекс по гос/наименование дисциплины

Вид материала

Содержание

Косов Александр Александрович, д-м физ.-мат. наук, проф.
Содержание учебно-методического комплекса
Федеральное агентство по образованию
I рабочая программа
Рекомендована к утверждению Рассмотрена и одобрена на
Ф.И.О. зав. кафедрой, подпись
1 ПОЯСНИТЕЛЬНАЯ ЗАПИСКА 1.1 Требования государственного образовательного стандарта к содержанию данной дисциплины
Квантовая теория.
1.2 Цели, учебные задачи дисциплины, место и роль учебной дисциплины в подготовке специалиста
1.3 Виды учебной деятельности студентов
2 Содержание программы
Актуальность и значимость курса.
Цель и задачи изучения курса.
Место дисциплины в профессиональной подготовке специалистов.
Структура учебной дисциплины.
Особенности изучения дисциплины.
Форма организации занятий по курсу.
Взаимосвязь аудиторной и самостоятельной работы студентов.
Требования к уровню усвоения содержания курса.
Объем и сроки изучения курса.
...
Полное содержание

Подобный материал:

1 2 3

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОУВПО «Марийский государственный университет»
Физико-математический факультет

Кафедра теоретической и прикладной физики

УТВЕРЖДАЮ

Декан физико-математического
факультета

«24» ноября 2009 г.

/Попов Н.И./

(

подпись/Ф.И.О)

УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКС ПО ДИСЦИПЛИНЕ

ОПД.Ф.015 Теоретическая физика: Квантовая теория

(индекс по ГОС/наименование дисциплины)

СПЕЦИАЛЬНОСТЬ/НАПРАВЛЕНИЕ

010701 – Физика

(код и наименование специальности/направления в соответствии с лицензией)

С

оставитель ^ Косов Александр Александрович, д-м физ.-мат. наук, проф.

(должность, Ф.И.О., ученая степень, звание автора программы)

Йошкар-Ола

2009

УТВЕРЖДЕНО

на заседании кафедры

теоретической и прикладной физики

(название кафедры)

П

ротокол № 4 от

«20» ноября 2009 г.

Зав. кафедрой /Косов А.А./

(

подпись/Ф.И.О)

УТВЕРЖДЕНО

на заседании УМК

П

ротокол № 1 (ВЗ) от

«23» ноября 2009 г.

П

редседатель УМК /А.В. Леухин/

(подпись/Ф.И.О)

^ СОДЕРЖАНИЕ УЧЕБНО-МЕТОДИЧЕСКОГО КОМПЛЕКСА

I Рабочая программа учебной дисциплины 4

II Методические рекомендации по изучению учебной дисциплины 25

III Учебно-методические материалы 25

IV Материалы текущего контроля, промежуточной аттестации и итогового контроля знаний 26

V Словарь терминов и персоналий 26

VI Программа государственного экзамена, итогового междисциплинарного
экзамена 27

VII Программное и методическое обеспечение практики 28

^ ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ

ГОУВПО «Марийский государственный университет»

Физико-математический факультет

УТВЕРЖДАЮ

Декан физико-математического

факультета

/Попов Н.И./

(

подпись/Ф.И.О.)

«24» ноября 2009 г.
^

I РАБОЧАЯ ПРОГРАММА

чебная дисциплина Теоретическая физика: Квантовая теория

(/наименование дисциплины)

ОПД.Ф.015

(индекс по ГОС)

С

пециальность 010701 – Физика

(

код и наименование в соответствии с лицензией)

Кафедра теоретической и прикладной физики

(

название)

К

урс 3 семестр 6 форма обучения очная

Л

екции 38

(кол-во часов)

Практические занятия 19

(

кол-во часов)

Лабораторные занятия –

(

кол-во часов)

Самостоятельная работа 46

(

кол-во часов)

Курсовая работа (проект)

(

семестр)

Зачет 6

(

семестр)

Э

кзамен

(семестр)

Программа разработана Косовым Александром Александровичем, д-м физ.-мат. наук, проф.

(

должность, Ф.И.О., ученая степень, звание автора программы)

Йошкар-Ола

2009
^

Рекомендована к утверждению Рассмотрена и одобрена на

решением учебно-методической заседании кафедры

комиссии (учебно-методического теоретической и прикладной

с

овета) физико-математического физики

факультета (название кафедры)

(название факультета / института, специальности)

п

ротокол заседания № 1 от протокол заседания № 4 от

«

11» сентября 2009 г. «20» ноября 2009 г.

Косов А.А. Косов А.А.

(подпись, Ф.И.О. председателя) (подпись, Ф.И.О., зав. кафедрой)

СОГЛАСОВАНО с выпускающей кафедрой общей физики

(название кафедры)

п

ротокол заседания № 1 от «31» августа 2009 г. / Леухин А.В.

(^ Ф.И.О. зав. кафедрой, подпись)

Учебный год	Решение кафедры (№ протокола, дата заседания кафедры, Ф.И.О., подпись зав. кафедрой)	Автор изменения (Ф.И.О., подпись)	Номер изменения

1 ПОЯСНИТЕЛЬНАЯ ЗАПИСКА

1.1 Требования государственного образовательного стандарта к содержанию данной дисциплины

ОПД	Общепрофессиональные дисциплины	1310
ОПД.Ф.01	Теоретическая физика.	870
ОПД.Ф.015	^ Квантовая теория. Дуализм явлений микромира, дискретные свойства волн, волновые свойства частиц. Принцип неопределенностей. Принцип суперпозиции Наблюдаемые и состояния. Чистые и смешанные состояния. Эволюция состояний и физических величин. Соотношения между классической и квантовой механикой. Теория представлений. Общие свойства одномерного движения гармонического осциллятора. Туннельный эффект. Квазиклассическое движение. Теория возмущений. Теория момента. Движение в центрально-симметричном поле. Спин. Принцип тождественности одинаковых частиц. Релятивистская квантовая механика. Атом. Периодическая система элементов Менделеева. Химическая связь, молекулы. Квантование электромагнитного поля. Общая теория переходов. Вторичное квантование, системы с неопределенным числом частиц. Теория рассеяния.	185

^ 1.2 Цели, учебные задачи дисциплины, место и роль учебной дисциплины в подготовке специалиста

Профессиональная деятельность специалиста по специальности «Физика», изучающего курс квантовая теория направлена на возможность освоения новых теорий и моделей; исследований и оценку состояния и обработки полученных результатов научных исследований на современном уровне и их анализ.

Студенты, окончившие курс «Квантовая теория», должны быть подготовлены к решению следующих задач:

научные исследования поставленных проблем;
формулировка новых задач, возникающих в ходе научных исследований;
разработка новых методов исследований;
выбор необходимых методов исследования;
освоение новых методов научных исследований;
освоение новых теорий и моделей;
обработка полученных результатов научных исследований на современном уровне и их анализ;
работа с научной литературой с использованием новых информационных технологий, слежение за научной периодикой.

^ 1.3 Виды учебной деятельности студентов

Лекции и практические семинарские занятия. В качестве внеаудиторной самостоятельной работы: работа с научной литературой с использованием новых информационных технологий, слежение за научной периодикой.

Самостоятельная работа также включает в себя:

изучение теоретического материала;
переработку материала лекций;
подготовку к практическим занятиям;
индивидуальную работу в компьютерном классе

1.4 Контроль знаний студентов

6 семестр – зачет.

^

2 СОДЕРЖАНИЕ ПРОГРАММЫ

Рабочая программа составлена на основании типовой программы курса «Квантовая теория» для специальности 010701 «Физика», утвержденной УМС по физике УМО классических университетов и полностью соответствует требованиям Государственного образовательного стандарта специальности 010400 «Физика».

^ Актуальность и значимость курса. Сегодняшняя жизнь не мыслима без приборов и механизмов, работающих по законам квантовой физики. Знание основных законов физики микромира будет еще более востребовано при переходе общества в эру нанотехнологий. Ну а понимание исследований на переднем крае физики, даже на уровне популярных статей, требует не только знаний основных закономерностей физики микромира, но и соответствующего математического языка их описания, но и логической структуры всей физики в целом, на всех ее уровнях.

Данный курс является основой для курсов «Физика конденсированного состояния», «Статистическая физика» и большинства курсов специальной подготовки.

^ Цель и задачи изучения курса. Целью данного теоретического курса - показать, почему перестали действовать законы классической физики в микромире и как строится новая физика, включающая классическую как составной элемент, но с ограниченной областью применимости. Важнейшей задачей курса является овладение специальным аппаратом квантовой физики, позволяющим читать современную литературу, и умение его применять для рассмотрения широкого круга физических явлений.
^ Место дисциплины в профессиональной подготовке специалистов. Курс "Квантовая теория", читаемый после разделов "Теоретическая механика" и "Электродинамика" курса теоретической физики, представляет собой теоретическую основу для последующих разделов курса теоретической физики. В нем вводятся основные понятия и методы квантовой теории, способы теоретического описания, количественного и качественного анализа квантовых процессов в системах, состоящих из одной или многих частиц, а также в системах с неопределенным или меняющимся числом частиц.
^ Структура учебной дисциплины. Курс «Квантовая теория» включает в себя следующие большие темы: Причины несостоятельности классической физики для описания явлений микромира; Уточнение основных положений физики, таких как физическая величина, состояние, закон движения, в виде постулатов квантовой теории; использование новых понятий в модельных задачах и качественное описание явлений микромира; Точно решаемые задачи квантовой теории; Методы приближенного решения задач и их использование для описания явлений.
^ Особенности изучения дисциплины. Курс рассчитан на студентов-физиков, имеющих подготовку по общей физике и математике в объеме обычной университетской программы. В частности, предполагается, что студенты знакомы с качественным описанием отдельных квантовых явлений из области атомной и ядерной физики, оптики, физики твердого тела, а также знакомы с элементами теории линейных операторов в гильбертовом пространстве.
^ Форма организации занятий по курсу. Организация занятий - традиционная. По курсу «Квантовая теория» читаются лекции и ведутся практические занятия по 2 часа в неделю в течении двух семестров.
^ Взаимосвязь аудиторной и самостоятельной работы студентов. Аудиторные занятия, лекции и практика, предполагают самостоятельную работу студентов по данному курсу. На лекциях предлагается для самостоятельного изучения дополнительные темы, самостоятельное проведение некоторых вычислений. На практических занятиях даются домашние задания для самостоятельного решения задач и упражнений по курсу «Квантовая механика».
^ Требования к уровню усвоения содержания курса. Понимание области применимости отдельных разделов физики и их взаимосвязь, владение «математическим языком» квантовой теории и причин, его использования, знание теоретического материала и его использование при решении конкретных задач, умение читать современную литературу по физике, понимание главных проблем этой науки, грамотное использование получаемых знаний и умений в специальных дисциплинах.
^ Объем и сроки изучения курса. Курс «Квантовая теория» читается на третьем (6 семестр) и четвертом (7 семестр) курсах: лекции – 2 часа в неделю (70 часов), практические занятия – 1 час в неделю (35 часов), самостоятельная работа студентов (90 часов).
^ Виды контроля знаний и их отчетности. Усвоение материала, излагаемого на лекциях, контролируется проведением контрольных работ по основным понятиям предыдущих лекций. В течении семестра проводятся контрольные работы по практическим занятиям. Усвоение отдельных больших тем контролируется проведением тестирования. Темы, выносимые на самостоятельное изучение, предполагают рефераты. В 6-м семестре промежуточной итоговой аттестацией является зачет, в 7-м – итоговый экзамен.
^ Критерии оценки знаний студентов по курсу. Для получения допуска к экзамену по курсу «Квантовая теория» требуется посещение аудиторных занятий и выполнение контрольных мероприятий. А именно: зачет в первом семестре ставится при выполнении контрольной работы, прохождения двух тестов, отсутствия «долгов» по домашним заданиям и сдачи коллоквиума по теоретическому материалу. Для допуска к экзамену – такие же требования. Оценка «хорошо» ставится при решении задачи экзаменационного билета. Задача считается решенной, если дано ее полное, правильное, поэтапное решение. Для получения оценки «отлично», кроме решения задачи, необходимо полно и с пониманием ответить на теоретический вопрос билета. Экзамен проводится письменно.

3 ТЕМАТИЧЕСКИЙ ПЛАН ИЗУЧЕНИЯ УЧЕБНОЙ ДИСЦИПЛИНЫ

№ п/п раздела	№ п/п темы	Наименование разделов и тем	Количество часов по учебному плану
			Всего	В том числе
				Аудиторная нагрузка			Самостоятельная работа
				Лекции	Практические (семинарские) занятия	Лабораторные занятия	Самостоятельная работа
1	2	3	4	5	6	7	8
	1	Введение	5	2	1		2
	2	Первый квантовый постулат – динамические переменные как операторы. Квантование физических величин	12	4	2		6
	3	Второй квантовый постулат – описание состояния в микромире. Смешанные и чистые состояния.	15	6	3		6
	4	Третий квантовый постулат – эволюция состояний. Представление Шредингера, Гейзенберга, принцип соответствия.	17	6	3		8
	5	Одномерное движение, модельные задачи	20	8	4		8
	6	Движение в центральном поле	17	6	3		8
	7	Приближенные методы решения задач квантовой механики	17	6	3		8
		ИТОГО:	103	38	19	–	46

4 ПРОГРАММА ЛЕКЦИОННЫХ ЗАНЯТИЙ

4.1 Тематический план лекций

N п/п	Наименование Тем и разделов	Всего (часов)	Аудиторные занятия		Самостоятельная Работа
N п/п	Наименование Тем и разделов	Всего (часов)	Лекции	Семинары	Самостоятельная Работа
1.	1-7	38	38	0	23
3.	итого	38	38	0	23

^ 4.2 Номер и наименование темы в соответствии с тематическим планом лекций

№№ п/п	^ Темы лекционных занятий	Кол-во часов
1	Введение	2
2	Первый квантовый постулат – динамические переменные как операторы. Квантование физических величин	4
3	Второй квантовый постулат – описание состояния в микромире. Смешанные и чистые состояния.	6
4	Третий квантовый постулат – эволюция состояний. Представление Шредингера, Гейзенберга, принцип соответствия.	6
5	Одномерное движение, модельные задачи	8
6	Движение в центральном поле	6
7	Приближенные методы решения задач квантовой механики	6
	Итого	38

^ 4.3 План темы

Введение. Основные положения классической физики: описание состояния и закон движения, измеримость. Причины несостоятельности классического подхода в микромире. История становления квантовой механики. Математический аппарат физики микромира (обзор).

^ Первый квантовый постулат - динамические переменные как операторы. “Эффект вмешательства” процесса измерения на состояние микрообъекта. Динамическая физическая величина с учетом ее измеримости. Дискретность. Операторы физических величин. Правила фон Неймана построения операторов физических величин. Квантовые скобки Пуассона. Постоянная Планка. Перестановочные соотношения. Уравнения квантования. Координатное представление. Практический рецепт построения операторов физических величин, имеющих классический аналог. Операторы координат, импульса, момента импульса, кинетической и полной энергии. Особая роль декартовой системы координат.

^ Второй квантовый постулат - описание состояния в микромире статистическим оператором. Задание микросостояния макро обстановкой, эквивалентные состояния, квантовые ансамбли. Процесс измерения и роль средних значений результатов измерений. Среднее значение физической величины как операторно-числовой функционал, оператор состояния и его свойства. Чистые и смешанные состояния, проектор, нормированный кет-вектор и волновая функция.

^ Статистический характер квантовой теории. Средние значения и отдельные измерения, квадратичная дисперсия. Отсутствие состояний с нулевой дисперсией для всех физических величин. Смысл собственных кет-векторов операторов физических величин, одновременная измеримость, полный набор физических величин. Соотношения неопределенностей. Соотношение неопределенностей Гейзенберга для координат и импульса. Когерентные и сжатые состояния.

^ Третий квантовый постулат - уравнение Шредингера. Эволюция чистого состояния, оператор эволюции и его свойства, гамильтониан. Уравнение Шредингера. Эволюция смешанных состояний, уравнение фон Неймана. Изменение средних со временем, интегралы движения. Представление Гейзенберга и принцип соответствия. Теоремы Эренфеста. Стационарные состояния. Соотношение неопределенности энергия-время. Вычисление вероятностей результатов измерений физических величин.

^ Одномерное движение. Свободная частица, волновые пакеты, связь с когерентными состояниями. Кусочно-постоянный потенциал. Движение в однородном поле. Квазиклассическое приближение. Туннельный эффект. Гармонический осциллятор: решение в координатном представлении и в общем виде, с использованием только перестановочных соотношений.

^ Движение в центральном поле. Общая теория движения в центральном поле, разделение переменных, радиальное уравнение Шредингера. Момент и его квантование. Кулоновское поле, полное решение задачи о движении водородоподобного атома.

^ Приближенные методы решения задач квантовой механики. Вариационный метод. Оценка энергии основного состояния атома гелия. Теория возмущений для стационарных задач: поправки первого и второго порядков в случае невырожденных уровней, теория возмущений при наличии вырождения. Эффект Штарка у атома водорода. Теория возмущений для нестационарных задач. Вероятность квантовых переходов под действием возмущения.

^ 4.4 Основные понятия и категории

Волновая функция, оператор, собственные значений и собственные функций эрмитовского оператора, соотношения неопределенностей, уравнение Шредингера, Туннельный эффект, интегралы движения, уравнение Гамильтона-Якоби, гармонический осциллятор, момент импульса микрочастицы, квантование энергии, теория возмущений, квантовые переходы, коэффициенты Эйнштейна, матрицы Паули.

^ 4.5 Список литературы

Рекомендуемая литература (основная).

Блохинцев Д.И. "Основы квантовой механики" М., Наука, 1983.
Давыдов А.С. "Квантовая механика" М., Наука, 1973.
Елютин П.В., Кривченков В.Д. "Квантовая механика с задачами", М., Наука, 1976.
Ландау Л.Д., Лифшиц Е.М. "Квантовая механика", М., Наука, 1989.
Соколов А.А., Тернов И.М., Жуковский В.Ч. "Квантовая механика", М., Наука, 1979.
Галицкий В.М., Корнаков Б.М., Коган В.И. "Задачи по квантовой механике" М., Наука, 1972.

Рекомендуемая литература (дополнительная).

Бом Д., "Квантовая теория", М., Наука, 1965.
Боум А. "Квантовая механика: основы и приложения", М., Мир, 1990.
Гольдман И.И., Кривченков В.Д. "Сборник задач по квантовой механике", М., Гостехиздат, 1957.
Флюгге З. "Задачи по квантовой механике" тт. 1, 2., М., Мир, 1974.
Тернов И.М. , Жуковский В.Ч., Борисов А.В. "Квантовая механика и макроскопические эффекты", М., Изд. Моск.Унивеситета, 1993.

Рекомендуемая литература (монографическая).

Вейль Г. "Теория групп и квантовая механика" М., Мир, 1997.
Дирак П.А.М. "Принципы квантовой механики" М., Мир, 1978.
Паули В. "Принципы волновой механики" М., Гостехиздат, 1948

5 ПРОГРАММА ПРАКТИЧЕСКИХ (СЕМИНАРСКИХ),
ЛАБОРАТОРНЫХ ЗАНЯТИЙ

5.1 Тематический план практических (семинарских) занятий, лабораторных
занятий

N п/п	Наименование Тем и разделов	Всего (часов)	Аудиторные занятия		Самостоятельная Работа
N п/п	Наименование Тем и разделов	Всего (часов)	Лекции	Семинары	Самостоятельная Работа
1.	1-7	19	0	19	23
3.	итого	19	0	19	23

^ 5.2 Номер и наименование темы в соответствии с тематическим планом практических (семинарских) занятий, лабораторных занятий

№№ п/п	^ Темы практических занятий	Кол-во часов
1	2	3
1	Введение	1
2	Первый квантовый постулат – динамические переменные как операторы. Квантование физических величин	2
3	Второй квантовый постулат – описание состояния в микромире. Смешанные и чистые состояния.	3
4	Третий квантовый постулат – эволюция состояний. Представление Шредингера, Гейзенберга, принцип соответствия.	3
5	Одномерное движение, модельные задачи	4
6	Движение в центральном поле	3
7	Приближенные методы решения задач квантовой механики	3
	Итого	19

^ 5.3 План темы (вопросы для подготовки)

1. Основные положения классической физики. Закон движения и уравнение движения, начальные условия (графическое решение задачи об одномерном движении частицы массы m в произвольном поле V(x)). Измеримость и волновые пакеты (получить выражение для амплитуды волнового пакета

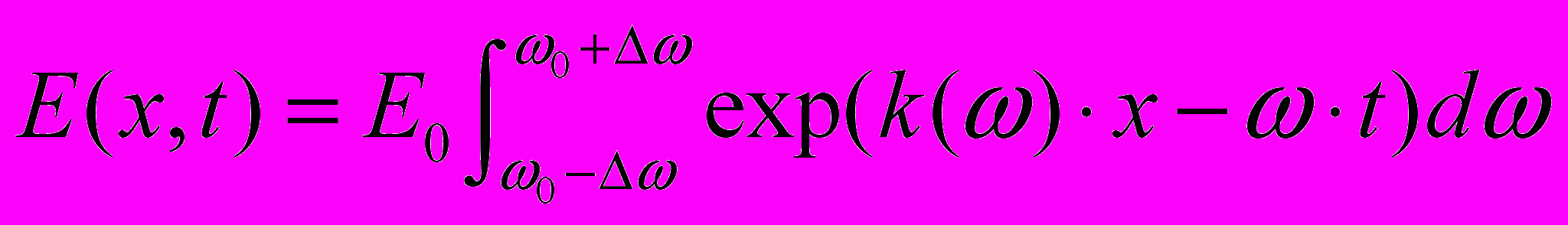и соотношения между областью локализации, временем "пребывания" в точке волнового пакета и его характеристиками (

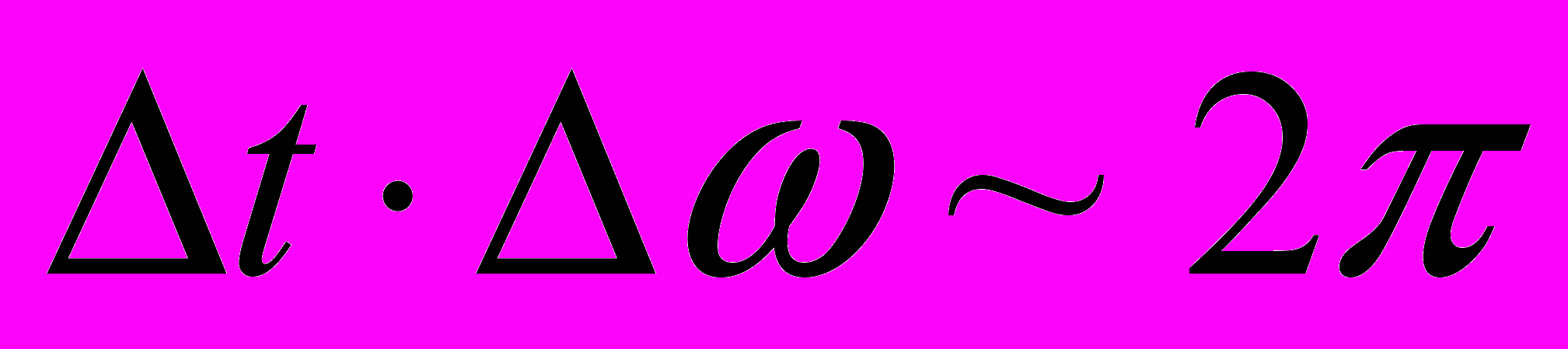)). Излучение (получить формулы спектрального распределения равновесного излучения Рэлея

и Планка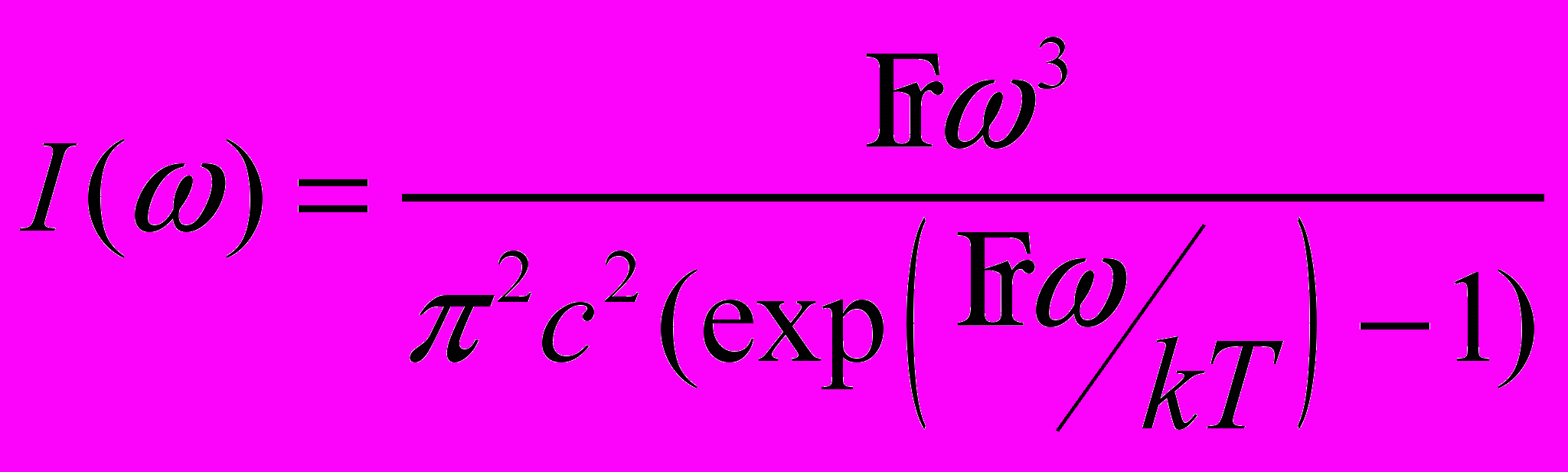

).

2. Математический аппарат квантовой теории. ([11], стр.73-75, №8-15, 23-29).

3. Квантование физических величин. ([10], №1.17-1.24, 1.32-1.34, [11], стр.76, №38,41-42).

4. Бозе-оператор, оператор числа частиц. ([13], стр.21, №6).

5. Стационарные состояния дискретного спектра. ([10], №2.1-2.5, 2.7).

6. Гармонический осциллятор. ([11], стр.76, №46-49, [10], 2.35).

7-8. Прохождение через потенциальные барьеры. ([11], стр.81-82, №103-106).

9. Радиоактивный распад. ([11], стр.82, №107).

10-11. Классические частицы в электромагнитном поле. ([10], №2.45, [11], стр.82-83, №108-112).

12-13. Момент импульса и его квантование. ([13], стр.12-16, стз.29-35).

14-15. Центрально-симметричное поле. ([10], №4.1-4.6, 4.23-4.24, 4.33).

16-17. Уравнение Шредингера. ([10], №7.1-7.3, 7.10, [11], стр.75, №37).

18. Представление Гейзенберга. ([10], №7.29-7.31, 7.33-7.36).

19-20. Атом водорода и водородоподобные ионы. (Для атома Не провести разложение уравнения Шредингера на части, связанные с движением центра масс и относительным движением электронов, [11], стр.77, №55-59).

21. Приближенные методы. Вариационный метод Ритца. ([11], стр.86, №140,142, [10], №2.29 - 2.31).

22. Приближенные методы. Стационарная теория возмущений, невырожденный спектр. ([10], №8.1, 8.3-8.5, 8.8).

23. Ангармонический осциллятор. Резонансные состояния. ([11], стр.84, №127).

24. Приближенные методы. Стационарная теория возмущений, вырожденный спектр. ([10], №8.13, [11], стр.85, №134, 132).

25-26. Приближенные методы. Нестационарная теория возмущений. Вероятности переходов. ([10], №8.23, 8.24, 8.30, 8.38, 8.39, 8.46).

^ 5.4 Основные понятия и категории

Волновая функция, оператор, собственные значений и собственные функций эрмитовского оператора, соотношения неопределенностей, уравнение Шредингера, Туннельный эффект, интегралы движения, уравнение Гамильтона-Якоби, гармонический осциллятор, момент импульса микрочастицы, квантование энергии, теория возмущений, квантовые переходы, коэффициенты Эйнштейна, матрицы Паули.

^ 5.5 Список литературы

Давыдов А.С. Квантовая механика: Учеб. Пособие. - М.: Наука, 1973. - 704с.
Блохинцев Д.И. Основы квантовой механики: Учеб. Пособие. - М.: Наука, 1976. - 664с.
Соколов А.А., Тернов И.М., Жуковский В.Ч. Квантовая механика. - М.: Наука, 1979. - 528с.
Балашов В.В., Долинов В.К. Курс квантовой механики. - М., изд-во МГУ, 1982. - 280с.
Левич В.Г., Вдовин Ю.А., Мямлин В.А. Курс теоретической физики, т.2. - М.: Наука, 1971. - 11-496 с.
Ландау Л.Д., Лифшиц Е.М. Квантовая механика (нерелятивистская теория).- М.: Наука, 1974. - 752с.
Мессиа А. Квантовая механика, т.1. - М.: Наука, 1978. - 480с.
Мессиа А. Квантовая механика, т.2. - М.: Наука, 1979. - 584с.
Фок В.А. Начала квантовой механики. - М.: Наука, 1976.- 376 с.
Галицкий В.М., Карнаков Б.М., Коган В.И. Задачи по квантовой механике. - М.: Наука, 1981. - 648 с.
Гречко Л.Г., Сугаков В.И., Томасевич О.Ф., Федорченко Ф.М. Сборник задач по теоретической физике. - М.: Высшая школа, 1984. - 320с.
Иродов И.Е. Задачи по квантовой физике. М.: Высшая школа, 1991. - 175с.

Д о п о л н и т е л ь н а я .

Кучин В.А. Основные принципы нерелятивистской квантовой теории. - Томск,

изд-во ТГУ, 1982. - 192 с.

Елютин П.В., Кривчинков В.Д. Квантовая механика. М.: Наука, 1976. - 334 с.
Дирак П.А. Принципы квантовой механики. - М.: Наука, 1979.- 480 с.
Шифф Л. Квантовая механика. - М.: Иностранная литература, 1959. - 475с.
Боум А. Квантовая механика: основы и приложения. - М.: Мир, 1990. - 720с.
Флюгге З. Задачи по квантовой механике, в 2 т. М.: Мир, 1974. Т.1-2.
Макки Дж. Лекции по математическим основам квантовой механики. М.: Иностранная литература, 1965. - 222с.

6 ПРОГРАММА САМОСТОЯТЕЛЬНОЙ РАБОТЫ

6.1 Тематический план самостоятельной работы

№№ п/п	^ Темы для самостоятельного изучения	Кол-во часов
1	Дуализм явлений микромира, дискретные свойства волн, волновые свойства частиц.	2
2	Решение стационарного уравнения Шредингера при разных потенциальных энергиях	2
3	Общие свойства одномерного движения гармонического осциллятора.	2
4	Операторы вторичного квантования.	2
5	Волновая функция электрона в водородоподобном атоме.	2
6	Теория момента импульса. Матрицы операторов момента импульса M_x, M_y_.	2
7	Спин. Принцип тождественности одинаковых частиц.	2

^ 6.2 Номер и наименование темы в соответствии с тематическим планом самостоятельной работы

В соответствии с пунктами 4.2 и 5.2.

6.3 План темы (вопросы для изучения)

Вопросы к курсу

Волновая функция, ее интерпретация, требования, налагаемые на нее. Плоская волна де-Бройля.
Понятие оператора. Линейность, эрмитовость. Операторы физических величин. Их явный вид.
Свойства собственных значений и собственных функций эрмитовского оператора.
Средние значения физических величин.
Общая теорема о соотношении неопределенностей для динамических переменных представляемых некоммутирующими операторами.
Условия одновременной измеримости динамических переменных. Понятие о полном наборе наблюдаемых.
Принцип микропричинности, уравнение Шредингера.
Уравнение непрерывности.
Стационарные состояния, их свойства.
Изменение средних значений физических величин, дифференцирование операторов по времени.
Интегралы движения, Теоремы Эренфеста.
Предельный переход от квантовых уравнений к классическим уравнениям Ньютона.
Предельный переход от уравнения Шредингера к уравнению Гамильтона-Якоби.
Частица в потенциальной яме.
Падение частицы на потенциальный барьер. Туннельный эффект.
Гармонический осциллятор: спектр энергии, собственные функции.
Гармонический осциллятор: матричные элементы координаты и импульса. Повышающий и понижающий операторы.
Координатное, импульсное, энергетическое представления для волновых функций и операторов.
Канонические преобразования.
Описание эволюции системы в представлениях Шредингера, Гайзенберга, взаимодействия.
Момент импульса микрочастицы, его свойства.
Операторы квадрата момента импульса и его проекции, их собственные значения и функции, четность состояния.
Радиальное уравнение Шредингера, анализ общих свойств решения в случаях положительной и отрицательной энергий, условия квантования энергии.
Атом водорода: собственные функции и собственные значения энергии, объяснение сериальных закономерностей в спектре.
Теория возмущений для стационарных задач, случай отсутствия вырождения, критерий применимости. Пример.
Теория возмущений в случае близко расположенных уровней или вырождения. Пример.
Теория возмущений для нестационарных задач. Вероятность квантовых переходов под действием возмущения.
Полуклассическая теория взаимодействия вещества с излучением, коэффициенты Эйнштейна, их связь с вероятностями квантовых переходов и электрооптическими параметрами системы.

^ 6.4 Основные понятия и категории

Волновая функция, оператор, собственные значений и собственные функций эрмитовского оператора, соотношения неопределенностей, уравнение Шредингера, Туннельный эффект, интегралы движения, уравнение Гамильтона-Якоби, гармонический осциллятор, момент импульса микрочастицы, квантование энергии, теория возмущений, квантовые переходы, коэффициенты Эйнштейна, матрицы Паули.

^ 6.5 Виды самостоятельной работы

Изучение теоретического материала по учебникам. Поиск нужной информации в интернете. Работа с прикладными пакетами компьютерных программ QUANT и др.

^ 6.6 Формы контроля

Проверка результатов контрольных работ. Тестирование в локальной информационной сети. Устный опрос студентов.

7 ТЕМАТИКА

^ 7.1 Контрольных работ

Основные действия с операторами вторичного квантования.

Эффект Штарка.

Работа с матрицами Паули.

7.2 Эссе, рефератов

Квантовые точки.

Квантовые компьютеры.

Сверхпроводимость – квантовое явление в макроскопических масштабах.

7.3 Курсовых работ (проектов)

Не предусмотрено учебным планом.

^

Blog

Учебно-методический комплекс по дисциплине опд. Ф. 015 Теоретическая физика: Квантовая теория индекс по гос/наименование дисциплины

Содержание

УТВЕРЖДАЮ