Реологические характеристики бетонных смесей (литературный обзор)

Вид материала

Документы

Содержание 3.Дискретной системы материальных точек случайно распределенных в непрерывной среде. В качестве уравнений формоизменения наиболее обоснованно применение линейных дифференциальных уравнений, общий вид которых Более общие зависимости дают уравнения состояния в интегральной форме Для описания объемоизменения смесей также могут применяться линейные дифференциальные уравнения с учетом двух принципиальных пол Рассмотрим теоретические и эмпирические модели цементного теста, раствора и бетона, которые приведены в литературных источниках. Исследование реологии цементных растворов авторами [17] проводилось на 3 песках с М Авторами [21] исследовано влияние цементов различной тонкости помола (2800-5500 см Список использованной литературы

Подобный материал:

• Рекомендации рк 06-2009 по устройству литых бетонных полов с применением сухих безусадочных, 326.09kb.
• 2. Технические характеристики, 53.54kb.
• «Создание предприятия по производству железо-бетонных изделий», 21.64kb.
• Оборудование для бетонных работ – обзор рынка раздел Двухроторные бетоноотделочные, 327.74kb.
• Номер и наименование программы тестирования ( 1 специалист сдает 1 тест по выбору), 289.22kb.
• Темы рефератов для поступления в аспирантуру по научной специальности 05. 20. 01 Технологии, 12.36kb.
• Методика оценки последствий аварийных взрывов топливно-воздушных смесей (рд 03-409-01), 414.51kb.
• 2. 3 Объекты и методики исследования 40 глава, 171.07kb.
• 1. Литературный обзор по вопросам исследований, 166.96kb.
• Требования к выдаче свидетельства о допуске к работам по монтажу сборных железобетонных, 33.04kb.

РЕОЛОГИЧЕСКИЕ ХАРАКТЕРИСТИКИ БЕТОННЫХ СМЕСЕЙ (ЛИТЕРАТУРНЫЙ ОБЗОР)

ссылка скрыта


 

К.т.н. Ильдар Каримов

Адрес для контакта: 450071, Россия, г.Уфа, а/я 21, Башкирский государственный аграрный университет, Кафедра теоретической и прикладной механики, Телефон/факс: (3472) 30-81-38, E-mail: dh@ufacom.ru

  

Данный литературный обзор освещает современные представления о реологических свойствах цементных бетонов.

 

Реология бетонных смесей, как и других структурированных материалов, связана с их структурой, изменяющейся в процессе твердения. В этой связи оценка реологических свойств смесей необходима в технологическом процессе производства строительных конструкций, особенно в процессе структурообразования.

Рассмотрим факторы, влияющие на реологические характеристики бетонных смесей. Разными авторами приводятся много факторов, которые по их мнению влияют на реологию бетонных смесей. Среди них можно выделить концентрацию, гранулометрию и форму частиц заполнителя; характер динамического воздействия на смесь; режим движения частиц, степень проявления тиксотропных свойств; фактор времени и другие параметры.

По мнению авторов [3], на реологические свойства бетонной смеси влияют два основных структурных фактора: величина поверхности мельчайших фракций и масса крупных заполнителей.

Авторами [6] предложена классификация факторов, влияющих на удобоукладываемость бетонной смеси, в соответствии с которой эти факторы делятся на внутренние и внешние. К внутренним относятся: текучесть цементного теста; тип заполнителя и отношение объема цементного теста к объему заполнителя. Текучесть цементного теста определяется В/Ц, типом цемента (в частности, его удельной поверхностью, содержанием С₃А, содержанием гипса, содержанием щелочей), наличием добавок. Тип заполнителя определяется максимальным размером, зерновым составом, содержанием мелких частиц (<300 мкм), пористостью. К внешним факторам относятся условия перемешивания, температура смеси и время выдержки от момента затворения (зависит от наличия ускоряющих или замедляющих добавок).

Однако авторы [18] считают, что химический и минералогический состав цемента мало влияет на реологические свойства цементного теста; исключение составляет цемент с регулируемыми сроками схватывания, который при прочих равных условиях образует цементное тесто повышенной вязкости. Отмечается, что при увеличении В/Ц вязкость цементного теста падает; такое же влияние оказывает более грубый помол цемента и перемешивание цементного теста во время гидратации.

Авторы [5] отмечают, что процессы течения, скольжения и внутреннего трения, которые имеют место в бетонной смеси в результате приложения сдвиговых деформаций обусловливаются передвижением частиц бетонной смеси относительно друг друга и во многом определяются состоянием воды, находящейся между зернами цемента и заполнителя и на их поверхности. Эту воду предлагается называть “межзерновой”. Большая роль отводится свойствам цементного теста, которые в свою очередь зависят от геометрии частиц цемента.

Согласно авторам [14] подвижность бетонной смеси определяется толщиной образующихся после затворения вокруг цементных частиц пленок воды, играющих роль своеобразной “смазки”, а также количеством цементного теста, окружающего зерна заполнителей. Зная зерновой состав твердой фазы бетонной смеси можно рассчитать объем пустого пространства, занимаемого водой, а по мере гидратации - цементным тестом, и тем самым толщину пленок воды вокруг зерен твердой фазы, играющих роль “смазки”. По мере химического связывания воды в процессе гидратации цемента уменьшается толщина указанных пленок, что наряду с заполнением пространства между зернами твердой фазы гидратными новообразованиями приводит к постепенной потере пластичности.

Авторы [16] также считают, что процесс течения бетонной смеси определяется реологическими характеристиками жидкости, находящейся между частицами твердой фазы, и трением между частицами.

Рассмотрим реологические характеристики, которыми предлагается характеризовать бетонную смесь. Согласно [5] к ним относятся: когезия (во многом определяется когезией цементного теста), вязкость (в частности, при приложении вибрационных воздействий) и внутреннее трение. Величина когезии в основном определяется количеством воды. Внутреннее трение зависит от количества и геометрии заполнителей.

Авторы [16] также считают, что реологическое поведение бетонных смесей определяется тремя фундаментальными параметрами: когезией, трением и вязкостью. Указанные величины зависят от сил, действующих в бетонной смеси. Это силы трения, капиллярные силы, силы коагуляционного структурообразования и коллоидного взаимодействия. Относительная значимость этих сил определяется размерами зерен и расстоянием между ними. Указанные силы изменяются во времени по мере того, как частицы цемента реагируют с водой. Проведенный анализ [16] показал, что для улучшения удобоукладываемости бетонной смеси необходимо уменьшать когезию, вязкость и трение в смеси. Однако чрезмерное уменьшение этих величин приводит к водоотделению и сегрегации в смеси, что влечет за собой резкое ухудшение эксплуатационных свойств бетона. Указанные недостатки могут быть частично устранены путем введения в смесь добавочного количества цемента. Однако, это может явиться причиной появления трещин в бетоне за счет повышенного тепловыделения.

Авторы [19] считают, что цементное тесто играет двоякую роль в обеспечении удобоукладываемости бетонной смеси: во-первых, отделяет частицы заполнителя друг от друга, предотвращая их взаимный контакт, во-вторых, являясь материалом с вязкими свойствами, наделяет бетонную смесь способностью к пластическим деформациям. При уменьшении количества цементного теста увеличивается интенсивность взаимодействия между твердыми частицами, что приводит к увеличению жесткости смеси. Там же отмечается, что традиционные реологические параметры, используемые для описания различных вязких систем, включая цементное тесто и раствор, не могут быть применены для бетонной смеси с крупным заполнителем. Реологические свойства таких смесей по Пауэрсу определяются следующими величинами: модулем деформации, когезионной прочностью и предельной деформативностью при срезе. Однако каждая из этих величин в отдельности полностью не определяет удобоукладываемость бетонной смеси. Так, модуль деформации уменьшается с увеличением количества цементного теста в смесях, имеющих одинаковую осадку конуса. Когезионная прочность является важнейшим фактором, определяющим удобоукладываемость, так как уменьшение ее ниже критической приводит к расслоению смеси, водоотделению и ухудшению перекачиваемости.

Как показал анализ литературных источников точной модели реологического поведения бетонных смесей в настоящее время не существует, из-за большого количества влияющих факторов.

Согласно Овчинникову П.Ф. [2] при построении реологических моделей бетонной смеси как многофазной структурированной системы, следует исходить из возможности ее представления в виде:

1.Дискретной системы физических материальных точек. Обычно в роли таких точек выступают частицы крупного заполнителя. Материальные точки могут быть свободными или связанными между собой силами. Если бетонная смесь представлена системой свободных материальных точек, то ее влияние на движение уплотняющих устройств учитывается в виде сил инерции точки, а также массовых сил веса. В случае представления бетонной смеси, связанной системой точек, к указанным выше силам добавляются упругие, вязкие и силы трения. Упругие силы описываются линейной непрерывной функцией от смещения точки, а также разрывной с конечным скачком, допускающей представление комбинацией функций Хевисайда. Вязкая сила содержит составляющую, определяемую предельным напряжением сдвига, и составляющую, зависящую от скорости, а также от смещения. Составляющая силы вязкого трения, зависящая от скорости и смещения, описывается линейной, квадратичной функцией скорости, а также разрывными функциями с бесконечным скачком типа функций Дирака. Природа вязких сил определяется возможностью смещения группы частиц, окружающих данную, как целого по отношению к соседним группам. Природа сил трения (сухого) определяется возможностью смещения данной частицы по отношению к соседним, то есть обычным скольжением частицы. Силу сухого трения можно описать функцией от нормальной силы. Если эту функцию разложить в ряд Маклорена по нормальной силе, то первое слагаемое будет представлять силу сцепления, которую в первом приближении можно представить капиллярными силами. Последнее существенно, так как это позволяет учесть влияние размера частиц заполнителя. Описанное равносильно представлению дискретной системы динамическими моделями реологических тел Гука, Ньютона, Кельвина, Сен-Венана, Шведова, Максвелла. Движение бетонной смеси будет описываться системой конечного числа дифференциальных уравнений второго порядка.

2.Непрерывной среды. Все деформационные процессы, происходящие в таких средах, описываются известными уравнениями механики сплошной среды, полученными из второго закона Ньютона, примененного к бесконечно малому элементу среды. Однако число неизвестных, входящих в них, более числа уравнений. Поэтому приходится отыскивать дополнительные условия, обеспечивающие их замыкание. Эти условия получили название реологических уравнений. Условия замыкания могут быть получены из эксперимента. Так появились экспериментальные кривые зависимости напряжения от скорости однородного сдвига (реологические кривые), а может быть и времени. Реологические уравнения по отношению к неизвестным напряжениям и деформациям, а также их производным являются нелинейными. Последние можно линеаризовать, получив обобщенные линейные относительно напряжений, деформаций и их производных реологические уравнения. Аналогично можно учесть и нелинейные эффекты, сохранив неизменными по форме реологические уравнения, если при этом соответствующие коэффициенты считать функциями от принятых переменных.

^ 3.Дискретной системы материальных точек случайно распределенных в непрерывной среде.

В этом случае реологические уравнения будут представлены простейшими реологическими телами, а также уравнениями смешанной структурированной системы.

Дифференциальные уравнения движения бетонной смеси будут состоять из системы обыкновенных дифференциальных уравнений с конечным числом неизвестных функций, уравнений сплошной среды и реологических уравнений [2].

 Гирштель Г.Б. в работе [1] излагает основные принципы математического моделирования в реологии бетонных смесей. Согласно [1] cвойства каждой среды описываются двумя реологическими уравнениями состояния: объемо- и формоизменения. Эти уравнения и входящие в них параметры позволяют описать напряженно-деформированное состояние среды в общем случае.

^ В качестве уравнений формоизменения наиболее обоснованно применение линейных дифференциальных уравнений, общий вид которых

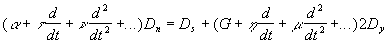, (1)

где , , , D_s, G, ,  - реологические параметры; D_n, D_y - девиаторы напряжений и деформаций; d/dt - оператор производной по времени.

Частными случаями уравнения (1) являются уравнения Гука, Ньютона, Максвелла, Бюргерса, Бингама, Джефриса и др. Порядок уравнений равен числу вязких элементов модели. Если в модели отсутствует непрерывная упругая связь, то в уравнение не входит деформация, а есть только ее производные.

Некоторое улучшение сходимости экспериментальных и теоретических данных могут дать дифференциальные уравнения в обобщенной форме, в которых периоды ретардации и релаксации заменены функциями распределения этих величин.

^ Более общие зависимости дают уравнения состояния в интегральной форме

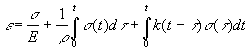, (2)

где  - деформация;  - напряжение; Е,  - мгновенный модуль и модуль пластической деформации (для ньютоновской жидкости  =t_релЕ).

В уравнение (2) почленно входят: мгновенная, пластическая и деформация последействия. Интегральные уравнения дают лучшую сходимость только для деформации последействия; так как процессы деформации смесей весьма скоротечны, а применение интегральных уравнений существенно усложняет решение задач, их использование в реологии смесей, очевидно нецелесообразно.

^ Для описания объемоизменения смесей также могут применяться линейные дифференциальные уравнения с учетом двух принципиальных положений:

- в уравнение должна в обязательном порядке входить деформация, а не только ее производные. Это значит, что при сколь угодно большем изотропном давлении деформации имеют конечные значения. Исходя В уравнение должна в обязательном порядке входить из этого, для описания объемоизменения могут быть использованы уравнения Гука, Кельвина-Фойгта, Френкеля и нельзя применять уравнения Ньютона, Сен-Венана, Бингама-Шведова, Бюргерса и Джефриса;

- объемоизменение носит линейный характер и линейные дифференциальные уравнения могут применяться только в узких диапазонах напряжений и деформаций, когда использование усредненных параметров не приводит к существенным для рассматриваемой задачи погрешностям [1].

^ Рассмотрим теоретические и эмпирические модели цементного теста, раствора и бетона, которые приведены в литературных источниках.

Авторами [7] предложена реологическая теория цементного раствора, рассматривающая раствор как ньютоновскую жидкость. При рассмотрении реологического поведения раствора принималось, что в начальный период после затворения влиянием гидратации на изменение реологических свойств можно пренебречь, а основной причиной изменения вязкости является флокуляция частиц.

В [15] описана структурная модель цементного теста, которая позволяет объяснить вязкопластичное и тиксотропное поведение бетонной смеси, подверженной вибрационному воздействию, в зависимости от концентрации цемента и его удельной поверхности. В предлагаемой модели два соседних зерна цемента удерживаются в состоянии равновесия, с одной стороны, электростатическими силами притяжения, а с другой - расклинивающим давлением по Дерягину. Отмечается, что цементное тесто ведет себя при приложении сдвиговых нагрузок как идеальная жидкость, и понятие “тиксотропия” не может быть применено к нему, так как предполагает полную обратимость свойств после окончания воздействия.

Авторами [9] принята модель цементного теста как концентрированной суспензии, состоящей из конгломерированных частиц сферической формы (флокул) и выведено уравнение для расчета вязкости цементного теста:

_r=1+3/(1/X+1/0,52), (3)

где _r- относительная вязкость цементного теста, X - кажущаяся объемная концентрация флокул.

В работе [10] приводятся результаты экспериментально-теоретических исследований вязкости бетонной смеси. Бетонная смесь рассматривается как высококонцентрированная суспензия. Вязкость смеси оценивается по формуле:

_r=1+dS_r/(1/X_v-1/X_vc)/2, (4)

где _r - относительная вязкость; d - средний диаметр частиц заполнителя; S_r - удельная поверхность заполнителя; X_v и X_vc - объемная концентрация и максимальная объемная концентрация заполнителя соответственно.

Экспериментальным и расчетным путем показано, что величина относительной вязкости смеси с увеличением объемного содержания заполнителя растет. Фактические данные совпадают с расчетными в интервале изменения величины максимальной объемной концентрации заполнителя 0,56-0,67.

^ Исследование реологии цементных растворов авторами [17] проводилось на 3 песках с М_кр=2,10; 2,66 и 3,22. Растворная смесь рассматривалась как бентамовское тело. Эффективная объемная концентрация песка (V_se) принималась равной геометрической объемной концентрации песка с добавлением объема адгезионного слоя цементного теста толщиной 10 мкм. Предельное напряжение сдвига _y (Па) выражалось зависимостью:

 _y=5,49 10^-18exp[(85,2-101V_se)V_c+61,9V_se], (5)

где V_c - объемная концентрация цемента в цементном тесте.

В тех же обозначениях пластическая вязкость _pl (Пас) описывалась выражением:

 _pl=9,84 10^-23exp[(98,9-115V_se)V_c+71,7V_se] (6)

Авторами [11], по результатам исследования реологических характеристик раствора и бетона на ротационном вискозиметре получено эмпирическое уравнение

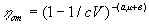, (7)

где _от - относительная вязкость; с - фактический объем твердых частиц; V - объемная концентрация твердых частиц;  - модуль крупности твердых частиц; а, в - постоянные (для раствора а=-0,57, в=3,40, для бетона а=-0,89, в=9,31). Использование данного уравнения для расчета пластической вязкости раствора и бетона показало небольшое расхождение между расчетными значениями и экспериментальными данными; для раствора их соотношение равно 0,81-1,28, для бетона 0,78-1,15. Было также определено уравнение для динамического напряжения сдвига  :

 =A logSL+B, (8)

где SL - осадка конуса в см; А и В для раствора равно -2,71 и 3,36, для бетона А=-4,83, В=7,29.

^ Авторами [21] исследовано влияние цементов различной тонкости помола (2800-5500 см²/г) и различного химического состава на текучесть и седиментационные свойства цементных суспензий, изготовленных при различных значениях величины В/Ц от 0,5 до 2,0. Текучесть цементных суспензий, выраженная через ее вязкость (_d), связана с величиной В/Ц (W), водопотребностью цемента (W_a), определенной по нормам DIN 1164, и удельной поверхностью (O_spez) уравнением:

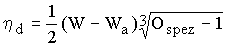. (9)

Влияние химико-минералогического состава цемента на текучесть цементной суспензии проявляется только через влияние на текучесть водопотребности цемента. Доля воды, влияющая непосредственно на текучесть цементных суспензий, определяется разностью между величиной W и W_a. С увеличением тонкости помола цемента при постоянной величине В/Ц текучесть цемента уменьшается, поскольку вязкость увеличивается. Бингамовский предел текучести цементных суспензий не удалось однозначно выразить определенной функцией. Стабильность цементных суспензий с В/Ц=0,6-2,0 можно достаточно точно описать функцией величины В/Ц, зернового состава цемента и содержания в цементе SiO₂. Особое влияние на седиментационные свойства суспензий оказывает фракция с размером зерен  8 мкм. С возрастанием доли этой фракции склонность суспензий к седиментации уменьшается.

Авторами [13] показана целесообразность использования для оценки консистенции бетонных смесей эмпирических уравнений, в которые входят такие факторы, определяющие консистенцию как абсолютный объем цементного теста, количество цементного теста, отнесенное к поверхности заполнителя, отношение количества песка к общему количеству заполнителя. На основании проведенных экспериментов предложено уравнение следующего вида:

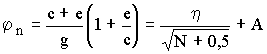, (10)

где 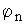- показатель консистенции; с - количество цемента; e- количество воды; g - количество заполнителя; N - жесткость смеси по Вебе в с; 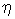и А - эмпирические коэффициенты. Показано, что показатель консистенции 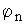не зависит от способа измерения консистенции.

Авторами [8] изучены реологические свойства цементного теста при действии сдвигающего усилия. исследования показали, что цементное тесто имеет существенно нелинейную реологическую кривую и не подчиняется закону Бингама. В ограниченном диапазоне В/Ц напряжение сдвига () связано с его предельным значением (_s) и скоростью сдвига (q) соотношением =_s+Kqⁿ, где K и n - константы. Используя модель Robertson и Stiff, получено выражение, связывающее напряжение сдвига с В/Ц (W):

 =(kW+l) q+(mW+p)(r/W+sl-W), (11)

где k,l,m,p,r - константы.

Авторами [4] предложена новая модель тиксотропного поведения цементного теста, базирующаяся на предположении о непостоянстве связей в процессе формирования структуры. Эксперименты, проведенные на ротационном вискозиметре при постоянной скорости сдвига (D), позволили получить зависимость напряжения сдвига () от времени (t) вида:

 =_e+(_m-_e)exp(-B_t-B_T(1-e^-t/T)), (12)

где _m - начальное максимальное напряжение сдвига при t=0, _е - равновесное напряжение сдвига при t= , B_ , и Т - константы.

Согласно [20] сопротивление сдвигу цементного раствора может рассматриваться аналогично поведению частично насыщенного связанного грунта. Сопротивление сдвигу (_r) связано с когезией (с), эффективным нормальным давлением () и коэффициентом внутреннего трения (tg) соотношением _r=C+tg. Для полностью уплотненного раствора справедлив закон Кулона-Терцали, согласно которому в уравнении сопротивления сдвигу  =-U_w, где U_w - давление жидкой фазы. При отсутствии давления можно определить когезию по предельному моменту сдвига при повороте лопаток крестообразной формы, погруженных в смесь, находящуюся в большом сосуде (M_r):

C=M_r/(2 r²(l+2/3r)), (13)

где r - радиус лопаток.

Исследование сопротивления сдвигу и когезии проводилось на растворах, приготовленных на стандартном песке и трех марках портландцемента. Раствор имел состав 1:3 и В/Ц=0,3-0,6. Скорость сдвига во всех опытах была постоянной, равной 0,1⁰/c. С увеличением удельной поверхности цемента при равном критическом водосодержании уменьшалась толщина водной пленки, что увеличивало силы взаимодействия между частицами и повышало когезию.

Авторами работы [12] рассмотрена модель растворной и бетонной смеси в виде вязкой жидкости (цементное тесто) с распределенными в ней заполнителями. Количество цементного теста на единицу объема заполнителей, необходимое для получения смеси с заданной удобоукладываемостью (A₀), называют функцией потребности и обозначают _s для мелкого заполнителя (крупность до 2 мм) и _g для крупного. Модуль поверхности заполнителя можно вычислять по Пауэрсу с использованием множителя 1 для фракции 0-0,125 мм, 0,5- для фракции 0,125-0,25 мм и т.д. Из уравнения абсолютных объемов было получено выражение

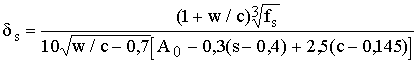, (14)

где w, c и s - абсолютные объемы воды, цемента и песка в долях единицы, f_s - модуль поверхности песка.

Жесткость бетонной смеси по Вебеметру (H_f) связана с жесткостью цементного раствора (H_z) соотношением

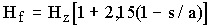, (15)

где а - общий объем заполнителей. Для крупного заполнителя с учетом его наибольшей крупности D_max и модуля поверхности f_g было получено выражение

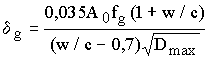, (16)

Проверка формул для 220 составов бетона с крупностью заполнителя до 20 мм и тремя типами песка дала среднюю ошибку 1,3% при отклонениях от -4% до +4%.

 

^ СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ

1. Гирштель Г.Б. Принципы математического моделирования в реологии бетонных смесей. Principles of mathematical modelling in rheology of concrete mixes. //Реология бетонных смесей и ее технологические задачи: Тез. докл. III Всес. симпоз. -Рига: РПИ, 1979. -С.5-7.
   
2. Овчинников П.Ф. Реологические модели бетонной смеси с учетом уплотняющих устройств. Rheological models of a concrete mix in view of packing devices. //Реология бетонных смесей и ее технологические задачи: Тез. докл. III Всес. симпоз. -Рига: РПИ, 1979. -С.8-10.
   
3. Смирнов А.В. К вопросу о взаимосвязи реологических характеристик и технологических параметров бетонных смесей. To a question on interrelation of the rheological characteristics and technological parameters of concrete mixes. /Куйбыш. фил. Всес. ин-та по проектир. орг. энерг. стр-ва. -Куйбышев: 1989. -7 с.
   
4. Atzeni Crillo, Maseldda Lurgi, Sanna Ulrico. Model for the Thixotropic Behavior of Cement Pastes. Модель тиксотропного поведения цементного теста //Ind. and Eng. Chem. Prod. Res. and Dev. -1986. -№3. -pp.499-504.
   
5. Bombled J.B. Rheologie du beton frais. Реологические свойства бетонной смеси. //Cim. beton, platres, chaux. -1978. -№1. -pp.27-29.
   
6. Collepardi M. The Influence of Admixtures on Concrete Rheological Properties. Влияние добавок на реологические свойства бетона //Cemento. -1982. -№4. -pp.217-242.
   
7. Hattori Kenichi, Izumi Koichi. The new rheological theory of cement mortar. Новая реологическая теория цементного раствора. //Дзайрё = J. Soc. Mater. Sci., Jap. -1983. -№356. -pp.461-470.
   
8. Jones T.E.R., Taylor S. A Mathematical Model Relating the Flow Curve of a Cement Paste to its water/cement ratio. Математическая модель зависимости кривой течения цементного теста от В/Ц. //Mag. Concr. Res. -1977. -№101. -pp.207-212.
   
9. Kakuta S., Akashi T. Evaluation of Viscosity of Cement Paste. Оценка вязкости цементного теста. //Rev. 32^nd Gen. Meet. Cem. Assoc. Jap. Techn. Sess., Tokyo, 1978, Synopses. -Tokyo. -1978. -pp.53-54.
   
10. Kakuta S., Fujii M., Akashi T. Evaluation of Viscosity of Fresh Concrete. Оценка вязкости бетонной смеси. //Rev. 33^nd Gen. Meet. Cem. Assoc. Jap. Techn. Sess., Tokyo, 1979, Synopses. -Tokyo. -1979. -pp.129-131.
    
11. Kikukawa H. Investigation of the viscosity equation of mortar and concrete. Исследование уравнения вязкости раствора и бетона. //Добоку гаккай ромбунсю = Proc. JSCE. -1990. -№414. -pp.109-118.
    
12. Kopycinsky Br. Formula Describing the Dependence of the Consistence of Cement Mortars and Concrete Mixes on their Composition. Формула, описывающая зависимость удобоукладываемости цементных растворных и бетонных смесей от их состава. //Bull. Pol. Acad. Sci.: Techn. Sci. -1985. -№3-4. -pp.155-163.
    
13. Kopycinsky B. Recherches sur la Consistance du Beton et l’application des Resultats. Исследование консистенции бетонных смесей. //Mater. Constr. -1979. -№71. -pp.359-366.
    
14. Krell Jorgen. Die Konsistenz von Zementleim, Mortel und Beton und ihre Zeitliche Veronderung. Консистенция цементного теста, раствора и бетона и ее изменение во времени. //Steinbruch und Sandgrube. -1986. -№12. -pp.680-681.
    
15. Legrand C. L’etat floculent des Pastes de Ciment avant Prise et Ses Consequences sur le Comportement Rheologique. Коагуляция частиц в цементном тесте и ее влияние на реологические свойства. //Cah. Groupe franc. rheol., 1981, num. spec.: Comport. rheol. et struct. mater. 15 eme Collog. Annu., Paris. -1981. -pp.129-136.
    
16. Massazza F., Costa U. Rheological Problems Related to the use of Cement. Реологические проблемы цементных бетонов. //Cemento. -1982. -№4. -pp.217-242.
    
17. Mizuguchi H., Ohyama R. Relation between Rheological Constants of Fresh Mortar and Grading of Fine Aggregate. Зависимость между реологическими константами растворной смеси и гранулометрией песка. //Rev. 35^nd Gen. Meet. Cem. Assoc. Jap. Techn. Sess., Tokyo, 1981, Synops. -Tokyo. -1981. -pp.80-82.
    
18. Odler I., Becker T., Weiss B. Rheological Properties of Cement Pastes. Реологические свойства цементного теста. //Cemento. -1978. -№3. -pp.303-310.
    
19. Popovics S. Effect of structure and Composition on the Rheology of Fresh Concrete. Влияние состава и структуры бетонной смеси на ее реологические характеристики. //13 Szilikatip. es szilikattud. konf., Budapest, Jun.1-5, 1981, Vol.2. -Budapest. -1981. -pp.140-145.
    
20. Rajgelj S. Cohesion Aspects in Rheological Behaviour of Fresh Cement Mortars. Когезия и реологические свойства цементного раствора. //Mater. et constr. -1985. -№104. -pp.109-114.
    
21. Rendchen K. Einflub Verschiedener Zemente auf das Fliebverhalten und die Stabilitat von Zementsuspensionen. Влияние различных цементов на текучесть и стабильность цементных суспензий. //Betontechn. Ber. -1976. -pp.123-133.
    

Публикация обзора без ссылки на автора запрещена.

 

Уважаемые коллеги

 Предлагаю Вам подборки статей по основным проблемам бетоноведения. Пожалуйста укажите публикации по указанным проблемам, которые не вошли в данный обзор по e-mail dh@ufacom.ru

 Напишу рецензию на Вашу статью, доклад, диссертацию по исследованию бетона.

 Дам рекомендации по основным направлениям исследований в механике бетона.

 Переведу на английский язык и окажу содействие в публикации Ваших работ в ведущих зарубежных изданиях.

Искренне желаю Вам успехов в дальнейшем развитии и совершенствовании новых бетонных составов и технологий и надеюсь на плодотворное сотрудничество.

 

С уважением,

Ильдар Каримов