Контрольное задание №1 Прогнозирование событий Цель лабораторной работы
| Вид материала | Документы |
- Задание для лабораторной работы Ввести в базу данных системы Monitor crm товары, менеджеров, 1563.17kb.
- Контрольное задание Тематика и методические указания к его выполнению для студентов, 75.93kb.
- Контрольное задание представляет собой реферативное исследование возможностей автоматизации, 82.16kb.
- Методические указания по выполнению контрольного задания контрольное задание по темам, 515.04kb.
- Методические указания к выполнению контрольного задания в форме реферата Контрольное, 272.86kb.
- Задание для выполнения лабораторной работы №1 средствами ms word, 50.12kb.
- Задание: занести в рабочую тетрадь: название и цель лабораторной работы, 330kb.
- Контрольное задание по цсп. Задание №27, 38.81kb.
- Задание на лабораторную работу по дисциплине, 699.22kb.
- Методические указания к лабораторной работе по исследованию статических характеристик, 104.56kb.

Контрольное задание № 1
Прогнозирование событий
Цель лабораторной работы: Освоить способы прогнозирования событий методом регрессионного анализа.
1. Задание для контрольного задания:
Провести регрессионный анализ статистических данных, представляющих взаимозависимость двух переменных, в целях определения прогнозируемых значений зависимой переменной.
^
2. Порядок выполнения контрольного задания:
- Изучите разделы методического указания.
- Составьте таблицу статистических данных по профилю своей работы (аналогично таблицы 1) для выполнения данной работы.
- Постройте точечную диаграмму для заданного ряда данных и добавьте линию тренда, характеризуемую линейным и нелинейным уравнениями (на отдельных диаграммах). Интерпретируйте полученные результаты. Определите прогнозируемые значения для нескольких точек независимой переменной. Сравните прогнозируемые данные.
- Проведите анализ связи переменных заданного ряда данных, используя инструмент анализа - функцию «Регрессия», при аппроксимации связи переменных линейным и нелинейным уравнениями. Интерпретируйте полученные результаты. Определите прогнозируемые значения для нескольких точек независимой переменной.
- Сравните результаты прогнозирования, полученные в пунктах 3, 4 настоящего задания, и сделайте вывод о лучшем способе прогнозирования для исследуемых данных.
3. Методические указания
3.1 Введение
Руководители разного ранга ежедневно сталкиваются с задачами, решение которых требует анализа имеющейся накопленной информации, в частности, для прогнозирования событий.
Прогнозирование всегда явно или неявно основывается на наборе данных. При этом следует иметь в виду, что, если используемые данные будут необъективны, неоднозначны или будут характеризоваться другими неточностями или погрешностями, то никакие самые изощренные методы не смогут компенсировать эти недостатки, и результаты анализа будут совершенно неадекватны существующей ситуации.
На практике при анализе каких-либо явлений обнаруживаются связи между несколькими различными параметрами (факторами). Например, заработная плата служащего зависит от его образования, места работы, объема выпускаемой предприятием продукции и т.д. Однако существуют определенные связи и между двумя параметрами, выделенными из списка взаимосвязанных параметров. Например, заработная плата служащего зависит от его образования. Поэтому часто проводят анализ зависимостей двух параметров.
В математических методах анализа существуют два базовых инструмента, с помощью которых анализируются взаимосвязи параметров. С помощью корреляционного анализа оценивается степень взаимосвязи параметров, а регрессионный анализ показывает, как можно предсказать поведение параметров (переменных), т.е. имеется возможность анализировать, как изменение одного параметра влияет на изменение другого.
Мера связи двух параметров определяется коэффициентом корреляции. Для его расчета имеется соответствующая методика, а в MS Excel имеется соответствующая функция. Коэффициент корреляции принимает значения в интервале -1
Регрессионный анализ представляет собой следующий этап статистического анализа и позволяет предсказать значения случайной величины на основании значений одной или нескольких независимых случайных величин. Поскольку здесь фигурируют взаимосвязи величин, то логично, что эти связи хорошо описываются аналитическими уравнениями и графически их можно отобразить в виде линий. Эти уравнения в регрессионном анализе называются уравнениями регрессии, а линии – линиями регрессии. Линия регрессии переменной Y, зависящей от независимой переменной X, является статистическим построением, которое представляет линию наибольшего "соответствия" данным. Для нахождения оптимального прохождения линии на графикеГРАФИК
-1) расписание, определяющее последовательность выполнения действий, протекания событий во време... регрессионного анализа в MS Excel используется методМЕТОД
- способ исследования явлений природы и общественной жизни, а в узком смысле - прием, способ или... наименьших квадратов1.
Регрессионный анализ может исследовать связи, как между двумя факторами, так и между несколькими. В последнем случае анализ носит название – многофакторный.
Наиболее важным параметром регрессионного анализа является коэффициент регрессии (коэффициент детерминации) - R2. Для линейной зависимости он равен квадрату коэффициента корреляции. Этот коэффициент дает количественную оценку меры анализируемой связи и изменяется от 0 до 1. Коэффициент детерминации показывает, насколько точно найденная функция регрессии описывает связь между исходными значениями факторов X и Y. Чем ближе R2 к 1, тем в большей степени уравнение регрессии объясняет изучаемый фактор.
Для проведения статистического анализа разработано ряд программных продуктов, среди которых, например, широко известны программные пакеты Statistica и Stadia. Но на практике они, к сожалению, не всегда доступны рядовому пользователю, а в то же время многие из задач статистического анализа можно достаточно успешно и просто решать, используя широко известный и распространённый MS Excel.
В MS Excel могут использовать следующие формы уравнений для описания взаимодействия параметров (факторов) исследуемого процесса:
Линейный - уравнение имеет вид: Y = a + bX;
логарифмический - Y = a + Ln(X);
степенной (показательный) - Y = a * Xb;
полиноминальный - Y = a + b1 X + b2 X2 + …+ bn Xn;
экспоненциальный - Y = ebx
Методика исследования закономерностей взаимодействия параметров может иметь варианты. Для целей прогнозирования наиболее приемлемой и достаточно доступной (по нашему мнению) технологией проведения регрессионного анализа с помощью MS Ехсеl является следующая:
___________________________________________
1 Метод наименьших квадратов - статистический метод определения параметров совокупности путем минимизации суммы квадратов (иногда средней суммы квадратов) отклонений между фактическими и расчетными данными.
(Yi—Y(Xі))2=min.
Yi -действительно наблюдаемые значения,
Y(Xі) - значения, которые получаются из уравнения регрессии.
- Формируется массив статистических данных исследуемых параметров по определенным интервалам.
- Строится точечная диаграмма, которая отражает связь исходных данных. К точечной диаграмме добавляется линия тренда с аппроксимирующим её уравнением.
- Проводится анализ с использованием функции «Регрессия».
- На основании результатов, полученных в пунктах 2 и 3, принимается решение о типе зависимости, которую можно использовать для прогноза с определенной доверительной вероятностью.
- Определяются необходимые данные прогноза.
^ 3.2 Прогнозирование с использованием
линии тренда
Рассмотрим технологию проведения регрессионного анализа с помощью MS Ехсеl на конкретных примерах.
Для получения прогноза наиболее наглядный способ исследования связи между двумя переменными базируется на использовании линии тренда. В качестве примера проведем анализ связи стоимости и площади объектов недвижимости. Исходные данные приведены в таблице 1.
Таблица 1
-
Площадь, м2
Цена, у.е.
52
26
66
31
69
37
74
34
78
39
82
38
88
39
92
31
96
37
101
38
104
43
106
44
^ Первым шагом является построение точечной диаграммы. Здесь и в дальнейшей работе принимается во внимание, что в MS Excel зависимую переменную называют Y-переменной, а независимую переменную называют Х-переменной.
Введите данные таблицы 1 на листе MS Excel. Выделите область данных без меток (заголовков), войдите в пункт меню «Вставка», затем «Диаграмма». Выберите – «Точечная диаграмма». Далее можно уточнить диапазон исходных данных для диаграммы и в пункте меню «Ряд» можно указать распределение столбцов (строк) по осям ординат. Затем укажите название диаграммы, двух её осей, место расположения диаграммы и легенду (название). При желании имеется возможность установить подписи для каждой точки диаграммы.
^ Следующий шаг - добавление линии тренда к точечной диаграмме и форматирование результатов:
- Выделите точки на диаграмме (щелкните на какой-либо точке данных) и в пункте меню «Диаграмма» (этот пункт появляется в главном меню, когда активизировано окно диаграммы) выберите «Добавить линию тренда» (такие линии часто также называют линиями среднего соотношения).
- В появившемся окне «Линия тренда» выберите тип линии, который будет соответствовать точечной диаграмме.
Для прогнозирования данных в нашем примере можем использовать различные типы линий тренда.
^ Линейный тренд. После построения точечной диаграммы (рис. 1.1) можно предположить, что линия тренда может быть линейная. Исследуем этот тип.
В окне «Линия тренда» выделите «Линейная». Щелкните по вкладке «Параметры» и включите опции: «Показывать уравнение на диаграмме» и «Поместить на диаграмму величину достоверности аппроксимации (R^2)». Убедитесь, что пункт «Пересечение кривой с осью Y в точке:» не отмечен. Нажмите OK. Результат представлен на рис. 1.1.
^ Имеется ряд возможностей редактирования диаграммы:
- изменить шрифт текста и получить большее количество десятичных знаков в формуле (дважды щелкните по области, где расположено уравнение, и в окне «Формат подписей данных» выполните необходимые действия).
- переместить и ввести дополнительный текст в область, где расположено уравнение (выделите эту область).
- установить параметры шкал осей, их вид и шрифт цифр (щелкните по оси графика, затем щелкните правой кнопкой на маркере и воспользуйтесь пунктами контекстного меню).
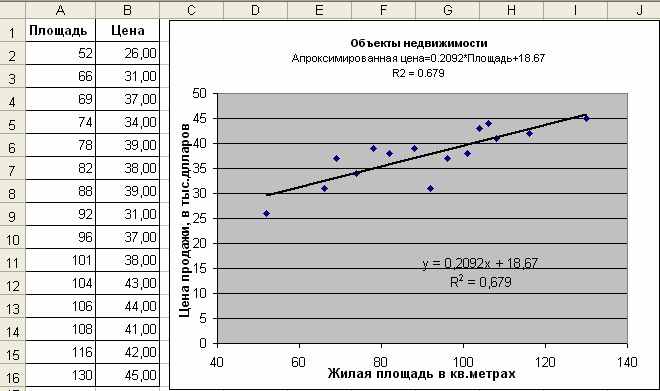
Рис.1.1
^ Интерпретация полученных результатов
Уравнение аппроксимации Y= 0,2092х + 18,67 можно переписать в виде: Предсказанная цена = 18,67 + 0,2092* Площадь.
Величина смещения по Y или постоянного члена в уравнении равна 18,67 и измеряется в тех же единицах, что и переменная Y. Величина 0,2092 является мерой наклона линии регрессии. Она показывает среднее изменение переменной Y при единичном изменении переменной X. Одним из самых распространенных способов ответить на вопрос «Насколько хорошо приближение» является исследование значения коэффициента детерминации (R2). Здесь значение R2 равно 0,679 и показывает, что примерно 68% колебаний стоимости от жилой площади может быть выражено линейной моделью. Возможно, остальные 32% колебаний могут быть выражены через другие параметры объектов в регрессионной модели с многими параметрами.
Для определения величины прогнозируемой цены «вперед» или «назад» выполните следующее.
Активизируйте область построения диаграммы или выделите точки на диаграмме. В пункте меню «Диаграмма» (этот пункт появляется в главном меню, когда активизировано окно диаграммы) выберите «Добавить линию тренда» или тот же пункт выберите в контекстном меню, щелкнув правой кнопкой по любой точке диаграммы. В появившемся окне «Линия тренда» выделите пункт «Параметры», в окне которого укажите задание на прогнозирование цены объекта недвижимости. Прогнозируемая величина появится на диаграмме.
^ Далее рассмотрим нелинейный тип линии тренда.
По изложенной выше методике постройте точечную диаграмму по данным таблицы 1. Затем при добавлении линии тренда в окне «Линия тренда» выберите, допустим, тип - «Логарифмическая». При этом следует иметь в виду, что свойства алгоритма предписывают, чтобы значения независимой переменной были положительными. Если же среди значений X имеются нулевые или отрицательные значения, то при добавлении линии тренда пиктограмма «Логарифмическая» на вкладке «Линия тренда» будет недоступна. Чтобы обойти это ограничение, можно добавить какое-либо число ко всем X.
Результаты построения точечной диаграммы и добавления логарифмической линии тренда приведены на рис. 1.2.
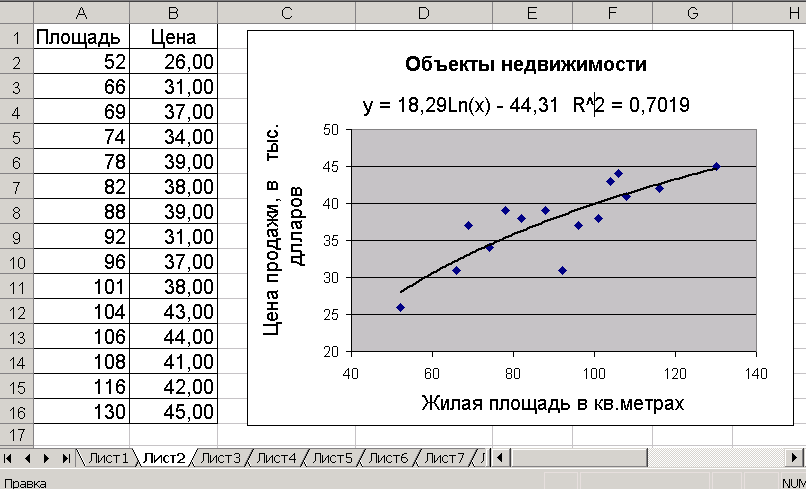
Рис. 1.2
В данном примере значение R2 равно 0.7019, это лучше результатов линейного моделирования.
^ 3.3 Анализ статистических данных с помощью
функции «Регрессия»
При необходимости выполнить более полный и точный расчет, включая вычисление остатков, стандартных ошибок, дисперсионный анализ и др. можно использовать функцию «Регрессия». Эта функция анализирует отношения переменных, связанных линейной зависимостью: Y=а+bX. Функция «Регрессия» входит в пакет «Анализ данных». Если же на Вашем компьютере пункт «Анализ данных» в меню «Сервис» отсутствует, то в меню «Сервис» - «Надстройки» выделите пункт «Пакет анализа» и щелкните ОК. После этого будет выполнена загрузка пакета из дистрибутива и подключение его к MS Excel.
Следуйте следующим инструкциям по использованию инструмента анализа «Регрессия»:
- Расположите данные на листе MS Excel, как и ранее, по столбцам: переменная X слева, переменная Y справа. Освободите место для результатов регрессионного анализа справа от данных, по крайней мере, 16 столбцов.
- Выберите функцию «Регрессия» и нажмите ОК. Появится диалоговое окно (рис. 1.3), в которое введите ссылки на интервалы значений Y и X. Если в диапазон включаются заголовки столбцов, то отметить пункт «Метки».
- Опция «Константа – ноль» включается для прохождения линии регрессии через начало координат.
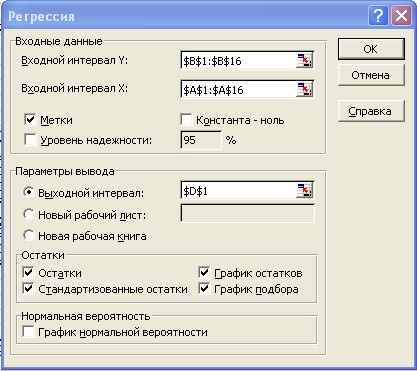
Рис. 1.3
3. «Выходной интервал» - область, где будут располагаться итоговые результаты и диаграммы. В этом поле достаточно ввести ссылку на левый верхний угол области шириной в 16 столбцов.
- Флажок «Остатки» устанавливается, если требуется включить столбцы с предсказанными значениями Y и остатками. Остатки – это разница между статистическими данными и предсказанными.
- Флажки: «График остатков» - выводятся точечные графики зависимости остатков от значений Xi; «График подбора» для вывода точечных графиков теоретических и статистических значений Yi; «График нормальной вероятности» (график вероятности нормального распределения) – зависимость Yi от автоматически формируемых интервалов персентелей1.
Ниже приведены примеры использования функции «Регрессия» для линейной и нелинейной зависимости исходных данных.
Результаты анализа для линейной зависимости представлены на рис. 1.4, где:
- Множественный R — коэффициент корреляции R;
- R-квадрат — коэффициент детерминации R2;
- Нормированный R - квадрат — нормированное значение коэффициента детерминации2;
- Стандартная ошибка - стандартная ошибка оценки 3;
- Наблюдения — это число исходных наблюдений (n).
Результаты дисперсионного4 анализа используются для проверки значимости коэффициента детерминации.
Здесь:
- df - число степеней свободы. Для строки «Регрессия» – число переменных (количество факторных признаков – m).
- SS - сумма квадратов отклонений. Для строки «Регрессия» - сумма квадратов отклонений теоретических данных от среднего ( (Yi—Y(Xі))2 ),
-------------------------------------
1 Это характеристика набора данных, которые выражают ранги (значения) пунктов шкалы данных в виде процентов (от 0 до 100%), а не в виде чисел от 1 до n. В нашем случае в виде персентелей представляются значения Xi.
2Нормированный R-квадрат – скорректированный (адаптированный, поправленный) коэффициент детерминации.
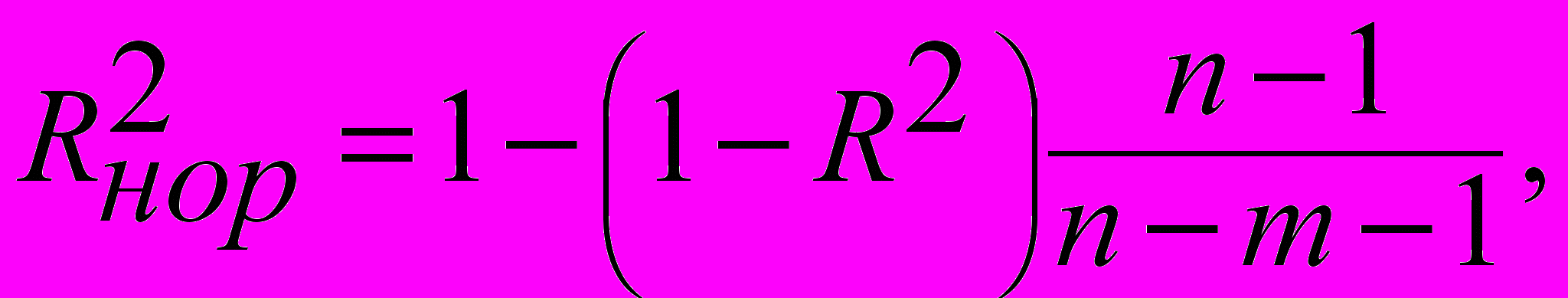
где n – число наблюдений, m - количество факторных признаков.
3Стандартная ошибка =
 , определение MS – приведено ниже.
, определение MS – приведено ниже. Для регрессионного уравнения в целом она выступает как степень точности прогнозов, которые базируются на уравнении. Стандартная ошибка — это мера ошибки предсказанного значения Y для отдельного значения X.
4 Дисперсия - мера рассеивания (отклонения от среднего) - средний квадрат отклонений индивидуальных значений признака от его средней величины. Дисперсия фактических значений результативного признака от вычисленных по уравнению определяется как
2 = (Yi—Y(Xі))2/n, где: Yi -действительно наблюдаемые значения,
Y(Xі) - значения из уравнения регрессии, n-количество наблюдений.
для строки «Остаток» - сумма квадратов отклонений эмпирических данных от теоретических, для строки «Итого» это сумма квадратов отклонений эмпирических данных от среднего.
- MS содержит значения дисперсии, которые рассчитываются по формуле MS=SS/df. Для строки Регрессия дисперсия называется факторной, для строки Остаток – остаточной.
- F – расчетное значение критерия Фишера. Вычисляется по формуле: F = MS(регрессия)/MS(остатки)
- Коэффициенты – это значения коэффициентов уравнения регрессии.
- Стандартная ошибка - стандартная ошибка коэффициентов уравнения регрессии.
- t – статистика - критерии вычисляемые как =коэффициет/стандартная ошибка.
- Нижние 95% и верхние 95% - границы доверительных интервалов для коэффициентов регрессии.
- В полученной таблице «Вывод остатка» «предсказанная цена» – данные в соответствии с уравнением регрессии, «остатки» – разница между статистическими и теоретическими данными.
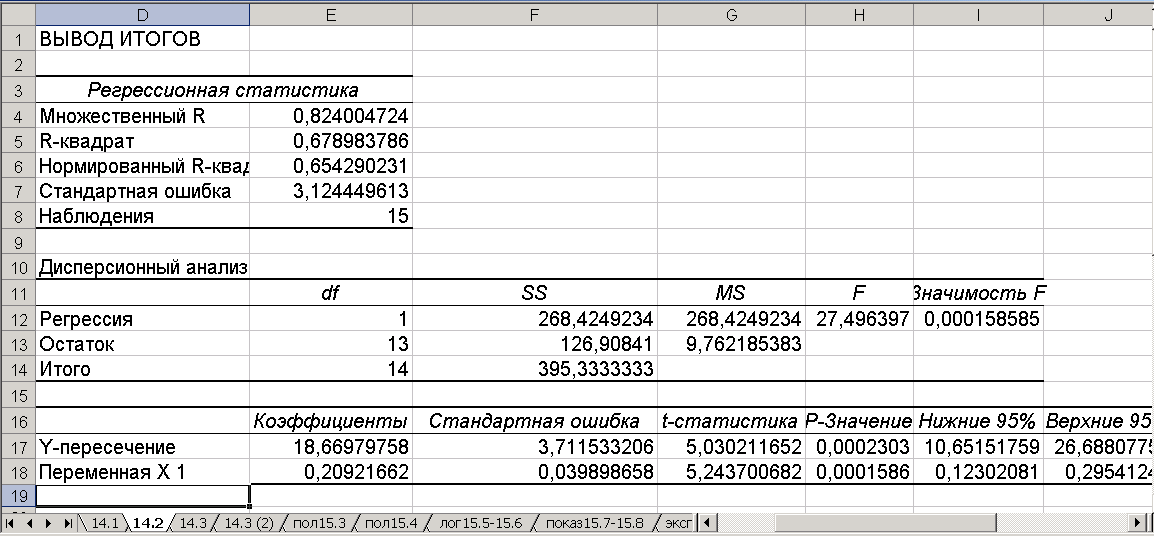
Рис. 1.4
^ Интерпретация полученных результатов
Смещение и коэффициент наклона аппроксимирующей прямой представлены в столбце «Коэффициенты» (рис. 1.4). Коэффициент Y- 18,66979 является постоянным членом уравнения линейной регрессии, а коэффициент 0,2092 (переменная Х1) является мерой наклона линии регрессии. Для осуществления прогноза стоимости объекта жилой площади используется формула:
Предсказанная цена = 18,6697 + 0,2092* Площадь.
Обычно для ответа на вопрос «Насколько хорошо приближение» используются следующие четыре характеристики: стандартная ошибка, R2, t-статистика и дисперсионный анализ.
Нормированный R-квадрат, приведенный в ячейке Е6, используется для сравнения выбранной модели с другими, имеющими дополнительные независимые переменные.
Значения t-статистики в ячейках G17:G18 являются частью проверок гипотез о коэффициентах регрессии (значения t-статистики =Коэффициент/стандартная ошибка). Нулевая гипотеза – это когда взаимозависимость исследуемых переменных отсутствует, то есть мера наклона линии регрессии равна нулю. В нашем примере мера наклона выборки (0,2092) со стандартной ошибкой коэффициента (оценка ошибки выборки = 0,0398) находится от нуля на расстоянии 5,2437 стандартных ошибок.
Р-значение (0,000159), приведенное в ячейке H18 является вероятностью получения данных результатов при выполнении нулевой гипотезы. Таким образом, нулевая гипотеза отвергается.
^ Графики функции регрессии
Инструмент анализа строит диаграммы:
- график остатков
- график подбора.
График подбора подобен графику с добавленной линией тренда, за исключением того, что предсказанные значения на этом графике отображаются маркерами без соединяющей их линии.
График остатков применяется для определения, является ли приемлемой форма аппроксимирующей кривой. Если график остатков имеет случайный рисунок, то линейное приближение может быть удовлетворительным. Если же график остатков имеет определенную структуру, то может потребоваться дополнительное моделирование.
^ Использование функции «Регрессия» для нелинейной зависимости
Методика проведения анализа взаимодействия параметров, связанных нелинейным уравнением, аналогична методики для линейных связей. Однако, механизм проведения анализа для нелинейных зависимостей, несколько отличается. В этом случае требуется интерпретация исходных данных для их соответствия характеру уравнения Регрессии.
Для примера рассмотрим один из указанных ранее четырех способов описания нелинейной зависимости двух переменных - логарифмический.
В логарифмической модели уравнение линии регрессии имеет вид: Y = a + Ln(X). Следовательно, исходными данными для функции «Регрессия» в данном случае будут Y и Ln(X). Поэтому в таблице исходных данных создаем дополнительный столбец Ln(X), т.е. Ln(площадь). Для быстрого заполнения ячеек В2 - В16 в ячейку В2 введите формулу «=Ln(А2)», а в остальные ячейки столбца «В» эту формулу скопируйте, выделив В2 и дважды щелкнув по маркеру заполнения в правом нижнем углу ячейки.
Далее активизируйте функцию «Регрессия». В диалоговом окне «Регрессия» (Рис. 1.5) введите ссылки на входной интервал Y (цена) и входной интервал Х (Ln(площадь)).
На рис. 1.5 приведены результаты после удаления части таблицы вывода итогов, относящейся к анализу дисперсии.
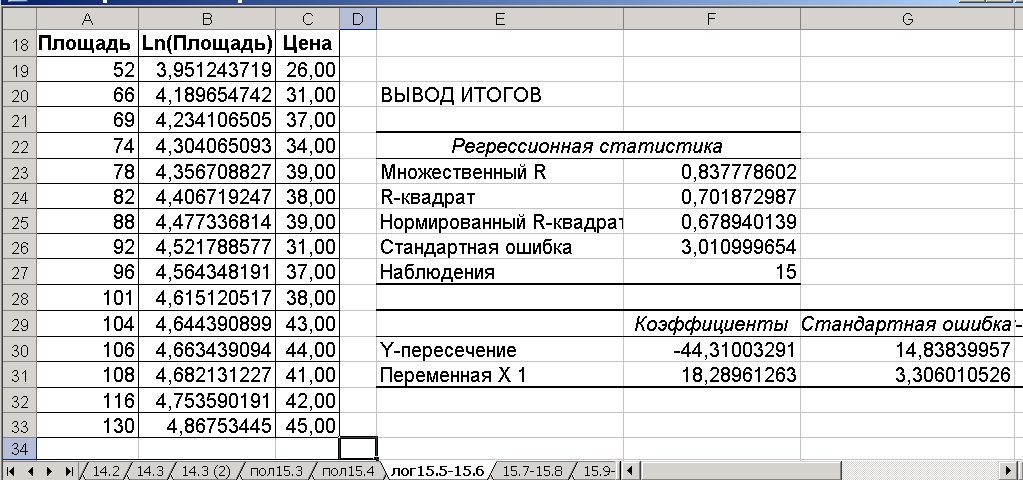
Рис. 1.5
По сравнению с линейной моделью данная логарифмическая модель имеет меньшую стандартную ошибку и большее R2, что говорит о её лучшем соответствии для описания зависимостей переменных.
Для осуществления прогноза стоимости объекта жилой площади можно воспользоваться формулой: = -44.31 + 18.289 * Ln(X)
Аналогично проводится регрессивный анализ степенного, экспоненциального и полиномиального моделирования.
^ 4. Вопросы для самопроверки
- Назовите два базовых инструмента MS Excel, которые используются для анализа взаимосвязи параметров ряда статистических данных.
- Что можно сказать о связи параметров ряда данных, если коэффициент корреляции близок к -1 или 1.
- Что называют дисперсией.
- В каких пределах изменяется коэффициент регрессии и что характеризуют величины этого коэффициента близкие к крайним точкам.
- Суть метода наименьших квадратов при построении линии тренда.
- Какой вид уравнения использует функция «Регрессия» для описания взаимодействия параметров (факторов) исследуемого процесса.
- Если взаимодействие параметров ряда статистических данных характеризуется нелинейным уравнением, то какие преобразования необходимо выполнить с этим уравнением для анализа процесса с помощью функции «Регрессия».
- Что необходимо выполнить для получения прогнозируемых величин с помощью линии тренда.
- Какие данные среди результатов работы функции «Регрессия» называют «смещением» и какие - мерой наклона линии регрессии.
- Как рассчитывается прогноз по данным, полученным с помощью функции «Регрессия».
- Назовите функции MS Excel, которые выполняют только отдельные частные этапы регрессионного анализа.
5. Примеры вариантов индивидуальных заданий лабораторной работы
Пример 1
-
Данные по Нижегородской области
год
Численность населения
Численность работников , занятых в органах гос. власти и местного самоуправления
1996
3691
25379
1997
3673
25969
1998
3655
26893
1999
3628
27501
2000
3594
26884
2001
3554
26280
2002
3515
28427
2003
3479
29537
2004
3445
30024
Провести регрессионный анализ зависимости количества работников, занятых в органах гос. власти, от численности населения.
Пример 2
-
Данные по Нижегородской области
год
Средние доходы населения (в месяц)
Усредненная продолжительность жизни
1996
535
66,17
1997
657
66,88
1998
725
67,18
1999
1172
66,09
2000
1718
65,05
2001
2407
64,66
2002
3215
64,27
2003
4000
63,64
2004
4794
63,75
Провести регрессионный анализ средних доходов населения по годам и усредненной продолжительности жизни от средних доходов населения. Вычислить значения прогнозируемых параметров на 2007-2009 гг.
Оригинальная версия данного документа находится на сайте www.izo.guu.ru. Документ получен из открытых источников, реквизиты правообладателей сохранены. Материалы представлены исключительно для ознакомления в учебных целях.
