Geum.ru

На предприятии имеется возможность выпускать n видов продукции

Вид материалаЗадача
Подобный материал:
Задача 1.

На предприятии имеется возможность выпускать n видов продукции 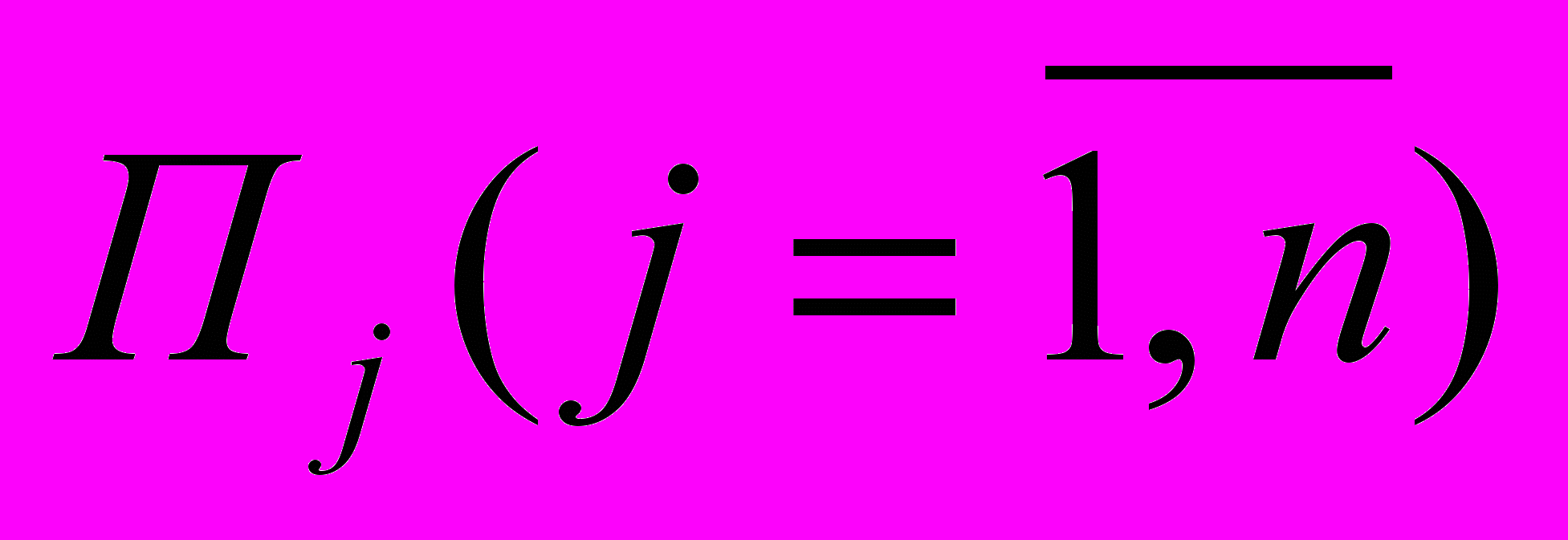. При ее изготовлении используются ресурсы Р1, Р2 и Р3. Размеры допустимых затрат ресурсов ограничены соответственно величинами b1, b2 и b3. Расход ресурса i-го 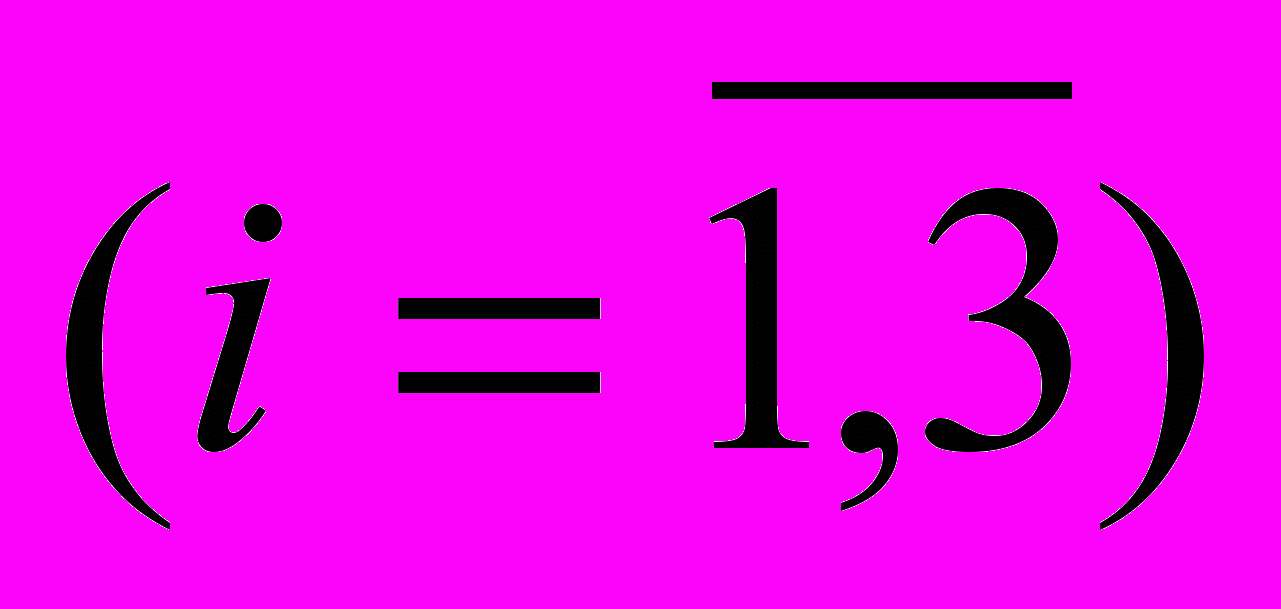вида на единицу продукции j-го вида составляет аij единиц. Цена единицы продукции j-го вида равна сj ден. ед.
а11
а12
а13
а14
b1






1
1
1
1
6000




а21
а22
а23
а24
b2
=



0.5
1
5
0.5
5000




а31
а32
а33
а34
b3






0.5
0.5
20
0.5
9000




с1
с2
с3
с4









80
100
300
80




Требуется:
  1. составить экономико-математическую модель задачи, позволяющую найти сбалансированный по ресурсам план выпуска продукции, обеспечивающий предприятию максимальный доход;
  2. симплексным методом найти оптимальный план выпуска продукции по видам; (дать содержательный ответ, раскрыв экономический смысл всех переменных, приведенных в решении задачи);
  3. сформулировать в экономических терминах двойственную задачу и составить ее математическою модель;
  4. найти компоненты оптимального плана двойственной задачи (двойственные оценки 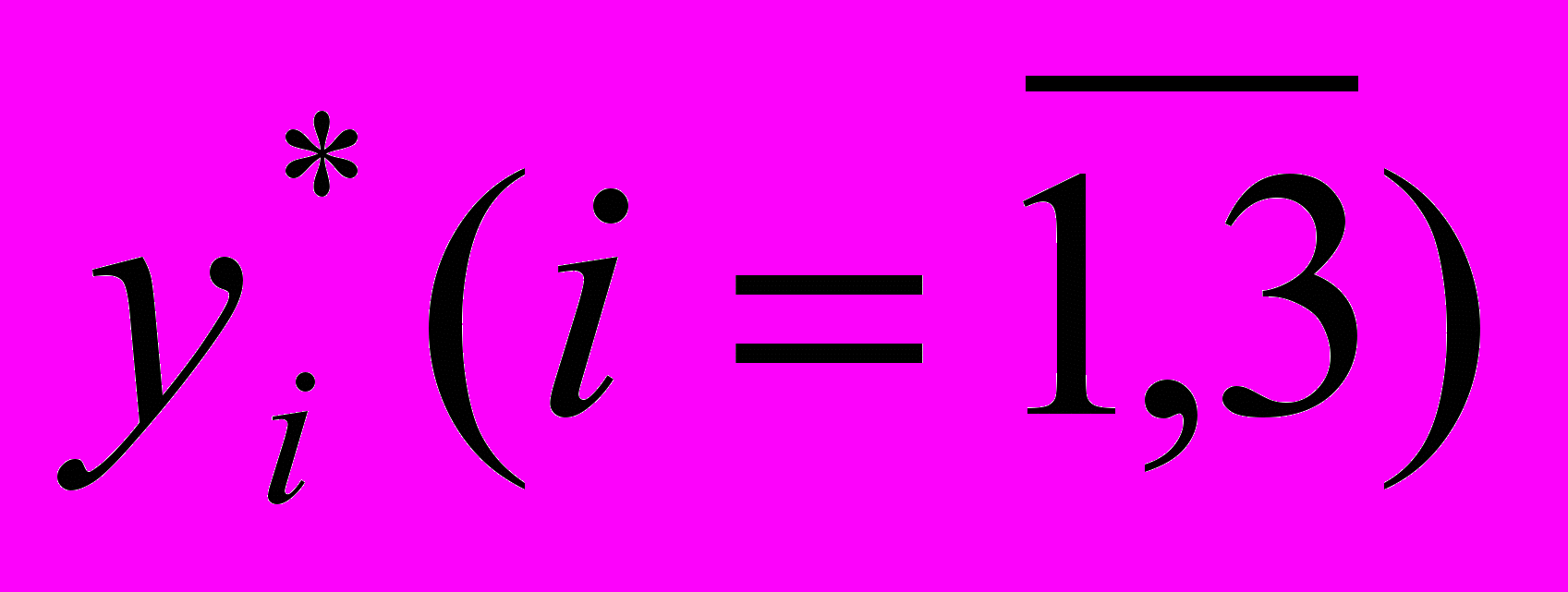используя решение исходной задачи и соответствие между двойственными переменными.

Решение



Обозначим через Х1 , Х2 , Х3-- количество единиц продукции соответственно П1, П2, П3, планируемой к выпуску, а через f--величину прибыли от реализации этой продукции. Тогда , учитывая значение прибыли от единицы продукции П1 =80 ден. ед., П2=100 ден. ед., П3=300 ден. ед., запишем сум­марную величину прибыли - целевую функцию - в следующем виде:

f = 80Х1 + 100Х2 +300Х3. (2.1)

Переменные Х1, Х2 , Х 3 должны удовлетворять ограничениям, наклады­ваемым на расход имеющихся в распоряжении предприятия ресурсов. Так, затраты ресурса P1 на выполнение плана (Х1 , Х2 , Х3) составят (Х1 +Х2 +Х3) ед., где Х1 - затраты ресурса P1на выпуск Х1 ед. продукции П1; Х2- затраты ресурсы P1 на выпуск Х2 ед. продукции П2 и т.д. Понятно, что указанная сумма не может превышать имеющийся запас P1 в 6000 ед., т.е.

Х1 +Х2 +Х3 ≤6000. (2.2)

Аналогично получаем ограничения по расходу ресурсов P2 и P3:

0.5 Х1 +Х2 +5Х3 ≤5000. (2.3)

0.5Х1 +0.5Х2 +20Х3 ≤9000. (2.4)

По смыслу задачи переменные Х1, Х2 , Х 3 не могут выражаться отрицатель­ными числами, т.е.

Хj ≥0 (j=1,3) (2.5)


Соотношения (2.1) - (2.5) образуют экономико-математическую модель данной задачи.

Итак, математически задача сводится к нахождению числовых значений Х1*, Х2*, Х 3* переменных Х1, Х2 , Х 3 , удовлетворяющих линейным нера­венствам (2.2) - (2.5) и доставляющих максимум линейной функции (2.1)


2. Прежде чем решать задачу линейного программирования симплекс-методом, ее модель приводят к канонической форме. Основным признаком канонической формы является запись ограничений задачи в виде равенств. В нашем же случае ограничения (2.2) - (2.4) имеют вид неравенств типа "≤". Чтобы преобразовать их в эквивалентные уравнения, введем в левые части неравенств дополнительные (балансовые) неотрицательные переменные Х4 , Х5 , Х6 , обозначающие разности между правыми и левыми частями этих нера­венств. В результате модель можно записать в виде

f = 80Х1 +100Х2 +300Х3 (max) (2.6)




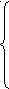
Х1 +Х2 +Х3 + Х4 = 6000

0,5Х1 +Х2 +5Х3 + Х5 =5000 (2.7)

0.5Х1 +0.5Х2 +20Х3 + Х6 =9000


Хj ≥0 (j=1,6) (2.8)


Заметим здесь же, что дополнительные переменные Х4 , Х5 , Х6 имеют вполне определенный экономический смысл - это возможные остатки ресур­сов соответственно P1, P2, P3 . Их еще называют резервами.

Анализируя каноническую модель (2.6) - (2.8), замечаем, что каждая из переменных Х4 , Х5 , Х6 входит только в одно из уравнений системы (2.7). Это обстоятельство свидетельствует о том, что в системе (2.7) переменные Х4 , Х5 , Х6 являются базисными, а остальные переменные Х1 , Х2 , Х3 - свободными. В связи с этим в первую симплекс-таблицу систему ограничительных урав­нений (2.7) можно записать в виде, разрешенном относительно базиса Х4 , Х5 , Х6 (табл. 2.1).


Таблица 2.1

БП
1
СП

- Х1
- Х2
- Х3

Х4=
6000
1
1
1

Х5=
5000
0.5
1
5

Х6=
9000
0.5
0.5
20

f
0
-80
-100
-300


Все элементы столбца свободных членов положительны, поэтому со­держащийся в табл. 2.1 план (0; 0; 0; 6000;5000; 9000), является опорным. Однако этот план не является оптимальным: в f — строке имеются отрицательные элементы.

Чтобы получить опорный план, более близкий к оптимальному, выпол­ним симплексное преобразование табл. 2.1. С этой целью выберем перемен­ные, участвующие в преобразовании базиса Х4 , Х5 , Х6 в новый базис. Наи­больший по модулю отрицательный элемент (-300) f-строки указывает, что в новый базис следует ввести переменную Х3 ,т.е. в качестве разрешающего в предстоящем симплексном преобразовании надо взять первый столбец. Что­бы определить переменную, выводимую из базиса, составляем симплексные отношения и выбираем наименьшее из них


Min(6000/1;5000/5;9000/20)=9000/20=450

Итак, из базиса надо исключить переменную, стоящую в третьей (разре­шающей) строке, т.е. Х6. На пересечении разрешающих столбца и строки на­ходится разрешающий элемент 20, с которым и выполняется симплексное преобразование (шаг жорданова исключения). В результате приходим к табл. 2.2.

В f-строке табл. 2.2 есть отрицательные элементы, значит, опорный

план (0;0; 450;5550;2750;0) оптимальным не является.


Таблица 2.2

БП
1
СП

- Х1
- Х2
- Х6

Х4=
5550
0.975
0.975
-0.05

Х5=
2750
0.375
0.875
-0.25

Х3=
450
0.025
0.025
0.05

f
135000
-72.5
-92.5
15


Рассуждая аналогично предыдущему, устанавливаем, что для улучшения этого плана надо выполнить очередное симплексное преобразование с раз­решающим элементом 0.875 . В результате получаем табл. 2.3

Таблица 2.3

БП
1
СП

- Х1
- Х5
- Х6

Х4=
2486
0.557
-1.11
0.229

Х2=
3143
0.429
1.143
-0.286

Х3=
371.4
0.014
-0.029
0.057

f
425714.3
-32.86
106
11.43

В f-строке табл. 2.2 есть отрицательные элементы, значит, опорный план оптимальным не является. Рассуждая аналогично предыдущему, устанавливаем, что для улучшения этого плана надо выполнить очередное симплексное преобразование с раз­решающим элементом 0.557 . В результате получаем табл. 2.4

Таблица 2.4

БП
1
СП

- Х4
- Х5
- Х6

Х1=
4462









Х2=
1231









Х3=
307.7









f
572307.7
59
40
2.05

Следовательно, опорный план (4462 ; 1231 ; 307.7 ; 0 ; 0 ; 0 ) является опти­мальным, а соответствующее ему значение 572307.7 целевой функции будет макси­мальным.

Итак, по оптимальному плану следует изготовить 4462 ед. продукции П1 , 1231 ед. продукции П2, 307.7 ед. продукции П3 .

При этом предприятие получит максимальную прибыль в размере 572307.7 ден. ед. Pесурсы будут израсходо­ваны полностью.

3. Двойственная переменная Yi. выступает коэффициентом при b i ,следовательно определяет зависимость целевой функции от изменения ресурсов b i на единицу.

Чтобы составить модель двойственной задачи, напишем матрицу ис­ходной

задачи (2.1)- (2.5) в следующем виде:


1
1
1
6
(2.9)
000

0.5
1
5
5000

0.5
0.5
20
9000

80
100
300
f max

Транспонируем матрицу (2.9). В результате получим матрицу (2.10) двойственной задачи:

1
0.5
0.5
8
(2.10)
0

1
1
0.5
100

1
5
20
300

6000
5000
9000
φ min


По матрице (2.10) легко написать модель задачи, двойственной к ис­ходной задаче:

φ =6000Y1 + 5000Y2 +9000Y3 (min) (2.11)




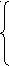
Y1 +0.5Y2 +0.5Y3 ≥80

Y1 +Y2 +0.5Y3 ≥100

Y1 +5Y2 +20Y3 ≥300 (2.12)


Yi ≥0 (j=1,3) (2.13)

4. Из теорем двойственности следует, что если решена одна из пары двойственных задач, то одновременно найдено решение и другой задачи. Компоненты оптимального плана этой задачи находятся в строке целевой функции последней симплекс - таблицы решенной задачи.

В п. 2 мы нашли оптимальный план исходной задачи, его компоненты находятся в

табл. 2.3. В f-строке этой же таблицы содержатся и компоненты Yi* оптимального плана двойственной задачи (2.11) - (2.13). Выписать ком­поненты Yi* поможет соответствие между переменными двойственных задач. Чтобы установить это соответствие, преобразуем ограничения-неравенства (2.12) в эквивалентные уравнения, вычитая из левых частей до­полнительные неотрицательные переменные Y1, Y2 и Y3 , равные разностям между левыми и правыми частями этих неравенств. Тогда модель (2.11)-- (2.13) запишется в виде

φ = 6000Y1 + 5000Y2 +9000Y3 (min)

Y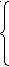1 +0.5Y2 +0.5Y3 - Y4=80

Y1 +Y2 +0.5Y3 - Y5=100

Y1 +5Y2 +20Y3 - Y6=300

Yi ≥0 (j=1,6)

В этой записи переменные Y4, Y5 и Y6 являются базисными, а Y1, Y2 и Y3 - свободными. В исходной задаче (2.6) - (2.8) переменные Х1 , Х2 и Х3 яв­ляются свободными, a Х4 , Х5 и Х6 - базисными.

Соответствие, о котором шла речь выше, устанавливают, сопоставляя базисным переменным одной задачи свободные переменные двойственной задачи и наоборот, т.е.

Х4  Y1, Х5  Y2, Х6  Y3, Х1  Y4, Х2  Y5, Х3  Y6, (2.14)


Воспользуемся соответствием (2.14) следующим образом. Как видно, переменная Y1 связана с переменной Х4 (поэтому их называют двойственными переменными. Y1 соответст­вует Х4, а в табл.2.4 под Х4 в f- строке находится элемент 59 ,следовательно, Y1* = 59. Точно так же устанавливается, что Y2* = 40, Y3* = 2.05; Y4* = 0 ; Y5* = 0 ; Y6* = 0 .

Из теорем двойственности следует, что экстремальные значения целе­вых функций разрешимых двойственных задач совпадают, поэтому φ min = f max =572307.7