Geum.ru

Программа курса «Mетоды теории групп в квантовой теории поля» (9 семестр, 64 часа)

Вид материалаПрограмма курса

Содержание


Экзаменационные вопросы к курсу
Подобный материал:

Программа


курса «Mетоды теории групп в квантовой теории поля»

(9 семестр, 64 часа)

  1. Представления группы Лоренца.
  1. Представления алгебр so(3,1) и sl(2,C)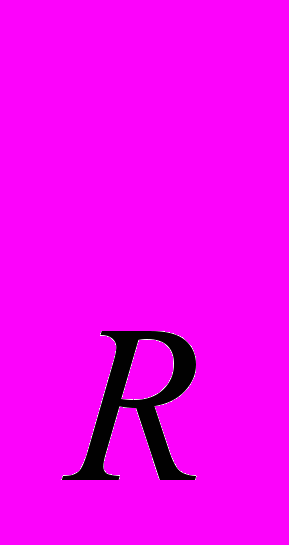. Пунктирные и непунктирные спиноры. Спин-тензоры.
  2. Представления подалгебры вращений в sl(2,C)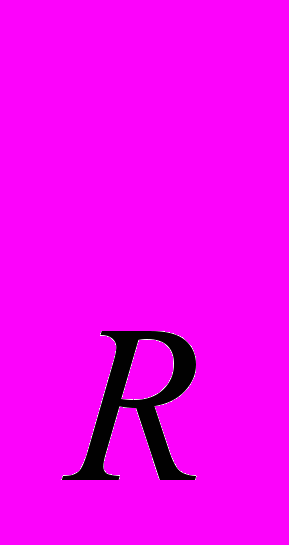. Интегрируемые представления группы Лоренца.



  1. Метод индуцированных представлений, представления группы Пуанкаре.
  1. Конструкция индуцированного представления. Критерий унитарности.
  2. Метод малой группы.
  3. Представления групп движения, построение представлений группы e(2).
  4. Индуцированные представления группы Пуанкаре. Классификация унитарных неприводимых представлений. Конструкция операторов представления.
  5. Представления группы Пуанкаре в спинорном базисе.
  6. Релятивистски инвариантные уравнения движения элементарных частиц.


Ш. Алгебраический анализ представлений групп.
  1. Максимальные торы в пространствах групп.
  2. Диаграмма и решетки. Экспоненциальное отображение единицы. Множество сингулярных точек. Центр группы как пересечение сингулярных множеств.
  3. Диаграмма группы. Центральная решетка. Единичная решетка. Фундаментальная решетка. Дискретные нормальные подгруппы универсальной накрывающей группы и решетки.
  4. Точные представления и представления локально изоморфных групп.
  5. Анализ представлений классических групп с помощью решеток.



  1. Метод орбит в теории представлений и геометрическое квантование.
  1. Коприсоединенное представление и кокасательное расслоение.
  2. Инвариантные формы на кокасательном пространстве.
  3. Коприсоединенное представление общей линейной группы. Орбиты как классы подобных матриц.
  4. Формы на однородных пространствах и функции на группе со структурным условием.
  5. Невырожденные замкнутые инвариантные формы на орбитах.
  6. Симплектические многообразия и симплектические формы. Орбиты коприсоединенного представления как симплектические многообразия.
  7. Гамильтоновы и строго гамильтоновы поля. Канонические преобразования.
  8. Строго однородные симплектические многообразия.
  9. Классификация орбит и классификация представлений. Орбиты как фазовые пространства гамильтоновых систем.
  10. Построение унитарных представлений индуцированных с одномерных представлений подчиненных подгрупп.
  11. Геометрическое квантование гамильтоновых систем.



Литература:
  1. В.Д. Ляховский, А.А. Болохов, Группы симметрии и элементарные частицы, Изд. ЛУ, 1983
  2. А.А. Кириллов, Элементы теории представлений, «Наука», 1978
  3. A.A. Kirillov, “Merits and Demerits of the Orbit Method”, Bulletin of the American Mathematical Society, V 36, N 4, p.p. 433-488
  4. М.Б. Менский, Метод индуцированных представлений, «Наука», 1976
  5. О. Лоос, Симметрические пространства, «Наука», 1985
  6. Теория алгебр Ли. Топология групп Ли, Семинар «Софус Ли», М., 1962
  7. Дж. Адамс, Лекции по группам Ли, «Наука», 1979
  8. А. Барут, Р. Рончка, Теория представлений и ее приложения, Т. I,II , М., 1980



^

Экзаменационные вопросы к курсу


«Mетоды теории групп в квантовой теории поля»

  1. Алгебра Ли как структура, индуцированная на касательном пространстве к группе Ли.
  2. Алгебра Ли инвариантных векторных полей.
  3. Спектр неприводимых конечномерных представлений алгебры sl(2,C)R.
  4. Интегрируемые и неинтегрируемые представления алгебры so(3,1).
  5. Присоединенное и коприсоединенное представления.
  6. Приводимые, вполне приводимые и неприводимые представления.
  7. Сплетающий оператор. Леммы Шура.
  8. Максимальные торы в пространствах групп.
  9. Диаграмма и решетки.
  10. Центральная решетка. Единичная решетка. Фундаментальная решетка.
  11. Анализ представлений групп SO(5) и SU(3) с помощью решеток.
  12. Представления группы Пуанкаре для массивных частиц.
  13. Представления группы Пуанкаре для безмассовых частиц.
  14. Представления группы Пуанкаре в спинорном базисе.
  15. Уравнения Дирака, Прока, Баргмана-Вигнера, Рариты-Швингера.
  16. Коприсоединенное представление и кокасательное расслоение.
  17. Производная Ли.
  18. Каноническая форма и уравнения Картана-Маурера.
  19. Инвариантные формы на кокасательном пространстве. Форма Кириллова.
  20. Коприсоединенное представление общей линейной группы. Орбиты как классы подобных матриц.
  21. Инвариантные тензорные поля на однородных пространствах и функции на группе со структурным условием.
  22. Невырожденные замкнутые инвариантные формы на орбитах.
  23. Орбиты коприсоединенного представления как симплектические многообразия.
  24. Гамильтоновы и строго гамильтоновы поля. Канонические преобразования.
  1. Строго однородные симплектические многообразия.
  2. Орбиты как фазовые пространства гамильтоновых систем.
  3. Построение унитарных представлений индуцированных с одномерных представлений подчиненных подгрупп.
  4. Унитарные неприводимые представления нильпотентных матричных групп.