Г. А. Евдокимова Е. В. Петрова Словарь терминов по начертательной геометрии и инженерной графике/ Новосиб гос аграр ун-т, ии; сост. Т. В. Семенова, Г. А. Евдокимова, Е. В. Петрова. Новосибирск, 2010. 120 с

Вид материала

Содержание

Концентрические окружности
Координатные оси.
Коробовая кривая
Косое сечение.
Косая плоскость
Косоугольная диметрия.
КРАН (гол. kraan). 1.
Кривая ошибок.
КРУГ. Часть плоскости, ограниченная окружностью. КУБ
Левая система осей.
Легированные стали
Лекальные кривые.
Линейчатые поверхности.
Линейчатый гиперболоид.
Линейчатый параболоид.
Линия выносная.
Линия выпуклая.
Линия зацепления
Линия кривая.
Линия ломаная
...
Полное содержание

Подобный материал:

1 2 3 4 5 6 7 8 9

б)

^ КОНЦЕНТРИЧЕСКИЕ ОКРУЖНОСТИ. Окружности различных радиусов, описанные из одного центра. Каждые две концентрические окружности эквидистантны.

КООРДИНАТА (лат. со — с, вместе, ordinatus — упорядоченный). 1. Число линейных единиц в данном отрезке. 2. Числа, определяющие положение точки в какой-либо системе отсчета (прямоугольной, косоугольной, полярной и др.). Для определения положения точки в плоскости необходимы две координаты, а в пространстве — три.

^ КООРДИНАТНЫЕ ОСИ. Для определения положения точки в плоскости пользуются системой двух пересекающихся осей, расстояния от которых и определяют точку. Координатные оси бывают прямоугольные, косоугольные (аффинные) и полярные. Для определения положения точки в пространстве пользуются системой трех пересекающихся осей. Наибольшее применение получила прямоугольная система Декарта. Точка пересечения осей называется началом координат.

^ КОРОБОВАЯ КРИВАЯ. Замкнутая или незамкнутая линия, состоящая из сопряженных дуг окружностей разных радиусов. Незамкнутую коробовую линию всегда можно превратить в замкнутую, если известна ось симметрии последней.

^ КОСОЕ СЕЧЕНИЕ. В проекционном черчении косым называется сечение детали проектирующей плоскостью, непараллельной плоскостям проекций. Построить косое сечение — значит найти истинную форму его (обычно методом переданы плоскостей проекций).

^ КОСАЯ ПЛОСКОСТЬ. Линейчатая поверхность, образованная непрерывным движением прямой, которая все время пересекает две скрещивающиеся прямые (направляющие) и остается параллельной заданной плоскости параллелизма. При этом направляющие не параллельны плоскости параллелизма. Косая плоскость иначе называется гиперболическим параболоидом или линейчатым параболоидом.

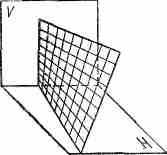
^ КОСОУГОЛЬНАЯ ДИМЕТРИЯ. Косоугольная аксонометрическая проекция с коэффициентами искажения, одинаковыми только по двум осям (например, р = r ≠ q).

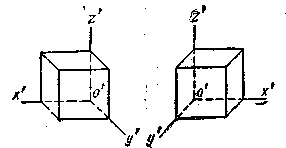
В черчении широко применяется косоугольная диметрия, у которой р = r = 1, q = 0,5, а система осей показана на рисунке. При этом проектирующие лучи падают на плоскость проекций под углом в 63° 30'.

^ КРАН (гол. kraan). 1. Устройство для ручного или автоматического выпуска жидкости или газа из трубопровода. Конструктивно и по назначению краны делятся на пробковые (двух- и трехходовые), водоразборные, смывные, запорные и др. 2. Грузоподъемная машина для поднятия и перемещения грузов. Конструктивно краны делятся на мостовые, консольные, козловые, стреловые, судовые, подъемно-транспортные и проч.

КРИВОНОЖКА. Вращающийся рейсфедер для проведения кривых линий от руки или по лекалу. Применяется в топографическом и архитектурно-строительном черчении. Благодаря тому, что рейсфедер вращается в ручке и имеет изогнутую форму щечек, при работе он плавно следует за движением руки.

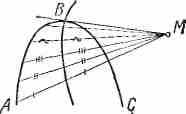
^ КРИВАЯ ОШИБОК. Вспомогательная кривая, которую строят при решении задачи: «Из данной точки М провести касательную к данной кривой АС». Для нахождения точки касания В строится кривая ошибок, как геометрическое место середин всех хорд, проходящих через точку М.

КРИВИЗНА. Величина, характеризующая степень отклонения кривой линии от прямолинейности, а также выпуклой или вогнутой поверхности от плоскостности. Кривизна плоской кривой обратно пропорциональна радиусу, т. е. чем больше радиус, тем меньше кривизна. Обозначается буквой К. Центр кривизны лежит на нормали кривой в сторону ее вогнутости.

КРОКИ (фр. croquis). 1. Наскоро сделанный от руки эскиз, план, рисунок. 2. В топографии — простейший план местности, выполненный приемами глазомерной съемки.

КРОНЦИРКУЛЬ. 1. Мерительный инструмент в виде циркуля с дугообразно изогнутыми ножками, служащий для измерения линейных размеров. Взятый раствор лапок кронциркуля сравнивается с масштабной линейкой, С его помощью измеряют наружные размеры деталей. 2. Чертежный, инструмент для откладывания небольших отрезков одинаковой длины. Состоит из двух раздвижныж ножек, раствор которых регулируется установочным винтом. На концах ножек имеются иголки, закрепленные прижимными винтами. 3. Циркуль для вычерчивания окружностей малых диаметров (от 0,6 мм до 12 мм). Называется падающим кронциркулем. Может работать и с карандашной ножкой или с рейсфедером.

^ КРУГ. Часть плоскости, ограниченная окружностью.

КУБ (греч. kybos — игральная кость). Один из пяти выпуклых правильных многогранников. Поверхность его образуется из шести квадратов. Правильный гексаэдр. Имеет 6 граней , 8 вершин и 12 ребер. Куб имеет тринадцать осей симметрии.

КУРВИМЕТР. Прибор для измерения длины кривых линий на картах, планах, чертежах.

Л

ЛАТУНЬ (нем. Latun). Название сплавов меди с цинком, обычно с добавкой небольшого количества других элементов (свинца, олова, марганца, алюминия, железа, никеля и др.). Латуни широко применяются в технике (прутки, трубы, листы, проволока) для изготовления часовых механизмов, оптических приборов, электрооборудования и др. Обозначается на чертеже условно, например, ЛС59—1, что означает: латунь с содержанием меди около 59%, свинца—1% и цинка около 40%.

^ ЛЕВАЯ СИСТЕМА ОСЕЙ. Начало координат расположено слева. В начертательной геометрии рекомендуется правая система.

^ ЛЕГИРОВАННЫЕ СТАЛИ (нем. legieren — легировать). Стали со специальными прибавками разных элементов: никеля, хрома, молибдена, вольфрама, ванадия, способствующих улучшению механических свойств или приданию стали особых физико-химических свойств, напр. кислотоупорности, жаропрочности, амагнитности и т. д. Различают стали низколегированные и высоколегированные.

^ ЛЕКАЛЬНЫЕ КРИВЫЕ. Нециркульные кривые линии, вычерчиваемые по точкам при помощи лекал (см. лекало). Эллипс, парабола, гипербола, циклоида, спираль Архимеда, эвольвента окружности, синусоида, косинусоида - относятся к лекальным кривым.

ЛЕКАЛО. 1. Тонкая пластина с криволинейными кромками, служащая для вычерчивания нециркульных кривых. Лекала изготовляют из дерева, пластмассы и других материалов. Форма и величина их бывает различной. Существуют универсальные гибкие лекала, устанавливаемые по точкам, между которыми необходимо провести плавную кривую. 2. Инструмент для контроля формы криволинейной поверхности изделия, изготовляемого из металла, дерева (шаблон).

ЛИНЕЙКА (лат. linеа — линия). Инструмент, служащий для проведения прямых линий на плоскости; так называемые чертежные линейки с миллиметровой шкалой или без нее. Изготовляются из дерева, пластмассы и других материалов. Линейки могут быть: мерительные, масштабные, штриховальные, рейсшины, разметочные, полиграфические и др. При решении некоторых классических задач геометрии имеют в виду идеальную линейку с единственной кромкой, которая совпадает с теоретической прямой линией. Идеальная линейка никаких делений не имеет.

^ ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ. Поверхности, образованные движением прямой линии в пространстве. Различают линейчатые поверхности развертывающиеся и косые. Первые из них могут быть наложены на плоскость без разрывов и складок, например, цилиндрические и конические. Косые — геликоид, однополостный гиперболоид не могут быть совмещены с плоскостью.

^ ЛИНЕЙЧАТЫЙ ГИПЕРБОЛОИД. Поверхность, образованная непрерывным движением прямой, которая все время пересекает три направляющие, не лежащие в одной плоскости (однополостный гиперболоид).

^ ЛИНЕЙЧАТЫЙ ПАРАБОЛОИД. См. косая плоскость.

ЛИНИИ ЧЕРТЕЖА. Для выполнения чертежей применяют несколько различных условных линий, тип, назначение, начертание и толщина которых установлены ГОСТом 2.303—68: а) сплошная основная, б) сплошная тонкая, в) сплошная волнистая, г) штриховая, д) штрихпунктирная тонкая, е) штрихпунктирная утолщенная, ж) разомкнутая, з) сплошная тонкая с изломами.

ЛИНИЯ (лат. linеа). Всякую линию можно представить себе как траекторию движущейся точки. Нельзя рассматривать линию как ряд точек; вместе с тем линия — его точечное множество. Все геометрические линии сплошные. На чертеже линии изображают условно (см. линии чертежа).

^ ЛИНИЯ ВЫНОСНАЯ. Тонкая сплошная линия для выноса размерной линии за контур изображения или на некоторое расстояние от измеряемого места. Выносная линия заходит за размерную на 2—3 мм. Толщина ее

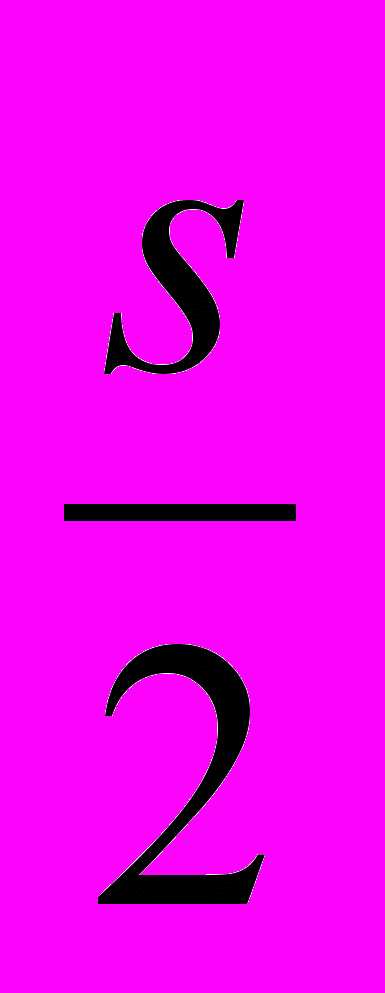и менее.

^ ЛИНИЯ ВЫПУКЛАЯ. Линия, которая со всякой прямой пересекается не более чем в двух точках. Во всякую выпуклую кривую можно вписать ломаную линию, а вокруг нее описать другую ломаную линию. Длина второй больше длины первой.

^ ЛИНИЯ ЗАЦЕПЛЕНИЯ (эвольвентного). Неподвижная относительно линии центров прямая (плоскость) NN, по которой в процессе работы перемещается точка (линия) касания сопряженных зубьев. Давление между зубьями направлено вдоль этой линии (плоскости) (см. угол зацепления).

^ ЛИНИЯ КРИВАЯ. Траектория непрерывно движущейся точки в постоянно изменяющемся направлении. Кривая, все точки которой принадлежат одной плоскости, называется плоской. Кривая, все точки которой не могут принадлежать одной плоскости, называется пространственной. Такая линия имеет двоякую кривизну. Кривые линии, как плоские, так и пространственные, могут быть закономерными или случайного вида. Свойства кривых изучаются в аналитической и дифференциальной геометрии, а также в топологии. Единственная кривая, изучаемая в элементарной геометрии, — окружность.

^ ЛИНИЯ ЛОМАНАЯ. Линия, составленная из отрезков прямых линий, не принадлежащих одной прямой. Ломаная линия может быть плоской или пространственной, простой или самопересекающейся. Она замкнутая, если концы ее сходятся в одну точку.

^ ЛИНИЯ НАИБОЛЬШЕГО НАКЛОНА ПЛОСКОСТИ. Прямая, принадлежащая данной плоскости и образующая с плоскостью проекций наибольший угол. Прямая эта перпендикулярна к соответствующему следу плоскости. Прямая, принадлежащая данной плоскости и перпендикулярная к ее горизонтальному следу, называется линией ската (по этой линии скатывается шар, поставленный на наклонную плоскость).

^ ЛИНИЯ ОСЕВАЯ. Тонкая штрихпунктирная линия, изображающая на чертеже ось симметрии данного изображения или ось вращения тела.

ЛИНИЯ ОЧЕРКОВАЯ (контурная). Линия видимого очертания предмета на его изображении (чертеже, рисунке). В машиностроительном черчении такая линия называется сплошной основной. Толщину основной линии (s) следует брать в пределах от 0,6 до 1,5 мм в зависимости от величины и сложности изображения, а также назначения и формата чертежа.

^ ЛИНИЯ ПУНКТИРНАЯ (нем. punktieren — ставить точки). Линия, составленная из точек или из очень коротких черточек.

ЛИНИЯ ЦЕНТРОВ. Прямая линия, соединяющая геометрические центры двух окружностей на чертеже.

^ ЛИНИЯ ПЕРЕСЕЧЕНИЯ ПОВЕРХНОСТЕЙ. Линия, получающаяся при пересечении двух поверхностей; каждая ее точка одновременно принадлежит и той и другой поверхности. Несколько примеров: а) линия пересечения двух плоскостей — прямая; б) линия пересечения двух сфер — окружность; в) линия пересечения поверхностей двух конусов, оси которых параллельны — гипербола (в общем случае); г) линия пересечения поверхностей двух многогранников — ломаная.

ЛИНИЯ ПЕРЕХОДА. 1. Условная линия на чертеже детали составной формы, показывающая плавный переход одной поверхности в другую. Линия эта воображаемая, заменяет собой линию пересечения и чертится тонкой сплошной линией. При явно выраженных скруглениях линию перехода не доводят до контурных линий детали.

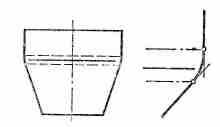
^ 2. То же, что линия пересечения.

ЛИНИИ ПОСТРОЕНИЯ. Геометрические построения, необходимые для выполнения изображения предмета, делают очень тонкими сплошными линиями, которые при обводке чертежа стирают резинкой. На некоторых чертежах линии построения сохраняют для того, чтобы показать ход геометрических построений.

^ ЛИНИЯ ПРОЕКТИРУЮЩАЯ (или проецирующая). Прямая линия, совпадающая с направлением проектирования; при ортогональном проектировании эта прямая перпендикулярна к плоскости проекций. Всякое проектирование осуществляется посредством таких линий.

^ ЛИНИЯ ПРЯМАЯ. Одно из основных неопределяемых понятий геометрии. Некоторые свойства прямой постулируются: а) через всякие две точки пространства можно провести прямую и притом только одну; б) если две прямые наложены одна на другую так, что какие-нибудь две точки одной прямой совпадают с двумя точками другой прямой, то эти прямые сливаются и во всех остальных точках; в) две прямые пересекаются только в одной точке; г) прямую линию можно продолжить в обе стороны. Некоторое представление о прямой дает туго натянутая тонкая нить.

^ ЛИНИЯ РАЗМЕРНАЯ. Тонкая сплошная линия, применяемая для нанесения линейных и угловых размеров на чертеже. Толщина ее

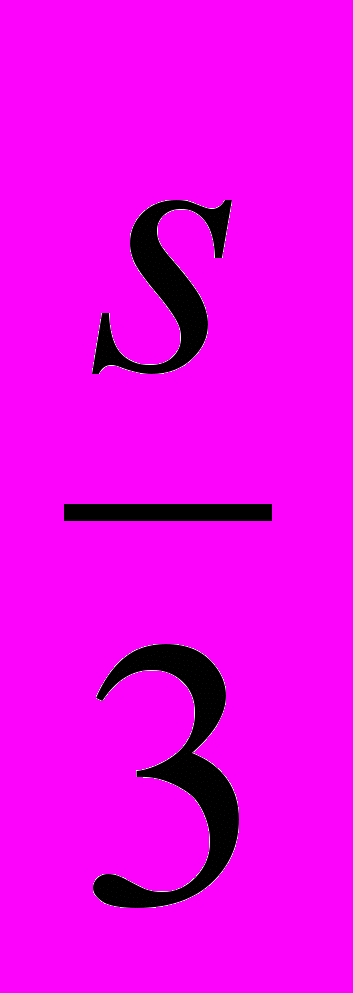и менее. Размерная линия снабжается одной или двумя размерными стрелками. Проводится параллельно линейному контуру или параллельно дуге.

^ ЛИНИЯ РАЗОМКНУТАЯ. В простейшем случае — линия, состоящая из двух штрихов длиной от 8 до 20 мм и толщиной от s до

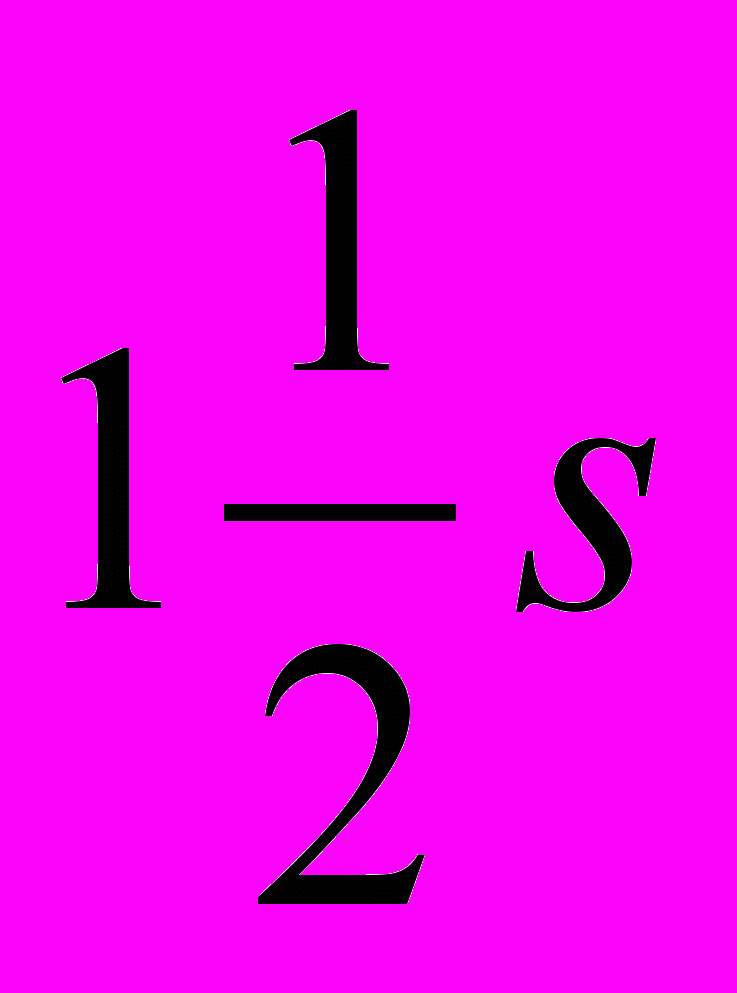, при помощи которой показывают на чертеже линию сечения (см. сечение). При выполнении более сложных разрезов штрихи проводят также у переломов линии сечения, а концы разомкнутой линии соединяют тонкой штрихпунктирной линией (см. ГОСТ 2.303—68).

^ ЛИНИЯ СВЯЗИ. Две проекции одной и той же точки лежат на одном перпендикуляре к оси проекций, который и называется линией связи этих двух проекций на комплексном чертеже точки.

^ ЛИНИЯ СЕЧЕНИЯ. Разомкнутая линия, которая указывает положение секущей плоскости выполненного на чертеже разреза или сечения. Начальный и конечный штрихи линии сечения не должны пересекать контур изображения. Разрезы и сечения на чертеже оформляют согласно указаниям ГОСТа 2.305—68.

^ ЛИНИЯ СРЕЗА. Некоторые детали машин (шатуны, рукоятки и др.) имеют формы, состоящие из различных тел вращения (шар, тор, конус и др.) и, кроме того, имеют плоские срезы, которые образуют на боковой поверхности их линии среза. На чертежах линии среза строят по точкам и при помощи лекала, в отдельных случаях они заменяются циркульными кривыми и прямыми линиями.

^ ЛИНИИ ОСОБОГО ПОЛОЖЕНИЯ В ПЛОСКОСТИ. Прямые, параллельные плоскостям проекций и лежащие в данной плоскости. Линия, параллельная горизонтальной плоскости проекций, называется горизонталью данной плоскости. Линия, параллельная фронтальной плоскости проекций, называется фронталью плоскости. Линия, параллельная профильной плоскости проекций, называется профильной прямой плоскости (см. также линии наибольшего уклона плоскости).

^ ЛИНИЯ ШТРИХОВАЯ. Линия, состоящая из штрихов и промежутков. Обычно промежутки в три-четыре раза меньше длины штрихов. Применяется для изображения на чертеже невидимого контура предмета. Толщина ее в два-три раза тоньше основной.

^ ЛИНИИ ЦЕНТРОВЫЕ. Взаимно перпендикулярные линии, проходящие через центр окружности или другой замкнутой кривой. Центровые линии чертят штрихпунктирной линией, а у окружностей малых диаметров — сплошной линией толщиной

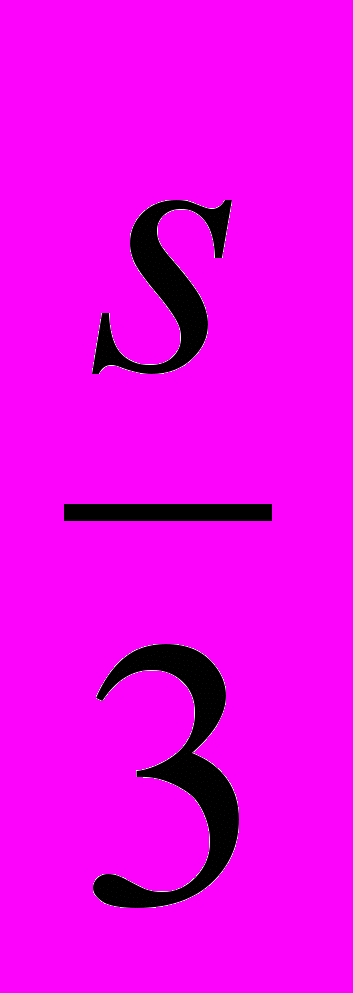и менее. Центровые линии выводятся за пределы кривой на 3—6 мм. Центр кривой во всех случаях отмечается пересечением линий (штрихов).

^ ЛИТЕЙНЫЙ УКЛОН. Стенки литых стальных, чугунных деталей имеют уклон порядка 1:20. Величина уклона зависит от размеров детали, от способа формовки и от других факторов. Уклон этот технологический, так как для извлечения модели из формы необходимо стенкам модели и ребрам, перпендикулярным к плоскости разъема, придавать некоторый уклон.

ЛИТЕРА (лат. litera — буква). Заглавная буква, проставляемая в одной из граф основной надписи чертежа или спецификации. Для эскизного проекта — Э, технического проекта — Т, опытных образцов — О, серийного или массового производства — Б, технического предложения — П, установочной серии — А, индивидуального производства — И, ремонта — Р, учебного чертежа - у.

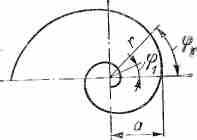
^ ЛОГАРИФМИЧЕСКАЯ СПИРАЛЬ. Одни конец спирали удаляется в бесконечность, другой конец делает около полюса бесконечное число оборотов, стремясь к нему, как к своей асимптотической точке. Логарифмическая спираль встречается в технике (направляющий аппарат гидротурбин, различные фрезы и проч.).

^ ЛЫСКА. Плоский срез на цилиндрической, конической или сферической части детали.

М

МАКЕТ (фр. maquette). Модель машины, здания, технического сооружения, микрорайона и др. Применяются при проектировании, на выставках, в учебных заведениях и т. п. Макеты бывают действующие (динамические) и неподвижные (статические). При плазовом методе производства, напр. в авиационной промышленности, макетами называют пространственные шаблоны.

МАРКИРОВКА. Нанесение на предмет производства (изделие) характеризующих его знаков, как-то: обозначения, порядковый номер, марка материала, группа селекции. Маркировку можно осуществить в литье, химическим или ударным способами.

МАССА (лат. massa — ком, кусок). Физическое свойство материи, мера ее инертности. Численно массу можно выразить как отношение силы, действующей на тело, к вызываемому этой силой ускорению тела. В технике массу измеряют в килограммах — единицей массы международного прототипа килограмма. В 5 графе основной надписи чертежа (ГОСТ 2.104—68) указывают массу детали или изделия в килограммах (в граммах, тоннах и др.).

МАСШТАБ (нем. Мав—мера, размер; Stab — палка). Мерительное приспособление для определения действительной длины отрезка по его изображению, которое может быть выполнено в натуральную величину, увеличено или уменьшено. Масштабы делятся на линейные (в том числе и поперечный), пропорциональные (угловые), аксонометрические, совмещенные (с совпадающими шкалами). Численные масштабы, сокращенно называемые в стандарте (ГОСТ 2.302—68) «масштабами», представляют собой математические выражения линейных масштабов.

^ МАСШТАБ ЛИНЕЙНЫЙ. Показываемая на картах или чертежах шкала размерности изображения в виде узкой прямолинейной полоски с нанесенными на ней делениями. Отрезок, принятый за единицу длины, называется основанием масштаба. Обычно основание делят на десять частей и откладывают влево от нулевого деления масштаба.

^ МАСШТАБ ЧИСЛЕННЫЙ (сокращенно М). Отношение линейных размеров изображения предмета к его действительным размерам. Численный масштаб обозначается простой дробью, которая показывает кратность увеличения или уменьшения действительных размеров предмета на его изображении. Численный масштаб уменьшения выражается дробью с единицей в числителе и некоторым числом в знаменателе (М 1:2 или М 1:5), а масштаб увеличения — дробью с единицей в знаменателе (М 2:1 или М 5:1). Численный масштаб М 1:1 означает, что изображение выполнено в натуральную величину. Масштабы для всех отраслей народного хозяйства установлены по ГОСТу 2.302—68.

МАШИНА (лат. machina — орудие). Сочетание механизмов для преобразования энергии или для производства работы. Двигательный, передаточный и исполнительный механизмы являются основными частями машины.

^ МАШИНОСТРОИТЕЛЬНОЕ ЧЕРЧЕНИЕ. Раздел курса черчения, в котором изучаются условности выполнения и оформления производственных чертежей для машиностроительной промышленности. В этом разделе рассматриваются чертежи: а) рабочие (эскизы деталей), б) сборочные, в) схематические и другие, в зависимости от специализации.

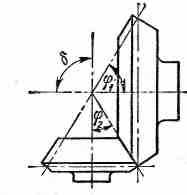
МЕЖОСЕВОЙ УГОЛ 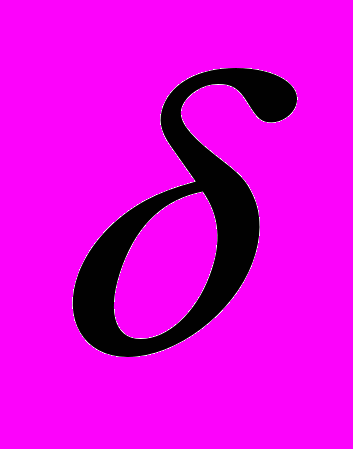. В конической зубчатой передаче угол между осями начальных конусов с совпадающими вершинами. Чаще всего 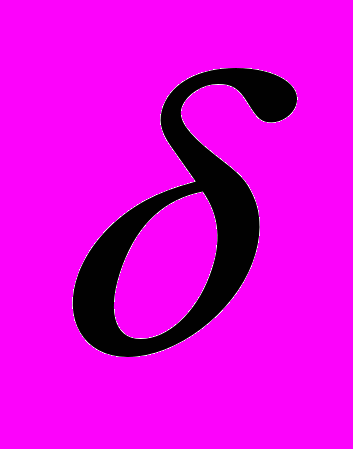= 90°. Межосевой угол равен сумме углов начальных конусов =

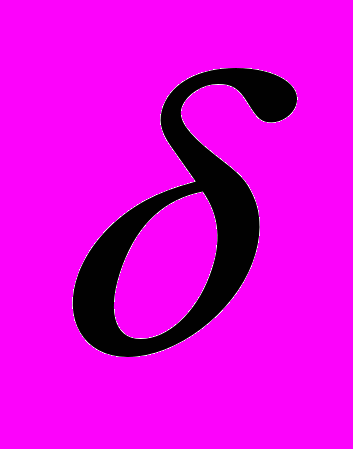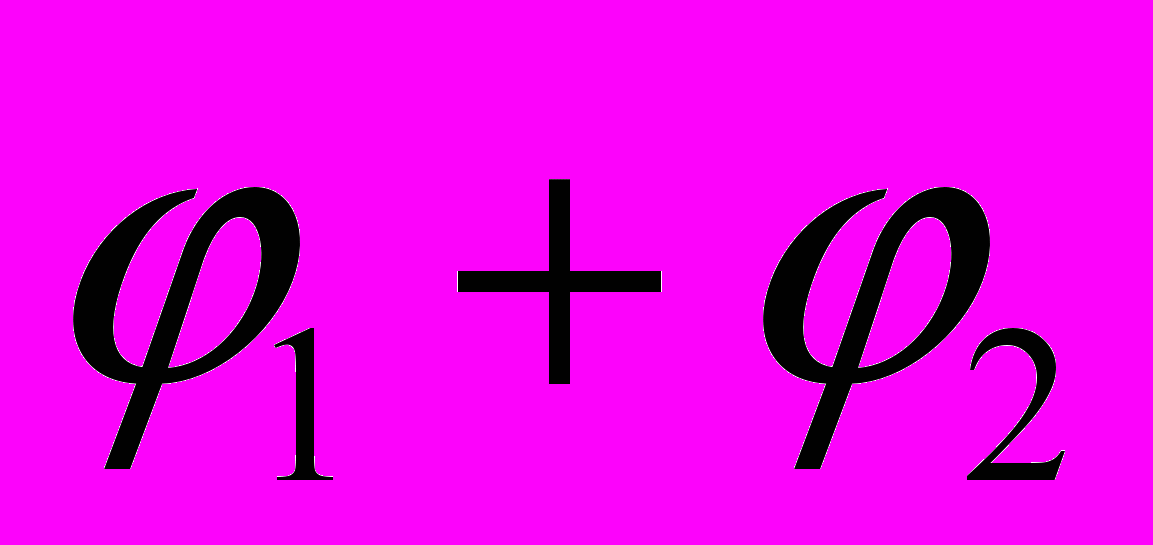МЕЖЦЕНТРОВОЕ РАССТОЯНИЕ (межосевое). Кратчайшее расстояние между осями вращения колес зубчатой или другой передач. Обозначается буквой А.

^ МЕСТНЫЙ ВИД. Изображение отдельного, ограниченного места на поверхности предмета. Применяется местный вид для пояснения формы и размеров какого-либо отдельного участка, когда полный вид давать нецелесообразно.

^ МЕТОД МОНЖА. В изображениях, выполненных методом Монжа, точка пространства ортогонально проектируется на две взаимно перпендикулярные плоскости — горизонтальную Н и фронтальную V. Получающиеся при этом изображения называются горизонтальной и фронтальной проекциями точки. Затем одна из плоскостей (Н) вращается вокруг оси проекций (линии пересечения плоскостей Н и V) до совмещения с другой плоскостью. После совмещения получается двухкартинное изображение, называемое эпюром Монжа, на котором две проекции точки лежат на одном перпендикуляре к оси проекций Ох. Этот перпендикуляр называется линией связи. Проекция точки на плоскости Н или V задается двумя координатами. Вторая проекция этой точки определяется путем задания третьей координаты, так как известно, что вторая проекция точки также лежит на линии связи. Тем самым положение точки в пространстве полностью определяется. С помощью метода Монжа оригинал определяется метрически точно. В некоторых исключительных случаях, например, когда изображается несколько прямых, лежащих в плоскости, перпендикулярной к плоскостям Н и V, пользуются третьей плоскостью проекций — профильной W для того, чтобы построить третью проекцию и сделать изображение определенным. Плоскость W перпендикулярна к Н и V.

МЕТОД ОСНОВНОЙ ПЛОСКОСТИ. Метод построения проекционных чертежей, разработанный Н. Ф. Четверухиным, является разновидностью аксонометрического метода изображений. Применяется в стереометрии.

МЕТОДИКА (греч. methodike). Составная часть дидактики. Учение о принципах и приемах преподавания учебных дисциплин. Методика исследует: а) цели и задачи предмета, б) содержание предмета, в) процесс преподавания и обучения, г) средства обучения. Существуют и частные методики, напр. методика проверки учебных чертежей и т. д.

МЕТАЛЛОКОНСТРУКЦИЯ. Узел или изделие, которое состоит из деталей (элементов), представляющих в своем большинстве отрезки и вырезки сортового, фасонного, листового, полосового и другого проката.

^ МЕТРИЧЕСКИ ОПРЕДЕЛЕННОЕ ИЗОБРАЖЕНИЕ. Изображение, по которому можно определить истинные размеры фигуры.

МЕТРОЛОГИЯ. Наука о системах мер и способах определения их образцов.

^ МЕХАНИЗИРОВАННАЯ РЕЙСШИНА. Чертежная рейсшина усовершенствованной конструкции: плавающая (на роликах и шнурах); с направляющими роликами или втулками и др.

МИЛЛИМЕТР (лат. mille — тысяча). Единица измерения длины, равная одной тысячной метра. Сокращенно обозначается мм. В машиностроительных чертежах все размеры указывают в мм без обозначения единицы измерения.

МНОГОГРАННИК. Тело, ограниченное со всех сторон плоскими многоугольниками (гранями). Различают многогранники правильные (10 шт.), полуправильные (14 шт.) и неправильные (все прочие). Многогранник называется выпуклым, если весь он расположен по одну сторону от плоскости любой его грани. Всякий многогранник можно разложить на треугольные пирамиды (тетраэдры).

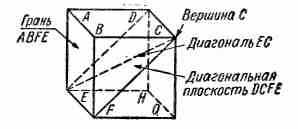
^ МНОГОГРАННИК ПРАВИЛЬНЫЙ. Многогранник, у которого все грани равны и представляют собой правильные многоугольники с равными углами. Всего имеется десять правильных многогранников: пять выпуклых и пять звездчатых (невыпуклых). Вокруг каждого правильного многогранника можно описать шар. Правильные многогранники могут быть составлены только из правильных треугольников, квадратов и пятиугольников. Тетраэдр (4 грани), куб или гексаэдр (6 граней), октаэдр (8 граней), додекаэдр (12 граней), и икосаэдр (20 граней) — правильные выпуклые (платоновы) многогранники.

МНОГОУГОЛЬНИК (сокращенно м-к). Фигура, ограниченная плоской замкнутой ломаной линией. Части этой линии называются сторонами; углы между каждыми соседними сторонами — углами м-ка, а их вершины — вершинами м-ка. По числу сторон м-ки называются треугольниками, четырехугольниками и т. д. Делятся они на простые и самопересекающиеся. Простой м-к называется выпуклым, если для любой его стороны все прочие стороны расположены по одну сторону от нее. М-ки бывают правильные и неправильные. Два м-ка, имеющие равные площади, называются равновеликими.

^ МНОГОУГОЛЬНИКИ ПРАВИЛЬНЫЕ. М-ки, имеющие равные стороны и равные углы. В правильный м-к можно вписать окружность. Каждая сторона его будет касательна к вписанной окружности. Радиус ее называется апофемой м-ка. Около правильного м-ка можно также описать окружность. Тогда все вершины его будут лежать на этой окружности. Площадь правильного м-ка равна произведению периметра на половину радиуса (R), а для м-ка, описанного около окружности — произведению периметра на половину апофемы.

^ МНОГОЦЕНТРОВАЯ КРИВАЯ. Плоская линия, составленная из нескольких плавно переходящих одна в другую дуг окружностей разных радиусов.

МОДЕЛЬ (фр. modelе). 1. Воспроизведение предмета в уменьшенном или увеличенном виде (модель атома, модель самолета, модель обуви). Модель может быть действующей (динамической) и недействующей (статической). Целой и составной (разборной). 2. Целая или составная копия отливаемой детали для изготовления литейной формы. Модель имеет несколько большие, чем деталь, размеры: на величину усадки и на величину припуска для механической обработки.

МОДЕЛИРОВАНИЕ. 1. Лабораторное исследование на моделях для изучения каких-либо физических свойств гидравлических устройств, аэродинамических качеств самолетов и т. п. 2. Изготовление моделей, проектирование с помощью моделей. 3. Создание геометрических моделей процессов и явлений.

^ МОДУЛЬ ЗАЦЕПЛЕНИЯ (т). Длина в мм, приходящаяся по диаметру делительной окружности на один зуб колеса: т =

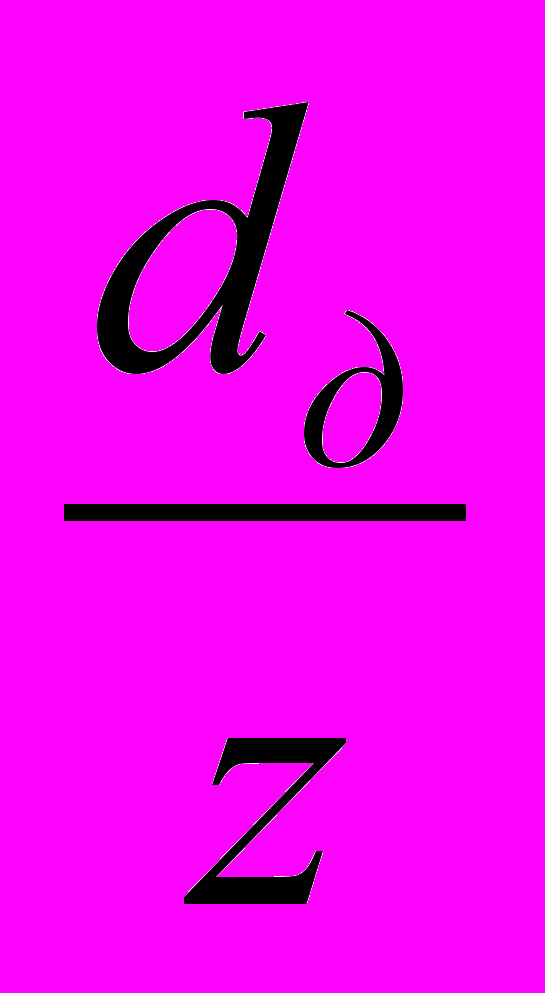мм. Численно модуль равен шагу, деленному на

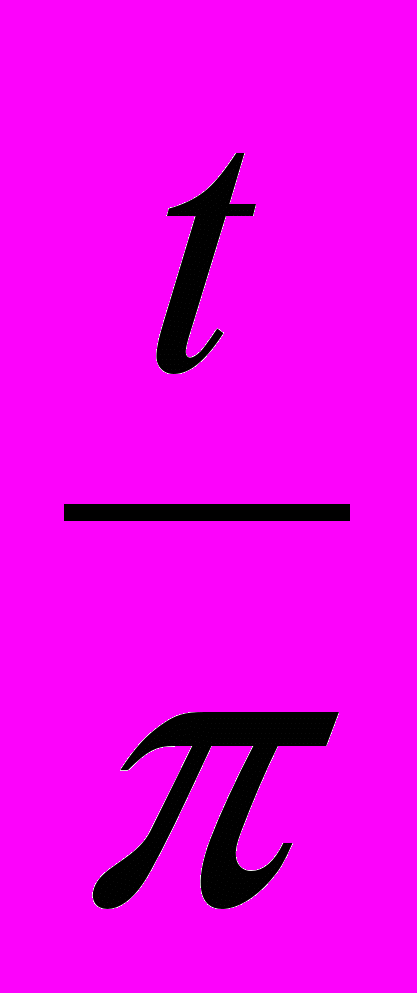: т = мм.

Величина модуля должна равняться указанным в ГОСТе 9563—60. Для цилиндрических колес с косым или шевронным зубом модуль определяется по нормальному шагу. В исключительных случаях допускается определение модуля в торцевом сечении. Для конических зубчатых колес модуль определяется по большему диаметру. Для червячных колес с цилиндрическим червяком модуль определяется в осевом сечении червяка.

МУФТЫ. 1. Устройства и механизмы, соединяющие валы в длину для передачи крутящего момента. Муфты могут включать в себя и предохранительные устройства, защищающие от поломки важные части машины при перегрузках. 2. Соединительные детали (фитинги) для наращивания труб в длину.

Blog

Содержание