Теория приближений
| Вид материала | Литература |
- Диофант (ок. III в.), 37.72kb.
- Паспорт специальности, 52.81kb.
- Правительстве Российской Федерации по адресу: 125468, г. Москва, Ленинградский проспект,, 715.82kb.
- Забрейко Петр Петрович доцент Кожич Павел Павлович Минск 2007 г. Оглавление Оглавление, 254.67kb.
- Хасанов Ильгизар Шамилевич трансакционный сектор экономической системы: национальное, 613.69kb.
- Правительство Российской Федерации Государственный университет Высшая школа экономики, 110.67kb.
- Институционально-экономическое развитие механизмов ценовой конкуренции, 427.47kb.
- Эффективные конструкции диофантовых приближений, 16.15kb.
- Оздоровительно развивающая программа «здравствуй!» Методические рекомендации для педагогов, 419.22kb.
- Теоретическая основа новых педагогических технологий, 40.28kb.
ТЕОРИЯ ПРИБЛИЖЕНИЙ
проф. В.М. Тихомиров
1 год
1. Критерии элементов наилучшего приближения.
2. Полиномы наименее уклоняющиеся от нуля.
3. Линейные функционалы на пространствах полиномов.
4. Неравенства для производных полиномов.
5. Теорема Вейерштрасса.
6. Средства аппроксимации – полиномы, гармоники, сплайны, вейвлеты.
7. Аппроксимация и гладкость (начала конструктивной теории функций).
8. Вложения функциональных пространств.
9. Приближения классов гладких функций суммами Фурье.
10. Уклонения классов гладких функций от пространств полиномов.
11. Поперечники и
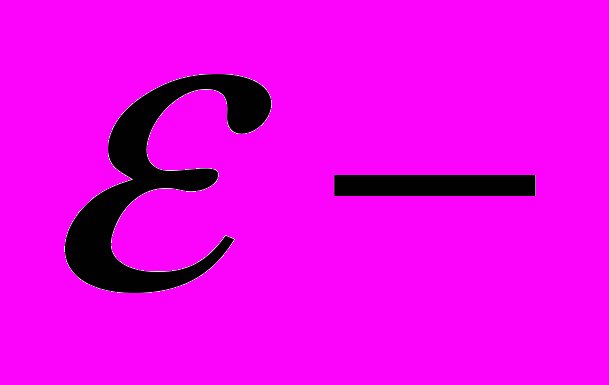энтропия.12. Поперечники конечномерных множеств.
13. Слабая асимптотика поперечников классов гладких функций.
14. Точные значения поперечников в гильбертовом пространстве.
15. Поперечники гладких и аналитических функций в равномерной метрике.
16. Поперечники и спектры.
17. Усреднённые характеристики аппроксимаций.
18. Геометрические аспекты теории приближений.
19. Оптимальное восстановление функционалов.
20. Оптимальное восстановление операторов.
Литература
1. Ахиезер Н.И. Лекции по теории аппроксимации. М., Наука, 1965.
2. Тихомиров В.М. Некоторые вопросы теории приближений. М., изд-во МГУ, 1976.
3. Магарил-Ильяев Г.Г., Тихомиров В.М. Выпуклый анализ и его приложения. М., Эдиториал УРСС, 2003.