Эффективные конструкции диофантовых приближений

Вид материала

Документы

Подобный материал:

• Диофант (ок. III в.), 37.72kb.
• Защита изображений на основе решения систем диофантовых уравнений и неравенств, 31.25kb.
• Удаленного решения линейных диофантовых уравнений в неотрицательных целых числах, 165.6kb.
• Институт Менеджмента Информационных Систем Изучаемая программа, 375.9kb.
• Государственный стандарт союза сср конструкции и изделия бетонные и железобетонные, 138.25kb.
• 6М073000 -производства строительных материалов, изделий и конструкции, 145.77kb.
• Теория приближений, 11.37kb.
• Контрольные вопросы по дисциплине «Строительные конструкции», 27.8kb.
• Лектор: доц. Педиков, 117.83kb.
• Металлические конструкции и их классификация, 34.64kb.

ЭФФЕКТИВНЫЕ КОНСТРУКЦИИ ДИОФАНТОВЫХ ПРИБЛИЖЕНИЙ

проф. Ю.В. Нестеренко

1 год

1. Меры иррациональности и линейной независимости чисел. Обзор свойств непре­рывных дробей (нерегулярные дроби). Непрерывная дробь числа 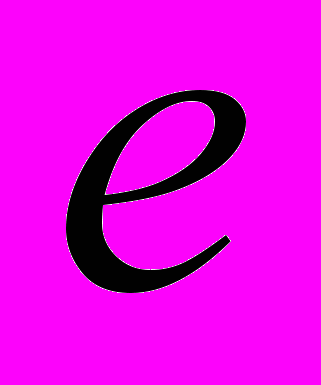и теорема Девиса о рациональных приближениях к 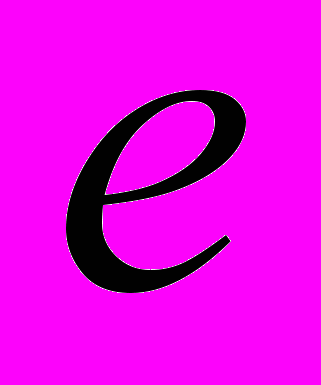. Теорема Тасоева о приближении чисел, представимых непрерывными дробями Гурвица. Показатель иррациональности числа. Теорема Данилова об оценке показателя иррациональности и ее следствия. Оценка показателя иррациональности числа log 2 с помощью непрерывной дроби. Теорема Рухадзе.

2. Гауссова гипергеометрическая функция (обзор свойств). Разложение в непре­рывную дробь отношения гипергеометрических функций. Представление остатков непрерывной дроби в интегральной форме. Теорема о сходимости гауссовой непре­рывной дроби, асимптотика остатков. Непрерывная дробь для гауссовой функции с одним из параметров 1. Теорема Аллади и Робинсона об оценке показателя иррацональности логарифмов рациональных чисел. Показатель иррациональности числа 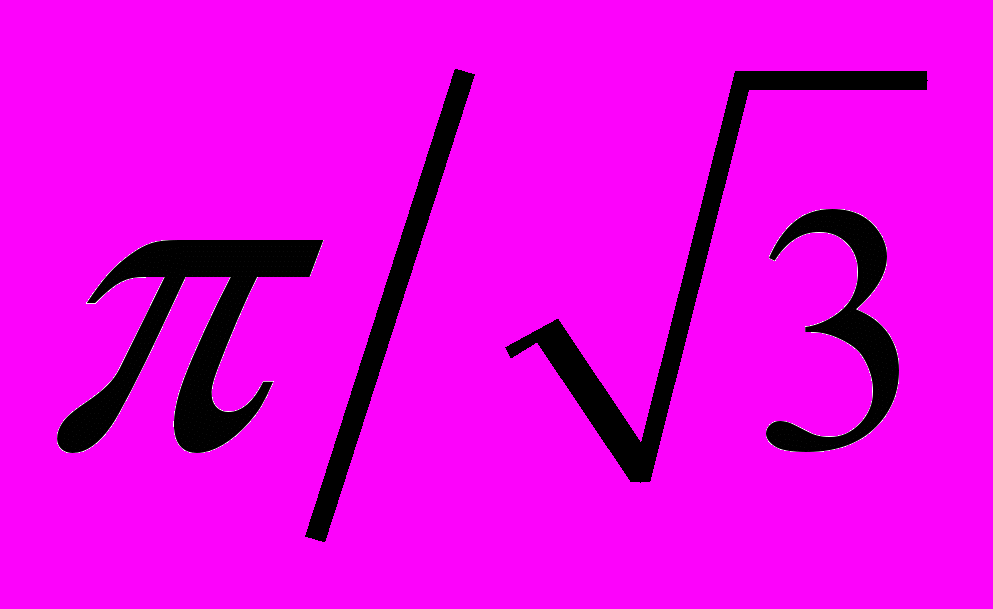. Оценка показателя иррациональности для корней из рациональных чисел. След­ствия для некоторых диофантовых уравнений.

3. Иррациональность 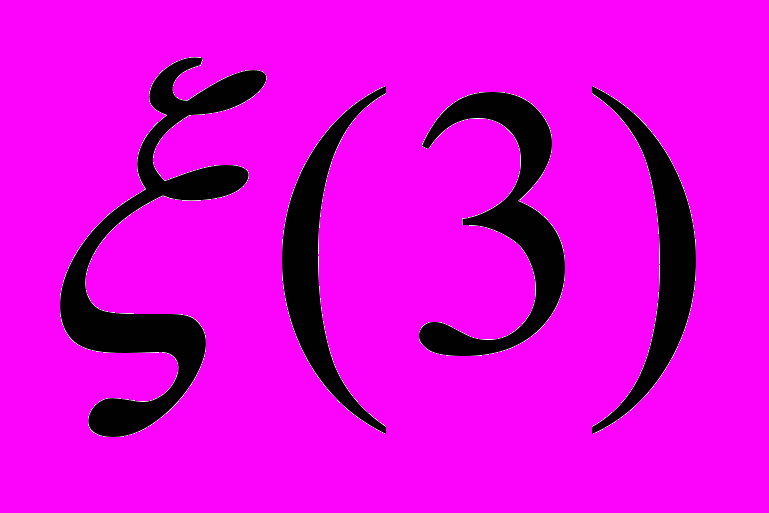и оценка показателя иррациональности этого числа.

4. Конструкция приближений Эрмита-Паде для обобщенных гипергеометрических функций. Многомерные непрерывные дроби и приближения Эрмита-Паде второго рода. Рекуррентные уравнения. Оценки знаменателей и величины коэффициентов приближений Эрмита-Паде. Показатель линейной независимости чисел и его свойства. Общие теоремы об оценке показателя линейной независимости. Оценка показателя линейной независимости для значений обобщенных гипергеометрических функций.

5. Полилогарифмические функции. Теорема о линейной независимости значений полилогарифмов. Конфлюентные гипергеометрические функции. Теорема Коробова-Галочкина о мере линейной независимости значений конфлюентных гипергеометри­ческих Е-функций.

Литература

1. Джоунс У., Трон В. Непрерывные дроби. М., Мир, 1985.

2. Feldman N.I., Nesterenko Yu.V. Transcendental Numbers, in. Encyclopedia of Mathematical Sciences, v. 44, Number Theory IV, Eds. Parshin A.N., Shafarevich I.R., Springer, 1998.