Geum.ru

Российской Федерации " мати"

Вид материалаРабочая учебная программа

Содержание


Вычислительная математика
1. Цели и задачи дисциплины. ее
2. Содержание дисциплины
3. Лабораторные занятия
4. Курсовые работы
Подобный материал:
Министерство образования и науки

Российской Федерации



“МАТИ” – РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ

ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ им. К. Э. ЦИОЛКОВСКОГО

    "УТВЕРЖДАЮ"




    Проректор по учебной работе




    ______________ С. В. Сухов




    "____" _____________ 2004 г.




    Кафедра “Высшая математика”


    Рабочая учебная программа по дисциплине

    ^ ВЫЧИСЛИТЕЛЬНАЯ МАТЕМАТИКА

    Направление: 5528 “Информатика и вычислительная техника”

Специализация: “1кт – Космические телекоммуникации”

    Факультет: № 2

Выпускающая кафедра: КТ

    Форма обучения: очная

    Часов всего по дисциплине: 153

    Цикл дисциплин: ЕНД

    Распределение времени студента по видам учебных занятий

    (часы аудиторных занятий / самостоятельная работа)



      Семестр

      6

    По уч. плану (АР / СР )

      64/89

    Лекции

      32/32

    Практические занятия



    Лабораторные занятия

      32/37

      Курсовая работа

      0/20

      Форма контроля

      экзамен



    Москва 2004 год

Рабочая учебная программа по дисциплине “Вычислительная математика” составлена в соответствии с требованиями Государственного образовательного стандарта и учебному плану по направлению 5528 “Информатика и вычислительная техника”.



Программа составлена: проф. Селиванов Ю. В.

    ст. преп. Балова Е. А.



Рабочая учебная программа рассмотрена кафедрой “Высшая математика” и одобрена 1 июля 2004 г.



    Зав. кафедрой “Высшая математика”

    ____________ К. Ю. Осипенко



Рабочая учебная программа по дисциплине “Вычислительная математика” рассмотрена и признана соответствующей требованиям ГОС и учебному плану по направлению 5528 “Информатика и вычислительная техника”.



    Декан факультета № 2

    ____________ В. П. Соколов


    Программа согласована с НМО

    Учебного управления МАТИ

    ____________ В. М. Морозов


    ^ 1. ЦЕЛИ И ЗАДАЧИ ДИСЦИПЛИНЫ. ЕЕ

    МЕСТО В УЧЕБНОМ ПРОЦЕССЕ



Предметом изучения дисциплины являются основные понятия и методы вычислительной математики. Целью преподавания дисциплины является обеспечение базовой математической подготовки специалистов в соответствии с требованиями Государственного образовательного стандарта РФ и учебному плану по направлению 5528 “Информатика и вычислительная техника”. Основные задачи изучения дисциплины состоят в обучении студентов методам численного решения важнейших математических задач (численные методы алгебры, численные методы в теории приближений, численные методы решения дифференциальных уравнений и их систем), выработке твердых навыков умения провести вычислительный расчет.



    В результате изучения курса студент должен:
  • освоить основные приближенные и численные методы алгебры и математического анализа, используемые в инженерной практике;
  • уметь практически применять эти методы;
  • приобрести твердые навыки организации и проведения вычислительной работы (решения задач вычислительной математики с доведением решения до практически приемлемого результата);
  • выработать начальные навыки математического исследования прикладных вопросов и умение при решении задач выбирать и использовать необходимые вычислительные методы и средства, а также таблицы и справочники.



Учебные дисциплины, владение которыми необходимо для изучения данной дисциплины: курсы математики и физики средней школы, курс алгебры и геометрии и курс математического анализа в МАТИ.



    ^ 2. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ

    6 СЕМЕСТР



Лекции — 32 часа, лабораторные занятия — 32 часа.



    ЛЕКЦИЯ 1. Ошибки. Представление ошибок. Относительные и абсолютные ошибки. Происхождение ошибок. Ошибки информации, ограничения и округления. Выражения для абсолютных и относительных ошибок для арифметических операций.

    ЛЕКЦИИ 2–3. Решение нелинейных уравнений. Корень уравнения. Простые и кратные корни. Геометрическая интерпретация корня уравнения. Локализация корней. Методы приближенного решения нелинейных уравнений: метод половинного деления, метод Ньютона, метод хорд. Скорости сходимости к точному решению.

    ЛЕКЦИИ 4–5. Решение систем линейных уравнений. Метод Гаусса. Итерационный метод Гаусса — Зейделя решения систем линейных уравнений. Решение систем из трех уравнений с тремя неизвестными. Обобщение на системы размерности 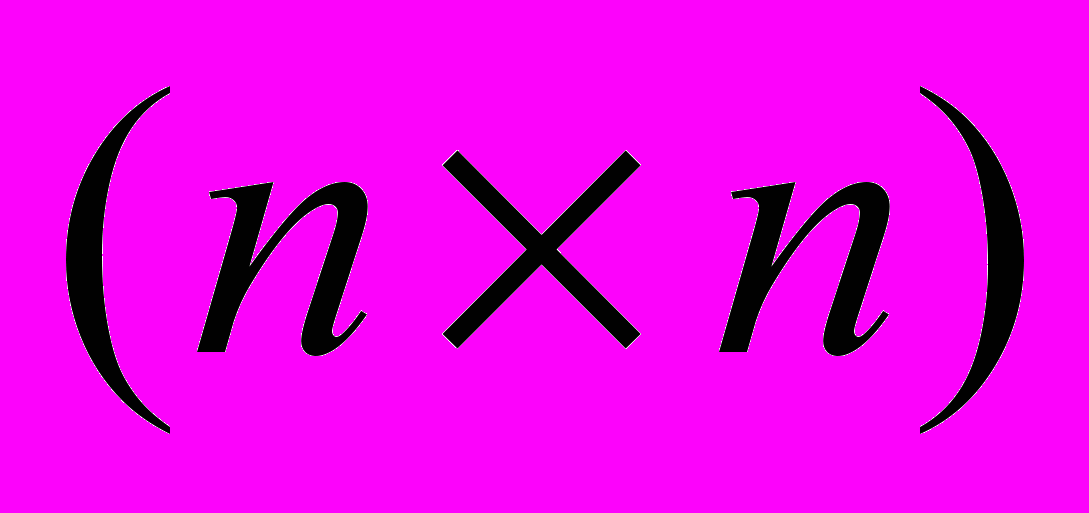. Достаточное условие сходимости метода Гаусса — Зейделя.

    ЛЕКЦИЯ 6. Аппроксимация функций многочленами. Многочлен Тейлора. Интерполяционный многочлен Лагранжа. Погрешность интерполяции.

    ЛЕКЦИЯ 7. Оптимальная интерполяция. Многочлены Чебышева. Интерполяция с равноотстоящими узлами.

    ЛЕКЦИЯ 8. Конечные и разделенные разности. Интерполяционный многочлен Ньютона. Интерполяция в начале и в конце сетки.


ЛЕКЦИЯ 9. Производная, ее геометрический смысл. Численное дифференцирование. Правая и левая разностные производные, центральная разностная производная, их геометрический смысл. Вычисление второй производной.


ЛЕКЦИИ 10–11. Оптимальный выбор шага. Формулы численного дифференцирования, получаемые с помощью интерполяционных многочленов Лагранжа и Ньютона.


    ЛЕКЦИЯ 12. Численное интегрирование. Понятие квадратуры. Основные проблемы численного интегрирования. Формула прямоугольников. Усложненная формула прямоугольников. Оценка погрешностей.

    ЛЕКЦИЯ 13. Квадратурные формулы Ньютона — Котеса. Формулы трапеций и Симпсона, оценка их погрешностей. Усложненные формулы трапеций и Симпсона. Правило Рунге. Уточнение приближенного решения по Ричардсону.

    ЛЕКЦИИ 14–15. Численные методы решения обыкновенных дифференциальных уравнений. Решение задачи Коши с помощью формулы Тейлора. Метод Эйлера и оценка его погрешности. Методы Рунге — Кутта и Адамса. Оценки погрешности одношаговых методов. Особенности интегрирования систем дифференциальных уравнений.

    ЛЕКЦИЯ 16. Метод наименьших квадратов. Линейная и квадратичная функциональные зависимости. Случай показательной функции.

    ^ 3. ЛАБОРАТОРНЫЕ ЗАНЯТИЯ

    ЗАНЯТИЕ 1. Ошибки.

    ЗАНЯТИЯ 2–3. Решение нелинейных уравнений. Выдача КР 1.

    ЗАНЯТИЯ 4–5. Решение систем линейных уравнений.

    ЗАНЯТИЕ 6. Приближение функций с помощью многочлена Тейлора.

    ЗАНЯТИЕ 7. Интерполяционный многочлен Лагранжа. Интерполяция с равноотстоящими узлами.

    ЗАНЯТИЕ 8. Конечные и разделенные разности. Интерполяционный многочлен Ньютона.

    ЗАНЯТИЯ 9–10. Численное дифференцирование.

    ЗАНЯТИЯ 11–12. Численное интегрирование.

    ЗАНЯТИЯ 13–14. Численные методы решения обыкновенных дифференциальных уравнений.

    ЗАНЯТИЯ 15–16. Метод наименьших квадратов. Прием КР 1.

    ^ 4. КУРСОВЫЕ РАБОТЫ



Помимо времени, предусмотренного студентам для подготовки к лекционным и практическим занятиям, предполагается выполнение ими курсовой работы. Она должна способствовать овладению студентами навыками самостоятельной работы и реализации индивидуального творческого мышления по темам курса “Вычислительная математика”.



    Контроль за выполнением курсовой работы проводится в два этапа.

    1). Предварительная проверка правильности письменного решения поставленной задачи;

    2). Защита курсовой работы.



КР 1. Решение нелинейных уравнений и систем уравнений с помощью методов простых итераций, Ньютона, половинного деления, а также с помощью встроенной процедуры root.

[18], § 14, [20], § 6 или [27], § 6.



    Цель задания — освоение студентами различных численных методов решения нелинейных уравнений и систем уравнений.



Литература

Основная

1. Бахвалов Н.С. Численные методы. М., Наука, 1973.

2. Бахвалов Н.С., Жидков Н.П., Кобельников Г.М. Численные методы. М., Наука, 1987.

3. Бахвалов Н.С., Лапин А.В., Чижонков Е.В. Численные методы в задачах и упражнениях. М., Высшая школа, 2000.

4. Березин И.С., Жидков Н.П. Методы вычислений, т.1. М., Наука, 1966.

5. Березин И.С., Жидков Н.П. Методы вычислений, т.2. М., Физматгиз, 1962.

6. Васильев Ф.П. Численные методы решения экстремальных задач. М., Наука, 1980.

7. Волков Е.А. Численные методы. М., Наука, 1982.

8. Годунов С.К., Рябенький В.С. Разностные схемы. М., Наука, 1973.

9. Дегтярев Ю.И. Методы оптимизации. М., Советское радио, 1980.

10. Демидович Б.П., Марон И.А. Основы вычислительной математики. М., Наука, 1966.

11. Марчук Г.И. Методы вычислительной математики. М., Наука, 1989.

    12. Осипенко К.Ю. Аппроксимация функций многочленами и численное дифференцирование. Методические указания по курсу “Численные методы”. М., МАТИ, 1994.

13. Осипенко К.Ю. Квадратурные формулы. Методические указания по курсу “Численные методы”. М., МГАТУ, 1995.

 

Дополнительная

14. Амосов А.А., Дубинский Ю.А., Копченова Н.В. Вычислительные методы для инженеров. М., Высшая школа, 1994.

15. Винокуров В.А., Горбацевич В.В., Тайманов В.А. Численные методы решения обыкновенных дифференциальных уравнений. Методические указания к лабораторной работе по курсу “Высшая математика”. М., МАТИ, 1988.

16. Жемерев А.В. Методические указания к выполнению лабораторной работы “Проведение вычислений в математическом пакете Mathcad”. М., МАТИ, 2000.

17. Жуков А.А., Осипенко К.Ю. Сплайн-интерполяция функций. Методические указания к лабораторной работе по курсу “Высшая математика”. М., МАТИ, 1989.

18. Зотов В.А. Методические указания и варианты домашних заданий по курсу “Вычислительная техника в инженерных и экономических расчетах”. Ч. I. “Численные методы решения алгебраических уравнений и систем уравнений”. М., МАТИ, 1983.

19. Зотов В.А. Методические указания и варианты домашних заданий по курсу “Вычислительная техника в инженерных и экономических расчетах”. Ч. II. “Аппроксимация функций, численное дифференцирование и интегрирование”. М., МАТИ, 1983.

20. Зотов В.А. Численные методы решения алгебраических уравнений и трансцендентных уравнений. Методические указания к лабораторной работе по курсу “Вычислительная техника в инженерных и экономических расчетах”. М., МАТИ, 1986.

21. Емельянова Н.З., Никулин А.М. Введение в Mathcad (Общие положения, функциональные возможности). Методические указания к лабораторной работе по курсу “Информатика”. М., МАТИ, 1999.

    22. Макаров Г.Д. Методические указания к выполнению лабораторной работы “Численные методы решения алгебраических и трансцендентных уравнений”. М., МАТИ, 1985.

23. Мысовских И.П. Лекции по методам вычисления. 2-е изд. М., Наука, 1994, (учебное пособие).

24. Плис А.И., Сливина Н.А. Лабораторный практикум по высшей математике. М., Наука, 1994.

25. Плис А.И., Сливина Н.А. Mathcad: математический практикум для экономистов и инженеров. М., Финансы и статистика, 1999.

26. Рябенький В.С. Введение в вычислительную математику. М., Наука, 1993.

27. Румшиский Л.З. Вычислительный лабораторный практикум по курсу высшей математики для втузов. М., Физматгиз, 1961.