Российской Федерации " мати"
| Вид материала | Рабочая учебная программа |
- Российской Федерации " мати", 90.04kb.
- Российской Федерации " мати", 84.47kb.
- В российской федерации, 645.64kb.
- Российской Федерации «мати», 79.28kb.
- Российской Федерации " мати", 150.39kb.
- Российской Федерации " мати", 249.71kb.
- Российской Федерации " мати", 202.31kb.
- Российской Федерации «мати», 105.42kb.
- Российской Федерации «мати», 66.69kb.
- Российской Федерации " мати", 205.88kb.
Министерство образования Российской Федерации
“МАТИ” - РОССИЙСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ им. К. Э. ЦИОЛКОВСКОГО
| | "УТВЕРЖДАЮ" |
| | Проректор по учебной работе |
| | ___________ В. Ф. Мануйлов |
| | "____" _____________ 2001 г. |
Кафедра “Высшая математика”
Рабочая учебная программа по дисциплине
"Математический анализ"
специальность 0104 "Физика"
Часов всего: 472
Дисциплина: по выбору
Цикл: Е
курс 1,2
-
Семестр
1
2
3
4
Итого
Всего часов
108
119
126
119
472
Всего: (ауд./с.р)
64/44
64/55
64/62
64/55
256/216
Лекции (ауд./с.р)
32/22
32/18
32/21
32/18
128/79
Лабораторные
работы (ауд./с.р)
-
-
-
-
-
Практические
занятия(ауд./с.р)
32/22
32/17
32/21
32/17
128/77
Курсовая работа (ауд./с.р)
-
0/20
0/20
0/20
0/60
Курсовой проект(ауд./с.р)
-
-
-
-
-
Форма контроля
Экз
экз
экз
экз
экз
Москва 2001 год
Рабочая учебная программа составлена в соответствии с требованиями
Государственного образовательного стандарта РФ (ГОС) и учебного плана
по специальности 0104 "Физика"
Программа составлена: проф., д.ф.-м.н. Шифриным Е.И.
Рабочая учебная программа рассмотрена кафедрой "Высшая математика"
и одобрена 2001 г.
Зав. кафедрой "Высшая математика" _______________ (Осипенко К.Ю.)
Рабочая программа рассмотрена методической комиссией факультета No 1
и признана соответствующей требованиям ГОС и учебному плану по
специальности 0104 "Физика"
Декан факультета _______________ (Фролов В.А.)
Программа согласована с НМО Учебного управления
_______________ (Морозов В.М.)
1. ЦЕЛИ И ЗАДАЧИ ДИСЦИПЛИНЫ. ЕЕ МЕСТО В УЧЕБНОМ ПРОЦЕССЕ.
1.1.Цели преподавания дисциплины.
Предметом изучения дисциплины является изложение фундаментальных основ математического анализа и вычислительных методов решения задач, связанных с физическими задачами в авиационной и космической технике. Целью преподавания курса высшей математики является формирование у студентов логического и творческого мышления, навыков доказательства теорем, опыта
формализации инженерно - технических и прикладных физических задач, исследования и решения их современными аналитическими методами.
1.2. Задачи изучения курса.
В результате изучения курса студент должен
ЗНАТЬ:
- содержание и прикладное значение основ математического анализа;
- основные приемы качественного и количественного анализа прикладных задач;
- методы формализации задач;
- какие методы целесообразны при решении конкретных задач.
УМЕТЬ:
- формализовать инженерную или прикладную физическую задачу;
- владеть логикой доказательства теорем;
- выбирать наиболее эффективные способы решения задач.
2. СОДЕРЖАНИЕ ДИСЦИПЛИНЫ.
2.1. Наименование тем, их содержание, объем в часах лекционных и практических занятий.
2.2. Список контрольных мероприятий (курсовых работ).
2.3. Рекомендуемая литература.
2.1. 1 СЕМЕСТР
Лекции - 32 часа, практика - 32 часа.
ЛЕКЦИИ
ЛЕКЦИЯ 1. Предмет математики. Физические явления как источник математических понятий. Понятие множества. Операции над множествами и их свойства. Отображение множеств. Общее понятие функции.
ЛЕКЦИЯ 2. Эквивалентность множеств. Теорема Кантора - Бернштейна. Понятие мощности множества. Счетные множества.
ЛЕКЦИЯ 3. Аксиоматическое введение множества вещественных чисел.Ограниченные числовые множества. Понятие точной верхней и точной нижней граней и их арифметические свойства. Принцип Архимеда.
ЛЕКЦИЯ 4. Теорема о вложенных отрезках. Покрытие отрезка интервалами. Теорема о выборе конечного подпокрытия. Комбинаторика. Метод математической индукции. Бином Ньютона.
ЛЕКЦИИ 5. Понятие предельной точки и предела последовательности. Теорема о единственности предела. Ограниченность сходящейся последовательности. Критерий Коши сходимости последовательности. Переход к пределу в неравенствах. Свойства пределов, связанные с арифметическими действиями над числовыми последовательностями.
ЛЕКЦИЯ 6. Монотонные последовательности. Предел монотонной последовательности. Число. Пределы некоторых последовательностей
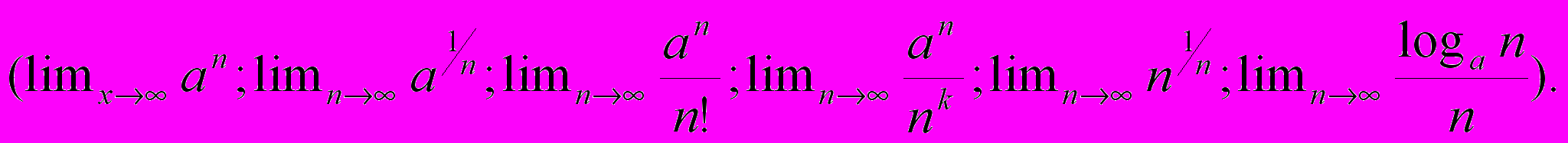
ЛЕКЦИЯ 7. Числовые ряды. Критерий Коши сходимости ряда. Необходимое условие сходимости. Расходимость гармонического ряда. Ряды с неотрицательными членами. Признаки сравнения. Сходимость ряда
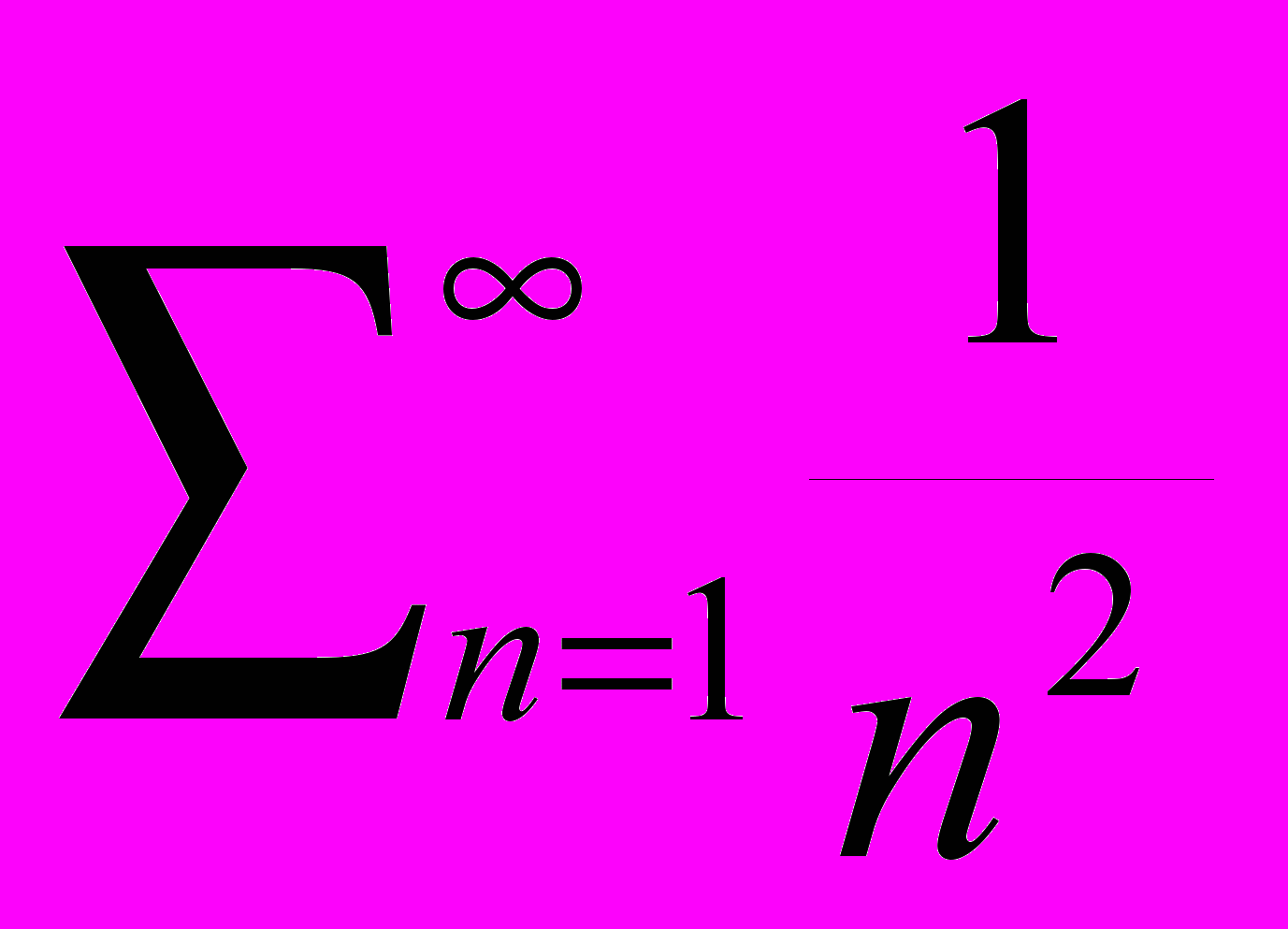
ЛЕКЦИЯ 8. Признак Даламбера. Признак Коши. Знакопеременные ряды. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимость рядов. Лемма Абеля. Признак Дирихле. Признак Абеля.
ЛЕКЦИЯ 9. Предел функции. Определение предела по Коши и по Гейне, их эквивалентность. Критерий Коши существования предела функции. Свойства пределов функции.
ЛЕКЦИЯ 10. Понятие бесконечно малых и бесконечно больших функций, их свойства. Сравнение функций в окрестности заданной точки. Первый замечательный предел. Односторонние пределы.
ЛЕКЦИЯ 11. Монотонные функции. Предел монотонной функции. Определение показательной функции и ее свойства. Второй замечательный предел.
ЛЕКЦИЯ 12. Непрерывность функции в точке. Свойства непрерывности. Классификация точек разрыва. Теорема об ограниченности и достижении наибольшего и наименьшего значений функцией, непрерывной на отрезке. Теорема о равномерной непрерывности функции, непрерывной на отрезке.
ЛЕКЦИЯ 13. Теорема о промежуточных значениях функции, непрерывной на отрезке. Теорема о существовании, монотонности и непрерывности функции, обратной к строго монотонной и непрерывной на отрезке функции. Непрерывность элементарных функций. Гиперболические функции.
ЛЕКЦИЯ 14. Дифференцируемость функции в точке. Непрерывность функции в точке существования производной. Геометрический и механический смысл производной. Свойства производной, связанные с арифметическими действиями. Производная обратной функции. Производная сложной функции. Производные элементарных функций.
ЛЕКЦИЯ 15. Понятие дифференциала функции в точке, его геометрический и механический смысл. Дифференциал сложной функции. Производные функций, заданных параметрически. Производные высших порядков от суммы и произведения функций. Производные высших порядков от сложной, обратной и параметрически заданных функций. Дифференциалы высших порядков.
ЛЕКЦИЯ 16. Понятие локального экстремума функции. Теорема Ферма. Теорема Ролля. Теорема Лагранжа. Теорема Коши. Раскрытие неопределенностей по правилу Лопиталя случаи
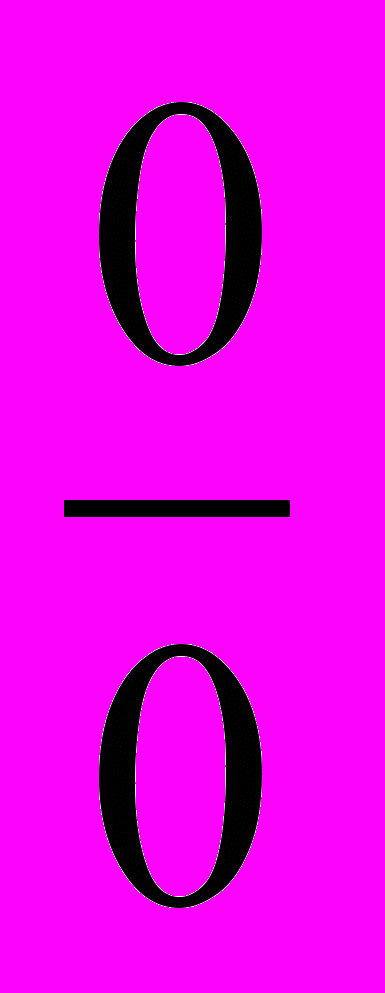 и
и 
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
ЗАНЯТИЕ 1. Множества, операции над ними.
ЗАНЯТИЕ 2. Мощность множества. Счетные множества.
ЗАНЯТИЕ 3. Верхние и нижние грани числовых множеств.
ЗАНЯТИЕ 4. Метод математической индукции. Комбинаторика. Бином Ньютона.
ЗАНЯТИЯ 5-6. Вычисление пределов последовательностей.
ЗАНЯТИЕ 7. Вычисление сумм простейших числовых рядов. Исследование на сходимость рядов с неотрицательными членами. Признаки Даламбера и Коши.
ЗАНЯТИЕ 8. Исследование на сходимость знакопостоянных рядов. Признаки сравнения. Исследование на сходимость знакопеременных рядов. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимость.
ЗАНЯТИЕ 9. Понятие предела функции. Вычисление пределов (простейшие случаи ).
ЗАНЯТИЕ 10. Предел функции ( продолжение ). Замечательные пределы.
ЗАНЯТИЕ 11. Сравнение бесконечно малых, применение к вычислению пределов.
ЗАНЯТИЕ 12. Понятие непрерывной функции. Классификация точек разрыва.
ЗАНЯТИЕ 13. Производная, ее вычисление.
ЗАНЯТИЕ 14. Дифференцирование параметрически заданных функций. Дифференциал и его применение для приближенного вычисления функций.
ЗАНЯТИЕ 15. Производные и дифференциалы высших порядков.
ЗАНЯТИЕ 16. Вычисление пределов функции с помощью правила Лопиталя.
2 СЕМЕСТР
Лекции - 32 часа, практика - 32 часа.
ЛЕКЦИИ
ЛЕКЦИЯ 1. Многочлен Тейлора. Формула Тейлора с остаточным членом в форме Пеано. Единственность представления. Разложение по формуле Тейлора элементарных функций.
ЛЕКЦИЯ 2. Применение метода выделения главной части для вычисления пределов. Разложение по формуле Тейлора с остаточным членом в форме Лагранжа. Разложение по формуле Тейлора с остаточным членом в форме Коши. Ряд Тейлора. Достаточные условия сходимости ряда Тейлора. Разложение в ряд Тейлора элементарных функций.
ЛЕКЦИИ 3-4. Признак монотонности функции. Необходимое и достаточное условия локального экстремума. Выпуклость вверх и выпуклость вниз функции, достаточные условия. Точка перегиба. Необходимое и достаточные условия. Асимптоты, их нахождение.
ЛЕКЦИЯ 5. Комплексные числа. Операции над ними. Геометрическая интерпретация. Тригонометрическая форма записи комплексных чисел. Формула Муавра. Показательная функция комплексного переменного. Формула Эйлера.
ЛЕКЦИИ 6-7. Многочлены. Деление многочленов с остатком. Свойства делимости. Наибольший общий делитель многочленов, его существование. Взаимно простые многочлены. Корни многочленов. Теорема Безу. Основная теорема алгебры и ее следствие. Многочлены с действительными коэффициентами. Рациональные функции. Правильные и простейшие дроби. Теорема о разложении правильной дроби в сумму простейших.
ЛЕКЦИЯ 8. Первообразная, неопределенный интеграл и их свойства. Таблица интегралов.
ЛЕКЦИЯ 9. Замена переменной в неопределенном интеграле. Интегрирование по частям. Интегрирование рациональных функций.
ЛЕКЦИЯ 10. Методы вычисления неопределенных интегралов. Интегрирование дробно - линейных иррациональностей. Интегрирование дифференциального бинома. Интегрирование тригонометрических выражений. Интегрирование квадратичных иррациональностей.
ЛЕКЦИЯ 11. Определенный интеграл Римана. Теорема об ограниченности интегрируемых функций. Верхние и нижние суммы Дарбу и их свойства. Верхние и нижние интегралы.
ЛЕКЦИЯ 12. Необходимое и достаточное условие интегрируемости функций. Интегрируемость непрерывных функций. Интегрируемость монотонных функций.
ЛЕКЦИЯ 13. Свойства определенного интеграла ( линейность, аддитивность, интегрируемость модуля интегрируемой функции, интегрируемость функции, отличающейся от интегрируемой лишь в конечном числе точек ). Интегрируемость кусочно - непрерывной функции.
ЛЕКЦИЯ 14. Свойства определенного интеграла (интегрирование неравенств, интегрируемость произведения интегрируемых функций, интегральная теорема о среднем). Непрерывность интеграла, как функции верхнего ( нижнего ) предела.
ЛЕКЦИЯ 15. Дифференцируемость интеграла по верхнему ( нижнему ) пределу. Формула Ньютона - Лейбница. Замена переменной в определенном интеграле. Формула интегрирования по частям. Формула Валлиса. Формула Стирлинга.
ЛЕКЦИЯ 16. Геометрические приложения определенного интеграла.
Понятие длины кривой и ее вычисление. Понятие площади плоского множества. Площадь криволинейной трапеции. Вычисление площадей в полярных координатах. Вычисление площади плоской области в случае, когда ограничивающий ее контур задан параметрически. Понятие объема трехмерной области. Объем тел вращения. Площадь поверхности тела вращения.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
ЗАНЯТИЕ 1. Формула Тейлора. Вычисление пределов с помощью формулы Тейлора.
ЗАНЯТИЯ 2-3. Исследование функций и построение их графиков.
Выдача КР2.
ЗАНЯТИЯ 4-5. Операции над комплексными числами. Тригонометрическая форма записи комплексных чисел. Геометрическая интерпретация.
ЗАНЯТИЕ 6. Нахождение наибольших общих делителей многочленов. Разложение рациональных функций на простейшие дроби.
ЗАНЯТИЕ 7. Вычисление неопределенных интегралов. Замена переменной. Интегрирование по частям.
ЗАНЯТИЕ 8. Интегрирование рациональных функций.
ЗАНЯТИЕ 9. Интегрирование тригонометрических функций.
ЗАНЯТИЕ 10. Интегрирование дробно - линейных и квадратичных иррациональностей.
ЗАНЯТИЕ 11. Интегрирование дифференциального бинома. Интегрирование гиперболических функций.
ЗАНЯТИЕ 12. Смешанные задачи на интегрирование.
ЗАНЯТИЯ 13-14. Вычисление определенных интегралов.
ЗАНЯТИЯ 15-16. Геометрические приложения определенных интегралов.
Прием КР2.
3 СЕМЕСТР
Лекции - 32 часа, практика - 32 часа.
ЛЕКЦИИ
ЛЕКЦИЯ 1. Несобственные интегралы, их типы и свойства. Примеры несобственных интегралов. Критерий Коши. Замена переменных и интегрирование по частям в несобственных интегралах.
ЛЕКЦИЯ 2. Признаки сходимости несобственных интегралов. Интегралы от
неотрицательных функций. Признаки сравнения. Сходимость интеграла от функции в случае, когда интеграл от ее модуля сходится. Абсолютная и условная сходимость. Признаки Дирихле и Абеля. Числовые ряды с неотрицательнымичленами. Интегральный признак сходимости.
ЛЕКЦИЯ 3. Понятие метрического пространства. Арифметическое n - мерное пространство. Сходимость последовательности в метрическом пространстве и Rn . Критерий Коши. Открытые и замкнутые множества, их свойства. Линейно связные множества. Понятие компакта. Теорема о компактности ограниченного и замкнутого множества в Rn .
ЛЕКЦИЯ 4. Функции многих переменных. Предел функции и его свойства. Непрерывность функции многих переменных в точке. Свойства непрерывных функций. Непрерывность композиции непрерывных функций. Непрерывность элементарных функций.
ЛЕКЦИЯ 5. Теорема об ограниченности и достижении наибольшего и наименьшего значений функцией, непрерывной на компакте. Теорема о промежуточных значениях функции, непрерывной на линейно связном множестве. Теорема о равномерной непрерывности функции, непрерывной на компакте. Частные производные. Дифференцируемость функции многих переменных в точке. Непрерывность дифференцируемой функции.
ЛЕКЦИЯ 6. Достаточное условие дифференцируемости функции многих переменных. Дифференцируемость композиции функций многих переменных. Дифференциал функции многих переменных. Инвариантность формы первого дифференциала. Геометрический смысл частных производных и дифференциала. Касательная плоскость, нормаль к поверхности. Производная по направлению. Градиент и его свойства.
ЛЕКЦИЯ 7. Частные производные высших порядков. Теорема о независимости смешанных производных от порядка дифференцирования. Дифференциалы высших порядков от функций многих переменных. Формула Тейлора с остаточными членами в форме Лагранжа и Пеано для функций многих переменных.
ЛЕКЦИЯ 8. Локальный экстремум функции многих переменных. Необходимое условие экстремума. Достаточное условие существования локального экстремума.
ЛЕКЦИЯ 9. Неявные функции, задаваемые одним уравнением. Теорема о существовании и непрерывности неявной функции. Дифференцирование неявной функции, задаваемой одним уравнением.
ЛЕКЦИЯ 10. Неявные функции, задаваемые системой уравнений. Матрица Якоби и якобиан системы функций. Условия разрешимости. Свойства якобианов отображений.
ЛЕКЦИЯ 11. Условный экстремум функций многих переменных. Метод неопределенных множителей Лагранжа. Необходимое и достаточное условия существования условного экстремума.
ЛЕКЦИЯ 12. Интегралы, зависящие от параметра. Собственные интегралы с постоянными пределами интегрирования, зависящие от параметра. Теореиы о непрерывности, дифференцируемости и перестановке порядка интегрирования. Собственные интегралы, зависящие от параметра, пределы интегрирования которых также зависят от параметра. Теоремы о непрерывности и дифференцируемости по параметру.
ЛЕКЦИЯ 13. Несобственные интегралы, зависящие от параметра. Область сходимости. Равномерная сходимость. Критерий Коши равномерной сходимости. Признаки равномерной сходимости. Признак Вейейрштрасса. Признак Дирихле. Теорема о непрерывности, дифференцируемости и перестановке порядка интегрирования.
ЛЕКЦИЯ 14. Применение свойств интегралов, зависящих от параметра, к вычислению интегралов. Вычисление интеграла Дирихле и интеграла Эйлера - Пуассона. Бета и гамма - функции и их свойства.
ЛЕКЦИЯ 15. Функциональные последовательности и ряды. Равномерная сходимость. Критерий Коши. Признаки равномерной сходимости. Признак Вейерштрасса. Признаки Дирихле и Абеля.
ЛЕКЦИЯ 16. Теоремы о непрерывности суммы равномерно сходящегося ряда непрерывных функций. Теоремы о почленном интегрировании и дифференцировании равномерно сходящихся рядов.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
ЗАНЯТИЕ 1. Исследование на сходимость несобственных интегралов. Исследование на абсолютную и условную сходимость.
ЗАНЯТИЯ 2-3. Исследование сходимости числовых рядов при помощи интегрального признака. Вычисление несобственных интегралов. Решение некоторых механических задач, приводящих к вычислению несобственных интегралов.
Выдача КР3.
ЗАНЯТИЕ 4. Функции многих переменных. Вычисление повторных пределов и пределов.
ЗАНЯТИЕ 5. Частные производные. Дифференциал функции многих переменных. Приближенное вычисление функции при помощи дифференциала. Производные и дифференциалы высших порядков.
ЗАНЯТИЕ 6. Дифференцирование сложной функции. Касательная плоскость и нормаль к поверхности.
ЗАНЯТИЕ 7. Производная функции по направлению. Градиент и его свойства.
ЗАНЯТИЕ 8. Неявные функции и их дифференцирование.
ЗАНЯТИЕ 9. Экстремум функции многих переменных.
ЗАНЯТИЕ 10. Условный экстремум. Метод неопределенных множителей Лагранжа.
ЗАНЯТИЯ 11-12. Собственные интегралы, зависящие от параметра. Вычисление пределов и дифференцирование по параметру. Вычисление интегралов путем дифференцирования по параметру и перестановки порядка интегрирования.
ЗАНЯТИЕ 13. Несобственные интегралы, зависящие от параметра. Нахождение области сходимости, исследование на равномерную сходимость.
ЗАНЯТИЕ 14. Дифференцирование и интегрирование по параметру несобственных интегралов, их вычисление.
ЗАНЯТИЕ 15. Определение области сходимости и исследование на равномерную сходимость функциональных последовательностей и рядов.
ЗАНЯТИЕ 16. Степенные ряды. Разложение функции в ряд Тейлора. Приближенное вычисление интегралов путем разложения интегрируемой функции в ряд.
Прием КР3.
4 СЕМЕСТР
Лекции - 32 часа, практика - 32 часа.
ЛЕКЦИИ
ЛЕКЦИЯ 1. Функциональные пространства. Скалярное произведение. Ортогональные и ортонормированные системы. Процесс ортогонализации. Примеры ортогональных систем функций. Коэффициенты Фурье. Единственность представления функции с помощью равномерно сходящегося на отрезке ряда по ортогональным функциям. Минимальное свойство коэффициентов Фурье. Неравенство Бесселя.
ЛЕКЦИЯ 2. Тригонометрический ряд Фурье. Свойства коэффициентов Фурье. Сходимость суммы квадратов коэффициентов Фурье для интегрируемой функции. Стремление к нулю последовательности коэффициентов Фурье. Ядро Дирихле. Сходимость ряда Фурье в точке.
ЛЕКЦИЯ 3. Принцип локализации. Ряды Фурье для четных и нечетных функций. Ряды Фурье для функций с произвольным периодом. Примеры разложения функций в ряд Фурье. Комплексная форма ряда Фурье. Условия равномерной сходимости ряда Фурье. Скорости стремления коэффициентов Фурье к нулю в зависимости от гладкости функции.
ЛЕКЦИЯ 4. Сходимость в среднем. Теорема о сходимости в среднем равномерно сходящейся последовательности функций. Полные и замкнутые системы функций. Равенство Парсеваля. Сходимость ряда Фурье в среднем - необходимое и достаточное условие замкнутости ортогональной системы. Равенство Парсеваля - необходимое и достаточное условие замкнутости ортогональной системы. Замкнутость тригонометрической системы функций.
ЛЕКЦИИ 5-6. Интеграл Фурье. Преобразование Фурье и его свойства.
ЛЕКЦИЯ 7. Мера плоских компактов, ее свойства.
ЛЕКЦИЯ 8. Двойные интегралы. Геометрический смысл. Примеры интегрируемых и неинтегрируемых функций. Верхние и нижние суммы Дарбу. Критерий интегрируемости ограниченной функции. Интегрируемость непрерывной функции.
ЛЕКЦИЯ 9. Свойства двойных интегралов. Теорема о среднем. Вычисление двойного интеграла в декартовых координатах. Сведение двойного интеграла к повторному.
ЛЕКЦИЯ 10. Замена переменных в двойном интеграле. Переход к полярным координатам. Криволинейные координаты. Геометрический смысл якобиана.
ЛЕКЦИЯ 11. Мера трехмерных компактов. Тройные интегралы, их свойства.
Вычисление тройных интегралов в декартовых координатах. Замена переменных в тройном интеграле. Переход к цилиндрическим и сферическим координатам. Механические приложения кратных интегралов.
ЛЕКЦИЯ 12. Криволинейные интегралы 1 - го рода. Криволинейные интегралы 2 - го рода, их свойства. Формула Грина. Условия независимости интеграла 2 - го рода от пути интегрирования. Механические приложения криволинейных интегралов.
ЛЕКЦИЯ 13. Поверхности. Первая квадратичная форма поверхности. Длина кривых на поверхности. Площадь поверхности. Ориентация поверхности.
ЛЕКЦИЯ 14. Поверхностные интегралы 1 - го и 2 - го рода. Представление поверхностных интегралов в виде двойных интегралов. Скалярные и векторные поля. Понятия дивергенции, циркуляции и потока векторного поля.
ЛЕКЦИЯ 15. Формула Гаусса - Остроградского. Формула Стокса.
ЛЕКЦИЯ 16. Регуляризация расходящихся интегралов. Основные понятия теории обобщенных функций.
ПРАКТИЧЕСКИЕ ЗАНЯТИЯ
ЗАНЯТИЯ 1-2. Разложение функций в тригонометрический ряд Фурье.
ЗАНЯТИЕ 3. Преобразование Фурье и его обращение.
ЗАНЯТИЕ 4. Вычисление двойных интегралов в декартовых координатах.
Выдача КР4.
ЗАНЯТИЕ 5. Замена переменных в двойном интеграле.
ЗАНЯТИЕ 6. Вычисление площадей плоских областей.
ЗАНЯТИЕ 7. Вычисление тройных интегралов в декартовых координатах.
ЗАНЯТИЕ 8. Замена переменных в тройном интеграле.
ЗАНЯТИЕ 9. Геометрические и механические приложения кратных интегралов.
ЗАНЯТИЕ 10. Вычисление криволинейных интегралов 1 - го рода.
ЗАНЯТИЕ 11. Вычисление криволинейных интегралов 2 - го рода.
ЗАНЯТИЕ 12. Формула Грина. Механические приложения криволинейных интегралов.
ЗАНЯТИЕ 13. Вычисление поверхностных интегралов 1 - го рода.
ЗАНЯТИЕ 14. Вычисление поверхностных интегралов 2 - го рода.
ЗАНЯТИЕ 15. Формулы Гаусса - Остроградского и Стокса.
ЗАНЯТИЕ 16. Приложения поверхностных интегралов.
Прием КР4.
2.2 КУРСОВЫЕ РАБОТЫ
2 СЕМЕСТР
КР 2. Работа состоит из трех разделов:
- исследование функций и построение их графиков;
- вычисление неопределенных интегралов;
- вычисление определенных интегралов.
Литература [4, раздел III, задачи 1 - 3, 5 - 10; раздел IV задачи 1, 3, 5, 6, 7, 13; раздел IV 2, 4, 8 - 12]
3 СЕМЕСТР
КР 3. Работа состоит из трех разделов:
- геометрические приложения определенных интегралов;
- исследование на сходимость и вычисление несобственных интегралов;
- дифференцирование функций многих переменных, нахождение их безусловных и условных экстремумов.
Литература [4, раздел IV, задачи 14 - 21]; [ 2, часть 1, отдел IV, п. 4];
[4, раздел VIII, задачи 1, 2], [2, часть 2, отдел VI, п. 7].
4 СЕМЕСТР
КР 4. Работа состоит из трех разделов:
- нахождение области сходимости функциональных рядов, степенные ряды, приближенное вычисление интегралов.
- кратные интегралы;
- криволинейные и поверхностные интегралы.
Литература [ 4, раздел VI, задачи 9 - 11, 14, 15; раздел VII, задачи 1 - 16; раздел VIII, задачи 4 - 12 ].
2.3 РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
1. Кудрявцев Л.Д. Краткий курс математического анализа. Изд - во Alfa, 1998, Т. 1, 2.
2. Демидович Б.П. Сборник задач и упражнений по математическому анализу. М., Наука, 1977.
3. Сборник задач по математике для втузов. Специальные разделы
математического анализа. (под ред. А.В.Ефимова, .П.Демидовича). М., Наука, 1981.
4. Кузнецов Л.А. Сборник заданий по высшей математике. Типовы расчеты. М., Высшая школа, 1994.
5. Бугров Я.С., Никольский С.М. Дифференциальное и интегральное исчисление. М., Наука, 1988.
6. Бугров Я.С., Никольский С.М. Дифференциальные уравнения.
Кратные интегралы. Ряды функции комплексного переменного. М.,Наука, 1985.
7. Берман Г.И. Сборник задач по курсу математического анализа. М., Наука,1973.
