М. В. Ломоносова В. И. Добреньков, А. И. Кравченко методы социологического исследования учебник

Вид материала

Учебник

Содержание Возраст, годы Глава 4. Анализ эмпирических данных Возраст, годы Таблица 4.15 Связь между образованием и Число лет образования (независимая переменная)

Подобный материал:

• Незарегистрированный брак как социальный механизм формирования брачно-семейных отношений, 370.79kb.
• Новые поступления литературы в библиотеку Ургупс в декабре 2006 года с социология, 276.4kb.
• Рабочий план социологического исследования. Функции и основные элементы программы социологического, 17.2kb.
• Программа социологического исследования. 27 Методы сбора социологической информации, 666.33kb.
• Гергенрейдер Татьяна Владимировна программа А. И. Кравченко «Обществознание», учебник, 53.33kb.
• Правительстве Российской Федерации ; под ред. О. И. Лаврушина. 7-е изд., перераб, 187.02kb.
• Особенности программы исследования кадровой деятельности. Методы социологического анализа, 29.53kb.
• Автор программы: Даудрих Н. И. Рекомендована секцией умс, 522.38kb.
• Программа дисциплины «Модели объяснения и логика социологического исследования» для, 127.71kb.
• Отчет о ходе и результате социологического исследования. Анкета (опросный лист), 138.6kb.

210

Такая таблица называется «кросстаб»²⁰, а процесс ее созда­ния — «кросстабуляция». Это один из основных способов ана­лиза, используемых для того, чтобы увидеть, какую связь пе­ременные имеют друг с другом. Вообще говоря, категории не­зависимой переменной могут размещаться как по строкам, так и по столбцам (или, что то же самое, — графам) кросстаба. Обычно независимую переменную помещают в верхней части кросстаба, формируя таким образом столбцы из значений зави­симой переменной. Однако на практике — чаще всего из сооб­ражений удобства — для наглядности и для того, чтобы умес­тить кросстаб на одной странице, его иногда конструируют так, чтобы сверху вниз шла переменная с большим числом категорий (т.е. значений, которые может принимать переменная). Реаль­но, конечно, не имеет значения, как будет сконструирован кросстаб: имея независимую переменную в верхней части таб­лицы (по горизонтали) или сверху вниз (по вертикали). Глав­ное — соблюсти правило: когда выбор сделан, процентные от­ношения в таблице должны вычисляться таким образом, что­бы проверить наличие связи. Давайте на примере кросстаба 17 посмотрим, как производится чтение таблицы — процесс, в ходе которого и выявляется наличие или отсутствие связи между переменными и ее параметры.

Прежде всего обратим внимание на крайний правый столбец и две нижние строки. Здесь сведены контрольные суммы. Смысл приведенных цифр таков: число в верхней правой ячейке гово- рит о том, что общее число опрошенных в возрасте от 18 до 24 лет составляет 46 человек; цифра в ячейке ниже сообщает, что это составляет 9,2% общей численности выборочного массива, (500 человек, которые и принимаются за 100%, — данные в клет-1 ках в правом нижнем углу таблицы); общее число опрошенных в возрасте от 25 до 29 лет — 55 человек, это составляет 11,0% общей численности выборочного массива и т.д. В самой нижней строке приведены контрольные суммы количества тех, кто дал различные ответы об участии в голосовании по всем возрастным группам. Так, общее число принимавших участие в голосовании («да») — 301 человек, что составляет 60,2% общего объема выбо­рочного массива; тех, кто не принимал участие («нет»), было в выборочном массиве 155, или Ъ\%,\\ т.д. Две ячейки в нижнем правом углу указывают на общую численность участников опро-

211

са, которая принимается за 100% для обеих исследуемых пере­менных. Контрольные суммы позволяют убедиться, что в про­цессе обработки были учтены ответы всех без исключения кате­горий респондентов.

Отметим также, что в этой таблице мы привели для макси­мальной полноты распределение по возрастам и тех, кто вообще не дал в анкете ответа на данный вопрос (столбец под заголов­ком «нет ответа»), а также тех, кто не смог точно вспомнить факта своего участия или неучастия (столбец «не помнят»). Во­обще говоря, содержимое этих столбцов не очень информатив­но, и в итоговом отчете их можно опустить (здесь они нужны скорее для того, чтобы убедиться, что сошлись контрольные сум­мы). Хотя порой знание о том, какое число (и какой процент) респондентов не дали ответа или в той или иной форме уклони­лись от него, бывает достаточно полезным — например, при ана­лизе осведомленности респондентов или степени заинтересован­ности их в какой-то проблеме. Кроме того, следовало бы под­вергнуть особому анализу обе категории (тех, кто не дал ответа, и тех, кто не помнит), если бы численность их оказалась стати­стически значимой.

Анализ проводят, отслеживая изменения значений зависи­мой переменной при переходе ее от одного значения к друго­му. В данном примере в качестве независимой переменной вы­ступает возраст респондентов, в качестве зависимой — их элек­торальная активность (выражаемая участием либо неучастием в голосовании). Процедуру отслеживания изменений значения зависимой переменной можно проводить как по строкам, так и столбцам. Двигаясь по строкам, мы начинаем с первого зна­чения независимой переменной (возраст) — 18—24 года. Мы видим, что здесь число принимавших участие в выборах замет­но — более чем в 1,5 раза — меньше числа тех, кто не участво­вал. Перейдя к следующей строке — 25—29 лет, мы убеждаем­ся, что в этой возрастной категории соотношение между чис­лом участвовавших и не участвовавших противоположное: первых уже более чем в 2 раза больше. Это соотношение еще более возрастает при переходе к следующим возрастным кате­гориям, хотя и несколько снижается для самой старшей груп­пы избирателей (старше 70 лет). Это позволяет нам сделать вы­воды: 1) о наличии связи между независимой (возраст) и зави­симой (участие в выборах) переменными; 2) о направлении этой связи, которая в данном случае является прямой или положи­тельной, поскольку ее можно выразить следующим простым описанием: чем больше значения независимой переменной (воз-212


раст), тем больше значения зависимой переменной (процент участия в выборах).

Фактически, как мы видим, непосредственному анализу здесь подвергались далеко не все цифры, а лишь некоторые из них — те, которые можно было бы свести в сокращенном варианте в виде табл. 4.14а.

Таблица 4.14а

Соотношения участия в выборах и абсентеизма²¹ в различных возрастных группах

^ Возраст, годы	Участвовали	Не участвовали
18-24	34,8	58,7
25-29	54,5	32,7
30-39	59,8	27,8
40-49	65,2	27,8
50-59	64,9	27,0
60-70	70,0	25,7
Старше 70	58,1	30,2

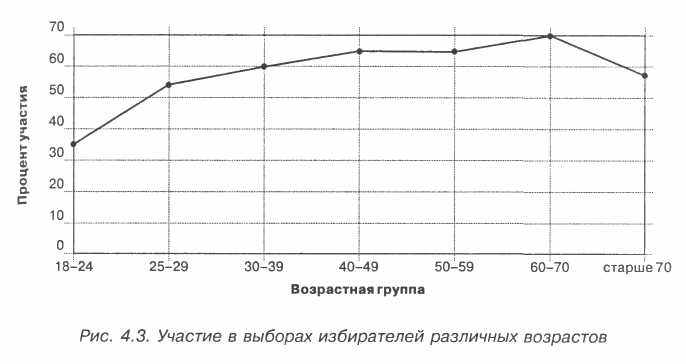
Данные, приведенные в табл. 4.14 и 4.14а и отраженные в виде графика на рис. 4.3, позволяют нам сделать следующие основные выводы: 1) существует отчетливо выраженная связь между воз­растом избирателей и их электоральной активностью; 2) эта связь в основном положительная — чем больше возраст, тем выше про­цент участия представителей этой возрастной группы в голосов вании; исключение составляет лишь самая верхняя возрастная группа, где электоральная активность по вполне понятным при­чинам снижается. Второй из указанных выводов основан на пра­виле, определяющем направление связи: когда низкие значения одной переменной ассоциируются с низкими значениями дру-гой переменной (и наоборот), имеет место положительная связь; например, «чем выше уровень образования у кого-то, тем выше уровень его политического интереса». Когда низкие значения одной переменной ассоциируются с высокими значениями дру­гой, между двумя переменными существует отрицательная связь; например, «чем выше чей-то доход, тем менее он либерален».

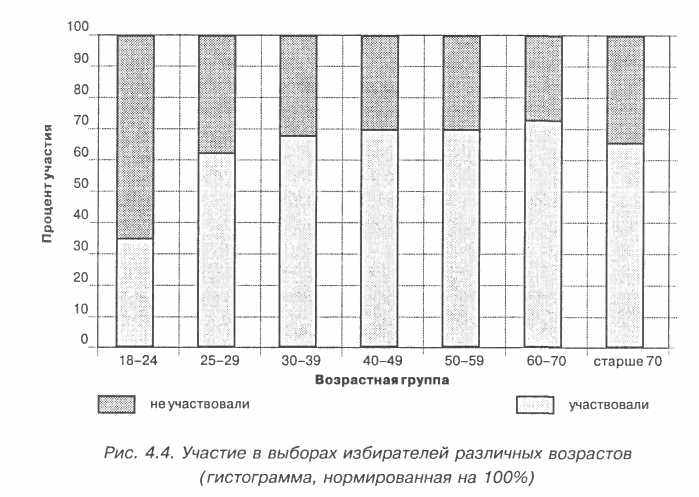
Мы могли бы построить графическое отображение и несколь­ко иным способом — в виде распределения, нормированного на 213

100%, где в столбцах диаграммы отражена доля каждой из кате­горий в общей сумме (рис. 4.4).






Иногда для большей наглядности и убедительности анализа используют различные индексы. Это специально создаваемые по­казатели, с помощью которых связь между переменнными прояв­ляется более зримо и отчетливо. Здесь должны прийти на помощь 214

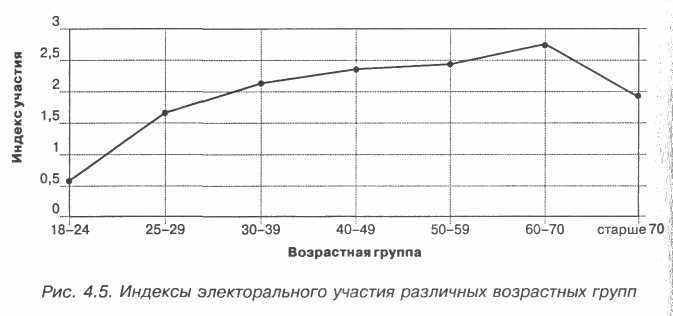
воображение и опыт. Мы могли бы, например, сконструировать по данным табл. 4.14а «индекс электорального участия», равный частному от деления числа принимавших участие в каждой из возрастных групп на число тех, кто не голосовал. Результаты от­ражены в табл. 4.146 и на рис. 4.5.

Таблица 4.146 | Индекс электорального участия в различных возрастных группах

Возраст, годы	Индекс участия
18-24	0,592845
25-29	1,666667
30-39	2,151079
40-49	2,345324
50-59	2,403704
60-70	2,723735
Старше 70	1,923841

Нетрудно убедиться, что формы кривых на рис. 4.3 и 4.5 со­вершенно идентичны (та же зависимость), хотя значения на оси ординат иные. Мы могли бы построить индекс иначе (скажем, не разделив, а вычтя одно из другого) и убедиться, что результат был бы таким же.




Теперь представим себе, что данные опроса были бы принци­пиально иными, такими, например, как это представлено в гипо­тетической табл. 4.14в.

Вывод, который мы могли бы сделать из такого рода данных, сомнения не вызывает: связи между возрастом и электоральной активностью не наблюдается. При этом мы опираемся на прави-ло, сформулированное в предыдущей главе: нет изменения — нет связи.

^ Глава 4. Анализ эмпирических данных 215

Понятие силы связи имеет отношение к тому, насколько суще­ственно различаются наблюдаемые значения зависимой переменной при изменении значений независимой переменной. Если, предполо­жим, характер голосования одной категории избирателей (к при­меру, мужчин) значительно отличается от характера голосования другой категории (женщин), тогда мы можем утверждать, что имеет место сильная связь между двумя переменными. Если сте­пень различия в характере их голосования мала, имеет место сла­бая связь.

Таблица 4.14в

Соотношения участия в выборах и абсентеизма в различных возрастных группах (в процентах к численности каждой возрастной группы)

^ Возраст, годы	Участвовали	Не участвовали
18-24	59,8	27,8
25-29	59,8	27,8
30-39	59,8	27,8
40-49	59,8	27,8
50-59	59,8	27,8
60-70	59,8	27,8
Старше 70	59,8	27,8

Источник: Гипотетические данные.

Наиболее сильная из возможных связей между двумя перемен­ными — это такая связь, при которой значение зависимой пере­менной для каждого случая в одной категории независимой пе­ременной отличается от каждого из случаев в другой категории. Такую связь называют совершенной, потому что зависимая пере­менная абсолютно ассоциируется с независимой переменной, не допуская никаких исключений. Совершенная связь между неза­висимой и зависимой переменными дает исследователю возмож­ность точно предсказать значение любого из случаев зависимой переменной, если известно значение независимой. Пример совер­шенной связи для гипотетического случая различий в голосова­нии приведен в табл. 4.14г. Между переменными может существо­вать как совершенная положительная, так и совершенная отрица­тельная связь, поскольку направление и сила — это разные свойства связи.

Строго говоря, в реальных распределениях социологических дан­ных крайне редко встречаются как совершенная связь, так и абсо­лютно полное отсутствие связи. Фактически отсутствие связи выра­жается в слабости связи. Слабой можно было бы считать такую связь, при которой различия наблюдаемых значений зависимой перемен-216

ной для различных категорий независимой переменной незначитель­ны. Фактически наиболее слабая связь — это такая, в которой рас­пределение было бы идентично для всех категорий независимой пе­ременной — другими словами, связь просто отсутствует.

Таблица 4.14г

Различия в голосовании за различных кандидатов в зависимости от пола избирателей

Кандидат	Голосование(%)
	Мужчины	Женщины
Иванов	100	0
Петрова	0	100
Всего	100	100

Источник: Гипотетические данные.

Пример из социологической практики. Американские социологи Раймонд Уолфингер и Стивен Розенстоун в своем анализе причин, J. по которым люди голосуют, использовали анализ кросстаба для про- ■ верки гипотезы, что чем выше уровень образования индивида, тем с большей вероятностью он примет участие в голосовании. Табл. 4.15 позволяет прийти к следующим выводам: 1) связь между образова- .; нием и явкой избирателя на выборы реально существует; 2) направ­ление ее таково, как определяет гипотеза; 3) связь довольно сильная. Это хороший пример кросстаба с независимой переменной, разме- * щенной сверху вниз таблицы, поскольку она включает много кате- i горий. В этом случае процентные отношения размешаются по стро- \ кам, а сравнение проводится вниз по столбцам.

^ Таблица 4.15

Связь между образованием и явкой на выборы

^ Число лет образования (независимая переменная)	Явка на выборы (зависимая переменная)
	Голосовали{%)	Не голосовали(%)	Общая доля в выборке (%)
0-4 года	38	62	4
5-7лет	49	51	6
8 лет	59	41	10
9-11 лет	55	45	16
12 лет	69	31	38
1-3 года колледжа	79	21	14
4 года колледжа	86	14	7
Sлетколледжа	91	9	4

217

Довольно часто используемым показателем силы связи выступа­ют различные коэффициенты корреляции²². Корреляция указывает на степень статистической взаимосвязи признаков. Одним из индек­сов такого рода при использовании порядковой шкалы измерения выступает коэффициент ранговой корреляции Спирмена, названный так по имени американского психолога Чарльза Спирмена, который использовал его в своих исследованиях вместо обычных коэффици­ентов корреляции. Формула расчета его имеет следующий вид:



где d_j — разность рангов; /— общее число сопоставляемых пар.

Понятно, что коэффициент ранговой корреляции Спирмена будет равен +1 (абсолютная положительная связь), если ответы рес­пондентов анализируемых групп будут в точности совпадать; он будет равен -1 (абсолютная отрицательная связь), если ответы всех респондентов обеих анализируемых групп будут прямо противопо­ложны; если r_s = 0, то это означает полное отсутствие всякой связи.

Строго говоря, коэффициент ранговой корреляции показы­вает, насколько одинаковыми или различными оказываются от­веты на один и тот же вопрос со стороны двух сравниваемых между собою групп респондентов. Рассмотрим процедуру рас­чета r_s на примере данных исследования о стереотипах сексу­ального поведения. Респондентов просили высказать степень своего согласия (выразив это в баллах от 5 — «полностью согла­сен», до 1 — «совершенно не согласен») с целым рядом сужде­ний, связанных с теми или иными сторонами интимной жиз­ни. После расчетов среднего значения были получены следую­щие результаты(табл. 4.16).

После ранжировки по степени согласия с тем или иным сужде­нием таблица приобретет несколько иной вид (табл. 4.16а). Рассчи­тав величину для каждого из значений, возведя ее в квадрат, а за­тем сложив, мы можем проделать в соответствии с формулой (4.2) следующую процедуру для расчета коэффициента корреляции:



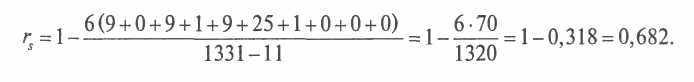
218

Таблица 4.16 Степень согласия с суждениями (в средних значениях по 5-балльной шкале)
Суждение		Мужчины	Женщины
Инициатива в интимных отношениях должна принадлежать юношам		3,42	3,55
Если девушка в 18—20 лет невинна, то, скорее всего, она никому не нужна		1,58	1,57
Без секса жизнь неинтересна		3,77	3,03
Любовь бывает исключительно в книгах, в фильмах, а в жизни—только секс		2,12	1,76
Верю, что в жизни у меня будет (есть) настоящая любовь		3,88	3,91
Девушка, ведущая беспорядочную половую жизнь, останется несчастной и одинокой		3,04	3,03
Курение и алкоголь — злейшие враги сексуальности		3,42	3,79
Прежде чем вступить в брак, надо проверить, подходитлитебе человек в сексуальном отношении		4,19	3,33
Без любви не стоит заниматься сексом		2,75	3,45
Наличие денег играет большую роль в выборе сексуального партнера		2,37	2,64
Интимная близость — это соединение, в первую очередь, не половых органов, а любящих душ		3,62	4,22
Таблица 4.16а
Суждение	Мужчины	Женщины		d	d*
Интимная близость — это соединение, в первую очередь, не половых органов, а любящих душ	4	1		3	9
Верю, что в жизни у меня будет (есть) настоящая любовь	2	2		0	0
Курение и алкоголь — злейшие враги сексуальности	6	3		3	9
Инициатива в интимных отношениях должна принадлежать юношам	5	4		1	1
Без любви не стоит заниматься сексом	8	5		3	9
Прежде чем вступить в брак, надо проверить, подходитлитебе человек в сексуальном отношении	1	6		-5	25
Без секса жизнь неинтересна	3	7		4	16
Девушка, ведущая беспорядочную половую жизнь, останется несчастной и одинокой	7	8		-1	1
Наличие денег играет большую роль в выборе сексуального партнера	9	9		0	0
Любовь бывает исключительно в книгах, в фильмах, а в жизни — только секс	10	10		0	0
Если девушка в 18-20 лет невинна, то, скорее всего, она никому не нужна	11	11		0	0

Это довольно высокий уровень корреляции, указывающий на относительную близость взглядов мужчин и женщин по всему комплексу приведенных суждений (несмотря на существенные расхождения по отдельным позициям).