Планирование в условиях неопределенности Литература
| Вид материала | Литература |
- Принятие решений в условиях неопределенности, 804.21kb.
- Бизнес-планирование инновационных проектов, 362.11kb.
- Стратегическое планирование в современных условиях обострения конкуренции и рыночной, 38.51kb.
- Университет им. Отто-фон-герике, 65.04kb.
- Программа семинара на тему «Оценка неопределенности измерений электрических величин», 32.3kb.
- Правовая социализация учащейся молодежи в условиях социальной неопределенности российского, 794.87kb.
- Темы Фамилия Управление инвестиционной деятельностью в современных условиях. Специфика, 53.18kb.
- Планирование очной ставки Планирование осмотра места происшествия Планирование проверки, 937.5kb.
- Учебный план курса «живая компания» (долгожительство в деловой среде в эпоху нестабильности, 50.04kb.
- Адаптационные стратегии российской молодежи на рынке труда в условиях социально-экономической, 526.77kb.
Планирование в условиях неопределенности
Литература
- Экономико-математические методы и модели: Учеб. пособие / В. Ю. Киселев. – Иваново, Иван. гос. энерг. ун-т, 1998. – 384 с. (см. стр. 251-259)
- Монахов А. В. Математические методы анализа экономики. (Серия "Краткий курс") – СПб.: Питер, 2002. – 176 с. (см. стр.129-130)
- Лотов А. В. Введение в экономико-математическое моделирование. – М.: Наука, 1984.
- ссылка скрыта
Детерминированные экономико-математические модели – это модели, в которых не учитывается влияние неопределенных факторов. Вместе с тем имеется большое количество экономических задач, в которых невозможно однозначно определить основные параметры и переменные модели изучаемого процесса или явления. В этом случае говорят, что принятие хозяйственных решений осуществляется в условиях неопределенности.
Различают два вида неопределенности. Первый – это стохастическая неопределенность, или неопределенность первого порядка, т. е. ситуация, в которой предполагается, что для неопределенных параметров может быть установлено вероятностное распределение. В этом случае часто прибегают к изучению функции плотности вероятностей, определяют среднее значение случайной величины, ее дисперсию и т. п., что в конечном счете позволяет сделать вывод о допустимом варианте хозяйственного решения по некоторому заранее определенному, как правило, пороговому критерию. Применение вероятностных методов моделирования экономических процессов оправдывает себя только в тех случаях, когда есть возможность накопить и обработать большое количество статистической информации, обеспечивающей репрезентативность анализируемых выборок.
Второй вид неопределенности – это неопределенность, при которой неизвестно вероятностное распределение интересующей величины, но определена область её изменения. Неопределенность такого вида называют неопределенностью второго порядка. Возникает неопределенность второго порядка по двум причинам: в связи с действием людей, преследующих иные цели в некоторой экономической ситуации, или в связи с поведением некоторых непредсказуемых природных факторов.
Для принятия решений в ситуации с неопределенностью предлагаются некоторые логические критерии принятия хозяйственных решений.
Пусть Y – множество значений неопределенного параметра, X – множество планов (или управлений). Мы должны выбрать такой план xX, который давал бы в некотором смысле наилучшее решение при всех возможных значениях неопределенного параметра yY. Далее мы будем предполагать, что множества X и Y конечны:
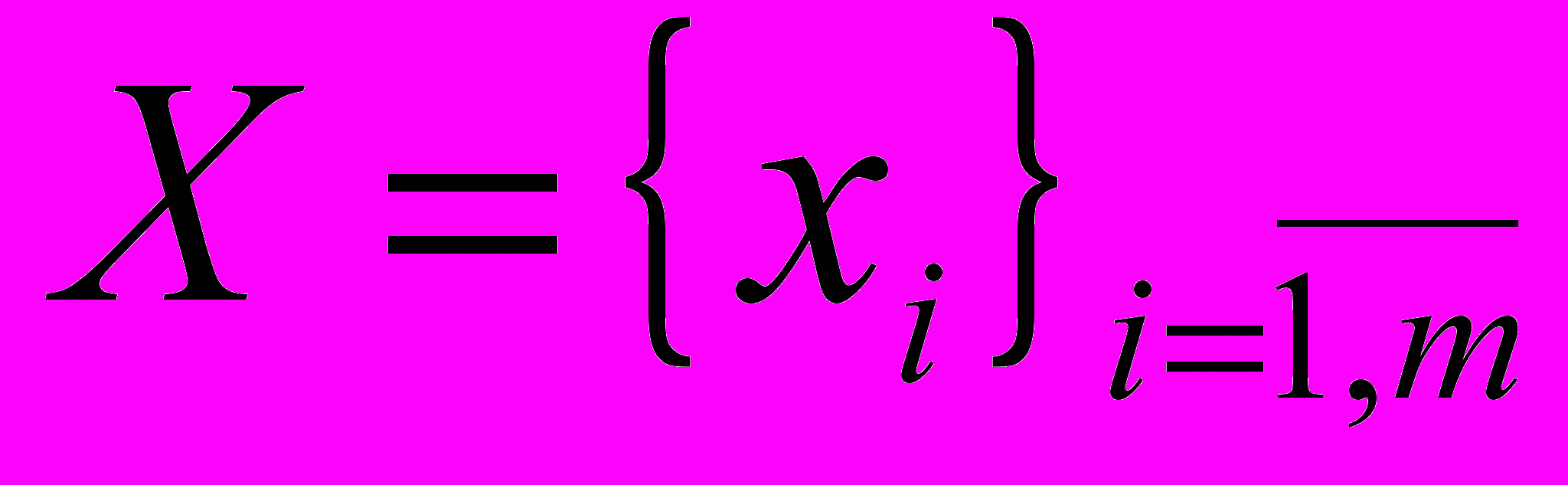 ,
, 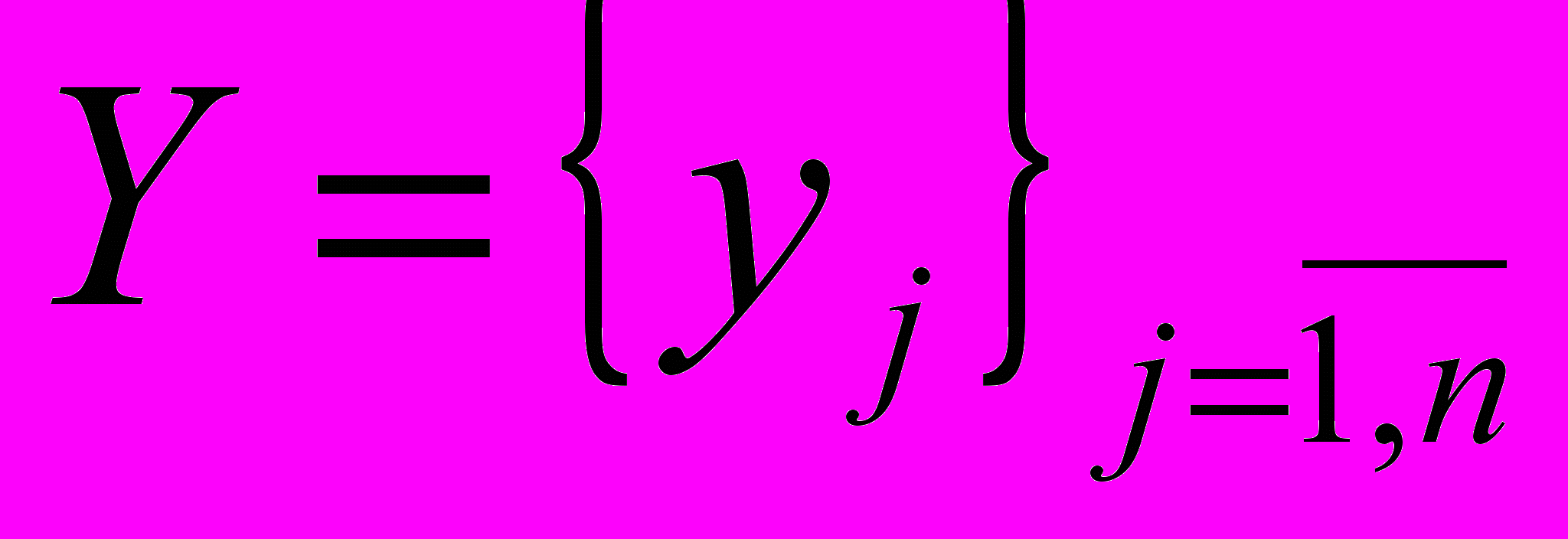 . Обозначим через Wij – значение выгоды (выигрыша) при выборе плана xi в ситуации, когда неопределенный фактор принимает значение yj.
. Обозначим через Wij – значение выгоды (выигрыша) при выборе плана xi в ситуации, когда неопределенный фактор принимает значение yj.Рассмотрим сначала случай неопределенности первого рода. Рассмотрим критерий принятия решения с учетом вероятности неопределенного фактора. Пусть известен вектор q = (q1, …, qn) – вероятностей, с которыми встречаются значения неопределенного фактора y. Среднее значение выгоды при выборе плана xi определяется числом
vi = Wi1q1 + Wi2q2 + … + Winqn , i = 1, …, m.
Очевидно, следует выбрать такой план, при котором достигается наибольшее значение средней выгоды vi. То есть в данном случае решением является такое x*, при котором достигается
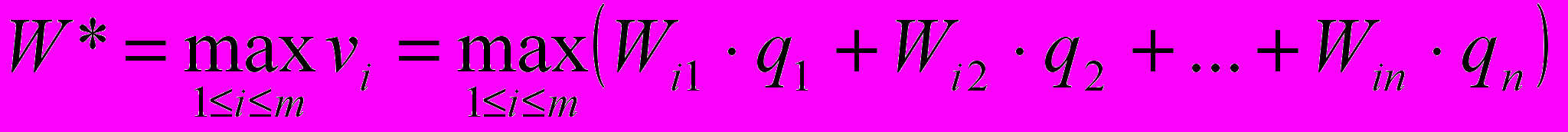 .
.Если необходимость выбора повторяется многократно, то можно каждый раз совершать один и тот же выбор (чистая стратегия) или выбирать разные планы xi с определенной вероятностью (смешанная стратегия). Можно доказать, что применение смешанной стратегии невыгодно, так как в таком случае выгода может только уменьшиться. Действительно, пусть вектор p = (p1, …, pm) – вероятности, с которыми осуществляется выбор планов из множества X. Среднее значение выгоды при многократном повторении выбора (с вероятностями p) определяется числом
vi(p) = v1p1 + v2p2 + … + vmpm.
Поскольку vi v* для любого i, а
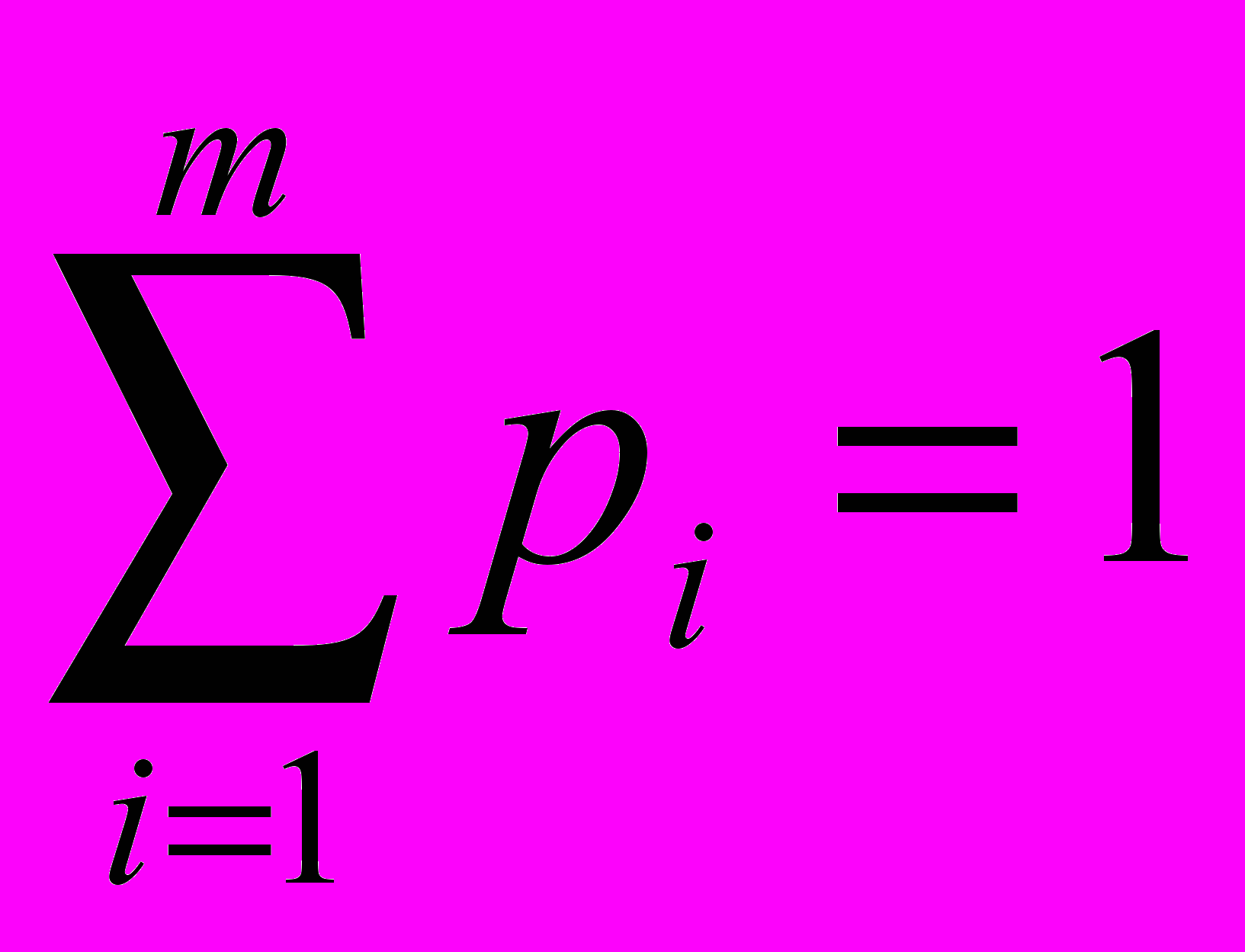 , то
, то v(p) = v1p1 + v2q2 + … + vmpm v*p1 + v*q2 + … + v*pm = v*
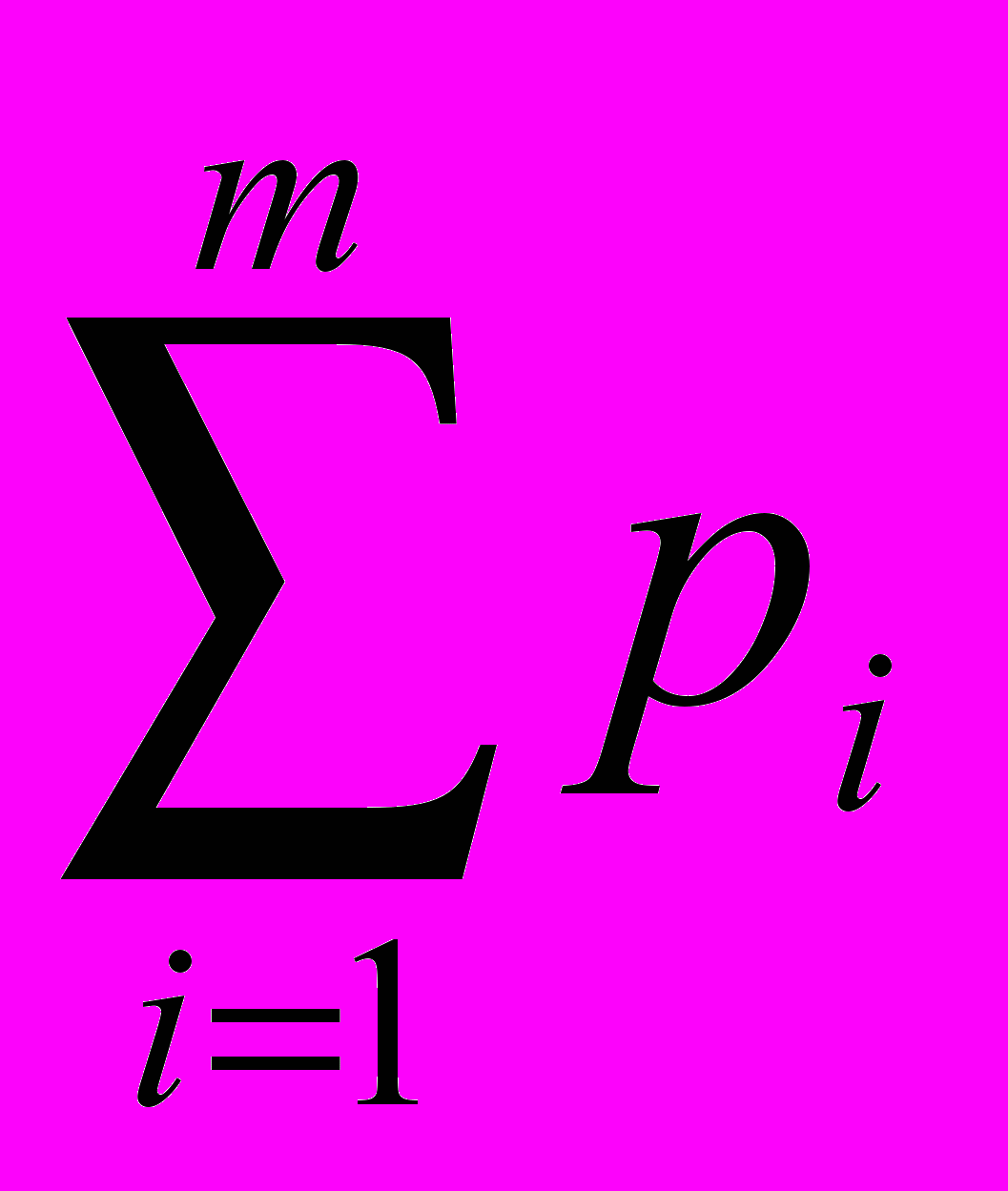 = v*,
= v*,что доказывает невыгодность смешанной стратегии.
Рассмотрим теперь случай неопределенности второго рода. Это значит, что неизвестен вектор вероятностей, с которыми встречаются значения неопределенного фактора y. Здесь возможны два случая: 1) выбор производится многократно, и требуется получить максимальное значение средней выгоды; 2) выбор производится только один раз.
Принцип недостаточного основания Лапласа. Если нет никаких оснований считать, что какая-либо стратегия природы имеет большую частоту (вероятность), чем какая-либо другая стратегия, то можно предположить, что вероятности всех стратегий природы одинаковы и равны 1/n. Тогда средний выигрыш от применения стратегии yi равен
vi = 1/n(Wi1 + Wi2 + … + Win).
Очевидно, для определения оптимальной стратегии достаточно сравнить между собой числа nvi = Wi1 + Wi2 + … + Win (то есть суммы элементов каждой строки матрицы выигрышей) и выбрать из них наибольшее. Таким образом,
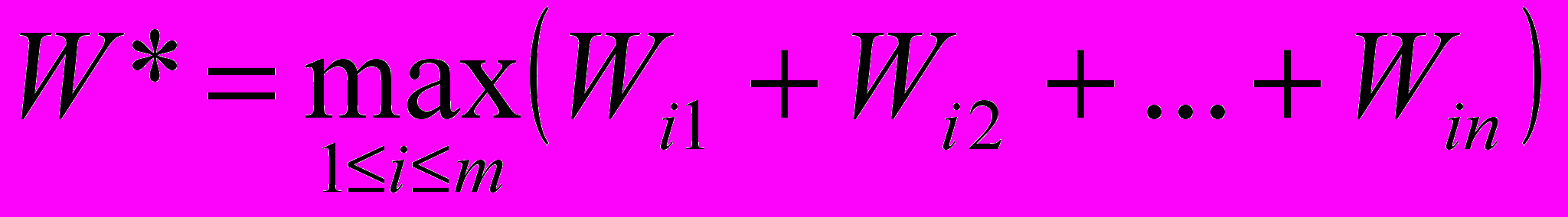 .
.Принцип максимизации приемлемого выигрыша. Пусть игроку важны большие значения выигрышей в некоторых отдельных играх последовательности игр и безразличны малые значения в прочих играх этой последовательности. Тогда игрок, надеясь, что «природа будет на его стороне», может (в зависимости от цели) выбирать в каждой игре
- либо ту стратегию, которая соответствует строке матрицы с наибольшим элементом матрицы;
- либо ту стратегию, которая соответствует строке матрицы, где находится наибольшее количество элементов (выигрышей), превышающих некоторый приемлемый уровень полезности выигрыша. В этом случае игрок может также применять смешанную стратегию, в которой каждая из чистых стратегий применяется с вероятностью, пропорциональной количеству элементов (выигрышей), превышающих некоторый приемлемый уровень полезности выигрыша в соответствующей строке матрицы выигрышей.
Если игра с природой проводится только один раз, то предыдущие два способа решения не используются, поскольку в их основе лежит идея многократного повторения игры и максимизации среднего выигрыша за несколько игр. При однократной игре нужно указать какую-либо одну чистую стратегию, которая оптимальна, исходя из некоторого критерия. При этом необходимо помнить, что все приведенные ниже известные критерии имеют высокую степень произвольности.
Принцип гарантированного результата. Его смысл состоит в том, что выбирается такой параметр x, определяемый нами, при котором некоторый интересующий нас показатель W(x,y) достигает наилучшего (наибольшего) значения при условии, что неопределенный параметр y принимает наихудшее значение. Математически решение с помощью принципа гарантированного результата определяется по следующему алгоритму.
- Для каждого управления x находится наихудшее значение показателя W(x, y):
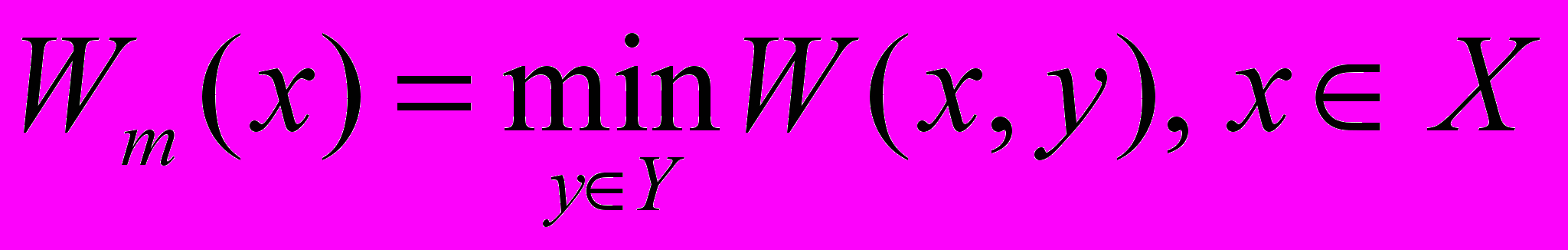 .
.- После этого выбирается такое управление xX, при котором достигается наибольшее значение Wm(x):
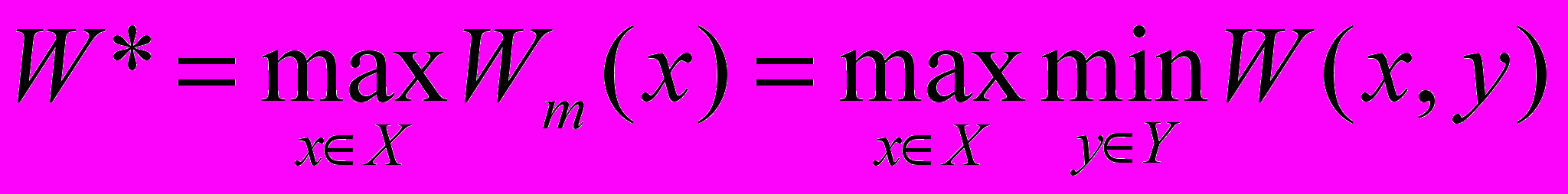 .
.Величина W* – это такое значение показателя W(x, y), которое мы можем гарантировать при наихудшем для нас поведении (значении) неопределенного параметра y. Этот критерий выбора называется критерием Вальда.
Принцип учета степени оптимизма. Противоположный принципу гарантированного результата подход основан на оптимистическом предположении, что неизвестный параметр y будет принимать наилучшие для нас значения. В этом случае выбор управляющего решения основывается на определении W* по формуле:
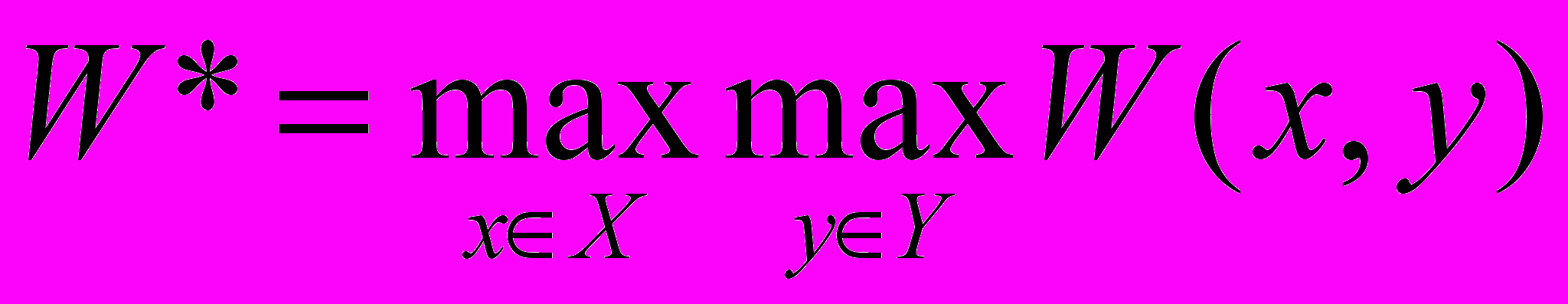
Однако этот критерий слишком оптимистичен, поэтому чаще применяется критерий Гурвица, состоящий в выборе такого управления x, при котором достигается
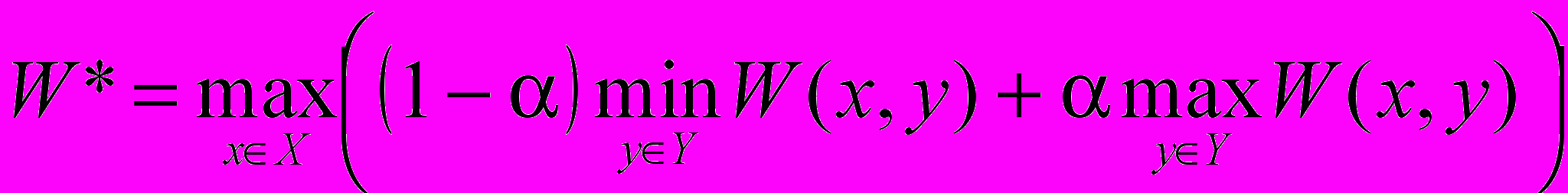
где принимает значение от 0 до 1 и представляет собой степень оптимизма. При =0 получается крайне пессимистический подход к принятию решения на основе принципа гарантированного результата, а при =1 – противоположный, крайне оптимистический подход. Объективных основ для выбора коэффициента не существует.
Принцип минимального риска. Интересен подход, предложенный Л. Сэвиджем. Он состоит в следующем. Для каждого значения y находится функция
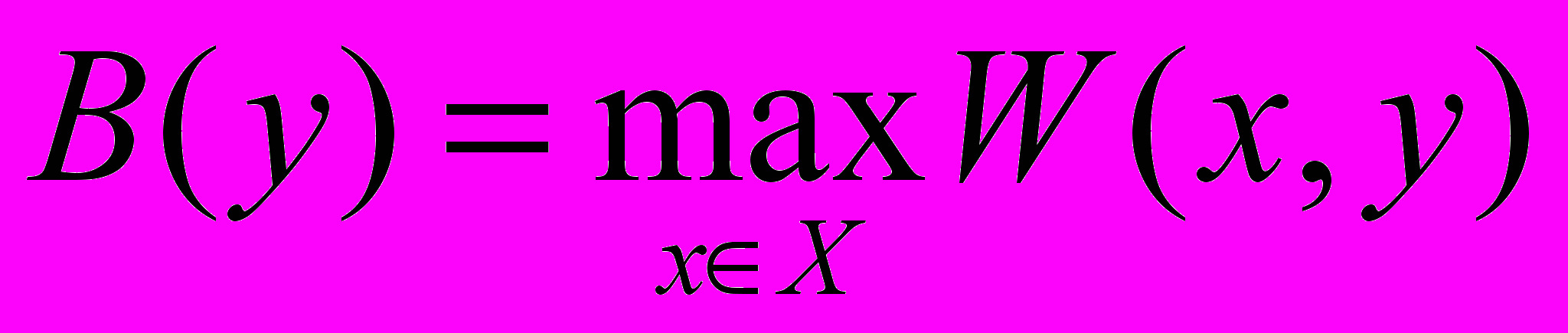 ,
,которая показывает, какое наилучшее значение показателя W(x, y) можно получить при каждом значении yY. Это значение показателя можно было бы получить, если бы было известно значение параметра y заранее. Далее строится новый показатель:
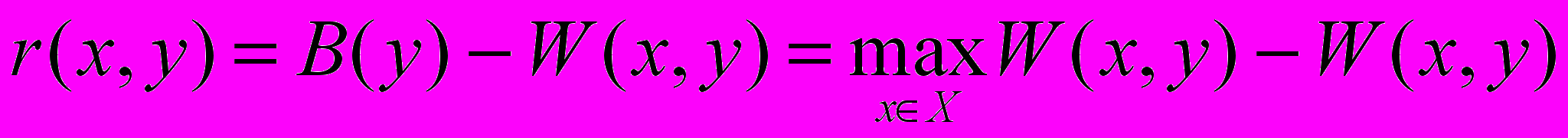 ,
,который называется функцией риска (функцией потерь или функцией сожалений). Он показывает потери (отклонения от наилучшего значения B(y)) для каждого управления xX при всех значениях параметра yY. Критерий Сэвиджа состоит в выборе решения на основе функции риска r(x, y) с использованием принципа гарантированного результата, т. е. ищется такое решение, при котором достигается:
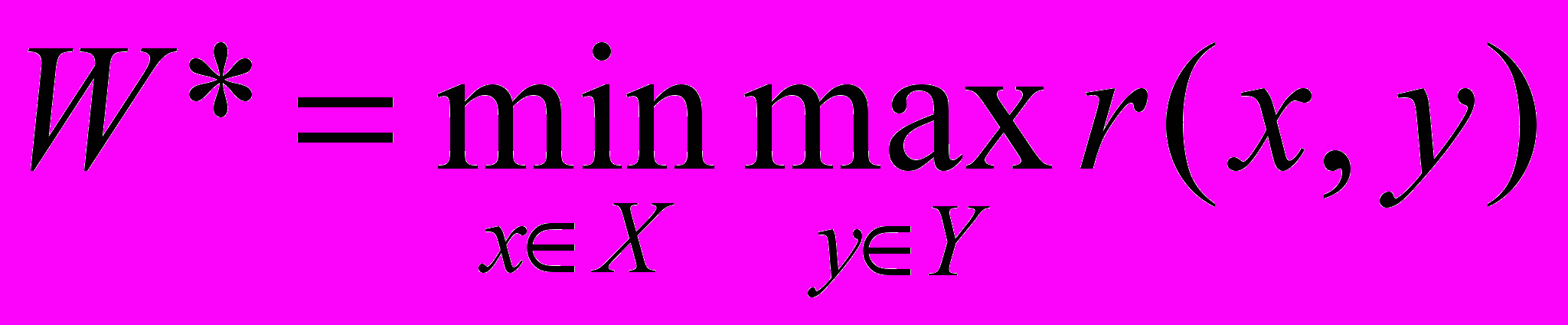
Использование этого подхода позволяет уменьшить риск при принятии решения.
Пример.
Предположим, что перед сельскохозяйственным предприятием стоит дилемма: засевать ли данное поле в данном календарном году кукурузой (стратегия x1) или овсом (стратегия x2). Погодными условиями (стратегиями природы) могут быть сухое теплое лето (y1), сухое холодное лето (y2), влажное холодное лето (y3) или влажное теплое лето (y4). В зависимости от комбинации (xi, yj) доход в условных единицах, который рассчитывает получить предприятие, определяется матрицей:
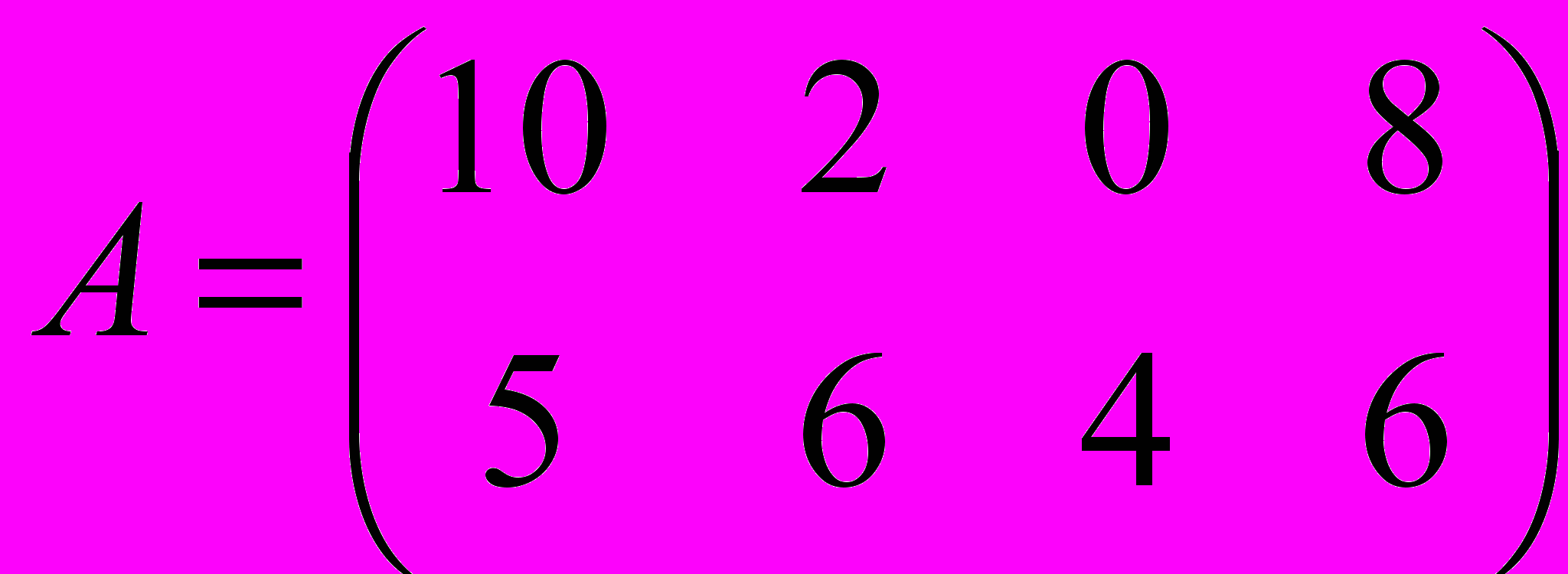 .
.Предприятие стремится увеличить свой доход. Какой культурой следует засеять поле?
Решить задачу в двух предположениях:
- из многолетних наблюдений известно, что ситуация y1 повторяется в 25 % летних сезонов, y2 – в 20 %, y3 – в 30 % и y4 – в 25 % сезонов (то есть известно распределение вероятности стратегий природы);
- статистических данных нет (то есть о вероятностях применения стратегий природой ничего не известно).
Решение
Используя критерий принятия решения с учетом вероятности неопределенного фактора, получаем, что среднее значение выгоды при выборе плана x1 определяется числом v1 = 4,9, а при выборе плана x2 – числом v2 = 5,15. Наибольшее значение средней выгоды достигается при выборе плана x2, то есть в среднем хозяйству овёс сеять выгоднее, чем кукурузу.
Пусть теперь отсутствуют статистические данные о вероятности наступления погодных условий.
По принципу недостаточного основания Лапласа имеем n v1 = 20, а n v2 = 21. Наибольшее значение средней выгоды достигается при выборе плана x2, то есть в среднем хозяйству овёс сеять выгоднее, чем кукурузу.
Рассмотрим результат применения принципа максимизации приемлемого выигрыша.
- Стратегия, которая соответствует строке матрицы с наибольшим элементом матрицы (он равен 10) – это x1 (сеять кукурузу). Заметим, что в этом случае больший средний доход получается за счёт хороших урожаев в хорошие годы при почти полном отсутствии дохода в неудачные годы. Такая стратегия является очень рискованной.
- Зададим некоторое значение уровня полезности выигрыша. Например, пусть = 4. Тогда в первой строке имеем два элемента со значением, не меньшим , а во второй строке таких элементов четыре. Значит, игроку следует выбирать план x2. Игрок может также применять смешанную стратегию, состоящую в том, чтобы выбирать план x1 с вероятностью 2/(2+4)=1/3, а план x2 – с вероятностью 4/(2+4)=2/3. При = 6 вероятности выбора плана x1 и x2 будут равны. А если взять > 6, то игроку следует выбирать план x1.
Пусть теперь игра с природой проводится только один раз.
Принцип гарантированного результата (критерий Вальда) даёт W1=0, W2=4, W* = 4, оптимальный план – x2.
Применим принцип учета степени оптимизма (критерий Гурвица). Находим сначала для каждого плана
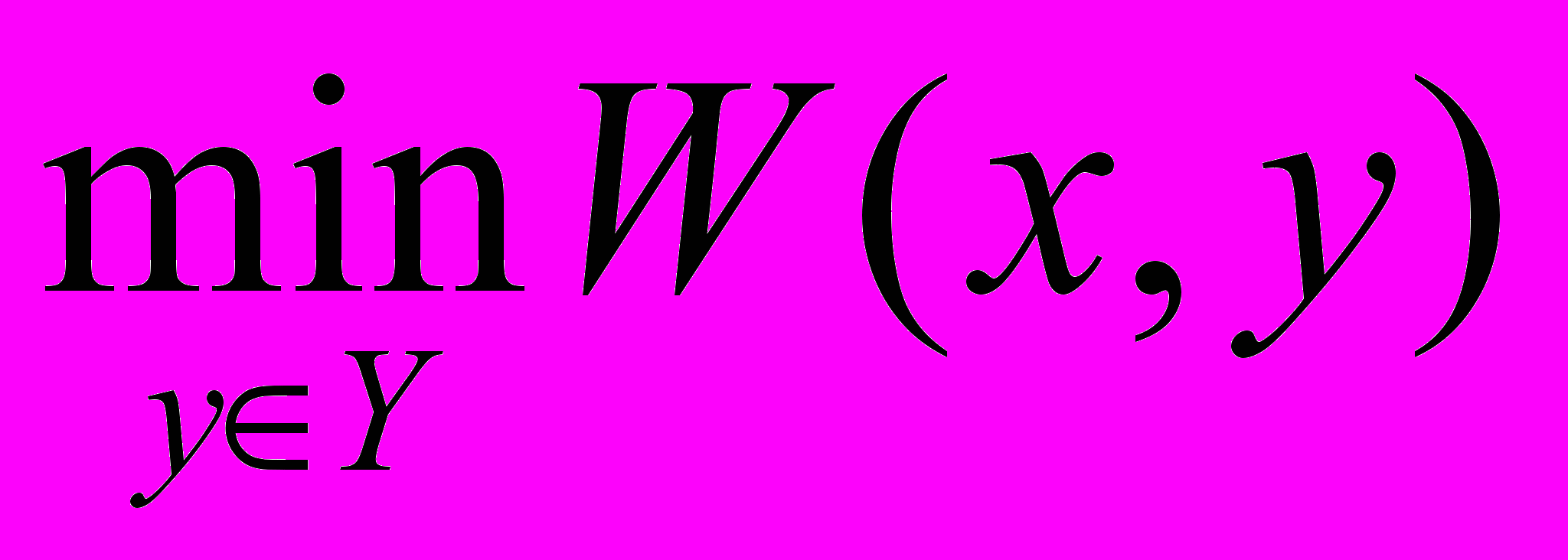 и
и 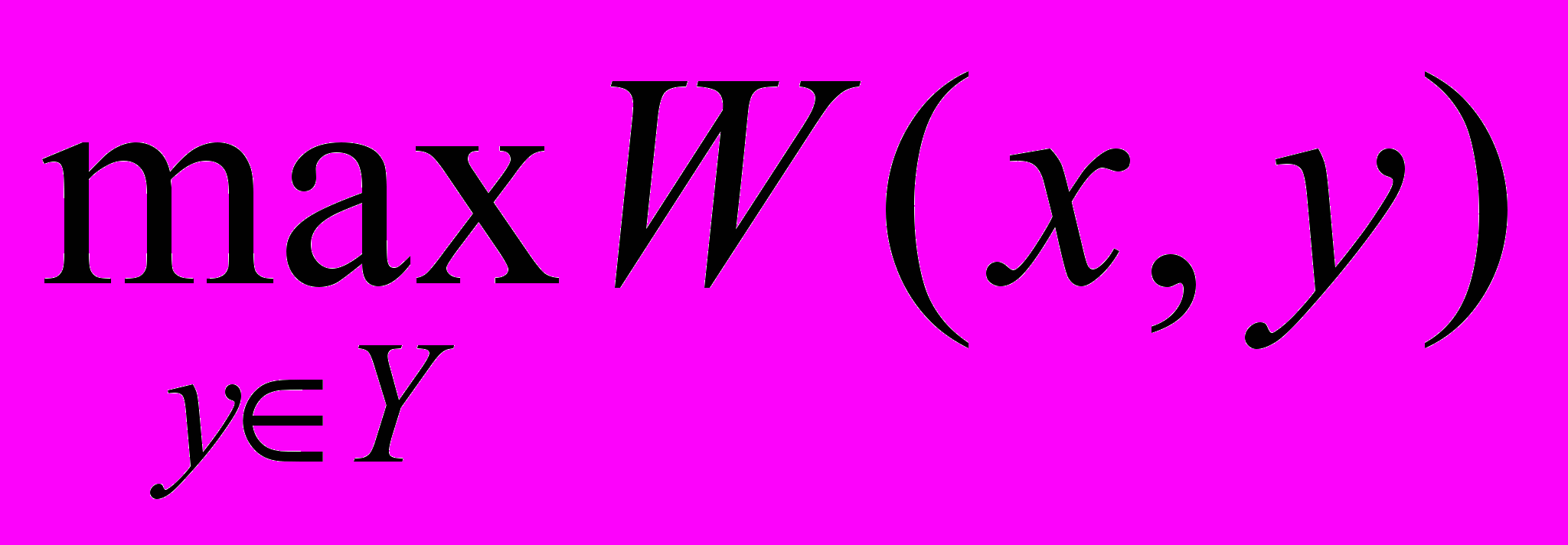 :
:| i | 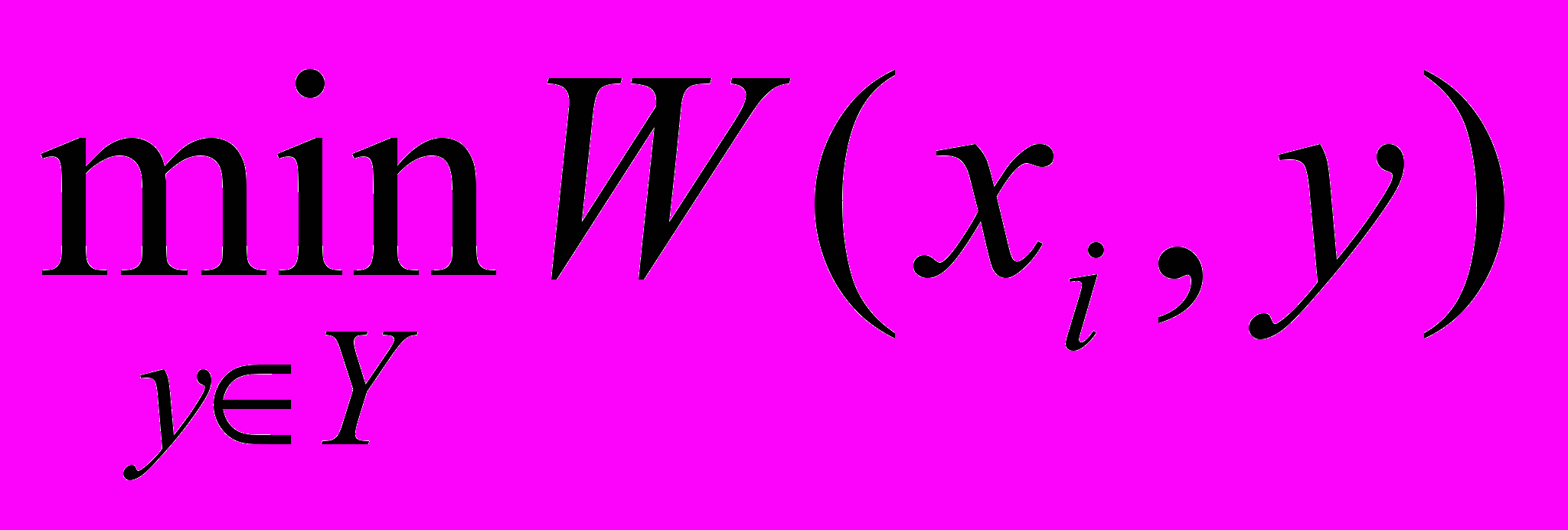 | 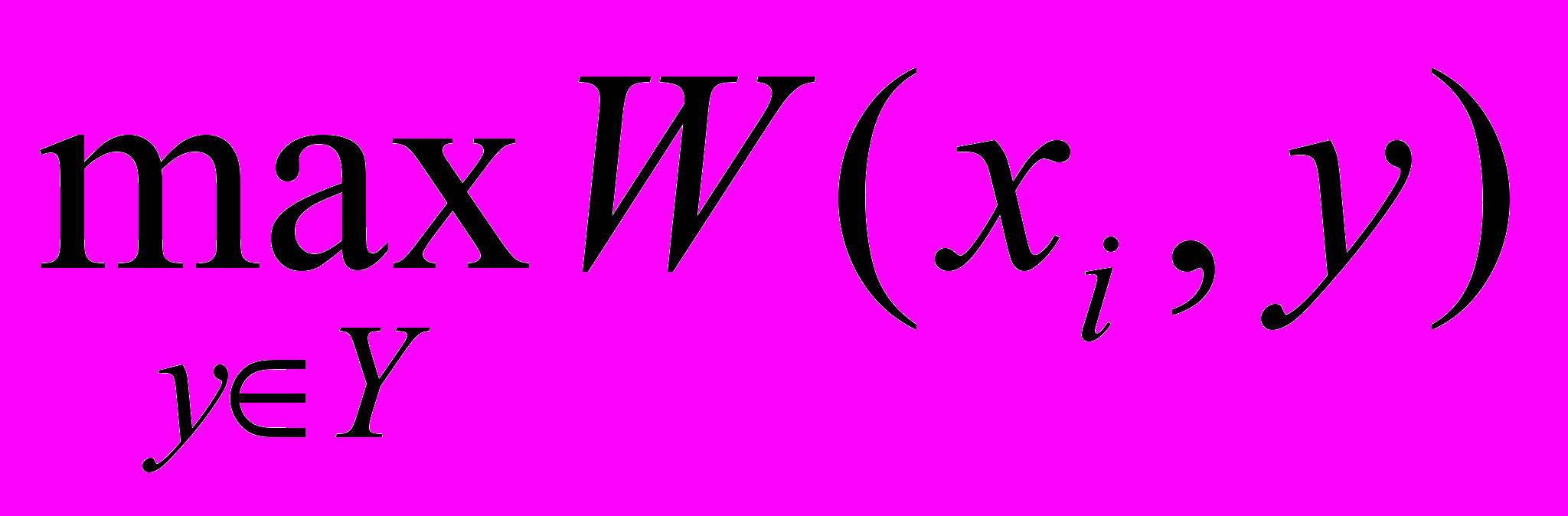 |
| 1 | 0 | 10 |
| 2 | 4 | 6 |
Тогда
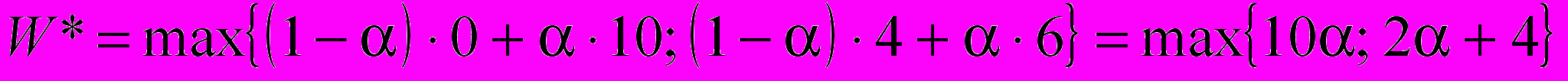 . Найдём W* при разных значениях параметра . Очевидно при =0,5 имеем 10 = 2+4, поэтому оба плана являются оптимальными. При <0,5 имеем 10 < 2+4, поэтому оптимальным является план x2. При >0,5 имеем 10 > 2+4, поэтому оптимальным является план x1. Это решение можно проиллюстрировать графически. Изобразим прямые W1() = 10 и W2() = 2+4 (см. рис. 1). Поскольку нам нужно выбрать максимум из этих двух выражений, то для каждого фиксированного отмечаем точку на той из двух прямых, которая расположена выше (см. синюю линию на рис. 2). Находим точку пересечения прямых: =0,5; W1(0,5) = W2(0,5) = 5. Поскольку при <0,5 прямая W2() расположена выше, то при таких значениях степени оптимизма оптимальным является план x2. Поскольку при >0,5 прямая W1() расположена выше, то при таких значениях степени оптимизма оптимальным является план x1.
. Найдём W* при разных значениях параметра . Очевидно при =0,5 имеем 10 = 2+4, поэтому оба плана являются оптимальными. При <0,5 имеем 10 < 2+4, поэтому оптимальным является план x2. При >0,5 имеем 10 > 2+4, поэтому оптимальным является план x1. Это решение можно проиллюстрировать графически. Изобразим прямые W1() = 10 и W2() = 2+4 (см. рис. 1). Поскольку нам нужно выбрать максимум из этих двух выражений, то для каждого фиксированного отмечаем точку на той из двух прямых, которая расположена выше (см. синюю линию на рис. 2). Находим точку пересечения прямых: =0,5; W1(0,5) = W2(0,5) = 5. Поскольку при <0,5 прямая W2() расположена выше, то при таких значениях степени оптимизма оптимальным является план x2. Поскольку при >0,5 прямая W1() расположена выше, то при таких значениях степени оптимизма оптимальным является план x1.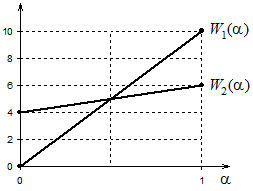
Рис. 1
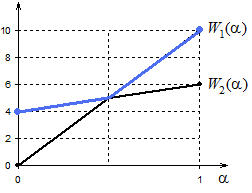
Рис. 2
Используем принцип минимального риска (критерий Сэвиджа). Сначала для каждого значения y находим
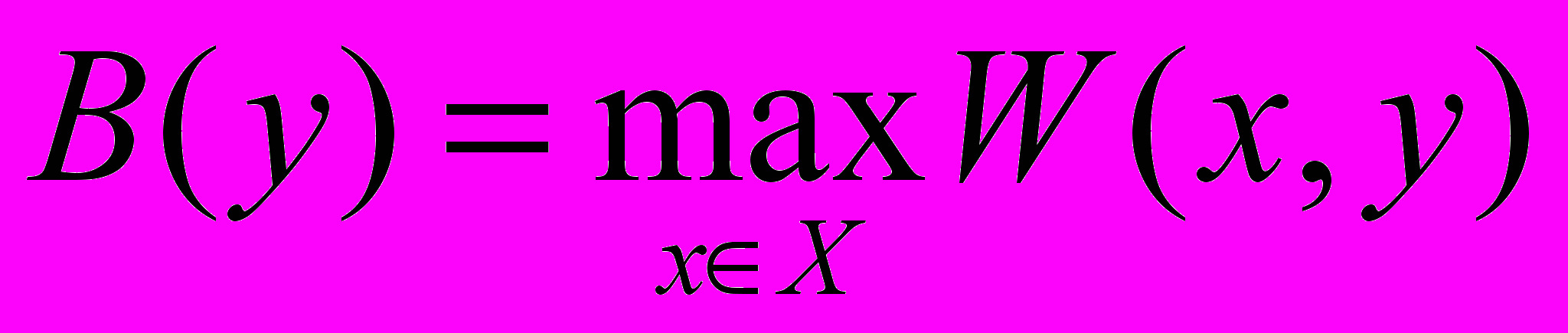 , то есть максимум в каждом столбце матрицы выигрышей, и составим матрицу рисков, вычитая из B(y) элемент матрицы (в каждом столбце значение B(y) свое):
, то есть максимум в каждом столбце матрицы выигрышей, и составим матрицу рисков, вычитая из B(y) элемент матрицы (в каждом столбце значение B(y) свое):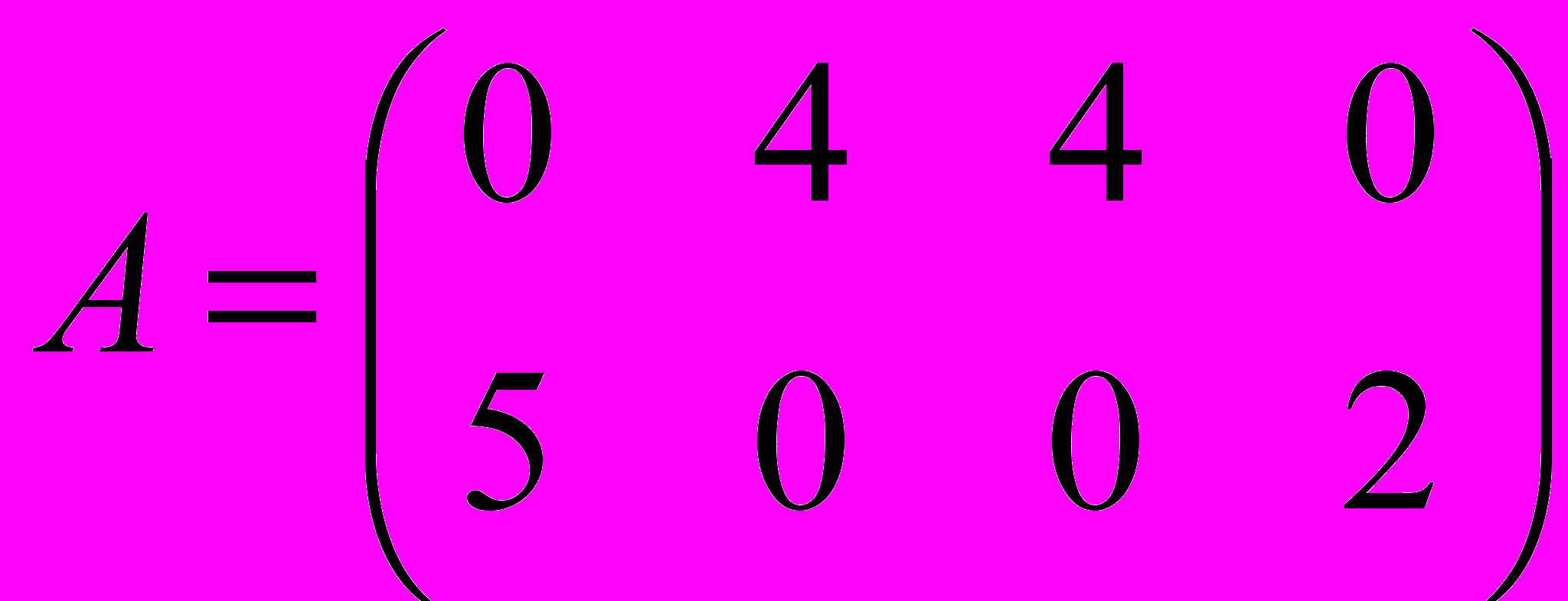 .
.Ищем теперь
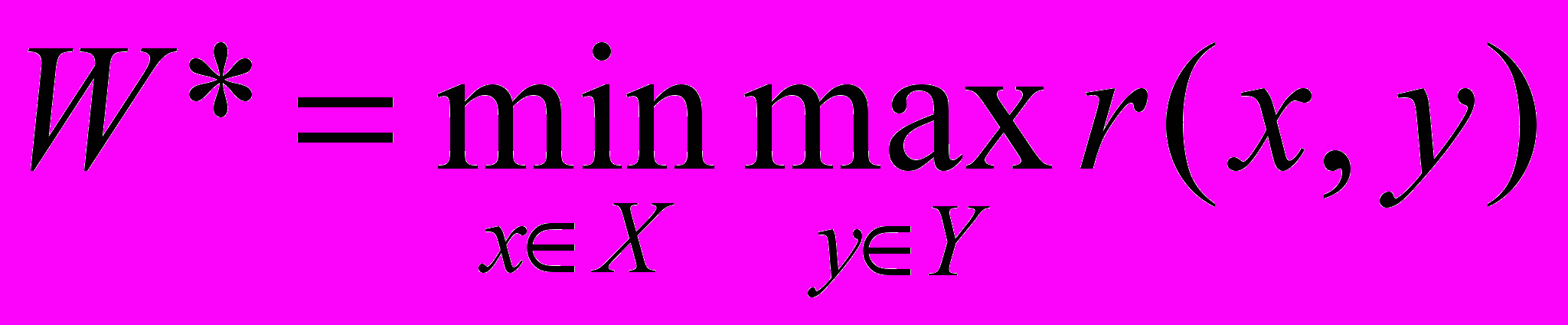 , то есть сначала находим максимум в каждой строке, а потом из них выбираем минимум. Поскольку W*= 4 достигается в первой строке, то оптимальным является план x1.
, то есть сначала находим максимум в каждой строке, а потом из них выбираем минимум. Поскольку W*= 4 достигается в первой строке, то оптимальным является план x1.Таким образом, использование различных принципов решения задачи приводит к различным оптимальным планам.
