Н. Э. Баумана Курсовая работа Теория автоматического управления Валиев А. М. Руководитель проекта: Рассадкин Ю. И. Москва, 2006 Содержание Курсовая

Вид материала

Курсовая

Содержание Техническое задание Вывод уравнения силовой части Построение желаемой ЛАЧХ Нахождение координат рабочей точки Построение желаемой ЛАЧХ Расчет параллельного корректирующего устройства

Подобный материал:

• Курсовая работа по дисциплине "Теория автоматизированного управления", 106.5kb.
• Программа дисциплины "Теория автоматического управления" Направление, 86.24kb.
• Службы курсовая работа по курсу «Система государственного управления» на тему: «Государственное, 376.12kb.
• Московский Государственный Университет технологий и управления курсовая, 5.68kb.
• Кафедра Экономического Анализа и Аудита курсовая, 512.81kb.
• А. Л. Шестаков 06 июня 2008 г. Группа Т62 стандарт организации система управления качеством, 966.21kb.
• Москва, 9-11 сентября 2009 г. Московский государственный технический университет им., 94.15kb.
• Методические рекомендации по выполнению курсовых работ курсовая работа по «Общей психологии», 54.44kb.
• Теория и методика математического развития, 63.97kb.
• Курсовая работа Социокультурные лакуны в статьях корреспондентов, 270.94kb.

Московский Государственный Технический Университет

имени Н. Э. Баумана

Курсовая работа

Теория автоматического управления

Выполнил:

Валиев А.М.

Руководитель проекта:


Рассадкин Ю.И.


Москва, 2006

Содержание

Техническое задание

Спроектировать следящую САУ, согласно Схеме 1, в соответствии со следующими параметрами:

1. Момент инерции приведенный к валу двигателя:[кг·м²],
   
2. Сопротивление якорной цепи: R_я = 1.7 Ом
   

3. Индуктивность якоря: L_я =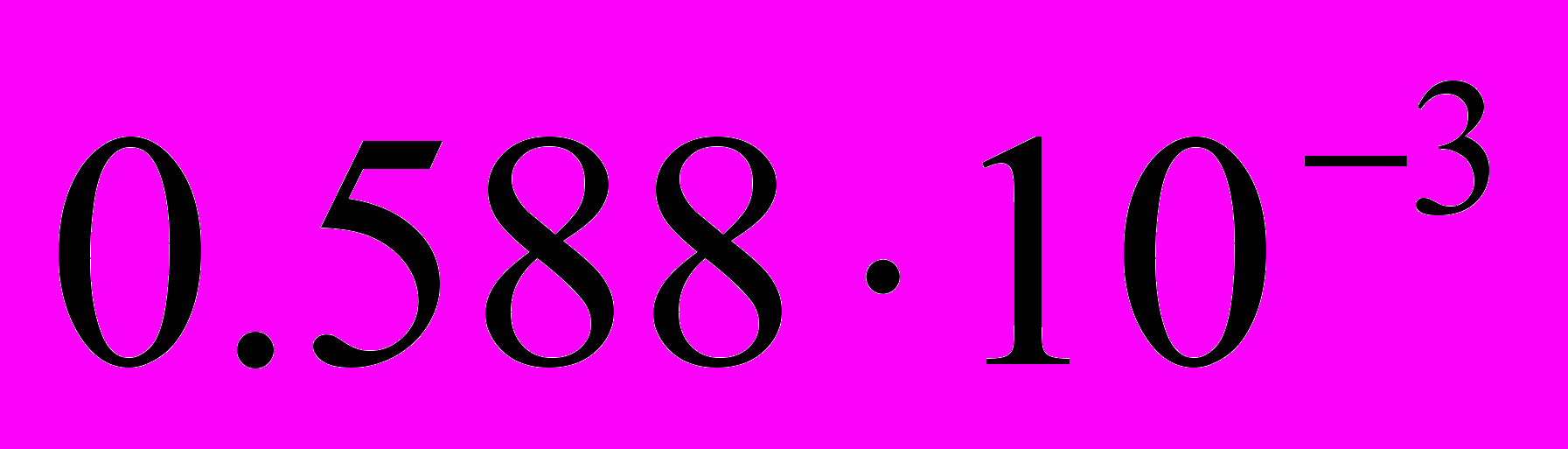Гн
   

4. Коэффициент противо-ЭДС (конструктивная постоянная двигателя):
   

=

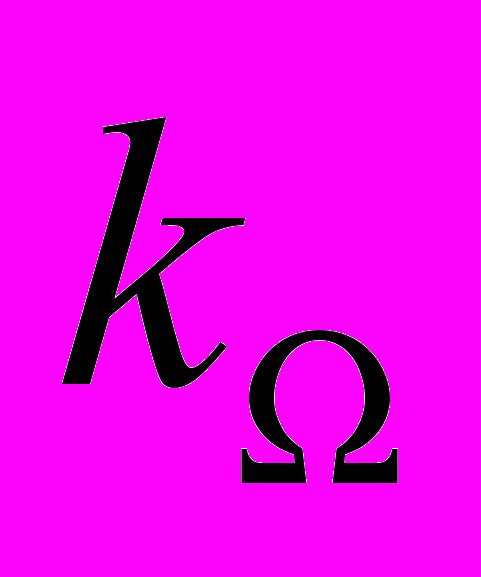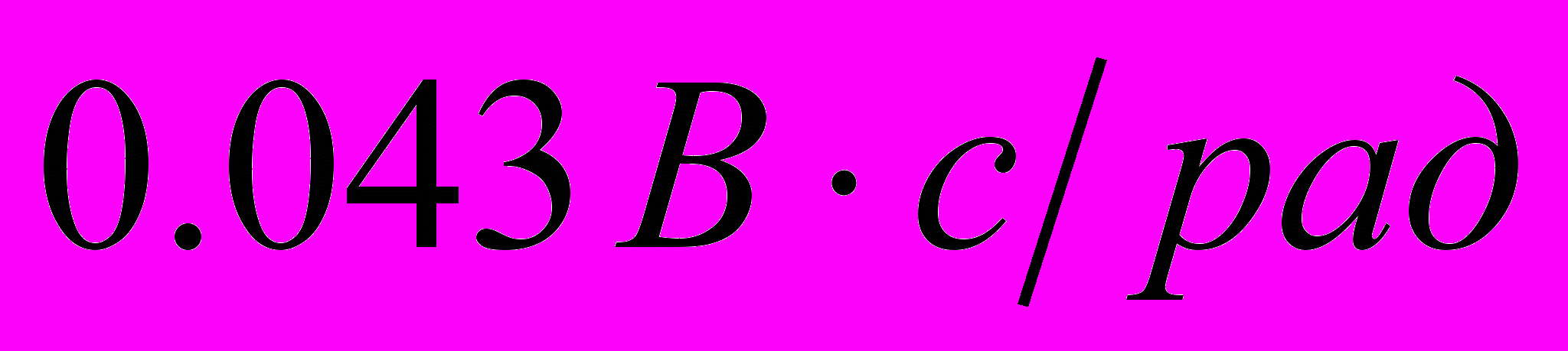
5. Конструктивная постоянная двигателя: k_м =
   

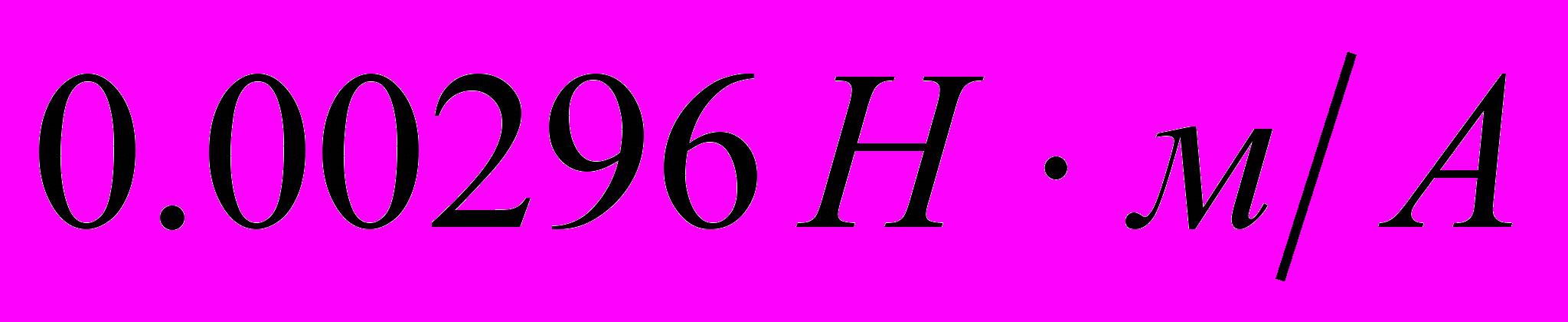
6. Скорость изменения управляющего воздействия:
   

7. 
   
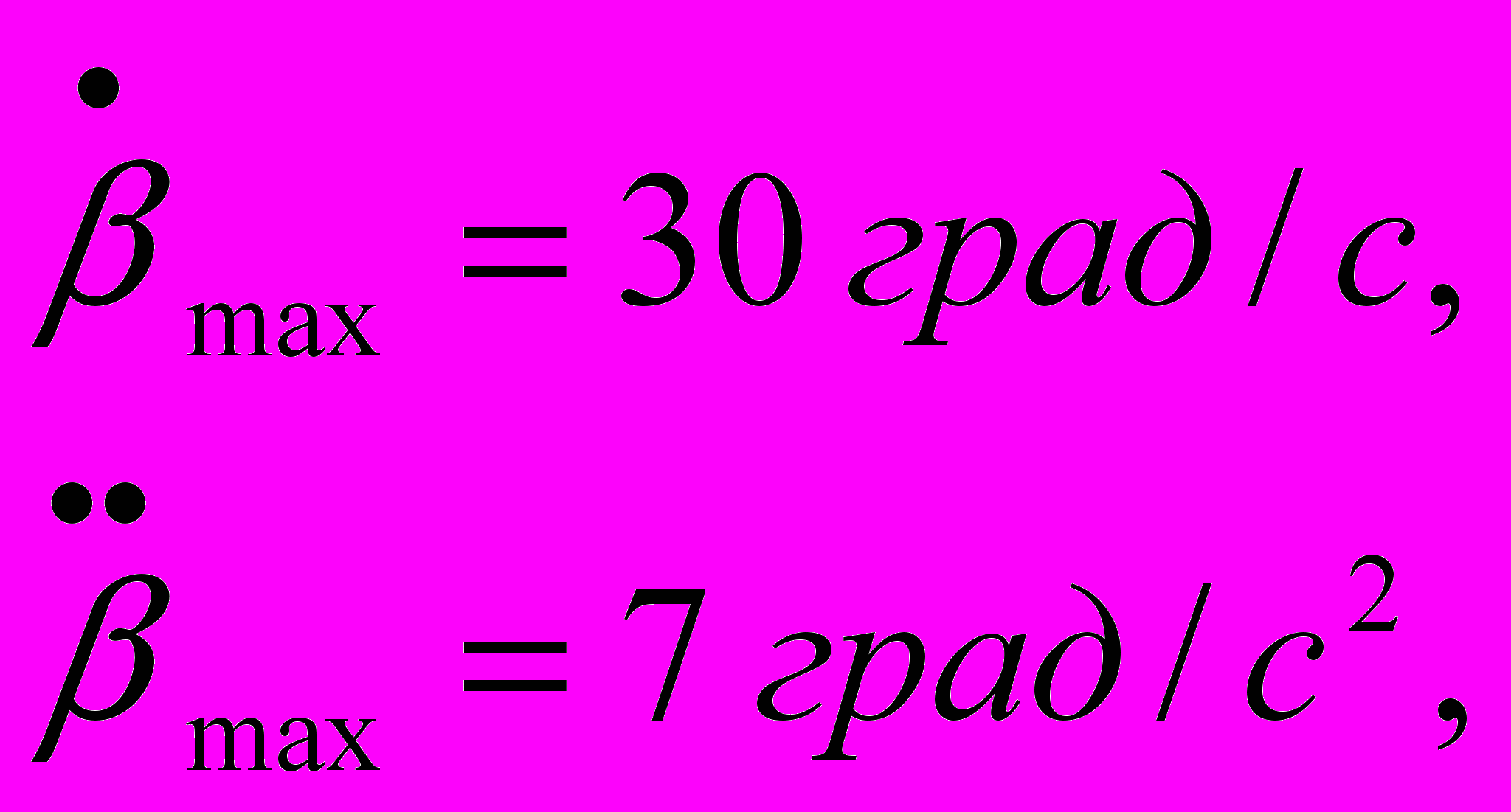
8. Максимальная ошибка:
   

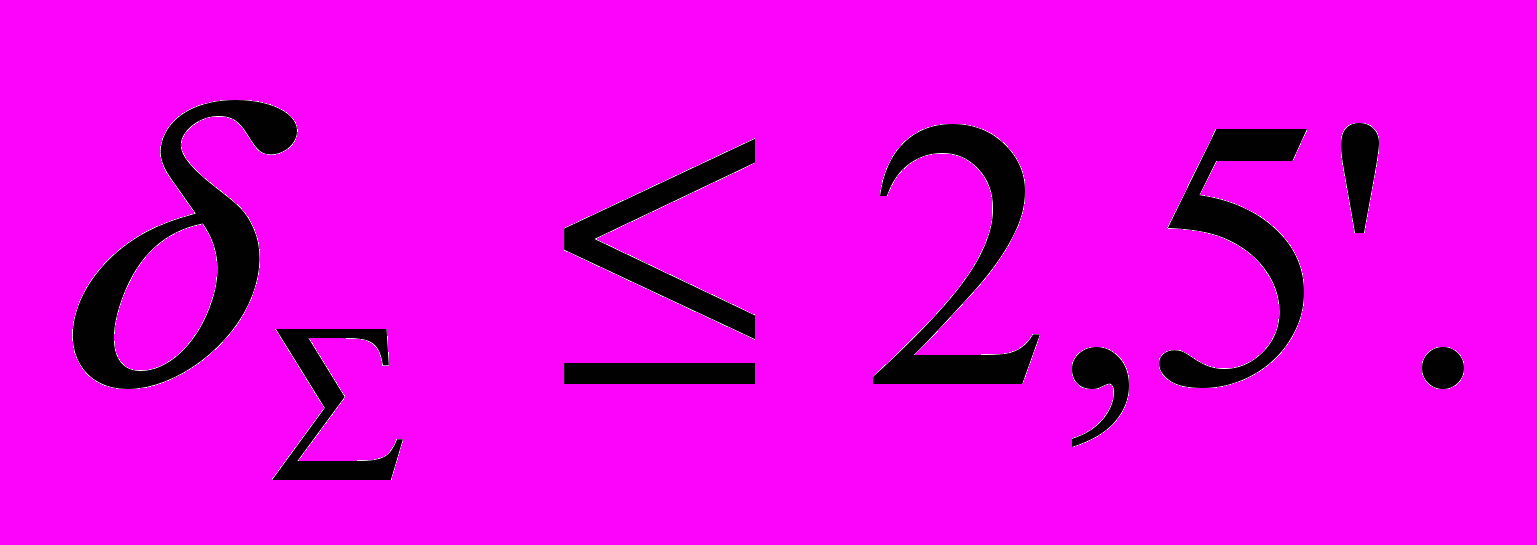
Вывод уравнения силовой части

Выведем уравнение исполнительной части следящей системы. В системе в качестве исполнительного двигателя используется двигатель постоянного тока независимого возбуждения, схема которого представлена на Рис. 1.





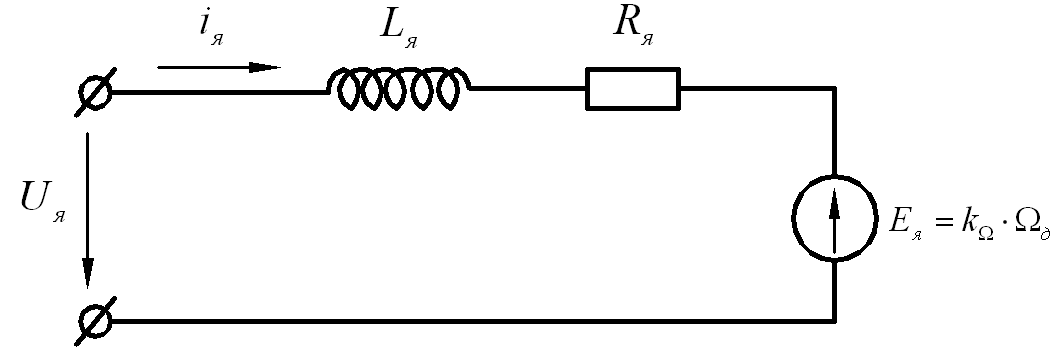
Запишем уравнения, согласно схеме замещения:


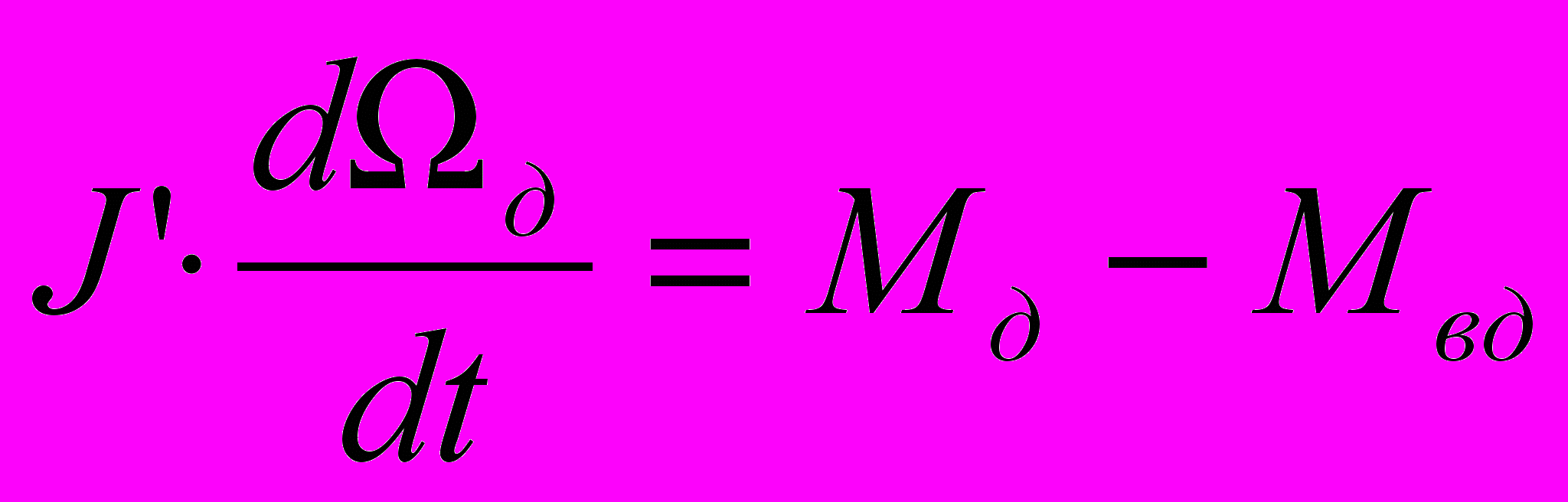(1.1),

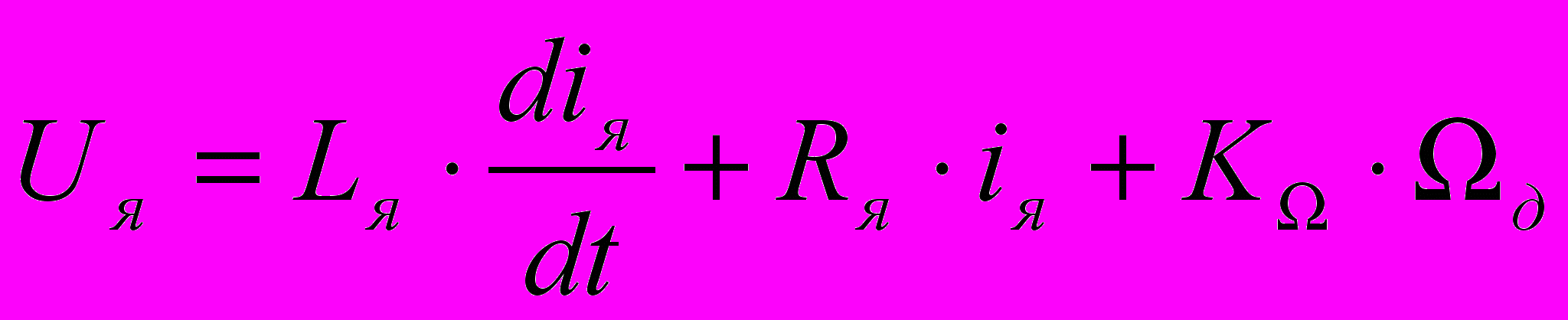(1.2),


где 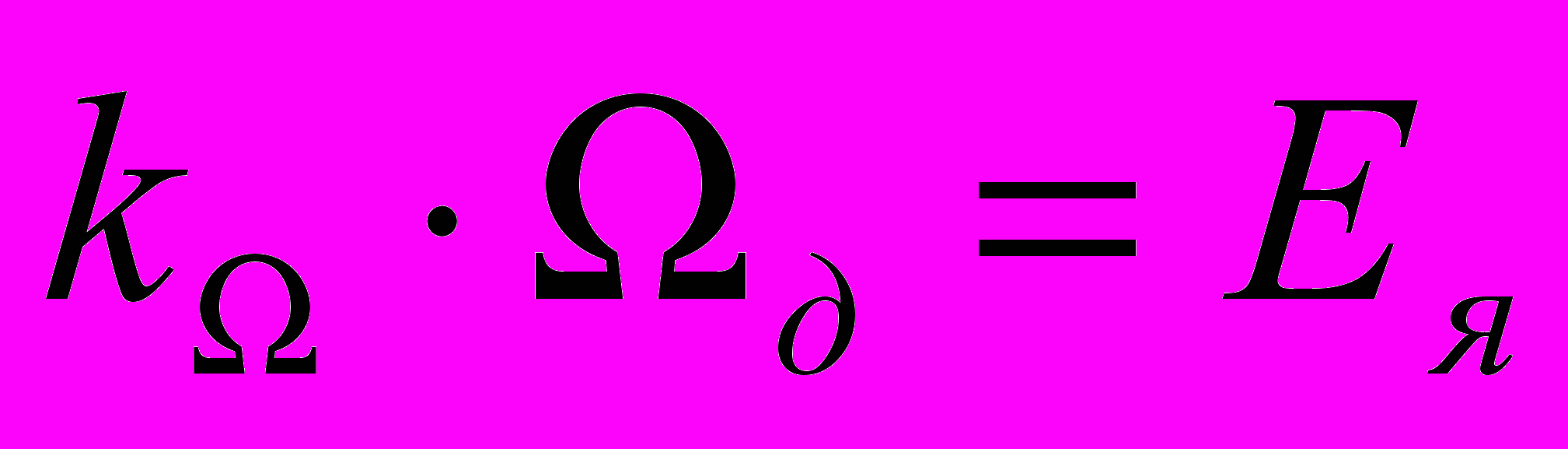(1.3),

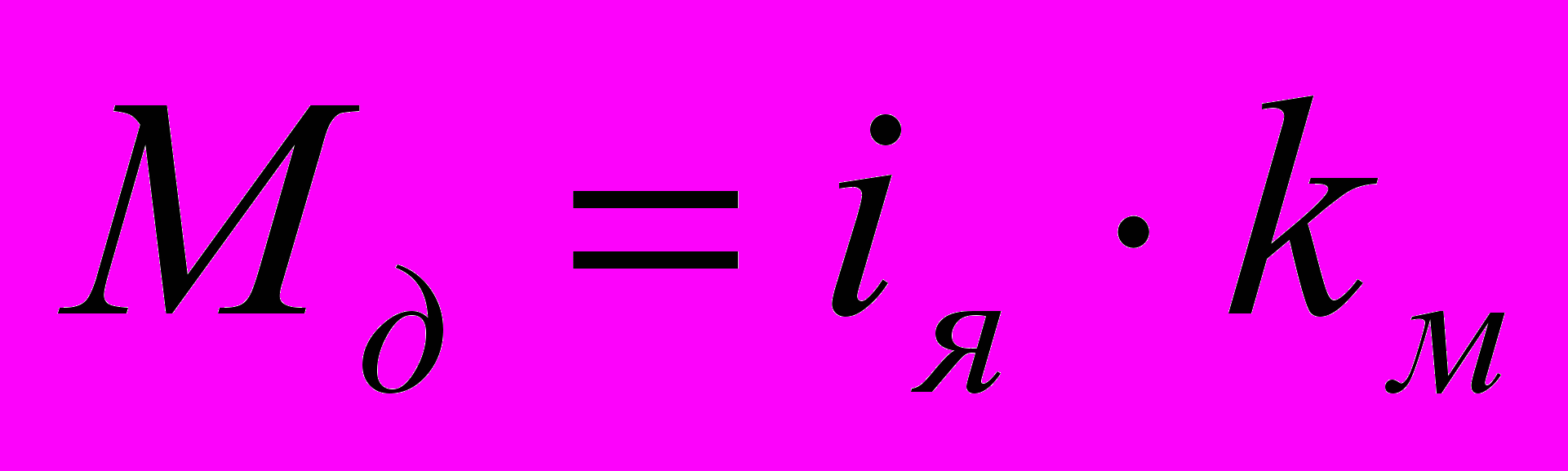(1.4).


U_я – напряжение якоря,

I_я – ток якоря,

L_я – индуктивность якоря,

R_я – активное сопротивление якоря,

J’ – суммарный момент инерции, приведенный к валу двигателя,

М_д – момент, развиваемый двигателем,

М_вд – момент возмущения, приведенный к валу двигателя,

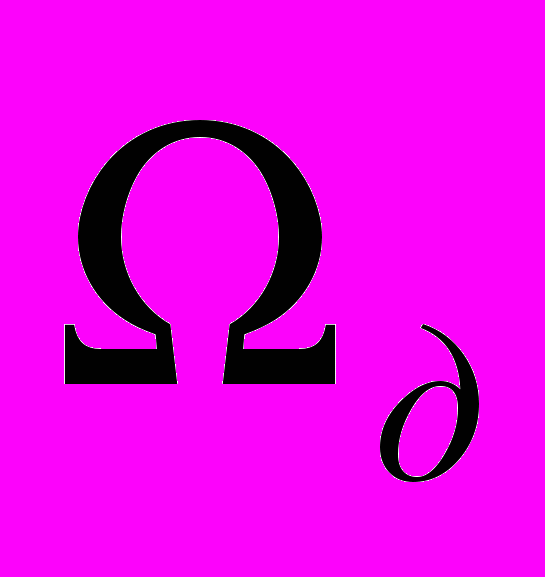- скорость вращения ротора двигателя,

Е_я – противо-ЭДС,

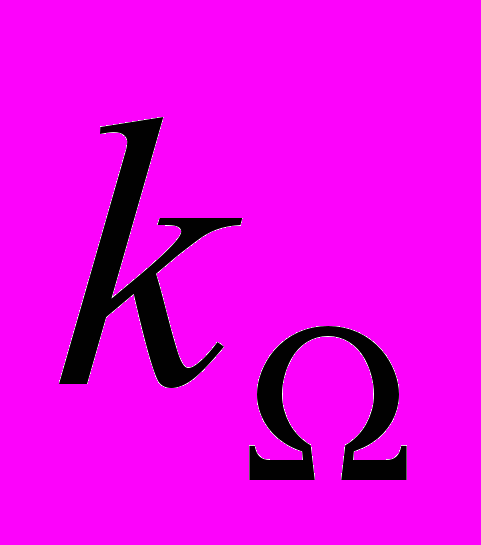- коэффициент противо-ЭДС (конструктивная постоянная двигателя),

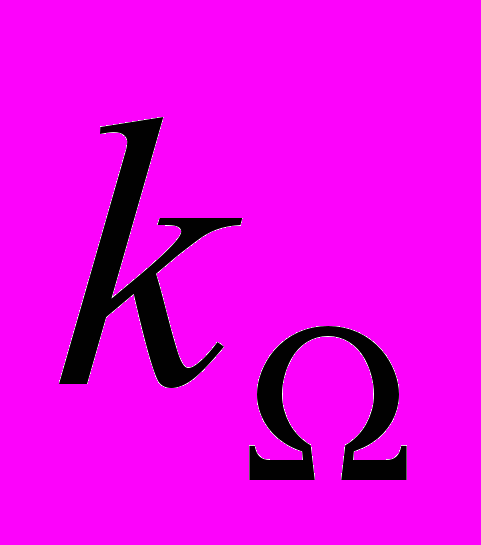k_м – конструктивная постоянная двигателя.


Рассмотрим уравнения (1) – (4).




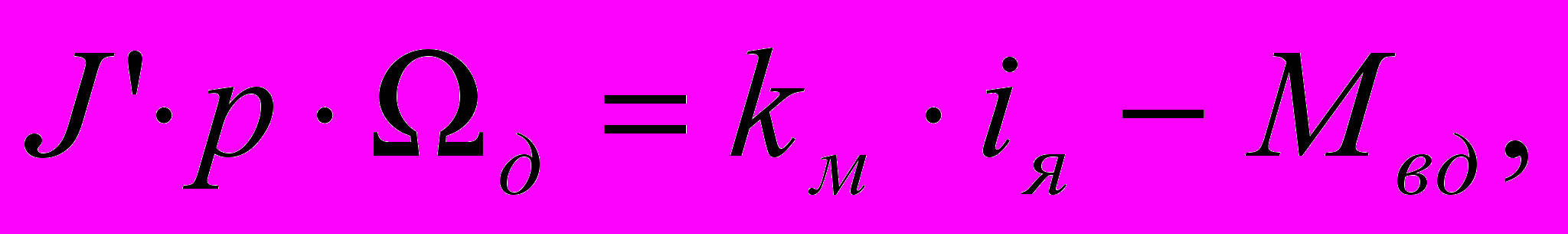
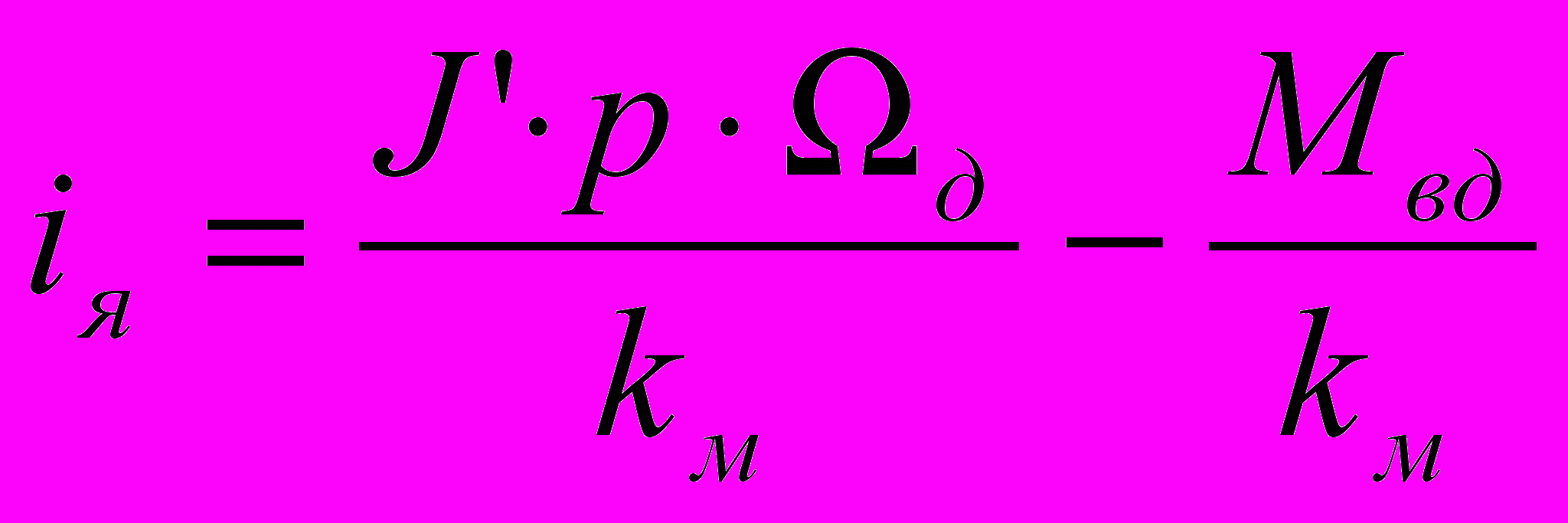(1.5).

,

,



.


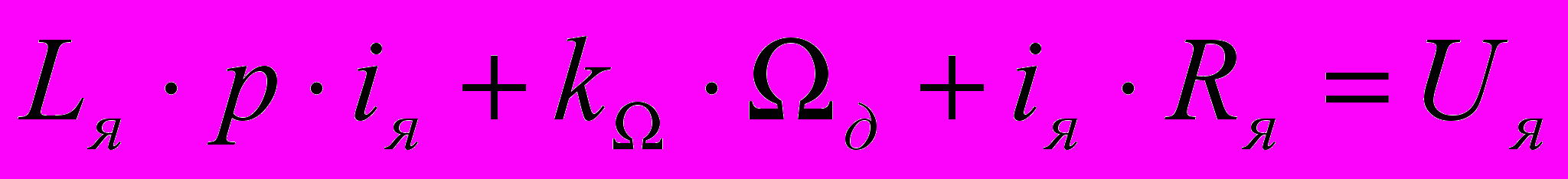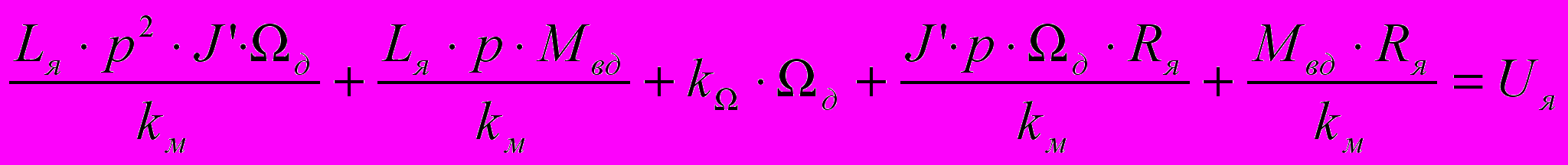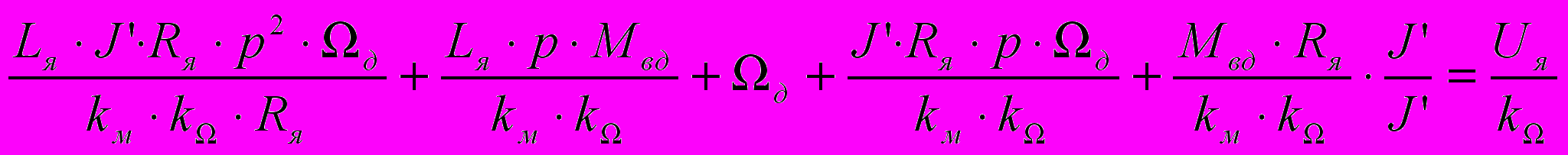Обозначим:


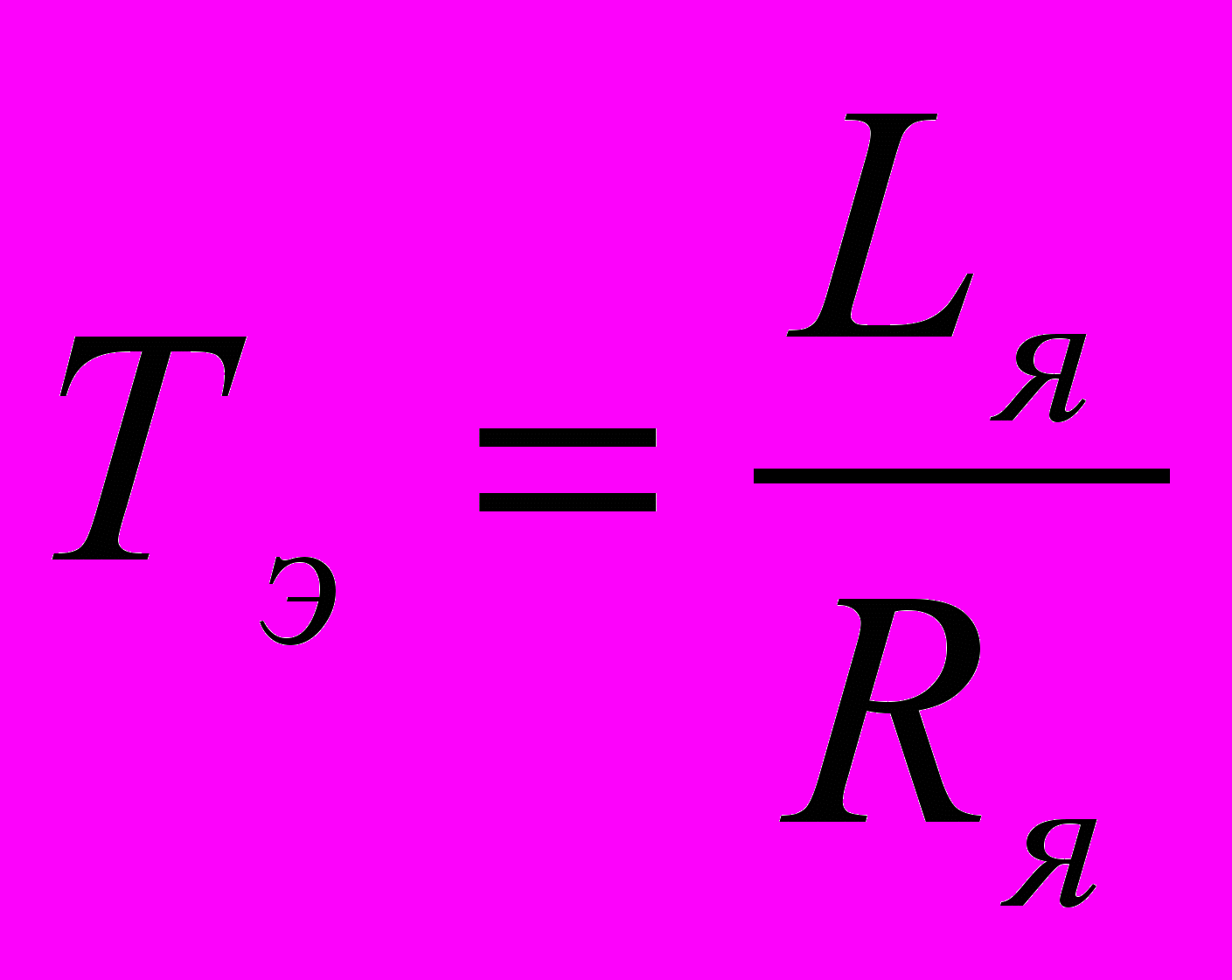- постоянная времени нарастания тока якоря (из-за наличия L_я) (1.6),

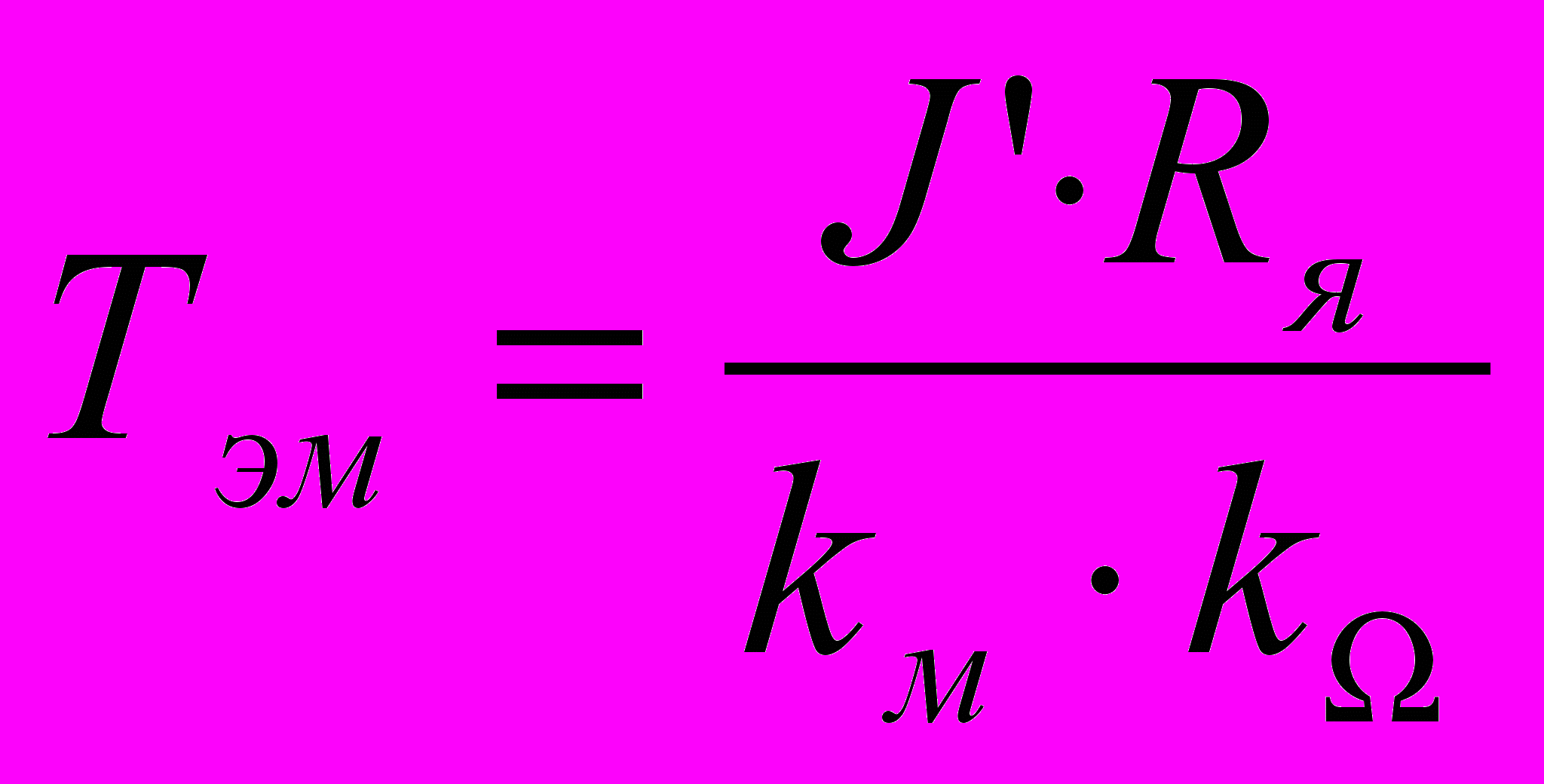- постоянная времени нарастания скорости ИД. (1.7).


Подставив данные обозначения получим:


,

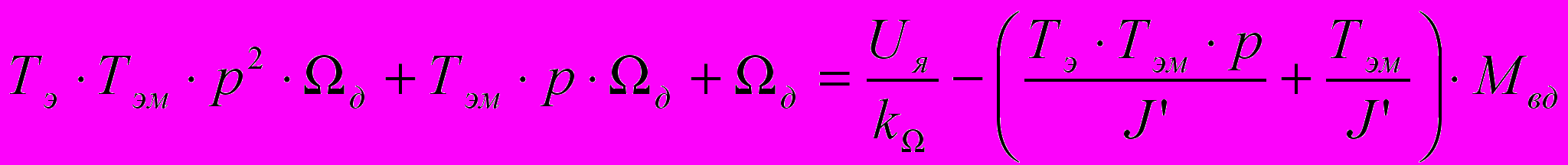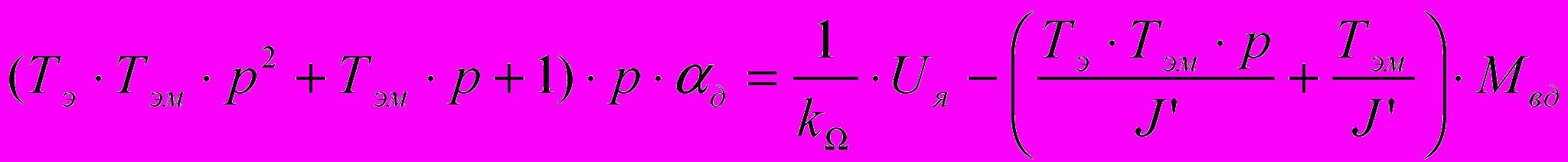(1.8),


Примем:


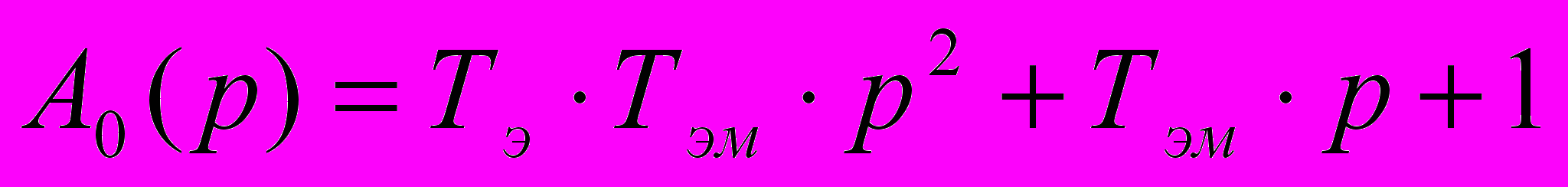(1.9).


Рассчитаем значение Т_э и Т_эм:


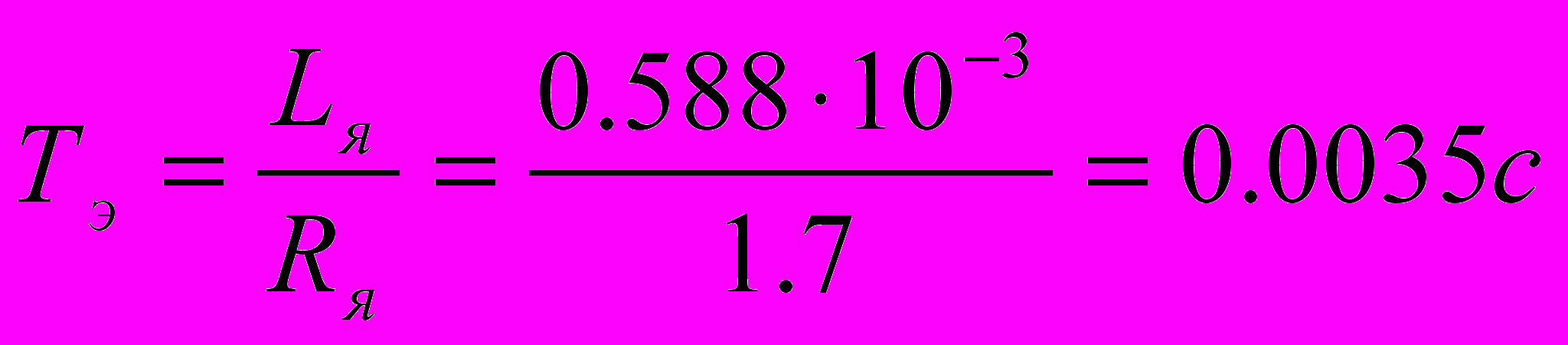(1.10)

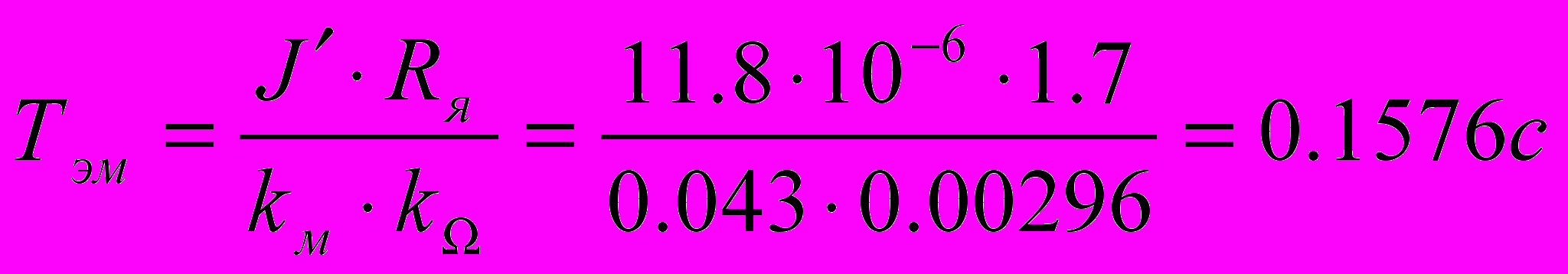(1.11)


Запишем уравнение (1.9) в виде: 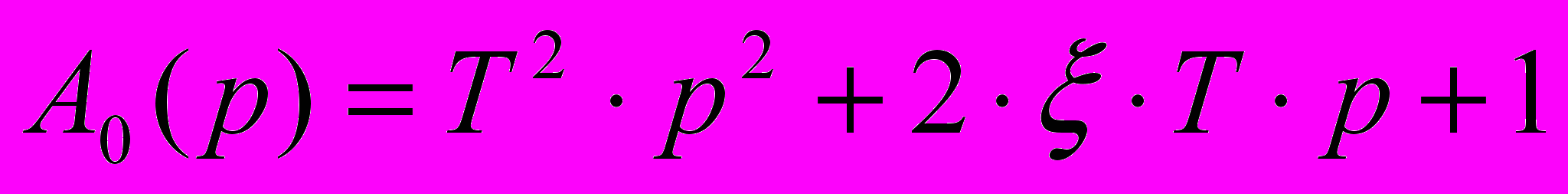(1.12),


где 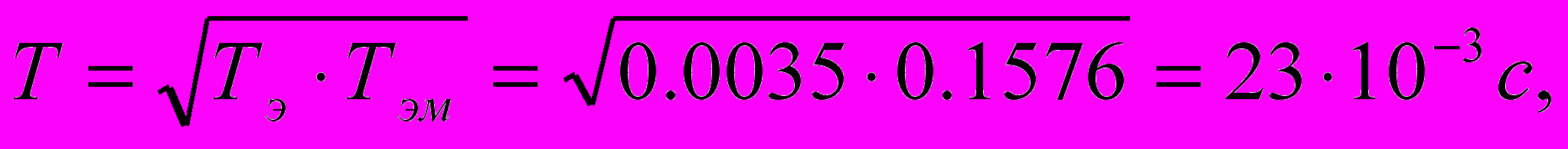(1.13)

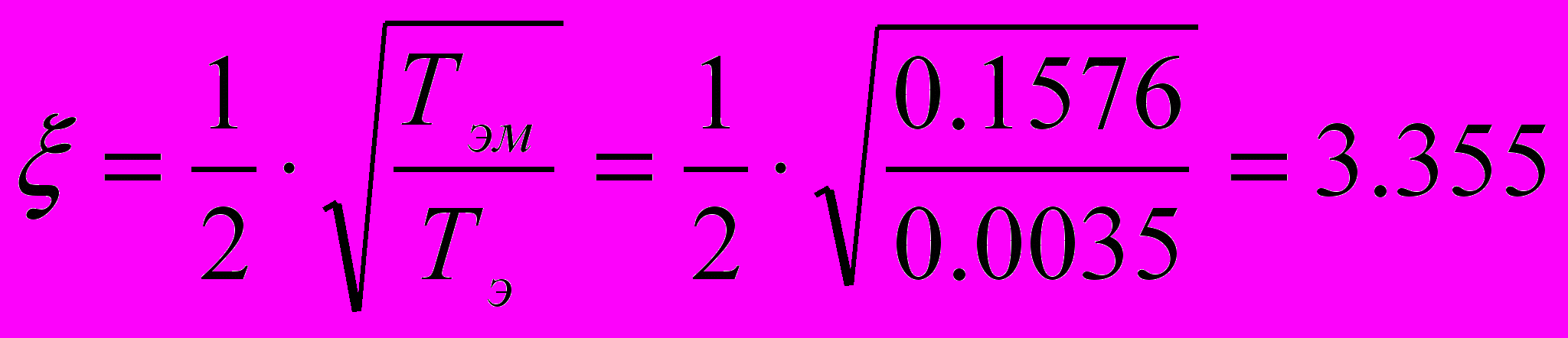(1.14).


Тогда передаточная функция неизменяемой части имеет вид:

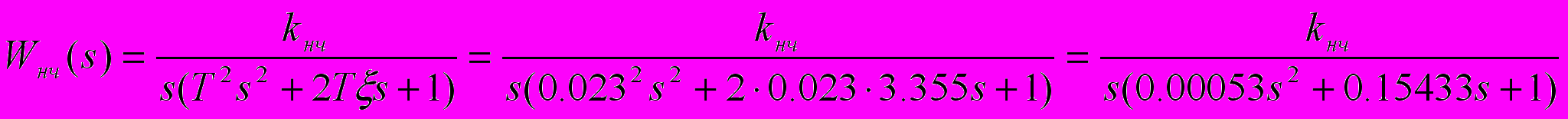
Построение желаемой ЛАЧХ

В соответствии с методикой, выбираем желаемую обратную ЛАЧХ 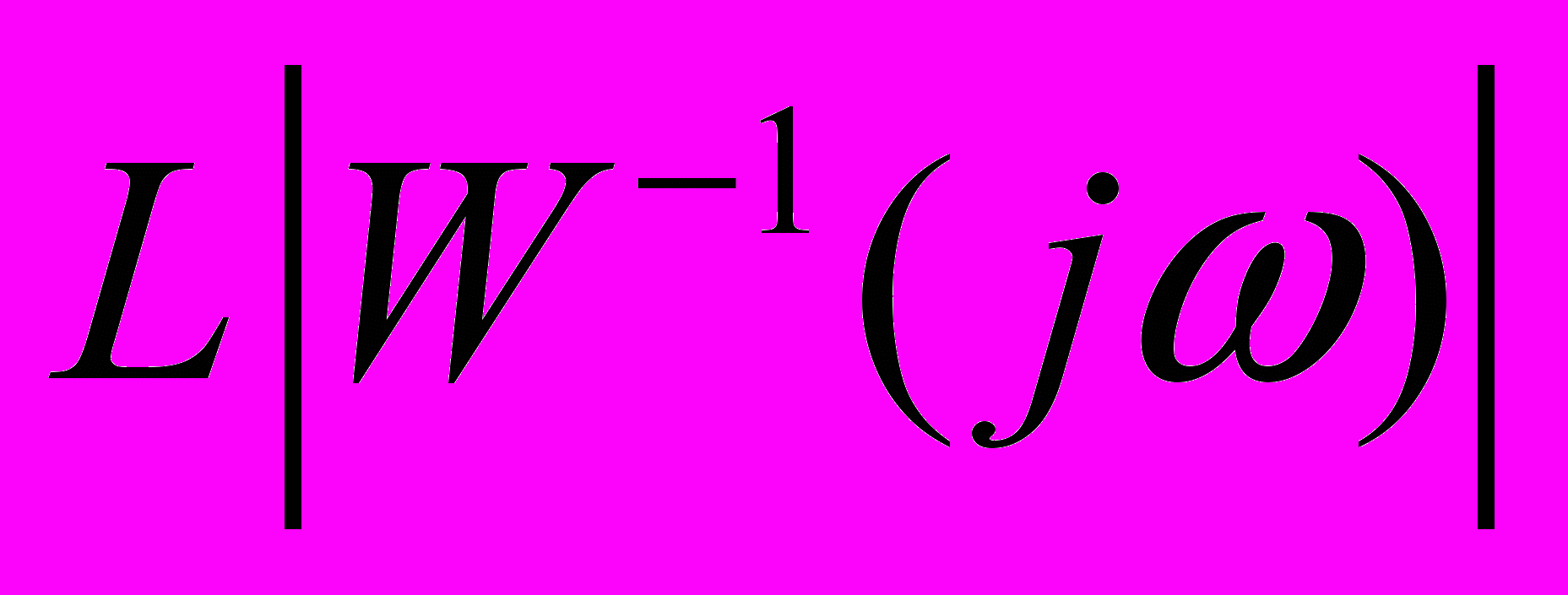второго типа. При этом для коррекции ЭСП используются обратные связи по скорости и моменту ИД, а также последовательное корректирующее устройство. Для упрощения реализации применяем общее корректирующее устройство во всех цепях обратных связей. В этом случае передаточная функция скорректированного разомкнутого СП будет иметь вид:


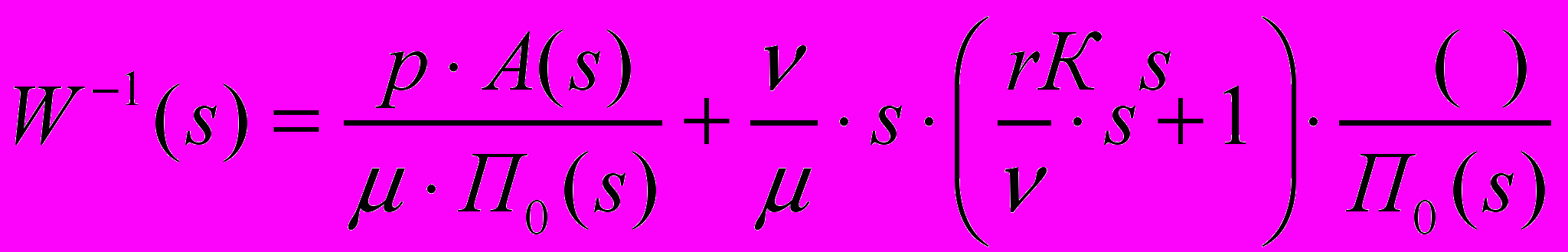(2.1),

где μ – коэффициент усиления разомкнутой системы;

υ – коэффициент усиления разомкнутого внутреннего контура связи по скорости при К(s)≡1;

r – коэффициент усиления разомкнутого внутреннего контура связи по моменту при К(s)≡1

Нахождение координат рабочей точки

Определим координаты т. В_р исходя из требований по точности системы.


Находим рабочую частоту:


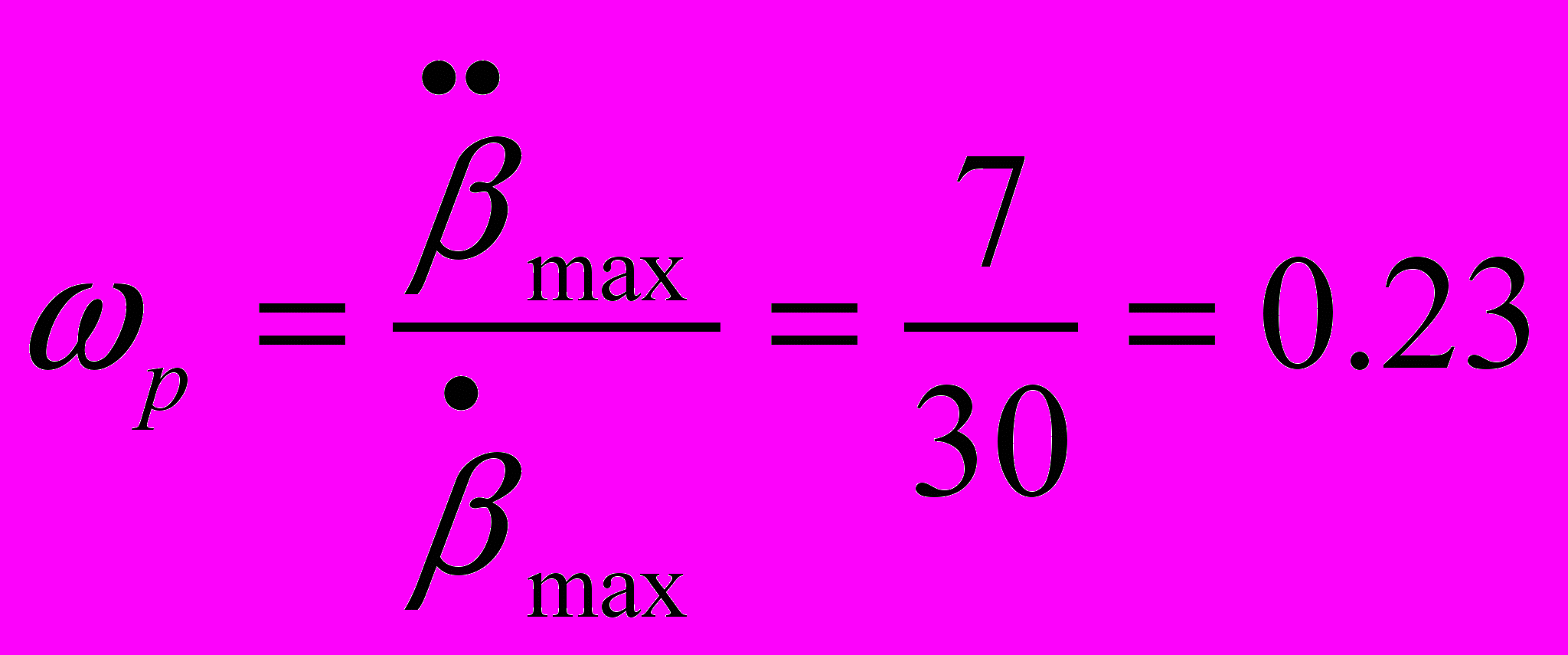с^-1


Определяем амплитуду гармонической составляющей управляющего воздействия:


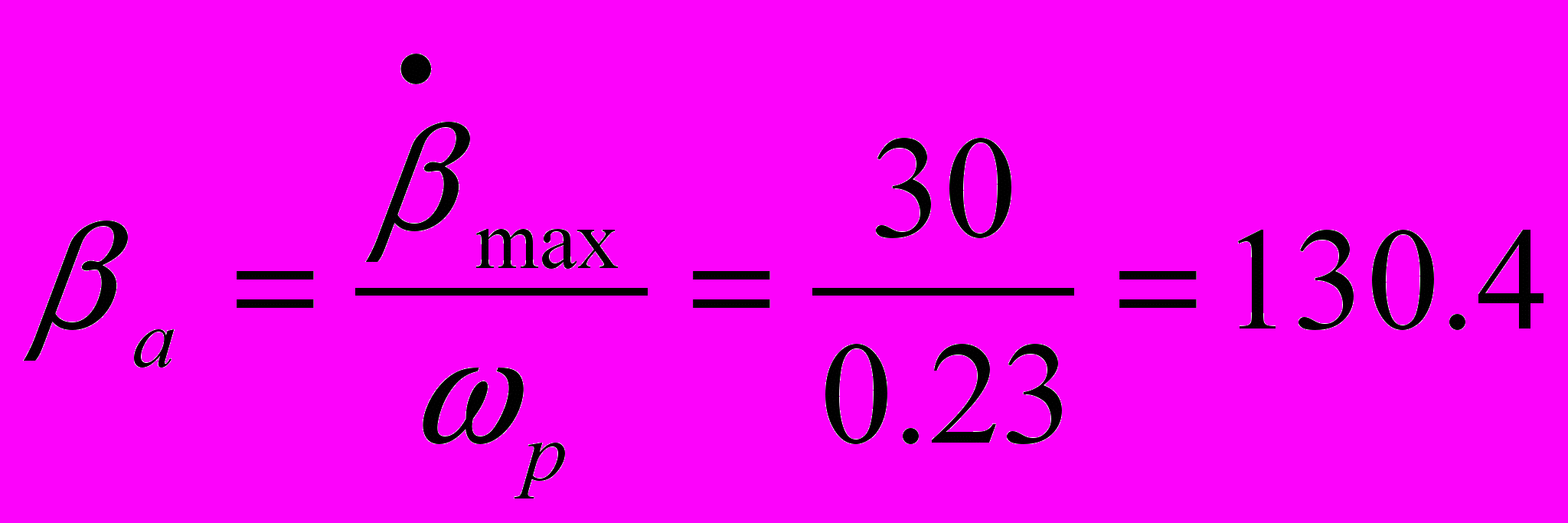град

Примем амплитуду гармонической составляющей ошибки равной 70% от заданной максимальной ошибки. Тогда:


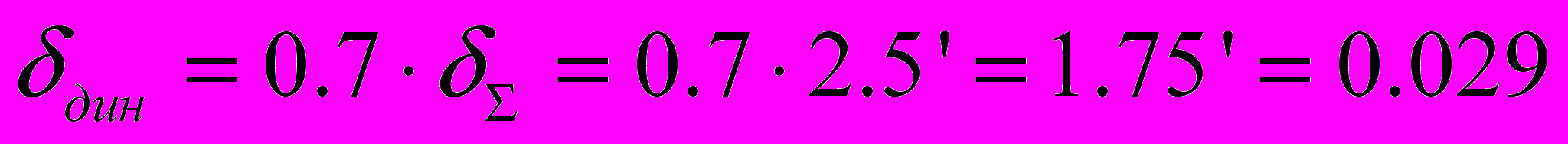град.


При этом ордината рабочей точки равна:


.


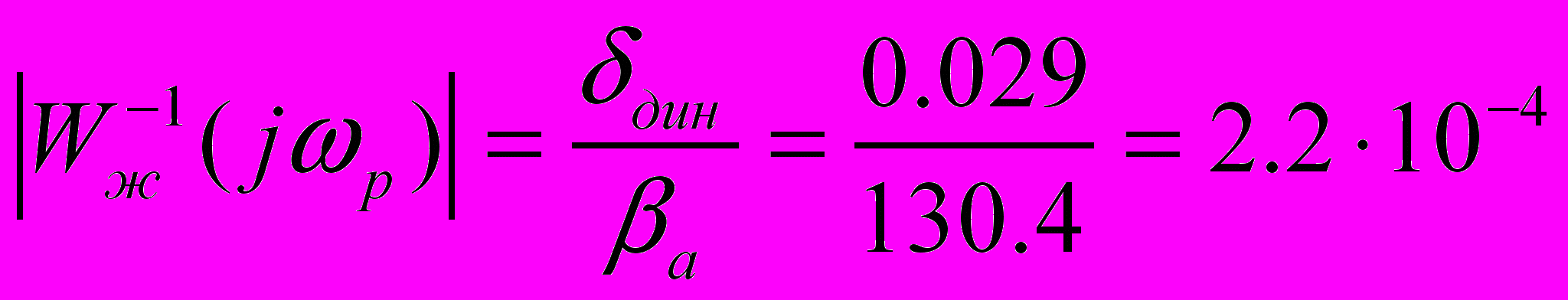Таким образом, координаты рабочей точки A_р будут иметь значения:


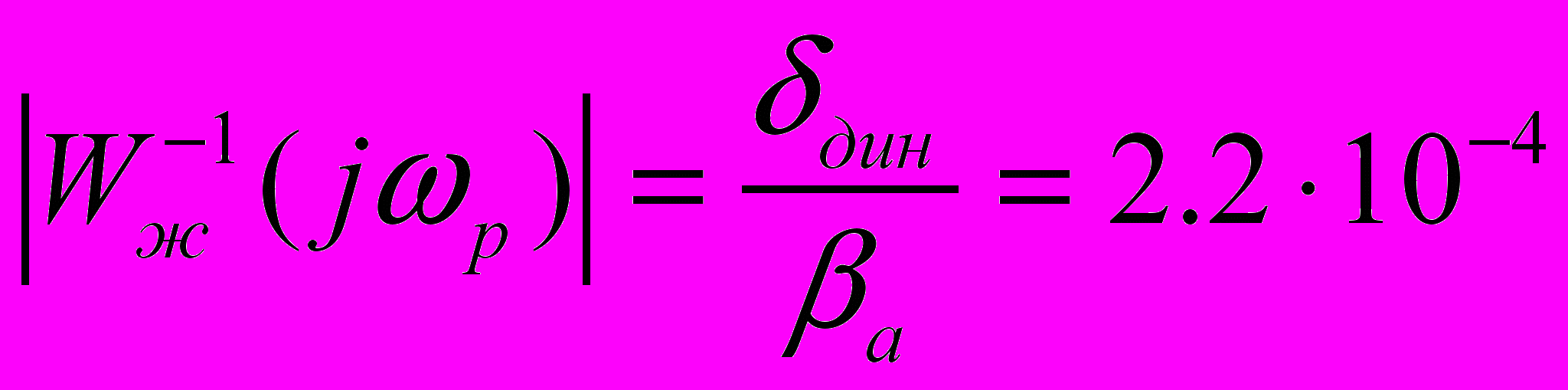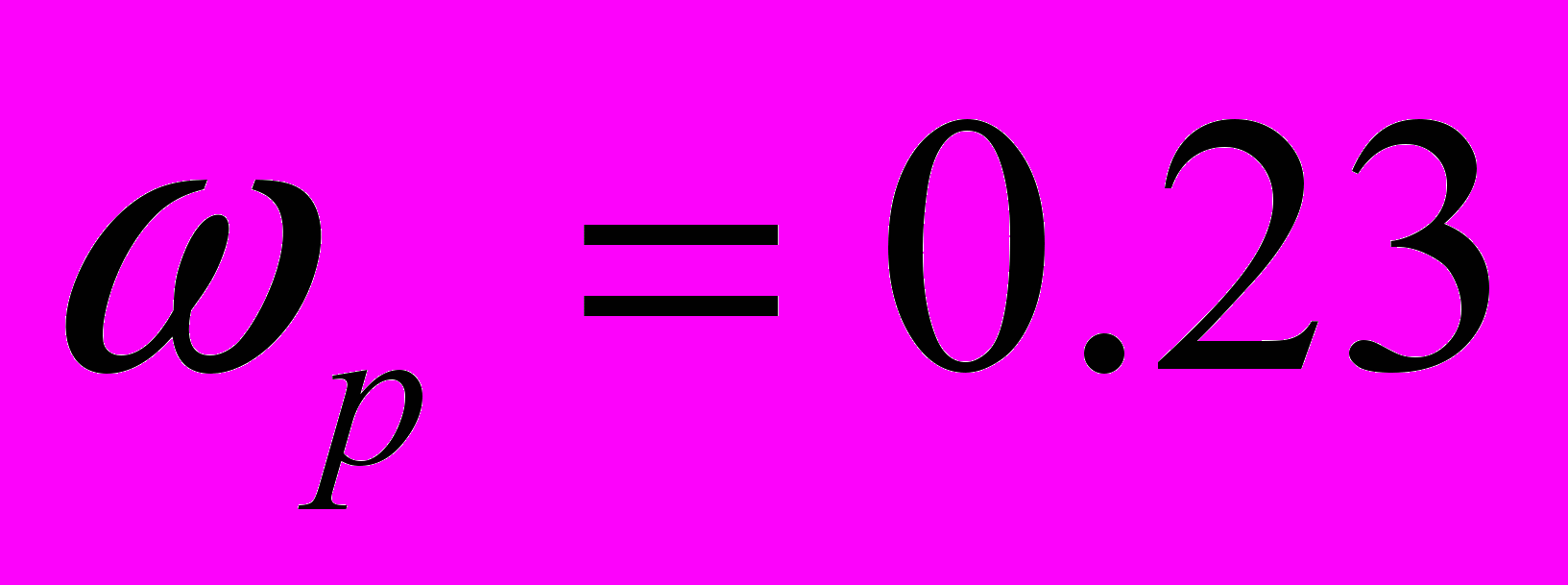; рад/с.

Построение желаемой ЛАЧХ

Передаточная функция неизменяемой части имеет вид:


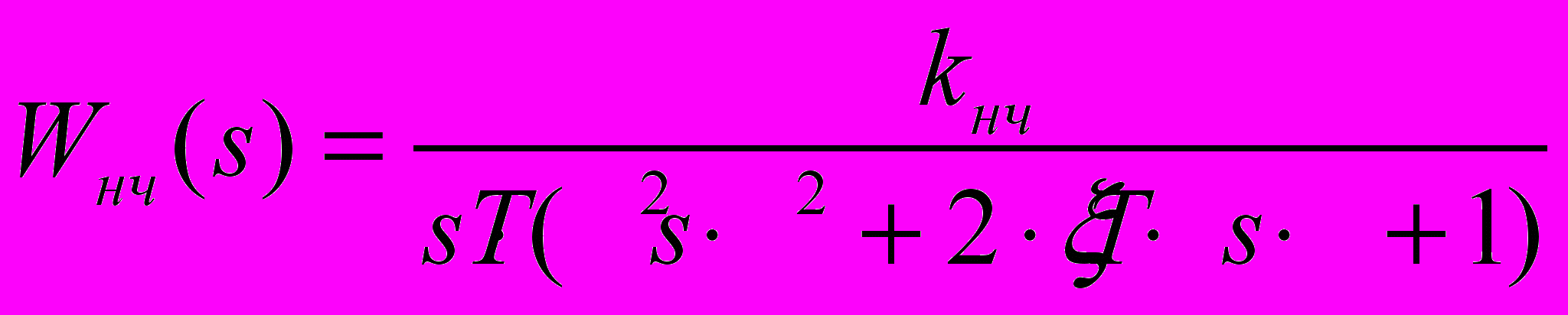(1.1)


Исходя из найденных значений координат рабочей точки, строим 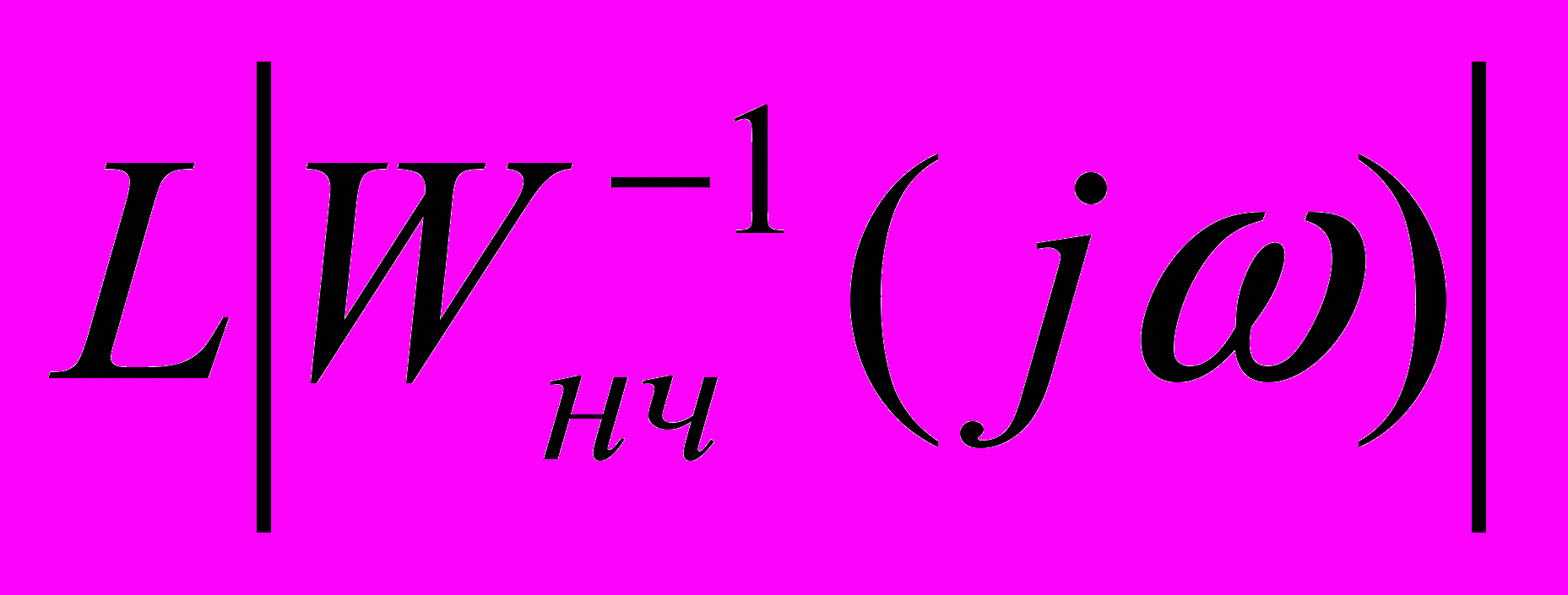. По построенному графику определяем значение коэффициента усиления разомкнутой системы:


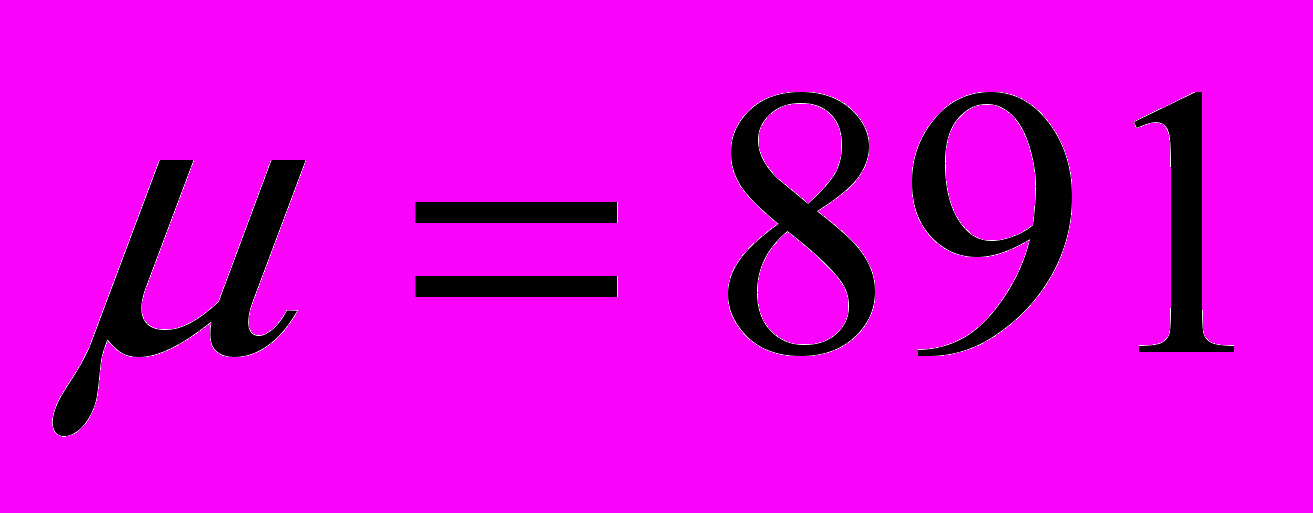с^-1


Из т. А_р проводим прямую с наклоном +40 дБ/дек до уровня – 13 дБ. Из полученной точки проводим прямую с наклоном +20 дБ/дек до пересечения с графиком 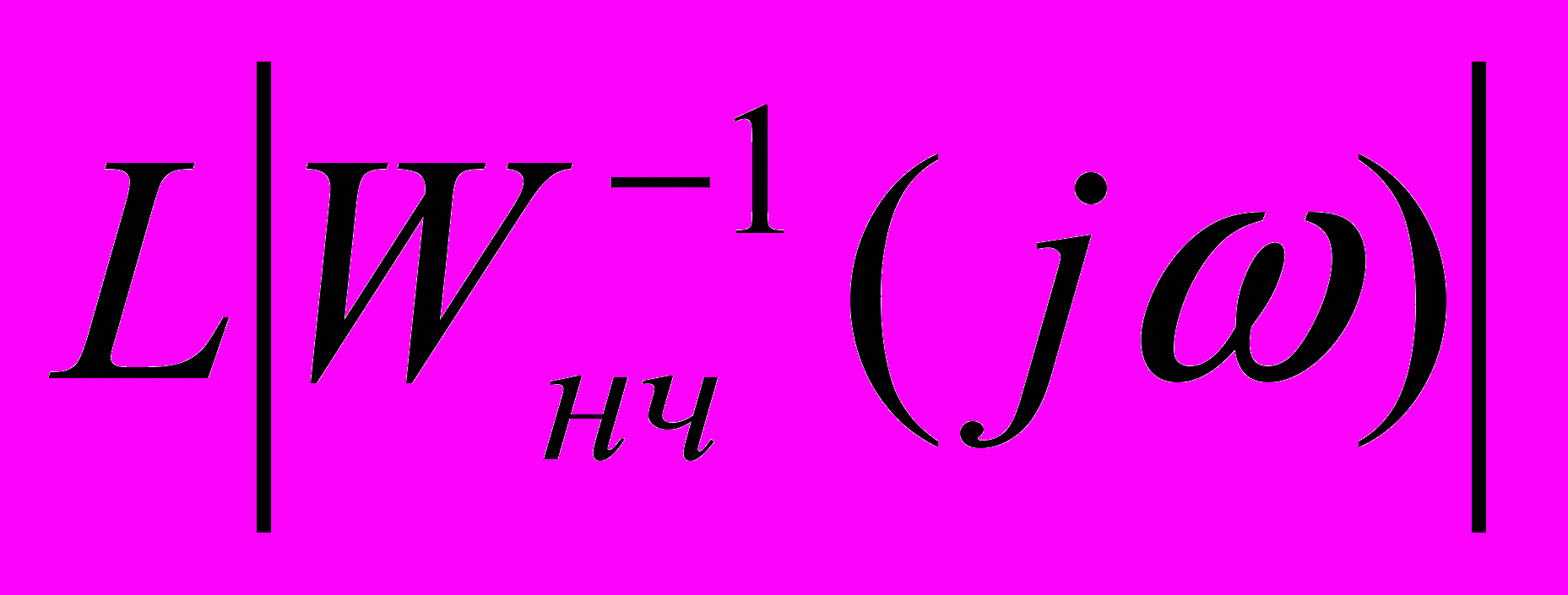. Так как высокочастотная и низкочастотная асимптоты построенной желаемой ЛАЧХ и ЛАЧХ неизменяемой части совпадают, то мы получили желаемую ЛАЧХ.

Частота среза системы, исходя из графика, равна:


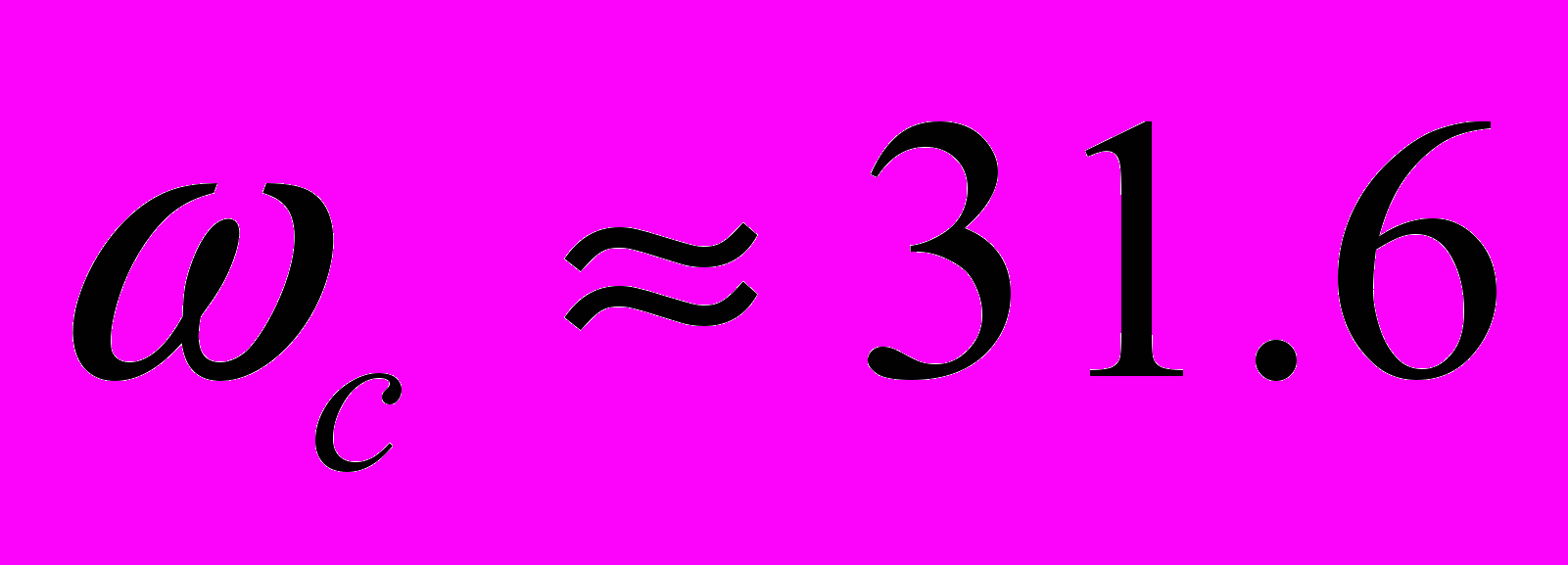с^-1


Пересечение 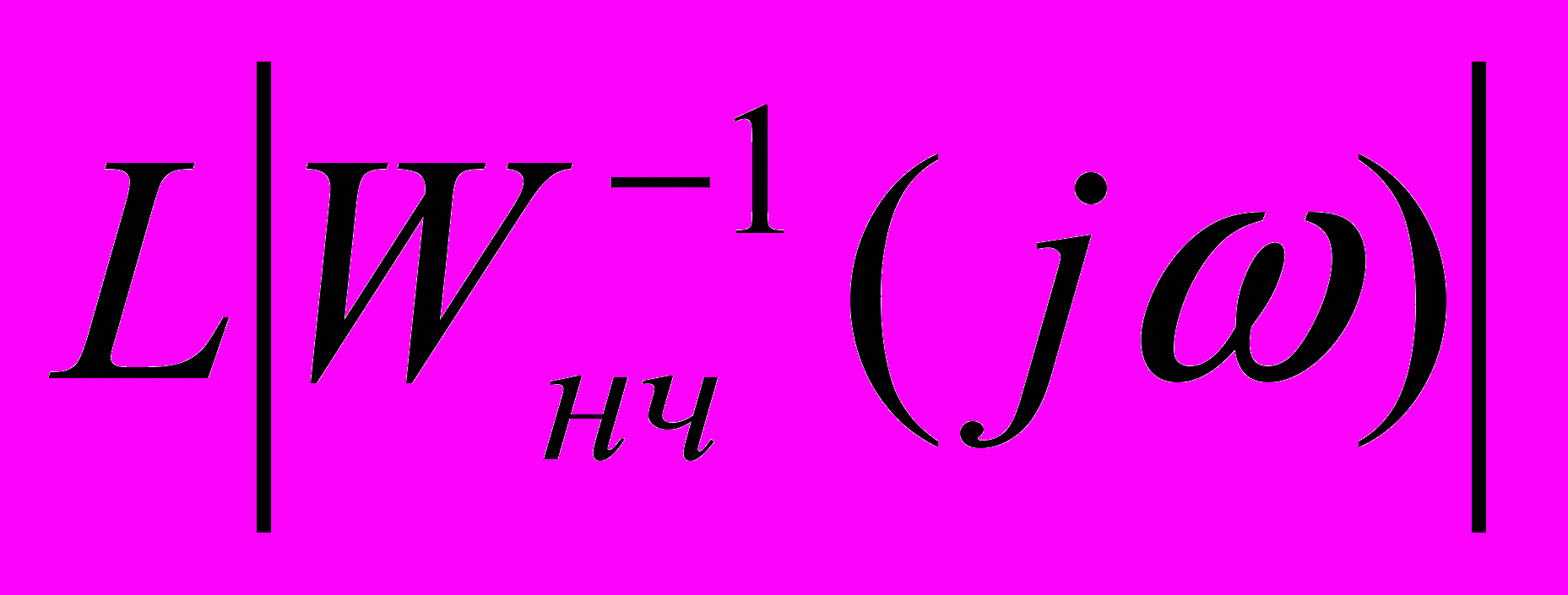и 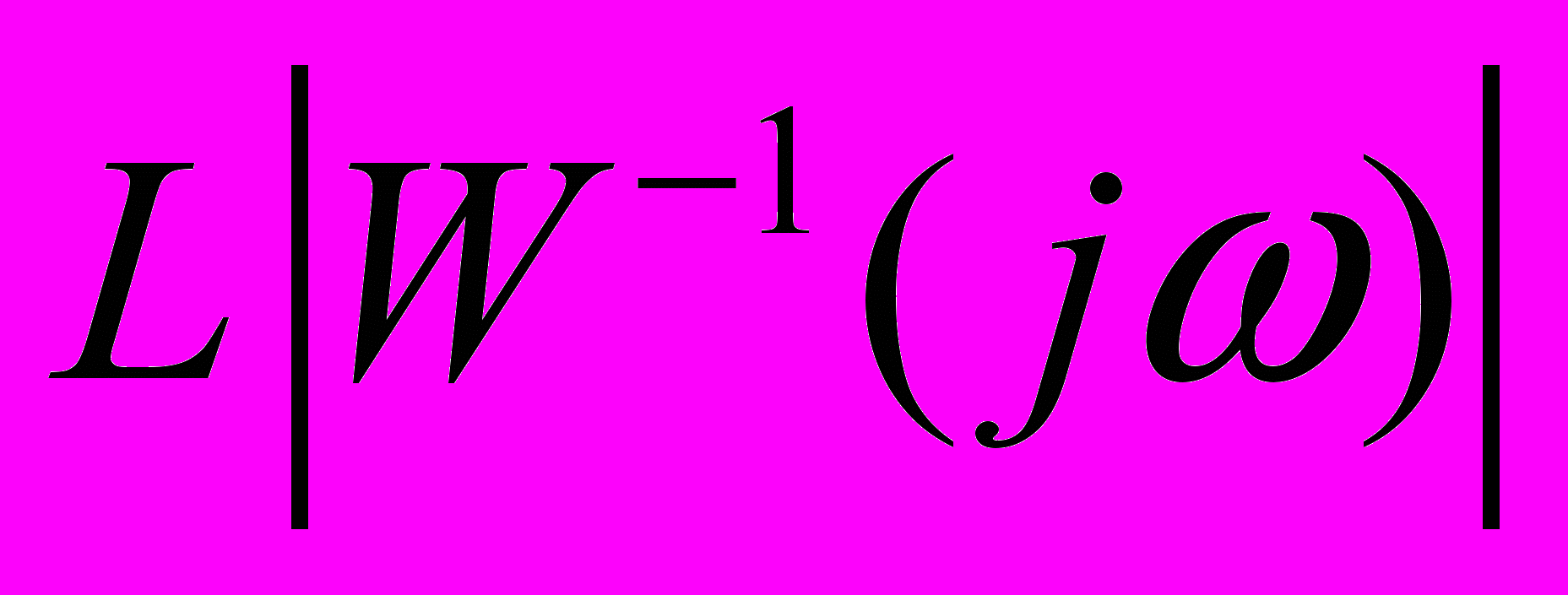произошло в точке B, значение амплитуды в которой равно 16 дБ. Таким образом, система удовлетворяет требованиям по устойчивости, и в введении последовательного корректирующего устройства нет необходимости: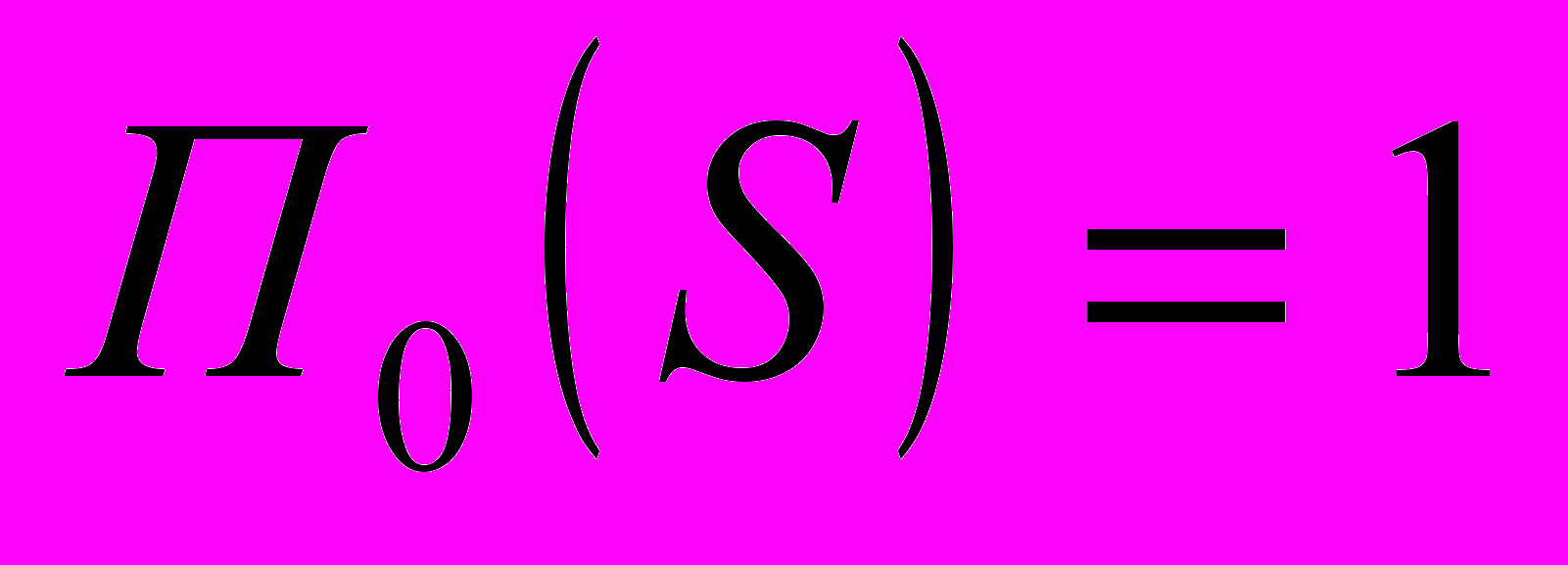




Желаемая ЛАЧХ выделена на графике штриховкой.

Частоты характерных точек построенной желаемой ЛАЧХ:

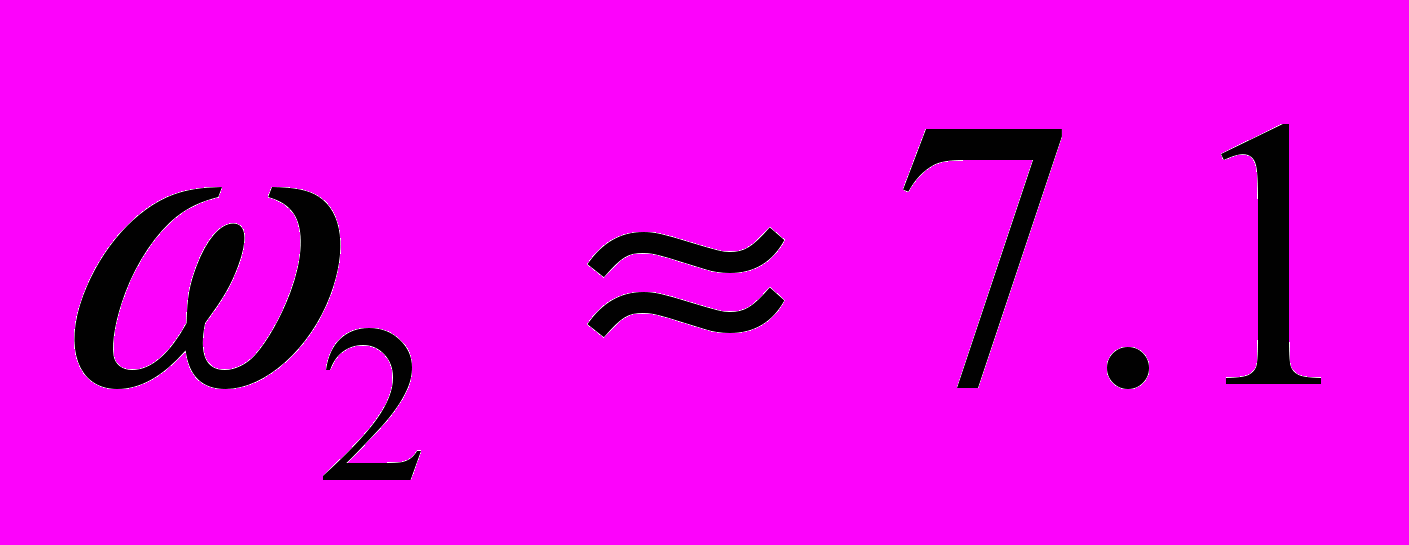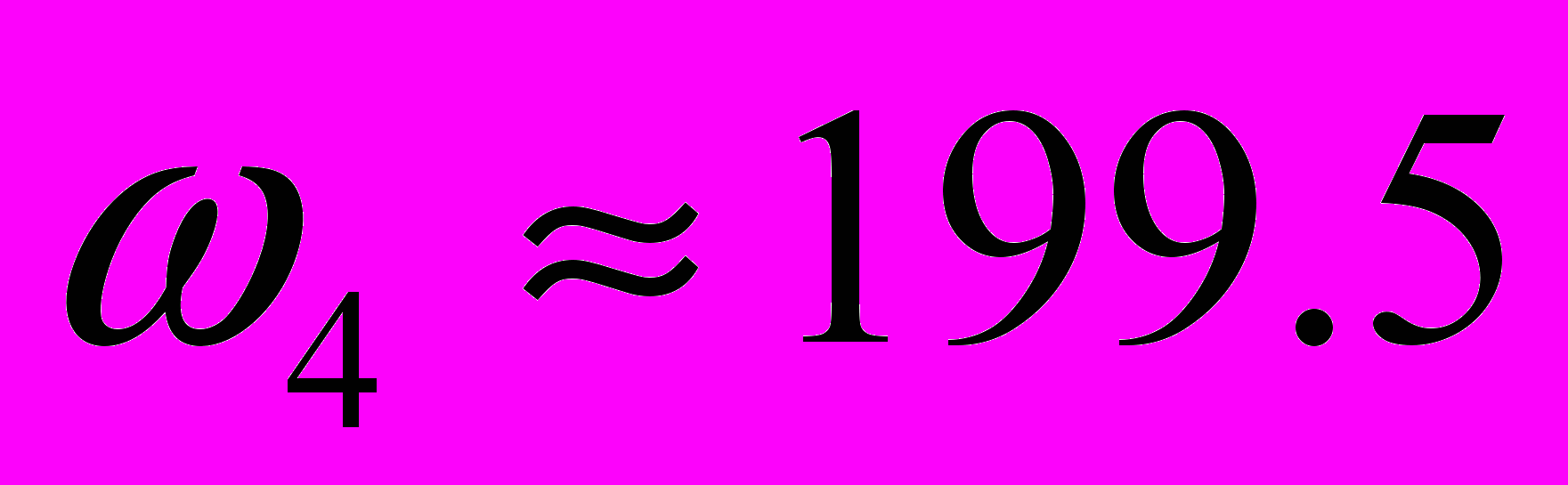с^-1

с^-1

Расчет параллельного корректирующего устройства

В общем виде обратную передаточную функцию системы можно представить в виде:

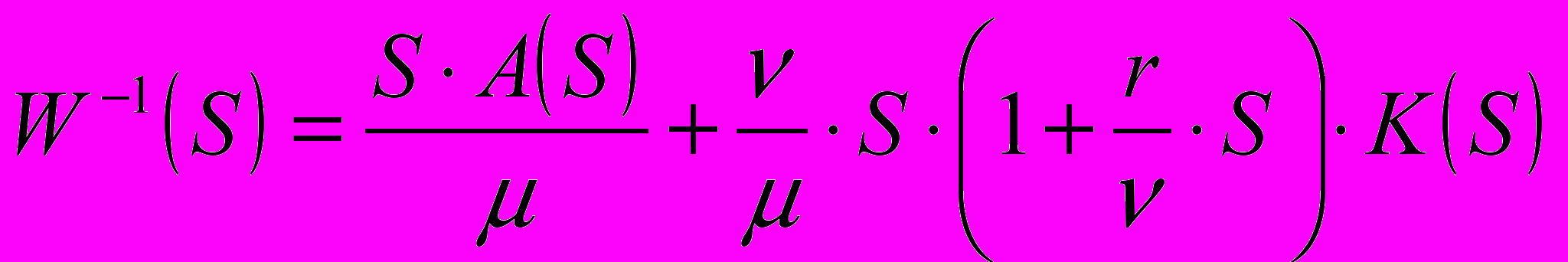. (2.1`)

Второе слагаемое характеризует 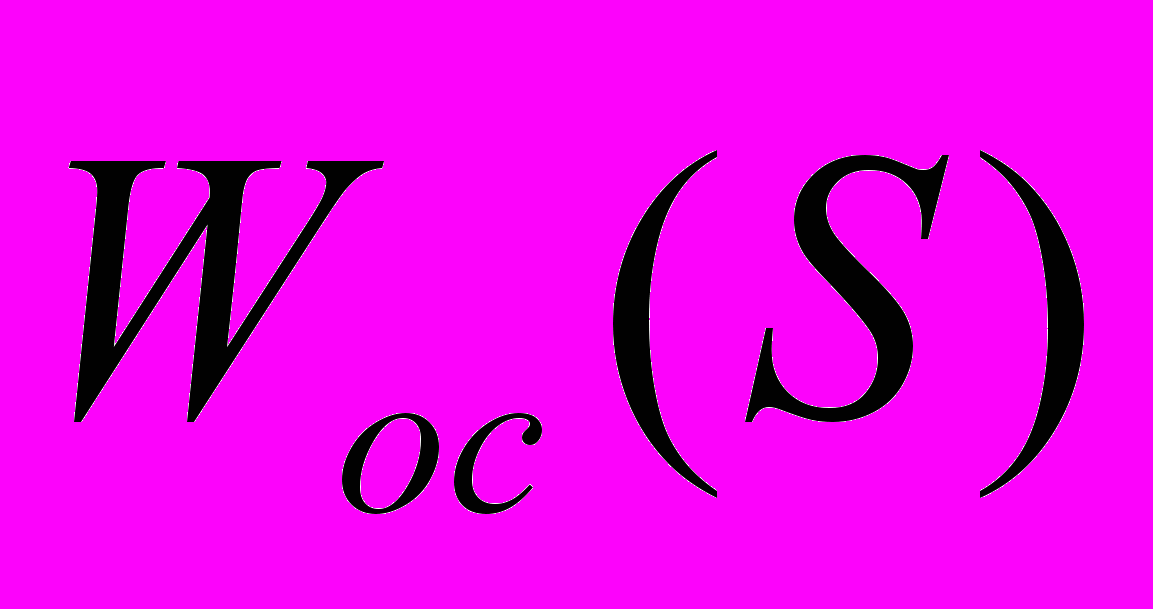. Запишем передаточную функцию, применив к ЛАЧХ, изображенной на графике, принцип сопоставления. Получим:

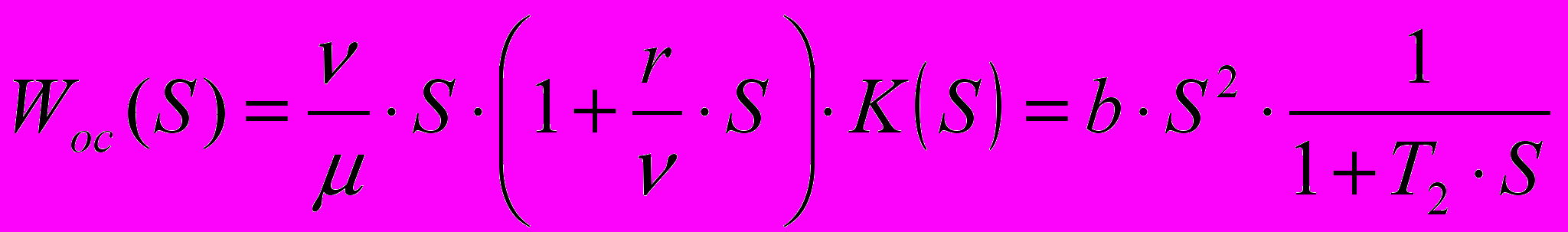; (2.2)

С целью упрощения реализации параллельного корректирующего устройства и улучшения параметров устойчивости проведем ЛАЧХ 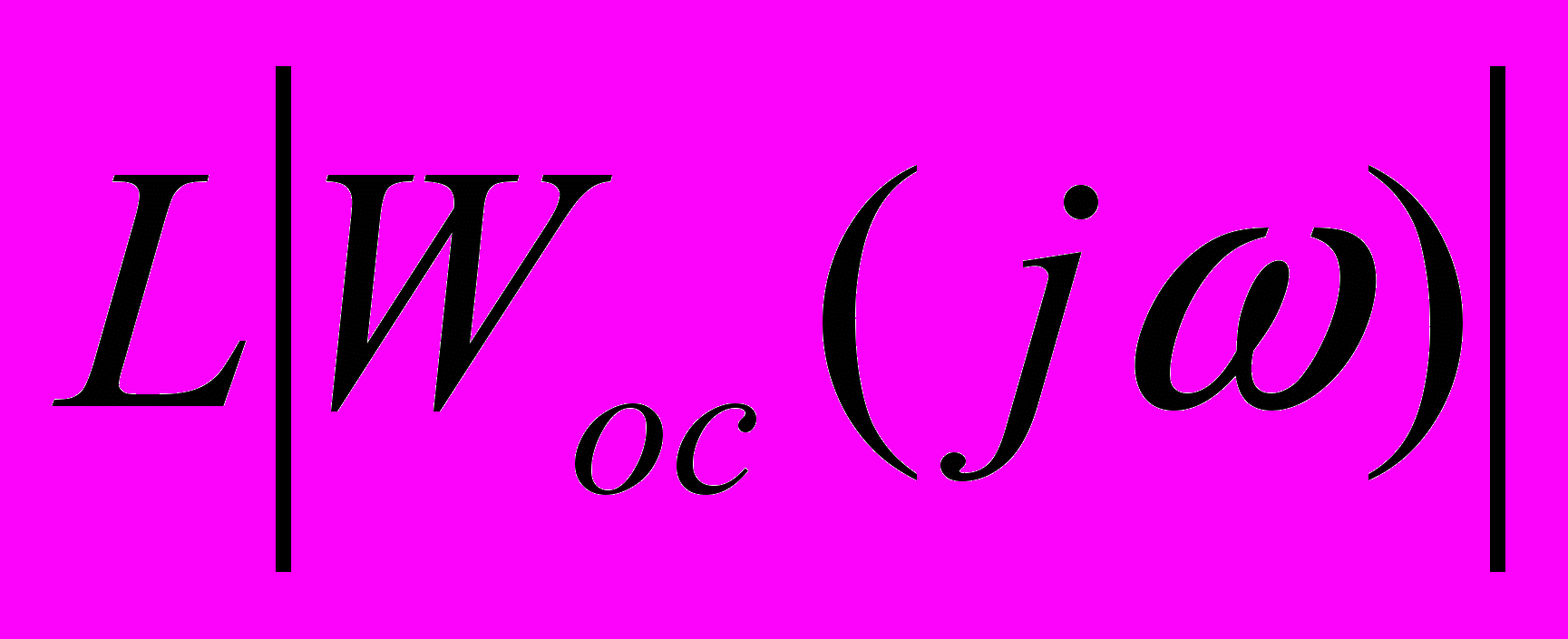начиная с точки В под наклоном +40 дБ/дек. В этом случае имеем:

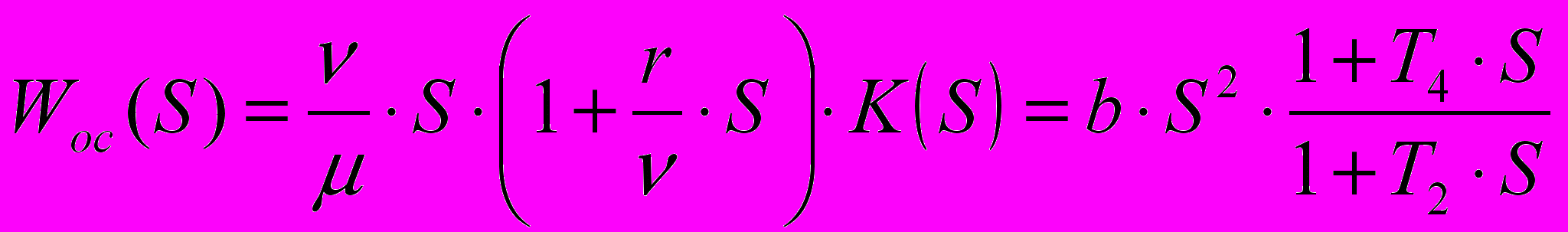; (2.3)

Из графика 1.1, найдем коэффициент усиления b:

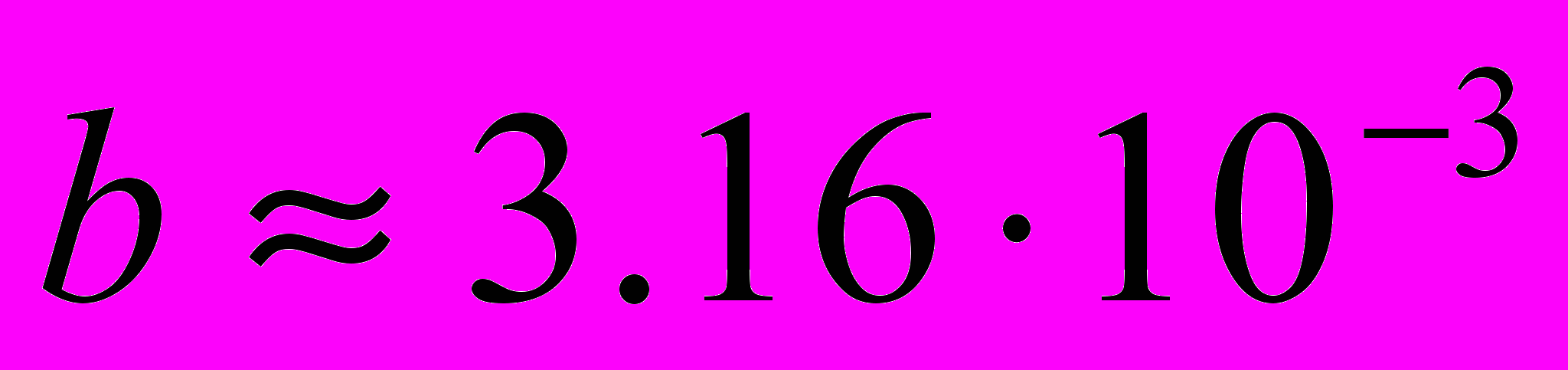c²; (2.4)

Потребуем, чтобы:

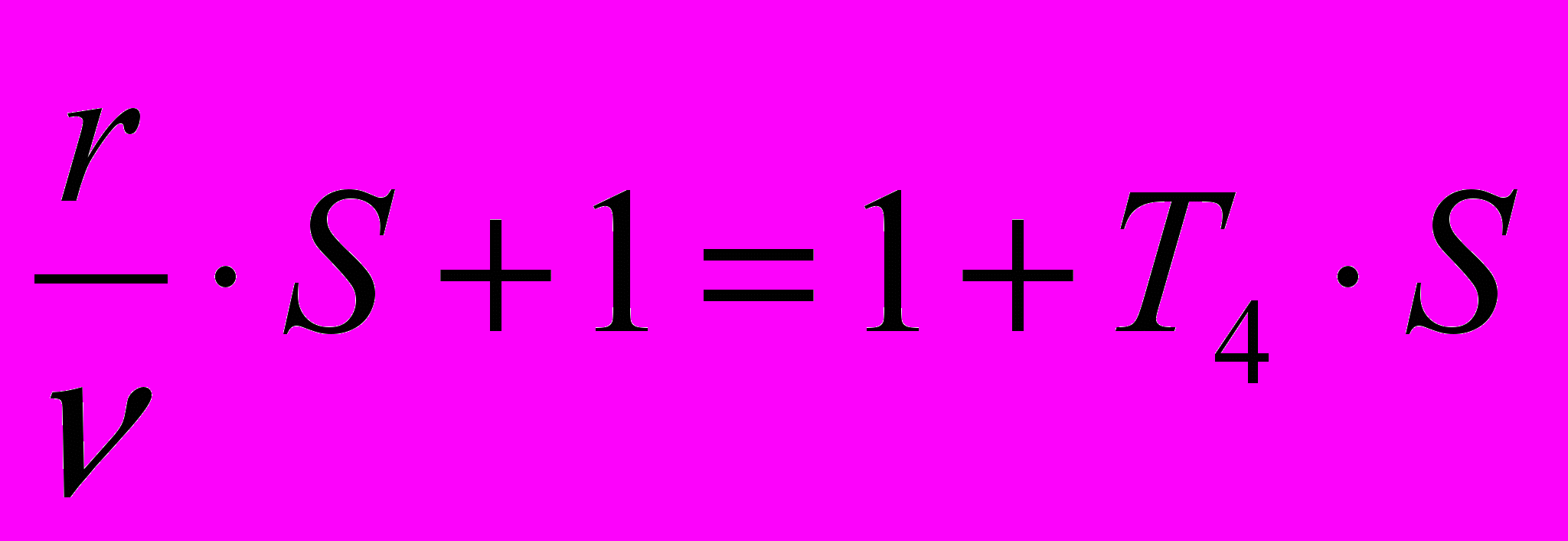; (2.5)

Тогда:

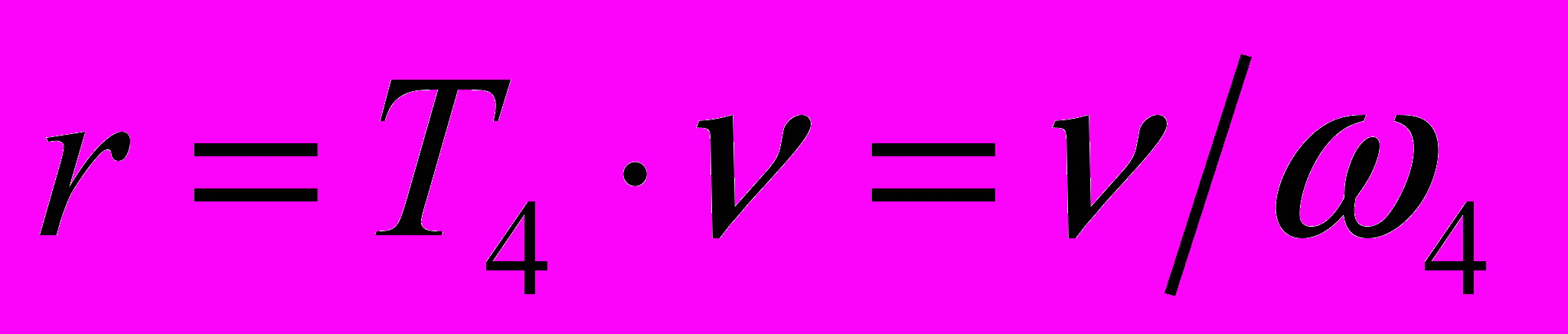; (2.6)

Исходя из (2.3), с учетом (2.4) получаем:

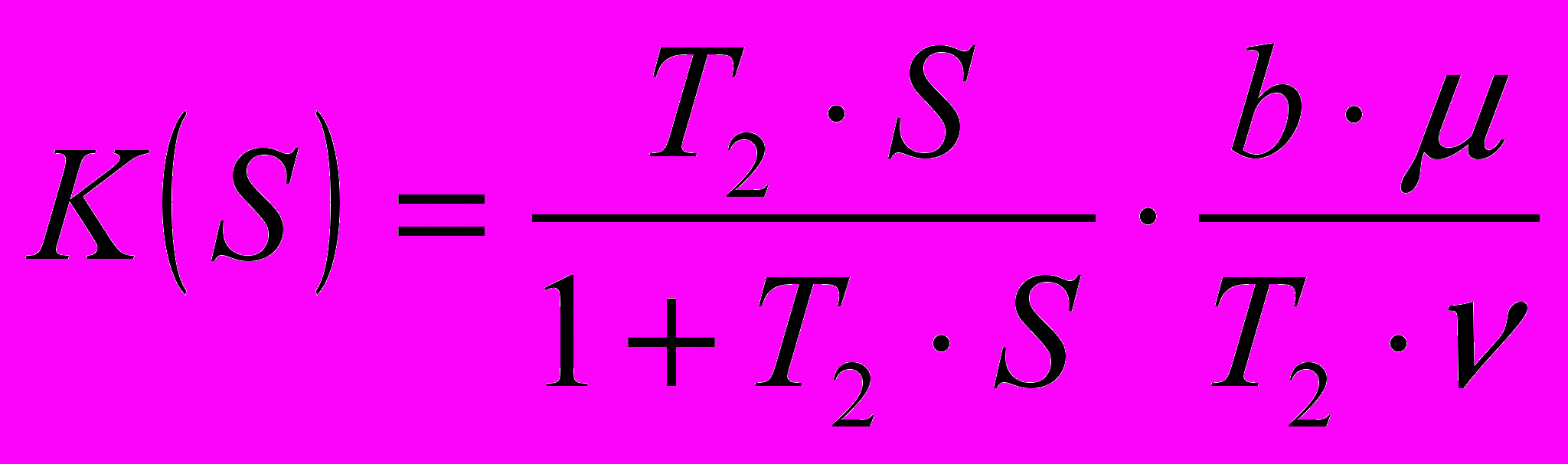; (2.7)

Потребуем, чтобы:

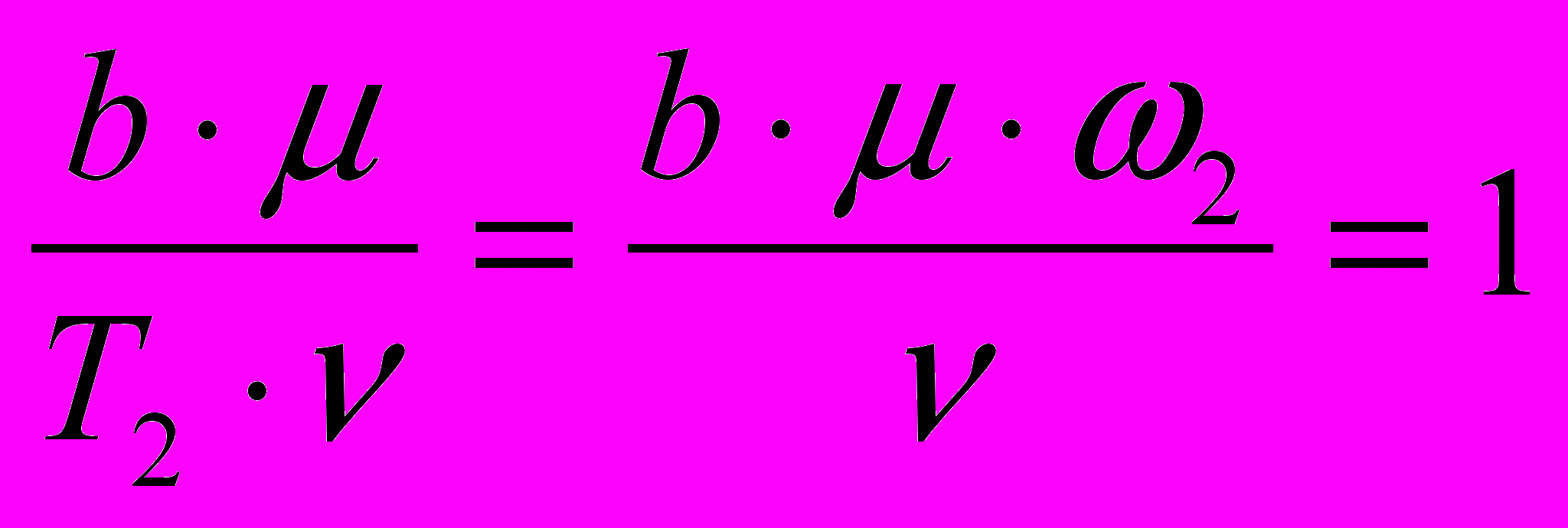; (2.8)


Откуда:

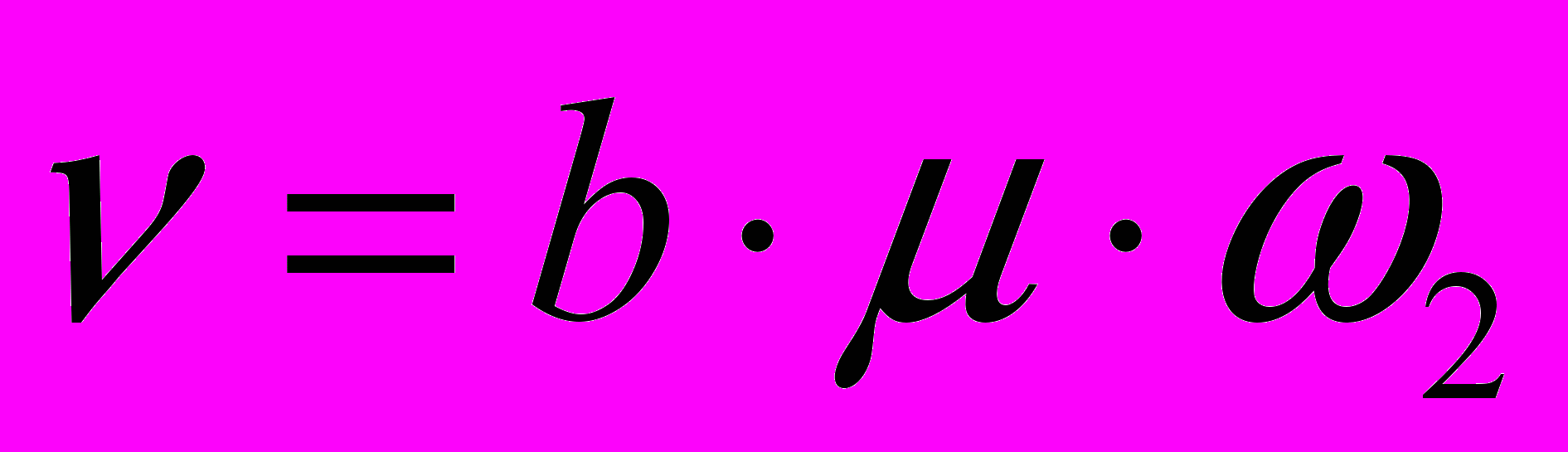; (2.9)

Подставим значения 2.4, 2.2 и 2.5 в формулу 2.9:

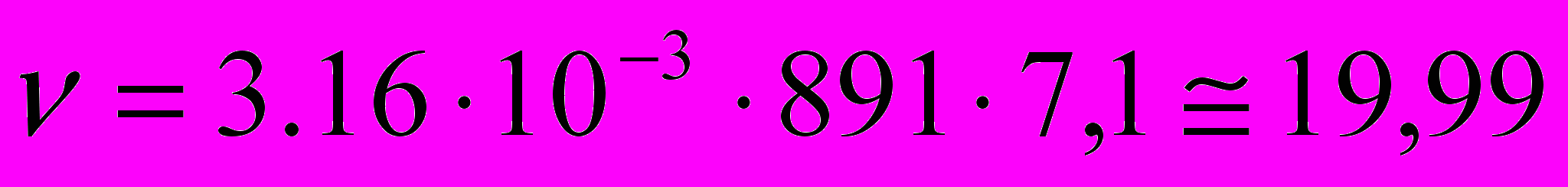; (2.9’)

Подставим в формулу 2.6 значения 2.9’ и 2.6:

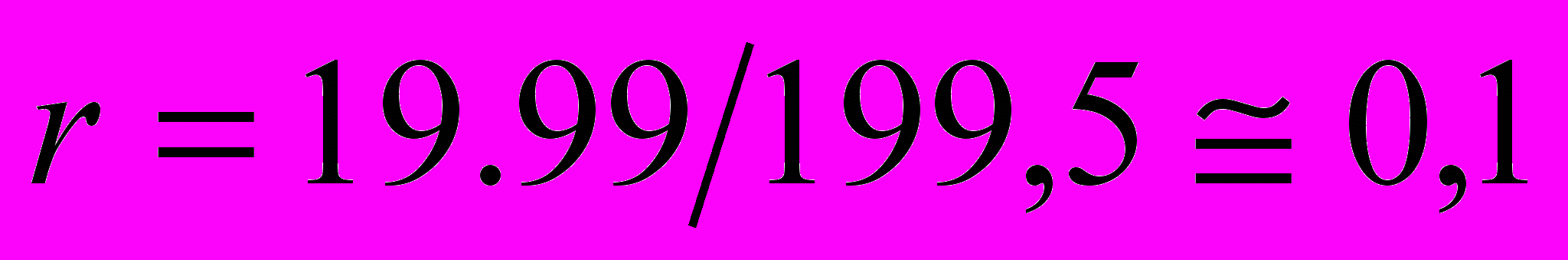с (2.6’)


Итак, передаточная функция параллельного корректирующего устройства имеет вид:

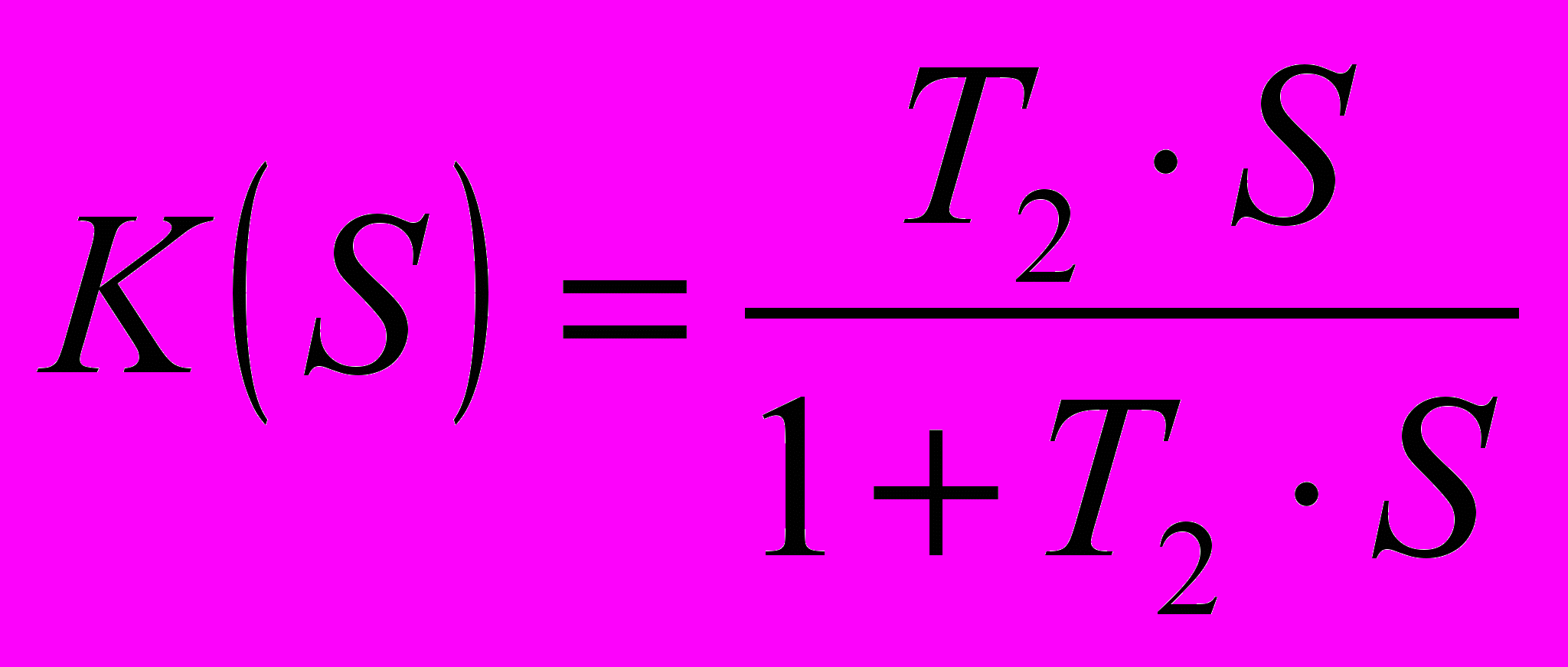, (2.10)

где

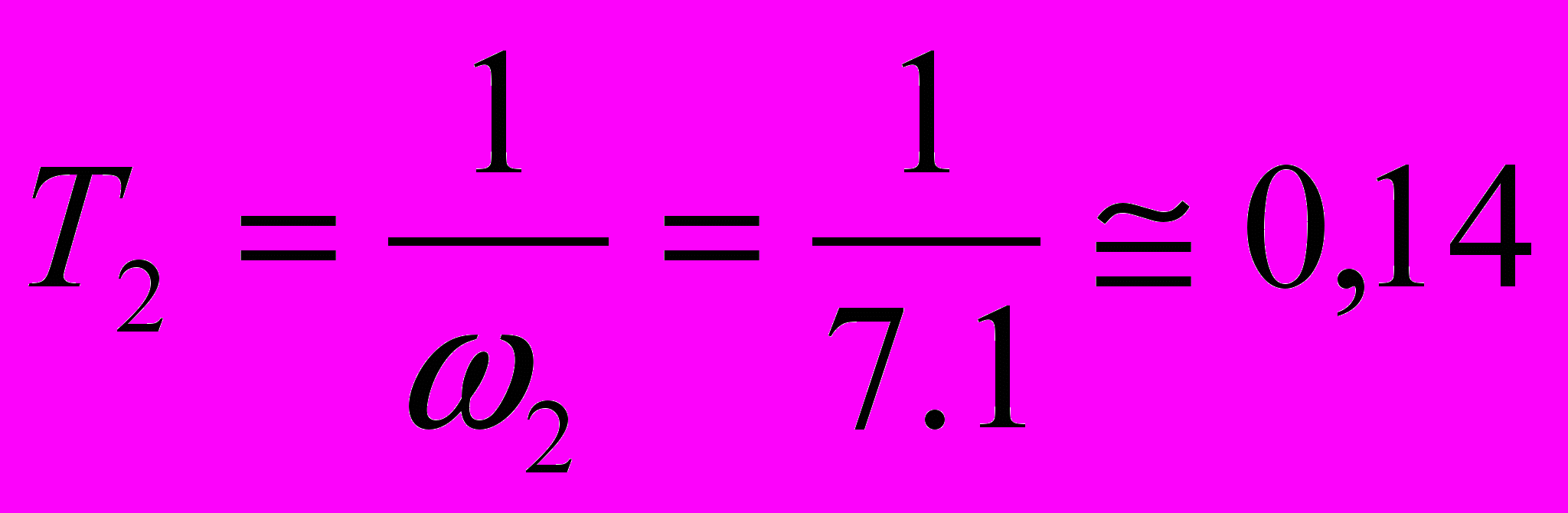с. (2.11)


Техническая реализация параллельного корректирующего устройства


Реализовывать корректирующее устройство будем посредством простейшей RC-цепочки.

Для 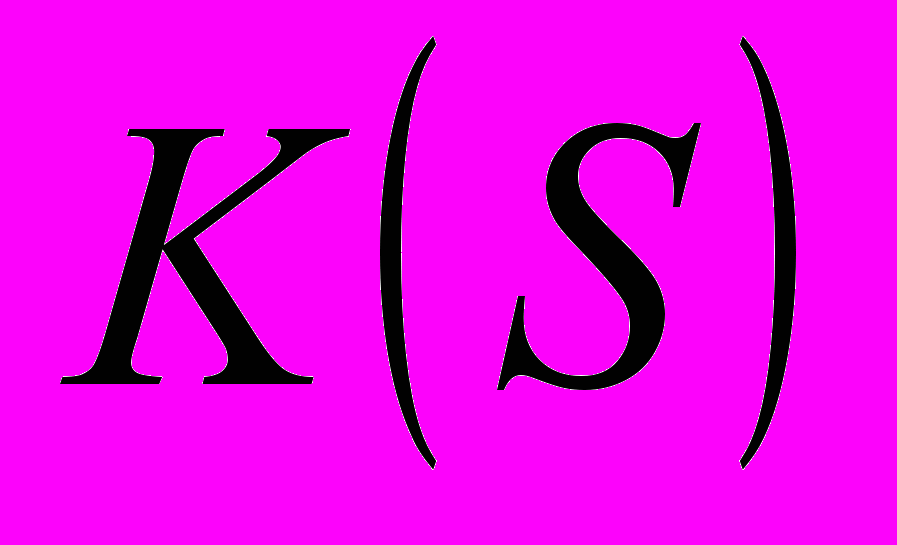вида 2.10 такая RC-цепочка имеет вид: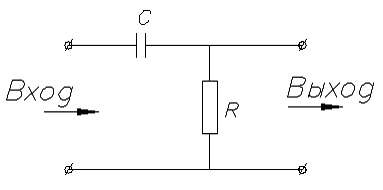



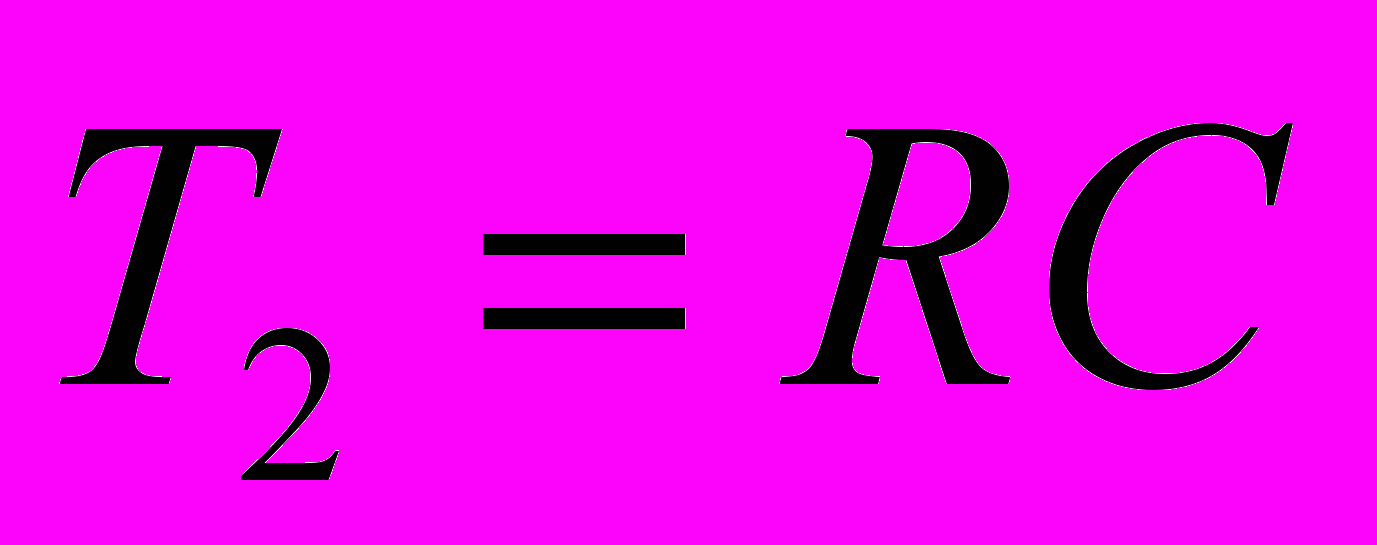; (3.1)

Примем C = 50 мкФ, тогда на основании формулы 3.1:

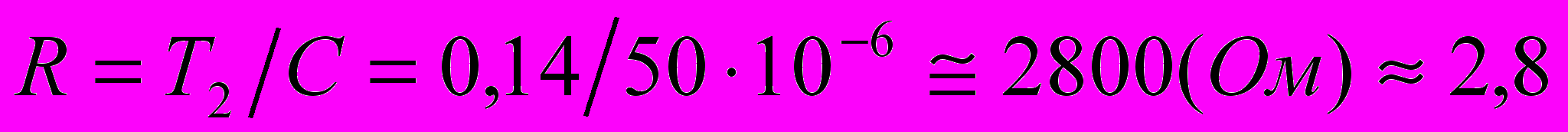КОм. (3.2)

Проверка устойчивости внутреннего контура


Определим запас устойчивости внутреннего контура:

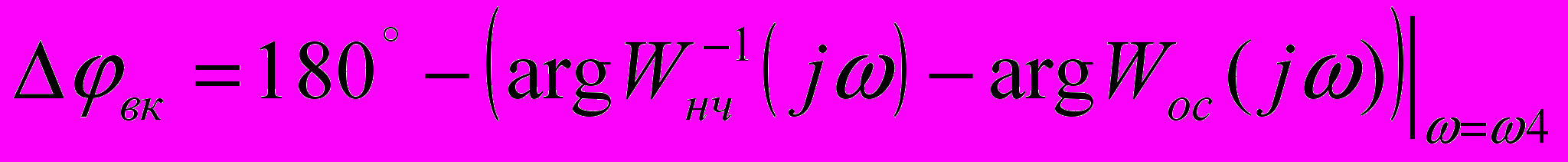; (4.1)


В соответствии с формулой 1.1 имеем:

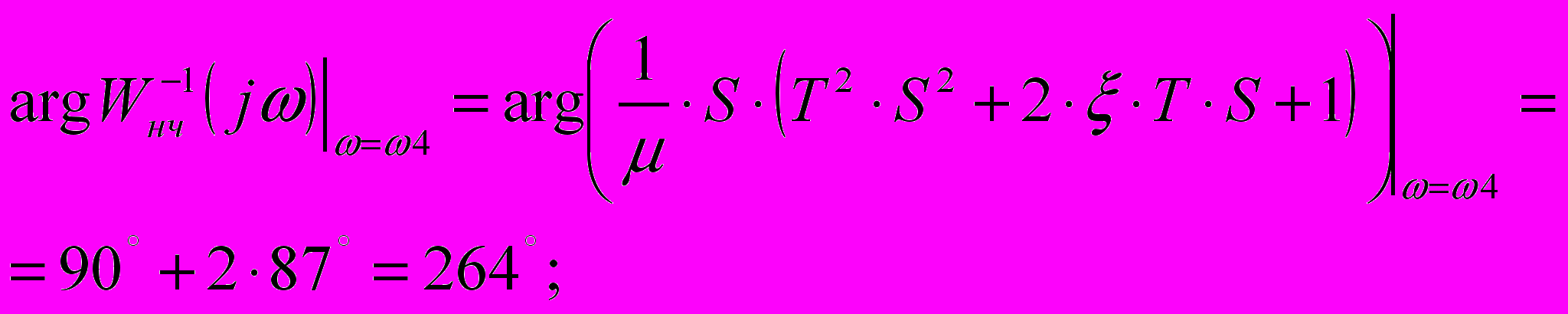(4.2)

В соответствии с формулой 2.3 имеем:

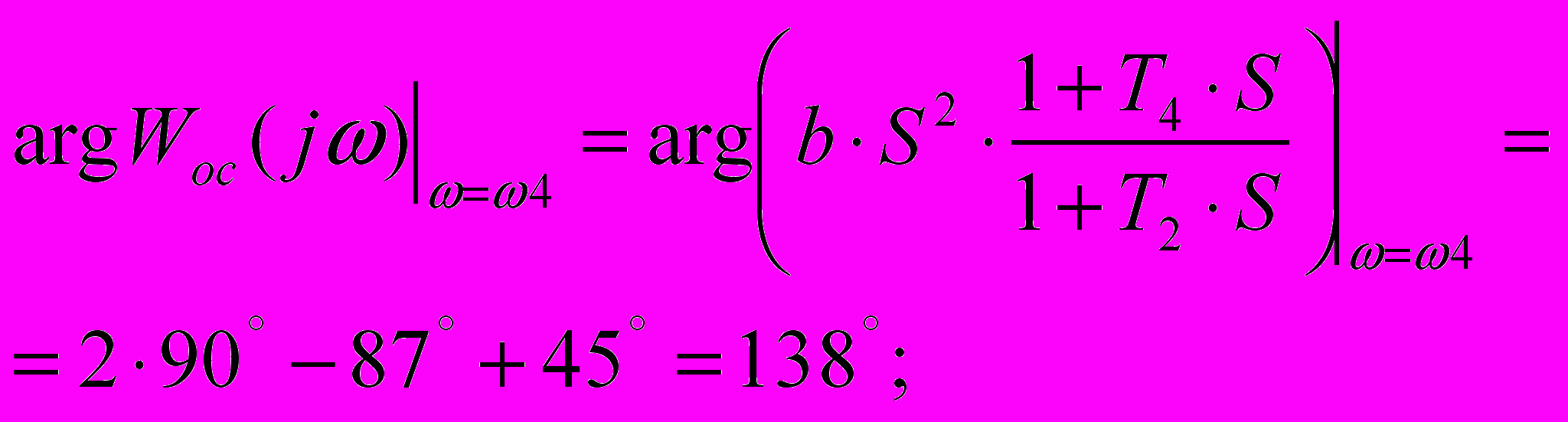(4.3)

Подставим значения 4.2 и 4.3 в уравнение 4.1:

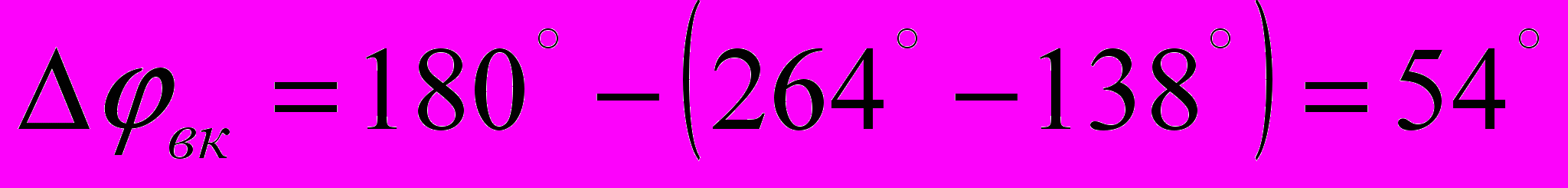; (4.1’)

Запас устойчивости внутреннего контура больше 30⁰, что благоприятно сказывается на устойчивости системы.


Проверка устойчивости всей системы


Определим запас устойчивости всей системы:

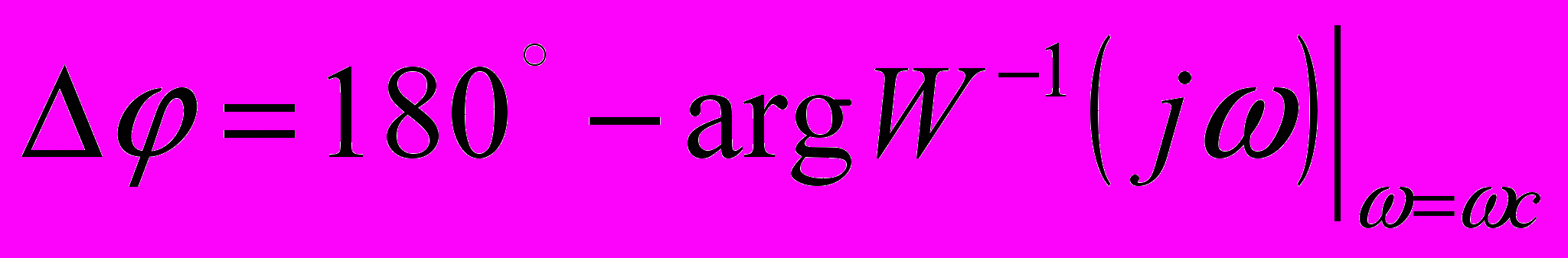(5.1)

Пользуясь желаемой ЛАЧХ, найдем :

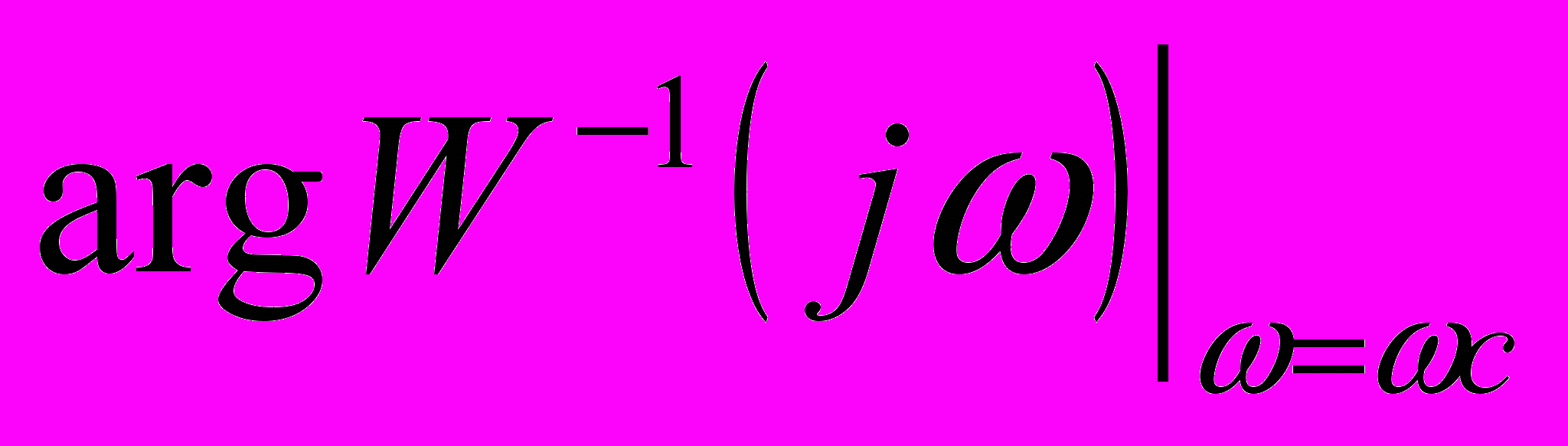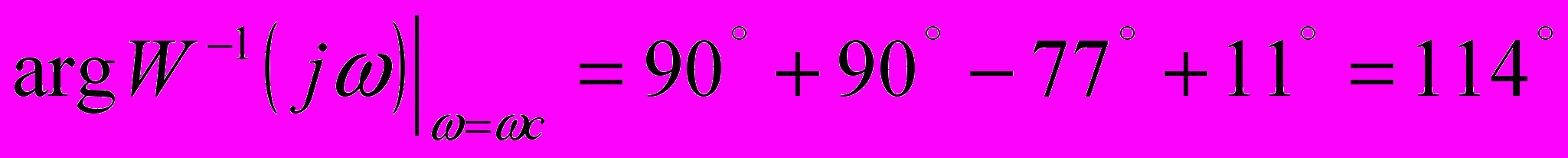; (5.2)

Подставим значение 5.2 в формулу 5.1:

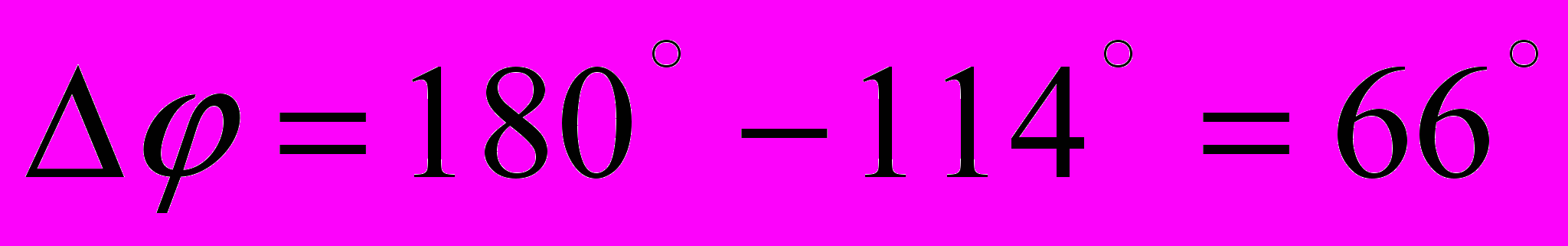; (5.3)

Запас устойчивости всей системы удовлетворяет требованиям по устойчивости.

Литература

1. Следящие приводы, том 1 / Под ред. Чемоданова Б.К. М.: Издательство МГТУ им. Н.Э.Баумана, 1999. 903 c.
   
2. Следящие приводы, том 2 / Под ред. Чемоданова Б.К. М.: Издательство МГТУ им. Н.Э.Баумана, 2003. 878 с.