Развитие теории оптимального проектирования механизмов грузоподъемных кранов пролетного типа

Вид материала

Автореферат

Содержание Общая характеристика работы Цель работы. Основная научная идея. Научные положения, выносимые на защиту Новизна научных положений Практическая значимость работы. Реализация результатов работы. Апробация работы. Структура и объем работы. Содержание работы В первой главе Вторая глава Lр и его стоимостью S U, т.е. решение, имеющее наименьшую метрику. Если несколько решений получат одинаковые значения метрики ρ(x В третьей главе Н сливается с осью OY Y примем за линию отсчета, а ось Х В четвертой главе U, т.е. решение, имеющее наименьшую метрику. Если несколько решений получат одинаковые значения метрики ρ(x В пятой главе ... Полное содержание

Подобный материал:

• Анкета –резюме Общие сведения, 52.08kb.
• Типовая инструкция для крановщиков (машинистов) по безопасной эксплуатации мостовых, 574.73kb.
• Типовая инструкция для крановщиков (машинистов) по безопасной эксплуатации мостовых, 603.15kb.
• Правила устройства и безопасной эксплуатации грузоподъемных кранов, 4085.92kb.
• Правила устройства и безопасной эксплуатации грузоподъемных кранов, 3600.74kb.
• Пособие для электромонтеров по обслуживанию и ремонту грузоподъемных машин литература, 1981.47kb.
• Закономерности проектирования механизмов для передачи и преобразования, 19.17kb.
• Пособие Для стропальщиков по безопасному производству работ грузоподъемными машинами, 1339.67kb.
• М. Л. Семенова, 2656.47kb.
• Правила устройства и безопасной эксплуатации грузоподъемных кранов (пб-10-382-00), 357.05kb.

На правах рукописи


ЧЕРНОВА НАТАЛЬЯ МИХАЙЛОВНА


РАЗВИТИЕ ТЕОРИИ ОПТИМАЛЬНОГО ПРОЕКТИРОВАНИЯ МЕХАНИЗМОВ ГРУЗОПОДЪЕМНЫХ КРАНОВ ПРОЛЕТНОГО ТИПА


Специальность: 05.05.04 – «Дорожные, строительные

и подъемно-транспортные машины»


АВТОРЕФЕРАТ

диссертации на соискание ученой степени

доктора технических наук


Новочеркасск – 2009

Работа выполнена в Государственном образовательном учреждении высшего профессионального образования «Балаковский институт техники, технологии и управления Саратовского государственного технического университета» на кафедре «Подъемно-транспортные и строительно-дорожные машины»


Научный консультант: доктор технических наук, профессор

Кобзев Анатолий Петрович


Официальные оппоненты: доктор технических наук, профессор,

Короткий Анатолий Аркадьевич;


доктор технических наук, профессор

Панасенко Николай Никитович;


доктор технических наук, профессор

Липатов Анатолий Степанович.


Ведущая организация: ГОУ ВПО «Тульский государственный университет».


Защита состоится 5 июня 2009 г. на заседании диссертационного совета Д 212.304.04 в Южно-Российском государственном техническом университете (Новочеркасском политехническом институте) по адресу: 346430, г. Новочеркасск, Ростовской обл., ул. Просвещения, 132, ауд.107 главного корпуса.


С диссертацией можно ознакомиться в библиотеке Южно-Российского государственного технического университета (Новочеркасского политехнического института).


Автореферат разослан « » 2009 г.


Ученый секретарь диссертационного совета

доктор технических наук, профессор В.С. Исаков

ОБЩАЯ ХАРАКТЕРИСТИКА РАБОТЫ


Актуальность работы. Механизация подъемно-транспортных, погрузочно-разгрузочных и складских работ в подавляющем большинстве осуществляется с помощью кранов различных типов. От эффективности работы кранов во многом зависит производительность и качество выполненных работ в строительстве, промышленности, судостроении, сельском хозяйстве, на транспорте.

Поэтому весьма актуальным является совершенствование приводов и металлоконструкций кранов с целью повышения производительности, точности позиционирования грузов, повышения безопасности производства работ. Особенную актуальность имеет задача повышения технического уровня специальных кранов, входящих в технологический цикл производства работ. К таким кранам относятся монтажные, металлургические, судостроительные краны, краны для обслуживания гидравлических, тепловых и атомных станций, перегрузочные краны портов. От эффективности работы механизмов кранов зависит их производительность, безопасность производства работ, надежность крана в целом. Приводы таких кранов отличаются большим многообразием по мощности, передаточному отношению трансмиссии, скоростям передвижения и подъема груза, точности посадки груза. При проектировании специальных кранов часто невозможно выбрать серийно изготавливаемый редуктор, главным образом по величине передаточного отношения, в этом случае заводам-изготовителям кранов или специализированным предприятиям приходится проектировать и изготавливать оригинальный редуктор. При этом требуется выполнить ряд ограничений: по массе, габаритам, передаточному отношению, уровню шума, эффективности передачи энергии. Таким ограничениям зачастую удовлетворяют планетарные редукторы. В настоящее время разработан ряд интересных схем планетарных зубчатых передач 2k-h, 3k, замкнутых дифференциальных механизмов. Методика расчета этих передач достаточно детально разработана, но методы выбора наилучшего решения по указанным выше ограничениям требуют дальнейшего развития.

Решение задач повышения эффективности работы кранов в современных условиях невозможно без применения методов оптимального проектирования, позволяющих снизить энерговооруженность и металлоемкость приводов, от чего, как известно, большей частью зависит их стоимость.

Методы оптимального и автоматизированного проектирования нашли широкое применение в краностроении. Однако в связи с развитием теории оптимального проектирования в целом, и развитием новых типов приводов и систем их управления, а также в связи с повышением требований к энерговооруженности, металлоемкости кранов и крановых механизмов прикладная теория оптимального и автоматизированного проектирования должна получить дальнейшее развитие.

Цель работы. Совершенствование приводов механизмов кранов пролетного типа с целью снижения металлоемкости и энерговооруженности на основе дальнейшего развития теории оптимального и автоматизированного проектирования.

Для достижения поставленной цели необходимо решить следующие основные задачи:

1. Выбрать методы оптимизации и модифицировать их применительно к решению задач оптимального проектирования механизмов кранов пролетного типа.
   
2. Разработать математические модели и выбрать критерии оптимального проектирования механизмов.
   
3. Обосновать методику и алгоритмы оптимального проектирования механизмов подъемов кранов и механизмов передвижения кранов и крановых тележек.
   
4. Разработать методику оптимального проектирования зубчатых передач соосного типа и автоматизированного выбора схем соосных зубчатых передач в зависимости от требуемых технологических, прочностных и качественных характеристик.
   
5. Составить алгоритм оптимального проектирования соосных зубчатых передач применительно к решаемой задаче.
   
6. Предложить методику инженерного расчета оптимального проектирования механизмов кранов пролетного типа на основании разработанной теории.
   

Основная научная идея. Разработка теории оптимального проектирования механизмов кранов пролетного типа с применением методов многокритериальной оптимизации..

Научные положения, выносимые на защиту:

1. Метод решения многокритериальной задачи оптимального проектирования приводов механизмов кранов пролетного типа, основанный на принципе Парето.

2. Методика формирования области возможных решений задачи оптимального проектирования механизмов подъема.

3. Методика формирования области возможных решений задачи оптимального проектирования механизмов передвижения кранов и крановых тележек.

4. Векторные критерии оценки качества решения задач оптимального проектирования механизмов подъема кранов.

5. Векторные критерии оценки качества решения задач оптимального проектирования механизмов передвижения кранов и крановых тележек.

6. Модификация метода целевого программирования для сужения области парето-оптимальных решений.

7. Метод решения многокритериальной задачи оптимального проектирования передаточных механизмов с большими передаточными отношениями на основе принципа Парето.

8. Теоретические положения оптимального проектирования соосных зубчатых передач.

9. Методика определения оптимальных параметров металлоконструкций барабанов механизмов подъема и металлоконструкций балансиров механизмов передвижения.

Новизна научных положений:

- впервые предложено решение многокритериальной задачи оптимального проектирования приводов механизмов кранов пролетного типа, основанное на принципе Парето, включающее три этапа: формирование области возможных решений; выделение области парето-оптимальных решений; определение оптимального решения;

- разработана методика формирования области возможных решений задачи оптимального проектирования механизмов подъема для кратностей полиспаста от 1 до 24, позволяющая учесть все возможные варианты по типам электроприводов и управляющих устройств, трансмиссий, канатов, муфт и тормозов;

- формирование области возможных решений задач оптимального проектирования механизмов передвижения кранов и крановых тележек рекомендовано осуществлять при дискретно изменяемых значениях диаметра ходового колеса от 250 мм до 1000 мм, что позволяет учесть все возможные конструктивные схемы компоновки механизмов;

- для механизма подъема предложен векторный критерий оценки качества решения, включающий в качестве составляющих девять критериев оптимальности: экономическую оценку двигателя и управляющего устройства, стоимость и габаритный размер передаточного механизма, массы барабана, каната, крюковой подвески, муфт, тормозов и коэффициент полезного действия механизма;

- предложен векторный критерий оценки качества решения при проектировании механизмов передвижения, состоящий из девяти критериев оптимальности: экономической оценки двигателя и управляющего устройства, стоимости и массы трансмиссии, масс балансиров, колес, рельсов, муфт, тормозов и коэффициента полезного действия механизма;

- разработана модификация метода целевого программирования для выбора оптимального решения задач проектирования механизмов подъема и передвижения из множества парето-оптимальных решений по минимальному значению метрики;

- впервые предложена методика многокритериального оптимального проектирования передаточных механизмов с большими передаточными числами: на первом этапе выполняется формирование области возможных решений на основе схем планетарных передач типа 2k-h, 3k, с учетом прочностных ограничений и требуемых качественных характеристик; на втором – формирование области парето-оптимальных решений в соответствии с предложенным векторным критерием оценки качества решения, включающим: массу и габаритный размер передачи, коэффициент перекрытия и коэффициент полезного действия; на третьем - выбор оптимального решения по минимальному значению метрики в соответствии с предложенной модификацией метода целевого программирования;

- разработан метод графического синтеза соосных зубчатых передач, позволяющий в зависимости от величины и знака передаточного отношения, а также требуемых качественных характеристик определять схему и геометрические параметры зубчатой передачи;

- обосновано применение модифицированного метода Хука-Дживса для определения оптимальных параметров барабанов механизмов подъема и балансиров механизмов передвижения, позволяющего получить конструкции минимальной металлоемкости.

Практическая значимость работы. Проведенные научные исследования и полученные результаты обеспечили возможность разработки методик автоматизированного оптимального проектирования механизмов кранов пролетного типа и их трансмиссий, а также позволили достичь снижения металлоемкости и энерговооруженности кранов, затрат труда конструкторов на стадии проектирования.

Достоверность полученных результатов подтверждается выбором соответствующих задаче физических предпосылок; применением апробированных законов механики, математики, теории механизмов и машин, методов математического моделирования, методов оптимизации; сопоставлением результатов аналитического исследования с данными математического моделирования; сравнительным анализом полученных результатов с известными.

Реализация результатов работы. Результаты исследований внедрены:

- в ЗАО Научно-производственная фирма «Авангард-ф» г. Саратов в виде технических предложений по выполнению конструктивных схем погрузочно-разгрузочных и подъемно- транспортных работ; методики расчета механизмов кранов пролетного типа;

- ОАО «Строймаш» г. Саратов в виде методики оптимального проектирования планетарных зубчатых передач грузоподъемных машин;

- ООО Инженерно-консультационный центр «Мысль» Новочеркасского государственного технического университета г. Новочеркасск в виде методики и алгоритма оптимального проектирования механизмов подъема.

- подразделении технопарка БИТТУ СГТУ и ООО ИКЦ «Крансервис» при выполнении модернизация механизмов подъема и передвижения пяти козловых кранов К 2×125 Нижегородской ГЭС; двух кранов К2×180/50 Саратовской ГЭС.

Результаты исследований используются в курсах лекций «Грузоподъемные машины», «Специальные краны», «Погрузочно-разгрузочные машины», «САПР ПТМ», «Теория механизмов и машин», которые читаются для студентов специальности 190205 «Подъемно-транспортные, строительные, дорожные машины и оборудование», а также в дипломном и курсовом проектировании. По материалам исследования опубликовано учебное пособие, методические указания к курсовому проектированию, которые широко используются в учебном процессе.


Апробация работы. Основные положения диссертации докладывались и обсуждались:

- на научно-технических конференциях «Перспективы развития подъемно-транспортной техники» (г. Одесса, 2002 г.); «Проблемы динамики и прочности исполнительных механизмов и машин» (г. Астрахань, 2002 г.); конференции, посвященной 100-летию Г.П. Ксюнина (г. Новочеркасск, 2005 г.); научно-технических конференциях Балаковского института техники, технологии и управления Саратовского государственного университета (1990-2008 гг.);

- заседаниях технического совета ОАО «Строймаш» (г. Саратов, 2002 г.);

- Всероссийской научно-технической конференции «Информационные технологии в науке, образовании, технологии» (г. Якутск, 2008 г.)

- межрегиональной научно-практической конференции «Дорожно-транспортный комплекс: состояние и перспективы развития» (г. Чебоксары, 2007 г.);

- Международных научно-технических конференциях «Перспективы развития подъемно-транспортных, строительных и дорожных машин» (г. Балаково, 2002 г.); «Проблемы исследования и проектирования машин» (г. Пенза, 2006, 2008 гг.); «Современные тенденции развития транспортного машиностроения» (г. Пенза, 2008 г.).

Публикации. По теме диссертации опубликовано 29 печатных работ, в том числе монография и учебное пособие. Из указанного числа работ 9 опубликованы в изданиях, входящих в перечень ВАК Министерства образования и науки РФ для докторских диссертаций.

Структура и объем работы. Диссертация состоит из введения, 6 глав, основных выводов, списка использованной литературы из 226 наименований. Основной текст исследования изложен на 372 страницах и включает 112 рисунков, 39 таблиц, 6 приложений на 137 страницах.


СОДЕРЖАНИЕ РАБОТЫ


Во введении обоснована актуальность проблемы, подтверждающая необходимость дальнейшего развития теории оптимального проектирования механизмов кранов пролетного типа, сформулирована цель работы, приведена общая характеристика работы с определением ее научной новизны и практической ценности.

В первой главе представлена оценка современного состояния теории оптимального проектирования механизмов кранов, определены направления диссертационного исследования, на основе проведенного анализа выбраны методы проектирования и тип математической модели, дана постановка задач диссертационного исследования.

В краностроении вариантное проектирование и применение методов оптимизации позволяют решать целый ряд задач: создание рациональных конструктивных схем, определение оптимальных значений их геометрических параметров и размеров отдельных элементов, получения крановых механизмов с наилучшими технико-экономическими показателями. При этом можно назвать выдающихся отечественных и зарубежных ученых, сделавших большой вклад в теорию оптимального и автоматизированного проектирования: В.И. Брауде, М.М. Гохберг, А.П. Кобзев, В.Г. Соловьев, А.С. Липатов, А.В. Олешкевич, В.Л. Лифшиц, И.А. Невзоров, И.М. Соболев, Р.Б. Статников, О.Н. Пылаев, Д. Хедли, Д. Уайлд, Б. Банди, В.Н. Демокритов, Фам Ван Хой, В.Я. Недоводеев, Н.Н. Панасенко, А.Н. Орлов, Е.М. Кудрявцев, Д.И. Батищев, Д.Н. Решетов, Г. Реклейтис, А. Рейнвиндран, К. Рэксдел, В.Н. Тарасов, и другие

Многочисленность возможных конструктивных решений, разнообразие и противоречивый характер требований к механизмам, большое число трудно формализуемых качественных требований приводят к тому, что на практике поиск оптимума при проектировании механизмов ведут путем разработки и сравнения ограниченного числа вариантов. В работах А.П. Кобзева, А.В. Олешкевича, И.Ю. Акимова, В.К. Тимошенко, В.Т. Баранова, А.С. Плотникова, В.Г. Соловьева рассматривается оптимизация параметров механизма подъема по критериям массы механизма или приведенных затрат. При этом оптимизируется кратность полиспаста, частота вращения двигателя, металлоемкость барабана, тип каната. При этом в ряде работ использован диалоговый режим, увеличивающий трудоемкость процесса оптимального проектирования.

В работах А. П. Кобзева, Д.А. Зотова обоснованы условия автоматизированного выбора оптимальных величин основных параметров механизма передвижения – числа ходовых колес, количества приводов движителей и числа подкрановых рельсов, параметров балансирных балок.

Однако в оптимизационных работах практически не рассматривается оптимальность схем приводов механизмов грузоподъемных машин с точки зрения применения современных типов приводов и управляющих устройств, позволяющих значительно улучшить эксплуатационные характеристики.

Кроме того, во всех вышеперечисленных работах при кинематическом расчете рассматривался вариант комплектации передаточного механизма преимущественно серийно выпускаемыми горизонтальными или вертикальными редукторами, имеющими ограничения по передаточному отношению.

Уникальные мостовые, козловые краны и перегрузочные мосты имеют сравнительно низкие скорости рабочих движений, поэтому требуют проектирования приводов с большими передаточными отношениями.

При оптимальном проектировании механизмов необходимо наравне с вариантами комплектации приводов серийными редукторами рассматривать возможности использования в приводах вновь проектируемых оригинальных редукторов. Проектируемые для уникальных кранов редукторы с большими передаточными числами зачастую обладают большими массами и низкими коэффициентами полезного действия, поэтому с учетом поставленной цели необходимо исследовать такие приводы на оптимальность. В этом отношении перспективными являются планетарные редукторы, находящие в мировой практике все большее распространение. Для механизмов подъема их применение позволяет создавать малогабаритные приводы, встроенные в барабан, а также многоскоростные двух- и трехдвигательные. Также очень перспективными из-за малых габаритов и малых масс являются планетарные редукторы для приводов механизмов передвижения кранов и крановых тележек. Особенно существенно упрощается компоновка механизмов передвижения многоколесных приводов, когда приходится редукторы устанавливать на балансирах. Передачи обладают большой компактностью, т.е. возможностью получения высоких передаточных отношений при малом количестве зубчатых колес, а также меньшей массой и габаритами по сравнению с рядовыми передачами.

В целом теория проектирования планетарных зубчатых передач достаточно разработана и освещена в литературе. Имеется обширный список работ, посвященных проблемам проектирования и выбора параметров планетарных передач. При решении оптимизационных задач возникают дополнительные требования к проектированию по условиям равнопрочности, энергоемкости, габаритов, что требует дальнейшего развития теории проектирования зубчатых передач применительно к решаемым задачам.

Для решения многокритериальной задачи оптимального проектирования механизмов подъемно-транспортных машин наиболее применим метод оптимизации, построенный на принципе Эдворта-Парето.

При применении данного принципа к решению задач многокритериальной оптимизации должны быть разработаны методика формирования области возможных решений задачи на применении принципов структурного синтеза и векторные критерии оценки качества решения, включающие в качестве составляющих критерии оптимальности рассматриваемых задач. В качестве метода сужения области парето-оптимальных решений может быть использован метод целевого программирования с модификацией применительно к решаемым задачам.

Для получения оптимальных параметров металлоконструкций барабана механизма подъема, а также балансиров механизма передвижения кранов и крановых тележек, наибольший интерес представляют методы прямого поиска, в частности, метод Хука-Дживса, который позволяет исследовать овражные функции. Однако данный метод применим только к задачам безусловной оптимизации. Поэтому требуется модифицировать метод Хука-Дживса так, чтобы можно было решать задачи оптимизации с ограничениями.

Вторая глава посвящена разработке теории оптимального проектирования механизма подъема груза.

На основе проведенного анализа методов оптимального проектирования сделан вывод, что наиболее эффективным для решения задачи оптимального проектирования механизма подъема груза является метод многокритериальной оптимизации, основанный на принципе Парето.

В качестве составляющих векторного критерия качества решения f =(f₁, … f₉) при оптимальном проектировании механизма подъема груза можно рекомендовать следующие критерии оптимальности.

Стоимость электропривода и управляющих устройств, а также эффективность их работы, учитывается экономической оценкой А (руб), согласно методике, предложенной д.т.н. М.М. Гохбергом:

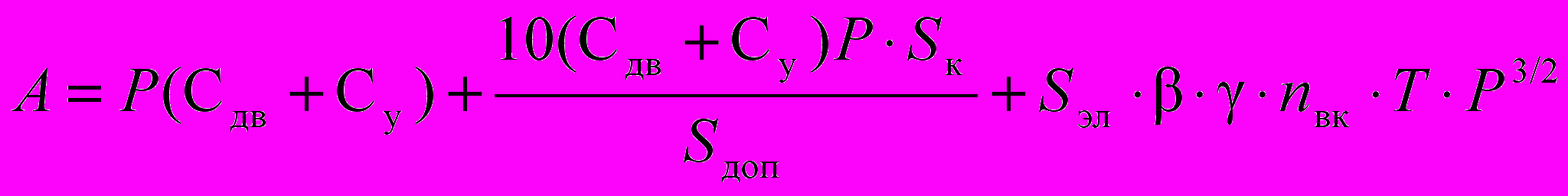, (1)

где Р – номинальная мощность электродвигателя, кВт; С_дв – удельная стоимость 1 кВт мощности двигателя, руб/кВт; С_у – удельная стоимость управляющего устройства на 1 кВт мощности двигателя, руб/кВт; S_к – число включений за год работы; S_доп – износостойкость электропривода (допустимое число включений до проведения капитального ремонта); S_эл - усредненная стоимость электроэнергии на пуск двигателя мощностью 1 кВт, руб/кВт; β – коэффициент, определяющий потери при пуске, торможении, регулировании скорости в зависимости от вида управляющих устройств; γ – коэффициент, характеризующий приведенные моменты инерции механизмов; n_вк – число включений в час; Т – число часов работы в год.

Выбор трансмиссии характеризуется двумя критериями: габаритным размером привода L_р и его стоимостью S_р. Остальные элементы привода: барабан, канат, крюковая подвеска, муфты, тормоза в векторном критерии учитываются в виде массы соответствующих частей привода: m_Б, m_к, m_п, m_м, m_т. При этом оптимальные параметры барабана по критерию металлоемкости определяются отдельно по рекомендованной модификации метода Хука-Дживса.

Для оценки эффективности в отношении передачи энергии различных вариантов компоновки привода принят коэффициент полезного действия механизма η.

Цель оптимального проектирования механизма подъема груза в математических терминах выражается в условии минимизации функции f =(f₁, … f₉):

f₁= A; f₂= L_р ; f₃= S_р; f₄= m_Б; f₅= m_к; f₆= m_п; f₇= m_м; f₈= m_т; f₉= - η, (2)

на множестве возможных решений задачи X.

Для формировании области возможных решений Х рассматриваются все возможные схемы компоновки электропривода: с двигателями постоянного и переменного тока, с применением контактно-контроллерных управляющих устройств, тиристорных регуляторов напряжения, тиристорных преобразоватей частоты; все возможные схемы компоновки передаточного механизма: с серийно выпускаемыми редукторами, с несерийными редукторами, полученными при проектировании из условия оптимальности при различных значениях значениями кратности полиспаста i_п на интервале [i_min; i_max].

Исключением из области возможных решений Х непарето-оптимальных решений формируется множество Парето P_f (X):

P_f (X) = {x* X | не существует такого x X , что f (x) ≤ f (x*)}. (3)

Для дальнейшего сужения множества Парето до множества выбираемых решений Sel(X) применяется модификация метода целевого программирования. Для этого на множестве P_f (X) формируется идеальный вектор U, состоящий из минимальных значений составляющих векторного критерия f:

U= (f _1min, f _2min, …, f _9min). (4)

Для каждого решения x_j Р_f(Х) X рассчитывается метрика ρ(x_j), представляющая собой неотрицательное число, определяющее расстояние критериального вектора f (x_j) от идеального вектора U. Величина метрики для каждого решения x_j рассчитывается: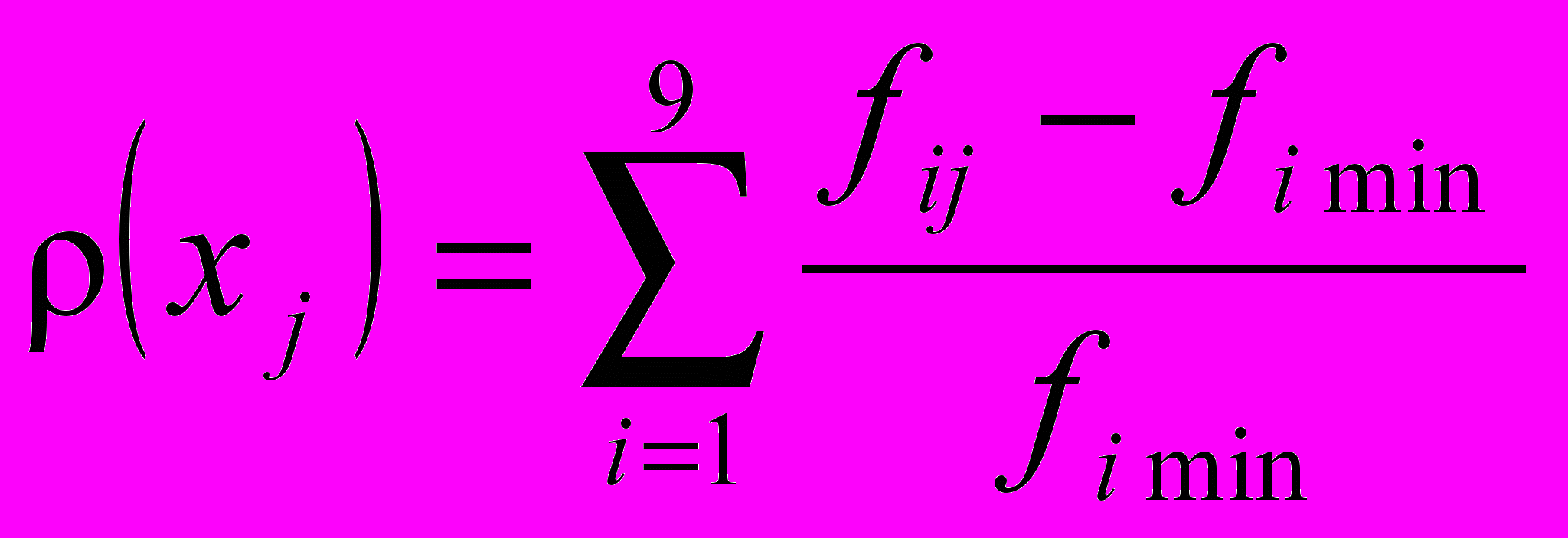

. (5)

Оптимальным является решение, расположенное как можно ближе к множеству идеальных оценок U, т.е. решение, имеющее наименьшую метрику. Если несколько решений получат одинаковые значения метрики ρ(x_j), окончательное решение об оптимальности того или иного варианта компоновки механизма принимает конструктор.

С учетом физической сущности задачи разработана система ограничений. Выбор и расчет деталей и узлов механизма подъема осуществляется на основе существующих методик с проверкой установленных ограничений.

Для подбора оптимальных параметров барабана предложена модификации метода покоординатного спуска Хука-Дживса для решения задач с ограничениями из условия минимума металлоемкости. Проверка ограничений выполняется в отдельной подпрограмме. Управляемые параметры выбираются при выполнении условий прочности по эквивалентным напряжениям от сжатия, изгиба и кручения в цилиндрических стенках барабанов с однослойной и многослойной навивкой каната, а также устойчивости цилиндрических стенок.

Модифицированный алгоритм Хука-Дживса включает в себя две процедуры: исследование окрестности базовой точки, которое проводится методом покоординатного спуска, и движение вдоль одной из координат, дающее наибольшее уменьшение функции цели. Выбор оптимального диаметра барабана производится методом покоординатного спуска по условию:

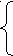D_Б+Δ D_Б, если m_Б^(r+1) < m_Б^r;

D_Б= (6)

D_Б, если m_Б^r ≤ m_Б^(r+1), (D_Б+Δ D_Б) > D_Бmax, L_Б> L_Бmax.

где ΔD_Б – первоначальное значение шага изменения диаметра барабана, назначаемое конструктором;

r – номер итерации по изменению диаметра барабана;

L_Бmax, D_Бmax – максимальная длина и максимальный диаметр барабана, получаемые конструктором расчетом из условий компоновки механизма подъема.

Переменное значение шага определяется по условию:

Δ D_Б, если m_Б^r ≥ m_Б^(r+1);

Δ D_Б = - Δ D_Б/2, если m_Б^r < m_Б^(r+1); (7)

0 , если ׀Δ D_Б׀ ≤ ε,

где ε – минимальное значение шага изменения диаметра барабана, назначаемое из условия точности нахождения минимума металлоемкости барабана.

Необходимость применения барабана с многослойной навивкой каната оценивается логическим оператором:

m₁, если D_Б ≤ D_Бmax, L_Б ≤ L_Бmax;

m₁= (8)

m₁+1, если D_Б > D_Бmax, L_Б > L_Бmax,

где m₁ – число слоев навиваемого на барабан каната.

Для формирования области возможных решений при изменении значения кратности полиспаста на интервале [i_min; i_max] (за первый вариант принимается вариант с минимальной кратностью, для которого можно подобрать канат необходимого диаметра, i_max=24) выполняется расчет привода по каждому варианту компоновки.

Управление работой алгоритма осуществляется переменной с тремя индексами: ns = ns(j, k, r), управляющей структурным синтезом механизма. Каждое значение переменной ns определяет схему компоновки механизма подъема. Значение переменной j предопределяет автоматизированное обращение к массиву двигателей; значение переменной k управляет обращение к массивам управляющих устройств; значение переменной r управляет обращением к серийно выпускаемым редукторам и, при необходимости, проектированию открытой зубчатой передачи или обращение к процедуре проектирования нового редуктора из условия оптимальности. Конструктор при проектировании может исключить из рассмотрения в программе ряд вариантов, заданием переменной ns= ns(j, k, r), соответствующей исключаемым номерам схем нулевого значения.

Алгоритм перехода к схеме с открытой зубчатой передачей управляется условием:

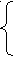u_p, если u≤ u_pmax;

u= (9)

u_p· u_оп, если u > u_pmax,

где u – общее передаточное число трансмиссии;

u_p – передаточное число редуктора;

u_pmax - максимального значения передаточного числа редуктора;

u_оп – передаточное число открытой зубчатой передачи.

Для проектирования несерийно выпускаемого редуктора механизма подъема применяется разработанные автором методика и алгоритм оптимального проектирования зубчатых передач.

В третьей главе разрабатывается метод графического синтеза соосных зубчатых передач, позволяющий однозначно получать схему и геометрические размеры звеньев передачи в зависимости от типа передачи, величины и знака передаточного отношения и введенных геометрических параметров Х_i.

При проектировании планетарных передач согласно существующим методикам, вначале выбирается схема передачи, а затем проводится кинематический расчет, и при этом часто оказывается, что выбранная схема не оптимальна или вообще не существует при заданных качественных характеристиках. Для решения задачи оптимального проектирования зубчатых передач, применяемых в механизмах подъемно-транспортных машин, был разработан новый метод графического синтеза соосных зубчатых передач.

В общем виде любую ступень зубчатого механизма можно считать частным случаем дифференциального редуктора. Так для двухступенчатого дифференциального редуктора (рис. 1), состоящего из солнечных колес 1 и 3, и сателлитных колес 2 и 2’, если передаточное отношение от первого к третьему солнечным колесам u₁₃=, получаем планетарный редуктор с неподвижным третьим колесом. Если передаточное отношение от первого солнечного колеса к водилу H u_1h=, получаем зубчатый механизм с неподвижными осями.

Рассмотрим метод графического синтеза дифференциального зубчатого механизма. Введем декартову систему координат XOY (рис. 1). По оси X отложим отрезок Оа, равный окружной скорости точки А, точки контакта первого солнечного колеса с сателлитным колесом 2:

.

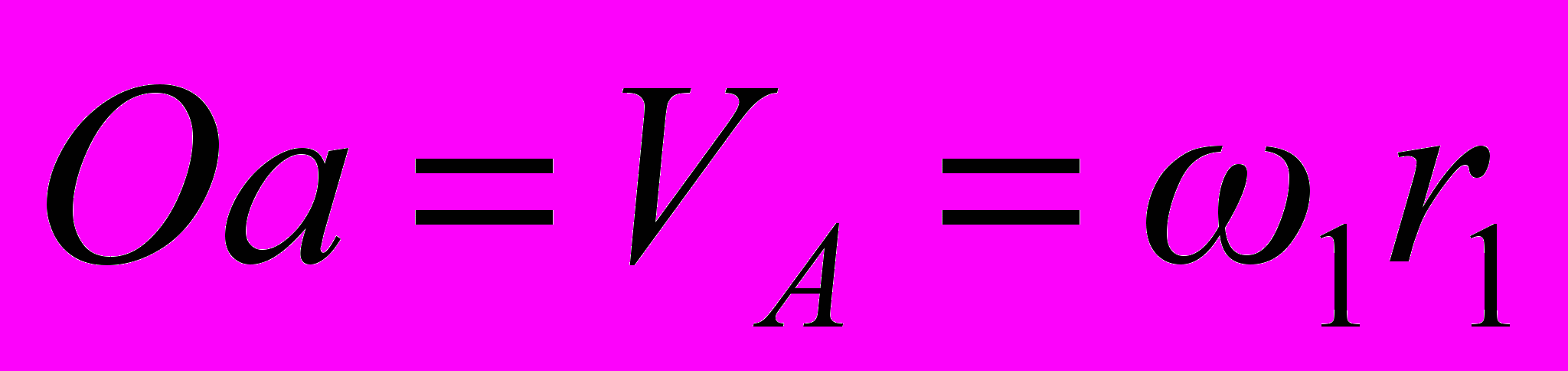Если при этом принять угловую скорость 1-го колеса ₁=1, то Оа примет значение r₁. От нуля вниз по оси Y отложим расстояние OD= r₁. Если соединить точки а и D, получим прямоугольный треугольник с равными катетами. Причем гипотенуза треугольника будет линией распределения скоростей точек 1-го колеса редуктора. Угол наклона этой линии к оси Y равен 45 градусам: ₁=45. Построим линию распределения скоростей водила, линию Н. Для этого из точки D проведем прямую под углом _H, определив данный угол из соотношения:



Для построения линии распределения скоростей 3-го солнечного колеса линию 3 под углом ₃ , который определим из соотношения:




Рис. 1. Графический синтез дифференциального редуктора




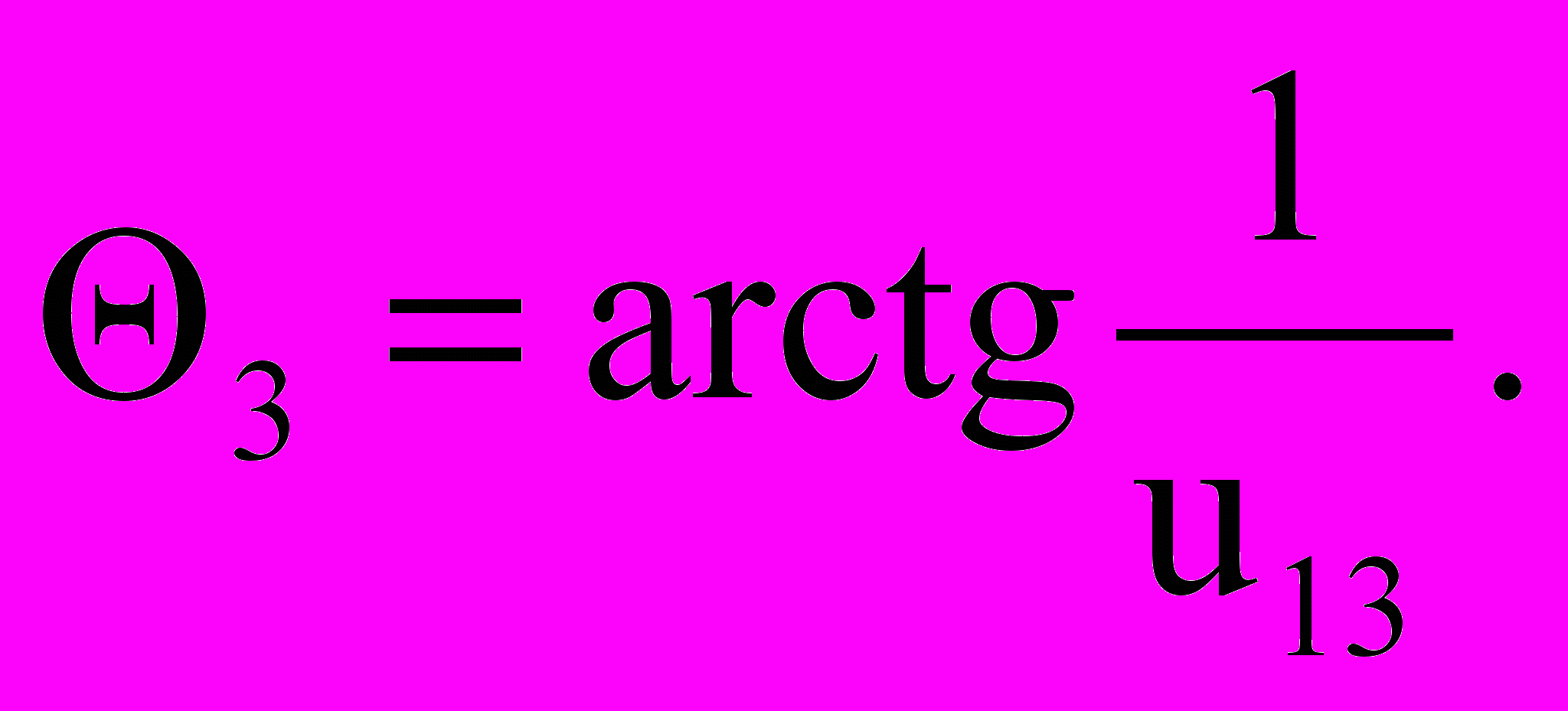
Выберем на линии Н точку b, которая соответствует точке В на схеме редуктора – оси вращения сателлитных блоков, задавшись значением параметра Х_b, который является координатой точки b во введенной системе координат. Через точки а и b проведем линию 2. Полученная линия будет линией распределения скоростей сателлитных колес 2 и 2’. Точка пересечения линий 2 и 3, точка с, соответствует точке контакта сателлитного колеса 2’ с солнечным колесом 3 на схеме редуктора. Полученное построение представляет собой план аналогов скоростей точек дифференциального редуктора, построенный в том же масштабе, что и схема редуктора. Положения точек а, b и с на плане однозначно определят схему и геометрические размеры проектируемого дифференциального редуктора: r₂= b’O; r_2’= c’O; r₃=c’D.

Следовательно, схема дифференциального зубчатого механизма и геометрические размеры колес однозначно определяются значениями передаточных отношений дифференциального зубчатого механизма u_1h и u₁₃, а также значением параметра x_b, который может задаваться в зависимости от назначения зубчатого механизма.

При проектировании планетарного зубчатого механизма u₁₃= получаем:



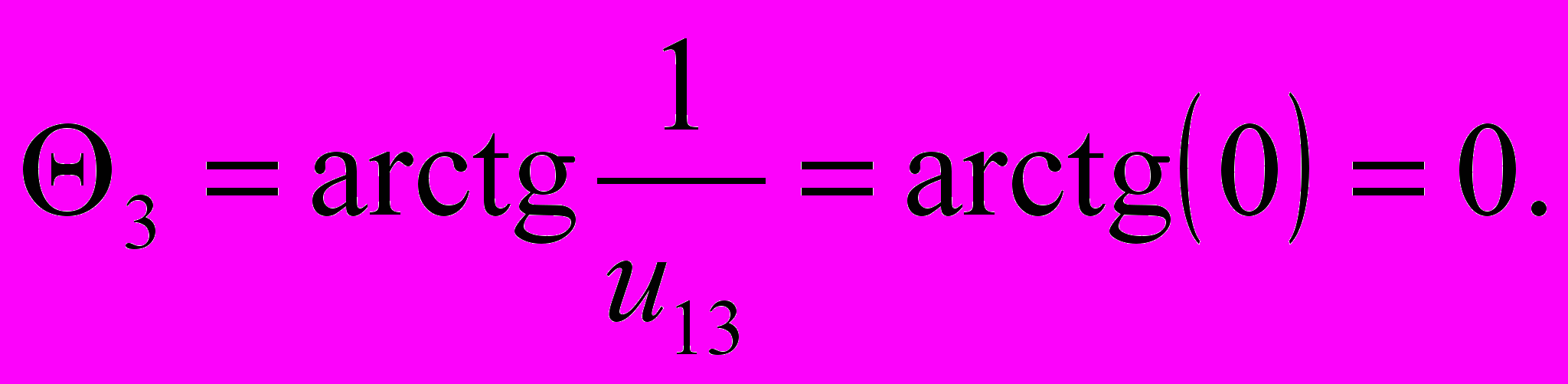
При проектировании зубчатого механизма с неподвижными осями u_1h=, получаем:



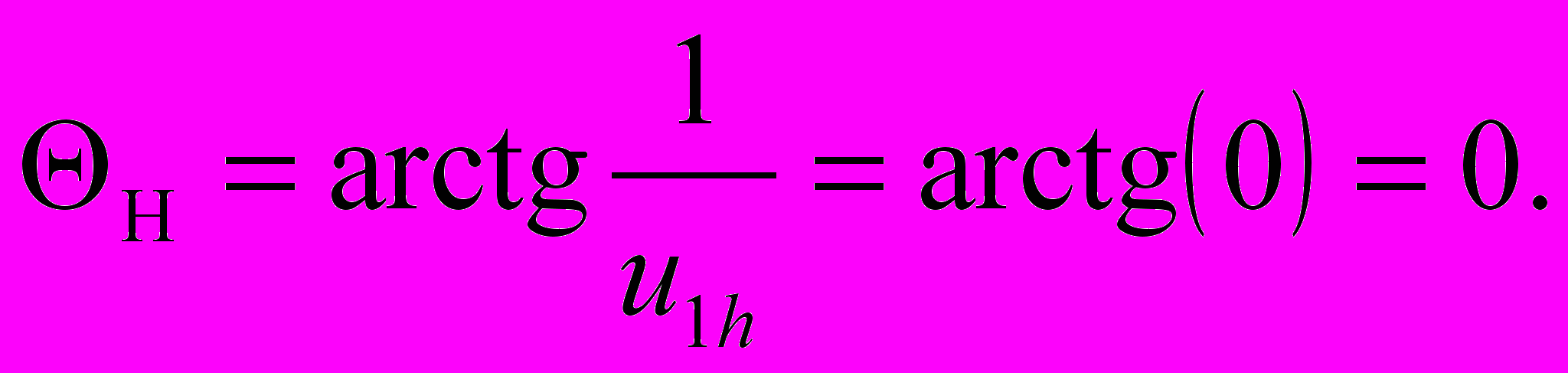
Линия распределения скоростей водила Н сливается с осью OY.

Из вышесказанного следует вывод, что предложенный метод графического синтеза может применяться при проектировании любого типа соосных зубчатых механизмов. Причем данный метод позволяет однозначно получить схему и геометрические размеры звеньев передачи.

На основании метода графического синтеза проведена классификация простейших схем планетарных редукторов и мультипликаторов типа 2k-h по четвертям декартовой системы координат с разделением на схемы с приводом на центральное колесо и с приводом на водило, а также классификация схем планетарных передач типа 3k.

Возможны двенадцать вариантов простейших схем планетарных механизмов с цилиндрическими колесами типа 2k-h в зависимости от модуля передаточного отношения, от того, какое из звеньев механизма будет ведущим - солнечное колесо или водило, а также в зависимости от знака передаточного отношения и вида зацепления солнечных колес с сателлитными шестернями. В предлагаемой работе следует задаваться только передаточным отношением зубчатого механизма и его знаком. При одноименном направлении вращения ведущего и ведомого звеньев зубчатых механизмов передаточное отношение положительное u_1h>0, при разноименном направлении вращения – отрицательное u_1h < 0.

Для редукторов с приводом на центральное колесо и приводом на водило можно выделить по четыре схемы, распределенные по четвертям декартовой системы координат (рис. 2 и 3). Аналогичное распределение выполнено для мультипликаторов с приводом на центральное колесо и водило.

Для зубчатых механизмов с приводом на центральное колесо (рис. 2) задается система координат, в которой ось Y примем за линию отсчета, а ось Х проводится через точку контакта ведущего звена с блоком сателлитных колес. Анализируя эти схемы, легко доказать, что некоторая точка b на плане скоростей, соответствующая точке В на схеме зубчатого механизма, находится только в одной четверти выбранной системы координат. Причем точка b представляет собой точку пересечения линии распределения скоростей ведомого звена (водила) с линией распределения скоростей сателлитных колес. По этому принципу механизмы с приводом на центральное колесо разделены по четвертям декартовой системы координат. Положительный знак передаточного отношения определяет схемы 1 и 4 четвертей декартовой системы координат. Отрицательный знак передаточного отношения определяет схемы 2 и 3 четвертей декартовой системы координат.





Рис. 2. Классификация редукторов типа 2k-h с приводом на центральное колесо


Аналогичным образом можно разделить по четвертям и зубчатые механизмы, выполненные по схемам с приводом на водило, задаваясь положением на плане скоростей точки а – пересечения линии распределения скоростей ведомого звена (первого зубчатого колеса) с линией распределения скоростей сателлитных колес, соответствующей точке А на схеме редуктора (рис.3) или мультипликатора. При этом ось Х вводимой системы координат ХОY проходит через ось вращения сателлитных блоков. Если на приведенных схемах строить картины не скоростей, а их аналогов, причем в том же масштабе, что и схемы механизмов, то координаты точек b и а определят размеры колес зубчатого механизма в том же масштабе.





Рис. 3. Классификация редукторов типа 2k-h с приводом на водило


Полученные расчетные соотношения для определения радиусов колес зубчатых механизмов типа 2k-h в зависимости от ведущего колеса и введенных параметров Х_b и Х_а представлены: для механизмов с приводом на центральное колесо в табл. 1, с приводом на водило – в табл. 2.

Для планетарных передач типа 3k могут быть получены 4 схемы различного исполнения в зависимости от того, какое из колес центральных колес является опорным и знака передаточного отношения. Для разработки методики оптимального проектирования планетарных зубчатых передач типа 3k, на основании метода графического синтеза были получены соотношения для определения начальных радиусов колес в зависимости от передаточного отношения и введенного геометрического параметра Х_i.