Развитие теории оптимального проектирования механизмов грузоподъемных кранов пролетного типа

Вид материала

Автореферат

Содержание В четвертой главе U, т.е. решение, имеющее наименьшую метрику. Если несколько решений получат одинаковые значения метрики ρ(x В пятой главе Х. Применение к полученной области возможных решений принципа Эджворта-Парето позволит сузить область Х X1, задаваемая дискретно с заданным приращением ΔX X корректируется согласно условию: ΔX В шестой главе Х задачи оптимального проектирования рассматривались варианты компоновки механизма при различных значениях кратности полиспаста Основные выводы и результаты работы Основные положения диссертации опубликованы в следующих работах

Подобный материал:

• Анкета –резюме Общие сведения, 52.08kb.
• Типовая инструкция для крановщиков (машинистов) по безопасной эксплуатации мостовых, 574.73kb.
• Типовая инструкция для крановщиков (машинистов) по безопасной эксплуатации мостовых, 603.15kb.
• Правила устройства и безопасной эксплуатации грузоподъемных кранов, 4085.92kb.
• Правила устройства и безопасной эксплуатации грузоподъемных кранов, 3600.74kb.
• Пособие для электромонтеров по обслуживанию и ремонту грузоподъемных машин литература, 1981.47kb.
• Закономерности проектирования механизмов для передачи и преобразования, 19.17kb.
• Пособие Для стропальщиков по безопасному производству работ грузоподъемными машинами, 1339.67kb.
• М. Л. Семенова, 2656.47kb.
• Правила устройства и безопасной эксплуатации грузоподъемных кранов (пб-10-382-00), 357.05kb.

Таблица 1

Геометрические размеры колес зубчатых передач типа 2k-h

с приводом на центральное колесо

Наименование	Формула	Примечание
r1		-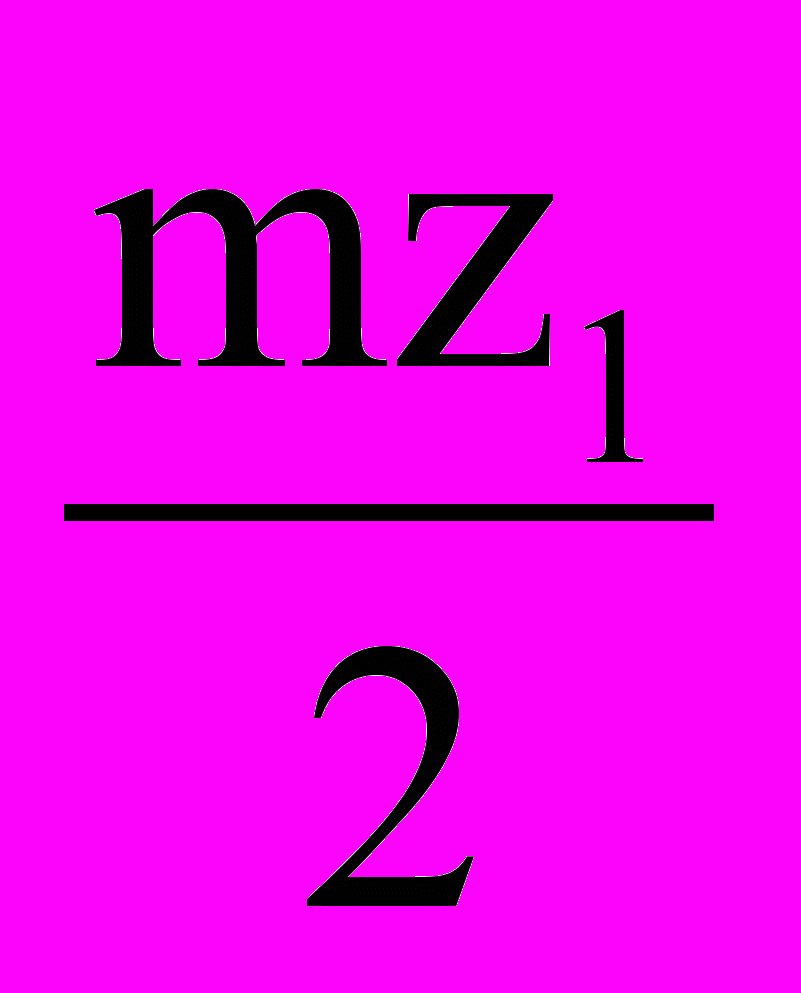
r2		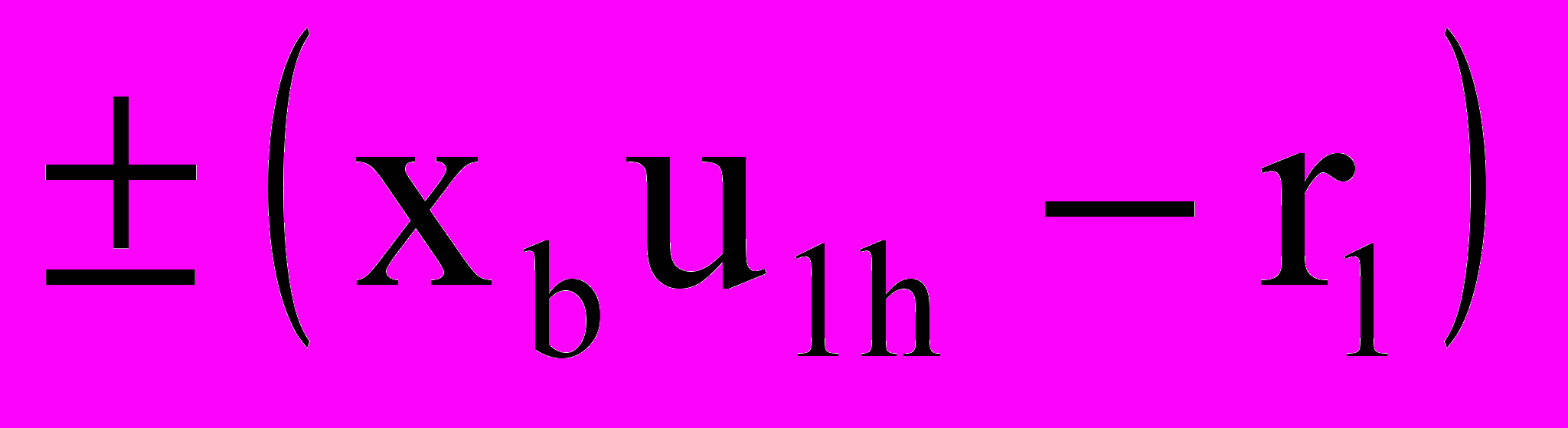Знак «-» для редукторов и мультипликаторов 3-х и 4-х четвертей
r2’		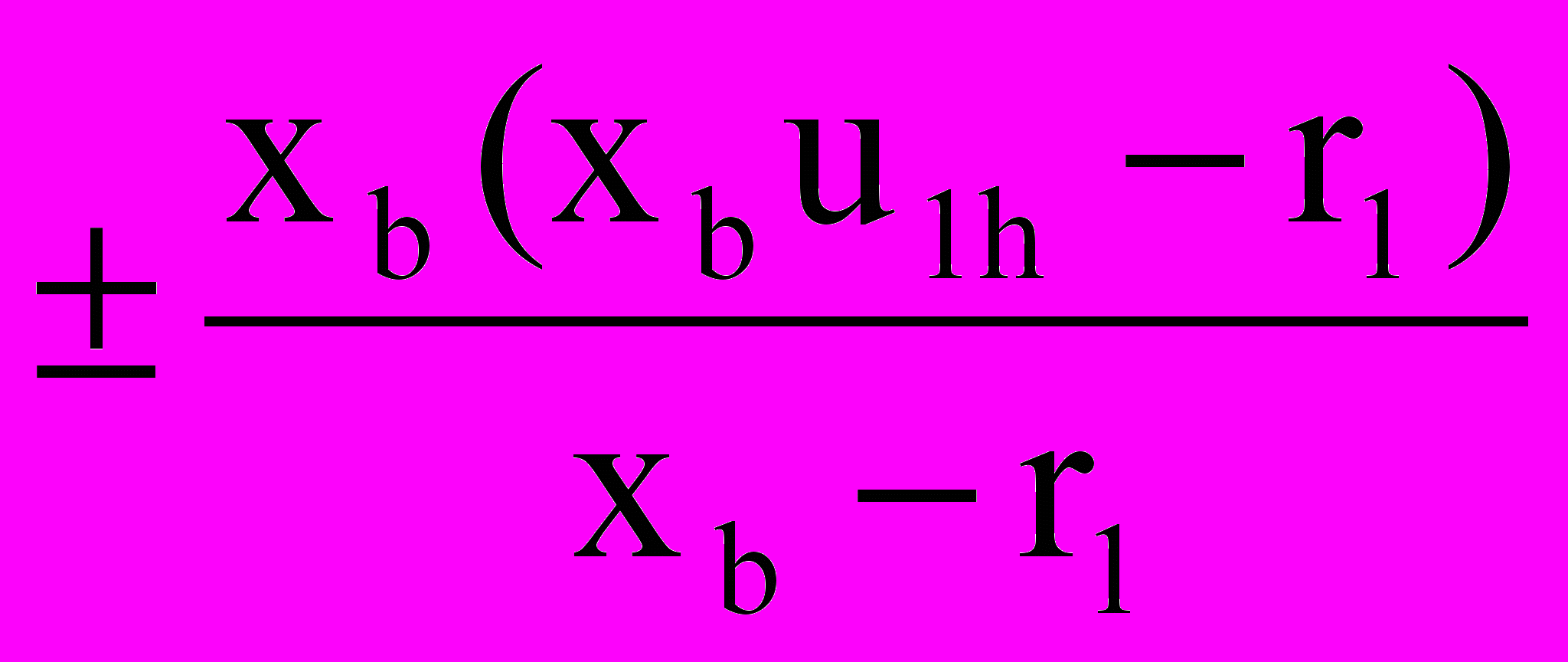Знак «-» для редукторов 1-й и 3-й четвертей и мультипликаторов 3-й и 4-й четвертей
r3		-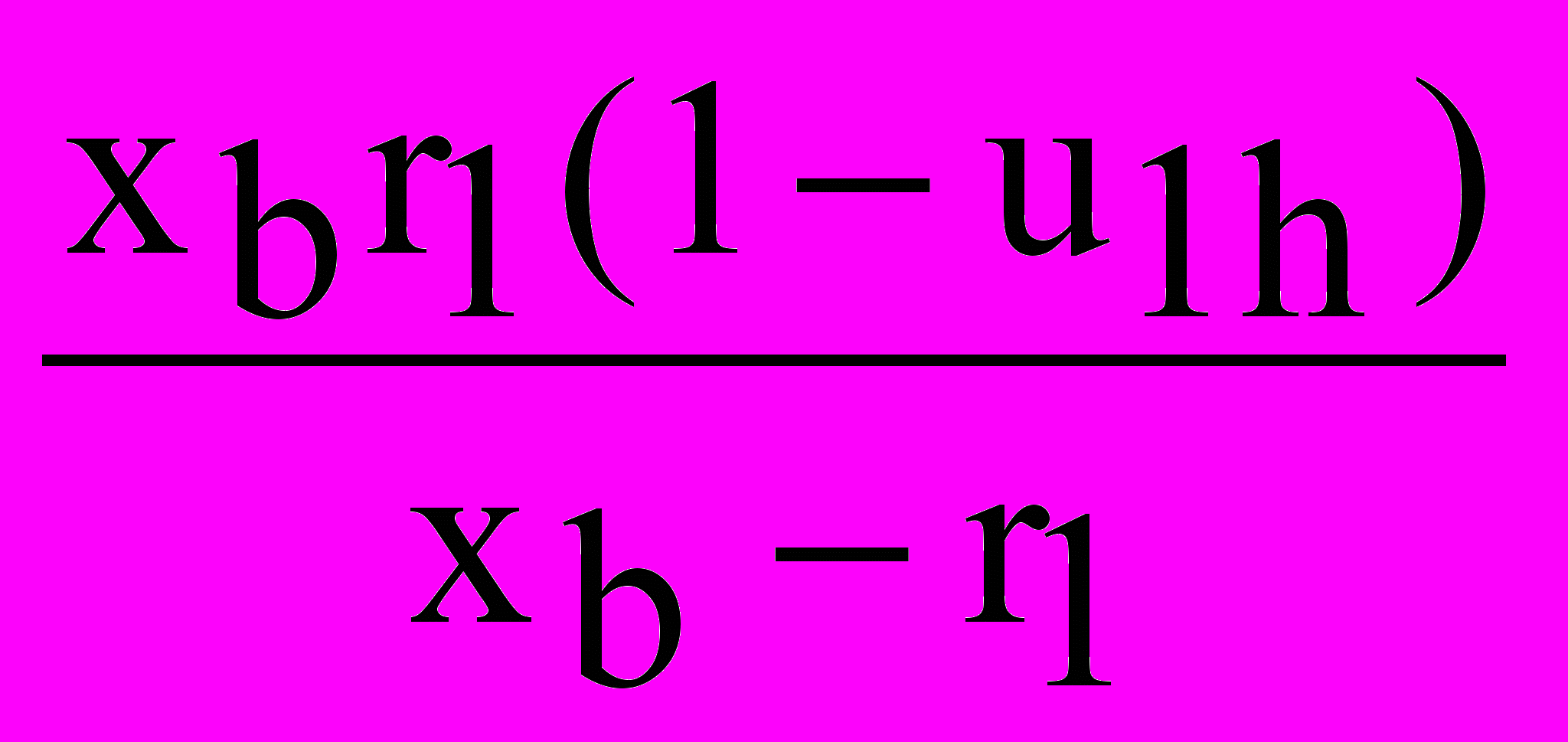

Таблица 2.

Геометрические размеры колес зубчатых передач типа 2k-h

с приводом на водило

Наименование	Формула	Примечание
r1		-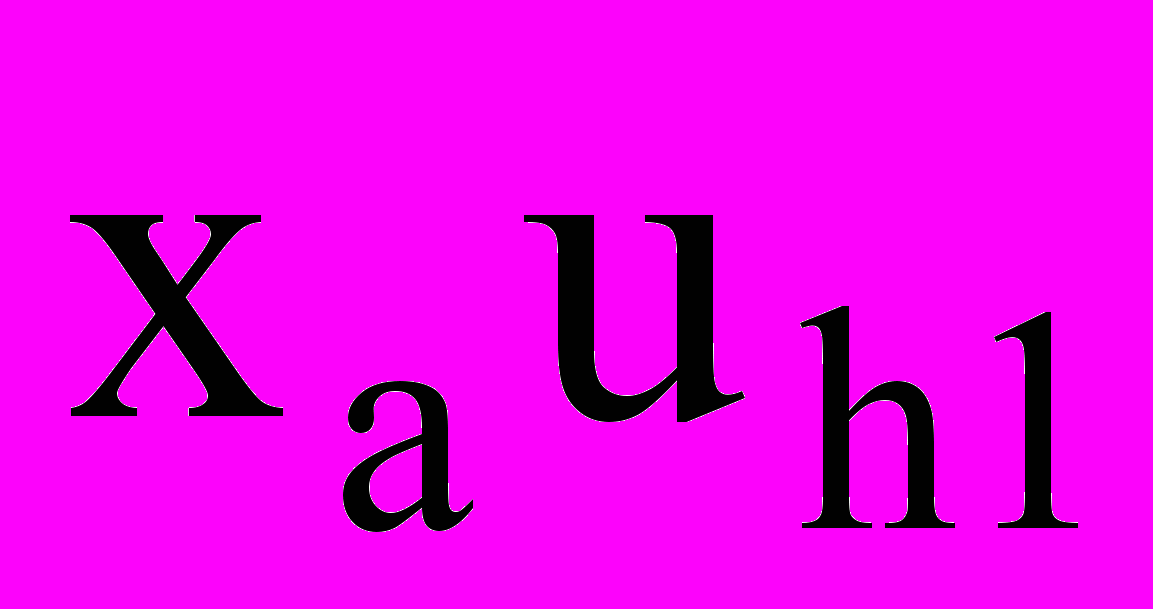
r2		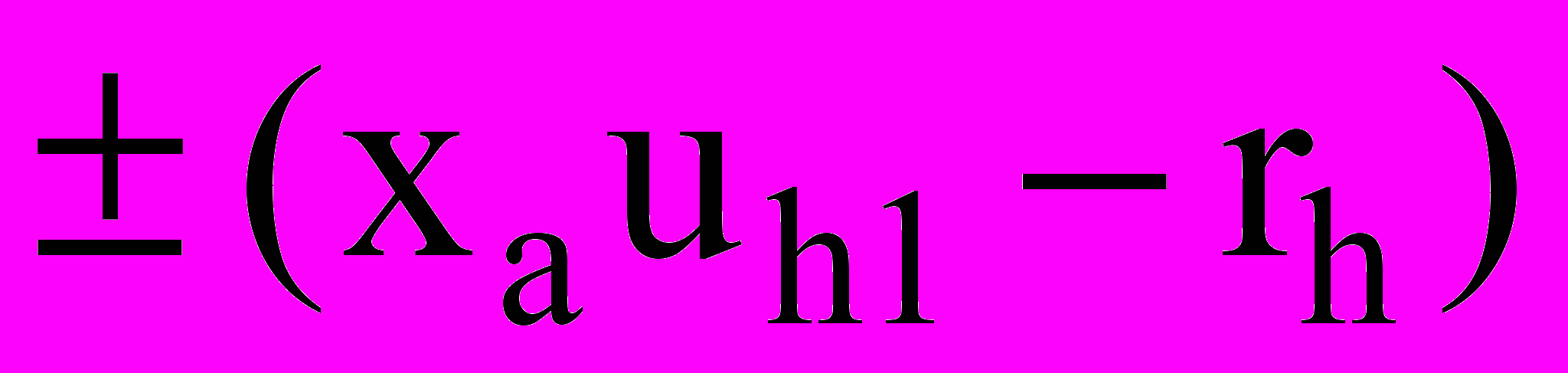Знак «-» для редукторов и мультипликаторов 3-х и 4-х четвертей
r2’		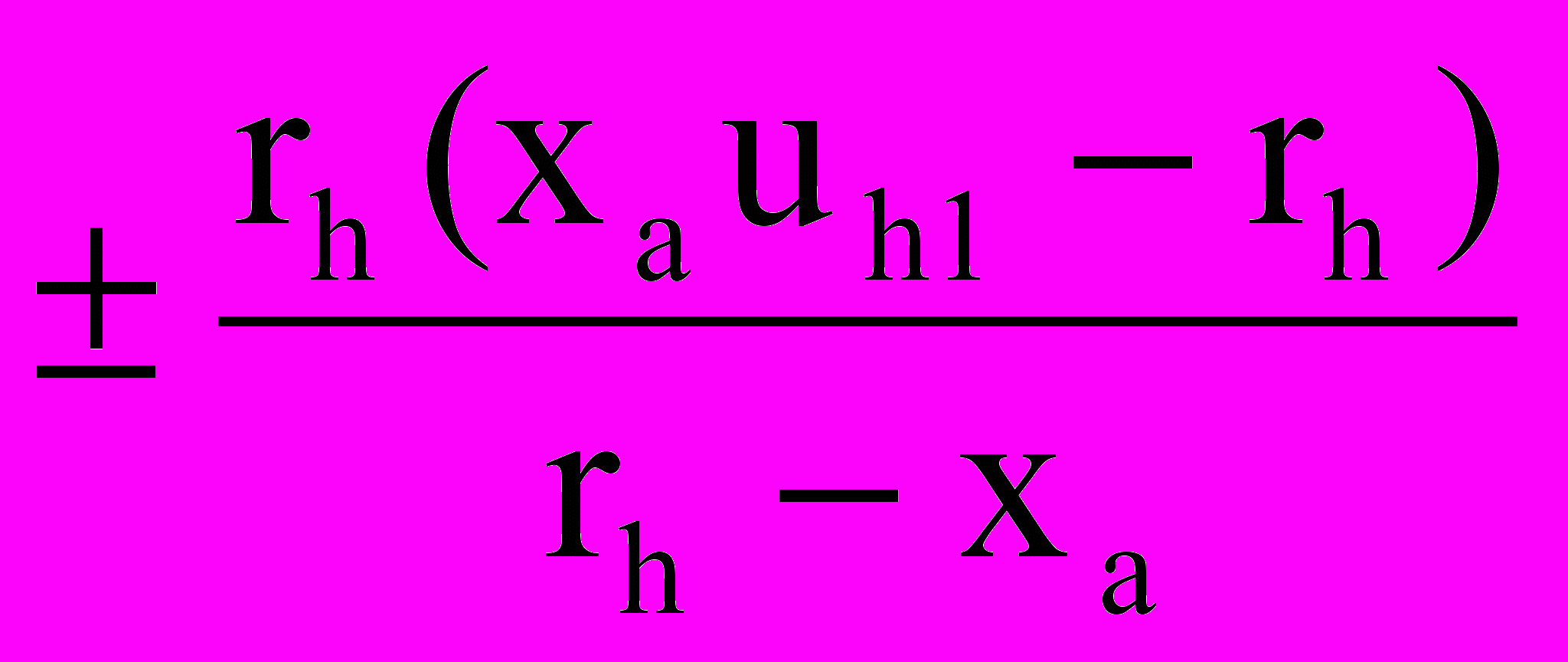Знак «-» для редукторов 3-й и 4-й четвертей и мультипликаторов 1-й и 3-й четвертей
r3		-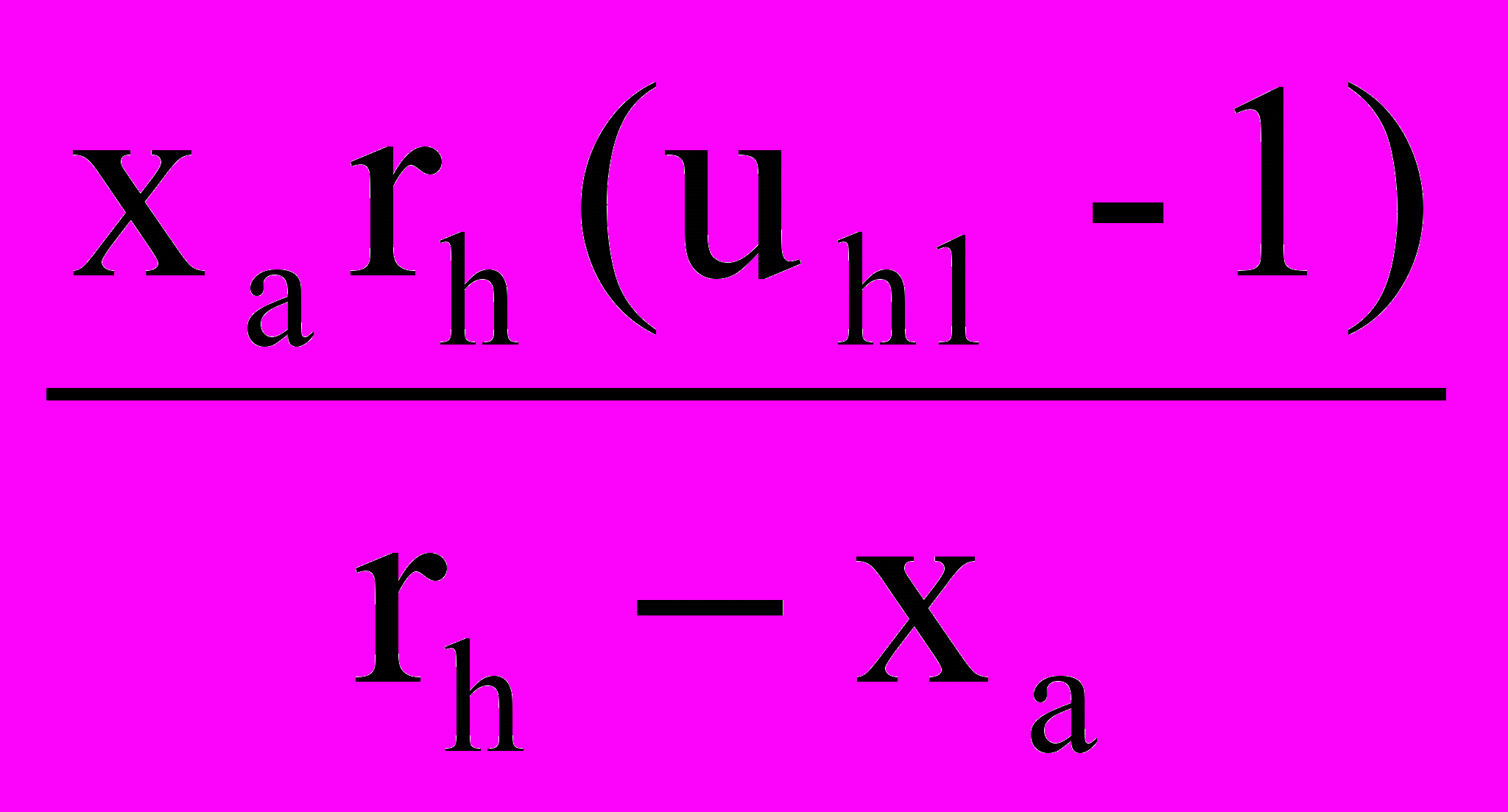

Введенные геометрические параметры Х_i следует выбирать, исходя из требуемых качественных характеристик зубчатого механизма. Такими характеристиками для крановых планетарных зубчатых механизмов могут быть: условие равной контактной прочности зубьев; условие наименьших габаритов; максимально возможный коэффициент перекрытия зубьев; максимально возможное число сателлитов; величина КПД.

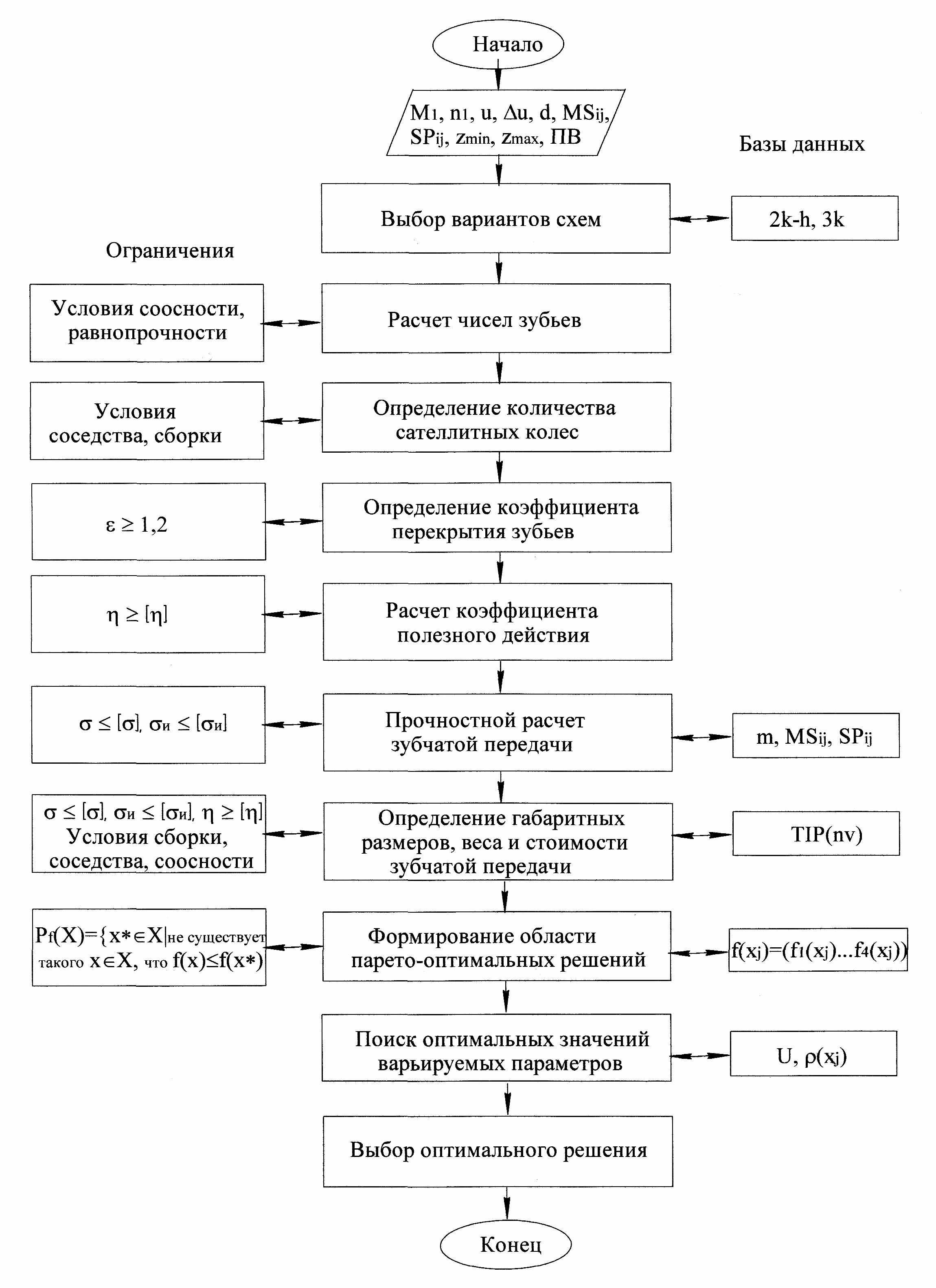
В четвертой главе приведена методика оптимального проектирования зубчатых приводов кранов: разработка математической модели, критериев оптимизации и алгоритмов.

Проектирование зубчатых механизмов представляет собой комплексную проблему, решение которой может быть разбито на несколько самостоятельных этапов. Первым этапом проектирования является установление кинематической схемы механизма, которая бы обеспечивала требуемый закон движения. Вторым этапом проектирования является разработка конструкции механизма, обеспечивающая его прочность, долговечность, высокий КПД и др.

При проектировании планетарных зубчатых передач возникает многовариантная задача выбора схемы передачи, удовлетворяющей требуемым кинематическим и динамическим условиям. Кроме того, задача оптимального проектирования планетарных зубчатых передач является многокритериальной, т.к. при выборе наилучшего варианта приходится учитывать много различных требований, и среди этих требований встречаются противоречащие друг другу. Однако почти все существующие методы оптимизации планетарных зубчатых передач предназначены для отыскания оптимального значения одного критерия, т.е. пытаются упрощениями свести многокритериальную задачу к однокритериальной. Так для решения задачи оптимального проектирования планетарных зубчатых в ряде работ предлагается принять радиальный оценочный габарит - половину полного радиального размера планетарного механизма, отсчитанного от центральной оси, т.е. оптимальной считается передача, которая при достаточном КПД имеет минимальный радиальный габарит. Однако функция цели при проектировании планетарных зубчатых передач должна учитывать не только габаритные размеры, но и качественные характеристики передачи, например, такие как плавность хода и шумовые характеристики, зависящие от назначения и технического задания на проектирование. Кроме того, в ряде силовых передач наиболее важной характеристикой является эффективность передачи энергии, определяемая КПД.

На основе проведенного анализа методов оптимального проектирования механических передач был сделан вывод, что наиболее эффективным для решения задачи оптимального проектирования планетарных зубчатых передач метод Парето. В качестве составляющих векторного критерия f рассматриваются следующие характеристики зубчатой передачи: металлоемкость передачи, габаритные размеры, коэффициент перекрытия одной из ступеней, коэффициент полезного действия:

f₁=m, f₂=L, f₃=ε, f₄=η. (10)

Область возможных решений задачи Х формируется при дискретном изменении передаточного отношения u с шагом Δu в области ±2% от величины заданного передаточного отношения и ограничениях, наложенных на прочностные и качественные характеристики проектируемой планетарной зубчатой передачи, с учетом условий соосности, сборки и соседства. Далее из области возможных решений выбирается множество парето-оптимальных решений Р_f(х) исключением решений, не улучшающих ни одного из критериев – не парето-оптимальных согласно условию (3). Для дальнейшего сужения множества возможных решений, применяется предложенная модификация метода целевого программирования.

В соответствии с методологией целевого программирования был составлен идеальный вектор U. Применительно к решению задачи оптимального проектирования зубчатой передачи, идеальный вектор U должен состоять из минимальных значений составляющих векторного критерия f₁ , f₂ и максимальных значений составляющих векторного критерия f₃ и f₄, которые выбираются в области парето-оптимальных решений:

U= (f _1min, f _2min, f_3max, f _4max). (11)

Для каждого решения x_j Р_f(Х) X рассчитывается метрика ρ(x_j), представляющая собой неотрицательное число, определяющее расстояние критериального вектора f (x_j) от идеального вектора U. Величина метрики для каждого решения x_j рассчитывается: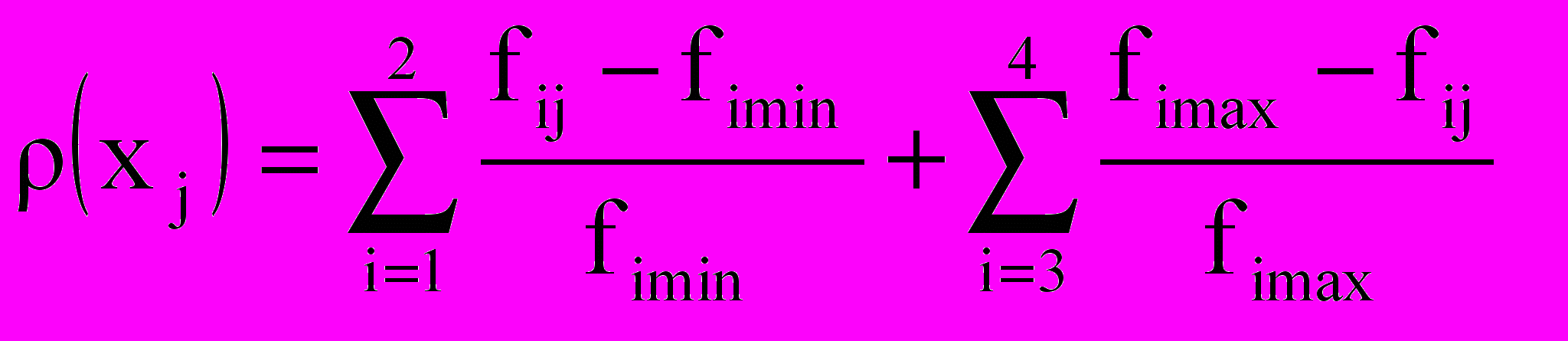

. (12)

Оптимальным является решение, расположенное как можно ближе к множеству идеальных оценок U, т.е. решение, имеющее наименьшую метрику. Если несколько решений получат одинаковые значения метрики ρ(x_j), окончательное решение об оптимальности того или иного варианта компоновки механизма принимает конструктор.

Для решения оптимизационной задачи проектирования планетарной зубчатой передачи была разработана система ограничений на числовые значения оптимизируемых параметров в виде прочностных и качественных требований, а также условий соосности, сборки, соседства, отсутствия заклинивания.

Так как основной причиной выхода из строя закрытых зубчатых передач грузоподъемных машин является выкрашивание, связанное с развитием усталостных трещин, наибольший интерес из прочностных характеристик вызывает равная контактная прочность зубьев колес. При допущениях, что все колеса планетарной передачи нарезаны без смещения и выполнены из одного материала, были получены расчетные соотношения для определения геометрических параметров Х_i, при которых выполняются условия равной контактной прочности. На основании полученных соотношений определены области существования планетарных зубчатых передач при условии равной контактной прочности зубьев колес. С учетом соотношений, полученных для геометрических параметров Х_i, разработаны формулы расчета геометрических размеров колес планетарных передач при условии равной контактной прочности.

Нередки случаи, когда в закрытых зубчатых передачах несущая способность по контактным напряжениям недоиспользуется, а выносливость зуба по изгибным напряжениям оказывается недостаточной. Такие расчетные ситуации возможны для закрытых зубчатых передач с мелкомодульными зубчатыми колесами, изготовленными из материалов с твердостью выше 350 НВ (цементированные, азотированные, закаленные нагревом т.в.ч.), для которых допускаемые контактные напряжения, пропорциональные твердости рабочих поверхностей, получаются большими. Поэтому расчеты на изгибную прочность и для закрытых зубчатых передач также могут иметь проектный характер.

Посредством смещения, рационального подбора чисел зубьев и термообработки можно достичь желаемой равнопрочности зубьев на изгиб. Если контактирующие зубчатые колеса изготовлены из одного материала, т. е. [s]_и1=[s]_и2, равнопрочность зубьев на изгиб может быть достигнута путем назначения коэффициентов смещения при которых: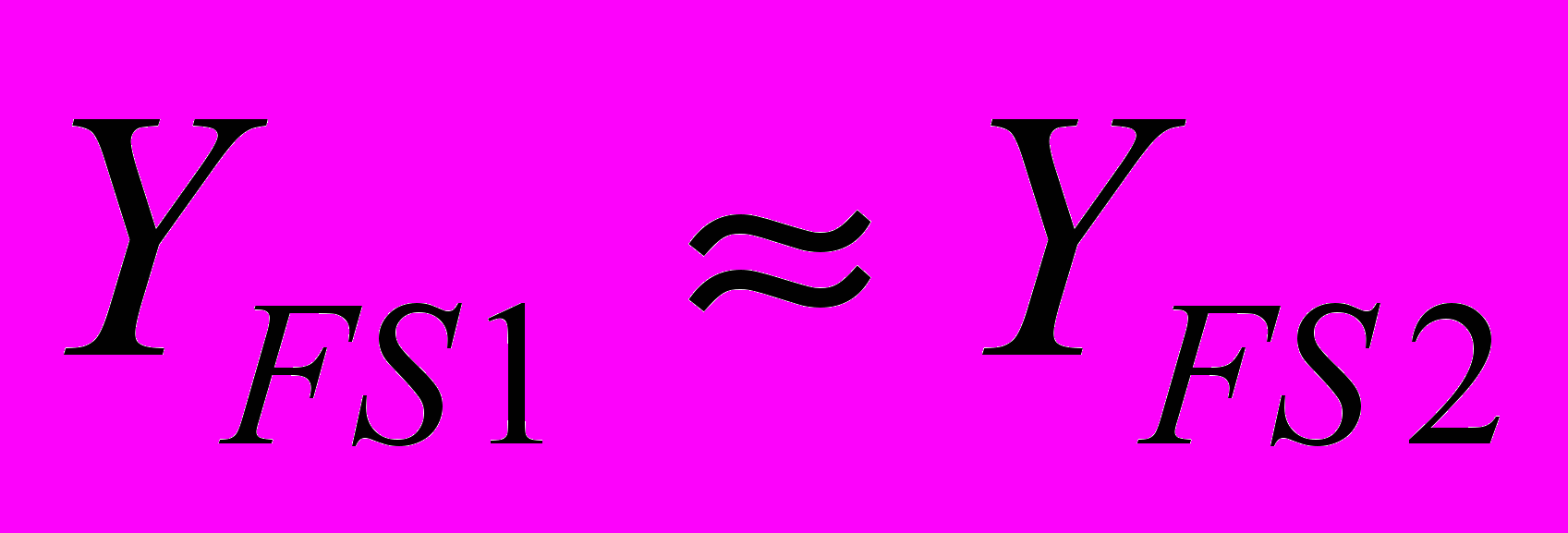, где Y_FS1, Y_FS2 – коэффициенты формы зуба шестерни и колеса.

Наибольшая изгибная прочность достигается смещением с возможно большим коэффициентом смещения. При применении равносмещенных передач x₁=–x₂ (x_S=0) изгибная прочность зубьев колеса уменьшается, а шестерни увеличивается. В связи с этим выбор коэффициентов смещения х₁ и х₂ должен ограничиваться такими значениями, при которых бы достигалась равная изгибная прочность шестерни и колеса при соблюдении ряда других условий: отсутствия заострения зубьев, получения коэффициента перекрытия не ниже допустимого значения.

Для оптимального проектирования зубчатых передач в случае, когда проектным является расчет на изгибную прочность, была разработана методика и получены расчетные соотношения для определения геометрических параметров Х_i, и размеров колес при условии равной изгибной прочности.

Для выполнения прочностных расчетов зубчатых механизмов, а также

для получения расчетных соотношений для автоматизированного расчета коэффициента полезного действия планетарных зубчатых передач выполнено исследование планетарных зубчатых передач по критерию эффективности передачи энергии с определением величин сил и моментов, действующих на звенья зубчатой передачи.

В работе проведено исследование планетарных зубчатых передач по коэффициенту перекрытия, учитывающему непрерывность и плавность зацепления, в результате которого получены поверхности распределения коэффициентов перекрытия планетарных зубчатых передач в зависимости от числа зубьев ведущего колеса (первого колеса для схем с приводом на водило) и передаточного отношения, позволившие уточнить области применения векторного критерия оптимальности решения f₃. На рис. 4 приведены графики зависимости коэффициента перекрытия от передаточного отношения и числа зубьев ведущего колеса для редуктора с приводом на центральное колесо первой четверти для первой (рис. 4 а) и второй ступени (рис. 4 б).

Для решения задачи оптимального проектирования соосных зубчатых передач разработана методика и алгоритм, составленный по модульному принципу. Структура алгоритма представлена на рис. 4 в. Входными данными для работы алгоритма являются: вращающий момент на быстроходном валу М₁, частота вращения быстроходного вала n₁, передаточное отношение привода u, точность вычисления передаточного отношения Δ%, количество шагов вычислений, марка стали MS_ij, из которой будут изготавливаться колеса, способ обработки поверхностей зубьев колес SP_ij, минимальное z_min и максимальное число z_max зубьев колес, режим работы. Для формирования области возможных решений задачи Х внешний цикл алгоритма построен на дискретном изменении передаточного отношения с шагом, определяемым заданной точностью вычисления и количеством шагов вычислений. Алгоритм включает основную программу, которая является управляющей и процедуры (подпрограммы). По величине и знаку передаточного отношения выбираются возможные варианты схем планетарных передач типа 2k-h и 3k. Рассчитываются числа зубьев передач при условии равнопрочности с округлением до целых величин и последующим уточнением передаточного отношения; из условия сборки с проверкой по условию соседства определяется количество сателлитных колес; рассчитываются коэффициент перекрытия зубьев и коэффициент полезного действия зубчатой передачи, для которого проверяется ограничение по допустимой величине, задаваемой конструктором. Модуль зацепления определяется из прочностных расчетов с округлением до стандартного значения. При известных значениях чисел зубьев и модуля зацепления выполняется определение габаритных размеров зубчатой передачи с корпусом, массы и стоимости передачи. Формируется векторный критерий оценки качества решения f=(f ₁,…f ₄) (10) для всех возможных схем зубчатой передачи с заданными характеристиками. На полученной области возможных решений Х формируется область парето-оптимальных решений Р_f(Х), идеальный вектор U (11), для каждого парето-оптимального решения определяется метрика ρ (12). Оптимальным считается решение, имеющее минимальную метрику.





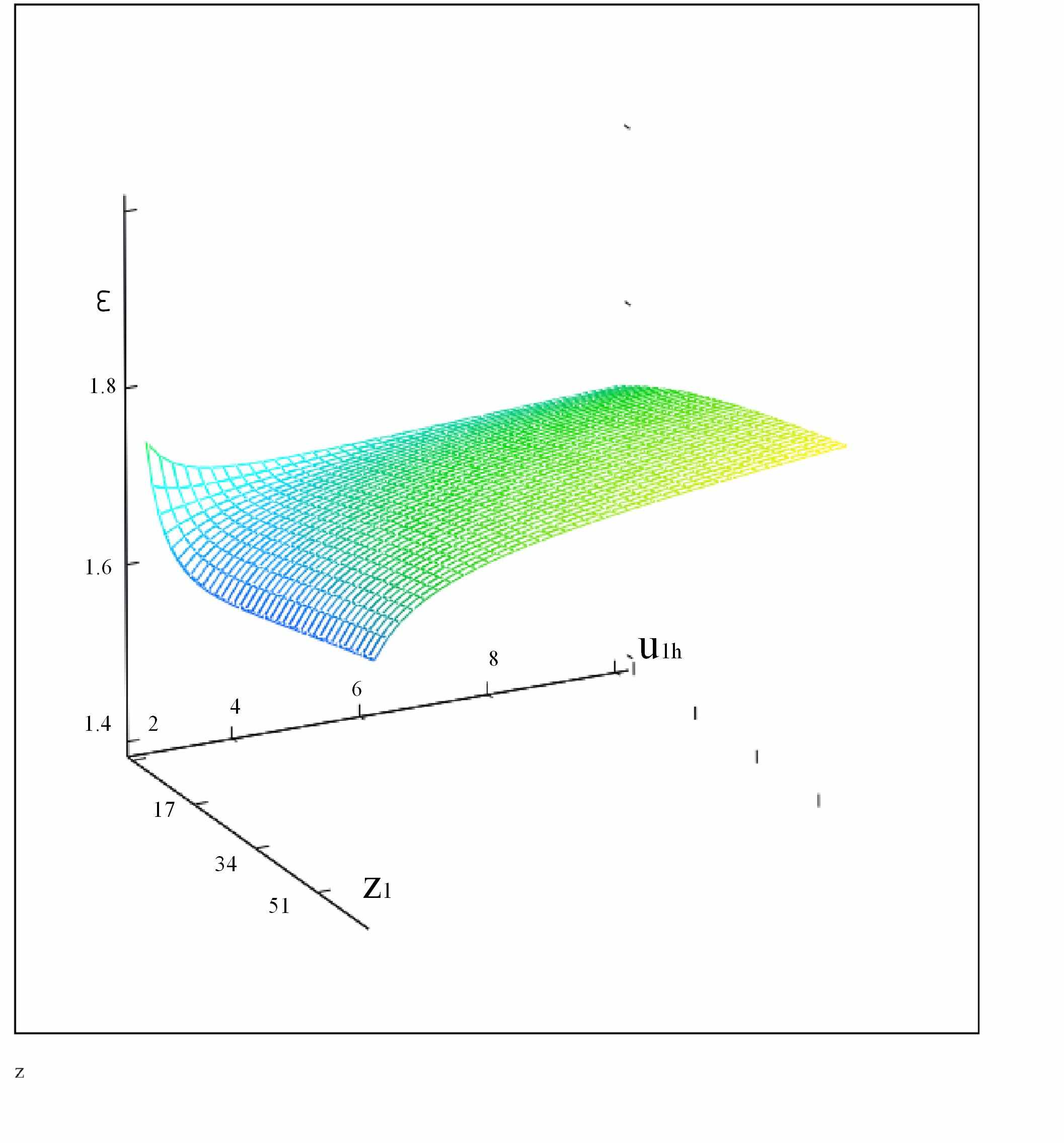
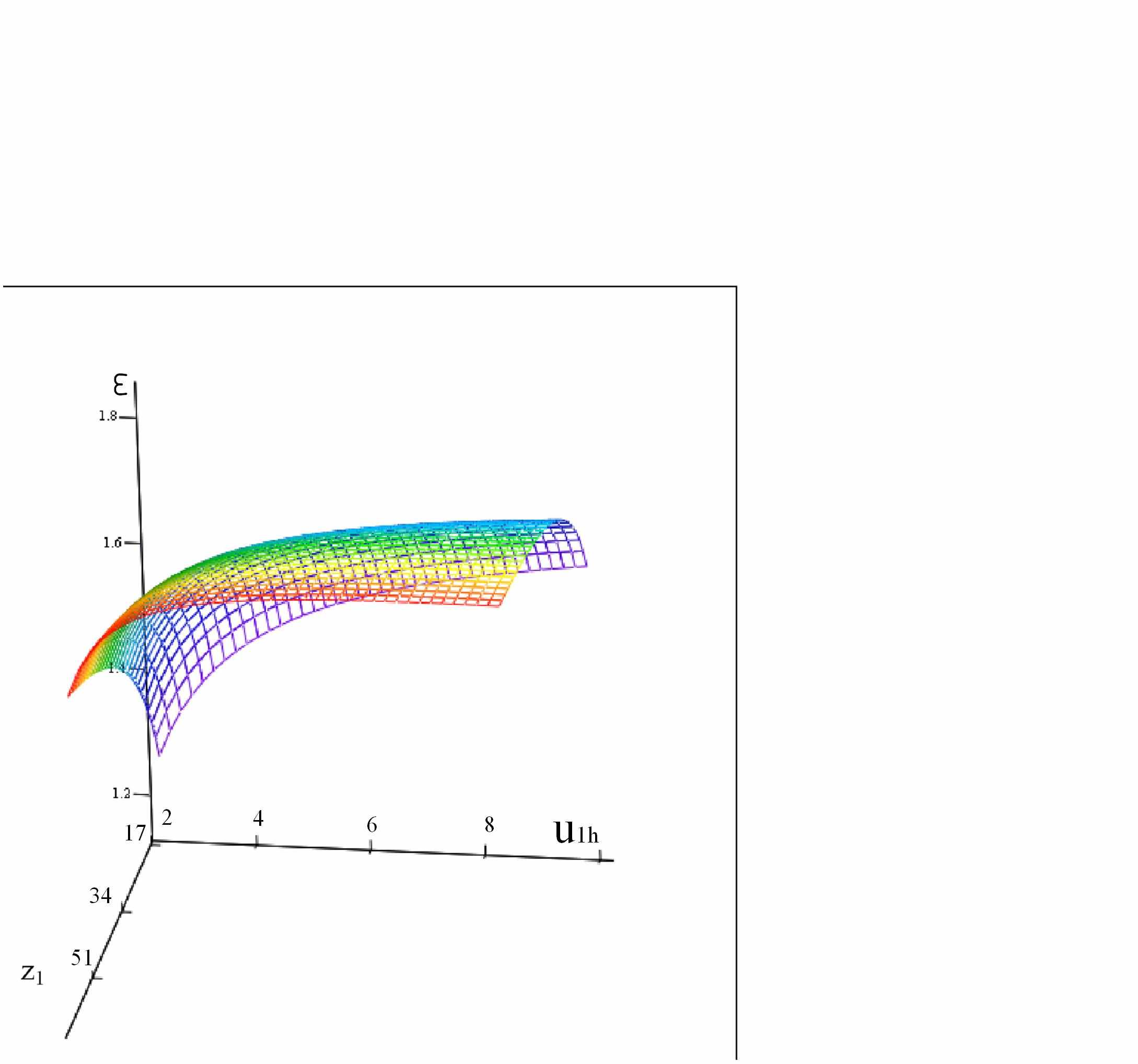
а) б)



в)

Рис. 4.

В пятой главе рассматривается теория оптимального проектирования механизмов передвижения кранов и крановых тележек.

При проектировании механизмов передвижения тяжелых мостовых, козловых кранов и мостовых перегружателей возникает многовариантная задача выбора кинематической схемы привода, балансирной схемы установки колес, их типа, диаметра колеса и числа опорных рельсов. При инженерном проектировании решается обычно задача обеспечения кинематики, мощности привода, прочности и надежности, однако на современной стадии развития науки и техники ставится задача оптимального проектирования механизмов передвижения.

Для решения многокритериальной задачи проектирования механизма передвижения крана и крановых тележек также предлагается метод Парето.

В качестве критериев оптимальности, входящих в векторный критерий качества решения f, предложены следующие характеристики схемы компоновки механизма передвижения: стоимость электродвигателя и управляющих устройств; стоимость трансмиссии S_тр и ее масса m_тр; массы муфт m_м, тормозов m_т, балансиров m_б, ходовых колес m_к, крановых рельсов m_р. Причем необходимо рассматривать все возможные схемы трансмиссии: с комплектацией серийно выпускаемыми редукторами, применением открытых зубчатых передач и серийно выпускаемых редукторов, вновь проектируемых из условия оптимальности редукторов с большими передаточными отношениями. В случае раздельного привода, в векторном критерии учитываются суммарные массы, соответствующие количеству приводов n_пр. При применении четыхрельсового кранового пути масса рельсов m_р должна входить в векторный критерий f с коэффициентом 2. Для учета эффективности использования энергии в векторный критерий оптимальности включен КПД привода, взятый со знаком «-». Таким образом, векторный критерий качества решения включает девять критериев оптимальности:

f₁= n_пр·A; f₂= n_пр·S_тр ; f₃= n_пр·m_тр; f₄= n_пр·m_м;

f₅= n_пр·m_т; f₆= m_б; f₇= m_к; f₈= n_p· m_р; f₉= - η, (13)

которые необходимо минимизировать на области возможных решений задачи Х.

Применение к полученной области возможных решений принципа Эджворта-Парето позволит сузить область Х до области парето-оптимальных решений Р_f(Х). Для дальнейшего сужения области парето-оптимальных решений до области принимаемых решений Sel(X) формируется идеальный вектор U, состоящий из минимальных значений полученных при решении задачи критериев оптимальности:

U= (f _1min, f _2min, …, f _9min). (14)

Для каждого решения x_j Р_f(Х) X рассчитывается метрика ρ(x_j), представляющая собой неотрицательное число, определяющее расстояние критериального вектора f (x_j) от идеального вектора U. Величина метрики для каждого решения x_j рассчитывается: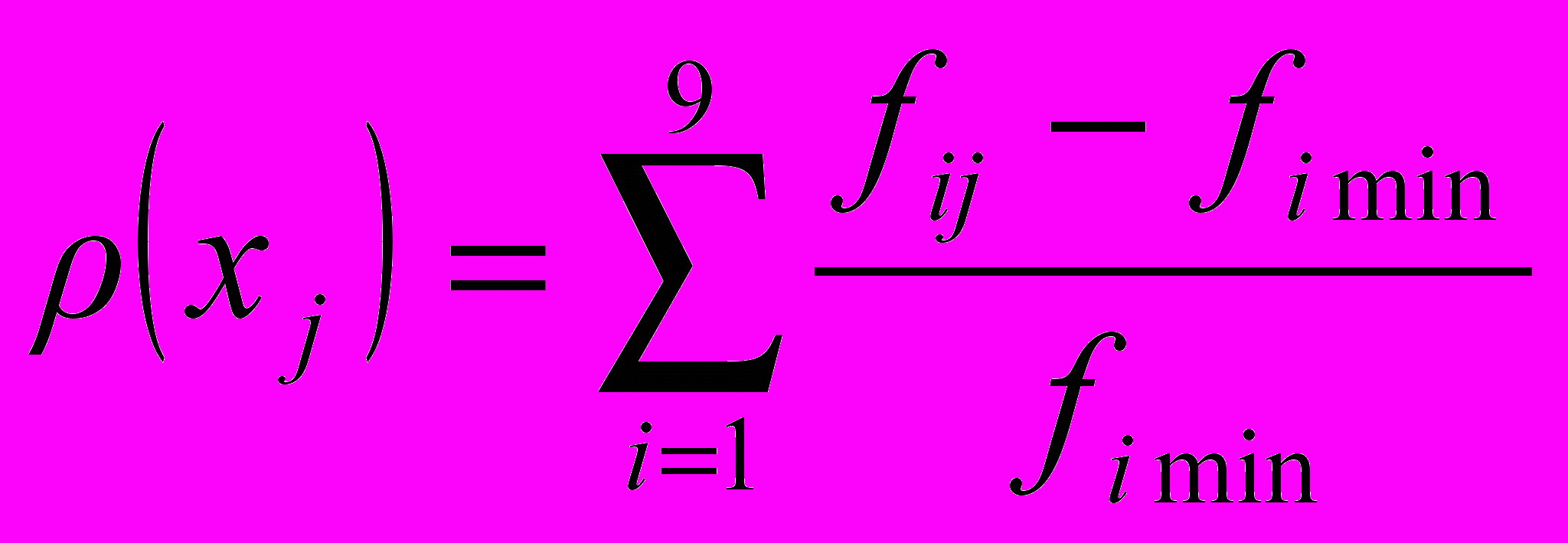

. (15)

Оптимальным является решение, расположенное как можно ближе к множеству идеальных оценок U, т.е. решение, имеющее наименьшую метрику.

При оптимальном проектировании механизма передвижения тележки прежде всего учитывается ее тип. Для консольных тележек, получивших распространение для однобалочных кранов, алгоритм выбора оптимальных параметров аналогичен выбору элементов привода механизма передвижения крана. Различие только в дополнительном проектировании поддерживающих колес от опрокидывания рамы тележки. Чаще всего они выбираются в виде конических колес, удерживающих раму тележки от опрокидывания за верхний пояс двутавра, устанавливаемого над стенкой главной балки с противоположной стороны опорного рельса.

При проектировании центрального привода передвижения тележки в алгоритме аналогичного привода механизма передвижения крана обнуляются критерии оптимальности f₆ и f₈.

Для формирования области возможных решений задачи оптимального проектирования механизма передвижения осуществляется перебор вариантов при дискретно изменяемых значениях оптимизируемых параметров. Для организации автоматизированного расчета были созданы базы данных, включающие в себя основные характеристики элементов привода. Основной цикл алгоритма построен на дискретном изменении диаметра ходового колеса D на интервале [D_min; D_max], при этом для каждого значения D выполняется подбор комплектующих и расчет привода по каждому варианту компоновки.

Каждому типу схем компоновки механизма передвижения, в зависимости от выбора типа привода, схемы электропривода и типа трансмиссии, присваивается номер варианта ns, представляющий собой переменную с четырьмя индексами: ns = ns(р, j, k, r). Значение переменной р определяет тип привода: центральный, раздельный, раздельных с формированием ходовых узлов. Значение переменной j предопределяет автоматизированное обращение к массиву двигателей; значение переменной k управляет обращение к массивам управляющих устройств; значение переменной r управляет обращением к серийно выпускаемым редукторам и, при необходимости, проектированию открытой зубчатой передачи или обращение к процедуре проектирования нового редуктора из условия оптимальности.

Алгоритм оптимального проектирование механизмов передвижения имеет ряд особенностей. Проектирование проводится для одной опоры из условия наибольшего давления на опору для случая, когда одна из грузовых тележек находится с номинальным грузом над этой опорой или на минимально возможном расстоянии от опоры. При этом учтена возможность выхода тележки на консоль (для козловых кранов) и возможность применения двух тележек, что необходимо учитывать при расчете нагрузки на опору. Расчет элементов приводов производится согласно существующим методикам.

Оптимизация балансирной подвески колес производится в подпрограмме на основе модификации метода Хука-Дживса по критерию металлоемкости. Рассматривается наиболее распространенная коробчатая конструкция балансиров. Переменной координатой при проведении исследований является высота балансира, назначаемая дискретно с заданным приращением ΔX, так как основная нагрузка на балансиры действует в вертикальной плоскости, поэтому ширину балансиров можно задавать по условиям компоновки. Толщина стенки назначается не менее 5 мм по условиям сварки.

Для того чтобы можно было использовать метод Хука-Дживса для решения задач с ограничениями, толщины поясов определяются методом перебора в отдельной процедуре, с учетом ограничений по условиям прочности, жесткости, устойчивости сжатых элементов сечения.

При определении нагрузки балансиров принимается, что усилие, действующее на опору, равномерно распределяется между тележками опоры. Нагрузка каждого балансира складывается из части нагрузки вышерасположенного балансира и давления ветра. Силой ветра можно пренебречь ввиду его малости, т.к. максимум нагрузки имеет место при рабочем состоянии крана. Распределение нагрузки между балансирами зависит от числа колес, на которые опирается нижерасположенный балансир.

Расчет исходных нагрузок и размеров балансиров при различном числе ходовых колес производится автоматизировано. Нумерация балансиров производится с верхнего балансира, расположенного под опорой. Схема распределения нагрузок на балансиры и размеры балансиров для различных схем расположения колес опор крана приведены на рис. 5.1. Для крановых тележек, перемещающихся по двухбалочным мостам, схема приложения нагрузки и размеры тележки приведены на рис. 5.1 д, ж, и.

Переменной координатой при проведении исследований является высота балансира X₁, задаваемая дискретно с заданным приращением ΔX. Толщина стенки балансира δ_с принимается минимальной (рис. 5.2) из расчетов по эквивалентным напряжениям при заданном коэффициенте запаса прочности (рис. 5.3) с учетом условий сварки. Высота балансира выбирается по минимуму металлоемкости m_б балансира, согласно модификации метода Хука-Дживса:

Х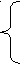₁+ΔX, если m_б ⁽ⁱ⁺¹⁾< m_б ⁱ,

X₁ =

Х₁, если m_б ⁽ⁱ⁺¹⁾≥ m_б ⁱ.

По методу Хука-Дживса движение к минимуму осуществляется с переменным шагом, уменьшающимся по мере приближения к минимуму целевой функции. Окончание исследования происходит при достижении минимального значения шага ε, назначаемого из условия получения необходимой точности решения.

Шаг движения к минимуму целевой функции Δ X корректируется согласно условию:

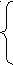ΔX, если m_б ⁽ⁱ⁺¹⁾< m_б ⁱ,

ΔX = -ΔX/2, если m_б ⁽ⁱ⁺¹⁾> m_б ⁱ,

0, если | ΔX|<ε.





Рис. 5.1. Схема распределения нагрузки, действующей на балансиры

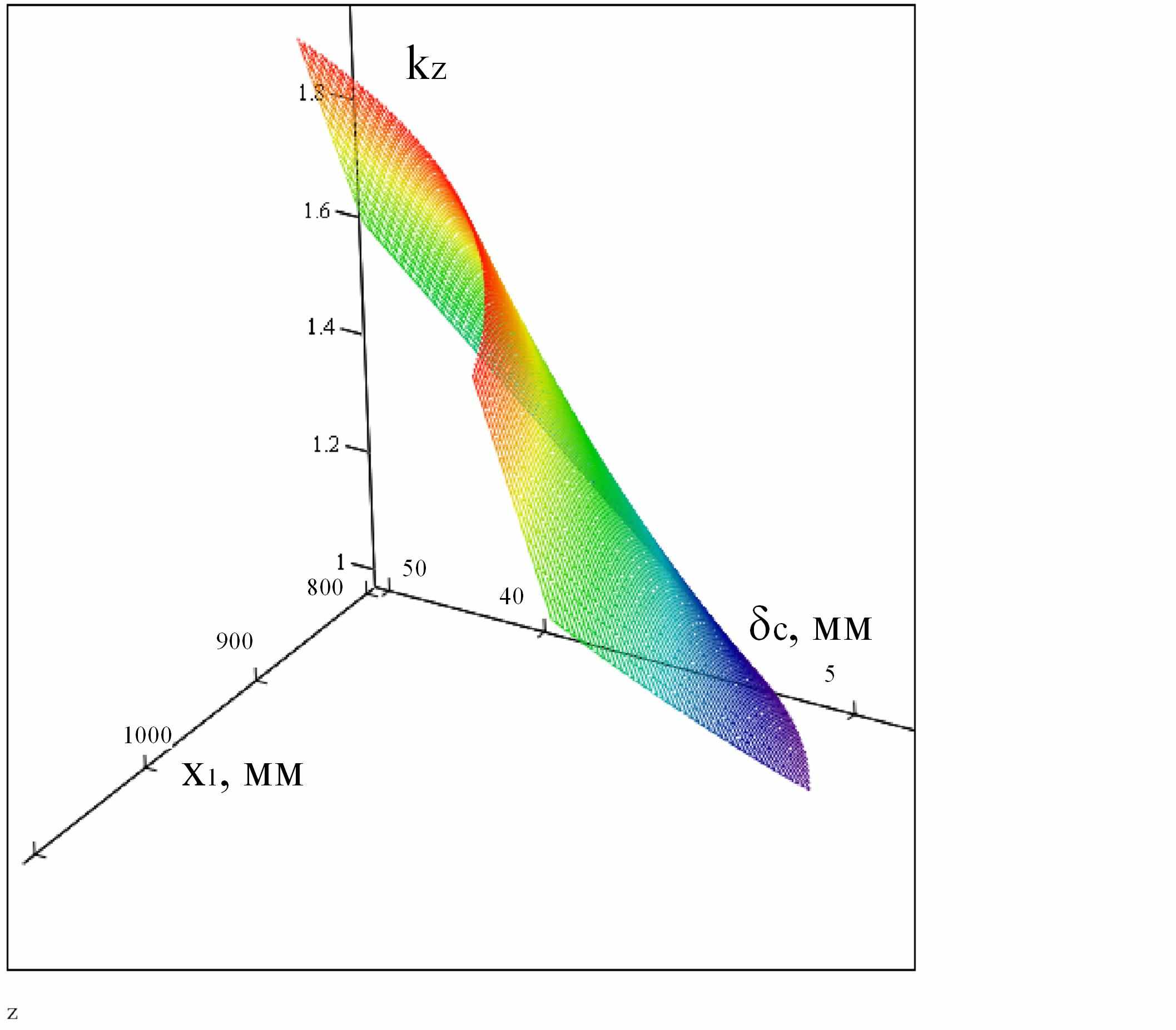
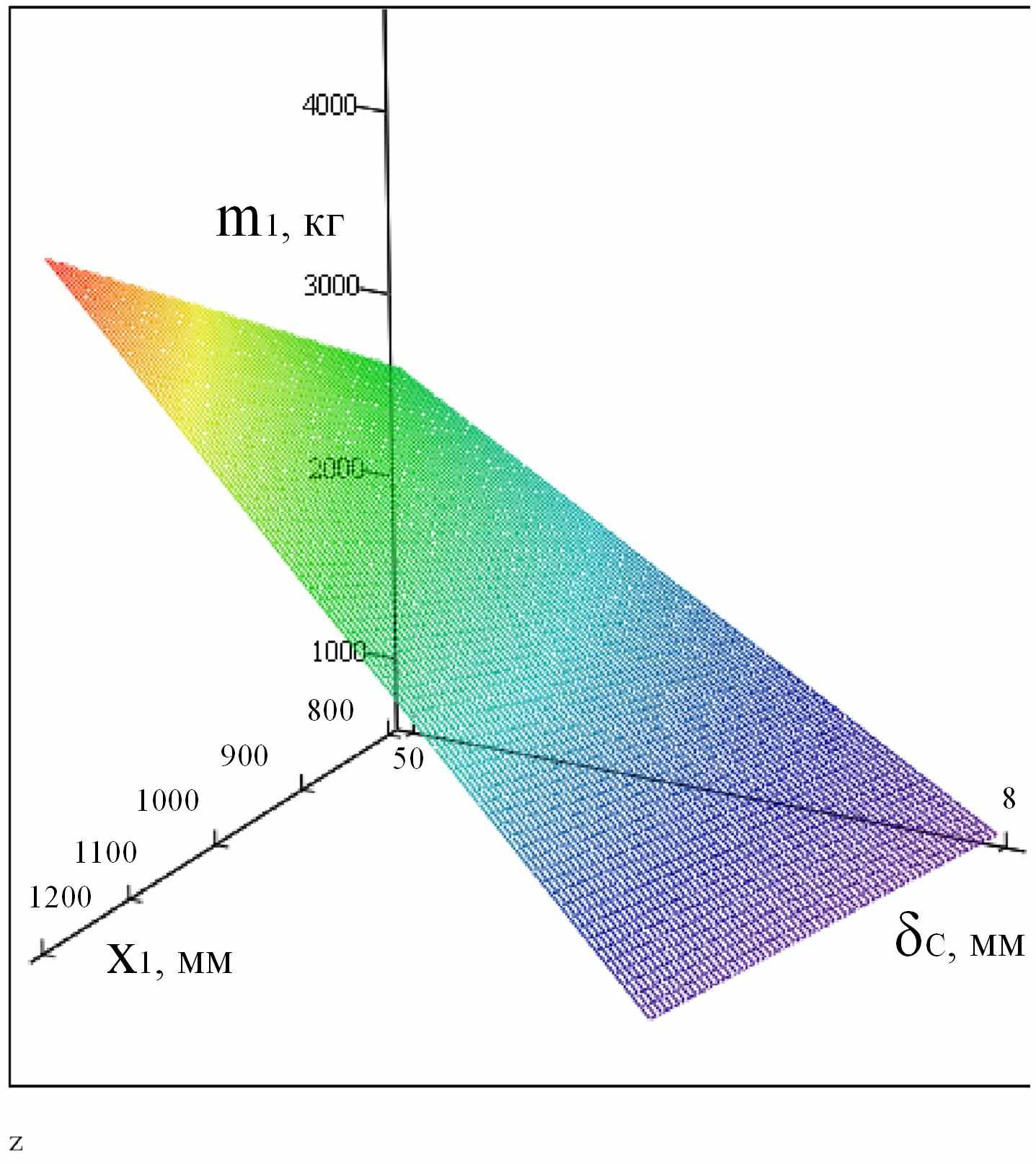
Рис. 5.2. Зависимость металлоемкости верхнего балансира механизма передвижения крана К2×180/50 от высоты балансира и толщины стенки

Рис. 5.3. Зависимость коэффициента запаса прочности по эквивалентным напряжениям верхнего балансира механизма передвижения крана К2×180/50 от высоты балансира и толщины стенки

В шестой главе предложена методика инженерного расчета оптимального проектирования механизмов подъема груза и механизмов передвижения кранов и крановых тележек, а также представлены результаты вычислительных экспериментов в разработанной программной среде автоматизированного проектирования, построенной на основе предлагаемого теоретического подхода.

В методике реализуется метод многокритериальной оптимизации, предложенный автором. Расчет основан на принципе Парето и впервые доведен до уровня инженерного расчета для механизмов кранов пролетного типа.

Указанный расчет начинается с анализа технического задания, из которого для заданного типа крана и его назначения выбираются все основные исходные данные для проектирования: группа режимов работы крана и механизма, грузоподъемность и скорость рабочих движений, конструктивное исполнение металлоконструкции и ее масса, конструкция грузовой тележки и их количество. В зависимости от назначения крана определяется потребность в проектировании многоскоростного привода. согласно классу ответственности крана назначается степень защиты от отказов элементов привода, заключающаяся в количественной и качественной комплектации механизмов наиболее надежными с точки зрения отказов элементами: двигателями, тормозами, приборами безопасности. Так для кранов атомной энергетики требуется по концепции безопасности не менее трехкратной степени защиты.

Поскольку по предложенной методике многокритериальной оптимизации необходимо создать область возможных решений по типам двигателей и систем управления, типам редукторов, барабанов, тормозов, муфт, канатов, в работе предложены методики и алгоритмы автоматизированного расчета всех вариантов, для чего разработаны базы данных вышеперечисленных элементов, которые, однако, могут дополняться при необходимости новыми решениями.

Для оптимального проектирования механизма подъема груза разработан алгоритм, структурная схема которого представлена на рис.6. Оптимальное проектирование механизма выполняется в три этапа. На первом этапе формируется область возможных решений задачи: для каждого значения кратности на интервале от 1 до 24 рассчитываются все возможные схемы комплектации механизма подъема по типам двигателей, передаточных механизмов, управляющих устройств, муфт, тормозов. Для механизмов режима нагружения 1М-3М предусмотрена возможность перехода к схемам с открытой зубчатой передачей согласно условию (9). По критерию минимума металлоемкости для каждой схемы рассчитаются оптимальные параметры барабана. Для каждого возможного решения определяются составляющие векторного критерия оценки качества решения (2). На втором этапе по значениям векторного критерия согласно условию (3) формируется область парето-оптимальных решений. На третьем этапе формируется идеальный вектор (4) и для каждого парето-оптимального решения по формуле (5) рассчитывается метрика, по минимальному значению метрики определяется оптимальное решение задачи. При близких значениях метрики (Δρ = 0,001) окончательное решение принимает конструктор.




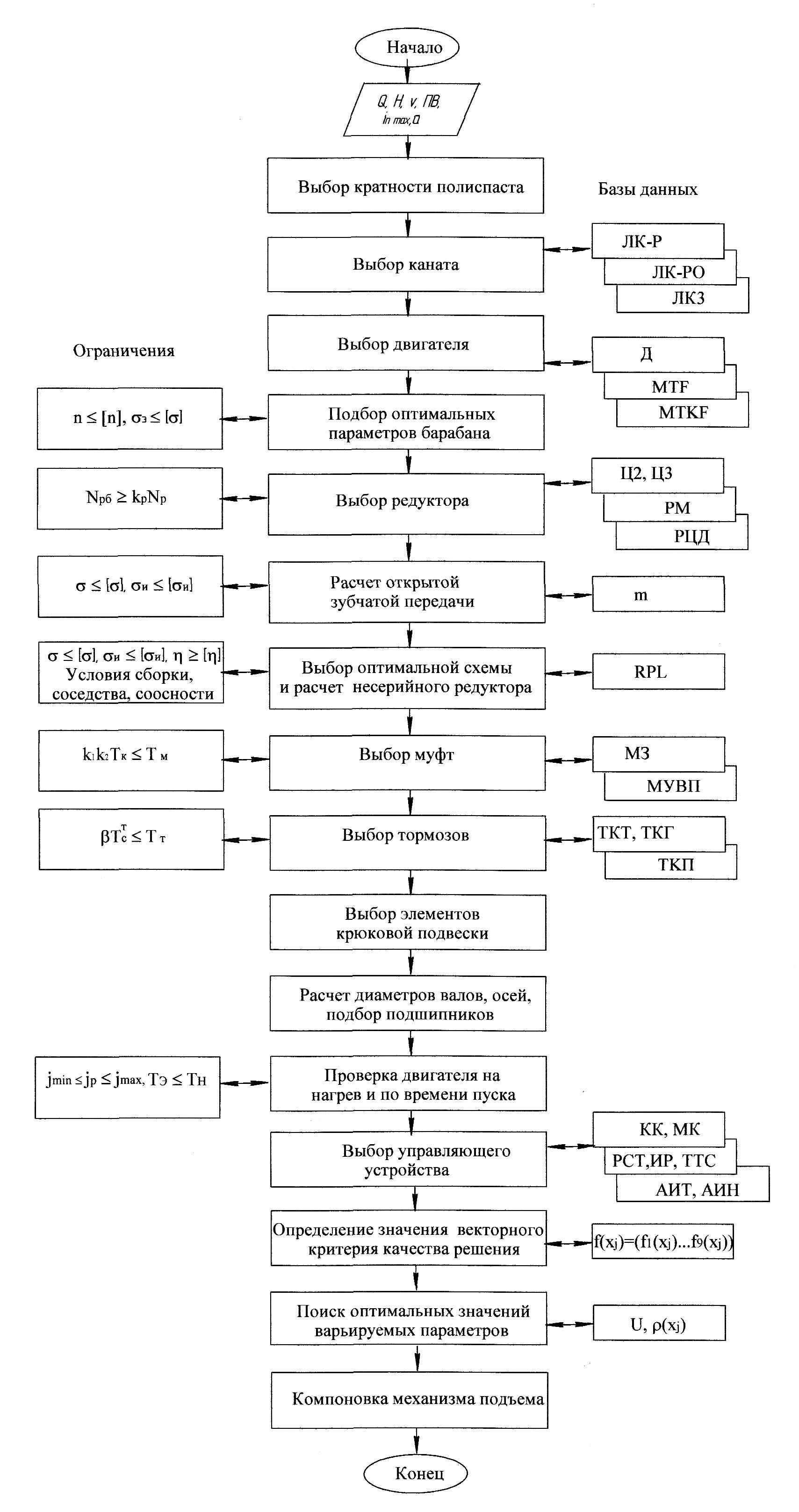
Рис. 6. Схема алгоритма оптимального проектирования

механизма подъема груза

Алгоритм включает в себя основную программу, которая является управляющей и подпрограммы: CRAT подбора диаметра каната и определения кратности полиспаста, DVIG, MUV, TOR, PODV – выбора двигателя, муфт, тормозов, подвески, для чего составлены соответствующие базы данных; RED, ZUB, INV – выбора редуктора, расчета и определения угла зацепления открытой зубчатой передачи; BAR - проектирования барабана с минимальной массой, для чего разработаны подпрограмма GB – определения силы веса барабана, DBAR - исследования влияния диаметра барабана на его металлоемкость; NAPR - определения эквивалентного напряжения в стенке барабана с учетом напряжений сжатия, изгиба и кручения; подпрограммы VAL, OS, POP - расчета валов, осей, подшипниковых опор барабана; RDPN - проверки выбранного двигателя по условиям пуска и нагрева; UPR – выбора управляющего устройства электропривода; MATPAR – формирования области парето-оптимальных решений и выбора оптимального решения на основе сужения данной области.

По предложенной выше методике выполнен проект модернизации механизма главного подъема полярного крана КМ 320/160/ 2×70 Балаковской АЭС. Механическая часть существующей схемы механизма главного подъема (рис.7 а) представляет собой два электродвигателя постоянного тока мощностью 40 кВт М1 и М2, которые через редуктор передают вращение на барабан. Редуктор состоит из дифференциальной части, включающей колеса z₁, z₂, z₃ и водило Н, и тихоходной части, представляющей собой трехступенчатую косозубую передачу, включающую колеса z₄, z₅, z_5’, z₆, z_6’, z₇. Передача вращения от двигателя М2 осуществляется через рядовую зубчатую передачу, состоящую из колес z₈, z₉, z₁₀, числа зубьев которой подобраны таким образом, чтобы двигатель М2 обеспечивал подъем номинального груза с заданной скоростью в случае отказа двигателя М1. Для регулирования скорости подъема в диапазоне от 0,1 до 1 м/мин в качестве управляющих устройств применяются тиристорные преобразователи постоянного тока. Применяется полиспаст с кратностью i = 10.

Существующая схема механизма главного подъема имеет ряд недостатков. Не выполняется концепция промышленной безопасности работы АЭС, согласно которой должна выполняться тройная защита при отказе любого механизма. Мощности применяемых двигателей не обеспечивают возможность подъема номинального груза 320 т при работе одного двигателя, для подъема номинального груза используется одновременная работа двух двигателей, что также противоречит концепции промышленной безопасности работы АЭС. Применяемая в существующей схеме тихоходная зубчатая передача, вес которой составляет 9750 кг, а габаритные размеры 3100×1150×1700 мм, вызывает сложности при компоновке и с учетом предлагаемых в работе методик может быть существенно реконструирована в сторону снижения габаритов и массы.





Рис. 7


Рассматриваемый механизм имеет следующие характеристики: грузоподъемность 320 т, высота подъема 45 м, номинальная скорость подъема 1 м/мин, посадочная скорость 0,1 м/мин, группа режима работы 4М.

Для обеспечения концепции промышленной безопасности работы АЭС предложено включить в схему третий двигатель М3 малой мощности, подключенный по схеме с микроприводом (рис. 7 б), что позволит обеспечить при незначительных затратах дополнительную защиту при отказе двигателей М1 и М2. Мощность двигателей М1 и М2 должна обеспечивать возможность работы механизма с номинальным грузом при работе каждого из двигателей.

При формировании области возможных решений Х задачи оптимального проектирования рассматривались варианты компоновки механизма при различных значениях кратности полиспаста на интервале [i_min, i_max]. В качестве минимального значения было принято значение кратности, при котором можно было подобрать канат. Рассматривался канат стальной двойной свивки типа ЛК-РО конструкции 6×36 (1+7+7/7+14)+1 о.с. (ГОСТ 7668-80). Применительно к решению данной задачи i_min= 8. Максимальное значение кратности i_max = 13 ограничено заданными конструктивно предельными значениями диаметра и длины барабана: D_Бmax= 2500 мм, L_Бmax= 6800 мм.

При неизменной дифференциальной части редуктора, для каждого значения кратности рассматривались следующие схемы компоновки тихоходной части: компоновка по схеме базового варианта; трехступенчатая передача, составленная из трех передач типа 2k-h однорядных (рис. 7 б) – А+А+А, согласно принятой классификации; двухступенчатая передача, составленной из двух передач типа 2k-h (рис. 7 в) – С+А; передача типа 3k (рис. 7 г). Параметры зубчатых передач определялись в отдельной подпрограмме из исследования на оптимальность. Для каждого значения кратности полиспаста определялись оптимальные параметры барабана по предложенной модификации метода покоординатного спуска Хука-Дживса для решения задач с ограничениями из условия минимума металлоемкости, при решении были приняты: первоначальное значение шага изменения диаметра барабана Δ D_Б = 100 мм, минимальное значение шага ε = 10 мм.

Путем удаления неулучшаемых решений на области возможных решений Х была сформирована область парето-оптимальных решений задачи Р_f(X), состоящая из 10 решений. Основные параметры данных решений приведены в таблице 3: i – кратность полиспаста; А – экономическая оценка; D_Б – диаметр барабана; m_Б – масса барабана; m_к – масса канатов; тип передачи тихоходной ступени редуктора; η_тс, m_тс, L_тс – коэффициент полезного действия, масса и длина тихоходной ступени редуктора; ρ – значение метрики. В первой строке таблицы 3 приведены параметры базового варианта.

Таблица 3

Основные параметры парето-оптимальных решений

при проектировании механизма подъема

№	i	А, тыс.руб	DБ, мм	mБ, кг	mк, кг	тип передачи	ηтс	mтс, кг	Lтс, мм	ρ
б/в	10	282,006	2500	9648	6499	-	0,86	9750	3100	2,097
1	10	317,272	2180	8628	6499	C+A	0,755	8800	1450	0,804
2	10	317,272	2180	8628	6499	А+А+А	0,93	9150	1570	0,759
3	11	317,272	2240	8267	6411	С+А	0,77	8000	1420	0,591
4	11	317,272	2240	8267	6411	A+A+A	0,93	8950	1560	0,665
5	11	435,331	2240	8267	6411	3k	0,72	7200	1300	0,855
6	12	317,272	2320	8362	6318	A+A+A	0,932	7200	1530	0,383
7	12	435,371	2320	8362	6318	3k	0,73	6900	1290	0,789
8	13	317,272	2460	8644	6160	A+A+A	0,932	8000	1510	0,492
9	13	317,272	2460	8644	6160	C+A	0,783	7800	1370	0,515
10	13	435,371	2460	8644	6160	3k	0,72	8100	1330	1,014

В качестве оптимального принят шестой вариант решения, выполненный по схеме рис. 7 в, т.к. он имеет минимальное значение метрики, т.е. расположен ближе всех остальных решений к идеальному вектору в многокритериальном пространстве. При этом получено: снижение металлоемкости барабана на 13 %; металлоемкости и габаритных размеров тихоходной ступени зубчатой передачи соответственно на 26% и 58 %. Результаты расчетов приведены в приложении 5 диссертации.

Структурная схема алгоритма оптимального проектирования механизмов передвижения кранов и крановых тележек представлена на рис. 7. Формирование области возможных решений задачи выполняется на первом этапе при дискретном изменении диаметра ходового колеса: при проектировании механизма передвижения крана от 250 мм до 1000 мм; при проектировании механизма передвижения тележки от 250 мм до 500 мм. Для каждого значения диаметра колеса рассчитываются все возможные схемы компоновки механизмов по типу привода, типу электродвигателей, трансмиссий и систем управления. Формирование области парето-оптимальных решений выполняется на втором этапе в зависимости от значений составляющих векторного критерия (13) по условию (3). Из минимальных значений критериев оптимальности на третьем этапе формируется идеальный вектор (14) и рассчитывается метрика (15) для каждого парето-оптимального решения, по минимальному значению которой определяется оптимальное решение задачи.

Для организации работы с программой оптимального проектирования механизмов передвижения кранов и крановых тележек в методике инженерного расчета даны рекомендации по выбору типа ходовых колес и рельсов из базы данных программы. Предложены возможности сокращения времени расчета за счет предварительного выбора схемы привода, исходя из технического задания на проектирование и типа крана.

Алгоритм построен по модульному принципу и включает в себя основную программу, которая является управляющей и подпрограммы: определения опорных давлений крана ROD (опорных давлений крановой тележки RODT); числа ходовых колес ZK; числа приводных колес в опоре и количество движителей привода ZKP; выбора двигателя DVIGP; управляющего устройства электропривода UPRР; выбор схемы и расчет трансмиссии выполняется в процедуре RED. Параметры открытой зубчатой передачи рассчитываются в процедуре ZUBР. Выбор оптимальной схемы и расчет вновь проектируемого редуктора выполняется в процедуре RPL. Параметры муфт и тормозов выбираются в подпрограммах MUV, TOR.

Оптимизация балансирной схемы по металлоемкости производится в процедуре BAL: в процедуре PB определяется нагрузка; в процедуре LBI длина балансиров; в процедуре MI изгибающий момент; в процедуре RGB подбирается сечение, определяется металлоемкость балансиров и проверяются условия прочности. Минимизация массы металлоконструкции производится модифицированным методом Хука-Дживса в процедуре DXP, где дискретно с заданным шагом определяется высота балансира и подбирается толщина поясов из условия прочности, которые проверяются в процедуре RGB. Исследования заканчиваются после прекращения убывания веса металлоконструкции балансиров и при заданном минимальном значении шага движения ε.



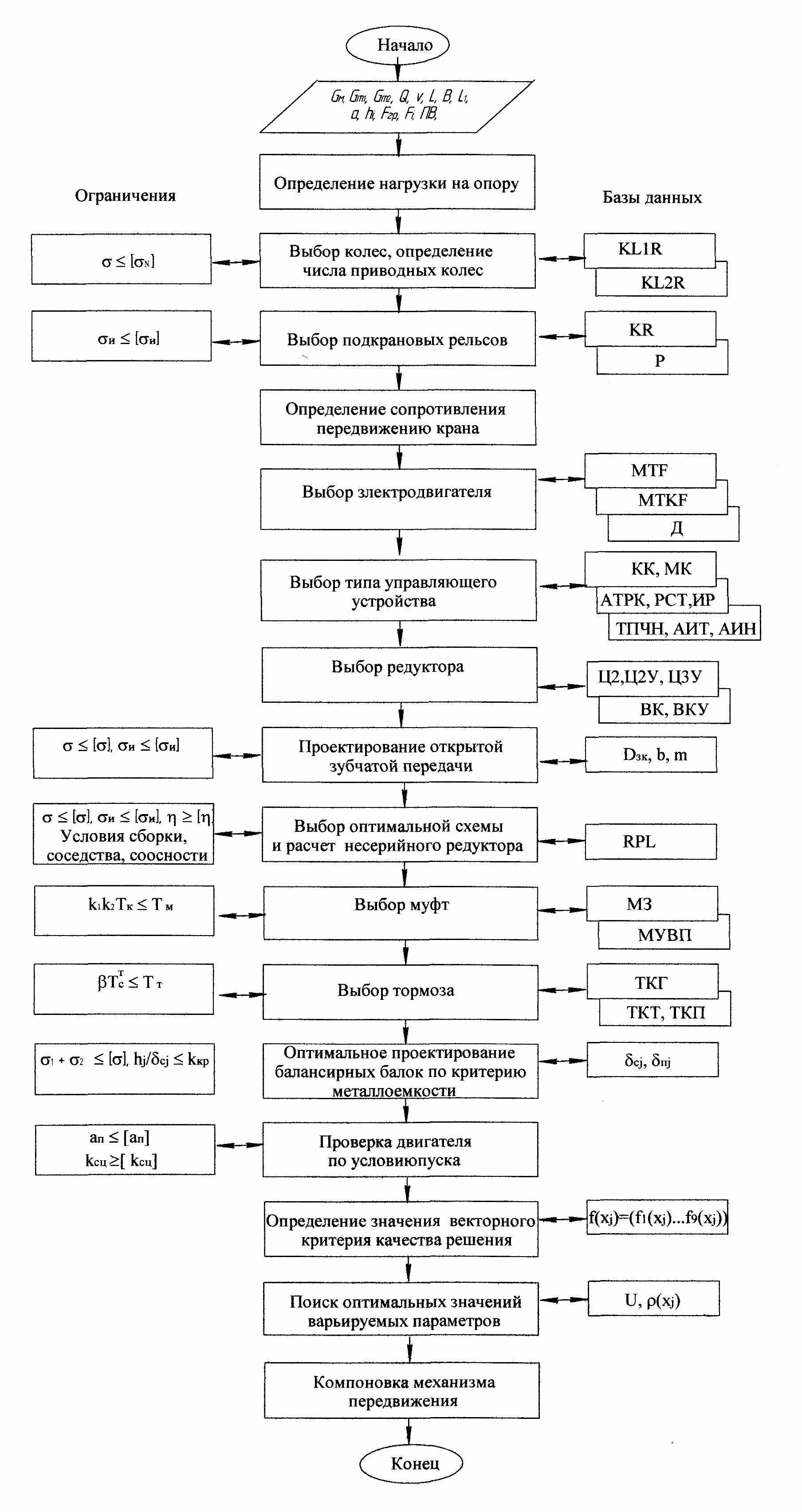
Рис. 7. Схема алгоритма оптимального проектирования механизмов передвижения кранов и крановых тележек

По окончании выбора всех комплектующих механизма проводится проверка двигателя по условиям пуска в процедуре RDP и, при необходимости, пересчитываются параметры механизма.

По полученным значениям расчетных параметров на каждом шаге работы алгоритма в процедуре МАТРАRР формируется матрица парето-оптимальных решений, идеальный вектор, рассчитываются метрики и выбирается оптимальное решение задачи.

В соответствии с предложенной методикой был выполнен проект модернизации механизма передвижения козлового крана К2×180/50 Саратовской ГЭС, схема которого представлена. Кинематическая схема существующего механизма передвижения представлена на рис. 8. Рассматриваемый механизм имеет следующие характеристики: масса крана 1106880 кг; грузоподъемность основного механизма подъема 360 т, вспомогательного 50 т; скорость передвижения крана 33 м/мин; пролет крана 26 м.



Рис. 8


П
Рис. 8
ри формировании области возможных решений задачи оптимального проектирования рассматривались три варианта компоновки механизма передвижения при различных значениях диаметра ходового колеса на интервале от 500 до 1000 мм: с определением необходимого числа ходовых колес по условию сцепления; с приводом на каждое колесо с применением серийно выпускаемых редукторов; с приводом на каждое колесо с применением оригинальных планетарных редукторов типа 3k, параметры которых определялиcь отдельно из исследования на оптимальность. Для каждого значения диаметра ходового колеса определялись оптимальные параметры балансиров по критерию минимума металлоемкости по предложенной модификации метода Хука-Дживса. Путем удаления неулучшаемых решений на области возможных решений была сформирована область парето-оптимальных решений, а также идеальный вектор. Для каждого парето-оптимального решения была рассчитана метрика, согласно методике, предложенной автором. По минимальному значению метрики определено оптимальное решение задачи проектирования.

Минимальное значение метрики получила схема с раздельным приводом на каждое колесо рис. 9, с применением оригинальных планетарных редукторов, имеющая следующие характеристики: диаметр ходового колеса 800 мм, число колес в одной опоре – 6.




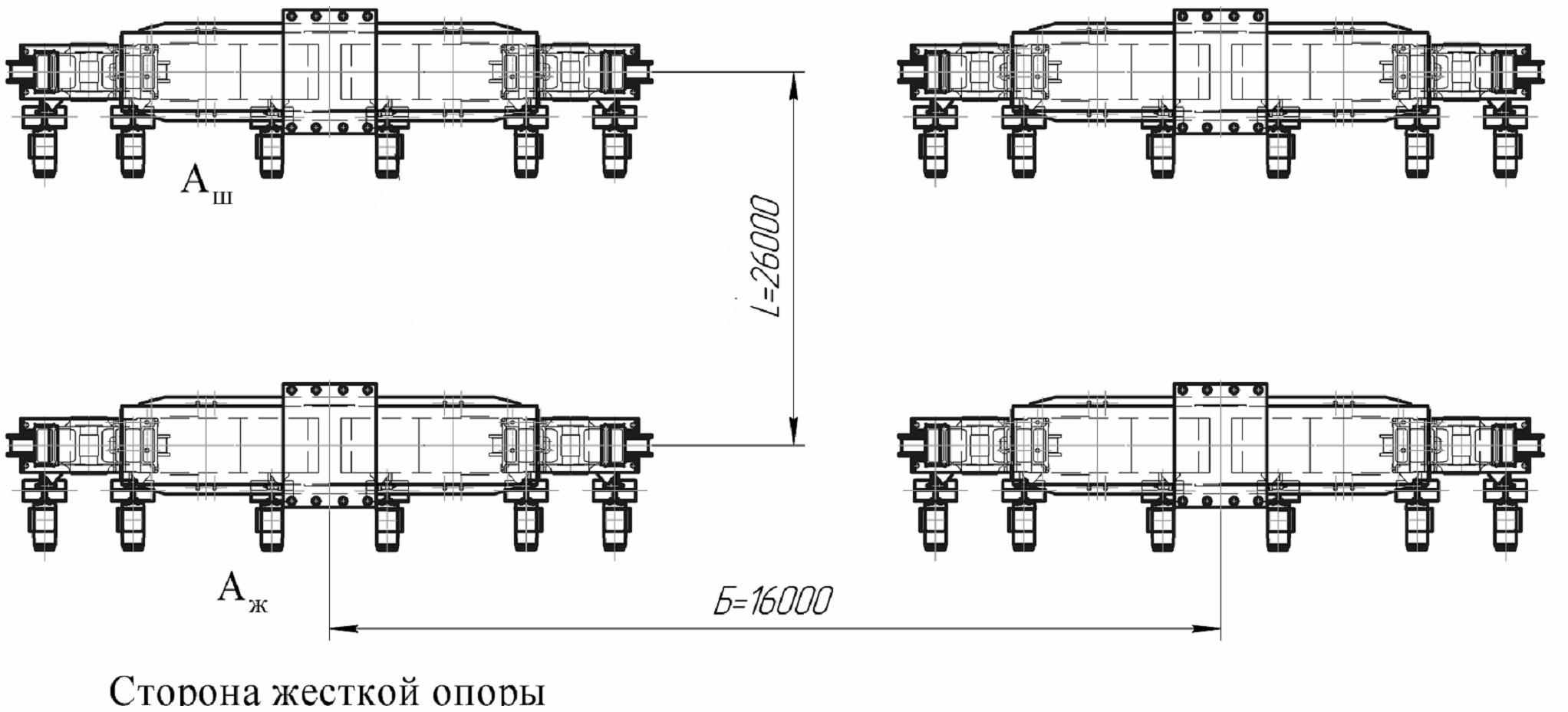
Рис. 9


По сравнению с базовым вариантом металлоемкость балансиров снизилась с 15,75 т до 8,647 т – на 45,1%; металлоемкость механизма передвижения в целом с 143,930 т до 70,307 т – на 51,1%. Снижение установленной мощности составило 4,5%: установленная мощность базового варианта равна 176 кВт - 8 двигателей по 22 кВт; оптимального варианта 168 кВт - 24 двигателя по 7 кВт. Результаты исследования приведены в приложении 6 диссертации.


ОСНОВНЫЕ ВЫВОДЫ И РЕЗУЛЬТАТЫ РАБОТЫ


В диссертации решена крупная научная проблема, имеющая важное хозяйственное значение для развития прикладной теории оптимального и автоматизированного проектирования приводов грузоподъемных машин, а именно: разработан новый теоретический подход к оптимальному и автоматизированному проектированию механизмов кранов пролетного типа с применением метода многокритериальной оптимизации.

В ходе выполнения работы получены следующие результаты, имеющие как научное, так и практическое значение:

1. Для решения задач оптимального проектирования приводов механизмов кранов пролетного типа, когда критерии оптимизации имеют различную природу, и недостаток в одном показателе не может быть скомпенсирован за счет достоинств другого, наиболее применимым является метод многокритериальной оптимизации, построенный на принципе Эджворта-Парето. В качестве метода сужения области парето-оптимальных решений применительно к данному типу задач, с дискретно изменяемыми параметрами оптимизации, предложена разработанная модификация метода целевого программирования.
   

Определение оптимальных параметров металлоконструкций барабана механизма подъема, а также балансиров механизма передвижения кранов и крановых тележек по критерию минимума металлоемкости предложено проводить модифицированным методом Хука-Дживса для решения задач оптимизации с ограничениями: при оптимизации все ограничения выполнять в подпрограммах, а основную управляющую программу построить по методу Хука-Дживса. В алгоритм Хука-Дживса ввести модификацию, заключающуюся в том, чтобы вместо изменения всех параметров «по образцу», изменять один, соответствующий минимуму целевой функции.

2. Для применения метода Парето к проектированию механизмов подъема предложен методика формирования области возможных решений при дискретном изменении кратности полиспаста на заданном интервале с расчетом всех возможных вариантов компоновки привода для каждого значения кратности, с подбором всех элементов: двигателей, управляющих устройств, редукторов, тормозов, муфт в зависимости от назначения крана, механизма и групп режима работы. Для выделения множества Парето-оптимальных решений разработан векторный критерий оценки качества решения, включающий в качестве составляющих девять критериев оптимальности: экономическую оценку двигателя и управляющего устройства, стоимость и габаритный размер передаточного механизма, массы барабана, каната, крюковой подвески, муфт, тормозов и коэффициент полезного действия механизма. Предложена модификация метода целевого программирования для сужения области парето-оптимальных решений с обоснованием выбора идеального вектора в многокритериальном пространстве, аналитической зависимостью для расчета метрики, по минимальному значению которой выбирается оптимальное решение.
   

Область возможных решений при проектировании механизмов передвижения крана и крановой тележки формируется в зависимости от типа и диаметра ходового колеса: для разных типов привода, двигателей, управляющих устройств, муфт, тормозов, трансмиссий, балансирной подвески колес, с учетом назначения и групп режима работы. Множество парето-оптимальных решений строится на основе векторного критерия оценки качества решения, включающего: экономическую оценку двигателя и управляющего устройства, стоимость и массу трансмиссии, массы балансиров, колес, муфт, тормозов рельсов и коэффициент полезного действия механизма. Оптимальное решение выбирается, как и для механизма подъема, по минимальному значению метрики, для расчета которой предложена аналитическая зависимость.

3. На основании предложенных математических моделей и критериев оптимизации разработаны методика и алгоритмы оптимального проектирования механизмов. Составлены базы данных всех комплектующих механизмов. Управление работой алгоритма оптимального проектирования механизма подъема осуществляется с помощью трехиндексной управляющей переменной, соответствующей схеме компоновки, значение индексов которой предопределяют автоматизированное обращение к массивам: двигателей, управляющих устройств и редукторов. Управление алгоритмом оптимального проектирования механизмов передвижения кранов и крановых тележек производится четырехиндексной переменной, первый индекс которой выбирает схему привода, а значения остальных индексов предопределяют автоматизированное обращение к массивам: двигателей, управляющих устройств и редукторов.

Для возможности автоматизированного проектирования трансмиссий механизмов кранов с большими передаточными отношениями разработана методика компоновки приводов как серийно выпускаемыми редукторами с переходом при необходимости к схемам с открытой зубчатой передачей для механизмов режима нагружения 1М-3М, так и вновь проектируемыми соосными редукторами с большими передаточными отношениями, с дальнейшим сравнением решений по критериям оптимальности.

4. Задача проектирования оригинального редуктора является многовариантной, поэтому для выбора оптимального решения предложено использовать метод Парето. Для формирования области возможных решений задачи разработана методика автоматизированного выбора схем соосных зубчатых передач на основе предложенного метода графического синтеза, позволяющего в зависимости от величины и знака передаточного отношения, а также качественных требований, предъявляемых к проектируемой передаче: равной контактной прочности, равной изгибной прочности, выбрать схему и определить параметры зубчатых колес. Составляющими векторного критерия оценки качества решения являются: масса и габаритный размер передачи, коэффициент перекрытия зубьев и коэффициент полезного действия. Для выбора оптимального решения получены аналитические соотношения построения идеального вектора и расчета метрики в соответствии с методом целевого программирования.

5. Разработан алгоритм оптимального проектирования соосных зубчатых передач, построенный по модульному принципу. Основной цикл алгоритма основан на дискретном изменении передаточного отношения с заданным шагом с точностью ± 2% от заданной величины.

6. В методике инженерного расчета изложен принцип организации многокритериальной оптимизации проектирования механизмов кранов пролетного типа на основе принципа Эджворта-Парето:

- на первом этапе формируется область возможных решений задачи: для механизмов подъема эта область включает все возможные решения для кратности полиспаста от 1 до 24 со всеми вариантами по двигателям, трансмиссиям, системам управления; для механизмов передвижения область возможных решений формируется в зависимости от типов и значений диаметров ходовых колес от 250 мм до 1000 мм со всеми вариантами по схемам привода, типам двигателей, трансмиссий и систем управления;

- на втором этапе путем исключения из области возможных решений не парето-оптимальных составляется область парето-оптимальных решений в соответствии с предложенными векторными критериями оценки качества решения;

- на третьем этапе выбирается оптимальное решение по минимальному значению метрики в соответствии с предложенной модификацией метода целевого программирования.

Если несколько решений получают близкие значения метрики, окончательное решение принимает конструктор, исходя из назначения и условий работы крана.

Предложенные теоретические основы доведены до конкретных систем проектирования механизмов кранов пролетного типа и апробированы применительно к реальной практике проектирования, годовой экономический эффект составил 1 млн. 680 тыс. рублей в год.


Основные положения диссертации опубликованы в следующих работах: