Geum.ru

Отчет по дисциплине: "Информатика"

Вид материалаОтчет

Содержание


Вывод теории Вывод консультации
ВЫХОДОписание программы
Введите через пробел значения х(1) и у(1): 1.4 0.9523
Подобный материал:
Министерство образования Российской Федерации

Алтайский государственный технический университет


Отчет по дисциплине: "Информатика”


Курсовая работа


"Интерполяция каноническим полиномом"


Выполнил:

студент гр. Э-13

Барсуков В.


Проверил:

ст. преподаватель

Деев Ю. В


г. Барнаул 2002 г.

Постановка задачи:

Данная программа предназначена для широко распостраненных в научно-технических расчетах дифференциальных уравнениях, которые часто имеют решения в виде ортогональных многочленов Лагерра, Лежандра, Эрмита и Чебышева. Итерполяция заключается в нахождении значений функции у(х), заданной n узлами, в промежитках между ними. При этом функция заменяется тем или иным полиномом Р(х), значения которого в узлах совпадают со значениями у(х).


Описание метода решения:

В данной программе использовался метод, реализующий интерполяцию с помощью интерполяционного полинома Лагранжа

Y(x)=B0(y)+B1(y)(x-x0)+B2(y)(x-x0)(x-x1)+…

+Bn(y)(x-x0)(x-x1)…(x-xn-1)

где коэффициенты B0(y)%Bn(y) являются функциями ординат у0% уn . Алгоритм их вычисления по схеме Эйткена поясняется таблицей№1. При известных B0(y)%Bn(y) вычисление у(х) для любого х можно произвести по схеме Горнера.

Таблица№1





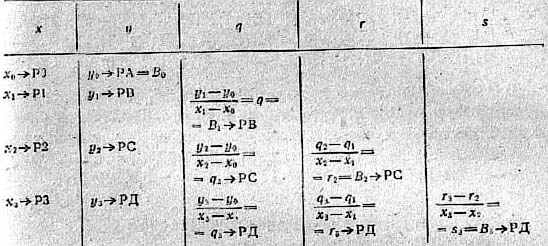
Блок-схема:


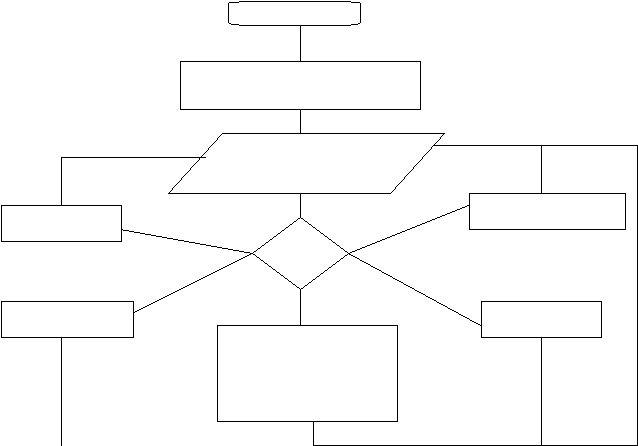ВХОД


Титульный лист


Выбор варианта работы

Программы

Вывод теории Вывод консультации


N=1 N=3

N

N=4 N=4


Выход N=2

Вывод справки

Основная программа пиот


в которой высчиты-

ваются коэффициенты


ВЫХОД


Описание программы:

Программа состоит из нескольких процедур. В процедуре Proga содержится основная часть программы(2-ой пункт меню), в которой и вычисляются коэффициенты. Процедура Shad используется, как вспомогательная для процедуры SingleRam, в которой создается рамка для пунктов меню.

Процедура Txt нужна для вывода текстов теории, справки и консультации постранично. Файл с именем theory.txt один, но он делится на 3 части, для каждой из которых создана сигнальная строка, которая передается процедуре в качестве параметра. Как только процедура находит строку, совпадающую со строкой, переданной в качестве параметра, то она начинает вывод текста на экран.

В основной программе содержится титульный лист, а так же меню выбора.


Текст программы:


Program Slava;

Uses Crt;

Var

ch :Char;

n,n1 :Integer;

s :array [1..5] Of String;

Procedure Proga;

{Сама программа - 2-ой пункт меню}

Var

n,i,j,k :Integer;

x,y,a,q :Array [1..10] Of Real;

c :Char;

Begin

c:='y';

While (c<>'n')and(c<>'N')Do

Begin

Clrscr;

Writeln(' Интерполяция каноническим полиномом');

Writeln;

TextColor(3);

Write('Введите кол-во узлов функции: ');

Readln(n);

For i:=1 to n do

Begin

Write('Введите через пробел значения х(',i-1,') и у(',i-1,'): ');

Readln(x[i],y[i]);

End;

a[1]:=y[1];k:=2;

For i:=1 to n do q[i]:=y[i];

For i:=2 to n do

Begin

For j:=i-1 to n do

q[j+1]:=(q[j+1]-q[k-1])/(x[j+1]-x[k-1]);

a[i]:=q[i];k:=k+1;

End;

TextColor(2);

Writeln('Коэффициенты полинома:');

For i:=1 to n do writeln('B(',i-1,')=',a[i]:4:4);

Writeln('Еще раз?(y/n)');

c:=readkey;

End;

End;

procedure shad(i,j:byte);

{Процедура для выбора рамки}

type scrarray=array[0..25,1..160] of byte;

var

Fn,Cl:byte;

screen:scrarray absolute $b800:$0000;

begin

Dec(j);

Fn:=trunc(screen[j,i*2]/16);

Cl:=screen[ j,i*2]-Fn*16;

If Fn<8 then Fn:=0 else Fn:=Fn-8;

if Cl<8 then Cl:=8 else Cl:=Cl-8;

screen[j,i*2]:=Fn*16+Cl;

end;

Procedure SingleRam(x1,y1,x2,y2,ch:byte);

{Процедура, создающая рамку, используя данные процедуры shad}

var

i:shortint;

s,p:string[80];

Begin

s:='';

while length(s)<(x2-x1-3) do s:=s+'=';

Gotoxy(x1,y1) ;write (' -',s,'¬ ');

p:='';

while length(p)<(x2-x1-3) do p:=p+' ';

for i:=(y1+1) TO (Y2-1) do

begin

Gotoxy(x1,i);write(' ¦',p,'¦ ');

end;

Gotoxy(x1,y2);

write(' L',s,'- ');

IF CH=1 THEN BEGIN

FOR I:=(X1+2) TO (X2+2) DO SHAD(I,Y2+1);

FOR I:=(Y1+1) TO Y2 DO

BEGIN

SHAD(X2+1,I);

SHAD(X2+2,I);

END;

END;

END;

procedure txt(saw:string);

{Процедура вывода теории, справки и консультации на экран}

label exx2;

var

i,j,qwer,k18 :word;

as :char;

asds :String;

f :Text;

mn :boolean;

begin

Assign(F,'theory.txt');

Reset (F);

TextAttr:=$6F;

For I:=0 to 275 do Write (' ');

GOTOXY(0,0);write('');

TextAttr:=$3C;

SingleRam(3,1,77,5,1);

TextAttr:=$3d;

gotoXY(29,3);write('Текст');

TEXTATTR:=$3c;

SingleRam(3,21,77,23,1);

TextAttr:=$3d;

gotoXY(18,22);write('КОГДА ПРОЧТЕТЕ, НАЖМИТЕ В В О Д');

Window (5,8,77,19);

TextAttr:=$0E;

ClrScr;

Window (5,8,77,18);

J:=0;qwer:=1;asds:='';k18:=0;mn:=false;

while not(mn) do begin

readln(f,asds);

if asds=saw Then k18:=1;

if k18<>0 then mn:=true;

end;

While qwer<72 do

Begin

Read(F,Ch);

Write (Ch);

If Ch=#13 then Inc(J);

If J=2 then

Begin

as:=readkey;

If as=#27 Then goto exx2;

J:=0;

qwer:=qwer+11;

End;

End;

exx2:

close(F);

window(1,1,80,25);

textattr:=$3f;

clrscr;

End;


Begin

clrscr;n:=0;

textattr:=$30;

singleram(2,1,78,25,0);

textattr:=$3f;

gotoxy(17,3);write('Алтайский Государственный Технический Университет');

gotoxy(30,4);write('им. И. И. Ползунова');

gotoxy(20,6);write('Курсовой проект по предмету "Программирование"');

gotoxy(35,9);write('ТЕМА: ');

gotoxy(23,11);write('ИНТЕРПОЛЯЦИЯ КАНОНИЧЕСКИМ ПОЛИНОМОМ');

gotoxy(50,16);write('Выполнил:ст. гр. Э-14');

gotoxy(60,17);write('Барсуков В.');

gotoxy(22,22);write(' ------------------------ ');

gotoxy(22,23);write(' - Нажмите клавишу Ввод - ');

gotoxy(22,24);write(' ------------------------ ');

readln;

textattr:=$3f;

ClrScr;

while n<>5 do begin

window(1,1,80,25);clrscr;

textattr:=$3f;

singleram(2,2,78,24,0);

delay(100);

S[1]:=' ТЕОРИЯ ';

S[2]:=' РАБОТА ПРОГРАММЫ ';

S[3]:=' КОНСУЛЬТАЦИЯ ';

S[4]:=' СПРАВКА ';

S[5]:=' В Ы Х О Д ';

Textattr:=$5f;

For N:=1 to 5 do

Begin

SingleRam(n*5+12,n*2+3,n*5+37,n*2+5,0);

GotoXY (n*5+14,n*2+4);

Write (S[N]);

End;

textattr:=$5f;

singleram(17,18,26,22,0);

singleram(53,18,62,22,0);

singleram(35,18,44,22,0);

gotoxy(21,19);write('_');

gotoxy(19,21);write('вверх');

gotoxy(39,19);write('_');

gotoxy(38,21);write('вниз');

gotoxy(56,20);write('ввод');

N:=1;

N1:=5;

Ch:=#0;

While Ch<>#13 do

Begin

Ch:=ReadKey;

If Ch=#0 then Ch:=ReadKey;

If ch=#27 Then halt(0);

If Ch=#72 then Dec(N);

If Ch=#80 then Inc(N);

If (N<1) or (N>5) then N:=Abs(N-5);

If N1<>N then

Begin

TextAttr:=$5F;

GotoXY (N1*5+14,N1*2+4);

Write (S[N1]);

TextAttr:=$F5;

GotoXY (n*5+14,N*2+4);

Write (S[N]);

N1:=N;

End;

End;

TextAttr:=$02;

ClrScr;

If n=1 Then Txt('theory');

If n=2 Then Proga;

If n=3 Then Txt('kons');

If n=4 Then Txt('spravka');

If n=5 Then Halt(0);

end;

End.


Инструкция пользователю:

Системные требования: монитор SVGA, процессор не ниже 386, оперативная память 1 Мb, клавиатура.

При загрузке программы выбрать нужный вам пункт меню. Остановимся подробнее на 2-ом пункте меню – самой программе. Сначала нужно ввести количество узлов функции(n>=2). Число должно быть натуральным. После чего через пробел вводятся координаты точек у(i) и x(i) . Результатом будет список коэффициентов B0(y)%Bn(y), которые и дополнят формулы интерполяционного полинома Лагранжа.


Заключение:

Данная программа является хорошим подспорьем для инженеров, которые занимаются дифференциальными вычислениями. Простота алгоритма вычисления коэффициентов, а также непритязательность к системным требованиям обеспечат ей, возможно, вполне конкурентоспособное место на рынке аналогичных программ.


Тесты программы:


Введите кол-во узлов функции: 3

Введите через пробел значения х(0) и у(0): 1.3 0.934

Введите через пробел значения х(1) и у(1): 1.4 0.9523


Введите через пробел значения х(2) и у(2): 1.5 0.9661

Коэффициенты полинома:

B(0)=0.9340

B(1)=0.1830

B(2)=-0.2250


Введите кол-во узлов функции: 4

Введите через пробел значения х(0) и у(0): 1.3 0.934

Введите через пробел значения х(1) и у(1): 1.4 0.9523

Введите через пробел значения х(2) и у(2): 1.5 0.9661

Введите через пробел значения х(3) и у(3): 1.6 0.9763

Коэффициенты полинома:

B(0)=0.9340

B(1)=0.1830

B(2)=-0.2250

B(3)=0.1500


Введите кол-во узлов функции: 5

Введите через пробел значения х(0) и у(0): 2.2 0.4860966

Введите через пробел значения х(1) и у(1): 2.3 0.4892759

Введите через пробел значения х(2) и у(2): 2.4 0.4918025

Введите через пробел значения х(3) и у(3): 2.5 0.4937903

Введите через пробел значения х(4) и у(4): 2.6 0.4953388

Коэффициенты полинома:

B(0)=0.4861

B(1)=0.0318

B(2)=-0.0326

B(3)=0.0190

B(4)=-0.0060


Список литературы:

  1. Дьяконов В.П. Справочник по расчетам на микрокалькуляторах.-2-ое изд., испр. Москва: Наука. Гл. ред. физ.-мат. Лит. 1986 г. – 224с.