Силовые механизмы
| Вид материала | Документы |
СодержаниеКлассификация силовых механизмов станочных приспособлений 3. Клин как средство зажима и самоторможения Условия самоторможения клина |
- Силовые узлы и устройства станочных приспособлений. Пневматические силовые узлы. Виды, 80.73kb.
- «основы тестирования и методики развития силовых и скоростных способностей учащихся», 235.77kb.
- Изобразить силовые линии магнитного поля проводника с током, 107.16kb.
- План лекции структура и содержание предмета «легкая атлетика» Содержание Классификация, 104.46kb.
- Задачи и методы исследования 18 Организация исследования 19 Глава Обработка результатов, 508.72kb.
- Б. Е. Большаков Механизмы формирования идеалов и ценностей для управления безопасностью, 924.23kb.
- Пути проведения боли и ее механизмы, 2596.89kb.
- Ы 35-47, 4444.46kb.
- Практическая работа «Механизмы макроэволюции», 93.04kb.
- Отражение синергетических свойств в отклике геологической среды на внешние силовые, 23.28kb.
СИЛОВЫЕ МЕХАНИЗМЫ
1. ЗАМЕЧАНИЯ О РАСЧЕТЕ ПОТРЕБНЫХ СИЛ ЗАЖИМА
Определив схему базирования и расположение установочных элементов, намечают схему закрепления деталей. Последняя должна удовлетворять следующим требованиям:
- в процессе зажима не должно нарушаться положение детали, заданное ей при базировании;
- силы зажима должны быть достаточными, чтобы исключить возможность смещения и вибраций детали в процессе обработки;
- силовые механизмы должны быть быстродействующими и легко управляемыми.
При построении схемы закрепления деталей определяют точки приложения величины и направления сил зажима исходя из схемы действия и значений сил резания и их моментов. Так, например, при фрезеровании деталей, учитывая наличие опрокидывающих моментов, боковые опоры и направленные на них силы зажима располагают как можно ближе к обрабатываемой поверхности. При построении схемы закрепления деталей в кондукторе учитывают действие осевой силы резания, крутящего момента и т.д. Линия действия силы зажима должна проходить через рабочую поверхность опоры (рис. 4.I) и перпендикулярно к ней. Соблюдение этого требования обязательно при закреплении нежестких деталей (планки, плиты, рамы, станины и т. п.).
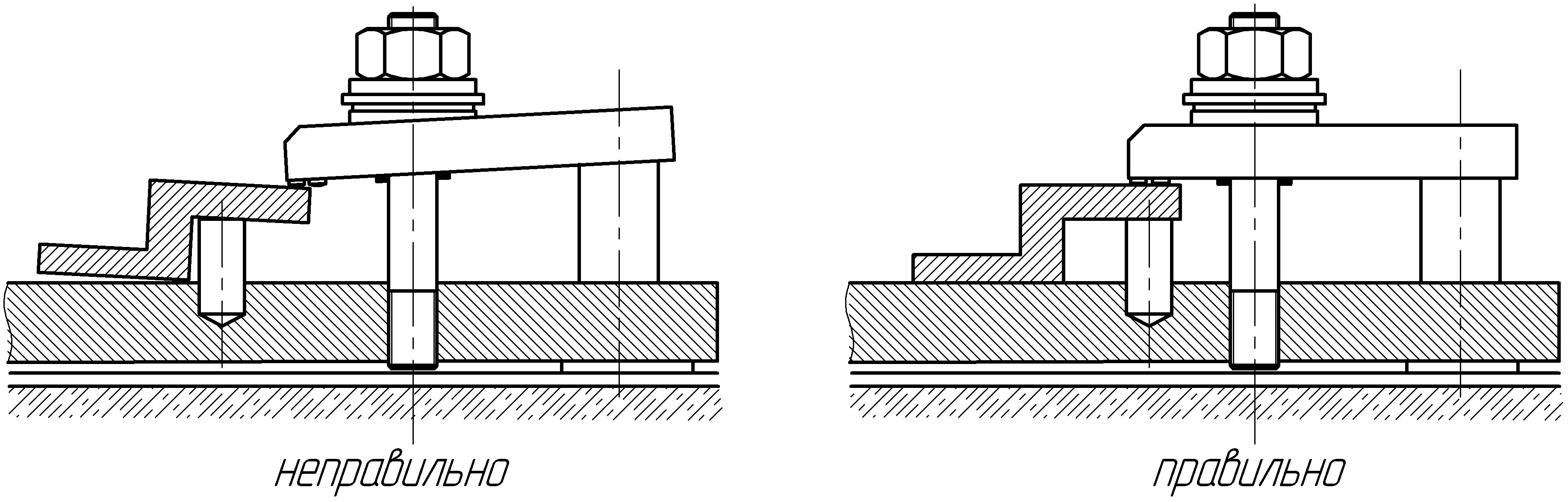
Рис. 4.1. Точки приложения сил зажима
Величины сил зажима можно определять, решая задачу статики на равновесие твердого тела под действием всех приложенных к нему сил и их моментов (сил резания, зажима, массы, реактивных сил и сил трения).
Значения сил резания и моментов рассчитывают по формулам из курса резания металлов или берут из таблиц нормативов, а затем, для большей надежности, увеличивают их на коэффициент запаса К = 1,5 . . . 2,5; меньшее значение К для случая чистовой обработки, большее - для черновой. На практике силы зажима обычно определяют приближенно, исходя из анализа взаимодействия сил резания и зажима и их моментов.

Рис. 4.2. Схемы взаимодействия сил резания и зажима
Рассмотрим пять характерных случаев такого взаимодействия.
- Силы зажима W и резания Р имеют одинаковое направление и действуют на опору (рис. 4.2, а). В этом случае сила зажима минимальна (Wmin).
- Силы имеют противоположное направление (рис. 4.2, б). Тогда
W = КР.
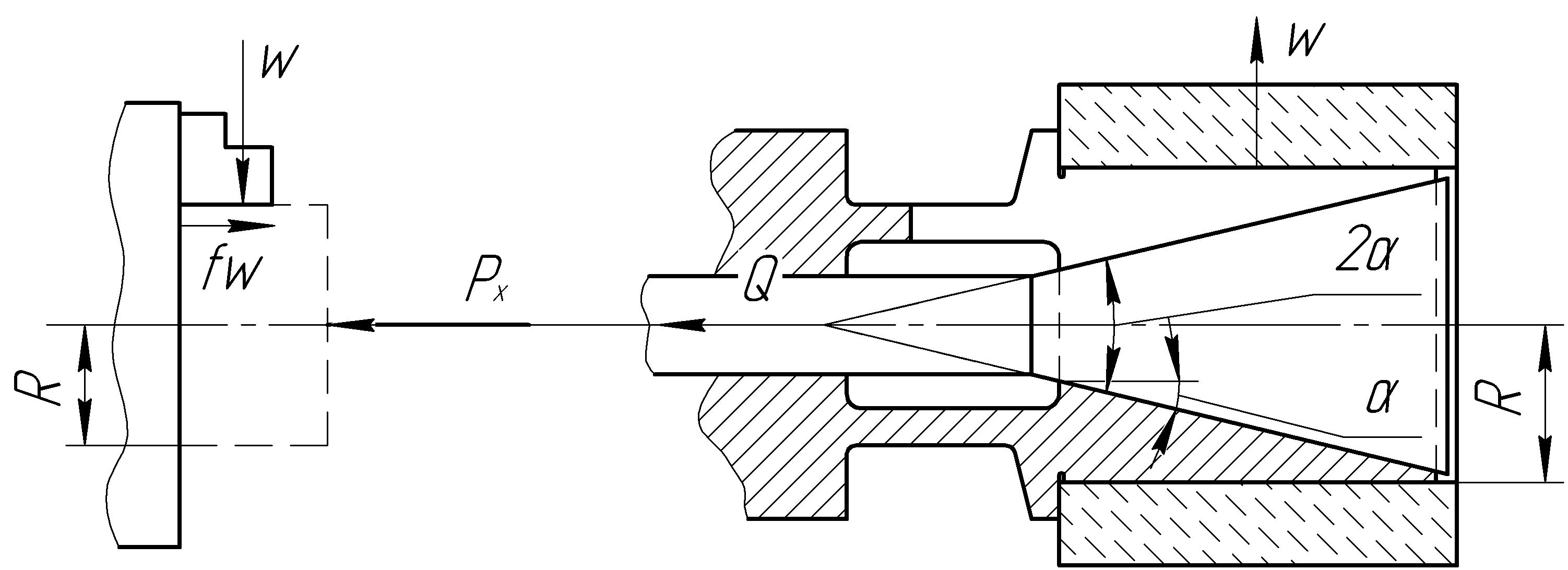
Рис. 4.З. Схемы для расчета сил зажима при обработке в патронах и на оправке
3. Силы направлены взаимно перпендикулярно, и силе резания противодействуют силы трения на опоре и в точке зажима (рис. 4.2, в). В этом случае
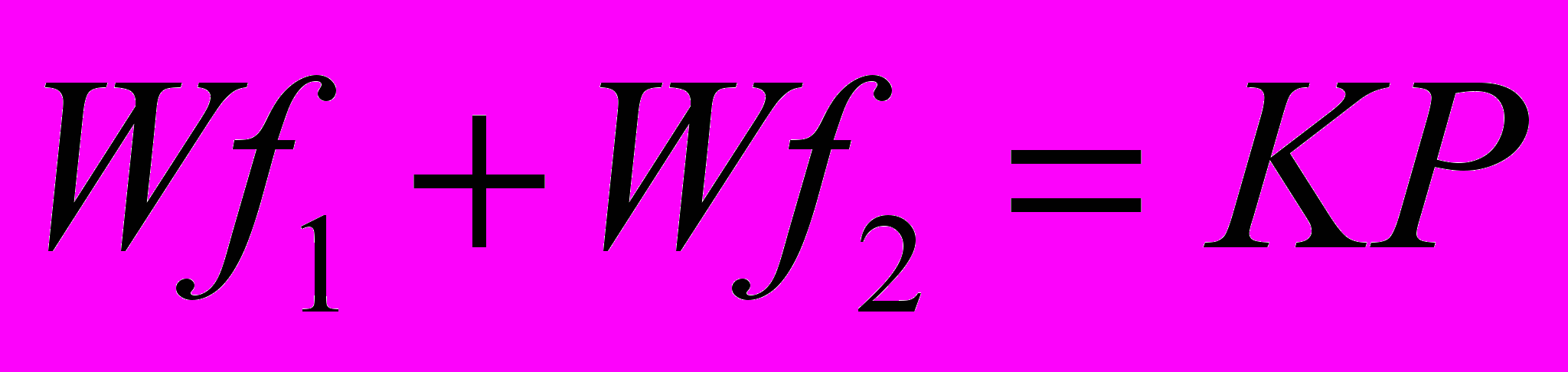
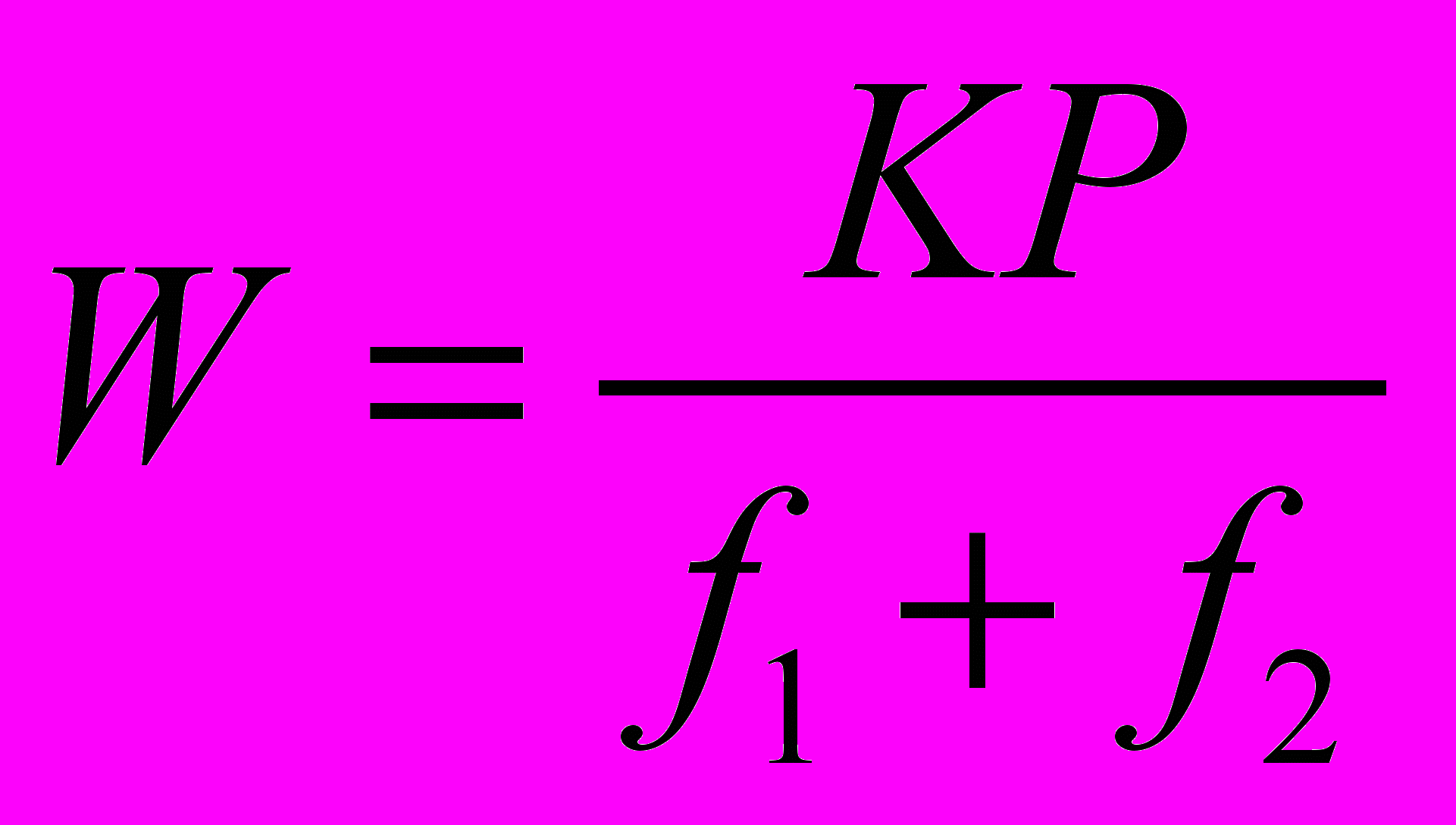
где f1, f2 — коэффициенты трения.
При f1 = f2 = 0,1
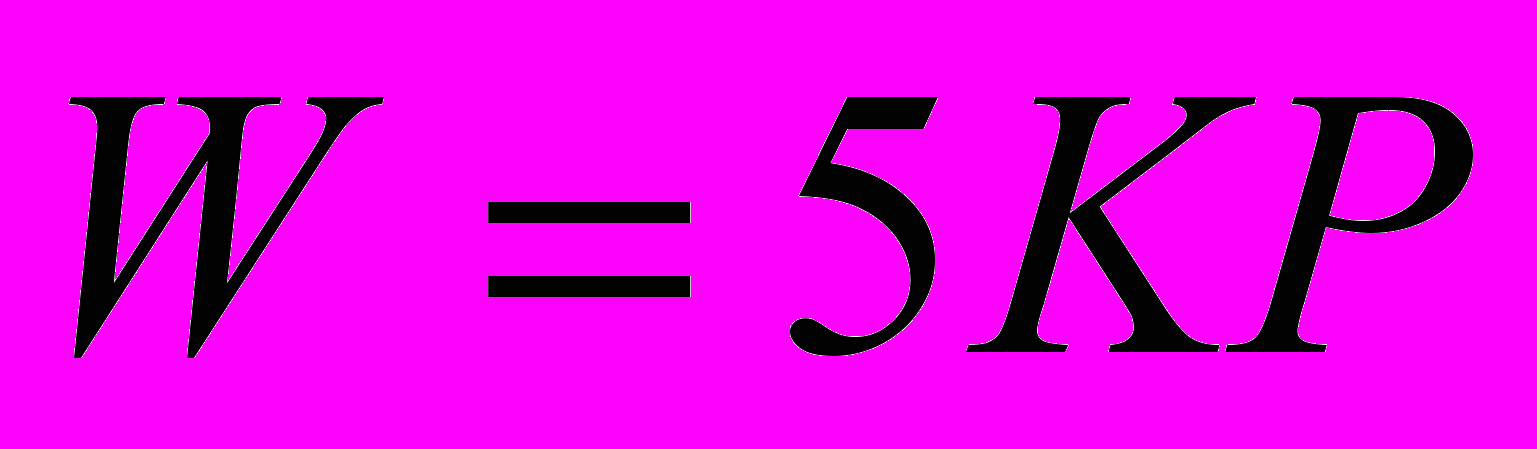
4. Заготовка, обрабатываемая в трехкулачковом патроне, находится под воздействием момента Мрез и осевой составляющей силы резания Рх. Из схемы, приведенной на рис. 4.3, а, находим
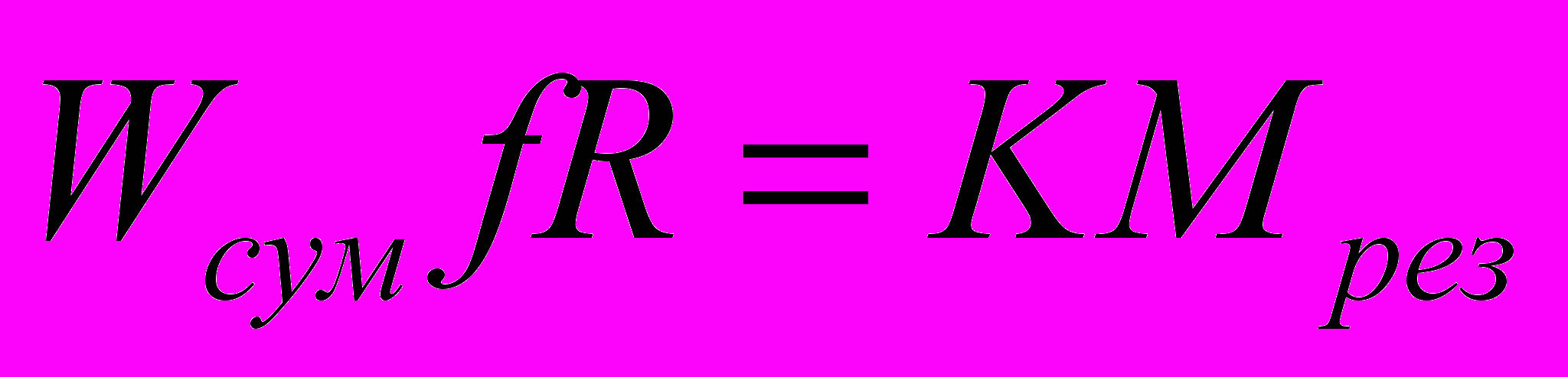
отсюда
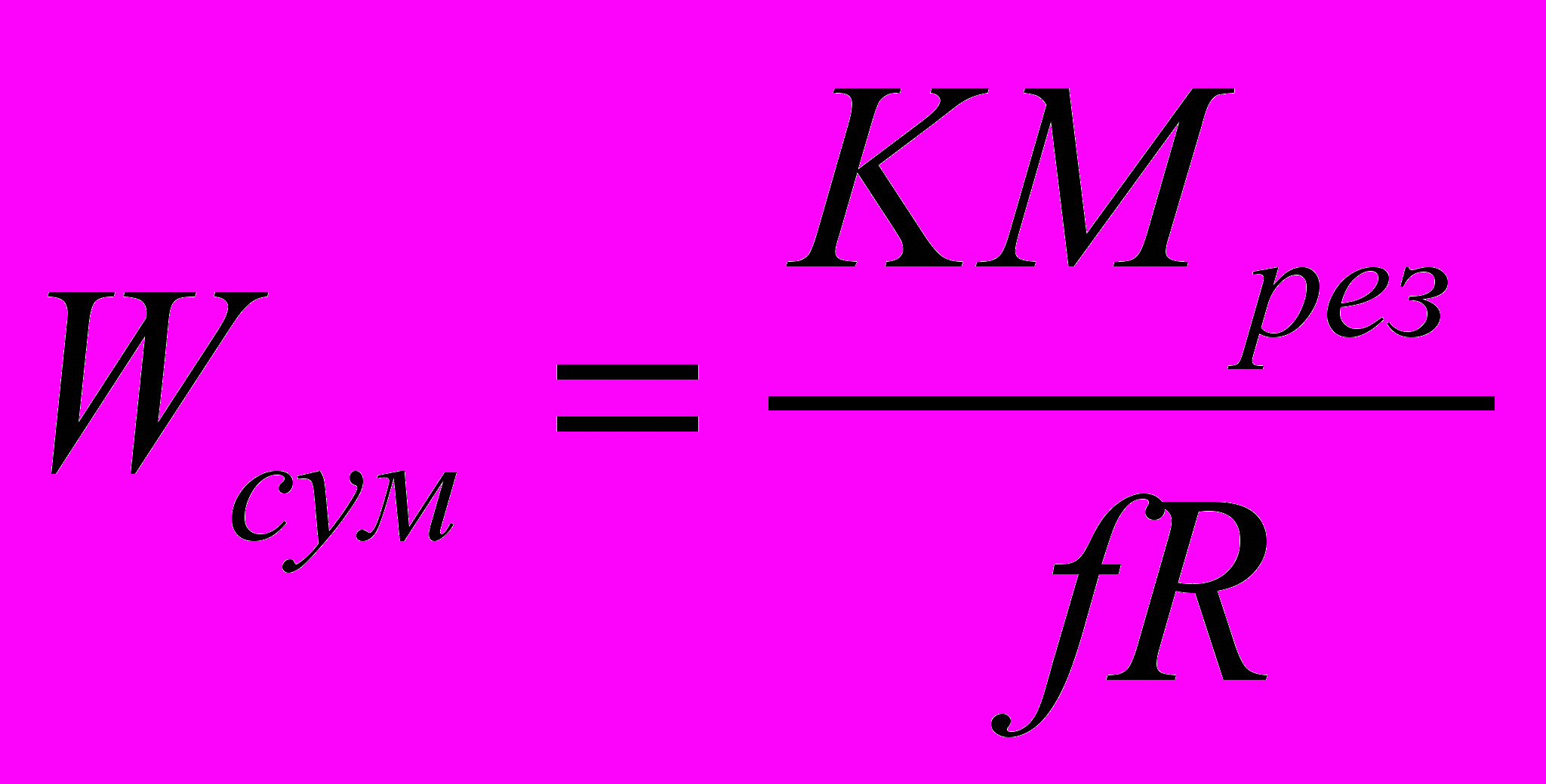 ,
, 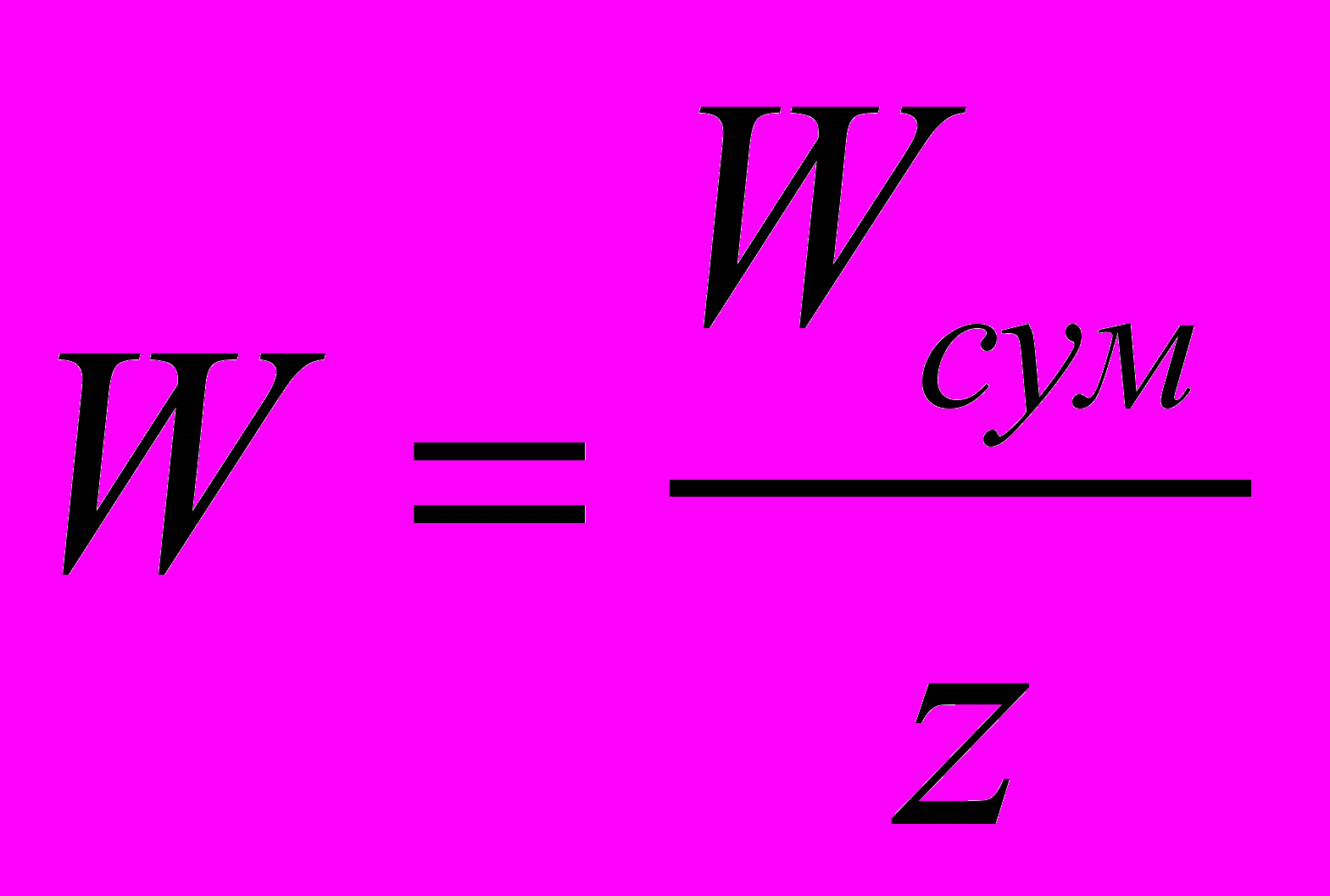
где Мрез – момент силы резания, Wсум - суммарная сила зажима всеми кулачками; W — сила зажима одним кулачком; z — число кулачков, R — радиус заготовки; К — коэффициент запаса; f — коэффициент трения.
Найденное значение Wсум проверяется на невозможность осевого сдвига заготовки
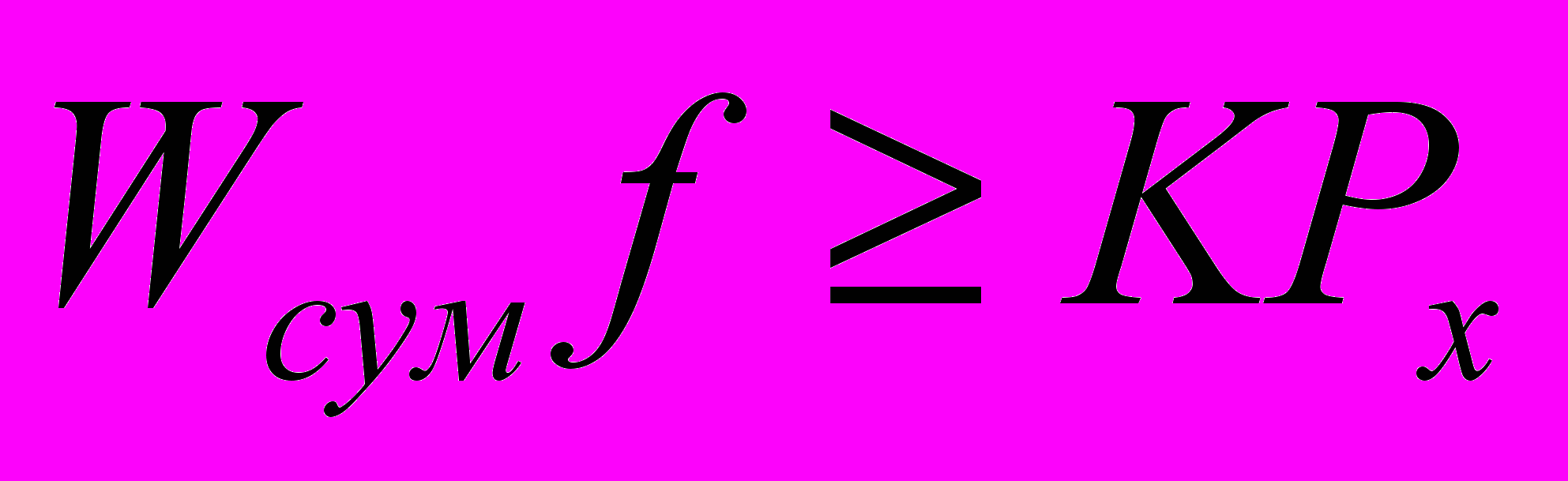
Отсюда
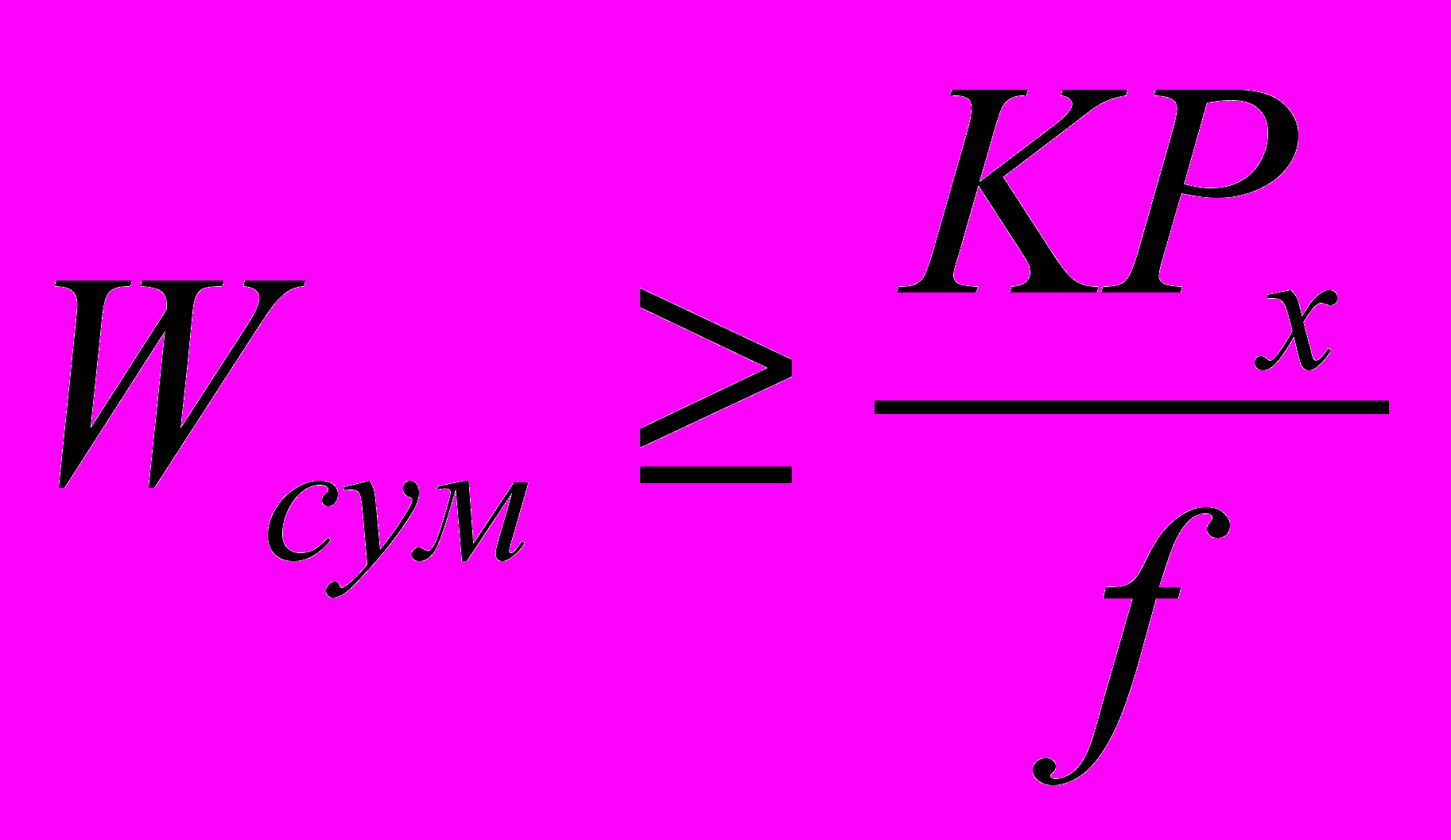
При расчетах средние значения коэффициента трения можно принимать равными:
1) при контакте обработанных поверхностей с опорными пластинами f = 0,1 … 0,15;
2) при контакте необработанных поверхностей с установочными штырями со сферической головкой f = 0,2 …0,3;
3) при контакте с закаленными рифлеными элементами (рифленые опоры, губки кулачков и т. п.) f < 0,7 в зависимости от рисунка и глубины насечки.
Силы зажима в каждой точке следует определять с возможно большей точностью, так как чрезмерное их завышение приводит к неоправданному увеличению габаритов и массы приспособлений, диаметров цилиндров, излишнему расходу сжатого воздуха, к увеличению деформации закрепляемых деталей.
Действительные силы зажима, развиваемые силовыми механизмами, должны быть равны или несколько больше расчетных. Значение этих сил зависит от величины исходной силы Q и передаточного отношения сил выбранного механизма.
Классификация силовых механизмов станочных приспособлений
Силовые механизмы приспособлений делятся на простые и комбинированные, т.е. состоящие из двух-трех сблокированных простых механизмов (см. схему).
К простым механизмам относятся клиновые, винтовые, эксцентриковые, рычажные, рычажно-шарнирные и др. Простые механизмы принято называть зажимами.
Комбинированные механизмы обычно выполняются как винто-рычажные, эксцентрико-рычажиые и т, п.
В тех случаях, когда простые или комбинированные механизмы используются в компоновках с механизированными приводами (пневматическими и др.), их называют механизмами-усилителями. По числу ведомых звеньев механизмы делятся на однозвенные, двухзвенные и многозвенные (многоточечные).
Каждый силовой механизм имеет ведущее звено, к которому прикладывается исходная сила, и одно или несколько ведомых звеньев (прижимных планок, плунжеров, кулачков), передающих обрабатываемой детали силы зажима. Многозвенные механизмы зажимают одну деталь в нескольких точках или несколько деталей в многоместном приспособлении одновременно и с равными силами.
Особую группу многозвенных механизмов составляют самоцентрирующие патроны и оправки.
По степени механизации силовые механизмы классифицируются на ручные, механизированные и автоматизированные.
Ручные механизмы требуют применения значительной мускульной энергии и утомляют рабочего. Механизированные работают от энергии, передаваемой приводом. Автоматизированные приводятся в действие перемещающимися столами, суппортами, шпинделями станков или центробежными силами вращающихся масс и осуществляют зажим и раскрепление изделий без участия рабочего.
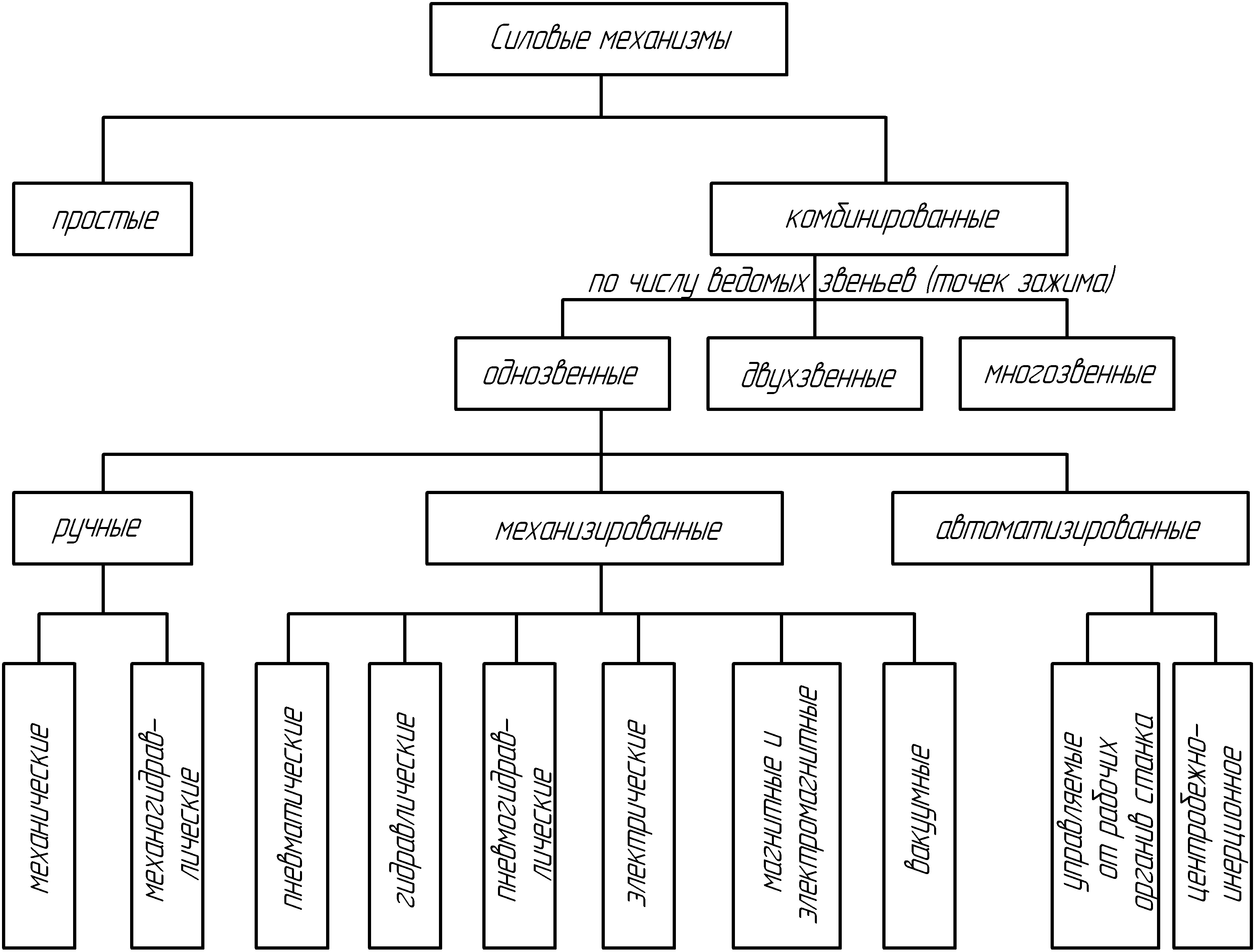
Рис. 4.4 Классификация силовых приводов
3. КЛИН КАК СРЕДСТВО ЗАЖИМА И САМОТОРМОЖЕНИЯ
Большинство силовых механизмов основано на действии клина, обладающего свойством самоторможения.
Разновидности клина
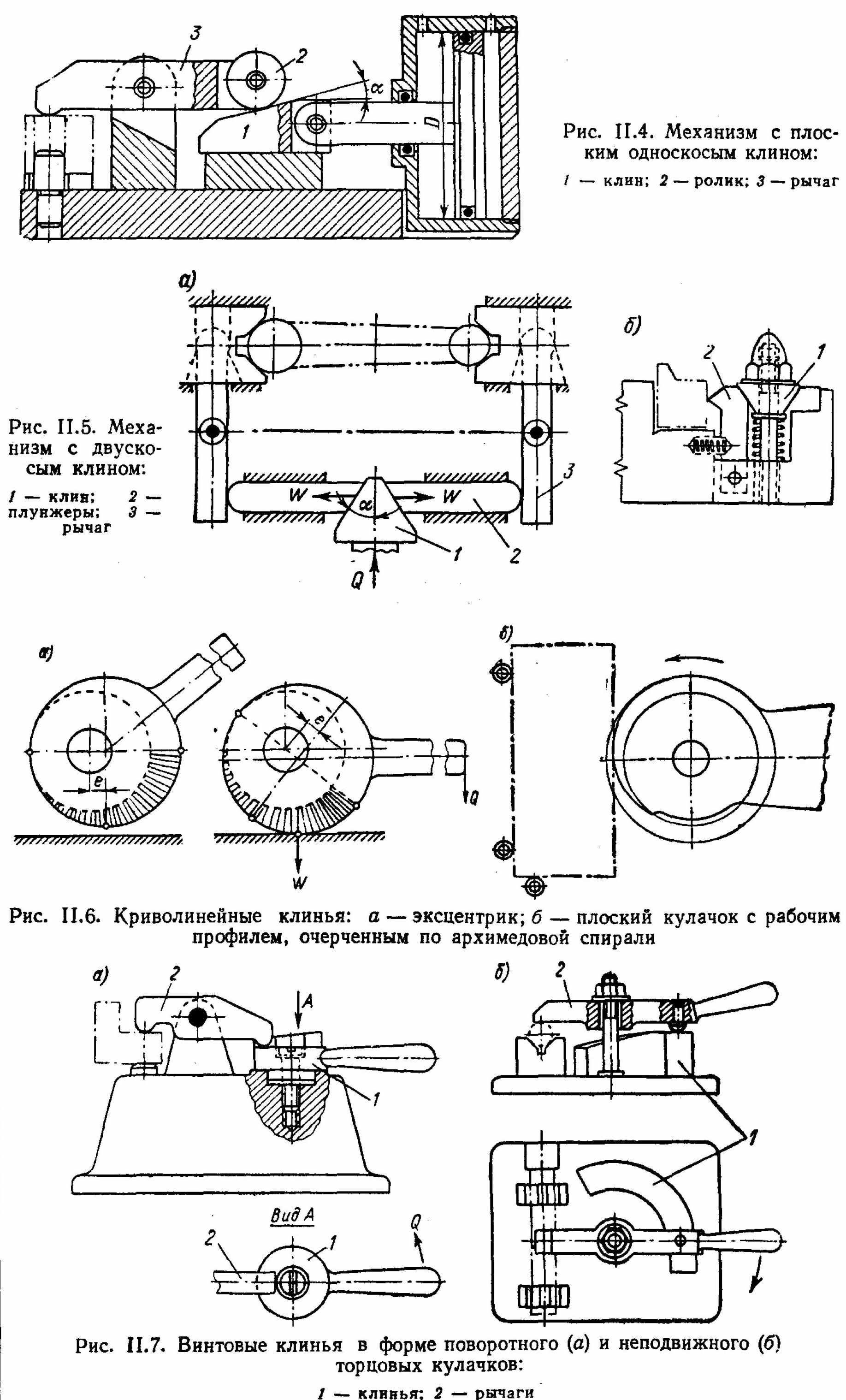
Клин применяется в следующих конструктивных вариантах:
- плоский односкосый (рис. II.4);
- двускосый (рис. II.5, а) или круглый (рис. II.5, б);
- криволинейный клин в форме эксцентрика или плоского кулачка (рис. II.б). В этих конструкциях основание односкосого клина как бы навернуто на окружность диска, а наклонная его плоскость превращена в криволинейную поверхность;
- винтовой клин в форме торцового кулачка (рис. II.7). Здесь односкосый клин как бы свернут в цилиндр; основание клина образует опору, а его наклонная плоскость — винтовой профиль кулачка (винт и гайка также работают па принципу торцового кулачка с трением по одной стороне резьбового профиля).
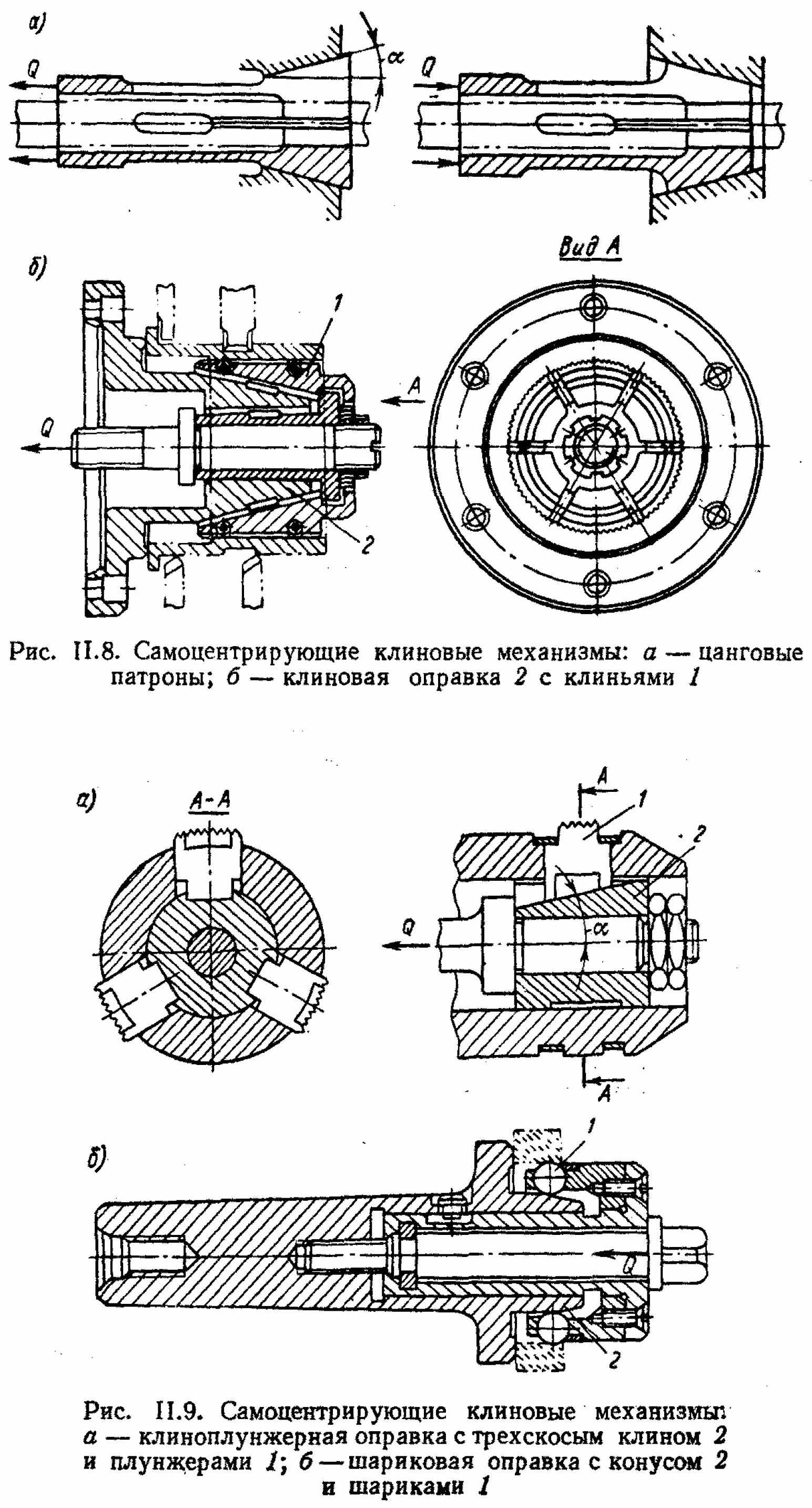
В самоцентрирующих клиновых механизмах (патроны, оправки) используются системы из трех и более клиньев. К таким механизмам относятся: цанговые и клиновые (рис. II.8, а и б), клиноплунжерные и шариковые (рис. II.9, а и б) и некоторые другие.
Условия самоторможения клина
В силовых механизмах клин может работать с трением на двух поверхностях (наклонной поверхности и основании клина) или с трением только на наклонной поверхности. Последний случай обычно встречается в самоцентрирующих клиновых механизмах. Так, например, если цанговый механизм снабжен упором 3 (рис. II.10, а), ограничивающим перемещение заготовки 2 (пруток), то каждый лепесток 1 цанги (клин) при зажиме преодолевает трение на двух поверхностях. Если механизм без упора, трение возникает только на конической поверхности, так как пруток в этом случае перемещается вместе с цангой и
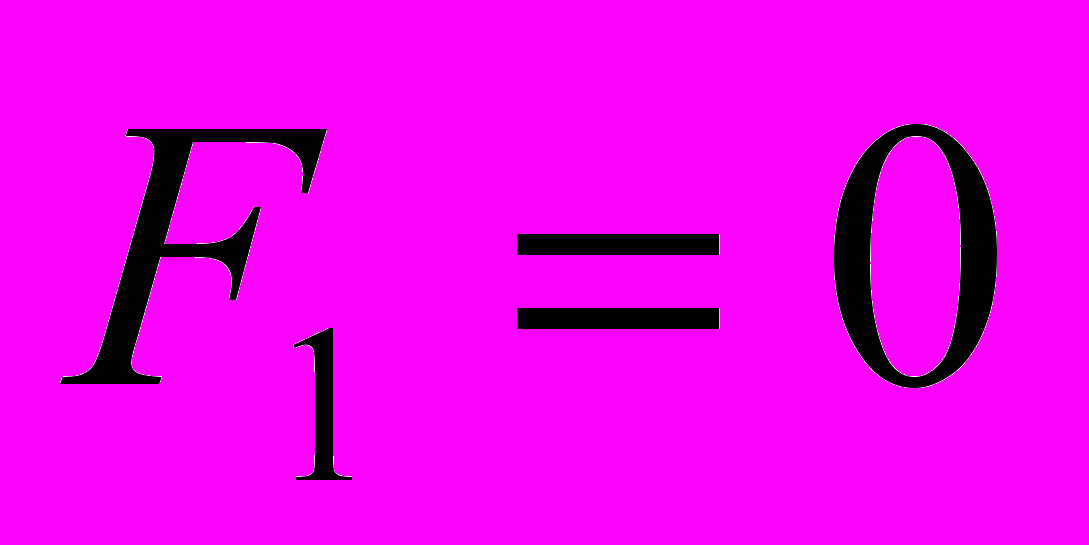 .
.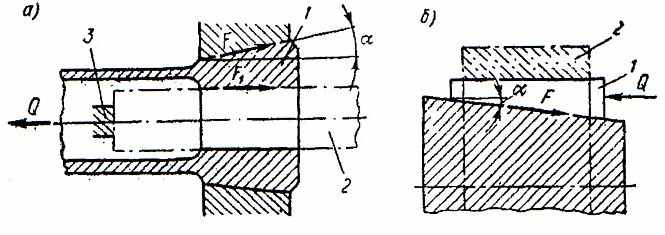
Рис. 4.5. Клиновые механизмы: а — с трением на обеих поверхностях
клиньев; б — с трением только на наклонной поверхности.
В клиновой оправке (см. рис. II.8, б) заготовка устанавливается до упора и каждый клин при зажиме имеет трение на двух поверхностях. Но если заготовка 2 не прилегает к упору (рис. II. 10, б), то клинья 1 преодолевают трение только на наклонной поверхности (
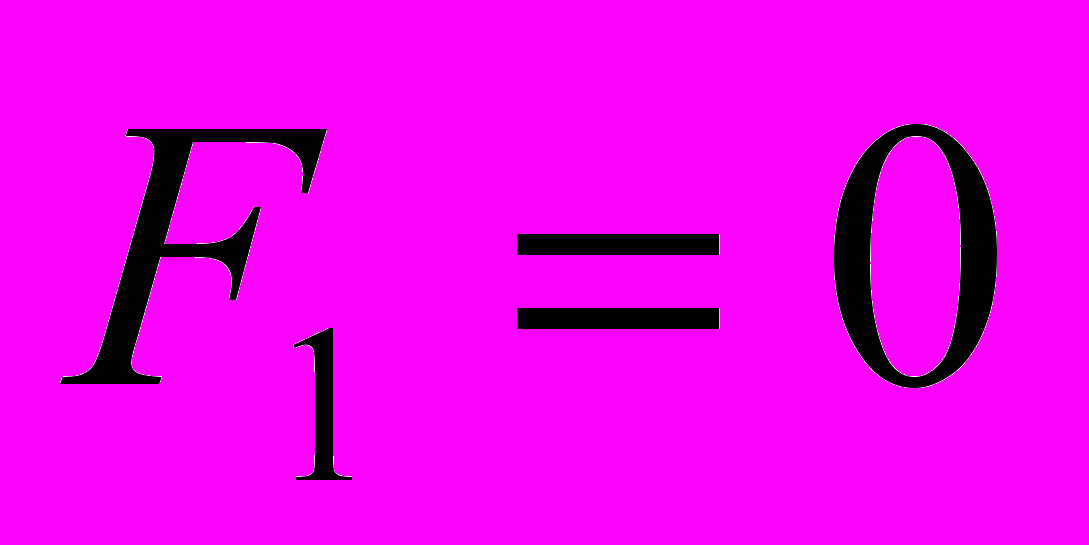 ).
).
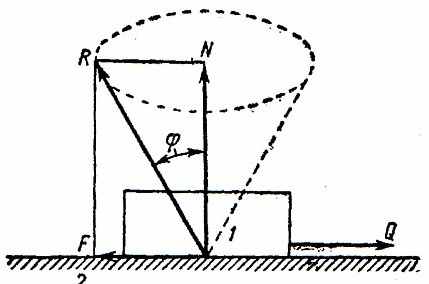
Для выяснения условий самоторможения рассмотрим рис. 11.11 и 11.12. Из механики известно, что если тело 1 (рис. 11.11), нагруженное нормальной реакцией N под действием силы Q равномерно перемещается на плоскости 2, то при наличии силы трения F полная реакция R отклоняется от направления нормали навстречу движению на некоторый угол
 , называемый углом трения.
, называемый углом трения.Из рисунка находим
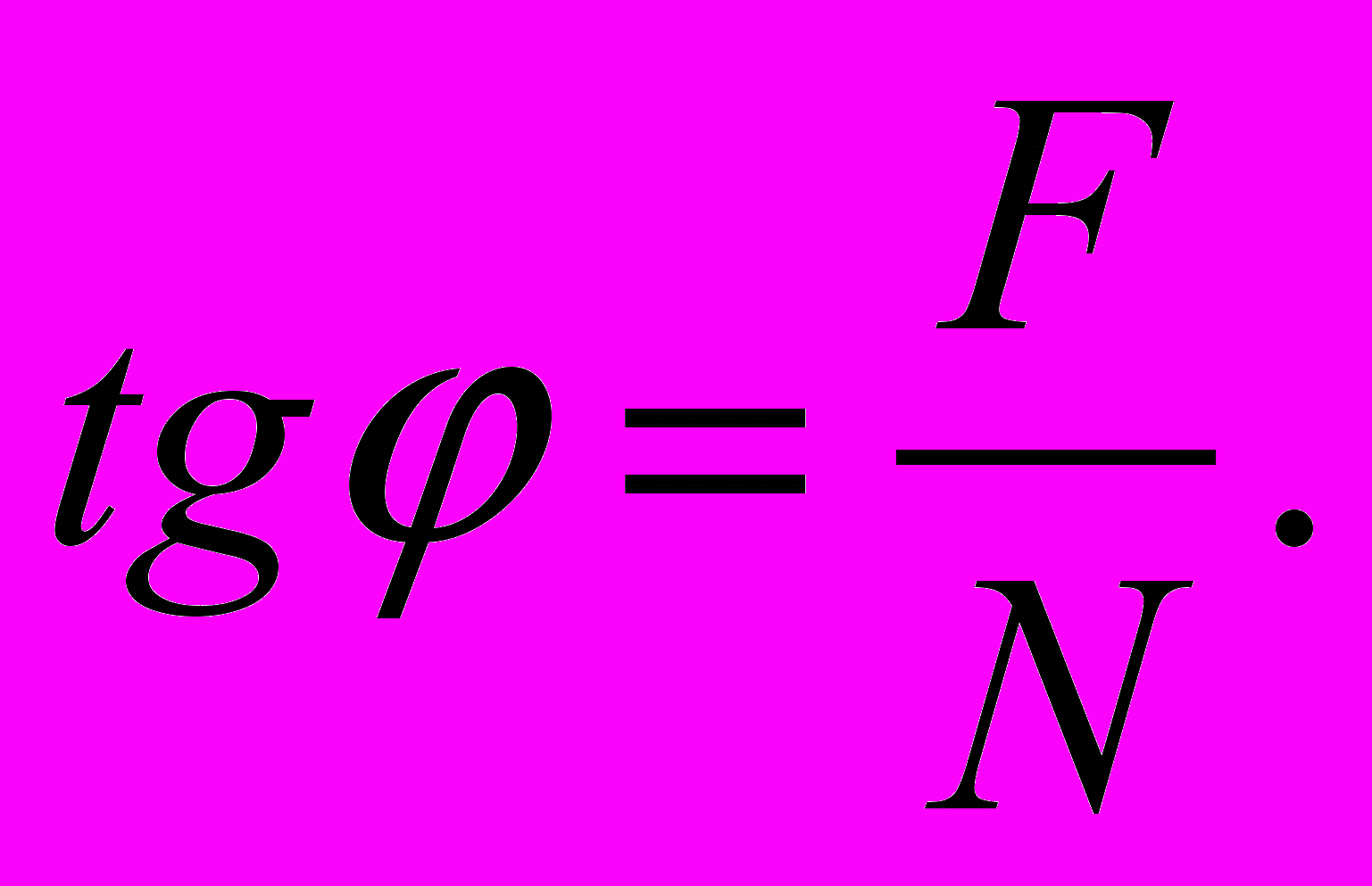
Так как коэффициент трения скольжения
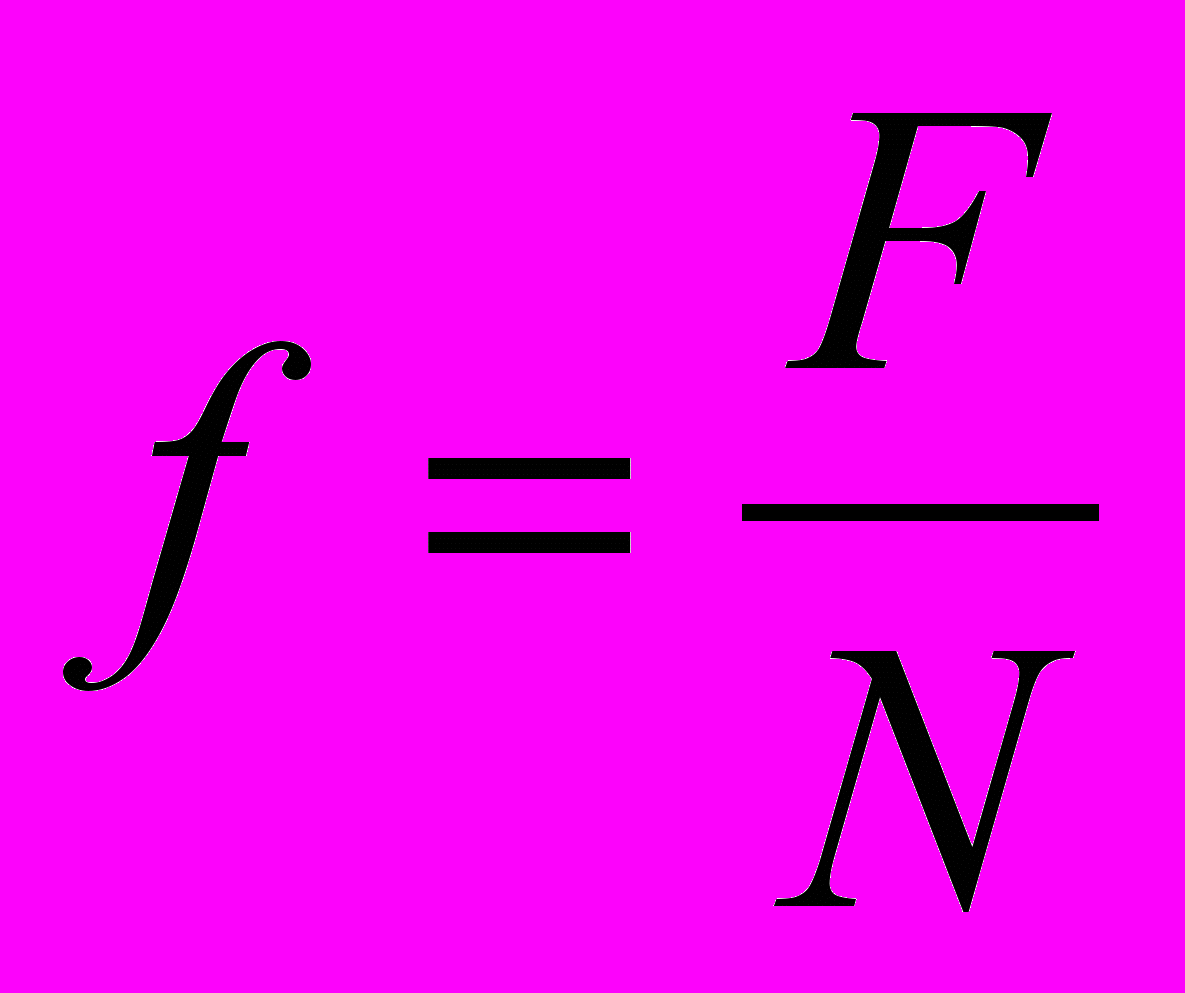 , то
, то .
.На рис. II.12, а показана схема сил, действующих на зажатый односкосый клин с трением на двух поверхностях. При любом угле скоса
 зажатый клин стремится вытолкнуть сила обратного действия
зажатый клин стремится вытолкнуть сила обратного действия  представляющая собой горизонтальную составляющую нормальной реакции N; W — ее вертикальная составляющая
представляющая собой горизонтальную составляющую нормальной реакции N; W — ее вертикальная составляющаяСиле
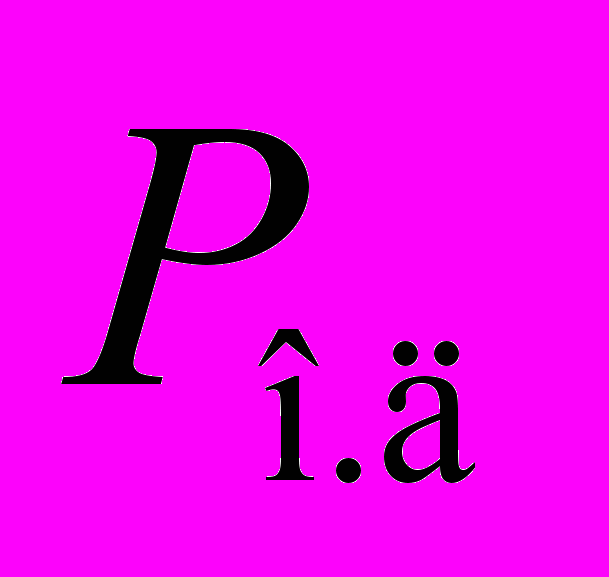 противодействуют сила трения
противодействуют сила трения 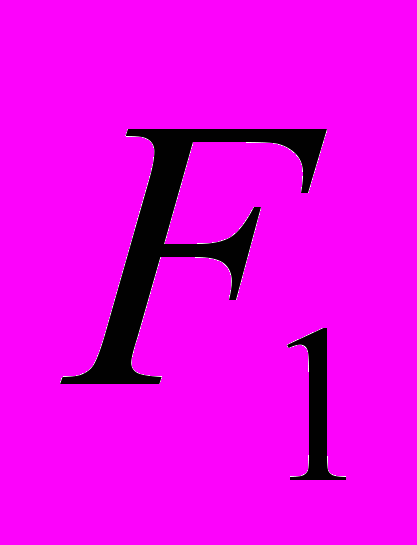 на основании клина и горизонтальная составляющая
на основании клина и горизонтальная составляющая 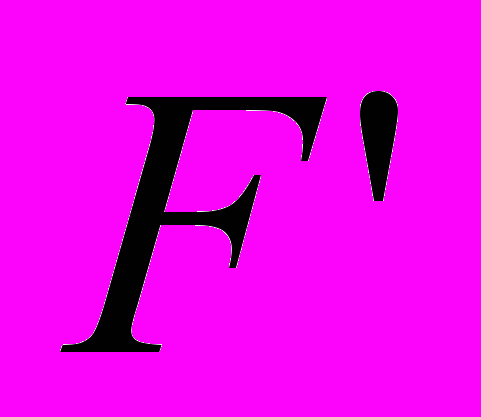 силы трения
силы трения  на наклонной поверхности клина.
на наклонной поверхности клина.Условие равновесия клина
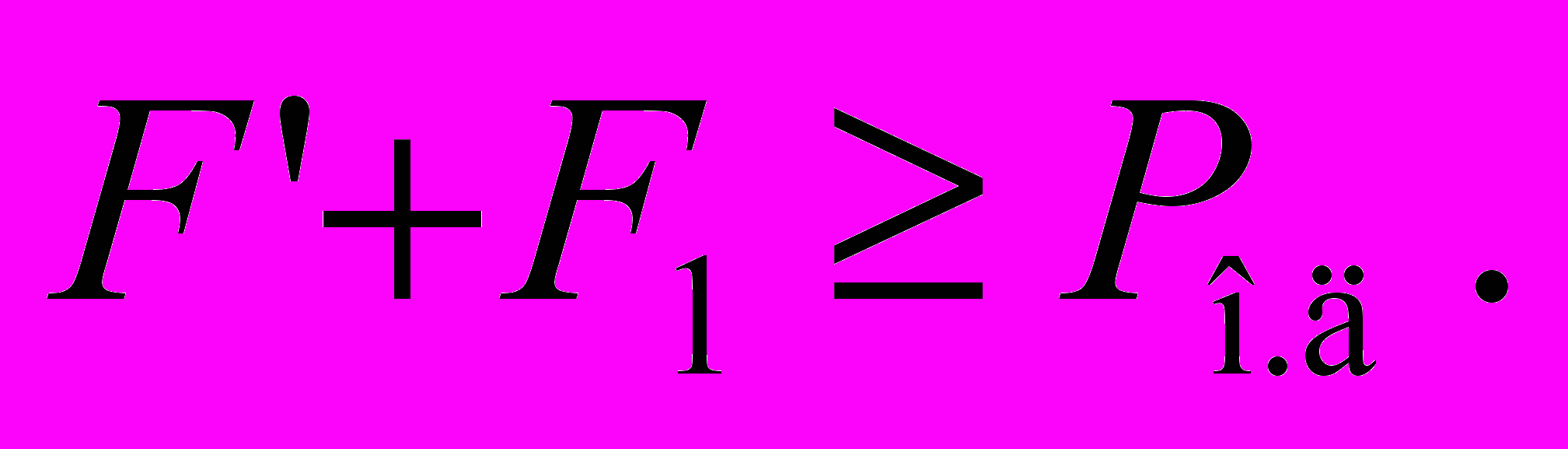
Из схемы сила трения
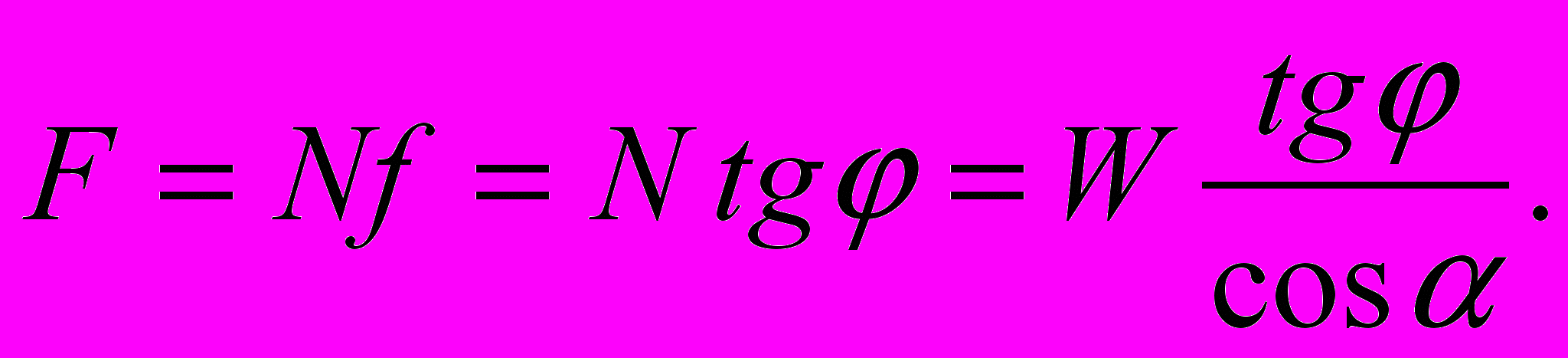
Ее горизонтальная составляющая
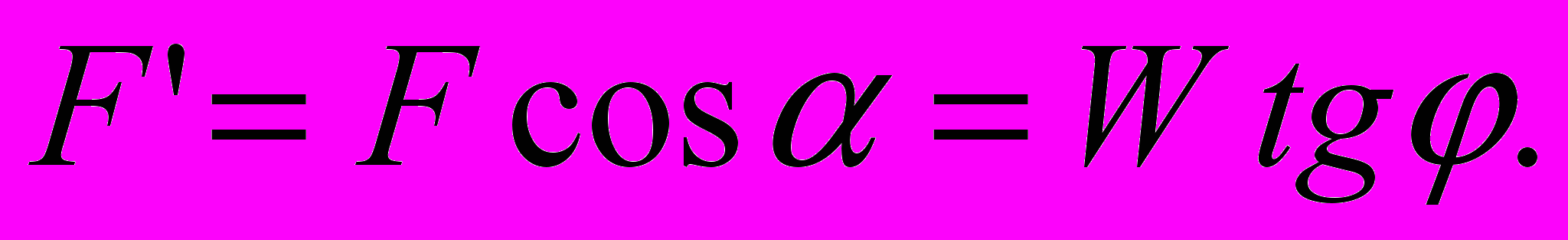
Вертикальная составляющая силу трения
 , равная
, равная 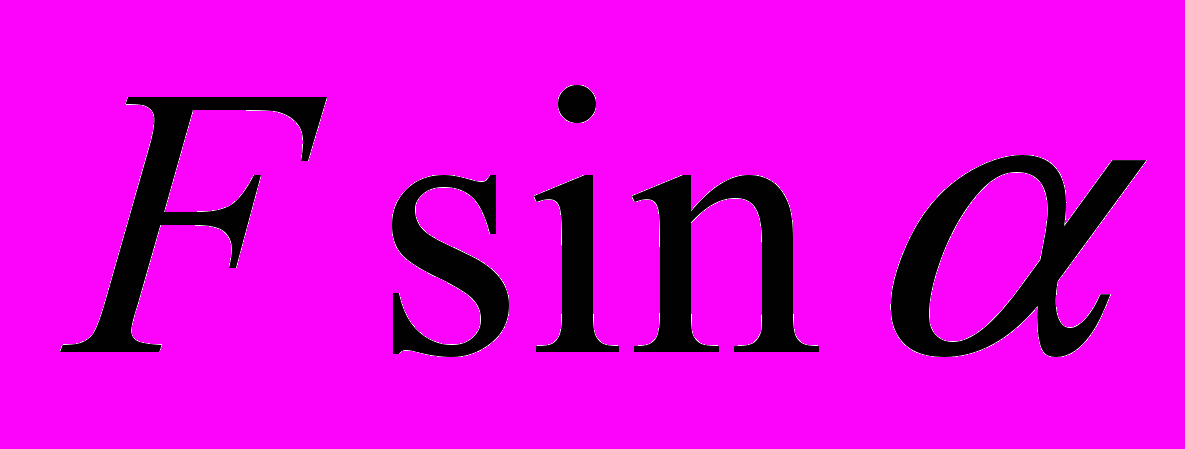 , суммируется с вертикальной составляющей W нормальной силы N. Соответственно величина нормальной реакции на основании клина
, суммируется с вертикальной составляющей W нормальной силы N. Соответственно величина нормальной реакции на основании клина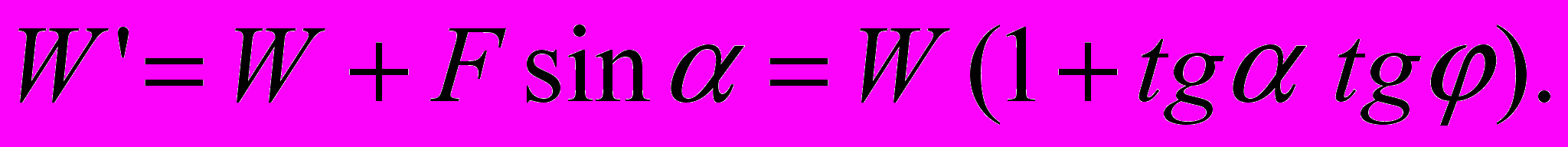
Формула (2) для предельного случая перехода самотормозящего клина в несамотормозящий приобретает вид
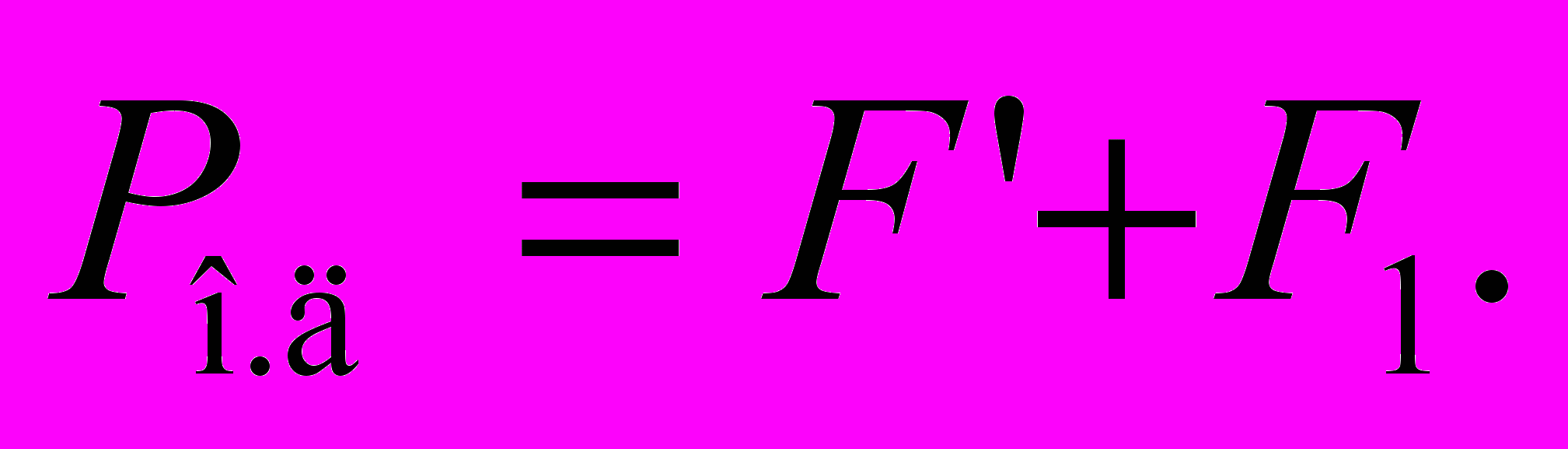
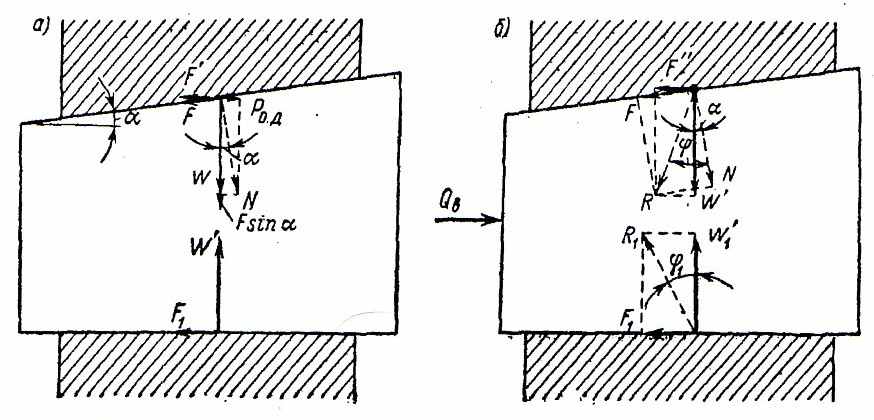
Рис. 11.12. Схема для выяснения условия самоторможения и запаса самоторможения
клина (а); схема для определения выталкивающей силы
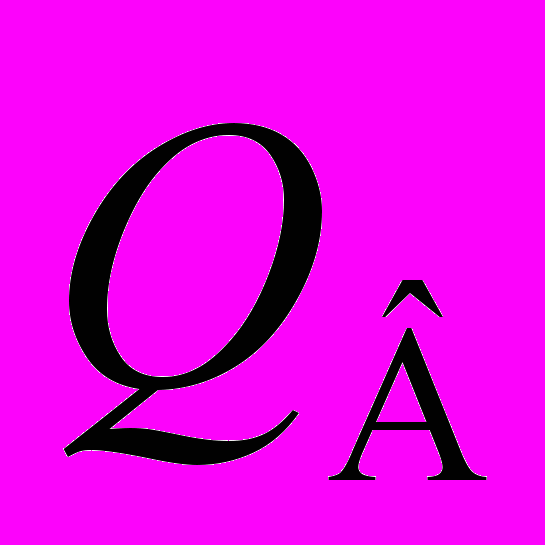 (б)
(б)Подставив в эту формулу значения сил, получим
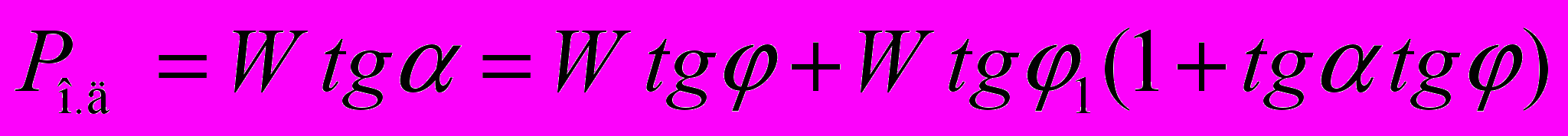
или
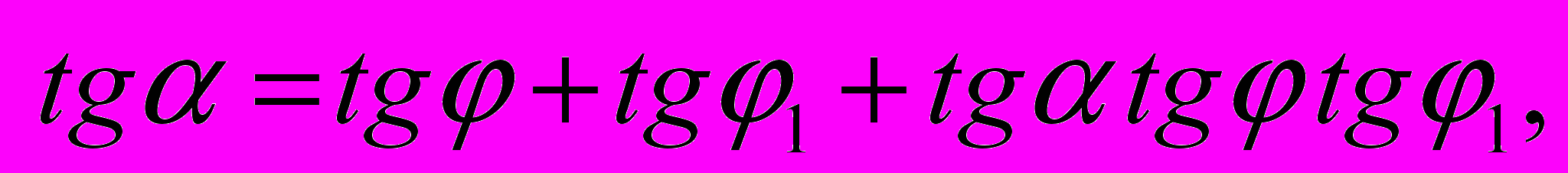
При малых углах а произведение
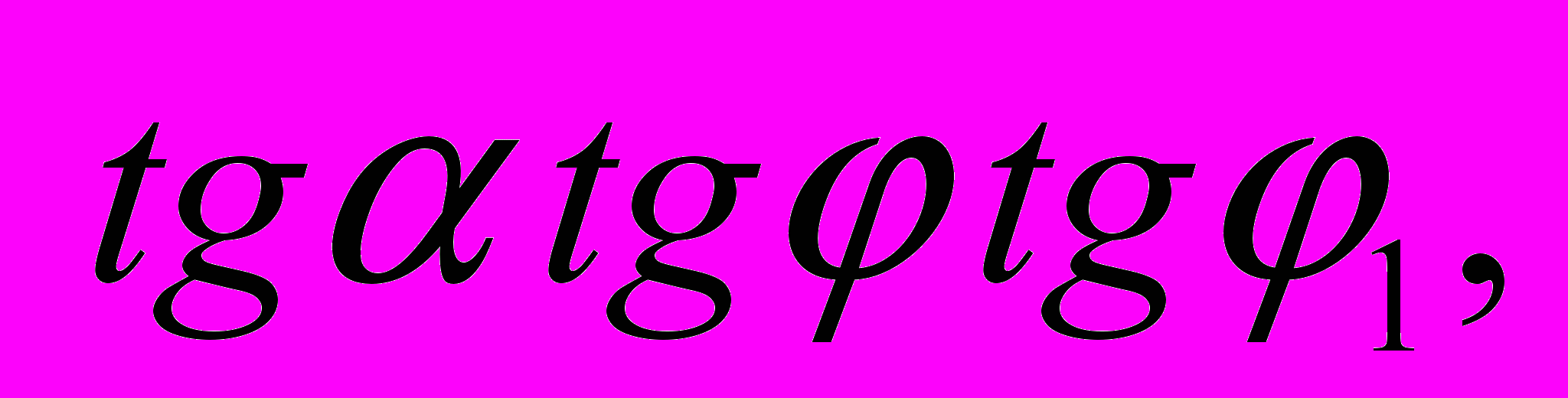 близко к нулю, а величина тангенсов углов близка к величине соответствующих углов в радианах.
близко к нулю, а величина тангенсов углов близка к величине соответствующих углов в радианах.Тогда условие предельного равновесия клина выразится равенством
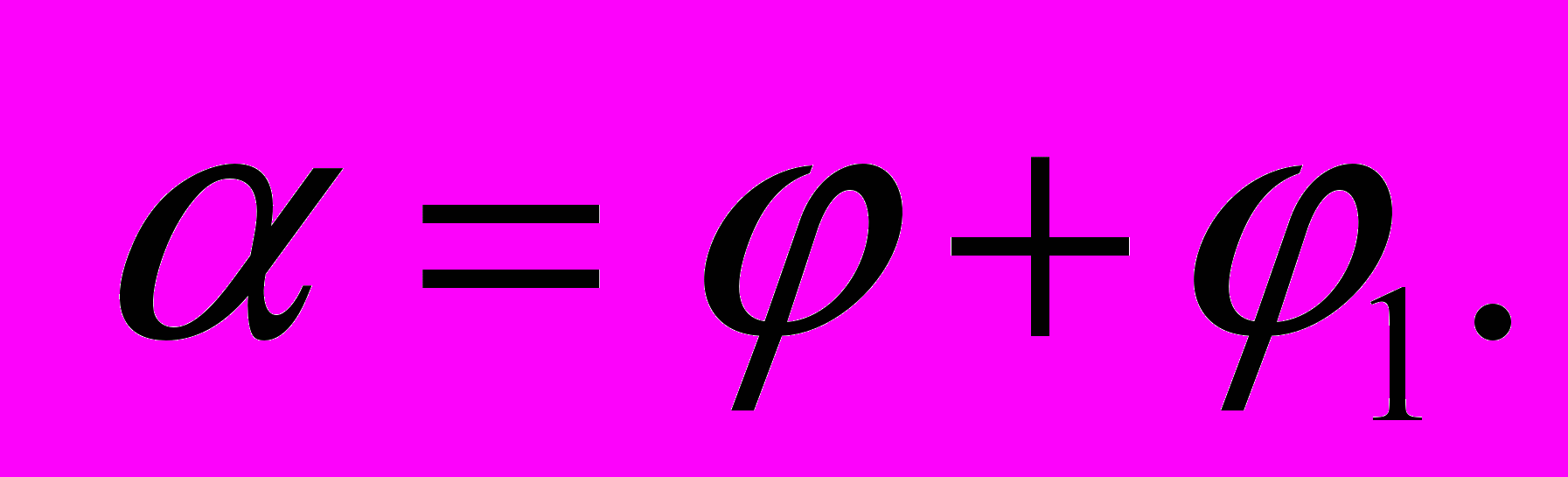
Полагая углы трения на обеих поверхностях клина одинаковыми, т. е.
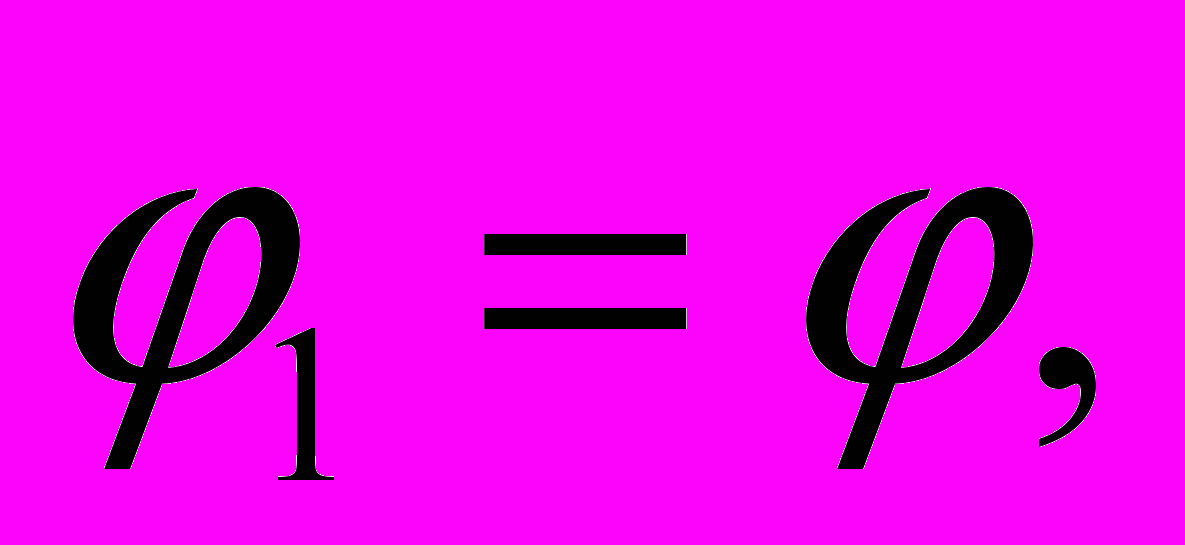 , получим
, получим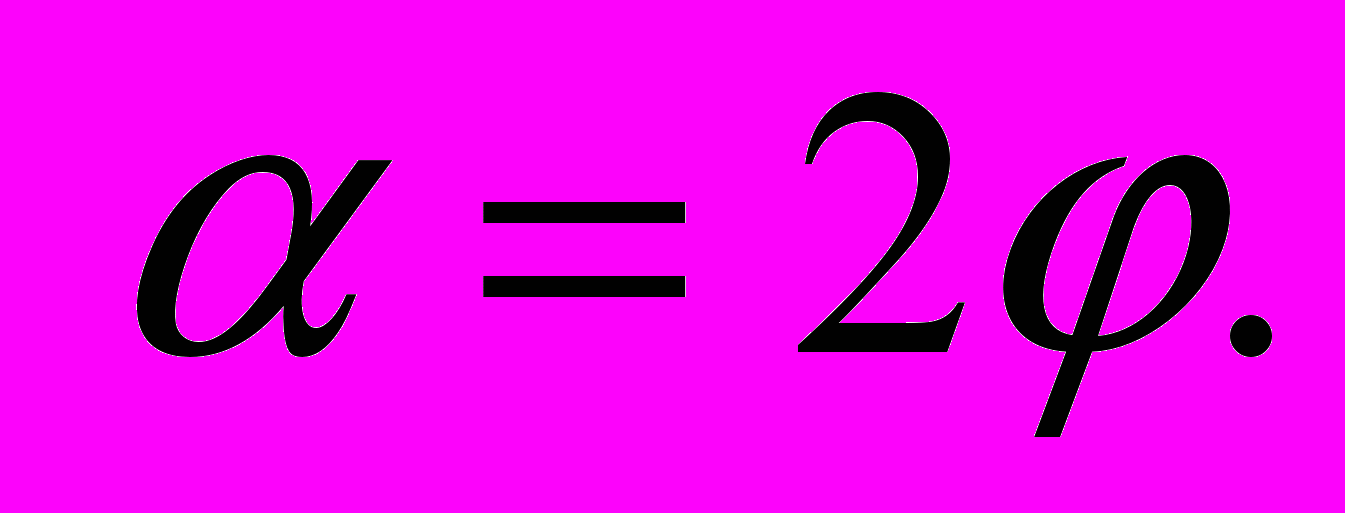
Для клина с трением только на наклонной поверхности (
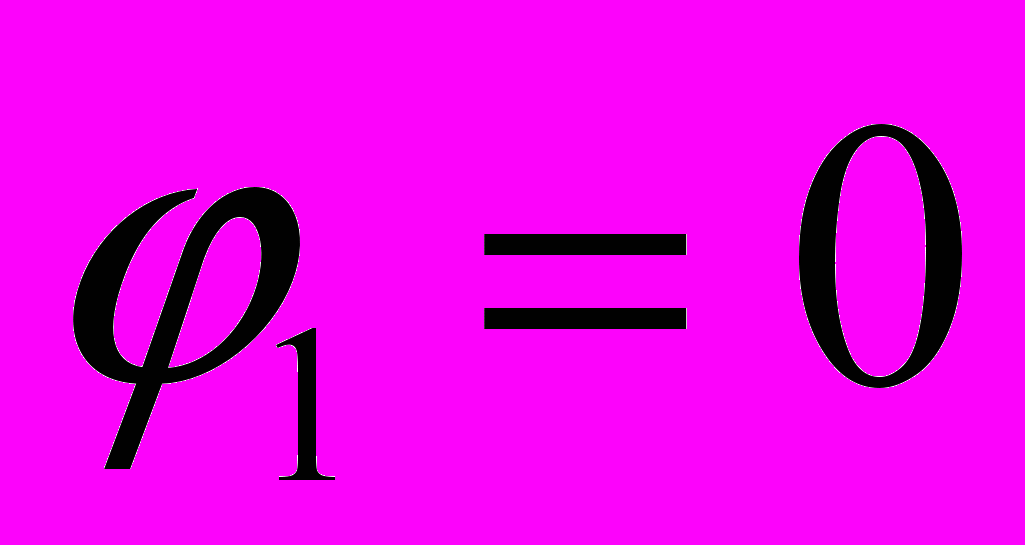 ) условие равновесия будет
) условие равновесия будет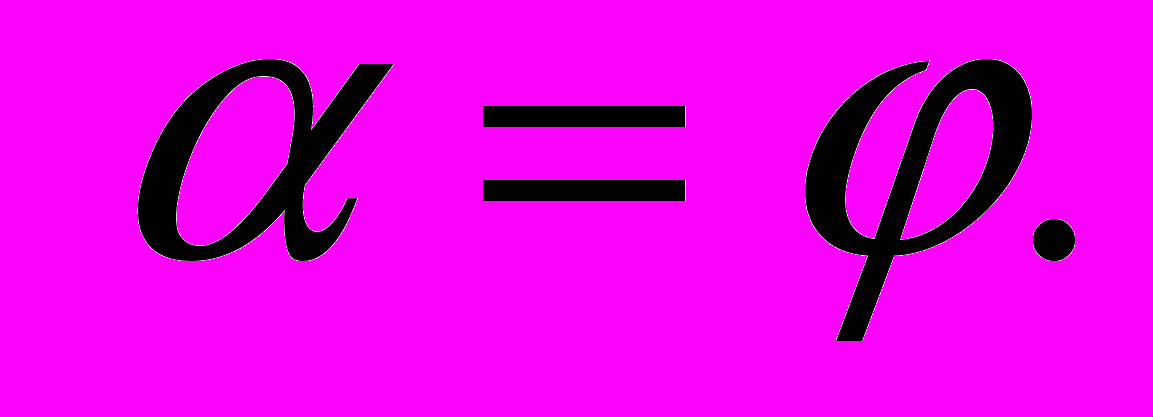
Очевидно, что в заторможенном состоянии клин будет находиться, если угол его скоса а меньше
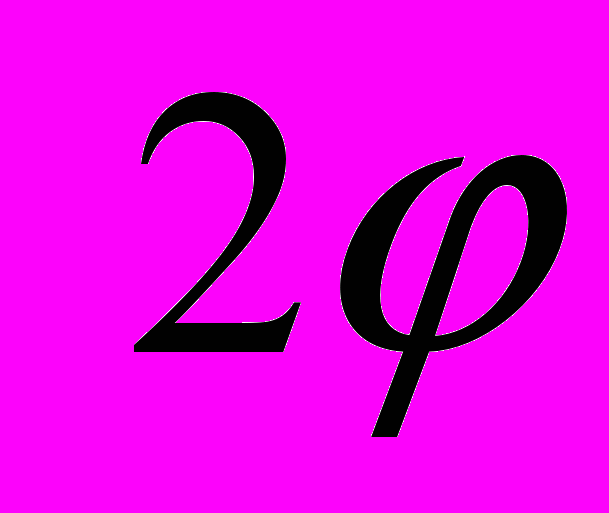 или
или  .
. Условия
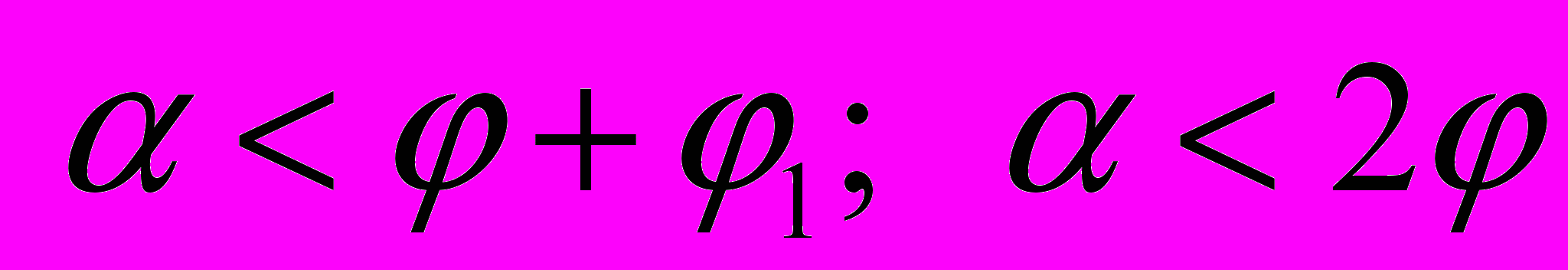 (4)
(4)или
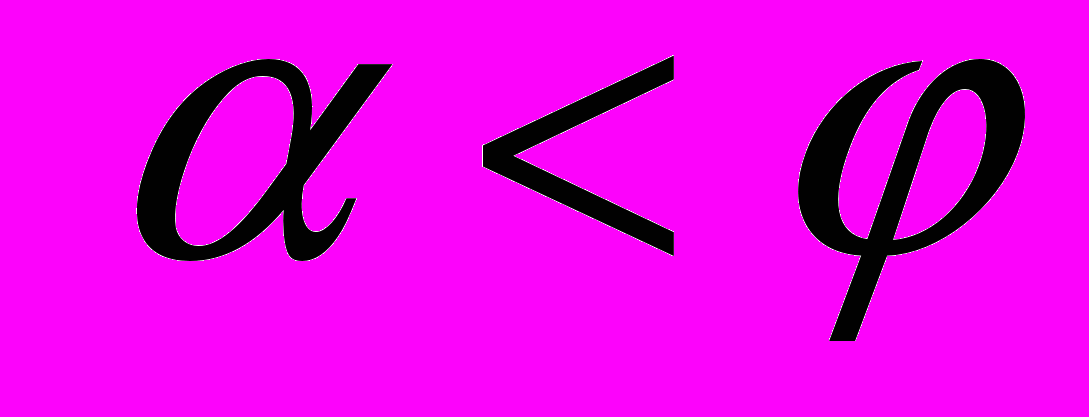 (4а)
(4а)называются условиями самоторможения клина с трением на двух поверхностях (4) и одной поверхности (4а).
Клин и сопряженные с ним детали обычно выполняются из стали, с чисто обработанными (шлифованными) поверхностями. Для этих поверхностей, в зависимости от условий работы клина, принимают
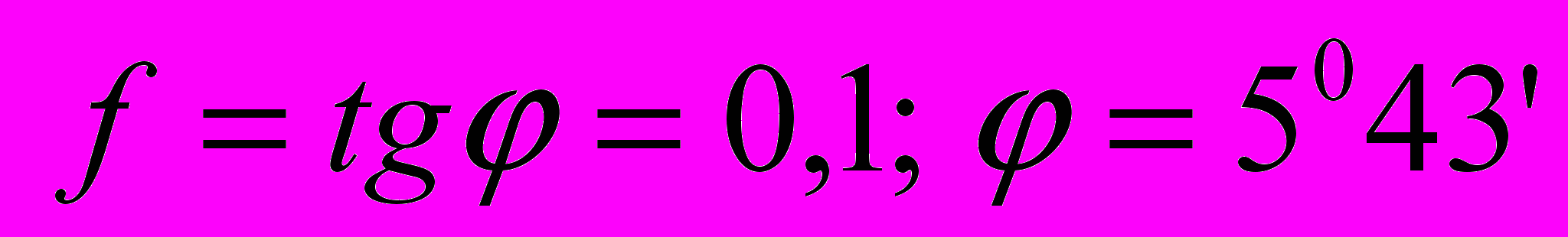
или
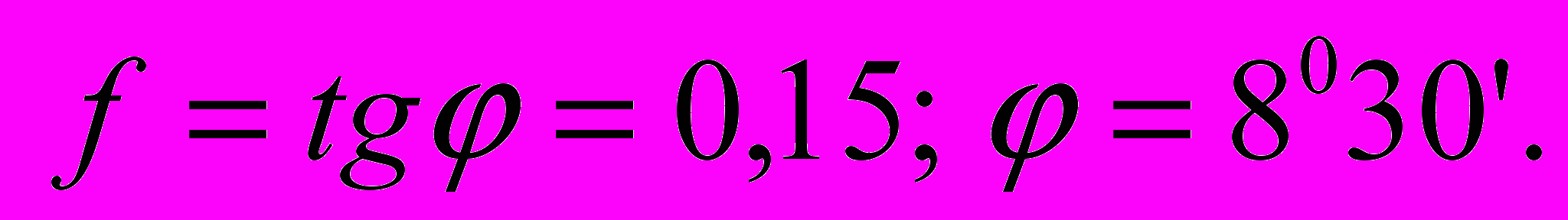
Тогда условия самоторможения соответственно будут:
для клина с трением на двух поверхностях
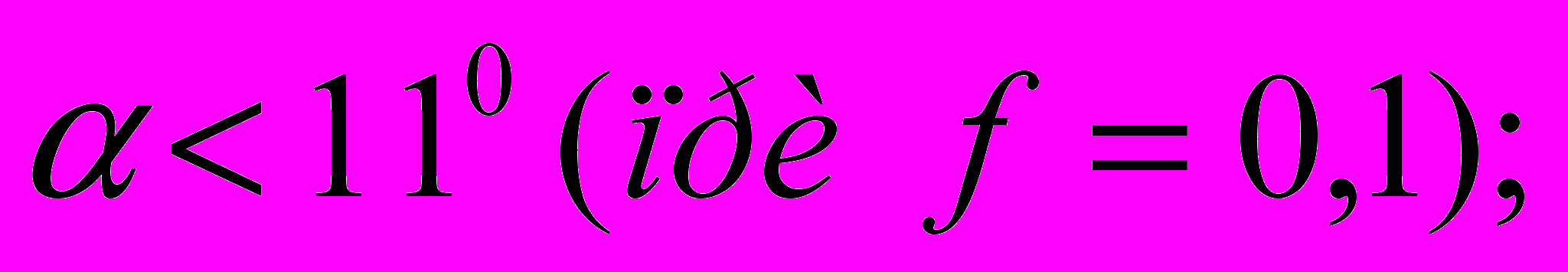
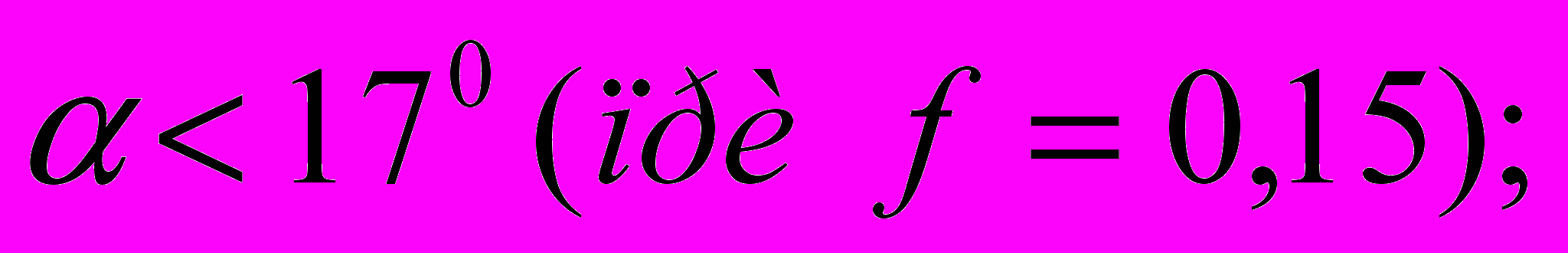
для клина с трением только на наклонной поверхности
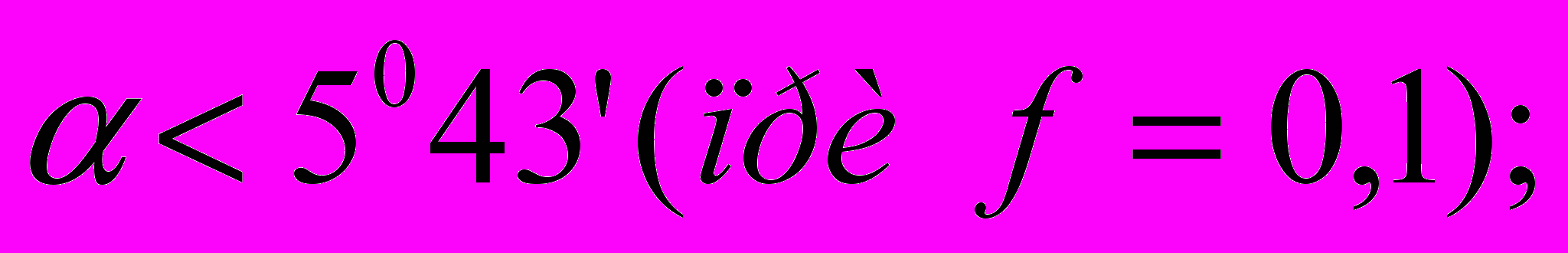
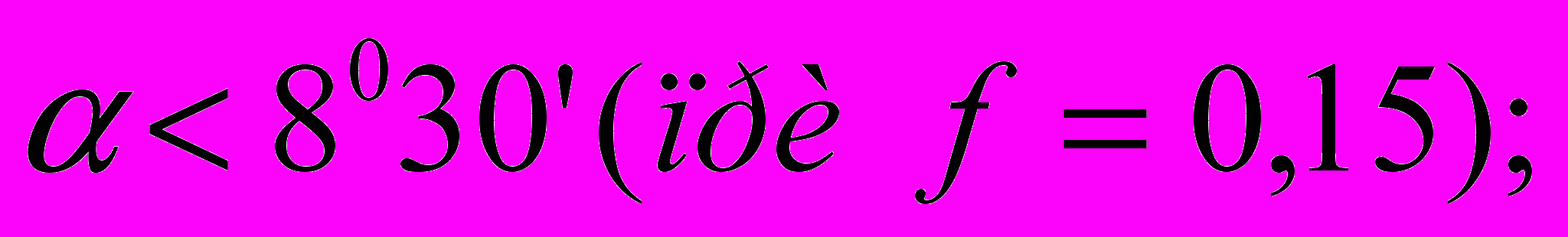
Для надежности заклинивания углы
 при расчетах берут меньше предельных, исходя из потребного запаса самоторможения (см. ниже).
при расчетах берут меньше предельных, исходя из потребного запаса самоторможения (см. ниже).Выталкивающая сила
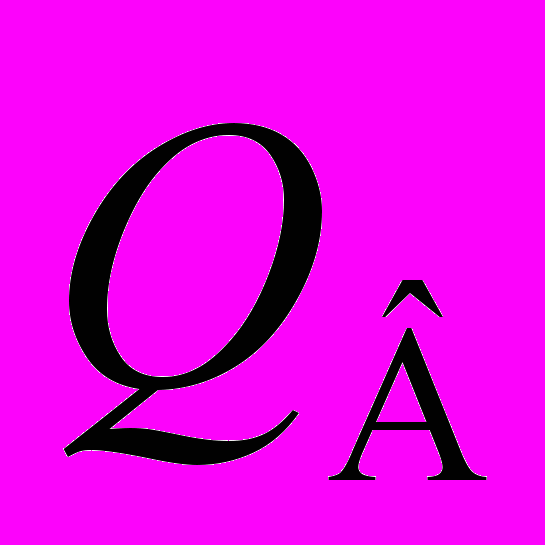 (рис. II.12, б), необходимая для расклинивания самотормозящего клина, определяется из следующих рассуждений.
(рис. II.12, б), необходимая для расклинивания самотормозящего клина, определяется из следующих рассуждений.Заменим силы N и F равнодействующей R и разложим ее на силы
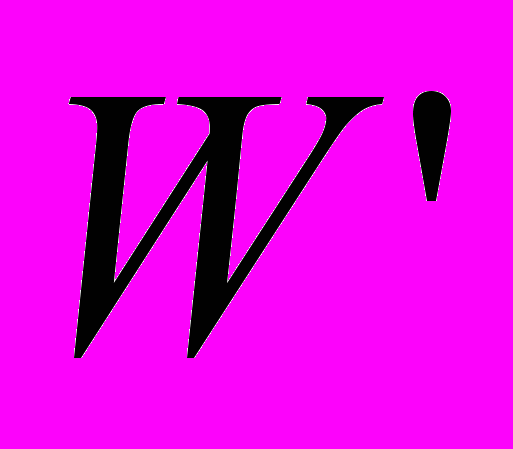 и F". На основании клина действуют нормальная сила реакции
и F". На основании клина действуют нормальная сила реакции 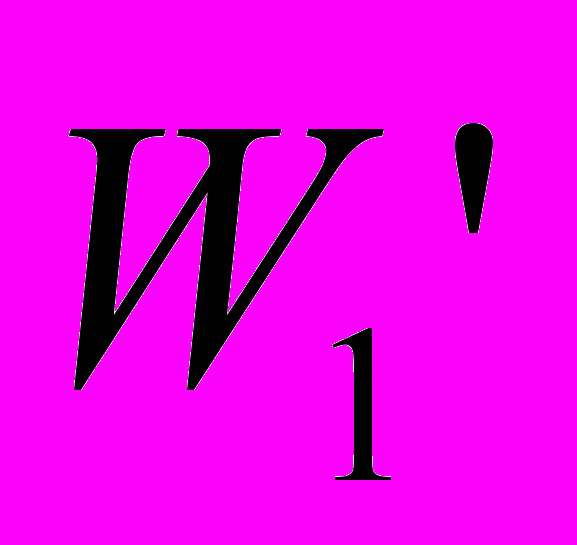 и сила трения
и сила трения 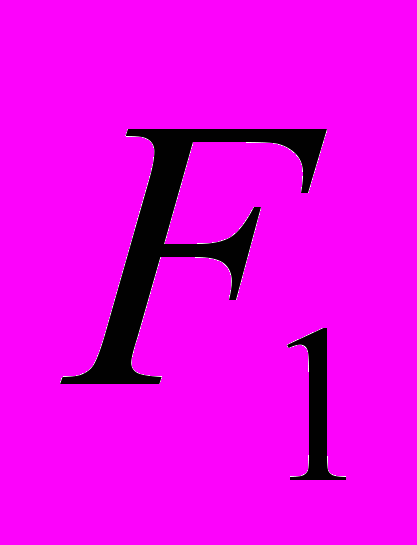 .
.Из условия равновесия клина находим:

Так как из схемы
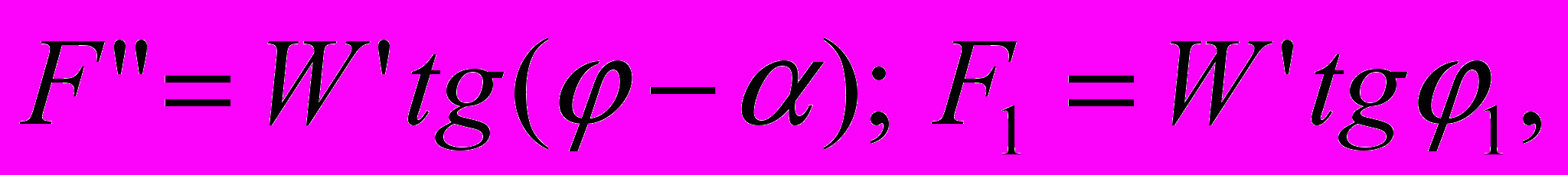
то
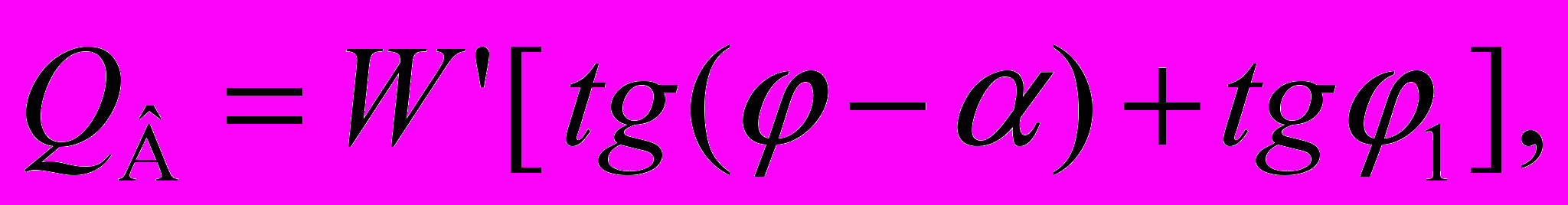 (5)
(5)или при
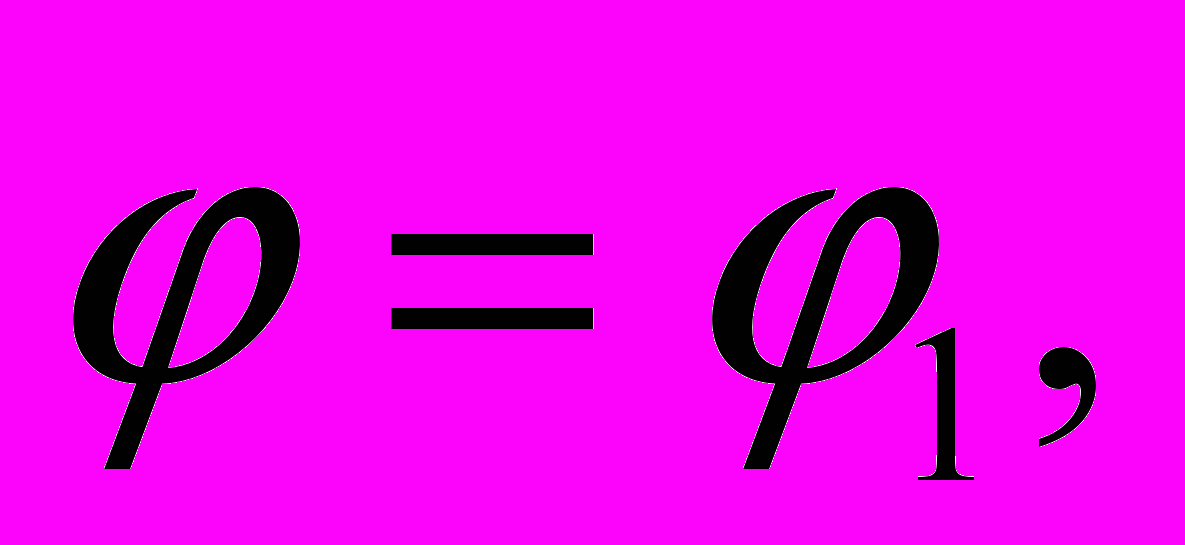
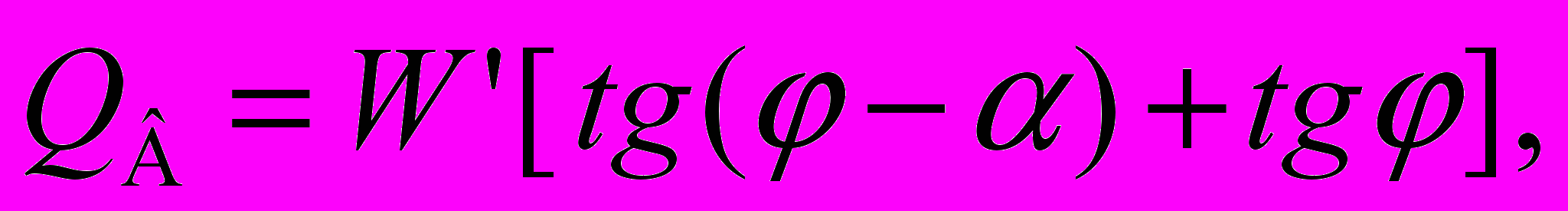 (6)
(6)Для клина с трением только по наклонной поверхности
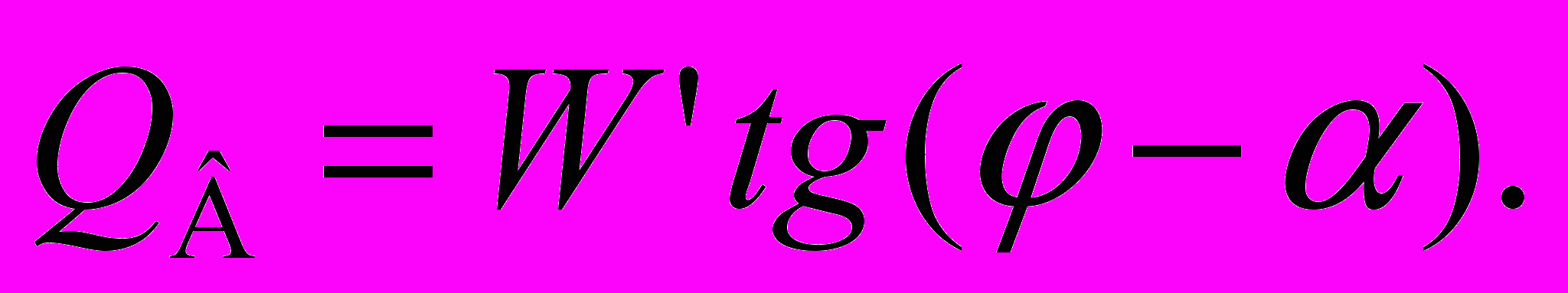 (7)
(7)Сила
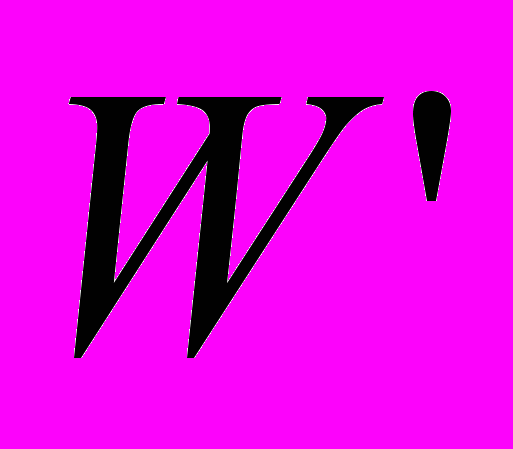 в формулах (6) и (7) подсчитывается по формуле (3). Для упрощения расчетов можно принимать
в формулах (6) и (7) подсчитывается по формуле (3). Для упрощения расчетов можно принимать 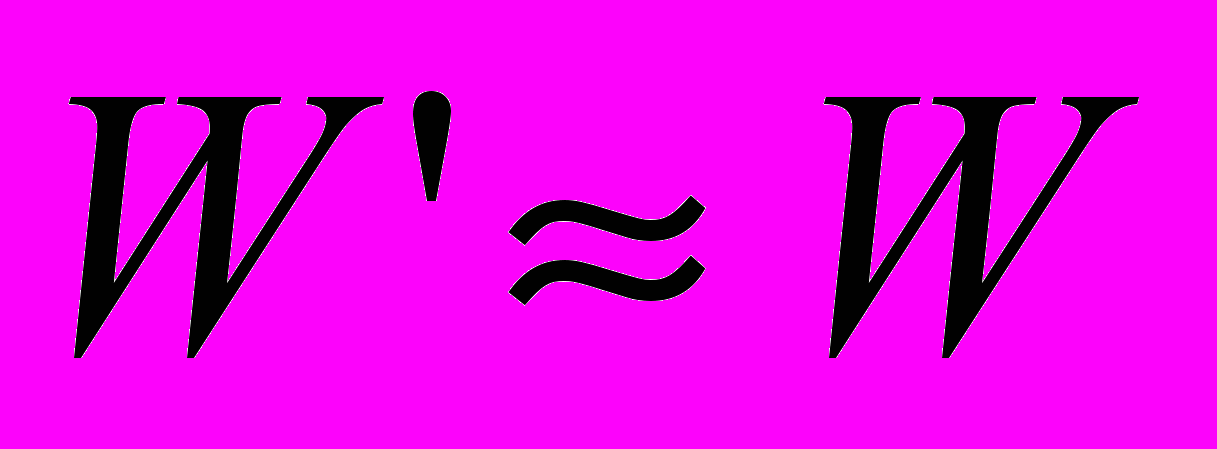 .
.- В какой из приведенных схем потребные силы зажима минимальны и максимальны?

Рис. 4.2. Схемы взаимодействия сил резания и зажима
- Приведите пример механизированных силовых механизмов.
- Сформулируйте условие самоторможения клина.
