К лекции 2 Структура себестоимости

Вид материала

Лекции

Содержание 1.2. Расчётная часть 2.2. Расчётная часть Таблица № 1 Давление паров над чистыми жидкостями, Рi = f(t) Таблица № 2 Результаты расчёта (х и у) 2.2.5. Определение высоты колонны 2.2.6. Материальный баланс 2.2.7. Расчёт диаметра верхней (d

Подобный материал:

• Методы учёта затрат и учёта себестоимости Понятие себестоимости. Виды себестоимости, 232.07kb.
• Нормативный метод калькулирования себестоимости как российский вариант «стандарт, 32.79kb.
• Такие разные лекции, 101.86kb.
• И. Г. Лекции по теории интегральных уравнений(7382) Петровский И. Г. Лекции, 55.62kb.
• Тема 7 Анализ себестоимости сельскохозяйственной, 555.39kb.
• «Статистические методы изучения уровня и динамики себестоимости продукции», 457.54kb.
• Планирование себестоимости продукции на предприятии. Ценовая политика на различных, 26.91kb.
• Задачи статистического изучения себестоимости. Основные показатели в анализе себестоимости, 92.6kb.
• Технический Университет «военмех», 1200.54kb.
• Управление персоналом вопросы для подготовки к экзамену, 23.69kb.

1.2. Расчётная часть

Задание. Определить поверхность теплопередачи кожухотрубчатого подогревателя (рис.1) для нагрева потока (2,6 кг/c) толуола от 20С до 100С с помощью конденсирующегося пара, имеющего температуру 115С.

При расчетах теплообменных аппаратов для установившегося процесса теплопередачи используют общее уравнение следующего вида:

Q = K Ft_ср ,

где Q – количество передаваемого тепла от горячего теплоносителя к холодному в единицу времени, вт или дж/c;

К – коэффициент теплопередачи вт/( с м²град) или дж/(с м²град). Его физический смысл – это количество тепла передаваемого через единицу поверхности теплообменника в единицу времени при температурном напоре (разности температур), равном одному градусу;

F – поверхность теплообменника, м²;

t_ср – средняя разность температур между паром и толуолом (усредненный температурный напор вдоль теплопередающей поверхности – длине теплообменника, или движущая сила процесса теплопередачи), град.

Последовательный расчет (Q), t_ср и затем (K) позволяет полчеить конечный результат, т. е. определить поверхность теплообменника (F).


1.2.1. Определение количества передаваемого тепла (Q) и t_ср

Количество тепла (Q), получаемого толуолом при его нагревании от начальной температуры t_н.тол. до конечной t_к.тол. можно рассчитать по уравнению:

Q = G_т. с_т. (t_н.тол. -t_н.тол.),

где G_т. – массовый расход толуола; кг/c

с_т. – средняя удельная теплоемкость толуола при средней температуре толуола t_ср.тол., дж./(кг град); для заданных условий t_ср.тол.= t_пара-t_ср. 72С;

с_т. = 1800 дж/кгград (по номограмме х₁ в [7], стр.562).

Среднюю (среднелогарифмическую) разность температур определяют по формуле:

,

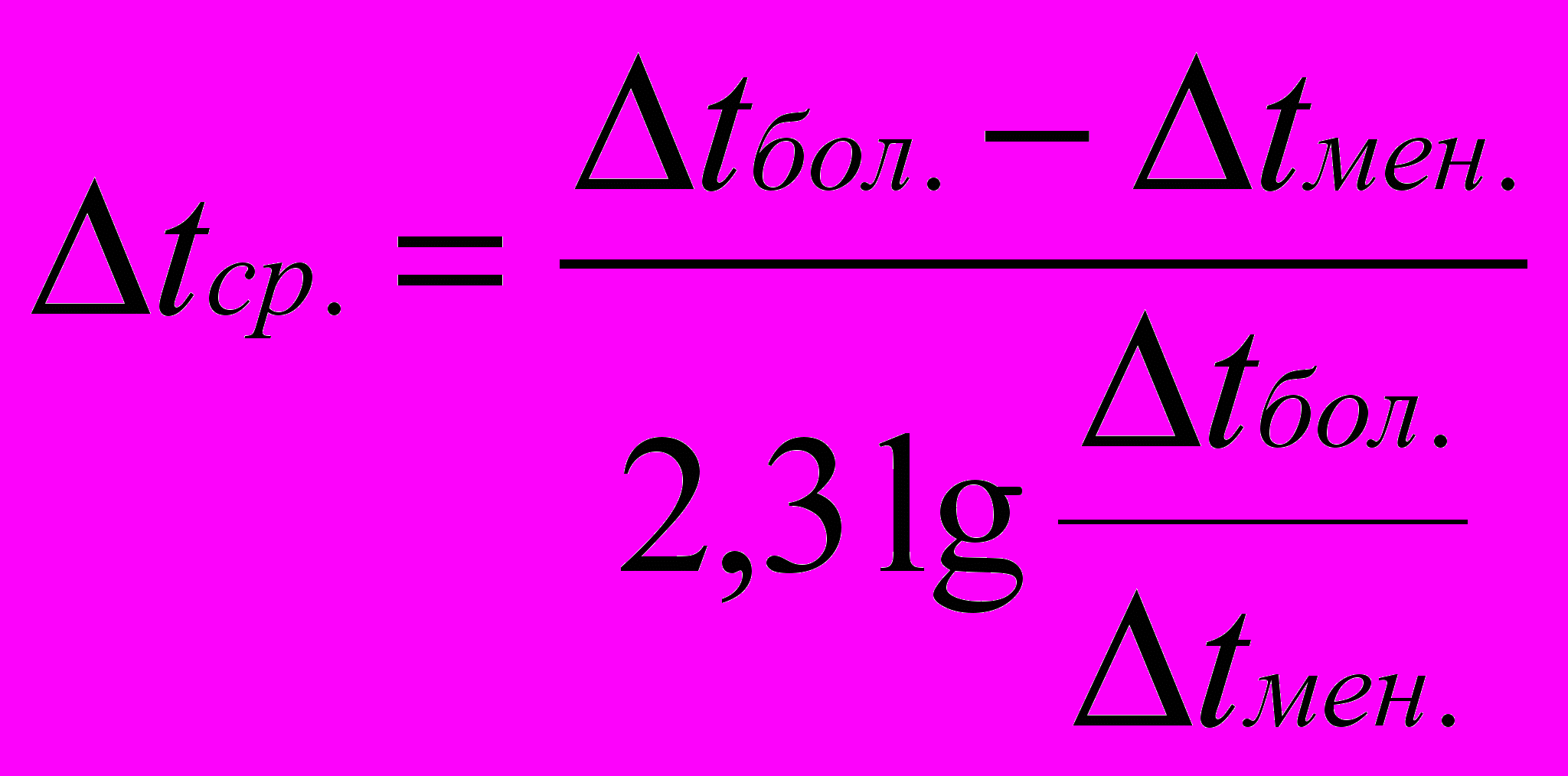где t_бол. и t_мен. – большая и, соответственно, меньшая разность температур на концах теплообменника, определяемая для случая противотока теплоносителей по графику:



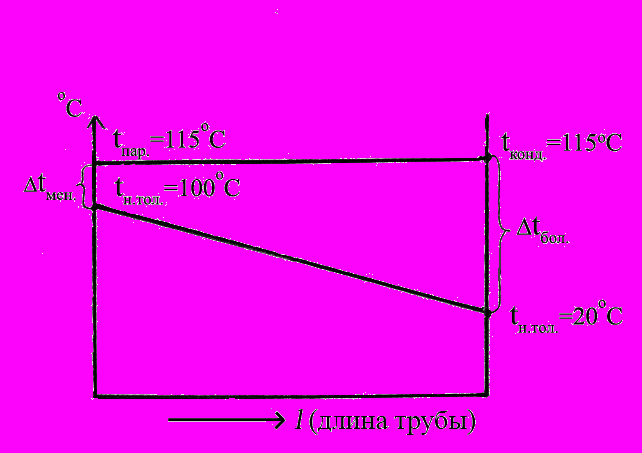
Рис. 2. График изменения температуры вдоль длины трубы


Расчет t_ср можно упростить при условии

0,5 t_бол./ t_мен. 2

В этом случае применима среднеарифметическая разность температур:

.

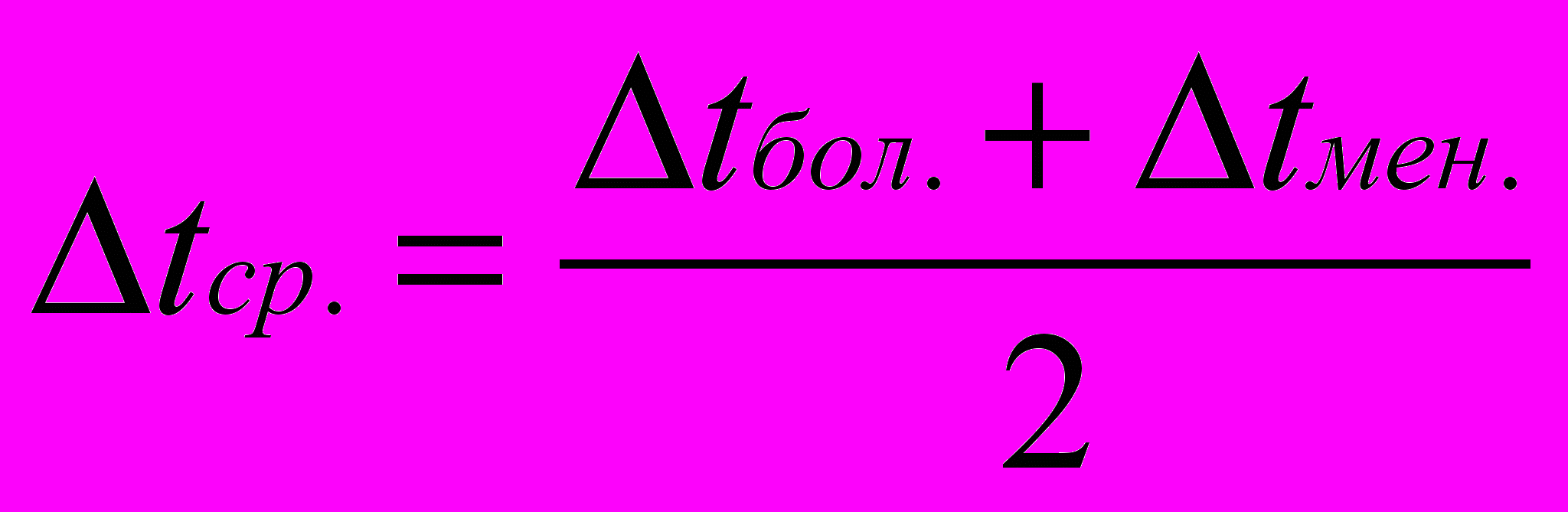После расчета t_ср определяем количество передаваемого тепла:

Q = 2,61800 t_ср

и анализируем размерность:

.

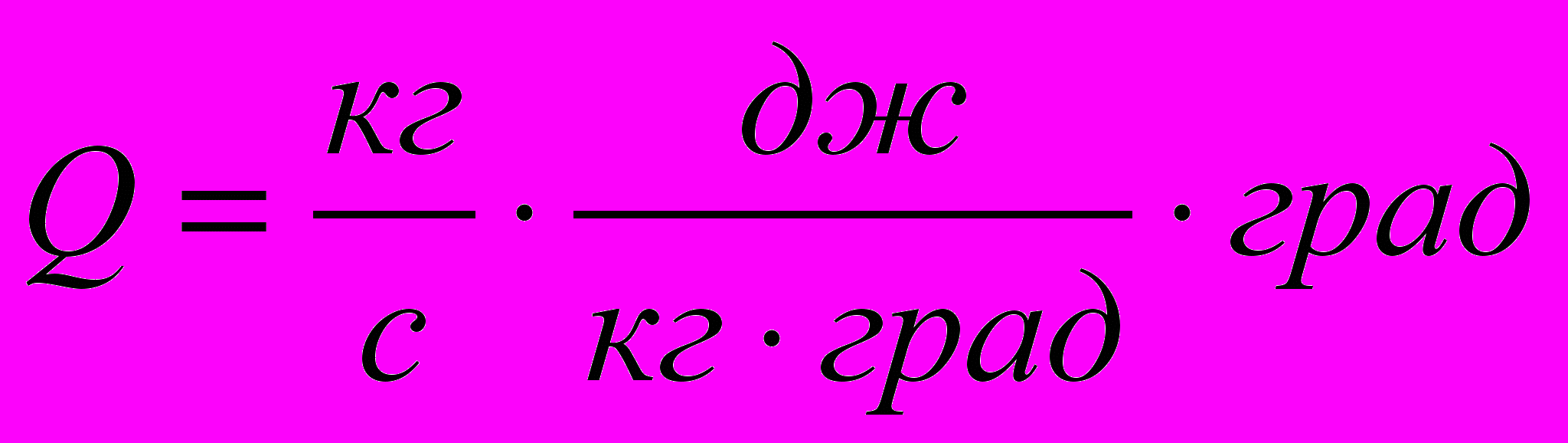После сокращений получаем Q [дж/c] или [вт].


1.2.2. Определение расхода теплоносителя

Полученная величина расхода тепла на нагревание известного массового потока толуола позволяет теперь определить требуемое для этой цели количество водяного пара G_г.п. по формуле:

G_г.п. = Q/r_в,

где r_в – удельная теплота конденсации водяного пара, равная при 115С 2222000 дж/кг (см.[7], стр.549, табл.57).


1.2.3. Определение коэффициента теплопередачи (К)

Коэффициент теплопередачи расчитывают по уравнению:

,

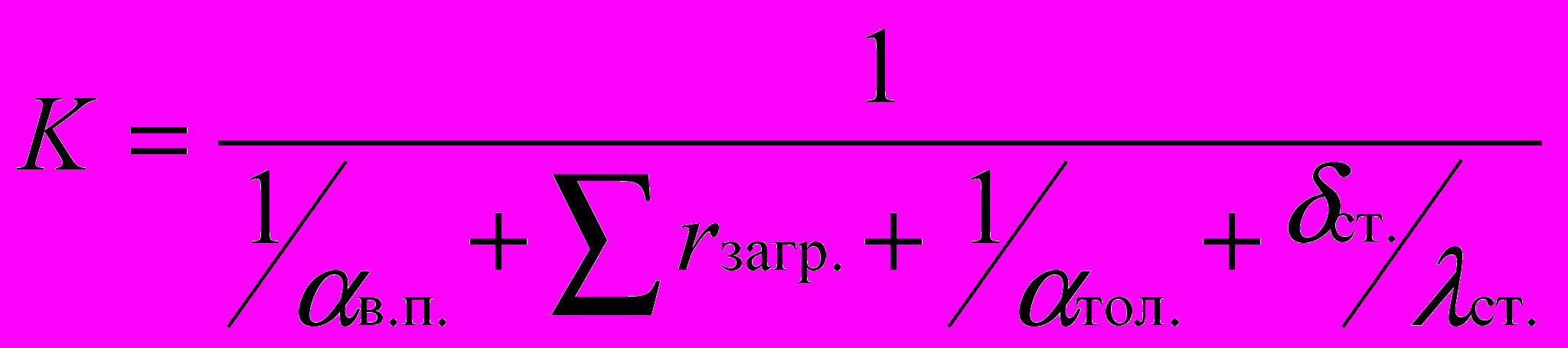где _в.п. и _тол. – частные коэффициенты теплоотдачи со стороны водяного пара и толуола, соответственно; _ст. – толщина стенки трубы; _ст. – коэффициент теплопроводности материала, из которого изготовлена труба.

1.2.3.1. Определение термического сопротивления стенки трубы

Для данного теплообменника выбираем стальные трубы размером 25 2 мм, где 25 – это внешний диаметр трубы в мм, а 2 – толщина ее стенки () в мм. Для стали выписываем коэффициент _ст.= 46,5 вт/мград (см.[7],табл. 28 на с. 523).

Тогда

_ст./_ст.= 0,002 м / 46,5 вт/мград = 4,30 × 10^-5 [(м²град)/вт].

В случае загрязненных теплоносителей на стенках труб образуется слой отложений, увеличивающий их термическое сопротивление при теплопередаче (r_загр)

r_загр. =1/r_в.п. + 1/r_тол. =1/5800 + 1/5800 = 3,45 × 10^-4 [вт/(м²град)],

где r_в.п. и r_тол. – сопротивление загрязнений со стороны конденсирующего пара и толуола (см.[7],табл. 31 на с. 531).

Перед тем, как определить коэффициенты (), проводят предварительное определение числа труб (n) в теплообменнике. Для этого запишем уравнение для секундного объёма (V_{тол. ,} м³/с) потока толуола внутри труб.

V_тол. = G_т./_т. = (d²Wn)/4 = 0,785 d²Wn ,

где _т. – плотность толуола для t_ср.тол.; d – внутренний диаметр труб, м ; W- линейная скорость потока толуола , м/с ;

Анализ размерности: G_{т. .}/_т = [кг/c / кг/м³] = [м³/c] ; d²Wn = [м² м/с] = [м³/c].

Откуда n = G_т./ ( 0,785 d²W).

Заменяя W на ее выражение (Rе)/(d), получаемое из формулы

Rе = (Wd)/,

имеем

n = G_т./ ( 0,785 d Rе_т) ,

где _т – динамический коэффициент вязкости толуола, равный 0,3710^-3 Па/с [или кг/(мс)] (см.[7], с. 556, рис V).

Задаваясь численным безразмерным значением критерия Рейнольдса (т.е., выбирая ламинарный, переходный или турбулентный режим движения толуола), рассчитываем (n), например, для развитого турбулентного режима R_e= 15000:

n = 2,6_./ ( 0,7850,02115000,00037);

Анализ размерности: [кг/c /м кг/мc] = [ штук ].

В случае подбора стандартного теплообменника по определенному выше числу труб, можно уточнить значение величины критерия Рейнольдса.

1.2.3.2. Определение коэффициента теплоотдачи со стороны жидкого теплоносителя (_тол)

Коэффициент теплоотдачи для толуола расчитываем из формулы:

,

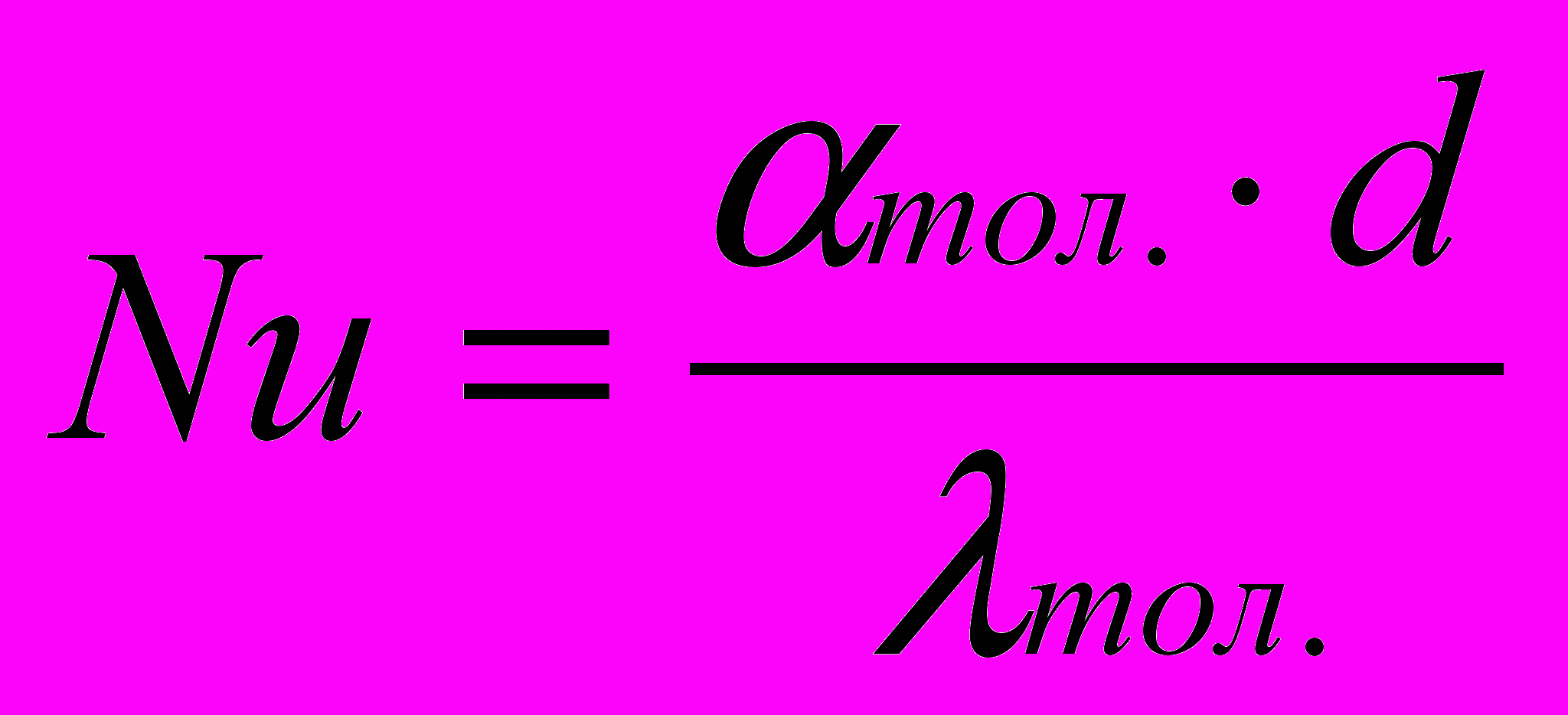где коэффициент теплопроводности _тол. = 0,125 вт/мград (см. рис.10, стр.561).

Откуда

_тол= ( Nu_тол)/d = ( Nu0,125)/0,021.

Поскольку толуол проходит внутри труб, не меняя агрегатного состояния, для расчета критерия Нуссельта (Nu) пользуются критериальными уравнениями:

Nu = 0,021 Re^0,8Pr^0,43(Pr/Pr_cт.)^0,25_l (при Re10⁴) или

Nu = 0,008 Re^0,9Pr^0,43 (при 10⁴  Re 2300)

В случае Rе  2300 принимаем Nu = 4 ([7], с. 188).

Принимаем _l = 1,0 ([7], с. 157) и (Pr/Pr _cт.)^0.25 = 1,0 (для нагревающихся жидкостей).

Критерий Прандтля (Рr =4,5) находим по [7] (рис. XIII, стр.564).

1.2.3.3. Определение коэффициента теплоотдачи со стороны конденсирующего пара (_в.п.)

Расчет проводят для пучка горизонтальных труб, пользуясь формулой ([7], глава 4):



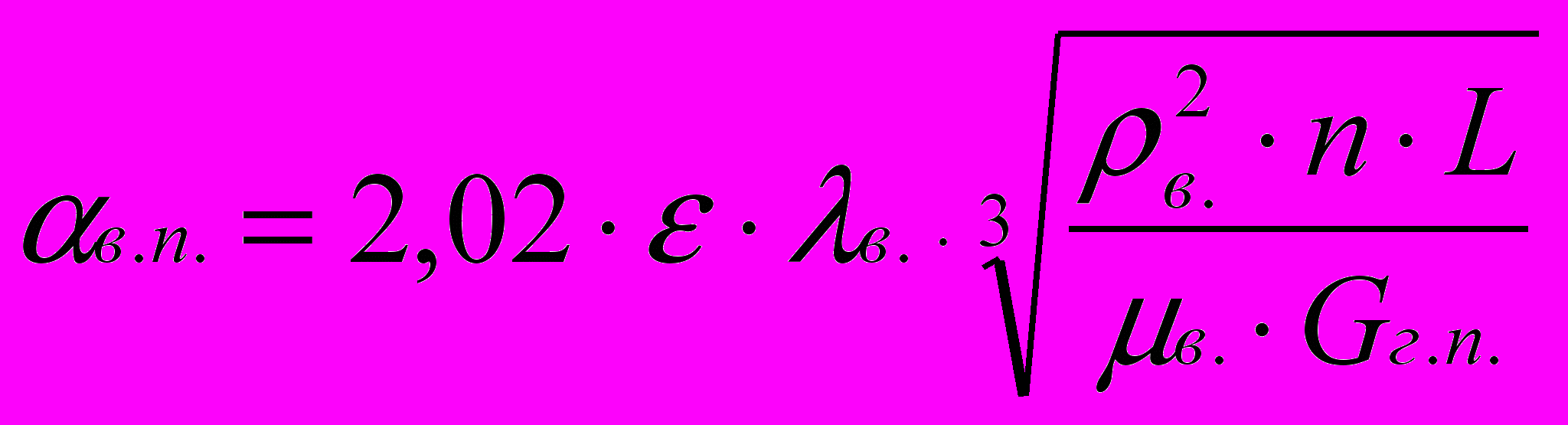
 = 0,6 – коэффициент, зависящий от расположения и числа труб в вертикальном ряду;

_в = 0,685 вт/мград – коэффициент теплопроводности конденсата (рис.10, стр.561);

_в. = 947 кг/м³ – плотность конденсата ([7], табл.39, стр.537);

L – длина трубы (задаемся длиной  1,0; 1,5; 2,0; 3,0; 4,0; 6,0 м);

_в = 0,24410^-3 кг/мс или Пас – динамический коэффициент вязкости конденсата ([7], табл.39,стр.537).




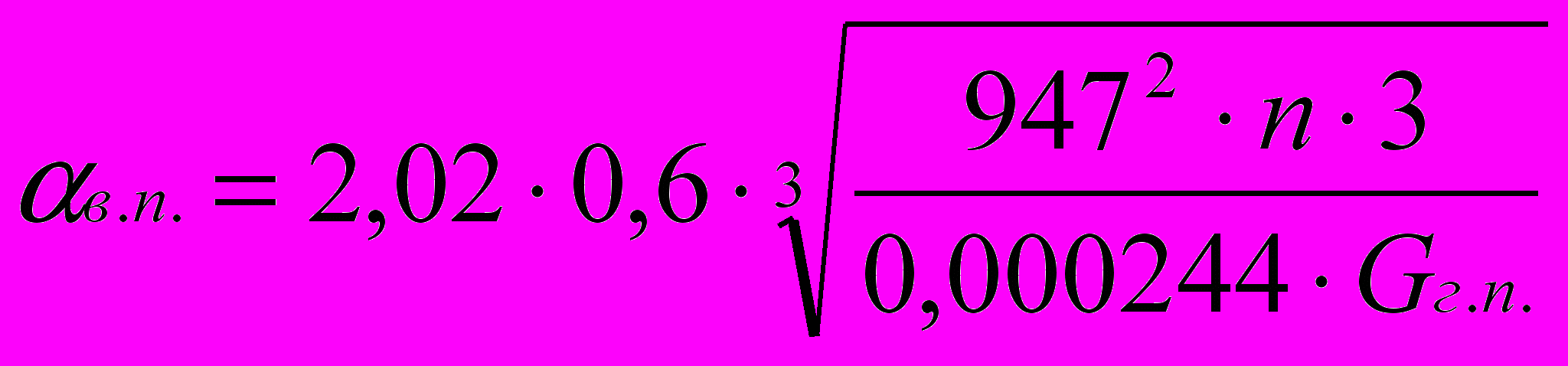
1.2.4. Нахождение требуемой площади поверхности подогревателя (F)

В заключении расчета теплообменника в первом приближении определяем площадь поверхности аппарата по формуле

F = Q/Kt_ср.

По найденной поверхности (F) можно подобрать стандартный теплообменник по каталогам и провести расчет во втором приближении по уточненным значениям числа труб, их длины и диаметру.

В работе [5] приведены методические указания по составлению компьютерной программы для расчета теплообменников на ЭВМ.


К лекции 8


Разделение жидкой гомогенной смеси веществ методом перегонки (дистилляции) основано на различии температур их кипения (летучести). В случае простой перегонки бинарной смеси происходит однократное испарение низкокипящего компонента (НК) с его последующей однократной конденсацией при охлаждении паров в вынесенном теплообменнике-конденсаторе. Высококипящий компонент (ВК), как правило, почти полностью остаётся в перегонном кубе при условии, что разница между температурами кипения НК и ВК велика. Однако при не очень больших различиях в их температурах кипения прибегают к более сложному случаю перегонки – ректификации, при которой наблюдается многократное частичное испарение и частичная конденсация разделяемых компонентов (НК и ВК). В этих случаях над перегонным кубом расположена колонна с насадкой или с тарелками ситчатого или колпачкового типа. Горячие пары смеси ВК и НК, образующиеся в кубе, поднимаются вверх по колонне и контактируют с относительно холодной жидкой смесью НК и ВК, опускающейся вниз. При этом между паровой и жидкой фазами, движущимися противотоком, происходят теплообменные процессы – пары охлаждаются, а жидкость нагревается, что в свою очередь вызывает массообменные процессы. По закону Коновалова при охлаждении паров конденсируется, прежде всего, ВК, а из нагреваемой жидкой фазы испаряется главным образом НК. Таким образом, поднимающийся вверх по колонне пар постепенно обогащается НК, а опускающаяся вниз жидкость обогащается ВК. В верхней части колонны отбирают сконцентрированный НК, который в виде флегмы частично возвращают в верхнюю часть колонны. Из кубовой части колонки отбирают ВК.

На рис.3 представлена схема установки ректификации непрерывного действия для разделения бинарной смеси с обозначениями массового (G) и мольного (G_m) потока исходной смеси, мольных потоков дистиллята (D), кубовой жидкости (W_o), паров в колонне (G_p), массовых (a) и мольных (х) концентраций этих потоков (для бинарной смеси приводят лишь долю НК, т.к. х_н.к.+х_в.к.=1, или 100%).

На рис.3 изображена схема непрерывно действующей ректификационной установки с тарельчатой колонной ректификации:



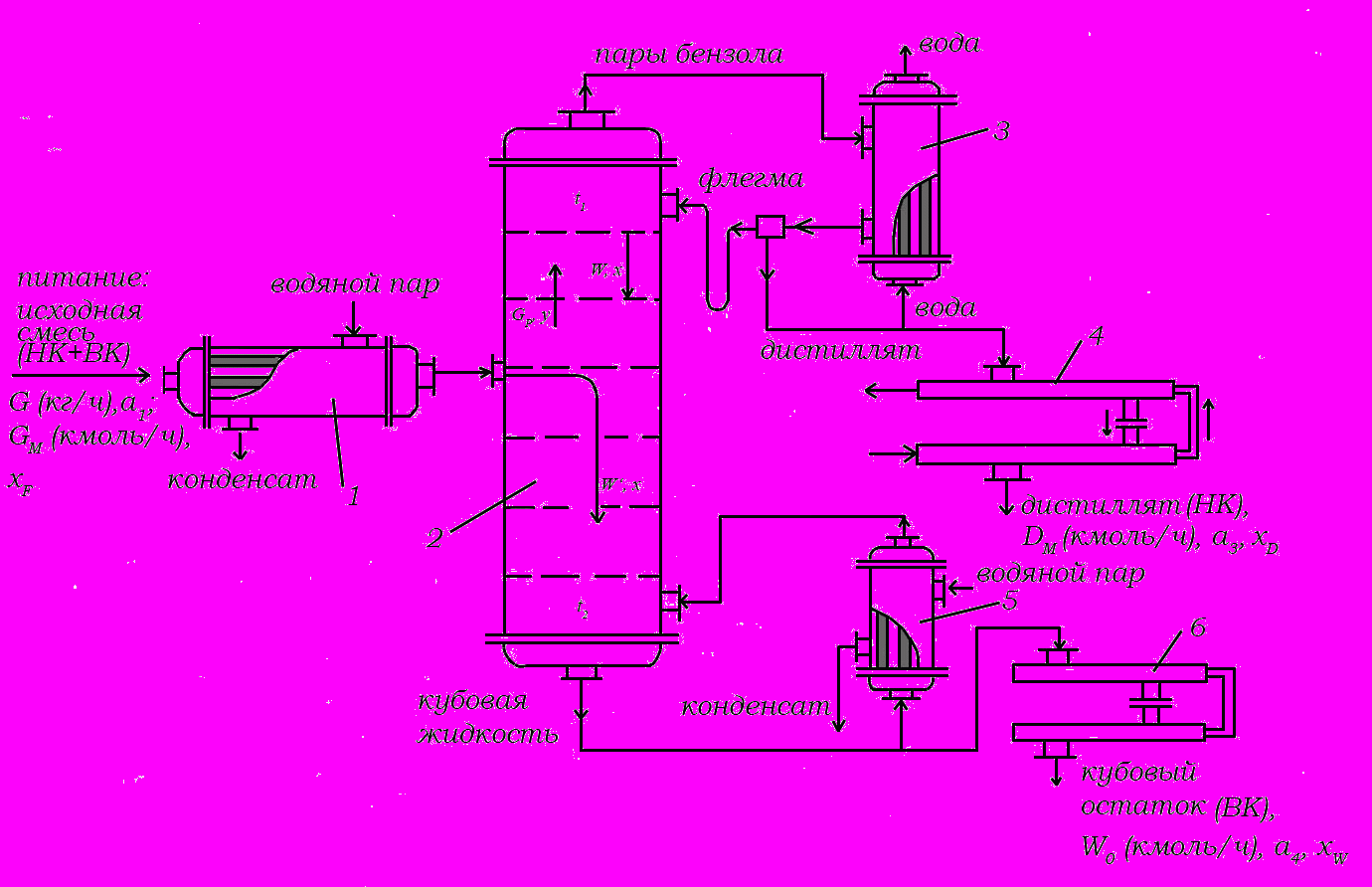
Рис.3. Схема ректификационной установки:

1 – подогреватель; 2 – колонна ректификационная; 3 – дефлегматор; 4 , 6 – холодильники «труба в трубе»; 5 – (кипятильник вынесенный).


2.2. Расчётная часть

2.2.1. Пример-задание

Определить графическим путём число тарелок ректификационной колонны непрерывного действия, её высоту и диаметр для разделения под атмосферным давлением 10000 кг/ч (G) жидкой смеси, состоящей из бензола (a₁ = 40% масс.) и толуола. Содержание бензола в дистилляте (a₃ = 96% масс.), содержание толуола в кубовом остатке 98% масс. (a₄ = 2% масс.). Исходная смесь подаётся в колонну при температуре кипения.


2.2.2. Пересчет массовых долей в мольные

Процесс ректификации удобнее рассчитывать в мольных потоках и концентрациях, т.к. отношения мольных теплот парообразования разделяемых компонентов к их температурам кипения не очень сильно отличаются друг от друга (правило Трутона). Это допущение приводит к тому, что для испарения 1 кмоля НК расходуется теплота, выделяемая при конденсации 1 кмоля ВК. Поскольку мольные теплоёмкости обоих компонентов близки (при допущении, что они мало изменяются с температурой по высоте колонны), то мольные потоки пара и жидкости допустимо мало изменяются по высоте колонны.

В связи с этим производят пересчёт массовых концентраций (a_i) в молярные (х_i).

По определению молярная доля – это отношение числа кмолей данного компонента (n_i) в смеси (n_i = a_i/M_i) к общему числу кмолей всех компонентов (n):



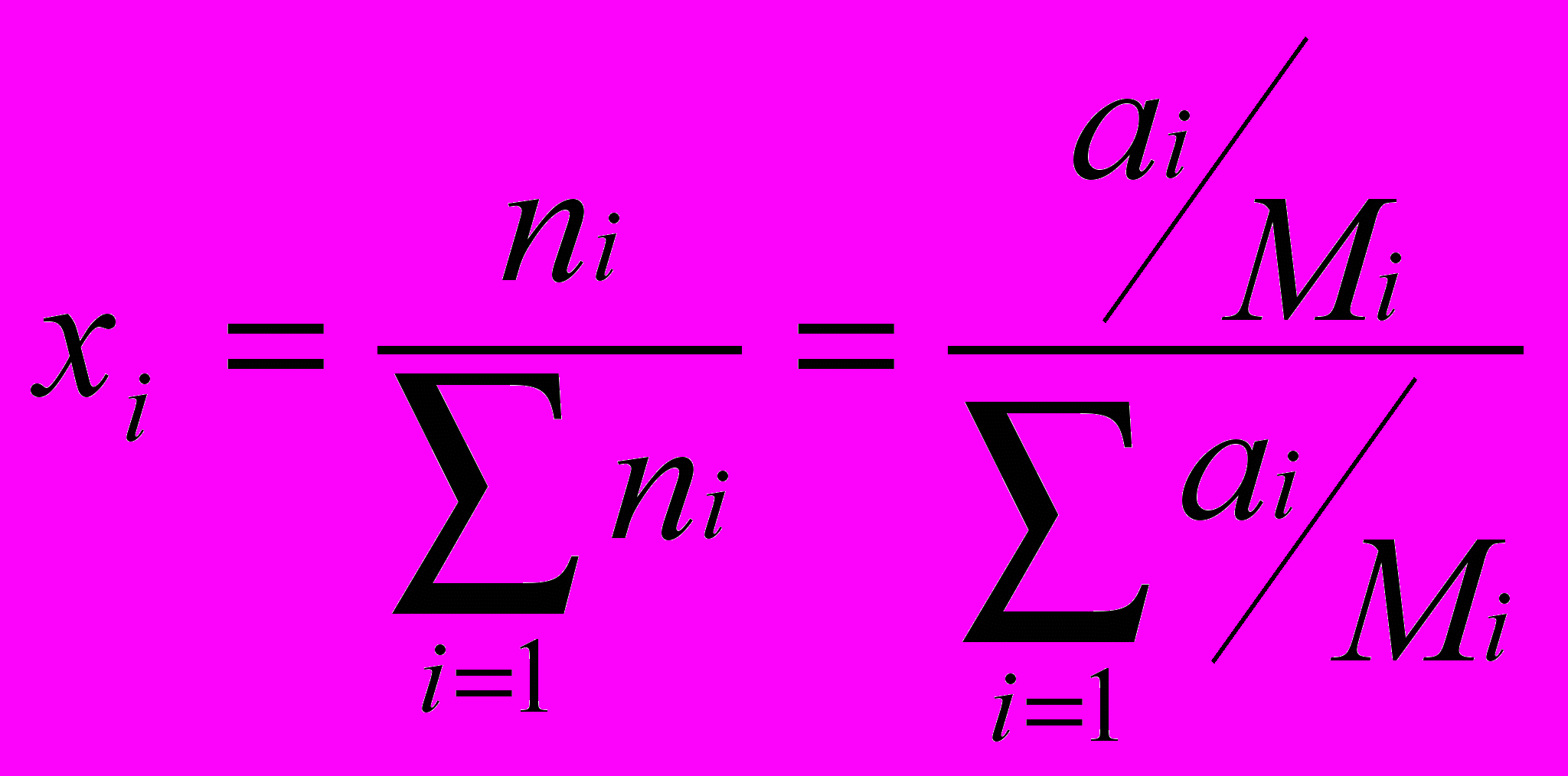
Для бинарных смесей (i=2) формула имеет вид



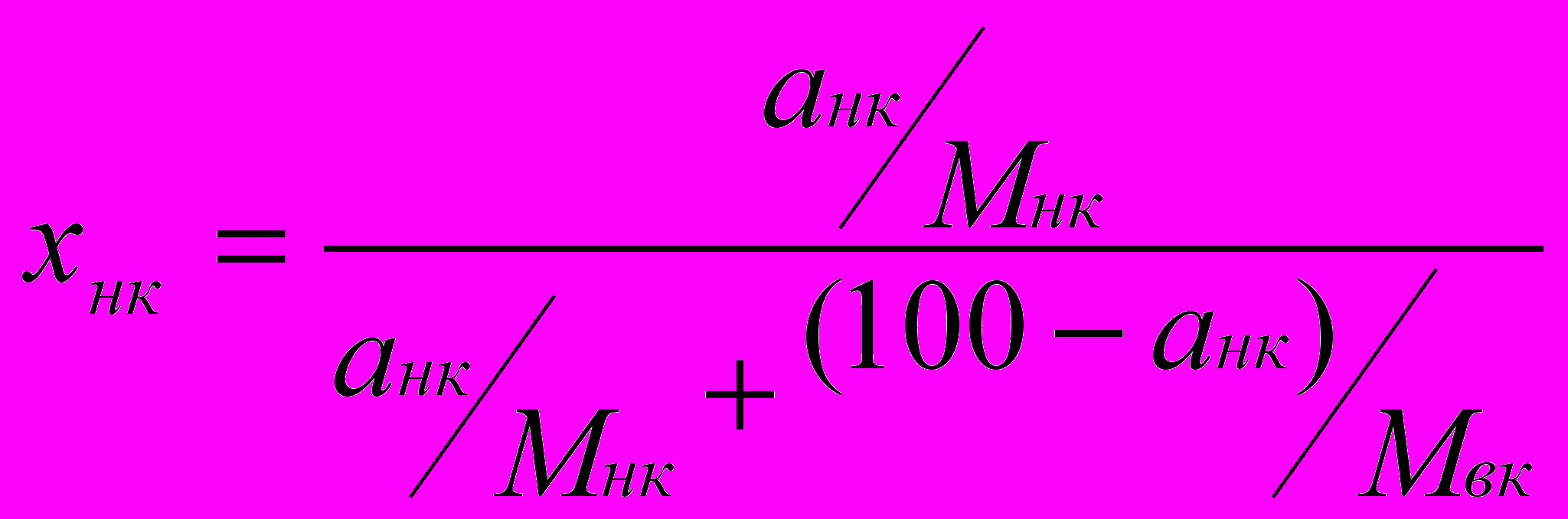
Выражение концентраций питания, дистиллята и кубового остатка в мольных долях. В выбранном примере имеем:

а) для питания:

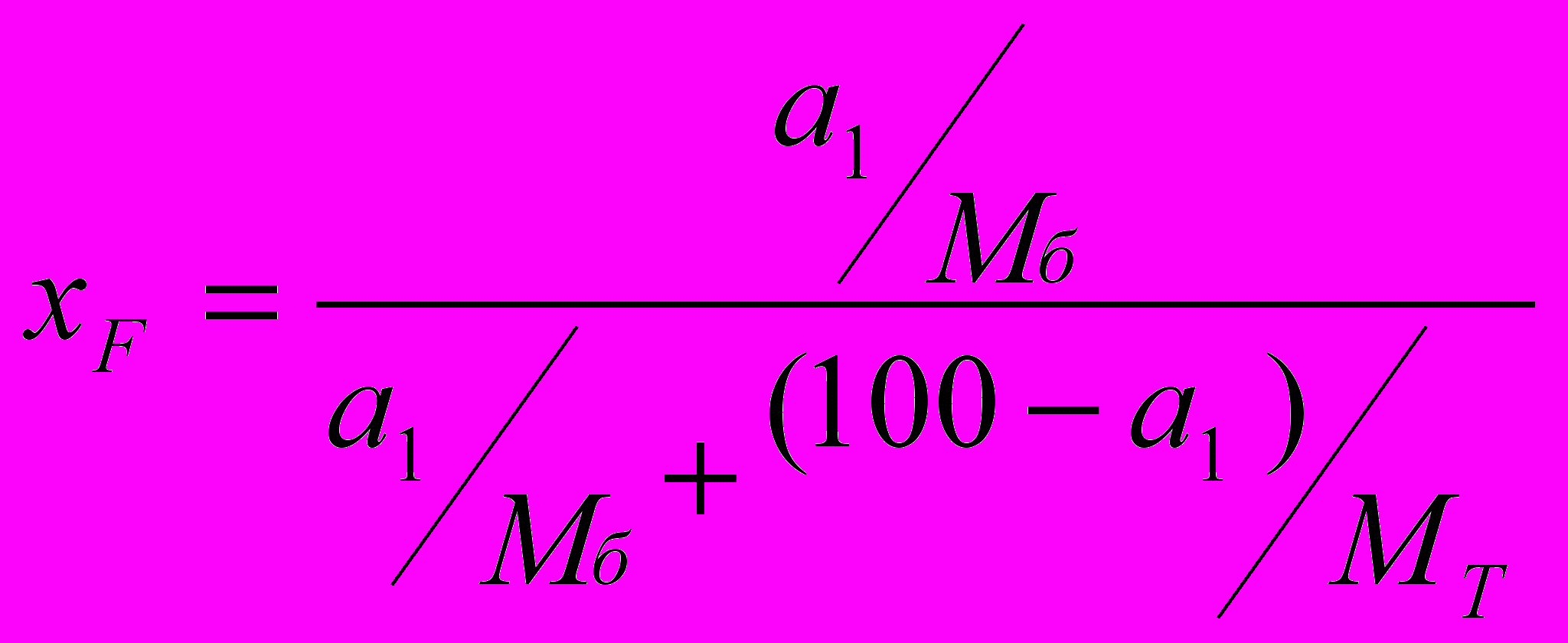
где х_F – мольная доля бензола в питании;

а₁ – исходная весовая концентрация бензола (%);

М_б – молекулярная масса бензола;

М_т – молекулярная масса толуола;

б) Для дистиллята:

;

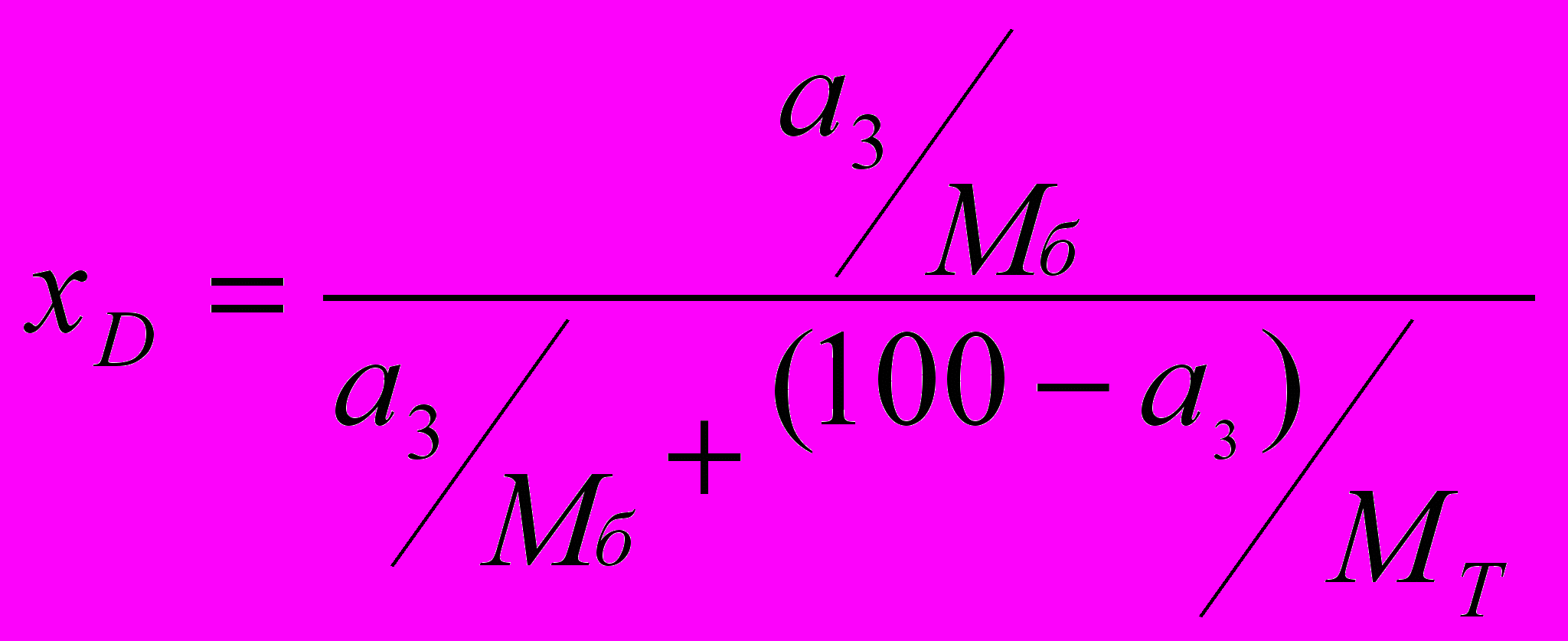в) для кубового остатка:



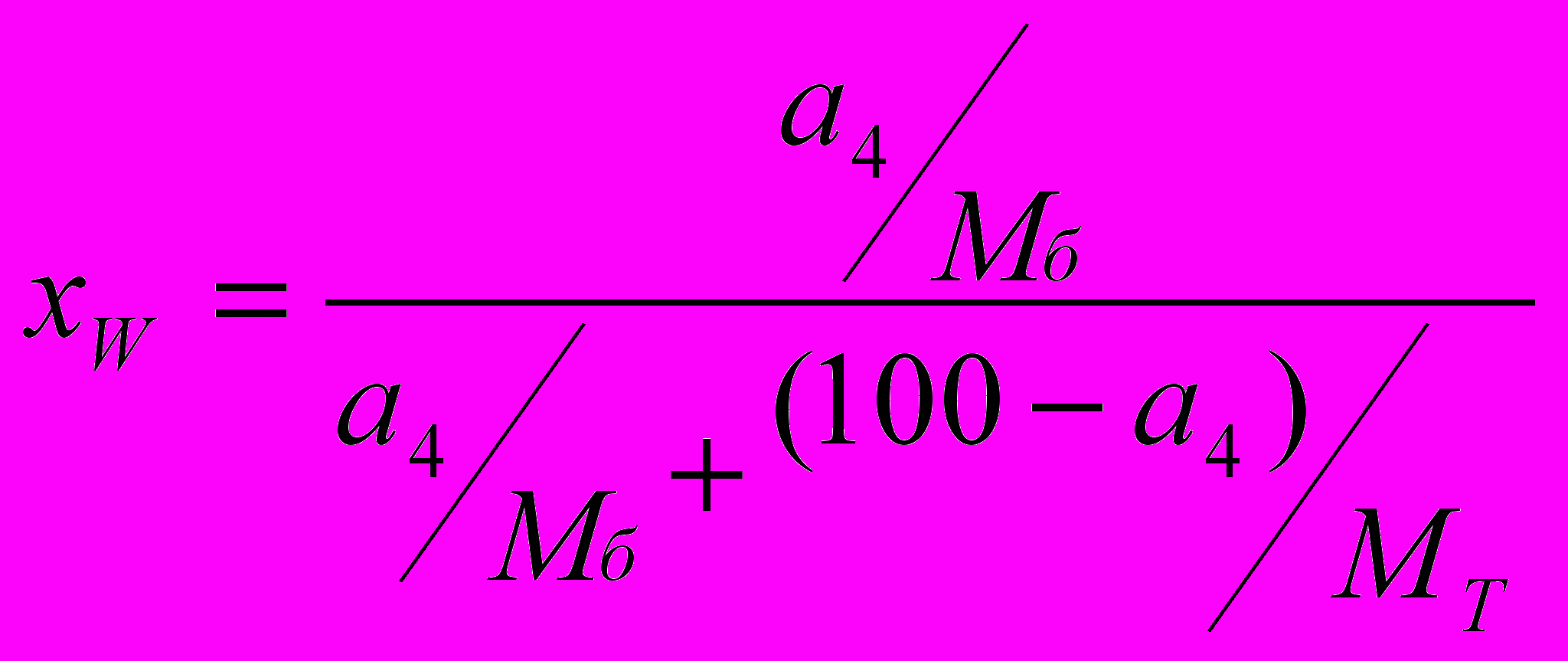
Рассчитанные значения х_F, х_D,, х_W лежат в пределах от 0 до 1,0.


2.2.3. Определение равновесных концентраций системы бензол-толуол для жидкой (х) и паровой (y) фаз в зависимости от температуры


По закону Рауля парциальное давление (р_i) паров компонента над жидкой смесью пропорционально его содержанию (х) в смеси и температуре (в приближении к идеальным смесям). Для бинарной смеси можно записать:

р_нк = Р_нк∙х_нк и р_нк = Р_вк∙(1-х_нк),

где Р_нк и Р_вк – давление паров, соответственно , НК и ВК над чистыми жидкими НК и ВК при данной температуре.

Полное давление пара смеси НК и ВК (Р_общ.) над их жидкой смесью составит

Р_общ = р_нк + р_вк = Р_нк∙х_нк + Р_вк∙(1-х_нк),

откуда Х_нк=(Р_общ-Р_вк)/(Р_нк-Р_вк). Эта формула показывает зависимость изменения молярной концентрации НК (и ВК) в жидкой фазе от температуры по всей высоте колонны ректификации.

Изменение молярной концентрации у_нк по определению представляет собой отношение парциального давления компонента (р_нк) к общему давлению пара над жидкостью (Р_общ).

y_нк = р_нк/Р_общ = Р_нк ∙х_нк/Р_общ

В таблице 1 приведены величины давления паров (Р_i) разделяемых компонентов над чистым (индивидуальным) жидким компонентом.


Таблица № 1

Давление паров над чистыми жидкостями, Р_i = f(t)

Вещество	Давление пара (мм рт. ст.) при Т, 0С
	60	70	80	90	100	110	120	130
Ацетон	861	1190	1611	2142	2797	3594	4547	5670
Бензол (Рб)	389	547	754	1016	1344	1748	2238	2825
Бутанол	59	112	165	255	386	572	433	1150
Вода	149	234	355	526	760	1075	1489	2026
Дихлорэтан	538	480	664	906	1220	1600	2040	2580
Изопропанол	289	455	692	1021	1480	2020	2790	3800
Метанол	625	927	1341	1897	2621	3651	4751	6242
Толуол (Рт)	147	204	299	408	571	751	973	1350

По результатам расчёта (х) и (у) составляется таблица 2 и строится диаграмма (t – x,y), рис. 4 и диаграмма равновесия (х – у), рис. 5.


Таблица № 2

Результаты расчёта (х и у)

T,0C	Pб	Рт	Робщ.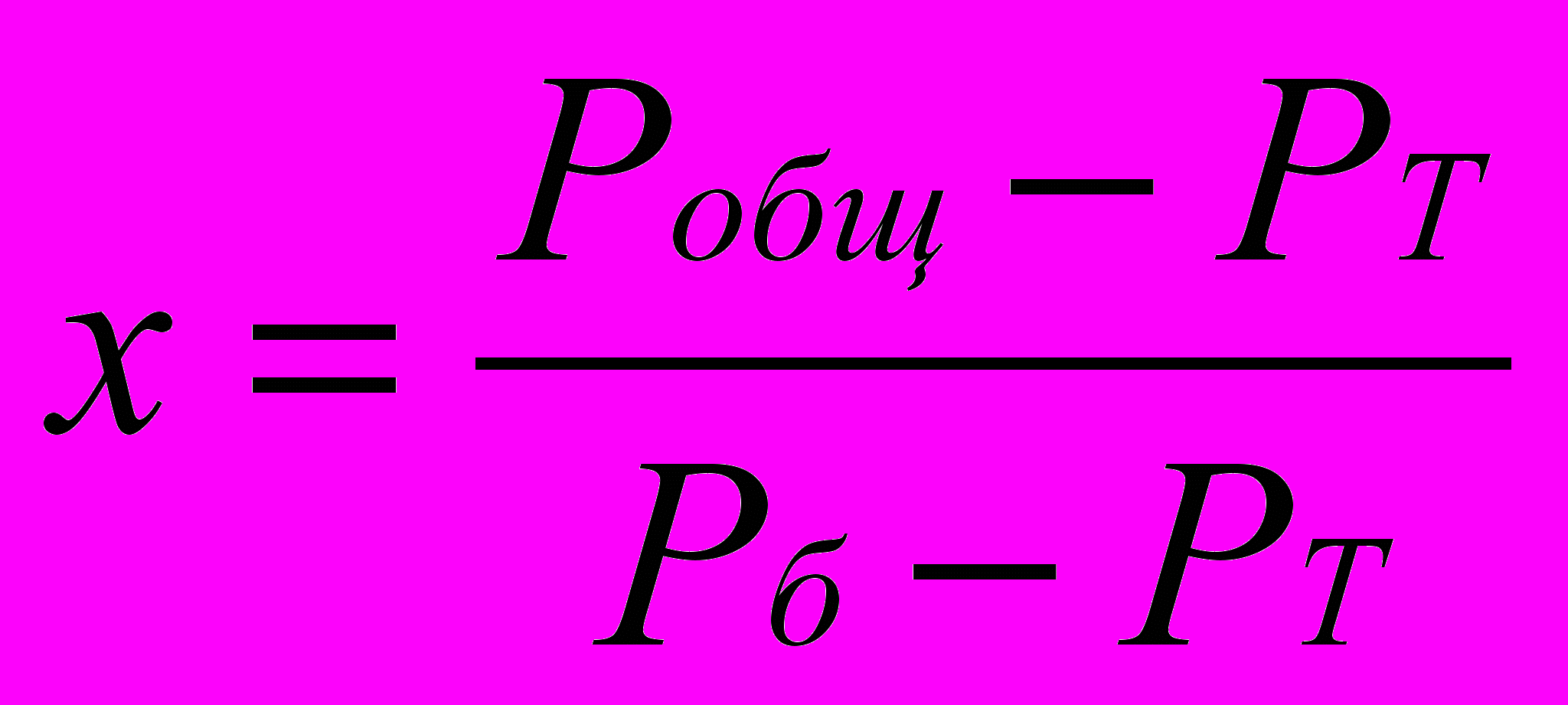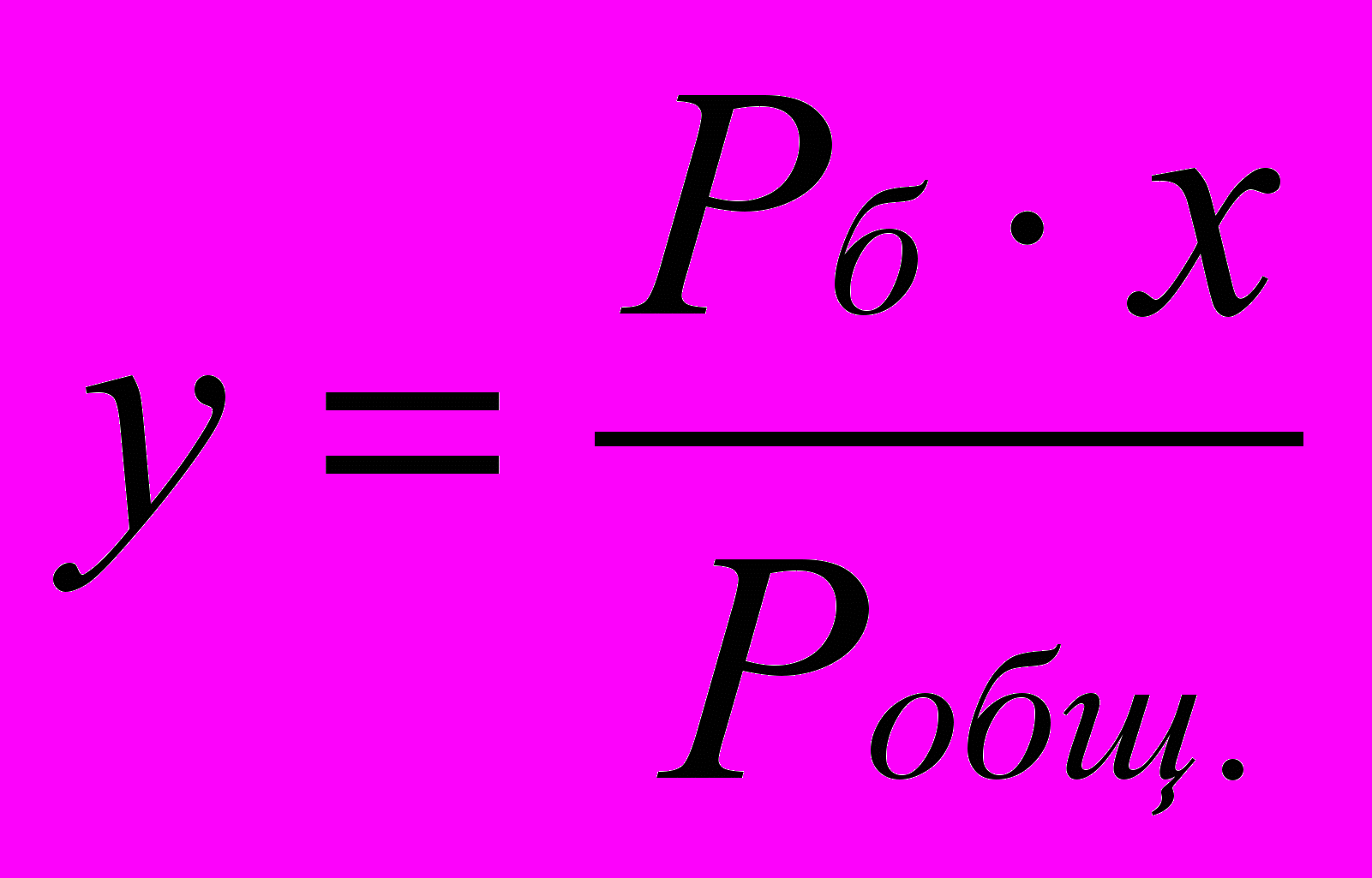
80	760	300	760	1	1
84	852	333	760
88	957	379,5	760
92	1078	432	760
96	1204	492,5	760
100	1344	559	760
104	1495	625	760
108	1695	704,5	760
110	1748	760	760	0	0

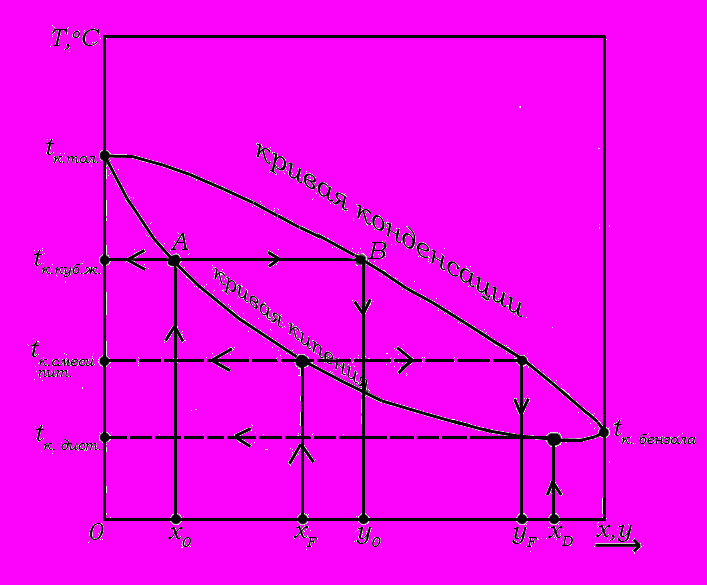
Рис.4. Диаграмма (t – x,y)



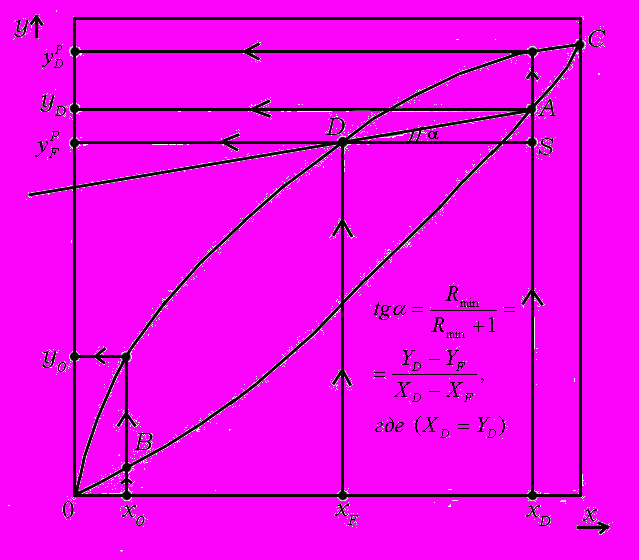
Рис.5. Диаграмма равновесия (х, у) и определение равновесных концентраций для расчёта R_min


По диаграмме (t – x,y) можно определить температуры кипения бинарных жидких смесей любого состава, а также составы получающихся при этом паров, например: х_оАВу_о. По диаграмме (х, у), на которой линией равновесия является кривая ОДС (прямая линия ОВАС – вспомогательная диагональная линия), определяют равновесные концентрации (например, х_F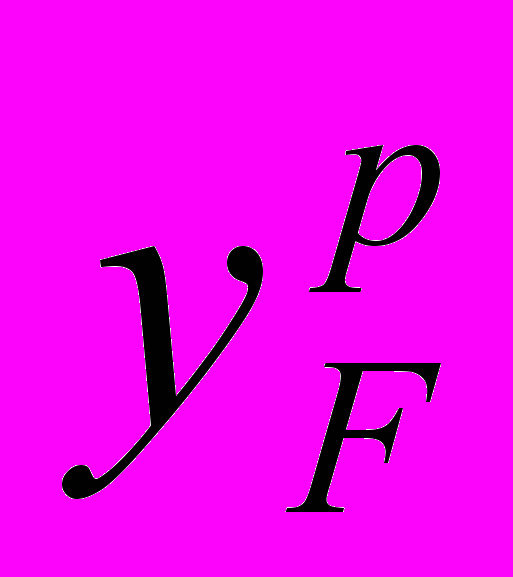), минимальное флегмовое число (R_min) и число теоретических ступеней (n_тт) массообмена (после построения рабочих линий для верхней и нижней части колонны).


2.2.4. Определение числа теоретических ступеней графическим построением

а) Сначала проводят расчёт рабочего флегмового числа (R).

Для этого определяют минимальное флегмовое число R_min), проводя из точки х_F диаграммы равновесия (х – у) проводят перпендикуляр до пересечения с линией равновесия в точке D (рис.4). Далее из точки D проводим прямую, параллельную оси абсцисс, до пересечения с осью “у”. Точка пересечения 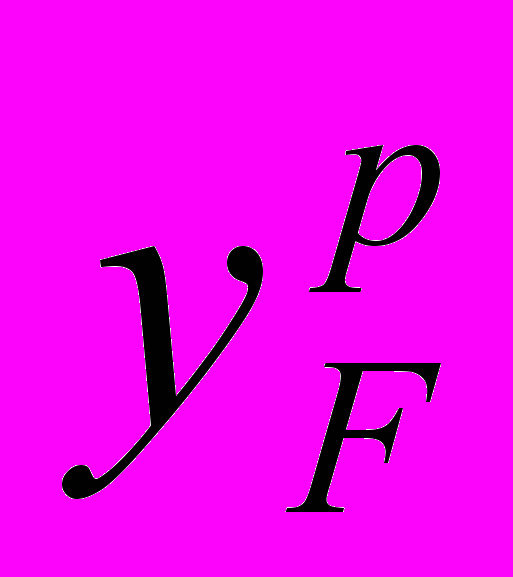даёт значение равновесной концентрации бензола в паре. Рабочее флегмовое число изменяется от R=∞ (когда весь дистиллят возвращается в колонну, и рабочая линия совпадает с диагональю, это режим начала ректификации) до R_min, когда рабочая линия проходит через точки А и D (этот режим требует слишком большого числа тарелок). Построив прямоугольный треугольник ASD можно определить через соотношения:

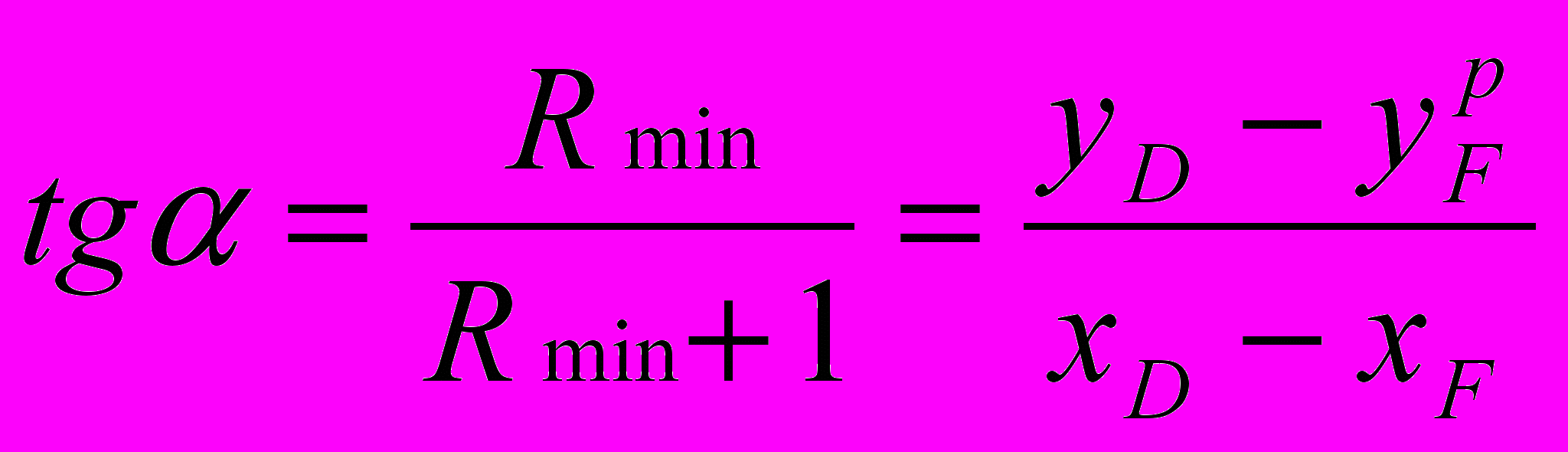, где y_D=x_D.

По найденным величинам рассчитываем R_min [7]:

.

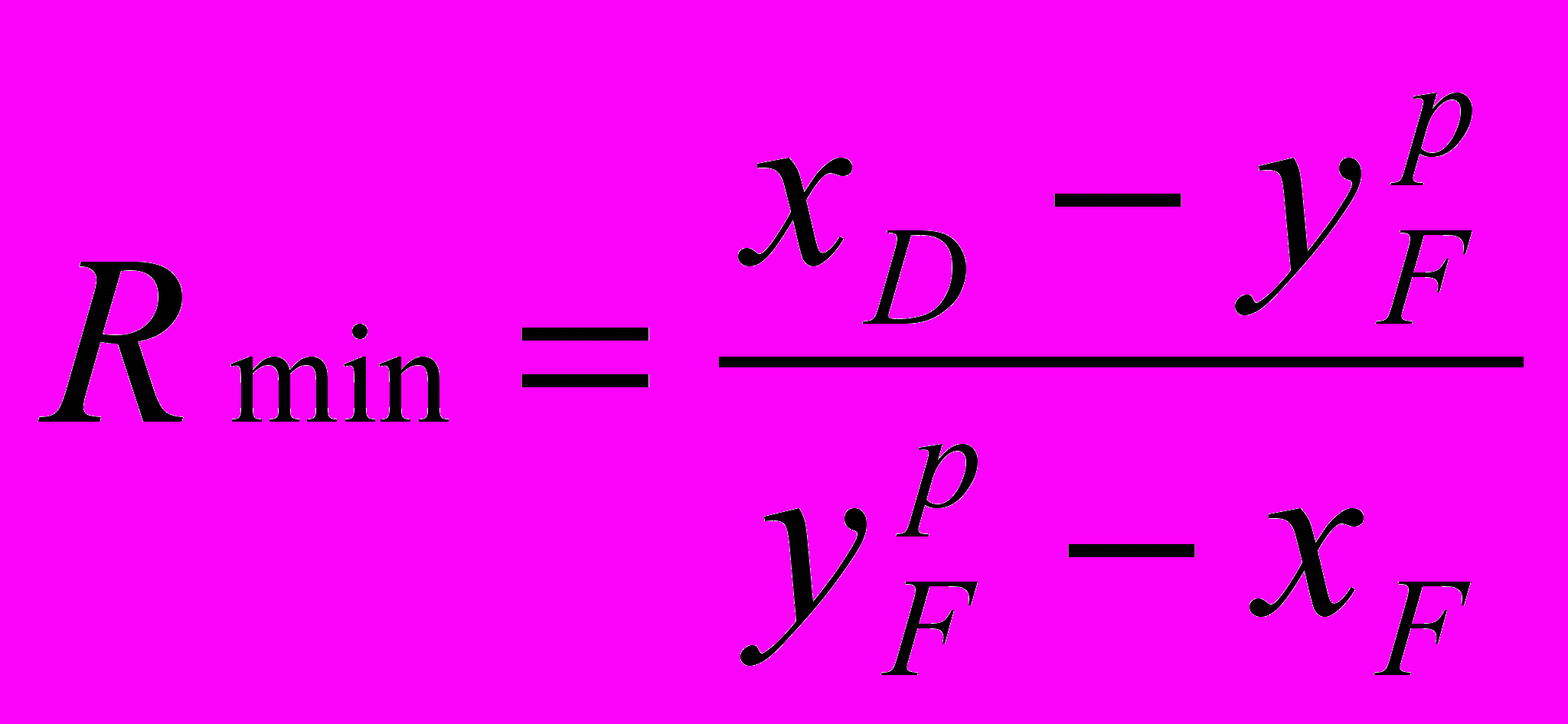Задаваясь коэффициентом () избытка флегмы (например, =2,5) рассчитываем рабочее флегмовое число ( R ) по уравнению:

R = R_min∙.

Флегмовое число показывает количество кмоль возвращаемого в колонну дистиллята (W) на каждый кмоль отбираемого дистиллята (D_M – готовый продукт), т.е. .

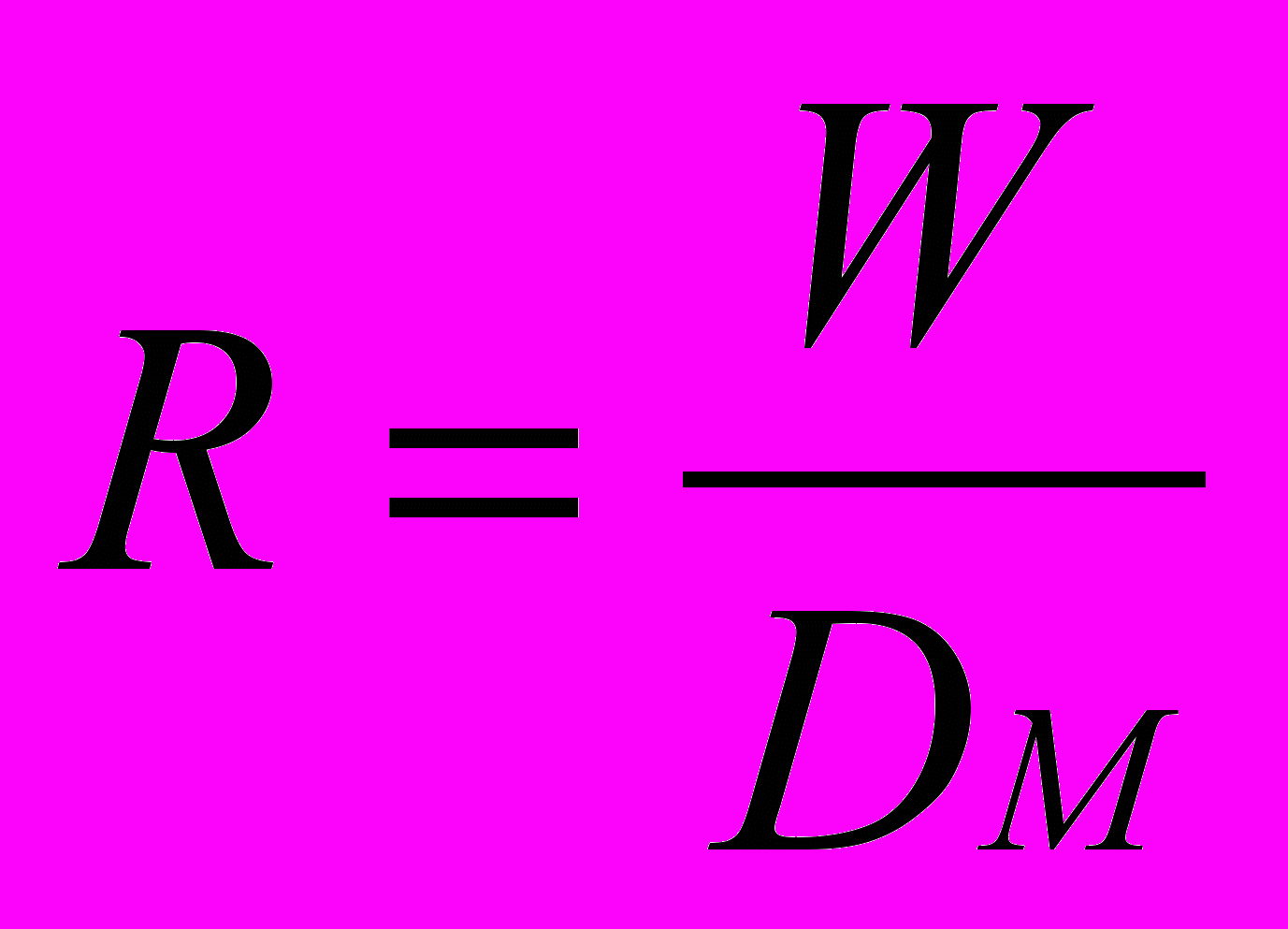б) Затем выписываем уравнения рабочих линий.

Для верхней части колонны:

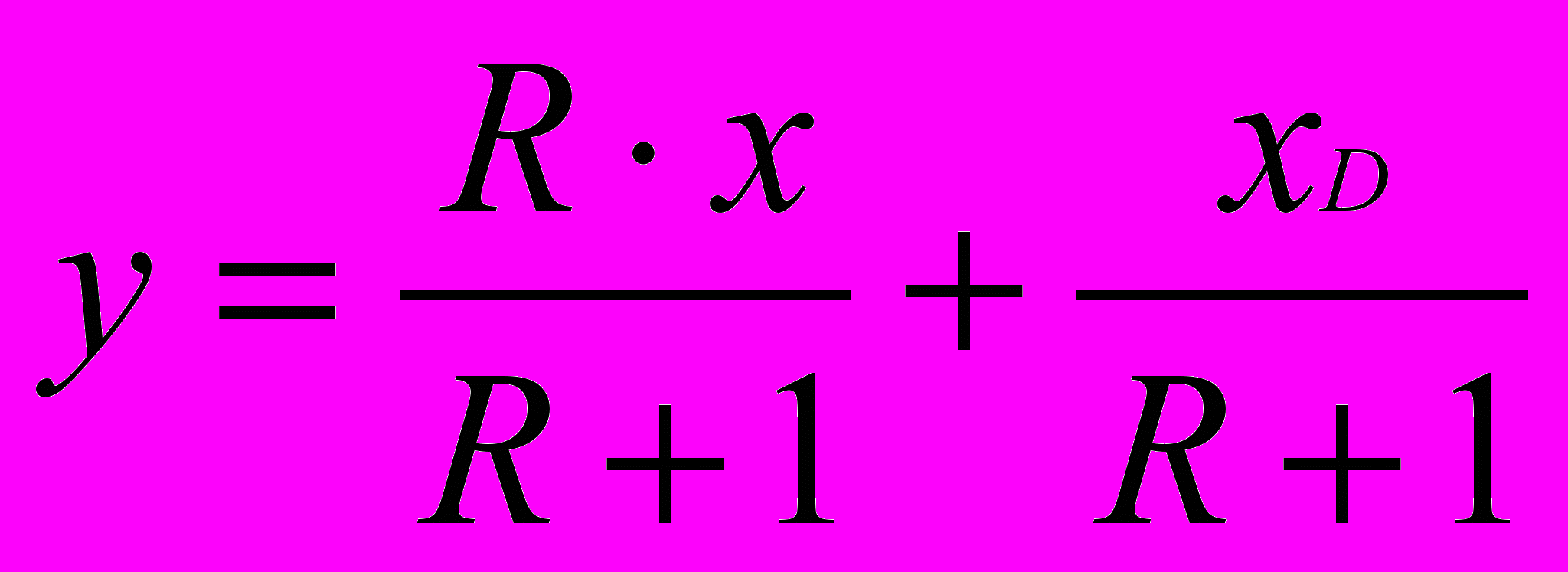, где у и х – переменные.

Для нижней части колонны:

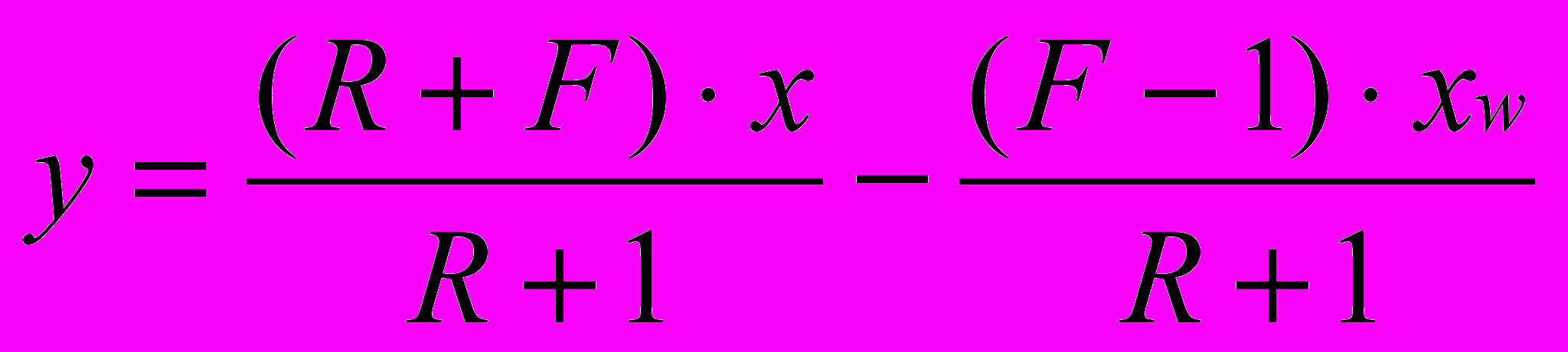, где .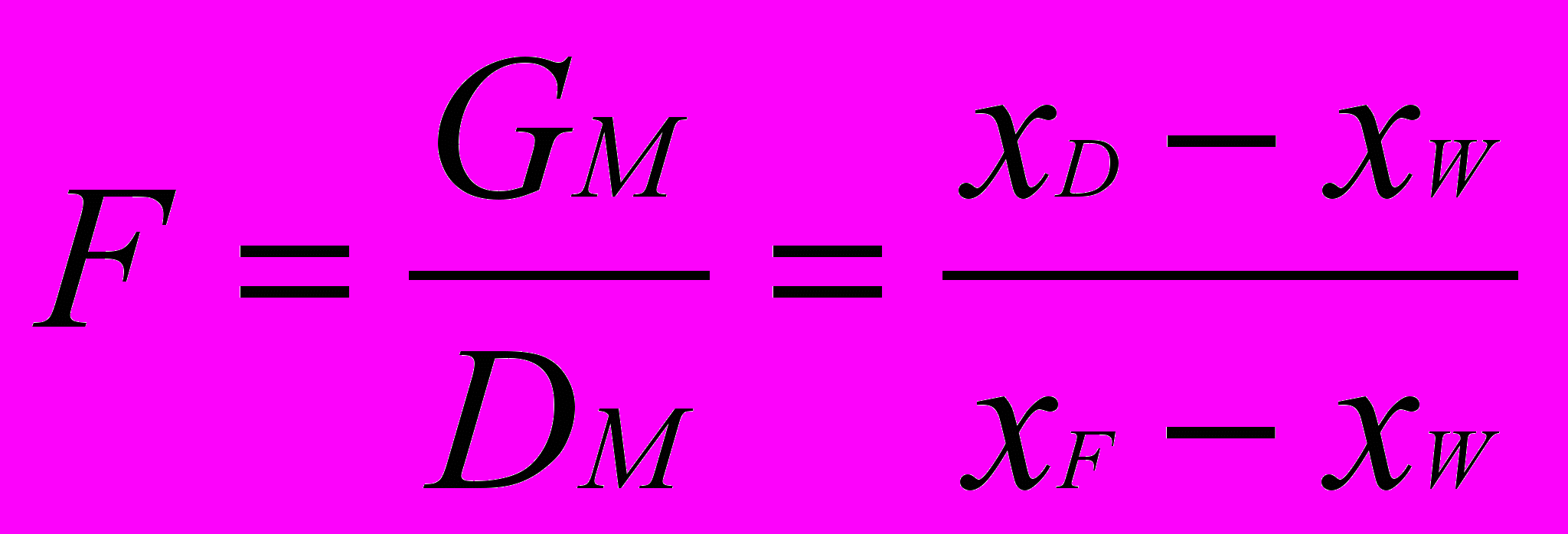


F – количество исходной смеси (питания) в кмолях, приходящейся на кмоль отбираемого дистиллята;

G_M – мольный расход питания в кмолях в час;

G_M = G/M_F,

где M_F – средняя молекулярная масса исходного потока,

;

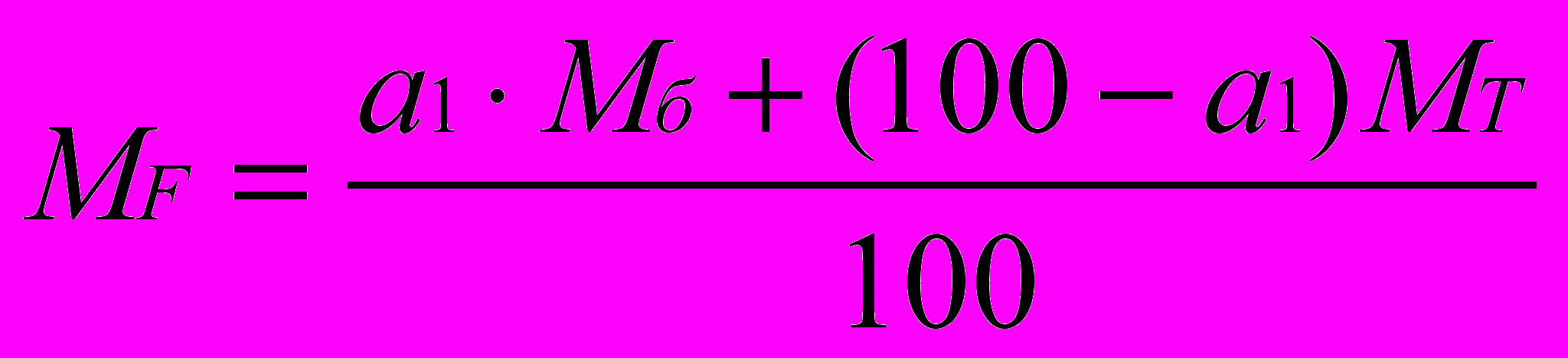D_M – мольный расход дистиллята в кмолях в час,

.

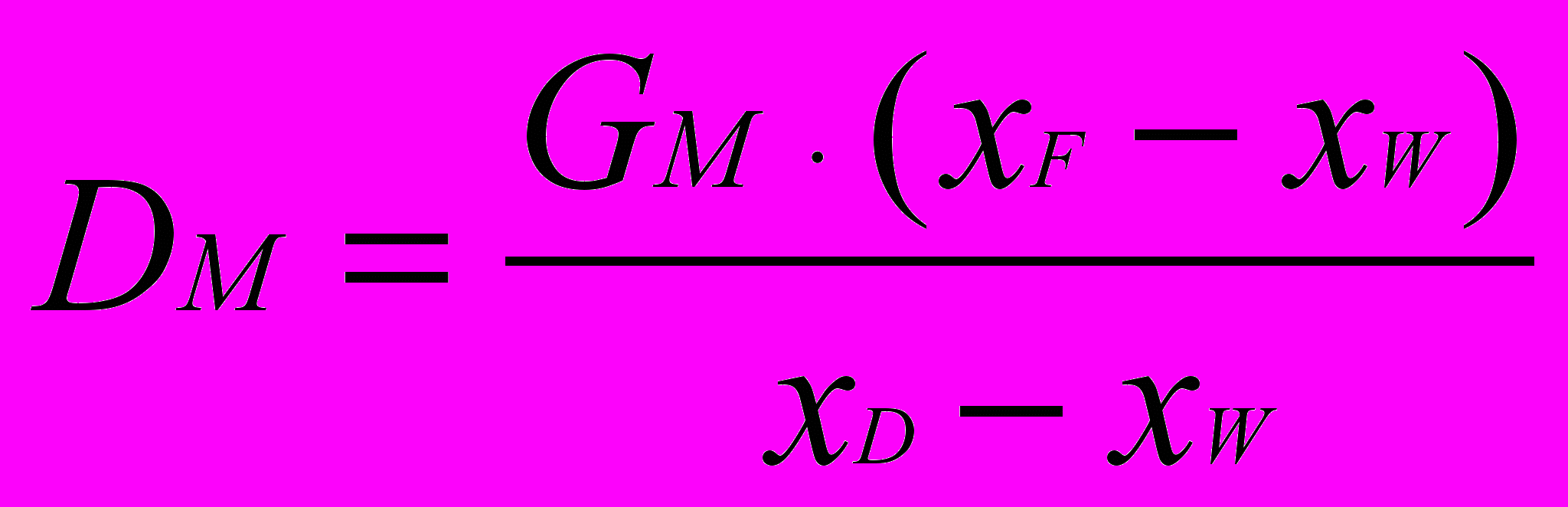в) Отложив на оси ординат свободный член уравнения для верхней части колонны (точку Е, получаем при х = 0, 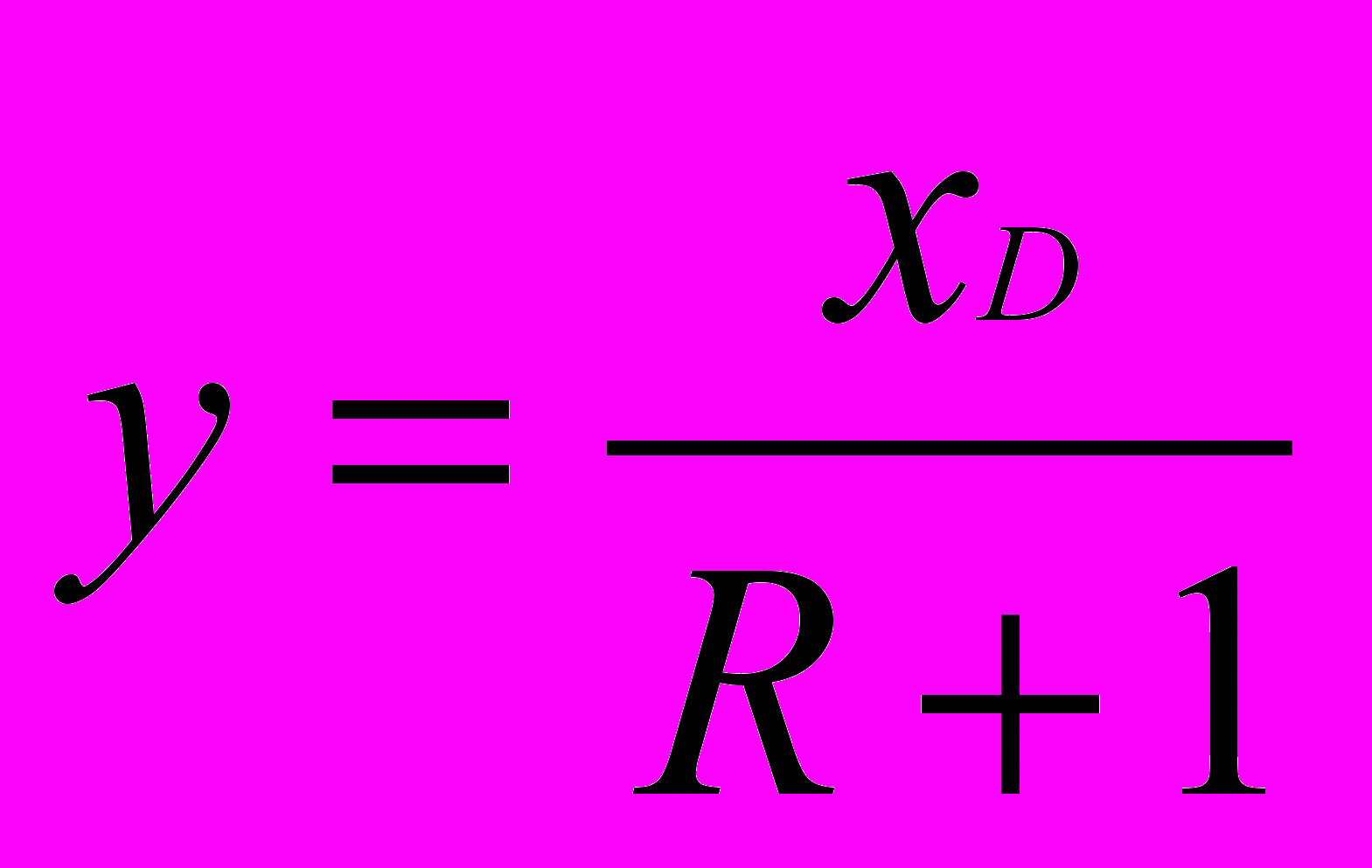) и восстановив перпендикуляр из точки х_D на оси абсцисс до пересечения с диагональю (в точке А, получаем при х_о = х_D), проводим прямую линию АЕ (рис. 5). Участок АК есть рабочая линия верхней части колонны (точку К получаем, восстановив перпендикуляр из абсциссы х_F до пересечения с рабочей линией). Аналогичное построение проводят для нанесения рабочей линии нижней части колонны (можно просто соединить прямой точку К с точкой В, полученной пересечением перпендикуляра, восстановленного из точки х_W c диагональю). Получаем рабочую линию ВК для нижней части колонны.

г) Затем выполняем на диаграмме (х-у) построение ломаной линии («лесенки»), начиная от точки А. Для этого из точки А, принадлежащей рабочей линии, проводят линию, параллельную оси абсцисс, до пересечения с кривой равновесия. Затем из этой точки пересечения опускают перпендикуляр до пересечения с рабочей линией. Таким образом, получают первую ступень в виде прямоугольного треугольника. Далее аналогичные построения продолжают вплоть до точки В. Подсчитывают число прямоугольных треугольников, заключённых между равновесной и рабочими линиями. Полученное число треугольников соответствует теоретическому (при условии достижения равновесия) числу ступеней изменения концентраций (числу испарений и конденсаций), необходимых для достижения заданной степени разделения. Для верхней части колонны оно составляет  5, а для нижней  7 (округляем в большую сторону). Всего теоретических тарелок (по рис. 6) n_тт равно 12.



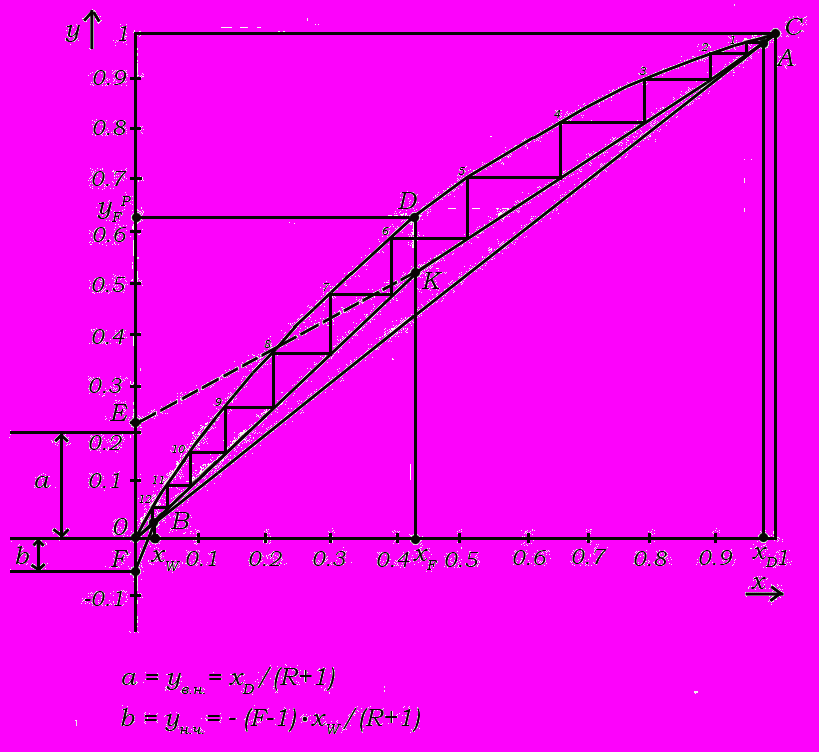
Рис. 6. Графическое построение для приближенного определения числа теоретических тарелок (n_тт).


2.2.5. Определение высоты колонны

Для определения действительного числа тарелок можно воспользоваться приближёнными значениями КПД тарелки . Его вводят, чтобы учесть реальные условия, при которых не достигается равновесия в массообмене. Значения КПД определяют экспериментально. Они находятся в пределах 0,3-0,8.

Принимая к расчёту КПД равный 0,7, получаем действительное число тарелок:

n_д.т. = n_т.т/

Суммарная высота нижней и верхней рабочих частей колонны (Н_р) составляет (принимая расстояние между тарелками h = 0,4 м):

Н_р = (n_д.т.-1)∙h.

Для получения общей высоты колонны (Н_об.) необходимо к рабочей высоте (Н_р) приплюсовать высоту (Н_с.п.) сепарационного пространства (для предотвращения уноса капель жидкости паром) и высоту (Н_к.) кубовой части колонны, в которой расположен встроенный кипятильник.

Н_об. = Н_р + Н_с.п. + Н_к.


2.2.6. Материальный баланс

а) мольный поток питания (G_M):

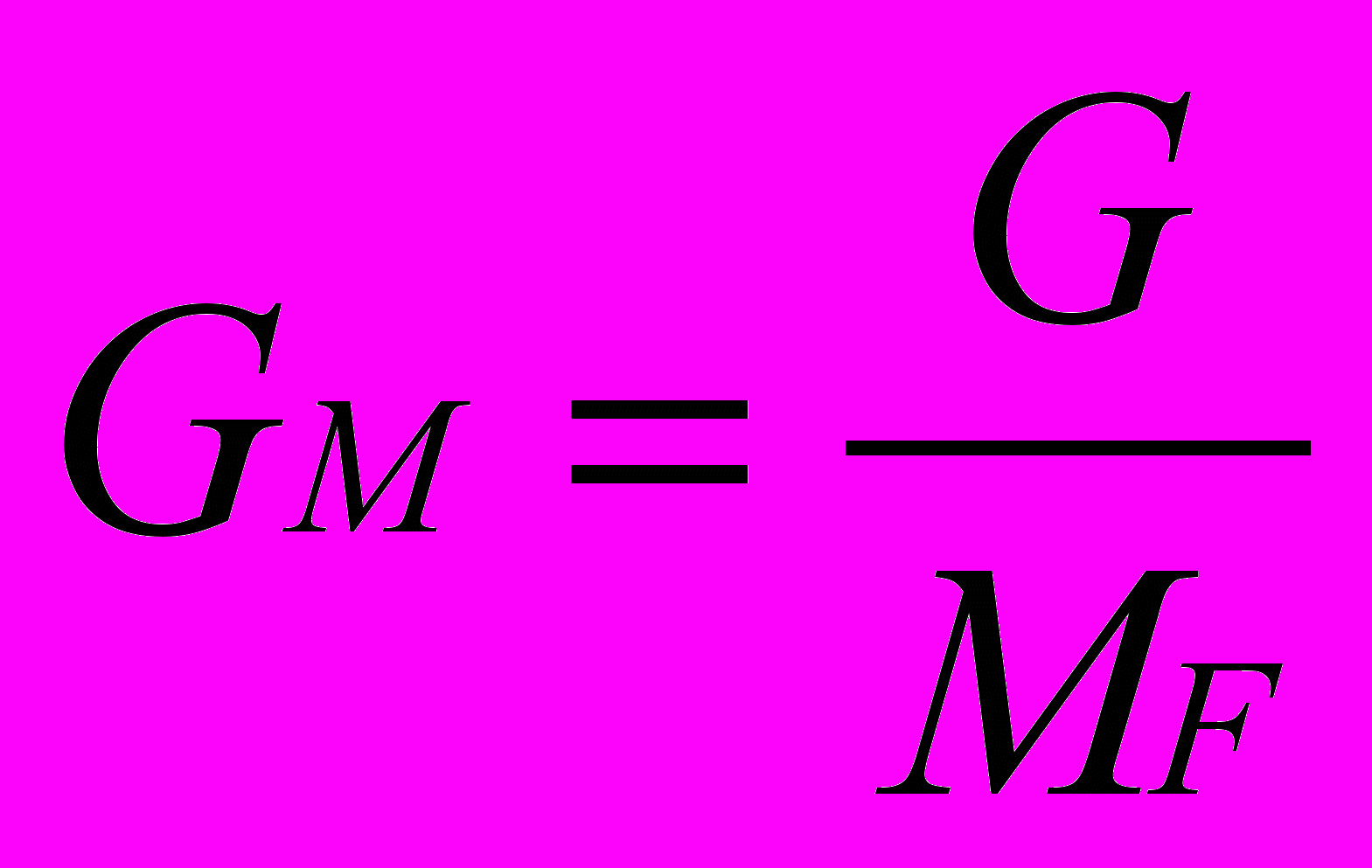, кмоль/ч,

где G – заданный массовый расход питания в кг/час;

M_F – молекулярная масса исходного потока, кмоль;

.

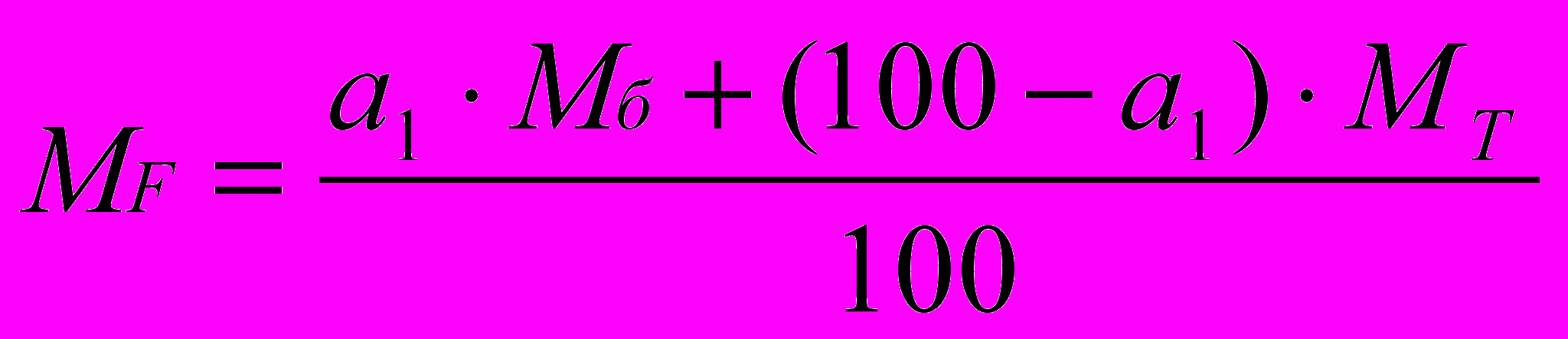Мольные потоки отбираемого дистиллята (D_M), кубовой жидкости (W_O), проходящего по всей высоте колонны пара (G_P) определяют из уравнений материального баланса по всей колонне по всем потокам смесей:

G_M = D_M+W_O

и по НК в этих потоках:

G_M∙х_F = D_M∙х_D+W_O∙х_W.

б) мольный поток дистиллята (D_M), кмоль/ч:

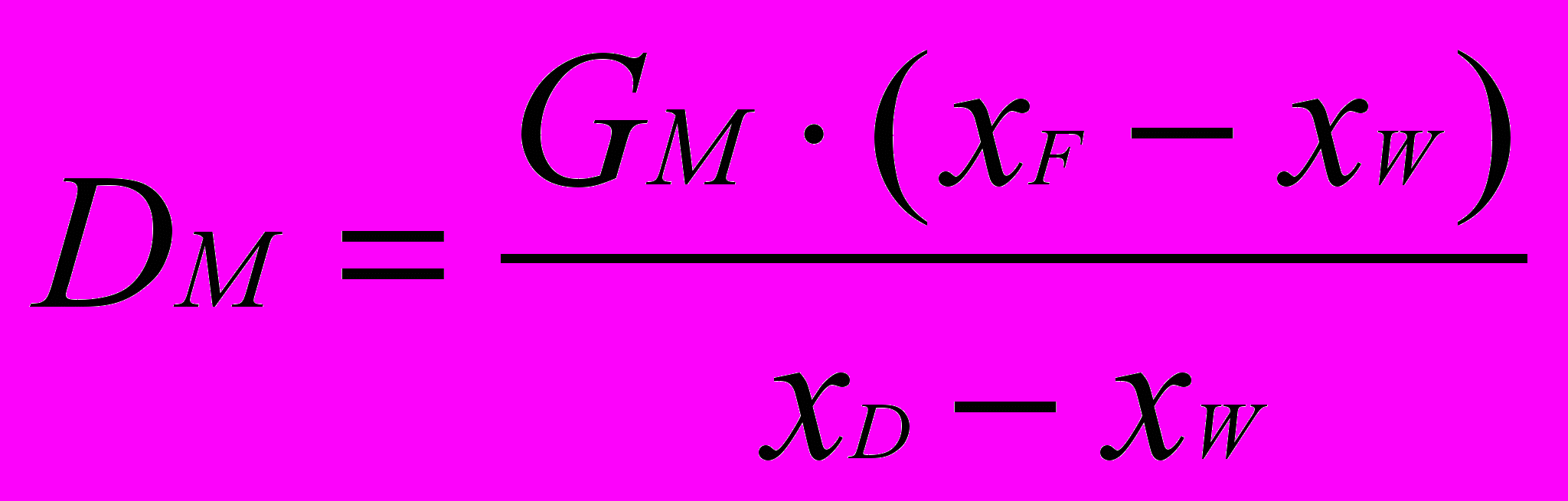или .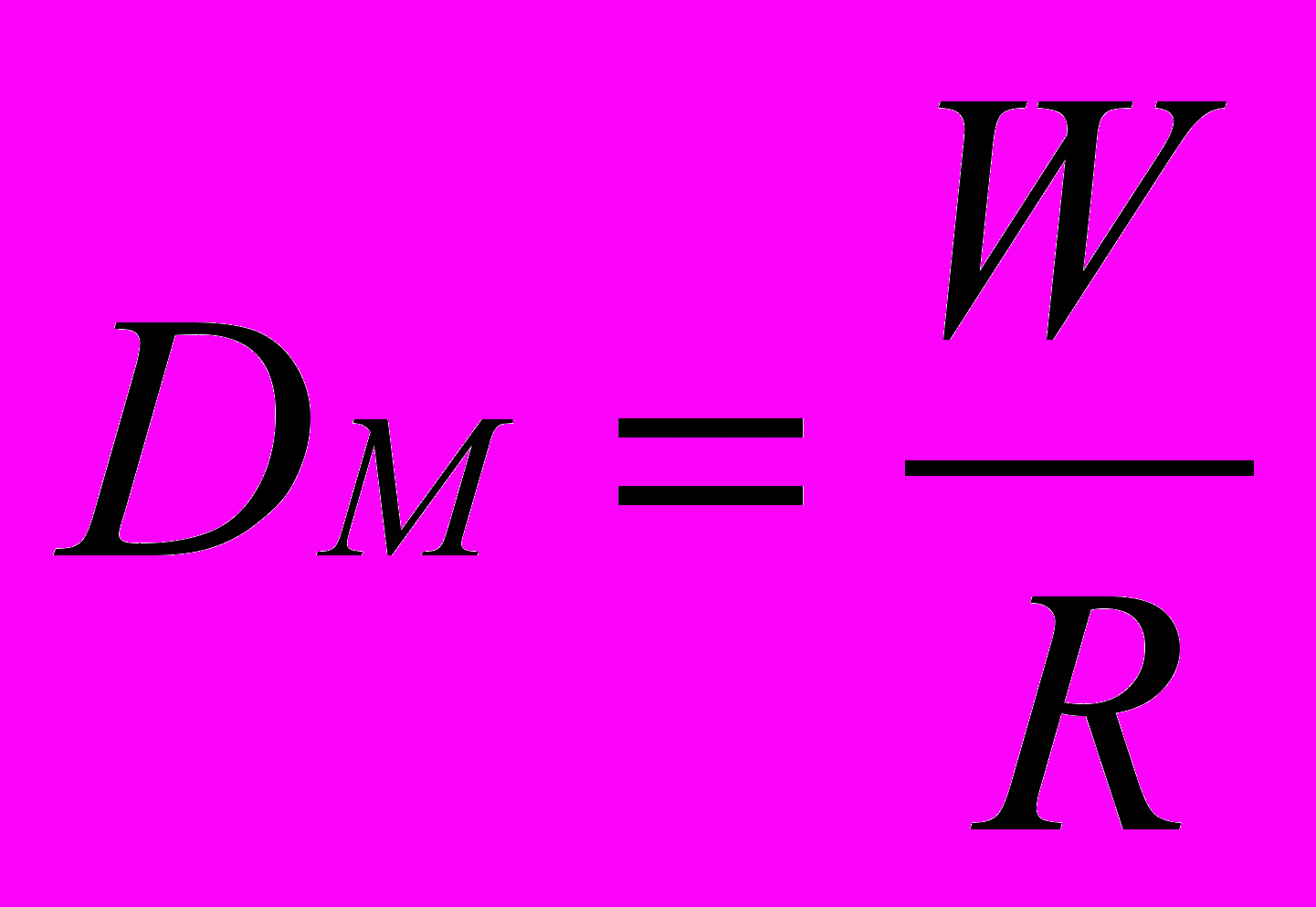

в) расчёт мольного потока паров в колонне (G_P), кмоль/ч:

G_P = G_M∙R+D_M .

г) Расчёт мольного потока кубовой жидкости, кмоль/ч:

.

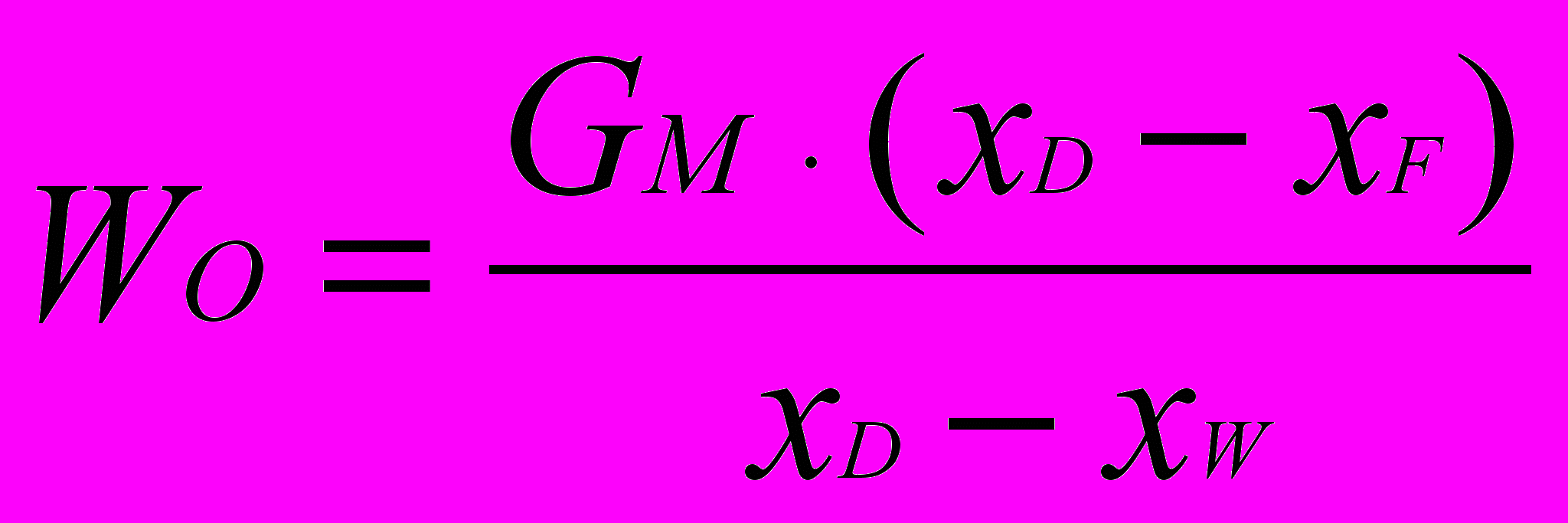д) Количество флегмы, возвращаемой в колонну, кмоль/ч:

W=D_M∙R.

При необходимости проводят пересчёт мольных потоков в час в массовые секундные:

D_MM = D_M∙M_D, G_PM = G_P∙M_P и W_OM = W_O∙M_O, где M_D, M_P и M_O – средние молекулярные массы дистиллята, паров в колонне и кубовой жидкости, которые рассчитывают следующим образом:

M_D = х_б∙M_б+(1−х_б) ∙M_т и т.д.


2.2.7. Расчёт диаметра верхней (d₁) и нижней (d₂) частей колонны

Из общего выражения 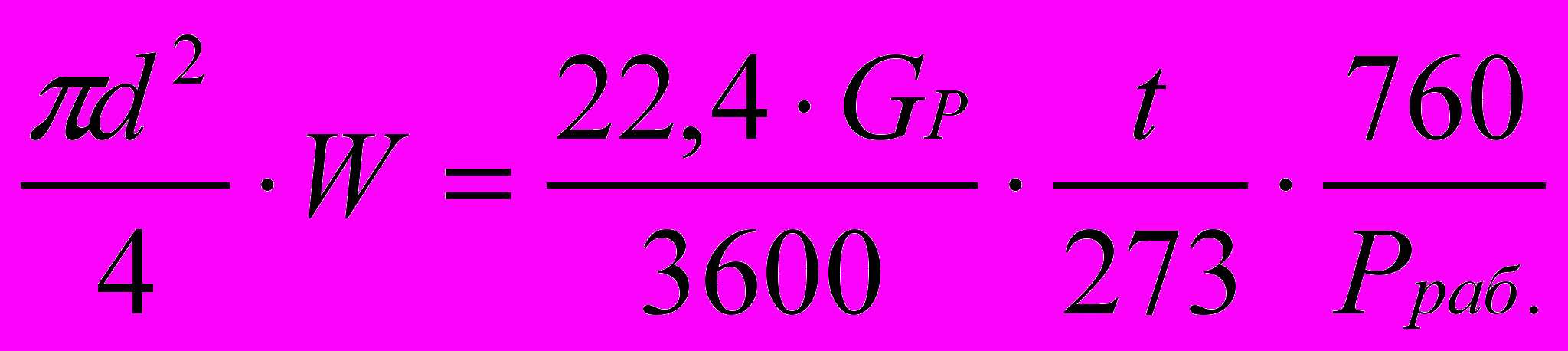, где

d – диаметр колонны,

W – линейная скорость паров, м/с,

t – температура в колонне, и принимая, что Р_раб. Мало отличается от атмосферного, имеем для верхней части колонны



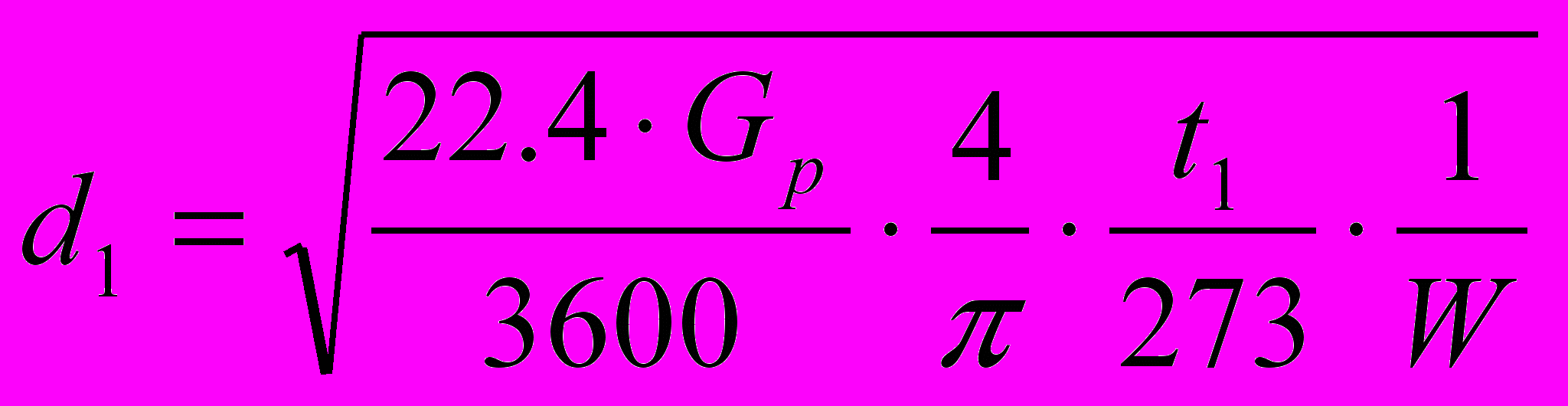
и для нижней части колонны

.

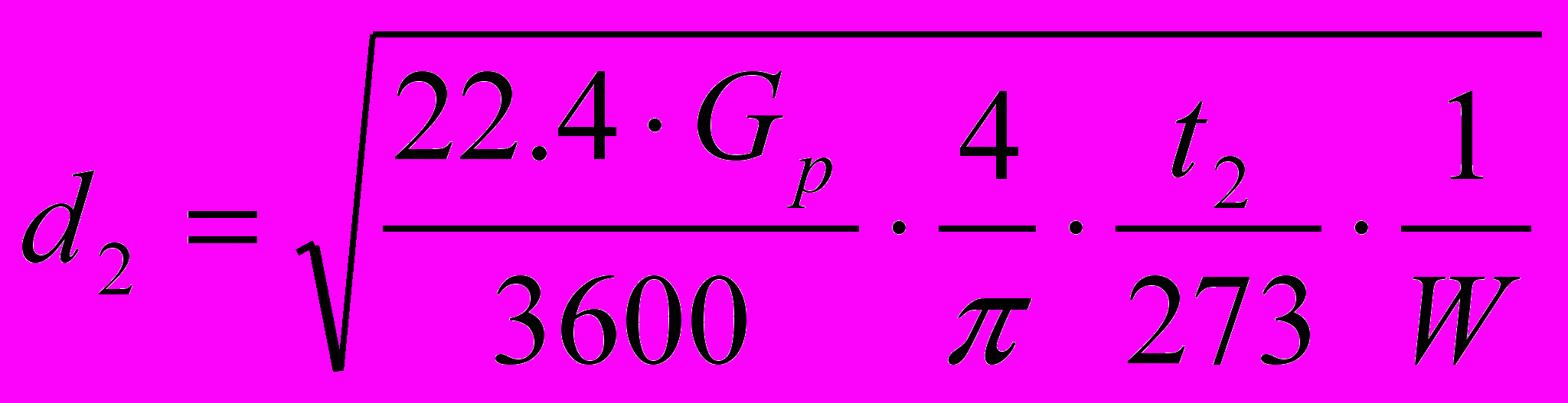К расчёту принимаем скорость паров 0,5 м/с (рекомендуется выбор в пределах 0,3-0,8 м/с), а t₁ и t₂ – температуры кипения дистиллята и кубового остатка, которые определяют по диаграмме (t – x,y) для состава х_D и х_W.

В работе [6] приведены методические рекомендации и компьютерные программы по расчёту ректификационных колонн.