Методы построения радионавигационных полей для информационного обеспечения автоматизированных систем управления движением судов

Вид материала

Содержание

Содержание работы
Во втором разделе
Р – мощность передатчика, W
Рпер – мощность передатчика, Р
В третьем разделе
Таблица 1. Результаты осреднения расчетной формы периметра зоны действия ККС
Осредненный и минимальный радиусы зоны действия ККС

Подобный материал:

1 2 3 4

СОДЕРЖАНИЕ РАБОТЫ

В первом разделе проведены анализ и обобщение установившихся в современной отечественной и зарубежной научно-технической литературе основных взглядов, принципов и приемов для проведения концептуальных исследований сложных организационно-технических систем.

Основное внимание в данном разделе было уделено принципам построения современных речных инфокоммуникационных систем и систем высокоточного позиционирования. Проанализированы существующие методы создания триадно-иерархических структур речных инфокоммуникационных систем типа: корпоративная речная информационная система (КРИС) – речная информационная служба (РИС) – автоматизированная система управления движением судов (АСУ ДС), а также вскрыт основной ряд факторов, определяющих эффективность указанных систем.

Проведен анализ и обобщены особенности целеполагания при проведении концептуальных исследований и выбора показателей эффективности для сложных организационно-технических систем. Рассмотрены основные принципы целеполагания, такие как: причинности, коммутативности, «от общего к частному», минимизации затрат при синтезе системы, системности, описания рабочих функций, полноты и точности изложения цели.

С позиции указанных принципов рассмотрены возможности основных трёх классов критериев. В качестве критериев была рассмотрена возможность адаптивности, пригодности и оптимальности указанных систем в целом, а также их сегментов и функциональных дополнений в отдельности.

Проведён анализ и обобщение мирового и отечественного опыта разработки, внедрения и использования речной иерархической триады КРИС – РИС – АСУ ДС и систем высокоточного местоопределения, строящихся на базе дифференциальных дополнений спутниковых радионавигационных систем ГЛОНАСС, GPS, который свидетельствует о том, что в настоящее время системы управления движением судов и системы высокоточного местоопределения, задействованные в процессе обеспечения безопасности судоходства, получили достаточно широкое распространение на внутренних водных путях многих Европейских стран, Азии и Северной Америки. Подобные системы в настоящее время также активно используются для осуществления качественного мониторинга и управления транспортным процессом на акваториях внутренних водных путей. Разработка, внедрение и информационное сопровождение инфокоммуникационных триад КРИС – РИС – АСУ ДС и высокоточных систем местоопределения на ВВП стран Евросоюза осуществляется в соответствии с Концепцией «Речных информационных служб», принятой в Европейском Союзе и подтвержденной Международной Ассоциацией маячных служб, что, несомненно, свидетельствует об актуальности внедрения таких систем и на ВВП России.

Выполнен анализ современных подходов, путей, принципов создания и архитектуры высокоточных систем местоопределения, строящихся на ис–пользовании дифференциальных дополнений спутниковых радионавигации–онных систем ГЛОНАСС, GPS, работающих для нужд внутреннего водного транспорта.

Проведен анализ современных основ создания и информационного обеспечения корпоративных речных информационных систем при ис–пользовании сетевого и комбинированного методов интеграции в случае её построения на ЕГС ВВП России. Здесь также рассматриваются весьма конструктивные алгоритмы и методы построения высокоточных систем местоопределения, а именно: сетевой метод интеграции, широкозональный метод интеграции, комбинированный метод (сетевой–сотовый–транкинго–вый), комбинированный метод (широкозональный–сотовый–транкинговый).

Рассмотрены основные принципы построения высокоточных систем местоопределения, строящихся на основе спутниковых радионавигационных систем (СРНС) второго поколения ГЛОНАСС/GPS. Здесь детально были проанализированы точностные характеристики и контроль целостности указанных СРНС с точки зрения их использования в решении навигационной задачи на ВВП России. Здесь также детально рассмотрены главные направления и пути решения задачи повышения точности навигационных местоопределений. С этой точки зрения исследованы физические основы реализации дифференциального режима. Причем было показано, что при реализации дифференциального режима на ВВП России удвоенная среднеквадратическая радиальная ошибка определения координат подвиж–ного объекта при использовании навигационных сигналов СРНС ГЛОНАСС может составлять

(1)

при вероятности 95%, а при использовании навигационных сигналов СРНС GPS

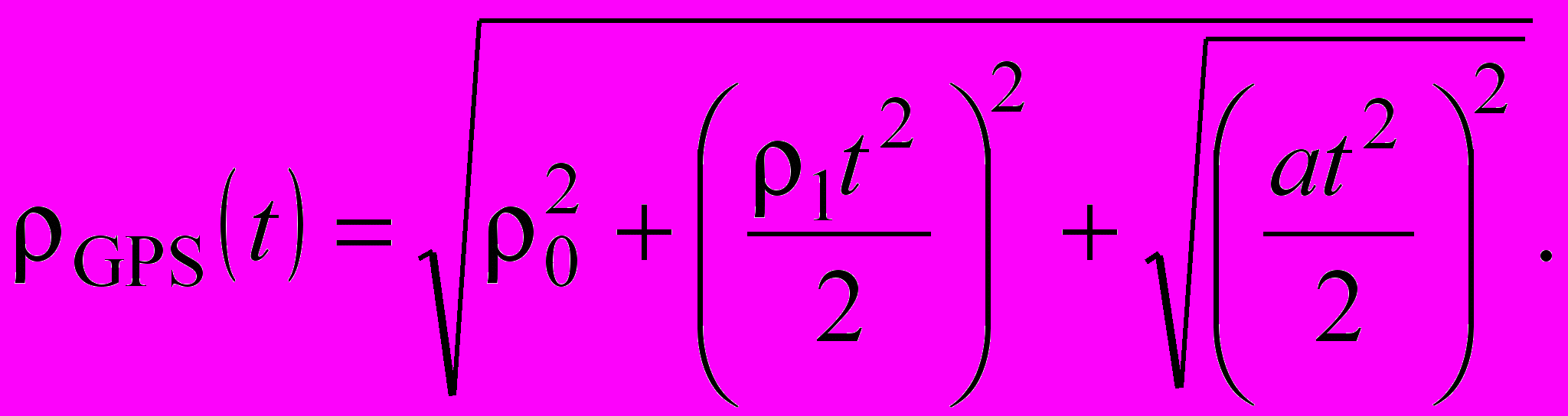
(2)

Принимая во внимание выражения (1) и (2), в данном разделе выполнен анализ основных реализаций дифференциального режима, что позволило с учетом принятой в мировой практике классификации дифференциальных дополнений исследовать архитектуру и особенности информационного фун–кционирования локальной дифференциальной подсистемы (ЛДПС) (рис. 1),

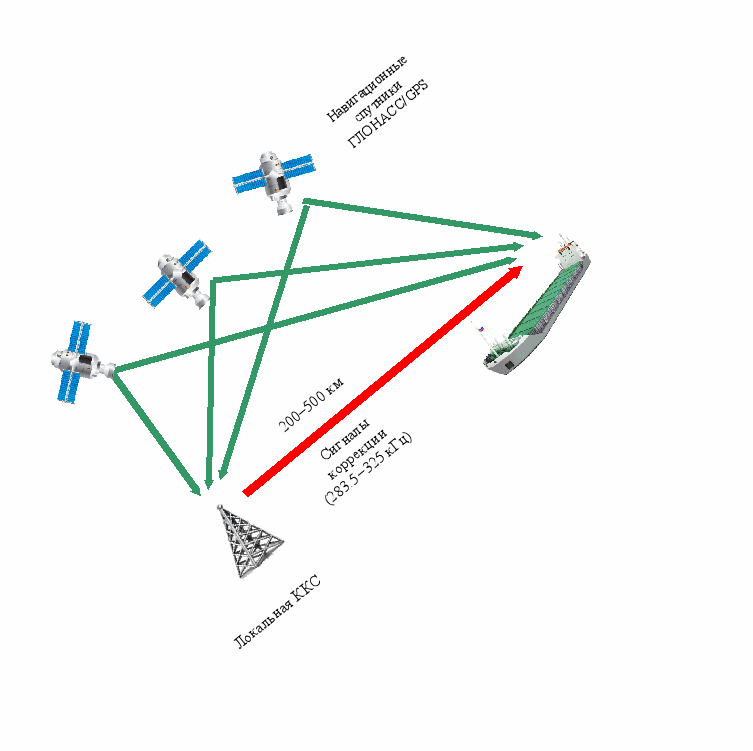
Рис. 1. Принципиальная схема построения ЛДПС.

что свидетельствует о необходимости сосредоточить, в первую очередь, внимание на задачах формирования сплошных дифференциальных полей высокоточного местоопределения для АСУ движением судов на ВВП России.

На основе анализа в терминах современного инженерно-кибернети–ческого подхода в данном разделе сформулированы и выделены для последующего исследования основные технологии высокоточного позиционирования, строящиеся на базе глобальных навигационных спутниковых систем ГЛОНАСС, GPS, или их объединенной группировки, где рассмотрены реализации дифференциальной технологии этих Глобальных навигационных спутниковых систем, функционируюих при помощи геостационарных космических аппаратов и получивших название широкозональные и региональные дифференциальные подсистемы глобальных навигационных спутниковых систем ГЛОНАСС, GPS, здесь же изучены локальные дифференциальные подсистемы этих глобальных навигационных спутниковых систем, строящиеся на базе контрольно-корректирующих станций, используемых на водным транспорте в крупнейших странах Европы, Америки и России.

При анализе мирового научно-технического опыта по решению проблемы формирования радионавигационных полей дифференциальной поправки в зонах действия АСУ движением судов и других инфокоммунакационных систем водного транспорта показаны основные проблемы определения топологии форм периметров зон действия ККС работающих в СВ диапазоне, в границах инфокоммуникационных триад внутреннего водного транспорта

В заключении раздела обоснованы целесообразность и необходимость дальнейшего исследования локальных дифференциальных подсистем Глобальных навигационных спутниковых систем ГЛОНАСС, GPS, строящиеся на базе цепи контрольно-корректирующих станций, а также топология высокоточных полей дифференциальной поправки, формируемых поверхностной волной диапазона средних волн, излучаемой такими контрольно-корректирующими станциями и в ультракоротковолновом диапазоне информационного канала, формируемого базовой станцией автоматизированной информационной системы.

Решению указанных задач посвящены последующие разделы диссертации.

Во втором разделе представлены результаты исследования комплекса задач анализа математического обеспечения определения дальности и форм зон действия контрольно-корректирующих станций локальной дифференциальной подсистемы.

В случае, когда приемная и передающая антенны подняты над поверхностью Земли, а расстояние между ними незначительно, тогда кривизной Земли можно пренебречь. Здесь предполагается, что подстилающая поверхность гладкая и однородная на протяжении всей радиотрассы. При таких условиях с помощью модели Шулейкина–Ван-дер-Поля можно определить напряженность электромагнитного поля, создаваемого передающим устройством ККС в СВ диапазоне: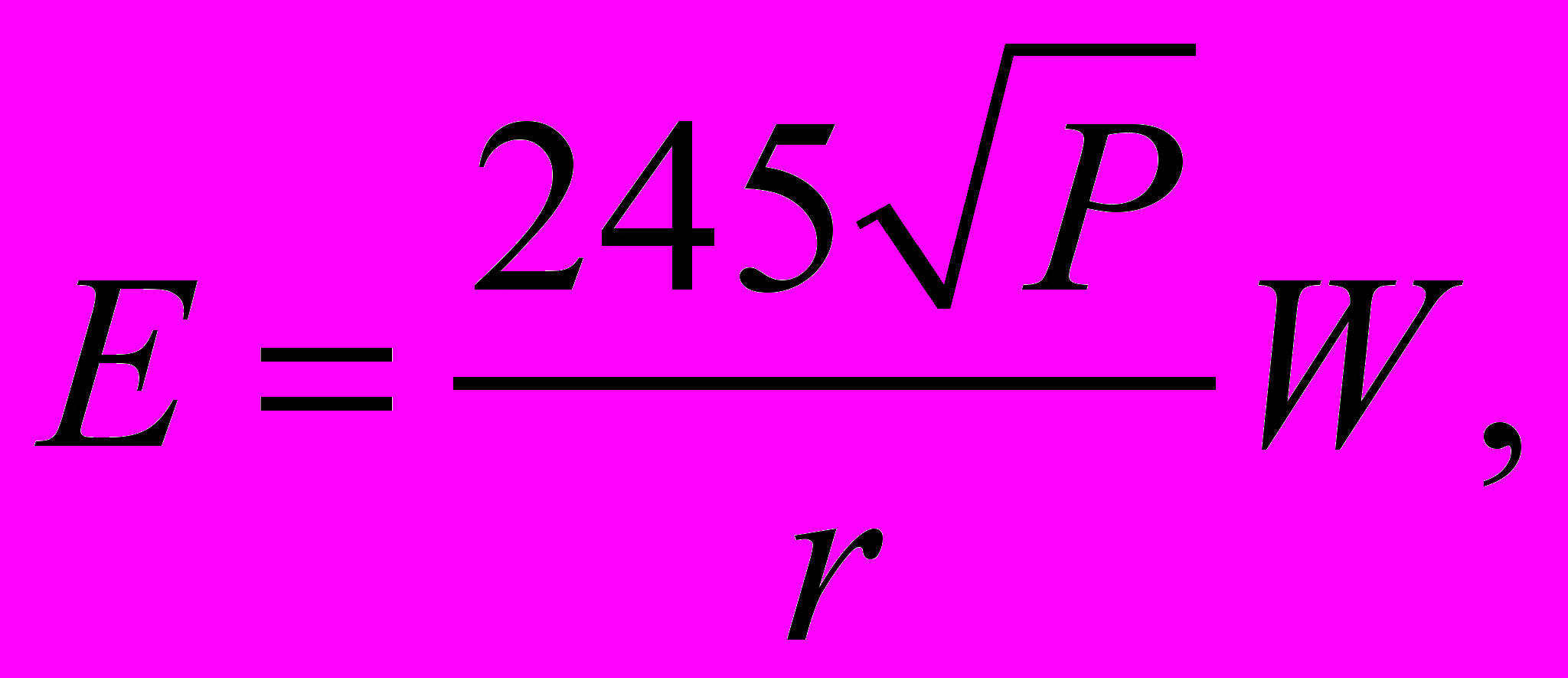

(3)

где Р – мощность передатчика, W – нелинейный множитель ослабления, r – удаленность от передатчика.

Множителем ослабления W является функцией численного расстояния ρ, которое представляет собой безразмерный параметр. Численное расстояние можно определить следующим образом:

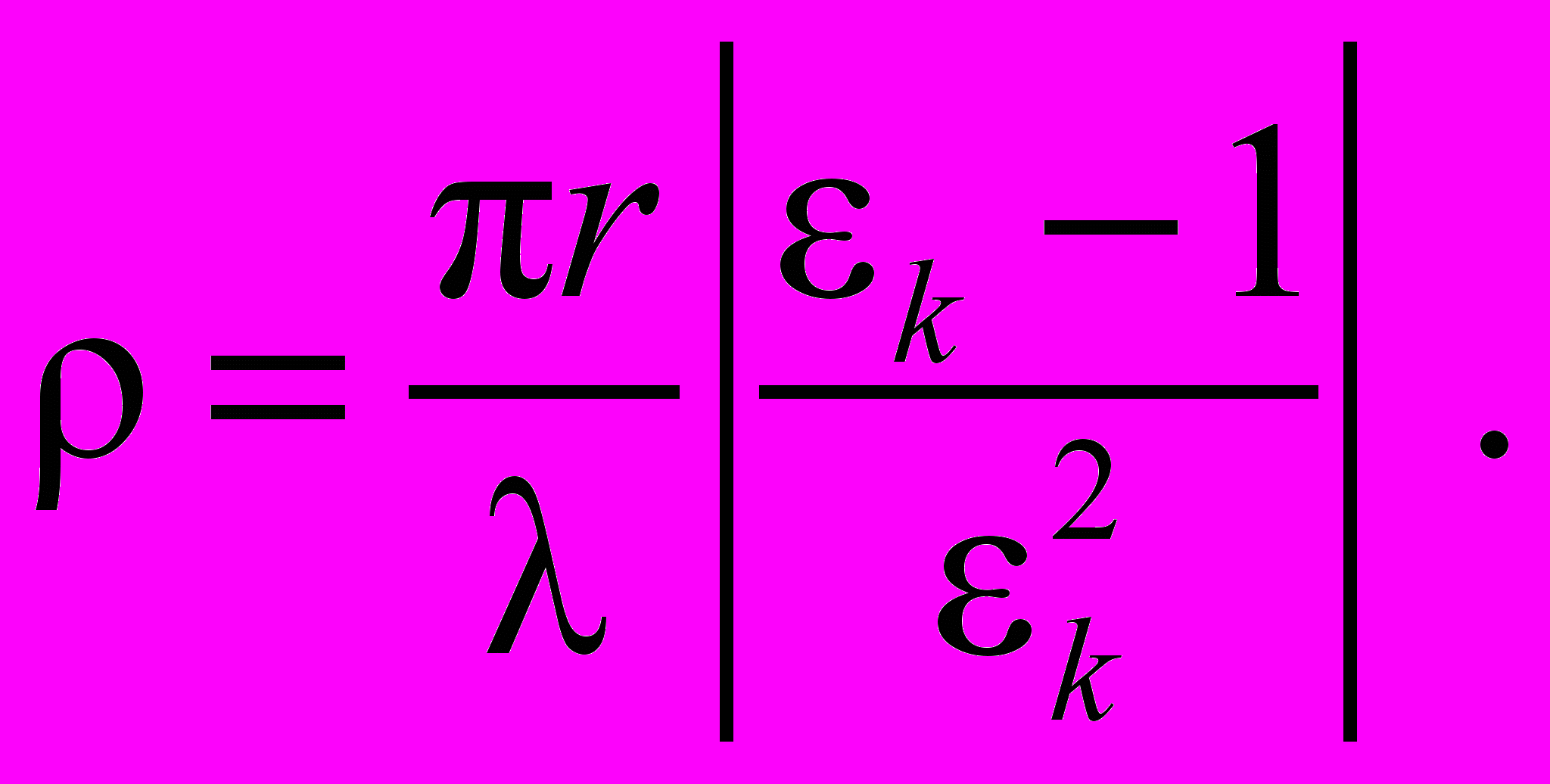
(4)

где ε – диэлектрическая проницаемость подстилающей поверхности.

Для определения W при известном ρ можно пользоваться графиками, составленными Берроузом, где в логарифмическом масштабе по оси абсцисс отложены различные значения ρ, на оси ординат расположены искомые значения W для двух видов поляризации и разных значений параметра

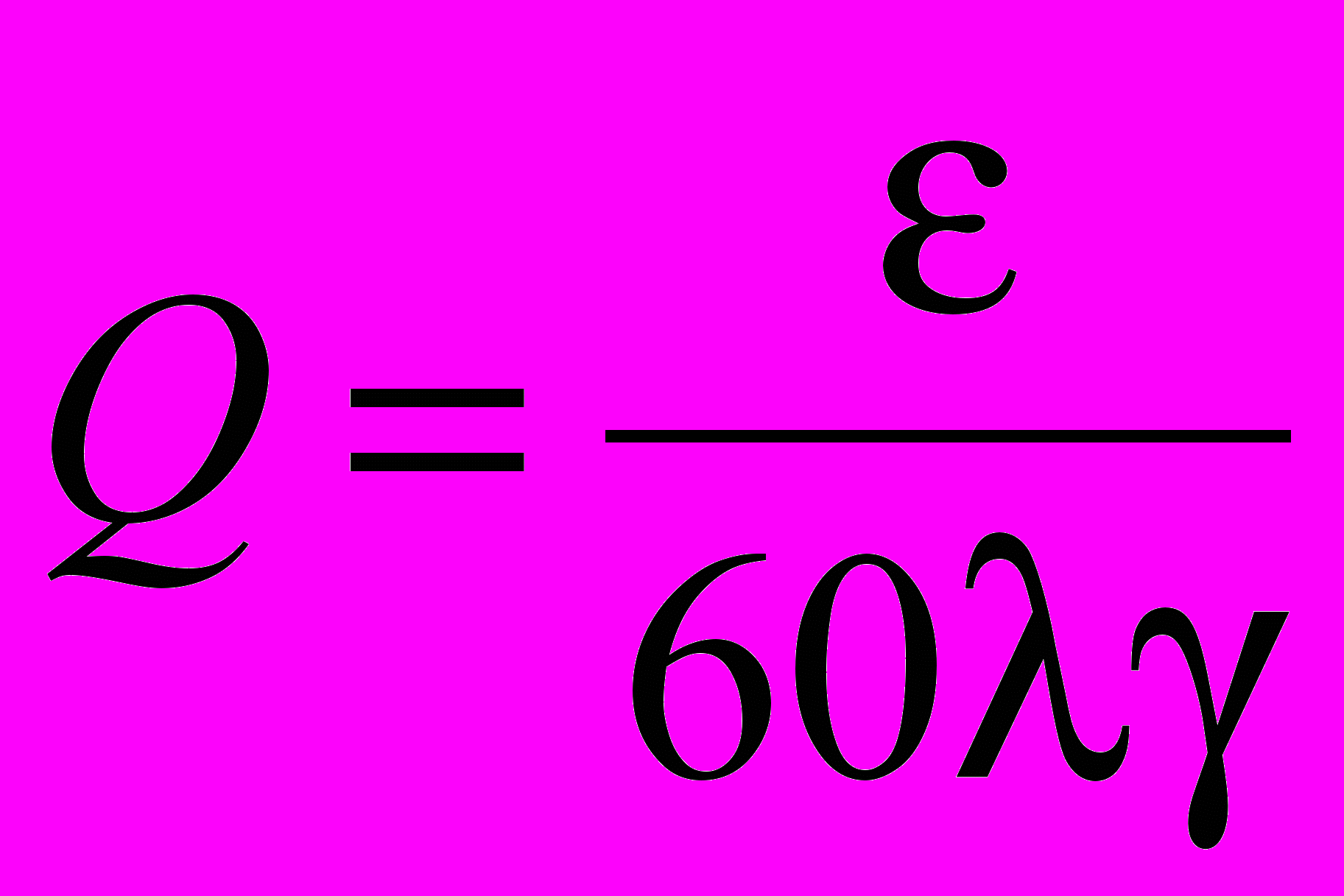. Модуль множителя ослабления также можно определить аналитическим путем по приближенной формуле

(5)

При ρ > 25 выражение (5) примет вид

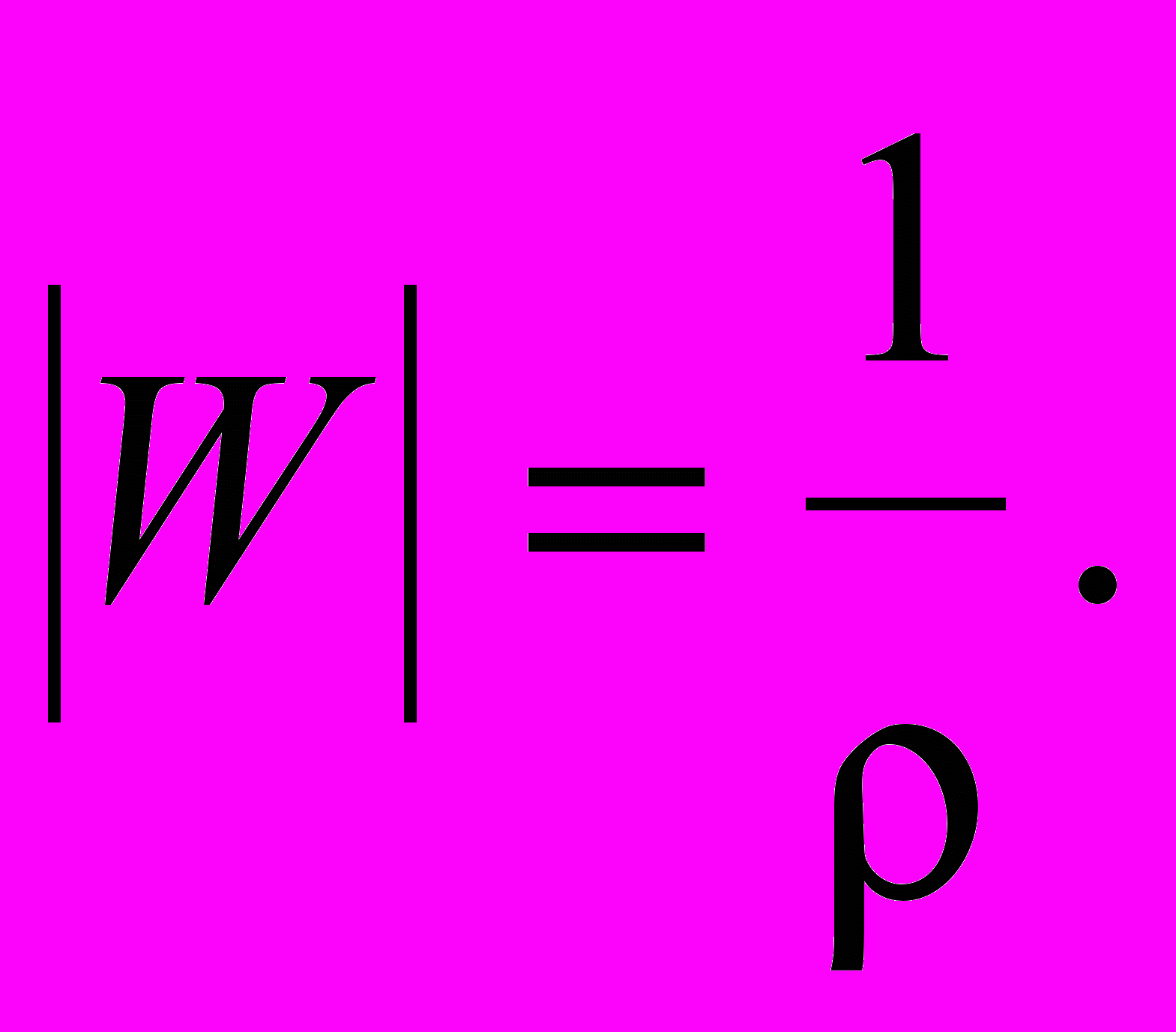
(6)

Данная модель достаточно актуальна при сравнительно малых расстояниях от передатчика, когда влиянием кривизны земной поверхности можно пренебречь.

В случае, когда дальность распространения поверхностных волн СВ диапазона составляет порядка нескольких сотен километров, необходимо учитывать кривизну земной поверхности. Для решения такой задачи можно использовать модель В.А. Фока. В указанной модели связь между функциями ослабления V и W для освещенной части поверхности можно записать так

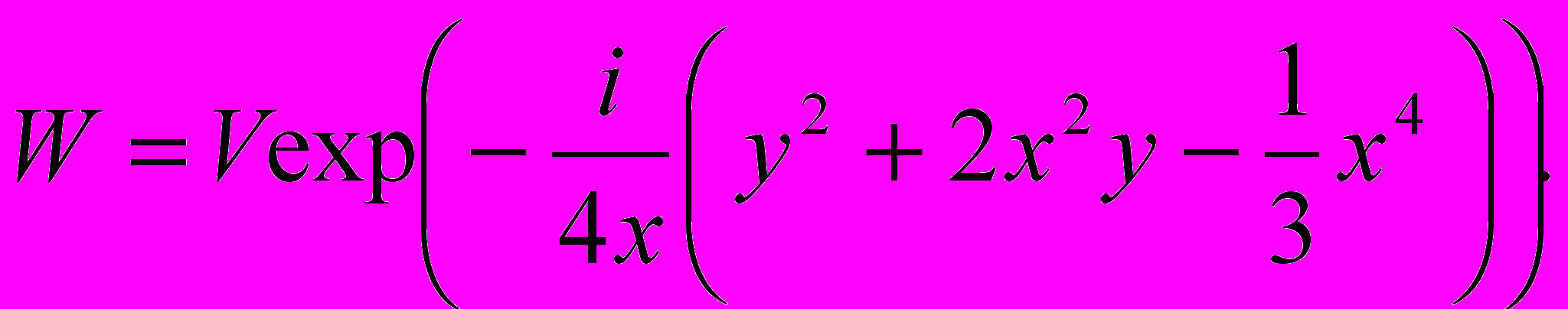
(7)

После определенных математических преобразований можно показать, что функция ослабления примет вид

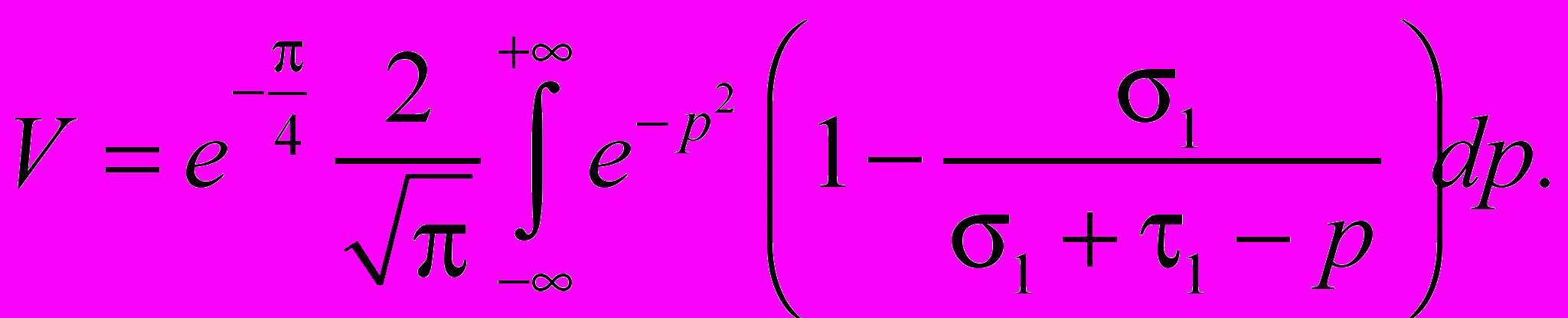
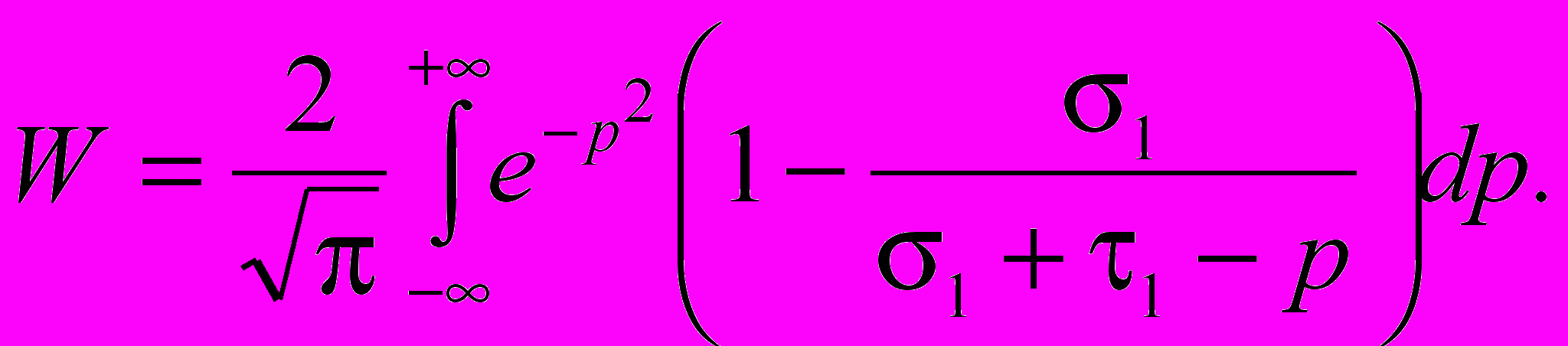
(8)

Тогда, при выполнении

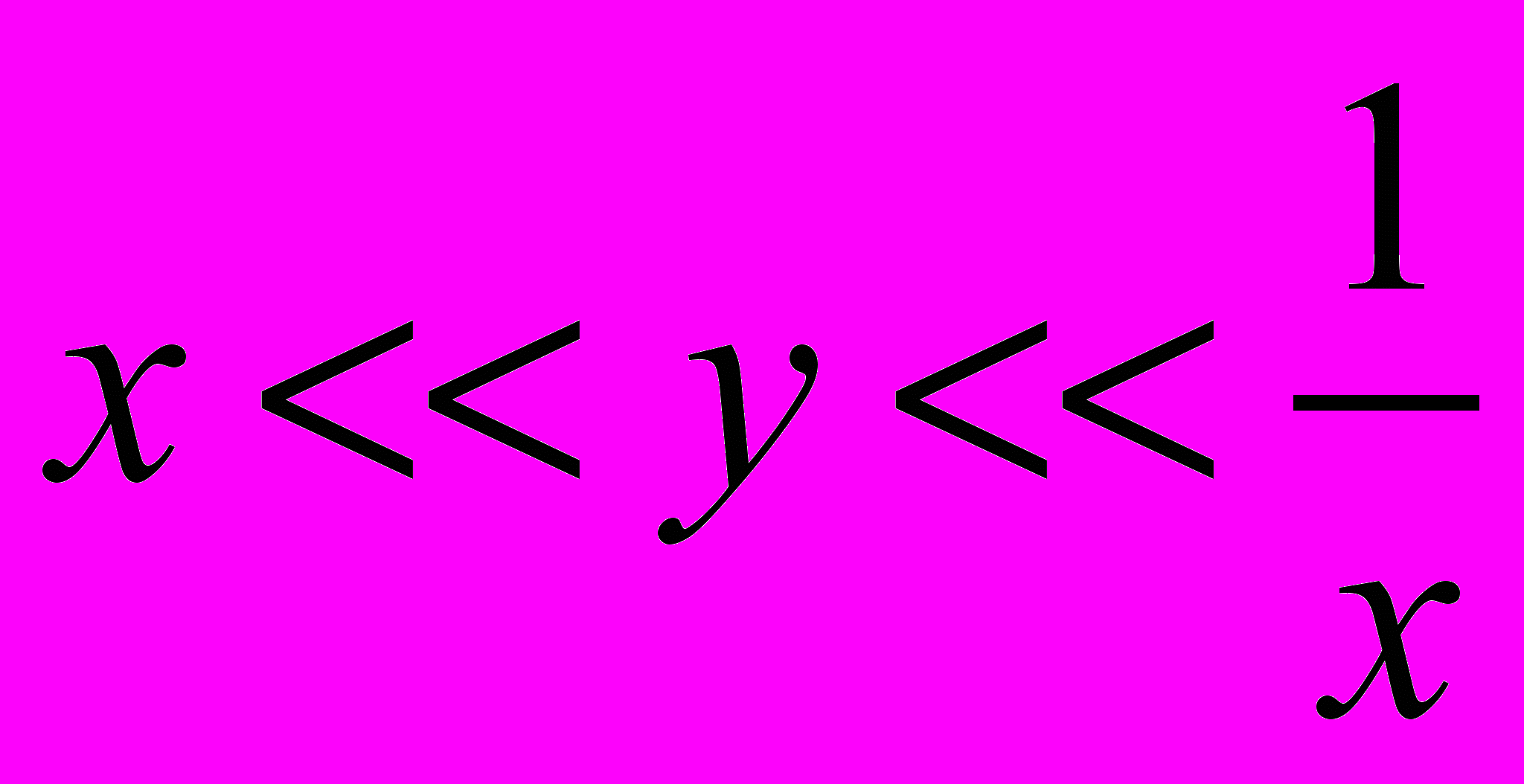, когда

, а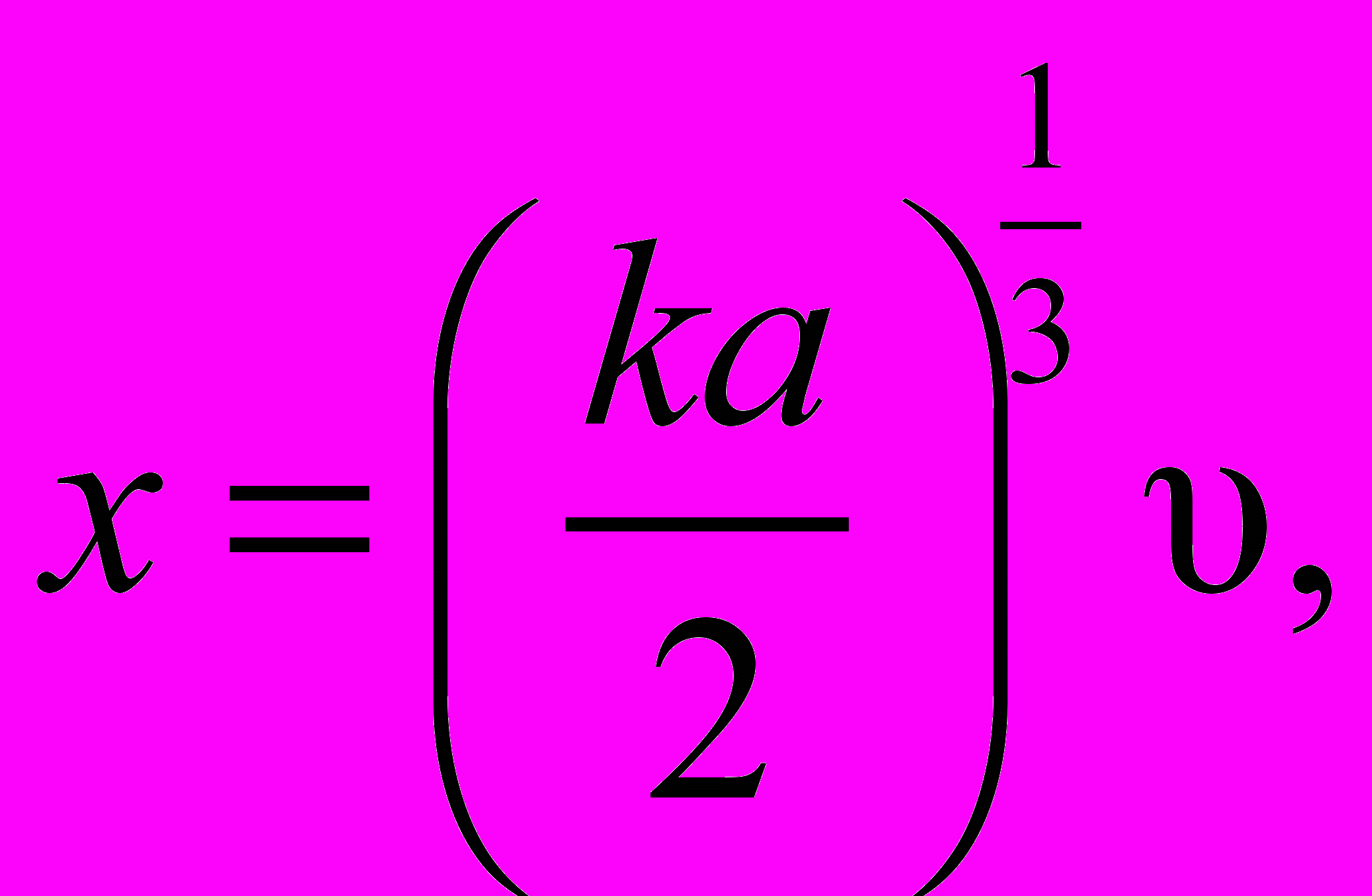

выражение для W дает формулу (9), следовательно, им можно пользоваться для освещенной области.

Для области полутени, когда

положительное или отрицательное число порядка единицы, т. е. область полутени, где явление дифракции играет главную роль. Для определения функции ослабления в области полутени можно использовать соотношение

(9)

где

, q – параметр, характеризующий свойства почвы.

В случае, когда величины х и у достаточно велики, причем пусть

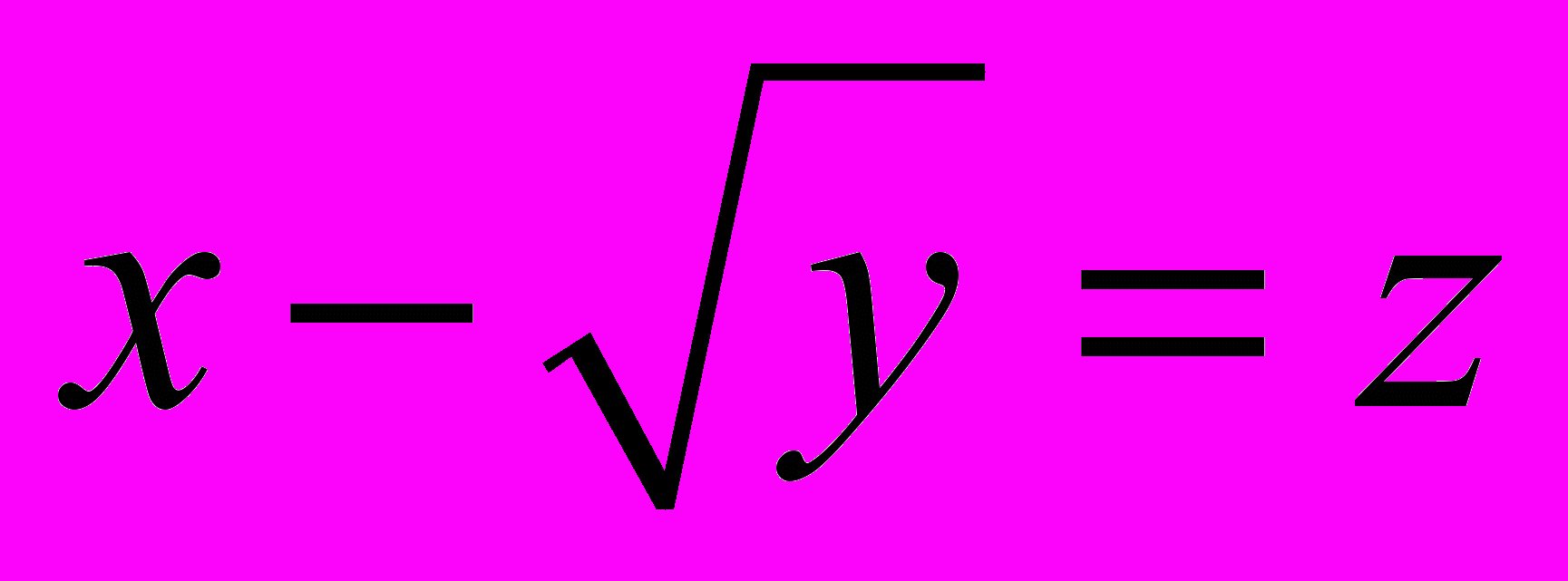конечна. Величина z представляет приведенное расстояние, считаемое не от источника, а от геометрической границы тени. В области геометрической тени z > 0, в «видимой» области – z < 0.

Для положительных (не слишком малых) z будет справедливым

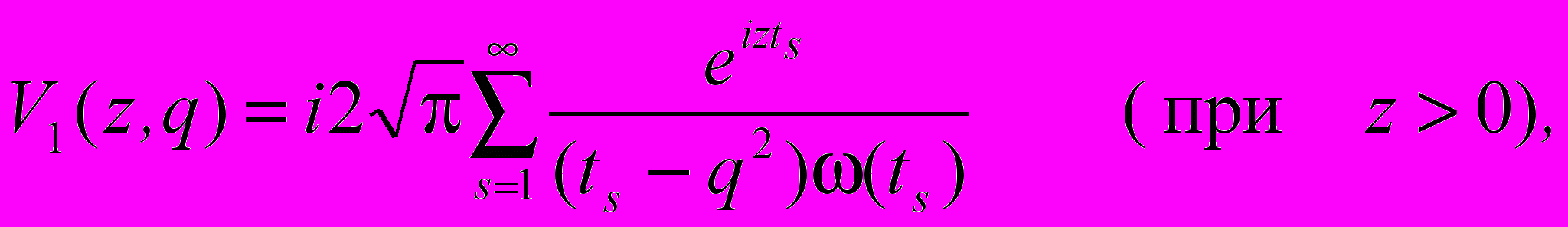
(10)

Ряд (10) сходится тем быстрее, чем больше z. При больших положительных z его сумма практически сводится к первому члену. Для отрицательных z ряд перестает сходиться.

Для области геометрической тени (z > 0) можно записать степенной ряд

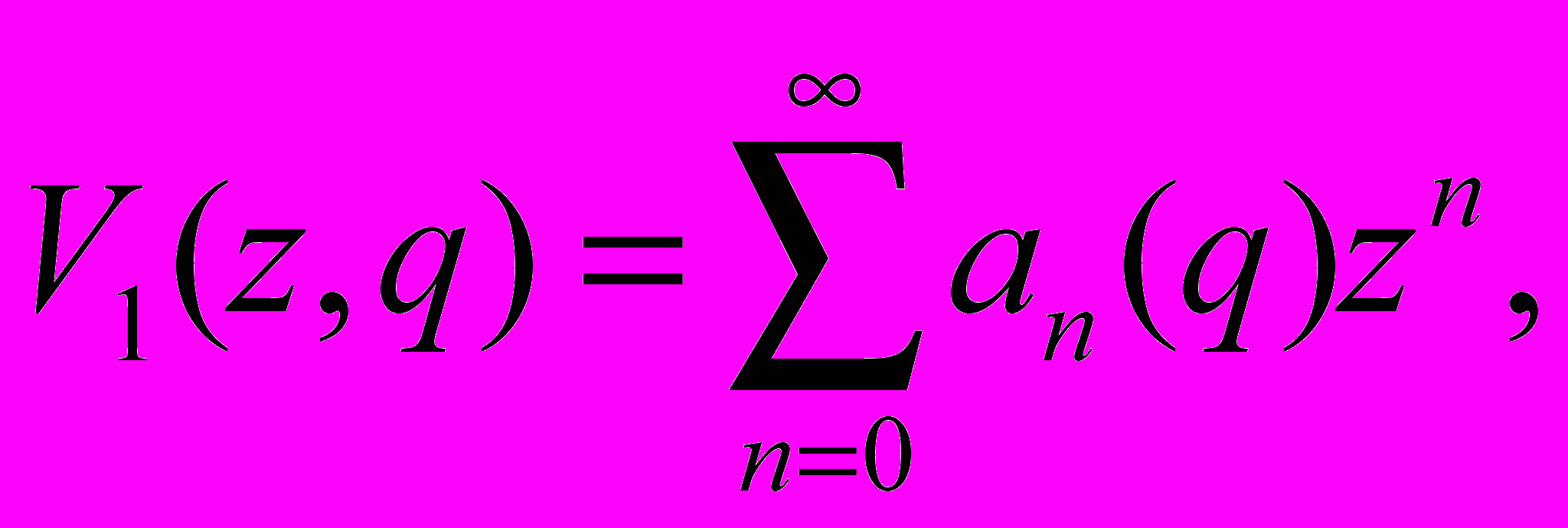
(11)

Представленный ряд (11) вполне пригоден для практического использования и может быть достаточно просто использован для определения множителя ослабления в теневой области.

Показанные модели позволяют выполнять вычисления только для однородных подстилающих поверхностей. Для определения напряженности поля с учетом неоднородности подстилающей поверхности можно использовать модель Фейнберга. Если трассой распространения радиоволн является первая зона Френеля, которая в случае z₀ = z_A = 0 имеет вид вытянутого эллипса с корреспондирующими точками в качестве его фокусов. Такая трасса может быть разбита на число участков N, каждый из которых обладает постоянными параметрами проводимости, причем переходные области между участками малы по сравнению с размерами самих участков. Тогда для z₀ = 0, y₀ = y(s₀ρ) когда

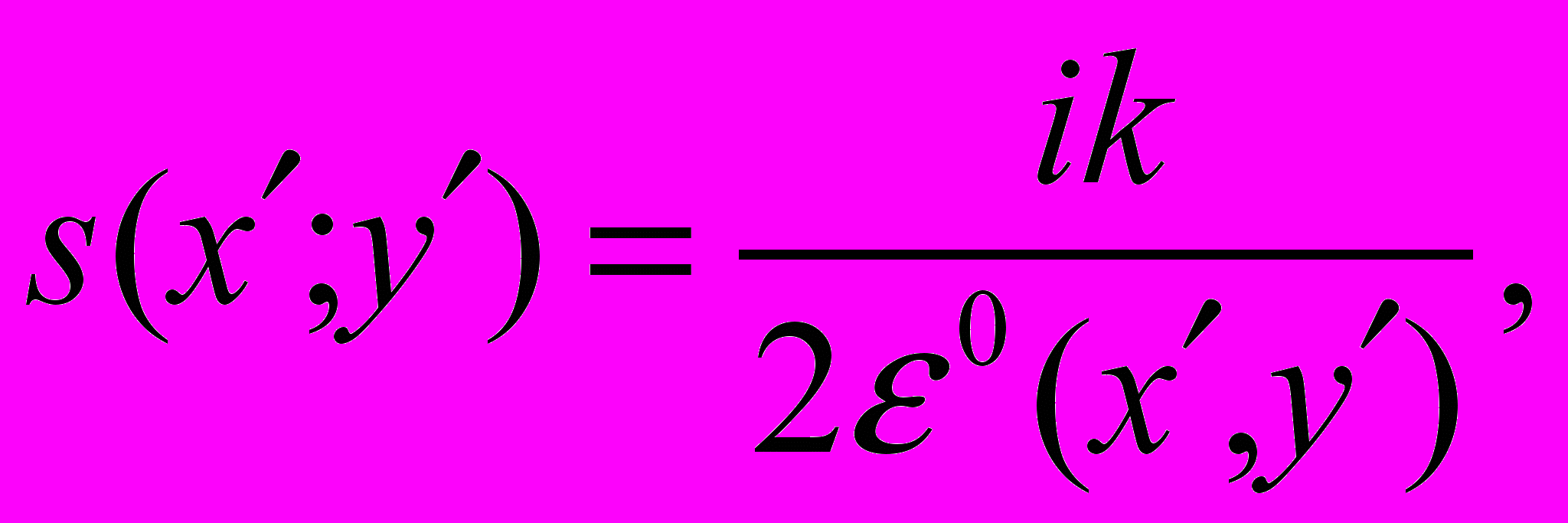
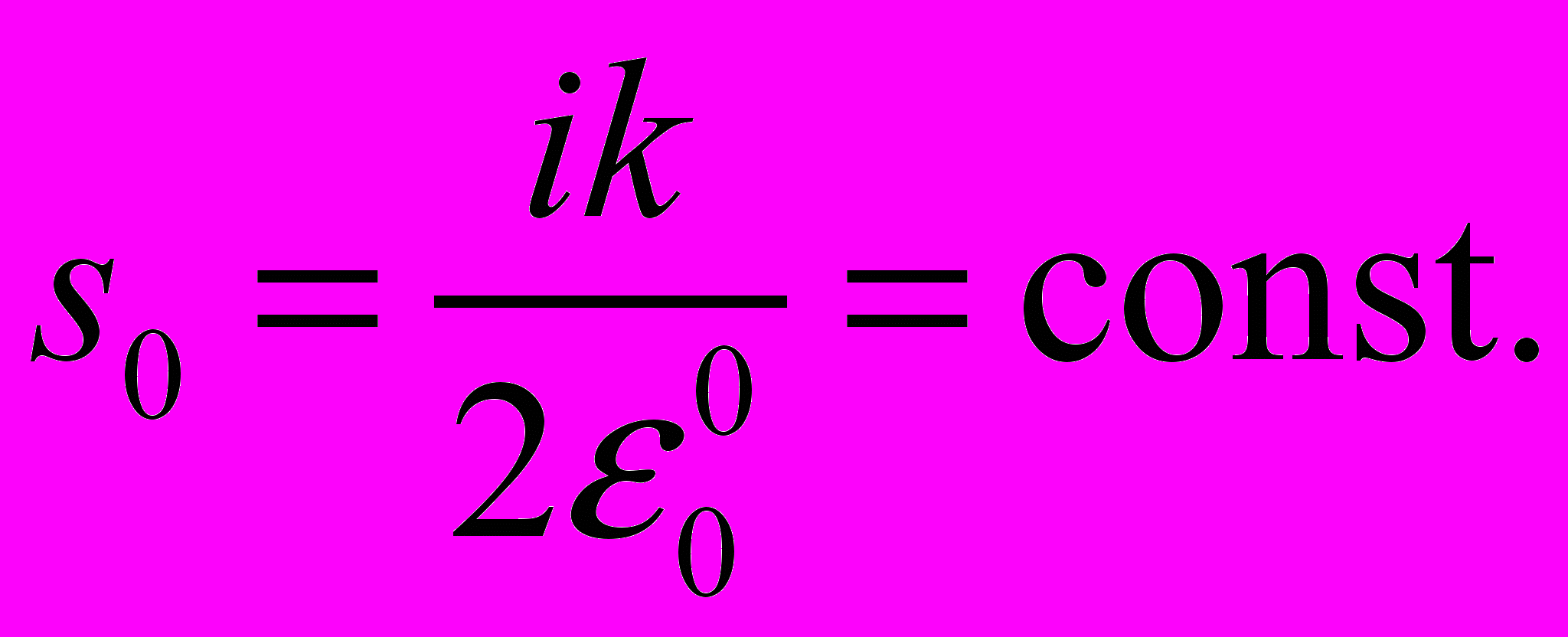будет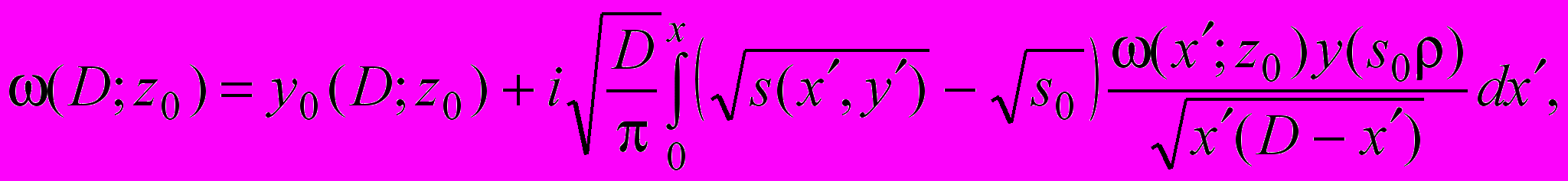

(14)

где k – абсолютная величина волнового вектора.

Разбивая такую подстилающую поверхность на однородные участки, по своим электромагнитным свойствам, это уравнение можно переписать так:

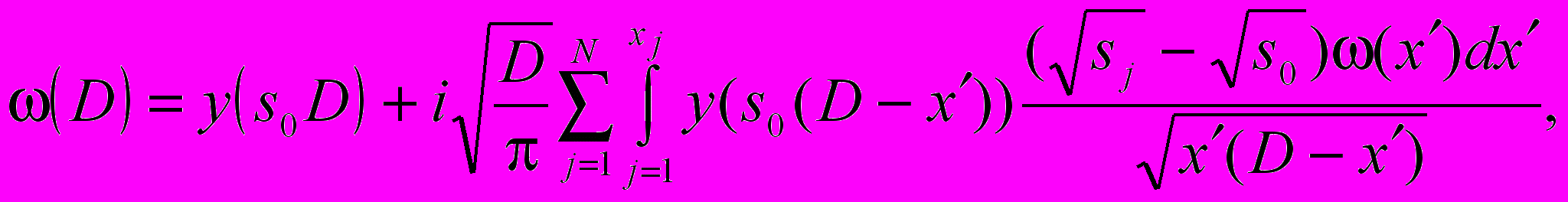
(15)

где

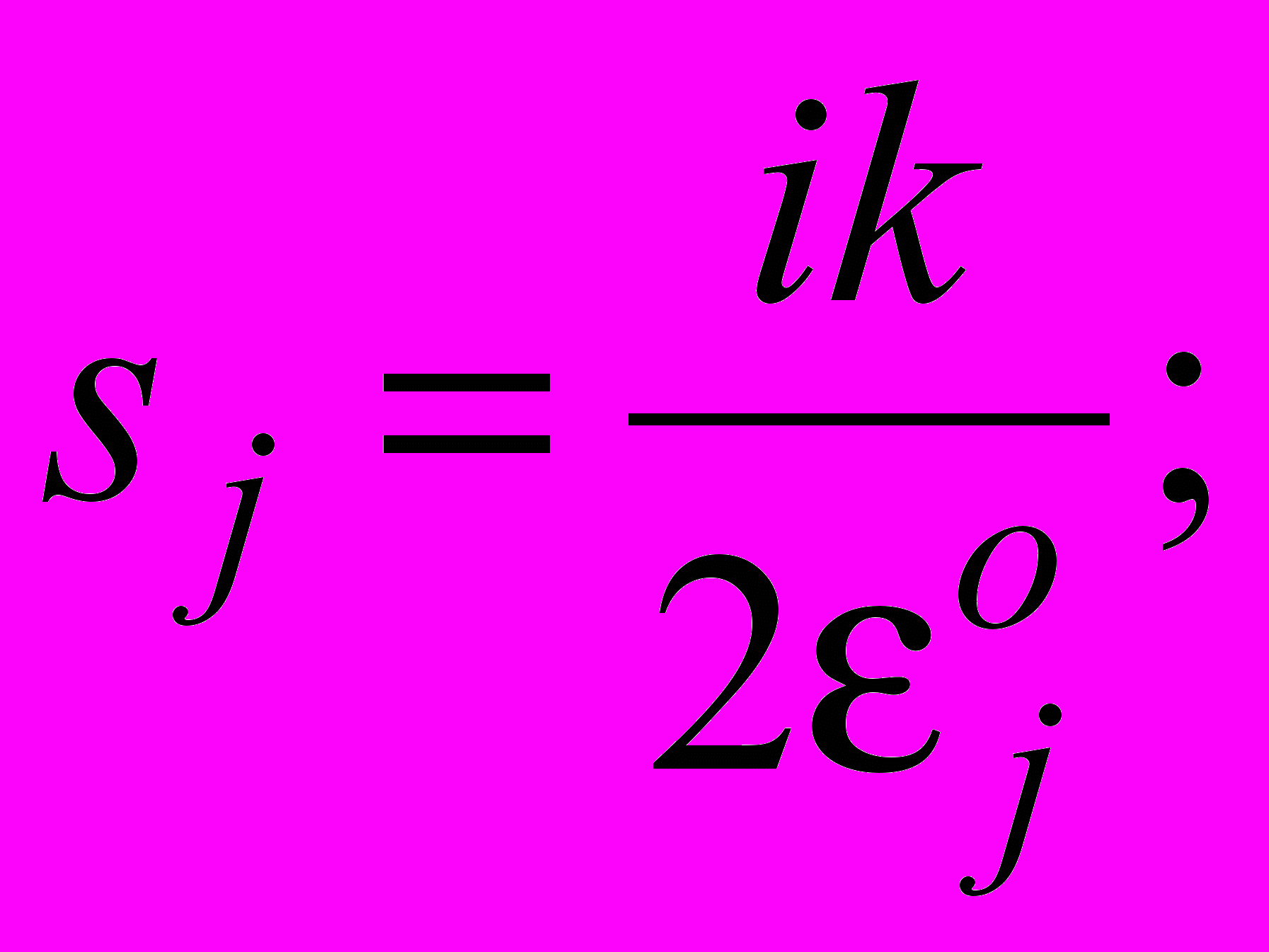x_j_–₁ и x_j – границы j-го участка, x₀ = 0, x_N = D.

Функция ослабления ω является сложной функцией расстояния от источника. При переходе каждой границы между участками может меняться и характер ее поведения. Поэтому, закрепив положение источника, особенно удобно на каждом участке обозначать ее определенным символом.

Для определения поля в любой точке необходимо выполнить интегрирование только по области значений x′, лежащей между источником и точкой. Для первого участка функция ослабления известна, это нормальная функция ослабления для соответствующего ε₀, а именно

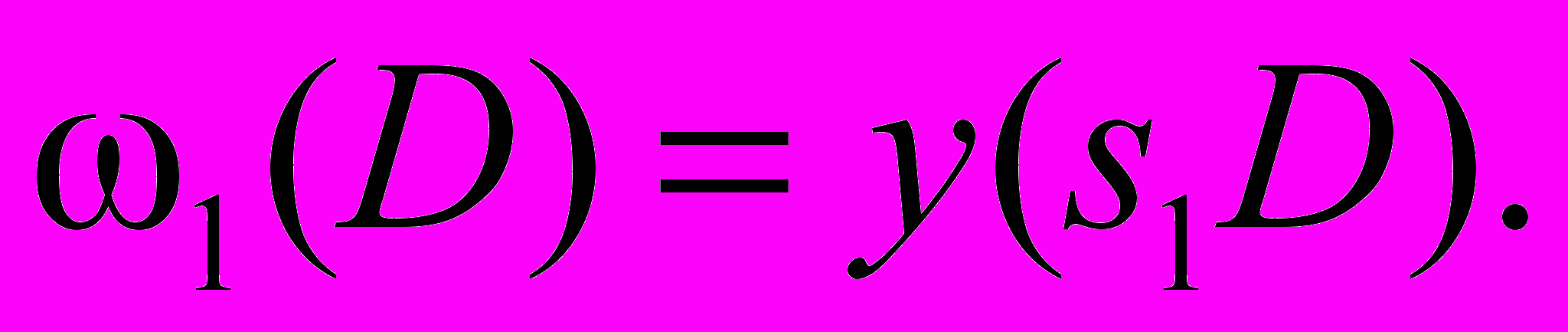
Для функции ослабления второго участка при х₁ < D будет справедливо

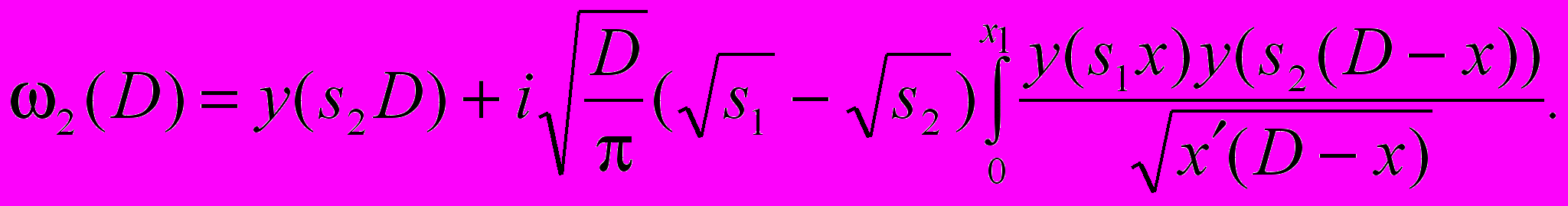
(16)

При условии

для концевого участка

(17)

В общем случае для k-го участка при

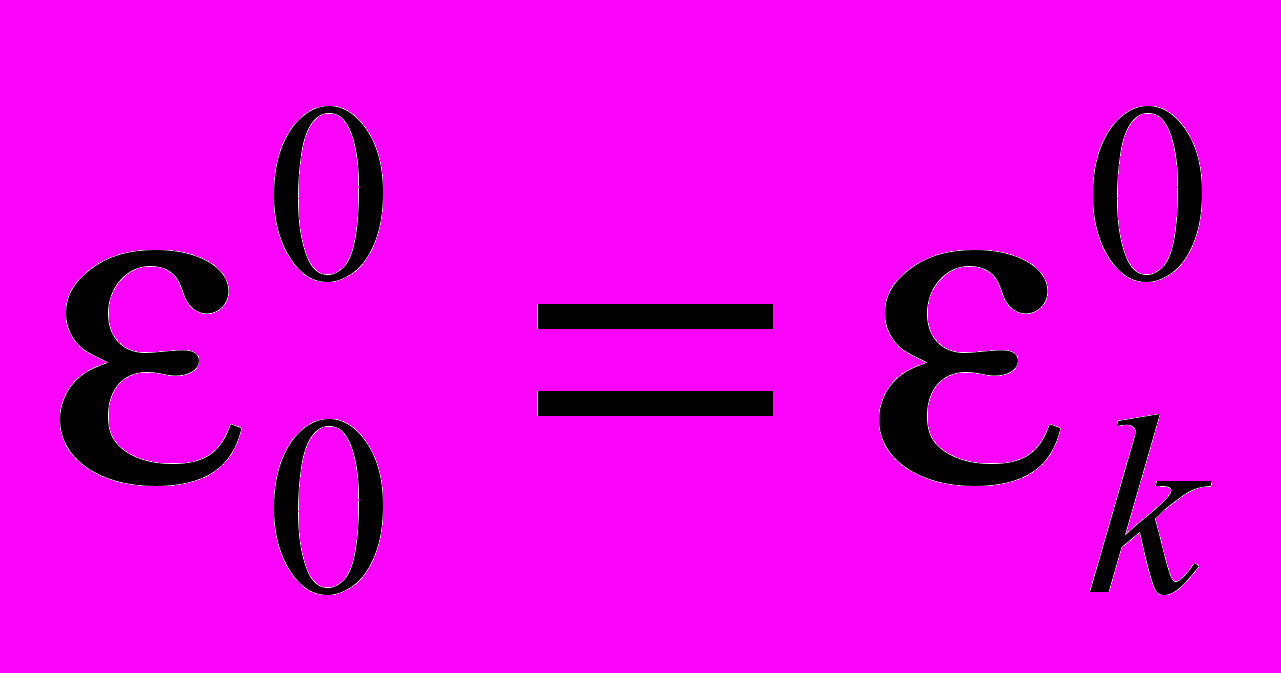может быть показано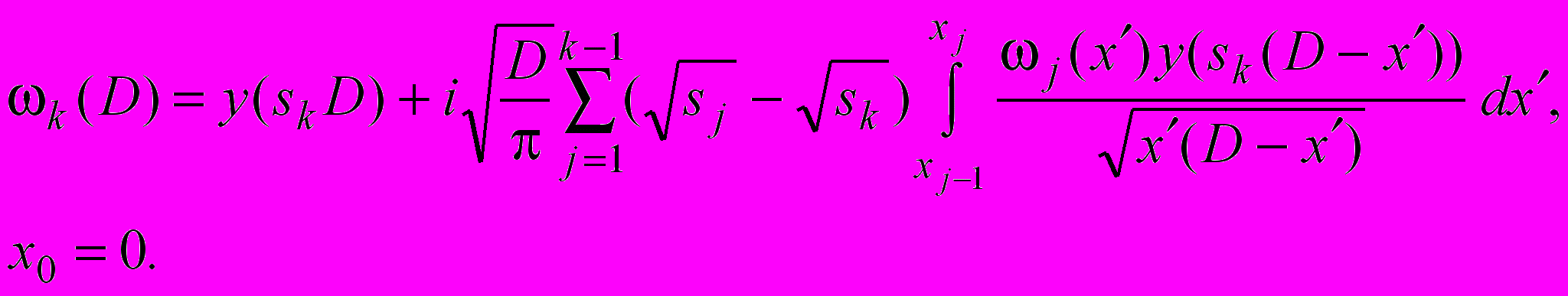

(18)

При использовании показанной модели в случае аппроксимации поликомпонентной подстилающей поверхности, состоящей из большого количества участков, принимая во внимание соотношение (21), могут возникать определенные затруднения вычислительного характера, связанные с определением функции ослабления каждого из участков. Для аппроксимации подобных подстилающих поверхностей могут быть использованы аппроксимационные модели сложных импедансов.

Модель средневзвешенного импеданса

(

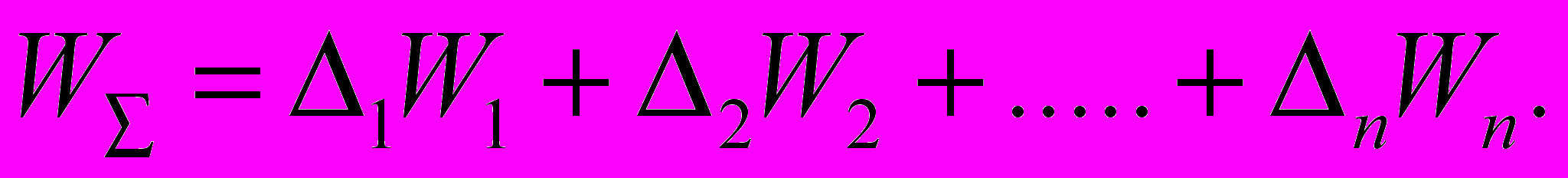19)

Модель обобщенного среднегеометрического импеданса

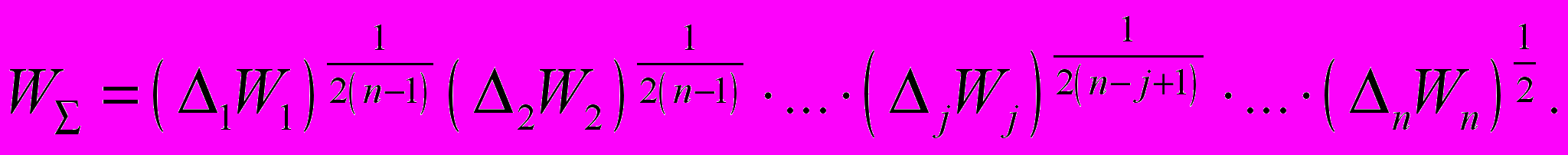
(20)

Модель квазипозиномиального импеданса

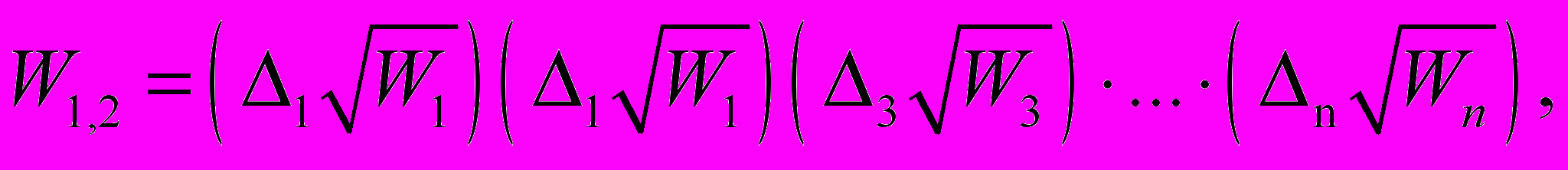
(21)

г

де

(22)

где W₁, W₂, W₃, W_n – неоднородные множители ослабления каждого из участков подстилающей поверхности; L₁, L₂, L₃, L_n – протяженность ее участков; Δ₁, Δ₂, Δ₃, Δ_n – весовые коэффициенты каждого из задействованных участков подстилающей поверхности.

Для аппроксимации любых подстилающих поверхностей может быть использована аппроксимационная сегментационная модель, строящаяся на использовании сегментационной теоремы

, где М = α + β – общее число сегментов, причем α = 0, 1, 2,… – число «двоек», а β = 0, 1, 2… – число «троек» участков.

Для двухкомпонентного сегмента будет

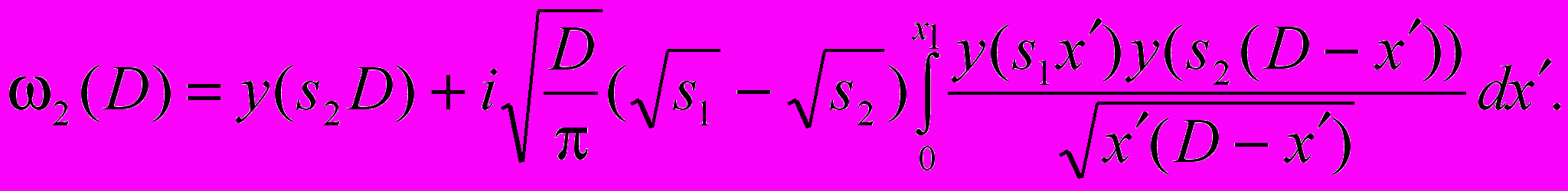
(23)

Для трехкомпонентного сегмента можно записать

(24)

При использовании сегментационной теоремы

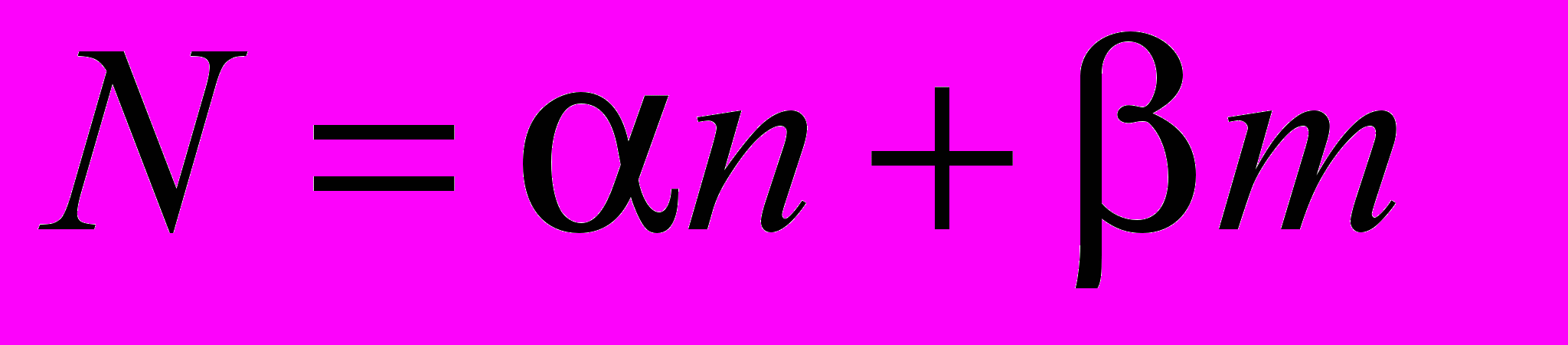с учетом алгоритмов оптимальности и сшивки граничных участков аппроксимационных сегментов представляется возможным достаточно просто определять нелинейный множитель функции ослабления для любого участка поликомпонентной подстилающей поверхности.

У

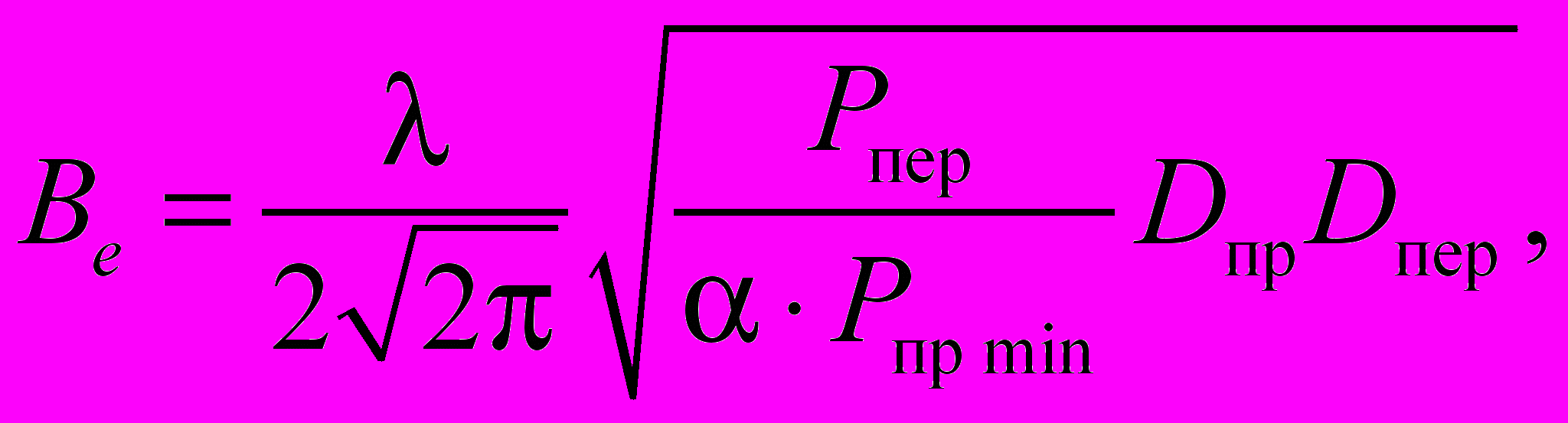становлено, что вводя в общее аппроксимационное решение граничное условие, учитывающее параметры приемопередающего оборудования, в данном случае можно определить непосредственно дальность действия ККС.

(25)

где λ – длина волны; Р_пер – мощность передатчика, Р_пр_min – чувствительность приемника; α – коэффициент, определяющий требуемую вероятность приема,

G_np и G_n_е_p – коэффициент усиления соответственно приемной и передающей антенн; η_npи η_nep – коэффициент полезного действия (к.п.д.) их антенно-фидерного тракта.

Сформулированная статистическая модель, доказанная сегментационная теорема

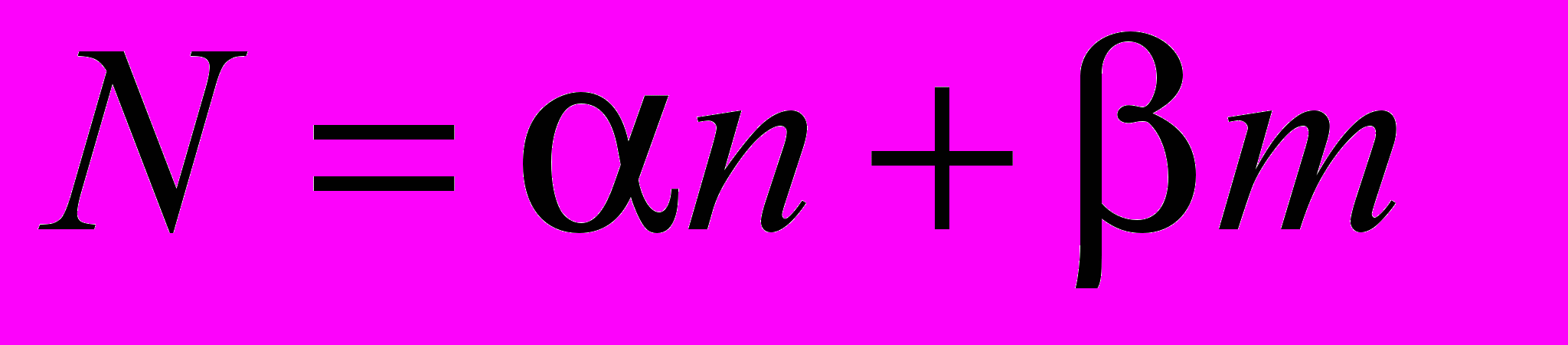и алгоритмы сшивки, как это подтверждается исследованиями последующих разделов весьма конструктивна для решения задач определения топологии и форм периметров зон действия ККС, работающих в СВ диапазоне с учетом неоднородности подстилающей поверхности. Для решения таких задач анализа разработаны, прежде всего, методика и алгоритмы решения многопараметрических стохастических задач количественной оценки дальности и формы зон действия ККС, работающей в СВ диапазоне.

Далее в разделе выявлена чувствительность указанной модели к зонам, содержащим нелинейные переходы, имеющие место в граничных областях соседних участков, обладающих различными проводящими способностями поликомпонентной подстилающей поверхности.

Важным выводом, имеющим экономические последствия при проектировании и строительстве цепей ККС, является особая роль «взлетной» и «посадочной» площадки поликомпонентной подстилающей поверхности, при определении дальности и формы зоны действия контрольно-корректирующих станций, работающей в средневолновом диапазоне.

Полученные в разделе результаты важны, во-первых, потому, что достаточно полно описывают тенденции и количественный характер поведения дальности распространения и формы зоны действия ККС, работающей в СВ диапазоне.

Во-вторых, они свидетельствуют о настоятельной необходимости исследований форм периметров зон действия как отдельных ККС, так и их цепей, особенно на ВВП.

В третьем разделе для решения задачи оптимизации топологии высокоточных радионавигационных полей, формируемых ККС в СВ диапазоне для речных инфокоммуникационных систем, разработаны методика и алгоритмы определения формы периметра зоны действия ККС при использовании аппроксимационных моделей, учитывающих влияние поликомпонентной подстилающей поверхности. Показано, что используя алгоритм

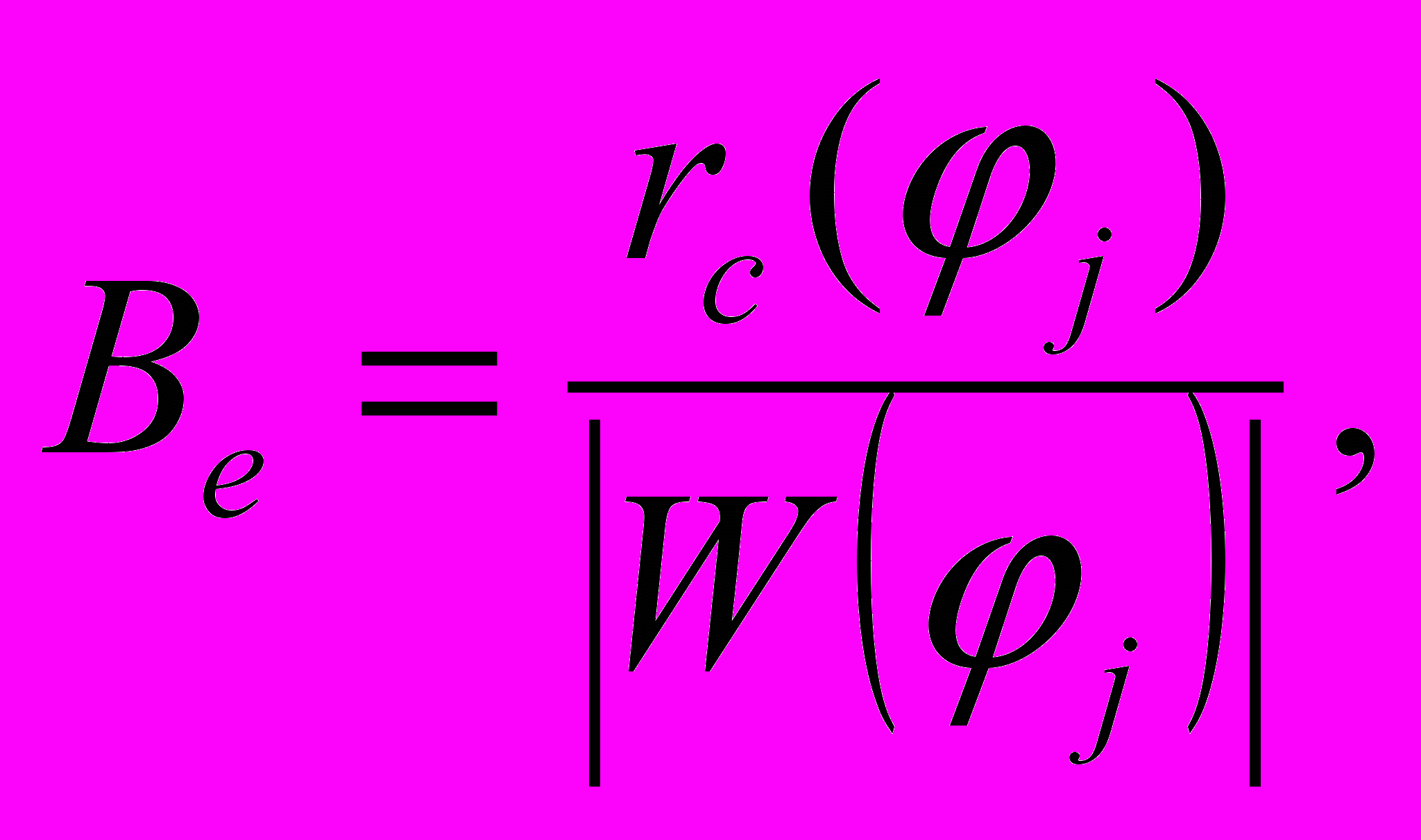
(26)

где r_c – дальность зоны действия ККС, │W│ – модуль нелинейного множителя ослабления, где φ_j – азимутальное j направление от ККС на НАП, j = 1,2,3,…,n где n – число выбранных азимутальных направлений для расчета.

В данном разделе на основе наиболее конструктивной из усредняющих обобщенных моделей – квазипозиномиального импеданса определен множитель ослабления составной трассы │W_{1, 2}│ и найдены зоны

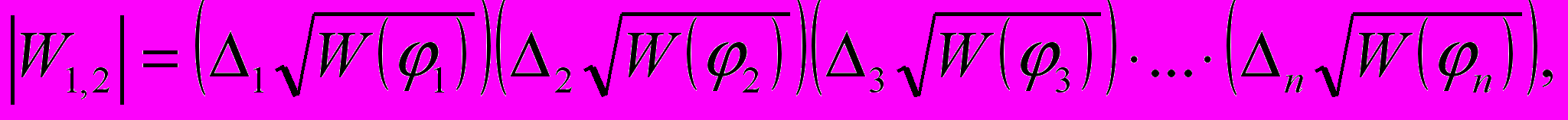
(27)

действия ККС для ряда опорных пунктов ЕГС России, а также выполнен сопоставительный анализ полученных результатов с результатом, полученным при использовании моделей (19) и (20). Также для рассмотренных случаев определены осредненные и минимальные зоны действия ККС для рассмотренных опорных пунктов (табл. 1).

Таблица 1.

Результаты осреднения расчетной формы периметра зоны действия ККС

№ п/п	Название опорного пункта	Осредненный радиус, км			Ближайшая ККС
№ п/п	Название опорного пункта	1	2	3	Дистанция, км	Опорный пункт
1	Маяк Шепелевский	495.8	270.7	235.8	537	Шексна
8	Шексна	520.8	194.0	148.0	461	Нижний Новгород
11	Нижний Новгород	517.1	207.1	107.4	328	Казань
12	Казань	499.5	180.1	144.6	289	Самара
13	Самара	484.1	211.0	144.1	348	Саратов
14	Саратов	504.8	187.8	107.2	309	Волгоград
15	Волгоград	509.4	218.3	145.1	322	Астрахань
16	Астрахань	514.3	198.9	183.5

Для практически важных вариаций двух компонентных подстилающих поверхностей типа «суша-море», «море-суша» с учетом соотношения

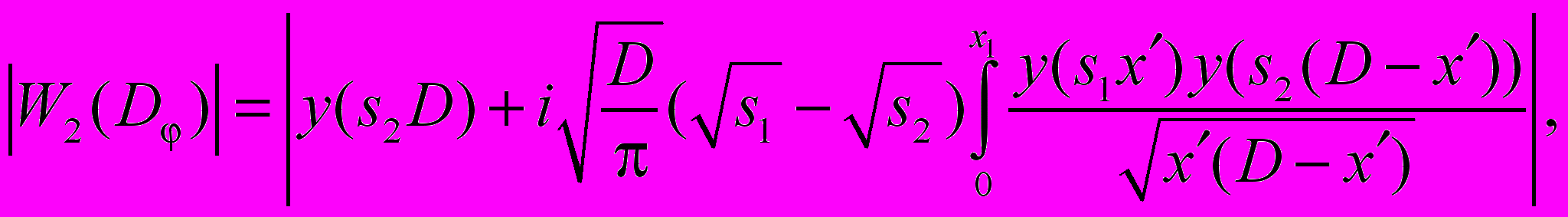
(28)

и

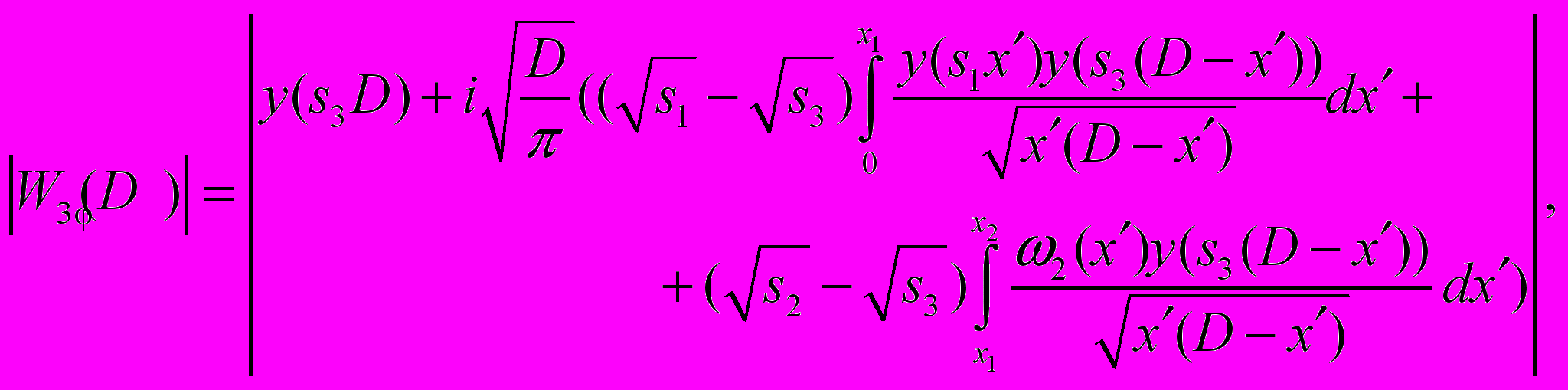трехкомпонентных подстилающих поверхностей типа «суша-море-суша», «море-суша-море» с учетом выражения

(29)

выполнен аналитический расчет функции ослабления и напряженности поля, с целью выявления чувствительности модели сегментации к нелинейным переходам напряженности поля граничных областей участков подстилающей поверхности (Рис. 2.а. кривая 1), а также с результатами аппроксимаций, полученных на основе квазипозиномиальной модели (Рис. 2.а. кривая 2).

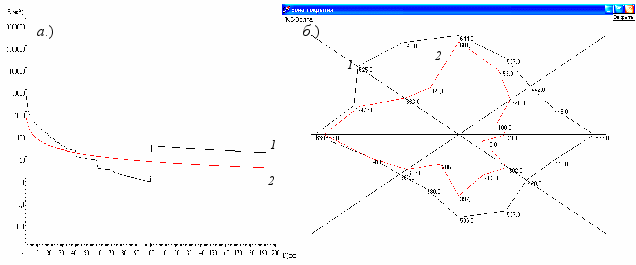
Рис. 2. Напряженность поля над поликомпанентной подстилающей поверхностью: а) двухкомпонентная подстилающая поверхность протяженностью 200 км; б) расчетная форма периметра зоны действия ККС.

С учетом алгоритмов сегментации и полученных условий показана возможность определения форм периметров зон действия ККС, работающих в СВ диапазоне с учетом параметров приемопередающего оборудования для любых поликомпонентных подстилающих поверхностей, отвечающих условию N = αn+βm, N ≥ 2. (Рис. 2.б.).

Проведен сопоставительный анализ результатов аналитических расчетов, полученных с использованием теоремы сегментации N = αn+βm с данными натурных испытаний рис. 3. На основании чего можно сделать вывод, что предложенная модель достаточно конструктивна для определения дальности и форм периметров зон действия речных ККС.

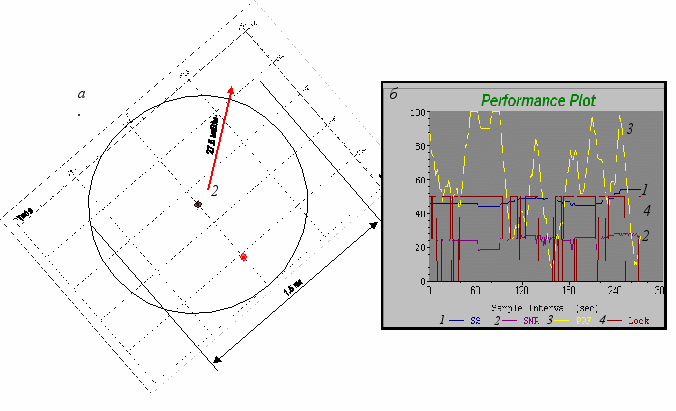
Рис. 3. Сопоставительный анализ расчетных результатов и данных натурных испытаний: а.) СКП при нормальном распределение с вероятностью 0.95; б.) параметры ККС Кочетовского гидроузла при удалении на 96.0 км.

Также в третьем разделе определены, нанесены на карту и исследованы, с учетом реальных условий распространения поверхностных волн средневолнового диапазона, топология осредненной (табл. 2) и уточненной зоны действия контрольно-корректирующей станции «Нижний Новгород», «Саратов», «Самара», «Казань», «Волгоград», «Астрахань», после чего была найдена и построена результирующая зона действия части цепи локальной дифференциальной подсистемы, ограниченная с севера контрольно-корректирующей станцией «Нижний Новгород», а с юга дифференциальной станцией «Астрахань» (рис 4).

Таблица 2.

№ п/п	Название ОП	Осредненный радиус, км.	Минимальный радиус, км.
1	Астрахань	481.6*	414*
2	Волгоград	335.2	220
3	Казань	339	182
4	Нижний Новгород	332	273
5	Самара	390	290
6	Саратов	417	363
* – в расчете принималась область в секторе 180° (запад-север-восток)

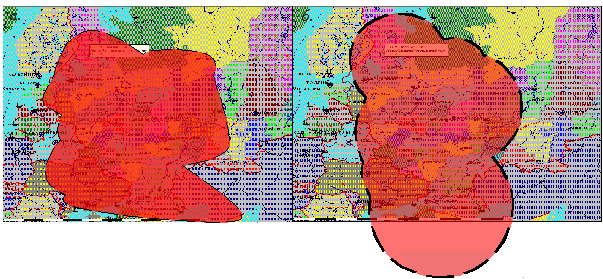
Осредненный и минимальный радиусы зоны действия ККС

Рис. 4. Форма зоны действия цепи ЛДПС состоящей из 8 ККС: а.) уточненная форма периметра; б.) минимальная форма периметра.

Blog

Методы построения радионавигационных полей для информационного обеспечения автоматизированных систем управления движением судов

Содержание