Рабочая программа по дисциплине «Исследование операций и математическое программирование» для специальности 080111 «Маркетинг» федеральный компонент, ен. Ф. 01
| Вид материала | Рабочая программа |
- Учебно-методический комплекс Специальность: 080111 Маркетинг Москва 2009, 1368.46kb.
- Рабочая программа по дисциплине: «Экономика организации ( предприятия)» Для специалистов, 725.21kb.
- Рабочая программа по дисциплине «международный маркетинг» для специальности 080111, 440.64kb.
- Рабочая программа по дисциплине «управление качеством» для специальности 080111 «Маркетинг», 646.15kb.
- Рабочая программа по дисциплине «маркетинговые коммуникации» для специальности 080111, 333.61kb.
- Рабочая программа по дисциплине «поведение потребителей» для специальности 080111 «Маркетинг», 501.4kb.
- Рабочая программа по дисциплине «управление маркетингом» для специальности 080111 «Маркетинг», 391.63kb.
- Рабочая программа по дисциплине «основы сегментации рынка» для специальности 080111, 301.91kb.
- Рабочая программа по дисциплине «конкурентоспособность товаров и фирм» для специальности, 466.75kb.
- Рабочая программа по дисциплине «ценообразование» для специальности 080111 «Маркетинг», 349.53kb.
Кроме того, заданы ресурсы производства:
- земли – не более 1800 га
- затраты тракторосмен – не более 300
- затраты труда человеко-дней - не более 8000
- потребности в культуре А – 10 000 ц; В – 7 500 ц
Критерий оптимальности - максимальная прибыль от реализации.
В-3
Завод производит продукцию двух видов А и В, используя сырье, запас которого составляет 570 т. Согласно плану выпуск продукции А должен составлять не менее 60% от общего объема выпуска. Расход сырья на изготовление 1 т продукции А и В составляет соответственно 10 и 70 т. стоимость 1 т продукции А и В соответственно 3 и 8 тыс. руб.
Определить план выпуска продукции А и В, при котором стоимость выпуска продукции будет максимальной.
| вариант | Вид ресурса | Объем ресурса | Норма расхода на 1 т изделия | Стоимость 1т изделия | ||
Вид изделий | А | В | А | В | ||
| 1 | алюминий | 570 | 10 | 70 | 3 | 8 |
Контрольная работа 2
№1
- Графический метод
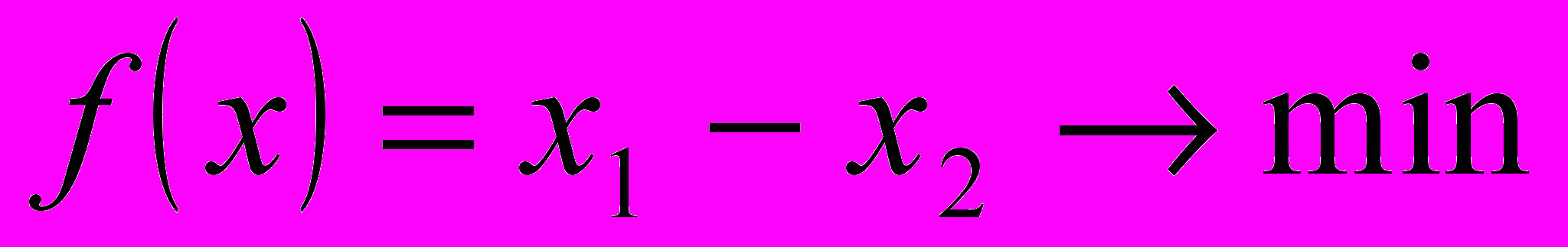
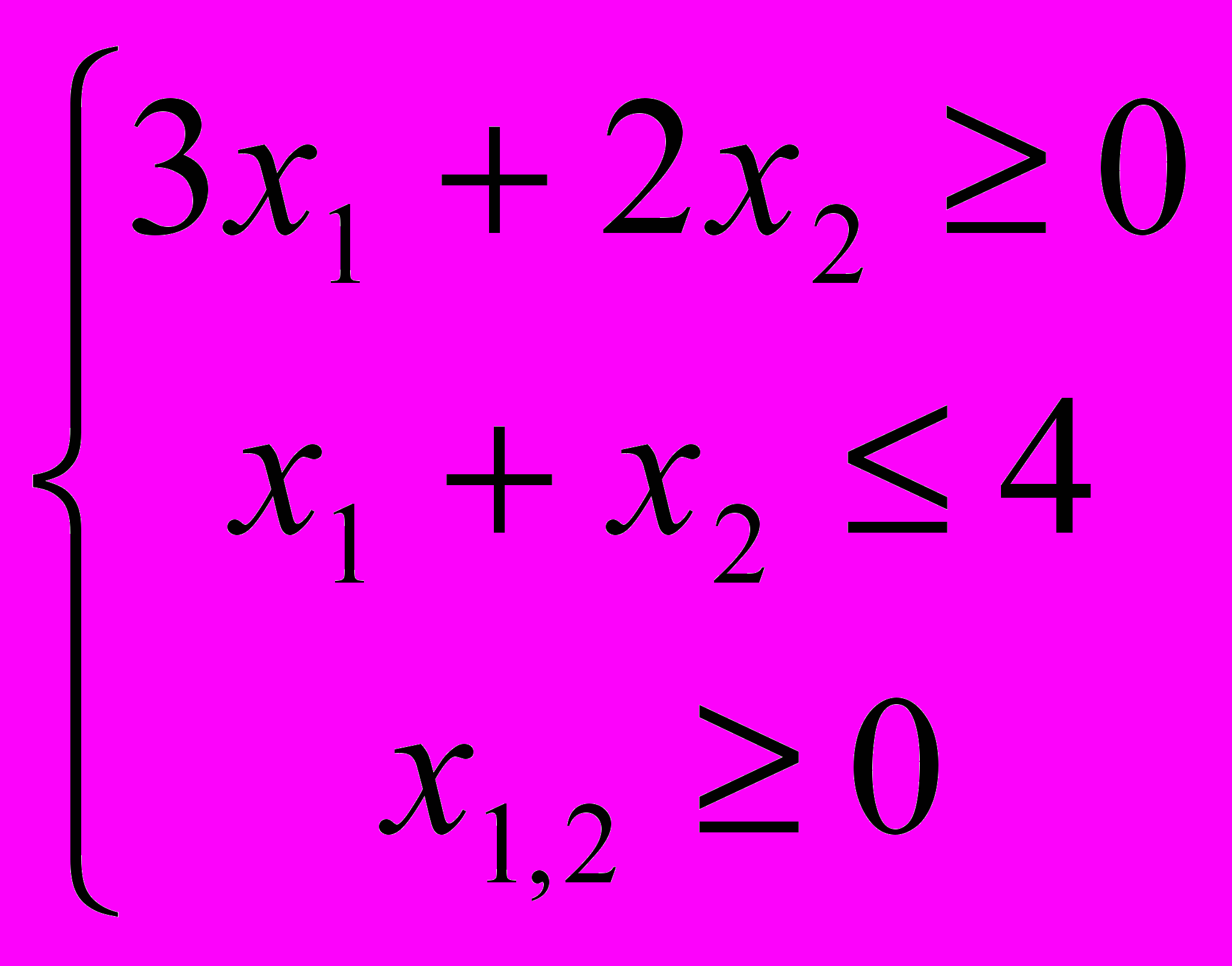
- Симплекс метод
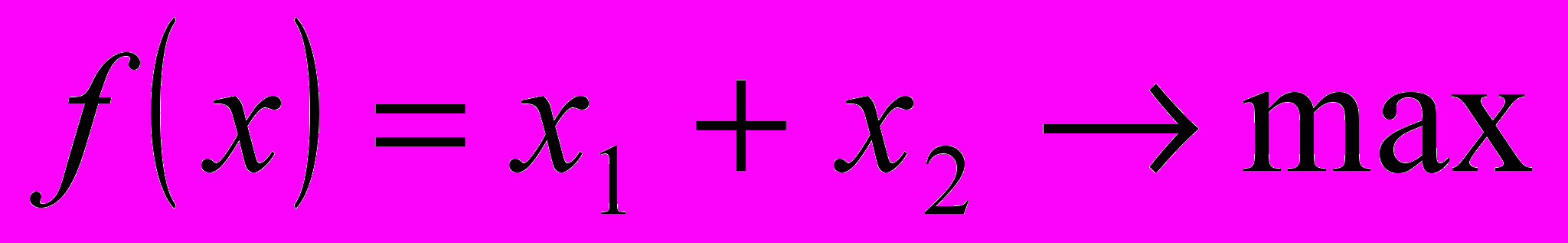
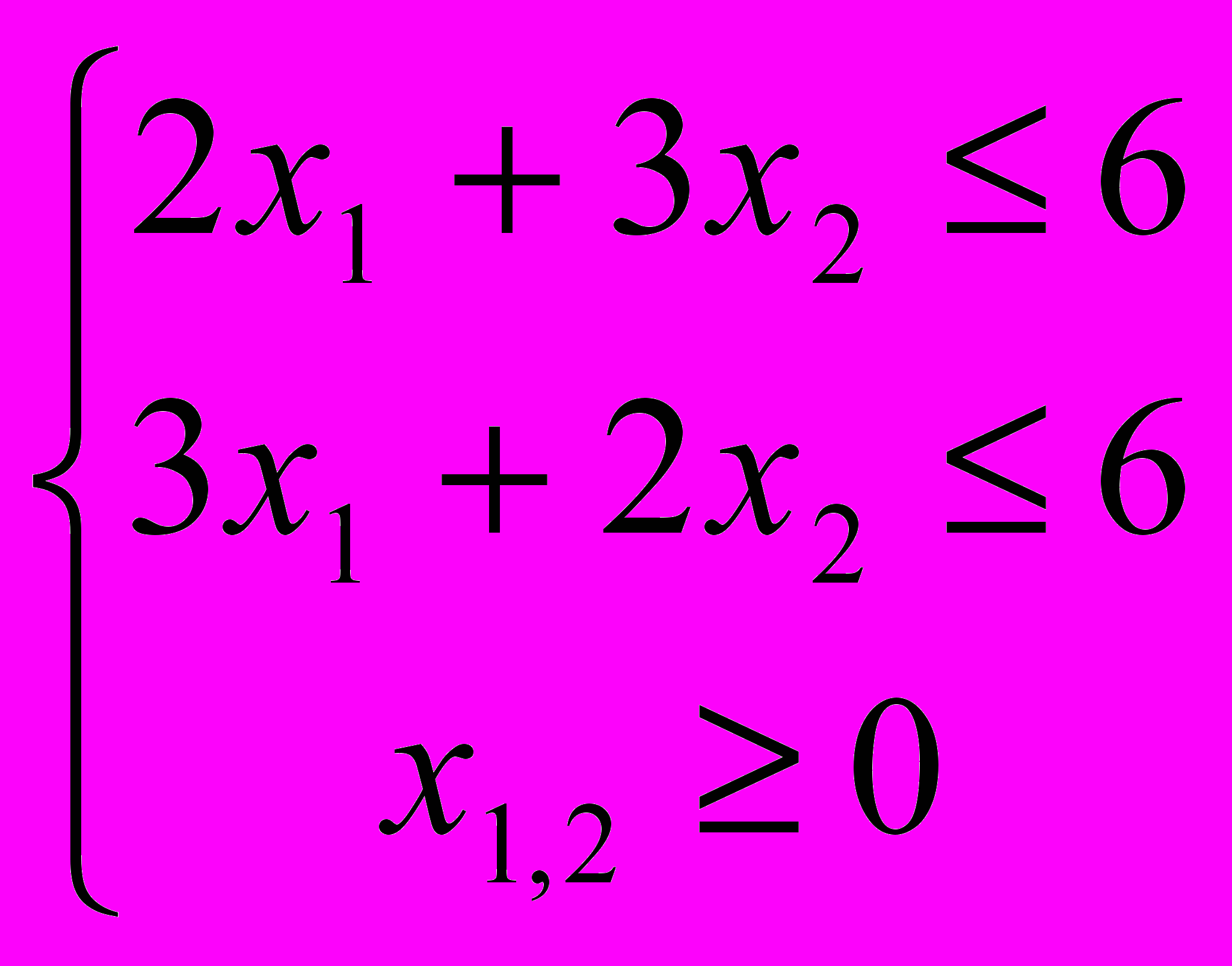
- Транспортная задача
a2 = 150, b2 = 100, a3 = 150, b3 = 70, b4 = 130, b5 = 110; |  |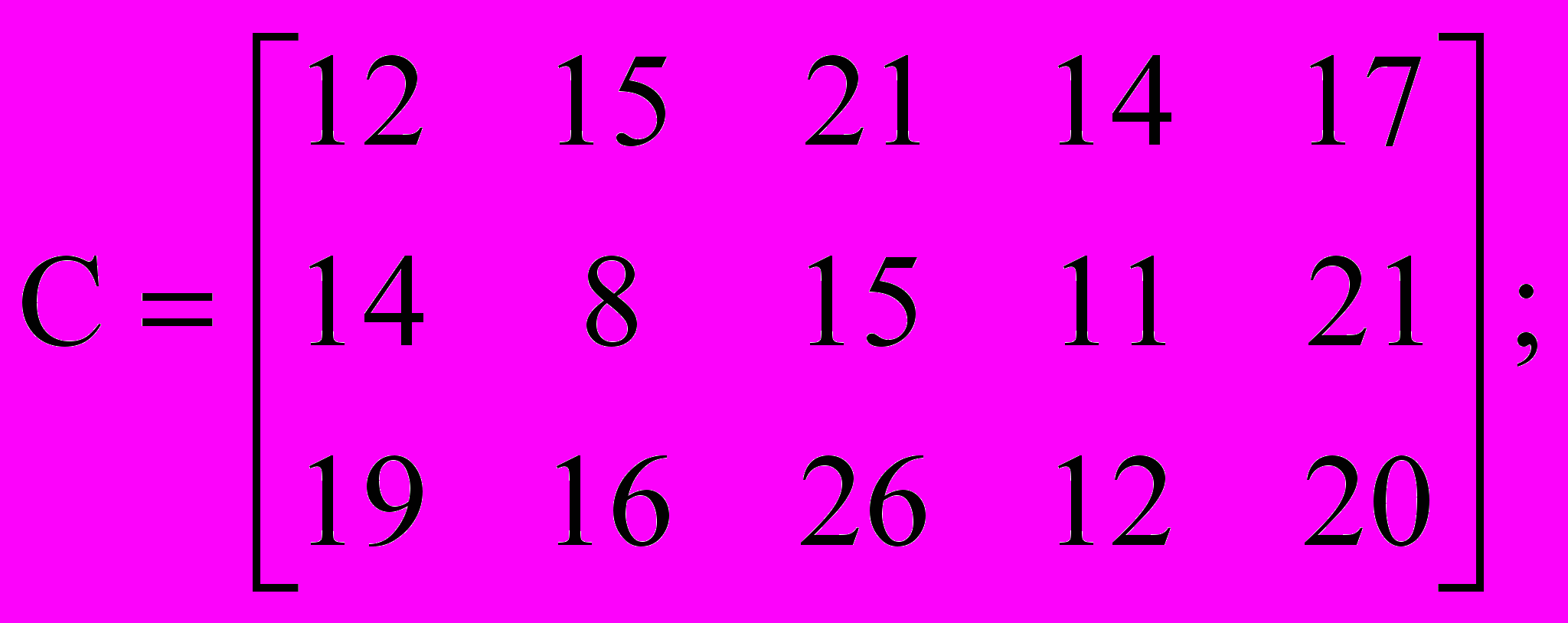
4 Решение матричной игры: а) показать существование или отсутствие чистых оптимальных стратегий; б) выполнить доминирование; в) свести исходную матричную игру к паре двойственных задач линейного программирования.
;5 Найти решение матричных игр.
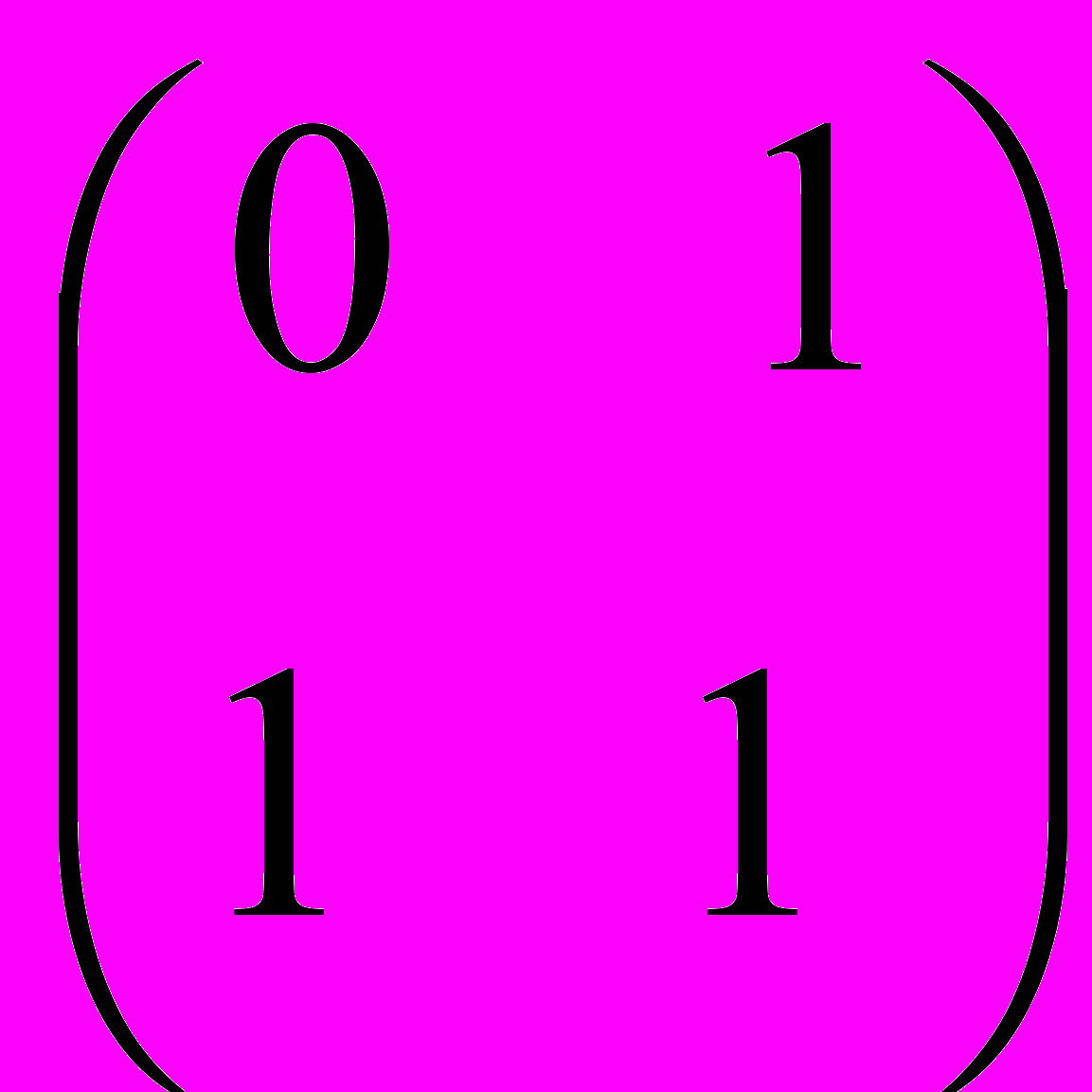
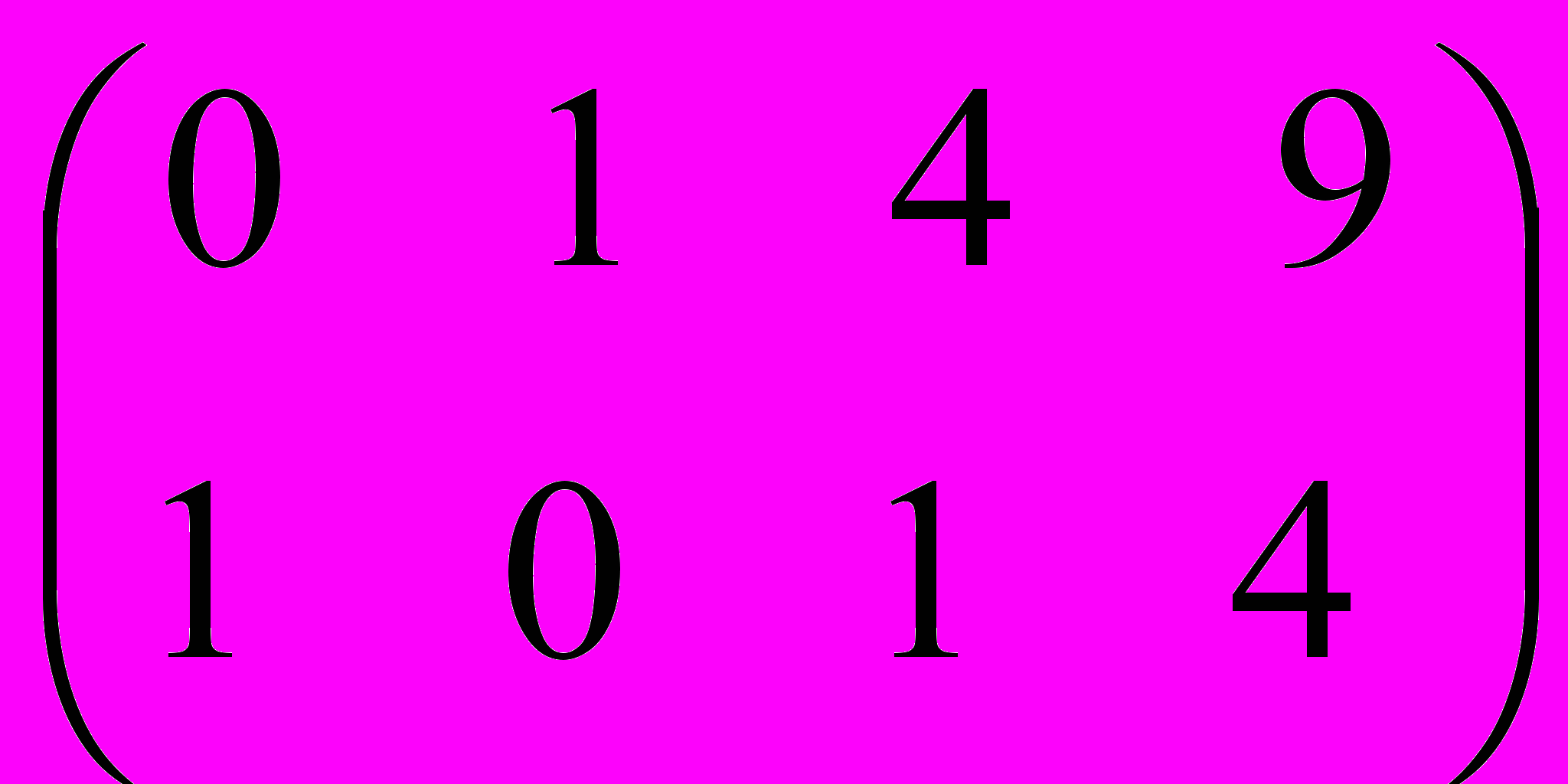
№2
- Графический метод
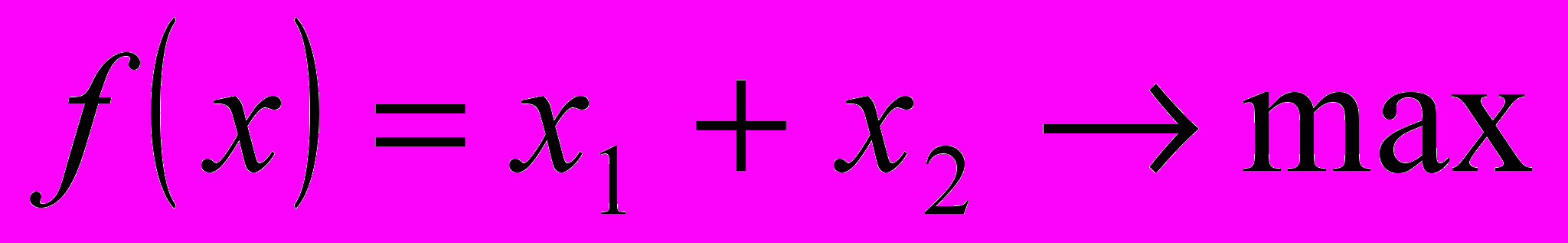
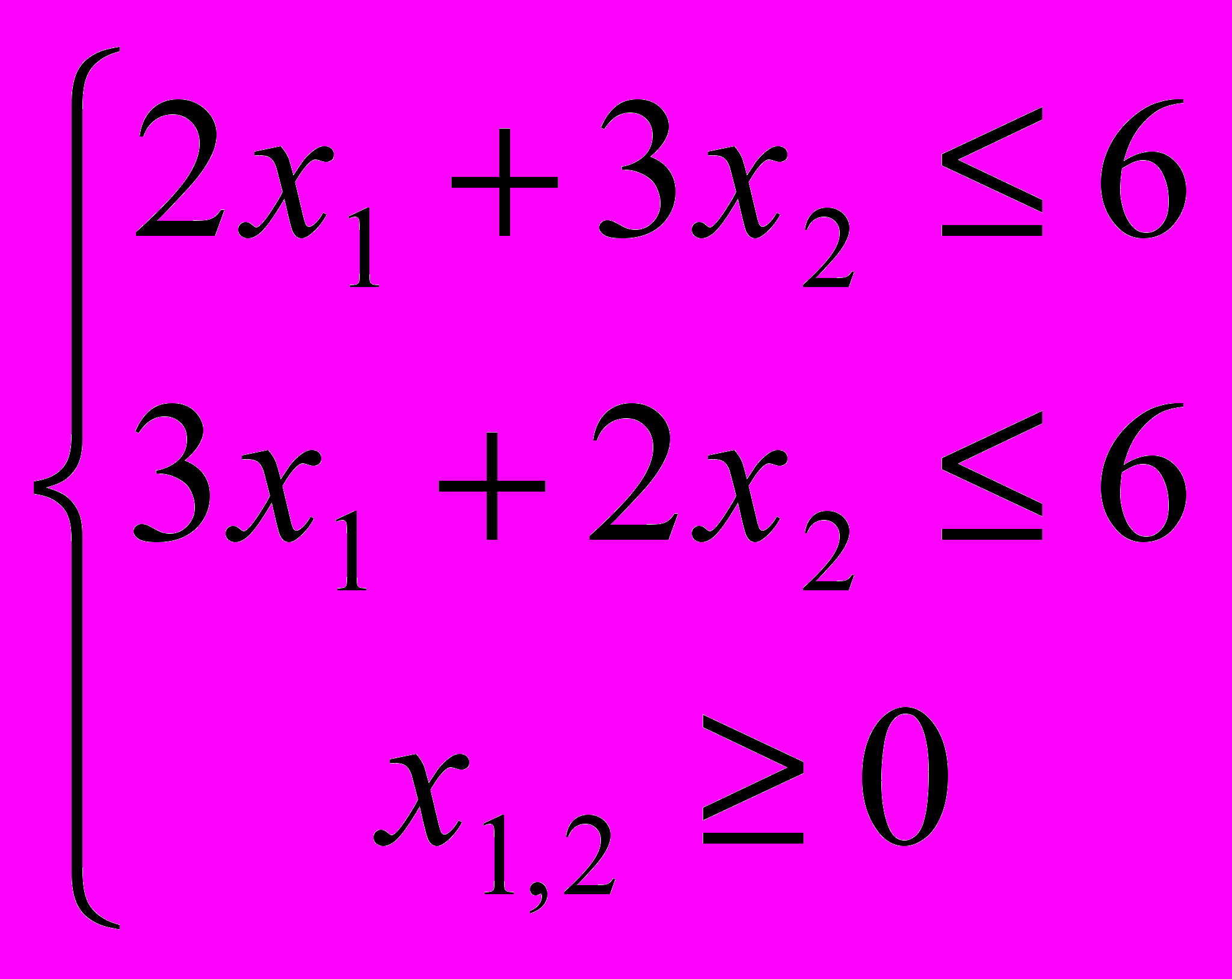
- Симплекс метод
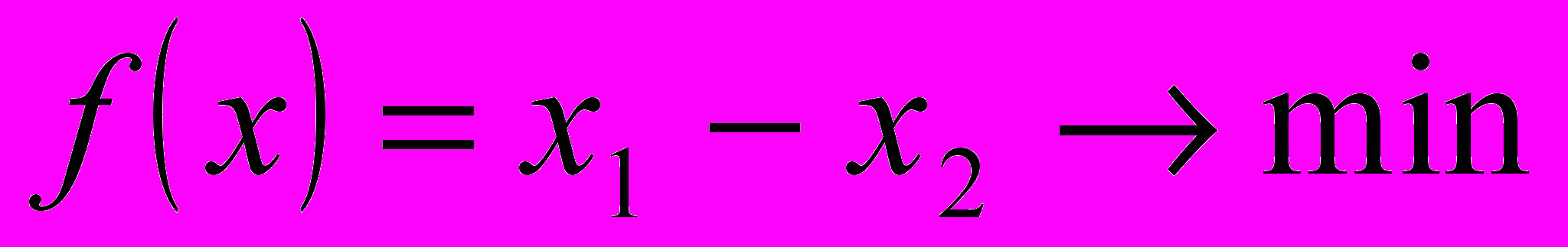
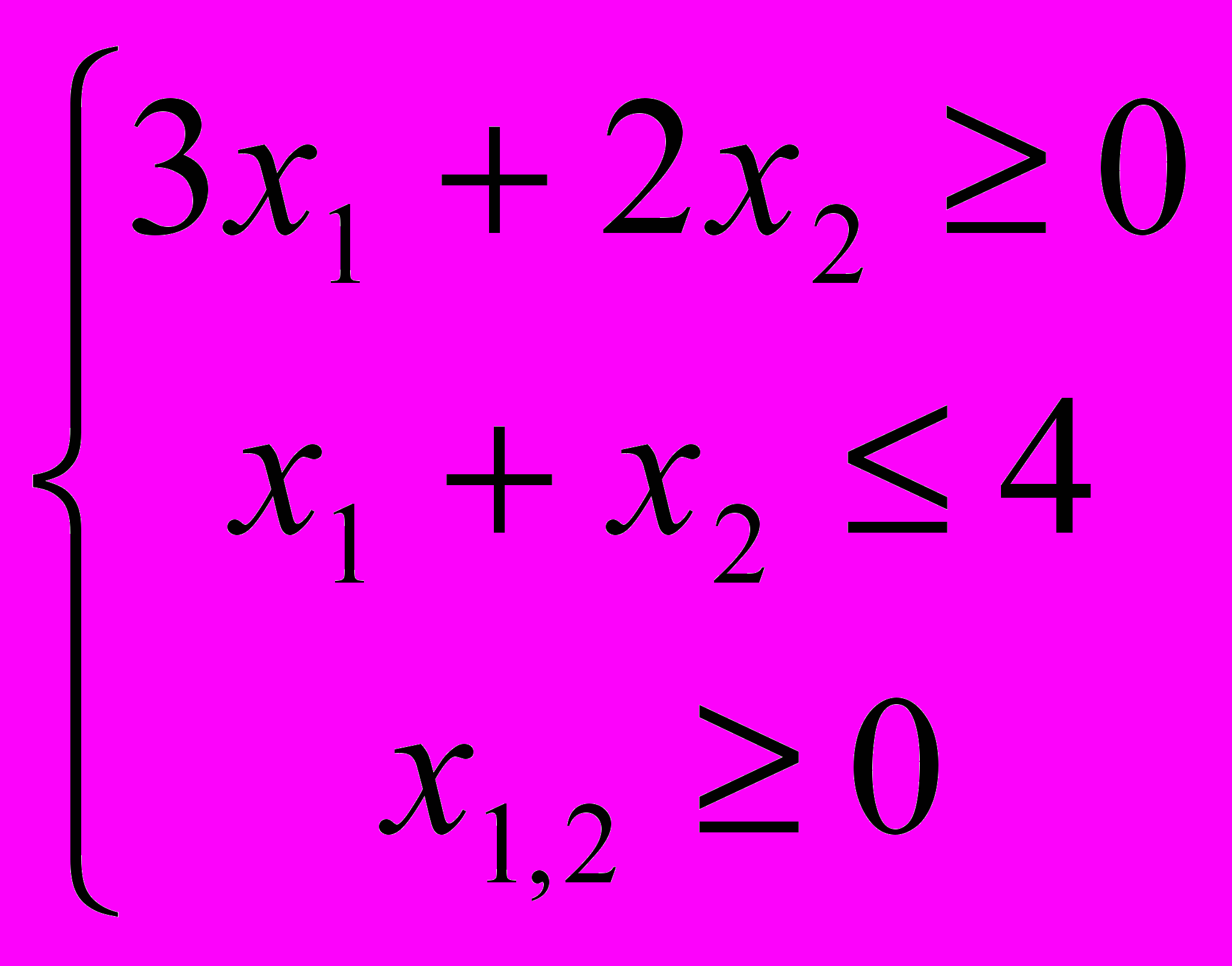
3. Транспортная задача
| a1 = 300, b1 = 180, a2 = 280, b2 = 140, a3 = 220, b3 = 190, b4 = 120, b5 = 170; |  |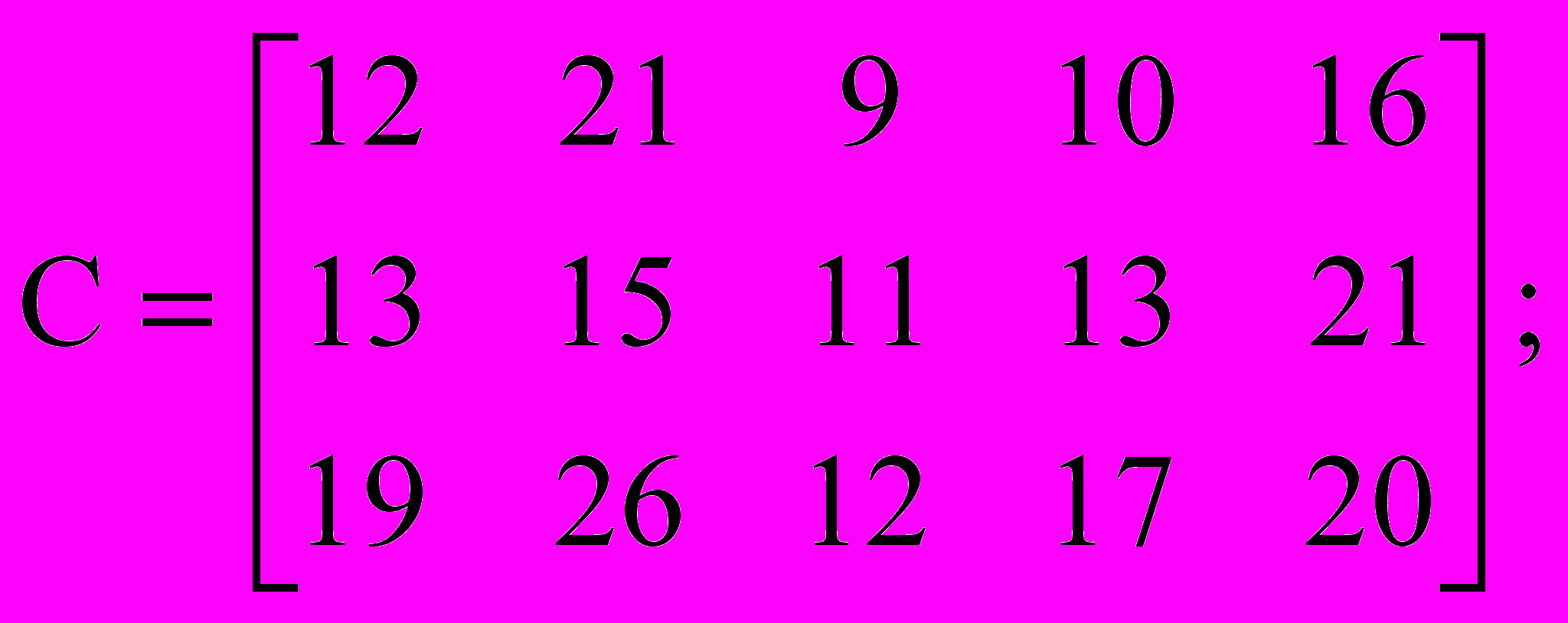
4. Решение матричной игры: а) показать существование или отсутствие чистых оптимальных стратегий; б) выполнить доминирование; в) свести исходную матричную игру к паре двойственных задач линейного программирования.
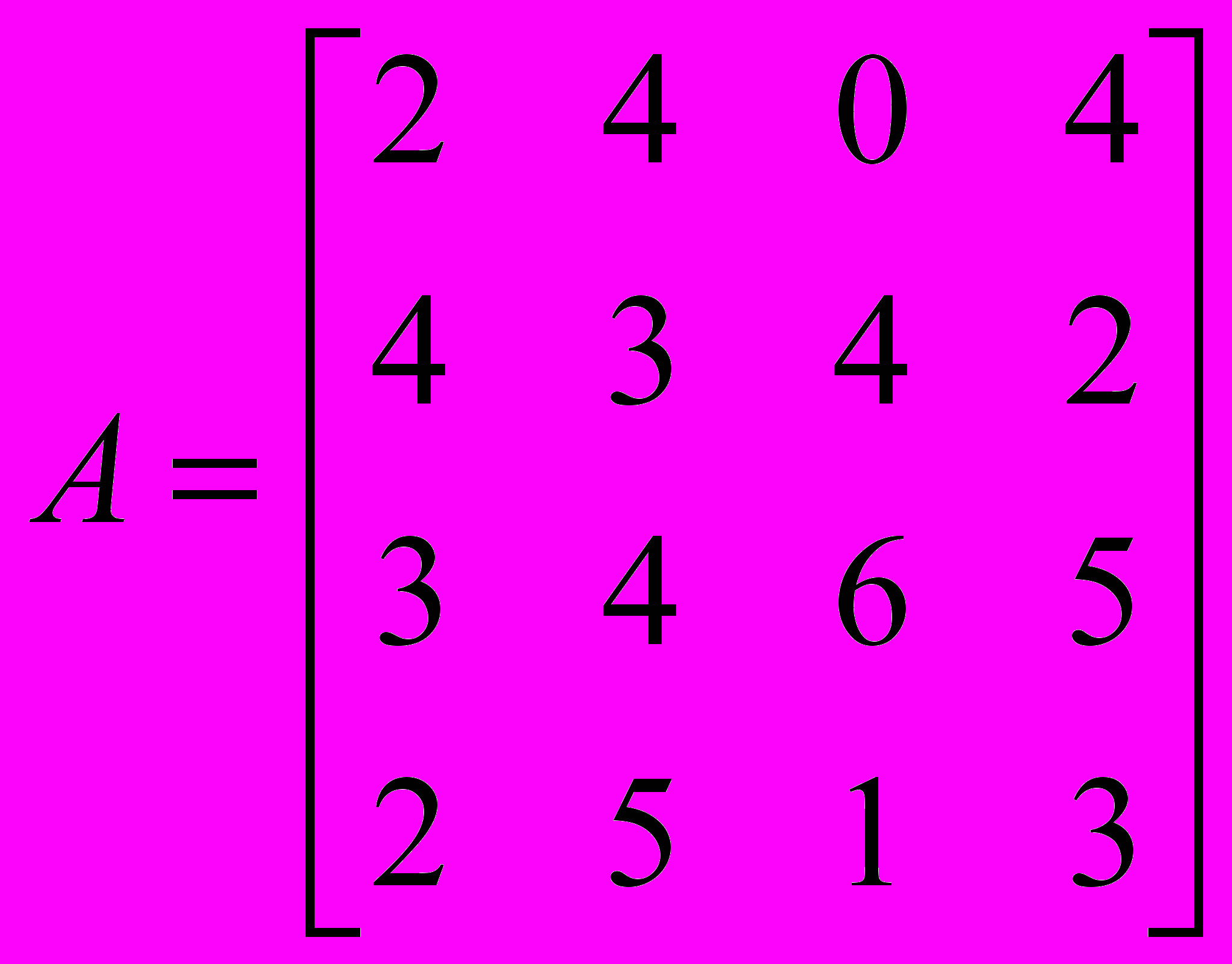;5 Найти решение матричных игр.
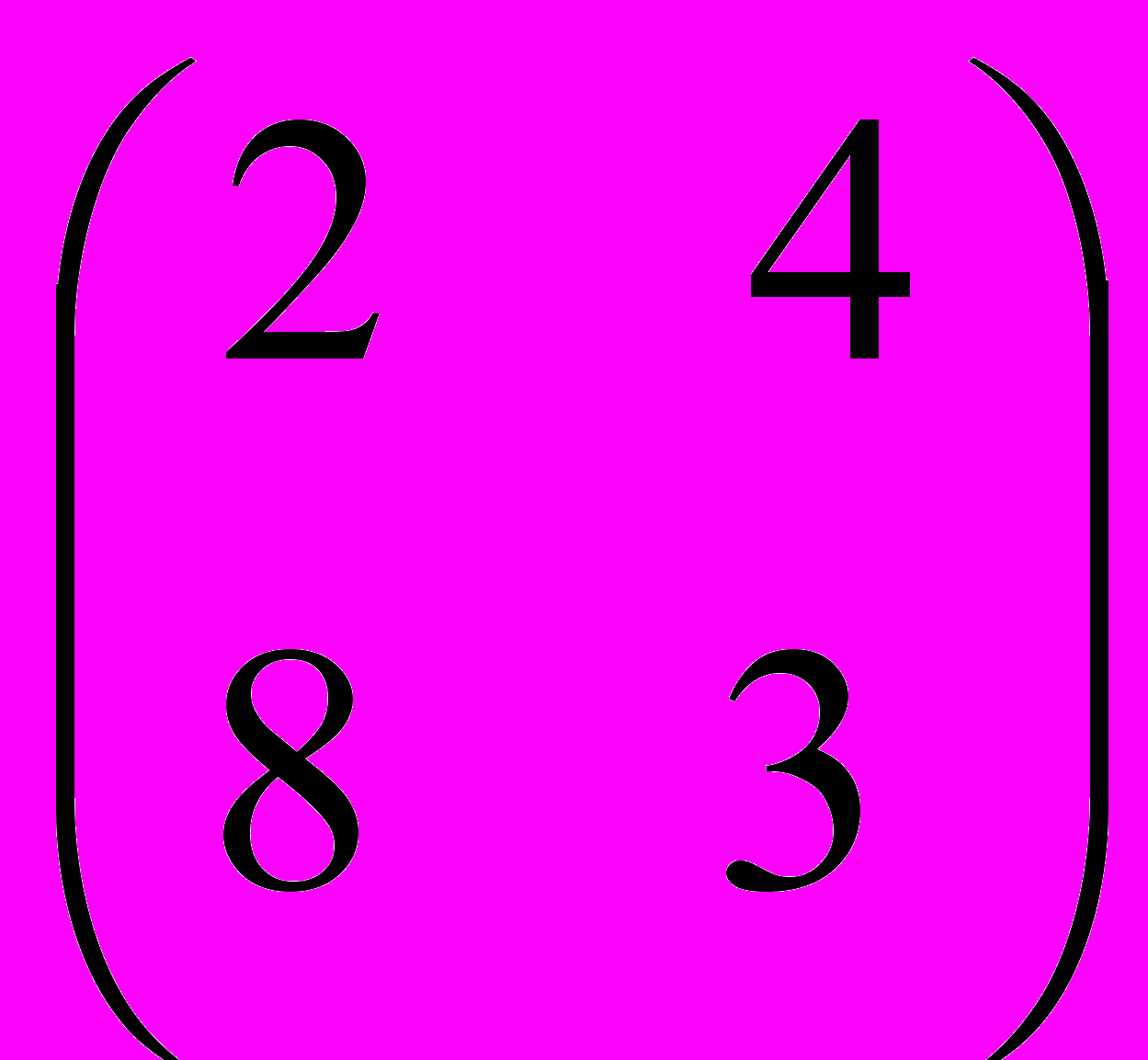
№3
- Графический метод
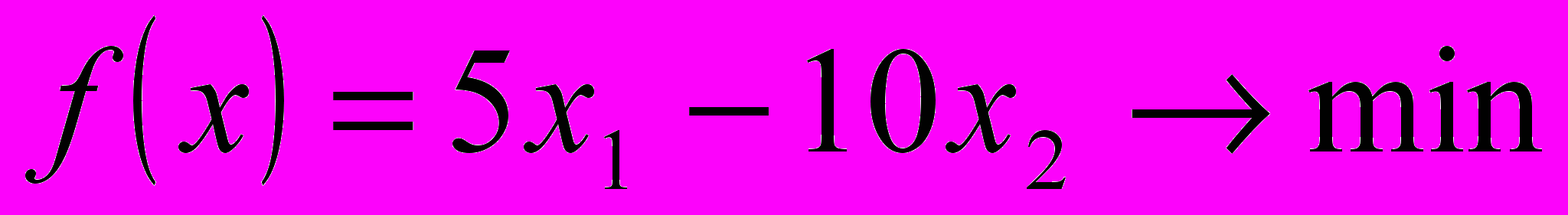
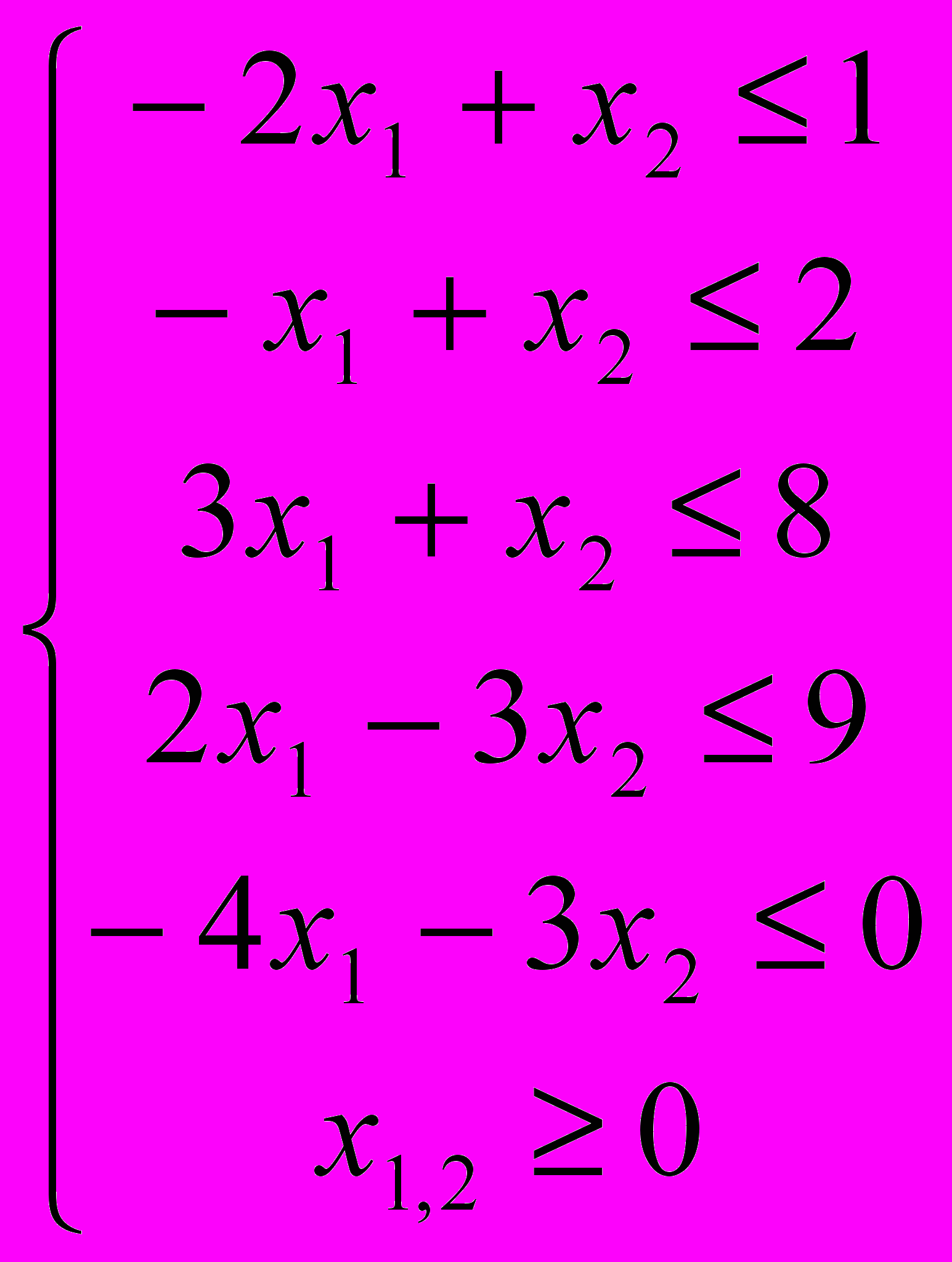
- Симплекс метод
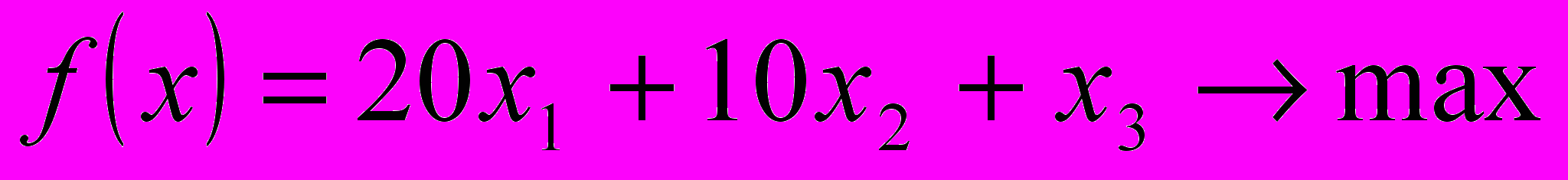
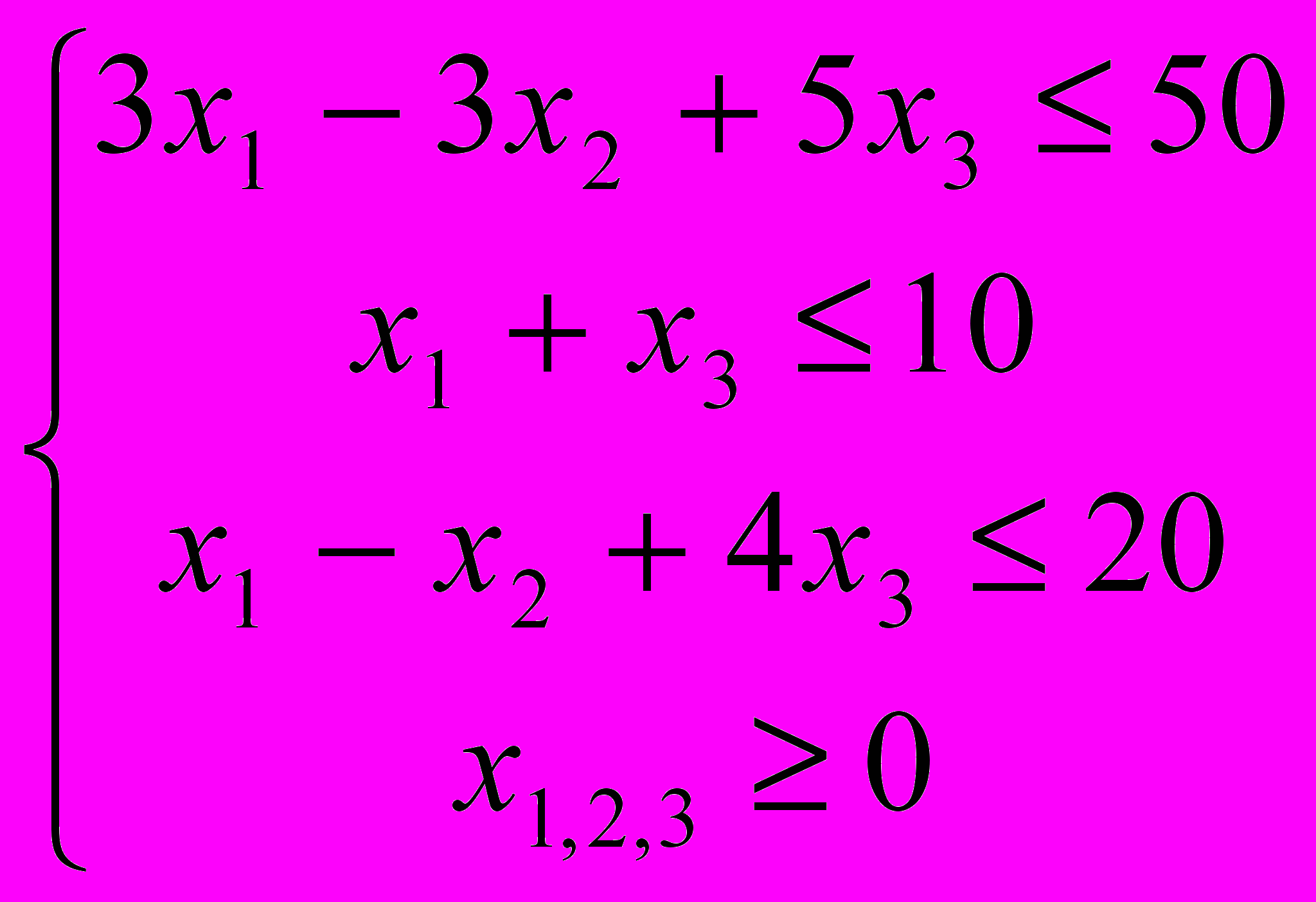
3. Транспортная задача
| a1 = 250, b1 = 180, a2 = 200, b2 = 120, a3 = 150, b3 = 90, b4 = 105, b5 = 105; |  |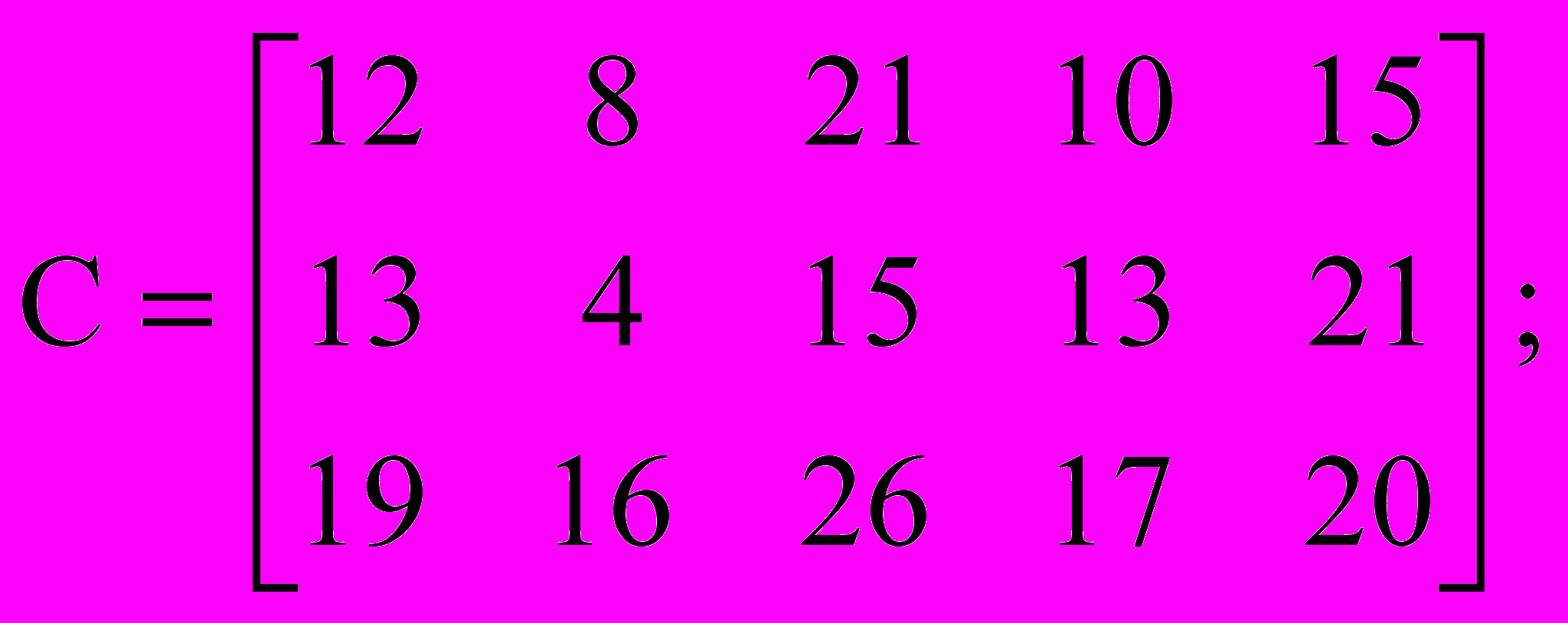
4. Решение матричной игры: а) показать существование или отсутствие чистых оптимальных стратегий; б) выполнить доминирование; в) свести исходную матричную игру к паре двойственных задач линейного программирования.
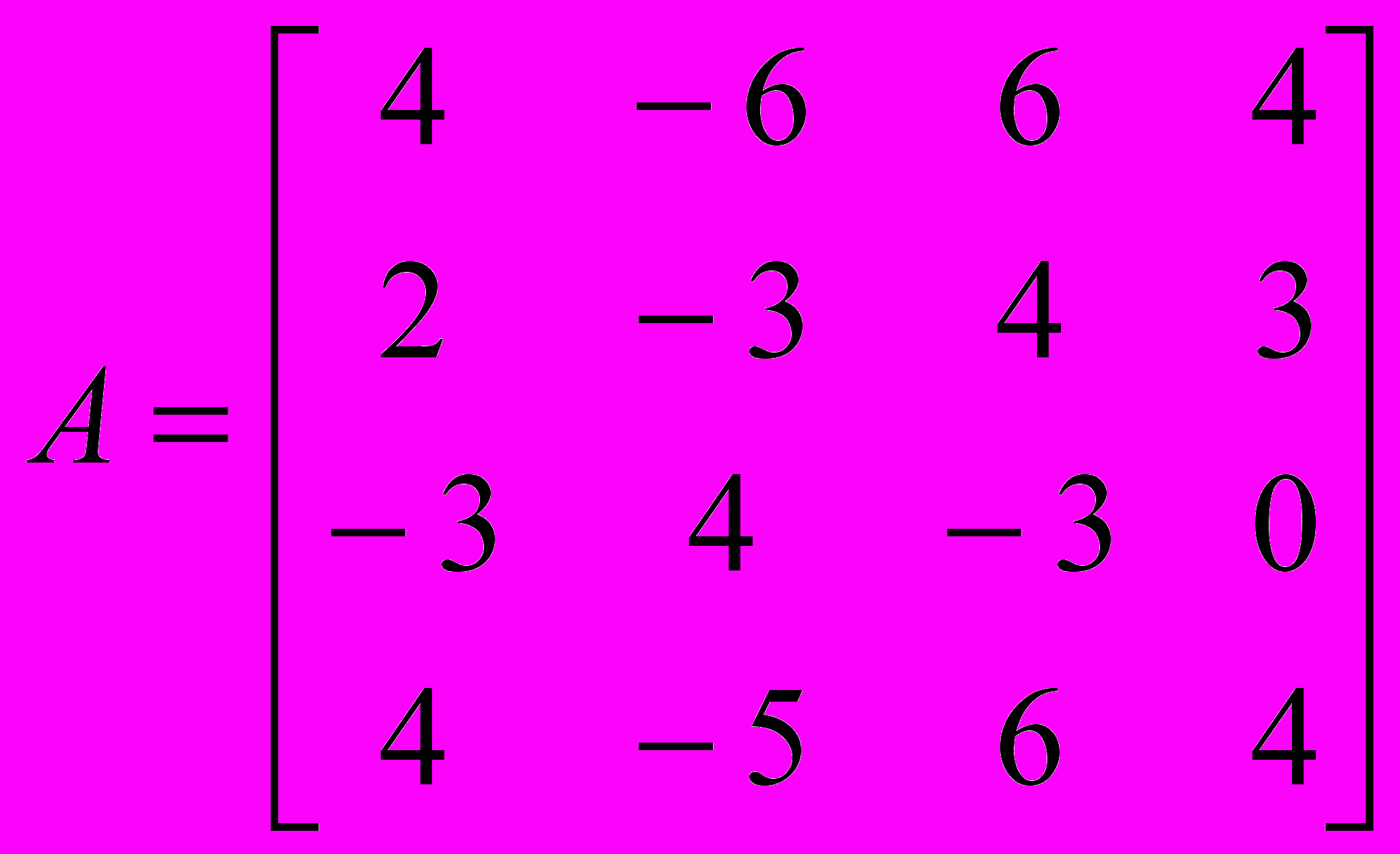;5 Найти решение матричных игр.
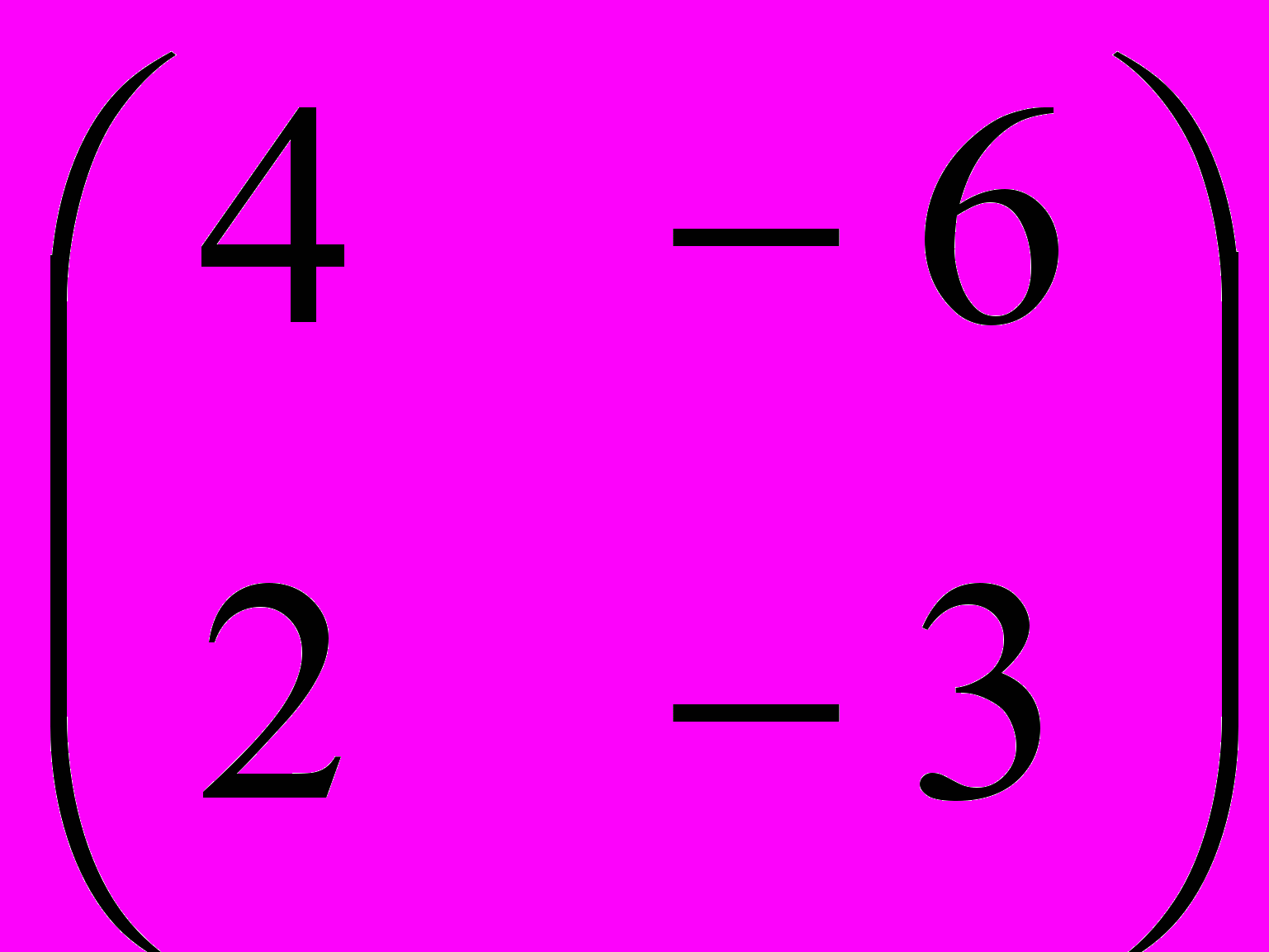
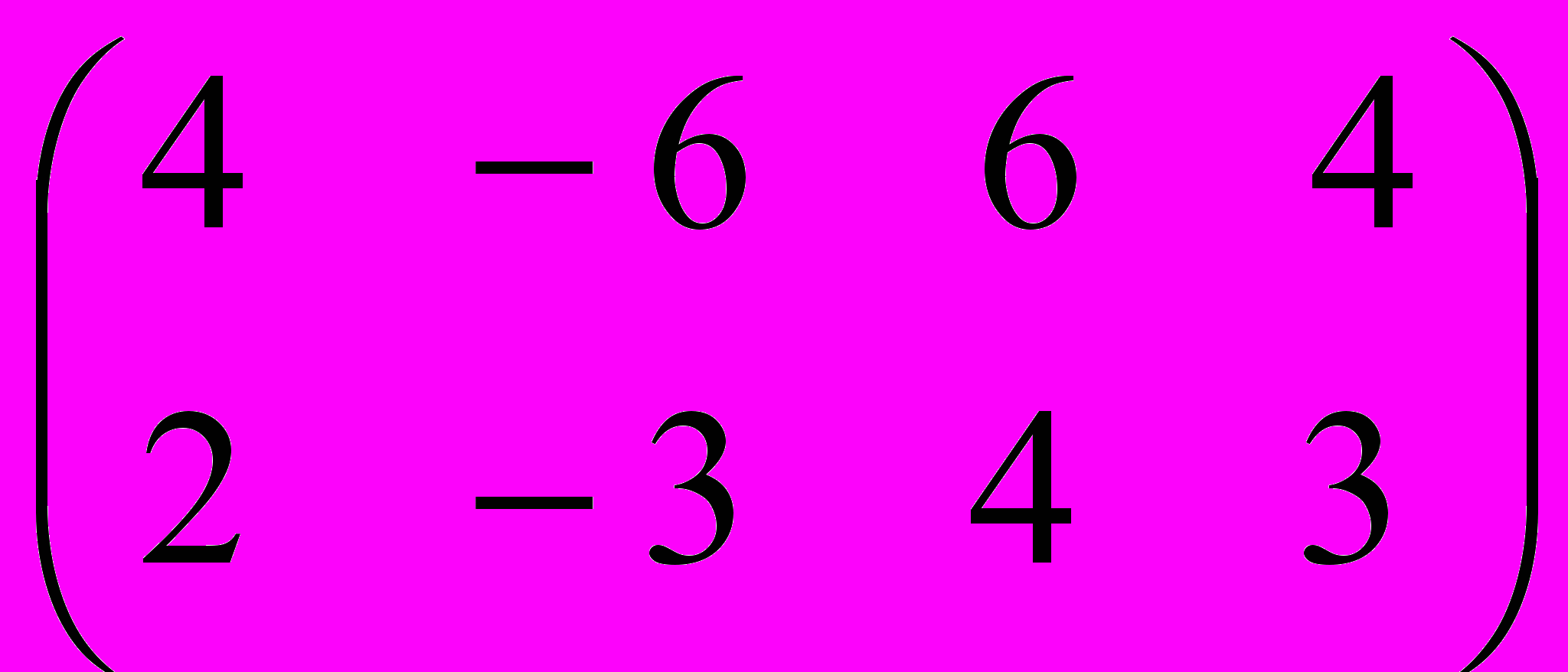
Контрольная работа 3
1. Правильно пронумеровать вершины графа. Построить календарный график работ. Числа в скобках – потребность в рабочей силе. Числа без скобок – длительность операции.
1(10) 8(5)
3(9)
3(5)2(8) 4(6) 2(4) 7(1)
2(2)
2(3) 3(8)
5(2) 3(1) 1(6) 4(7)
9(4)
8(5) 5(8)2
. Правильно пронумеровать вершины графа. Построить календарный график работ. Числа в скобках – потребность в рабочей силе. Числа без скобок – длительность операции.1(4)
1(3)
5
(2)
8(7) 2(7)3
(3)
9(5)
10(2) 3(1)
1(2)7(6)
4(7)
8(4)
6(5)
6(8)Приложение 2
Изменения и дополнения в рабочей программе на текущий учебный год
| № изменения | Учебный год | Содержание изменений | Преподаватель-разработчик программы | Рабочая программа пересмотрена и одобрена на заседании кафедры | Внесенные изменения утверждаю: Первый проректор КемГУ (декан) |
| | | | | Протокол №__ «__»_____200_ | _____________ «__»_____200_ |
| | | | | Протокол №__ «__»_____200_ | _____________ «__»_____200_ |
| | | | | Протокол №__ «__»_____200_ | _____________ «__»_____200_ |
| | | | | Протокол №__ «__»_____200_ | _____________ «__»_____200_ |
| | | | | Протокол №__ «__»_____200_ | _____________ «__»_____200_ |
| | | | | Протокол №__ «__»_____200_ | _____________ «__»_____200_ |
| | | | | Протокол №__ «__»_____200_ | _____________ «__»_____200_ |
| | | | | Протокол №__ «__»_____200_ | _____________ «__»_____200_ |
Методические рекомендации для студентов по изучению дисциплины «Исследование операций и математическое программирование»
1. Советы по планированию и организации времени, необходимого для изучения дисциплины. Рекомендуется следующим образом организовать время, необходимое для изучения дисциплины:
Изучение конспекта лекции в тот же день после лекции – 10-15 минут.
Повторение лекции за день перед следующей лекцией – 10-15 минут.
Изучение теоретического материала по учебнику и конспекту – 1 час в неделю.
Подготовка к практическому занятию – 1,5 часа.
Тогда общие затраты времени на освоение курса исследование операций и математическое программирование студентами составят около 3 часа в неделю.
2. Описание последовательности действий студента («сценарий изучения дисциплины»). При изучении курса исследование операций и математическое программирование следует внимательно слушать и конспектировать материал, излагаемый на аудиторных занятиях. Для его понимания и качественного усвоения рекомендуется следующая последовательность действий:
1. После окончания учебных занятий для закрепления материала просмотреть и обдумать текст лекции, прослушанной сегодня, разобрать рассмотренные примеры (10-15 минут).
2. При подготовке к лекции следующего дня повторить текст предыдущей лекции, подумать о том, какая может быть следующая тема (10-15 минут).
3. В течение недели выбрать время для работы с литературой по математической экономике в библиотеке и для решения задач (по 1 часу).
4. При подготовке к практическим занятиям повторить основные понятия и формулы по теме домашнего задания, изучить примеры. Решая упражнение или задачу, – предварительно понять, какой теоретический материал нужно использовать. Наметить план решения, попробовать на его основе решить 1-2 аналогичные задачи.
3. Рекомендации по использованию материалов учебно-методического комплекса. Рекомендуется использовать методические указания и материалы по курсу исследование операций и математическое программирование, текст лекций, а также электронные пособия, имеющиеся на факультетском сервере.
4. Рекомендации по работе с литературой. Теоретический материал курса становится более понятным, когда дополнительно к прослушиванию лекций изучаются и книги по исследованию операций и математическому программированию. Литературу по курсу исследование операций и математическое программирование желательно изучать в библиотеке. Полезно использовать несколько учебников, однако легче освоить курс, придерживаясь одного учебника и конспекта. Рекомендуется, кроме «заучивания» материала, добиться понимания изучаемой темы дисциплины. С этой целью после прочтения очередной главы желательно выполнить несколько простых упражнений на соответствующую тему. Кроме того, очень полезно мысленно задать себе и попробовать ответить на следующие вопросы: о чем эта глава, какие новые понятия в ней введены, каков их смысл, для чего служат и какими свойствами обладают используемые здесь математические модели. При изучении теоретического материала всегда полезно рисовать схемы или графики.
5. Советы по подготовке к экзамену. Дополнительно к изучению конспектов лекций необходимо пользоваться учебниками по исследованию операций и математическому программированию. Вместо «заучивания» материала важно добиться понимания изучаемых тем дисциплины. При подготовке к экзамену нужно освоить теорию: разобрать определения всех понятий и постановки математических моделей, рассмотреть примеры и самостоятельно решить несколько типовых задач из каждой темы. При решении задач всегда необходимо комментировать свои действия и не забывать о содержательной интерпретации.
6. Указания по организации работы с контрольно-измерительными материалами. При выполнении домашних заданий и подготовке к контрольной работе необходимо сначала прочитать теорию и изучить примеры по каждой теме. Решая конкретную задачу, предварительно следует понять, что требуется от Вас в данном случае, какой теоретический материал нужно использовать, наметить общую схему решения. Если Вы решали задачу «по образцу» рассмотренного на аудиторном занятии или в методическом пособии примера, то желательно после этого обдумать процесс решения и попробовать решить аналогичную задачу самостоятельно.
Методические указания для преподавателей
Исследование операций и математическое программирование — комплексная научная дисциплина, имеющая важное методологическое значение в системе подготовки современного экономиста. В ней наиболее четко реализуется одна из основных идей изучения курса высшей математики в экономическом вузе — идея математического моделирования экономических процессов.
Круг проблем, изучаемых данной дисциплиной, еще недостаточно определен. В соответствии с государственными общеобразовательными стандартами для экономических специальностей комплекс вопросов, относящихся к исследованию операций в экономике, изучается в рамках математических дисциплин
В первой части рассмотрены модели линейного программирования — постановка и примеры типовых задач, теоретические основы, теория двойственности, симплексный метод решения задач и транспортная задача. Учитывая то, что к задачам линейного программирования могут быть сведены некоторые модели "конфликтных" ситуаций целесообразно далее изложить элементы теории игр.
Вторая часть посвящена моделям нелинейного программирования: описываются классические методы оптимизации: методы нахождения условного экстремума функции нескольких переменных и, в частности, метод множителей Лагранжа, модели динамического программирования, используемые при решении таких актуальных задач, как задача об оптимальном распределении средств между предприятиями, ресурсов между отраслями за ряд лет, задача о замене оборудования.
Учитывая, что приведенные задачи и наглядные способы их решения являются лишь условными примерами оптимизационных экономико-математических моделей, служащими для иллюстрации их сущности далее целесообразно (если позволяют временные рамки) рассмотреть вопросы применения ЭВМ для решения реальных, многоразмерных задач математического программирования.
В третьей части рассматриваются специальные модели исследования операций: модели сетевого планирования и управления, модели управления запасами. Эти модели, весьма отличные друг от друга по своей содержательной постановке, представляют основные, типичные классы задач исследования операций.
На лекционных занятий целесообразно рассмотреть решение одной задачи всеми методами начиная с построения математической модели, решения ее графическим и симплексным методами, провести ее экономическую интерпретацию с помощью теории двойственности.