Geum.ru

Рабочая программа по дисциплине «Исследование операций и математическое программирование» для специальности 080111 «Маркетинг» федеральный компонент, ен. Ф. 01

Вид материалаРабочая программа

Содержание


Решите транспортные задачи методом потенциалов
5.3 Вопросы к коллоквиуму.
5.4 Примерные варианты контрольных работ
Подобный материал:
1   2   3   4

Решите транспортные задачи методом потенциалов

  1. a1 = 350, b1 = 120,

a2 = 400, b2 = 110,

a3 = 250, b3 = 230,

b4 = 170,

b5 = 200;


  1. a1 = 250, b1 = 120,

a2 = 250, b2 = 110,

a3 = 200, b3 = 85,

b4 = 195,

b5 = 190;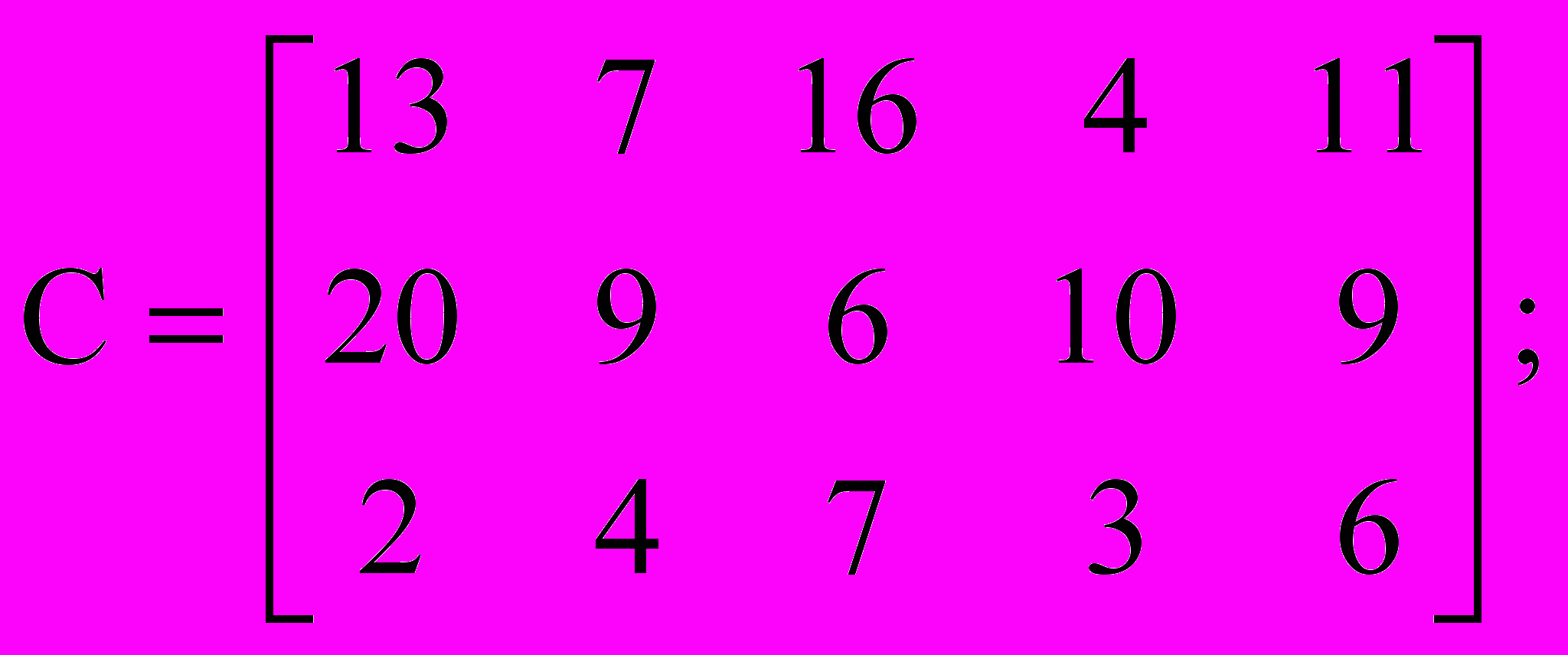


  1. a1 = 250, b1 = 160,

a2 = 180, b2 = 120,

a3 = 270, b3 = 100,

b4 = 150,

b5 = 170;


  1. a1 = 350, b1 = 160,

a2 = 300, b2 = 160,

a3 = 350, b3 = 180,

b4 = 220,

b5 = 280;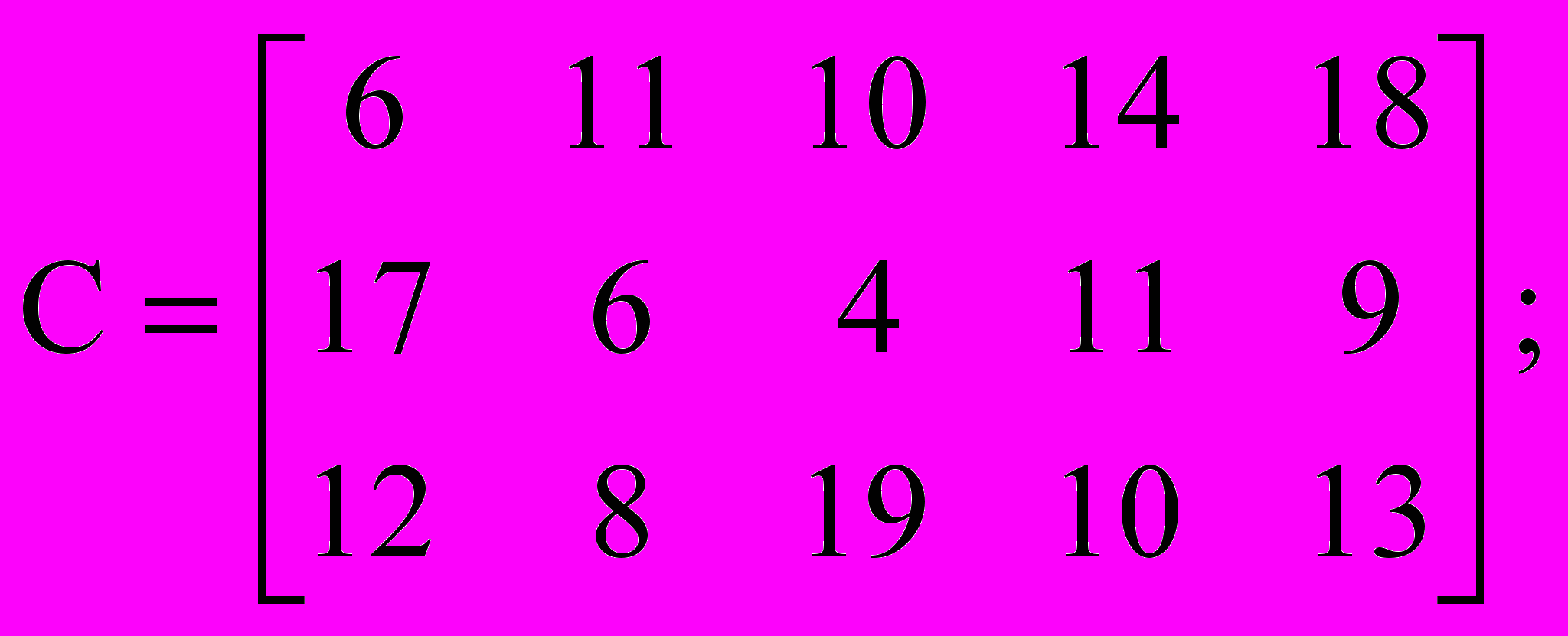



Решить матричные игры: а) показать существование или отсутствие чистых оптимальных стратегий; б) выполнить доминирование; в) выполнить графоаналитический метод либо свести исходную матричную игру к паре двойственных задач линейного программирования.

;

;

;

;


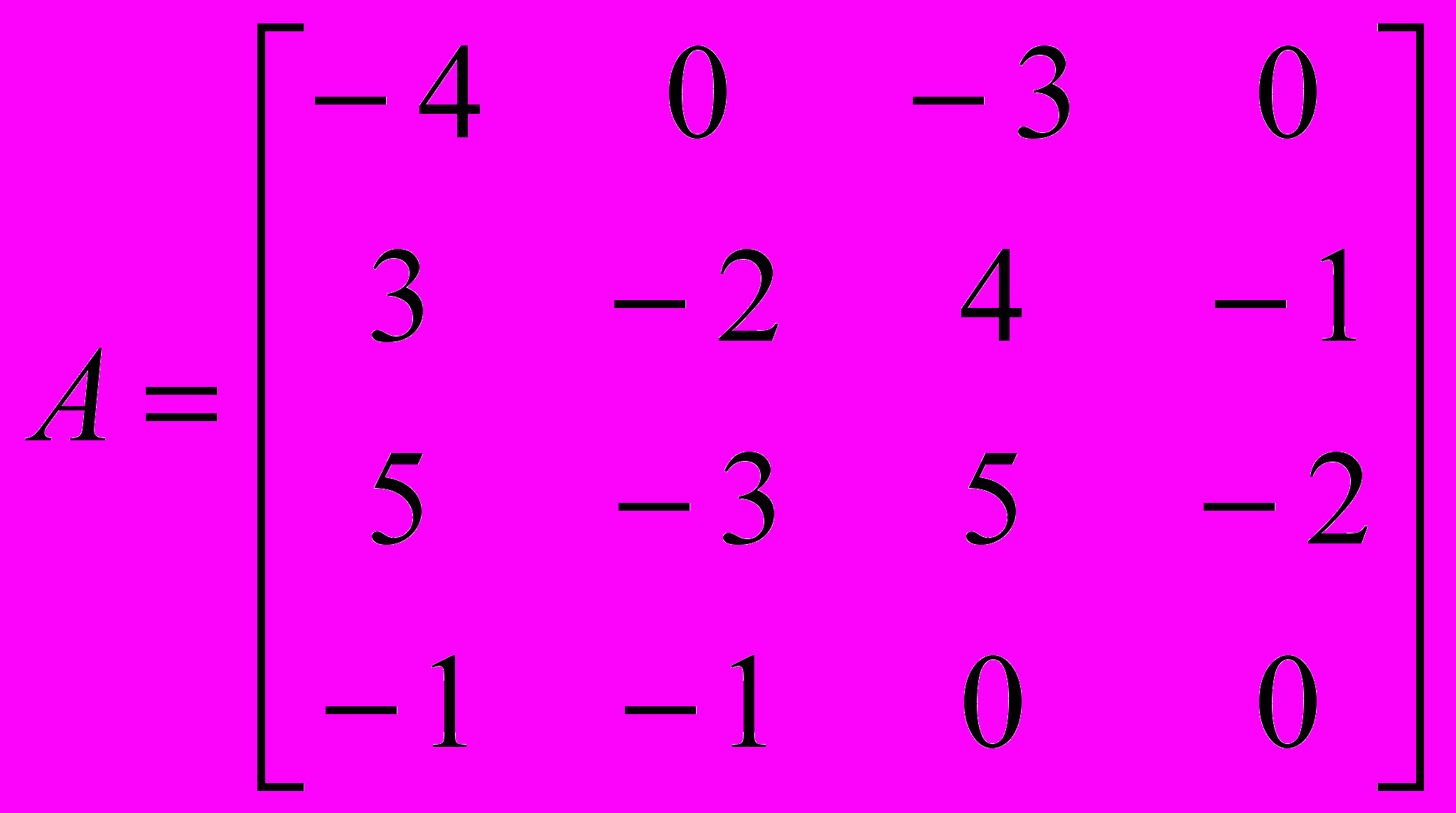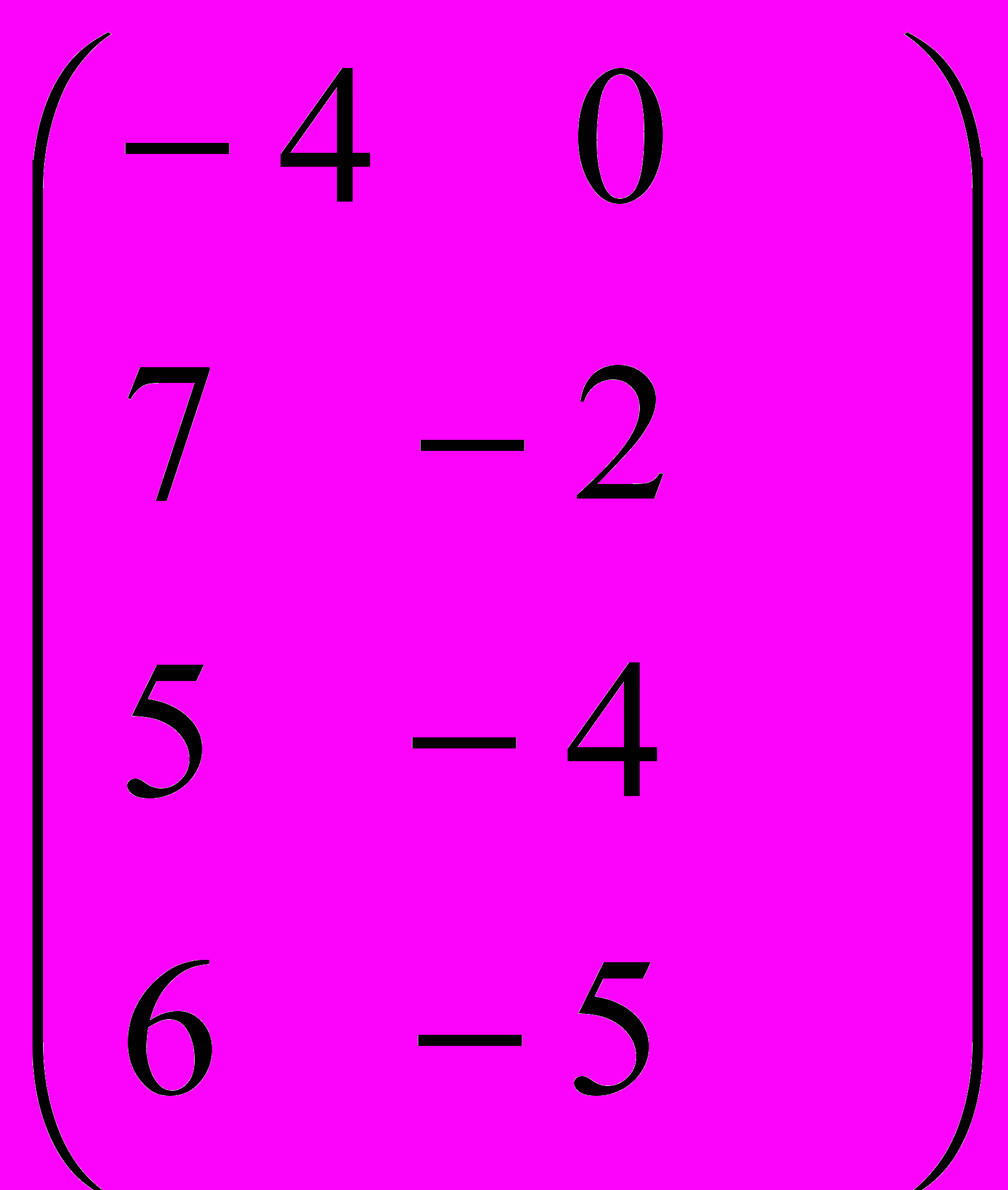
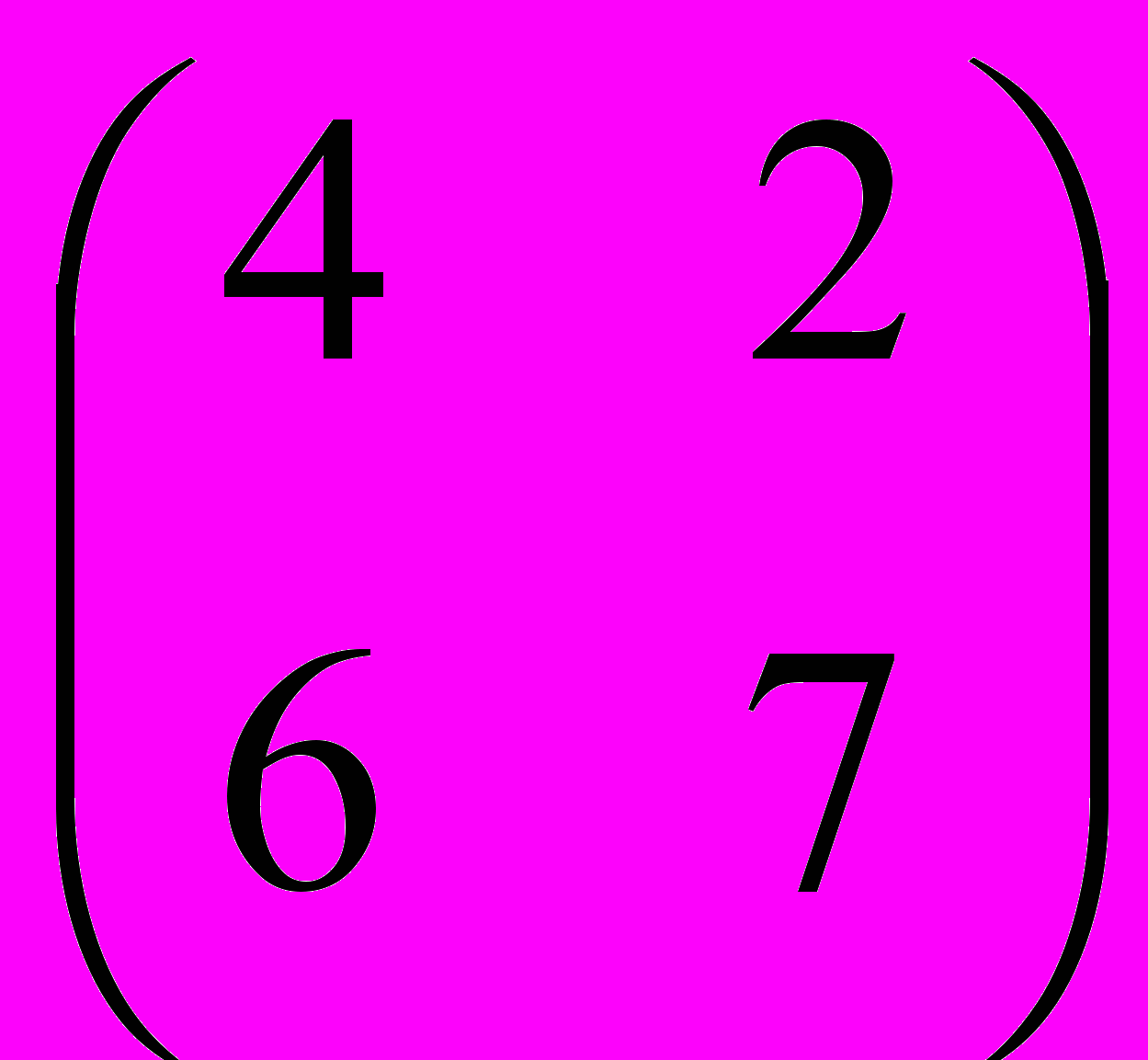
Правильно пронумеровать вершины графа. Построить календарный график работ. Числа в скобках – потребность в рабочей силе. Числа без скобок – длительность операции. Вычислить резервы событий и работ.


7(8)


10(8)

2(4)


9(8) 3(7)


12(1)


8(4)


10(9)


4(2) 3(6)


5(5)





5.2 Вопросы к экзамену

  1. Предмет исследования операции. Цели, задачи, область применения.
  2. Решение матричных игр симплекс – методом.
  1. Математическое моделирование задачи принятия решения. Требования, свойства и этапы.
  2. Понятия смешанных стратегий и смешанного решения игры.
  1. Описание этапов процесса исследования операций.
  2. Игровые задачи исследования операций.
  1. Теоремы двойственности в линейном программировании.
  2. Матричные игры. Постановка и основные понятия.
  1. Математические модели и методы в экономике. Примеры.
  2. Принцип минимакса в матричных играх.
  1. Принципы оптимального поведения в различных задачах исследования операций.
  2. Теорема о минимаксе. Применение.
  1. ЗЛП, их виды и постановки. Понятие оптимального решения задачи.
  2. Методы решений матричных игр (решение игры 2х2, графоаналитический метод решения mх2, 2хn- игр).
  1. Понятие слабых и искусственных переменных в симплеск-методе. Их предназначения и отличия.
  2. Модели управления запасами. Обобщенная модель управления запасами.
  1. Существование оптимальных решений в задачах линейного программирования.
  2. Матричные игры, чистые и смешанные стратегии. Определения следовой точки в чистых и смешанных стратегиях и их содержательная интерпретация.
  1. Постановка задачи линейного программирования. Геометрическая интерпретация.
  2. Матричные игры. Понятия следовой точки в матричных играх и основная теорема.
  1. Графический метод решения задач линейного программирования. Алгоритм.
  2. Типы моделей управления запасами. Виды затрат.
  1. Транспортная задача. Математическая постановка и экономическая интерпретация.
  2. Однопродуктовая статическая модель. Формула Уилсона.
  1. Каноническая, стандартная форма ЗЛП и понятие допустимого базисного решения.
  2. Игровые задачи исследования операций. Основные классы игр.
  1. Способы вычисления начального допустимого базисного решения в задачах линейного программирования.
  2. Однопродуктовая статическая модель с “разрывами” цен.
  1. Двойственные задачи линейного программирования. Правила построения и взаимосвязи между ними.
  2. Основные понятия и этапы календарного планирования программ сетевыми методами.
  1. Постановка задачи линейного программирования и алгоритм симплекс-метода.
  2. Правила построения сетевой модели.
  1. Транспортная задача. Математическая постановка. Необходимое и достаточное условие существования оптимального плана перевозок.
  2. Определение критического пути. Расчет сетевой модели.
  1. Методы вычисления начального опорного плана в транспортной задаче. Алгоритм.
  2. Календарный план распределения ресурсов. Определение резервов времени.
  1. Применение градиента и линии уровня целевой функции в графическом методе решения задачи линейного программирования. Случаи единственного и бесконечного множества оптимальных решений.
  2. Принцип минимакса в матричных играх.
  1. Метод искусственного базиса (двухфазный симплекс-метод). Алгоритм.
  2. Понятия смешанных стратегий и смешанного расширения игры.
  1. Связь между решениями прямой и двойственной задачи.
  2. Применение определения следовой точки в смешанных стратегиях при преобразовании матричной игры в виде пары двойственных задач линейного программирования.
  1. Экономическая интерпретация двойственности в задачах линейного программирования
  2. Методы решений матричных игр (решение игры 2х2, графоаналитический метод решения mх2, 2хn- игр).
  1. Метод потенциалов. Основные этапы алгоритма. Случаи вырожденности.
  2. Понятие седловой точки в смешанных стратегиях и приведение матричной игры к задачам линейного программирования.
  1. Постановка задачи линейного программирования. Геометрическая интерпретация. Случаи единственности, бесконечности и отсутствия оптимального решения.
  2. Принцип минимакса в матричной игре. Основная теорема матричных игр.
  1. Существование оптимального решения в задачах линейного программирования. случаи отсутствия оптимального решения.
  2. Модели управления запасами. Обобщенная модель управления запасами.
  1. Транспортная задача. Критерий проверки оптимальности плана в методе потенциалов.
  2. Типы моделей управления запасами. Виды затрат.
  1. Формализация принципов оптимального доведения в исследовании операций.
  2. Определение критического пути. Расчет сетевой модели.
  1. Метод искусственного базиса (двухфазный симплекс-метод). Алгоритм.
  2. Основные понятия и этапы календарного планирования программ сетевыми методами. Правила построения сетевой модели.
  1. Двойственные задачи линейного программирования. Теоремы двойственности в линейном программировании.
  2. Однопродуктовая статическая модель с “разрывами” цен.
  1. Определение двойственной задачи и правила ее построения. Связь между решениями прямой и двойственной задачи.
  2. Однопродуктовая статическая модель. Формула Уилсона.
  1. Каноническая, стандартная форма ЗЛП и понятие допустимого базисного решения.
  2. Правила построения сетевой модели. Определение критического пути. Расчет сетевой модели.
  1. Решение задачи линейного программирования симплекс-методом. Алгоритм.
  2. Календарный план распределения ресурсов. Определение резервов времени.


5.3 Вопросы к коллоквиуму.


Вариант 1
  1. Можно ли улучшить значение целевой функции, заменяя в линейной модели

знаки ограничений  или , на знак =.
  1. Различны ли условия оптимальности, используемые в симплекс-методе для

случаев максимизации и минимизации целевой функции.
  1. Всегда ли прямая задача должна быть задачей максимизации.

Вариант -2
  1. Может ли замена знака  на знак = в ограничении линейной модели привести к более жесткому ограничению пространства решений.
  2. Всегда ли прямая задача должна быть задачей максимизации.
  3. Каков принцип оптимальности при решении транспортной задачи методом потенциалов.

Вариант -3
  1. Сколько точек может содержать решение задачи ЛП.
  2. Какой будет задача двойственная к двойственной задаче.
  3. Изменятся ли оптимальные значения Хij, если ко всем коэффициентам Сij прибавить одно и то же число.



5.4 Примерные варианты контрольных работ


Контрольная работа 1


В-1.

Текстильный комбинат производит 2 вида ткани: вид А состоит из 80% шерсти и 20% синтетического волокна, вид В состоит из 20% шерсти и 80% синтетики.

Ткань производится партиями (большими рулонами, бабинами). Время изготовления каждого рулона – 2 часа времени технологического процесса. Технологический процесс может длиться сутки (24 часа). Ткацкий станок может переключаться с производства одного вида ткани на другой.

Для производства ткани вида А ткацкий станок использует 4 ед. шерстяной пряжи и 1 ед. синтетических волокон. Для производства ткани вида В – 1 ед. синтетического волокна и 4 ед. шерстяного волокна. В сутки станок расходует 36 ед. синтетического волокна и 24 ед. шерстяного волокна.

Стоимость 1 рулона ткани вида А – $ 2000, ткани вида В -$ 1000.

Сколько рулонов каждого вида ткани нужно выпускать в день, чтобы выручка была максимальной ?


В-2

Необходимо распределить площадь пашни между двумя культурами по следующим данным:


культура
Урожайность (ц\га)
Затраты

тракторо-смен на 1га
Цена

(руб. за ц)
Затраты (человеко-дней на 1 га)

А
10
0,1
6
2

В
15
0,24
8
10