Учебное пособие Издательство спбгпу санкт-Петербург

Вид материала

Учебное пособие

Содержание Теоретическая часть: модели и методы 6 Лабораторный практикум: средства и протоколы 40 Список литературы 158 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ: МОДЕЛИ И МЕТОДЫ Телематический подход к исследованию процессов в компьютерных сетях Модели процессов в компьютерных сетях и их характеристики Описание программных средств анализа трафика Вставить про Пример: Agent/TCP set window_ 100; # влияет на класс Agent/TCP set window_ 20 Agent/TCP set packetSize_ 1000 Agent/TCP set slow_start_restart_ true;# использование механизма медленного старта (1/0). Включено по умолчанию Agent/TCP set cwnd_ 0;# текущее значение окна переполнения (packets) Agent/TCP set srtt_ 0;# сглаженное (среднее) rtt Инструмент имитационного моделирования AnyLogic_5.3 Принципы построения AnyLogic. Моделирование систем с дискретными событиями. Агентное моделирование. Системная динамика ЛАБОРАТОРНЫЙ ПРАКТИКУМ: СРЕДСТВА И ПРОТОКОЛЫ Анализ пакетного трафика Уберите маркер напротив опции «Capture packets in promiscuous mode» для захвата только «своих» кадров (кадры с широковещательным ... Полное содержание

Подобный материал:

• Учебное пособие Санкт-Петербург Издательство спбгпу 2003, 5418.74kb.
• Методические указания Санкт-Петербург Издательство спбгпу 2007, 1378.97kb.
• Учебное пособие Санкт-Петербург 2011 удк 621. 38. 049. 77(075) Поляков, 643.33kb.
• Учебное пособие Санкт-Петербург Издательство спбгэту «лэти» 2004, 1302.72kb.
• Учебное пособие Санкт-Петербург 2009 удк 802., 485.15kb.
• Учебное пособие Санкт-Петербург Издательство спбгэту «лэти» 2006, 1935.03kb.
• Учебное пособие Санкт-Петербург Издательство спбгэту «лэти» 2006, 648.91kb.
• Новые поступления в библиотеку балтийского русского института, 158.89kb.
• Учебное пособие издательство санкт-петербургского государственного университета экономики, 3398.77kb.
• Учебное пособие Санкт- петербург 2010 удк 778. 5 Нестерова Е. И, Кулаков А. К., Луговой, 708kb.

Заборовский В.С., Мулюха В.А., Подгурский Ю.Е.


СЕТИ ЭВМ И ТЕЛЕКОММУНИКАЦИИ


ИССЛЕДОВАНИЯ ПРОЦЕССОВ В КОМПЬЮТЕРНЫХ СЕТЯХ: ТЕЛЕМАТИЧЕСКИЙ ПОДХОД


Учебное пособие


Издательство СПбГПУ

Санкт-Петербург

2009

УДК 061.68 (075.8)

Учебное пособие соответствует дисциплинам ОПД Ф10 «Сети ЭВМ и телекоммуникации» государственного общеобразовательного стандарта направления 552800 «Информатика и вычислительная техника».

Данное пособие развивает тематику лабораторных работ в направлении расширения инструментальных средств анализа и моделирования трафика. Учебное пособие включает в себя краткое описание возможностей программы Wireshark, предназначенной для анализа сетевых протоколов, и программы MTraffic, для анализа различных параметров сети, программы Network Simulator 2, для моделирования сетевых процессов, программы Anylogic, для моделирования различных механизмов TCP и содержит методические рекомендации и материалы к циклу работ студентов.

В пособие предлагается телематический подход к изучению материала, заключающийся в комплексном рассмотрении телекоммуникационной составляющей и изучении сетевых сервисов.

Лабораторные работы в учебном пособии предназначены для практического освоения материала студентами старших курсов специальностей «Информатика и вычислительная техника», «Сети ЭВМ и телекоммуникации».

Табл. XX. Ил. XX. Библиогр.: назв. XX

СОДЕРЖАНИЕ




СПИСОК ИСПОЛЬЗУЕМЫХ СОКРАЩЕНИЙ


МУЗ - медленно убывающая зависимость

ПО – программное обеспечение

ПС – пропускная способность

УЛК - учебно-лабораторный комплекс

ARP - Address Resolution Protocol

ICMP - Internet Control Message Protocol

IP – Internet Protocol

ТСР – Transmission Control Protocol

RTCP

UDP – User Datagram Protocol

ВВЕДЕНИЕ

Постоянный контроль работы сети необходим для поддержания ее в работоспособном состоянии. Использование средств контроля помогает администратору сети выявить проблемные участки и устройства сети, а их отключение или реконфигурацию он может выполнять в этом случае вручную.

Процесс контроля работы сети обычно делят на два этапа - мониторинг и анализ [1]. На этапе мониторинга выполняется более простая процедура - процедура сбора данных о работе сети.

Далее выполняется этап анализа, под которым понимается более сложный и интеллектуальный процесс осмысления собранной на этапе мониторинга информации, сопоставления ее с данными, полученными ранее, и выработки предположений о возможных причинах замедленной или ненадежной работы сети.

Процедура проведения измерений любых параметров сети не из простых и содержит множество подводных камней [2].

Не следует ограничиваться единственным измерением какого-нибудь параметра – например, времени передачи одного пакета. Нужно повторить измерения несколько раз и вычислить среднее значение. Чем больше будет выборка, тем выше окажется точность оценки среднего значения и его среднеквадратичного отклонения. Погрешность может быть вычислена при помощи стандартных формул статистики.

Выборка должна быть репрезентативной. Следует повторить всю последовательность измерений параметров в различное время суток и в разные дни недели, чтобы заметить влияние различной загруженности системы (сети) на измеряемые параметры. Результаты измерений зависят не только от сети, но и от операционной системы клиента и сервера, аппаратного интерфейса сетевых карт, их драйверов и других факторов.

На основе этих данных уже строится модель, и делаются дальнейшие прогнозы.

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ: МОДЕЛИ И МЕТОДЫ

Телематический подход к исследованию процессов в компьютерных сетях

Телематический подход при изучении компьютерных сетей заключается в комплексном рассмотрении телекоммуникационной составляющей и изучении сетевых сервисов. Сервис определяет семантику передаваемых данных.

Модели процессов в компьютерных сетях и их характеристики

Исключительно важным параметром компьютерных сетей, как и любых других систем связи, характеризующим эффективность использования сетевых ресурсов, является пропускная способность (ПС). Согласно сложившемуся подходу ПС определяется в стационарном режиме как среднее число по всем реализациям дошедших безошибочно до приемника пакетов (битов, байтов) в единицу времени. Для компьютерных сетей в связи c фрактальными свойствами протекающих в них случайных процессов вышеуказанную формулировку необходимо пересмотреть.

Для решения поставленной задачи и выработки соответствующих рекомендаций необходимо предварительно ознакомиться с имеющимися материалами по фрактальным процессам в сетях, дополнив их результатами анализа длительной работы сетей [3, 4, 5, 6]. Рассматривается наиболее коррелированный из TCP-процессов: режим быстрой повторной передачи, преобладающий при доставке пакетов на транспортном уровне. На рис. 1.1 (график 1) изображена одна из реализаций модели этого режима, аппроксимируемой линейным законом увеличения числа посланных пакетов с интенсивностью один пакет в условную единицу времени.

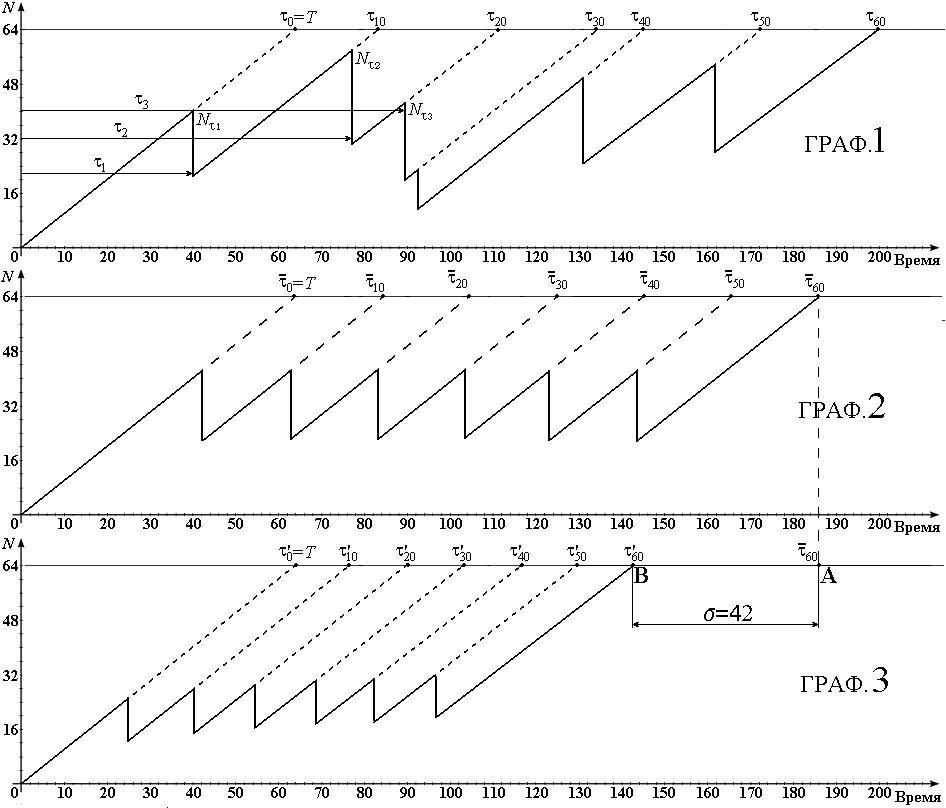
1. Модели режима повторной передачи пакетного трафика
   

Уровень 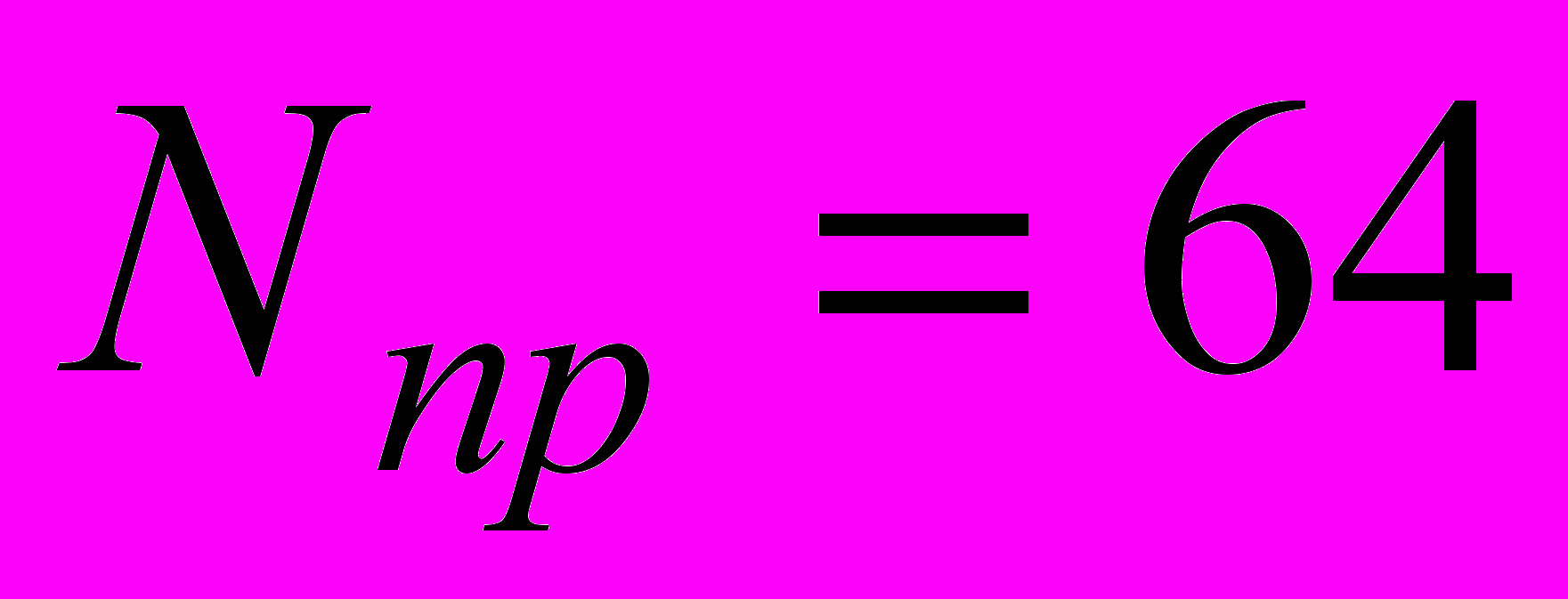соответствует окну приемника. При благоприятном исходе число переданных пакетов достигает максимально возможного, но не более размера окна приемника. Распределенные равномерно временные отсчеты 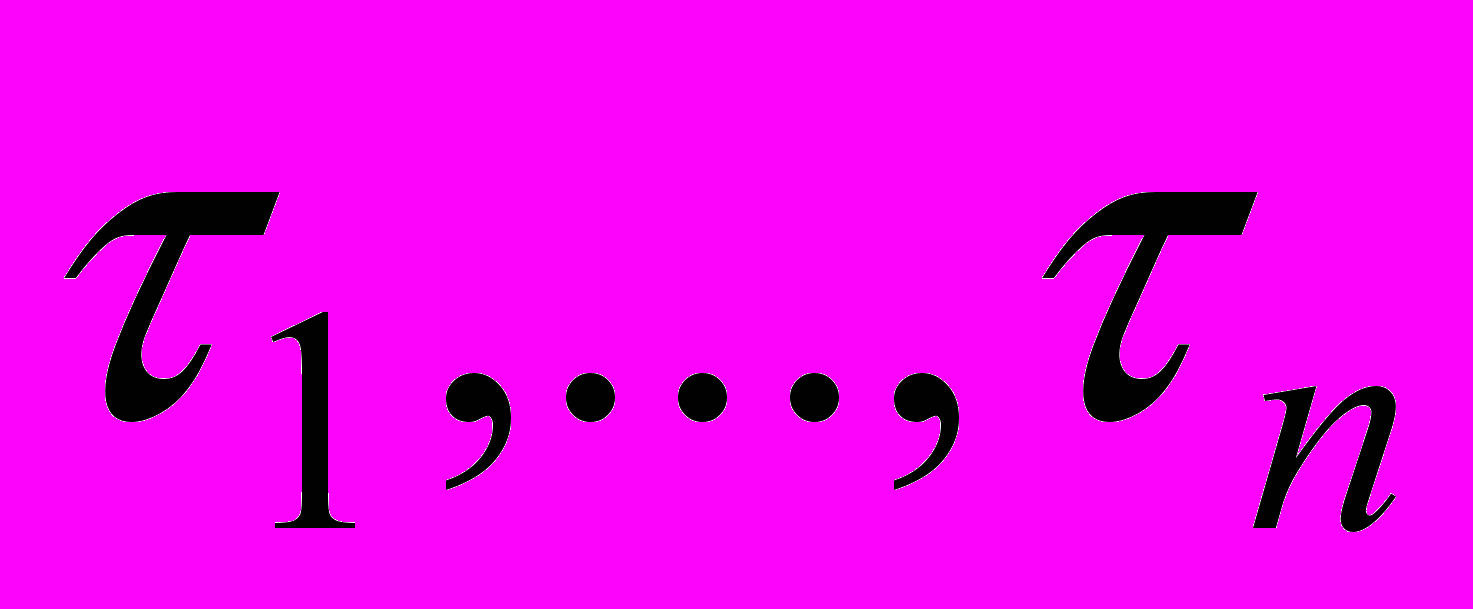- случайные моменты релаксации, вызванные перегрузкой в сети. Определению подлежат статистические характеристики временных моментов (задержек) 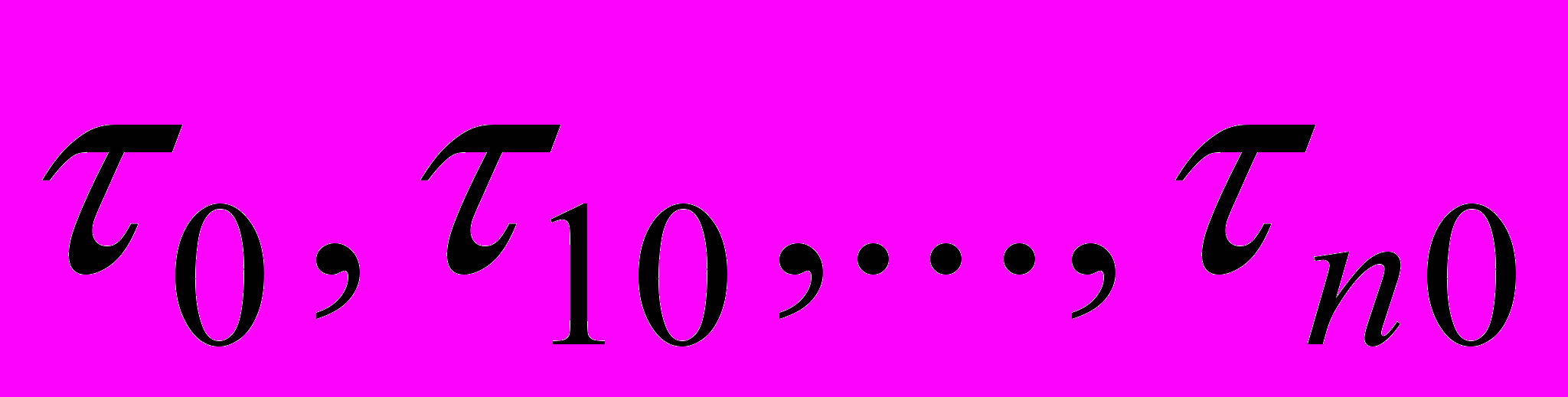, характеризующих благоприятные исходы в определенных сериях передачи. Моменты 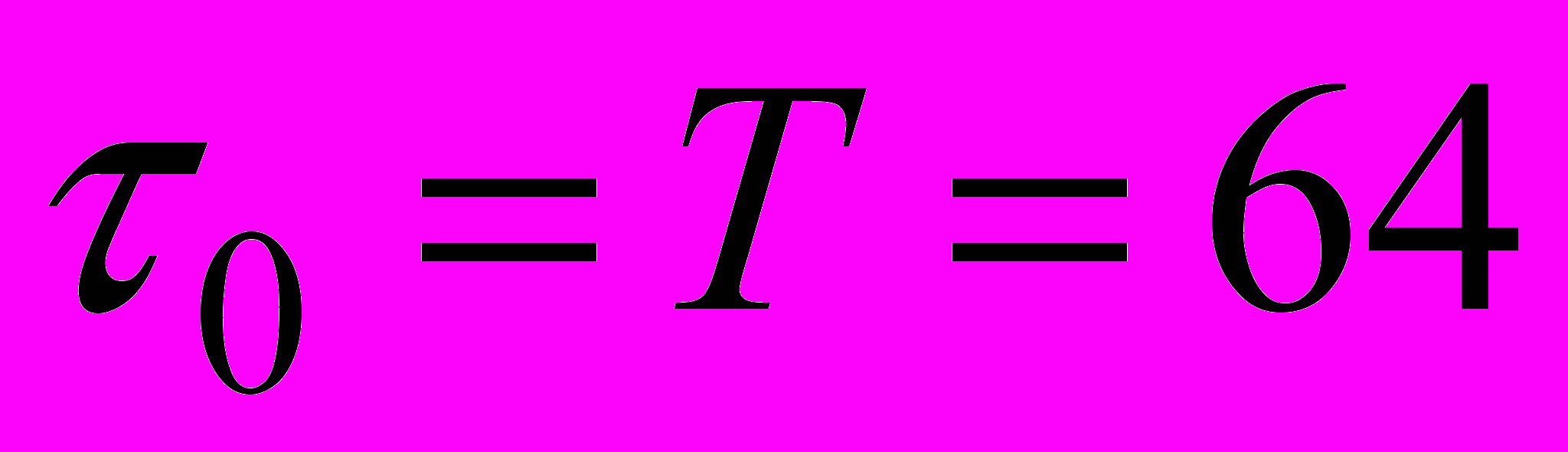полагаем наименьшим временем благоприятного исхода (в нулевой серии).

В момент релаксации значение окна перегрузки (задаваемое на стороне отправителя число пакетов, которое можно передать в сеть до получения подтверждения) уменьшается в два раза. Согласно представленной выше формулировке ПС пропорциональна площади под кривой среднего фрагмента режима повторной передачи, деленного на временной интервал этого фрагмента (Рис.1.1, график 2). Анализ статистических характеристик выявил корреляционную зависимость моментов релаксации каждой последующей серии от параметров функции распределения моментов релаксаций всех предыдущих серий. Это выразилось в характере изменения дисперсий задержек по закону 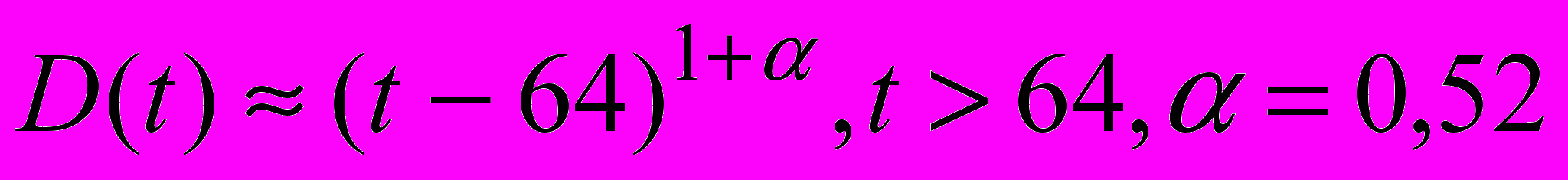- фрактальный параметр (Рис. 1.2, кривая 1). Методика решения приведена в [6].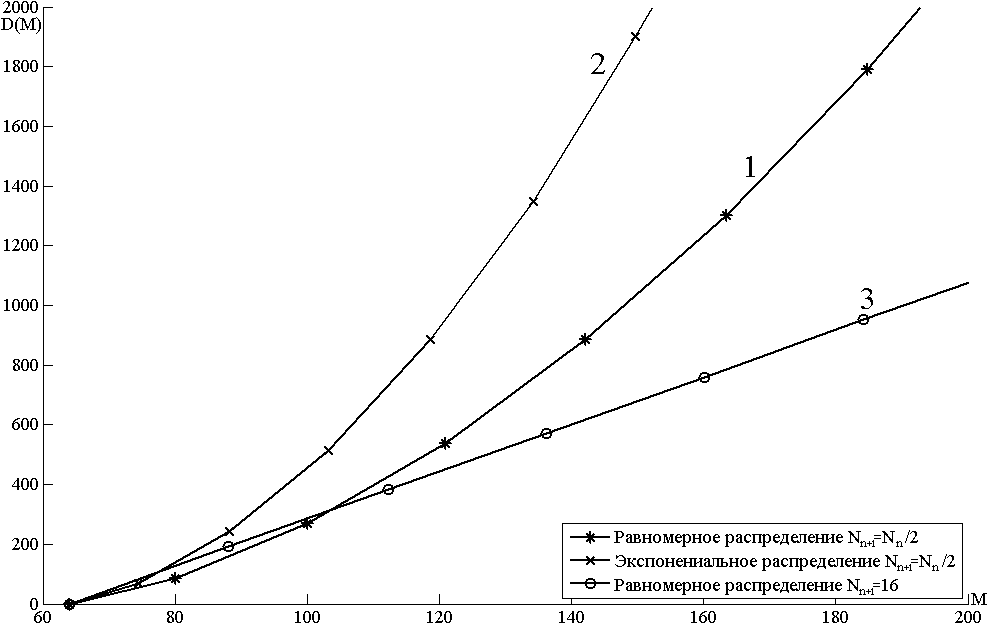

2. Расчетные зависимости дисперсии от математического ожидания
   

Наряду с равномерным распределением в процессе нормальной эксплуатации наблюдаются моменты релаксации, распределенные по экспоненциальному закону:.

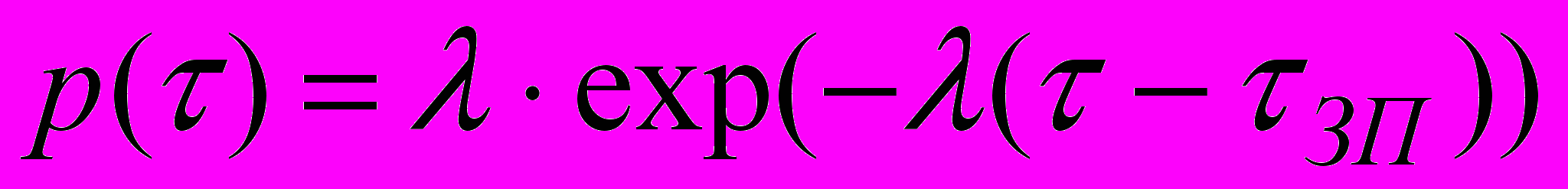Это имеет место, когда моменты релаксации группируются главным образом в районе малых значений окон перегрузки. Здесь зависимость дисперсии от времени имеет вид 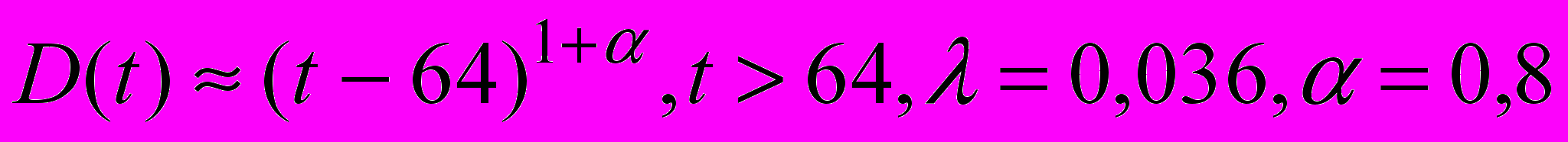(Рис. 1.2, кривая 2).

В качестве еще одного третьего альтернативного варианта рассматривается режим повторной передачи, в моменты релаксации которого окно перегрузки изменяется до постоянной величины, например, до нуля или, как в нашем примере до уровня 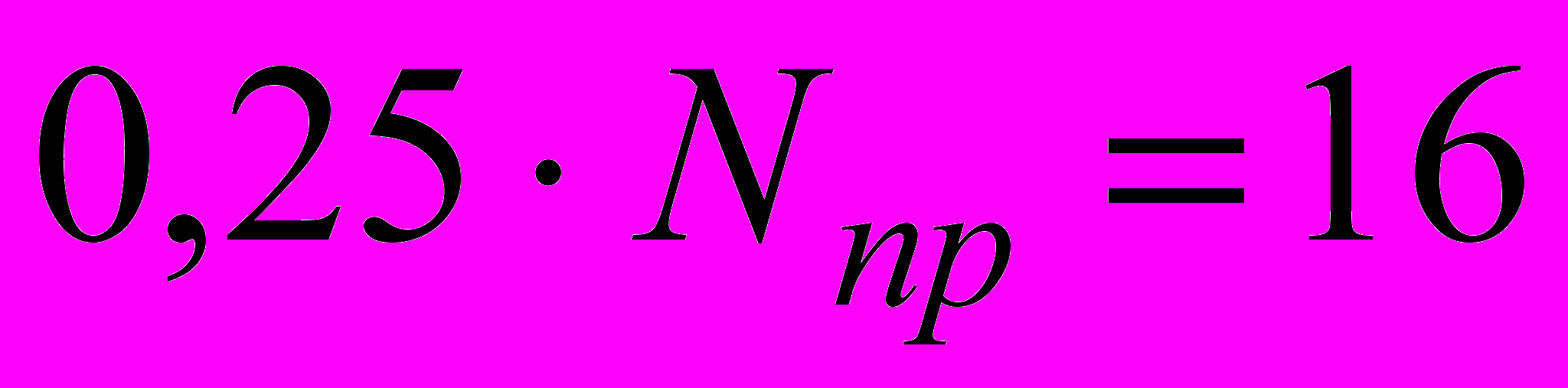(рис. 1.3, график 1 – реализация, график 2 – усредненный фрагмент, для уровня ).

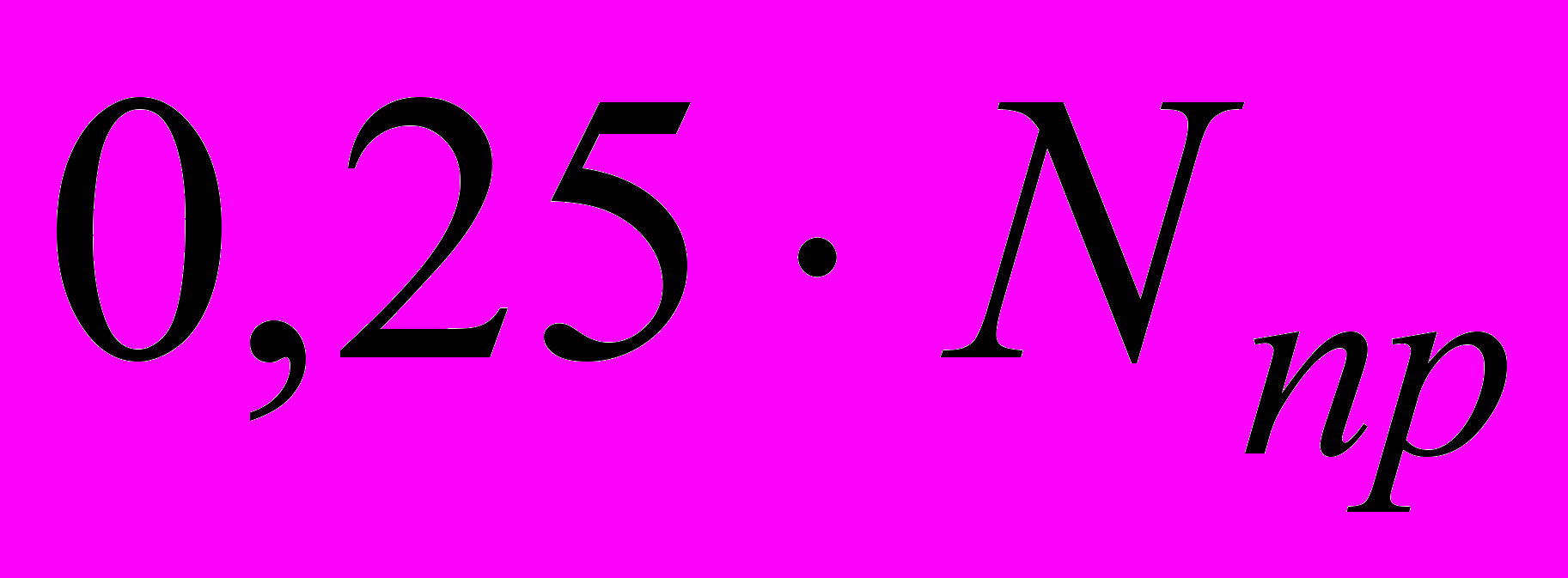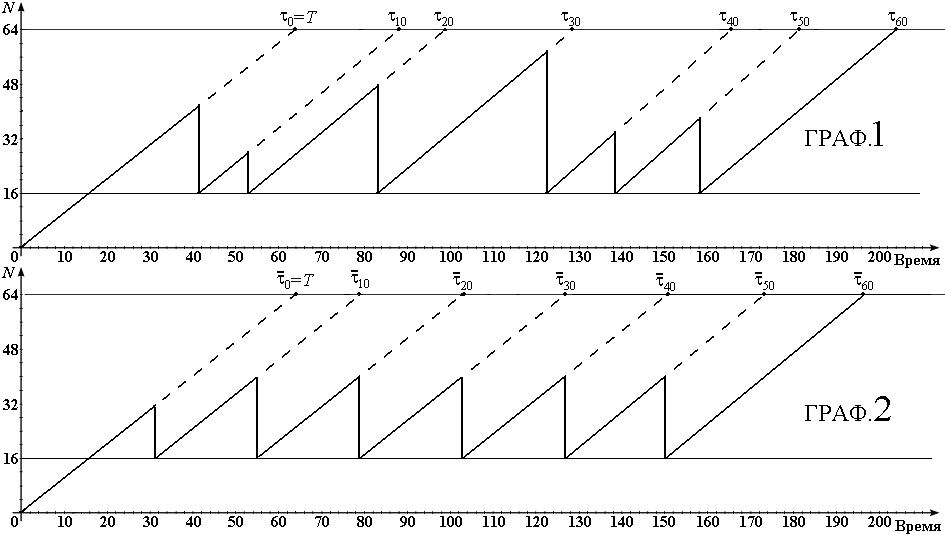
3. Модели режима передачи пакетного трафика независимыми блоками
   

При этом моменты релаксации в каждой серии некоррелированны (статистически независимы), а дисперсия задержек изменяется по линейному закону 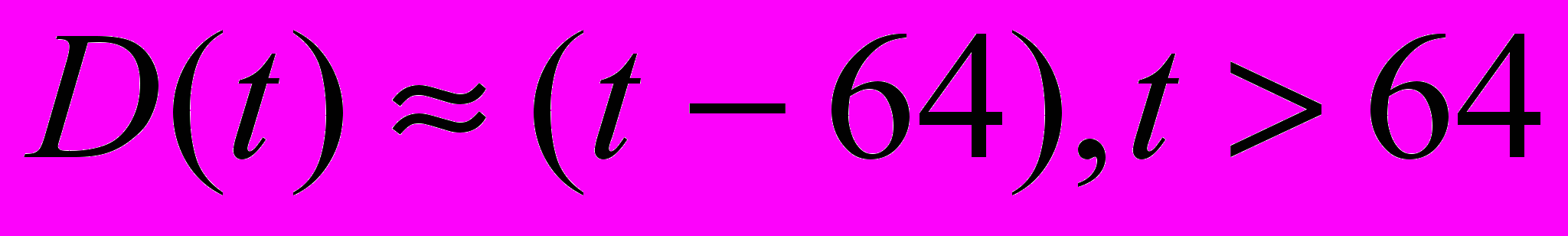(рис. 1.2, кривая 3). Сравнивая эти варианты, приходим к выводу, что площади под усредненными фрагментами за одинаковый интервал времени в первом варианте больше по сравнению с третьим и, следовательно, для пропускных способностей выполняется неравенство ПС1 > ПС3.

Перейдем к обсуждению причин, объясняющих необходимость пересмотра последнего результата. Начнем с того, что фрактальные процессы в режиме быстрой повторной передачи обладают протяженными или, как их еще называют, «тяжелыми» распределениями, аналитическая запись которых имеет вид 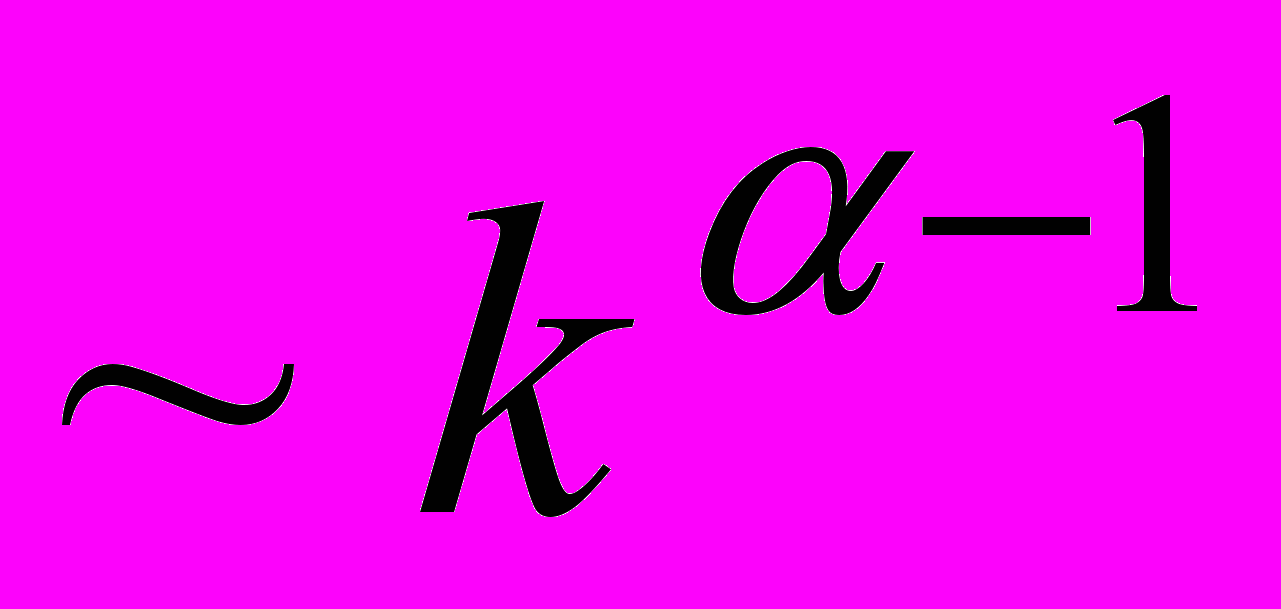или 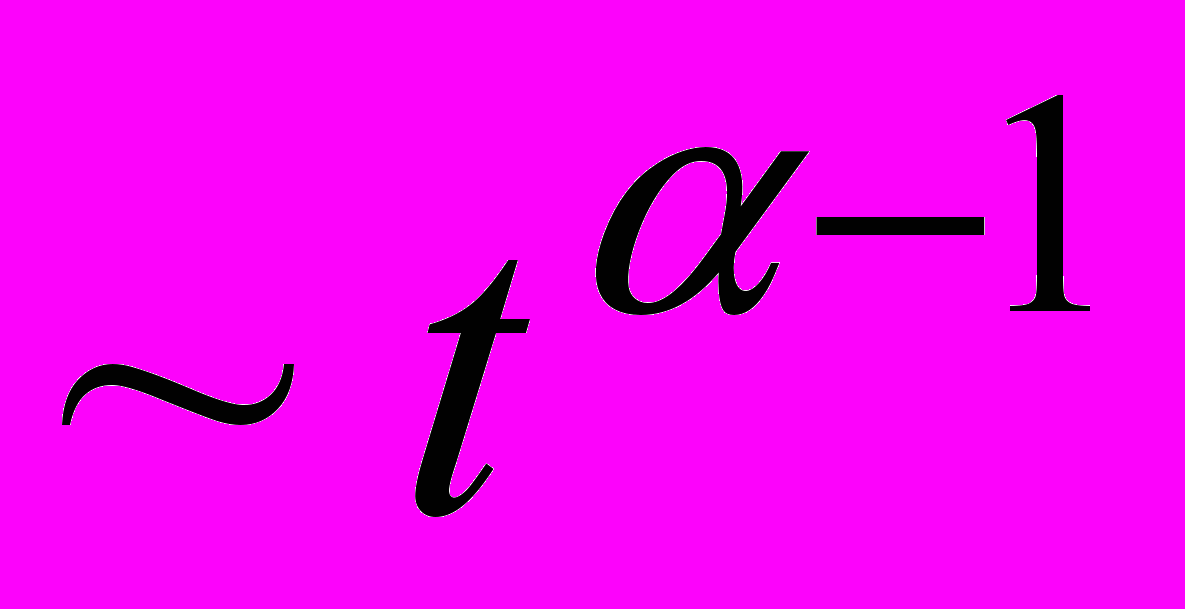( – фрактальный параметр, 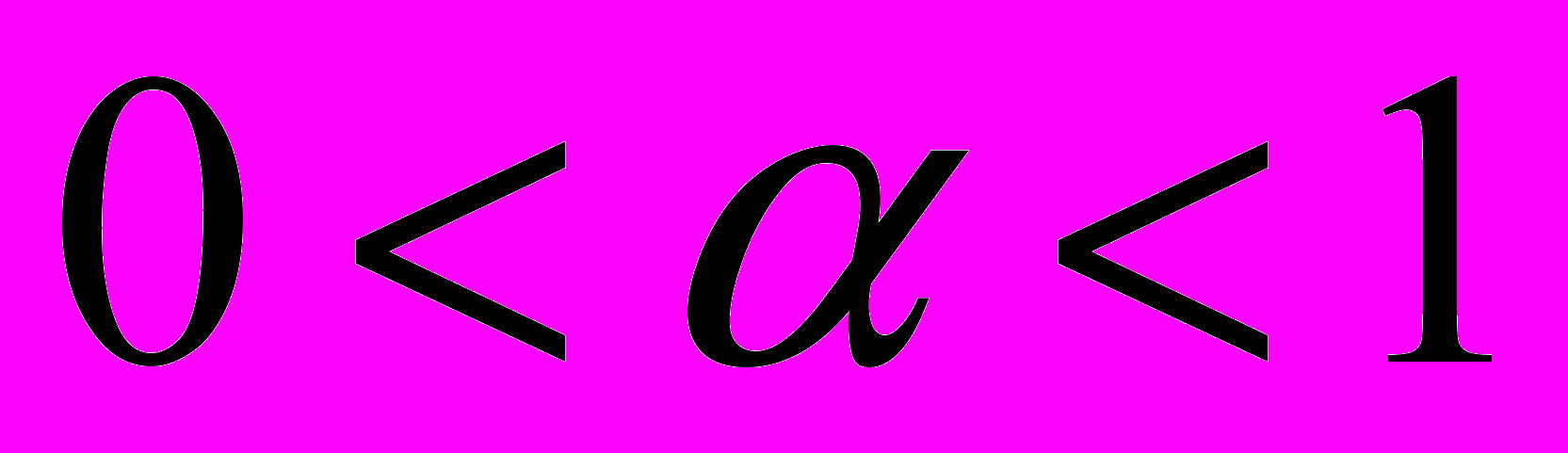). В первом случае этим выражением аппроксимируются корреляционные функции стационарных приращений фрактального винеровского процесса ( 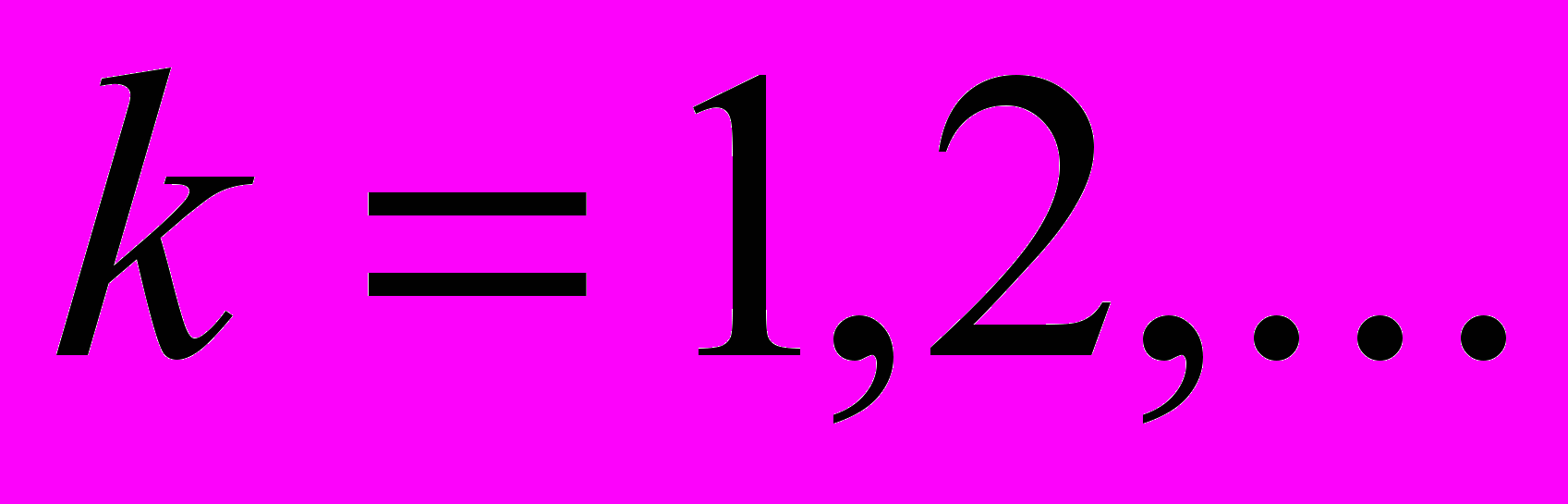– параметр смещения приращений процессов на интервалах одинаковой длительности Т), во втором – корреляционную функцию стационарной фрактальной плотности (t – текущее время). В последнем случае корреляционная функция участвует в формировании статистических характеристик задержек 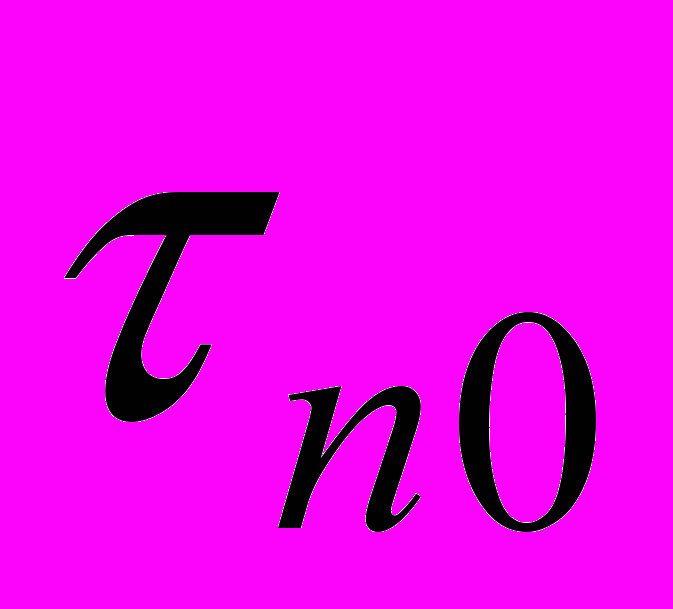[4, 6].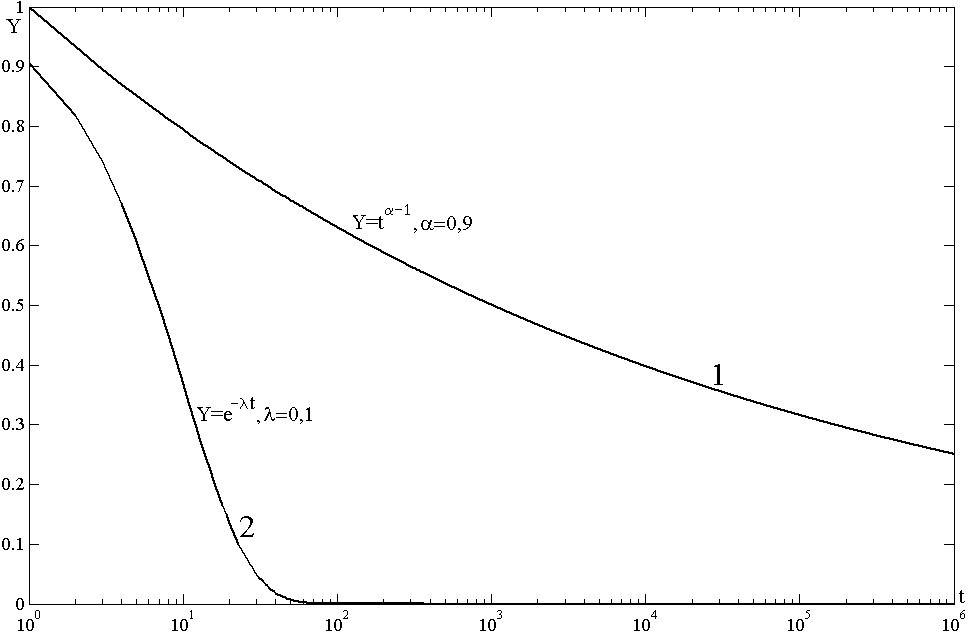

4. Корреляционные функции процессов
   

Как следует из рис. 1.4, она представляет собой при 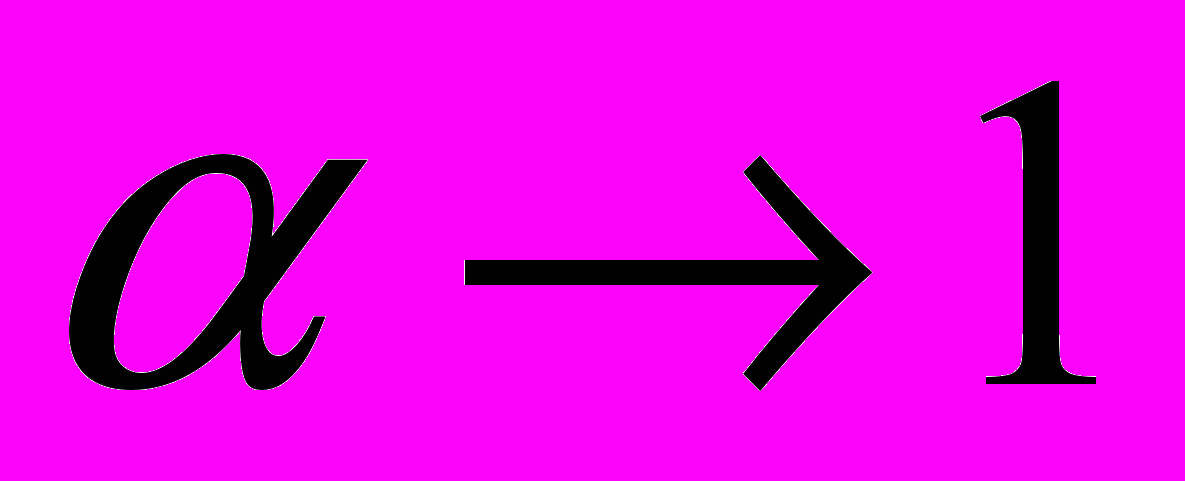слабозатухающую (протяженную) в течение нескольких часов функцию (кривая 1). Для сравнения на этом же рисунке приведена обычная короткопротяженная функция (кривая 2).

Оценим спектральные характеристики фрактального процесса. Введем параметр, называемый интервалом корреляции 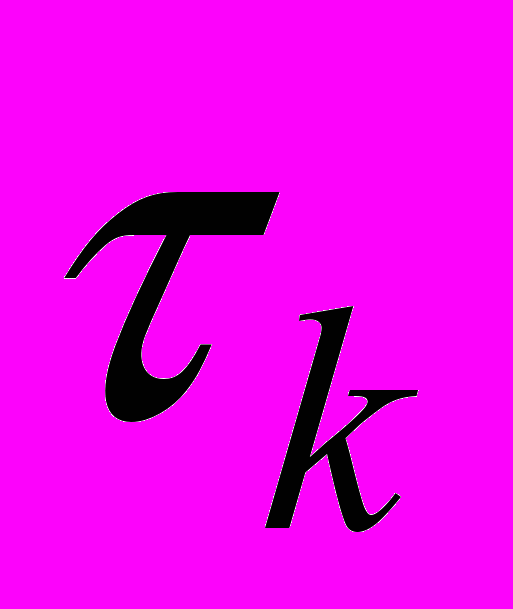. Он определяется как половина ширины основания прямоугольника с высотой равной дисперсии 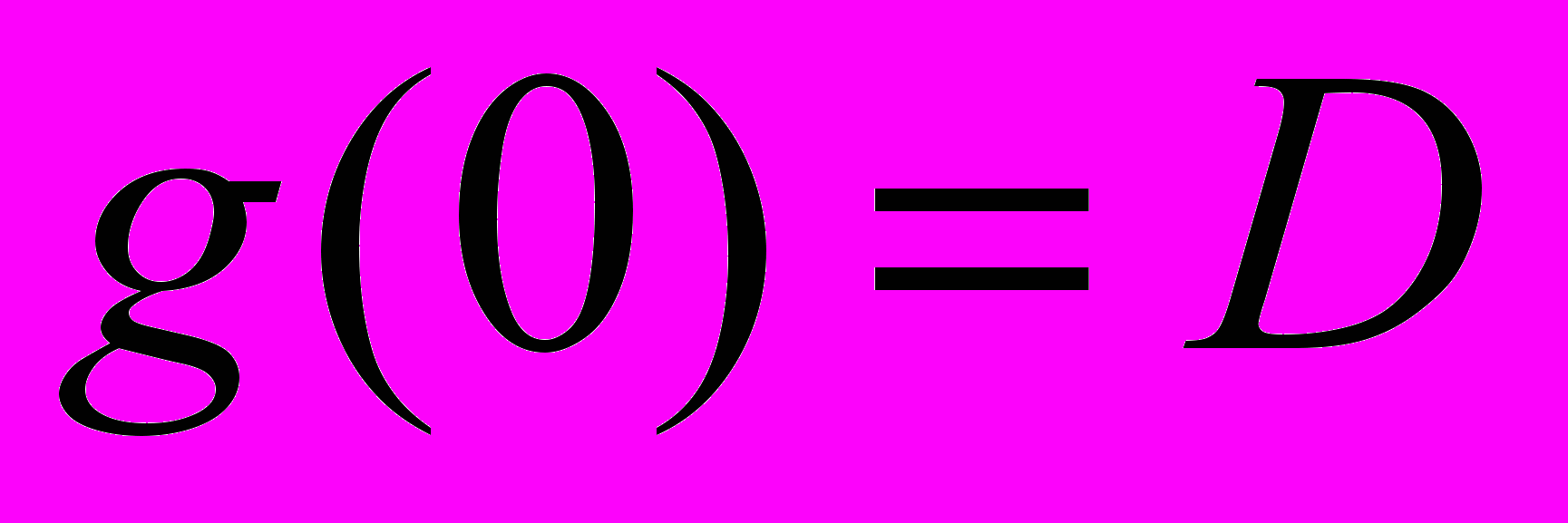, площадь которого равна площади под кривой модуля корреляционной функции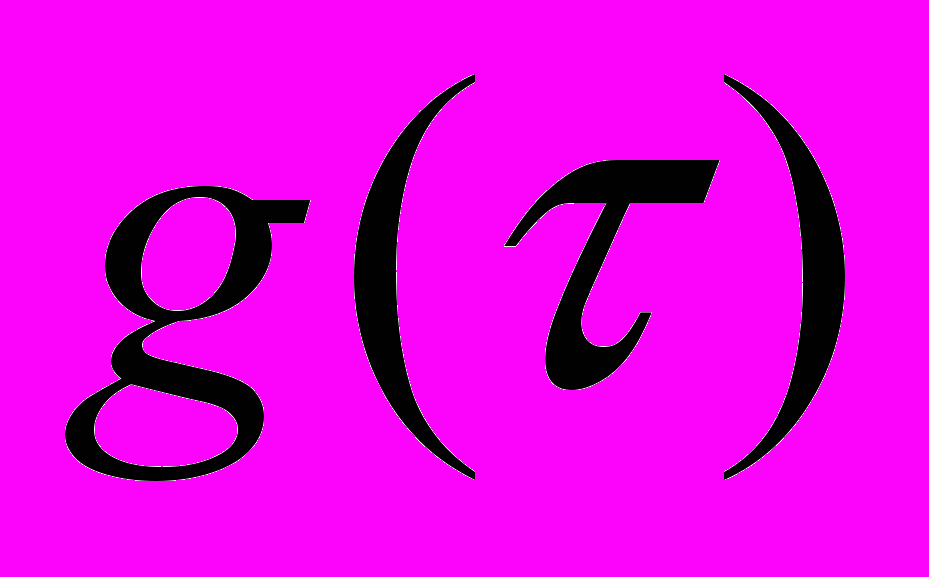



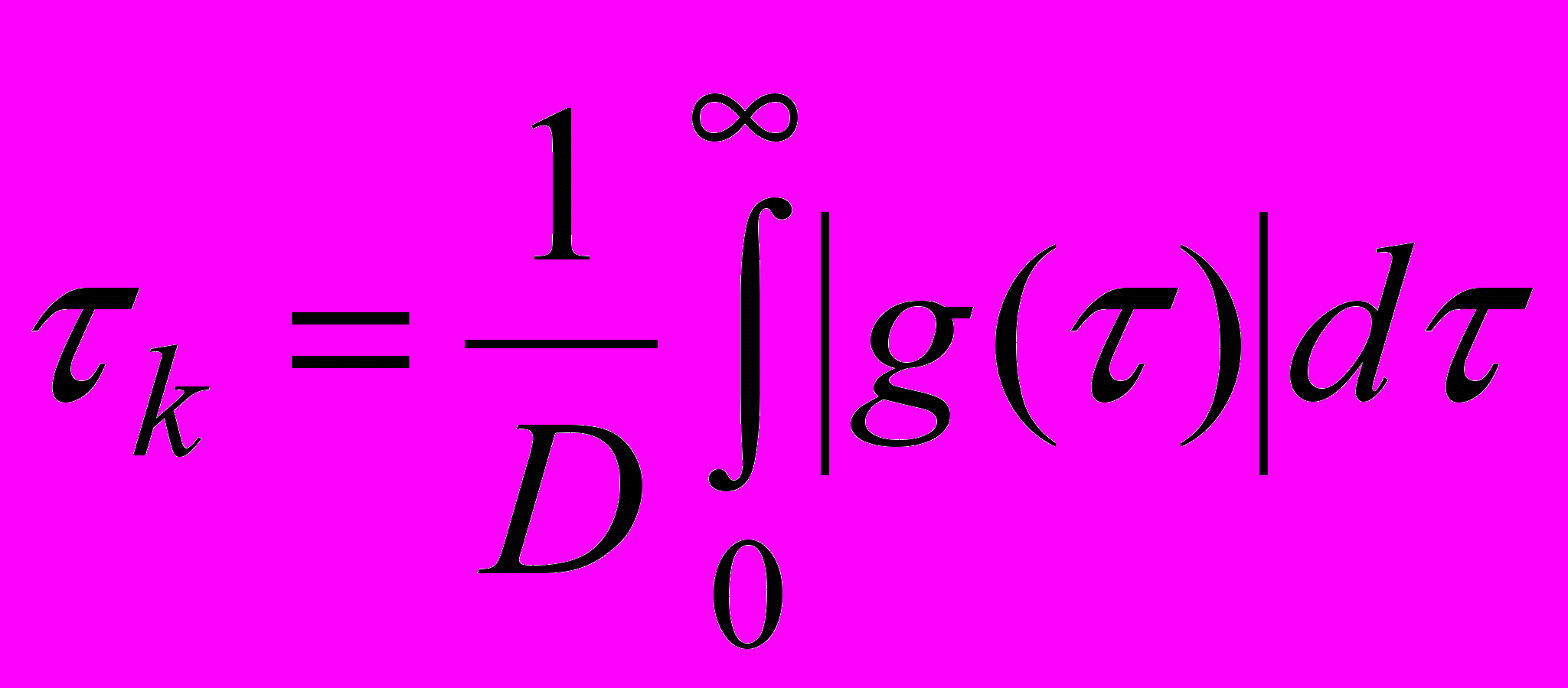
Другой параметр – ширина полосы спектра 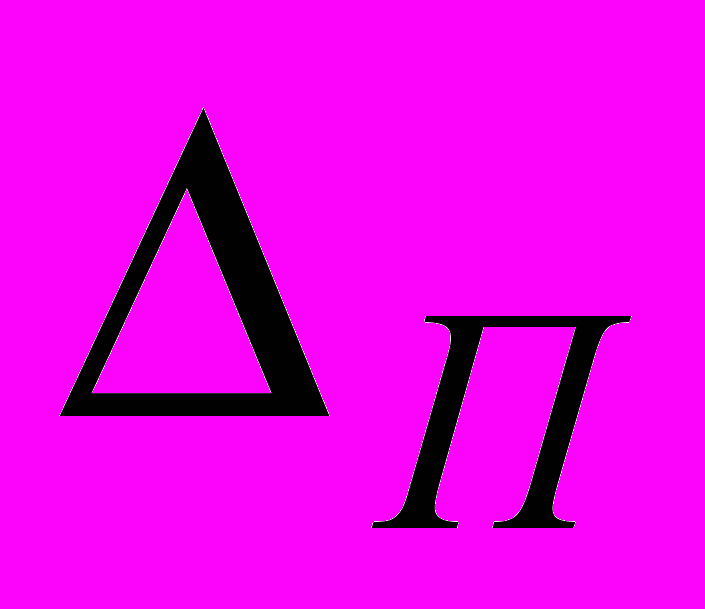, определяется как величина площади под кривой спектральной плотности 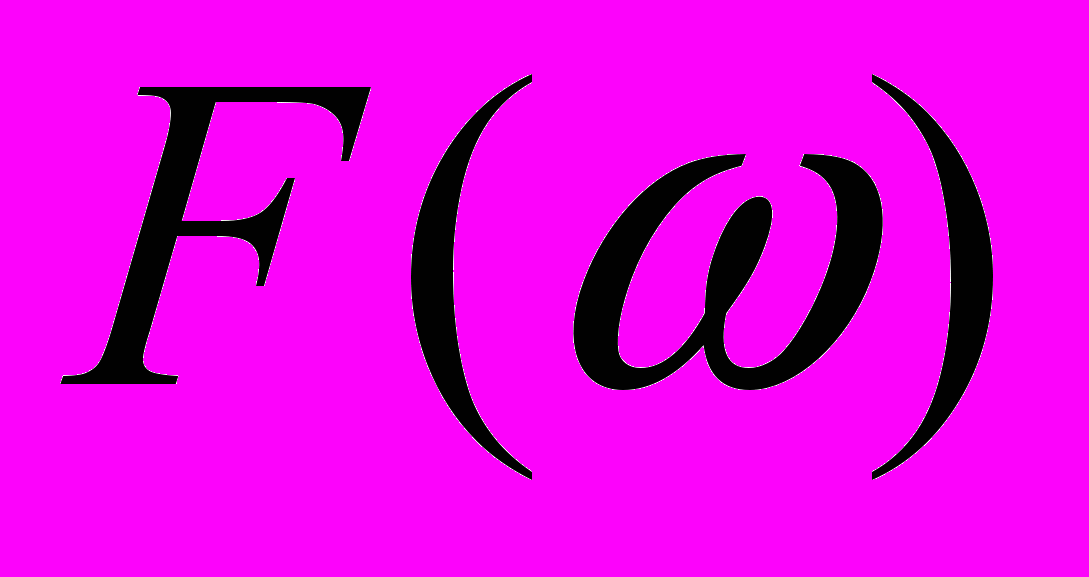, отнесенной к спектральной плотности на нулевой частоте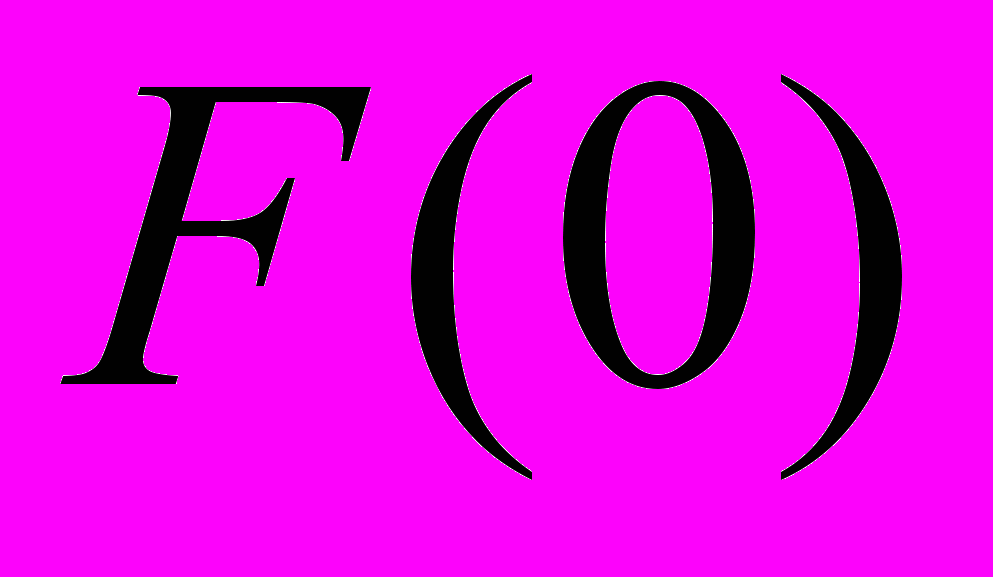



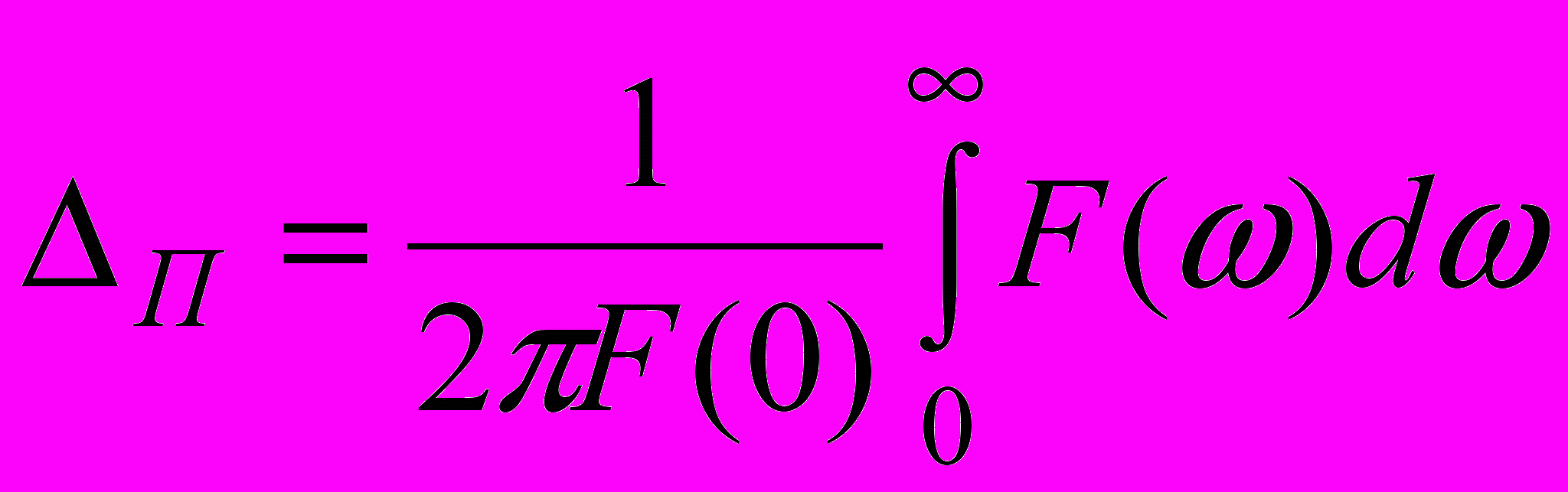
Воспользуемся следующим утверждением: произведение интервала корреляции на ширину полосы спектра 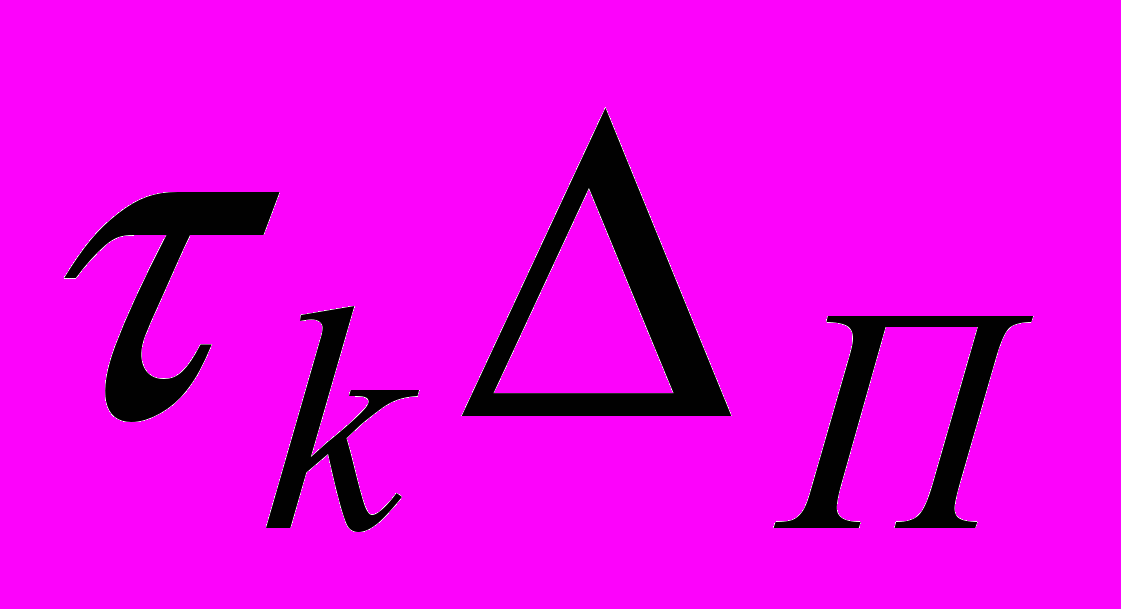– величина постоянная для семейств спектральных плотностей заданной формы [7]. Как следует из этой зависимости, чем уже корреляционная функция, тем протяженнее спектр, и наоборот, чем протяженнее корреляционная функция, тем уже спектр.

Возвращаясь к кривой 1 рис. 1.4, приходим к следующему результату: при 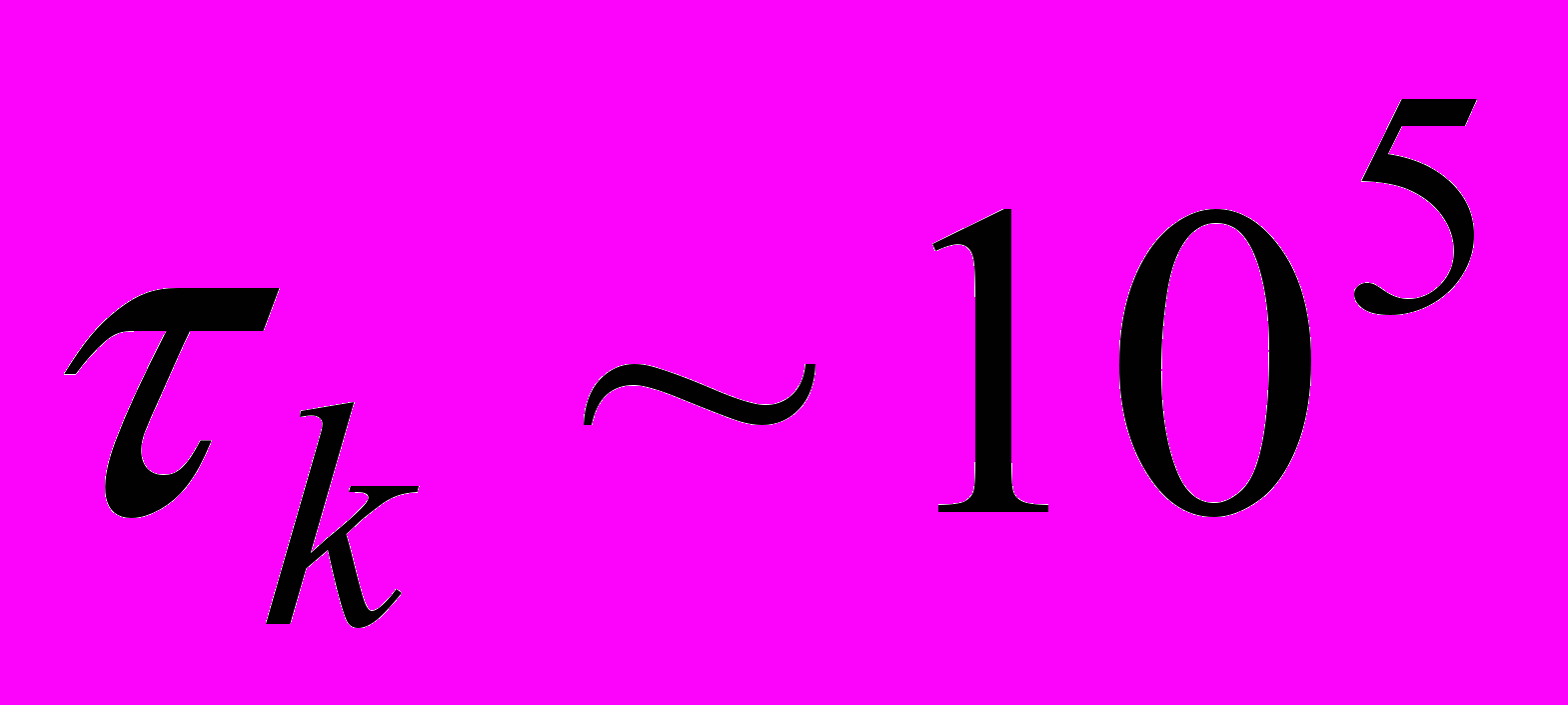сек. ширина полосы спектра 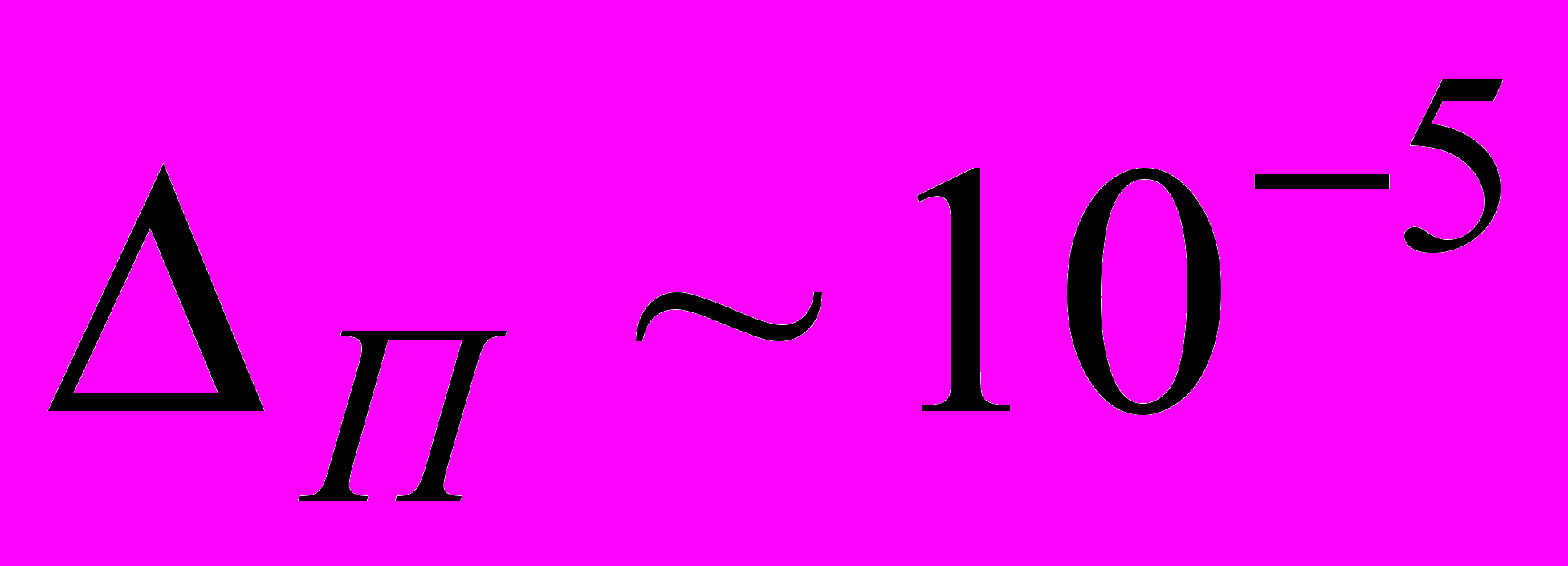1/сек, т.е. в спектре фрактальных процессов присутствуют в основном гармоники, периоды которых десятки минут и даже несколько часов. Таким образом, состояние фрактальных процессов задержек 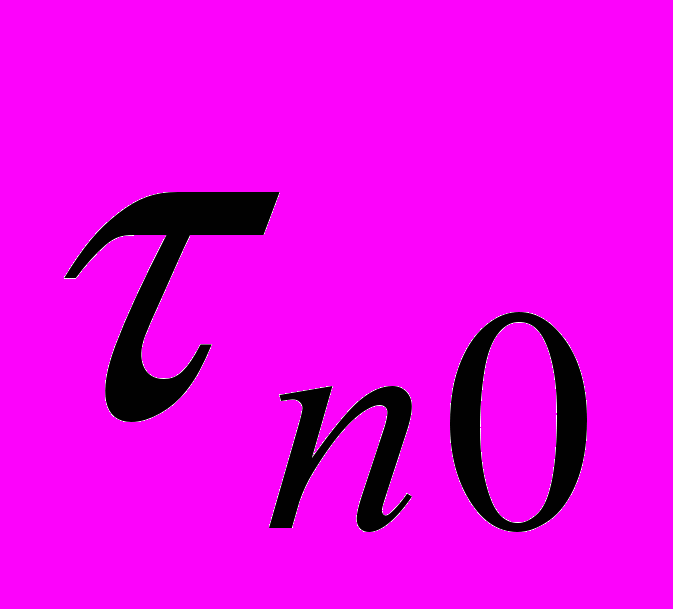характеризуется большими по величине и длительными по времени отклонениями от средних значений. Причем, чем больше моментов релаксации прошло, тем эти отклонения становятся больше и длительнее. Это объясняется существенным возрастанием дисперсии с увеличением точек (моментов) релаксации (рис. 1.2, кривые 1 и 2).

В задачах определения статистических характеристик при временах выборки значительно меньше 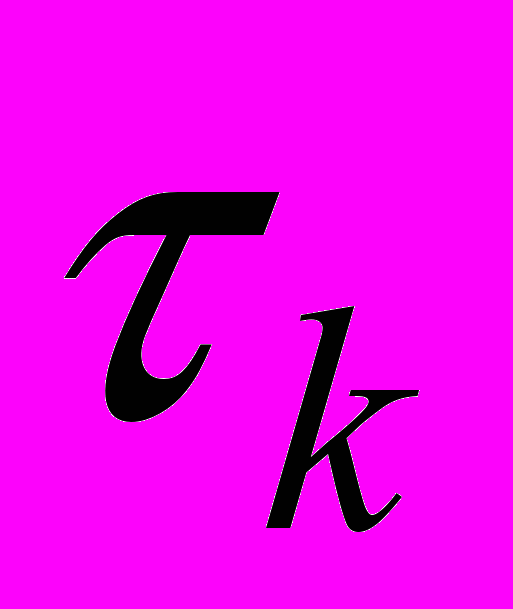создается видимость изменения по времени этих характеристик: режим как бы становится нестационарным. Оказывается при более детальном рассмотрении задачи определение ПС в режиме быстрой повторной передачи необходимо учитывать не только среднее значение, полученное через усредненный фрагмент передачи трафика, но и дополнительную составляющую, вызванную длительным и большим отклонением дисперсий моментов задержек 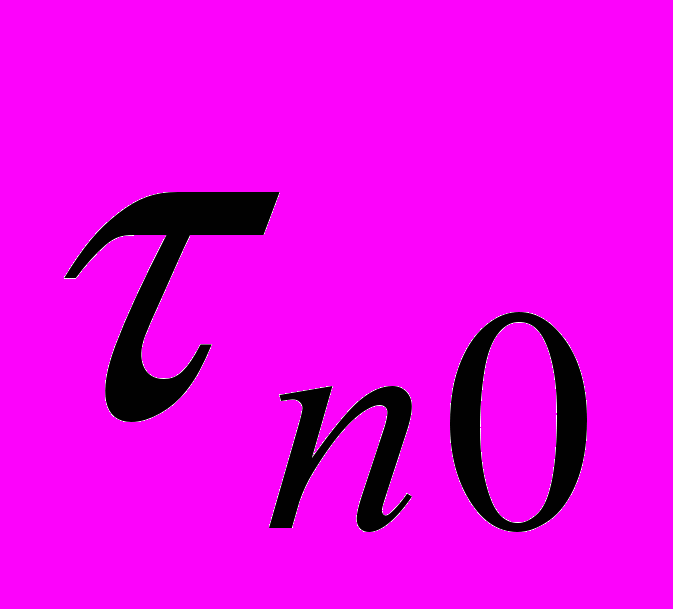. Это позволяет объяснить ряд парадоксов при передаче трафика: понижением ПС при длительной сопровождающейся большим числом релаксаций работе в этом режиме.

В качестве примера рассмотрим в режиме повторной передачи отклонение от среднего в сторону уменьшения текущего времени для шестого момента релаксации (от точки А к точке В, рис 1.1, график 3)¹. Это отклонение выбираем равным корню квадратному из дисперсии для шестой точки кривой 1 рис. 1.2: 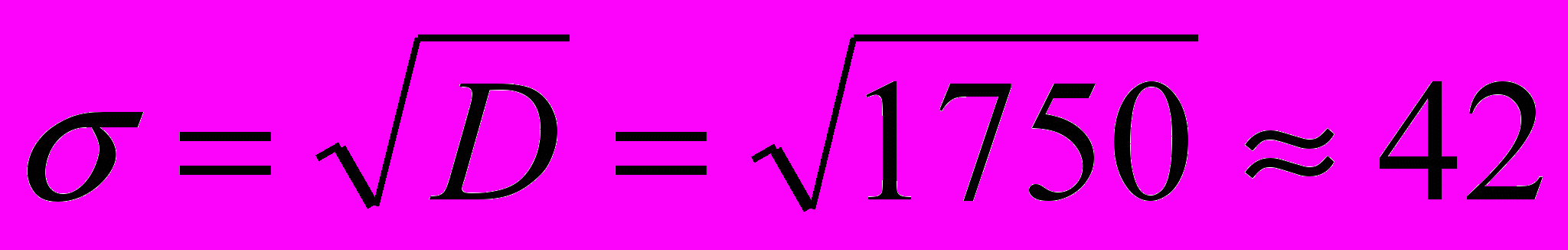. В этом случае усредненный фрагмент режима принимает вид графика 3 рис. 1.1 и, учитывая вышесказанное, может находиться в нем достаточно долго. Сравним этот режим с альтернативным вариантом 3, когда информация передается в виде независимых блоков, а усредненный фрагмент представляет собой график 2 рис. 1.3. Спектр этого режима имеет сравнительно высокочастотные гармоники, и случайный процесс задержек неоднократно пересекает средние значения из-за статистической независимости этих блоков. Здесь 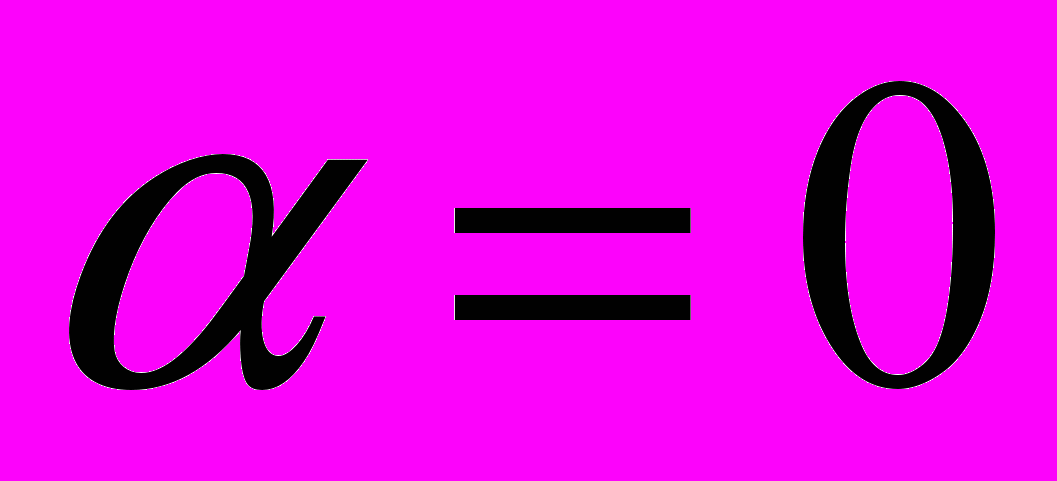и фрактальность в этом режиме отсутствует. Сравнивая площади под усредненными фрагментами графика 3 рис 1.1 и графика 2 рис 1.3, приходим к результату ПС1<ПС3. Это означает, что пропускная способность в режиме повторной передачи с увеличением числа релаксаций уменьшается по сравнению с пропускной способностью режима передачи информации независимыми блоками.

В заключение изложим полученные в работе основные результаты.

В режиме быстрой повторной передачи из-за корреляционной зависимости степенного вида поведение некоторых параметров, например моментов задержек 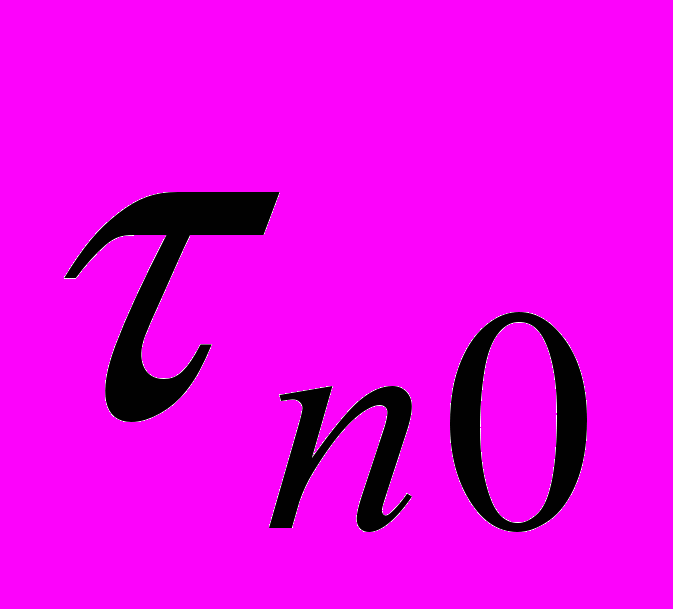, описывается фрактальными процессами. Эти изменения сопровождаются большими по величине и длительными по времени отклонениями от среднего значения.

Из-за фрактального характера процессов при определении пропускной способности необходимо учитывать не только среднее значение, но и дополнительную составляющую, зависящую от длительных и больших отклонений дисперсии.

С увеличением числа релаксаций и, следовательно, длительности режима повторной передачи пропускная способность уменьшается и становится меньше пропускной способности режима передачи информации независимыми блоками.

Уровень фрактальности характеризуется величиной фрактального параметра 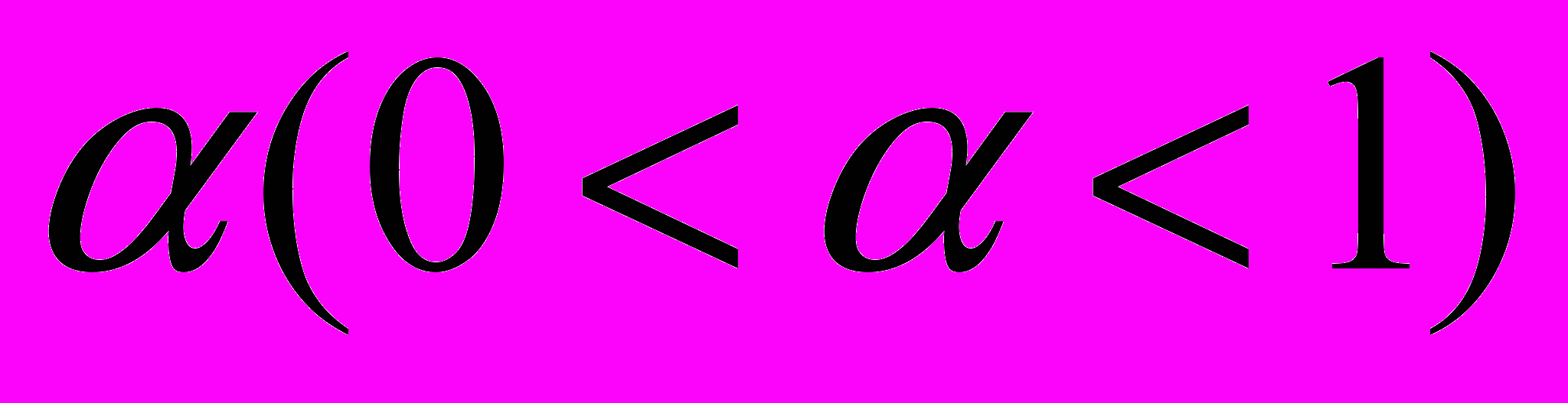. При переходе от равномерного к экспоненциальному распределению моментов релаксации этот параметр увеличивается. Следствием этого является усиление влияния рассмотренных в статье неблагоприятных факторов на пропускную способность.