Анализ финансовой отчетности сооо «Мобильные ТелеСистемы» Для анализа динамики развития сооо «Мобильные ТелеСистемы» идальнейшего прогноза деятельности компании рассмотрим основные финансовые показатели за 2006 2009 год
| Вид материала | Отчет |
- Информация о сооо «Мобильные ТелеСистемы», 214.74kb.
- Вице-президент ОАО «Мобильные ТелеСистемы»: Арендовать участок земли для работы операторам, 14.45kb.
- Оао «Мобильные ТелеСистемы»: история развития компании, 384.92kb.
- Портрет предприятия: ОАО "Мобильные ТелеСистемы" (мтс), 284.48kb.
- Акционерное Общество «Мобильные ТелеСистемы», 1308.59kb.
- «Мобильные ТелеСистемы», 3050.42kb.
- Информационные материалы, предоставляемые акционерам при подготовке к проведению Годового, 88.83kb.
- Пресс-служба ОАО «Таттелеком» Дайджест сми, 773.44kb.
- Заместитель генерального директора по развитию сооо «феликс», 117.83kb.
- 1. 1Общие сведения о процедуре запроса предложений, 3991.42kb.
2. Эконометрический анализ финансовой отчетности СООО «Мобильные ТелеСистемы»
Для анализа динамики развития СООО «Мобильные ТелеСистемы» и дальнейшего прогноза деятельности компании рассмотрим основные финансовые показатели за 2006 – 2009 годы. Данные взяты нами с сайта СООО «Мобильные ТелеСистемы» и представлены в таблице 2.1.
Введем обозначения рассматриваемых показателей:
S – количество абонентов, тыс. чел.;
WR – выручка от реализации, товаров, работ, услуг (за минусом НДС, акцизов и иных аналогичных обязательных платежей), млн. руб;
ARPU - средняя ежемесячная выручка от продажи услуг в расчете на одного абонента, USD/ абон.;
MOU – средний коммерческий трафик на одного абонента за месяц, мин./абон.;
KV – капитальные вложения, млн. руб.
Рассматриваемые нами показатели финансовой отчетности относятся к временным рядам. Чтобы рассмотреть взаимосвязь данных показателей, а так же оценить динамику их развития, мы должны вначале рассмотреть данные ряды отдельно, выявить присущую им тенденцию, а так же установить стационарность данных рядов.
Для установления стационарности временных рядов в данной работе мы будем использовать расширенный тест Дики-Фулера, далее ADF-тест. Для эконометрических расчетов мы воспользуемся приложением “Gretl”.
2.1. Анализ временных рядов финансовой отчетности деятельности СООО «Мобильные ТелеСистемы».
2.1.1. Анализ временного ряда абонентской базы.
Рассмотрим временной ряд показателя количество абонентов, представленный на рисунке 2.1.
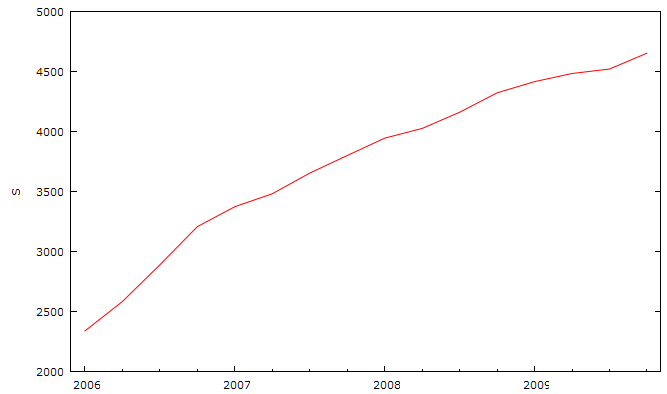
Рис. 2.1. Динамика развития абонентской базы.
Как видно из рисунка данный ряд имеет четко выраженный линейный тренд, т. е. скорость роста абонентской базы можно считать постоянной. Особого внимания заслуживает тот факт, что мировой финансовый кризис никак не повлиял на развитие абонентской базы.
Рассмотрим ряд первых разностей числа абонентов, представленный на рисунке 2.2.
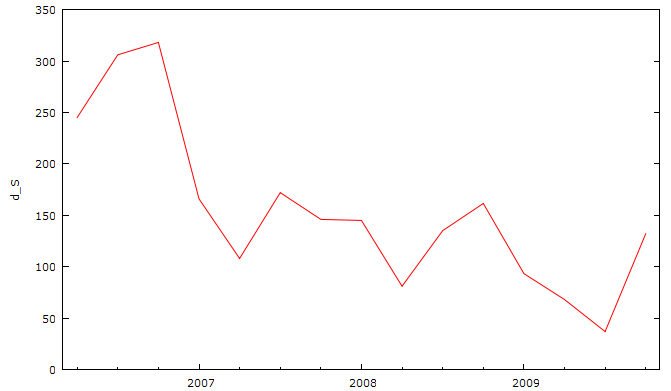
Рис. 2.2. Первые разности ряда абонентской базы.
Как видно из графика первых разностей наибольшие приросты абонентской базы наблюдаются с первого по третий квартал 2006 года. Долее приросты колеблются вокруг отметки 120 тысяч.
Рассмотрим стационарность данных временных рядов, используя ADF-тест.
Результаты ADF-теста для уровней ряда абонентской базы:


Как видно из результатов теста временной ряд абонентской базы можно признать стационарным относительно тренда, так же ряд можно признать стационарным относительно константы, так как значение вероятность принятия нулевой гипотезы составляет 0,0365, что меньше допустимого 0,05.
Результаты ADF-теста для первых разностей ряда абонентской базы:

Как видно из результатов теста ряд первых разностей абонентской базы нельзя признать стационарным.
Коррелограмма ряда абонентской базы представлена на рисунке 2.3.
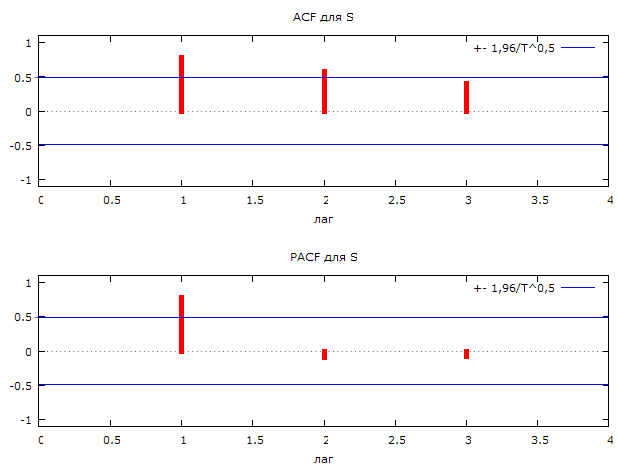
Рис. 2.3. Коррелограмма ряда абонентской базы.
Представим значения ACF – автокорреляционная функция и PACF – частная автокорреляционная функция:

По виду коррелограммы ряд абонентской базы можем идентифицировать как ряд авторегрессии.
Построим модель данного временного ряда, использую средства Gretl. В для моделирования модели воспользуемся моделью временного ряда ARIMA(q, ∆, p). Где q-параметр авторегрессии; ∆- величина разностей уровней ряда, p – параметр скользящего среднего. В результате подбора параметров модели, проверки их значимости, лучшей оказалась модель ARIMA(1, 0, 0) с константой.

Мы получили следующую модель временного ряда:
St = 510,7 + 0,903∙St-1 (2.1)
(t) (7,507) (49,66)
Так же модель можем записать в виде:
∆St = St – St-1 = 510,7 + 0,903∙St-1 – St-1 = 510 – 0,087∙ St-1 (2.2)
Полученную модель (2.1) можем признать удачной, все коэффициенты в модели являются статистически значимыми, в модели отсутствует автокорреляция, остатки модели стационарны и имеют нормальное распределение. Так же можем отметить, что информационные критерии Акаике и Шварца имеют лучшие значения, нежели в моделях рассмотренных нами ранее. Предшествующие модели мы не рассматриваем в данной работе, так как они имеют гораздо худшие показатели.
По полученной модели (2.2) можем сказать, что с каждым последующим кварталом прирост числа абонентов уменьшается, пропорционально значению абонентской базы предшествующего периода, с коэффициентом пропорциональности -0,087.
Рассчитаем максимальное число абонентов, до которого возможен рост абонентской базы:
Smax = 510/0,087 = 5862 тыс. чел.
Т. е. можем сказать, что после достижения компанией абонентской базы в размере 5862 тыс. чел. будет наблюдаться равновесное состояние абонентской базы. Действительно, при уменьшении значения St-1, будет увеличиваться значение прироста и наоборот.
Произведем прогноз численности абонентов на 2010 год. График прогноза представлен на рисунке 2.3.
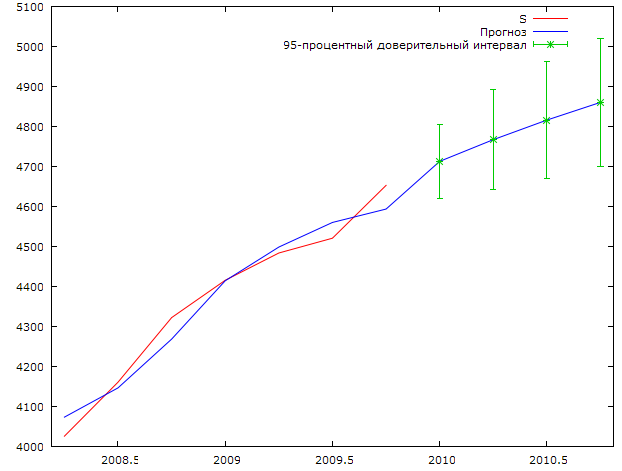
Рис 2.4. Прогноз численности абонентов на 2010 год.
Как видно из графика положительная динамика абонентской базы в 2010 году сохраниться, однако величины ежемесячных приростов будут меньше. К концу года величина абонентской базы может достигнуть значения 4860,5 тыс. чел. Данная величина не превышает критическую, поэтому в 2011 можем так же рассчитывать на прирост абонентской базы. Ниже приведены прогнозные значения по подученной нами модели (2.1), а так же стандартные ошибки прогнозов и доверительные интервалы для прогнозов.

Окончательно можем сделать вывод, что временной ряд абонентской базы является стационарным. Модель временного ряда является моделью авторегрессии первого порядка.
2.1.2. Анализ временного ряда выручки от реализации товаров, работ, услуг.
Рассмотрим временной ряд выручки от реализации, представленный на рисунке 2.5.
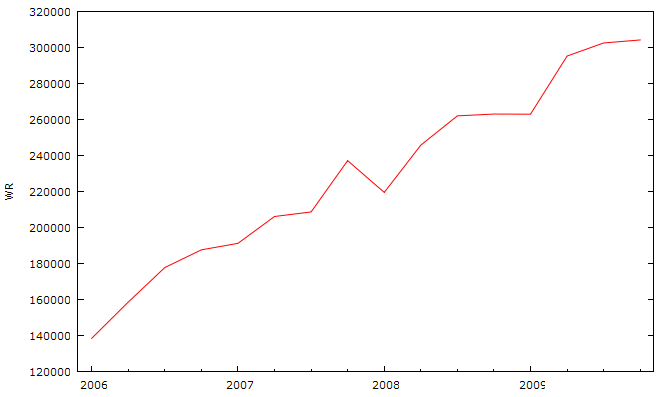
Рис. 2.5. Динамика выручки от реализации товаров и услуг.
Как видно из рисунка данный ряд имеет четко выраженный временной тренд, т. е. значения выручки от реализации колеблются от воображаемой линии тренда. Особого внимания заслуживает тот факт, что мировой финансовый кризис никак не повлиял на развитие абонентской базы.
Рассмотрим ряд первых разностей выручки от реализации, представленный на рисунке 2.6.
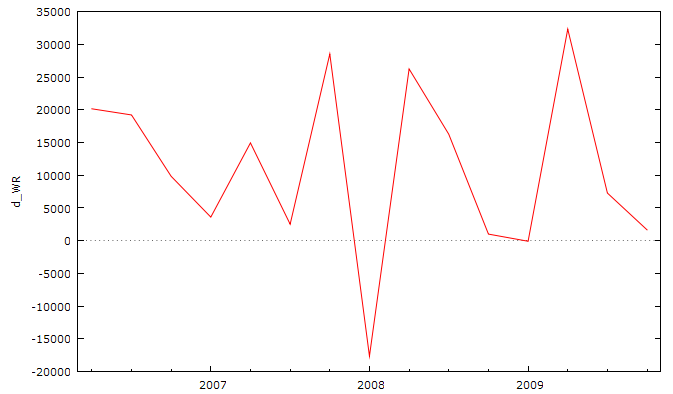
Рис. 2.6. Первые разности ряда выручки от реализации.
Как видно из графика первых разностей приросты выручки от реализации колеблются относительно некоторой воображаемой прямой линии. Отрицательный прирост выручки от реализации мы наблюдаем в начале 2008 года. До этого наблюдались только положительные приросты в выручке. Однако в данный период мировой финансовый кризис ещё не наступил, и мы это снижение не можем связать с ним. А вот в период финансового кризиса мы наблюдаем только положительные приросты в выручке от реализации. Мы можем связать это с гибкой политикой управления компанией в период кризиса, с адаптацией к новым условиям работы.
Рассмотрим стационарность данных временных рядов, используя ADF-тест.
Результаты ADF-теста для уровней ряда абонентской базы:

Как видно из результатов теста временной ряд выручки от реализации можно признать стационарным относительно тренда, так как значение вероятность принятия нулевой гипотезы составляет 0,0019, что намного меньше допустимого 0,05.
Результаты ADF-теста для первых разностей выручки от реализации:

Как видно из результатов теста ряд первых разностей выручки от реализации можно признать стационарным относительно константы.
Коррелограмма ряда выручки от реализации представлена на рисунке 2.7.
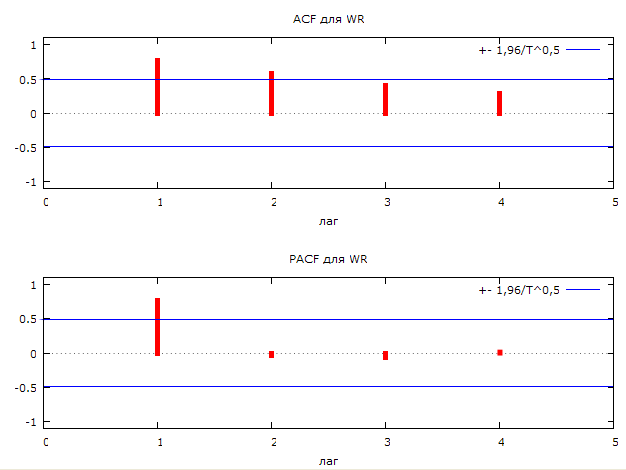
Рис. 2.7. Коррелограмма ряда выручки от реализации.
Представим значения ACF – автокорреляционная функция и PACF – частная автокорреляционная функция:

По виду коррелограммы ряд выручки от реализации можем идентифицировать как ряд авторегрессии.
Построим модель данного временного ряда, использую средства Gretl. В для моделирования модели воспользуемся моделью временного ряда ARIMA(q, ∆, p). Где q-параметр авторегрессии; ∆- величина разностей уровней ряда, p – параметр скользящего среднего. В результате подбора параметров модели, проверки их значимости, лучшей оказалась модель ARIMA(1, 0, 0) без константы.

Мы получили следующую модель временного ряда:
WRt = 1,044∙WRt-1 (2.3)
(t) (49,66)
Так же модель можем записать в виде:
∆WRt = WRt – WRt-1 = 1,044∙WRt-1 – WRt-1 = 0,044∙ WRt-1 (2.4)
Полученную модель (2.3) можем признать удачной, все коэффициенты в модели являются статистически значимыми, в модели отсутствует автокорреляция, остатки модели стационарны и имеют нормальное распределение. Так же можем отметить, что информационные критерии Акаике и Шварца имеют лучшие значения, нежели в моделях рассмотренных нами ранее. Предшествующие модели мы не рассматриваем в данной работе, так как они имеют гораздо худшие показатели.
По полученной модели (2.4) можем сказать, что с каждым последующим кварталом прирост выручки от реализации товаров и услуг увеличивается на 4,4% по сравнению с выручкой предшествующего периода.
Произведем прогноз выручки от реализации товаров и услуг на 2010 год. График прогноза представлен на рисунке 2.8.
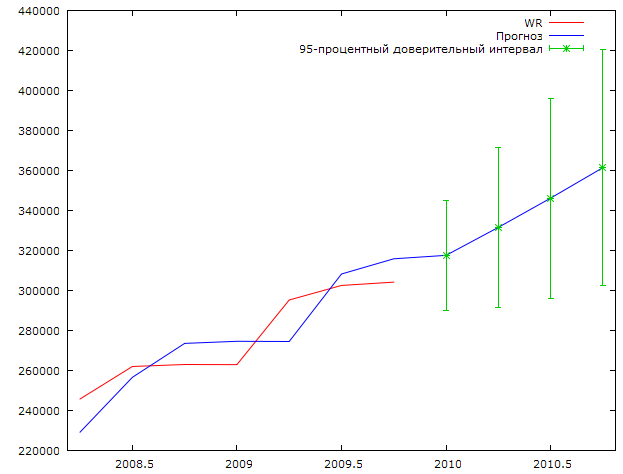
Рис 2.8. Прогноз выручки реализации товаров и услуг на 2010 год.
Как видно из графика положительная динамика выручки от реализации товаров и услуг в 2010 году сохраниться. К концу года величина выручки от реализации может достигнуть значения 361448 млн. р. Ниже приведены прогнозные значения по подученной нами модели (2.3), а так же стандартные ошибки прогнозов и доверительные интервалы для прогнозов.
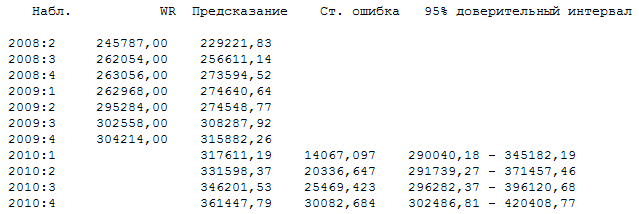
Окончательно можем сделать вывод, что временной ряд выручки от реализации товаров, работ и услуг является стационарным. Модель временного ряда является моделью авторегрессии первого порядка.
2.1.3. Анализ временного ряда ARPU, средней ежемесячной выручки от продажи услуг в расчете на одного абонента (USD/ абон.).
Рассмотрим временной ряд ARPU, представленный на рисунке 2.9.
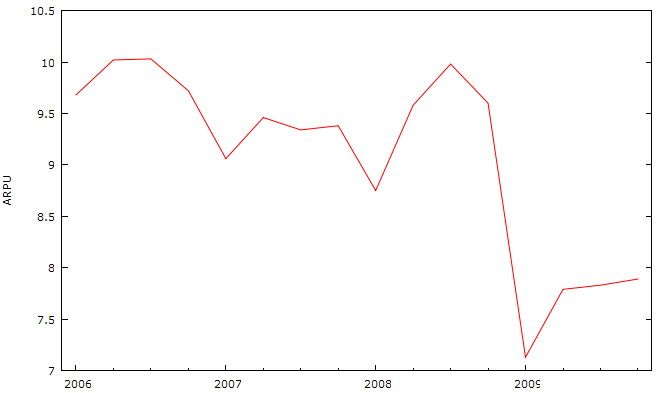
Рис. 2.9 Динамика величины ARPU.
Как видно из рисунка данный ряд не имеет временного тренда. Значения ряда колеблются вокруг некоторой константы. В третьем квартале 2008 года наблюдаем резкое снижение выручки на одного абонента. Данное резкое снижение можем связать с влиянием глобального экономического кризиса. Затем наблюдаем незначительный подъем средней выручки на одного абонента. Т. е. можем отметить, что компания приспособилась к новым условиям видения бизнеса.
Рассмотрим ряд первых разностей средней выручки на одного абонента, представленный на рисунке 2.10.
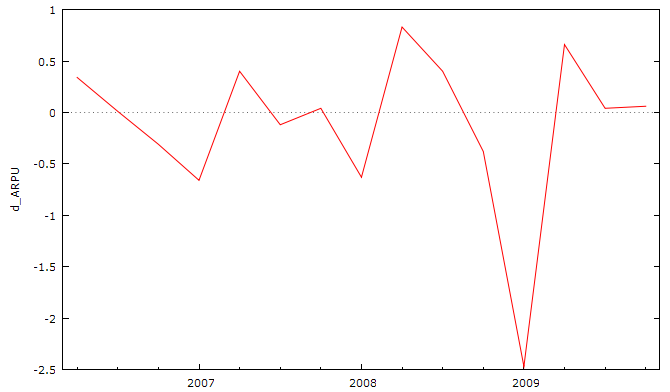
Рис. 2.10. Первые разности ряда ARPU.
Как видно из графика первых разностей приросты средней выручки на одного абонента колеблются относительно нулевой линии. Отрицательные приросты средней выручки, сменяются положительными приростами. Наибольший отрицательный прирост наблюдается в четвертом квартале 2008 года. Затем мы имеем только положительные приросты средней выручки на одного абонента. Так же можем отметить, что отрицательные приросты средней выручки на одного абонента наблюдаются в конце каждого года.
Рассмотрим стационарность данных временных рядов, используя ADF-тест.
Результаты ADF-теста для уровней ряда ARPU:



Как видно из результатов теста временной ряд средней выручки на одного абонента нельзя признать стационарным ни по одной из спецификаций, так как значения вероятности принятия нулевых гипотез составляет 0,3266; 0,5817; 0,2495 соответственно, что намного больше допустимого 0,05.
Результаты ADF-теста для первых разностей ряда средней выручки на одного абонента:

Как видно из результатов теста ряд первых разностей средней выручки на одного абонента можно признать стационарным со спецификацией без константы. Следовательно, временной ряд средней выручки на одного абонента является стационарным относительно взятия первых разностей, т. е. относится к классу DS-рядов.
Коррелограмма ряда первых разностей средней выручки от реализации на одного абонента представлена на рисунке 2.11.
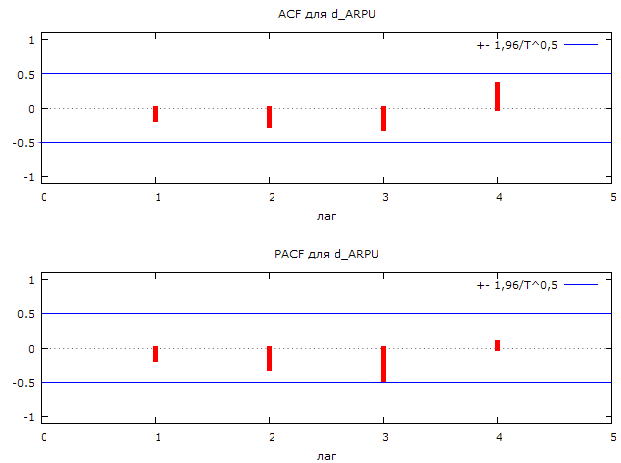
Рис. 2.11. Коррелограмма ряда первых разностей средней выручки от реализации на одного абонента.
Представим значения ACF – автокорреляционная функция и PACF – частная автокорреляционная функция:

По виду коррелограммы ряд средней выручки на одного абонента можем идентифицировать данный ряд, как процесс ARIMA.
Построим модель данного временного ряда, использую средства Gretl. В для моделирования модели воспользуемся моделью временного ряда ARIMA(q, ∆, p). Где q-параметр авторегрессии; ∆- величина разностей уровней ряда, p – параметр скользящего среднего. В результате подбора параметров модели, проверки их значимости, лучшей оказалась модель ARIMA(0, 1, 1) с константой.

Мы получили следующую модель временного ряда:
∆ARPUt = -0,1423 + at – at-1 (2.5)
(t) (-4,202) (-3,854)
Полученную модель (2.5) можем признать удачной, все коэффициенты в модели являются статистически значимыми, в модели отсутствует автокорреляция, остатки модели стационарны и имеют нормальное распределение. Так же можем отметить, что информационные критерии Акаике и Шварца имеют лучшие значения, нежели в моделях рассмотренных нами ранее. Предшествующие модели мы не рассматриваем в данной работе, так как они имеют гораздо худшие показатели.
Произведем прогноз средней выручки на одного абонента на 2010 год. График прогноза представлен на рисунке 2.12.
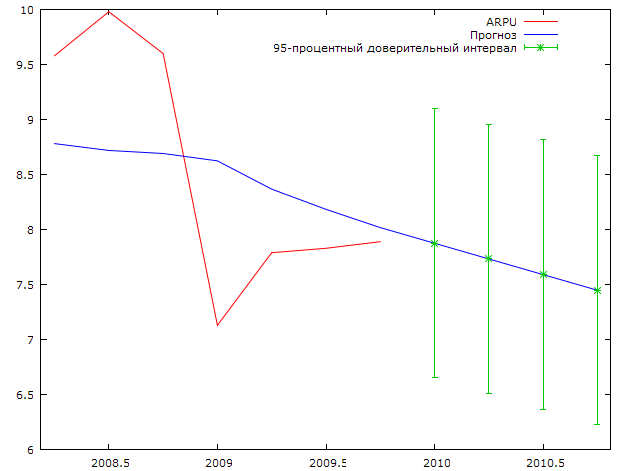
Рис 2.12. Прогноз средней выручки на одного абонента на 2010 год.
По полученным результатам прогноза трудно охарактеризовать значение средней выручки на одного абонента в следующем году, так как доверительные интервалы для прогнозируемой величины достаточно велики. Ниже приведены прогнозные значения по полученной нами модели (2.5), а так же стандартные ошибки прогнозов и доверительные интервалы для прогнозов.
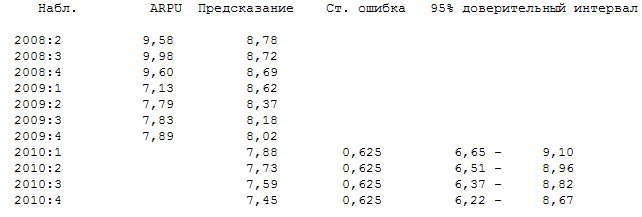
Окончательно можем сделать вывод, что временной ряд средней выручки на одного абонента является стационарным относительно взятия первых разностей. Модель временного ряда является процессом ARIMA.
2.1.4. Анализ временного ряда MOU, средний коммерческий трафик на одного абонента за месяц, (мин./абон.).
Рассмотрим временной ряд MOU, представленный на рисунке 2.13.
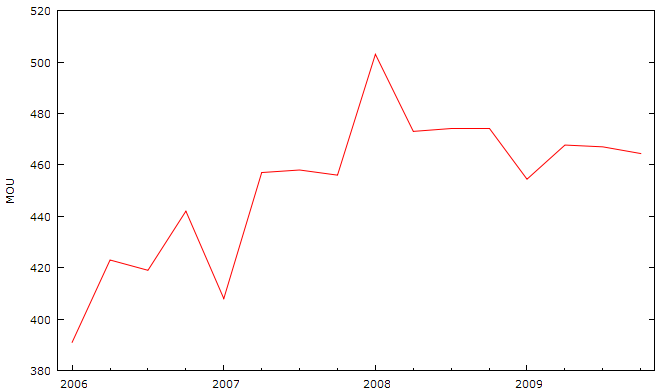
Рис. 2.13. Динамика величины MOU.
Как видно из рисунка до начала 2008 года ряд имеет положительную динамику, средний коммерческий трафик имеет тенденцию роста. А вот с начала 2008 года наблюдается отрицательная динамика, происходит снижение среднего коммерческого трафика.
Рассмотрим первые разности ряда среднего коммерческого трафика на одного абонента, представленный на рисунке 2.14.
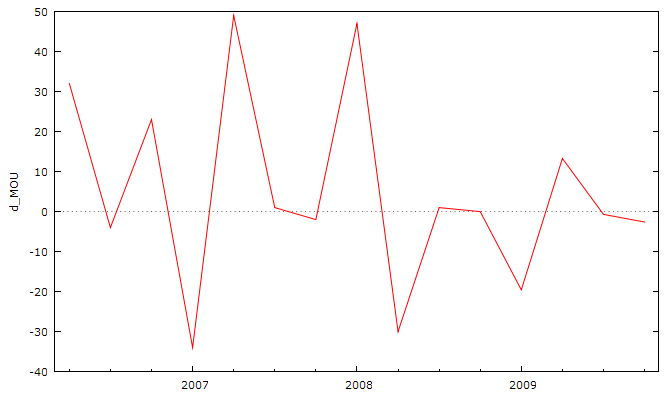
Рис. 2.14. Первые разности ряда МОU.
Как видно из графика первых разностей приросты средней среднего коммерческого трафика на одного абонента колеблются относительно нулевой линии. Отрицательные приросты среднего коммерческого трафика, сменяются положительными приростами. Наибольший отрицательный прирост наблюдается в четвертом квартале 2007 года.
Рассмотрим стационарность данных временных рядов, используя ADF-тест.
Результаты ADF-теста для уровней ряда ARPU:



Как видно из результатов теста временной ряд средней выручки на одного абонента нельзя признать стационарным ни по одной из спецификаций, так как значения вероятности принятия нулевых гипотез составляет 0,911; 0,3536; 0,1891 соответственно, что намного больше допустимого 0,05.
Результаты ADF-теста для первых разностей ряда средней выручки на одного абонента:

Как видно из результатов теста ряд первых разностей среднего коммерческого трафика можно признать стационарным со спецификацией без константы. Следовательно, временной ряд среднего коммерческого трафика на одного абонента является стационарным относительно взятия первых разностей, т. е. относится к классу DS-рядов.
Коррелограмма ряда первых разностей среднего коммерческого трафика на одного абонента представлена на рисунке 2.15.
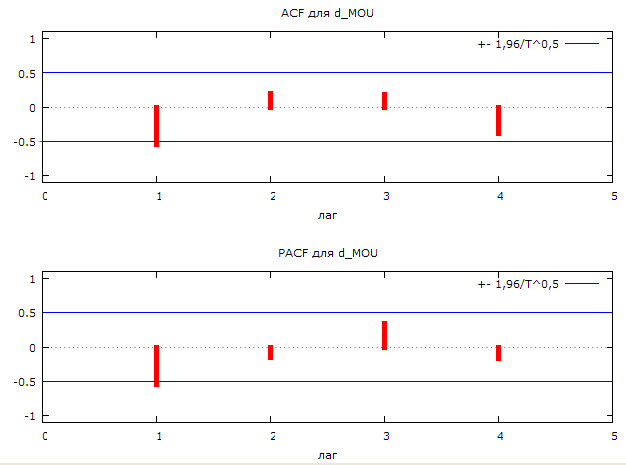
Рис. 2.15. Коррелограмма ряда первых разностей среднего коммерческого трафика на одного абонента.
Представим значения ACF – автокорреляционная функция и PACF – частная автокорреляционная функция:

По виду коррелограммы, ряд среднего коммерческого трафика на одного абонента можем идентифицировать, как процесс ARIMA.
Построим модель данного временного ряда, использую средства Gretl. В для моделирования модели воспользуемся моделью временного ряда ARIMA(q, ∆, p). Где q-параметр авторегрессии; ∆- величина разностей уровней ряда, p – параметр скользящего среднего. В результате подбора параметров модели, проверки их значимости, лучшей оказалась модель ARIMA(0, 1, 2) без константы.

Мы получили следующую модель временного ряда:
∆МОUt = at – 0,4136∙at-1 + at-2 (2.6)
(t) (-2,422) (2,933)
Полученную модель (2.6) можем признать удачной, все коэффициенты в модели являются статистически значимыми, в модели отсутствует автокорреляция, остатки модели стационарны и имеют нормальное распределение. Так же можем отметить, что информационные критерии Акаике и Шварца имеют лучшие значения, нежели в моделях рассмотренных нами ранее. Предшествующие модели мы не рассматриваем в данной работе, так как они имеют гораздо худшие показатели.
Произведем прогноз среднего коммерческого трафика на одного абонента на 2010 год. График прогноза представлен на рисунке 2.16.
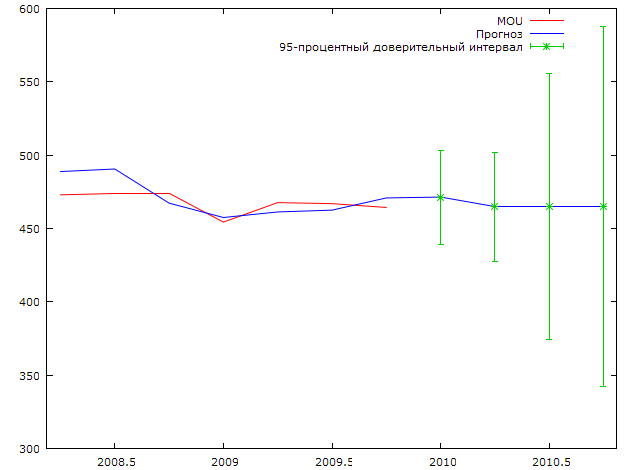
Рис 2.16. Прогноз среднего коммерческого трафика на одного абонента на 2010 год.
По полученным результатам прогноза трудно охарактеризовать значение среднего коммерческого трафика на одного абонента в следующем году, так как доверительные интервалы для прогнозируемой величины достаточно велики. С наибольшей вероятностью можем сказать, что значение среднего коммерческого трафика на одного абонента останется на уровне 2009 года. Ниже приведены прогнозные значения по полученной нами модели (2.6), а так же стандартные ошибки прогнозов и доверительные интервалы для прогнозов.
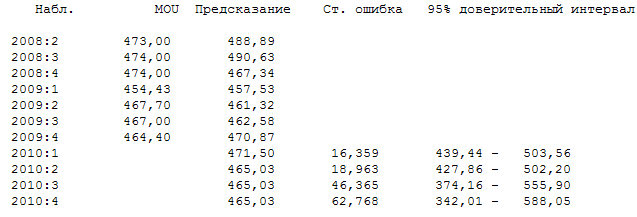
Окончательно можем сделать вывод, что временной ряд среднего коммерческого трафика на одного абонента является стационарным относительно взятия первых разностей. Модель временного ряда является процессом ARIMA.
2.1.5. Анализ временного ряда капитальных вложений.
Рассмотрим временной ряд капитальных вложений, представленный на рисунке 2.17.
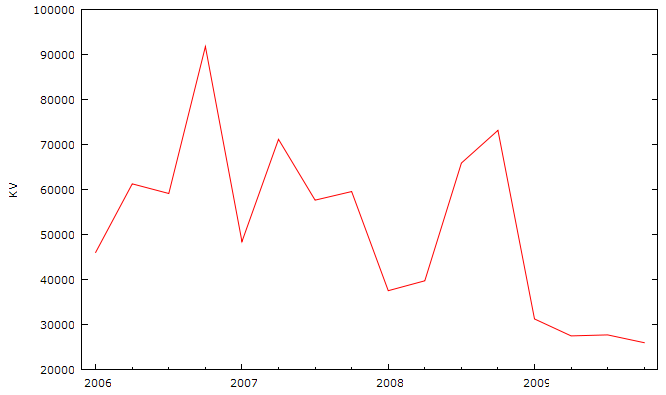
Рис. 2.17. Динамика величины капитальных вложений.
Как видно из рисунка величина капитальных вложений подвержена значительным колебаниям. Если провести воображаемую линию тренда, относительно которой происходят колебания величины капитальных вложений, то можно отметить отрицательную динамику. В 2009 году наблюдаем плавное снижение величины капитальных вложений.
Построим график первых разностей ряда капитальных вложений. График представлен на рисунке 2.18.
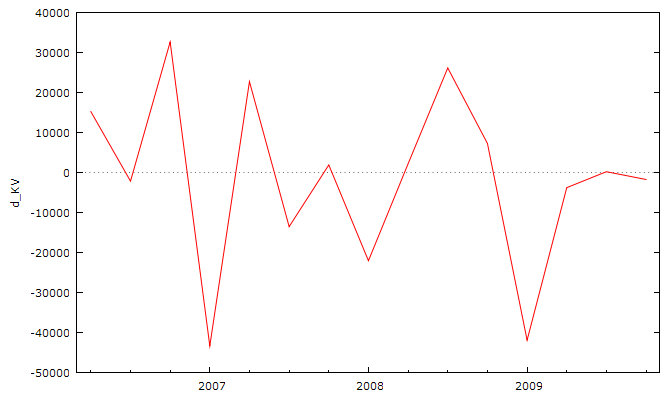
Рис. 2.18. Первые разности ряда капитальных вложений.
Как видно из графика первых разностей приросты капитальных вложений колеблются относительно нулевой линии. Отрицательные приросты капитальных вложений, сменяются положительными приростами. Наибольший отрицательный прирост наблюдается в четвертом квартале 2007 года.
Рассмотрим стационарность данных временных рядов, используя ADF-тест.
Результаты ADF-теста для уровней ряда капитальных вложений:



Как видно из результатов теста временной ряд капитальных вложений нельзя признать стационарным ни по одной из спецификаций, так как значения вероятностей принятия нулевых гипотез составляет 0,3151; 0,183; 0,0518 соответственно, что больше допустимого 0,05.
Результаты ADF-теста для первых разностей ряда капитальных вложений:

Как видно из результатов теста ряд первых разностей капитальных вложений можно признать стационарным со спецификацией без константы. Следовательно, временной ряд капитальных вложений является стационарным относительно взятия первых разностей, т. е. относится к классу DS-рядов.
Коррелограмма ряда первых разностей капитальных вложений представлена на рисунке 2.19.
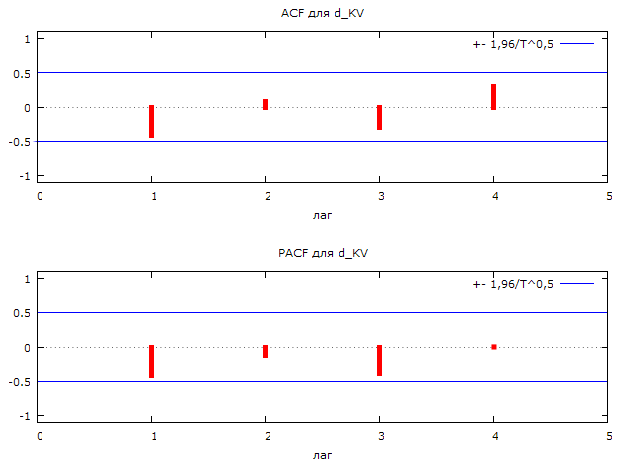
Рис. 2.19. Коррелограмма ряда первых разностей капитальных вложений.
Представим значения ACF – автокорреляционная функция и PACF – частная автокорреляционная функция:

По виду коррелограммы, ряд капитальных вложений можем идентифицировать, как процесс ARIMA.
Построим модель данного временного ряда, использую средства Gretl. В для моделирования модели воспользуемся моделью временного ряда ARIMA(q, ∆, p). Где q-параметр авторегрессии; ∆- величина разностей уровней ряда, p – параметр скользящего среднего. В результате подбора параметров модели, проверки их значимости, лучшей оказалась модель ARIMA(0, 1, 1) с константой.
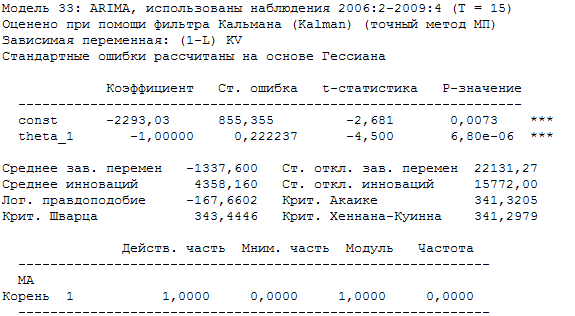
Мы получили следующую модель временного ряда:
∆МОUt = -2293 + at – at-1 (2.7)
(t) (-2,681) (-4,5)
Полученную модель (2.7) можем признать удачной, все коэффициенты в модели являются статистически значимыми, в модели отсутствует автокорреляция, остатки модели стационарны и имеют нормальное распределение. Так же можем отметить, что информационные критерии Акаике и Шварца имеют лучшие значения, нежели в моделях рассмотренных нами ранее. Предшествующие модели мы не рассматриваем в данной работе, так как они имеют гораздо худшие показатели.
Произведем прогноз капитальных вложений на 2010 год. График прогноза представлен на рисунке 2.20.
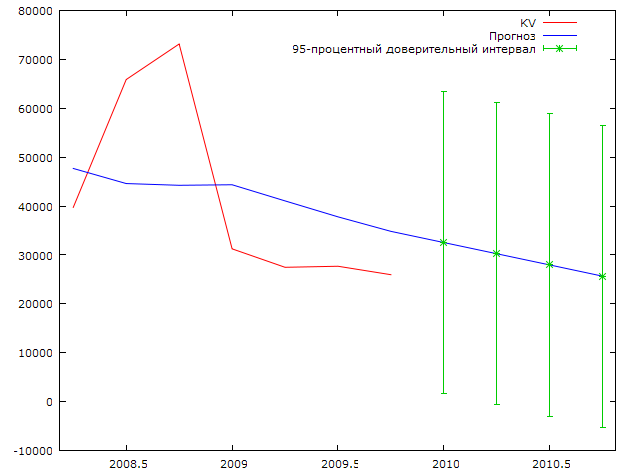
Рис 2.20. Прогноз величины капитальных вложений на 2010 год.
По полученным результатам прогноза трудно охарактеризовать величину капитальных вложений в следующем году, так как доверительные интервалы для прогнозируемой величины достаточно велики. С наибольшей вероятностью можем сказать, что величина капитальных вложений в 2010 году будет иметь тенденцию снижения. Ниже приведены прогнозные значения по полученной нами модели (2.7), а так же стандартные ошибки прогнозов и доверительные интервалы для прогнозов.
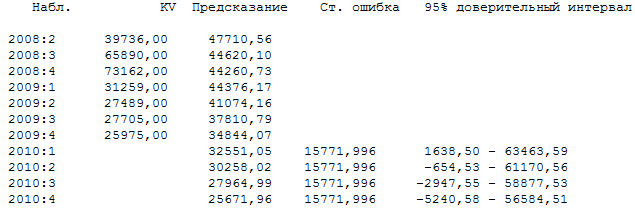
Окончательно можем сделать вывод, что временной ряд капитальных вложений является стационарным относительно взятия первых разностей. Модель временного ряда является процессом ARIMA.
Подводя итоги, проделанной нами работы в данной главе можем отметить, что рассматриваемые нами временные ряды относятся к различным классам. Временные ряды числа абонентов и выручки от реализации товаров и услуг являются стационарными. А вот ряды средней выручки на одного абонента, среднего коммерческого трафика на одного абонента и величины капитальных вложений являются стационарными относительно взятия их первых разностей, т. е. относятся к классу DS-рядов.
Следовательно, коинтегрированными будут ряды числа абонентов и величины денежной выручки, с порядком коинтегрированности I(0). Временные ряды средней выручки с одного абонента, среднего коммерческого трафика одного абонента, величины капитальных вложений будут коинтегрированы с порядком I(1).
Временной ряд величины денежной выручки мы рассматривали в белорусских рублях. Но рассмотрение данного показателя в национальной валюте не отражает реальную динамику изменения денежной выручки, так как в стране происходят не только инфляционные процессы, но и имеет место девальвация национальной валюты. Влияние данных процессов не будут учитываться, если оценивать динамику показателя денежной выручки в национальной валюте. Поэтому необходимо перейти от белорусских рублей в оценке показателя денежной выручке к мировой резервной валюте – долларам США.
Введем показатель: WRU - выручка от реализации, товаров, работ, услуг (за минусом НДС, акцизов и иных аналогичных обязательных платежей), млн. USD.
Рассмотрим временной ряд капитальных вложений, представленный на рисунке 2.21.
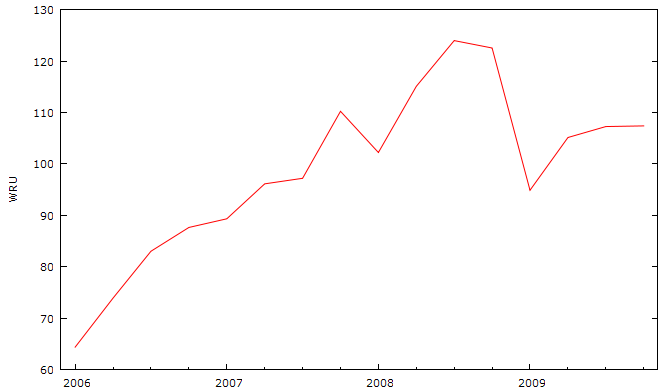
Рис. 2.21. Динамика выручки от реализации товаров и услуг.
Как видно из рисунка до третьего квартала 2008 года наблюдается положительная динамика выручки от реализации. Затем мы наблюдаем резкий спад выручки от реализации. Начиная с первого квартала 2009 года, наблюдается плавный подъем выручки от реализации. Можем отметить, что имеет место влияние финансового кризиса на результаты финансовой деятельности компании. Период высокого роста сменился падением, но несмотря на это мы наблюдаем возрастающий тренд после резкого падения.
Рассмотрим стационарность данного временного ряда, используя ADF-тест.
Результаты ADF-теста для уровней ряда капитальных вложений:



Как видно из результатов теста временной ряд выручки от реализации нельзя признать стационарным ни по одной из спецификаций, так как значения вероятностей принятия нулевых гипотез составляет 0,8585; 0,1693; 0,5438 соответственно, что больше допустимого 0,05.
Результаты ADF-теста для первых разностей ряда выручки от реализации:

Как видно из результатов теста ряд первых разностей выручки от реализации можно признать стационарным со спецификацией без константы. Следовательно, временной ряд капитальных вложений является стационарным относительно взятия первых разностей, т. е. относится к классу DS-рядов.
2.2. Исследование факторов влияния на величину денежной выручки от реализации товаров, услуг, работ.
Установим, имеет ли влияние размер абонентской базы на величину денежной выручки при реализации товаров и услуг. В предыдущем разделе мы установили, что временной ряд выручки от реализации, исчисляемый в белорусских рублях и временной ряд величины абонентской базы являются стационарными относительно линии тренда.
Построим модель регрессии в которой объясняемой переменной будет величина выручки при реализации. В результате получим следующую модель:
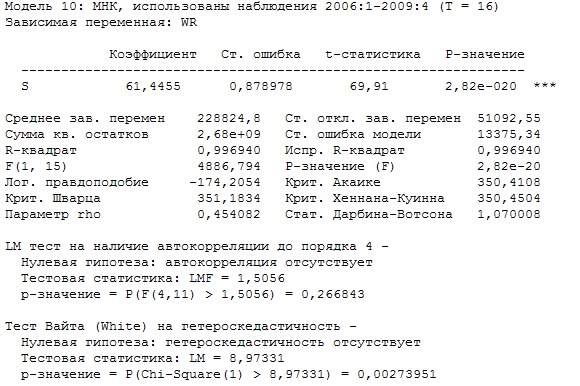
На первый взгляд мы имеем регрессионную зависимость. Но при более детальном рассмотрении, данную зависимость можем признать ложной. Тест Вайта на гетероскедастичность, подтвердил ее наличие, статистика Дарбина-Уотсона близка к единице и сравнима с значением коэффициента детерминации. Введем в полученную модель переменную тренда, в результате имеем:
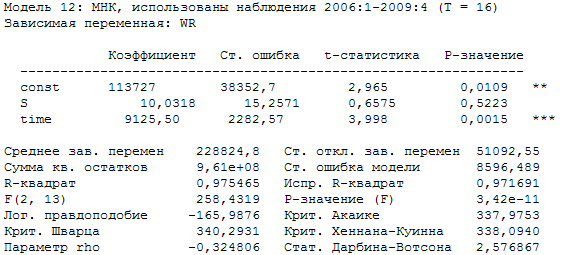
При введении переменной тренда, коэффициент регрессии при переменной величины абонентской базы оказался статистически незначимым. Это подтверждает ложную регрессионную зависимость между числом абонентов и величиной денежной выручки.
Как было установлено нами ранее, прирост величины абонентской базы равен -8,7% от величины предшествующего периода плюс постоянная, которая равна 510 тыс. абон. А прирост величины выручки от реализации составляет 4,4%. Мы имеем разные тенденции. Так же можем отметить, что величина 4,4% прироста не намного больше квартальной величины инфляции, которая примерно составляет 3%. Следовательно, реальная величина прироста будет гораздо меньше.
Обобщая, можем отметить, что величина выручки от реализации товаров и услуг не зависит от величины абонентской базы.
Далее рассмотрим другие факторы влияния на величину выручки от реализации. Временные ряды выручки от реализации в долларах США, средней выручки на одного абонента, среднего коммерческого трафика на одного абонента и величины капитальных вложений имеют порядок коинтегрированности I(1). Следовательно, на основании этих рядов можем построить модель множественной регрессии. Объясняемой переменной в нашем случае является величина выручки от реализации товаров и услуг.
В результате получим следующую модель:

Исключая незначимые переменные получаем следующую модель:
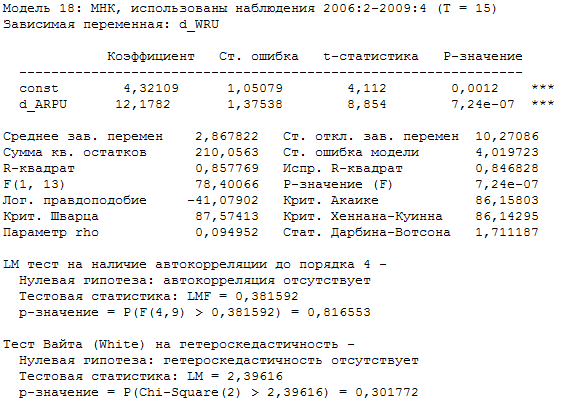
Модель можем записать в виде:
∆WRU = 4,32109 + 12,1782 ∙ ∆ARPU (2.8)
(t) (4,112) (8,854)
Все коэффициенты регрессии в полученной модели являются статистически значимыми, коэффициент детерминации имеет высокое значение и составляет 85,8%. Проведенные тесты на гетероскедастичность и автокорреляцию дали отрицательные результаты. В модели отсутствует гетероскедастичность и автокорреляция. Проверим модель (2.8) на наличие структурных изменений, для этого введем в модель фиктивную переменную d1, которая до начала 2009 года равна нулю, а сначала 2009 года равна единице.
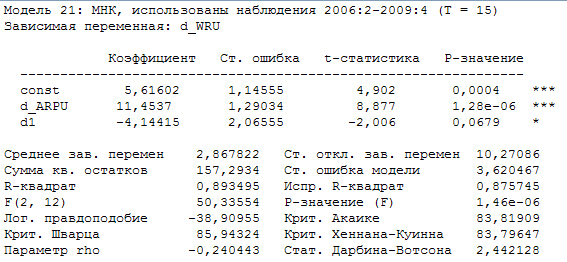
Модель можем записать в виде:
∆WRU = 5,616 + 11,4537 ∙ ∆ARPU – 4,14∙d1 (2.9)
(t) (4,902) (8,877) (-2,006)
Р-значение для включенной фиктивной переменной оказалось выше допустимого 5% уровня, следовательно, она не является статистически значимой. И структурные изменения не оказали влияния на модель. Действительно произведя тест Чоу в модели (2.8) получим тот же результат. Результаты теста Чоу модели (2.8):
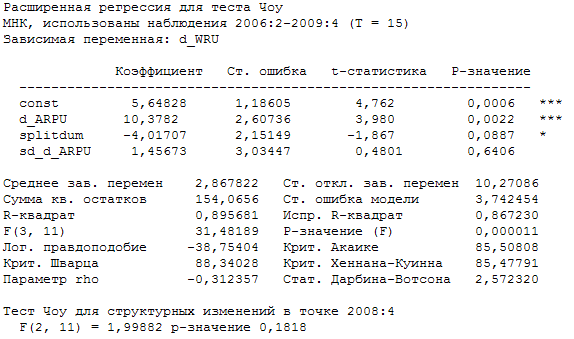
Включим в модель (2.8) переменную величины абонентской базы в результате получим следующую модель:
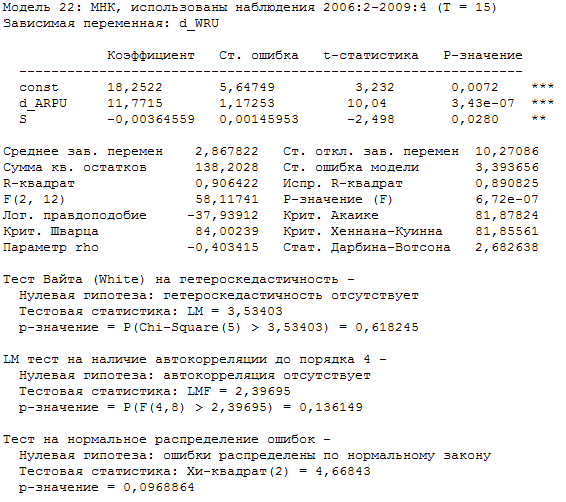
Модель можем записать в виде:
∆WRU = 18,2522 + 11,7715 ∙ ∆ARPU – 0,0036∙S (2.10)
(t) (3,232) (10,04) (-2,498)
Проведенные тесты на гетероскедастичность и автокорреляцию дали отрицательные результаты. В модели отсутствует гетероскедастичность и автокорреляция. Так же тест на нормальность распределения остатков дал положительный результат. Проведенный тест на мультиколинеарность, подтвердил её отсутствие в модели. Все коэффициенты регрессии в полученной нами модели являются статистически значимыми. Величины информационных критериев Акаике и Шварца в модели (2.10) лучше соответствующих величин критериев в модели (2.8). Исходя из этого полученную модель (2.10) можем признать наиболее удачной.
Представим на рисунке 2.22 наблюдаемые и расчетные значения прироста выручки от реализации товаров и услуг.
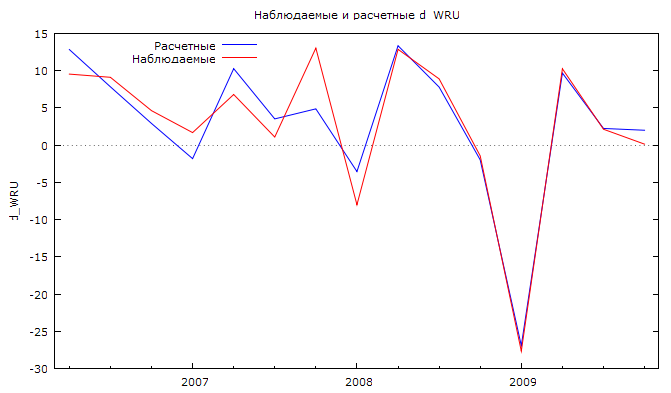
Рис. 2.22. Приросты выручки от реализации товаров и услуг (млн.USD) .
В полученной нами модели (2.10) коэффициент детерминации составляет 0,906. Это достаточно высокое значение. Следовательно, на 90,6% изменения переменной прироста денежной выручки зависит от изменения прироста денежной выручки на одного абонента и изменения величины абонентской базы, остальные 9,4% изменении обуславливаются случайными факторами, не включенными в данную модель.
Выводы.
Задачей расчетного раздела является выявление тенденций развития наиболее крупного из мобильных операторов в республике, СООО «Мобильные ТелеСистемы», и установление приоритетных направлений развития данного оператора. Для анализа мы взяли квартальные финансовой отчетности, представленные на официальном сайте компании.
Взятые нами данные представляют собой временные ряды. В первом подразделе расчетной части проекта мы рассмотрели отдельно каждый из временных рядов рассматриваемых показателей финансовой отчетности компании. Задачей данного раздела было выявление тенденции каждого из временных рядов, установление стационарности ряда, т. е. определение класса ряда DS или TS, для дальнейшей их коинтеграции при построении моделей множественной регрессии. Так же построение модели временного ряда с целью дальнейшего прогнозирования.
Ряд величины абонентской базы имеет четко выраженный линейный тренд, исходя из графического анализа, скорость роста абонентской базы можно считать постоянной. Особого внимания заслуживает тот факт, что мировой финансовый кризис никак не повлиял на развитие абонентской базы.
Временной ряд абонентской базы является стационарным. Модель временного ряда представляет собой процесс AR – процесс авторегрессии.
В результате моделирования временного ряда мы получили следующую аторегрессионную модель:
St = 510,7 + 0,903∙St-1,
Которую можем записать в виде:
∆St = St – St-1 = 510,7 + 0,903∙St-1 – St-1 = 510 – 0,087∙ St-1
По полученной модели можем сказать, что с каждым последующим кварталом прирост числа абонентов уменьшается, пропорционально значению абонентской базы предшествующего периода, с коэффициентом пропорциональности -0,087. По данной модели мы можем получить максимальное число абонентов, до которого может расти величина абонентской базы.
После достижения компанией абонентской базы в размере 5862 тыс. чел. будет наблюдаться равновесное состояние абонентской базы. Действительно, при уменьшении значения St-1, будет увеличиваться значение прироста и наоборот.
По результатам прогноза можем сказать, что положительная динамика абонентской базы в 2010 году сохраниться, однако величины ежемесячных приростов будут меньше. К концу года величина абонентской базы может достигнуть значения 4860,5 тыс. чел. Данная величина не превышает критическую, поэтому в 2011 можем так же рассчитывать на прирост абонентской базы.
Ряд выручки от реализации в белорусских рублях имеет четко выраженный временной тренд, т. е. значения выручки от реализации колеблются от воображаемой линии тренда. Особого внимания заслуживает тот факт, что мировой финансовый кризис никак не повлиял на развитие абонентской базы.
Временной ряд абонентской базы является стационарным. Модель временного ряда представляет собой процесс AR – процесс авторегрессии.
В результате моделирования временного ряда мы получили следующую аторегрессионную модель:
WRt = 1,044∙WRt-1
Так же модель можем записать в виде:
∆WRt = WRt – WRt-1 = 1,044∙WRt-1 – WRt-1 = 0,044∙ WRt-1
По полученной модели можем сказать, что с каждым последующим кварталом прирост выручки от реализации товаров и услуг увеличивается на 4,4% по сравнению с выручкой предшествующего периода. Однако если рассматривать реальную выручку, т. е. с учетом инфляции, то реальные темпы прироста окажутся гораздо меньшими, если взять квартальный темп инфляции 3%, то реальный прирост составит 1%.
По результатам прогноза можем сказать, что положительная динамика выручки от реализации товаров и услуг в 2010 году сохраниться. К концу года величина выручки от реализации может достигнуть значения 361448 млн. р.
Ряд средней выручки на одного абонента не имеет временного тренда. Значения ряда колеблются вокруг некоторой константы. В третьем квартале 2008 года наблюдаем резкое снижение выручки на одного абонента. Данное резкое снижение можем связать с влиянием глобального экономического кризиса. Затем наблюдаем незначительный подъем средней выручки на одного абонента. Т. е. можем отметить, что компания приспособилась к новым условиям видения бизнеса.
Можем сделать вывод, что временной ряд средней выручки на одного абонента является стационарным относительно взятия первых разностей, т. е. относится к классу DS-рядов. Модель временного ряда является процессом MA, скользящего среднего.
По полученным результатам прогноза трудно охарактеризовать значение средней выручки на одного абонента в следующем году, так как доверительные интервалы для прогнозируемой величины достаточно велики.
Для ряда среднего коммерческого трафика на одного абонента можем отметить, что до начала 2008 года ряд имеет положительную динамику, средний коммерческий трафик имеет тенденцию роста. А вот с начала 2008 года наблюдается отрицательная динамика, происходит снижение среднего коммерческого трафика.
Можем сделать вывод, что временной ряд среднего коммерческого трафика на одного абонента является стационарным относительно взятия первых разностей, т. е. относится к классу DS-рядов. Модель временного ряда является процессом MA, скользящего среднего.
По полученным результатам прогноза трудно охарактеризовать значение среднего коммерческого трафика на одного абонента в следующем году, так как доверительные интервалы для прогнозируемой величины достаточно велики. С наибольшей вероятностью можем сказать, что значение среднего коммерческого трафика на одного абонента останется на уровне 2009 года.
Величина капитальных вложений подвержена значительным колебаниям. Если провести воображаемую линию тренда, относительно которой происходят колебания величины капитальных вложений, то можно отметить отрицательную динамику. В 2009 году наблюдаем плавное снижение величины капитальных вложений.
Можем сделать вывод, что временной ряд величины капитальных вложениий является стационарным относительно взятия первых разностей, т. е. относится к классу DS-рядов. Модель временного ряда является процессом MA, скользящего среднего.
По полученным результатам прогноза трудно охарактеризовать величину капитальных вложений в следующем году, так как доверительные интервалы для прогнозируемой величины достаточно велики. С наибольшей вероятностью можем сказать, что величина капитальных вложений в 2010 году будет иметь тенденцию снижения.
Подводя итоги, проделанной нами работы в данной главе можем отметить, что рассматриваемые нами временные ряды относятся к различным классам. Временные ряды числа абонентов и выручки от реализации товаров и услуг являются стационарными. А вот ряды средней выручки на одного абонента, среднего коммерческого трафика на одного абонента и величины капитальных вложений являются стационарными относительно взятия их первых разностей, т. е. относятся к классу DS-рядов.
Следовательно, коинтегрированными будут ряды числа абонентов и величины денежной выручки, с порядком коинтегрированности I(0). Временные ряды средней выручки с одного абонента, среднего коммерческого трафика одного абонента, величины капитальных вложений будут коинтегрированы с порядком I(1).
Временной ряд величины денежной выручки мы рассматривали в белорусских рублях. Но рассмотрение данного показателя в национальной валюте не отражает реальную динамику изменения денежной выручки, так как в стране происходят не только инфляционные процессы, но и имеет место девальвация национальной валюты. Влияние данных процессов не будут учитываться, если оценивать динамику показателя денежной выручки в национальной валюте. Поэтому необходимо перейти от белорусских рублей в оценке показателя денежной выручке к мировой резервной валюте – долларам США.
Во второй главе расчетной части работы мы производили эконометрический анализ изменения величины выручки от реализации товаров и услуг с целью установления факторов влияния на динамику данной величины. Для этого мы рассмотрели несколько моделей множественных регрессий, построенных по вышерассмотренным временным рядам, с учетом их коинтеграции.
В результате моделирования и выбора наилучшей модели мы пришли к зависимости: ∆WRU = 18,2522 + 11,7715 ∙ ∆ARPU – 0,0036∙S.
В полученной нами модели (2.10) коэффициент детерминации составляет 0,906. Это достаточно высокое значение. Следовательно, на 90,6% изменения переменной прироста денежной выручки зависит от изменения прироста денежной выручки на одного абонента и изменения величины абонентской базы, остальные 9,4% изменении обуславливаются случайными факторами, не включенными в данную модель.
Прирост средней выручки на одного абонента имеет положительное влияние на значение результативного признака, при положительном приросте средней выручки на одного абонента мы имеем положительный прирост общей выручки от реализации. А вот величина абонентской базы имеет отрицательное влияние на значение результативного признака, при увеличении величины абонентской базы, мы наблюдаем уменьшение прироста общей выручки от реализации. Действительно, при увеличении прироста средней денежной выручки на одного абонента на 1 USD, значение прироста всей денежной выручки возрастет на 11,7715 млн. USD, при неизменности показателя абонентской базы. При увеличении абонентской базы на 1 тыс. абон., значение прироста выручки от реализации сократиться на 0,0036 млн. USD, при неизменности показателя прироста средней выручки на одного абонента.
Обобщая вышесказанное, можем отметить дальнейшее увеличение величины абонентской базы, не приведет к приросту выручки от реализации товаров и услуг. Т. е. величина абонентской базы достигла некоторого порога насыщения и дальнейшее увеличения числа абонентов не приведет к увеличению выручки от реализации. На конец 2009 года величина абонентской базы составляла 4,653 млн. – это практически половина населения страны. Полученная нами выше, при моделировании временного ряда абонентской базы, цифра 5,8 млн. характеризует максимально возможное число абонентов компании, при превышении данной цифры временной ряд скорректирует данный прирост. Поэтому мы можем ориентироваться на цифру 5,8 млн. чел., выше которой величина абонентской базы подняться не сможет. Теоретически мы имеем запас в 1,2 млн. человек, на который может увеличиться величина абонентской базы.
Единственный путь увеличения выручки от реализации товаров и услуг – это увеличение средней денежной выручки с одного абонента. Увеличение средней денежной выручки с одного может быть достигнута за счет предоставления абоненту дополнительных услуг. В данном случае становится актуальной тема высокоскоростного мобильного интернета по новой технологии 3G. Это новый сегмент услуг, которые могут оказывать мобильные операторы, данный вид связи позволяет предоставлять такие услуги как видео-звонки, мобильное интернет телевидение. С развитием данной технологии мобильный интернет может конкурировать с проводным интернетом, цены на который достаточно высоки по сравнению с развитыми европейскими странами. Т. е. со временем мобильный интернет может потеснить на рынке интернет стационарный. Поэтом в данный момент тема мобильного интернета актуальна для всех мобильных операторов.
