Лекция какая-то…

Вид материала

Лекция

Содержание Оценивание параметрических моделей. Оценивание спектров и частотных характеристик

Подобный материал:

• Тема 7 / Topic 7, 508.88kb.
• Лекции по истории русской литературы ХХ века. (40-е 90-е гг.) Война и свобода в «Книге, 315.61kb.
• Исследование художественного текста и, в частности, текста поэтического, никогда, 368.95kb.
• Психологические типы профессий /По Е. А. Климову, 224.46kb.
• Произведения для заучивания наизусть в 10 классе, 8.33kb.
• «Социальная стратификация и социальная мобильность», 46.19kb.
• Организация ЭВМ, 791.74kb.
• Войтеховского Даниила «Кто лучше?», 6kb.
• Вкакой памяти сохраняются программы bios? Какая информация сохраняется в энергонезависимой, 5.13kb.
• Широкая, быстрая река Кубань течёт через весь Краснодарский край. Поэтому край наш, 22.72kb.

Лекция какая-то…


Ставится задача определить след. Характеристики случайной величины x:

1. Мат. Ожидание
   
2. Дисперсию
   

Использование строгого определения величин см. слайд 8 – как правило невозможно, т.к. не известна функция распределения, поэтому на практике довольствуются оценкам, здесь и далее для оценки – символ с крышечкой Один из возможных методов указанных величин – слайд 12. Используется N независимых наблюдений. Называются – выборочная средняя и выборочная дисперсия. Подстрочный индекс говорит о том, что оценка смещенная (см. далее). N это размер выборки.


Свойства для установления качества оценки статистических величин:

1. Желательно чтобы оценка обладала свойством несмещенности. Несмещенной называется оценка, мат ожидание которой равно оцениваемому параметру. Например, мат. Ожидание среднего = самому среднему, кот характерно для данного процесса.
   
2. Оценка должна быть эффективной. Средне квадратическая ошибка оценки должна быть наименьшей из всех возможны оценок.
   
3. Оценка должна быть состоятельной.
   

Оценка должна сходиться к оцениваемому параметру с вероятностью стремящейся к единице по мере увеличения размера выборки. Можно показать, что оценка среднего по указанной выше формуле на сладе 12 не смещена состоятельно и эффективно, обладает всеми необходимыми качествами. Оценка дисперсии – проблемы, она состоятельна, но смещена. Для получения несмещенной, используют видоизмененную формулу





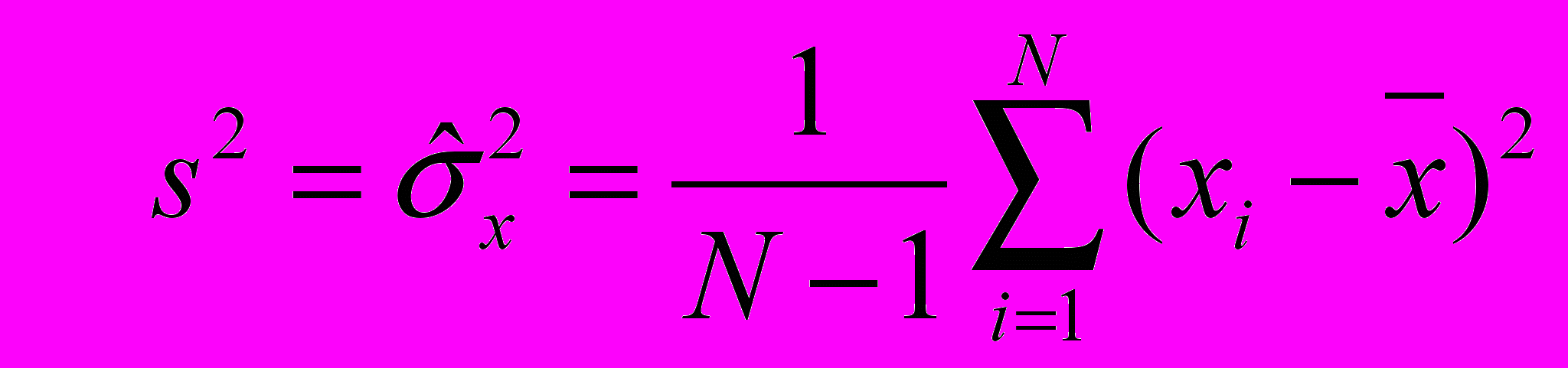
Формулы для оценки стационарны случайных процессов, в отличие от предыдущих формул – оцениваются одновременно протекающие процесса, минимум два - процесс X и Y.






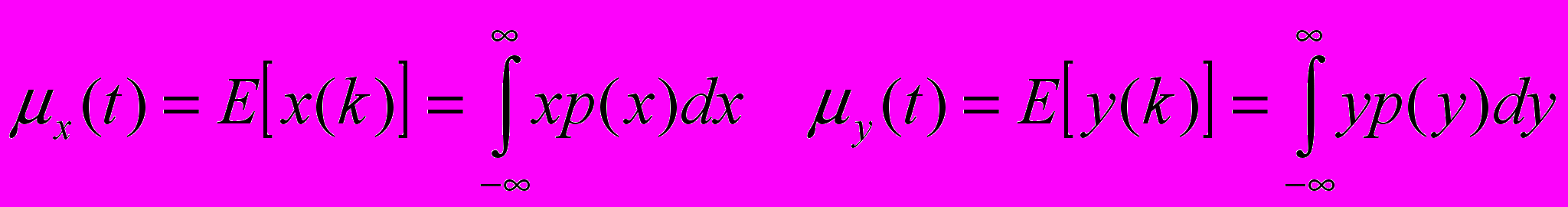
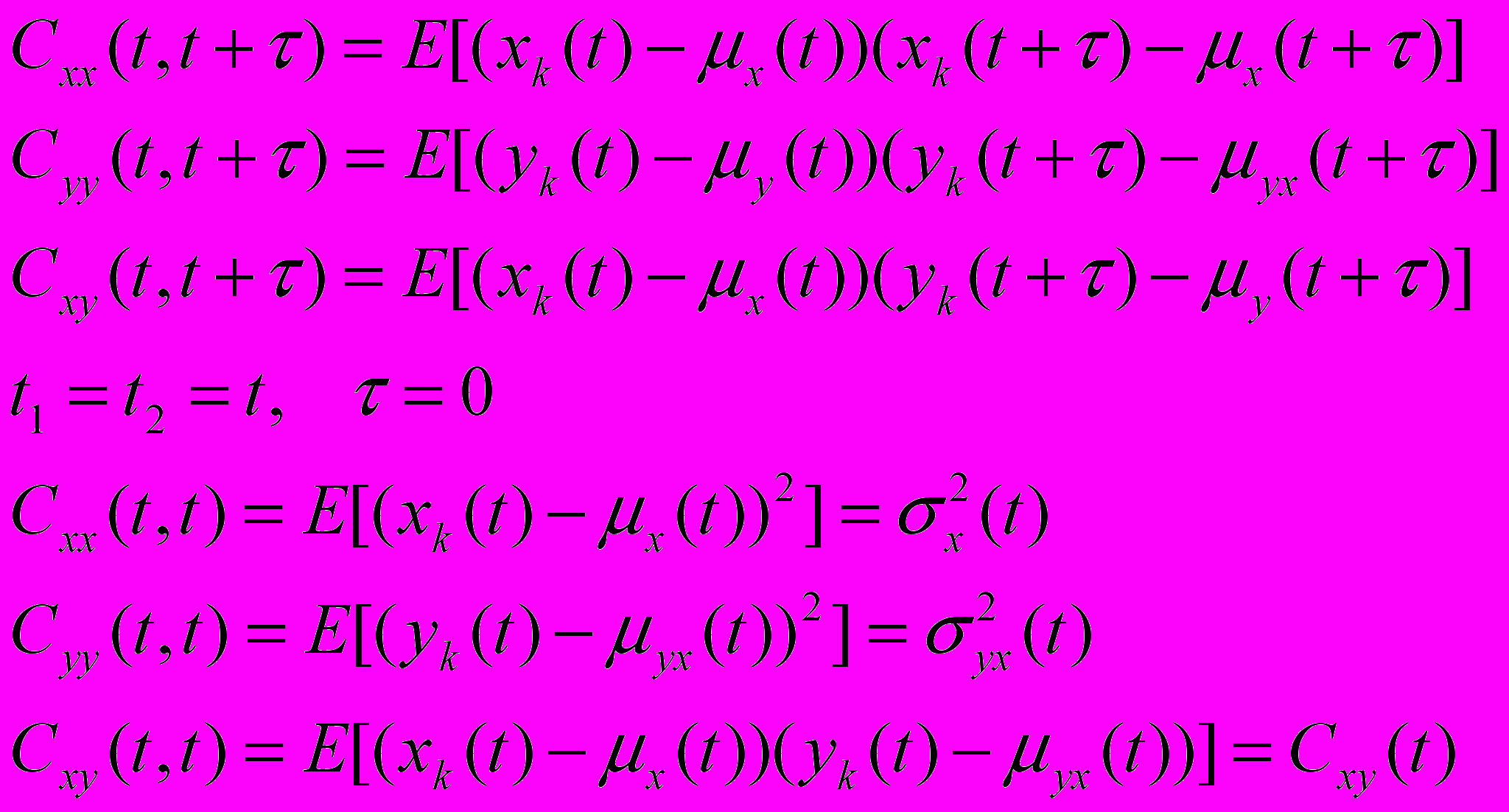
Первые три формулы – набор корреляционных функций. Если рассматриваем внутри одного процесса – “автокорреляционные”.


Для стационарных процессов ковариационные функции:




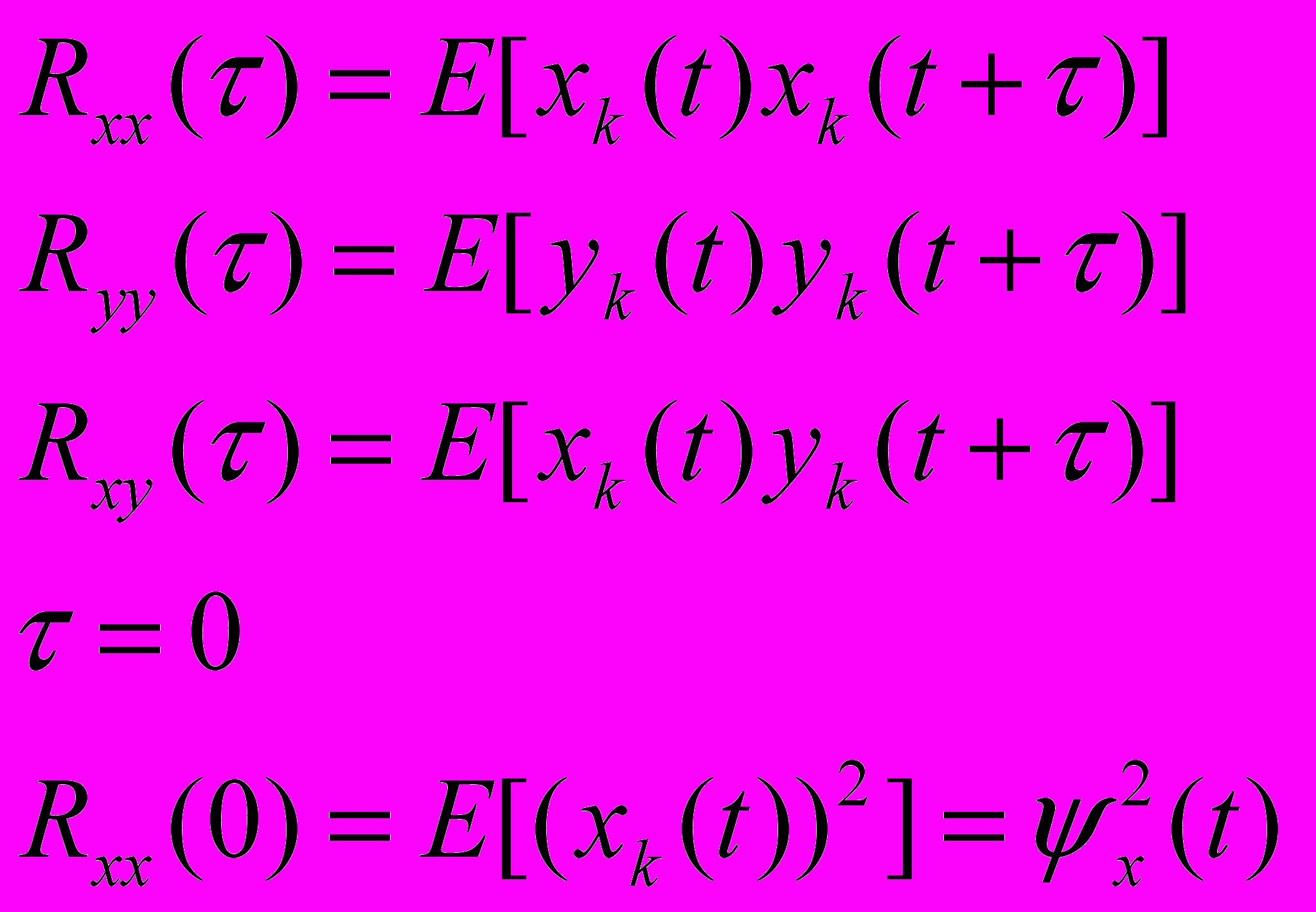
Два процесса называются некоррелированными, если корреляционная функция равняется нулю для всех сдвигов t (тау). Корреляционная функция стационарного процесса показывает меру зависимости его значений, сдвинутых относительно друг друга на определенный интервал времени. Практическая оценка корреляционной функции выполняется следующим образом – рассматривается … , сдвигается на величину сдвига …, перемножается на … и полученное произведение усредняется по всей реализации или по её отрезку.


Спектральная плотность


Выполнить оценки величин рассогласования между сигналами первичной модели и сигналами, полученными по результатам идентификации этой модели и добиться того, чтобы ошибка этого стремилась к минимуму -= решить задачи минимизации ошибки критерия качества.


Оценивание параметрических моделей.


Метод прогноза ошибок.


Модель исследуемого объекта имеет вид обобщенной линейной модели:





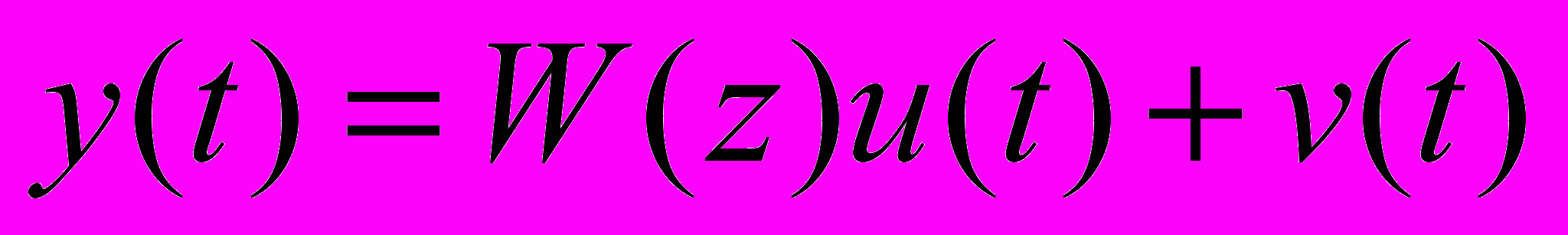
u(t) – входное воздействие

v(t) – шум процесса. Может быть получен из сигнала дискретного белого шума e(t) путем пропускания его через формирующий фильтр h(z). Будем интерпретировать величину e как ошибку оценивания и с первой и второй формул получим формулу для этой ошибки оценивания. Критерий качества для нашей системы – квадратичный. W(N).

Пытаемся определить оценку правильности полученных в результате процедуры идентификации передаточных функций W и H. Оценки получаются в результате решения задачи минимизации.





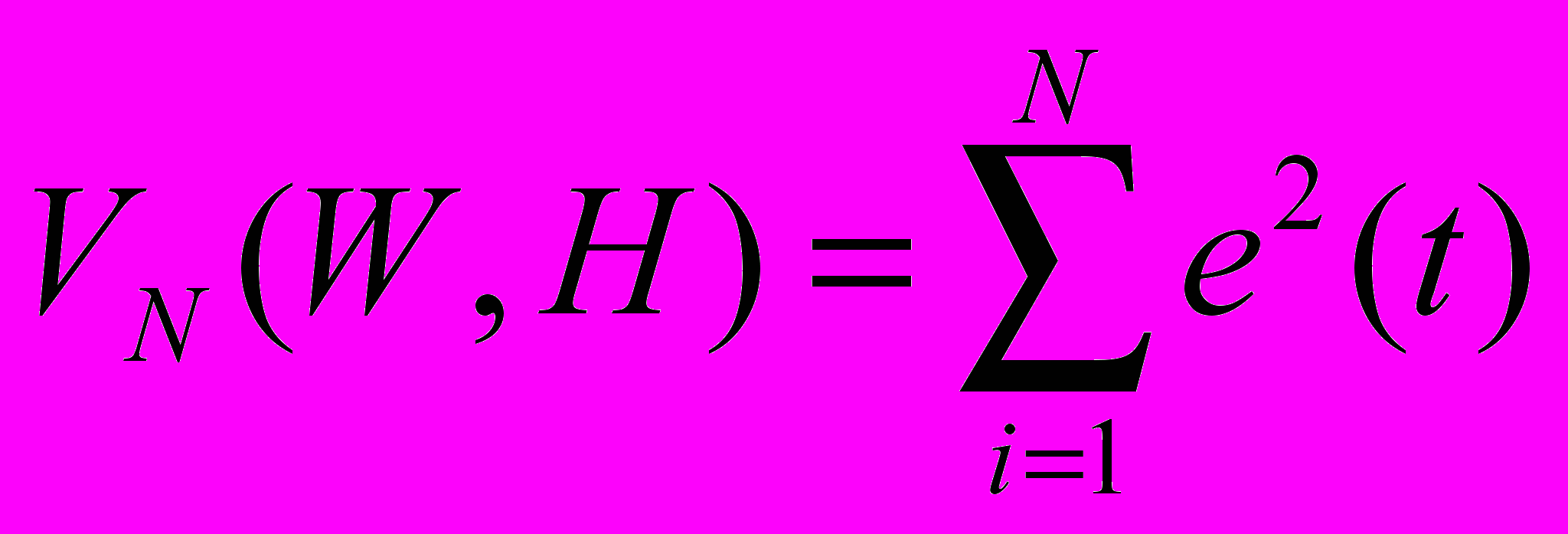
решение такой задач путем применения методов линейной оптимизации весьма трудоемко, ещё более сложной является процедура для линейных моделей, поэтому на практике задачу оценивания решают для модели достаточно простых структур и следующее оценивание импульсных характеристик.


Предполагается что входной сигнал имеет нулевое математическое ожидание и является дискретным белым шумом. Тогда автокорреляционная функция процесса записывается:





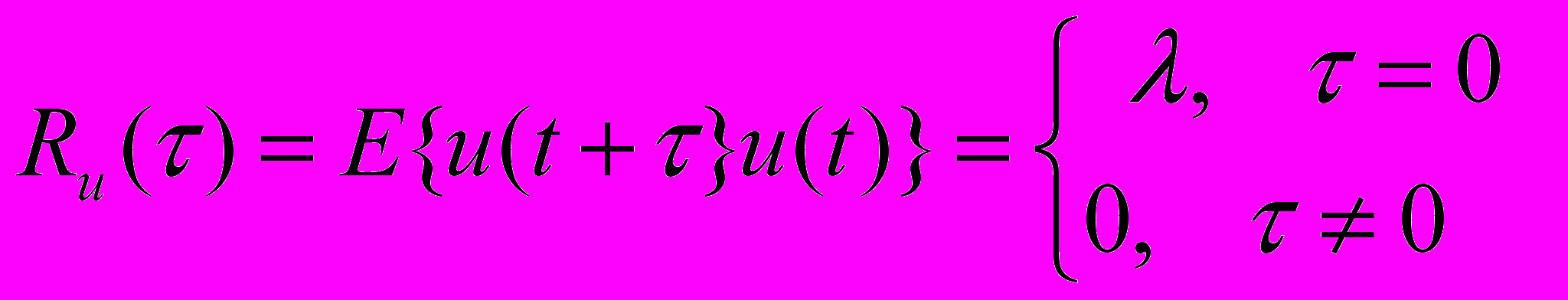
Лямбда – интенсивность сигнала.


Предполагается, что наш входной сигнал не коррелирован с сигналом шума или ошибки E(t):





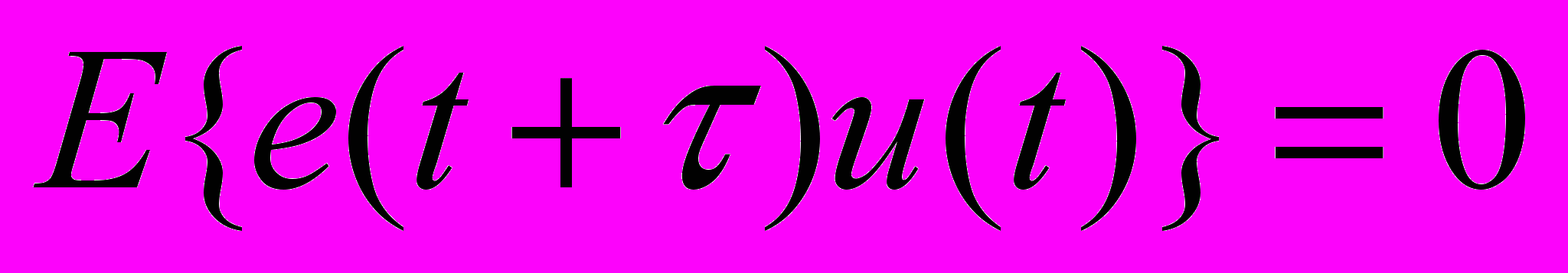
Тогда воспользуемся уравнение свертки, запишем дискретный аналог этого уравнения и рассмотрим установившийся режим. Выходной сигнал при этих условиях:





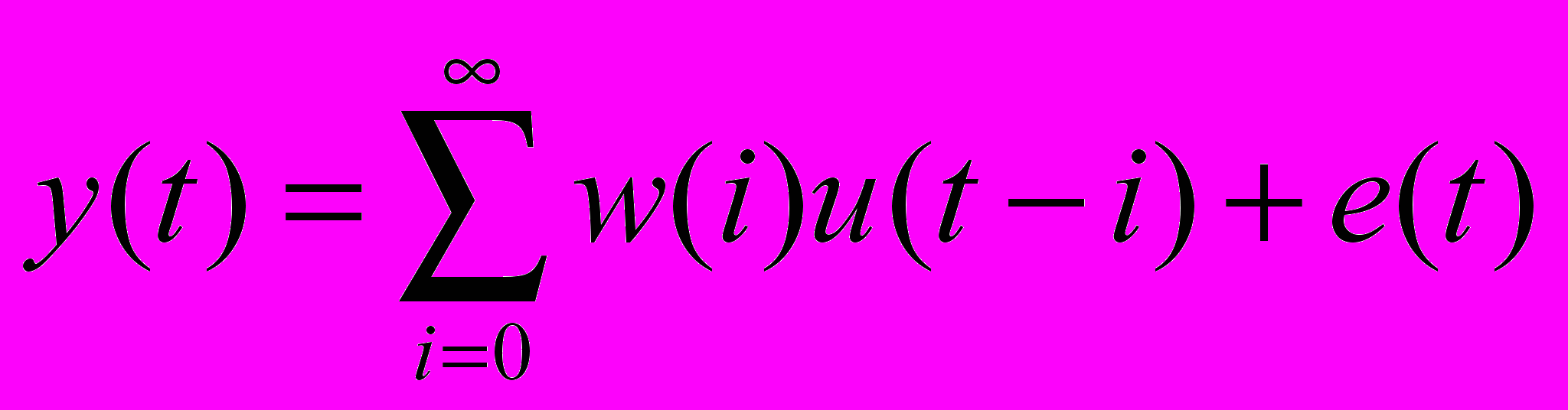
Попробуем рассчитать ковариционную функцию двух процессов: С учетом принятого положения можно показать, что R равно:







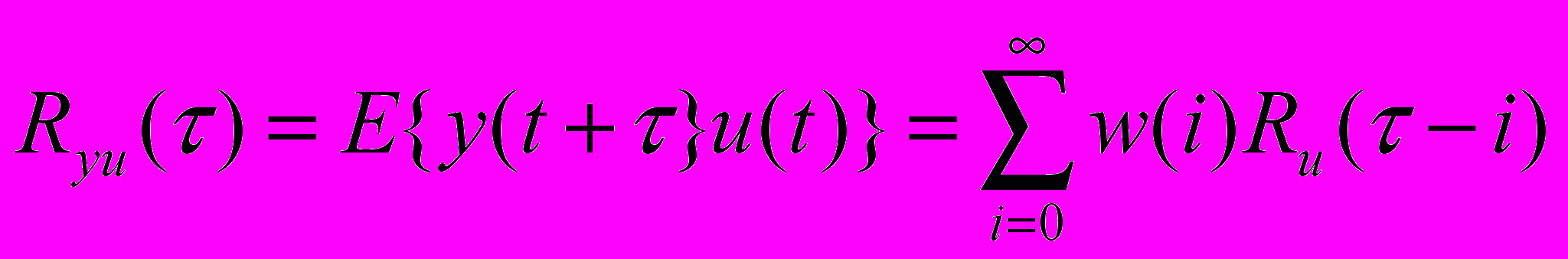
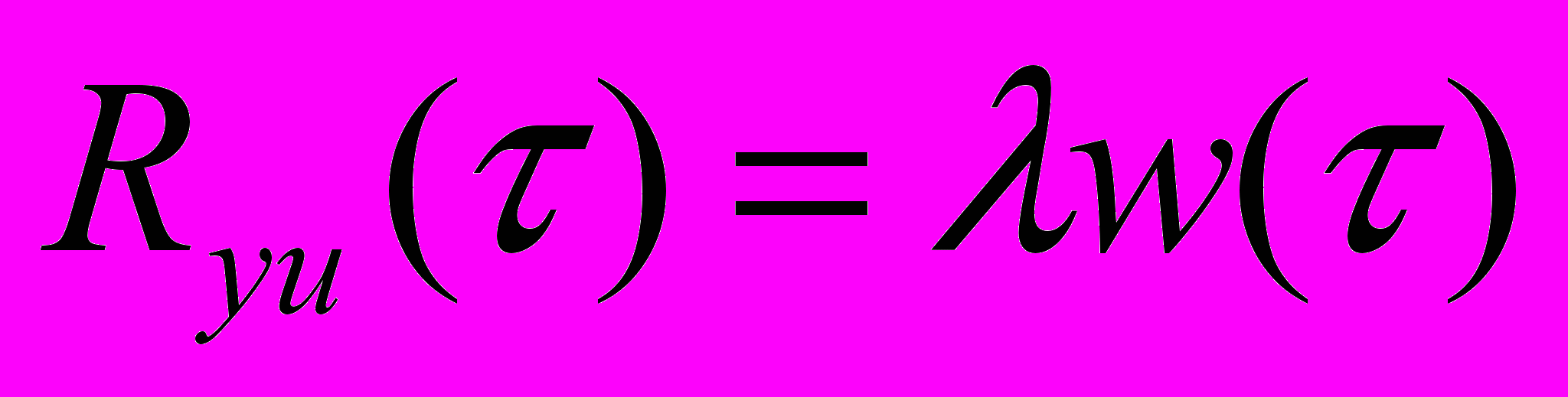
Сама оценка:





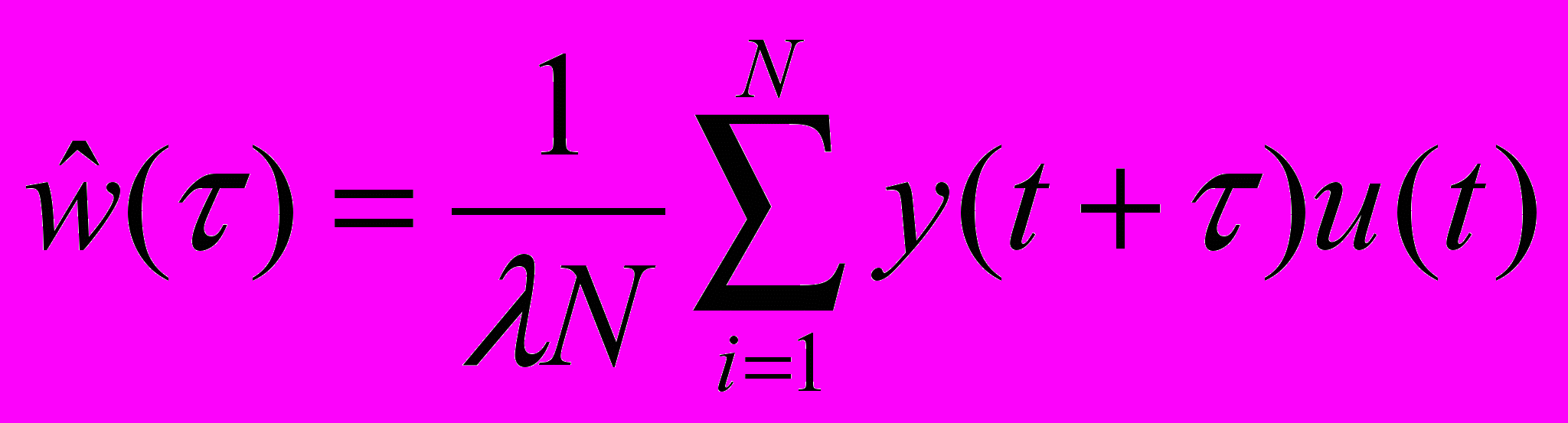
Сумма в правой части представляет собой оценок взаимной корреляционной функции сигналов Y и U, выполненную по выборкам измерения Y и U. Указанную формулу можно использовать и в том случае, когда сигнал не является.


Оценивание спектров и частотных характеристик


Центральным понятием – понятие спектральных плотностей сигналов. Прикладной задачей является;

1. генерация сигналов заданной спектральной плотностей
   
2. Оценка
   

11.11.09 - лекция


Спектральный анализ


Основной задачей спектрального анализа является выявление гармонического спектра исследуемого сигнала, т.е. определение частот отдельный гармоник, кот в совокупности составляют исследуемый сигнал.


Выделяют:


амплитудный спектр – частотный спектр

фазовый спектр


Спектральный анализ используется не только по своему прямому назначению, но и как средство решения других задач моделирования таких как идентификация систем. В основе спектрального анализа лежит принципиальная возможность преобразования информации о системе полученной во временной области представлению этой системы в частотной области. Фактически мы получаем частотную характеристики системы, имея её временную реализацию. В связи с этим очевидно использование теории Фурье, которую успешно использовали для получения обычных ЧХ.


Методы спектрального анализа, очевидно, более широкие по сравнению с методикой получения характеристик обычных систем. Эти методы позволяют извлекать информацию о частотных составляющих, или наборов частот для сигналов произвольной формы. Самым простым случаем является гармонический сигнал в детерминированной постановке, т.е. сигнал, не имеющий случайных составляющих.


Гармонический сигнал является частным случаем периодического процесса. Может представлять собой сумму гармоник. Идеи, которые первоначально лежали в основе расчета частотных характеристик для периодических и других сигналов послужили основой для исследования сигналов произвольного вида.


В основе спектрального анализа лежит теория Фурье о разложении любого апериодического процесса с периодом T в бесконечную, но счетную сумму гармонических составляющих.


Любой периодический процесс может быть представлен в виде ряда Фурье:


Получение временной последовательности по информации о гармониках с индексом





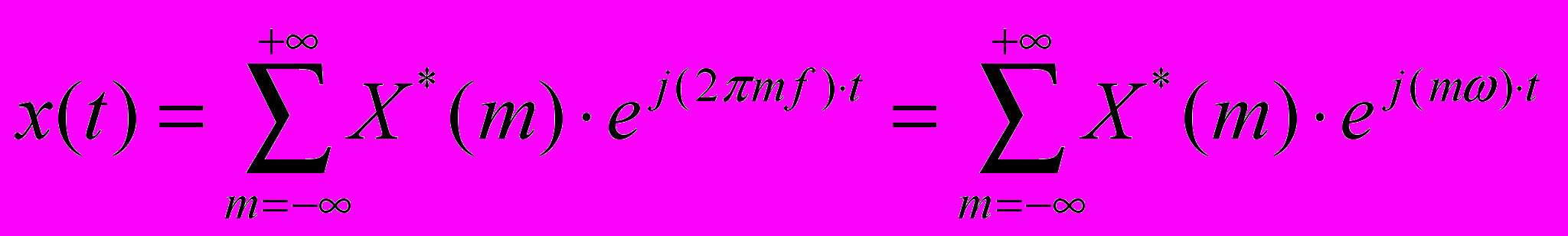
m – число гармоник

X*(m) - комплексные амплитуды гармонических составляющих


Получение отдельных гармоник по результатам исследования




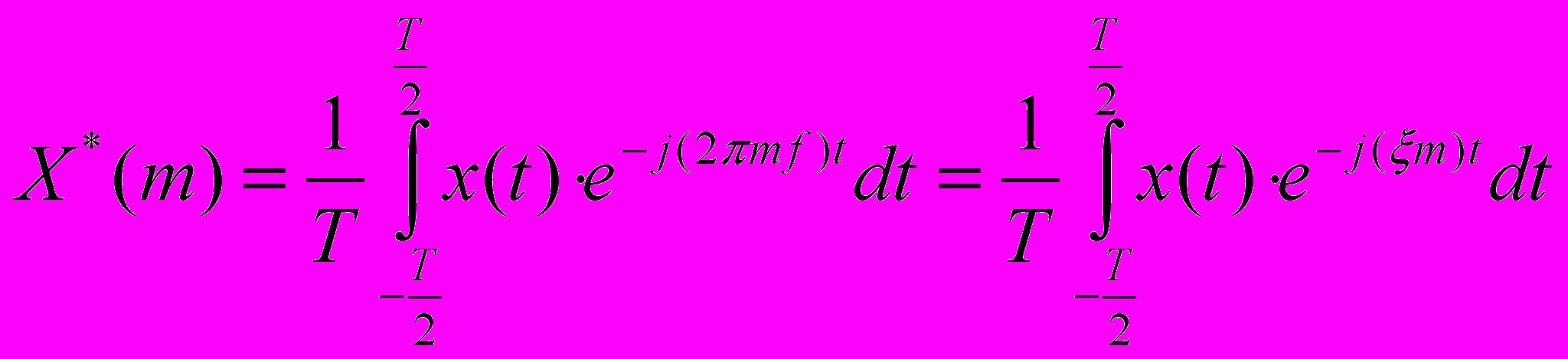
Частотный спектр периодического сигнала состоит из частот кратных базовой частоте f


f – базовая частота





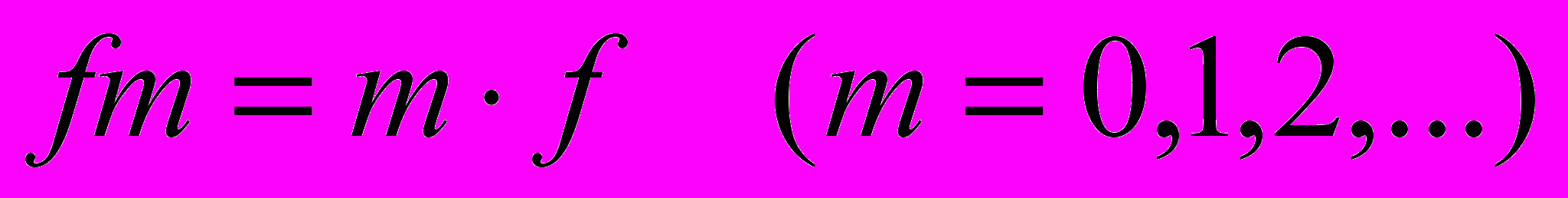
Поскольку в формуле 2 определяется комплексная амплитуда, в общем случае амплитуда является комплексным числом, мы можем выделить действительные и мнимые части этих амплитуд. Если мы соберем отдельно действительные части, получим действительный спектр сигнала. Собрав мнимые части – получим мнимый спектр периодического сигнала.


Комплексное число может быть представлено в форме экспоненты:





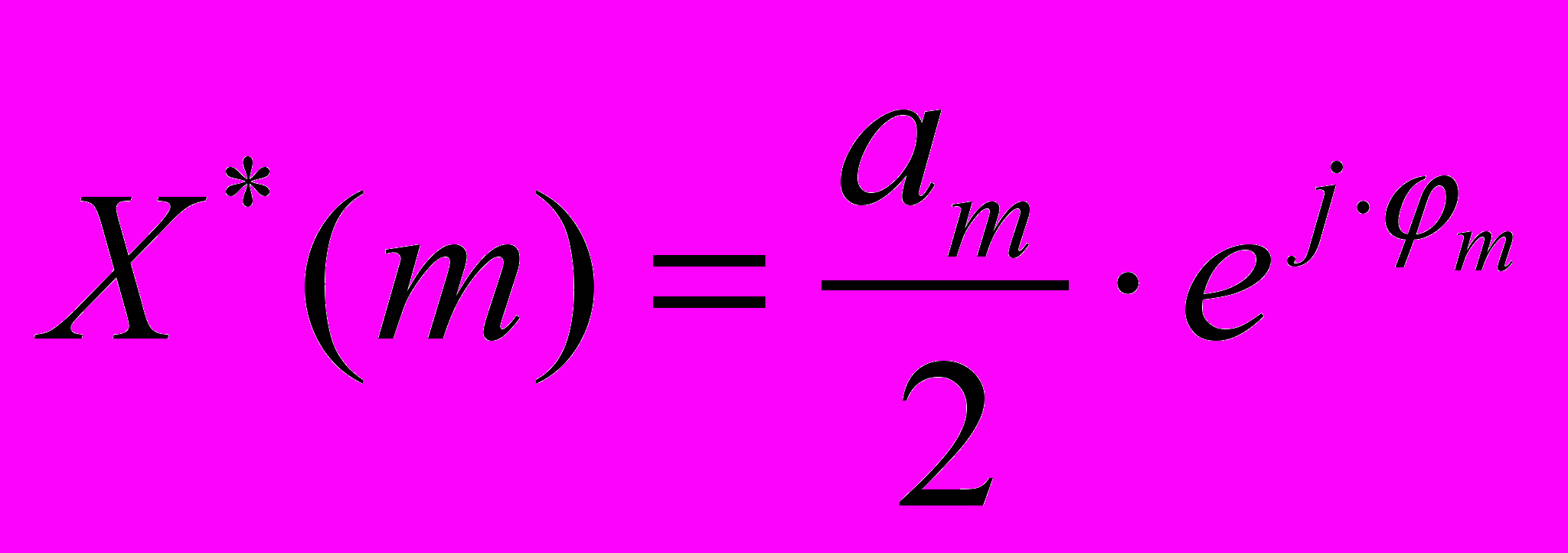
Am – амплитуда гармонической составляющей, относящейся к fm

ФИm – начальная фаза гармоники


Принято гармонический процесс описывать в виде косинусоиды;




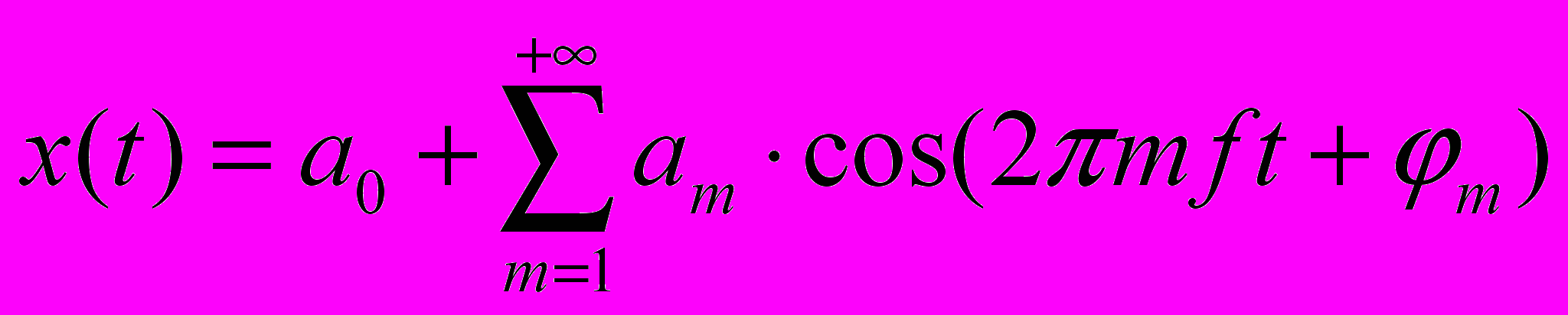
это и есть ряд Фурье


Если процесс по своей физической сути действителен, то:





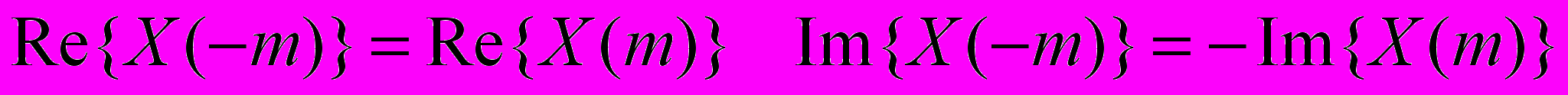
Действительная часть спектра – четная функция частоты


Мнимая часть спектра – нечетная функция частоты


2 и 5 позволяют рассматривать совокупность амплитуд как изображение периодического процесс в частотной области


Следующий шаг – желание распространить методы первоначально сформулированные для периодического процесса к процессам произвольного вида, в т.ч. непериодические.


Для этого вводится понятие Фурье изображения:





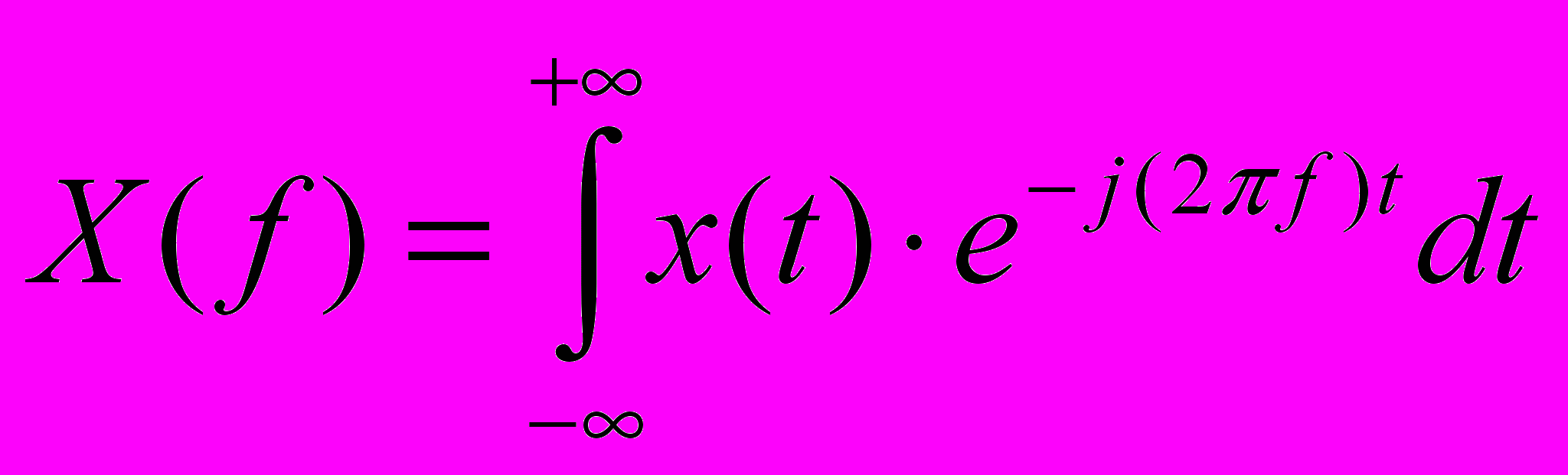
Сравним Фурье изображение по указанной формуле с изображением 2 для комплексных коэффициентов. Можно выявить отличия:

1. Физическая размерность комплексной амплитуды совпадает с размерностью самой величины. ….что-то там… умноженное на время
   
2. Интеграл Фурье изображения существует, т.е. является сходящимся к конечной величине только для так называемых двусторонне сходящихся процессов, т.е. процессов, которые затухают как при t-> бесконечности, так и минус бесконечности. Этот метод нельзя применять к стационарным или автоколебаниям.
   

Для Фурье изображения существует обратное преобразование


Очевидно что обратное преобразование представляет собой некий аналог комплексного ряда Фурье периодического процесса. Поскольку на практике наблюдения ведутся на конечном интервале времени, и сам процесс задается в ограниченном числе точек, несколько смягчается проблема сходимости рассматриваемого интеграла.


Последние две формулы, соответствующие прямому и обратному Фурье изображению для практических нужд подвергаются дискретизации – получаем дискретные аналоги дискретных изображений. Область непрерывного изменения частот мы заменяем набором дискретных частот в узловых точках. В простейшем случае мы используем равномерную сетку, так что точки на оси частот отличаются друг от друга на величину дельта f, тогда вместо вычисления интеграла Фурье изображения мы рассчитываем сумму:





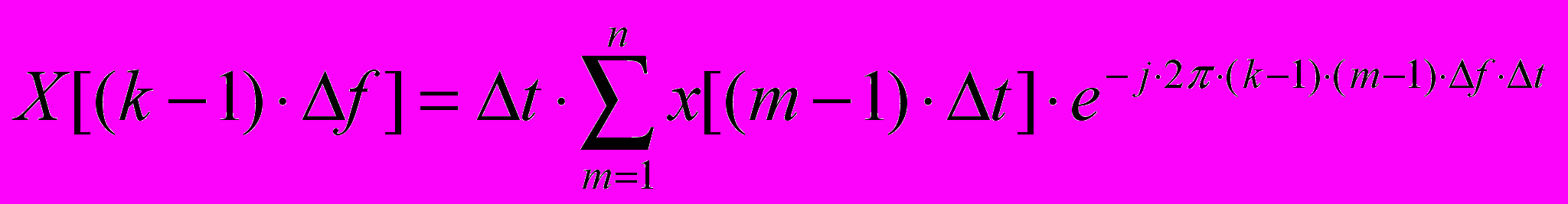
В формуле дискретного аналога Фурье изображения осуществляются следующие замены:

1. непрерывный интеграл заменяется ограниченно суммой площадей прямоугольников, одна из сторон прямоугольника = дельта t, вторая – мгновенному значению процесса в данный момент времени.
   
2. Непрерывное время заменено дискретными значениями в номере m – точки от начала процесса
   
3. Непрерывные значения частоты заменены дискретными значениями. Дельта f – приращение частоты, величина обратная 1/T. T – период или промежуток времени на котором задан процесс.
   
4. Дифференциал по времени dt заменен дискретным значением времени
   

25.11 Цифровая обработка сигналов: синтез фильтров.


Общая цель разработки фильтров (аналоговых или цифровых) – обеспечение частотно-зависимого цифрового сигнала, т.е. обеспечение заданной частотной характеристики. Предполагается, что имеется входная временная послед. В общем случае состоящая из основного несущего сигнала и шумовой составляющей. Природа может быть как внешней (шумы процесса), так и внутренней (шумы измерений и наблюдений) Назначение цифр. Фильтра

1. Удаление шумов (Внешних и внутренних)
   
2. Выделение из спектра основного входного сигнала необходимых гармоник (для разработки фильтра НЧ создать такое устройство, кот обеспечивало идеал. Пропускание сигналов в полосе пропускания (от нуля до границы этой полосы) и задерживание сигнала в остальном диопазоне частот.
   

Принято рассматривать обратную ЛАЧХ для таких фильтров, т.е. мы рассматриваем хар-ку как хар-ку затухания.


Идеальный фильтр предполагает полное пропускание полезного сигнала в полосе пропускания (или pass) и полное задерживание (stop).

Идеальные характеристики очевидно нельзя воплотить в жизнь, но можно к ним приблизиться, ставится вопрос о качестве фильтрации.


Качество фльтрации определяется отклонением частотной хар-ки в полосах пропкскания и задерживания, кот может быть интерпретирована в величине, которую далее будем использовать при построении конкретного фильтра, Rs – минимальное задерживание.





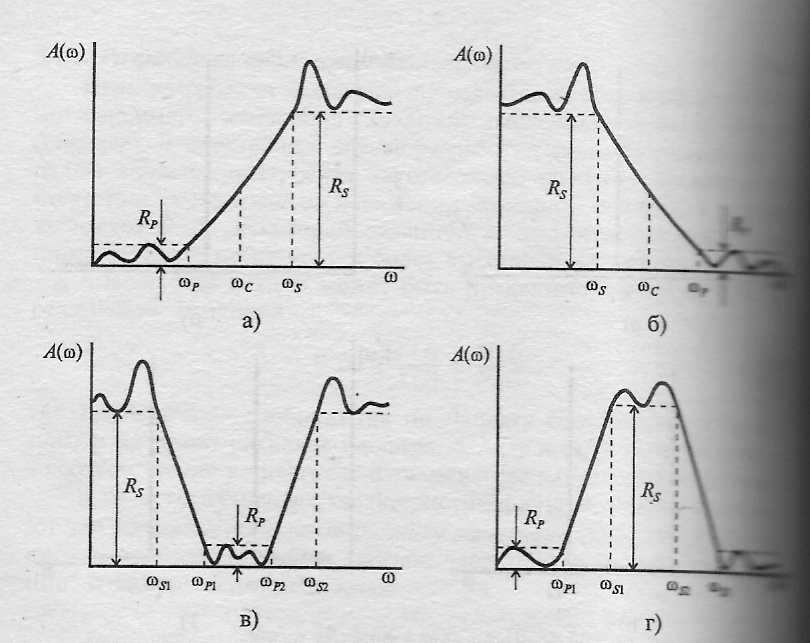
Рисунок а)


Идеальный фильтр НЧ обладает след хар-кой затухания:


В полосе задерживания равно бесконечности.


Wp (омега p) – частота относится к полосе пропускания

Wx (омега c) – задерживания


В связи с тем, что область переключения между пропусанием и задерживанием отлична от нуля, одним из требований к фильтрам может быть величина этой области. Вторым отличием реального фильтра от идеального – наличие пульсации.


Wp < Wc < Ws


Пульсации в полосах носят разные названия:

1. Пропускание – максимальное подавление в полосе пропускания. Мы должны его ограничивать, т.к. само наличие приводит к изменению амплитуды сигнала.
   
2. Задерживание - минимальное подавление в полосе задерживания
   

Рисунок б)


Фильтр высоких частот, он решает обратную задачу. Пропускает частоты в верхней частотной области и подавляет в нижней. Все характеристики меняются местами. Важным условием для интерпретации задачи построения фильтра – соотношение частот.


Пакет MATLAB анализирует отношение между частотами и при выполнении первого условия или второго условия, автоматически синтезирует фильтры либо высоких либо низких частот.


Рисунок в)


Полосно-пропускающий фильтр


Границы частот представляют собой векторы , состоящие из двух компонент – имеется две частоты пропускания и две частоты задерживания.


Ws1 < Wp1 < Wp2 < Ws2


Рисунок г)


Полосно-задерживающий фильтр


Wp1 < Ws1 < Ws2 < Wp2


Частоты представляю собой единичный или вектор из двух элементов.


Процесс проектирования фильтра заключается в проведении двух операций.

1. Вычисление порядка фильтра и частоты среза. Входной информацией является пульсации rp rs и приемлемые границы для полос пропускания и задерживания.
   
2. По определенному порядка фильтра и частотам среза для полосного фильтра – 2 частоты, определяются коэффициенты проектируемого фильтра.
   

Имеются очевидные различия между аналоговыми и цифровыми фильтрами.


Программно для того, чтобы рассчитать аналоговый фильтр среди параметров указывается “s” – признак того, что рассматриваем.


Частоты для проектируемого аналогового фильтра задаются в радианах в секунду и могут быть любыми.


Для цифрового фильтра используется нормированная частота. Очевидная характеристика цифрового фильтра связана с периодом квантования, поэтому величины частот, которые являются нормализованными располагается в (0,1). Единица для цифрового фильтра интерпретируется как половина частоты дискретизации или дискретности или частоты Найквиста.


Для проектирования всех четырех типов фильтра указываются значения граничных частот:

Тип фильтра	Условия задерживания (Stopband) и пропускания (Passband)	Задерживание (аналоговыйфильтр) (цифровой фильтр)	Пропускание (аналоговыйфильтр) (цифровой фильтр)
ФНЧ(lowpass)	Wp	(Ws,∞) (Ws,1)	(0,Wp) (0,Wp)
ФВЧ(highpass)	Wp>Ws, оба скаляры	(0,Ws) (0,Ws)	(Wp, ∞) (Wp,1)
Полосно-пропускающий(Bandpass)	Интервал, определяющий Ws,содержит интервал, определяющий Wp Ws(1)	(0,Ws(1)) (Ws(2),∞) (0,Ws(1)) (Ws(2),1)	(Wp(1),Wp(2)) (Wp(1),Wp(2))
Полосно-задерживающий(режекторный) фильтр (Bandstop)	Интервал, определяющий Wp,содержит интервал, определяющий Ws Wp(1)	(0,Wp(1)) (Wp(2),∞) (0,Wp(1)) (Wp(2),1)	(Ws(1),Ws(2)) (Ws(1),Ws(2))

Баттерворт - полоса граничная размыта.

Выбор порядка фильтра


[n, Wn] = buttord(Wp, Ws, Rp, Rs)

[n, Wn] = buttord(Wp, Ws, Rp, Rs, 's')


Группа функций buttord позволяет выбрать минимальный порядок цифрового или аналогового фильтра Баттерворта, имеющего следующие параметры:

Wp - частота пропускания (частота среза);

Ws - частота задерживания;

Rp - максимально допустимые пульсации в полосе пропускания, дБ;

Rs - минимальное затухание в полосе задерживания, дБ. Применение при расчете цифровых фильтров

Цифровые фильтры завязаны на частоту дискретности.


Передаточная функция спроектированного фильтра:





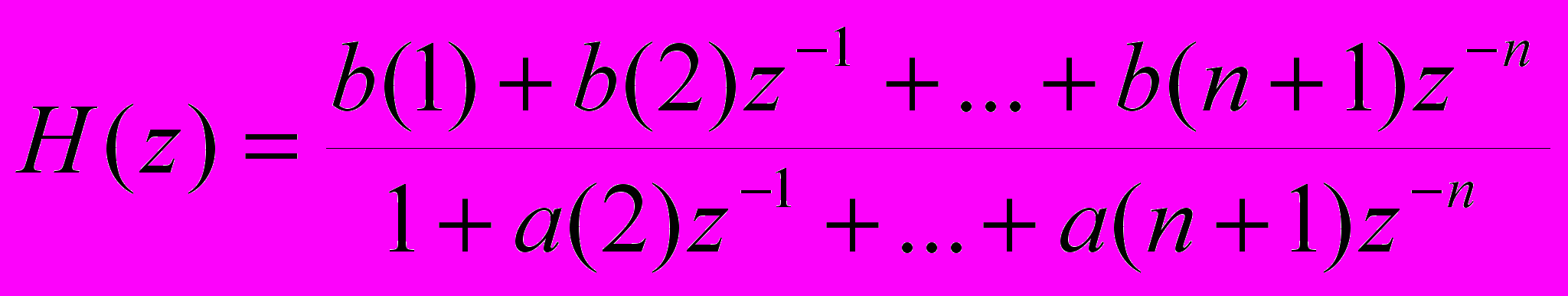
Формула для аналогового фильтра:





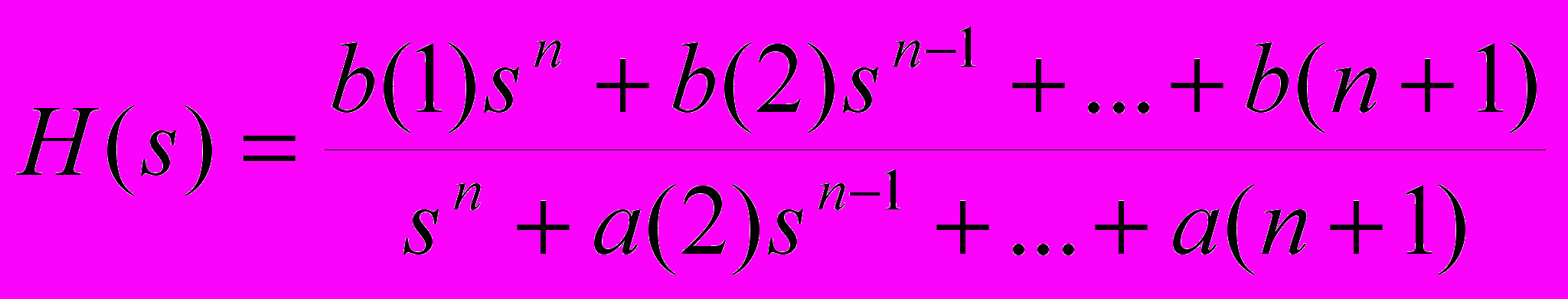
Практика интерпретация (комментарии)


Процесс представляется собой сумму трех гармоник. В примерах рассматривается задача пропускания одних и задерживание других. По свой сути процесс дискретный, важнейшей характеристикой – скорость выборки.


Если интервал выборки обозначить TS то частота обратная величина – 1/TS. Особое значение – половина выборки (частота Найквиста F). Физический смысл – можно восстановить … на которой в одном периоде выполнено не менее двух измерений. В конечном итоге частота измерений должна быть не менее чем в два раза выше, чем частота наблюдаемого процесса.


Для заданной частоты наблюдений можно распознать гармоники, частота которых меньше частоты Найквиста.


1) Процесс проектирования и исследования:

1. Формирование гармонических процессов s1 s2 s3
   
2. Задание на проектирование состоит в том, чтобы пропустить первую гармонику и пропустить … Для реализации – фильтр НЧ, полоса пропускания которого 0..100 Гц, полоса задерживания от 150 Гц … до частоты Найквиста. Частота дискретизации связана с особенностями генерации исходных гармонических сигналов. 1000 Гц
   

Порядок действий. Базовый фильтр Баттерворта проектируется аналоговый фильтр. Для аналогового фильтра рассматриваем диапазон 0 .. 10 Гц. Затухание 3 дБ. Пересчитываем частоты в радианы в секунды – появляется число pi.


По заданным показателям обращаемся к функции Баттерворта. Ответ Матлаба – порядок фильтра 5, частота среза


2) Расчет фильтра по заданным параметрам


freq(s) – частотная характеристика


Далее преобразуем герцы.


Моделирование процесса фильтрации


Пересчет радианы в секунды (умножить на 2pi)


Расчет частотной характеристики freqs(b, a)

Используется обратное преобразование -> герцы (для дальнейшего преобразования единиц измерения в герцы, градусы)


Fs – частота отсчета


Lsim – моделирует реакцию системы, имя которой H на входное воздействие U общего вида, подаваемое в моменты времени t.


Fft – позволяет получить прямое преобразование Фурье временной последовательности s – используется 512 точек.


Для Фурье принято брать количество измерений 2(x)


Вручную рассчитывается характеристика распределения спектра (или спектральная плотность). Заключительной фазой – перерасчет частот.


Строим графики


Дополнительное задание


Проверить, изменятся ли характеристики при изменении частот.


Тип фильтра


Тип фильтра: Баттерворда

Искажение: тоже самое


Пример 2


Полосовой фильтр


Пример 3


Частота Найквиста 500 Гц. Необходимо частоты отмасштабировать по отношению к частоте Найквиста – поэтому делится на 500 обе частоты.


Лекция. Задача большой размерности.


Источником являются физический уравнения, описывающие свойств сплошной среды. Например, уравнение тепловых процессов, деформаций и т.д. Процесс численного решения таких уравнений заключается в процедуре дискретизации таких моделей, т.е. к замене сплошной среды “ячейками” конечного размера и количества. Очевидно, для полного отображения таких моделей требуется сотни тысячи обыкновенных дифференциальных уравнений. Методы численных решений уравнений в частных производных такие как метод конечной разности, элементов и т.д. в полном обхеме решаются с помощью сложных вычислительных систем – распараллеливанне вычислительный процессов. В инженерной постановке на этапе эскизного проектирования представляется возможность выполнить сокращение порядка модели или редукцию модели.


Одним из плодотворных способов – для упругих систем описание движения их в модальном представлении.


Ограничиваются модами колебаний соответствующим низким частотам, считая что ВЧ колебания фильтруются системой.


Вторым примером усечения порядка модели являются модели электрических двигателей, например, асинхронных двигателей. Модель электромагнитных процессов, которые выливаются в классической модели асинхронного двигателя, предполагается, что используются только первые гармоники в процессах электромагнитной индукции.


Летательные аппараты, биологические объекты, климатический процессы.


Исследуется модель на первом этапе движения, выделяются параметры, которые медленно меняются на этом этапе, в системе дифференциальных уравнений остаются только существенно меняющиеся фазовые переменные.


Классы:

1. Сокращение порядка модели.
   
2. Упрощение систем управления (получение упрощенных регуляторов).
   

• Синтез регуляторов пониженной размерности, использующих информацию с пониженного числа датчиков.
  
• Сокращение порядка цифровых фильтров.
  

Среди методов редукции можно выделить:

1. Аналитический подход на основе анализа модели системы. Априорно информации (наличие быстрой и медленной составляющей)
   
2. Метод частотных характеристик – подбирается частотная характеристика, которая аппроксимирует с заданной точностью, но с меньшим порядком.
   
3. Выделение доминирующих обратных связей регулятора. Последовательно обрываются связи с каждого из датчиков и сравнивается реакция системы в полной и усеченной постановке. Если моделирование процессов является обязательной фазой но предварительно при выделении доминирующих связей сравниваются собственные значения или корни полной и усеченной систем (замкнутых). Оценка по корням. Относится не только к методам редукции, но и к проблеме оценке чувствительности систем. По корням используются не только для регуляторов, но и для построения редуцированных моделей.
   

Методы редукции системы в пакете Matlab сосредоточены в основном в пакете identification tool box. Задача редукции – неотъемлемая часть процесса идентификации, в нем получаем тем или иным способом набор моделей, каждую из моделей верифицируем )путем сравнения с исходными экспериментальными данными), пытаясь при этом получить модель возможно меньшего порядка.