Колебания системы материальных точек, имеющих несколько степеней свободы
| Вид материала | Задача |
- Лекция 8 Лекция колебания в системах со многими степенями свободы, 172.81kb.
- Совокупность материальных точек, движение которых взаимосвязаны. Масса системы = сумме, 51.86kb.
- Основы термодинамики, 381.85kb.
- Программа государственного экзамена по физике Специальность 010400 -физика, 72.86kb.
- 1-й вопрос билетов к государственному экзамену для студентов физического факультета, 72.21kb.
- Программа Государственного экзамена по биохимической физике Специальность 014200 Биохимическая, 93.2kb.
- Иерархия моделей теории колебаний, 18.86kb.
- Программа и вопросы вступительного испытания для поступающих в магистратуру по направлению, 71.57kb.
- Занятие №57 Механические колебания. Гармонические колебания. Резонанс. Колебания, 227.41kb.
- Василий Михайлович Доцент, к ф. м н. Головнев Игорь Федорович Доцент, к ф. м н. Медведев, 28.79kb.
Колебания системы материальных точек, имеющих несколько степеней свободы
Данная задача обобщает предыдущую.
Рассмотрим колебательное движение двух тождественных МТ. По прежнему ограничимся малыми колебаниями. Но теперь нужно учесть, что энергии частиц, составляющих единую систему, будут функциями обобщенных координат и скоростей обеих частиц:
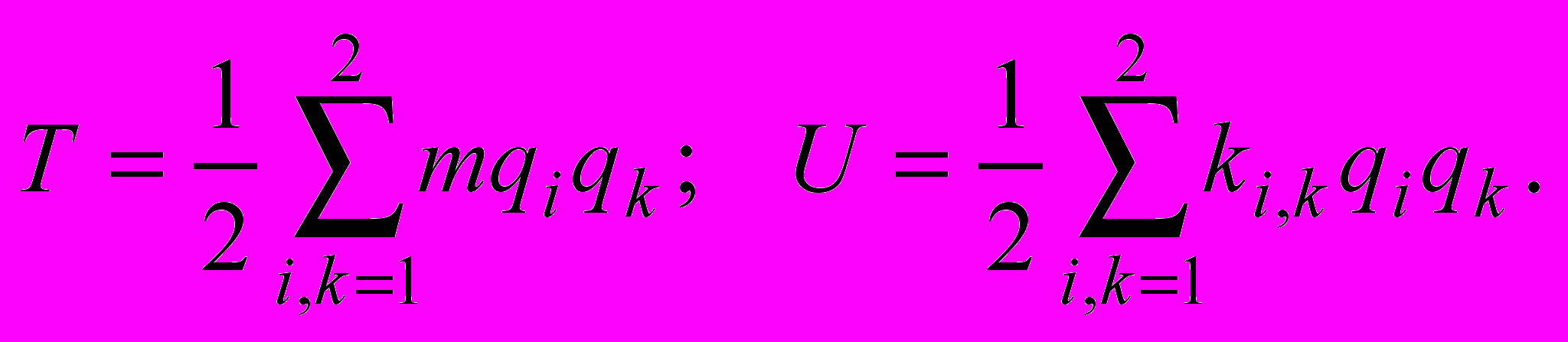
Составим уравнения движения, используя метод Лагранжа. Функция Лагранжа двух МТ имеет вид:
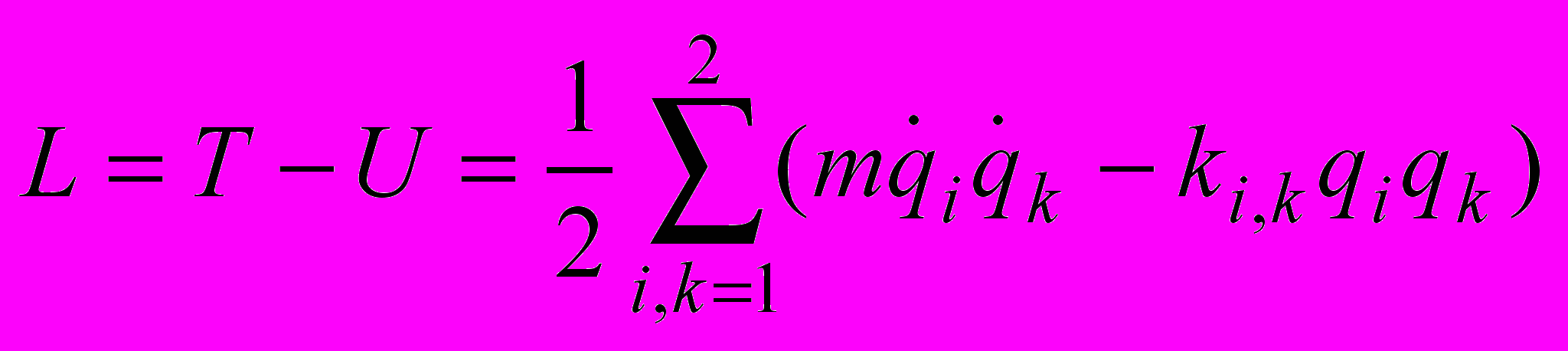.Тогда для каждой колеблющейся точки уравнение Лагранжа
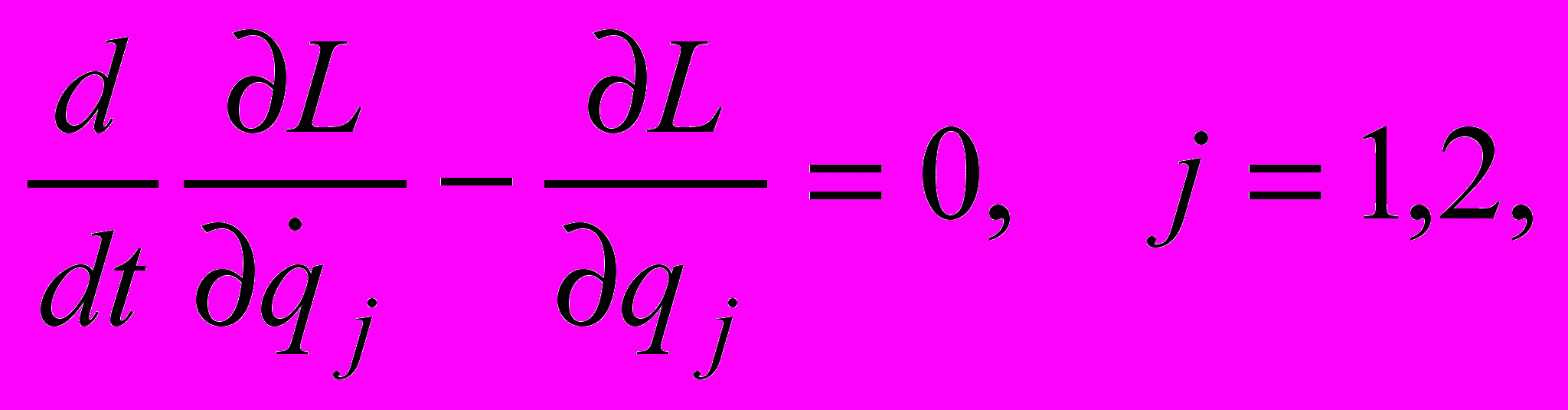запишется так: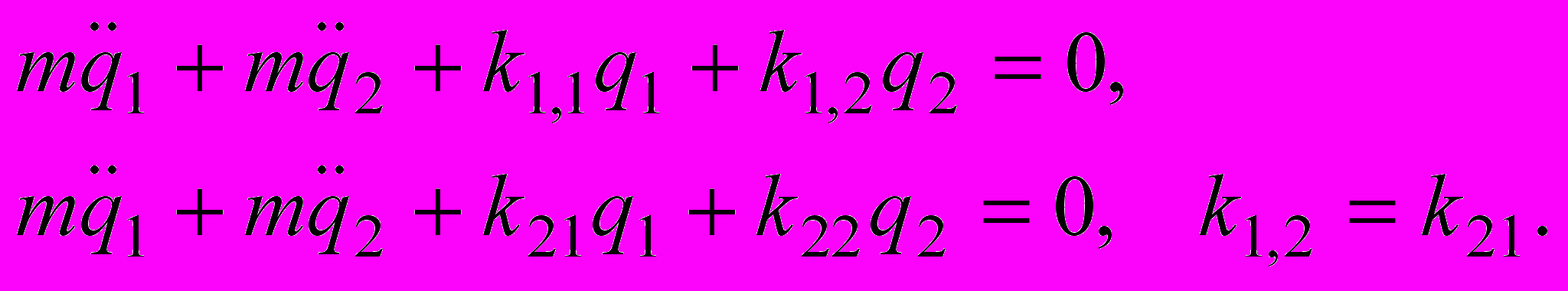
Будем находить решение в виде следующих функций:
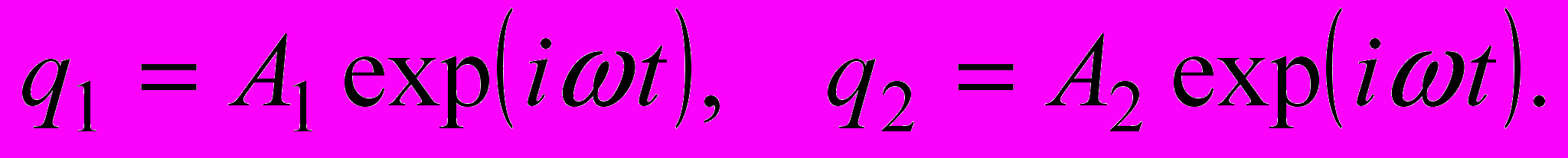
Подставляя эти функции в предыдущую систему уравнений, получим систему уравнений, которая будет иметь нетривиальное решение, если определитель, составленный из коэффициентов при величинах
, будет равен нулю:
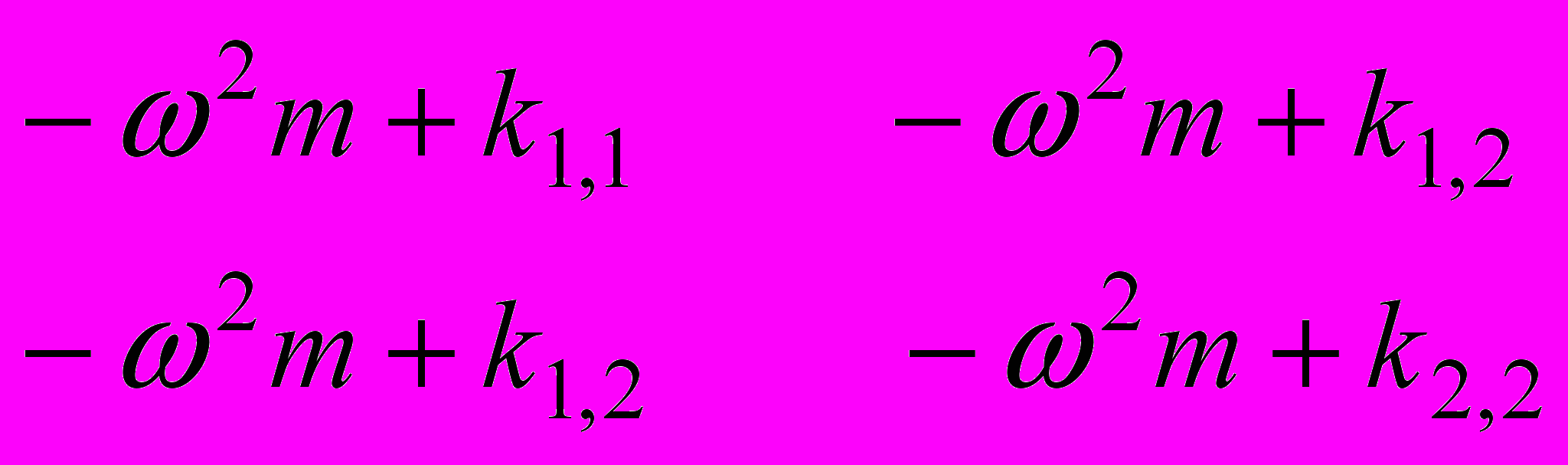=0 (*)Уравнение (*) называется характеристическим или вековым. Оно биквадратное относительно частоты. Но вещественных решений будут два:
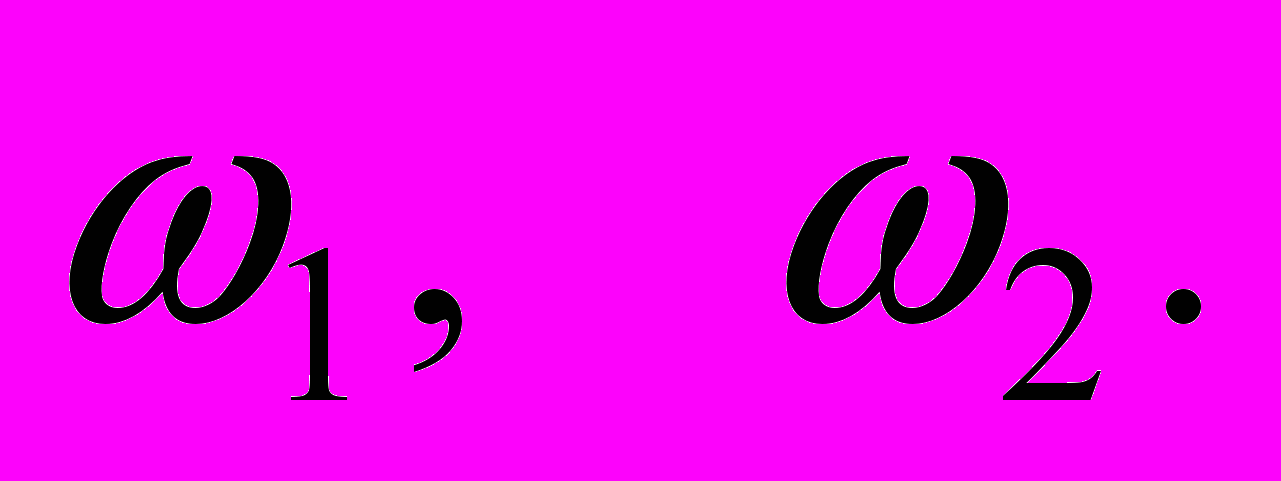, их число всегда равно числу степеней свободы системы колеблющихся частиц. Найдя частоты, затем находим координаты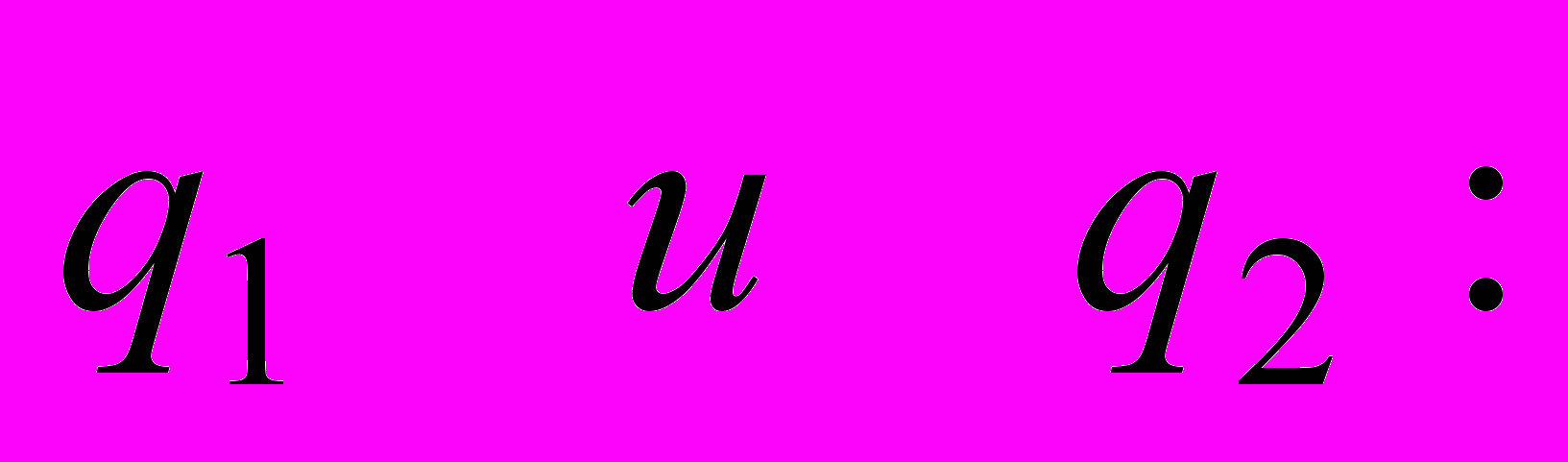 
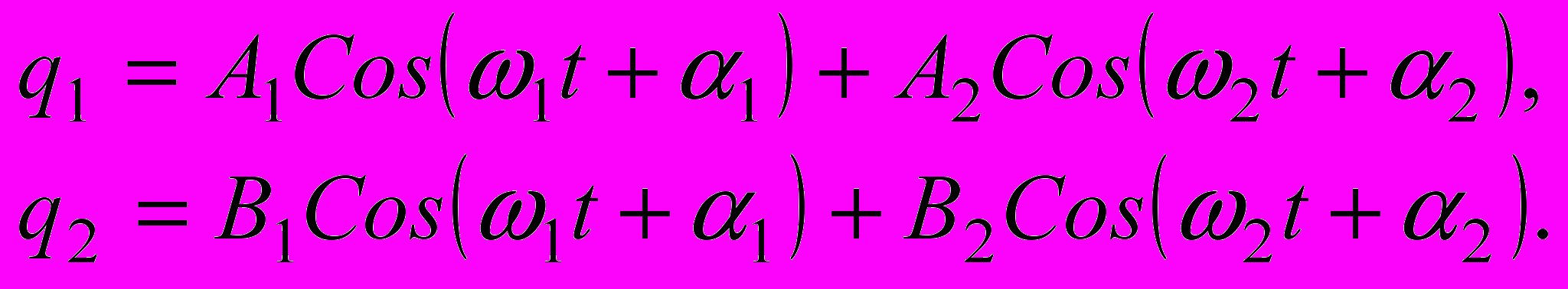
Из вида решения следует то новое, что отличает данную задачу от предыдущей: происходит наложение друг на друга гармонических колебаний двух частиц системы.