Программа дополнительного образования для круглогодичных школ интеллектуального роста авторы проекта
| Вид материала | Программа |
- График проведения круглогодичных школ интеллектуального роста, школ художественно-эстетического, 171.43kb.
- Администрация Муромского района Управление образования, 2425.95kb.
- Программа по литературе для школ и классов с углубленным изучение литературы Авторы:, 5585.49kb.
- Примерная программа для общеобразовательных школ, гимназий, лицеев алгебра и начала, 622.43kb.
- Казачкова Лариса Леонидовна, педагог дополнительного образования Бражное 2007 г пояснительная, 271.72kb.
- Федерального Государственного Учреждения «Санкт-Петербургский научно-исследовательский, 1055.69kb.
- Курс «Eвропейские науки» для продолжающих, 669.25kb.
- Н. В. Жаткина 2011г положени, 17.03kb.
- Авторская программа для общеобразовательных школ, гимназий, лицеев Краснодарского края:, 239.96kb.
- Программа составлена на основе проекта федерального компонента Государственного стандарта, 729.68kb.
КРАСНОЯРСКИЙ ГОСУДАРСТВЕННЫЙ ПЕДАГОГИЧЕСКИЙ УНИВЕРСИТЕТ ИМЕНИ В.П.
АСТАФЬЕВА
«... важнейшими качествами личности становятся инициативность, способность творчески мыслить и находить нестандартные решения...»
Президент РФ Д.А. Медведев
ПРОГРАММА ДОПОЛНИТЕЛЬНОГО ОБРАЗОВАНИЯ ДЛЯ КРУГЛОГОДИЧНЫХ ШКОЛ ИНТЕЛЛЕКТУАЛЬНОГО РОСТА
Авторы проекта:
Залезная ТА., доцент кафедры методики преподавания физики, к.пед.н., доцент;
Зданович О.В., ст. преподаватель кафедры алгебры и MOM, аспирант 3-го года обучения;
Латынцев СВ., доцент кафедры методики преподавания физики, к.пед.н., доцент;
Литвйнцева М.В., доцент каф. мат. анализа и методики его преподавания, к.пед.н., доцент;
Патрушев Г.О., доцент кафедры общей физики, к.ф.-м.н., доцент;
Подольский Н.Н., ст. преподаватель кафедры общей физики;
Семина Е.А., ст. преп. кафедры геометрии и методики ее преподавания, аспирант 3-го года
обучения;
Шимов А.В., ст. преподаватель кафедры общей физики;
Якушевич В.И., зав. лаб. кафедры общей физики;
Направление программы школы: физико-математическое
Название проекта школы: «НАША НОВАЯ ШКОЛА» - ШКОЛА ГАЛИЛЕЯ
Целевая группа: учащиеся 8-10 классов Количество дней/часов: 4 дня / 36 часов
Аннотация
Каким должно быть обучение в эпоху информационных взрывов? Может такая формулировка проблемы вообше неверна? Невозможно «научить» ребенка всем тонкостям предмета - нельзя объять необъятное. Учитель скорее должен помочь ученику организовать самостоятельный процесс познания. Тогда модель обучения должна выглядеть так: учитель создает информационно-образовательную среду, в которой ученик выбирает индивидуальную траекторию обучения в соответствии со своими образовательными потребностями и возможностями, а также с особенностями своего мышления и личностными предпочтениями, связанными с изучением предмета в дальнейшем и применении физических и математических знаний в будущей профессиональной деятельности.
Именно поэтому для решения задач развития интеллектуальных и творческих способностей, познавательных интересов учеников в процессе изучения математики и физики следует уделять внимание формированию умений и навыков исследовательской деятельности учащихся. Понятно, что учащиеся не могут в процессе обучения систематически делать объективно новые открытия и изобретения. Но они могут делать открытия и изобретения для себя. На этом и строится предлагаемый нами курс.
Программа школы состоит из двух модулей - физического и математического, в каждом из которых школьникам будет предложен набор исследовательских задач по соответствующей тематике. Учащийся выбирает один из модулей и за три рабочих дня проходит все три его лаборатории. Четвертый день отведен на заключительную конференцию — презентацию результатов исследовательских работ школьников.
Каждый модуль включает в себя 3 тематические лаборатории:
Математический -
- Вероятность случайного события;
- Геометрия;
- Исследовательские задачи в математике: уравнения с параметром.
Физический -
- Интерактивный музей физики;
- Лаборатория экспериментальной физики;
- Лаборатория методологии физики.
Тематика каждой лаборатории представляет собой относительно независимый блок материала, соприкасающегося с соответствующим материалом программы основной школы, однако не дублирующий его, а расширяющий и углубляющий знания учащихся в предметной области.
Формы работы - чередование кратковременных (20-30 минут) общих лекций-бесед, лабораторных работ в малых группах (3-4 человека в группе и 25-30 минут на одну работу) и общих семинаров, на которых представители малых групп докладывают основные результаты своей работы.
Формы организации процесса обучения и применяемые методы обучения носят интерактивный характер и сочетаются с самостоятельной внеаудиторной учебной деятельностью учащихся.
Содержание предметного учебного материала интегрировано с практико-ориентированными учебными задачами.
Количество и состав исполнителей, их обязанности в педагогической
команде
Реализация настоящей программы предполагается силами преподавателей кафедр факультетов математики и физики Красноярского педагогического университета
- кафедра методики преподавания физики
- кафедра общей физики
- кафедра алгебры и MOM
- кафедра геометрии и методики ее преподавания
- кафедра математического анализа и методики его преподавания
Исполнители проекта
'Залезная Т.А., доцент кафедры методики преподавания физики, к.пед.н., доцент; ХЗданович О.В., ст. преподаватель кафедры алгебры и MOM , аспирант 3-го года обучения; Латынцев СВ., доцент кафедры методики преподавания физики, к.пед.н., доцент; Н Литвинцева М.В., доцент каф. мат. анализа и методики его преподавания, к.пед.н., доцент; /Патрушев Г.О., доцент кафедры общей физики, к.ф.-м.н., доцент; £ Подольский Н.Н., ст. преподаватель кафедры общей физики;
Семина Е.А., ст. преп. кафедры геометрии и методики ее преподавания, аспирант 3-го года /обучения;
Шимов А.В., ст. преподаватель кафедры общей физики;
Якушевич В.И., зав. лаб. кафедры общей физики.
Все исполнители являются преподавателями с большим стажем и навыками работы не только в ВУЗе, но и в школе. Роль в процессе проведения школы - лектЬры, тьюторы учебных групп, руководители семинаров.
Пояснительная записка
Настоящая программа дополнительного образования (физико-математического направления) разработана для реализации в круглогодичных школах интеллектуального роста для одаренных детей на базе межрайонных ресурсных центров.
Основная цель программы:
Цель проекта: создание системы индивидуального сопровождения учащихся.позволяющей создавать и реализовывать их индивидуальные образовательные маршруты отражающие их интересы, возможности и потребности через творческую образовательную среду.
Для достижения сформулированной цели программа ориентирована на решение следующих задач:
- Определение структуры содержания индивидуального сопровождения учащихся.
- Описание последовательности действий, пригодных для индивидуального сопровождения
учащихся.
- Создание условий для формирования и развития познавательного интереса и
познавательной мотивации учебной деятельности учащихся школы интеллектуального роста.
- Создание условий для формирования таких личностных качеств учащихся как
самостоятельность в определении целей своей учебной деятельности, принятии решений и
ответственности за их последствия.
- Развитие метапредметных умений учащихся: самостоятельно выбирать способ решения
учебной задачи, осуществлять самоконтроль собственной деятельности, произвести
обоснованную оценку и самооценку результатов деятельности и приобретенного опыта, а также
умений работать над решением учебной задачи как индивидуально, так и в команде, с учетом
занимаемой позиции (лидера, участника); приобретение учащимися опыта учебно-
исследовательской и учебно-проектной деятельности, использования информационно-
коммуникационных технологий.
- Формирование у учащихся школы предметных умений, способов деятельности,
соответствующих классу решаемых задач (определенных тематическим планом),
приобретение опыта решения олимпиадных задач.
- Укрепление физического и психического здоровья одаренных детей, создание условий для их
успешной социализации.
Настоящая программа реализует компетентностный подход в образовании в следующих аспектах: а) планируемые результаты обучения являются составляющими ключевых, метапредметных и предметных (математической и физической) компетенций выпускника основной школы; б) формы организации процесса обучения и применяемые методы обучения носят интерактивный характер и сочетаются с самостоятельной внеаудиторной учебной деятельностью учащихся; в) содержание предметного учебного материала интегрировано с практико-ориентированными учебными задачами.
Актуальность проекта
В связи с потребностью общества в неординарной творческой личности проблема одаренности становится в наше время все более значимой. Неопределенность современной окружающей среды требует не только высокой активности человека, но и наличия у него особых умений по работе в нестандартной ситуации. Именно поэтому образовательная система стала вмешать в себя огромное количество нововведений.
В новой национальной образовательной стратегии «Наша новая школа» выделено 5 основных направлений в программе развития Российской школы:
- Создание условий обучения, при которых дети в школе могли бы раскрыть свои возможности,
подготовится к жизни в конкурентной борьбе.
- Выстраивание системы поиска и поддержки талантливых детей.
- Освоение новых образовательных технологий, которые смогут помочь детям выбрать
профиль обучения физики в школе.
- Изменение облика школ, как по форме, так и содержанию.
- Применение индивидуального подхода для сохранения здоровья школьников в процессе
обучения.
Для выполнения поставленных задач требуется специально разработанная обучающая программа для поиска и поддержки талантливых детей, направленная на индивидуальное обучение учащихся и сохранение здоровья школьников в процессе обучения,
Раннее выявление, обучение и воспитание одаренных и талантливых детей составляет одну из главных задач совершенствования системы образования. Бытует мнение, что одаренные дети не нуждаются в помощи взрослых, в особом внимании и руководстве. Однако в силу личностных особенностей такие дети наиболее чувствительны к оценке их деятельности, поведения и мышления. Грамотно выстроенная образовательная траектория способствует приобретению ими навыков самостоятельной работы: умений формулировать цель, задачи и предмет исследования; выдвигать гипотезу; находить и анализировать информацию; планировать и проводить многочисленные эксперименты; анализировать результаты экспериментов; формулировать выводы; находить практическое применение полученным результатам; намечать перспективы дальнейших исследований.
Планируемые результаты и образовательные эффекты
Результаты обучения учащихся в школе интеллектуального роста должны быть следующие:
- Приобретение (обогащение) учащимися опыта учебно-исследовательской и учебно-проектной
деятельности.
- Формирование у учащихся умений и навыков работы:
- В компьютерной среде «Живая геометрия»;
- В образовательном комплексе «1С: Математика»;
- С нестандартным физическим оборудованием;
- Формирование физической грамотности - знакомство с теорией механических колебаний на
уровне аргументированного анализа уравнений движения тел в свободных линейных
колебательных системах с различной природой возвращающей силы без затухания и с
затуханием, а также в линейных системах с гармонической вынуждающей силой;
- Формирование методологической грамотности - учащиеся должны уверенно и
аргументированно отвечать на вопросы типа: «Что такое физика и как она устроена? В чём
состоят основные методы физической науки, с помощью которых она познаёт мир? Чем
методология физики существенно отличается от методологии искусства и религии?».
- Формирование у учащихся школы предметных умений, способов деятельности,
соответствующих классу решаемых задач, приобретение опыта решения олимпиадных задач.
Ожидаемым образовательным эффектом является развитие познавательного интереса одаренных детей в области физики и математики, получение положительного опыта самостоятельной творческой деятельности в избранной области и получения ориентиров для дальнейшего развития в выбранном направлении.
Перечень содержательных блоков по модулям
Модуль 1 (Математика)
Лаборатория «Геометрия: метод геометрического места точек в задачах на построение».
Геометрические построения на плоскости. Основные понятия. Этапы решения задач на построение. Элементарные задачи на построение. Геометрические места точек (ГТМ). Понятие ГМТ. Простейшие и некоторые специальные ГМТ. Решение задач на построение методом ГМТ. Задачи на построение треугольников по заданным элементам.
Лаборатория «Исследовательские задачи в математике: уравнения с параметром»
Основные понятия: параметр, уравнение с параметром, общий алгоритм решения уравнений с параметром; основные методы и приемы решения уравнений с параметрами.
Лаборатория «Вероятность случайного события: геометрические вероятности, метод Монте-Карло и его приложения»
Понятие геометрического определения вероятности как обобщения классического определения вероятности. Применение геометрических вероятностей для решения задач практического содержания. Задача Бюффона (использование геометрического определения вероятности для определения приближенного значения числа л). Метод Монте-Карло (статистических испытаний) и его применение для приближенного вычисления площадей фигур.
Модуль 2 (Физика)
Лаборатория экспериментальной физики
Сила трения (покой, скольжение, качение), гидравлический удар, стробоскопическое исследование движения, сложение колебаний (фигуры Лиссажу), определение положения центра масс, баллистические методы измерений, закономерности течения идеальной жидкости (закон Бернулли), геометрическая оптика линз и призм.
Лаборатория методологии физики
Теория механических колебаний, уравнение и закон движения, гармонические колебания, свободные и вынужденные колебания, линейные колебательные системы с различной природой возвращающей силы без затухания и с затуханием, линейные системы с гармонической вынуждающей силой.
Интерактивный музей физики
Исследовательские работы в области истории физики - капельница Галилея, формула Эйлера, опыты Фарадея, дифракция Фраунгофера и Френеля.
Формы работы
Формы работы - чередование кратковременных (20-30 минут) общих лекций-бесед, лабораторных работ в малых группах (3-4 человека в группе и 25-30 минут на одну работу) и общих семинаров, на которых представители малых групп докладывают основные результаты своей работы.
Формы организации процесса обучения и применяемые методы обучения носят интерактивный характер и сочетаются с самостоятельной внеаудиторной учебной деятельностью учащихся.
Режим дня школы
- 7.30. Подъем.
- 7.45-8.15. Утренняя зарядка.
- 8.30. Завтрак.
- 9.00-12.00. Учебные занятия
- 12.00 - 12.45. Учебные занятия (игровые, соревновательные формы).
- 13.00-13.30. Обед.
- 14.00 - 15.30 Учебные занятия.
- 16.00. Полдник.
- 16.30 - 17.30. Учебные занятия (игровые, соревновательные формы).
10.18.00 - 19.00 Самостоятельная работа над проектами, консультации с преподавателями.
- 19.00. Ужин.
- 20.00 - 22.00. Культурно-массовые мероприятия, спортивные соревнования,
спортивные секции.
- 22.00 Отбой.
Информация об организации-заявителе
| | | |
| 1 | Организационно правовая форма и наименование заявителя | Государственное образовательное учреждение высшего профессионального образования Красноярский государственный педагогический университет им. В.П. |
| 2 | ИНН/КПП | 2466001998/246601001 |
| 3 | ОГРН | 1022402653008 |
| 4 | ОКПО | 02079135 |
| 5 | ОКАТО | 04401377000 |
| 6 | Основной код экономической деятельности | 80.30.1 |
| 7 | Юридический адрес, адрес места нахождения | 660049 г.Красноярск, ул. А.Лебедевой, 89 |
| 8 | Адрес для корреспонденции, факс, телефон, электронный адрес | 660049 г.Красноярск, ул. Л.Лебедевой, 89 (391) 211-31-77 (приёмная ректора, секретарь Карпова Ольга Сергеевна), (391) 211-07-29 (факс, отдел кадров). drozdov@kspu.ru, chiganov@imfi.kspu.ru |
| 9 | Куратор программы | Патрушев Глеб Олегович, (391) 227-09-28 ст. 8913-832-94-73 |
14
ПРИЛОЖЕНИЯ
Лаборатория МЕТОДОЛОГИИ ФИЗИКИ
Основная цель лаборатории — формирование у старших школьников основ методологической компетентности.
Главная задача — организовать активное участие школьников в учебно-познавательной деятельности, направленной на построение теории механических колебаний, в результате которой они смогли бы осознанно и аргументировано отвечать на вопросы типа: «Что такое физика и как она устроена? В чём состоят основные методы физической науки, с помощью которых она познаёт мир? Чем методология физики существенно отличается от методологии искусства и религии?».
1. Содержание учебных занятий (пояснительная записка для учителя)
Теория механических колебаний является чрезвычайно важным и выигрышным разделом физики в смысле организации эффективной учебно-исследовательской деятельности старших школьников. Обратим внимание на несколько особенностей данной физической теории, которые могут служить достаточно очевидной аргументацией в пользу высказанного утверждения.
Во-первых, теория механических колебаний является прикладной физической теорией в том смысле, что все её закономерности логически и математически выводятся из законов Ньютона и свойств сил, действующих на колеблющиеся тела. Ньютоновская механика, в свою очередь, в курсах физики школ изучается достаточно глубоко и подробно. Всё это позволяет утверждать, что старшие школьники при изучении механических колебаний вполне осознанно могут заниматься учебно-исследовательской деятельностью физико-технического характера.
Во-вторых, теория механических колебаний (несмотря на свой прикладной физический статус) является важнейшей общефизической теорией, имеющей широчайшие применения в самых различных областях физики. Можно даже сказать, что язык и основные идеи теории механических колебаний стали элементом общефизической культуры. Поэтому глубокое изучение теории механических колебаний существенно поможет учащимся в понимании и других более сложных разделов физики.
В-третьих, несмотря на то, что ньютоновской физике уже более 300 лет и, казалось бы, механические колебания должны быть полностью изучены, за последние 50-60 лет в теории механических колебаний были сделаны чрезвычайно важные физико-математические открытия. Удивительно то, что эти открытия связаны с изучением на первый взгляд очень простых механических систем. Однако при их исследовании фактически появилась новые разделы физики и математики: хаотические колебания, фракталы, солитоны и пр. Это обстоятельство даёт возможность учащимся довольно глубоко познакомиться с некоторыми фундаментальными проблемами современной физической науки.
Всё это делает теорию механических колебаний весьма удобным содержанием для организации учебно-исследовательской (проектной) деятельность старших школьников, интересующихся физико-техническими науками. Важнейшим результатом учебно-исследовательской деятельности школьников (кроме сформированности у них собственно физических знаний и умений) может стать достаточно глубокое усвоение методологических основ физической науки.
Прежде, чем начинать систематическое изучение теории механических колебаний, необходимо, на наш взгляд, решить две дидактические задачи.
Во-первых, нужно сформировать у обучаемых первоначальные (полуинтуитивные) представления о механических колебаниях как о специальном классе природных явлений. Это необходимо для того, чтобы обучаемые в общих чертах сумели обозреть огромное многообразие реальных колебательных движений и поняли основную идею выбора простейших колебательных систем, с которых целесообразно начинать изучение закономерностей механических колебаний.
15
Во-вторых, целесообразно замотивировать для обучаемых важность изучения механических колебаний. Это можно сделать, например, наглядно показав практическую значимость знания основных законов, управляющих поведением колеблющихся тел.
При классификации колебательных систем мы из всего их многообразия выбираем только наиболее важные с позиции физики и техники.
Основная идея отбора физического содержания, подлежащего изучению, состоит в том, что прежде всего, все существующие колебательные системы мы делим на два больших класса: системы с одной степенью свободы и системы с многими степенями свободы. При этом мы специально не отделяем поступательные степени свободы от вращательных, так как с физической точки зрения это не принципиально. Хотя, конечно, для школьников в силу большей наглядности лучше было бы остановиться на изучении только поступательных движений колеблющихся тел.
Так как системы с одной степенью свободы гораздо проще для понимания, то естественно начать изучение механических колебания целесообразнее именно с них.
Колебательные систем с одной степенью свободы, в свою очередь, мы делим на свободные и вынужденные, в зависимости от того, не действует или действует на колеблющееся тело вынуждающая (внешняя) сила.
Свободные колебания тел естественно делятся на незатухающие, происходящие в системах без сопротивления (консервативные системы) и затухающие, происходящие в системах с сопротивлением (неконсервативные системы).
Как незатухающие, так и затухающие колебательные системы в современной физике деляться на линейные и нелинейные в зависимости от того, линейным или нелинейным дифференциальным уравнением (представляющим второй закон Ньютона) описывается колебательная система. При этом, линейные системы теоретически изучаются количественно, а нелинейные — только качественно. Отсюда видна особая важность экспериментального модуля для понимания поведения нелинейных колебательных систем.
Вынужденные колебания мы делим несколько нетрадиционным способом.
Во-первых, рассматриваются линейные колебательные системы с гармонической вынуждающей силой. Эти чрезвычайно важные (как в физическом, так и техническом аспекте) системы изучаются полностью (точно).
Во-вторых, выделяются параметрические колебания в нелинейных системах с периодической вынуждающей силой. С теоретических позиций такие системы изучаются качественно. Поэтому важное значение имеет экспериментальное наблюдение поведения параметрических колебательных систем.
В-третьих, выделяются автоколебания, происходящие в нелинейных системах с непериодическим внешним воздействием. Для этих систем так же чрезвычайно важное значение имеет использование экспериментального метода исследования.
Наконец, мы специально рассматриваем так называемые хаотические колебания, происходящие в нелинейных системах с периодической вынуждающей силой. Как уже указывалось в начале раздела, хаотические колебания физики начали систематически изучать только около 50-ти лет назад. В настоящее время этот раздел физики чрезвычайно бурно развивается и имеет огромное значение, как для самой физики, так и для техники. Это важное обстоятельство даёт возможность студентам и старшим школьникам познакомиться с некоторыми фундаментальными проблемами современной науки и техники.
Что же касается колебательных систем с многими степенями свободы, то, во-первых, выделяются системы с их конечным числом степени свободы (две, три и четыре) и экспериментально изучаются их главные типы колебаний (так называемые моды); во-вторых, изучаются непрерывно распределённые одномерные системы (так называемые стоячие волны). В этом случае использование экспериментальных установок сильно облегчают усвоение теоретического материала.
Вышеизложенная классификация колебательных систем представлена на следующей схеме:
16
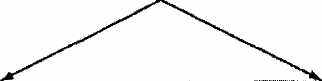
 КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
КОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ






 Системы с одной степенью свободы
Системы с одной степенью свободы Системы с многими степенями свободы
| Затухающие колебания в неконсервативиых системах | ||
| | | |
| —»> | Линейные системы с затуханием | |
| | | |
| | Нелинейные системы с затуханием | |
СВОБОДНЫЕ КОЛЕБАНИЯ (Внешнего воздействия нет)
| Незатухающие колебания в консервативных системах | ||
| | | |
| | Линейные системы без затухания | |
| | | |
| | Неинейные системы без затухания | |
Системы с конечным
числом степеней свободы
Системы с бесконечным
числом степеней свободы
| ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ (Внешнее воздействие есть) | ||
| | | |
| | Вынужденные колебания в линейных системах с гармонической вынуждающей силой | |
| | | |
| | Параметрические колебания в нелинейных системах с периодической вынуждающей силой | |
| | | |
| | Автоколебания в нелинейных системах с непериодическим внешним воздействием | |
| | | |
| | Хаотические колебания в нелинейных системах с периодической вынуждающей силой | |
Для реализации дидактического принципа «от простого к сложному» предлагается следующая последовательность изучения приведённых типов колебательных систем:
- Теоретическое и экспериментальное исследования 8-ми линейных колебательных системы
без затухания с различной физической природой возвращающей силы;
- Экспериментальное исследование особенностей поведения линейной колебательной системы
с затуханием;
- Экспериментальное исследование особенностей поведения вынужденных колебаний в ли
нейных системах с гармонической вынуждающей силой ;
- Экспериментальное исследование особенностей поведения колебательной системы с не
сколькими (2, 3, 4) степенями свободы ;
- Экспериментальное исследование особенностей поведения колебательной системы с бес
конечным числом степеней свободы (одномерные поперечные и продольные стоящие волны
на длинной пружине);
- Экспериментальное исследование особенностей поведения нелинейных колебательных сис
темы с малым затуханием (математический маятник с большой амплитудой и пружинные
системы с зазорами);
17
- Экспериментальное исследование особенностей параметрических колебаний (математиче
ский маятник с переменной длиной и переменным эффективным ускорением силы тяжести);
- Экспериментальное исследование особенностей автоколебательной системы (модели гейзера
и скрипичной струны);
- Экспериментальное исследование особенностей поведения существенно нелинейных
хаотических колебаний.
На заключительным этапе работы лаборатории будет организована лекция-беседа (40 минут) на тему: «Наука, религия, искусство — различные формы познания мира, "изобретённые" человечеством ».
2. Формы организации учебных занятий
В основном будет использоваться чередование кратковременных (20-30 минут) общих лекций-бесед, лабораторных работ в малых группах (3-4 человека в группе и 25-30 минут на одну работу) и общих семинаров, на которых представители малых групп докладывают основные результаты своей работы.
3. Конспект вводного учебного занятия «Что такое механические колебания и почему их
нужно изучать?»
3.1. Первоначальные представления о колебательном движении
1. Какие движения тел в самом общем смысле называют колебательными? Каким образом
молено классифицировать типы колебательных движение по их сложности?
Во-первых, очевидно, что из всех тел природы (твёрдых, жидких, газообразных) самыми простыми телами (в смысл изучения их движений) являются твёрдые тела, которые для простоты мы будем даже полагать абсолютно твёрдыми, то есть такими, форма которых при движении не изменяется.
Вообще говоря, колебательным движением твёрдого тела можно считать такое его движение, при котором тело всё время остаётся в некоторой ограниченной области пространства. При колебательном движении положения и скорости точек тела (точно или приблизительно) через некоторые промежутки времени (не обязательно равные) повторяются.
Другими словами, колебательное движение твёрдого тела есть (в точном или приближённом смысле) повторяющееся движение этого тела.
В силу того, что колебательные движения твёрдых тел чрезвычайно распространены, разумно повнимательнее к ним присмотреться и тщательно изучить их закономерности. Начинать, однако, такое изучение нужно с простейших типов колебательных движений.
Ясно, что самыми простыми колебательными движениями твёрдых тел являются поступательные колебательные движения, так как в этом случае все точки тела движутся совершенно одинаково. Следующим по сложности является вращательное колебательное движение твёрдого тела. И, наконец, самым сложным является комбинированное (одновременно поступательное и вращательное) колебательное движение тела.
2. Почему разумно разделить колебательные движения твёрдого тела на поступательные и
вращательные?
Дело в том, что динамика вращательного движения твёрдого тела намного сложнее динамики поступательного движения этого же тела.
Действительно, если тело движется поступательно, то все его точки движутся совершенно одинаково. Следовательно, при описании движения тела можно мысленно заменить его одной материальной точкой с массой, равной массе тела.
18
При вращательном же движении тела в нём обязательно найдутся точки, движущиеся по различным траекториям и с различными скоростями. Поэтому механику (кинематику и динамику) вращающегося твёрдого тела невозможно свести к механике одной материальной точки.
Таким образом, разумно сперва изучить поступательное колебательное движение твёрдых тел и только потом взяться за изучение вращательных колебательных движений.
3. Какое колебательное движение твёрдого тела является наиболее простым ?
Вообще говоря, существует бесконечно много различных типов (видов) поступательных колебательных движений твёрдого тела. В любых поступательных колебаниях все точки тела движутся совершенно одинаково (траектории одинаковы и законы движения по этим траекториям также одинаковы).
В самых сложных ситуациях нам заранее не известна даже та траектория, по которой будут двигаться все точки колеблющегося тела. Это обстоятельство позволяет выбрать простейшую физическую ситуацию.
Самым простым типом колебательного движения твёрдого тела является его поступательное колебательное движение по заранее заданной неподвижной траектории.
В этом случае очевидно, что положение колеблющегося тела в прастранстве полностью задаётся одним параметром, например, длиной траектории от мгновенного положения тела до произвольно фиксированной точки траектории.
В механике число независимых параметров, знание которых полностью задаёт её положение в пространстве, называется числом степеней свобода механической системы. В дальнейшем изложении мы почти всегда будем обсуждать именно этот простейший тип поступательного колебательного движения с одной степенью свободы.
3.2. О научной и практической важности изучения механических колебаний
Теперь попытаемся убедиться в необходимости всестороннего изучения механических колебаний. Можно, конечно, просто сообщить обучаемым, что учебной программой по физике предусмотрено обязательное изучение данного раздела физики. Лучше, однако, подобрать несколько важных и интересных примеров научного и практического применения знаний о механических колебаниях. В данном разделе мы приведём несколько таких примеров, из которых важнейшая роль отводится последнему примеру о маятнике Капицы.
3.2.1. Проблема конструирования точных механических часов
Наш первый пример относится к важной научной и технической проблеме точного измерения промежутков времени. Принцип действия часов (прибор для измерения промежутков времени) может быть основан на различных физических процессах. В настоящее время самые точные часы работают на основе атомной и ядерной физики. Несмотря на это, остаётся актуальной и проблема изготовления точных механических часов, основной частью которых является твёрдое тело (маятник), совершающее колебательное движение.
При конструировании точных механических часов нужно особо позаботиться о том, чтобы промежутки времени, через которые происходит повторение положения маятника, были бы строго одинаковыми. Причём, чем лучше выполняется это условие, тем точнее часы. Для того, чтобы решить эту проблему нужно знать законы, управляющие колебательным движением маятника. В противном случае прогресс в области создания высокоточных механических часов просто невозможен.
В качестве простейшего маятника механических часов можно взять металлический предмет малого размера (например, металлическую гайку) и прикрепить его на длинной нити (длина не менее 0,5 метра) к неподвижной точке. Если нить маятника отклонить от вертикали и отпустить, то он начнёт свершать колебательное движение. Важнейшей характеристикой этого движения является период колебаний, под которым понимают тот промежуток времени, по истечении которого положение и скорость маятника начинают повторяться.
Какой тип колебательного движения (поступательное, вращательное или комбинированное) совершает описанный выше маятник?
19

 4.
4.менее 3 Mb, не менее 2-х ядер
Экран: не менее 17.3", широкоформатный, глянцевое покрытие, разрешение матрицы не менее 1600 х 900
Память: не менее 4GB, DDR3
Жесткий диск: не менее 500 Гб SATA 2.5"
Накопители:
DVD+RW
Устройство чтения/записи карт памяти SD/MMC
Видео: дискретный адаптер, не менее 1024 Мб GDDR3, поддержка DirectX 11
Звуковая подсистема:
Встроенные динамики
Встроенный Микрофон
Дополнительные устройства:
Веб-камера, не менее 0.3 Мп.
Средства коммуникации:
Не менее lxLAN не менее 100 Мб/с
Wi-Fi 802.11
Порты и разъемы:
Не менее 4xUSB 2.0
Не менее lxRJ45
Не менее lxD-SUB
Линейный аудиовход, выход для наушников, вход для микрофона.
Устройства ввода:
Полноразмерная клавиатура
Манипулятор TouchPad с поддержкой Multi-touch
Габариты и вес:
Размеры, не более (ширина х высота х глубина), 41 х 3.8 х 27.5 см.
Аккумулятор:
Не менее 4400 mAh
Манипулятор «мышь»:
Тип мыши оптическая, количество кнопок мыши не
менее 3-х, интерфейс USB, разрешение не менее 1000
dpi
Поставляемый товар должен быть полностью
укомплектованным и обеспечивать полную
функциональность, необходимую для данного типа
товара.
Интерактивная доска с напольным креплением Smart Board 680D или эквивалент согласно следующим характеристикам:
Доска прямой проекции, диагональ не менее 77" (195
см), резистивная технология, интерфейс USB, размер
рабочей поверхности не менее 1565x1172 мм,
разрешение 4000x4000 на прикосновение, напольное
крепление в комплекте.
Документ-камера SMART SDC-280 или эквивалент согласно следующим характеристикам:
эффективное разрешение не менее 1077x788, оптическое увеличение не менее 5.3Х, рабочая область не менее 229 х 305 мм, выходные разъемы RGB, вес не более 2,9 кг.
55 000,00
4
 0 000,00
0 000,0055 000,00
40 000,00
Я понимаю, конечно, что ось стержня будет непрерывно вибрировать вследствие работы двигателей. Поэтому мне обязательно нужно проанализировать влияние этой вибрации на показания прибора.
Рассуждаю следующим образом. Пусть стержень занимает в данный момент некоторое положение, например, отклонен от вертикали на некоторый угол. При отсутствии вибрации стержень под действием силы тяжести неуклонно стремился бы к вертикальному положению вниз. Если в этот момент ось стержня быстро передвинется на малое расстояние вверх, то сам стержень также быстро повернется на малый угол к направлению вниз. Если наоборот точка подвеса дернется вниз, то стержень получит толчок, в результате которого он повернется на малый угол к направлению вверх. (Такое поведение стержня, кстати, лучше отдельно пронаблюдать на опыте.) Если теперь ось стержня будет симметрично дрожать (колебаться) вверх-вниз, то стержень также будет дрожать около рассматриваемого нами положения. Так как частота вибрации оси большая, а стержень довольно массивен, то размах дрожаний стержня будет мал. Причем, чем больше частота вибраций оси подвеса стержня, тем меньше размах его дрожаний около любого положения.
Таким образом, делаем вывод о том, что высокочастотная вибрация оси подвеса стержня не окажет принципиального влияния на работу моего прибора. Иначе говоря, стержень при любом положении самолета неизбежно будет направлен к земле.
После такого анализа принимается решение о передаче моей конструкции на завод-изготовитель
Теперь представим себе, что я летчик-испытатель и мне поручено опробовать прибор в деле. В качестве модели самолета и прибора лучше всего использовать специально изготовленную установку. С этой установкой и проведем наши испытания.
При малых оборотах двигателя стержень действительно все время стремится к нижнему относительно Земли положению независимо от ориентации корпуса модели самолета. Так что мой прибор надежно указывает вертикальное вниз направление.
При увеличении скорости вращения двигателя, однако, наступает такая ситуация, когда верхнее положение стержня также становится устойчивым, как и нижнее. Такое необычное поведение стержня хорошо наблюдается на нашей модели. Таким образом, при больших оборотах двигателя пилот не может отличить "верх" от "низа". Если самолет ориентирован относительно Земли строго горизонтально, а случайный толчок забросит стрелку прибора в верхнее положение, она так и останется в нем. Это явление может дезориентировать пилота, что вернее всего приведет к трагическим последствиям. Если же такое случайного толчка не было, но пилот станет поворачивать самолет вокруг продольной оси, то он с удивление обнаружит, что стрелка прибора неподвижна относительно самолета. Из этого факта пилот должен сделать вывод, что: 1) либо самолет не поворачивается относительно Земли (неисправны рули), 2) либо стрелку прибора заклинило (неисправен прибор).
Итак, испытания показали, что моя конструкторская идея порочна. Она совершенно неработоспособна при больших частотах вибрации оси подвеса стержня.
Таким образом, практическая важность знания законов, управляющих влиянием высокочастотной вибрации точки подвеса жесткого маятника на его поведение продемонстрирована (на наш взгляд) достаточно эффектно и убедительно. Отсюда следует острая практическая необходимость всестороннего изучения теории механических колебаний.
21
Лаборатория ЭКСПЕРИМЕНТАЛЬНОЙ ФИЗИКИ
Конспект занятия «Гидравлический удар или о прочности стекла на разрыв»
Цели занятия:
- Ознакомиться с теорией гидравлического удара
- Рассчитать предел прочности стекла на разрыв, используя данную идеологию
Решаемые задачи:
- Получить расчетную формулу
- Методами покадрового анализа и энергетическим рассчитать скорость молотка в момент удара
- В серии опытов измерить среднее значение массы жидкости, создающее критическое для стекла
давление
- Оценить достоверность полученного результата
Занятие начинается с обсуждения вопроса, почему поток воды можно достаточно быстро перекрыть водопроводным краном, но для такого действия на трубопроводе приходится долго вращать штурвал колеса.

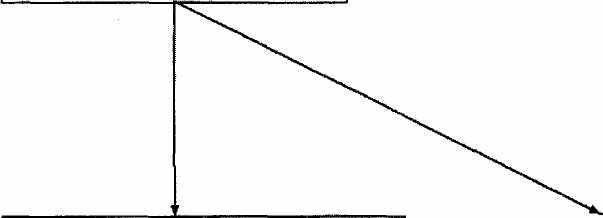
Рассматривается модель мгновенной остановки потока жидкости в трубе и делается вывод о величине возникающего при этом давления.
т' = pScr m'v = Fr- PSr P = pcv
Проводится эксперимент по выбиванию дна у бутылки с водой и рассматривается схема этого эксперимента.
М И

СТ
| Г? | | ■ | | ■ |
| | | т | | |
| | | | | |
| | | |||
| | 1 | |
t У r=0 V=0
Выясняется, что при равных массах молотка и бутылки они обмениваются энергией и в конечном итоге вся энергия молотка передается воде
MV
22
Выводится формула для давления жидкости на дно бутылки
Р = pcv= рсЛ—V V т
Сила, действующая на дно
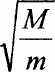
Механическое напряжение в стекле
F
= рсл\—У-т
дна


дна
Проводятся эксперименты по определению скорости удара молотка о горлышко бутылки

Учащиеся в режиме мелких групп проводят измерения критической массы воды, необходимой для разбивания бутылки, а также измеряют основные параметры эксперимента.
23
М = 0,45 кг с = 1450 м/с
м
'м2
SdHa = 3,4-Ю'м
Scme=6,2-10~4M2
V = 2,5 м/с
Получают значение для предела прочности стекла на разрыв и сравнивают его с табличным, попутно оценивая точность полученного результата.
а = 2,1-107 Па Табличное значение
Аа = 0,2-107 Па ° = 2-ь2,5407 Па
24
Лаборатория «Исследовательские задачи в математике: уравнения с
параметром»
План-конспект по теме: Линейные уравнения с параметрами
Цель: формирование у учащихся умений решать линейные уравнения, содержащие параметр; умений анализировать вид уравнения, обобщать.
Форма занятия: практикум План занятия:
- Организационный момент
- Целеполагание
- Актуализация знаний
- Основная работа
- Подведение итогов
Средства: интерактивная доска, карточки с заданиями (обязательный и дополнительный блоки). Основные вопросы занятия:
1. Общий метод решения уравнения вида ах = Ь, решение линейных уравнений с параметрами,
сводящихся к виду ах - Ъ ;
2. Линейные уравнения с параметрами, содержащие дополнительные условия (корень равен данному
числу, прямая проходит через точку с заданными координатами, уравнение имеет отрицательное
решение и т.д.).
Ход занятия
Организационный момент
Целеполагание. Сообщение темы и целей занятия.
Актуализация знаний:
- График линейной функции, свойства.
- Линейное уравнение, методы его решения.
- Сколько решений может иметь линейное уравнение
