Программа дополнительного образования для круглогодичных школ интеллектуального роста авторы проекта
| Вид материала | Программа |
- График проведения круглогодичных школ интеллектуального роста, школ художественно-эстетического, 171.43kb.
- Администрация Муромского района Управление образования, 2425.95kb.
- Программа по литературе для школ и классов с углубленным изучение литературы Авторы:, 5585.49kb.
- Примерная программа для общеобразовательных школ, гимназий, лицеев алгебра и начала, 622.43kb.
- Казачкова Лариса Леонидовна, педагог дополнительного образования Бражное 2007 г пояснительная, 271.72kb.
- Федерального Государственного Учреждения «Санкт-Петербургский научно-исследовательский, 1055.69kb.
- Курс «Eвропейские науки» для продолжающих, 669.25kb.
- Н. В. Жаткина 2011г положени, 17.03kb.
- Авторская программа для общеобразовательных школ, гимназий, лицеев Краснодарского края:, 239.96kb.
- Программа составлена на основе проекта федерального компонента Государственного стандарта, 729.68kb.
Теоретическая часть
Линейные уравнения могут иметь:
а) единственное решение;
б) отсутствие решений;
в) бесконечное множество решений.
Алгоритм решения такого типа уравнений:
- Определить «контрольные» значения параметра. В таких уравнениях «контрольными» значениями
параметров, как правило, являются значения, обращающие в нуль коэффициенты при х.
- Решить уравнение относительно х, при контрольных значениях параметра.
- Решить уравнение относительно х, при значениях, отличных от «контрольных».
- Записать ответ в виде:
25
Ответ: 1) при значениях параметра..., уравнение имеет корни ...;
- при значениях параметра ..., уравнение имеет корни ...;
- при значениях параметра ..., уравнение корней не имеет.
Решение задач
Задание 1. Решить уравнение с параметром 2а{а-2)х -а-2.
Задание 2. В зависимости от значений параметра а решить уравнение (а2 -1)х = 2а2 + а -3.
Задание 3. Решить уравнение с параметром Ь2х-1 - 49х + Ь .
Задание 4. Указать, при каких значениях параметра а уравнение ах + 7 = 2х + 3 имеет корень, равный а) 1; б) 2?
Дополнительные задания.
- b(b + x) = 49-7x;
- Найдите все значения параметра а, при которых уравнение За + 14х = 12х + 3я имеет корень,
меньший 1.
Перечень примерных заданий по теме «Линейные и квадратные уравнения с параметрами» Линейные уравнения с параметрами.
- х - 4 = ах;
- (а + 1)х = а + 1;
3) 4)
5)
- Зх -1 = а + 2х + 3;
- При каких значениях а уравнение 5(х-±)-3(я-2) = 5 имеет корень, принадлежащий
промежутку 1 < х < 6 ?
- При каких а уравнение [а2 - 5а + брс -а-2 не имеет корней; корнем является любое число?
- Указать, при каких значениях параметра а уравнение 0,5(5х -1) = 4,5 - 2а(х - 2) имеет
бесконечное множество решений.
- (a2 -l)x = a2 -а-2;
- Зх + 9-а\а — х);
- *=0;
х-2
- 4 + гах = Зх + 1;
- = = 0;
х-1
15) 3 ■■ * ;
кх-12 Зх-А;
16) тх +1 = х + т;
2
17) За + х = ;
Ь + х
18) 2wx + —— = 0;
У х-10
26
19) ах + 2х + 3 = х +1; 20)
a(xl)+
а +1 а\х~\)
Квадратные уравнения, содержащие параметры
- Найти все те значения параметра р , при которых корни квадратного уравнения рх2 - 2х +1 = 0
больше ,чем -1.
- При каких значениях параметра а один из корней квадратного трёхчлена
23) f{x) = х2 + 2bx + b-3 отрицателен при всех х, удовлетворяющих условию 2< х <3?
24) При каких значениях параметра к число -2 заключено между корнями уравнения
-х2
25) При каких значениях параметра а число 3 заключено между корнями уравнения
х2 -
- Найдите все значения параметра а, при которых квадратное уравнение
Зх2 - 4(3о - 2)д; + о + 2 = 0 имеет корни хги х2, удовлетворяющие условию х1 < а < х2.
- При каких значениях параметра t уравнение (t + l)x2 +tx-l = 0 имеет единственный корень?
- При каких значениях параметра а уравнение (а + 9)х2 + ах-1 = 0 имеет единственный корень?
- При каких значениях Ъ уравнение Ьх2 -5х + 0,256 = 0 имеет два корня?
- Найдите все значения параметра а, при которых уравнение ах2 -(2я+ 6)х + За + 3 = 0имеет
единственный корень?
- При каких значениях параметра Ь уравнение (Ь + 5)х2 + (2Ь+ 10)х + 4 = 0 имеет только один
корень?
- При каком значение а уравнение ах2 +10д: + а = 0 имеет два корня?
- Определите количество корней уравнения
= а при всех неотрицательных значениях
параметра а.
27
Лаборатория «Геометрия: метод геометрического места точек в задачах
на построение»
План-конспект по теме: Некоторые специальные геометрические места точек
Цель: Сформировать у учащихся целостное представление о сущности метода геометрических мест, используемого при решении задач на построение; рассмотреть некоторые специальные ГМТ; формирование навыков применения метода геометрических мест точек к решению задач на построение.
Оборудование: проектор, инструменты для измерений и построений фигур на плоскости. ПЛАН ЗАНЯТИЯ: I. Обоснование актуальности изучения геометрических мест точек в школьном курсе геометрии.
Учащиеся знакомятся с понятием ГМТ в 7 классе на примерах окружности, геометрического места точек, равноудаленных от концов отрезка и биссектрисы угла. Эти три ГМТ часто встречаются и при дальнейшем прохождении материала. Однако, понятие ГМТ, как показывает практика, трудно усваивается учащимися и быстро ими забывается. Для сознательного и прочного усвоения учащимися понятия ГМТ необходимо рассматривать больше примеров, чем их дано в учебнике.
Главное значение ГМТ заключается в том, что с их помощью решаются весьма многие и разнообразные геометрические задачи на построение. Очень часто, когда решение задачи на построение сводится к отысканию положения точки или нескольких точек на плоскости, задача легко, удобно и изящно решается путем использования двух подходящих ГМТ.
Следовательно, крайне необходимо уделять большее внимание на изучение разнообразных ГМТ.
II. Рассмотрение некоторых специальных ГМТ.
Знакомство учащихся с некоторыми м
специальными ГМТ осуществляется
преподавателем на проблемной лекции,
помощью компьютерной динамической
системы «Живая геометрия» наглядно
демонстрируется схема построения ГМТ
осуществляется анализ всевозможных
условий существования этих
геометрических мест точек.
Планируется рассмотрение
следующих ГМТ:
1. ГМТ, из которых данный отрезок
под данным углом.
и
виден
2. ГМТ, разность квадратов расстояний
которых до двух данных точек есть данная постоянная величина.
от
28
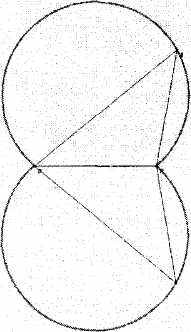
3. ГМТ, сумма квадратов расстояний от которых до двух данных точек есть данная постоянная величина.
1
ш
| Ф CD = 5,7* c« ■ | ■; . | | | . ■ :| |
| | | | \ | ■ - ■ ■ Ш \ ■■■.... 1 |
| | LL | | | M . . : s |
| | | | | / ' -г- I |
4. Окружность Аполлония - ГМТ, отношение расстояний от которых до двух данных точек, есть данная постоянная величина, отличная от единицы.
К
на
Планируется следующих
метода мест при
• решение
| | тгё | | -1 |
| | | | : |
| | | | |
| | | | |
| | | / i | 1 |
| | | | |
заданным элементам.
III. Применение изученных ГМТ решению задач построение.
рассмотрение вопросов:
• применение
геометрических
решении задач на
построение;
задач на
построение
треугольников по
29
hu, rna, Ia - высота, медиана, биссектриса, проведенные соответственно из вершины А. Р -периметр треугольника, р - полупериметр треугольника, г - радиус окружности, вписанной в треугольник, R - радиус окружности, описанной около него.
1. Постройте треугольник ABC по заданным его элементам:
а) /.A, la, ha;
б) ZB,lb,r;
в) a, R, К;
г) с, тс, Z С;
д)я, ZA, Ьъ\
е) ZA, hb, ma;
ж) a, ha, n, если п2=Ь2+с2;
з) a, ha, n, если п2=Ь2-с2;
и) Z A, a, q, если q Ъ +с ; к) a, ma,f если/=£2-с2; л) ZA, a,f, еслиf=Ъ -с";
м) a, ha, p, q, если - = —; с q
Форма занятия: практикум.
Учащиеся в группах по 2-3 человека осуществляют работу над поиском решения выбранной задачи, обязательно прохождение всех этапов работы над задачей (анализ, построение, доказательство, исследование). Результаты оформляются в компьютерной среде «Живая геометрия». Преподаватель выступает в роли консультанта.
Полученные результаты презентуются на итоговом занятии перед всей группой учащихся.
Оценка проекта осуществляется по следующей схеме:
Оценка проекта
учащихся
класса
о/к - оценка консультанта, с/о - самооценка, о/г - оценка группы
| о/к | с/о | о/г | итог |
| 1 2 3 | 1 2 3 | 12 3 | |
30
Смета расходов
Смета расходов школы должна включать оплату работы преподавателей, ведущих лекционные и лабораторно практические занятия с группами учащихся. Таблица составлена из расчета на одну группу учащихся (всего 6 групп):
| Вид деятельности | Количество дней | Количество часов в день | Полное количество часов |
| Лекция | 3 | 3 | 9 |
| Лабораторно-практические занятия | 3 | 4 | 12 |
| Игровые тренинги | 3 | 2 | 6 |
| Индивидуальная работа с учащимися | 3 | 2 | 6 |
| Рецензирование контрольных и олимпиадных работ | 3 | 1 | 3 |
| Оценка результатов исследовательской работы учащихся (итоговая конференция) | 1 | 3 | 3 |
| Итого на одного преподавателя в течение всей школы | | 39 | |
Полное количество часов на всю школу
39x6-234 часа
10
Аудиторный фонд и учебное оборудование
- Зал для заключительной конференции, способный вместить всех учащихся школы (100 чел.) с
проектором -1 шт.
- Лекционная аудитория (на 50 чел.) с проектором, интерактивной доской - 2 шт.;
- Аудитории для практических занятий (на 15-20 чел.) - 6 шт.; в том числе с проектором и
звуковыми колонками (интерактивной доской и звуковыми колонками) - 4 шт.
- Компьютерный класс (не менее 10 комп.) с проектором - 2 шт.
- Ноутбуки для групповых занятий - 4 шт.
Формы последующего сопровождения
- Рекомендация к зачислению в «Заочную естественно-научную школу (ЗЕНШ) при
Сибирском федеральном университете»; курирование поступления в «Заочную физико-
техническую школу» (ЗФТШ) при МФТИ.
- Организация дистанционного обучения (организация мини-групп типа «коллективный
ученик», работающих над выбранной на последнем этапе проведения данной школы
темой).
3. Продолжение обучения в школах интеллектуального роста в течение
2012-2013 гг.
Формы и критерии оценки деятельности учащихся
Предполагается рейтинговая оценка деятельности учащихся школы.
Баллы начисляются за все виды учебной деятельности учащегося школы интеллектуального роста:
- Решение учебных задач на практических занятиях;
- Участие (с учетом полученных результатов) в олимпиаде по математике и физике);
- Участие (с учетом гюлученных результатов) в играх «Математическая карусель»,
«Квест», «Физбой», «Крокодил»
- Выполнение учебного проекта и его презентация на конференции.
Учебно-тематический план
| № | Наименование разделов (тем) | Количество часов | |
| теория | практика | ||
| Модуль 1 | | | |
| Лаборатория «Геометрия» | | | |
| 1 | Геометрические построения на плоскости | 1 | |
| 2 | Основные понятия | 1 | |
| 3 | Этапы решения задач на построение | | 1 |
| 4 | Элементарные задачи на построение | | 2 |
| 5 | Геометрические места точек (ГТМ)Простейшие и некоторые специальные ГМТ | | 1 |
| 6 | Решение задач на построение методом ГМТ | | 2 |
| 7 | Задачи на построение треугольников по заданным элементам | | 1 |
| Лаборатория «Исследовательские задачи в математике: | | | |
| уравнения с параметром» | |||
| 1 | Параметр, уравнение с параметром | 1 | 1 |
| 2 | Общий алгоритм решения уравнений с параметром | 1 | 2 |
| 3 | Основные методы и приемы решения уравнений с параметрами | 1 | 3 |
| Лаборатория «Вероятность случайного события: | | | |
| геометрические вероятности, метод Монте-Карло и его | |||
| приложения» | |||
| 1 | Понятие геометрического определения вероятности | 1 | 1 |
| 2 | Применение геометрических вероятностей для решения задач практического содержания | | 2 |
| 3 | Задача Бюффона | | 2 |
| 4 | Метод Монте-Карло | 1 | 2 |
| | | | |
| Модуль 2 | | | |
| Лаборатория экспериментальной физики | | | |
| 1 | Сила трения | | 1 |
| 2 | Гидравлический удар | 1 | 1 |
| 3 | Стробоскопическое исследование движения, сложение колебаний (фигуры Лиссажу) | | 1 |
| 4 | Определение положения центра масс | | 1 |
| 5 | Баллистические методы измерений | | 1 |
| 6 | Закономерности течения идеальной жидкости | | 1 |
| 7 | Геометрическая оптика линз и призм | 1 | 1 |
| Лаборатория методологии физики | | | |
| 1 | Теория механических колебаний | 1 | 1 |
| 2 | Уравнение и закон движения | 1 | |
| 3 | Гармонические колебания | | 2 |
| 4 | Свободные и вынужденные колебания | | 2 |
| 5 | Линейные колебательные системы | | 2 |
| Лаборатория Интерактивный музей физики | | | |
| 1 | Капельница Галилея | | 1 |
| 2 | Формула Эйлера | 1 | 2 |
| 3 | Опыты Фарадея | 1 | 2 |
| 4 | Дифракция Фраунгофера и Френеля | 1 | 1 |
| | | | |
| | | | |
