Джон Р. Хикс. "Стоимость и капитал"

Вид материала

Документы

Подобный материал:

• 1 Стоимость и капитал, 550.67kb.
• Считается, что термин «интеллектуальный капитал» ввел в оборот Дж. Гэлбрейт. Существует, 129.05kb.
• Учет уставного капитала, 64.1kb.
• Капитал предприятия характеризует общую стоимость средств в денежной, материальной, 3330.22kb.
• -, 67.47kb.
• Финансовый капитал и динамика империализма, 118.88kb.
• Джон Стюарт Милль. Всвоем учебник, 239.09kb.
• Экономическая теория Дж. Р. Хикса, 2756.7kb.
• Изменение человеческого капитала России под воздействием миграционных процессов Лисовская, 41kb.
• Уставной капитал, 49.83kb.

[Очевидно, должны быть случаи, когда количества всех, кроме одного, факторов и соответствующих продуктов выбираются на­угад, и оказывается, что никакого количества этого одного фактора но хватает, чтобы произвести данный набор продуктов. Если количество продуктов очень велико, а в распоряжении фирмы имеет­ся лишь немного всех, кроме одного, факторов, то даже огромных объемов этого фактора может не хватить (при условии, что его не так легко использовать в различных целях). Однако представля­ется, что эта трудность не имеет особого значения. Развивая ана­лиз, мы всегда будем начинать с положения равновесия, т. е. с набора величин, отражающих соответствующие количества. И больше нет необходимости предполагать, что возможны те или иные отклонения от этого положения. Все это, я полагаю, допустимо. ].

Пусть задан набор соответствующих величин, отража­ющий некоторое количество факторов и продуктов; при этом движение производства может быть как угодно сложным - его можно свести к следующим видам (или к одному из них): (1) производство одного из продуктов может быть расширено за счет производства другого продукта, т. е. может произойти замещение одним продуктом другого; (2) один фактор может заменить другой; (3) количества одного фактора и одного продукта могут быть одновременно увеличены (или уменьшены) [В ходе исследования даже этот вопрос без особой необходи­мости усложнен-ведь первые два вида могут быть сведены к третьему. Так, можно считать, что замещение продуктом Х другого продукта-продукта У - состоит из: (1) одновременного возра­стания количеств продукта Х и фактора А; (2) одновременного уменьшения количеств фактора А а продукта Г; при этом количества фактора и продукта так приводятся в соответствие, что разнонаправленные изменения количества фактора взаимно погашают­ся. Таким образом, у нас при желании нет необходимости рас­сматривать выделенные два вида изменений. Но я думаю, что удобнее будет все-таки сохранить такое разделение.].

Если, с точки зрения предприятия, цены всех продук­тов и всех факторов заданы, то количество производствен­ных факторов, которые оно будет применять, и количество продуктов, которые оно произведет, будут определены условием, согласно которому прибыль максимальна. Тем самым подразумевается, что ее нельзя тем или иным путем увеличить. Таким образом, мы получим следующие условия равновесия.

(1) В соответствии с тем, что цена в условиях равнове­сия равна предельным издержкам, мы имеем три вида условий:

а) соотношение цен всяких двух продуктов должно равняться предельной норме замещения между ними (те­перь это будет производственная норма замещения).

б) соотношение цен всяких двух факторов должно равняться соответствующей предельной норме замещения.

в) соотношение цен всякого фактора и всякого про­дукта должно равняться предельной норме трансформа­ции между фактором и продуктом (иначе говоря, предельному продукту фактора, выраженному в соответствующем продукте).

(2) Теперь пришла очередь условий стабильности.

Преобразование фактора в продукт потребует, чтобы со­блюдалось определенное условие (оно уже установлено для случая с одним фактором и одним продуктом) - убывание предельной нормы преобразования или убывание предельного продукта. Чтобы осуществилось замещение одного продукта другим, необходимо соблюдение условия «возрастания предельной нормы замещения», иначе гово­ря, возрастание предельных издержек, выраженных в из­держках производства другого продукта (предельных издержек альтернативных возможностей); чтобы осущест­вилось замещение одного фактора другим, необходимо «убывание предельной нормы замещения» [Предельная норма замещения продуктов возрастает, так как совокупная стоимость выпускаемых продуктов должна быть мак­симизирована; предельная норма замещения факторов убывает, так как совокупная стоимость факторов должна быть минимизирована. Эти условия легко проверить графически, если предположить, что количество всех факторов и продуктов известно, а значения двух заданных продуктов (или факторов) откладываются по осям координат.].

Справедливость этих условий сохраняется не только для случая, когда осуществляются единичные процессы замещения или преобразования (замещение одного про­дукта одним продуктом, одного фактора - одним факто­ром, преобразование одного фактора в один продукт), но и для случая, когда в процессе замещения или преобразования участвуют группы товаров и факторов. Предельная норма замещения между любой парой товарных групп должна расти, а предельная норма замещения между любой парой групп факторов - уменьшаться; предельная норма преобразования между любой группой факторов и группой товаров должна уменьшаться [Иначе говоря, пусть количество каждого фактора из некоторой группы увеличивается на некоторую произвольную величину, и известны соответствующие значения приростов для количеств продукта, выпуск которого становится возможным благодаря увеличению количества фактора. Далее, пусть количество каждого фактора возрастает вторично на такую же величину; тогда этого приращения окажется недостаточно, чтобы количество продукта возросло на первоначальную величину (см. правило, приведенное в гл. I, § 5).].

В результате действия последнего правила предельные издержки производства определенного продукта должны с ростом выпуска увеличиться, даже если предложение всех факторов (за исключением заданных производствен­ных возможностей), как считается, изменяется.

(3) Наконец, вместо единственного условия, предполагающего, что прибыль выражается положительной вели­чиной, мы получили целый «набор» условий. Прибыль должна быть положительной, чтобы не оказалось выгод­ным прекратить сразу все производство. Но также не должно быть выгодным частичное прекращение производ­ства с целью исключить из него какой-либо из продуктов X, Y, Z и т. д. или какую-либо группу этих продуктов. Следовательно, средние издержки производства каждого продукта должны увеличиваться, как и средние издержки производства группы товаров, включая целую их группу из всех товаров. Только последнее из рассмотренных условий (все, что было сказано выше в настоящей главе о средних издержках, связано с этим условием), как я полагаю, действительно может вызвать заметную озабо­ченность. Ведь довольно легко допустить, что единичный продукт (или подгруппа товаров), входящий в совмест­ный продукт, будет обыкновенно производиться при воз­растающих средних издержках (сильно растущих пре­дельных издержках). Производство товаров, входящих в такую подгруппу, окажется серьезно ограниченным, если выпуск прочих продуктов не будет расширяться.

Таковы условия равновесия для общего случая. Теперь можно продолжать исследование, как мы это делали в части I. Допустим, что условия равновесия (2) и (3) справедливы для положений, близких к положению рав­новесия. Таким образом, мы затем и выведем законы рыночного поведения фирмы.

> Часть II. Общее равновесие - Глава VII. Дополняемость и заменяемость в сфере производства

1. Теперь нам необходимо рассмотреть вопрос о том, что происходит, если определенные цены на продукты и факторы производства, принадлежащие фирме, находив­шейся в состоянии равновесия, изменяются. Фирма ис­пользовала бы определенные количества факторов и про­изводила бы определенные количества продуктов; каким образом изменение цен скажется на этих количествах?

Эта проблема в точности совпадает с той, которую мы рассматривали в главах II и III применительно к частно­му лицу; наше исследование будет продолжено в том же направлении, хотя и неудивительно, что на этот раз нам придется обратить внимание на несколько иное множество точек.

Начнем с самого простого случая, с того, который мы подробно обсуждали в предыдущей главе. Производственные возможности самого предпринимателя ограничены; и противном случае он применяет только один фактор производства и производит только один продукт. Тогда его положение равновесия показано на рис. 19 в предыдущей главе; оно опять представлено точкой Р на рис. 20 ниже. Предположим теперь, что цена фактора производства па­дает. Непосредственным результатом этого (до того, как предприниматель как-то изменит объем производства) станет увеличение прибыли с ОК до ОК₁. Но так как РК₁ не касается кривой производства, то ОК₁ не является мак­симальной прибылью, которую может обеспечить себе предприниматель в новых условиях. В его интересах пе­реместиться вдоль кривой производства в точку Р', каса­тельная Р'К₂ к которой параллельна РК₁.



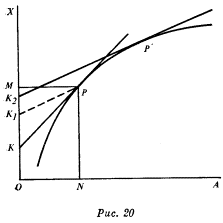
Так как кривая производства выпукла вверх (что со­ответствует уменьшению предельного продукта или возрастанию предельных издержек), точка Р', в которой касательная к этой точке поднимается не так круто, как касательная в точке Р, должна лежать правее точки Р. Та­ким образом, паде­ние цены на фактор производства приво­дит к его более ин­тенсивному использо­ванию и к увеличе­нию выпуска продук­ции.

Повышение цены продукта, которое также выражается в уменьшении наклона касательной, приве­дет к точно таким же последствиям.

Эти следствия крайне просты, но методы, при помощи которых они были получены, позволяют вывести и другие, более интересные заключения. Точно так же, как и в слу­чае с частным лицом, изменение цен перемещает фирму в положение, которое графически можно представить как точку касания новой прямой, имеющей другой наклон. Но когда речь шла о частном лице, новая прямая каса­лась другой кривой, когда же речь идет о фирме, она касается той же самой кривой. Таким образом, если стоит вопрос о производстве, нам не приходится сталкиваться с чем-либо подобным эффекту дохода, с которым было столько хлопот в теории полезности. Единственный на­блюдаемый здесь «эффект производства» в чем-то похож на эффект замещения; он выражается движением вдоль кривой (в данном случае вдоль кривой производства, рань­те-вдоль кривой безразличия), свойства которой извест­ны нам из условий стабильности.

Но эффект производства, так же как и эффект заме­щения, таит в себе другую трудность - трудность, связан­ную с дополняемостью. Этот вопрос оказывается на самом деле в теории производства более запутанным, чем в тео­рии полезности. Если в теории полезности нам необходи­мо было просто рассмотреть отношения между товарами, которые можно было считать (в определенном смысле слова) одинаковыми, то здесь мы имеем дело с товарами двух видов - с факторами производства и производимыми продуктами. Нам предстоит распуты­вать и отношения между товарами од­ного вида, и отноше­ния между товарами различных видов.

2. В качестве пер­вого шага на этом пу­ти воспользуемся до­вольно причудливым примером, в котором нас не будет беспоко­ить соотношение фак­торов и продуктов. Предположим, что объем продукции, ко­торый должна произ­вести фирма, опреде­лен, так что он не может измениться под влиянием обыч­ных колебаний цен. Предположим, однако, что исполь­зуются два производственных фактора - А и В. Тогда задача состоит в том, чтобы произвести заданный объем продукции с минимальными издержками. Это можно изобразить графически (см. рис. 21). Кривая производства будет иметь такую же форму, как и кривая безразличия: она обращена выпуклостью вниз (т. е. речь идет об убывании предельной нормы замещения между факторами). Точка Р, в которой РК касается кри­вой производства, будет положением равновесия, если соотношение цен на факторы производства такое же, как соотношение МК и РМ. Предположим теперь, что цепа фактора А падает. Количество фактора В, равное по стоимости количеству ON фактора А, сократится с МК до MK₁; а совокупные издержки производства (измеренные в единицах фактора В) уменьшатся с ОК до ОК₁. Но так как РК₁ не касается кривой производства, то издержки будут уменьшаться еще (до величины ОК₂), если переме­щаться вдоль кривой производства к точке Р', где Р'К₂ параллельна PK₁.



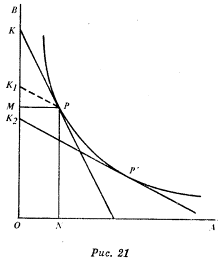
В новой точке равновесия используется больше факто­ра А и меньше фактора В - произошло замещение фак­тора В фактором А. Этот результат совершенно так же однозначен, как и в случае, когда применяется один фак­тор и выпускается один продукт. Тогда падение цены фактора А приводило к увеличению продукта X, здесь оно приводит к сокращению спроса на фактор В. Каждое из этих последствий неизбежно.

3. Так же как и в теории полезности, нам следует ожидать, что такого рода неизбежные результаты в этих двух случаях получаются потому, что каждый раз мы работали всего с двумя переменными - одним фактором и одним продуктом - или с двумя факторами. Можно пола­гать, что, как только мы перейдем к более сложным слу­чаям, такая определенность исчезнет.

Предположим, что фирме опять надо произвести за­данный объем продукции, но теперь она использует три фактора: А, В, С. Предположим, далее, что цена факто­ра А падает. Тогда, поскольку отношение цен факторов В и С не изменяется, их можно (как в теории полезно­сти) рассматривать как единичный фактор [Как и в теории полезности, это можно обосновать математи­чески, анализируя условия стабильности. См. сноску к гл.II п.4.]. Следователь­но, спрос на фактор А должен опять неизбежно возрасти, а спрос на факторы В и С (взятые вместе) должен сокра­титься. Неизбежно произойдет замещение фактором А остальных факторов, вместе взятых.

Как и прежде, однако, не обязательно, чтобы происхо­дило замещение каждого из прочих, кроме A, факторов. Фактор В может быть дополняющим по отношению к фактору А; в этом случае спрос на фактор В возрастет. Произойдет замещение факторами А и В фактора С.

Как и в теории полезности, условие взаимодополняе­мости факторов A и В заключается в том, чтобы замеще­ние фактором А фактора С (при постоянном количестве фактора В) сдвигало бы предельную норму замещения фактором В фактора С «в пользу» В.

Таким образом, пока объем продукции остается неизменным и пока мы рассматриваем только замещение од­ них факторов другими, можно вывести в точности такие же правила, как и те, что мы установили, изучая эффект замещения в бюджете потребителя. Ясно, к каким выводам мы в действительности придем, если рассмотрим случай, когда фирма использует постоянное количество производственных факторов и (под влиянием изменения цен) изменяет объем производства совместных продуктов. Новым будет лишь то, что повышение цены вызовет замещение этим продуктом всех других продуктов, а также, быть может, и замещение какими-либо дополняющими продуктами.

4. Что же произойдет теперь, если изменяться будут и количества факторов, и количества продуктов? Это самый важный случай.

Предположим, что фирма производит один продукт Х и использует два фактора производства - А и В. Тогда спрос на фактор А должен неизбежно увеличиться, если его цена падает, - ведь отношение, связывающее количество факторов с количеством продукта, обнаруживает свойства, аналогичные тем, с которыми мы знакомы. Но как падение цены повлияет на предложение товара Х и спрос на фактор В? Если мы будем рассматривать здесь продукт отдельно, то может показаться, что его предложение должно непременно увеличиться (см. рис. 20); если рассматривать сам по себе спрос на производственный фактор, то может показаться, что он непременно должен уменьшиться (см. рис. 21). Такой ход рассуждений будет, однако, неправильным. Если бы так рассуждать можно было применительно к случаю, когда используются три фактора (который мы только что обсудили), то оказалось бы, что спрос на фактор А должен увеличиться за счет спроса на фактор В и за счет спроса на фактор С. Мы знаем, что это не обязательно так: либо В, либо С могут быть дополняющими к А.

Если использовать понятие дополняемости при анализе случая двух факторов и одного продукта, то станет ясно, что расширение спроса на фактор А может быть уравновешено трояким образом.

(1) Предложение продукта Х может увеличиться, а спрос на фактор В - сократиться (нет никакой дополняемости) .

(2) Предложение продукта Х может увеличиться, но может возрасти и спрос на фактор В (здесь А и В - взаимодополняемые факторы).

(3) Спрос на фактор В может сократиться, но и предложение продукта Х может также уменьшиться. В этом cлучае обнаруживается необычная «обратная» дополняе­мость между фактором и продуктом. Становится ясно (и это действительно непосредственно следует из сравнения рис. 20 и рис. 21), что обычное отношение между факто­ром и продуктом, при котором расширение использования фактора приводит к увеличению производства продукта, имеет много общих черт с отношением заменяемости меж­ду товарами, между факторами или между продуктами. Но если это обычное отношение соответствует замещаемости, то должно быть, по-видимому, нечто такое, что соот­ветствует дополняемости. Здесь мы и сталкиваемся с этим нечто. Назовем его «регрессией» (regression). Если фак­тор А и продукт Х регрессивны, то замещение фактором А фактора В уменьшит предельный продукт фактора В, выраженный в единицах X, и, таким образом (при дан­ных ценах В и X), вызовет сокращение предложения X.

У меня такое чувство, что в этом месте читатель протрет глаза и скажет, что в наших рассуждениях что-то не так. Регрессия является таким странным отношением, что его трудно согласовать со здравым смыслом. Кажется, мы упустили из виду нечто такое, что или исключает возмож­ность регрессии, или хотя бы очень резко ограничивает вероятность ее существования. Посмотрим, что же это мо­жет быть.

5. Если третий способ уравновесить расширение спро­са на фактор А (А и Х регрессивны) представляется весь­ма маловероятным, то второй (A и В - взаимодополняе­мы) легко согласуется со здравым смыслом. В этом, как мы увидим, и состоит ключ к решению задачи. Существу­ют причины, позволяющие нам расположить три наших способа в следующем порядке по степени их вероятности. Скорее всего, А и В будут факторами взаимодополняемы­ми; затем, вероятно, что не будет отношений ни дополняе­мости, ни регрессии; наконец, наименее вероятно, что бу­дет наблюдаться регрессия. Причины всего этого взаимо­связаны.

Прежде всего возьмем крайний случай, когда можно доказать, что два фактора должны быть взаимодополняе­мы. Как мы помним, два фактора взаимодополняемы, если увеличение количества применяемого фактора А (при по­стоянном количестве фактора В) и соответствующее уве­личение объема выпускаемого продукта Х «сдвигает» предельную норму трансформации фактора В и Х «в пользу» B, иными словами, повышает значение предель­ного продукта фактора В. Следовательно, критерием взаимодополняемости факторов является нe что иное, как давно используемый и известный критерий «совместного функционирования» факторов; увеличение количества од­ного из них повышает предельный продукт другого [См.: А. Пигу. Экономическая теория благосостояния, часть IV, гл. 3.]. В этом случае у нас нет необходимости менять принятые в настоящее время определения [Однако мое определение в точности совпадает с определени­ем проф. Пигу только в случае, когда рассматриваются один продукт и два фактора. Если же факторов больше чем два, мой кри­терий будет зависеть от того, что произойдет с предельным продуктом фактора В (его количество неизменно), если предложение остальных факторов (С и др.) не постоянно, а изменяется таким образом, что величины их предельных продуктов остаются без из­менения.] .

Рассмотрим теперь, что происходит при тех особых ус­ловиях производства, когда не существует ограничения, задаваемого фиксированными «производственными ресур­сами» предприятия [Таким образом, в рассматриваемом случае объем производст­ва продукта Х является линейно-однородной функцией количеств факторов А и В. Этот случай иногда называют «постоянной доход­ностью, обусловленной расширением масштабов производства».], так что издержки не растут, хотя объем выпускаемой продукции увеличивается, когда от­сутствует экономия, обусловленная расширением масшта­бов производства, и издержки не снижаются при расширении объема выпускаемой продукции, а ситуация точно соответствует условиям совершенной конкуренции. Из­держки (и средние, и предельные) постоянны: прибыль равна нулю; если цена единицы каждого фактора равна его предельному продукту, то стоимостной объем продук­та в точности покрывает стоимостной объем издержек3. Так как предельные издержки постоянны, то увеличение объема продукта, обусловленное одновременным пропор­циональным увеличением обоих факторов, предельный продукт двух факторов, взятых вместе, также должно быть постоянным. Но этот совместный предельный продукт складывается из четырех частей:

(1) предельною продукта фактора А при постоянной количестве фактора В;

(2) приращения (положительного или отрицательного) этого предельного продукта, обусловленного одновременным увеличением количества фактора В. Приращение будет положительным, если А и В - взаимодополняемые факторы, отрицательным - если они заменители;

(3) предельного продукта фактора В при постоянном количестве фактора А;

(4) аналогичного приращения (положительного или отрицательного), обусловленного увеличением количества фактора А. Здесь приложимо указанное выше правило.

Теперь мы знаем, что при увеличении количества ис­пользуемых факторов первая и третья части уменьшают­ся. Но мы знаем также, что целое не уменьшается. Сле­довательно, уменьшение частей (1) и (3) должно быть компенсировано положительным приращением частей (2) и (4). Таким образом, факторы А и В должны быть взаи­модополняемыми.

Итак, если заданные «производственные возможности» не ограничивают размеров производства, два фактора дол­жны быть взаимодополняемыми. Как только «производ­ственные возможности» начинают ограничивать расшире­ние производства, два фактора уже не обязательно будут взаимодополняемыми. Но некоторая вероятность такого отношения между ними сохраняется, если предельный продукт двух факторов, взятых вместе, снижается мед­ленно. Когда для изготовления одного продукта применя­ются только два фактора и объем производства этого про­дукта колеблется, факторы могут быть взаимозаменяемы­ми лишь при выполнении двух условий: ресурсы предпри­нимателя, объем которых фиксирован, должны заметно способствовать расширению производства, а сами факто­ры должны быть такими, чтобы служить близкими заме­нителями при производстве данного количества продук­ции.