Е. О. Омаров Канд с-х наук Г. Е. Омарова
| Вид материала | Документы |
- Пособие для врачей и среднего медицинского персонала Минск, 5480.63kb.
- Тезисы докладов, 4290.75kb.
- М. А. Ляшко доц., канд физ мат наук; Т. Н. Смотрова доц., канд, 2299.13kb.
- Гост 17623-87, 138.94kb.
- Гост 5382-91, 1729.88kb.
- Кузбасса Кемерово «скиф», 5054.76kb.
- Міністерство України у справах сім’ї, молоді та спорту становище сімей в україні, 4532.43kb.
- «тк велби», 7624.26kb.
- -, 5971.32kb.
- Надійності та безпеки в будівництві, 692.13kb.
1 2
-
 Особые мнения экспертов
Особые мнения экспертов
Обратная связь между второй и первой процедурой алгоритма позволяет эксперту, который не попал в основную группу ранжировок, после дополнительного изучения и анализа проблемы изменить свое мнение и представить откорректированную ранжировку ряда.
Литература
1. Желтов С.Ю., Инвалев А.С., Киряков К.Р., Степанов А.А. Особенности реализации 3D ГИС. «Информационный бюллетень». ГИС – Ассоциации. – М. № 5 (12), 1997.
2. Полшков Е.А. Особенности ГИС – технологий при математическом моделировании геоэкологических объектов. «Информационный бюллетень». ГИС – Ассоциации. – М. № 4 (16), 1998.
3. Арефьев Н.В., Баденко В.Л., Осипов Г.К., Тараканов А.Е. Оценка геоэкологического потенциала геосистемы «речной бассейн» с использованием ГИС – технологий? Межвузовский сб. научных трудов. МГСУ и СПбГТУ, М., 2000.
4. Васильев В.С.., Арефьев Н.В., Кононова М.Ю. Природно-технический монитиринг энерго-водохозяйственных комплексов. Система обработки информации. Методические указания. СПГТУ, 1997.
5. Сенников М.Н. Совершенствование способов поддержания оросительных сис-тем в рабочем состоянии. Уч. пособие. ТарГУ, 2000.
Таразский Государственный университет им. М.Х.Дулати, Тараз
ЖЕР БЕТІНІҢ САНДЫҚ МОДЕЛІН ҚҰРУ
Техн.ғыл.докт М.Н.Сенников
Е.О.Омаров
А-ш.ғыл.канд. Г.Е.Омарова
В.Л.Сенникова
Т.С.Колбачаев
А.Е.Әубәкірова
Су электр станцияларындағы әр объектінің оқыс жағдайларының ерекшеліктері ескерілген.
THE CRTATION IN FIGUZES LAEND MODEL
Doct.tech.sci. M.N.Sennikov
E.O.Omarov
G.Y.Omarova
B.L.Sennikova
T.C.Kolbajaev
A.E.Aubakirova
The considez questchens emezqency situations on Dudzo. Ilectzic station and calculation object.
УДК 661.9:532.529
МОДЕЛИРОВАНИЕ ОБТЕКАНИЯ ТРЕУГОЛЬНОГО УСТУПА
ГАЗОВЫМ ПОТОКОМ
Докт.техн.наук Б.Р.Исмаилов
С.К.Мельдебекова
Канд.техн.наук С.В.Викторов
Рассматривается модель плоского течения газа в канале с треугольным уступом при ламинарном режиме. Решая уравнения Навье-Стокса численными методами, составлена математическая модель для нахождения значений функции тока и вихря. Приведен алгоритм для решения уравнений Навье-Стокса.
Повышение требований к колонным массообменным аппаратам /1/ системы «газ-жидкость» - эффективность, низкое гидравлическое сопротивление, низкая материалоемкость и др. требует от разработчиков проведения тонких исследований закономерностей обтекания насадочных тел. Известно, что наиболее общие законы обтекания тел газовым потоком в ламинарном режиме (в приближении плоской задачи) моделируются системой уравнений Навье-Стокса /2/:
 (1)
(1) (2)
(2)Система (1)-(2) в работе /3/ была решена численно для задачи обтекания пластин, регулярно расположенных в канале массообменного аппарата с многоступенчатым взаимодействием фаз.
В данной работе рассматривается плоское ламинарное течение газа, в сечении канала с предположением, что ширина канала достаточно велика (рис.1).
Расчетная область и качественная картина линий тока
в задаче об обтекании треугольного уступа
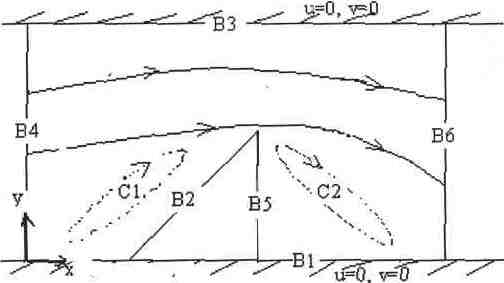
В1 - нижняя граница канала; B2 - лобовая сторона треугольника;
В3 - верхняя граница канала; В4 - входная граница канала;
В5 - основание уступа; В6 - выходная граница;
Cl, C2 - застойные зоны перед и за уступом.
Рисунок 1
Для уравнений (1)-(2) ставятся начальные и граничные условия:
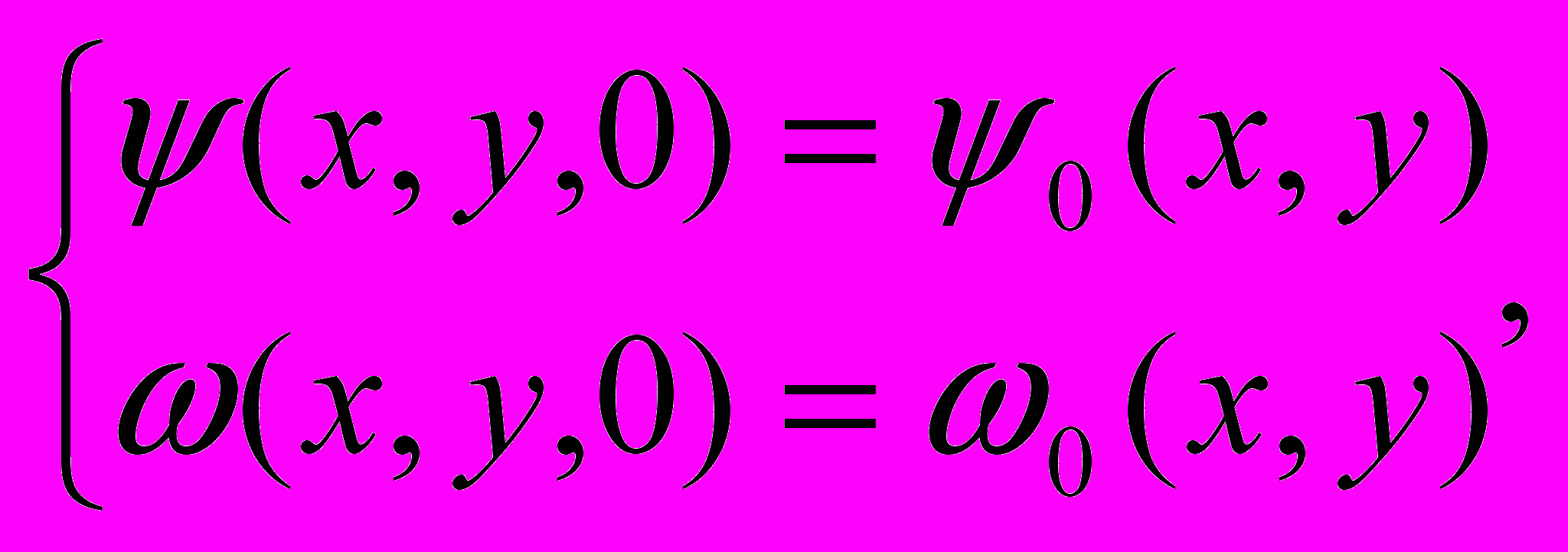 (3)
(3)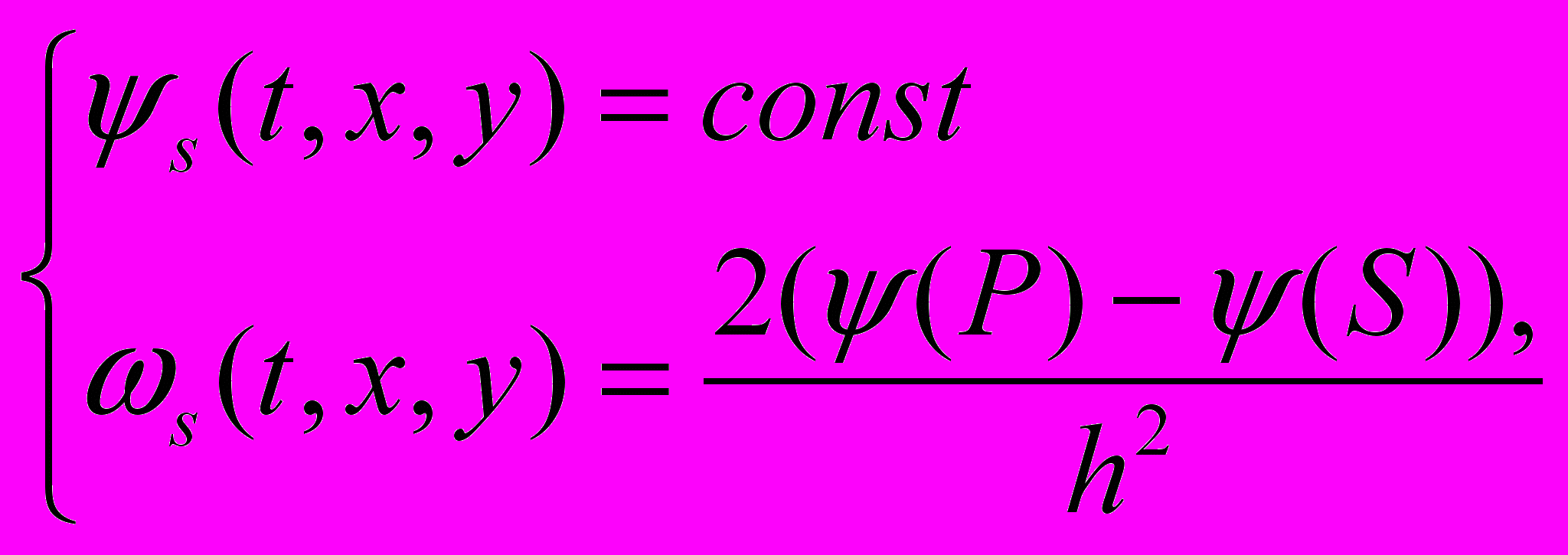 (4)
(4)где Р - приграничный узел, S - граничный узел.
Для решения задачи (1)-(4) применяем конечно-разностный метод с установлением.
В данной работе приводятся результаты математического моделирования обтекания ламинарным газовым потоком треугольного уступа в прямоугольном канале, как первого методического приближения моделирования турбулентного обтекания, соответствующего реальному рабочему режиму, возникающего при среднерасходной скорости газа от 1 до 5 м/с.
Покрываем канал равномерной сеткой с шагом h: xi=ih, yj=jh. В начальный момент времени задаем равномерное распределение по ψ от 0 до 1 с шагом h:
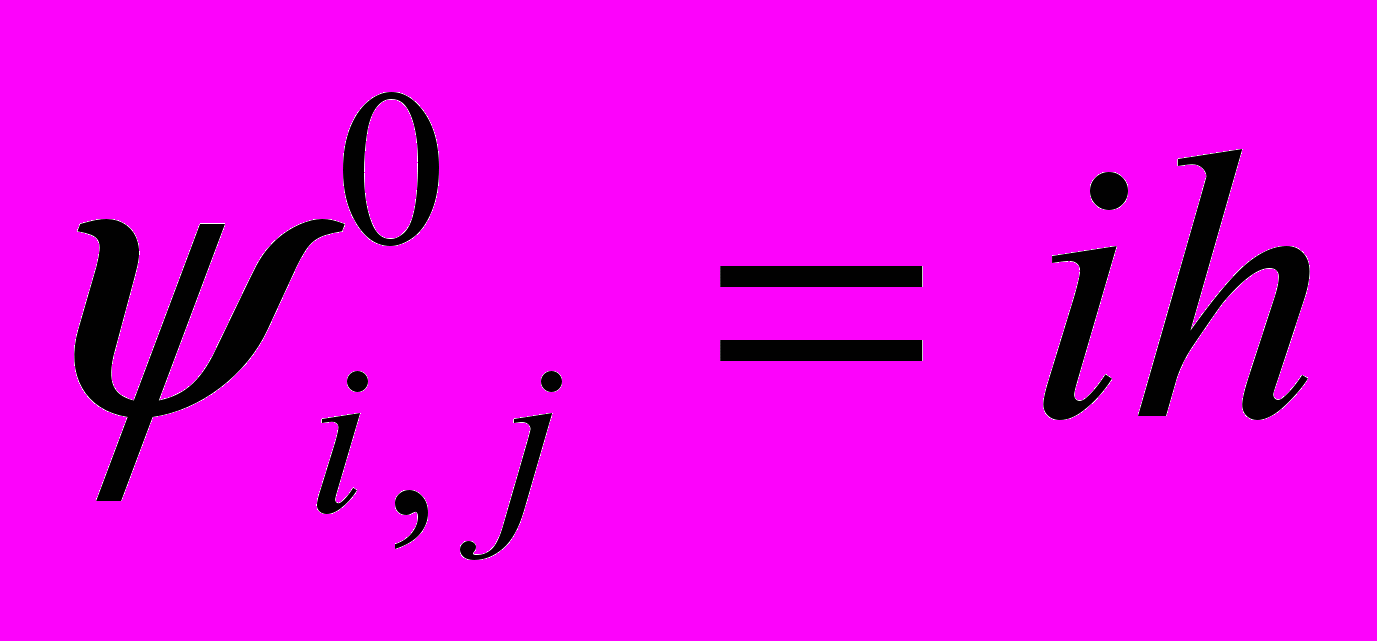 . Начальные условия для вихря имеют вид:
. Начальные условия для вихря имеют вид: 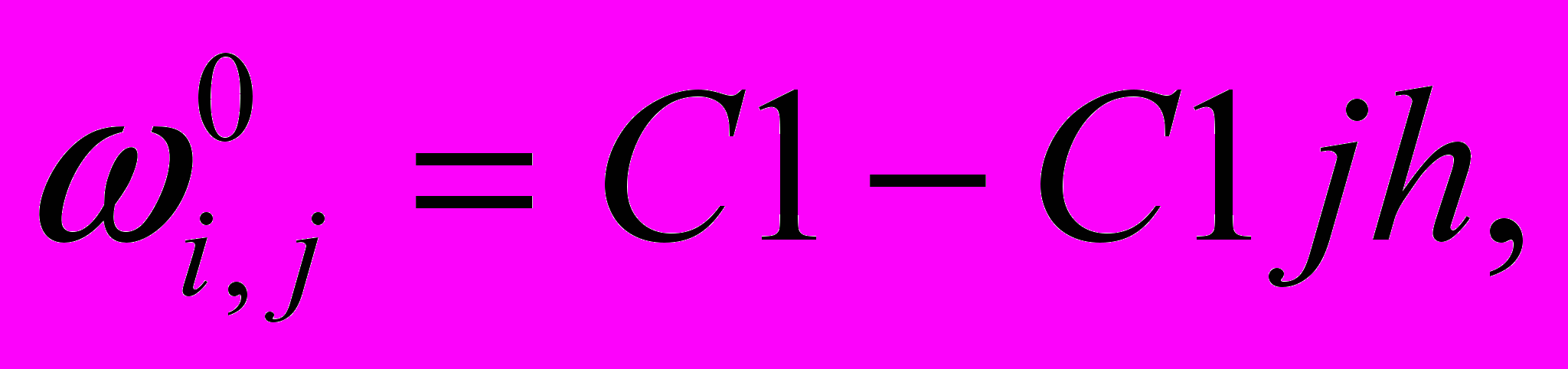 где
где 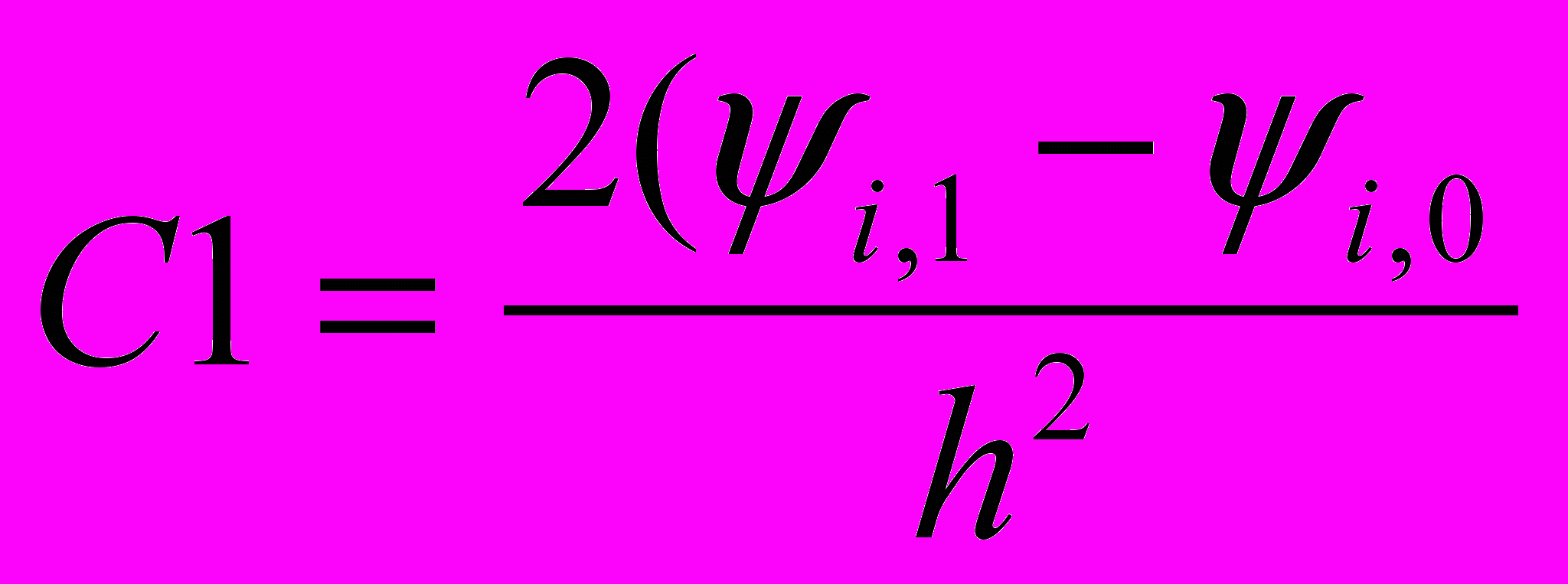 . Допустим, что в канале внезапно появляется уступ. Аппроксимируем граничные условия:
. Допустим, что в канале внезапно появляется уступ. Аппроксимируем граничные условия: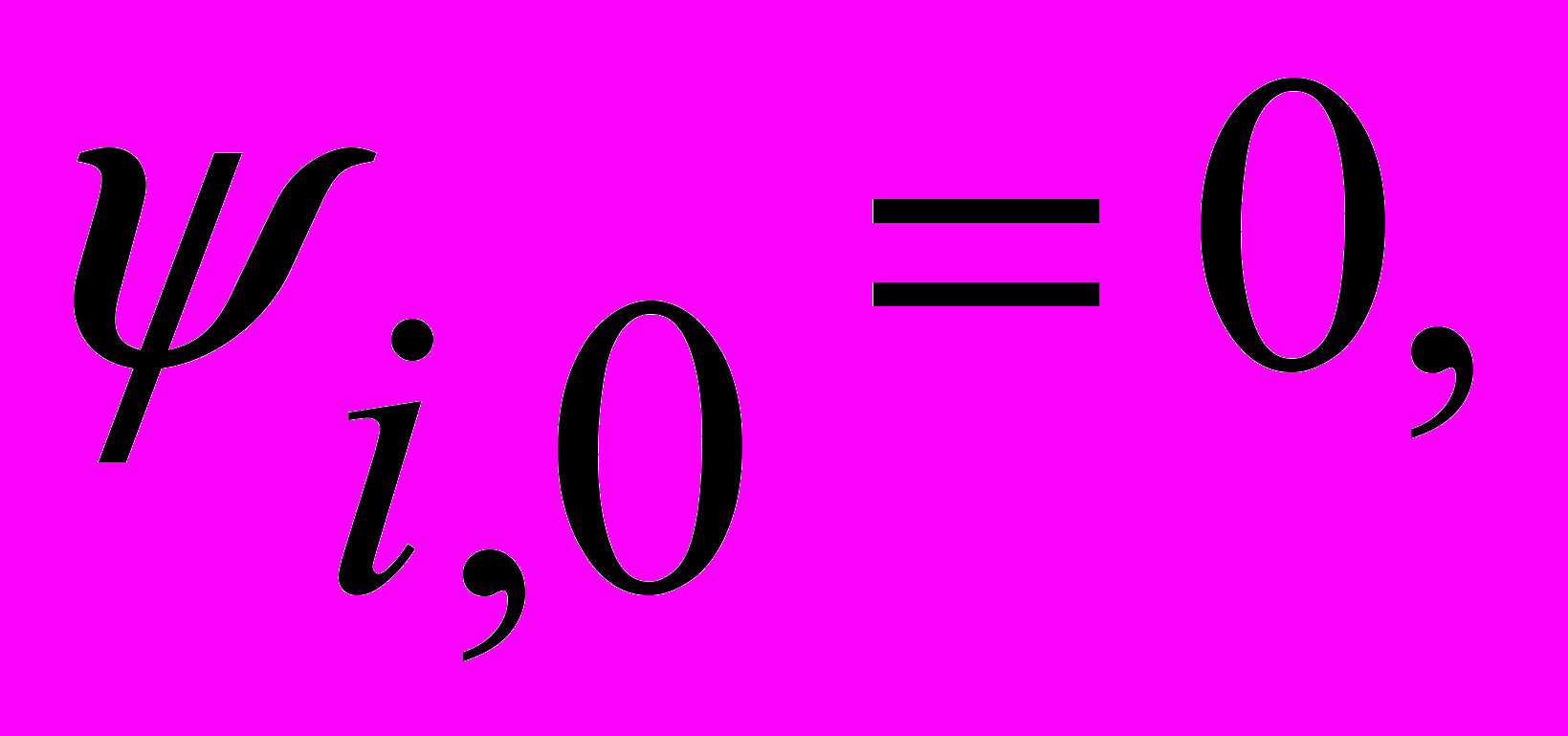
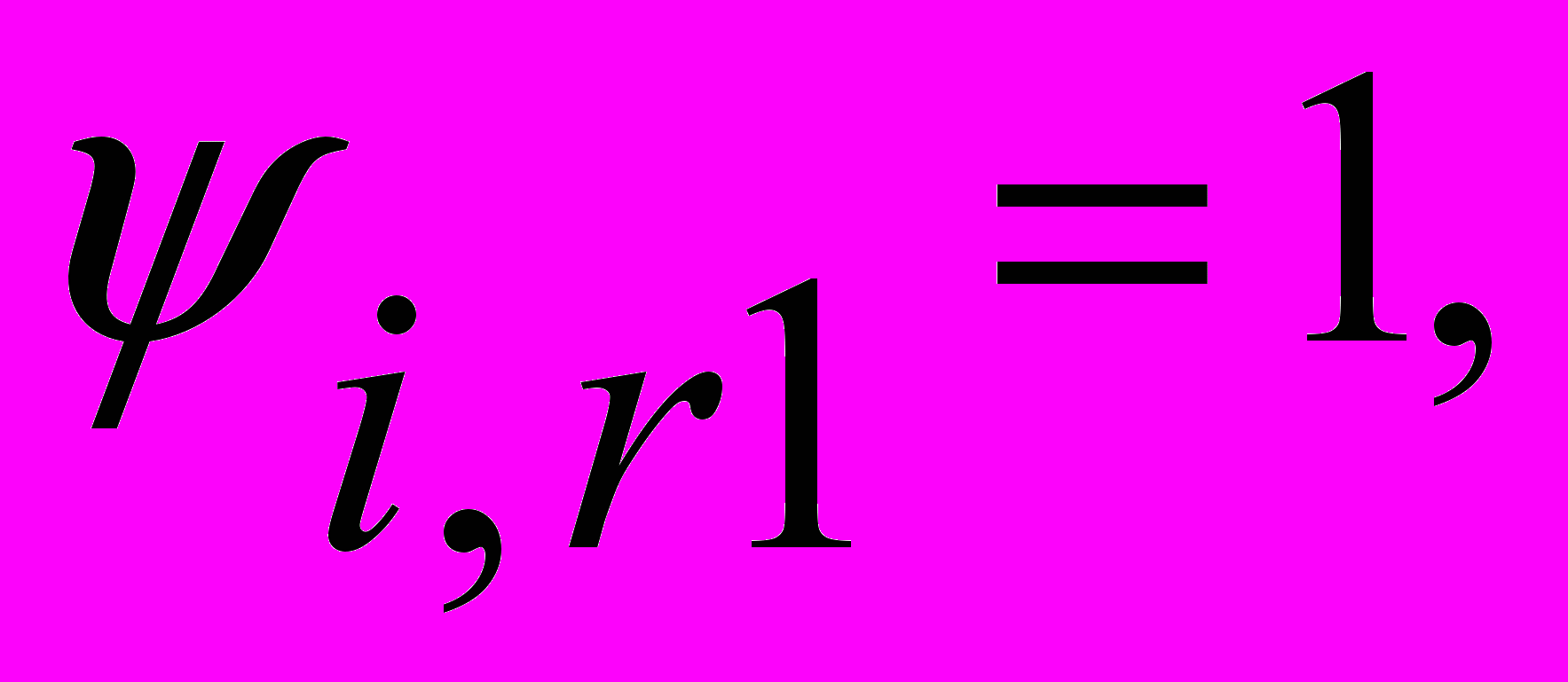
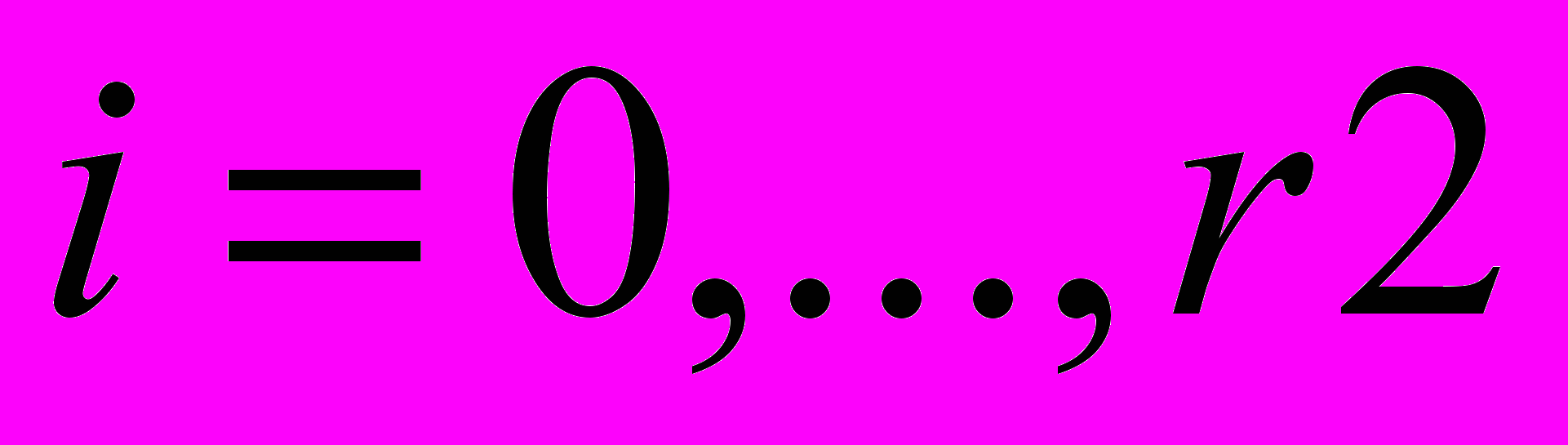
(5)
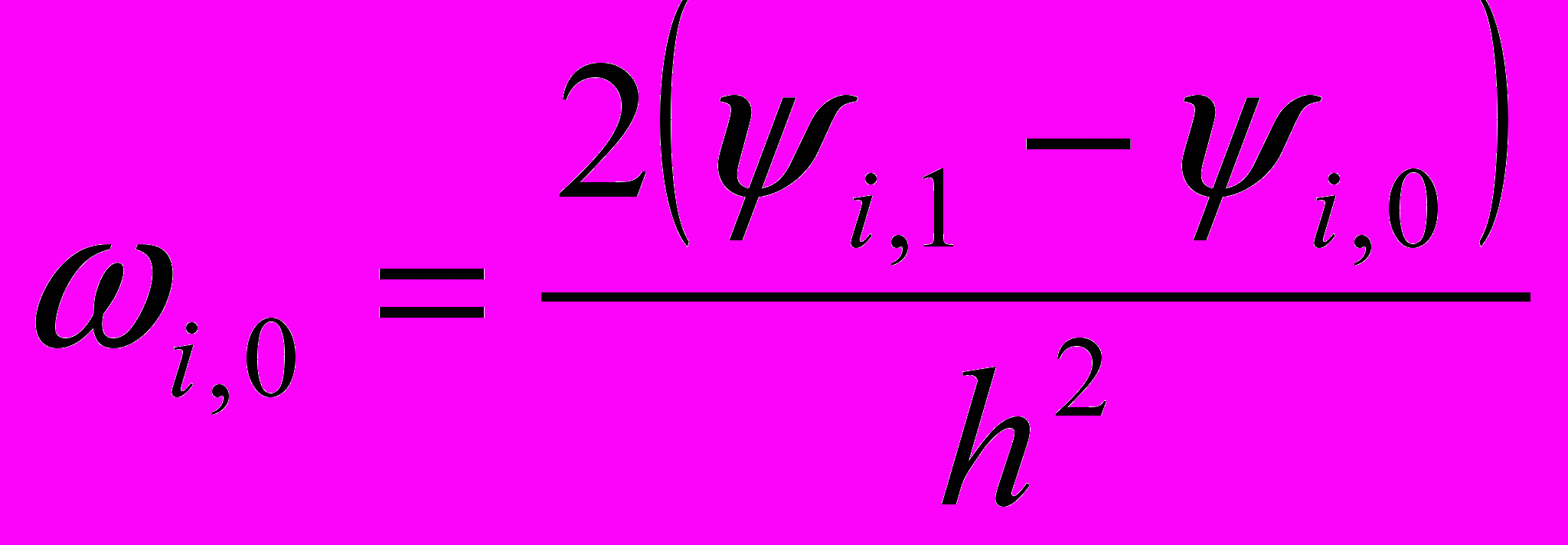
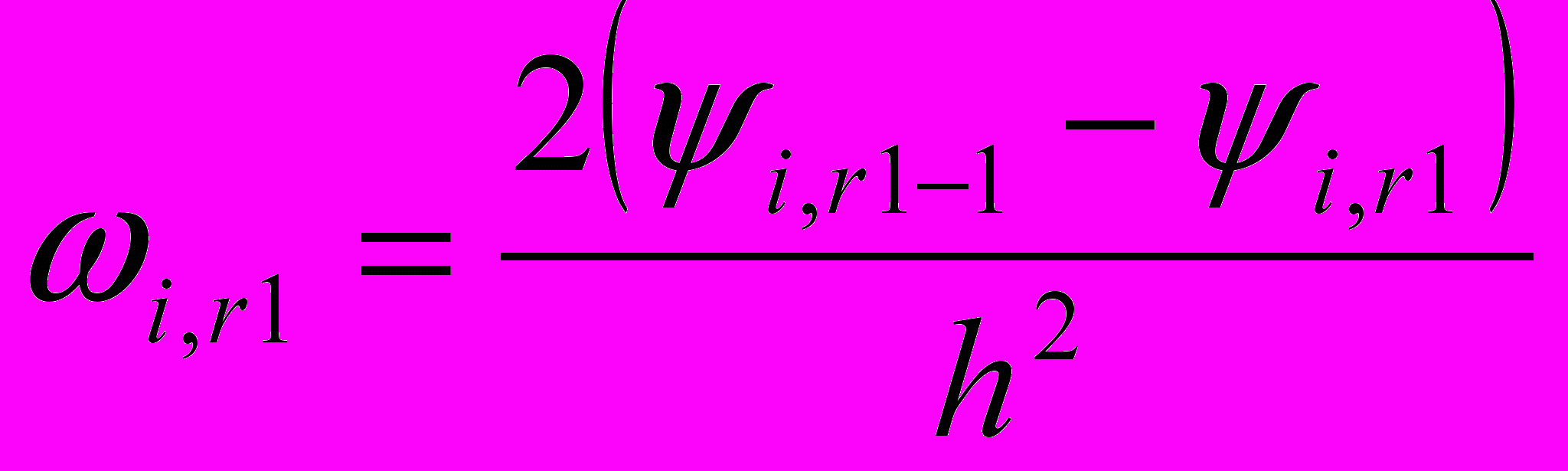
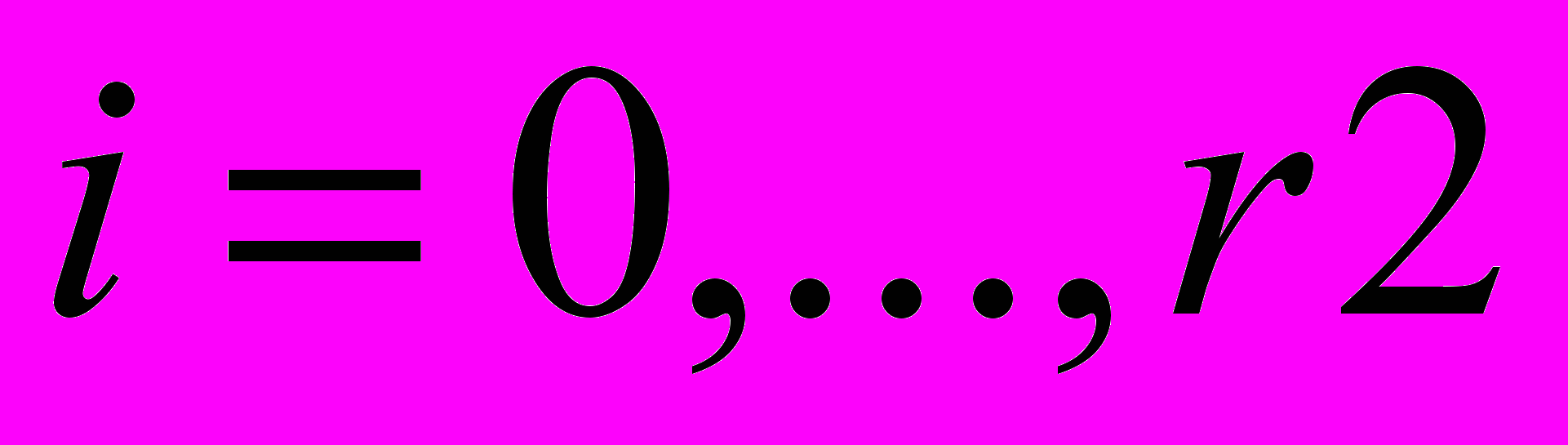
rl, r2 - число делений сетки.
Аппроксимация вихря проводится «против потока», т.е. в качестве вычисляемого узла все время берется узел, расположенный ближе к входу канала. Это было предпринято в связи с тем, что Сполдинг Д. доказал абсолютную устойчивость таких схем даже для турбулентных течений /4/. Введем следующее обозначение:
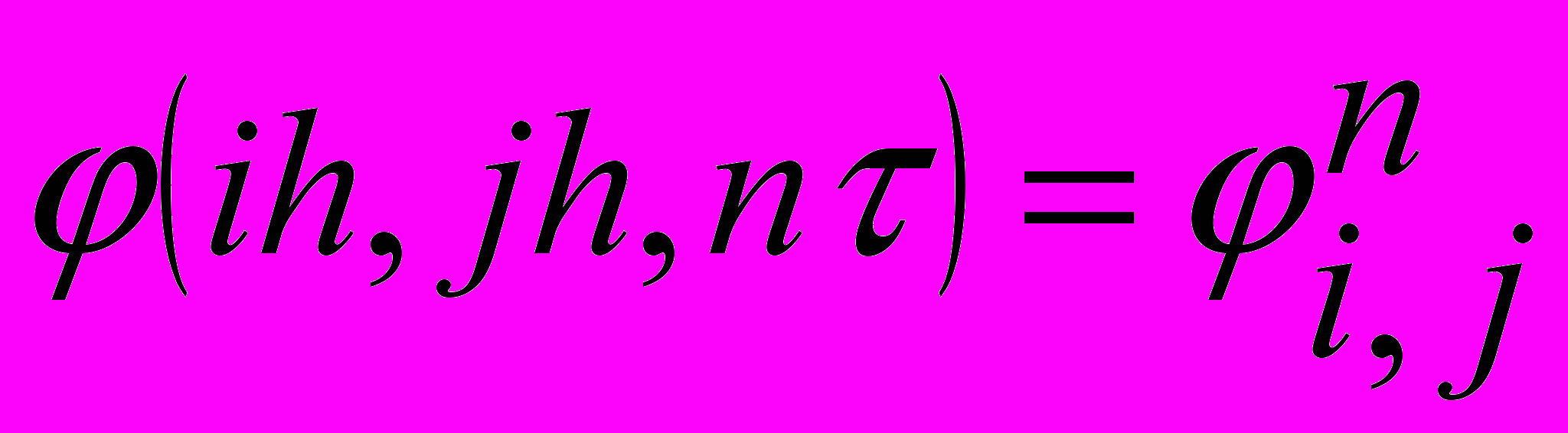 . Производные по пространственным переменным будем
. Производные по пространственным переменным будем аппроксимировать центральными разностями, а производные по времени заменим разностным отношением «вперед». Тогда получим следующую явную схему для уравнения вихря:
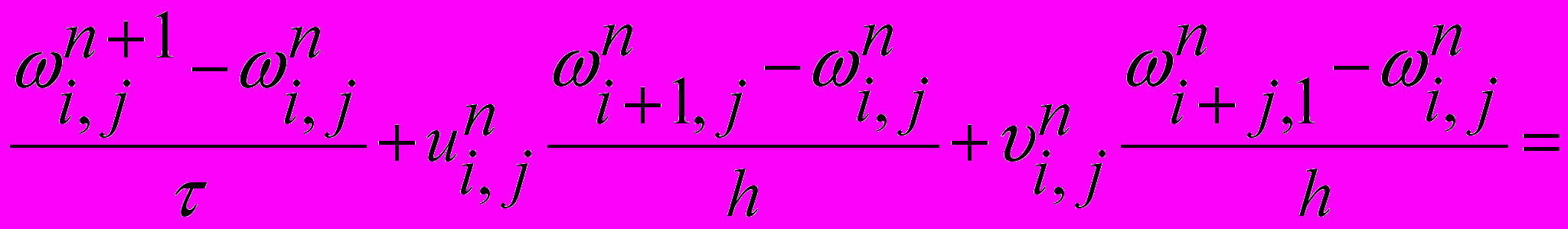
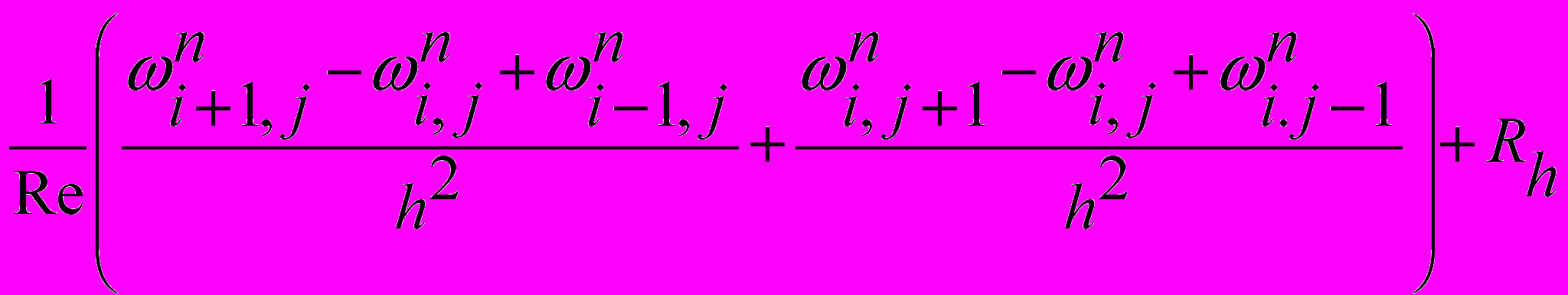 , (6)
, (6)Rh - остаточный член, порядок которого O(h). По этой формуле по известным в момент времени tn значениям функции тока и вихря в расчетной области, включая ее границу, можно вычислить значения вихря за новый момент времени п+1. Связи, определяемые этой схемой, имеют локальный характер, т.к. для определения значения вихря для нового момента времени требуется знать значения вихря для предыдущего момента времени в пяти точках:
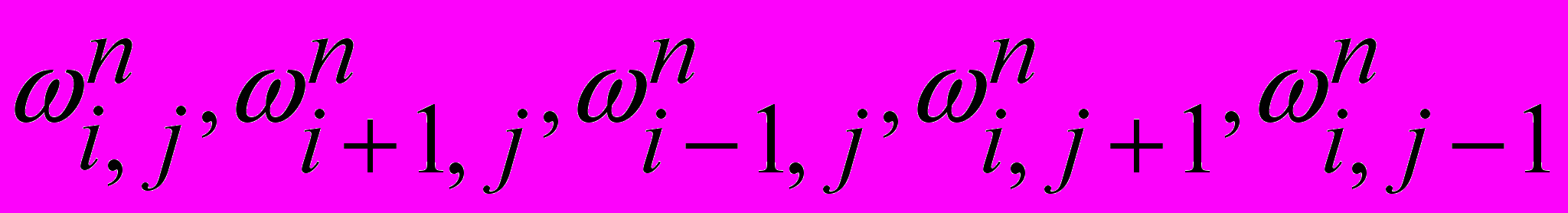
Перейдем теперь к решению уравнения Пуассона для функции тока (1). В отличие от уравнения вихря, это уравнение стационарно. Это значит, что для получения решения системы на одном временном слое нужно найти стационарное решение (1), где правая часть - вихрь
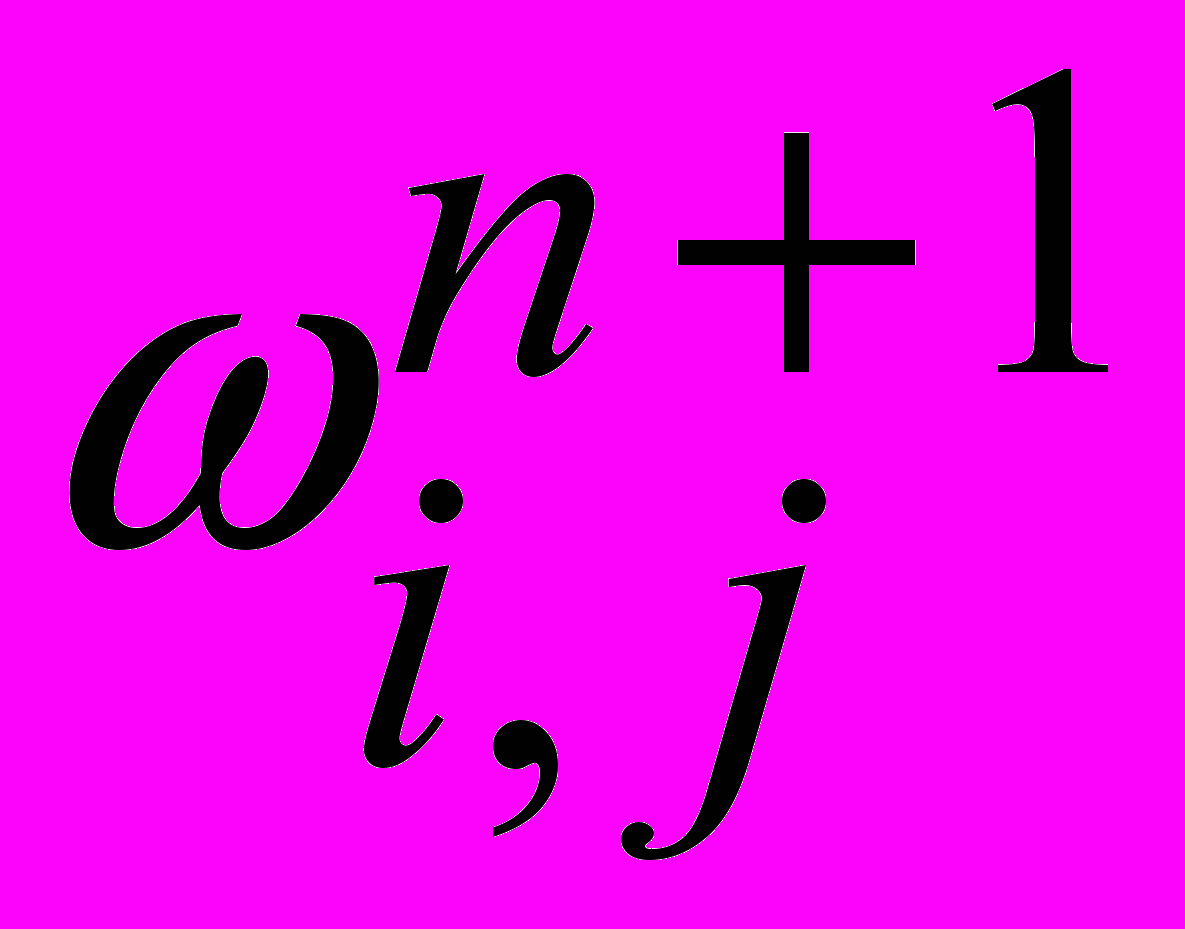 определена ранее. Для этого мы применим простейший явный итерационный метод. Его можно сформулировать по аналогии с решением нестационарного уравнения, если ввести фиктивное время σ следующим образом:
определена ранее. Для этого мы применим простейший явный итерационный метод. Его можно сформулировать по аналогии с решением нестационарного уравнения, если ввести фиктивное время σ следующим образом: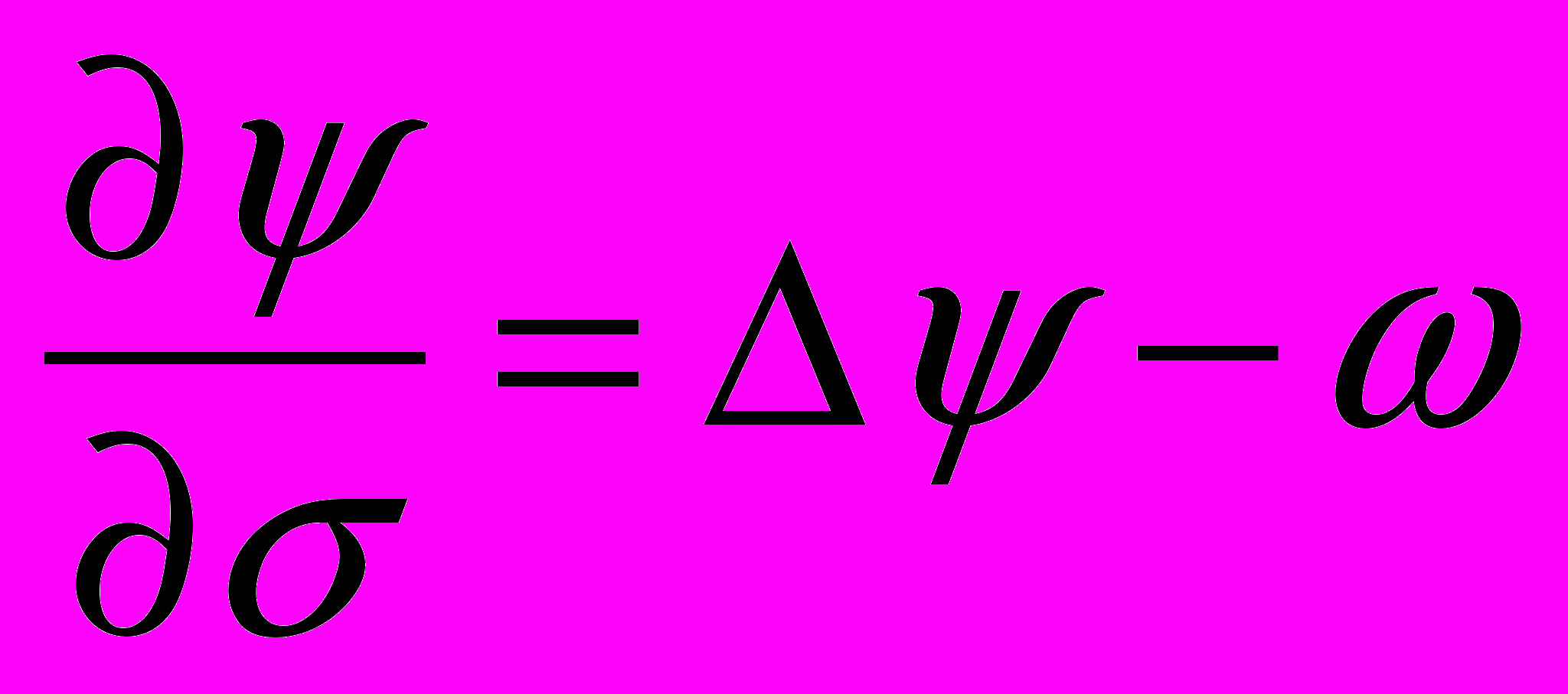 . (7)
. (7)Обозначим через s индекс внутреннего цикла, запишем схему для решения этого уравнения на временном слое n+1 в виде:
 , (8)
, (8)После преобразований (8) можно представить в виде
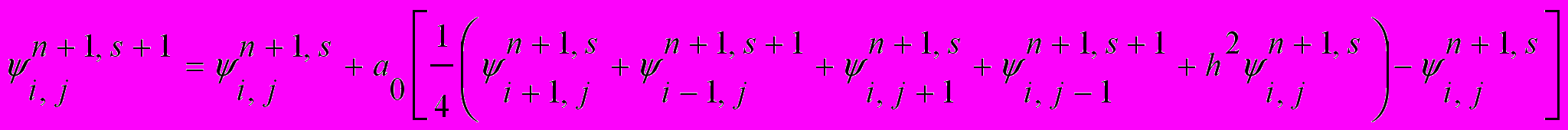 , (9)
, (9)где a0 - итерационный параметр, определяемый через сеточные параметры
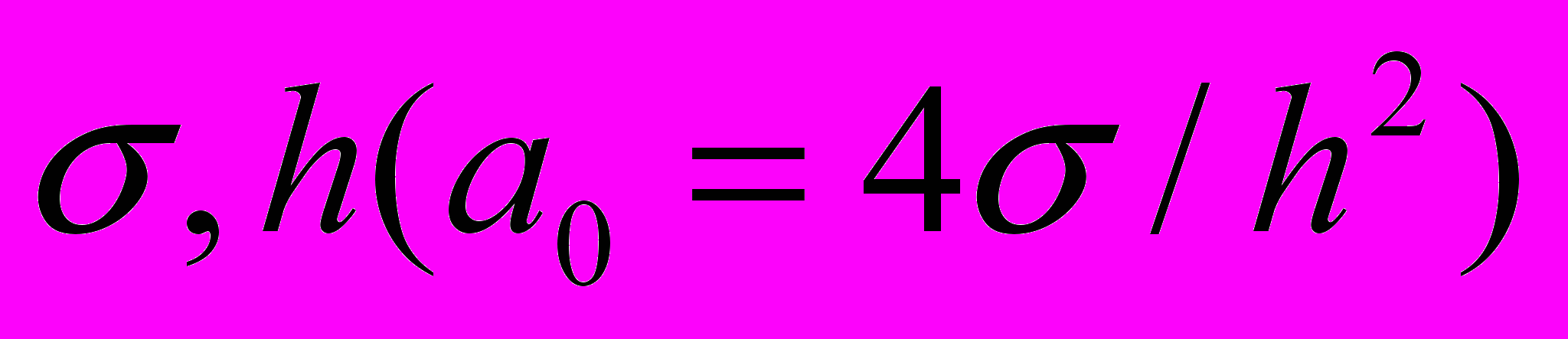 .
.Граничным условием при расчете по формуле (9) является условие
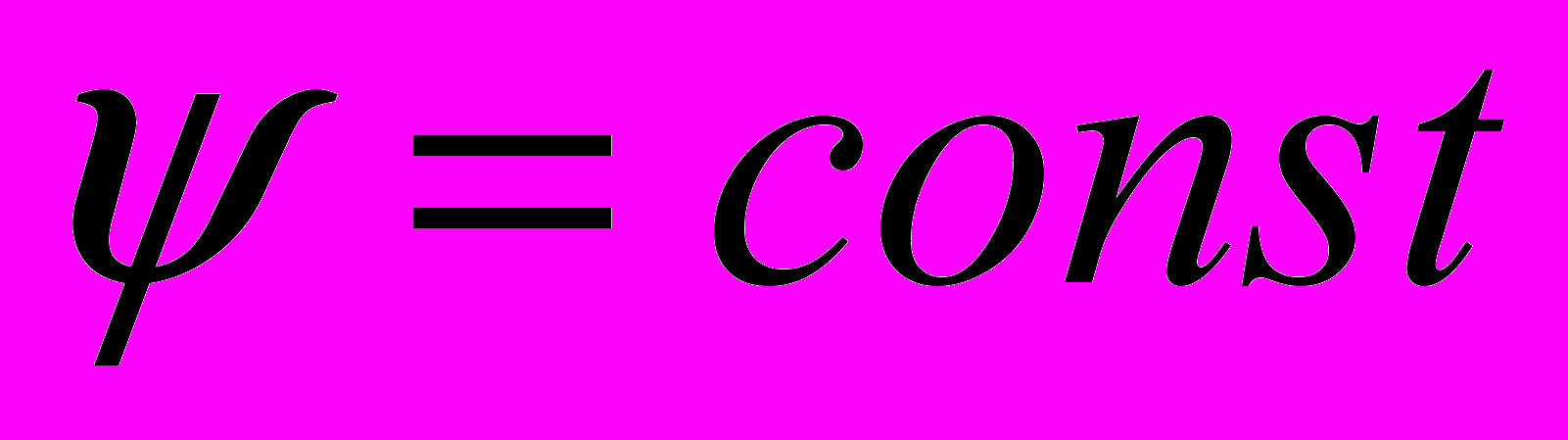 , задаваемое на границе области (другое из граничных условий
, задаваемое на границе области (другое из граничных условий 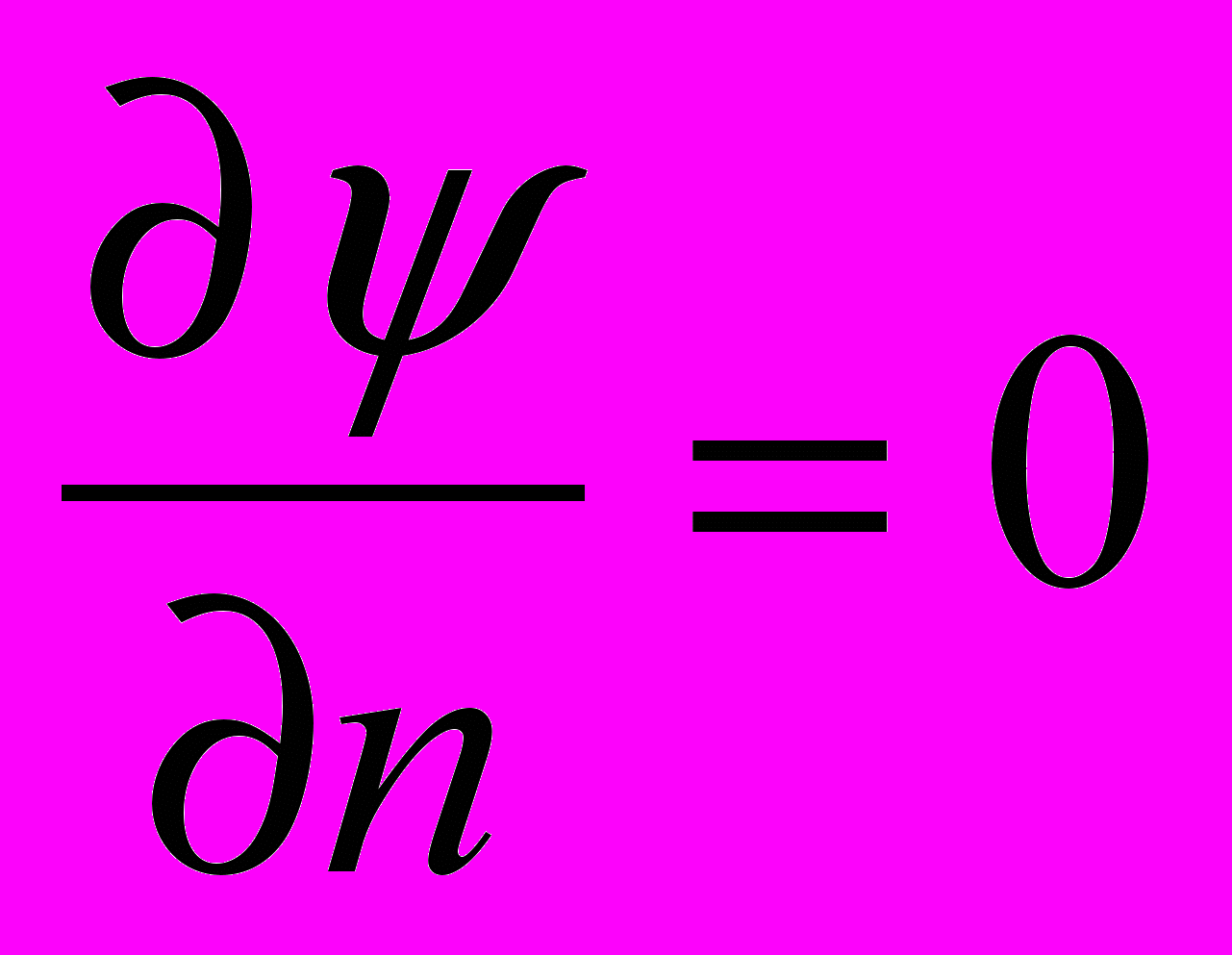 уже было использовано при получении граничного условия для вихря).
уже было использовано при получении граничного условия для вихря).Расчет поля функции тока по формуле (9) проводится до получения стационарного решения. Это значит, что внутренний итерационный цикл с параметром s должен заканчиваться при определенном условии, которое характеризует достижение стационарного режима. При плавном изменении ψi,j, в процессе итераций можно использовать самое простое из этих условий, состоящее в том, что разность значений функции тока в двух соседних итерациях s и s+1 не превосходит некоторой заданной величины
max
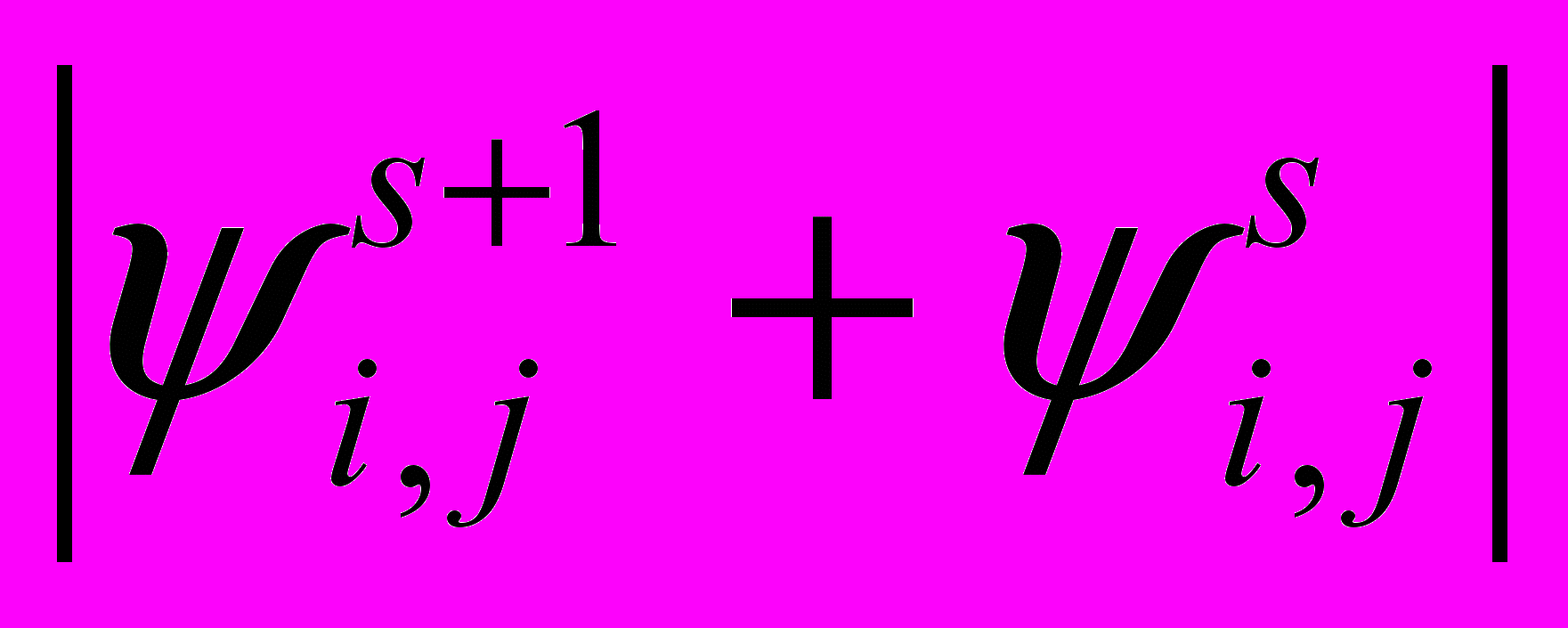 <ε (10)
<ε (10)При выполнении условия (10) расчет уравнения Пуассона по формуле (9) прекращается, и мы имеем поле вихря и поле функции тока, удовлетворяющее разностным аналогам уравнений для ψ и ω на временном слое п+1. Для получения решения в следующий момент рассмотренная выше процедура повторяется, с той лишь разницей, что в качестве начальных значений теперь используются найденные величины полей
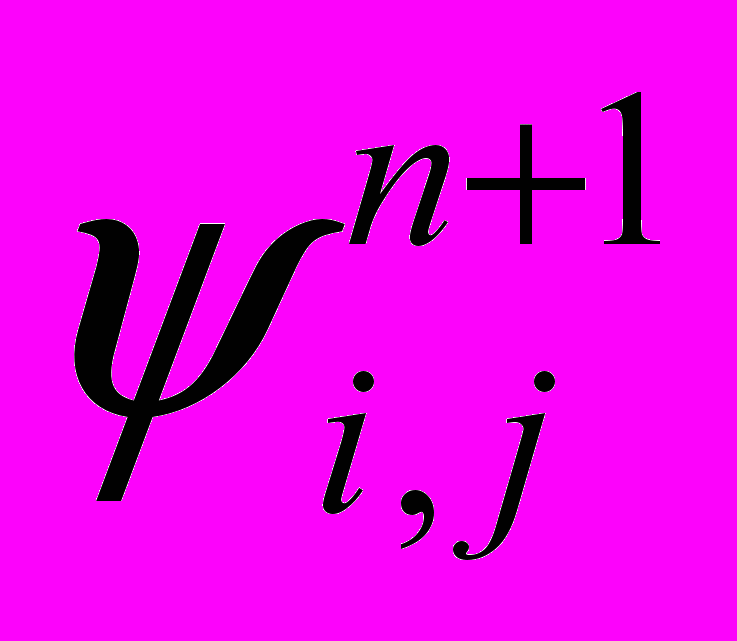 ,
, 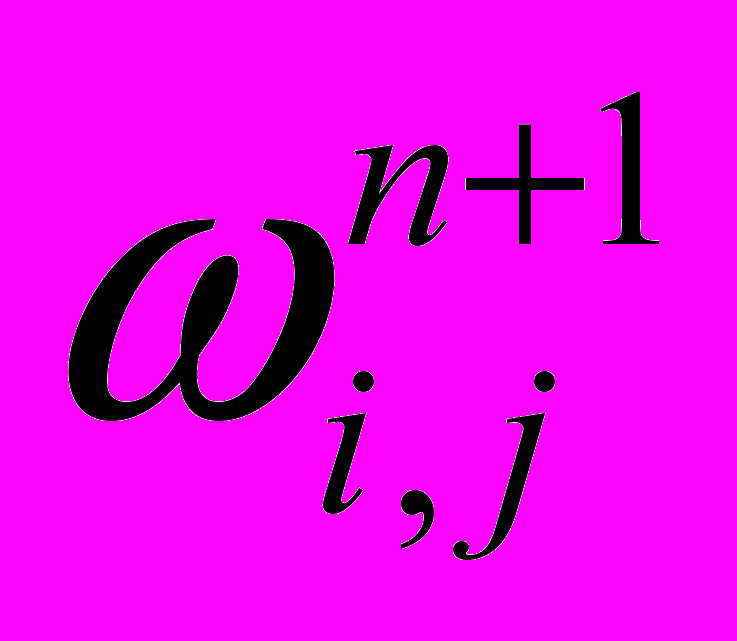 .
.Подытоживая, алгоритм решения УНС можно сформулировать следующим образом:
1. Вводим начальные и граничные условия: (3), (4), задаем Re, h, σ, удовлетворяющие условиям сходимости.
2. Проводим расчет вихря
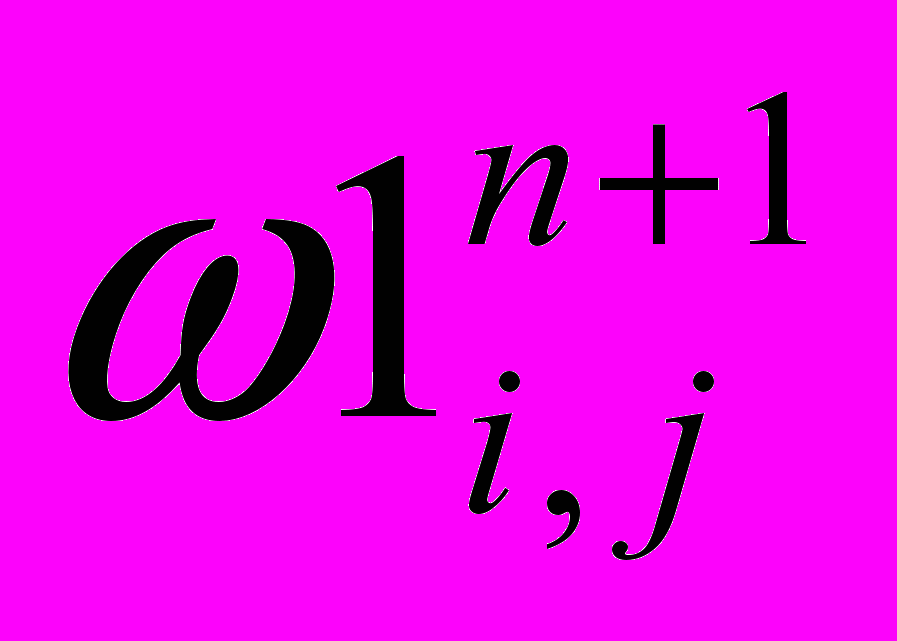
3. Рассчитываем функцию тока
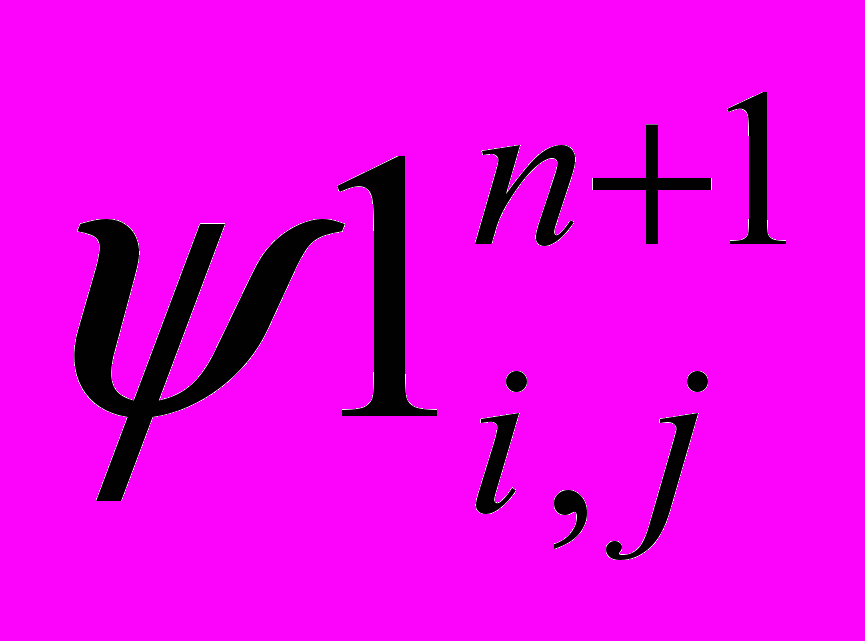
- Устанавливаем функцию тока по соотношению:
max
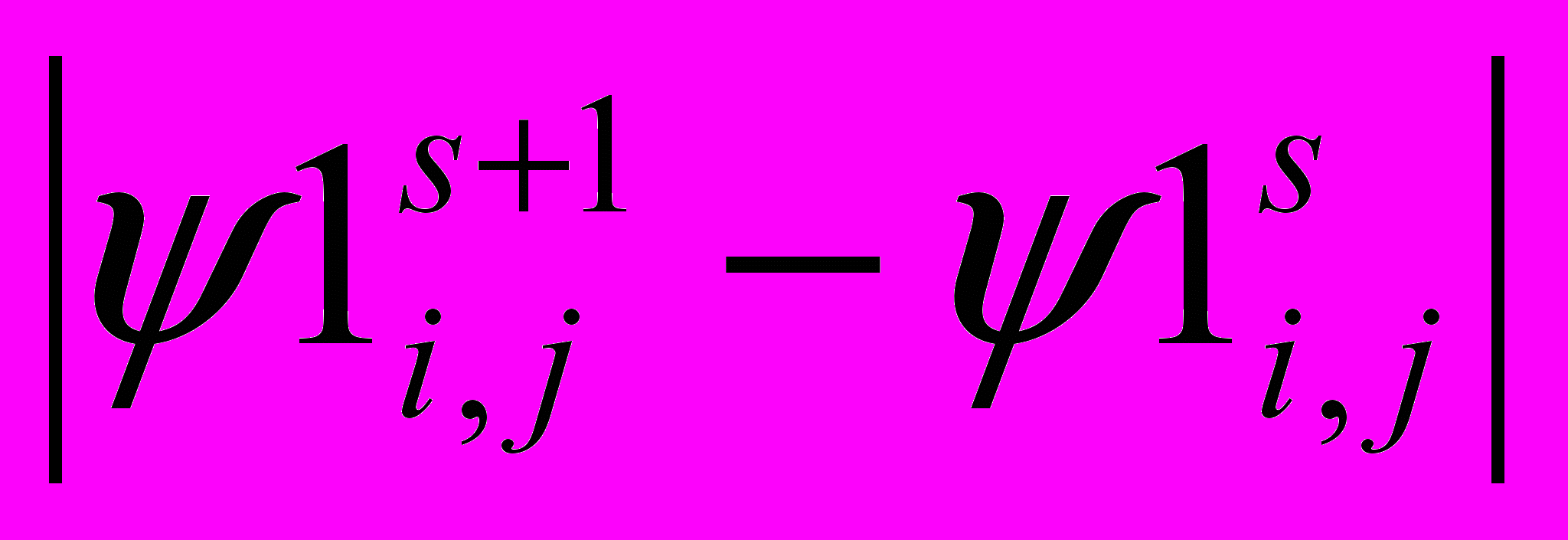 <εψ (11)
<εψ (11) Если (11) не выполняется, то возвращаемся к пункту 3, в противном случае переходим к следующему пункту.
- Устанавливаем вихрь:
max
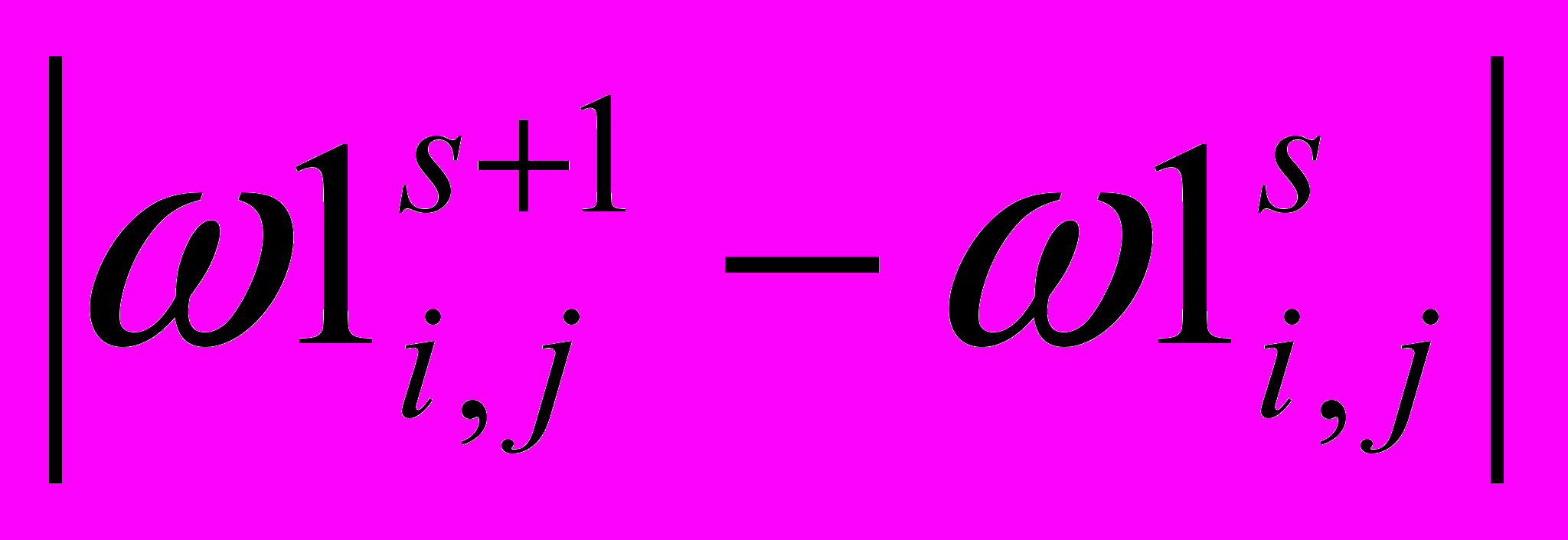 <εω (12)
<εω (12)Если (12) не выполняется, то возвращаемся к пункту 2, в противном случае переходим к следующему пункту.
6. Сохраняем установившиеся значения:
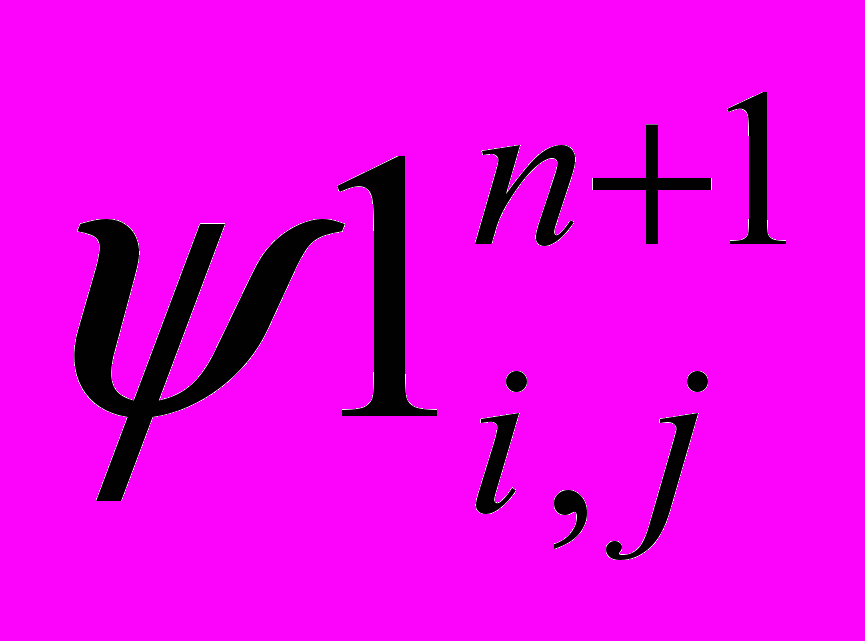 ,
, 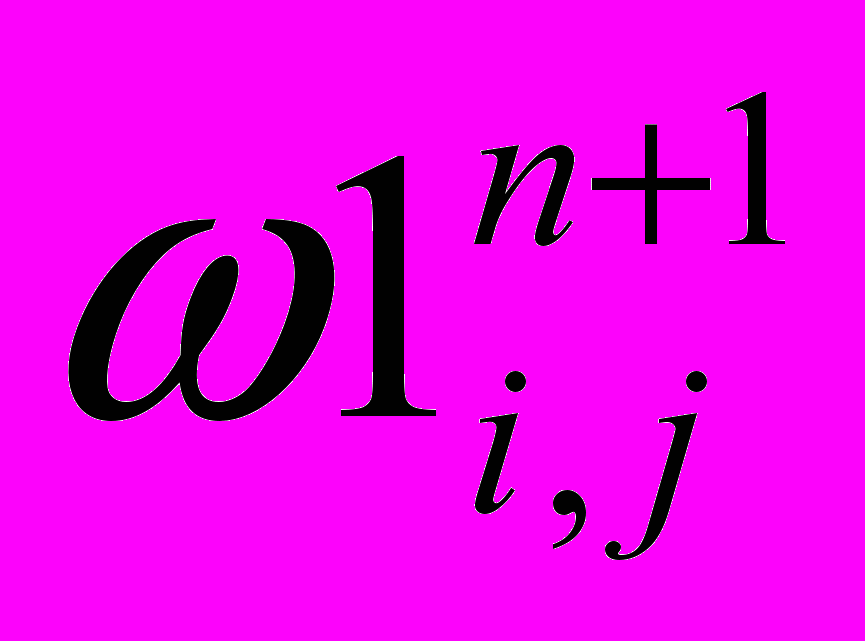
7. Переходим на следующую ступень контакта, т.е. полагаем выходные данные предыдущей ступени входными данными следующей ступени контакта
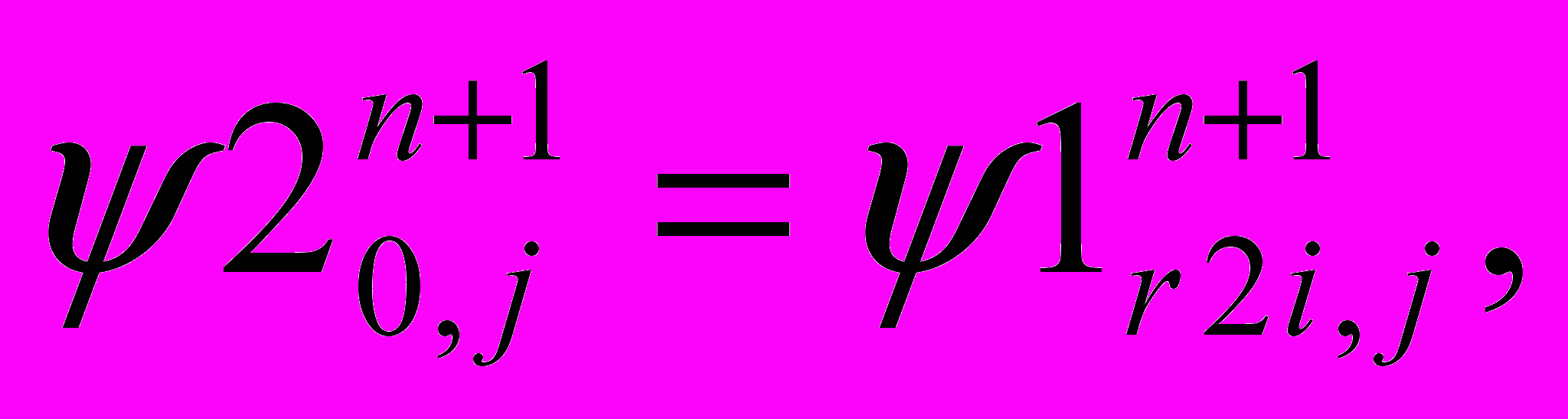
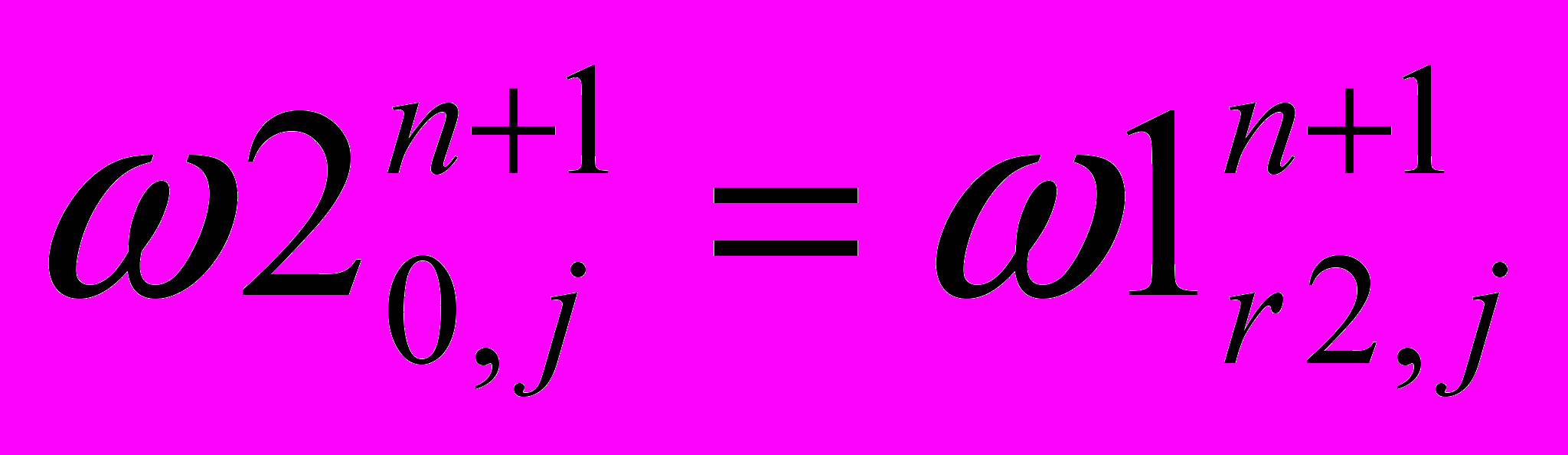
8. Расчета
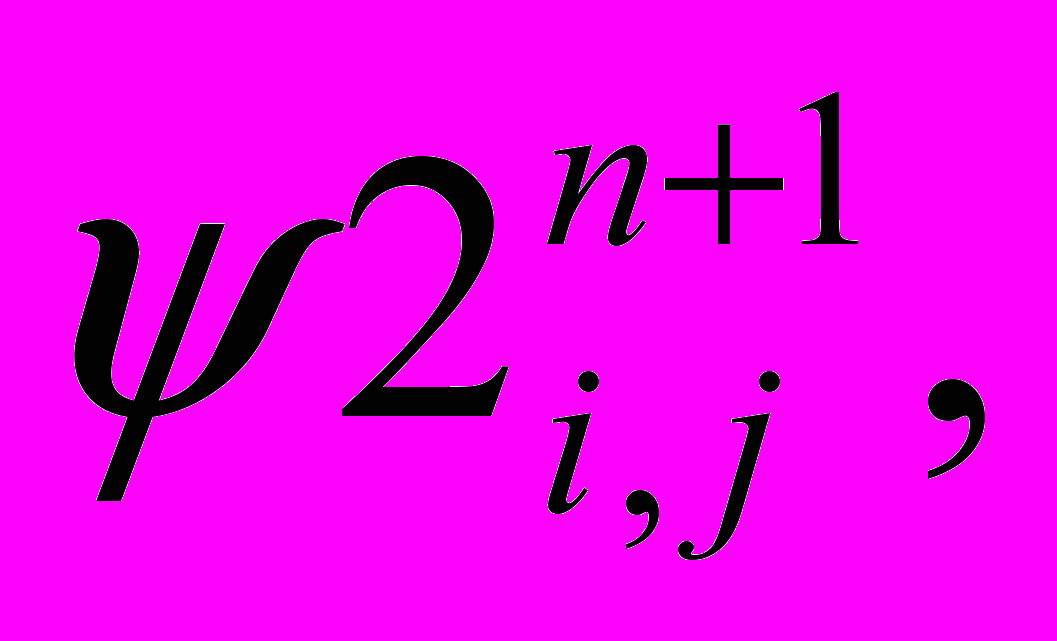
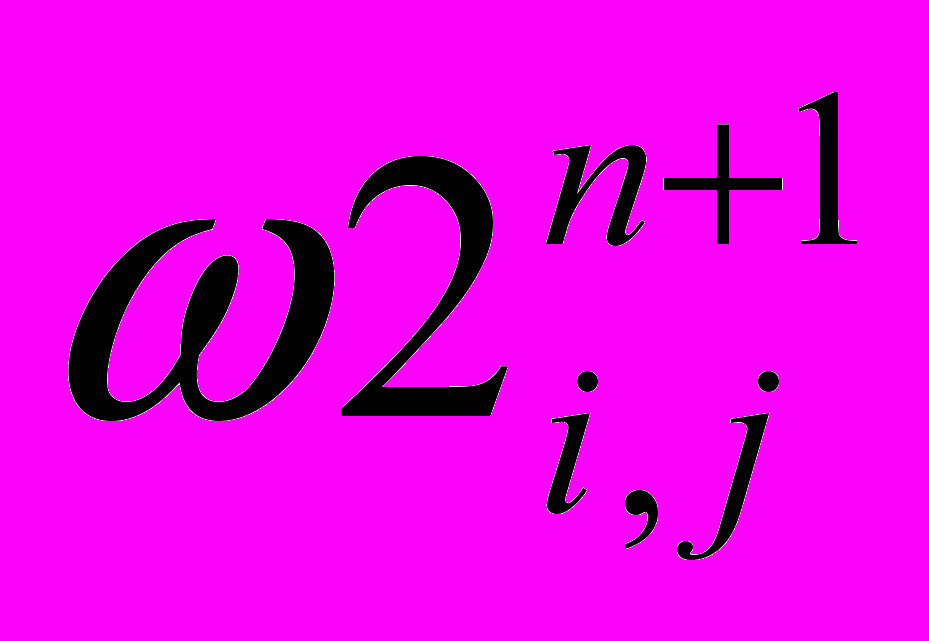
9. Устанавливаем функцию тока по (11), вихрь по (12).
10. Сохраняем установившиеся значения
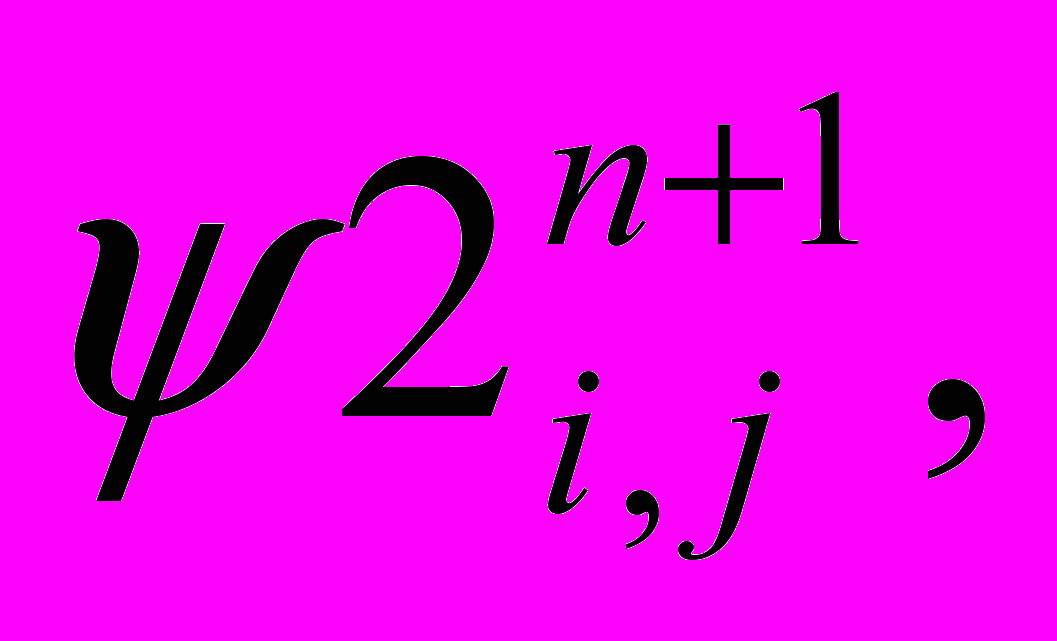
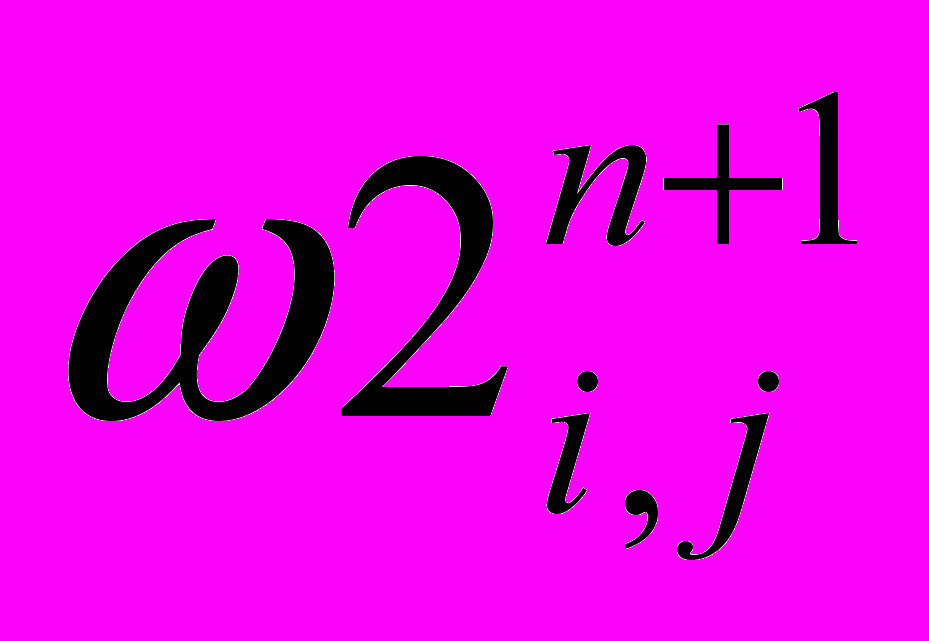
- Сравниваем картину данной ступени с предыдущей ступенью контакта по формулам: max
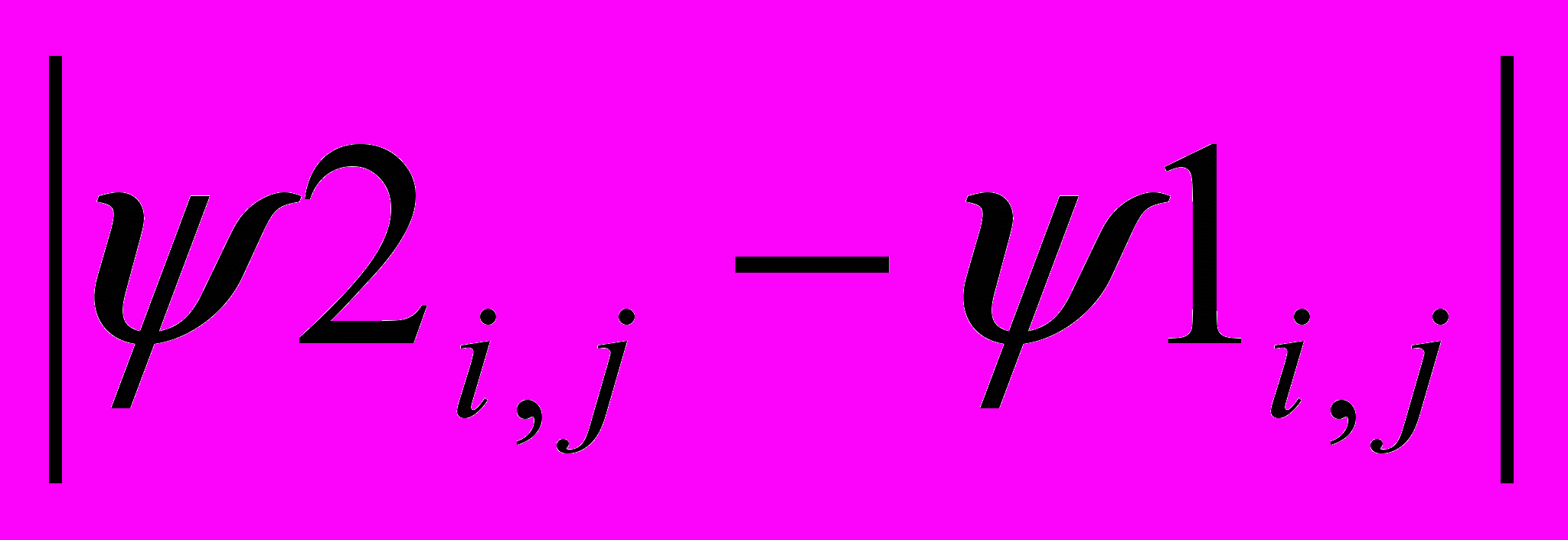 <εψ,
<εψ,
max
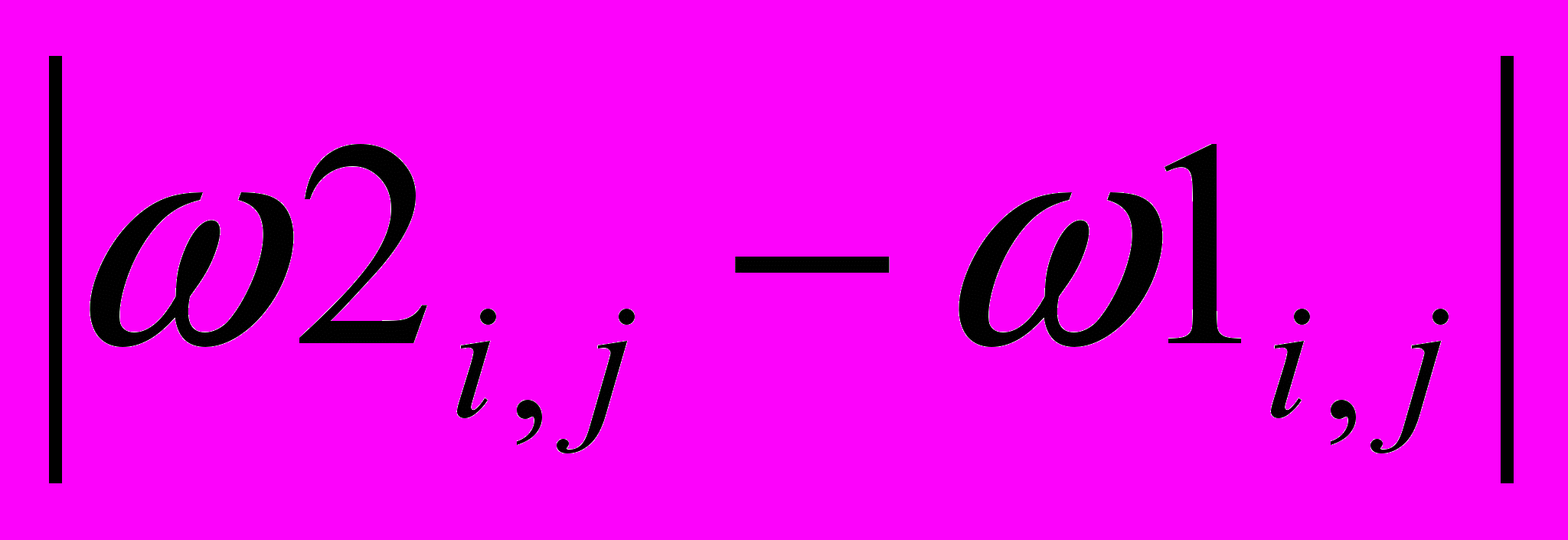 <εω (13)
<εω (13)Если (13) выполняется, то печатаем
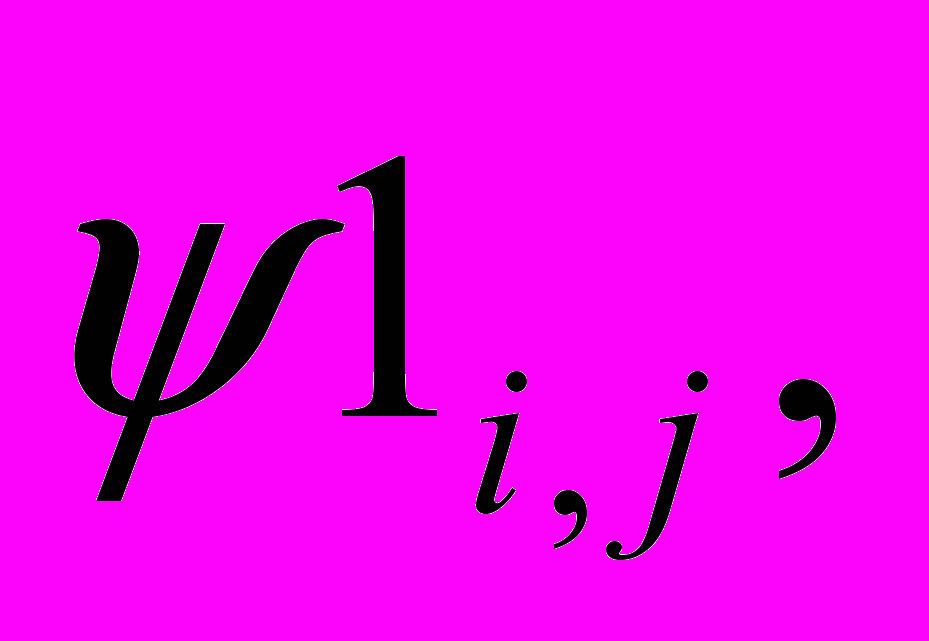
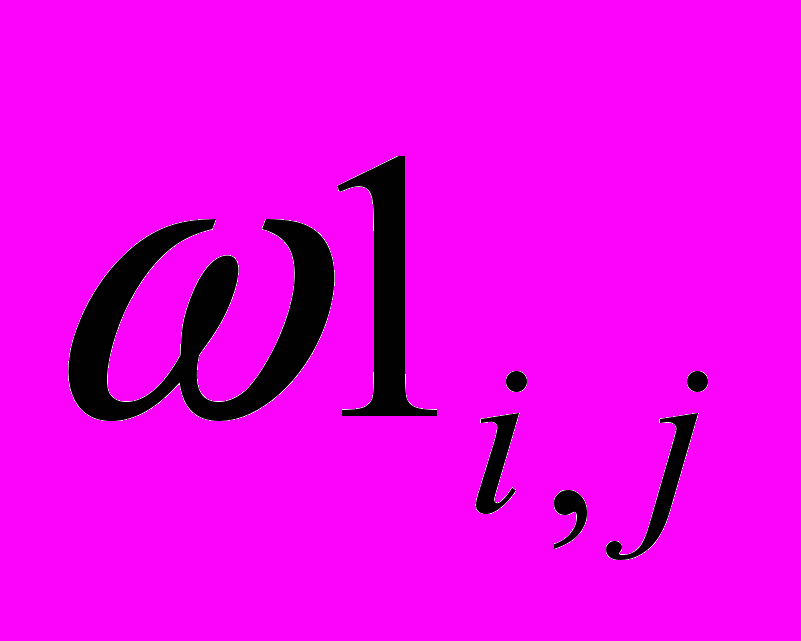 . В противном случае переходим на следующую ступень контакта и возвращаемся к пункту 6. Реализация приведенного выше алгоритма позволит получить закономерности образования зоны с максимальными значениями скорости, рассчитать поле давлений без решения уравнения Пуассона применением функции диссипации энергии.
. В противном случае переходим на следующую ступень контакта и возвращаемся к пункту 6. Реализация приведенного выше алгоритма позволит получить закономерности образования зоны с максимальными значениями скорости, рассчитать поле давлений без решения уравнения Пуассона применением функции диссипации энергии.Литература
1. Пасконов В.М., Полежаев В.И., Чудов Л.А. Численное моделирование процессов тепло- и массообмена.-М.: Наука, 1984.-284с.
2. Балабеков О.С. Закономерность взаимодействия вихрей, возникающих при отрывном обтекании потоком газа или жидкости дискретно расположенного вдоль него тел. Диплом об открытии № 144, 2000г.
3. Исмаилов Б.Р. Моделирование многоступенчатого взаимодействия газа и жидкости. - Алматы. Кітап палатасы, 2001. -103с.
4. Сполдинг Д. Численное исследование течений вязкой жидкости. -М.:Мир,1979.-349с.
Южно-Казахстанский Государственный университет им. М.Ауезова, Чимкент
Таразский Государственный университет им. М.Х.Дулати, Тараз
ГАЗДЫ АҒЫННЫҢ ҮШБҰРЫШТЫ БӨГЕТТІ
АЙНАЛЫП ӨТУІН МОДЕЛДЕУ
Техн.ғыл.докт. Б.Р.Исмаилов
С.К.Мелдебекова
Техн.ғыл.канд. С.В.Викторов
Үшбұрышты бөгеті бар канал ішіндегі ламинар режимдегі газдың жазық ағысының үлгісі қарастырылады. Навье-Стокс теңдеулерін сандық әдіспен шешу арқылы тоқ функциясы мен құйынның мәндерін анықтаудың математикалық моделі құрылған. Навье-Стокс теңдеулерін шешудің алгоритмі келтірілген.
MODELING current around TRIANGULAR LEDGE by GAS FLOW
Doct.tech.sci. B.R.Ismailov
S.K.Meldebekova
Kand.tech.sci. S.V.Viktorov
The model of the flat current of the gas is сonsidered in channel with triangular ledge at laminar flow. Solving equations Navie-Stoks numerical methods, is formed mathematical model for finding of importances of the function of the current and curl. The broughted algorithm for decision of the equations Navie-Stoks.
УДК 631.6: 338.111: 504.064.36
МЕТОДИКА СОЗДАНИЯ ЦИФРОВОЙ ТОПОГРАФИЧЕСКОЙ
ОБСТАНОВКИ В ЗОНЕ ВЛИЯНИЯ ВОДОХОЗЯЙСТВЕННЫХ СИСТЕМ
Докт.техн.наук М.Н.Сенников
Канд.с-х.наук Г.Е.Омарова
А.Е.Аубакирова
Т.С.Колбачаев
Рассмотрены новые методы работ по созданию цифровых моделей топографической поверхности.
При проведении проектных работ традиционными методами рельеф местности представлялся в виде образно-знаковых моделей посредством топографических и географических карт. Однако в последние годы выявилось, что при использовании ЭВМ для автоматизации проектирования исходная информация о рельефе местности должна быть задана в другой форме. Такой формой является интерпретация рельефа местности множеством точек, заданных числами. Вместо образно - знаков моделей для ЭВМ целесообразно использовать математические модели, относящиеся к классу цифровых /3/.
В специальной литературе начиная с 70-х годов используются термины «цифровая модель местности», «цифровая модель рельефа» и др.
В инженерных кругах, занимающихся моделированием топографической поверхности, применяется термин «цифровая модель местности», который несколько шире термина «цифровая модель рельефа».
Некоторые специалисты /1,3,5/ определяют ЦМР как модель поверхности рельефа в численной (дискретной) форме. Это определение не отражает сущности цифровой модели рельефа. В действительности нет возможности ввести в память машины бесконечно большое множество точек рельефа. Основой ЦМР служит совокупность исходных точек, определяемых пространственными координатами X,У,Z которые являются как бы каркасом ЦМР. Вторым компонентом модели является алгоритм аппроксимации, способный воссоздать по совокупности точек каркаса отметку любой точки рельефа.
Большинство данных о территории, необходимых для проектирования собирается в определенных точках на местности, которые при формировании данных для цифровых моделей называются точками взятия образцов. В основном эти измерения проводятся в некоторых характерных точках, например, местах расположения буровых исследовательских скважин, вдоль курса самолета, производящего аэрофотосъемку, или наземных траверсов геодезической съемки и проч. Точки взятия образцов могут располагаться как произвольно так и регулярно. Например, данные дистанционного зондирования, которые представляют собой растровые изображения, также можно рассматривать как источник информации в регулярно расположенном наборе точек. В дальнейшем эти точки и формируют узлы каркаса цифровых моделей местности используемых при автоматизации проектных работ.
Таким образом под цифровой моделью рельефа (ЦМР) понимается совокупность координат точек поверхности земли, связанных с ними значений высотных отметок, и алгоритм аппроксимации, по которому можно получить для любой точки А(X,У) значение отметки поверхности земли Zа.. Точка А, конечно, должна лежать внутри области, охватываемой ЦМР.
Многие компьютерные методы пространственного анализа, первоначально разрабатывались при решении задач по созданию различных моделей рельефа Земли [6,7]. В программном обеспечении геоинформационных систем заложены широкие возможности для создания и работы с цифровыми моделями рельефа и инженерных объектов.
С математической точки зрения подобные модели являются двумерными (2В), но в отличие от «плоских» полей орошения, ЦМР на двухмерном пространстве монитора или графопостроителя "полностью" отобразить нельзя, поэтому используют специальные методы представления, например, с помощью изолиний, изометрических изображений и т.д. Для того, чтобы выделить такого рода модели, для них используют специальное название 2,5D цифровые модели, подчеркивая тем самым, что реально такая двумерная модель может быть отображена только в трехмерном пространстве. Системы, позволяющие работать с такими моделями, называют соответственно 2,5П ГИС.
При проведении проектных работ в среде ГИС, чаще других требуется проводить пространственные преобразования типа "точка-область" и "точка-точка". Задача преобразования "точка-область" состоит в том, чтобы перейти от характеристик территории в точках взятия образцов к характеристикам местности для заданных координат, проектируемых или реконструируемых пространственных объектов (полей орошения). Для решения этих задач в среде ГИС создается специальный тематический слой векторного или растрового типа, который будет представлять, либо непрерывную, либо кусочно-непрерывную «поверхность», отображающий изменение значений характеристик местности. Способ преобразования "точка-область" зависит от шкалы измерения значений рассматриваемых характеристик (количественная или качественная шкала).
Выбор метода преобразования "точка-область" и "точка-точка" определяется многими факторами и в частности тем, какова структура расположения исходных данных - точек взятия образцов. При этом можно выделить три возможности:
- точки расположены регулярно на прямоугольных или гексагональных сетках;
- точки расположены нерегулярно в произвольных точках;
- точки расположены «полурегулярно» или равномерно на изолиниях профилях и др.
Для точечных исходных данных методы преобразования к площадным объектам могут быть подразделены на две группы по признаку, применяется или нет пространственная интерполяция. При моделировании поверхностей пространственно-непрерывных полей переменных часто используют интерполяцию из набора нерегулярно расположенных точек отбора образцов к регулярной сетке, которую можно рассматривать как растровое представление в ГИС, причем каждая интерполируемая точка определяет ячейку, внутри которой характеристика постоянна.
Основой методов ГИС-технологий работающих с такой пространственной информацией и не использующих интерполяцию (по сложившейся терминологии «интерполяционные методы 0-го порядка»), является построение полигонов, с которыми связывается одна или несколько характеристик узловой точки (точки взятия образцов). Если полигон строится по нескольким узловым точкам, то используется операция осреднения для определения значений характеристик полигона, которая зависит от шкалы, по которой заданы значения характеристик узловых точек. В большинстве случаев используются стандартные ГИС-алгоритмы автоматического построения полигонов по узловым точкам, хотя в некоторых случаях используются методы, в которых полигоны строятся «вручную» на основе субъективных мнений проектировщиков [8,9,10]. Некоторые примеры применения таких методов представлены на рис.2. На рис.2А представлено расположение набора узлов (точек взятия образцов).
В простейшем случае площадные объекты (поля орошения), для которых необходимо определить характеристики по исходным точкам, (рис.2Б), представляют собой регулярно расположенные ячейки некоторой сетки, каждая исходная точка связывается с соответствующей ей ячейкой. Если в ячейку не попадает ни один узел, то такой ячейке назначается либо значение характеристики ближайшего узла, либо значение, вычисляемое как некоторая функция, усредняющая данные соседних ячеек. Характеристики ячеек, которые содержат более чем один узел, определяются путем агрегирования значений в этих узлах согласно выбираемому правилу, такому как вычисление среднего, медианы, моды, максимального или минимального значения (в зависимости от шкалы измерения характеристики или смысла задачи).
Другой простой метод состоит в построении полигонов в виде правильного вписанного многоугольника или круга вокруг исходных узлов (рис.2В). Этим полигонам назначаются характеристики исходных узлов. Непокрытые области получают пустые значения ближайших узлов. Этот вариант метода хорошо работает, когда узлы распределены более или менее равномерно, без особых сгущений (отсутствует кластеризация), иначе для перекрывающихся полигонов необходимо применять не всегда простые операции для определения формы новых полигонов и агрегирования характеристик. Преимущество этого подхода состоит в том, что при построении полигонов радиус круга может быть выбран для отражения субъективного мнения о размере зоны влияния узлов.
Применение метода, основанного на использовании полигонов Тиссена (называемых также полигонами Вороного), позволяет исключить проблему полигонов либо не имеющих точек, либо содержащих несколько точек (рис.2Г). Полигоны всегда содержат только один узел. Такие полигоны образуются посредством проведения серединных перпендикуляров к отрезкам, соединяющих ближайшие узлы. Преимуществом этого метода является то, что отсутствуют непокрытые области и могут быть определены "естественные" соседи для каждого узла. Недостатком этого метода является то, что размер полигонов обратно пропорционален плотности узлов и отдельный узел может иметь очень большое влияние, (соответствующий полигон имеет большую площадь), несоразмерное смыслу задачи. Один из возможных выходов из этой ситуации может состоять в комбинировании полигонов Тиссена с предыдущим методом. Результат такого комбинирования представлен на рис.2Д. Последний метод часто применяется в том случае, когда точки взятия образцов расположены, например, вдоль некоторых траверзов обследования (например, русла рек), а расстояние между траверзами велико.
Иногда более удобно пользоваться полигонами неправильной формы, построение которых зависит от смысла задачи. Такой метод применяется в том случае если, например, стоит задача создания геохимической карты крупного масштаба по образцам воды и осадка, которые брались вдоль притоков водотока Зоны влияния в виде полигонов для таких исходных точек не могут определяться ни одним из представленных выше методов Построение таких полигонов осуществляется путем выделения водосборов каждого притока, что отвечает смыслу задачи (рис.2Е). При этом для выделения границ водосбора методами ГИС могут использоваться автоматизированные процедуры, которые опираются на ЦМР. Они работают достаточно удовлетворительно в областях с хорошо выраженным склоном поверхности земли. Поэтому в тех случаях, когда точки расположены, не достаточно плотно, границы полигонов, которые построены специалистом в предметной области (топографом, геологом, почвоведом), будут давать более удовлетворительный результат, чем автоматическое построение полигонов Тиссена.
Методы, не использующие интерполяцию, больше подходят в том случае, когда характеристики измеряются по качественной шкале, хотя они годятся и для случая измерения значений по порядковой, интервальной или относительной шкале. Алгоритмы реализации этих методов достаточно универсальны и они широко представлены в виде специальных модулей ПО ГИС.
Интерполяционные методы преимущественно применяются в резкоизменяющихся непрерывных характеристиках местности (геополей), например, отметок поверхности пересеченного рельефа. Эти методы, обычно, применяются для какой-либо одной характеристики, хотя иногда используются интерполяции векторных полей (высотная отметка, тип грунта и т.д.). В качестве основного картографического средства отображения в ГИС пространственного распространения геополей используется построение линий равного значения (изолиний). При этом точечные данные преобразовываются либо в линейные объекты, с которыми связывается определенная характеристика (собственно изолинии), либо в полигоны между изолиниями.
Альтернативой интерполяции на регулярной сетке является построение триангуляционной нерегулярной сети. Для целей реконструкции оросительных систем целесообразно использовать следующие специальные интерполяционные методы ГИС.
В триангуляционном методе точки взятия образцов соединяются линиями для образования мозаики треугольников. Предпочтительным является использование триангуляции Делоне, при построении которой получаются треугольники наиболее близкие к равносторонним /10/. Этот способ особенно хорошо использовать для моделирования топографических поверхностей, т.к. этим способом легко представляются разрывы поверхности Земли, такие как обрывы, реки и т.д. На рис.3 представлен пример для иллюстрации применения триангуляционного метода.
Внутри каждой треугольной фасетки функция изменяется линейно:
z = а + bх + су (1)
Неизвестные коэффициенты находятся отдельно для каждого треугольника. Так на рис.3 неизвестная точка лежит внутри треугольника, для вершин которого можно записать следующие уравнения:
-
42 = а + Зb + 5с
32 = а +4b + 2с
(2)
28 = а + 2b + Зс
Решение этой системы дает а = 4.8, b = 4.4, с = 4.8. Таким образом, оцениваемая отметка поверхности может быть вычислена для любой точки в треугольнике:
z = 4.8 + 4.4х + 4.8у (3)
т.о. значение в точке (3,4) равно 37.2.
При триангуляции генерируемая поверхность проходит через каждый узел с известным значением характеристик интерполируемого геополя. Такое построение сетки эффективно, если ошибки в определении данных в узлах малы, например, если высотные отметки, определены высокоточными геодезическими приборами. Другая особенность заключается в том, что в триангуляционном методе зона влияния каждой точки ограничена окружающими треугольниками и зависит от плотности узлов.
Литература
1. Желтов С.Ю., Инвалев А.С., Киряков К.Р., Степанов А.А. Особенности реализации 3D ГИС. «Информационный бюллетень». ГИС – Ассоциации. – М. № 5 (12), 1997.
2. Полшков Е.А. Особенности ГИС - технологий при математическом моделировании геоэкологических объектов. «Информационный бюллетень». ГИС – Ассоциации. – М. № 4 (16), 1998.
3. Арефьев Н.В., Баденко В.Л., Осипов Г.К., Тараканов А.Е. Оценка геоэкологического потенциала геосистемы «речной бассейн» с использованием ГИС – технологий? Межвузовский сб. научных трудов. МГСУ и СПбГТУ, М., 2000.
4. Васильев В.С.., Арефьев Н.В., Кононова М.Ю. Природно-технический монитиринг энерго-водохозяйственных комплексов. Система обработки информации. Методические указания. СПГТУ, 1997.
5. Сенников М.Н. Совершенствование способов поддержания оросительных систем в рабочем состоянии. Уч. пособие. ТарГУ, 2000.
Таразский Государственный университет им. М.Х.Дулати, Тараз
СУ ШАРУАШЫЛЫҒЫ ЖҮЙЕЛЕРІНДЕГІ ЖЕРДІҢ
САНДЫҚ ТОПОГРАФИЯЛЫҚ ӘДІСІН ҚҰРУ
Техн.ғыл.докт. М.Н.Сенников
А.-ш.ғыл.канд Г.Е.Омарова
А.Е.Әубәкірова
Т.С.Колбачаев
Топографиялық жер бетінің су шаруашылық жүйелеріндегі зоналардың сандық моделі құрастырылған.
THE METHOD CREATION JIGUZES TOPOGZOPFZICAL SITUATION IN ZONE ON INFLNENCE WOTEZ THZIFTY SYSTEMS
Doct.tech.sci. M.N.Sennikov
G.Y.Omarova
A.E.Aubakirova
T.C.Kolbajaev
The creation in jiquzes model topoqzopfzical country for zone woter thrifty systems.
УДК 621.43.065
МОДЕЛИРОВАНИЕ БОКОВОЙ ДИНАМИЧЕСКОЙ УСТОЙЧИВОСТИ
ТРАКТОРА КЛАССА 14-20 Кн ПРИ РАБОТЕ НА СКЛОНАХ
Докт.техн.наук М.Н.Сенников
Е.О.Омаров
А.Е.Аубакирова
Т.С.Колбачаев
Определенные основные методы соединения конструкций трактора с различными условиями движения на местности. Рассмотрены причины и определены основные показатели динамического бокового опрокидывания.
Боковое опрокидывание четырехколесных тракторов в основном может быть вызвано методом соединения конструкции собственного трактора и рабочих орудий, а также условиями движения трактора и профилем местности.
Первую причину можно отнести к категории внутренних причин, которые определяются распределением массы и положением центра тяжести трактора, причем наиболее типичной характеристикой, определяющей эти факторы, является угол статического бокового опрокидывания.
Данные исследование посвящено анализу величины угла динамического бокового опрокидывания в зависимости от коэффициента упругости шин, высоты переезжаемого препятствия, скорости движения трактора и величины угла статического бокового опрокидывания. Анализ проводили для случая, когда при движении четырехколесного трактора по трассовой линии верхние (по склону) колеса трактора (без навесных орудий) переезжают через единичное препятствие типа бугра.
Проведение экспериментального исследования на реальном тракторе требует многократного повторения эквивалентных измерений и, кроме того, связано с вероятным техническим ущербом опрокидывании машины. В этой связи при испытаниях реальной машины приходится устанавливать стенд с дистанционным управлением, а также предусматривать соответствующую технику безопасности, предотвращающую возможной технический ущерб при опрокидывании. В результате этого удается получить лишь несколько экспериментальных значений с различными положениями центра тяжести, которые отличаются от реальной машины.
В этой связи весьма удобно использовать малогабаритную модель машины, при опрокидывании которой не возникает технического ущерба. Однако, в этом случае необходимо предварительно рассматривать условия подобна модели и натурного образца, а также подтвердить справедливость экспериментальной методики.
В качестве первого этапа рассмотрели условия подобия при динамическом боковом опрокидывании относительно легкого 12-сильного реального трактора, снабженного экспериментальным стендом дистанционного управления, а также соответствующим устройствами техники безопасности и геометрической модели этого трактора. На втором этапе исследования, используя полученные условия подобия, были выбраны экспериментальные методы, позволяющие на модели, обладающей характеристиками среднестатистического серийного трактора, изучать поведение реального серийного трактора.
Эксперименты позволили исследовать задачу для случая, когда при движении четырехколесного трактора по трассовой линии только верхние (по склону) колеса трактора переезжают через единичное препятствие. В качестве такого препятствия для модели была использована криволинейная стальная трехмиллиметровая пластина с профилем поперечного сечения вида
Н = Но sin (πx /2Hо) (1)
где Н - высота единичной неровности;
X - горизонтальная длина по основанию;
Но - высота препятствия единичной неровности.
Сводка основных физических параметров, связанных с задачей динамического бокового опрокидывания при движении трактора в указанных выше условиях, в общем виде представлена в табл.1.
Таблица 1
Параметры и размерности, влияющие на величину угла
динамического бокового опрокидывания четырехколесного трактора
| Параметры | Обозначение | Размерность |
| 1 | 2 | 3 |
| Коэффициент упругости задних колес | k | МТ-3 |
| Коэффициент реституции задних колес | e | - |
| Угол динамического бокового опрокидывания | α d | - |
| Угол вращения передней оси относительно центрального шарнира | φ | - |
| Колея трактора | d | м |
| Колесная база | ℓ | м |
| Высота центра тяжести | h | м |
| Расстояние между задней осью и центром тяжести трактора | α | м |
| Высота центрального шарнира передней оси | | м |
| Масса трактора | W | кг |
| Инерция трактора | J | кг м2 (нм2) |
| Высота препятствия | Ho | м |
| Скорость движения | V | м/с |
| Ускорения силы тяжести | q | м/с2 |
Динамическое взаимодействие шины колеса трактора и препятствия можно выразить с помощью одного из двух методов, с применением коэффициента реституции шины колеса или с применением коэффициента упругости. В последующем изложении проводится анализ пригодности каждого из этих двух методов для решения рассматриваемых задач.
Первоначально рассмотрим метод выражения динамических характеристик взаимодействия и препятствия с помощью коэффициента реституции (метод А). Функциональную зависимость между величиной угла динамического бокового опрокидывания и различными факторами, непосредственно связанными с величиной этого угла, можно выразить соотношением (2).
α d = f (ℓ, α, d, ℓ, h, a, H1, Ho, V, q, W) (2)
Используя Гипотезу (Бакинзэма) /3/, можно преобразовать это соотношение в безразмерным виде к следующей функции:
π1 = F (π2, π3….., π10) (3)
Каждый из членов П формулы (3) можно определить по следующим уравнениям:
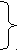
π1 = αd; π2 = α; π3 = d/ℓ; π4 = h/ℓ; π5 = a/ℓ;
π6 = H1/ℓ; π7 = Hо/ℓ; π8 = е; π9 = V2/ℓq; π10 = V2/ℓ3W
Если функциональное соотношение (3) правильно отражает сущность угла динамического бокового опрокидывания четырехколесного трактора, а также зависимости между основными параметрами, непосредственно влияющими на его величину, то, задавая однозначно величины параметров от П2, П3 до П10, можно получить однозначно величину опрокидывающего угла П1.
Действительно, обозначая для условий подобная индексами р параметры, относящиеся к прототипу, а m - параметры, относящиеся к модели, можно записать соотношение.
πip = πim (i = 1,2,3,….10) (5)
Обозначив далее через 1/п коэффициент подобия модели и прототипа и подставляя в формулу (5) значения по равенствам формулы (4), можно записать условия подобия в виде следующих соотношений:
φm = φp (6)
ℓm = ℓр (7)
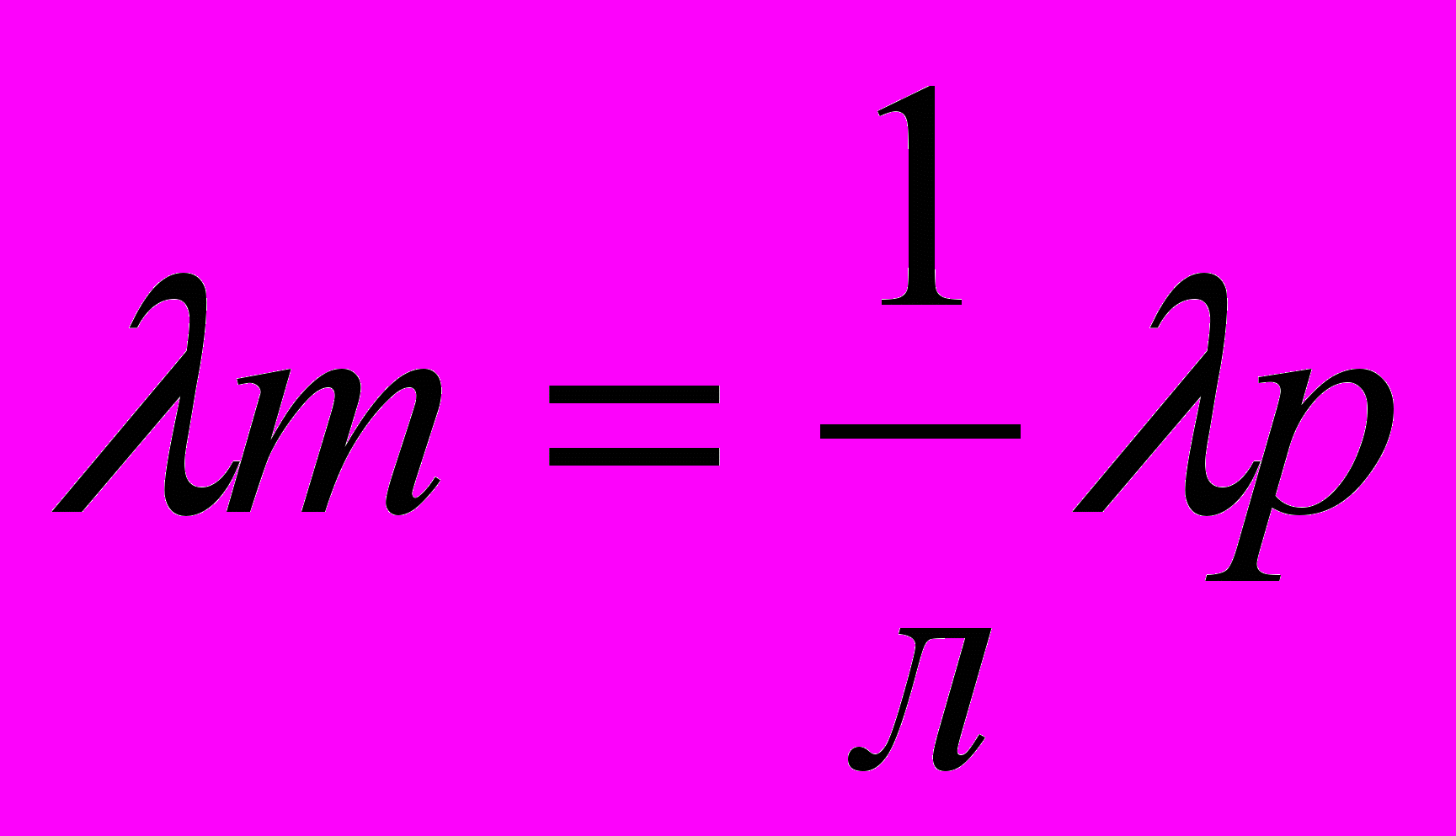 (8)
(8)где λ - единый параметр, обозначающий размерность длины для параметром d1, a, 1, Ho, H1
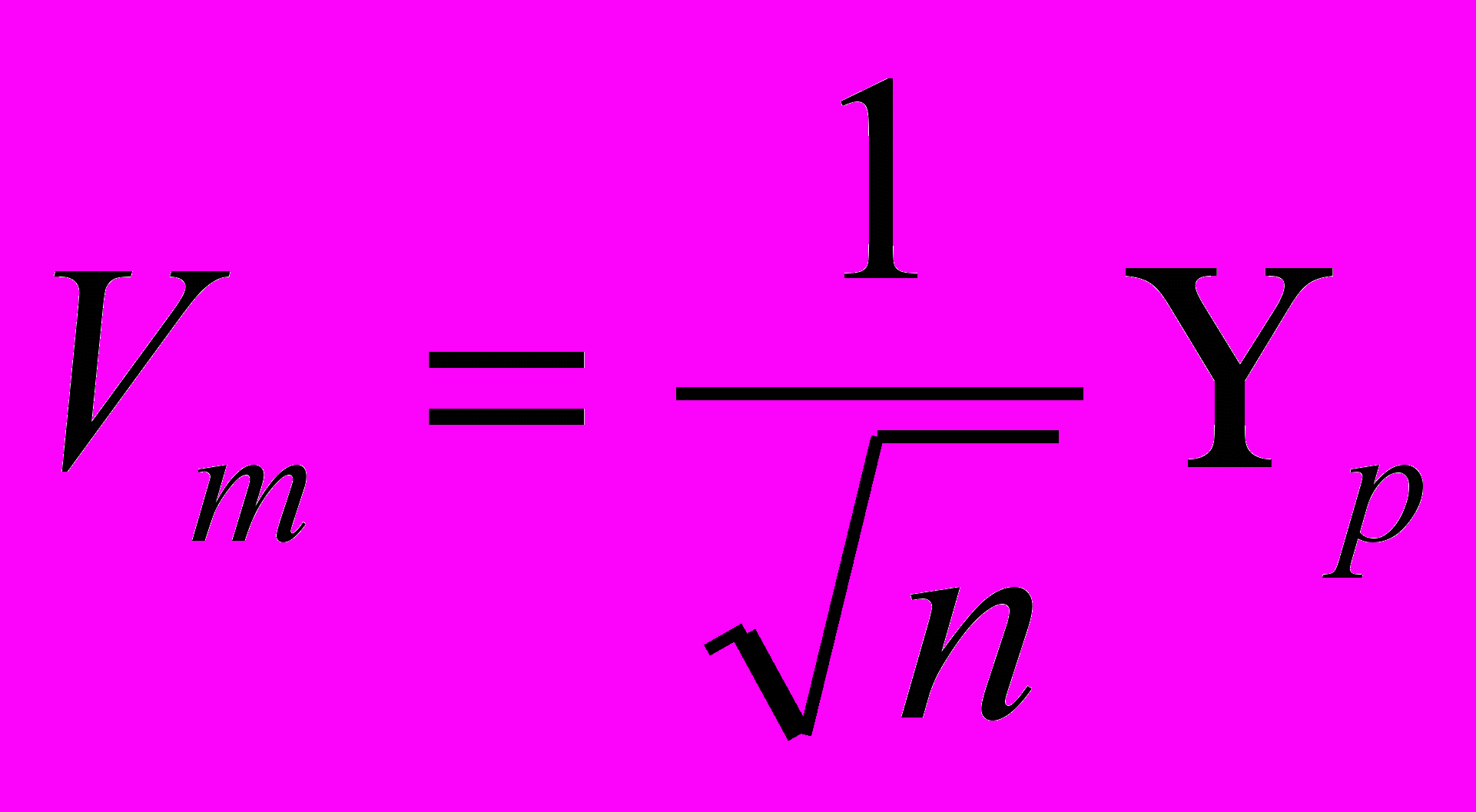 (9)
(9)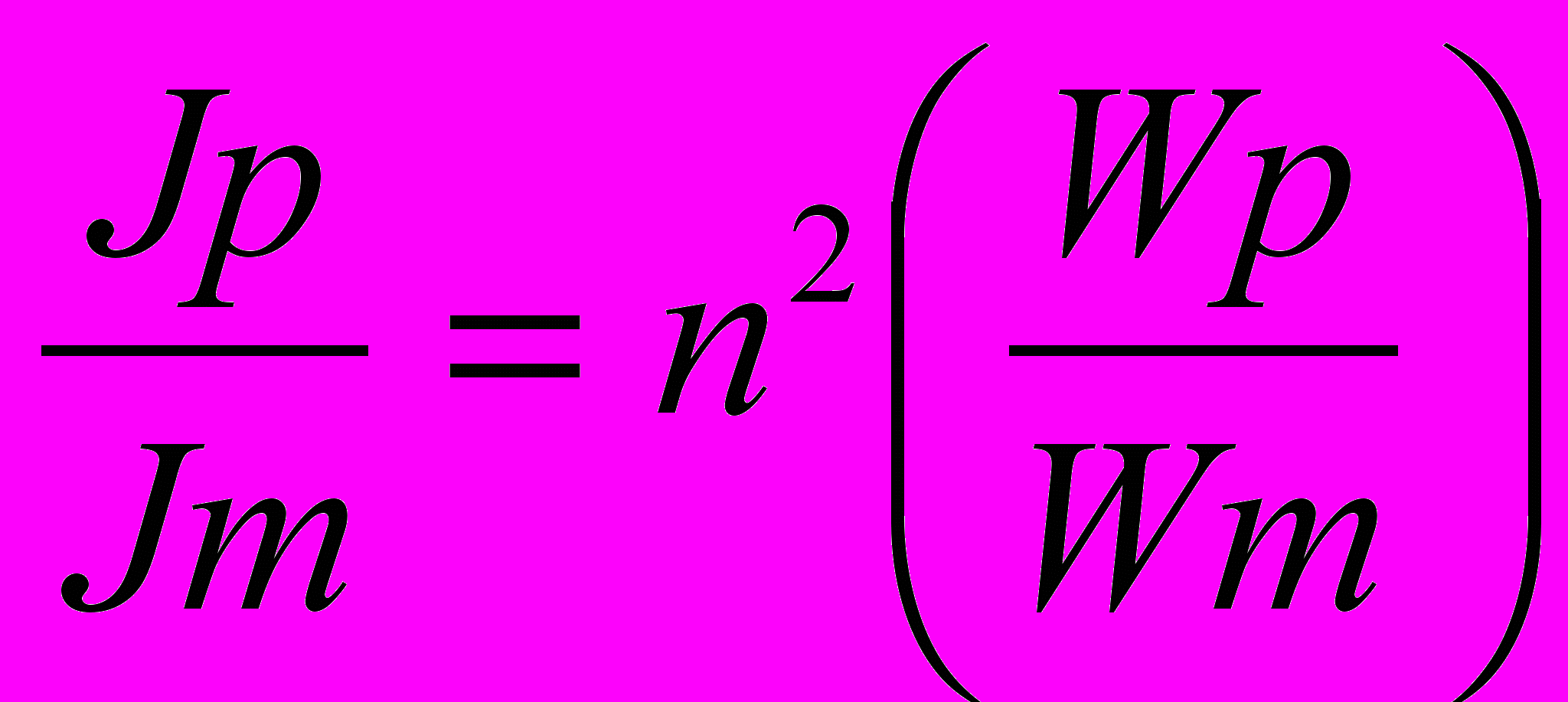 (10)
(10)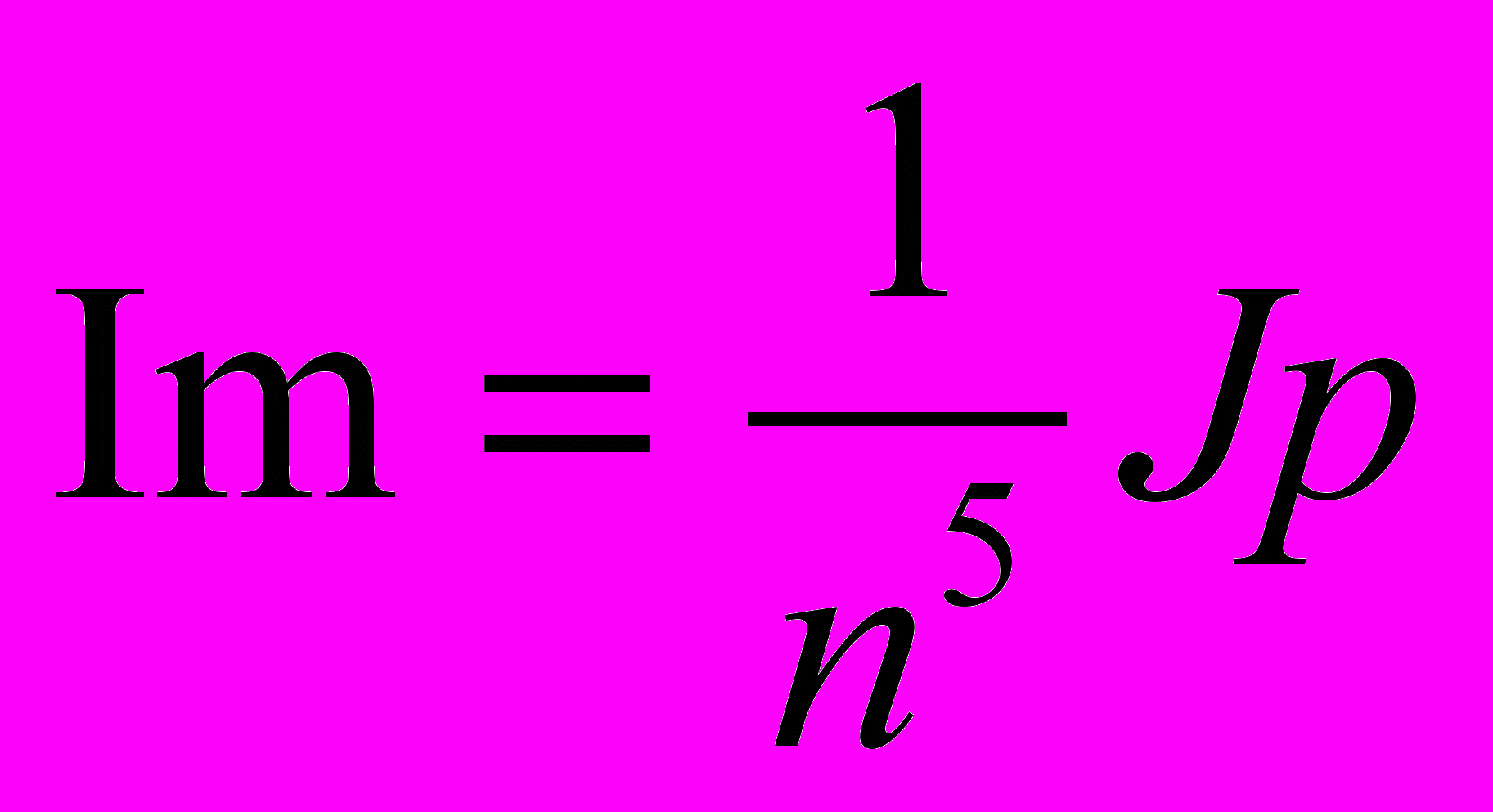 (11)
(11)Соотношение (10) можно преобразовать к следующему виду:
Далее рассмотрим метод (В) выражения динамических характеристик взаимодействия шины и препятствия с помощью коэффициента упругости (метод В).
Функциональная зависимость между величиной угла динамического бокового опрокидывания и различными параметрами, непосредственно влияющими на величину этого угла, может быть выражена в виде:
α d = f (к, α, d, ℓ, h, a, H1, Ho, V, q, W, J) (13)
Введя по аналогии с методом (А) в соотношении с формулой (3) параметр П, получим соотношение
π11 = F (π21, π31….., π101) (14)
Каждый из членов П формулы (14) может быть определен следующим образом:
π11 = π1 = αd π21 = π2 = α
π31 = π3 = d/ℓ π41 = π4 = h/ℓ
π51 = π5 = а/ℓ π61 = π6 = H1/ℓ
π71 = π7 = Ho/ℓ π81 = π8 = ℓк/W
π91 = π9 = V2/ℓq π101 = JV2/ℓ4к (15)
В полном соответствии с методом (А) получаем из формулы (15) условия подобия
φm = φp (16)
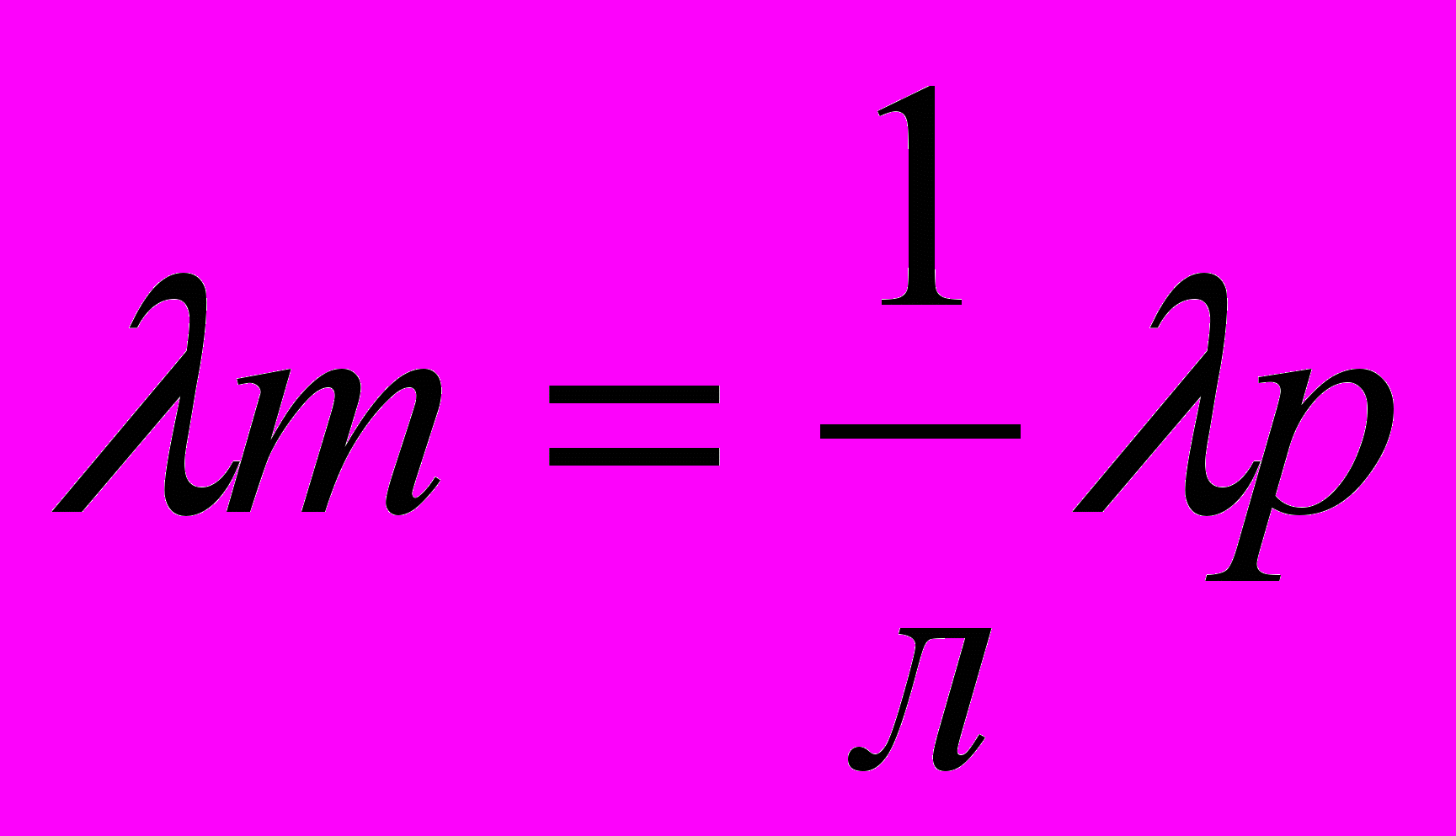 (17)
(17)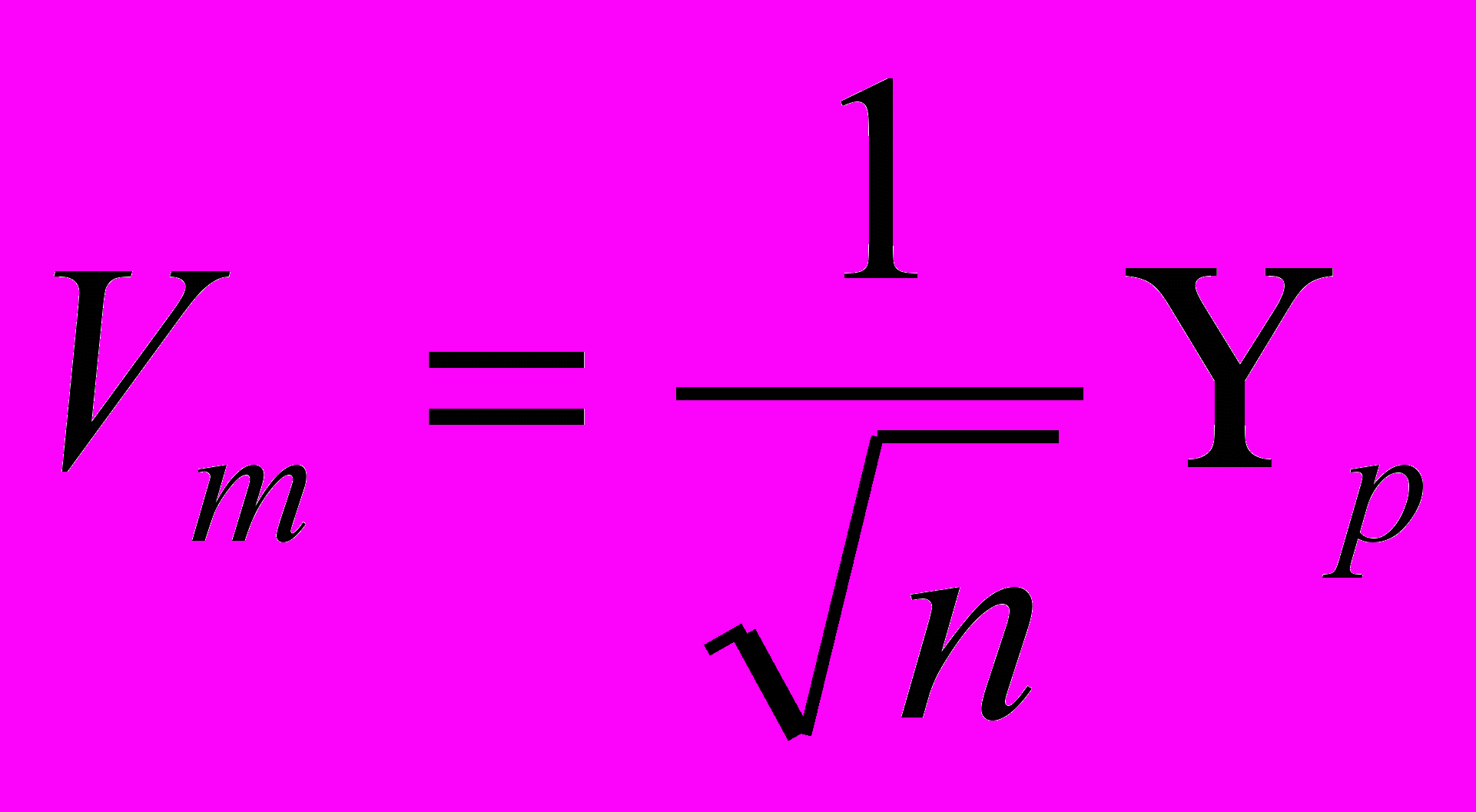 (18)
(18)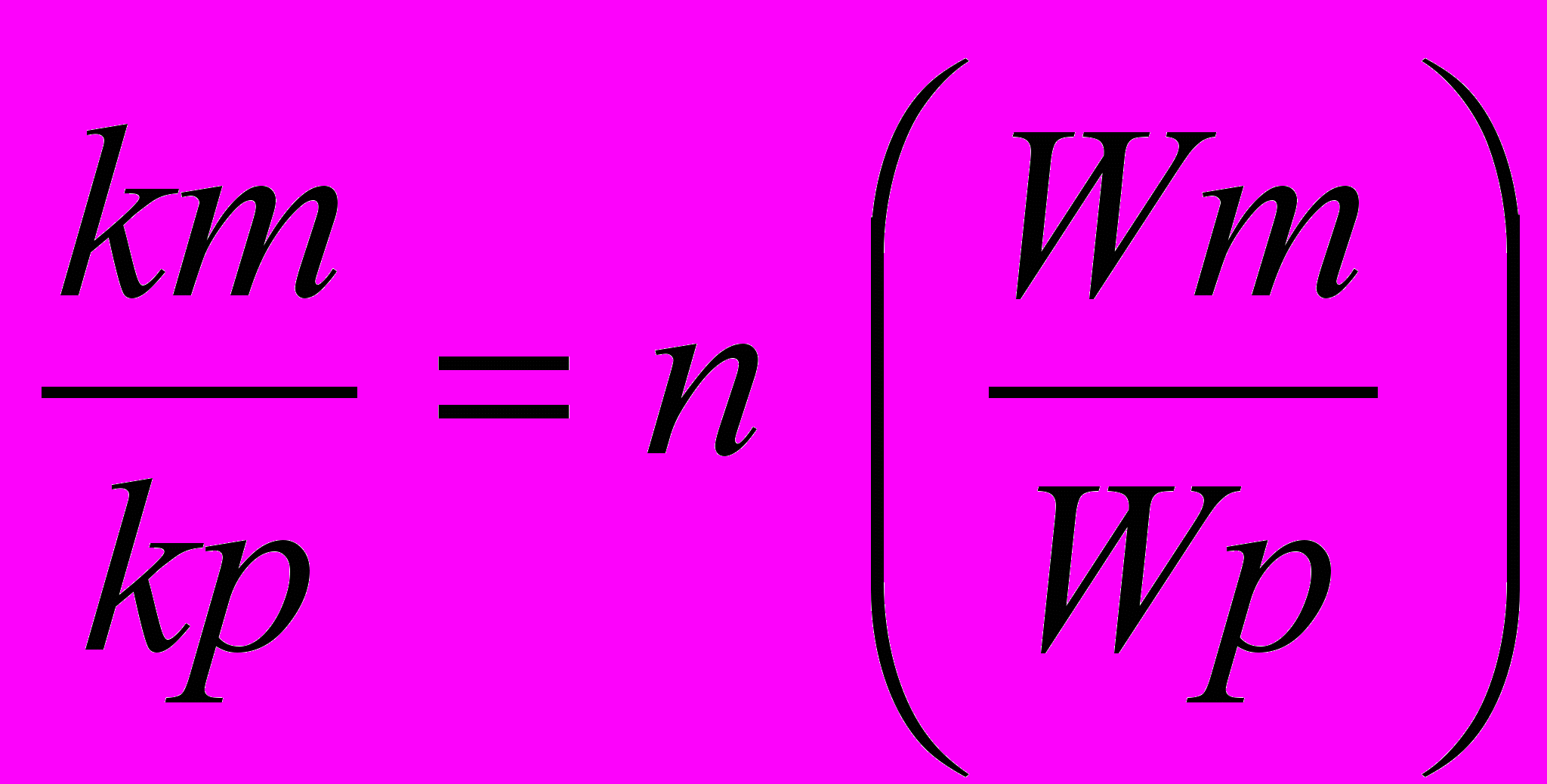 (19)
(19)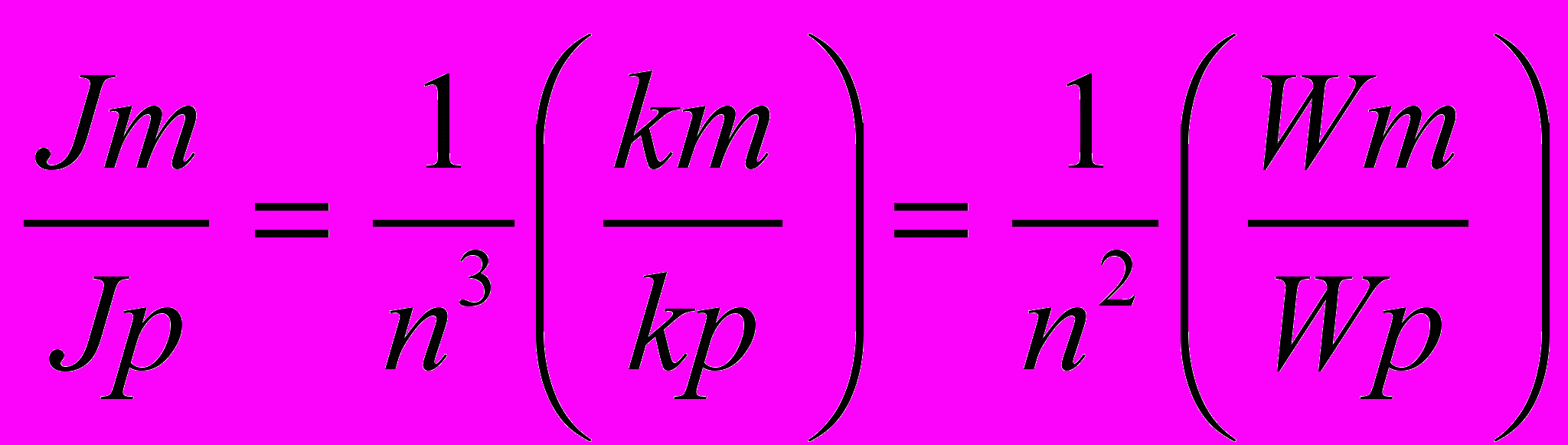 (20)
(20)Подставляя затем по аналогии с формой (11)
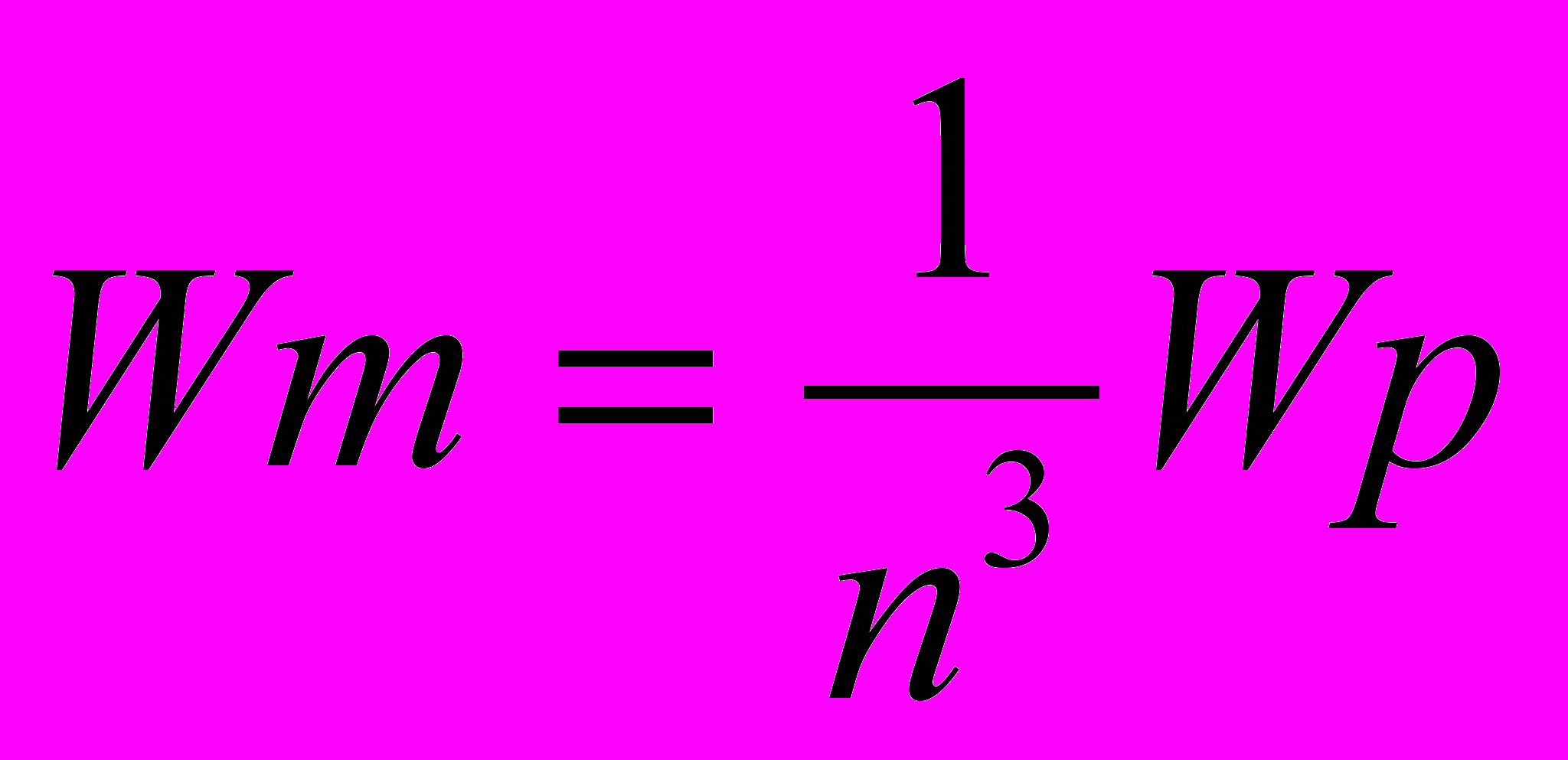
Преобразуем формулу (20) к следующему виду:
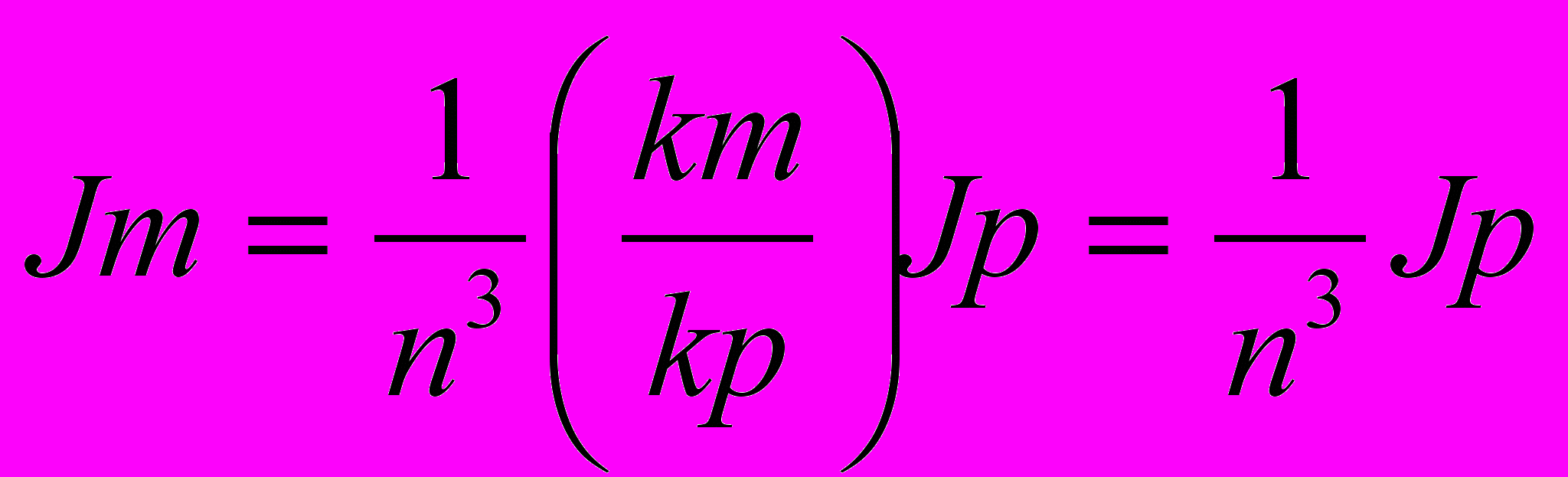 (21)
(21)Задаваясь указанными в предыдущем изложении условиями подобия и пологая, что физические закономерности, отражающие влияние различных параметров на величину угла динамического бокового опрокидывания были выражены достаточно точно, можно считать справедливым следующее равенство:
Выводы
Условия подобия обоих методов характеризуется уравнениями (4) и (5). Было установлено, что для решения рассматриваемой задачи пригодны оба метода. Тем не менее (А) дает возможность получить более точные результаты, чем метод (В), поэтому что у этих тракторов типа МТЗ-80 (МТЗ-100) нет упругой задней подвески.
Литература
1. Ш.Я.Кереселитье, К.К.Гонкрелидзе, О.П.Мышнилдадзе, А.А.Мелашвили. Поперечная устойчивость четырехколесного трактора с шарнирным упором переднего моста. «Труды ВНИГорсселмаш» Тбилиси, 1973.
2. Коновалов. Устойчивость и управляемость машинно - тракторных агрегатов. Пермь, 1969.
3. Мацуема и др. боковой опрокидывающий угол четырехколесного трактора при работе на горных склонах (Сообщение 1), «Ночь» какой гаккай 1970, т.32, № 2 с. 111-116.
4. Омаров Е.О., Подсевалов М.П. Результаты тяговых испытаний тракторов МТЗ-5214 на склонах гор. Сборник научных трудовых факультета механизации сельскохозяйственного производства КиргСХИ. Фрунзе, 1973.
5. Роспелов Ю.А. Устойчивость трактора. М.: Машиностроение.
Таразский Государственный университет им. М.Х.Дулати, Тараз
14-20 Кн КЛАСТЫ ТРАКТОРДЫҢ БІРЖАҚТЫ ДИНАМИКАЛЫҚ ТҰРАҚТЫЛЫҒЫН ТАУ ЕТЕГІНДЕ ЖҰМЫС ІСТЕГЕНДЕГІ МОДЕЛІ
Техн.ғыл.докт. М.Н.Сенников
Е.О.Омаров
А.Е.Әубәкірова
Т.С.Колбачаев
Жер ерекшеліктерін ескере отырып трактордың конструкциясын және жұмыс жүйелерін құру әдісі келтірілген.
THE WORING IN TZASCTOR 14-20 KN MODEL
LATEZAL DINAMIC STEADY
Doct.tech.sci. M.N.Sennikov
E.O.Omarov
A.E.Aubakirova
T.C.Kolbajaev
The zesults in method the creation conztraction tzacbor and worind instzument, condition motion with calculation especially country.
