Валентин Максимилианович Макаров Концепции современного естествознания. Часть I учебное пособие
| Вид материала | Учебное пособие |
СодержаниеРазвитие представлений о пространстве и времени. А отнесено к декартовой системе, координаты которой обозначены без штрихов (например, X Эрнст Мах Н. И. Лобачевский Вильям Клиффорд |
- Н. И. Константинова концепции современного естествознания учебное пособие, 2191.08kb.
- Учебное пособие Москва, 2007 удк 50 Утверждено Ученым советом мгупи, 1951kb.
- Высшее профессиональное образование т. Я. Дубнищева концепции современного естествознания, 9919.17kb.
- А. А. Горелов Концепции современного естествознания Учебное пособие, 3112.99kb.
- Ю. Б. Слезин Концепции современного естествознания Учебное пособие, 2161.2kb.
- Елена Юрьевна Матвеева. Концепции современного естествознания. Словарь основных терминов:, 1529.96kb.
- В. М. Найдыш Концепции современного естествознания, 8133.34kb.
- Концепции Современного Естествознания, 274.86kb.
- Учебно-методический комплекс дисциплины концепции современного естествознания Специальность, 187.08kb.
- Программа курса «Концепции современного естествознания», 168.05kb.
Развитие представлений о пространстве и времени.
Во второй половине XIX в. физики все чаще анализируют фундаментальные основания классической механики. Прежде всего, это касается понятий пространства и времени, их ньютоновской трактовки. Предпринимаются попытки придать понятию абсолютного пространства и абсолютной системы отсчета нового содержания взамен старого, которое им предал еще Ньютон. Так в 70-е гг. XIX в. было введено понятие α - тела как такого тела во Вселенной, которое можно считать неподвижным и принять за начало абсолютной системы отсчета. Некоторые физики предлагали принять за α - тело центр тяжести всех тел во Вселенной, полагая, что этот центр тяжести можно считать находящимся в абсолютном покое.
Вместе с тем рядом физиков высказывалось и противоположное мнение, что само понятие прямолинейного абсолютного и равномерного движения как движения относительно некоего абсолютного пространства лишено всякого научного содержания, как и понятие абсолютной системы отсчета. Вместо понятия абсолютной системы отсчета они предлагали более общее понятие инерциальной системы отсчета (координаты) не связанное с понятием абсолютного пространства. Из этого следовало, что понятие абсолютной системы координат также становится бессодержательным. Иначе говоря все системы, связанные со свободными телами, не находящиеся под влиянием каких-либо других тел, равноправны.
И
 нерциальные системы – это системы, которые движутся прямолинейно и равномерно относительно друг друга. Переход от одной инерциальной системы к другой осуществлялся в соответствии с преобразованиями Галилея. Именно преобразования Галилея характеризуют в классической механике закономерности перехода от одной системы отсчета к другой.
нерциальные системы – это системы, которые движутся прямолинейно и равномерно относительно друг друга. Переход от одной инерциальной системы к другой осуществлялся в соответствии с преобразованиями Галилея. Именно преобразования Галилея характеризуют в классической механике закономерности перехода от одной системы отсчета к другой. Если система отсчета Х1О1Y1 (Рис. 1) движется прямолинейно и равномерно со скоростью υ относительно системы отсчета XOY в течение времени t, то
ОО1 = υ.t,
а координаты точки Р в этих системах отсчета связаны между собой следующими соотношениями:
X1=X- υ.t; Y1=Y; t1=t
Преобразования Галилея в течение столетий считались само собой разумеющимися и не нуждающимися в обоснования. Они замечательны тем, что предъявляют определенное требование формулировке закона механического движения: эти законы должны быть сформулированы так, чтобы оставались инвариантными (т. е. неизмененными в любой инерциальной системе отсчета).
Развивая идею Галилея о системе отсчёта объектов (движущихся или покоящихся) Рене Декарт дает большую степень отточенности этому понятию: он ввел формализованную (идеализированную) систему прямоугольных пространственных координат, названную его именем – декартовая система координат.
И хотя до сих пор системой отсчета могут называться реальные объекты, но при этом всегда подразумевается отнесенность объекта в декартовой системе координат. Благодаря декартовой системе координат галилеевский принцип относительности движения, а также понятие галилеевых преобразования получили более четкое точное выражение.
Теперь, галилеевы преобразования можно представлять как взаимное проецирование не самых физических объектов, а декартовых систем координат, к которым отнесены объекты.
П
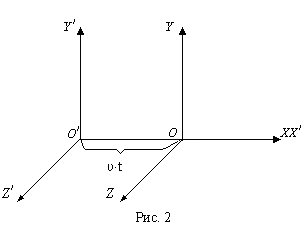 усть некоторое тело А отнесено к декартовой системе, координаты которой обозначены без штрихов (например, X, Y, Z), а нам нужно определить параметры тела в параллельной координатной системе со штрихами. Для простоты будем определять параметры одной точки тела и совместим координатную ось X1 c ось Х. Примем также, что координатная система со штрихами покоится, а без штрихов – движется равномерно и прямолинейно. Тогда правила галилеевых преобразований (т. е. перехода от одной системы отсчета к другой) примет вид:
усть некоторое тело А отнесено к декартовой системе, координаты которой обозначены без штрихов (например, X, Y, Z), а нам нужно определить параметры тела в параллельной координатной системе со штрихами. Для простоты будем определять параметры одной точки тела и совместим координатную ось X1 c ось Х. Примем также, что координатная система со штрихами покоится, а без штрихов – движется равномерно и прямолинейно. Тогда правила галилеевых преобразований (т. е. перехода от одной системы отсчета к другой) примет вид: В
X1=X- υ.t;
Y1=Y;
t1=t
Z1=Z
отличие от Галилея и Декарта Ньютон изучал движение в общем виде, поэтому пространство и время (как условие движения) он брал в предельно общем виде. С этой целью он выдвину два крайне абстрактных понятия – «абсолютное пространство» и «абсолютное время».
По Ньютону, пространство это абсолютное, неподвижное, однородное, изотропное, бесконечное вместилище всех тел (т.е. пустота). А время – это чистая, однородная, равномерная и непрерывная длительность процессов.
Поскольку пространство абсолютно и мыслится в отрыве от движущейся материи как пустота, то оно ни от чего не зависит и всюду одинаково. Поэтому любая его фиксированная точка может стать точкой отсчета для определения абсолютного движения. Нужно лишь сверить свои часы с абсолютным временем, которое опять таки не зависит ни от каких материальных процессов, а также и от пространства. Абсолютность времени выражается его одинаковостью во всех точках Вселенной.
Из разрозненности и абсолютности пространства и времени вытекают правила галилеевых преобразований.
Из оторванности движущихся тел от пространства и времени вытекает правило сложения скоростей в классической механике: оно состоит в простом сложении или вычитании скоростей двух тел, движущихся относительно друг друга.
Если, например, в движущемся вагоне пассажир идет в направлении движения поезда, то скорость движения пассажира и вагона нужно суммировать, чтобы получить скорость движения пассажира относительно железнодорожного полотна. Складывать можно любые, в том числе сколь угодно большие скорости. Отсюда вытекает связь механистической картины мира (МКМ) с принципом дальнодействия, согласно которому действия и сигналы могут передаваться в пустом пространстве со сколь угодно большой скоростью.
В XIX столетии МКМ продолжала оставаться господствующей, но это не значит, что небо над ней было безоблачным. Тучи критики стали сгущаться уже в середине столетия. Вторая половина XIX в. характеризуется оживленной дискуссией о фундаментальных понятиях классической физики– силе, масс, инерции, действии и противодействии, пространстве и времени. Еще в начале XIX в. Сади Карно (1796–1832 гг.) обратил внимание на оккультную и метафизическую природу ньютоновской силы. В 1876 г. Густав Кирхгоф определял силу чисто аналитически через понятия пространства, времени, массы. Французский математик и философ Анри Пуанкаре (1854–1912 гг.) отмечал критически тот факт, что механика Ньютона помещает относительное движение в абсолютное пространство и время, что внутренне противоречиво и является чистой условностью.
В конце XIX в. с резкой критикой ньютоновской представление об абсолютном пространстве выступил немецких физик и философ Эрнст Мах (1838–1916 гг.). В основе представлений Маха лежало убеждение в том, что «движение может быть равномерным относительно другого движения. Вопрос, равномерно ли движение само по себе, не имеет никакого смысла. Это представление Мах переносит не только на скорость, но и на ускорение. В ньютоновской механике ускорение (в отличие от скорости) рассматривалось как абсолютная величина: для того чтобы судить об ускорении достаточно самого тела, испытывающего ускорение. Иначе говоря, ускорение – величина абсолютная и может рассматриваться относительно абсолютного пространства, а не относительно других тел. Этот вывод и оспаривал Мах.
Ньютон аргументировал это положение примером с вращающимся ведром, в которое налита вода. Этот опыт показывал, что движение воды относительно ведра не вызывает центробежных сил и можно говорить о его вращении само по себе, без относительно другим телам, т.е. остается лишь отношение к абсолютному пространству.
Он обвинил Ньютона в отступлении от принципа, согласно которого в теорию должны вводиться только величины, непосредственно выводимые из опыта.
Несмотря на субъективно-идеалистический подход к проблеме относительности движения, в соображениях Маха были интересные идеи, которые способствовали появлению общей теории относительности. Речь идет о так называемом принципе Маха, согласно которому инерциальные силы следует рассматривать как действие общей массы Вселенной. Этот принцип в последствии оказал значительное влияние на А. Эйнштейна. Рациональное зерно принципа Маха состояла в том, что свойства пространства – времени обусловлены гравитирующей материи.
К новым идеям о природе пространства и времени подталкивали физиков и результаты математических исследований, открытие неевклидовых геометрий. Дело все в том, что пространственно-временные представления классической физики полностью согласуются с тем, как они описываются геометрией Евклида. Поэтому критика евклидовой геометрии является косвенной критикой классической механики.
В первой половине XIX в. отечественной математик Н. И. Лобачевский (1792–1856 гг.), критически осмысливая процедуру построения геометрии Евклида, нашел возможным создать иную (неевклидову) геометрию, построение которой реализуется на поверхности отрицательной кривизны типа седловидной. Позже немецкий математик Берн Хард Риман (1826–1866 гг.) разработал еще одну неевклидову геометрию, построения которой реализуются на поверхности положительной кривизны типа сферической. Эти геометрии также вступали в противоречие с пространственно-временными представлениями классической физики, но поскольку Лобачевский и Риман не могли указать физических объектов, которым бы соответствовали их теории, то они фактически не опровергали абсолютного пространства и времени Ньютона.
В 70-е гг. XIX в. английский математик Вильям Клиффорд (1845–1879 гг.) высказывает идею о том, что многие физические законы могут быть объяснены тем, что отдельные области пространства подчиняются неевклидовой геометрии. Более того, он считал, что кривизна пространства может изменяться со временем, а физику можно представить как некоторую геометрию. Клиффорд предложил нечто вроде полевой теории материи, в которой материальные частицы представляют собой сильно искривленные области пространства, а « изменение кривизны пространства и есть то, что реально происходит в явлении, которое мы называем движением материи, будь она весомая или эфирная». Вследствие искривления пространства действительная геометрия мира подобна «холмам» на равной местности, а перемещение частиц материи есть ничто иное, как перемещаемые «холма» от одной точки к другой. Клиффорд принадлежит к ряду немногочисленных в XIX в. провозвестников Эйнштейновской теории гравитации.
Контрольные вопросы
- Что называется инерциональными системами?
- В чём суть преобразований Галилея и что нового внёс в них Декарт?
- Какое требование к формулировке законов механического движения предъявляют преобразования Галилея?
- Как трактовались Ньютоном «абсолютное пространство» и «абсолютное время»?
- Какие учёные выступали с критикой механики Ньютона?
- Что означает принцип дальнодействия?
- Какое положение механики Ньютона подвергал сомнению Мах?
- В чём суть принципа Маха?
- В чём отличие геометрий Лобачевского и Римана от геометрии Евклида?
- В чём суть идеи Клиффорда?
