Г. Д. Ковалев (Санкт-Петербургская академия мвд россии) доктор социологических наук О. В попова (Санкт-Петербургский государственный университет) Артемов Г. П. А86 Политическая социология: Учебное пособие

Вид материала

Содержание

Таблица 4 Примерный вид «простой структуры»
Таблица 5 Значения переменных после вращения
Многомерное шкалирование
Основные выводы
Основные понятия
Наиболее важные термины

Подобный материал:

1 2 3 4 5 6 7 8 9 ... 18

Взаимосвязь голосования за различные партии и блоки

Партия, блок	КПРФ	«Выбор России»	«Яблоко»	ЛДПР
КПРФ	1,0	-0,57	-0,32	+ 0,08
«Выбор России»	-0,57	1,0	+ 0,36	-0,53
«Яблоко»	-0,32	+ 0,36	1,0	-0,63
ЛДПР	+ 0,08	-0,53	-0,63	1,0

Авторы отмечают, что высокие значения (больше 0, 4) коэффициента корреляции свидетельствуют о наличии линейной связи между голосованием за сравниваемые партии и блоки. Знак «минус» означает, что чем больше голосов определенная группа избирателей отдает за одну из сравниваемых партий, например за «Яблоко», тем меньше она отдает голосов за другую, например за ЛДПР (г = - 0,63). Знак «плюс» означает, что чем больше голосов группа избирателей отдает одной партии, например «Выбору России», тем больше она отдает голосов и другой сравниваемой партии, например «Яблоку» (г = +0,36). Значения г < 0,4 свидетельствуют лишь о слабой выраженности линейной связи между голосованием за разные партии, но это не исключает наличия другой формы связи (нелинейной).

В статье подчеркивается, что сам факт положительной или отрицательной корреляции говорит только о возможном механизме перераспределения голосов избирателей между партиями и блоками, а не о сходстве или различии их политических позиций. Эти наблюдения в определенной мере подтверждаются результатами корреляционного анализа голосования за партии и блоки по ито-

[52]

гам парламентских выборов 1995 г., проведенного А.Е. Любаревым [Любарев А.Е. Корреляционный анализ результатов парламентских выборов 1995 года // Политические исследования. 1996. N° 5. С. 117—129]. Автором статьи были получены значения коэффициентов корреляции, приведенные в табл. 3.

ТаблТаблица 3 Взаимосвязь голосования за различные партии и блоки

Партия, блок	КПРФ	ДВР	«Яблоко»	ЛДПР
КПРФ	1,0	-0,34	-0,45	+ 0,15
ДВР	-0,34	1,0	+ 0,67	-0,60
«Яблоко»	-0,45	+ 0,67	1,0	-0,48
ЛДПР	+ 0,15	-0,60	-0,48	1,0

Как правило, на признаки изучаемого явления влияет множество причин, поэтому для выявления полной картины недостаточно только анализа парных корреляций, нужна группировка этих корреляций и выявление на этой основе комплексов скрытых (латентных) переменных, которые называются факторами (рис. 2).

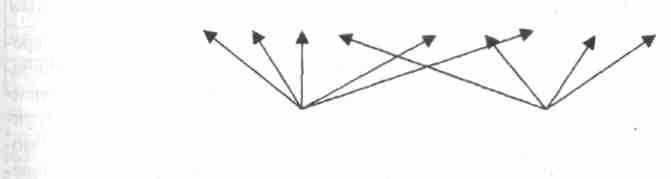
Переменные П1 П2 ПЗ П4 П5 П6 П7 П8 П9

Факторы Ф1 Ф2

Рис. 2. Графическая структура факторного анализа

Необходимость факторного анализа обусловлена тем, что мы не можем воспринимать большое число сопоставляемых пар признаков и вынуждены прибегать к помощи вычислительной техники. Факторный анализ основан на измерении доли влияния каждого из выделенных нами комплексов (независимых) переменных на изменение изучаемых признаков явления (зависимых переменных) и обнаружении причинной обусловленности этих изменений. Факторы выражают внутренние (скрытые) свойства системы переменных, характеризующих изучаемое явление.

Исходной информацией факторного анализа служит матрица \ (система чисел, размещенных в прямоугольной таблице в виде п столбцов и т строк) парных коэффициентов корреляции [Харман, 33] всех отобранных нами переменных. На основе матрицы выяв-

[53]

ляются скопления переменных, тесно связанных друг с другом и слабо связанных с переменными, входящими в другие скопления. Эти скопления переменных образуют факторы (рис. 3).

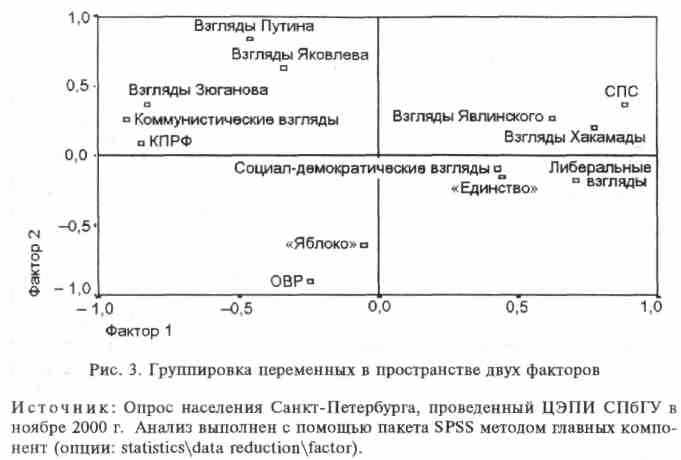
Первый фактор (горизонтальная ось графика) образуют переменные, характеризующие ориентации на коммунизм или либерализм. Второй фактор (вертикальная ось графика) образуют ориентации на власть или оппозицию. Следует учесть, что данная структура существовала в сознании населения Санкт-Петербурга на момент опроса (ноябрь 2000 г.). Со временем эта конфигурация переменных может измениться.

Целью факторного анализа служит выявление так называемой простой структуры. Согласно Терстоуну, эта структура должна удовлетворять следующим условиям [Харман, 114]:

В каждой строке факторной матрицы должно быть хотя бы одно нулевое значение (нулевыми считаются также значения, первый разряд которых начинается с 1).
В каждом столбце факторной матрицы число нулевых значений должно быть не меньше числа факторов.
В каждой паре столбцов должно быть несколько переменных, которые имеют значения, равные нулю в одном из столбцов и не равные нулю — в другом.
В каждой паре столбцов имеется мало переменных, значения которых в обоих из них отличны от нуля.

[54]

В качестве примера такой структуры можно привести результаты факторного анализа данных упомянутого выше опроса населения Санкт-Петербурга (табл. 4).

Таблица 4 Примерный вид «простой структуры»*

Переменные	Компоненты
Переменные	1	2	3	4
Коммунистические	+0,771	-0,411	+0,310	-0,192
Либеральные	-0,202	+0,796	-0,473	0,000
Взгляды Зюганова	+0,731	-0,337	+0,412	-0,142
Взгляды Путина	+0,434	0,000	+0,721	-0,398
Взгляды Хакамады	-0,477	+0,662	0,000	0,000
Взгляды Яковлева	+0,275	-0,176	+0,795	+0,321
Взгляды Явлинского	0,000	+0,866	0,000	+0,279
«Единство»	-0,730	0,000	0,000	-0,174
«Отечество—Вся Россия»	-0,106	- 0,601	- 0,708	0,000
КПРФ	+0,872	-0,210	0,000	-0,376
СПС	-0,627	+0,679	+0,237	+0,104
«Яблоко»	+0,452	+0,132	-0,754	+0,379

* В таблицу включены переменные, характеризующие приверженность взглядам и голосование за избирательные объединения на парламентских выборах 19 декабря 1999 г. Анализ выполнен с помощью пакета 8Р85, методом главных компонент.

Переменные для факторного анализа отбираются в соответствии с определенными критериями. Считается, что эти переменные должны быть измерены с помощью интервальной шкалы [Факторный, дискриминантный и кластерный анализ, 63]. Для порядковых переменных не существует факторных моделей, поскольку операции сложения для них невозможны. Надо иметь в виду, что в данном случае «допускается лишь эвристическое использование таких моделей без статистической интерпретации резулътатов»(курсш мой. — ТА.) [Там же]. Это значит, что можно подвергать факторному анализу переменные, измеренные с помощью порядковых шкал, однако в данном случае нельзя оперировать собственными значениями факторов и определять более и менее значимые факторы.

[55]

На порядковом уровне с помощью факторного анализа можно лишь устанавливать кластерную структуру переменных [Там же, 65]. Часто предполагается, что порядковым переменным можно присваивать числовые значения, не нарушая их внутренних свойств. Например, можно присвоить числовые значения 5, 4, 3, 2, 1 позициям порядковой шкалы: целиком согласен, согласен, безразличен, не согласен, полностью не согласен. «Если искажения корреляций, вносимые при шкалировании порядковых переменных, не слишком велики, вполне законно использовать эти переменные в качестве числовых» [Там же, 63]. В отечественной социологии такие случаи встречаются довольно часто. Считается, что если основой факторного анализа служит матрица корреляций, а данные, полученные на порядковых шкалах, позволяют подсчитывать коэффициенты корреляции, то это дает право использовать факторный анализ, но с учетом отмеченного выше ограничения — недопустимости статистической интерпретации собственных значений выделенных факторов. Здесь приходится ограничиваться лишь выявлением распределения переменных по скоплениям (кластерам).

Существует множество методов факторного анализа. Наиболее часто используется метод главных компонент. В нем факторы являются линейными функциями от наблюдаемых переменных. Задача в данном случае заключается не в объяснении корреляций между переменными, а в объяснении доли каждого скопления независимых переменных в дисперсии (отклонении от средней) интересующей нас зависимой переменной. В процессе факторного анализа определенная последовательность наблюдаемых переменных преобразуется в другую последовательность. Сначала вычисляются парные коэффициенты корреляции между переменными и строится корреляционная матрица, которая образует основу факторного анализа. Затем последовательно строится матрица компонент. При двухфакторном анализе первая компонента определяется таким образом, чтобы в ней содержалась максимальная доля дисперсии изучаемой переменной. Вторая компонента определяется аналогичным образом, но ее ось должна располагаться перпендикулярно первой. Выделенные компоненты должны объяснять не менее 50% суммарной дисперсии изучаемой переменной (например, мотивации голосования за определенного кандидата в президенты). При трехфакторном анализе принцип определения главных компонент тот же самый, что и при двухфакторном: ось второй компоненты располагается перпендикулярно первой, ось третьей компоненты — перпендикулярно двум первым (рис. 4). Анализ проведен с помощью пакета 8Р88.

[56]

Число переменных, отобранных для факторного анализа, должно превышать число факторов не менее, чем в два раза. В каждом факторе должно быть не менее трех переменных с максимальными значениями коэффициентов [Факторный, регрессионный и кластерный анализ, 28, 67].

На первом этапе анализа определяется минимальное число факторов, адекватно воспроизводящих наблюдаемые корреляции. После этого осуществляется процедура вращения, с помощью которой устанавливаются легко интерпретируемые факторы. Графический способ вращения заключается в проведении новых осей, которые обеспечивают воспроизводство вышеупомянутой простой структуры. Если после вращения обнаруживаются скопления точек (значений переменных), явно отделенных друг от друга, то это означает, что нам удалось провести оси через эти скопления.

Аналитический способ вращения осуществляется на основе определенного объективного критерия. Этот способ включает два вида вращения: ортогональное и косоугольное. Наиболее часто используется ортогональное вращение с помощью метода варимакс (поиск максимальных значений 1-го фактора). Метод основан на Упрощении описания столбцов факторной матрицы, в результате него достигается лучшее разделение факторов (четче выделяется главный фактор). Целью любого способа вращения является полу-

[57]

чение наиболее простой факторной структуры, которая легче поддается содержательной интерпретации.

Число факторов определяется с помощью различных критериев:

1. Критерий собственных чисел: отбираются факторы с собст
венными числами, превышающими 1, остальные не принимаются
во внимание.

Критерий воспроизводимой дисперсии: обычно отбирают факторы, объясняющие 50 — 60% общей дисперсии изучаемой переменной.
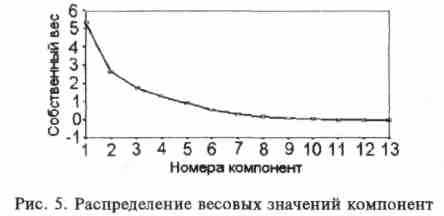
Критерий отсеивания: на графическом изображении собственных чисел корреляционной матрицы заканчивают отбор на том факторе, после которого кривая принимает вид, близкий к горизонтальному (рис. 5).

[58]

Знаки «плюс» и «минус» факторных значений интерпретируются как увеличение или уменьшение значения переменной, т.е. просто как разные направления. «Знак факторных нагрузок сам по себе не имеет внутреннего содержания и не несет информации о зависимости между переменной и фактором. Однако стоит сопоставлять знаки разных переменных при одном факторе» [Факторный, дискриминантный и кластерный анализ, 67]. Факторные нагрузки меньше 0,3 считаются несущественными [Там же, 60]. Интерпретация факторов сводится к анализу величины и знаков нагрузок. Рассмотрим эту процедуру на примере приведенного выше двухфакторного решения (см. рис. 3). Два вьщеленных фактора объясняют 61% дисперсии и включают переменные, указанные в табл. 5.

Таблица 5 Значения переменных после вращения*

Переменные	Факторы
Переменные	1	2
Взгляды Зюганова	- 0,823	+0,368
Взгляды Пугина	- 0,454	+0,777
Взгляды Хакамады	+0,776	+0,202
Взгляды Яковлева	-0,340	+0,679
Взгляды Явлинского	+0,627	+0,261
«Единство»	+0,443	-0,151
«Отечество—Вся Россия»	- 0,232	- 0,872
КПРФ	-0,842	0,000
СПС	+0,884	+0,366
«Яблоко»	0,000	-0,642
Коммунистические взгляды	-0,898	+0,258
Социал-демократические взгляды	+0,427	0,000
Либеральные взгляды	+0,708	-0,187

* Матрица получена методом главных компонент в пакете SPSS.

Выпишем наибольшие значения переменных по выделенным факторам. Фактор 1: отрицательное направление (взгляды Зюганова, коммунистические взгляды, КПРФ), положительное направление (взгляды Хакамады, либеральные, СПС). Фактор 2: отрицательное направление (ОВР, «Яблоко»), положительное направление (взгляды Путина, Яковлева). Содержание первого фактора состав-

[59]

ляет идеологический раскол (коммунисты — либералы), содержание второго фактора — политический раскол (власть — оппозиция). При интерпретации этих данных следует учитывать, что петербургские сторонники ОВР и «Яблока» в основном голосовали против Путина на президентских выборах 2000 г., а само петербургское отделение «Яблока» (Региональная партия центра) находилось в оппозиции губернатору Яковлеву. Эти расколы определяли политическое поведение населения Санкт-Петербурга в 2000 г. (факторный анализ осуществлен на основе данных общегородского опроса, проведенного ЦЭПИ СПбГУ в ноябре 2000 г.). \ Кластерный анализ (от англ. с1и$1ег — пучок, группа) — это процедура, позволяющая классифицировать различные объекты. С его помощью можно разбить респондентов на группы, сходные по ряду признаков. На дендрограмме «дерева признаков» признаки соединяются линиями, образуя отдельные пучки («ветви»), связанные с другими пучками («ветвями»). Эти пучки и называют кластерами. Чем короче линия, связьшающая переменные, тем ближе они находятся в пространстве признаков. В процессе кластеризации происходит объединение сходных объектов во все более сложные группы («разветвление»). Кластерный анализ представляет собой разновидность многомерной статистической процедуры, упорядочивающей объекты в относительно однородные группы. Переменные для кластерного анализа выбираются в соответствии с теорией (концепции, гипотезы), которая лежит в основе классификации [Факторный, дискриминантный, кластерный анализ, 153]. Перед началом анализа они должны быть преобразованы в биноминальные, принимающие значение «1» при наличии признака и «0» при его отсутствии. В статистическом пакете SPSS эта операция осуществляется в опции: 1гап$Гогт\гесоде. Кроме того, из анализа следует исключить альтернативы: «затрудняюсь ответить», «другое» и пр.

Важную роль в кластерном анализе играют «меры сходства». Наиболее часто в качестве такой меры употребляется коэффициент корреляции Пирсона, первоначально использовавшийся для определения зависимости переменных. Кластеры обладают рядом свойств, среди которых наиболее важными являются плотность, дисперсия, форма, отдельность. Плотность — это близость отдельных точек скопления, позволяющая отличать его от других областей многомерного пространства, содержащих либо мало точек, либо не содержащих их совсем. Дисперсия характеризует степень рассеяния точек в пространстве относительно центра кластера. Отдельность характеризует взаимное расположение скоплений точек в пространстве [Там же, 165—166]. Кластеры можно рассматривать

[60]

как «непрерывные области пространства с относительно высокой плотностью точек, отделенные от других таких же областей областями с относительно низкой плотностью точек» [Там же, 166].

Наиболее известными методами кластерного анализы являются методы одиночной, полной и средней связи, а также метод Уорда [Там же, 191]. Метод Уорда (\УагсР8 те1под) позволяет создавать кластеры приблизительно равных размеров [Там же, 171]. Он сначала объединяет самые близкие объекты, затем к уже образованным кластерам присоединяются сходные с ними объекты. Мерой сходства в данном случае является 1 — коэффициент корреляции Пирсона.

На основе анализа содержания переменных, входящих в отдельные кластеры, строится группировка респондентов по признакам, включенным в процесс кластеризации. Рассмотрим эту процедуру на примере (рис. 6)*

0,2 0,4 0,6 0,8 1,0 1,2 1,4 1,6 1,8

Рис. 6. Дендрограмма мотивов голосования за кандидатов в Президенты России на выборах 1996 г.

Условные обозначения переменных: персональные электоральные предпочтения респондентов на президентских выборах 1996 г. (Ельцин, Зюганов, Явлинский); мотивация этих предпочтений (1.1. «Он мне нравится», 1.2. «Не хочу перемен», 2.1. «Меня устраивает его программа», 2.2. «Он знает, как решить проблемы страны», 3.1. «Я ему доверяю», 3.2. «Ему нет достойной замены»); мотивация голосования за списки политических партий на парламентских выборах 1995 г. (4.1. «Они заставят правительство думать о народе», 4.2. «Они смогут решить проблемы страны», 4.3. «Устраивает программа партии»). Анализ выполнен с помощью пакета «Statistica» по методу Уорда.

Кластерный анализ основных альтернатив ответа на вопрос о том, за кого намерены голосовать (опрос проводился в мае 1996 г.) респонденты («Ельцин», «Зюганов», «Явлинский»), и вопрос о мотивах предстоящего голосования позволили обнаружить особые

[61]

структуры мотивации электорального выбора у сторонников отдельных кандидатов в Президенты России на выборах 1996 г. (см.: перечни мотивов в кластерах Ельцина, Зюганова и Явлинского).

Многомерное шкалирование представляет собой процедуру, с помощью которой оценивается степень сходства/различия между переменными. С его помощью мы можем представить набор изучаемых переменных в виде скоплений точек (каждой переменной соответствует одна точка). Этот метод позволяет находить в массиве данных комплексы сходных друг с другом и отличающихся друг от друга переменных. В геометрическом пространстве сходные переменные (тесно связанные между собой в сознании респондентов) располагаются близко друг от друга и образуют скопления точек, отделенные пустым пространством от других скоплений сходных переменных. Чем больше сходства зафиксировано у изучаемых переменных, тем ближе находятся обозначающие их точки на графике. Чем меньше сходства наблюдается у включенных в анализ переменных, тем дальше друг от друга располагаются соответствующие им точки на графике.

Данный метод дает возможность наглядно (на графике) представить множество переменных и увидеть особенности их конфигурации в геометрическом пространстве (чаще всего в двумерном). Подобная процедура используется при сопоставлении значительного числа переменных, которое трудно анализировать без визуализации. Перед началом многомерного шкалирования осуществляется процедура преобразования переменных в биноминальные, как и в кластерном анализе.

Рассмотрим пример такой визуализации на основе набора переменных, характеризующих идентификацию респондентов с различными взглядами (источник данных тот же, что и в примечании к рис. 6).

На графике рис. 7 видны четыре группы точек, отделенных друг от друга пустым пространством. Эти группы располагаются в рамках двух измерений. Первое измерение основано на противопоставлении власти и общественности, второе — на противопоставлении коммунизма и либерализма. Эти оппозиции наблюдались в политическом сознании населения Санкт-Петербурга в конце 2000 г.

Специфическим методом обработки социологической информации является вторичный анализ данных. Он применяется для получения дополнительной информации по уже прошедшему первичную обработку массиву данных. Обычно вторичный анализ используют при повторной обработке результатов «чужих» или собственных исследований. Можно выделить два типа вторичного ана-

[62]

Рис. 7. Конфигурация переменных в пространстве двух измерений* (политическая идентификация и партийные предпочтения на выборах)

лиза: монографический и сравнительный. В первом случае осуществляется повторный анализ одного массива первичных данных, во втором — сопоставляются несколько массивов первичных данных (например, электронные таблицы данных в системе 8Р88), полученные отдельными социологическими центрами в разное время, на разных выборках и по различным программам. Разнотипность исследований и используемых в них переменных порождает необходимость их стандартизации как условия сопоставимости результатов исследований [Социальные исследования: построение и сравнение показателей. М., 1978. С. 134—139].

Сопоставлять можно лишь однородные переменные, но для обеспечения этой однородности нужно, чтобы сравниваемые первичные данные по этим переменным были получены на однотипных выборках, одинаковыми методами и с помощью однотипных шкал. Если у нас нет информации о том, кого и как репрезентирует выборка, какие методы были использованы для сбора и анализа данных, как были сформулированы вопросы и какие альтернативы предлагались респондентам для ответа на них, то вторичный анализ становится невозможным.

Нельзя в строгом смысле слова назвать вторичным анализом часто используемое сопоставление частотных распределений внешне сходных переменных, взятых из отчетов по итогам массовых опросов населения, опубликованных в научных изданиях или газетах. Как правило, в этом случае авторы не выясняют степень

* Многомерное шкалирование выполнено с помощью пакета SPSS, опции: statistics\scale\multidimensional scaling.

[63]

однородности сравниваемых массивов информации, а между тем за каждым числовым значением признака стоит определенное качество. Не выяснив, насколько однородна качественная определенность переменных, отобранных из разных массивов данных, мы не можем их сопоставлять.

Для проведения вторичного анализа необходимо изучить описание выполненных исследовательских проектов, по которым имеется первичная информация в существующих отечественных и зарубежных архивах данных [см., например: Банк социологических данных, 1990 (Информационные ресурсы социологических центров СССР). М., 1990; Международный журнал социальных наук. Май. 1995. № 9. Европейские базы данных по социальным наукам); Мангейм Дж.-Б., Рич Р.-К. Политология. Методы исследования. М., 1997. С. 220—221]. В архивах нужно отобрать необходимые массивы данных, получить разрешение на их использование от руководства соответствующих центров и, сделав с них копии файлов, провести вторичный анализ.

Можно выделить несколько видов сравнительного вторичного анализа: сравнительно-типологический (синхронный), или анализ первичных данных исследований, проведенных в одно и то же время; сравнительно-генетический (диахронньш), или анализ результатов исследований, проведенных в разное время. В любом случае предварительное изучение переменных с целью определения степени их однородности и пригодности для сравнения представляет собой обязательное условие вторичного анализа. Важно отметить и то, что в процессе вторичного анализа мы, по существу, мысленно воспроизводим все этапы сопоставляемых исследований и одновременно осуществляем самостоятельное исследование, в ходе которого концептуализируем изучаемую проблему, выдвигаем собственные гипотезы, операционализируем понятия и т.д. Вторичный анализ означает новое, дополнительное исследование старых массивов первичных данных.

Основные выводы

Социологическое исследование проходит несколько этапов: подготовительный, полевой, аналитический.
Технологии сбора и обработки данных, основанные на использовании количественных (основанных на измерении параметров политического действия) и качественных (основанных на понимании смысла явлений политического действия) методов существенно отличаются.
Основным документом, направляющим весь процесс исследования, является программа, в которой излагаются цель, зада-

[64]

чи, объект, предмет, концепция, гипотезы, методы и график проведения исследования.

Исходным пунктом исследования является определенная проблема, решение которой имеет значение для политической социологии и практики.
Всякое исследование должно заканчиваться разработкой практических рекомендаций, способствующих совершенствованию технологии политического действия.
В процессе сбора эмпирических данных используются общесоциологические методы: наблюдение, опрос, анализ документов, которые включают конкретные методики, например включенное наблюдение, телефонное интервью, фокус-группы, контент-анализ, анализ биографий и т.д.
При обработке данных в политической социологии используются методы, заимствованные из прикладной статистики: анализ статистических таблиц, корреляционный, факторный, кластерный анализ и многомерное шкалирование.
Для воспроизведения явлений политической жизни желательно использовать различные методы, каждый из которых позволяет проверять стабильность результатов, полученных другим.

Основные понятия

Концептуализация

Квантификация

Репрезентация

Наблюдение

Анализ документов

Корреляционный анализ

Кластерный анализ

Наиболее важные термины

Пилотажное исследование

Номинальная шкала

Интервальная шкала

Генеральная совокупность

Социальная выборка

Кодировка данных

Стандартизованный остаток

Вращение

[65]

Контрольные вопросы, и задания для самостоятельной работы

Какие задачи решаются на подготовительном этапе социологического исследования политической жизни?
Назовите составные части программы социологического исследования.
Для чего осуществляется концептуализация проблемы социологического исследования?
В чем суть операционализации понятий?
Каким образом обеспечивается репрезентативность исследования?
Назовите уровни измерения признаков в социологическом исследовании.
Какие задачи решаются при интерпретации данных?
Чем отличаются количественные и качественные методы сбора данных?

9. Назовите явления политической жизни, которые можно изучать с
помощью наблюдения.

Какие стороны политического сознания и поведения людей изучаются с помощью массовых опросов?
Что дает анализ документов для изучения происхождения политической элиты?
Как с помощью критерия хи-квадрат и стандартизованных остатков определяется наличие или отсутствие взаимосвязи признаков?
Какие коэффициенты корреляции применяются на порядковом и интервальном уровне измерения?
Чем отличается функциональная связь между признаками от причинной?
На каком уровне измерения возможно применение факторного анализа?
Что дает для изучения политического сознания кластерный анализ?
В чем состоит главная цель многомерного шкалирования?
Без соблюдения каких условий нельзя проводить вторичный анализ данных?

Blog

Содержание