Geum.ru

Рекомендации по выполнению контрольной работы по дисциплине «Статистика» № вопроса

Вид материалаУчебники

Содержание


Средние величины.
Ряды динамики.
Статистические графики.
Наименование тканей
Наименование тканей
Подобный материал:
1   2   3

Задача. Расходы потребительского общества по отдельным статьям издержек обращения.

Показатели
Сумма издержек обращения тыс. руб.
Уровень издержек обращения
  1. Расходы на перевозку товаров
  2. Заработная плата
  3. Расходы по кредиту
  4. Прочие расходы

Всего

Розничный товарооборот
246,0

760,0

88,2

1407,8

2502,0

13510
1,82

5,63

0,65

10,42

18,52

Относительная величина интенсивности (уровень издержек обращения).

246 : 13510 · 100 = 1,82%; 760 : 13510 · 100 = 5,63%

88,2 : 13510 · 100 = 0,65%; 1407,8 : 13510 · 100 = 10,42; 2502 : 13510 · 100 = 18,52%. Таким образом, расходы потребительского общества составили на перевозку товаров 1,82% на 100 руб. оборота и т.д.

Средние величины.

Задача. Имеются следующие данные о товарообороте за 1 квартал.

За январь - 2980 тыс. руб.

За февраль - 3150 тыс. руб.

За март - 3490 тыс.руб. Вычислить среднемесячный товарооборот.

Решение

1. Так как в условии задачи приведен один ряд чисел (товарооборот), значит, данные приведены в не сгруппированном виде. В этом случае применяется либо средняя арифметическая простая (ха) или средняя хронологическая (хh).

Далее необходимо посмотреть, как даны исходные данные, т.к. они даны за месяц (за определенный период), то используется средняя арифметическая простая. Ха = Хn : п = (2980 + 3150-3490) : 3 = 3206,7 тыс. руб.

2. Имеются следующие данные о товарных запасах в магазине на 1.01. - 306 тыс.руб., на 1.02 - 410тыс.руб., на 1.03. - 370 тыс. руб., на 1.04. – 418 тыс.руб.

Вычислить средние токарные запасы за I квартал

Решение
  1. Одни ряд чисел - данные не сгруппированы.

2. Данные даны па определенную дату, значит, используется средняя хронологическая.
Хh = (Х1 : 2) + Х2 + … + (Хn : 2) : (п – 1)

Хh = (306/2 + 410 + 370 + 418/2) : (4-1) = 380,7 тыс. руб.


3. За два месяца по цехам завода имеются следующие данные:

№ цеха
Сентябрь
Октябрь

Численность
Средняя месячная зарплата, руб.
Средняя месячная зарплата, руб.
Фонд заработной платы, руб.

1

2

3
140

200

260
1780

1800

1665
1800

1790

1670
243000

375900

417500

Определить среднюю заработную плату одного работника за сентябрь и октябрь.

Решение
  1. так как дано 2 ряда чисел (численность работников и средняя месячная зарплата). Значит, данные сгруппированы.
  2. В этом случае используется или средняя арифметическая взвешенная (Хaf) или средняя гармоническая взвешенная (Хhm).
  3. Для выбора конкретной средней попробуем перемножить численность работников на среднюю зарплату и так как их перемножить численность работников на среднюю зарплату и так как их перемножение дает третий результат (фонд заработной платы), значит, применяем среднюю арифметическую взвешенную Хaf = ΣХn · fn : Σfn, в формуле которой и стоит перемножение.
  4. Выбираем признак (х), т.к. требуется определить среднюю месячную зарплату, то месячную зарплату обозначим х, тогда вторая величина (численность работников) – f – частота. Хaf = (1780 · 140 + 1800 · 200 + 1665 · 260) : (140+200+260) = 1042100 : 600 = 1736,8 руб.

Октябрь.
  1. Данные сгруппированы – два ряда чисел.
  2. Среднюю месячную зарплату нельзя умножить на фонд заработной платы, поэтому применяем среднюю гармоническую.

Хhm = Σmn : Σ(mn : хn)
  1. Индивидуальный признак

Х – средняя месячная зарплата

m – фонд заработной платы

Хhm = (243000 + 375900 + 417500) : [(243000 : 1800) + (375900 : 1790) + (417500 : 1670)] = 1036400 : 595 = 1741,8 руб.

4. Распределение рабочих участка по стажу работы следующее:

Стаж работы, лет х
Количество рабочих, f
Центр интервала, х
Х · f

До 5

5-10

10-15

свыше 15

итого
2

6

15

7

30
2,5

7,5

12,5

17,5
5

45

187,5

122,5

360

Решение

1. Так как признак дан в интервальной форме и первый и последний интервал открытые, то: а) Закрываем первый интервал. Находим интервал второй группы

10-5=5 лет

Группа от 0 до 5

б) Закрываем последний интервал. Находим интервал предпоследней группы

15-10 = 5 лет

Находим конец последней группы

15+5 = 20 лет

Группа от 15 до 20
  1. определяем среднее значение в каждой группе (центр интервала).

(0+5) : 2= 2,5 лет; (5+10) : 2= 7,5 лет и т.д.
  1. Далее расчет выполняется по средней арифметической взвешенной Хaf = (ΣХn · fn) : Σfn = 360 : 30 = 12 лет


Задача. Проведена группировка магазинов по размерам товарооборота.

Группы магазинов по величине товарооборота, тыс. руб.
Численность магазинов

До 30

От 30,2 до 50

От 50,1 до 70

От 70,1 до 90

От 90,1 до 110

Свыше 110
1

12

3

2

2

1

Определить средний размер товарооборота магазина, используя метод отсчета от условного нуля.

Решение

Расчет среднего товарооборота магазина.

Группы магазинов по величине товарооборота, тыс. руб. х
Число магазинов f
Центр интервала х
Х - а
(х – а) : i
(х – а) : i · f

До 30

От 30,1 до 50

От 50,1 до 70

От 70,1 до 90

От 90,1 до 110

Свыше 110

Итого
1

12

3

2

2

1

21
20

40

60

80

100

120
-20

0

20

40

60

80
-1

0

1

2

3

4
-1

0

3

4

6

4

16

Решение

1).Из средних значений признака (центр интервала) выбираем вычитаемое число «а», с наибольшей частотой, это число 40.

2). Вычислите от каждого признака «х», число «а».

20-40=-20; 40-40=0; 60-40=20; и т.д.

3). Из полученных чисел (х - а), выбираем общий делитель «I». Для этих чисел общий делитель будет 20.

i= 20 И каждый полученный признак делим на 20.

(-20): 20 = -1; 20 : 20 = 1; 40 : 20 = 2; и т.д.

4) Из полученных признаков (упрощенных,) рассчитываем среднюю арифметическую

Взвешенную.

Х= [(х-а): i] · fn : Σfn = 16:21- 0,76.

5). Так как согласно свойствам средней арифметической, если каждый признак разделить на какое-то число, то средняя уменьшается во столько же раз.

Если из каждого признака вычесть какое-то число, то средняя уменьшится на это же число, тогда для перехода к средней из первоначальных вариантов, используем следующее

Хаf = хaf · i + а хaf = 0,76 · 20 + 40 = 55,2 тыс. руб.

Ряды динамики.

Задача. Имеются следующие данные по объединению о производстве промышленной продукции.

(млн. руб.)

1992 1993 1994 1995 1996 1997

67,7 73,2 75,7 77,9 81,9 84,4

а) средний уровень ряда

б) цепные и базисные

1 абсолютные приросты

2 средний абсолютный прирост

3 темп роста

4 средний темп роста

5 темп прироста

6 средний темп прироста

7 абсолютное значение 1 % прироста.

Результаты расчетов изложить в таблице.


Решение

Анализ производства промышленной продукции по объединению.

Года
Объем пр-ва промыш. прод. мл.
Абсолютный прирост (млн. руб.)
Темп роста, %
Темп прироста, %
Абсолютное значение 1 % прироста млн. руб.

цепной
базисный
цепной
базисный
цепной

базисный
цепной
базисный

1992
67,7






100,0
100,0












1993
73,2
5,5
5,5
108,1
108,1
8,1
8,1
0,68
0,68

1994
75,7
2,5
8,0
103,4
111,8
3,4
11,8
0,74
0,68

1995
77,9
2,2
10,2
102,9
115,1
2,9
15,1
0,76
0,68

1996
81,9
4,0
14,2
105,1
121,0
5,1
21,0
0,78
0,68

1997
84,4
2,5
16,7
103,1
124,7
3,1
24,7
0,81
0,68

Решение

1. Средний уровень ряда динамики.

Ха = Σхn : n = (67,7 + 73,2 + 75,7 + 77,9 + 81,9 + 84,4) : 6 = 76,8 млн. руб.

2. Абсолютный прирост (∆)

а) Цепной (с переменной базой).

∆ = yi - yi – 1

73,2 – 67,7 = 5,5 млн. руб.; 75,7 – 73,2 = 2,5 млн. руб.; 77,9 – 75,7 = 2,2 млн. руб. и т.д.

б) Базисный (с постоянной базой).

∆ = yi –yk

73,2 – 67,7 = 5,5 млн. руб.; 75,7 – 67,7 = 8,0 млн. руб.; 77,9 – 67,7 = 10,2 млн.руб.

3. Средний абсолютный прирост (∆)

∆ = Σ∆ : (n – 1) = (5,5 + 2,5 + 2,2 + 4,0 + 2,5) : 5 = 3,34 млн. руб.
  1. Темп роста

а) Цепной

Тр = yi : (yi-1) · 100

73,2 : 67,7 · 100 = 108,1 %; 75,7 : 73,2 · 100 = 103,4; 77,9 : 75,7 · 100 = 102,9 % и т.д.

б) Базисный

Тр = yi : (yi-1) · 100

73,2 : 67,7 · 100 = 108,1 %; 75,7 : 67,7 · 100 = 111,8%; 77,9 : 66,7 · 100 = 115,1% и т.д.

5.Среднегодовой темп роста

Тр= 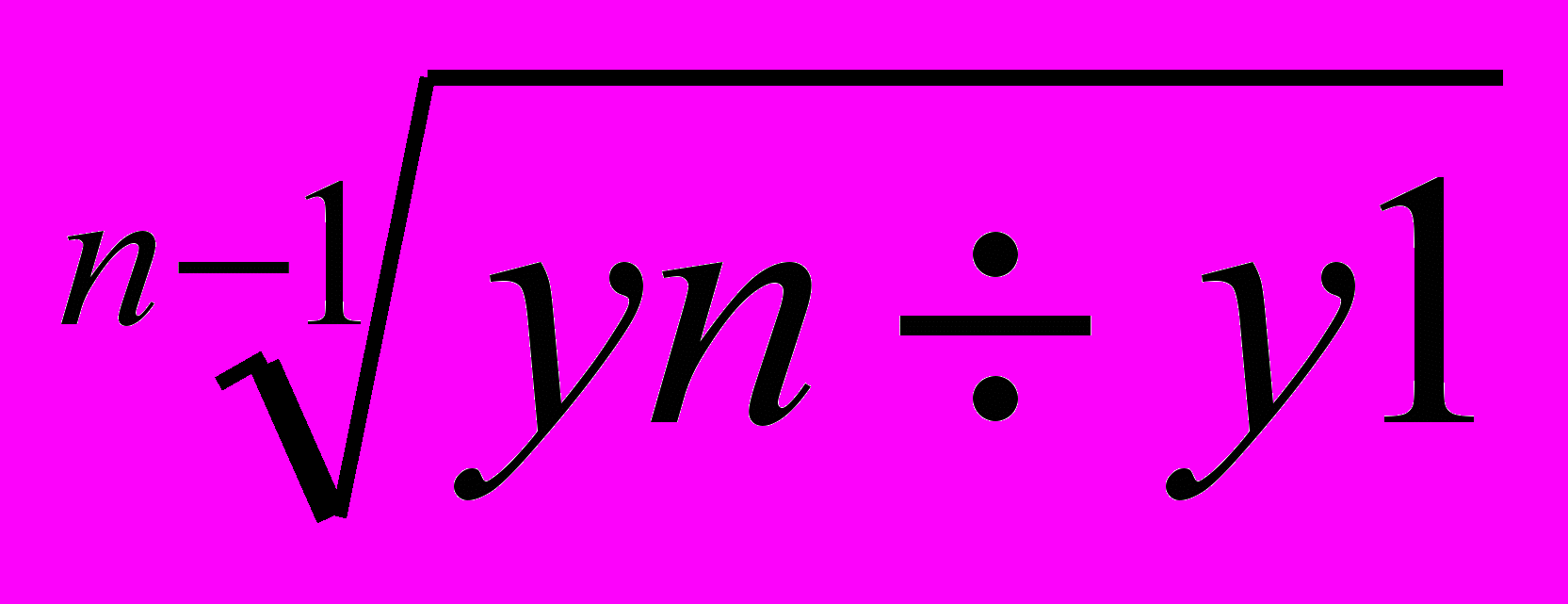· 100 = 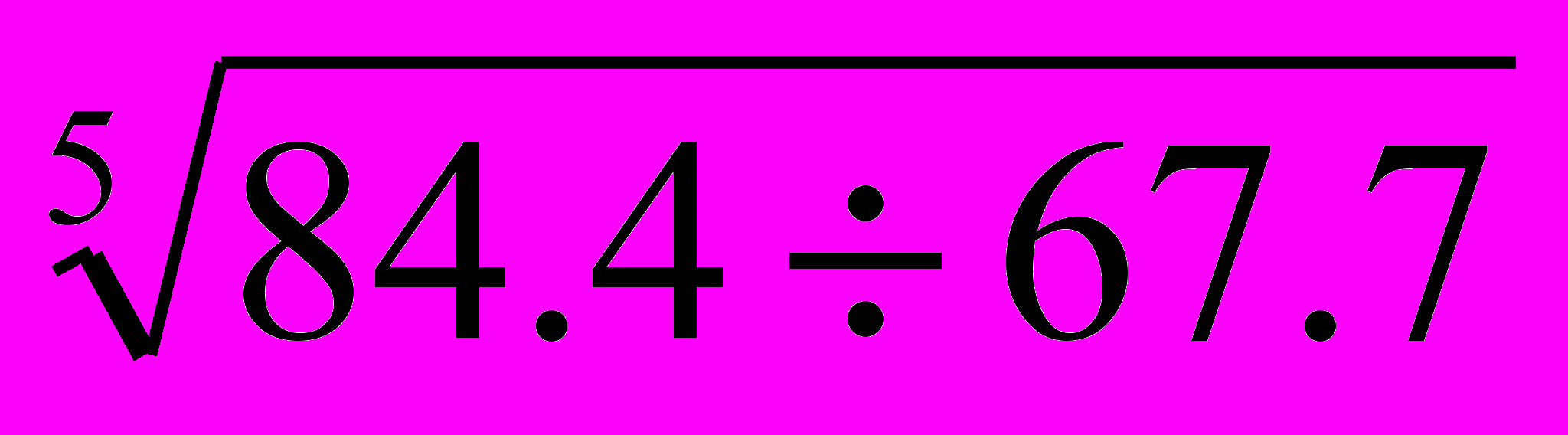· 100 = 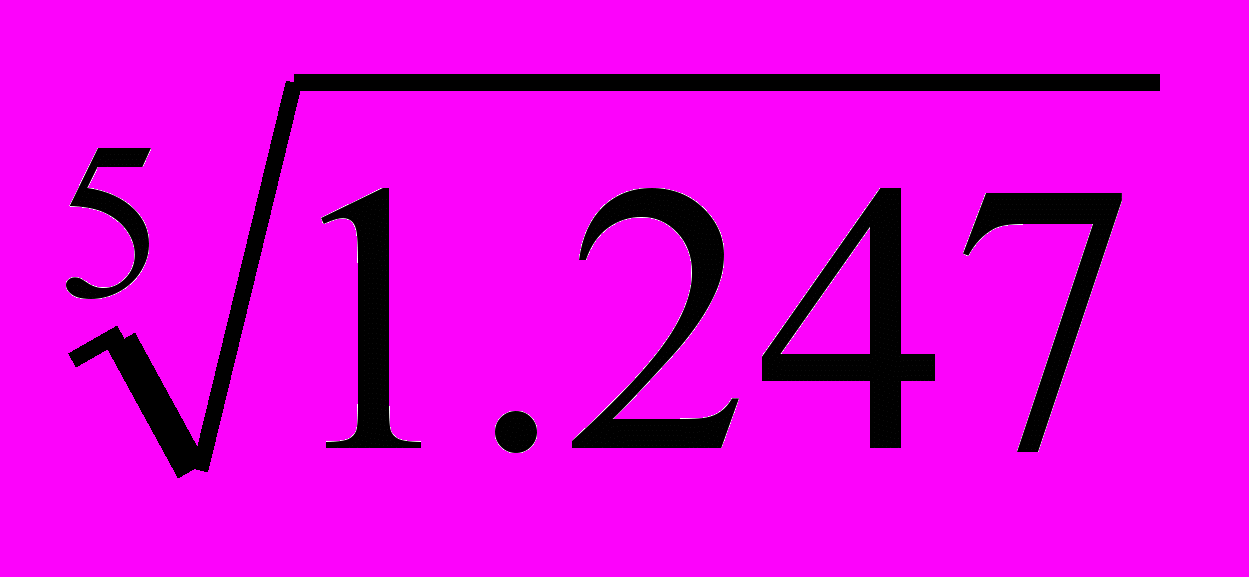· 100 = 1.045 · 100 = 104.5%

6. Темп прироста

а) Цепной

Тn = Тp – 100

108,1 – 100 = 8,1%; 103,4 – 100 = 3,4%; 102,9 – 100 = 2,9 % и т.д.

б) Базисный

Тn1 = Тр1 – 100

108,1 – 100 = 8,1%; 111,8 – 100 = 11.8%; 115,1 – 100 = 15,1% и т.д.

7.Среднегодовой темп прироста

Тn = Тp – 100 = 104,5 – 100 = 4,5%

8.Абсолютное значение 1% прироста

а) Цепной

А = ∆ : Тn

5,5 : 8,1 = 0,68 млн. руб.; 2,5 : 3,4 = 0,74 млн. руб.; 2,2 : 2,9 = 0,76 млн. руб.

а) А = ∆ : Тn = 5,5 : 8,1 = 0,68 млн. руб.; 8,0 : 11,8 = 0,68 млн. руб. и т.д.

Статистические графики.

Задача. При помощи столбиковой диаграммы изобразите данные о числе браков, заключенных населением России, тыс. чел.

1992 1993 1994 1995 1996

1320 1277 1054 1107 867

Решение

1.На основе данного ряда динамики, рассчитаем ценные темпы роста.

Показатели


Года

1992

1993

1994

1995

1996

Число браков
1320
1277
1054
1107
867

Темпы роста по годам
100,0
96,7
82,5
105,0
78,3

2.Выбираем масштаб графика.

1 см. = 25%

и рассчитаем высоту каждого столбика в см.

1992=100% / 25%

1993= 96,7% / 25%

1994=82,5 / 25%

3.Строим столбиковую диаграмму.

Динамика числа браков, заключенных населением России



1992 1993 1994 1995 1996

Задача. Объем производства промышленной продукции составил, млн. руб.

1992 1993 1994 1995 1996 1997

67,7 73,2 75,7 77,9 81,9 84,4

Изобразите динамику объема производства линейной диаграммой.

Решение

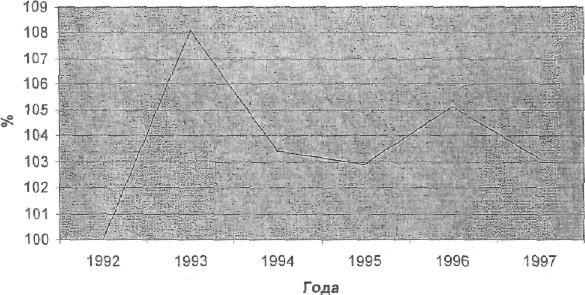
Динамика объема производства промышленной продукции.

Показатели


Года

1992

1993

1994

1995

1996

1997

Объем производства, млн. руб.


67,7


73,2


75,7


77,9


81,9


84,4

Цепные темпы роста

100,0

108,1

103,4

102,9

105,1

103,1


Выбираем масштаб.

В таких графиках, чтобы укрупнить масштаб, точку пересечения осей координат можно взять за 100 % и следовательно откладывать не 108,1%, а 8,1 % и т.д.

Тогда М = 1 см = 1%




Задача. Имеются следующие данные о производстве тканей на предприятии.

Наименование тканей
1999
2000

Хлопчатобумажные
6634
6974

Шерстяные
740
774

Льняные
1508
1725

Шелковые
295
410

Итого
9177
9883

Рассчитайте структуру производства тканей и постройте сложную столбиковую и секторную диаграммы.

Решение.

Структура производства тканей (%)

Наименование тканей
1999
2000

Хлопчатобумажные
72,3
70,6

Шерстяные
8,1
7,8

Льняные
16,4
17,5

Шелковые
3,2
4,1

Итого
100
100


а)Сложная столбиковая диаграмма производства тканей.

1.Строится 2 столбика по 100%.

Выбирается масштаб.

М=1см:20%


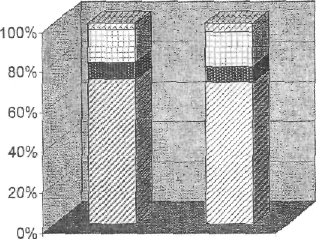
1.Шелковые

2.Льняные

3.Шерстяные

4.Хлопчатобумажнын


1999 2000

Делим каждый столбик на части, пропорционально удельных весов, т.к.

1ст.=20%

х- 72,3%

х = 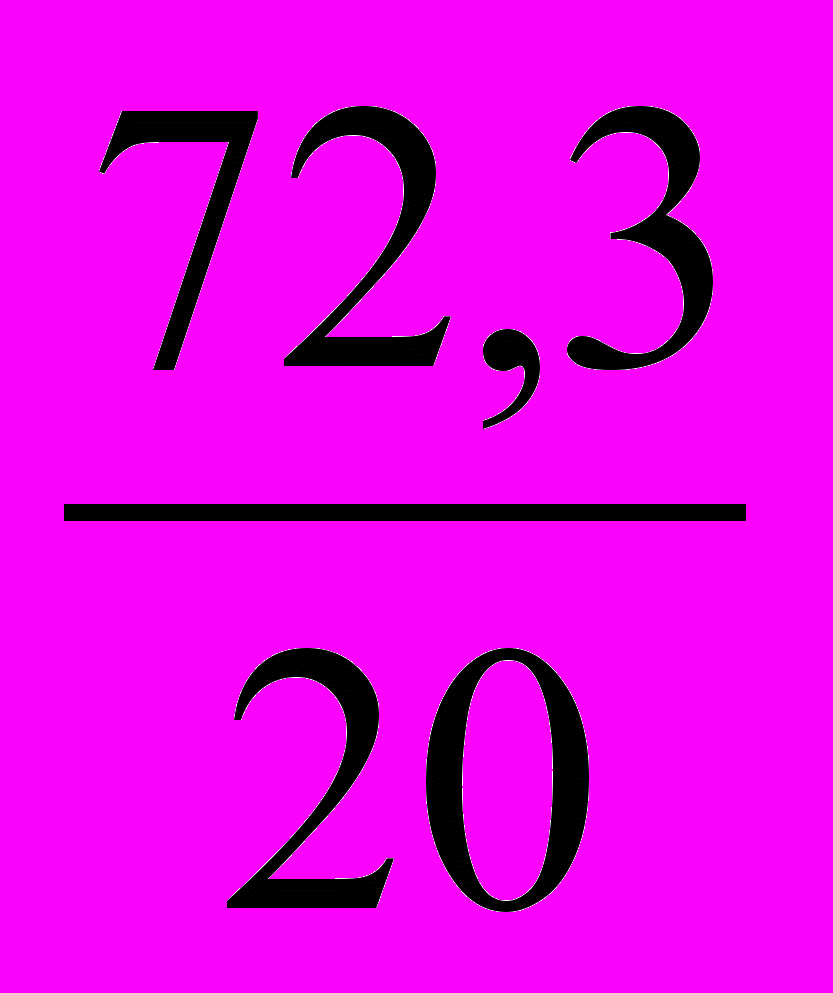= 3,6см

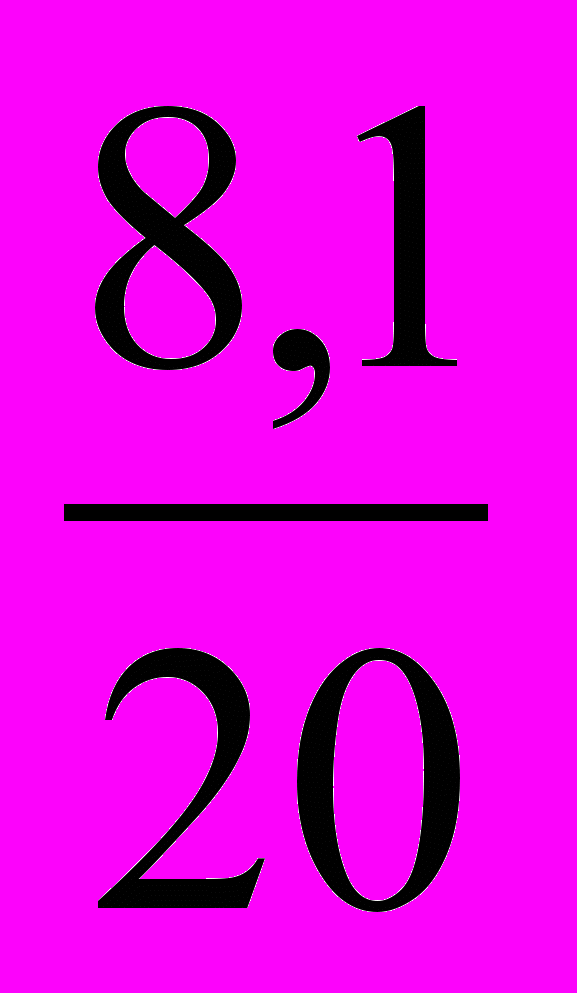= 0.4см 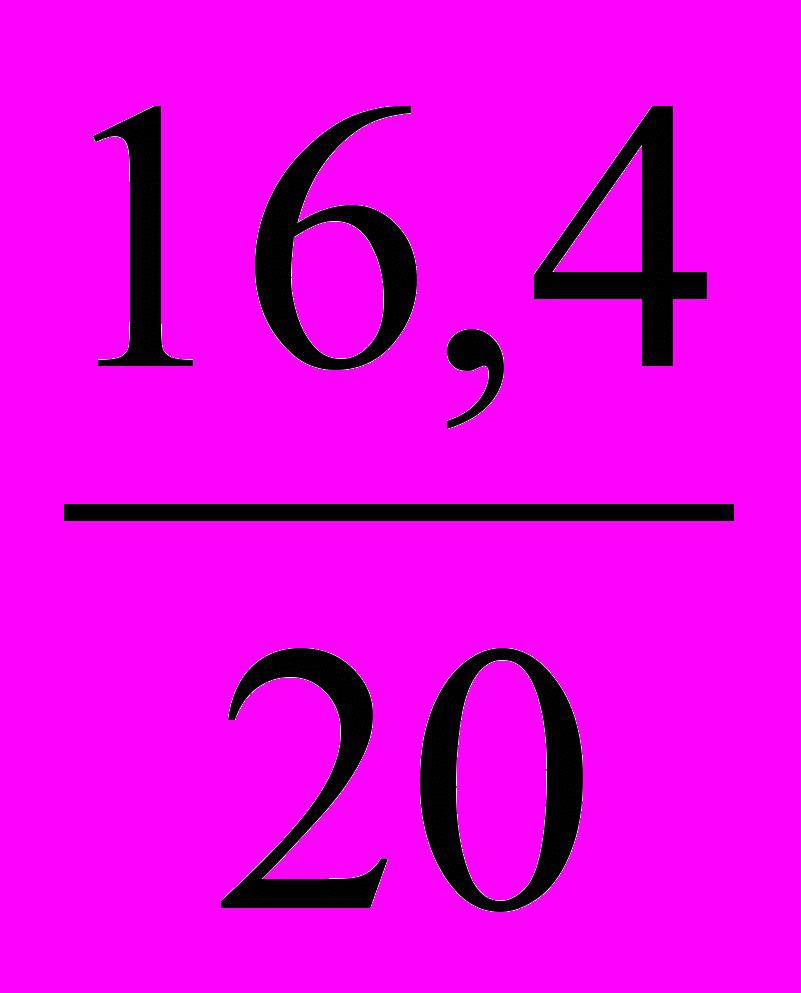= 0.8 см 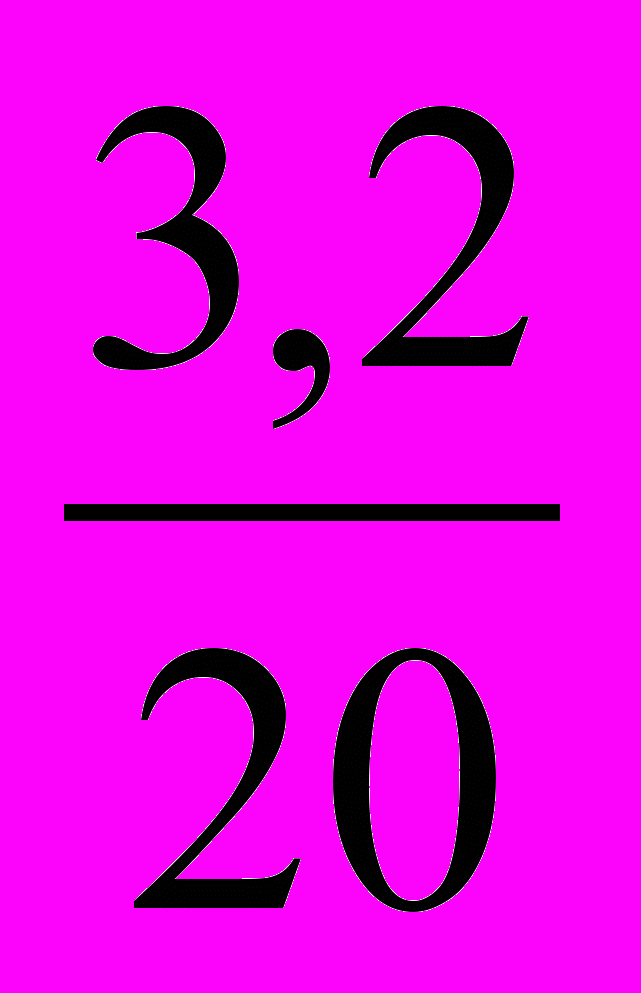=0,2 см

б) Секторная диаграмма производства тканей

1. Строится 2 окружности (1.Хлопчатобумажные, 2.Шерстяные,3.Льняные, 4.Шелковые).





(1.Хлопчатобумажные, 2.Шерстяные, 3.Льняные, 4.Шелковые).

3.Определяется угол откладываемого сектора, т.к.

100%=3600

1%=3,60

72,3% · 3,60 = 260,30

8,1% · 3,60 = 29,20

16,4% · 3,60 = 59,00

3,2% · 3,60 =

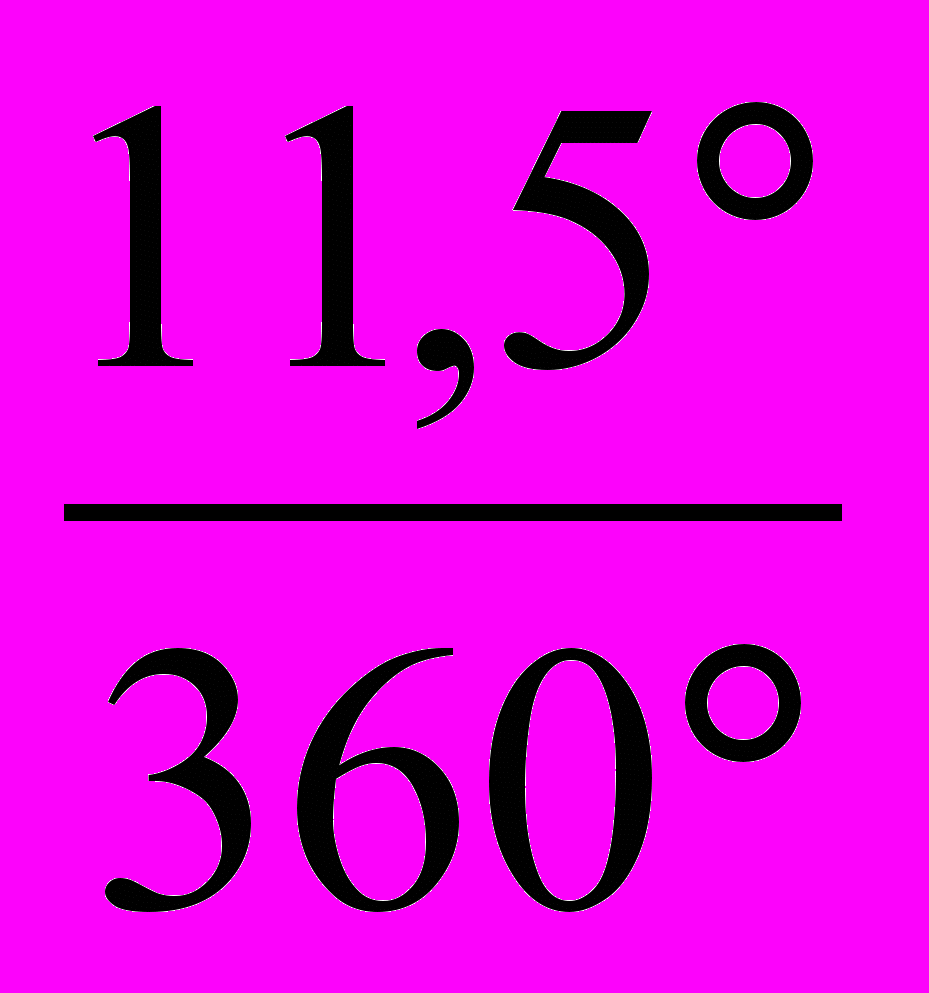
Индексы.

Задача. По предприятию имеются следующие данные о реализации продукции:

Вид изделия
Выпуск, шт.
Отпускная цена за шт. тыс. руб.

I квартал
II квартал
I квартал
II квартал

Плуги навесные
2500
2610
4,8
5,4

Плуги прицепные
3000
2950
7,1
7,6

Культиваторы навесные
3600
3700
5,0
5,7


Определить:

1.Изменение цен по каждому изделию и в целом.

2.Изменение объема реализации по каждому виду ив целом.

3.Изменение общей стоимости реализованной продукции.

4.Абсолютное изменение общей стоимости продукции, в т.ч. за счет изменения цен и количества реализованной продукции.


Решение.

Реализация продукции и отпускные цены по предприятию.

Вид изделия
Выпуск, шт.
Отпускная цена, тыс. руб.
Общая стоимость реализованной продукции тыс. руб.

I кв.g0

II кв. g1
Iкв.p0
IIкв. g1
I кв. p0 g0
IIкв. p1 g1

IIIкв. p0 g1

Плуги навесные
2500
2610
4,8
5,4
12000
14094
12528

Плуги прицепные
3000
2950
7,1
7,6
21300
22420
20945

Культиваторы навесные
3600
3700
5,0
5,7
18000
21090
18500

Итого:
-
-
-
-
51300
57604
51973

1) Для характеристики изменения цен по каждому виду продукции используются индивидуальные индексы цен.

Ip =


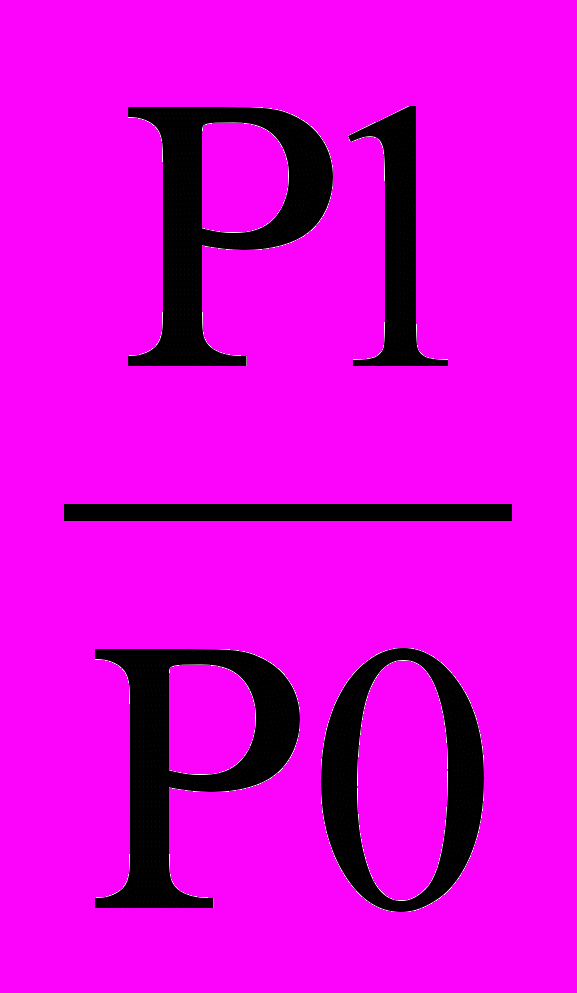
Плуги навесные Ip = 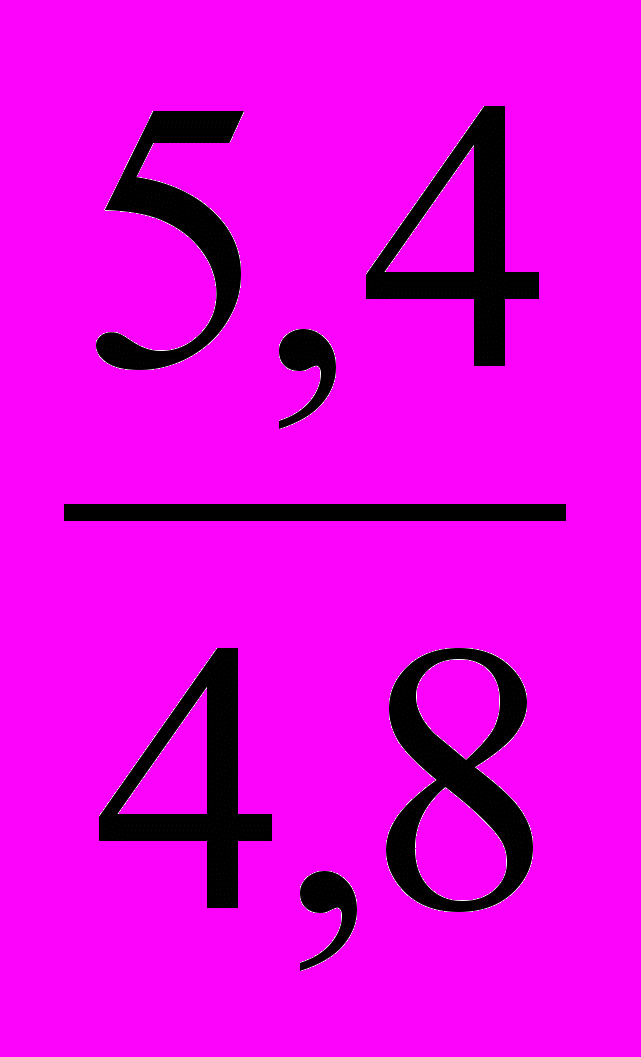= 1,125 или 112,5%, следовательно цена повысилась на 12,5% (112,5-100)

Плуги прицепные Ip = 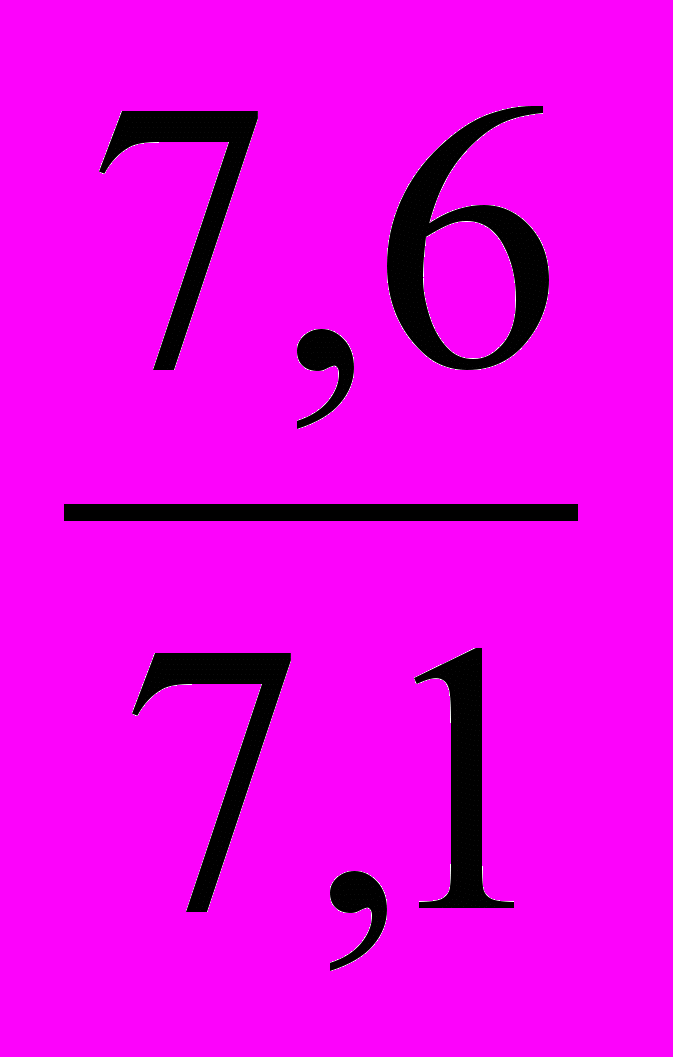= 1,070 или 107%, т.е. цена возросла на 7%.

Культиваторы навесные Ip = 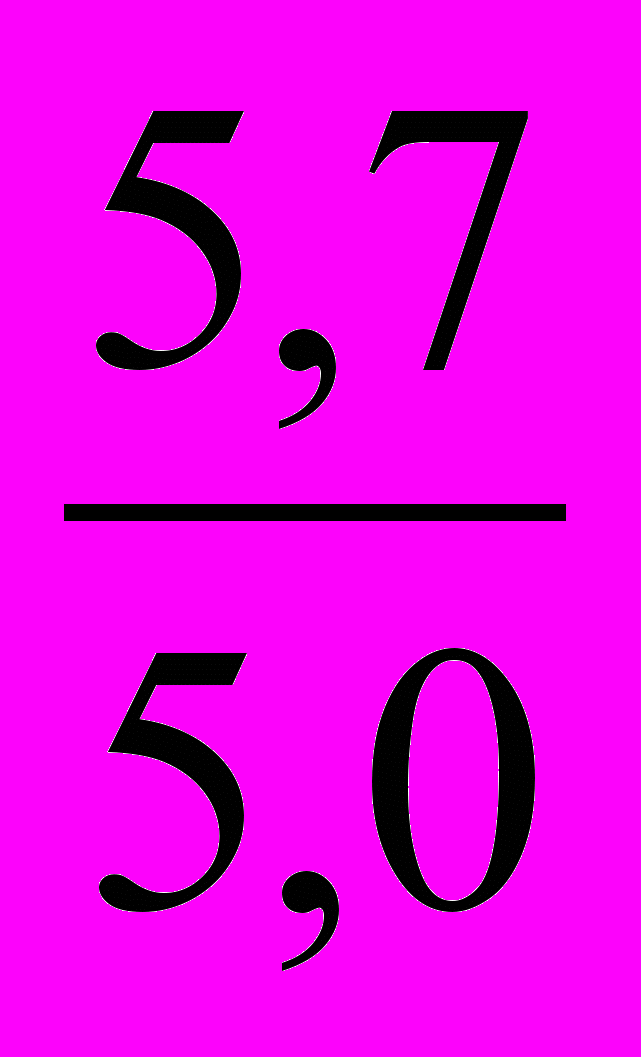= 1,140 или 114,0%, т.е. увеличение цены на 14%

Среднее изменение цены в целом определяется по формуле:

Jp = 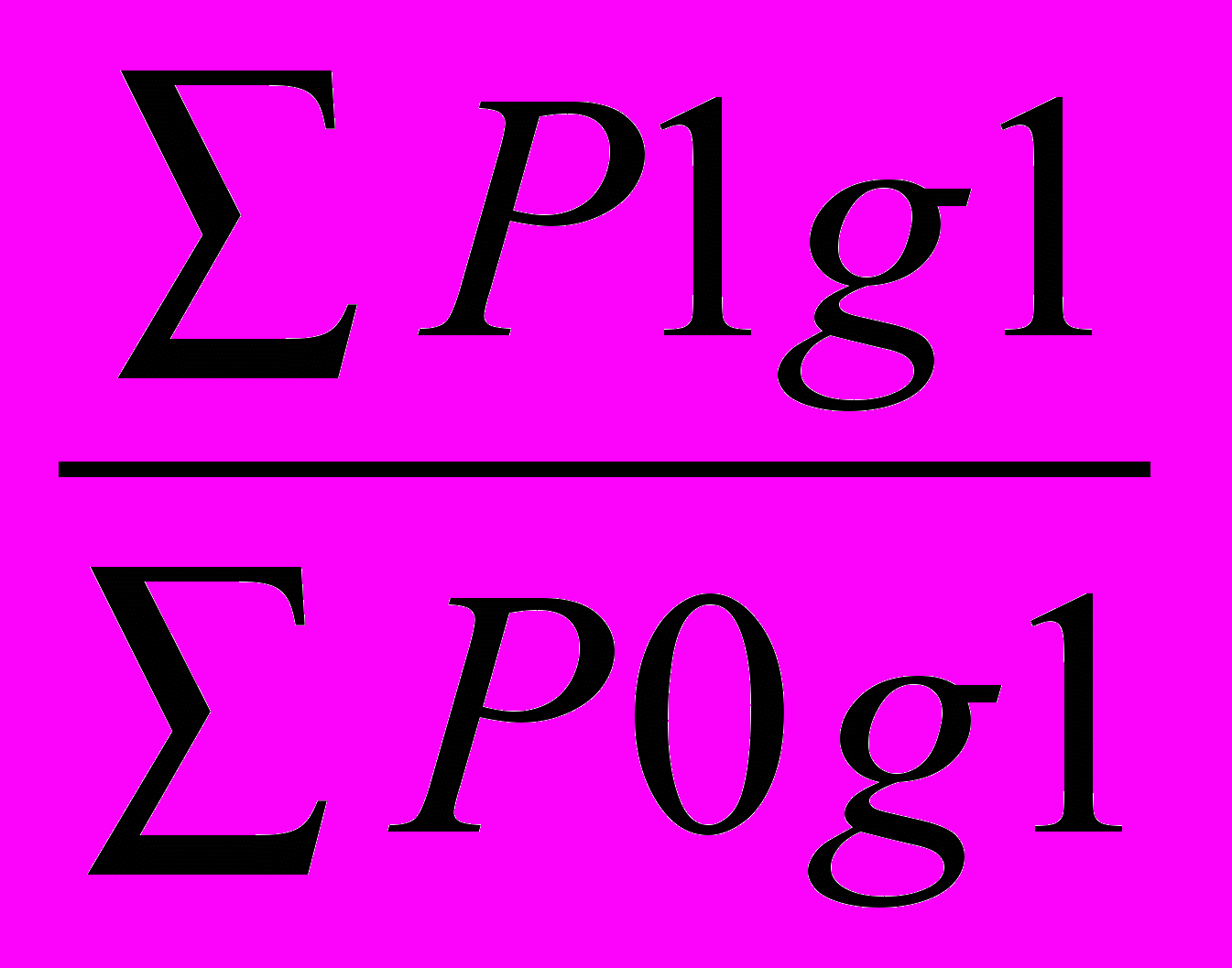= = 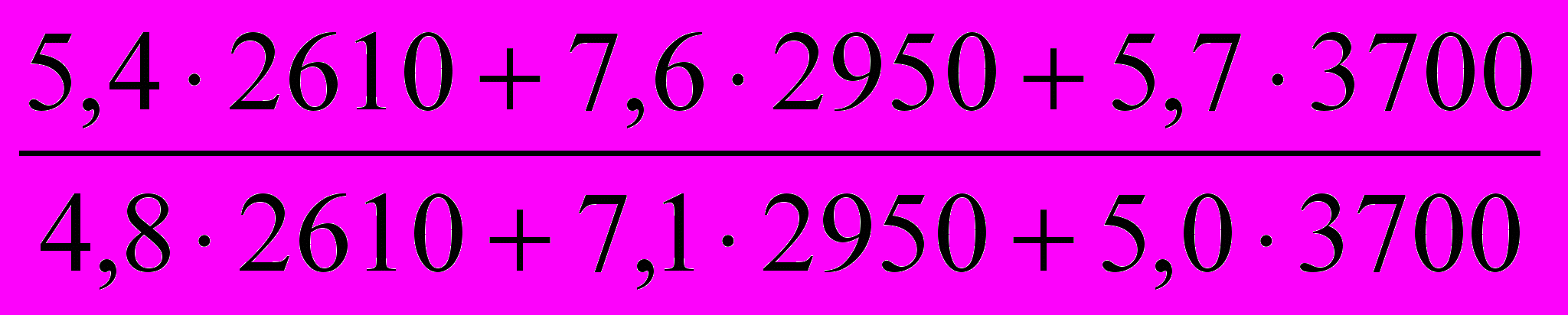= 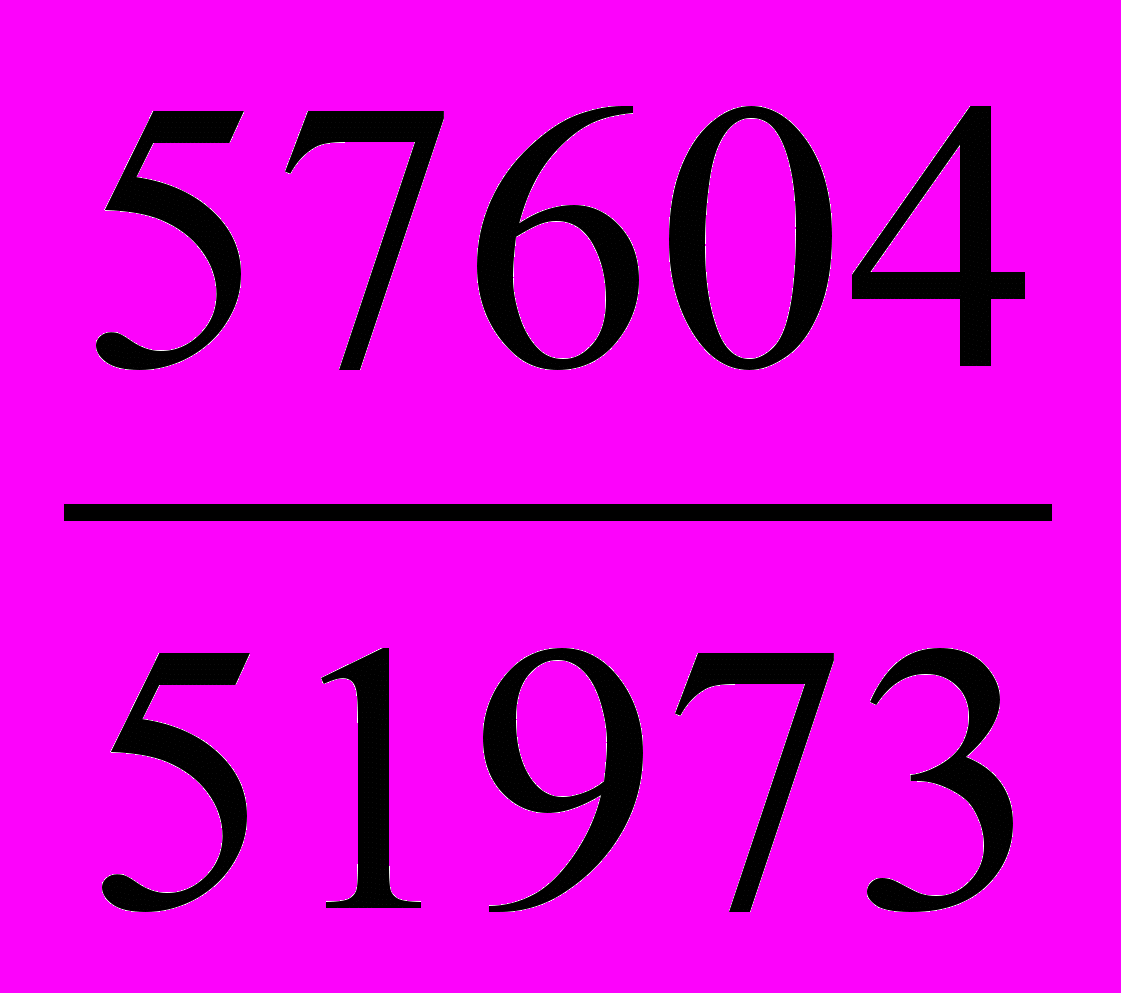1,108 или 110,8%

Таким образом, цены на продукцию повысились в среднем на 10,8%.

2)Изменение объема реализованной продукции по каждому виду определяется по индивидуальному индексу физического объема.

Ig =

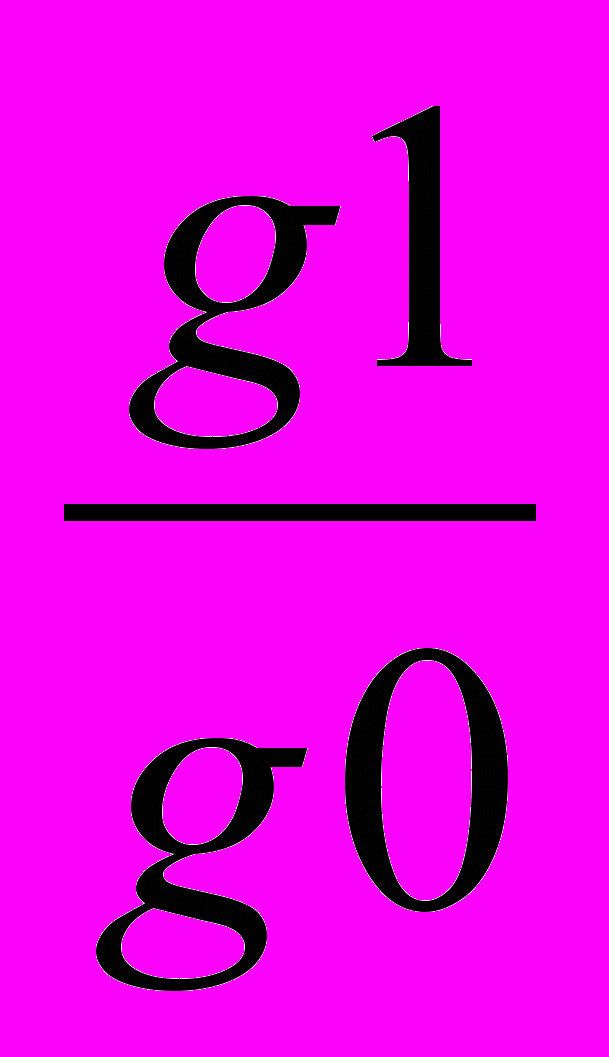
Плуги навесные Ig = 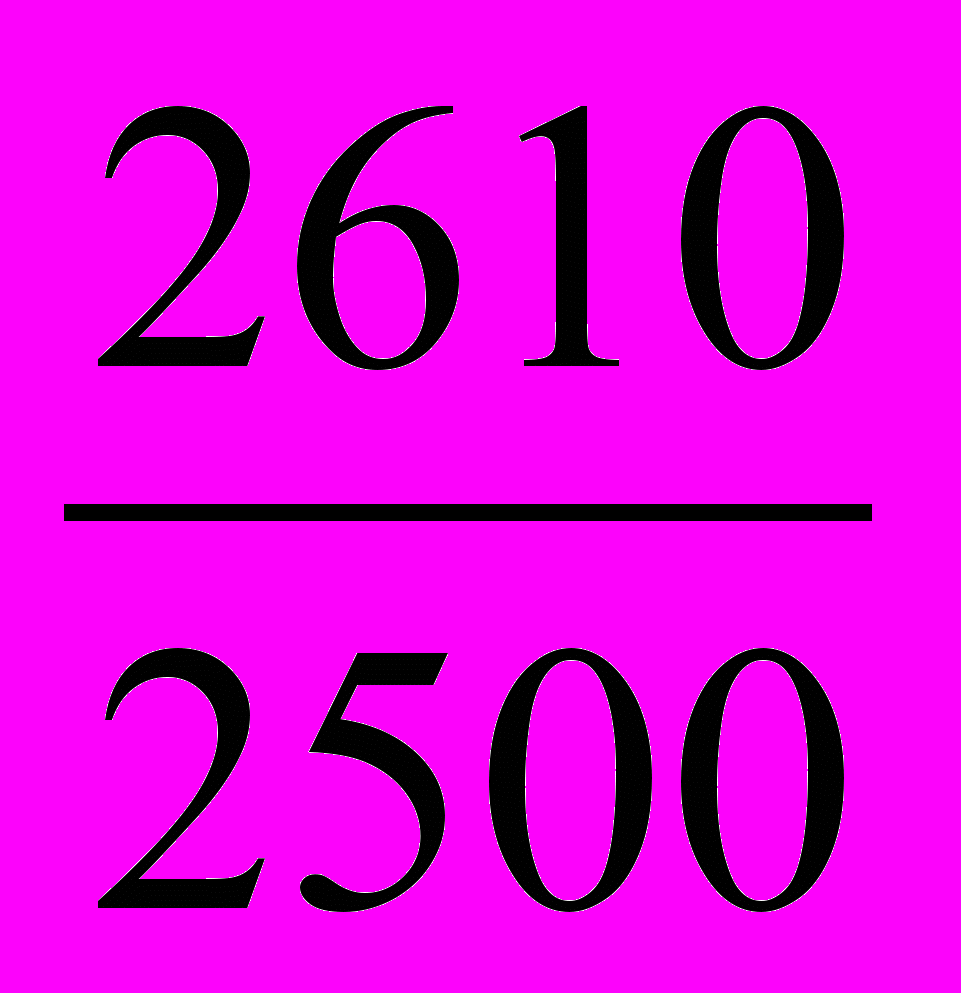= 1,004 или 104,4% т.е. количество реализованной продукции увеличилась на 4,4%.

Плуги прицепные Ig = 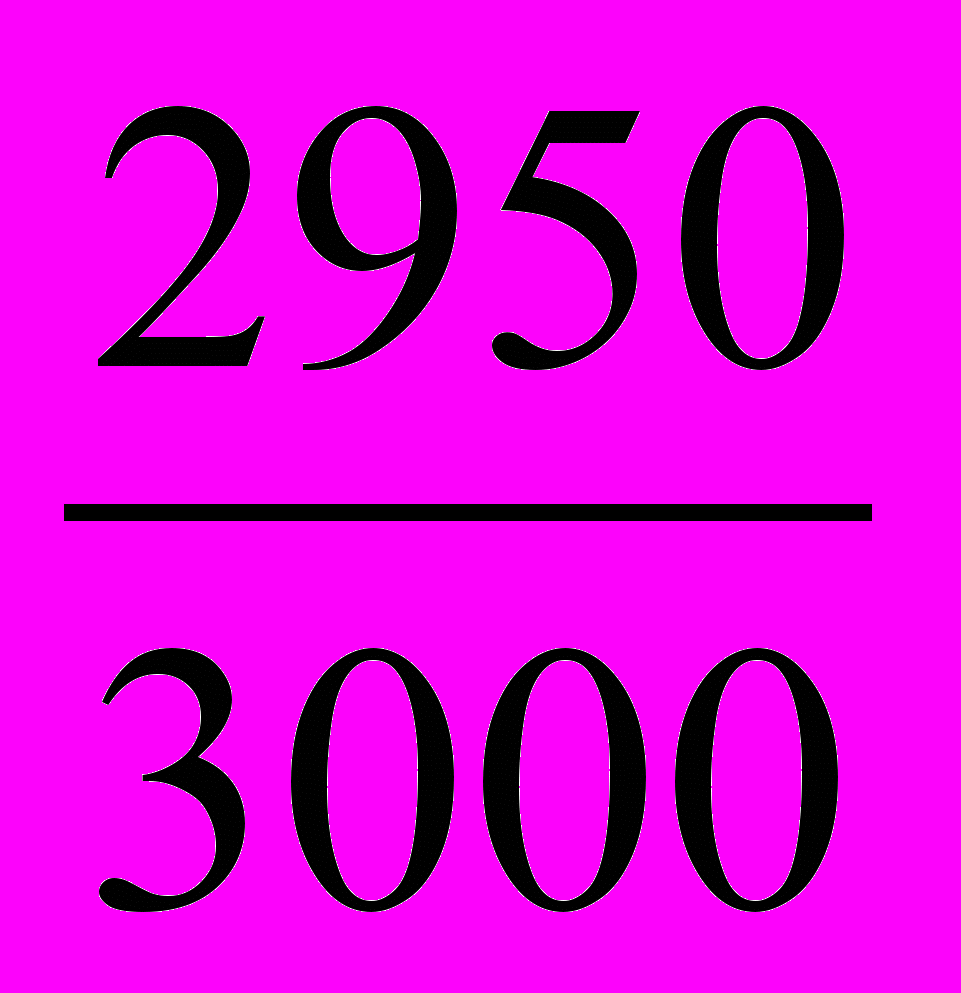= 0,983 или 98,3% т.е. количество реализованной продукции снизилась на 1,7%.

Культиваторы навесные Ig = 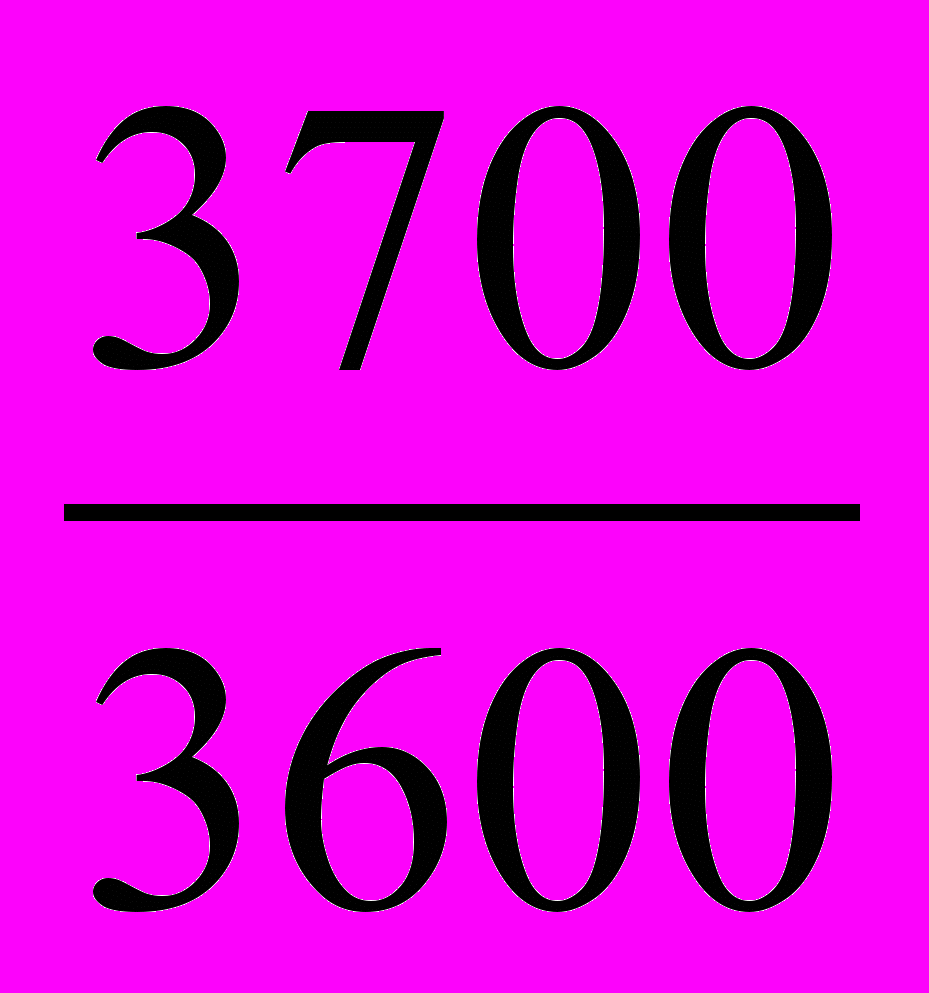= 1,028 или 102,8% т.е. увеличение реализации на 2,8%

Для характеристики изменения количества реализованной продукции в целом по предприятию исчисляется агрегатный индекс физического объема.

Ig = 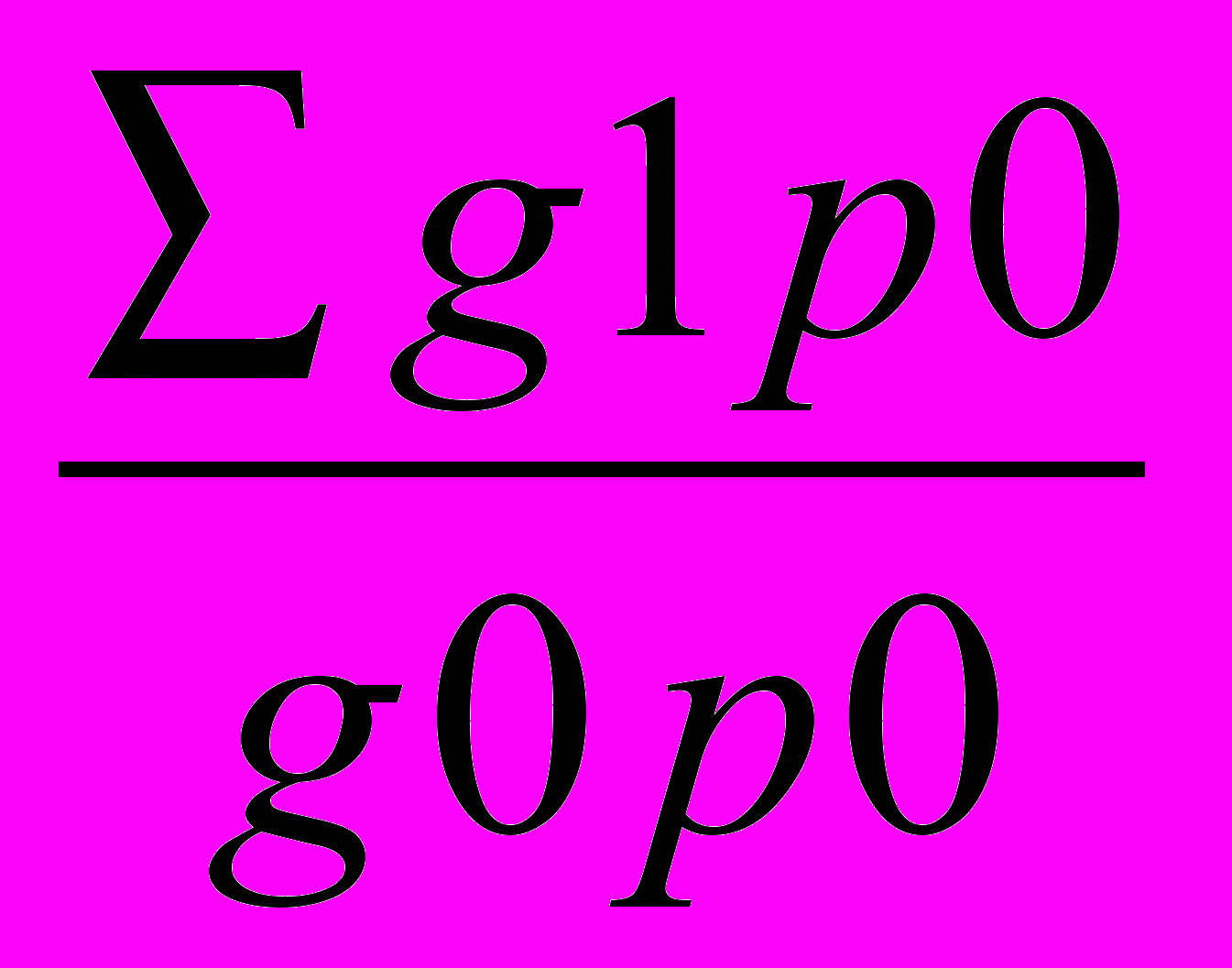= = 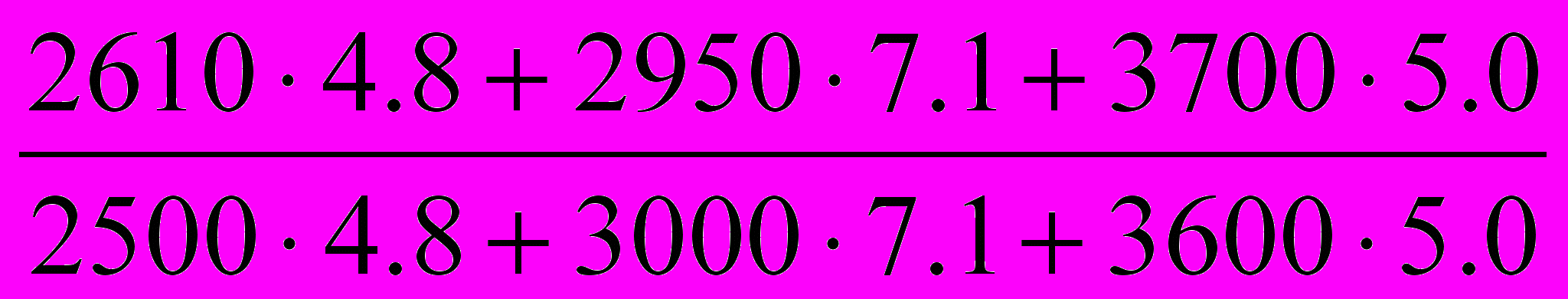= 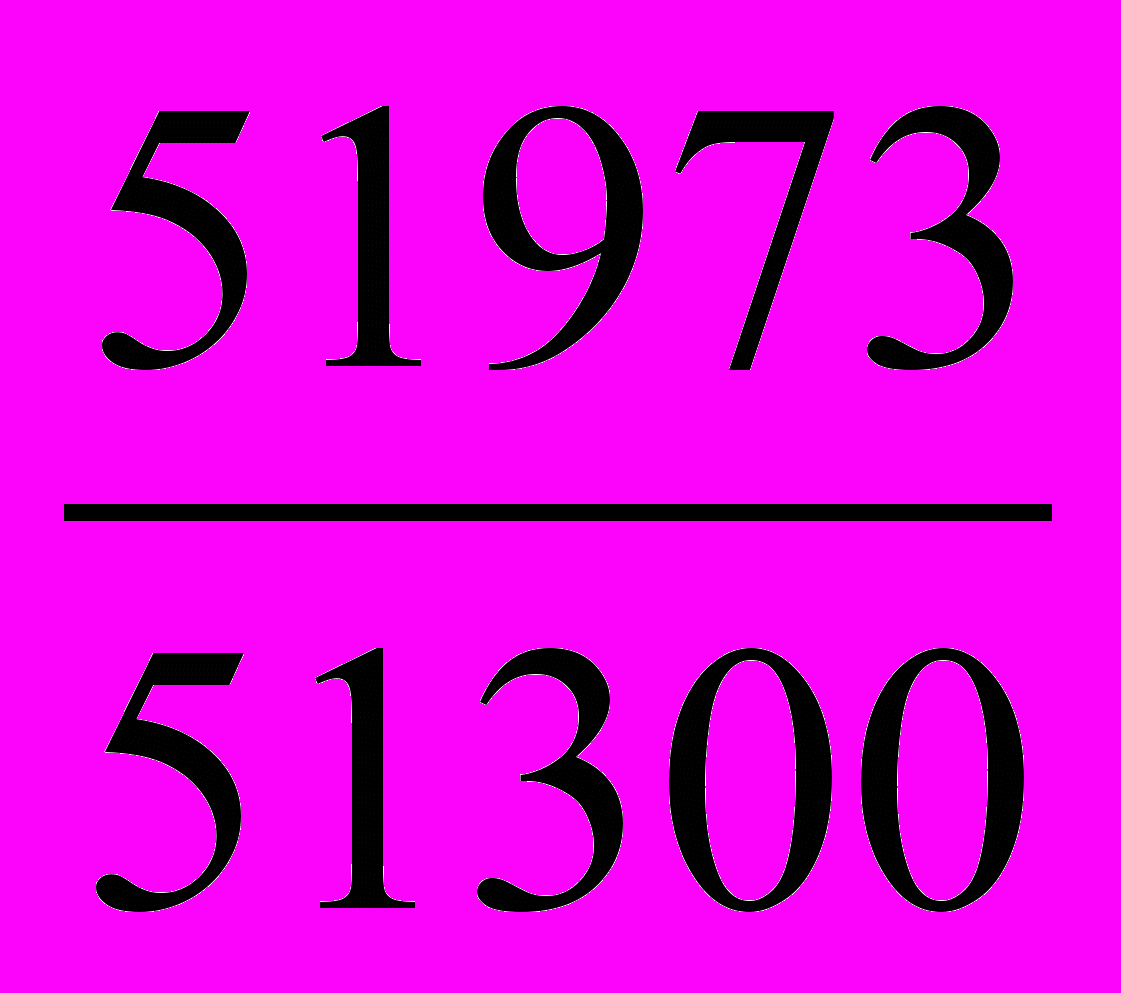1.013 или 101.3% т.е. в целом по предприятию реализация продукции возросла на 1.3%

3)Для характеристики изменения общего объема реализации продукции исчисляется агрегатный индекс фактического объема оборота.

Jpg = 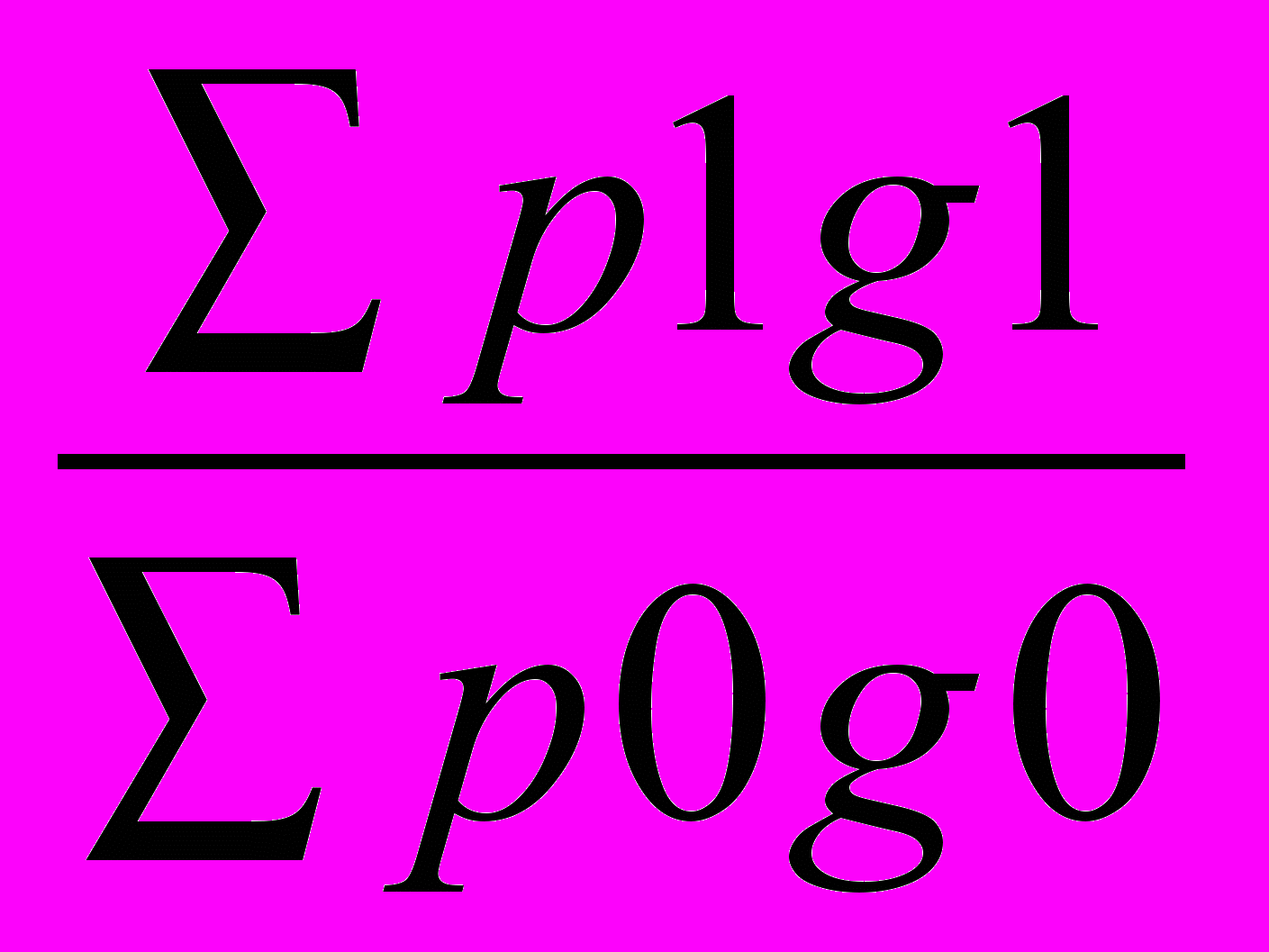= = 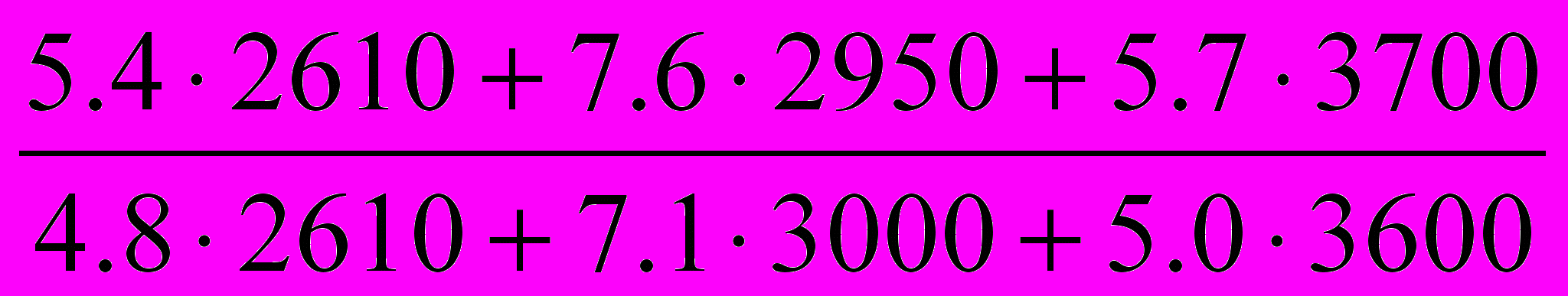= 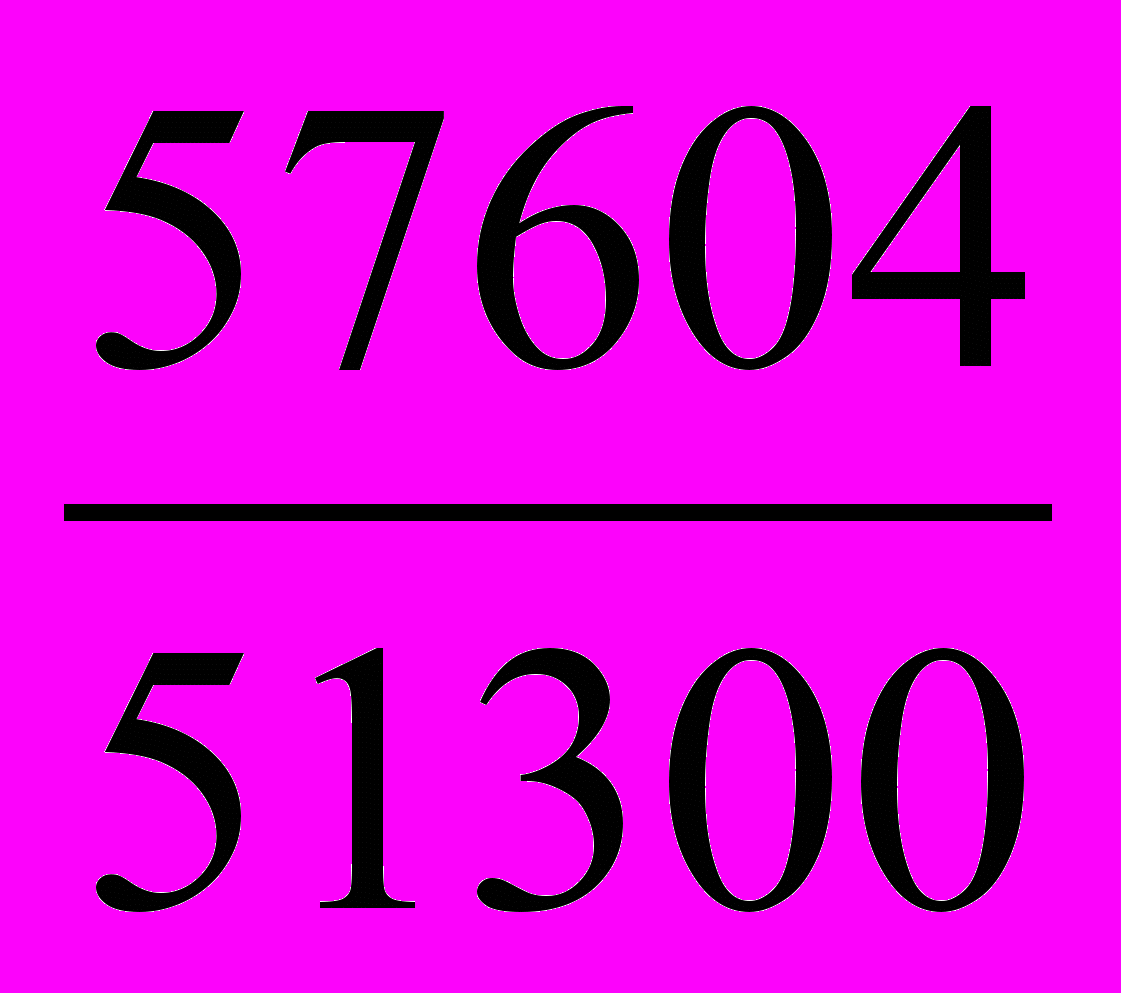1,123 или 112,3% т.е. в целом по предприятию объем реализации продукции возросла на 12%. Тоже самое можно рассчитать через взаимосвязь между индексами:

Jpg =Jp·Jg

Jpg = 1.108 · 1.013 = 1.123

4)Абсолютное изменение стоимости объема продукции определяется по формуле

∆pq = Σp1q1 – Σp0q0

∆pq = 57604 – 51300 = +6304 тыс. руб. т.е. общий объем реализованной продукции возрос на 6403 тыс. руб. в т.ч. рост стоимости реализованной продукции произошел:

а)за счет изменения цен определяется по следующей формуле

∆ppq = Σp1q1 – Σp0q1

∆ppq = 57604 – 51973 = +5631 тыс. руб. т.е. за счет среднего роста цен объем реализации возрос на 5631 тыс. руб.

б)за счет изменения количества реализованной продукции определяется по следующей формуле

∆ppq = Σq1p0 - Σq0p0

∆ppq = 51973 – 51300 = + 673 тыс. руб. т.е. за счет среднего увеличения количества реализованной продукции, объем реализации возрос на 673 тыс. руб.

Баланс факторов

6304=5631+673

По аналогии рассчитываются индексы себестоимости, количества выпущенной продукции, затрат производства.

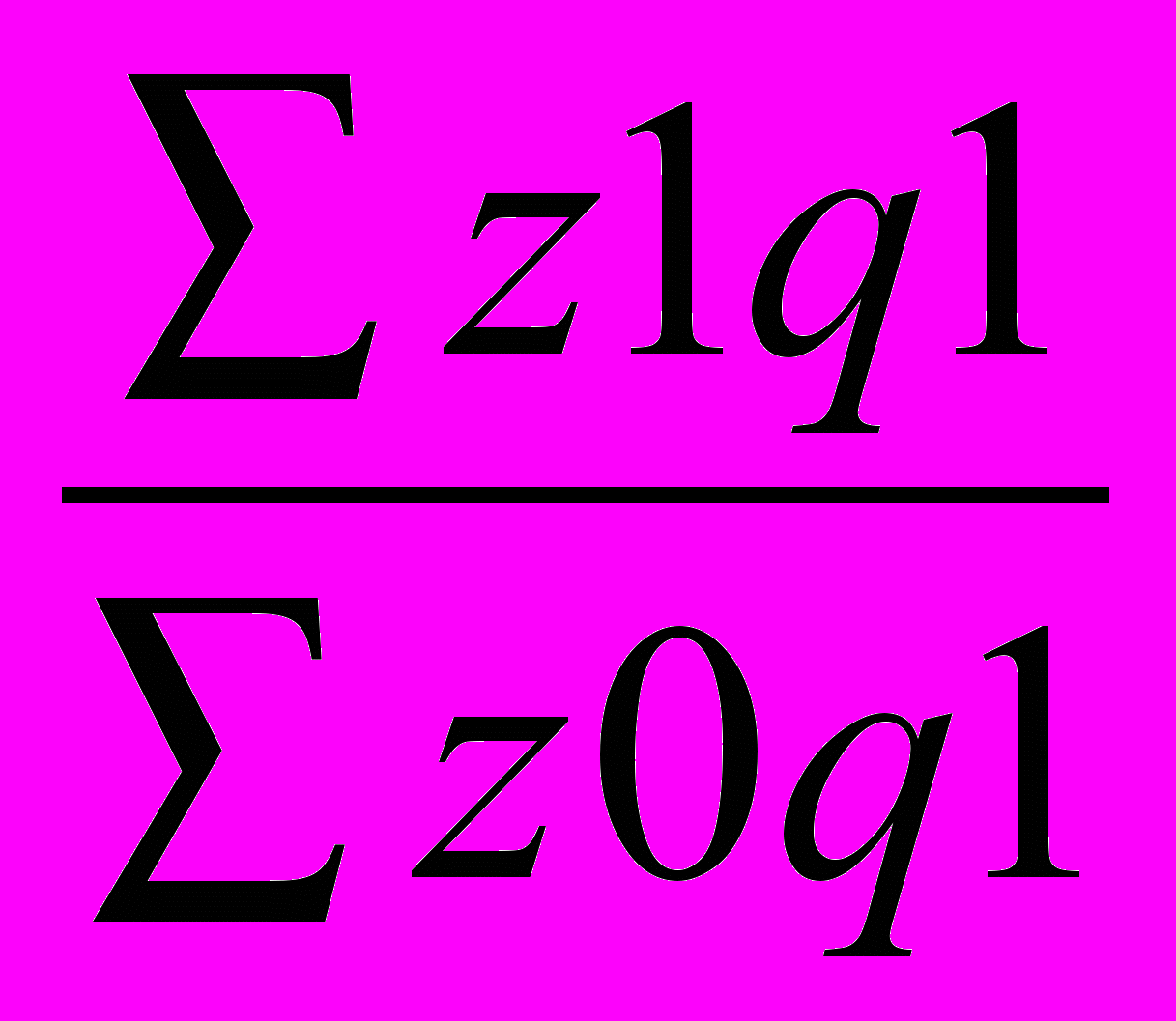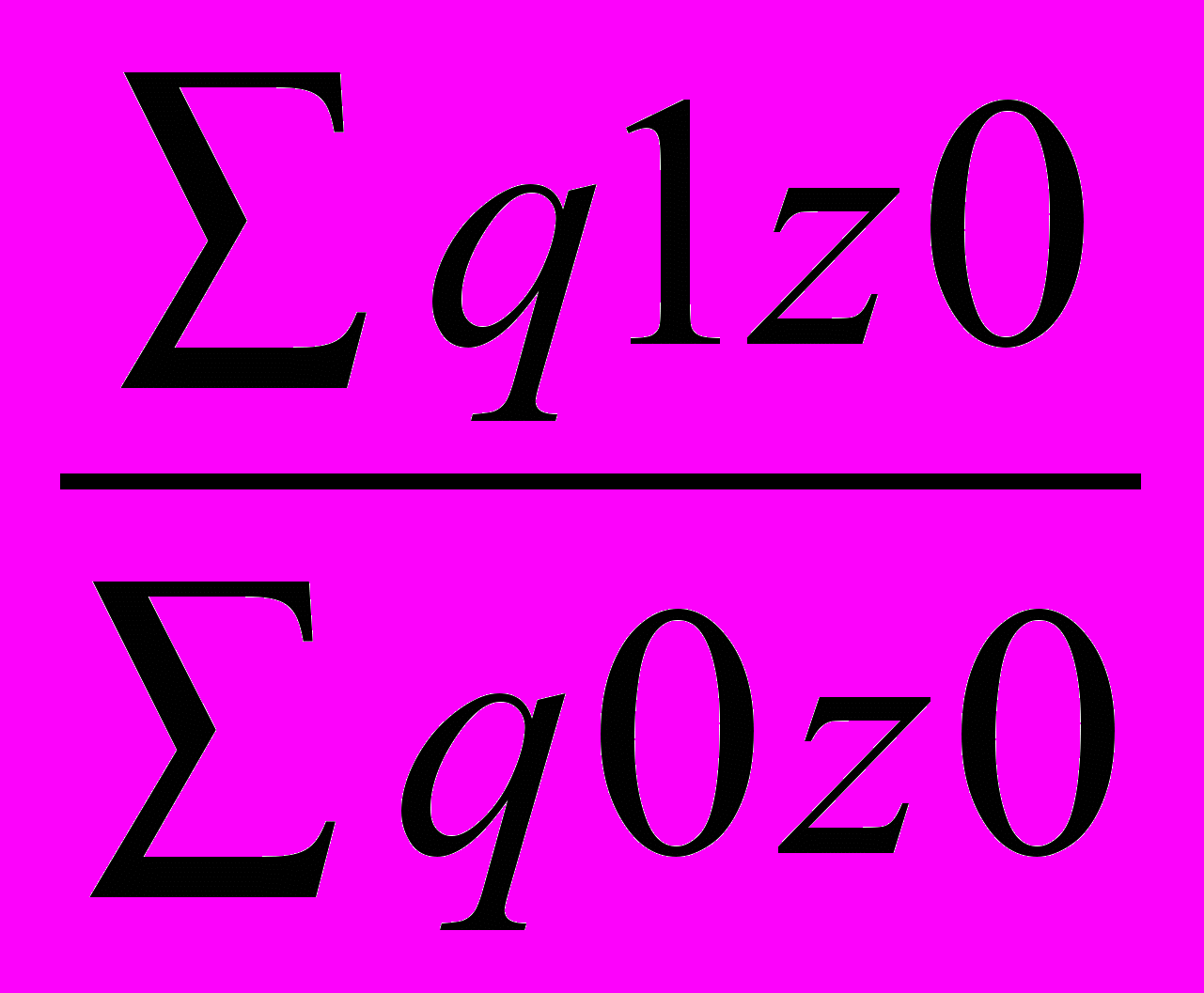Jz = Jq = Jzq = 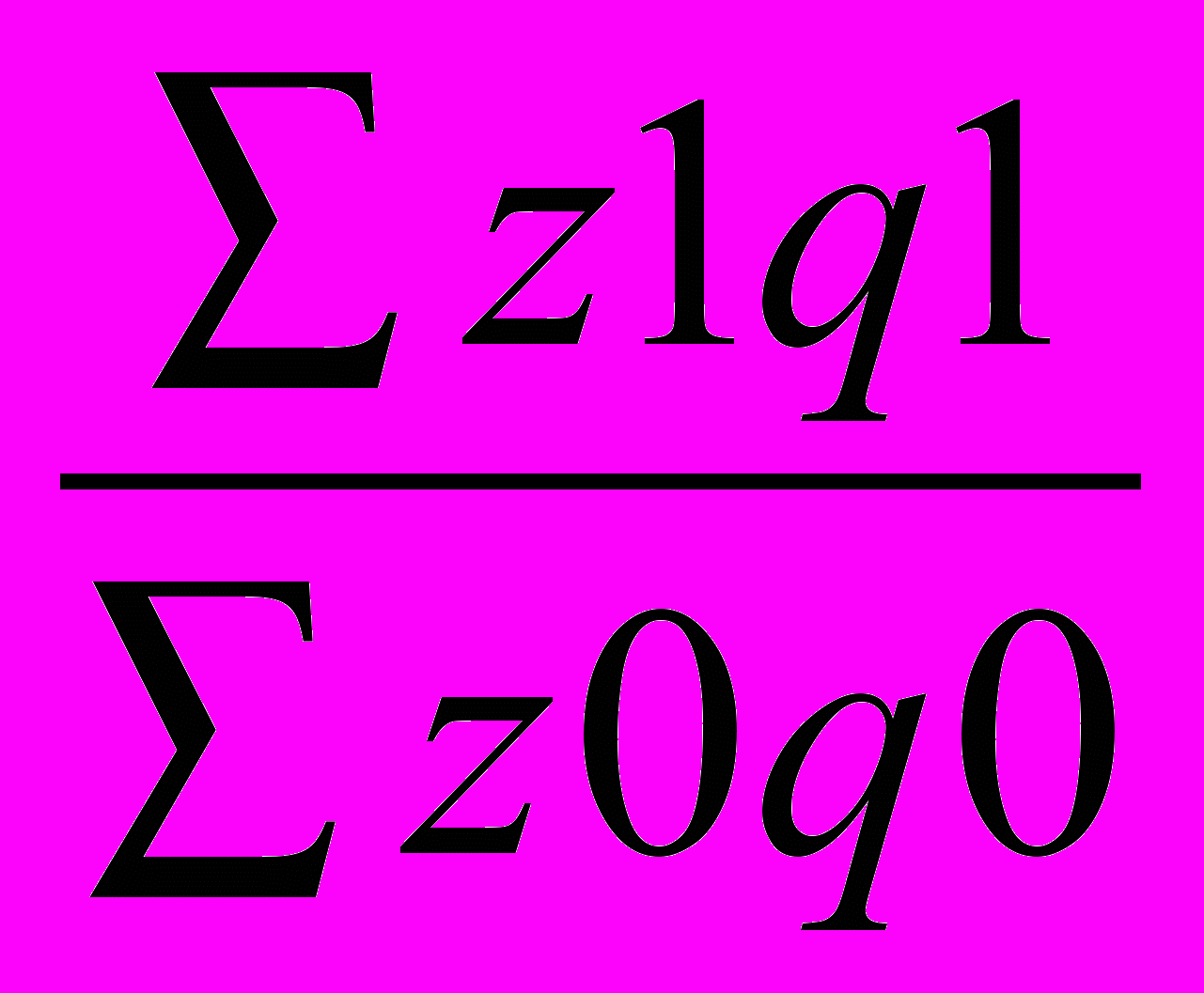Jzq = Jz · Jq

∆zq = Σz1q1 – Σz0q0 ∆zzq = Σz1q1 – Σz0q1 ∆qzq = Σz0q1 – Σz0q0


Индексы производительности труда

а)исходя из объема выработки на 1 работника

JB

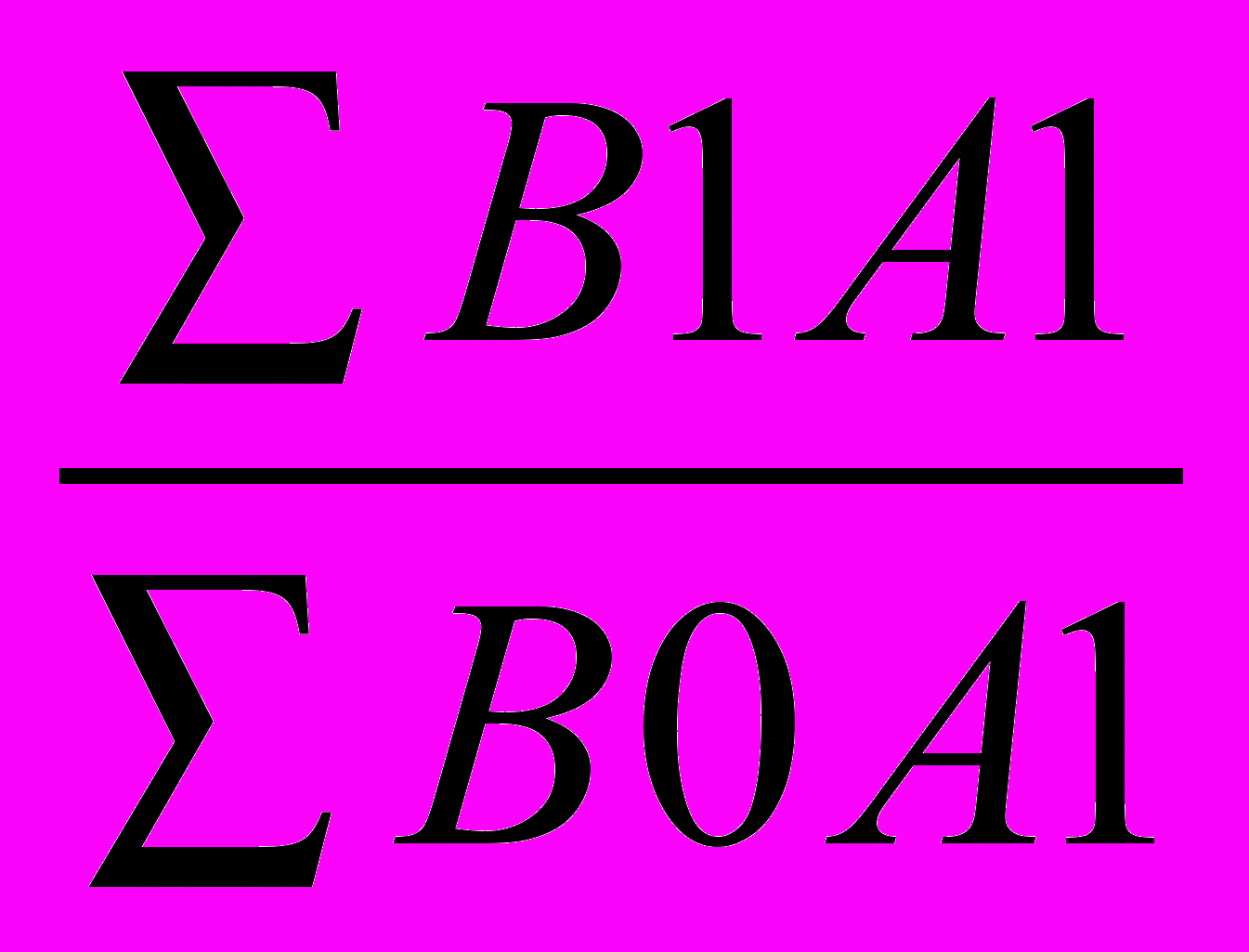
б)исходя из затрат времени на единицу продукции

Jt =