Geum.ru

Рекомендации по выполнению контрольной работы по дисциплине «Статистика» № вопроса

Вид материалаУчебники
Подобный материал:
1   2   3

Задача. Имеются данные о товарообороте и изменениях цен по товарам.

Товарные группы
Товарооборот, тыс. руб.
Изменение цен в отчетном году по сравнению с прошлым %

прошлый год
отчетный год

Молоко
565
553
+30

Творог
644
780
Не изменились

Сметана
226
186
+20

Итого
1435
1519



Определить:

Среднее изменение цен

Средний индекс физического объема товарооборота

Средний индекс фактического товарооборота, используя взаимосвязь между индексами.

Абсолютное изменение товарооборота, в т.ч. за счет изменения цен и количества проданных товаров.

Решение.

Товарооборот и изменение цен по товарам.

Товарные группы
Товарооборот, тыс. руб.
Изменение цен в отчетном по сравн. с прошлым, %


Ip
Сопоставимый т/оборот, тыс. руб. p0q0 = p1q1 : ip

прошлый год p0q0
отчетный год p1q1

Молоко
565
653
+30
1.300
502.3

Творог
644
780



1.000
780.0

Сметана
226
286
+20
1.200
238.3

Итого
1435
1719






1502.6

1) Так дано изменение цен по товарам, на основе этого записываем индивидуальные индексы цен.

Ip = 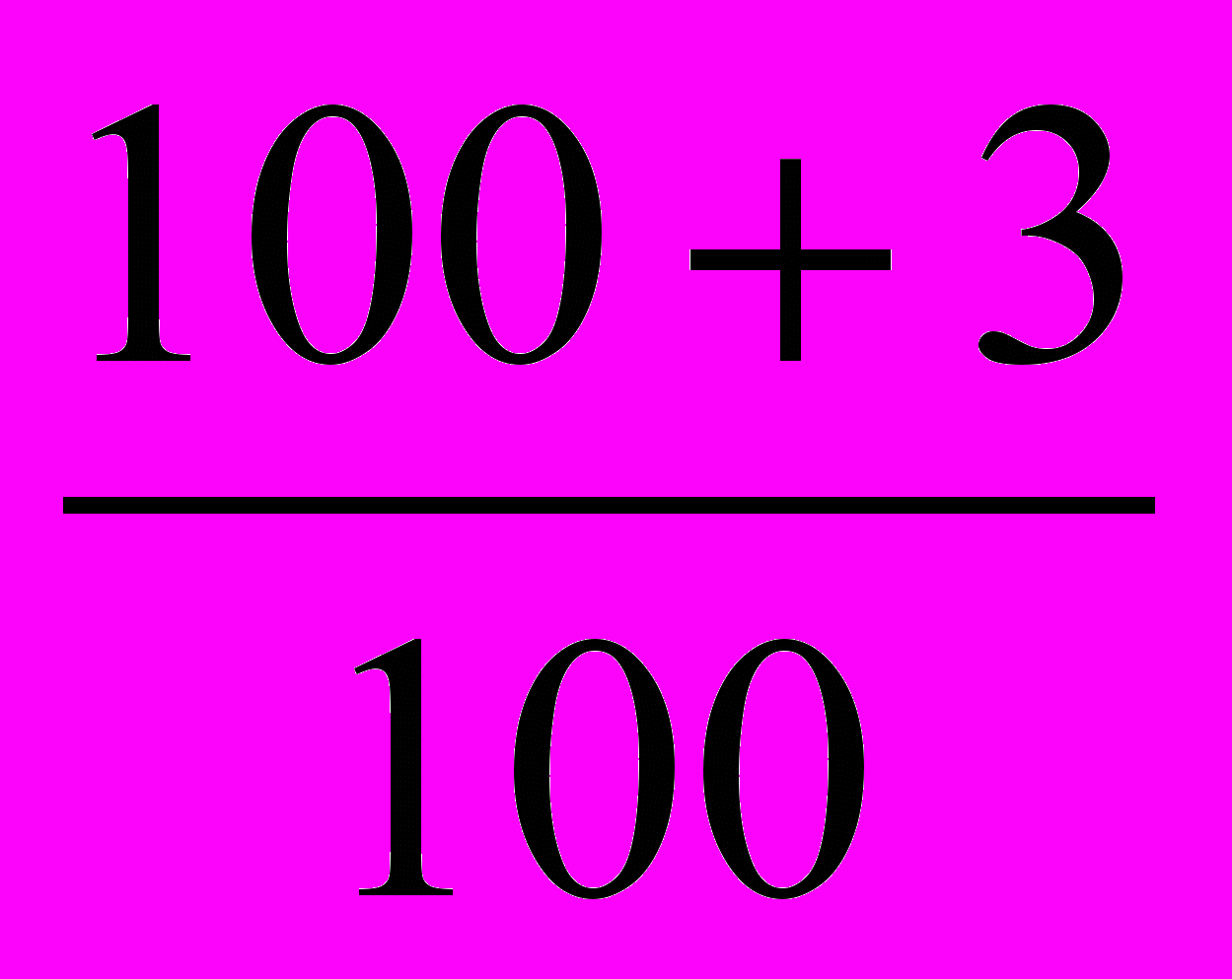= 1.300 Ip = 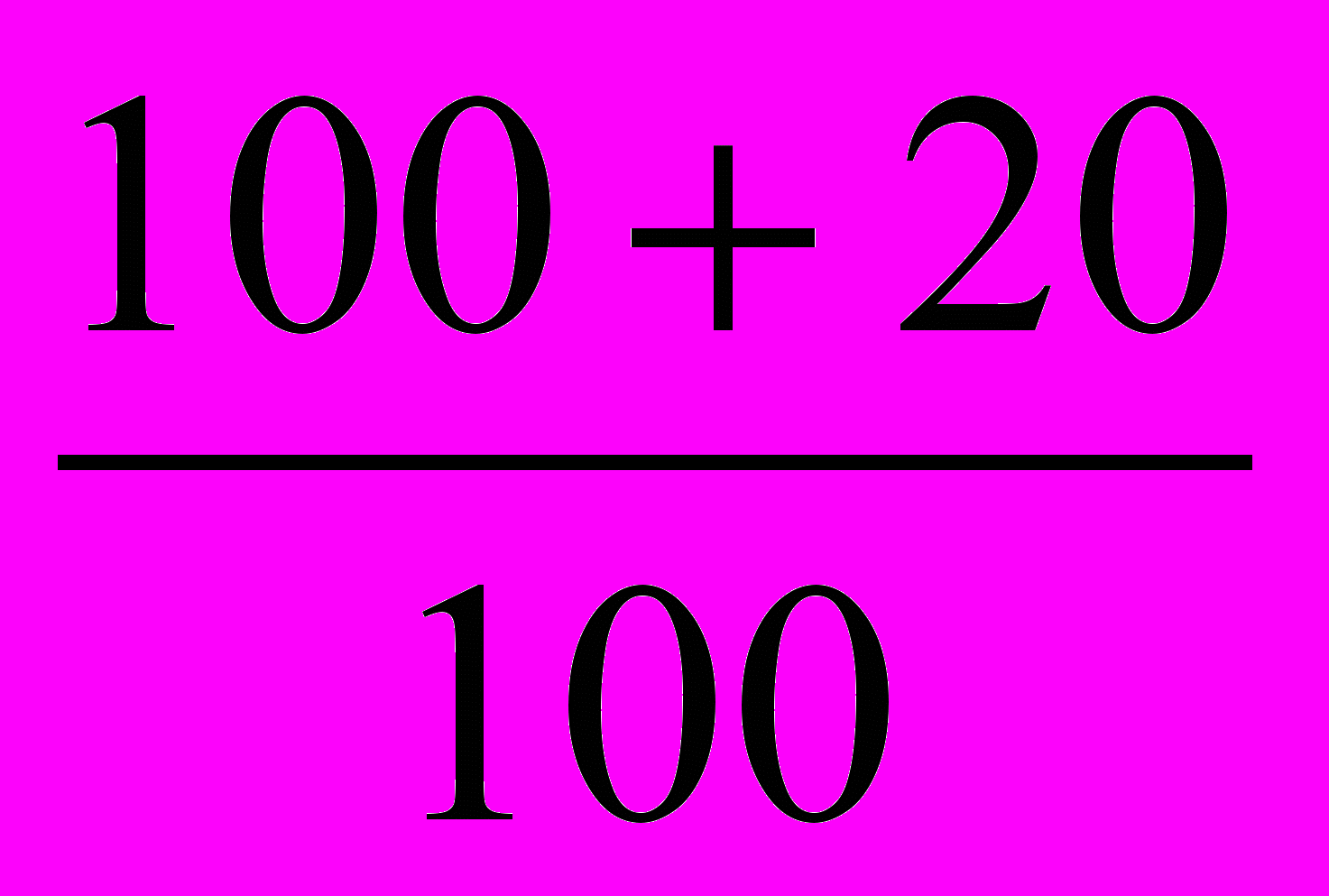= 1.200


2) Общий индекс цен рассчитываем по формуле среднего гармонического индекса.


Jph = 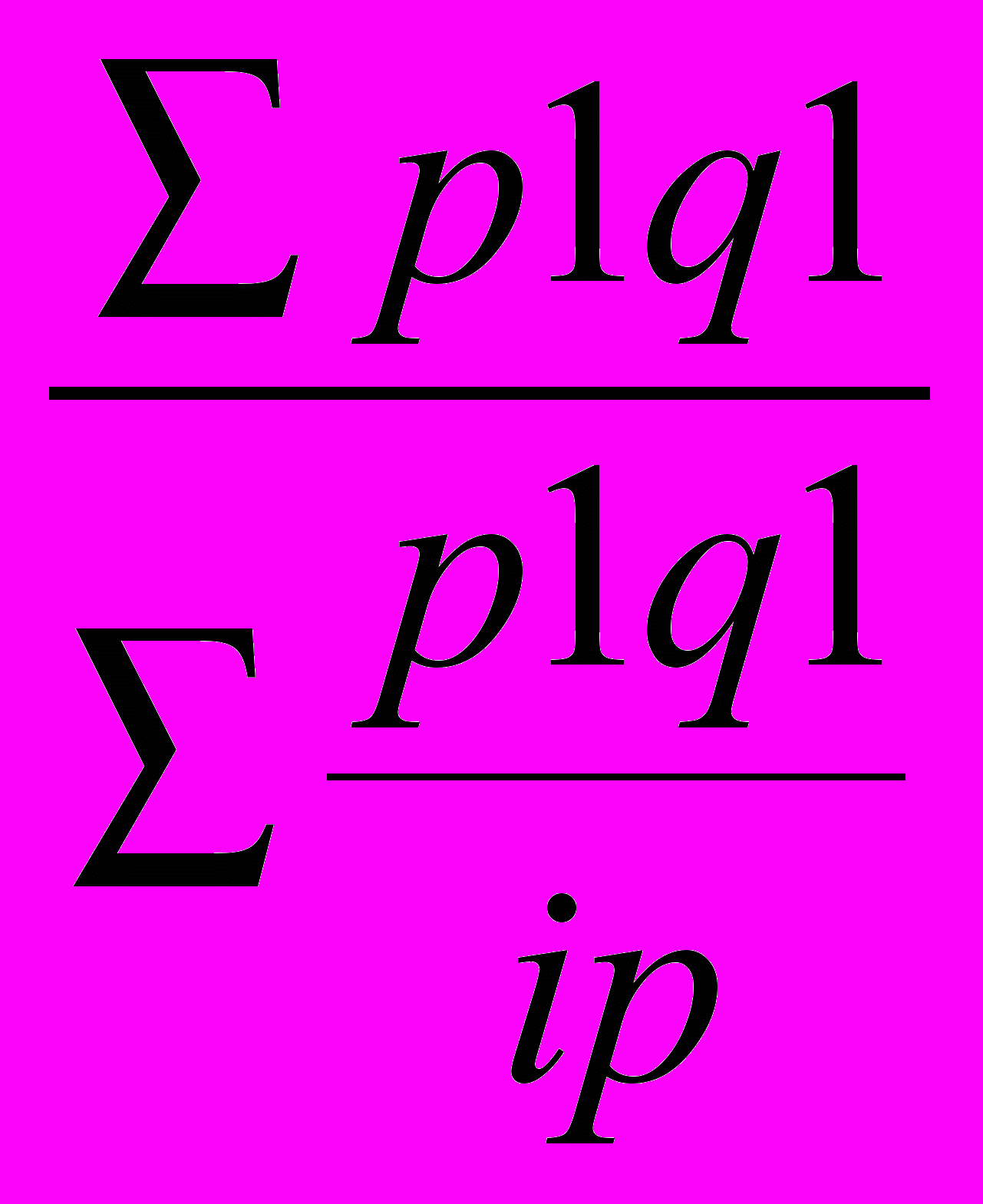= = 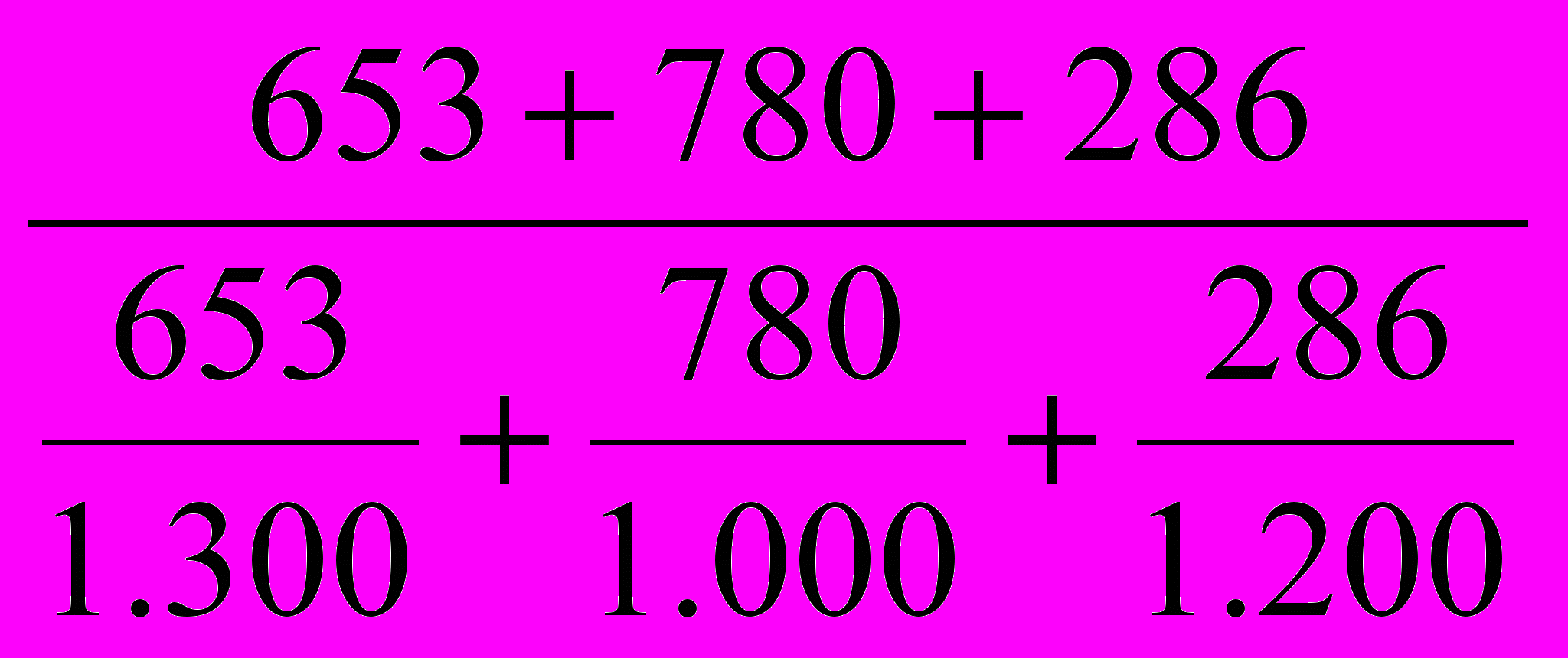= 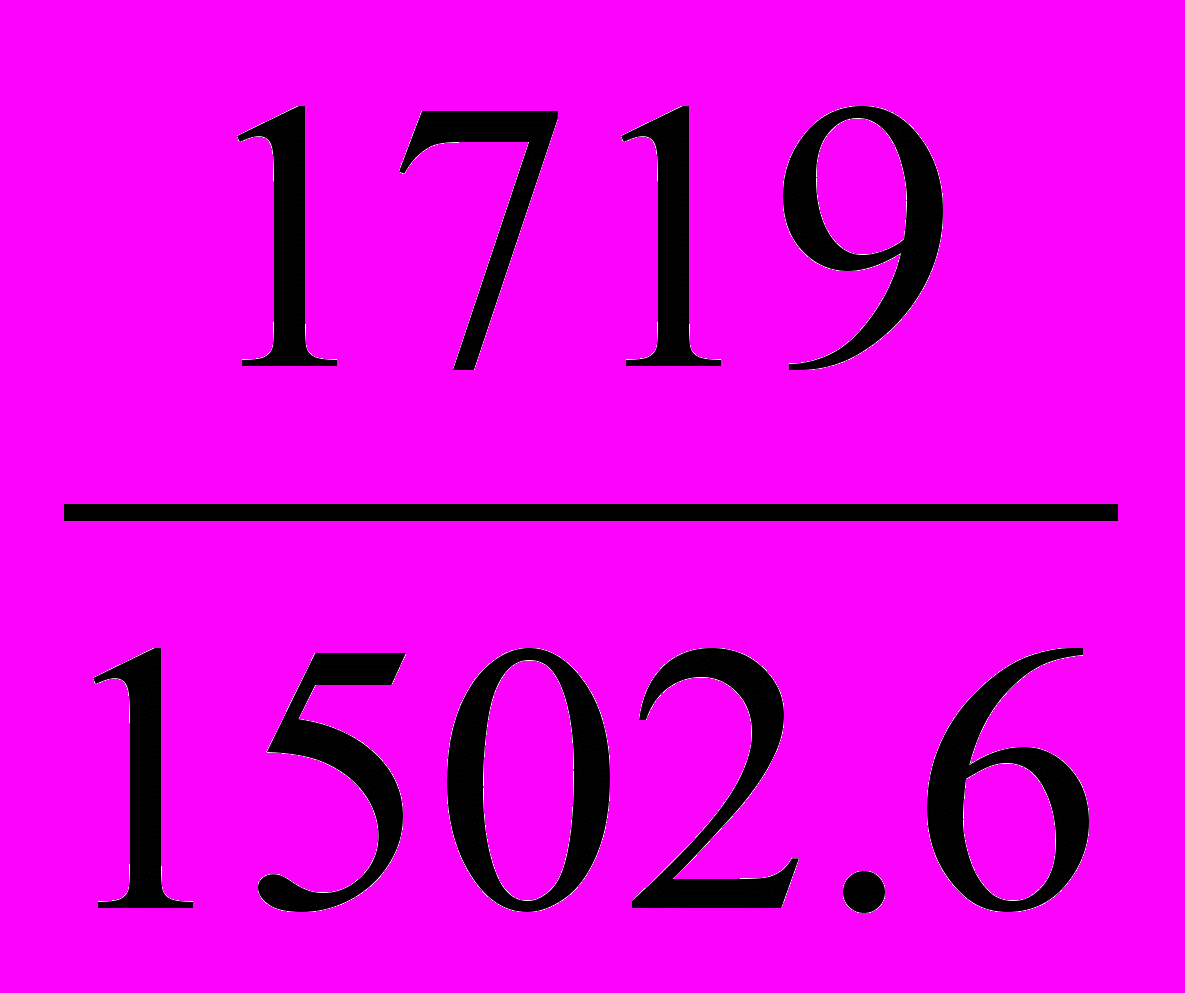1.144 или 114,4%, т.е. в среднем цены на товары возросли на 14,4%.

3) Средний индекс физического объема товарооборота

Jp = 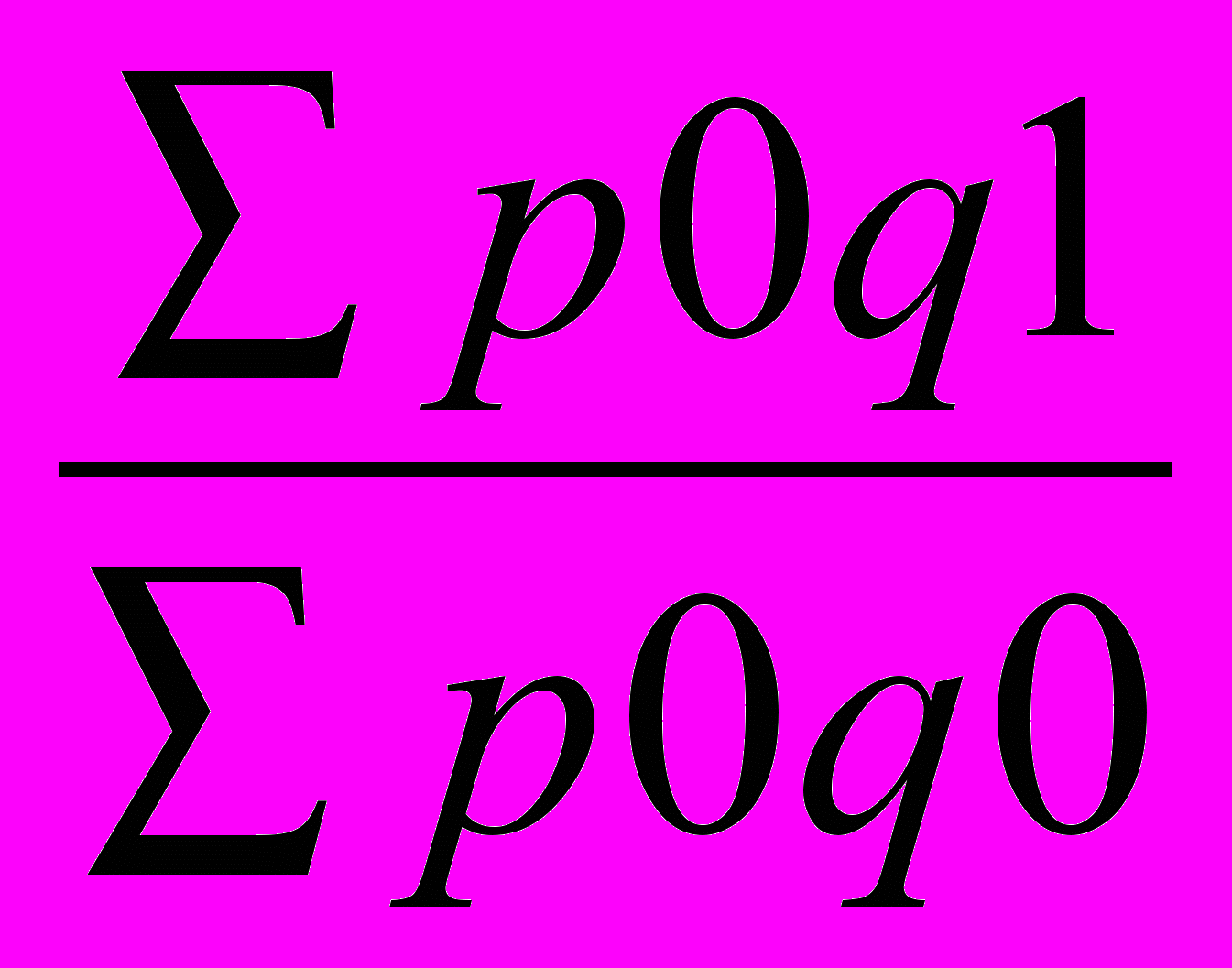= = 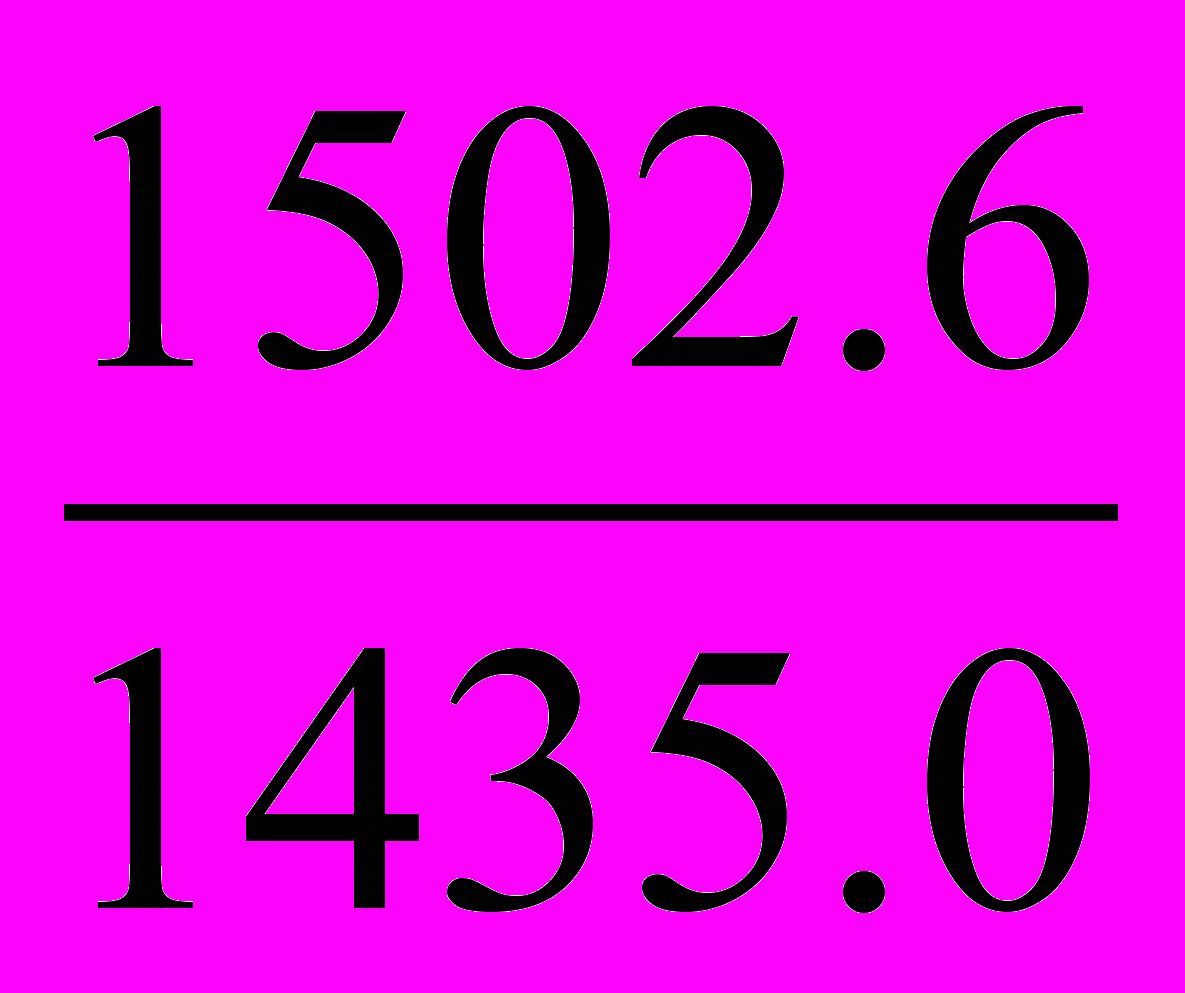1,047 или 104,7%, т.е. количество проданных товаров возросло на 4,7%.

4)Средний индекс фактического объема товарооборота

Jpq = Jp · Jq = 1.144 · 1.047 = 1.198 или 119.8%, т.е. фактический товарооборот возрос на 19.8%

5)Абсолютное изменение

а)товарооборота

∆pq = Σp1q1 – Σp0q0 = 1719 – 1435 = +284 тыс. руб.

б) в т.ч. за счет изменения цен

∆ppq = Σp1q1 - Σp0q1 = 1719 – 1502.6 = +216.4 тыс. руб.

За счет изменения количества реализованных товаров

∆ppq = Σp0q1 - Σp0q0 = 1502.6 – 1435 = +67.6 тыс. руб.

Задача. Имеются данные о товарообороте и изменениях количества реализованных товаров.

Товарные группы
Товарооборот, тыс. руб.
Изменение количества реализованных товаров в отчет., по сравнению с прошлым %

прошлый год
отчетный год

Мясо
270
280
-10

Рыба
160
153
-22

Овощи
170
172
+5

Итого
600
605



Определить.

1)Средний индекс физического объема товарооборота.

2)Средний индекс цен, фактического объема товарооборота.

Решение.

Товарооборот и изменения количества реализованных товаров.

Товарные группы
Товарооборот, тыс. руб.
Изменение количества реал. тов. %


Ip
Сопоставимый т/оборот, тыс. руб. p0q0 = p1q1 : ip

прошлый год p0q0
отчетный год p1q1

Мясо
270
280
-10
0.90
243

Рыба
160
153
-22
0.78
124.8

Овощи
170
172
+5
1.05
178.5

Итого
600
605






546.3

1) так как дано изменение физического объема реализации, запишем индивидуальные индексы

Jq = 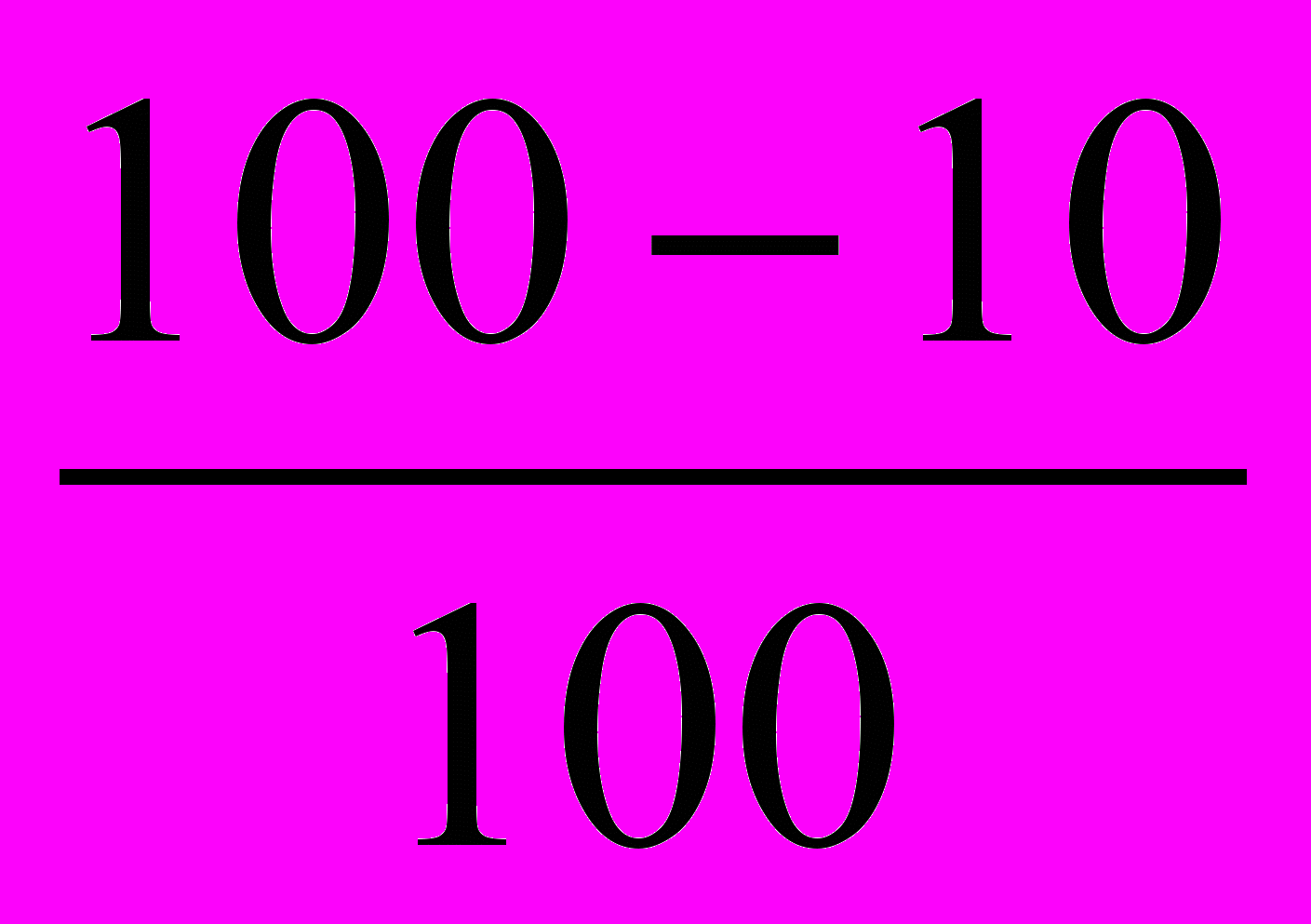= 0.90 Jq = 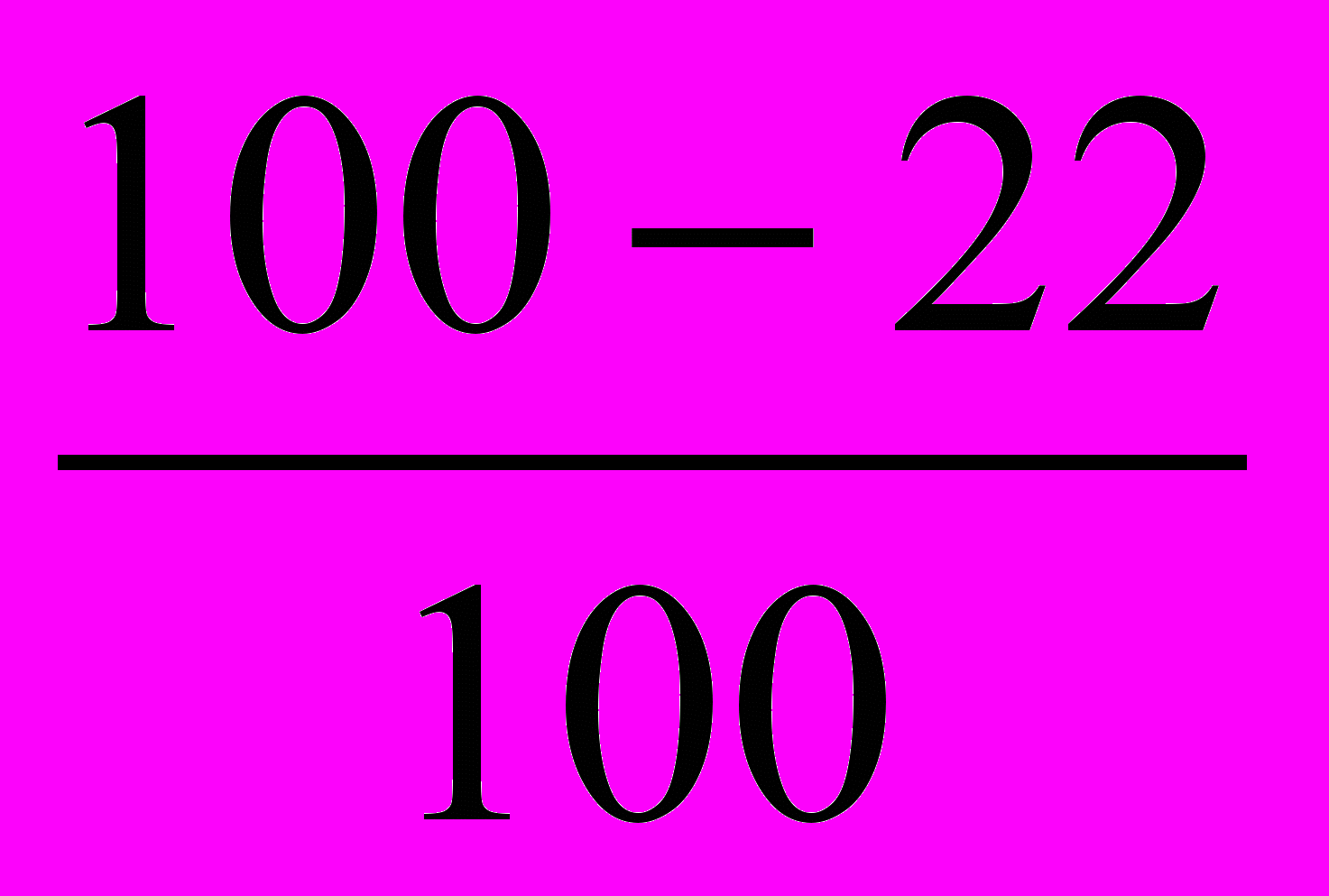= 0.78 Jq = 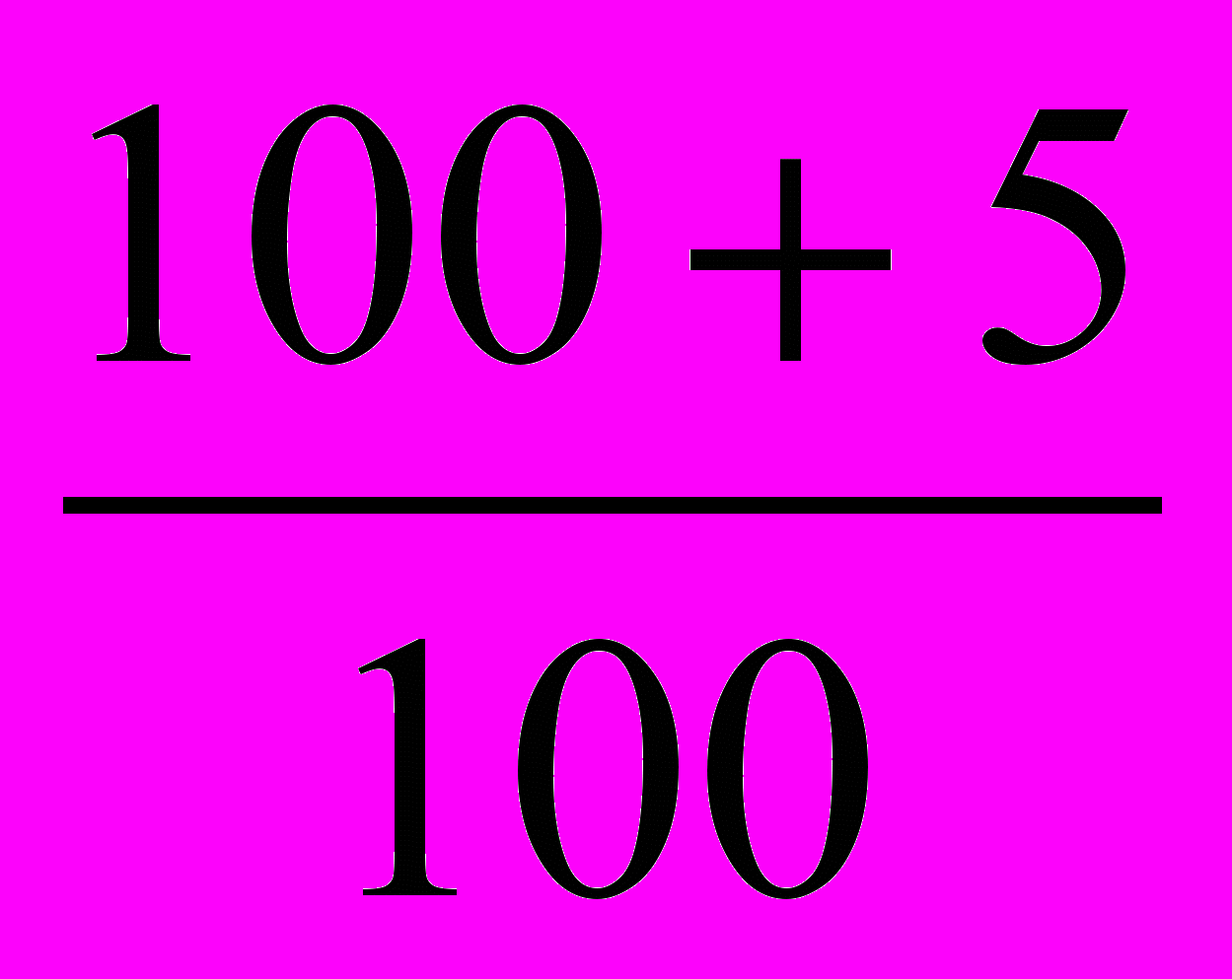= 1.05

2)Средний индекс физического объема товарооборота рассчитываем по формуле среднеарифметического индекса

Jpq =

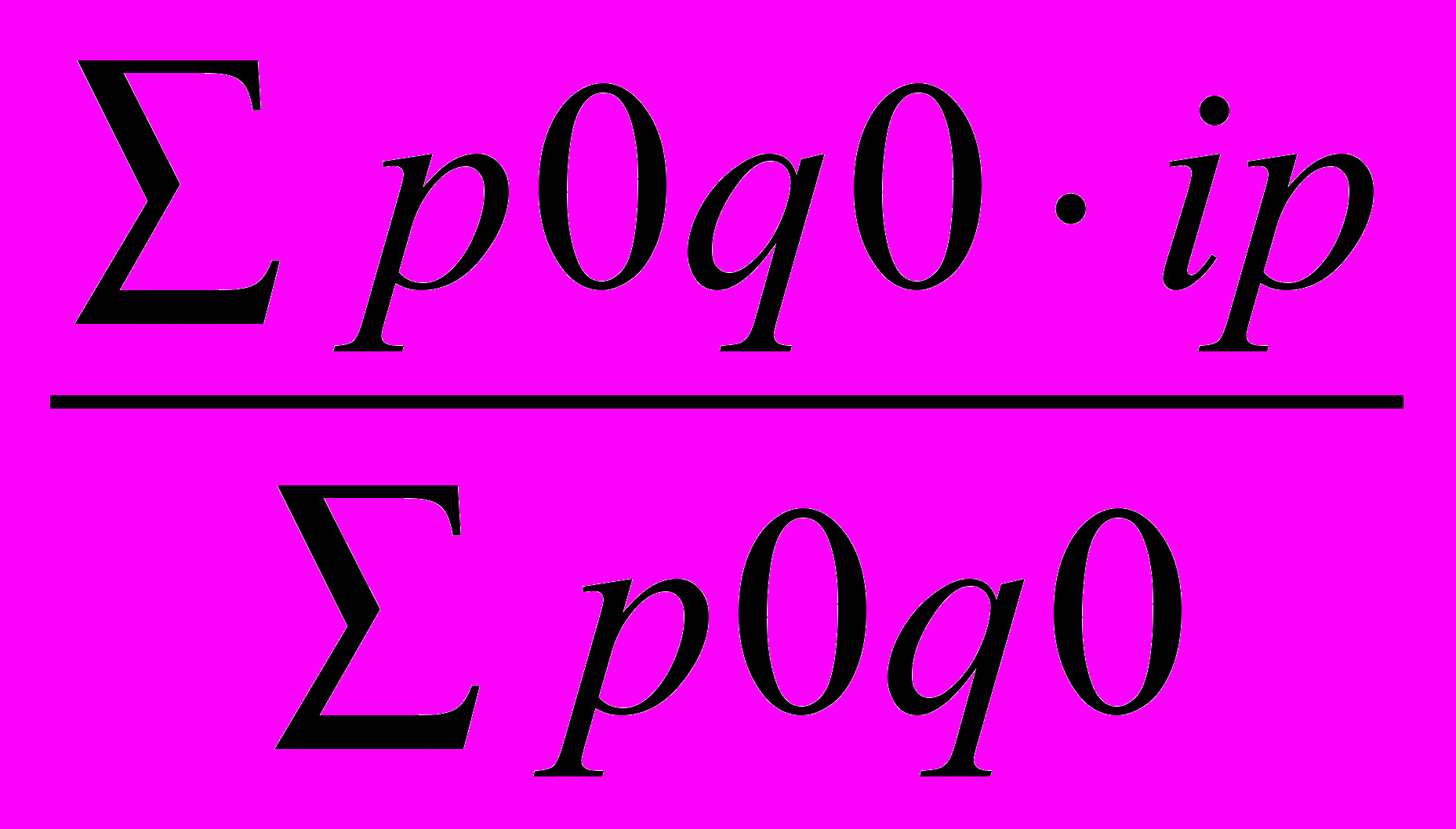
Jpq = 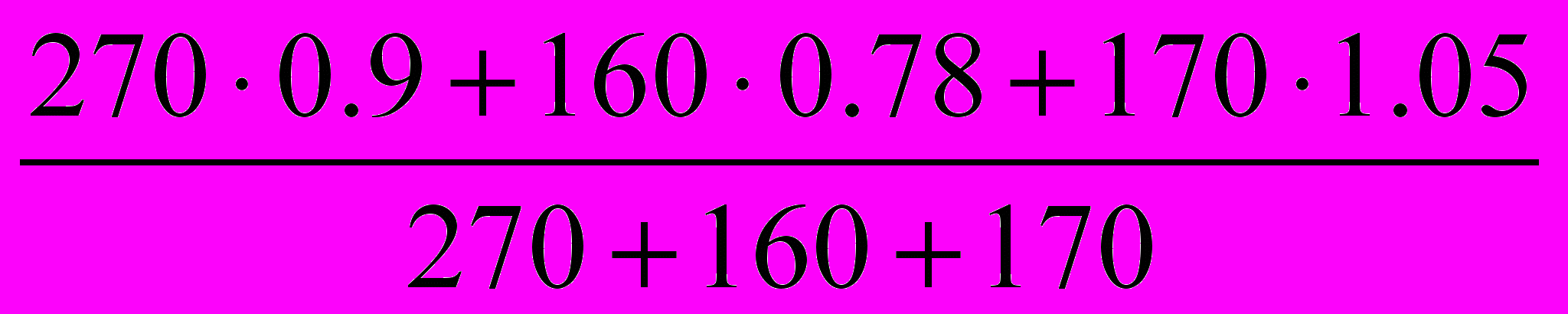= = 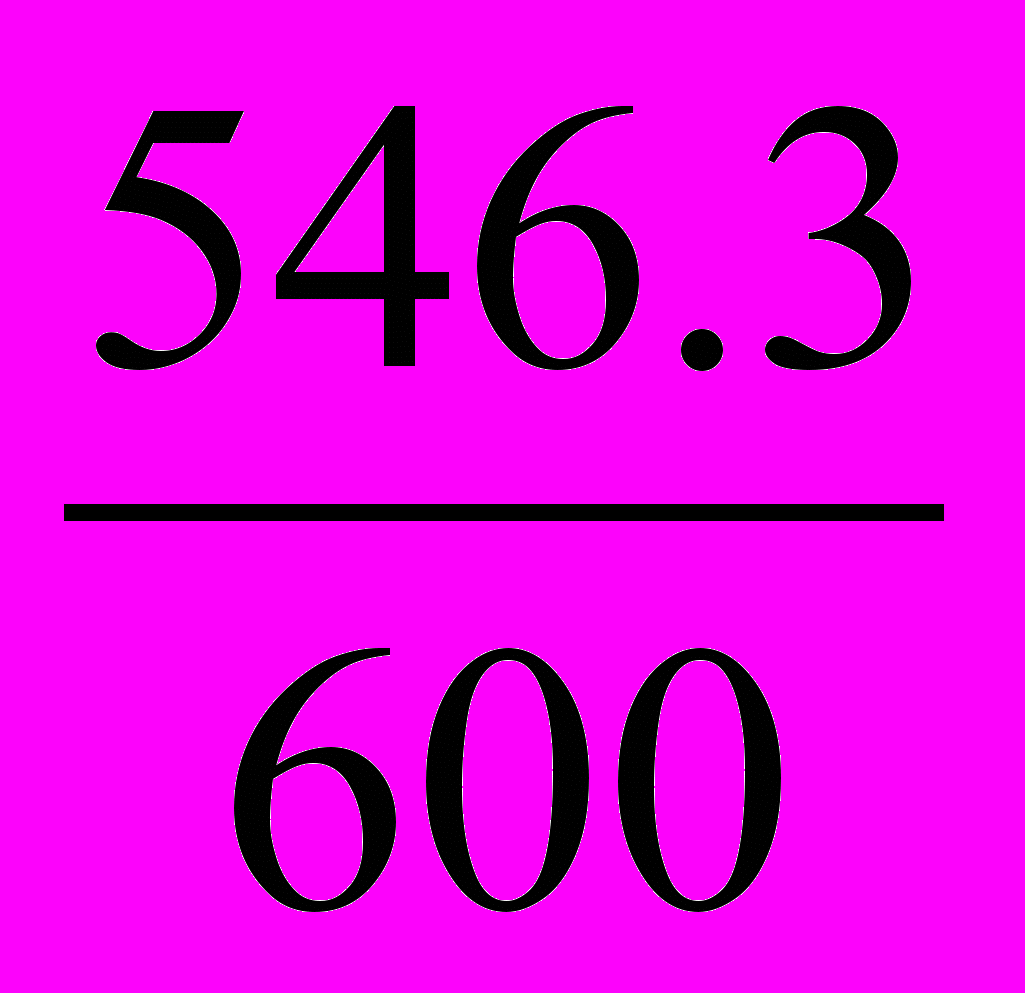0.911 или 91.1%, т.е. количество реализованных товаров снизилось на 8.9%.

Абсолютный прирост товарооборота за счет изменения количества

∆qpq = 546.3 – 600 = -53.7 тыс. руб.

3)Средний индекс цен

Jp = 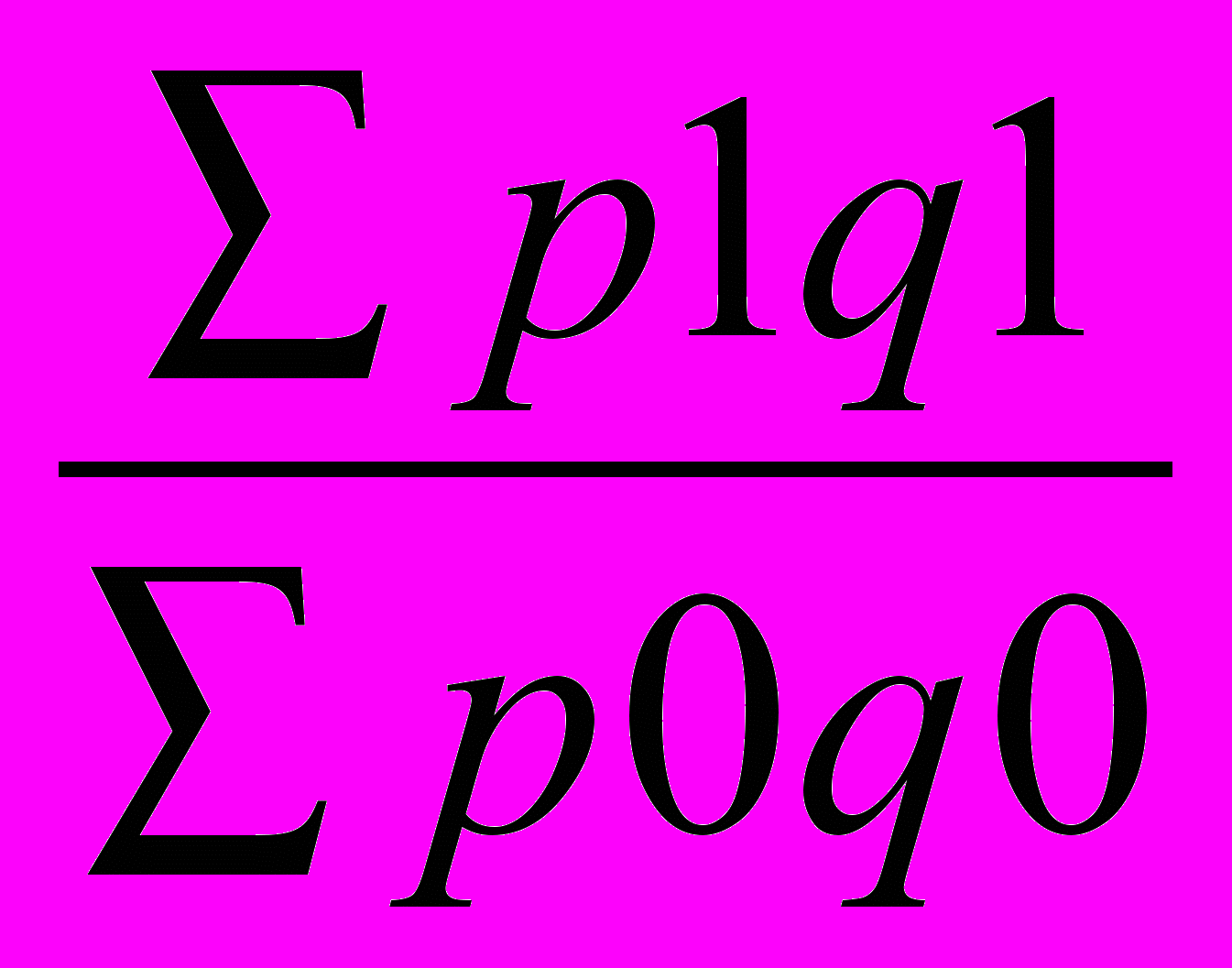= = 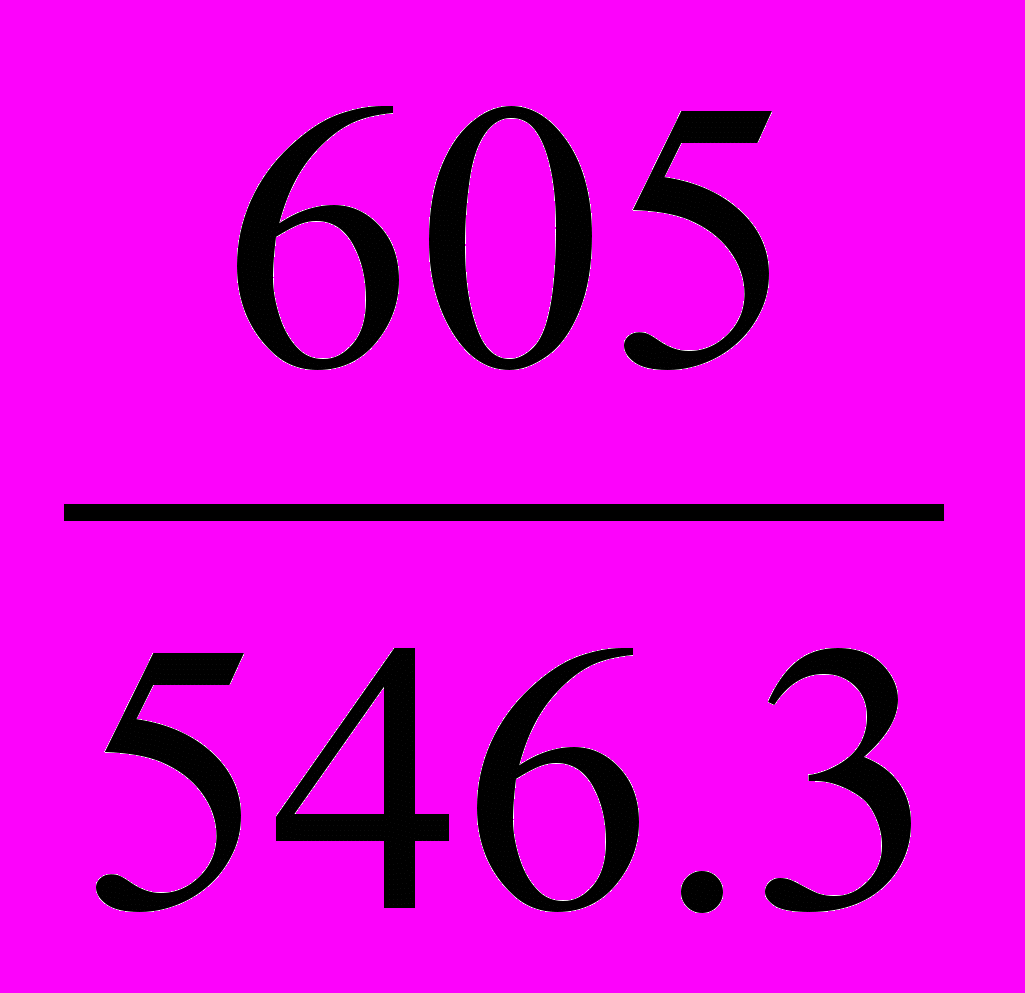1.107 или 110.7%, т.е. в среднем цены возросли на 10.7%

Абсолютное изменение товарооборота за счет изменения цен

∆ppq = 605-546.3 = +58.7 тыс. руб.

4)Средний индекс фактического объема товарооборота.

Jpq = 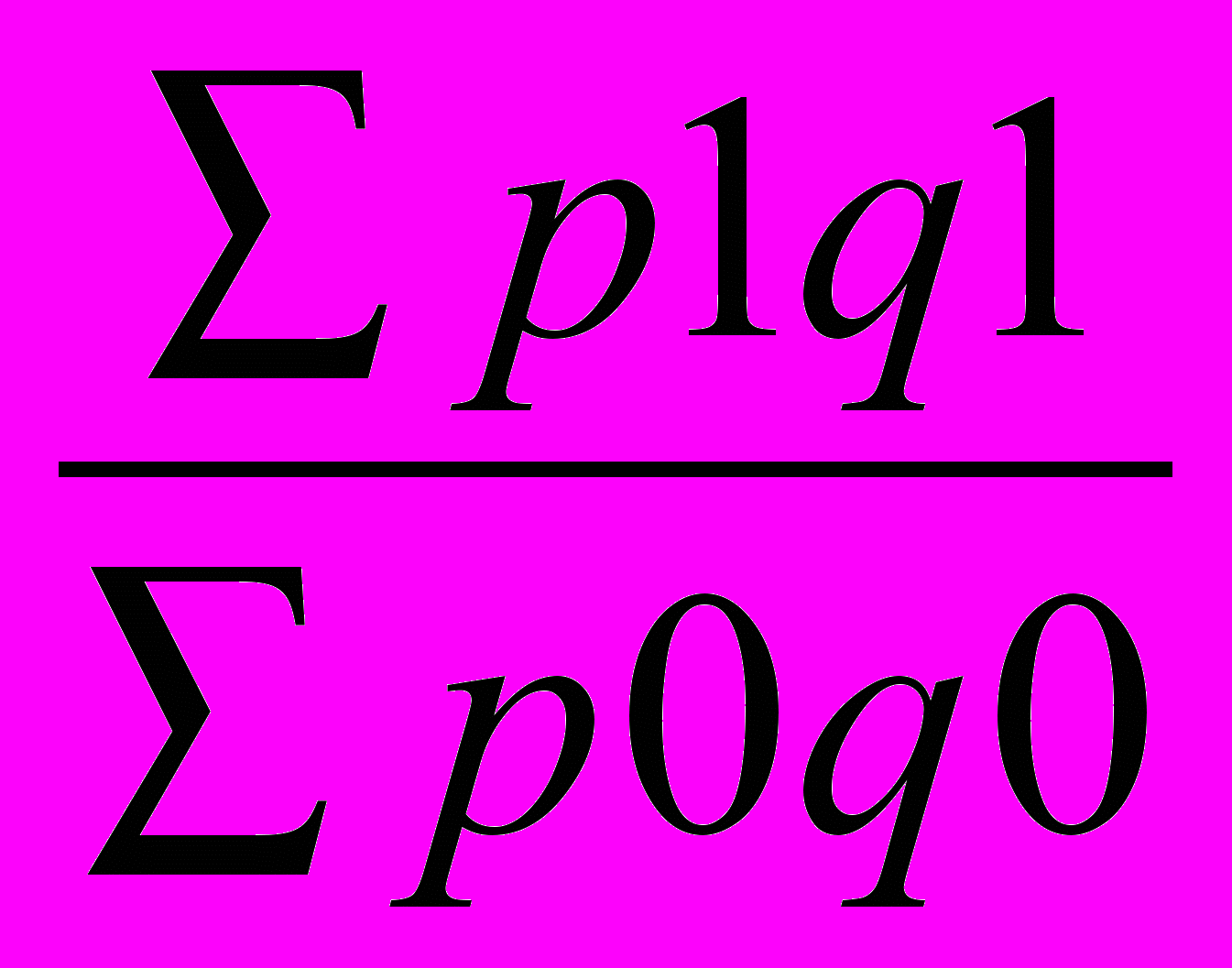= = 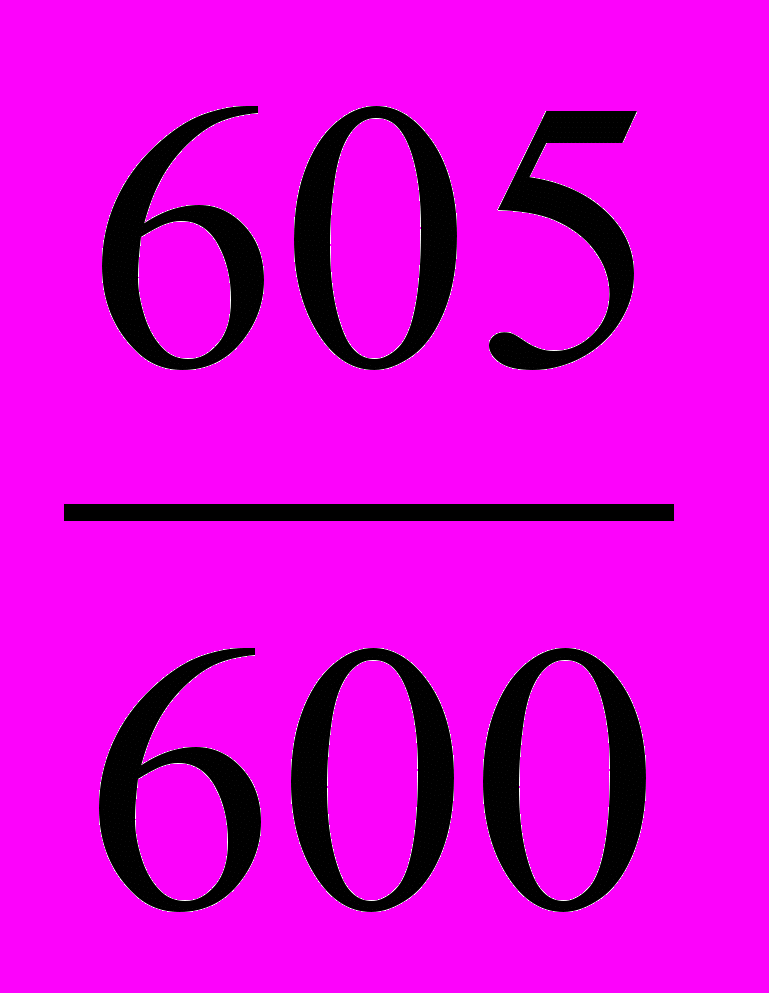1.008 или 100.8%, т.е. товарооборот возрос на 0.8%

Абсолютное изменение фактического объема товарооборота

∆pq = 605-600 = +5 тыс. руб.

Основы корреляционного анализа.

Задача. Имеются следующие данные о доле сортовых посевов пшеницы и ее урожайности по группе хозяйств.

№ хозяйств
1
2
3
4
5
6
7
8
9
10

Доля сортовых посевов

15

19

21

23

22

24

40

60

30

42

Урожайность ц. га
13
15
16
18
18
20
35
40
33
30

Исчислить:
    1. линейное уравнение связи между долей сортовых посевов и уровнем урожайности.
    2. Линейный коэффициент корреляции.
    3. Рассчитать ожидаемый уровень урожайности, если доля сортовых посевов составляет 50%.

Решение.

1) Так между долей сортовых посевов и урожайностью существует линейная регрессия, то необходимо построить уравнение прямой Ух = а + bх

2) для его построения необходимо найти параметры а и b, по формулам:

b = 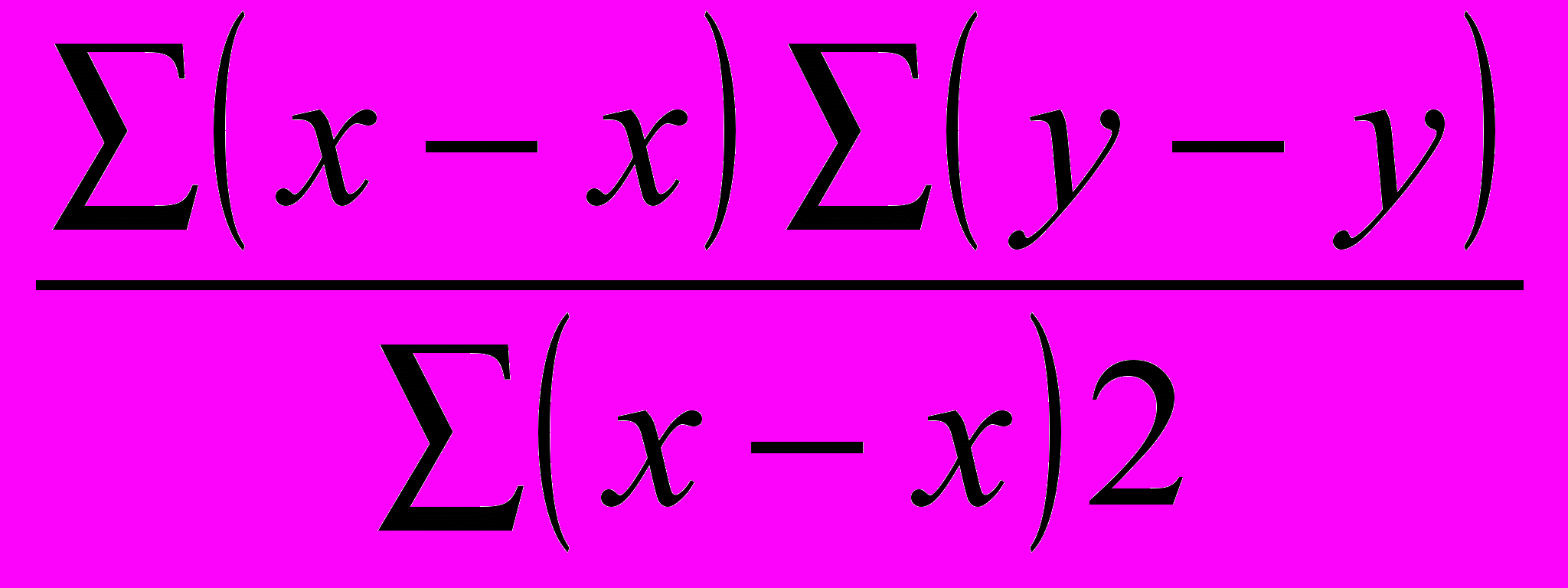; а = y - bx

№ хозяйств
Для сортовых посевов %, Х
Урожайность ц/га, У
(х-х)
(у-у)
(х-х)(у-у)
(х-х)2
Ух
(у-у)2

1
15
13
-14.6
-10.8
157.68
213.6
14.13
116.64

2
19
15
-10.6
-8.8
93.28
112.36
16.51
77.44

3
21
16
-8.6
-7.8
67.08
73.96
18.21
60.84

4
23
18
-6.6
-5.8
38.28
43.56
19.51
33.64

5
22
18
-7.6
-5.8
44.08
57.76
18.86
33.64

6
24
20
-5.6
-3.8
21.23
31.36
20.16
14.44

7
40
35
10.4
11.2
116.48
108.16
30.56
125.44

8
60
40
30.4
16.2
492.48
924.16
43.56
262.44

9
30
33
0.4
9.2
3.68
0.16
24.06
84.64

10
42
30
12.3
6.2
76.88
153.76
31.86
38.44

Итого
296
238
-
-
1111.2
1718.4
-
847.6

а)Определим среднюю долю сортовых посевов

х = 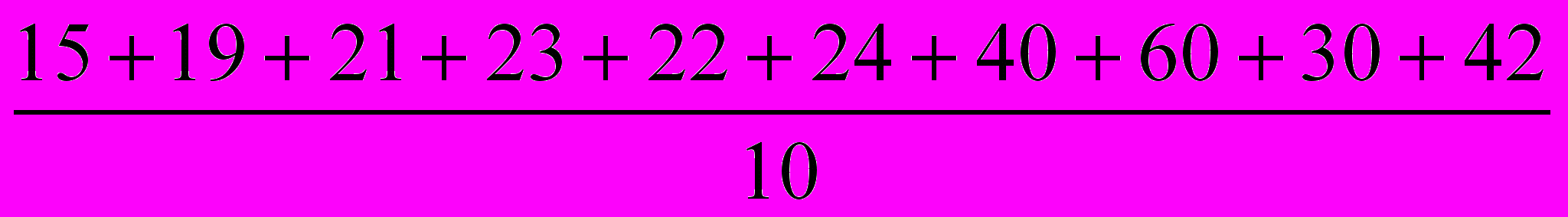= 29.6%

б)Определяем среднюю урожайность

у = 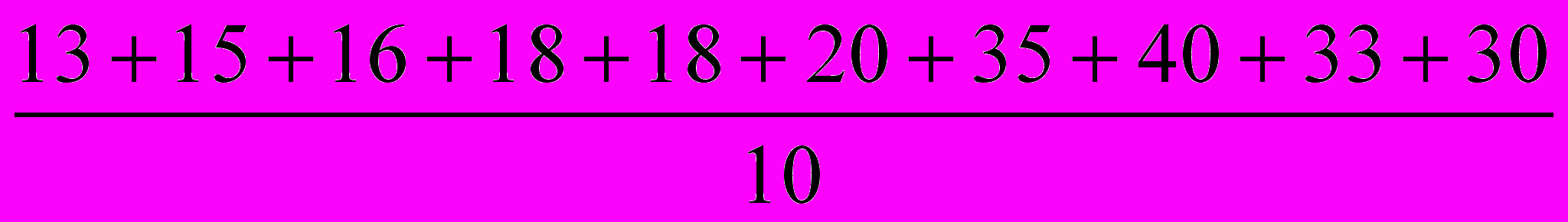= 23.8

тогда параметры

b = 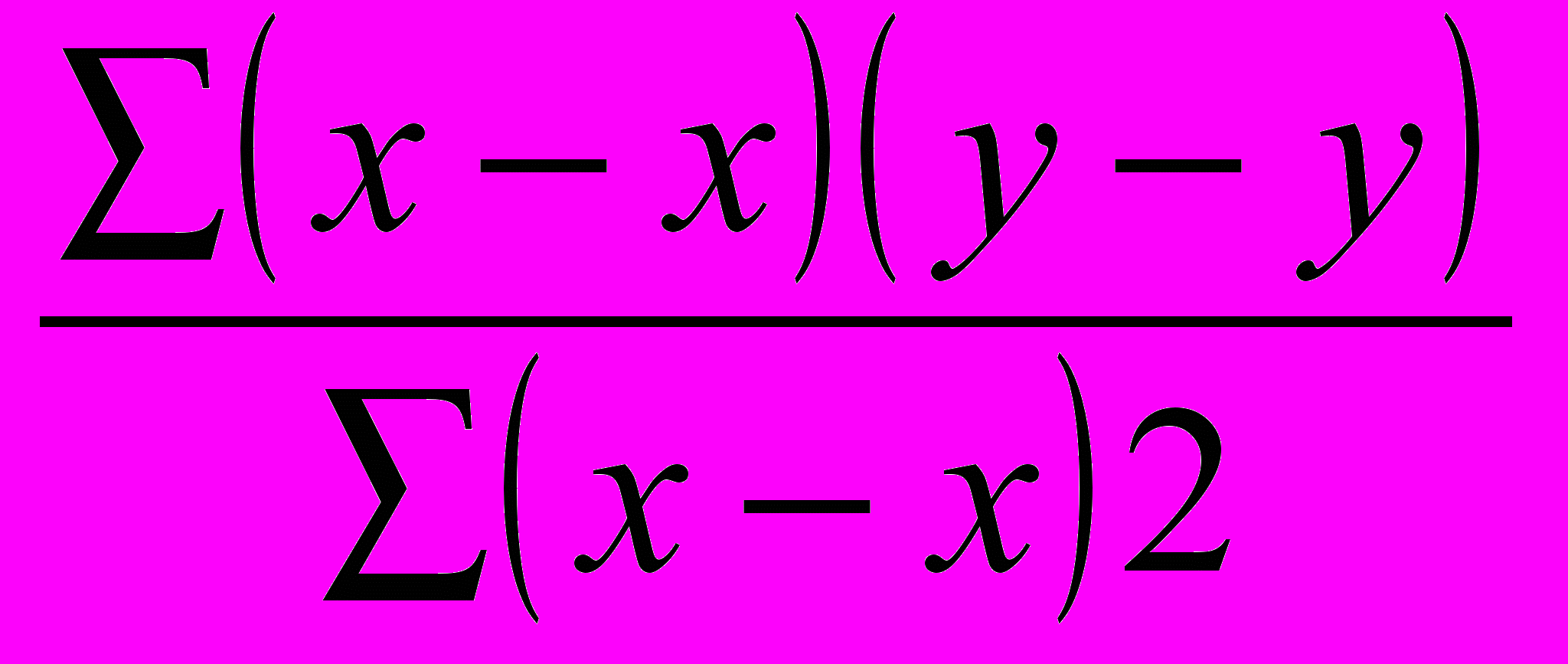= = 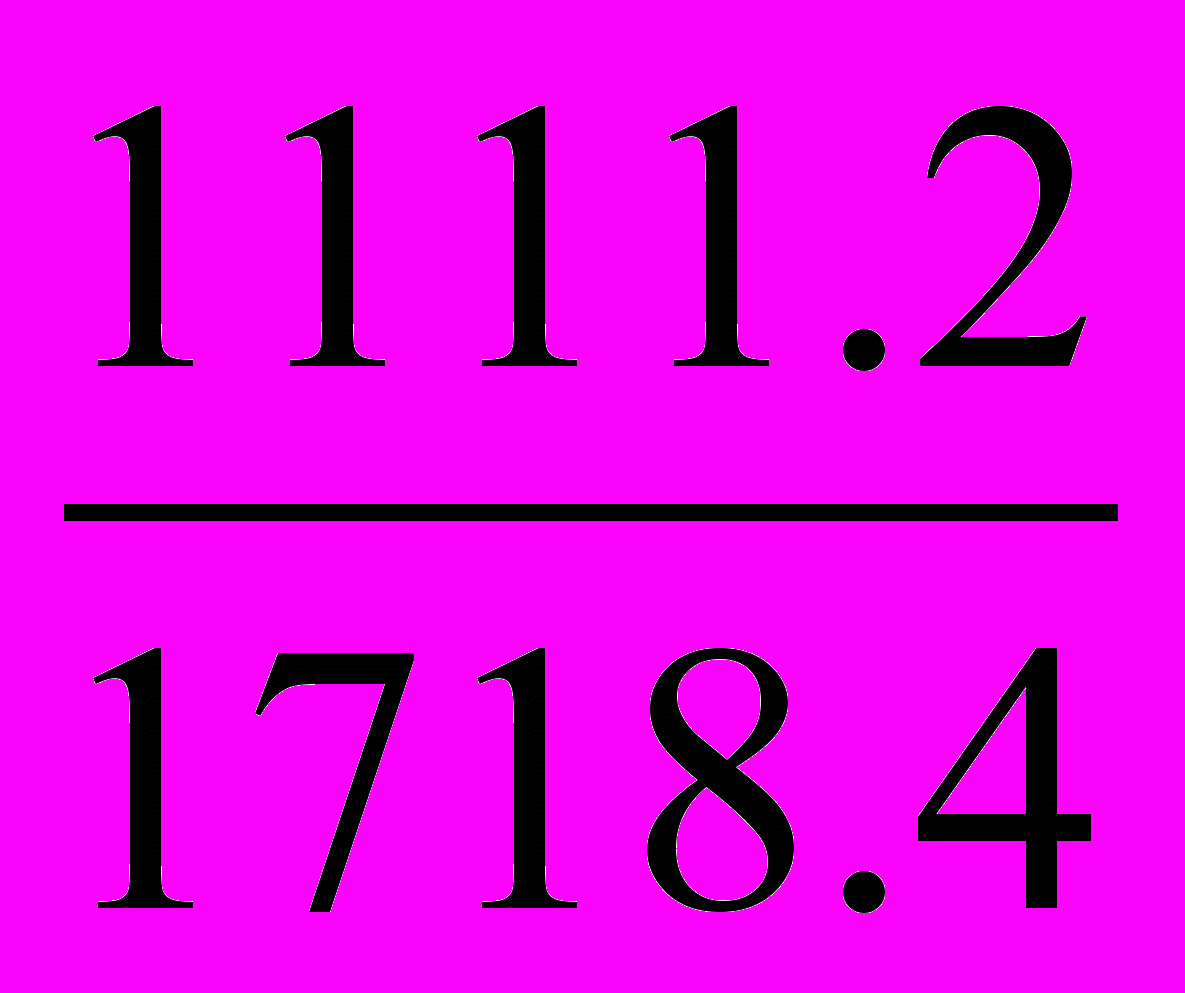0.65

означает, что каждый % увеличение сортовых посевов увеличивает урожайность на 0.65.

а = у - bх, а = 23.8 - 0.65 · 29.6 = 4.56

Составляем уравнение прямой. Ух = 4.56 + 0.65 · х

Теперь в полученной уравнение подставляем значение Х и рассчитываются точки выравнивания (теоретической линии).

Ух1 = 4.56 + 0.65 · 15 = 14.31 ц.

Ух2 = 4.56 + 0.65 · 19 = 16.91 ц.

Ух3 = 4.56 + 0.65 · 21 = 18.21 ц. и так далее.


3) Рассчитываем коэффициент линейной корреляции для измерения тесноты связи.

R =

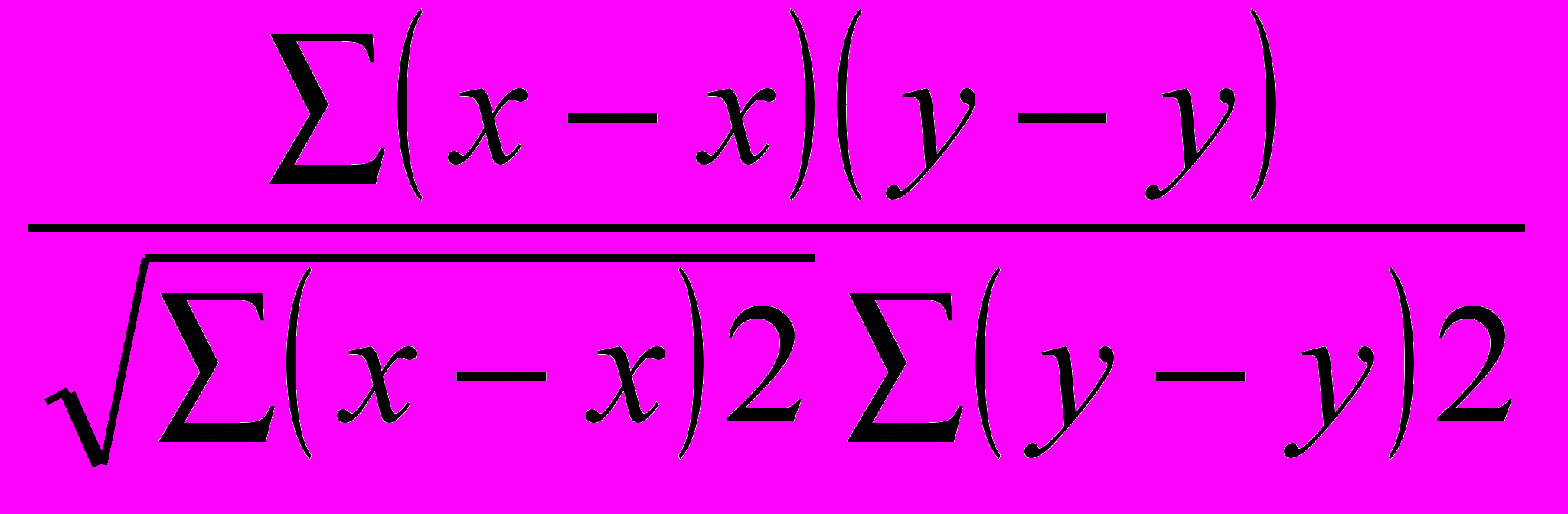
В таблице есть уже необходимые расчеты, следует дорасчитать (у-у)2 и подставляем результаты в формулу:

R = 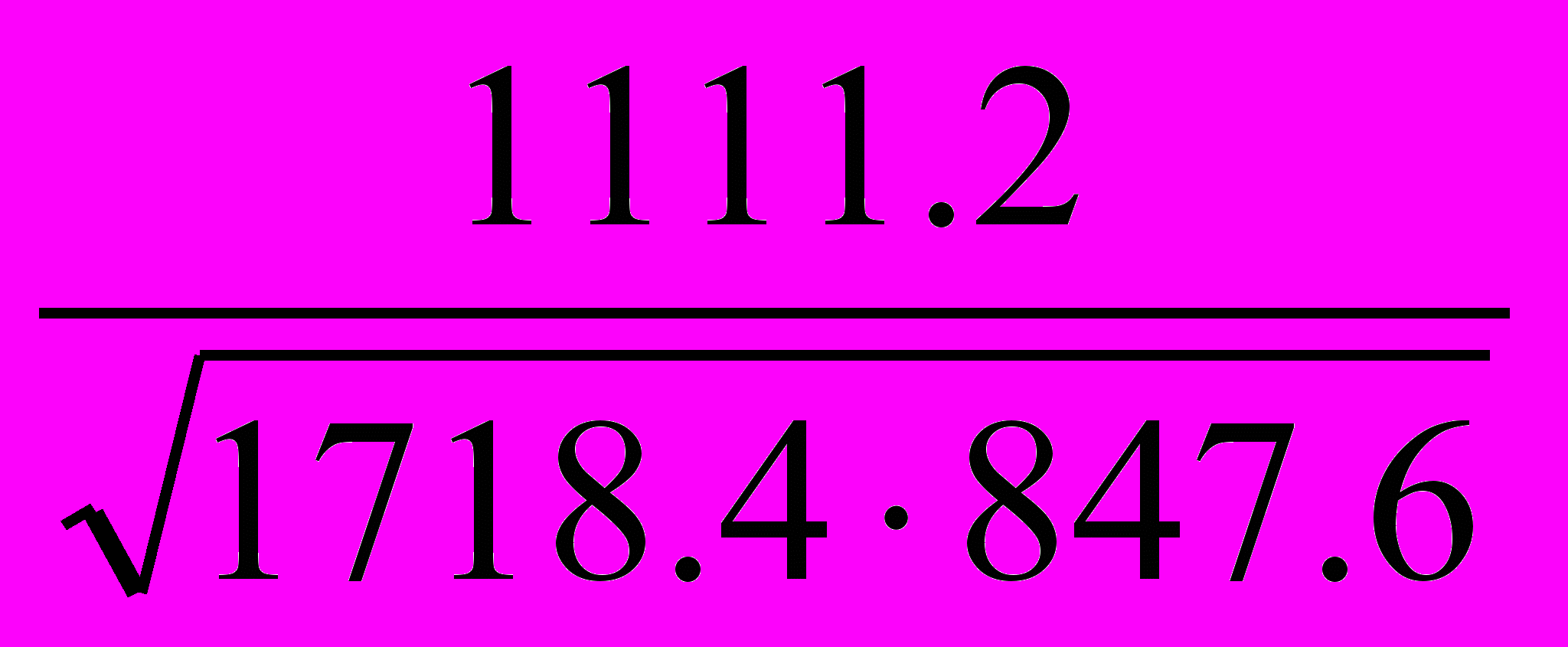= = 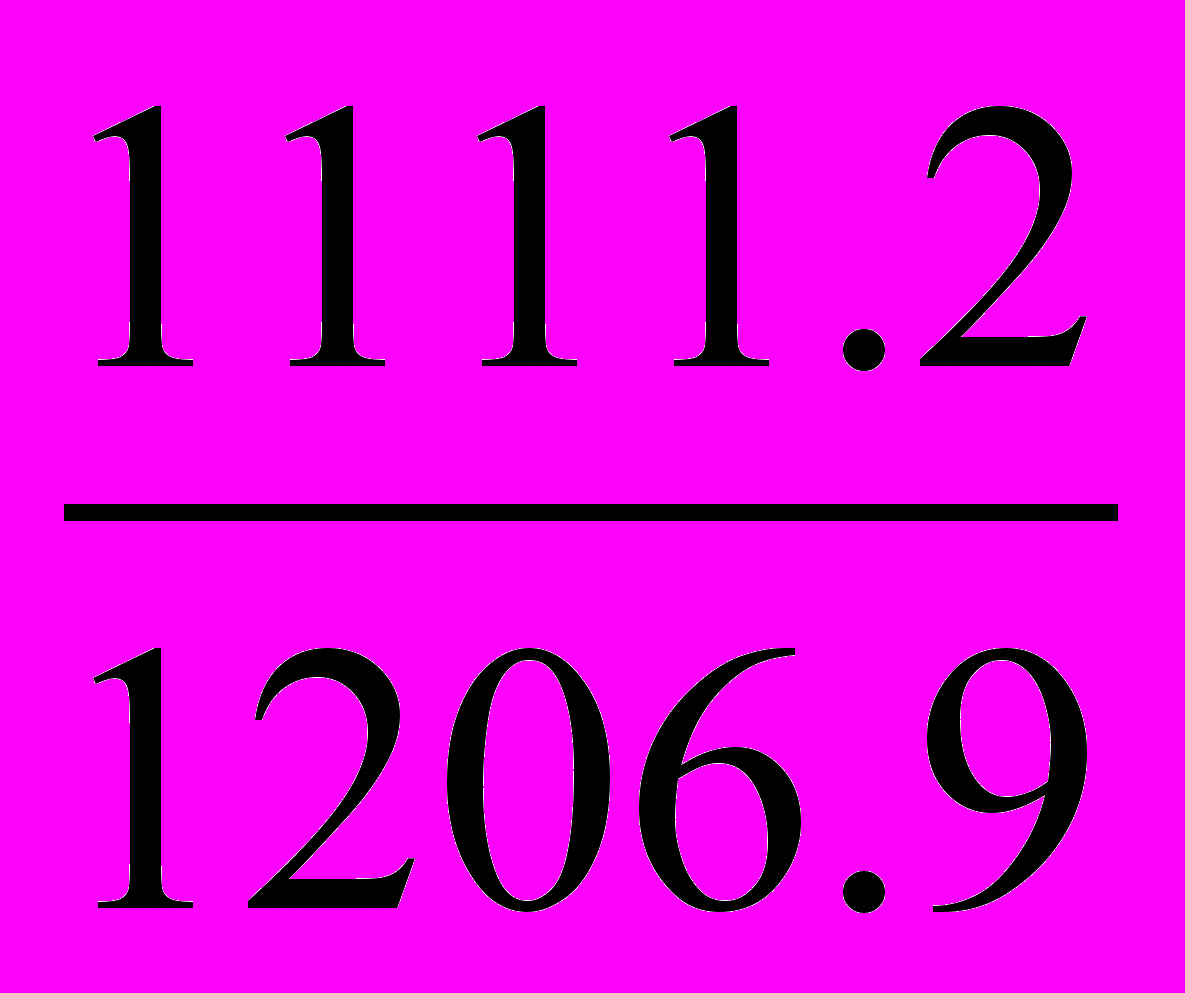0.921, т.е. на 92.1% урожайность зависит от доли сортовых посевов, связь очень тесная.

Выборочное наблюдение.

Задача. Методом механического отбора проведено 5% обследования веса расфасованного груза, в результате чего установлено:

Р =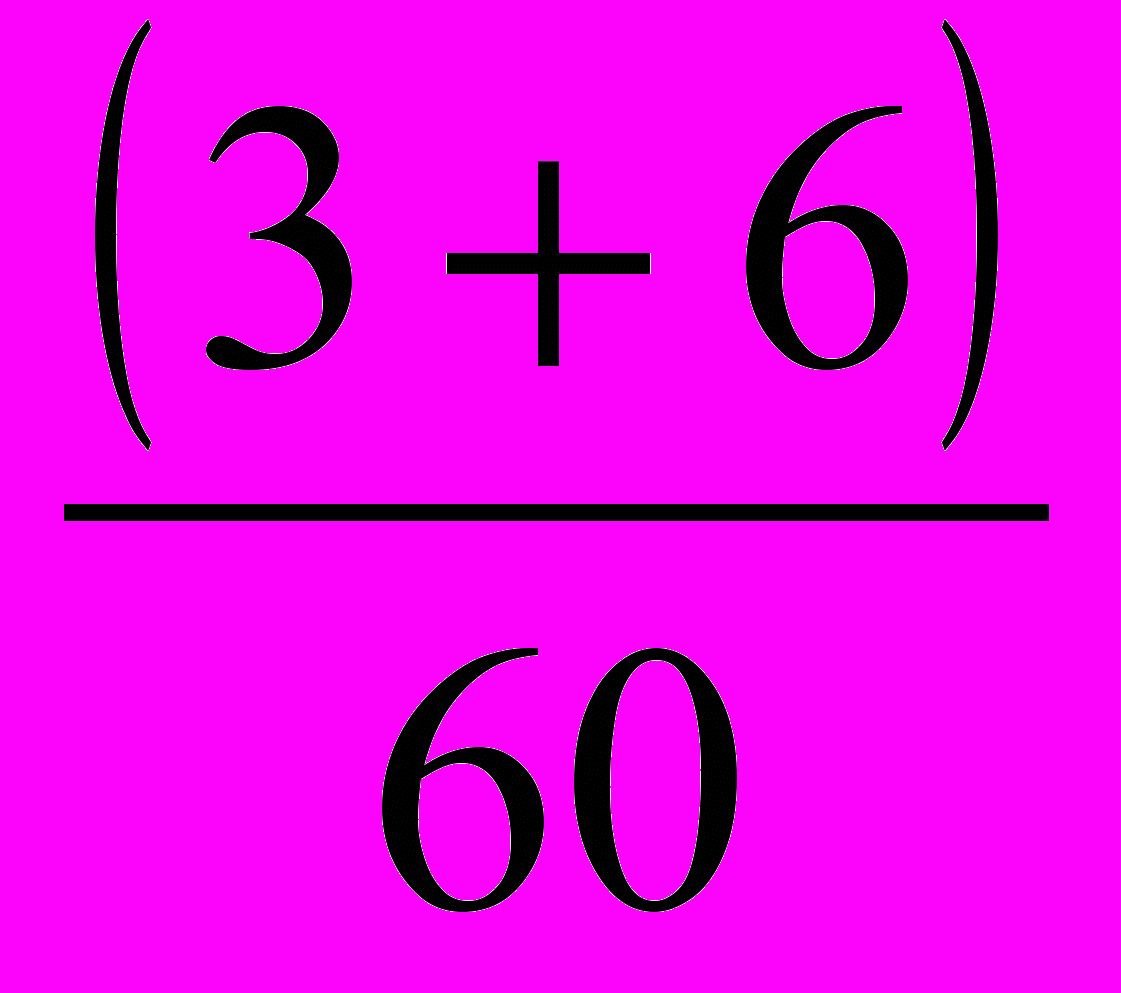= 0.15

(3+6) - число мешков муки вес которых до 50 кг.

Р - удельный вес этих 9 мешков в общем количестве.

3)С вероятностью 0.954 пределы, в которых может быть гарантирован средний вес мешка муки.

Доверительные пределы выборочной средней в генеральной совокупности определяется по формуле: х - ∆х ≤х0≤+∆х

Для этого следует рассчитать предельную ошибку выборки для средней при бесповторном отборе.

∆х =

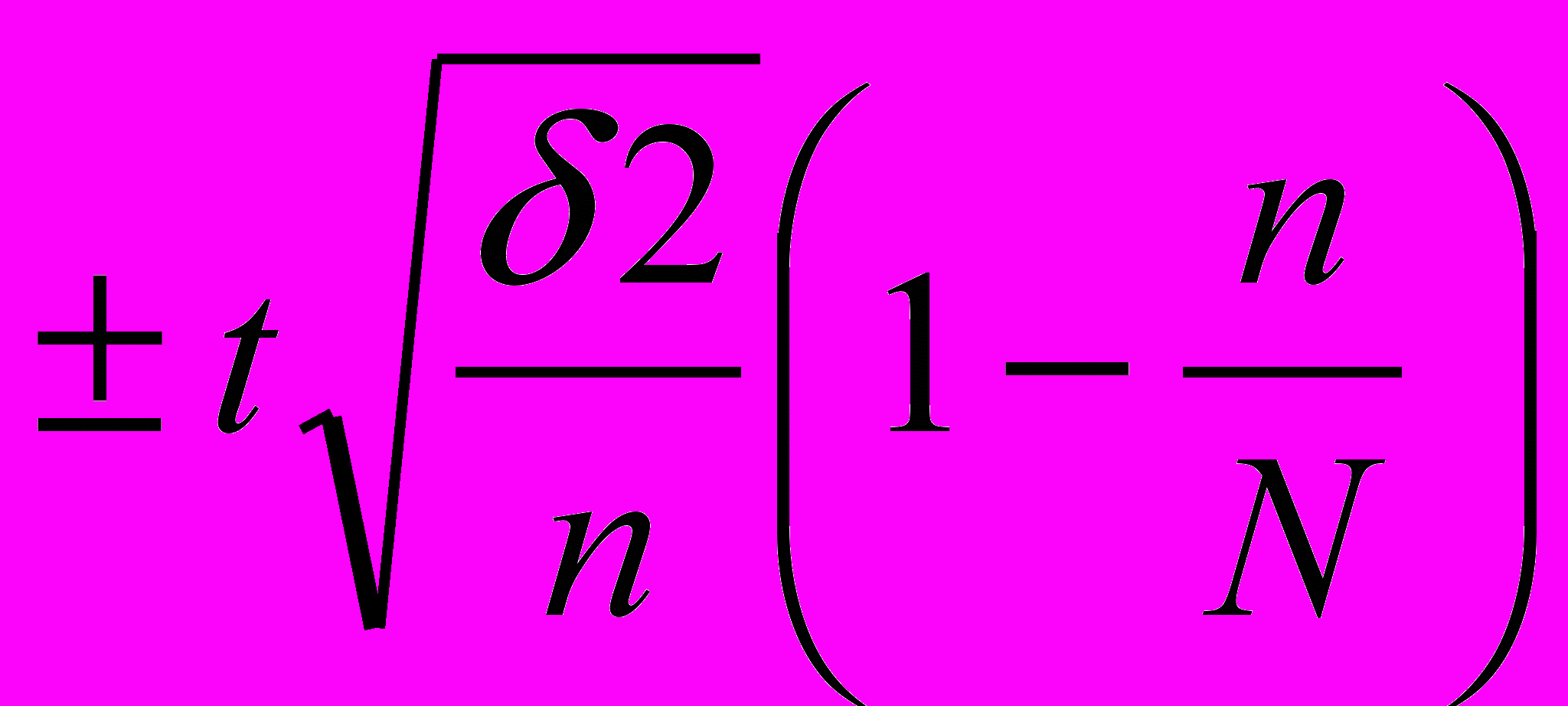
где t с вероятностью 0.954 определяется по таблице «Значения интеграла вероятностей закона нормального распределения»

при F(t) = 0.954 t=2

Определяем дисперсию по формуле

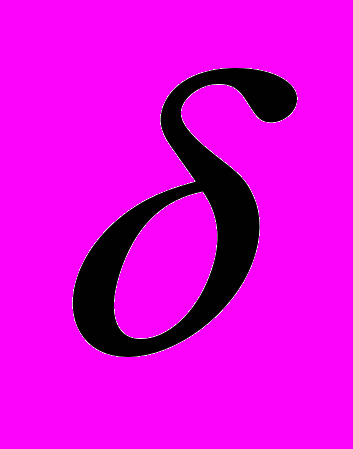2 = 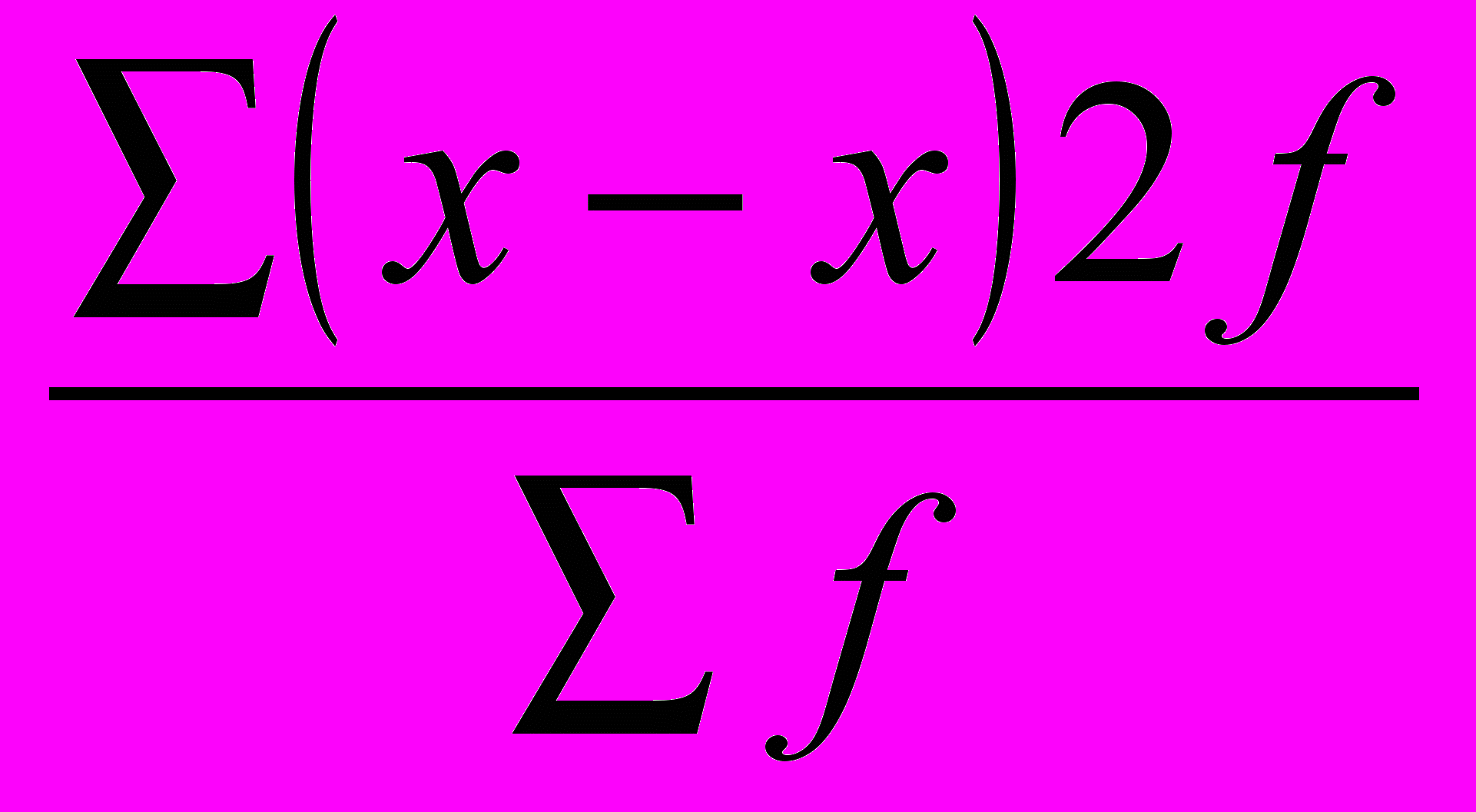= (расчеты занесем в таблицу).

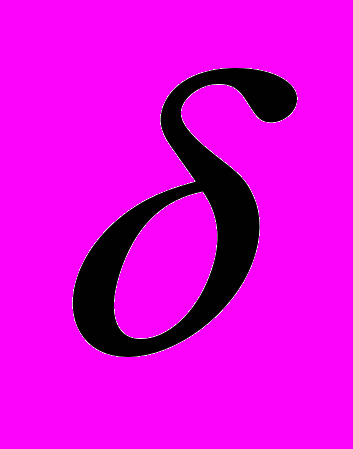2 = 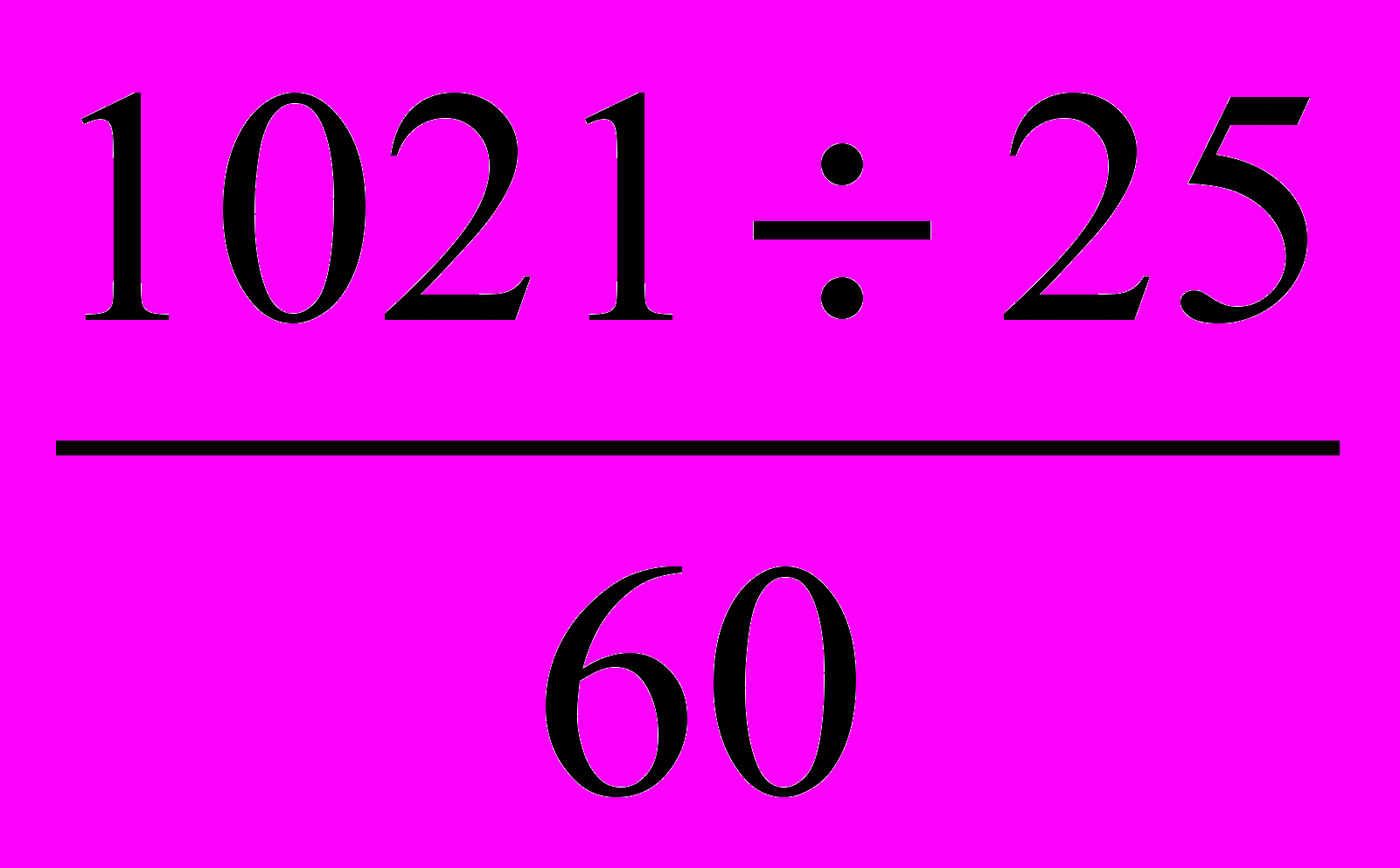= 17 n = 60 меш. При 5% выборке N = 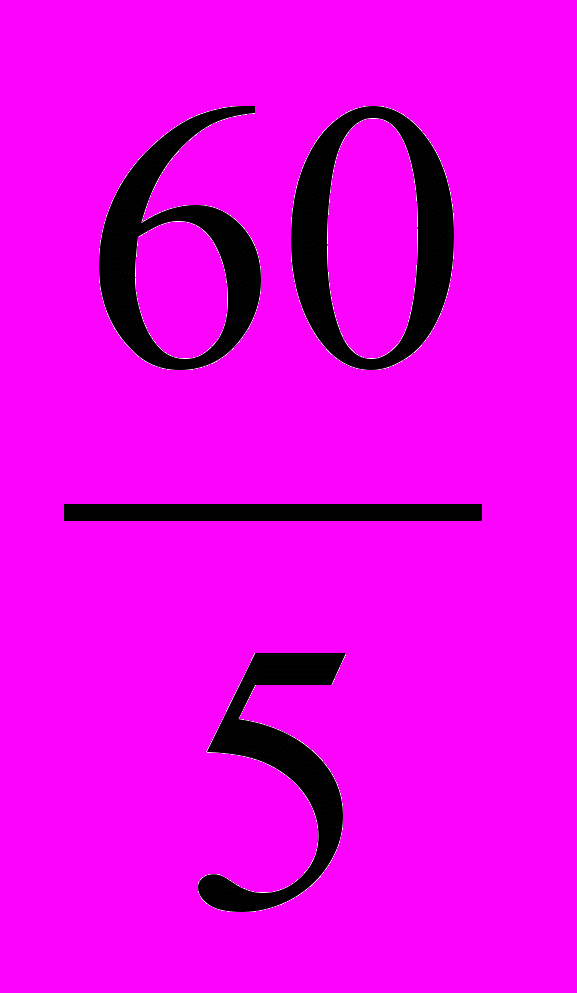· 100 = 1200 мешков.

Тогда ∆х = 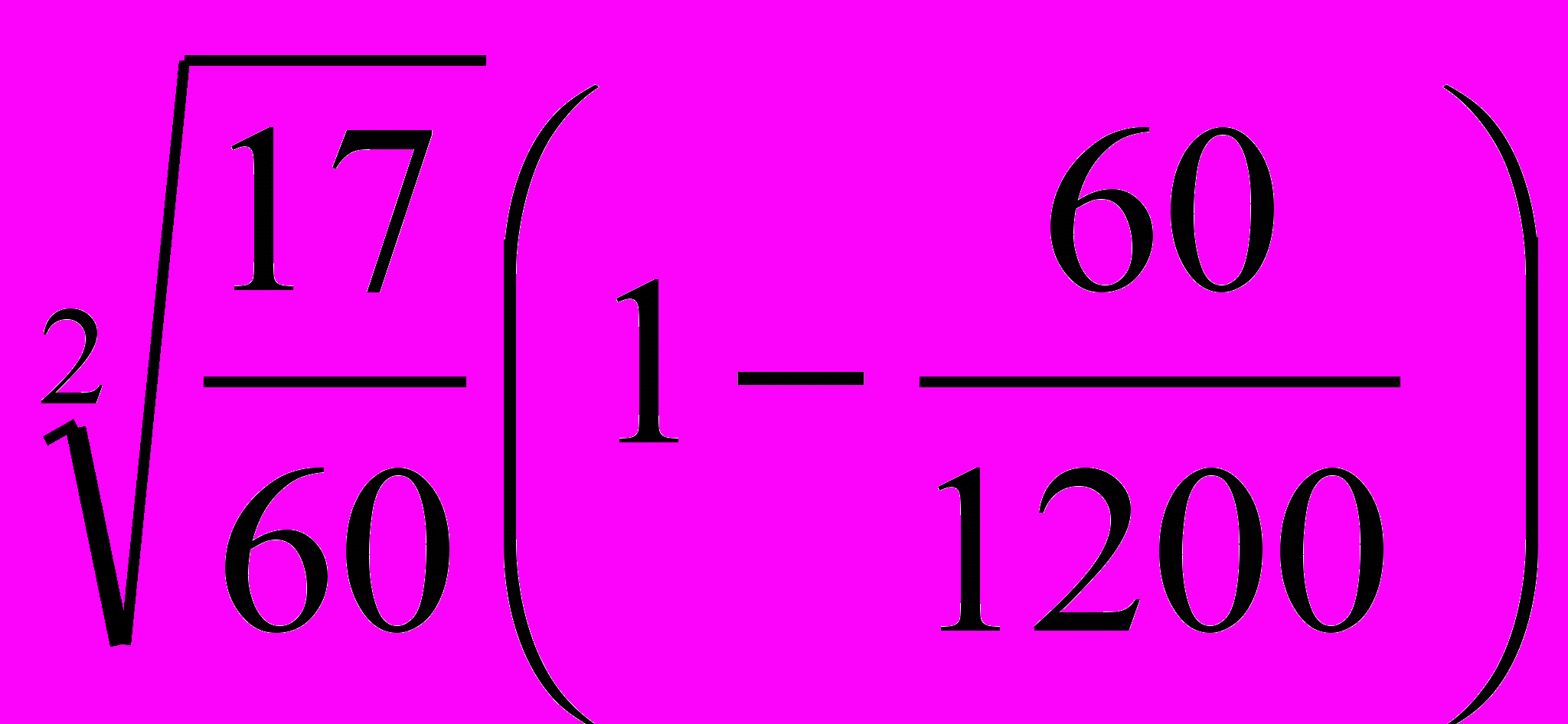= 1 кг

Доверительные пределы выборочной средней в генеральной совокупности запишется так.

52.71-1≤ х0 ≤52.75 + 1 51.75 кг≤ х0 ≤кг

Средний вес мешка муки в генеральной совокупности находится в пределах от 51.75 кг до 53.75 кг.

4)С вероятностью0.954 пределы, в которых находится доля мешков с весом менее 50 кг, определяется по формуле:

р-∆р≤ р0 ≤ р + ∆р.

Для этого рассчитываем предельную ошибку выборки по формуле

∆р =

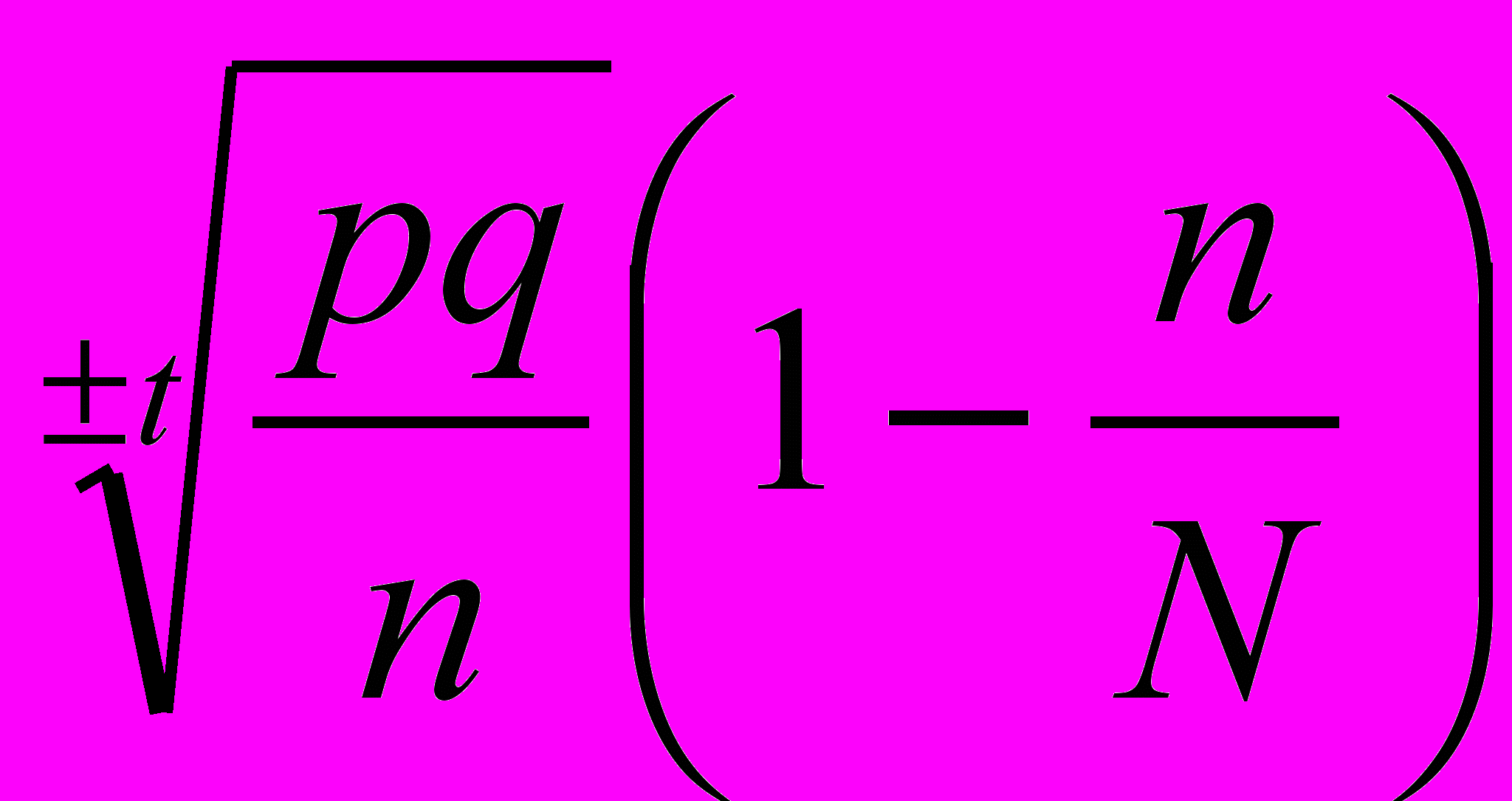
При F(t) = 0.954 t = 2 р = 0.15 q = 1-р = 1-0.15 = 0.85

∆р =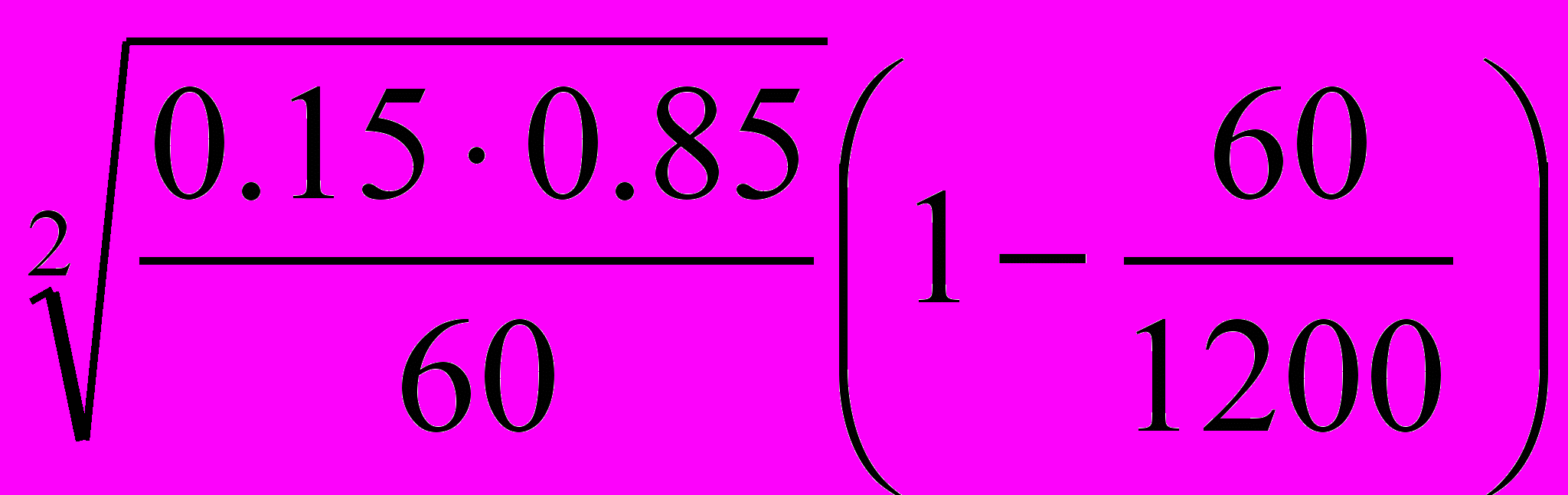= 0.09

Доверительные пределы доли мешков в генеральной совокупности составят

0.15-0.09 ≤ р0 ≤ 0.15+0.09 0.09≤ р0 ≤ 0.24 9% ≤ р0 ≤ 24%

т.е. с вероятностью 0.954 можно утверждать, что доля мешков с весом менее 50 кг находится в пределах от 9% до 24%.

5) Необходимый объем выборки, чтобы с вероятностью 0.997 ошибка выборки не превысила 0.5 кг.

n = 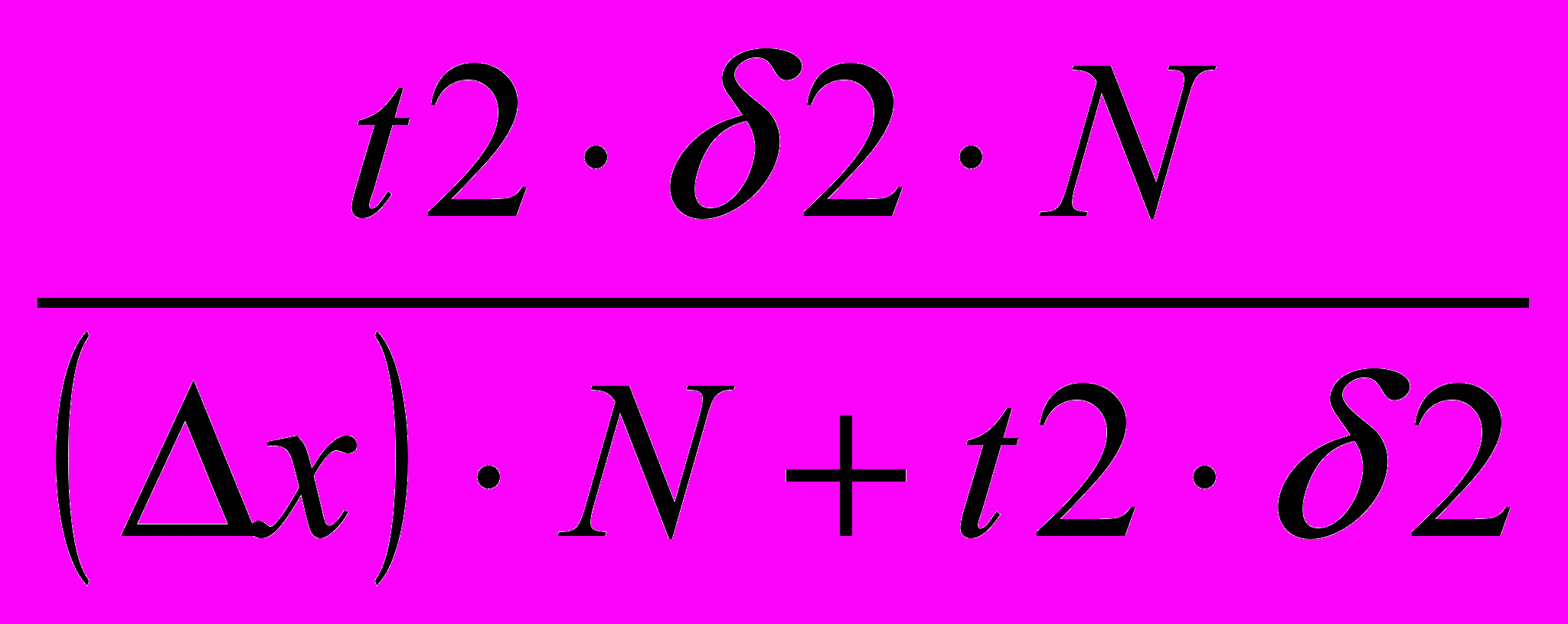, где, при F(t) = 0.997 ; t = 2.97; 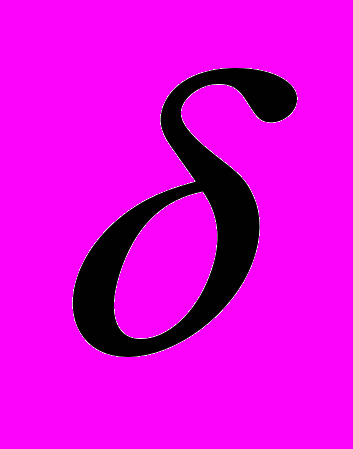2х = 17; N = 1200; ∆х = 0.8

n = 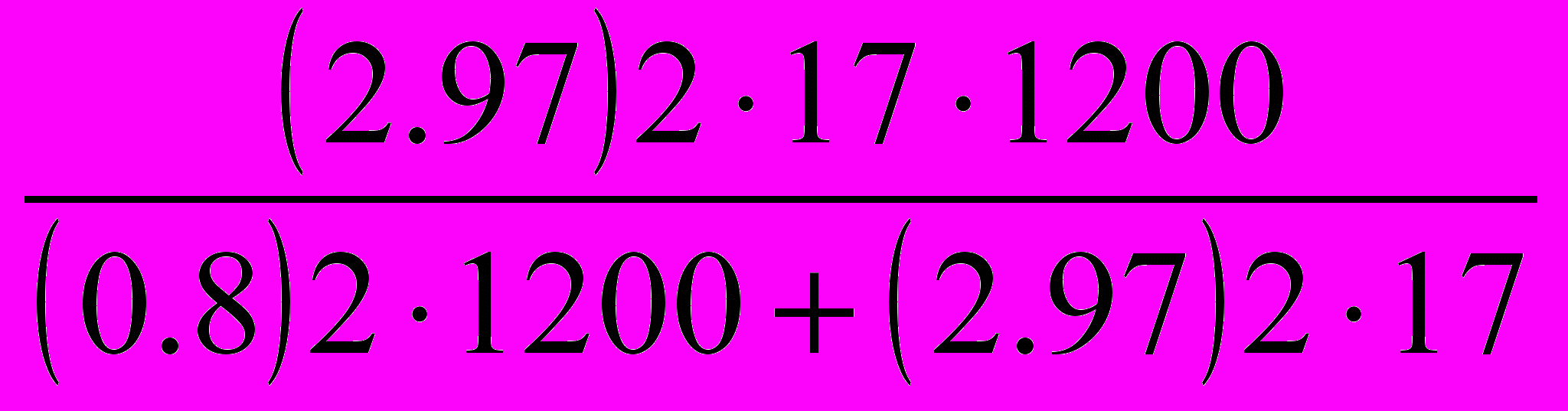= = 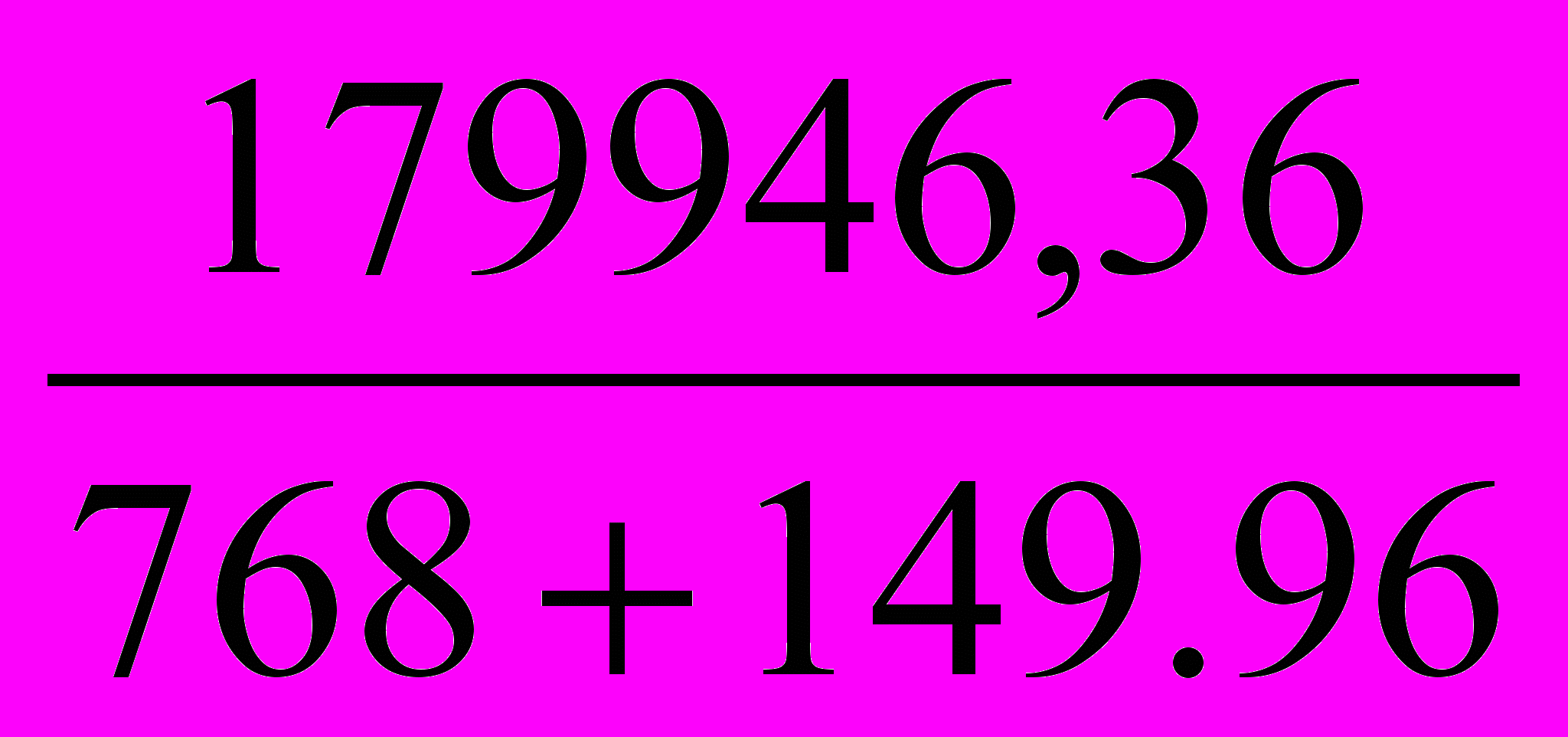196 мешков

Изучение курса заканчивается в группах по специальности 080110»Экономика, бухгалтерский учет и контроль» семестровым экзаменом, по специальности 080501 «Менеджмент»4-х часовой контрольной работой.