Теоретическая часть Глава

Вид материала

Подобный материал:

1 2 3 4 5

F(V) = ∫ e d t, где V =

2 П - ∞ σ

3. Логарифмическая нормальная распределения зависит от 2 – х параметров: математическое ожидание а и среднеквадратического отклонения σ случайной величины у (логарифмический доход)

а

= Е (у) = Е (ln х), σ² = var(у) = var (ln х)

Первый параметр а вычисляется по формуле а = ln х – σ² / 2

г

де х – средний денежный доход в целом по генеральной совокупности за отчетный период, который определяется по данным баланса денежных доходов и расходов населения.

Ряды распределения используются для установления характера распределения и выявления закономерностей развития явления.

2.2. Структурные средние

Наиболее распространенной формой статистических показателей, используемых в социально – экономических исследованиях, является средняя величина, представляющая собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени.

Сущность средней заключается в том, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные деятельностью случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагировать от индивидуальных особенностей, присущих отдельным единицам.

Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитывается по качественно однородной совокупности.

Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности.

В статистике применяются различные виды средних; арифметическая, гармоническая , квадратическая, геометрическая и структурные средние. Выбор формы средней зависит от исходных данных и содержания определяемого показателя.

Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. К таким показателям относятся мода и медиана.

Модальный доход М0 – это уровень дохода, встречающийся наиболее часто среди населения (имеющий наибольшую частоту).

В интервальных рядах распределения с равными интервалами мода вычисляется по формуле:

f мο – f мο - 1

Мο = x мο + i мο

(f мο – f мο – 1) + (f мο – f мο + 1)

где М0 – мода;

x мο – нижняя граница модального интервала;

i мο – величина модального интервала;

f мο – частота модального интервала;

f мο – 1 – частота интервала, предшествующая модальному;

f мο + 1- частота интервала, следующего за за модальным.

Модальный интервал определяется по наибольшей частоте.

Мода широко используется в статистической практике при изучении покупательского спроса, регистрации цен и т.д.

Медианный доход Ме – это уровень дохода, делящий совокупность на две равные части: половина населения имеет среднедушевой доход, не превышающий медианный, а другая половина – доход не меньше медианного.

Значение медианы вычисляется по формуле:

0,5 Σ f – S ме – 1

Ме = Х ме + i ме

f ме

где Ме – медиана;

Х ме – нижняя граница медианного интервала;

i ме – величина медианного интервала;

Σ f – сумма частот ряда;

S ме – 1 – сумма накопленных частот ряда, предшествующих медианному интервалу;

f ме – частота медианного интервала.

Мода и медиана в отличие от степенных средних являются конкретными характеристиками, их значение имеет какой – либо конкретный вариант в вариационном ряду.

Мода и медиана, как правило, являются дополнительными к средней характеристиками совокупности и используются в математической статистике для анализа формы рядов распределения.

Аналогично медиане вычисляются значения признака, делящие совокупность на четыре равные части – квартели, на пять равных частей – квинтели, на десять частей – децели, на сто частей – перцентели.

2.3. Ряды динамики

Процесс развития, движения социально – экономических явлений во

времени принято называть динамикой. Для отображения динамики строят ряды динамики. Они представляют собой ряды изменяющихся во времени значений статистического показателя, расположенных в хронологическом порядке. Процесс экономического развития изображается в них в виде совокупности показателей соответствующих периодов времени.

Составными элементами ряда динамики являются показатели уровней ряда y и показатели времени (годы, кварталы, месяцы, сутки) t.

Уровни ряда – это показатели, числовые значения которых составляют динамический ряд. Время – это моменты или периоды, к которым относятся уровни.

Построение и анализ рядов динамики позволяет выявить и измерить закономерности развития общественных явлений во времени. Выявление основной тенденции в изменении уровней, именуемой трендом, является одной из главных задач анализа рядов динамики.

Виды рядов динамики можно классифицировать по следующим признакам:

В зависимости от способа выражения уровней ряды динамики подразделяются на ряды абсолютны, относительных и средних величин;
В зависимости от того, выражают ли уровни ряда величину явления на определенные моменты времени или его величину за определенные интервалы времени, различают моментные и интервальные ряды динамики.

Моментным рядом называется ряд, уровни которого характеризуют состояние явления на определенный момент времени.

Интервальным рядом динамики называется ряд, уровни которого характеризуют размер явления за конкретный период времени.

Ряды динамики могут быть изображены графически. Графическое изображение позволяет наглядно представить развитие явления во времени и способствует проведению анализа уровней. Наиболее распространенным видом является линейная диаграмма. Также широко используется столбиковая диаграмма, секторная и др.

Важнейшим условием правильного построения рядов динамики является сопоставимость всех входящих в него уровней.

Статистические данные должны быть сопоставимы по территории (одни и те же границы территории).

Сопоставимость по кругу охватываемых объектов означает сравнение совокупности с равным числом элементов. При этом нужно иметь в виду, что сопоставляемые показатели динамического ряда должны быть однородны по экономическому содержанию и границам объекта, который они характеризуют.

Сопоставимость по времени регистрации для интервальных рядов

обеспечивается равенством периодов времени, за которые приводятся данные.

При определении уровней динамического ряда необходимо использовать единую методологию расчета сопоставимых цен.

Несопоставимость может возникнуть в следствии изменения единиц измерения или единиц расчета. Нельзя сравнивать цифры о производстве зерна, если за один год одни представлены в тоннах, а другие - в центнерах.

Для того, чтобы привести ряды динамики к сопоставимому виду, можно прибегнуть к приему, называемому смыкание рядов динамики. Под смыканием понимается объединение в один ряд двух или несколько рядов динамики, уровни которого исчислены по разной методологии или разным территориальным границам.

Анализ скорости и интенсивности развития явления во времени осуществляется с помощью статистических показателей, которые получаются в результате сравнивания уровней между собой. К таким показателям относятся: абсолютный прирост, темп роста и прироста, абсолютное значение одного процентного прироста. При этом принято сравниваемый уровень сравниваемый уровень называть отчетным, а уровень, с которым происходит сравнение – базисным.

Абсолютный прирост (цепной) Абсолютный прирост(базисный)

Δ у ц = у i – у i – ı (1) Δ у б = у i – у 0 (2)

где у i – уровень сравниваемого периода;

у i – ı - уровень предшествующего периода;

у 0 – уровень базисного периода.

Темп роста (цепной) Темп роста (базисный)

у i у i

Т

р ц = * 100 (3) Т р б = * 100 (4)

у i – ı у 0

Абсолютное значение 1 % прироста

у i – ı

А % = (5)

100

Для обобщающей характеристики определяются:

Средний уровень ряда:

∑ у

У = (6)

n

С

реднемесячный абсолютный прирост: ∑ ∆ у ц

∆ у ц = (7)

n

С

реднемесячный темп роста и прироста:

Т р = К р · 100 (8) Т пр = Т р – 100 (9)

Р А С Ч Е Т Н А Я Ч А С Т Ь

Задание 1

По материалам 1% - механической выборки домашних хозяйств региона получены следующие данные о распределении домохозяйств по величине среднедушевых доходов (табл. 1)

Таблица 1

Распределение домохозяйств по величине среднедушевых доходов

Среднедушевые денежные доходы в месяц, руб.	Число домохозяйств
до 1000	184
1000 - 2000	916
2000 - 3000	280
3000 - 4000	140
свыше 4000	80

По данным обследования определить:

Структуру домохозяйств по среднедушевому доходу.
Среднедушевой доход домашних хозяйств.
Показатели вариации: дисперсию, среднее квадратическое отклонение, коэффициент вариации. Оцените качество (однородность) совокупности.
Моду, медиану, первый и девятый децили.
Рассчитайте децильный коэффициент дифференциации доходов.
С вероятностью 0,954:

а) возможные пределы среднедушевого дохода домашних хозяйств региона;

б) возможные пределы удельного веса домашних хозяйств, имеющих доход менее 2000 руб.

Сделайте выводы.

Решение

Построим разработочную таблицу 2.

Таблица 2

Разработочная таблица

Среднедушевые денежные доходы в месяц, руб.	Число домохозяйств	Удельный вес к % в итоге

до 1000	184	11,5
1000 - 2000	916	57,25
2000 - 3000	280	17,5
3000 - 4000	140	8,75
свыше 4000	80	5
ИТОГО	1600

Вывод: Из данных таблицы следует, что наибольший число домохозяйств 1196 или 74,3 % имеет среднедушевой денежный доход от 1000 – 3000; 220 или 13,75 % имеют среднедушевые доходы свыше 3000 рублей и наименьшее число 11,5 % имеют среднедушевые денежные доходы от 0 – 1000 рублей.

1. На основании таблицы 2 определим структуру домохозяйств по среднедушевому доходу.

до 1000 – 184 /1000 * 100 = 11,5

1000 – 2000 – 916 / 1600 * 100 = 57,25

2000 – 3000 – 280 / 1600 * 100 = 17,5

3000 – 4000 – 140 / 1600 * 100 = 8,75

свыше 4000 – 80 / 1600 * 100 = 5

Из данных таблицы 2 следует, что наибольший вес домохозяйств 1196 или 74,25 % имеют среднедушевой доход от 1000 до 3000 рублей.

Для выполнения пункта 2, 3 построим разработочную таблицу 3.

Таблица 3

Разработочная таблица

Среднедушевой денежный доход, руб.	Число домохозяйств, f	Середина интервала, xi	xi f	(xi – x)²	(x – x)² f
до 1000	184	500	92000	1918225	352953400
1000 - 2000	916	1500	1374000	148225	135774100
2000 - 3000	280	2500	700000	378225	105903000
3000 - 4000	140	3500	490000	2608225	365151500
свыше 4000	80	4500	360000	6838225	547058000
ИТОГО	1600	12500	3016000		1506840000

. Среднедушевой доход домашних хозяйств.

х = ∑ xi f 3016000

∑ f = 1600 = 1885 руб.

3. Дисперсия.

σ

² = Σ (х – х)² f 1506840000

Σ f = 1600 = 941775

Среднее квадратическое отклонение.

σ

= σ² = 941775 = 970,45 руб.

Коэффициент вариации.

σ 970,45

V = х * 100 = 1885 * 100 = 51,48 = 52 %

Коэффициент вариации равный 52 % говорит о том, что ряд распределения домохозяйств по среднедушевому доходу не однороден, а среднедушевой доход 1885 рублей – не типичен, для данного ряда распределения.

4. Для того, чтобы определить моду и медиану построим разработочную таблицу 4:

Таблица 4

Разработочная таблица

Среднедушевой денежный доход в месяц, руб.	Число домохозяйств	Сумма накопленных частот, S
до 1000	184	1100
1000 - 2000	916	1196
2000 - 3000	280	420
3000 - 4000	140	220
свыше 4000	80

f мο – f мο - 1

Мο = x мο + i мο

(f мο – f мο – 1) + (f мο – f мο + 1)

По наибольшей частоте признака определяем модальный интервал. Наибольшее число домохозяйств 916 –имеют среднедушевой денежный доход в интервале 1000 – 2000, который и является модальным.

916 - 184

М

ο = 1000 + 1000 · = 1535,088 руб.

(916 - 184) + (916 - 280)

Медиана.

0,5 Σ f – S ме – 1

М

е = Х ме + i ме

f ме

Наибольшее число домохозяйств 916 – имеют среднедушевой доход в интервале 1000 – 2000, это и есть медианный интервал.

0,5 * 1600 - 184

М

е = 2000 + 1000 = 2672,489 руб.

916

Нижний дециль определяется по формуле:

Σ f / 10 – S d1 - 1

d

1 = х d1 + i d1

f d1

1600 / 10 - 0

d

1 = 0 + 1000 = 869,565 руб.

184

Верхний дециль определяется по формуле:

9 Σ f / 10 – S d1 - 1

d

9 = х d9 + i d9

f d9

9 * 1600 / 10 - 1100

d

9 = 2000 – 1000 = 3214,286 руб.

280

5. Децильный коэффициент дифференциации доходов составляет:

d9 3214,286

К

d = = = 3,7 раза.

d1 869,565

Децильный коэффициент дифференциации доходов населения показывает, что среднедушевой денежный доход, выше уровня которого имели доход выше 10% населения (высокодоходная группа), в анализируемом году превышал в 3,7 раза уровень дохода, ниже которого имели доход 10% населения(низкодоходная группа).

а) х – Δ х < х < х + Δ х

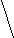
х = t σ² * (1 – n / N)

n

Δ

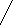
х = 2 941775 * 0,99 / 1600 = 48 руб.

Σ х i 3016000

х

= = = 1885 руб.

Σ f 1600

1

885 – 48 <х< 1885 + 48

1837 < х <1933

Таким образом можно утверждать, что среднедушевой доход домашних хозяйств будет находиться в пределах от 1837 до 1933 рублей.

б) Удельный вес домохозяйств имеющих доход менее 2000 рублей находится в пределах:

w – Δ w < p < w + Δ w

N 184 + 916

w

= = = 0,688

n 1600

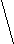w (1 – w)

Δ

w = t * (1 – n / N)

n

Δ

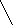w = 2 0,688 (1 – 0,688) * 0,99 / 1600 = 0,023

0,688 – 0,023 < р < 0,688 + 0,023

0,665 < р < 0,711

66,5 % < р < 71,1 %

Таким образом с вероятностью 0,954 можно утверждать, что удельный вес домохозяйств имеющих доход менее 2000 рублей находится в пределах 66,5 % < р <71,1 %.

Blog

Теоретическая часть Глава

F(V) = ∫ e d t, где V =