Лекция Элементы специальной теории относительности в курсе физики средней школы
| Вид материала | Лекция |
- Методика изучения электродинамики в школьном курсе физики раздел «электродинамика», 808.93kb.
- Методика изучения прямолинейного равномерного движения в курсе физики полной средней, 19.55kb.
- Всемирный Год Физики: переосмысление относительности, 146.79kb.
- Урок физики Учитель физики Долгова С. А. Тема: Элементы Специальной теории относительности, 105.07kb.
- Курс 1 семестр 2 количество кредитов, 29.05kb.
- Элементы специальной (частной) теории относительности, 301.45kb.
- Дударева Татьяна Викторовна Формирование и развитие основных понятий геометрической, 514.99kb.
- Лекция №1 Содержание курса физики система научного знания, 539.84kb.
- Лекция №1 Содержание курса физики система научного знания, 539.95kb.
- Физика изучение физики в старшей школе на профильном уровне направлено на достижение, 200.25kb.
Лекция 4. Элементы специальной теории относительности в курсе физики средней школы
§ 1. Пространство и время в ньютоновской механике
Теория относительности – это физическая теория, рассматривающая пространственно-временные закономерности, справедливые не только для механических, но и для других физических процессов. Основным объектом изучения данной теории – свойства пространства и времени. Теорию относительности условно подразделяют на общую теорию и частную (специальную) теорию относительности.
Общая теория относительности или теория тяготения – наиболее общая теория пространства и времени, так как согласно этой теории свойства пространства и времени в данной области определяются действующими в ней полями тяготения. Специальная теория относительности изучает свойства пространства и времени, справедливые с той точностью, с какой можно пренебречь действием тяготения.
В средних общеобразовательных учреждениях изучаются элементы специальной теории относительности (СТО). Сфера применимости СТО огромна. Её идеи и результаты пронизывают все «здание» современной физики, касаются вопросов происхождения, развития и структуры звезд, галактик и Вселенной в целом.
Возникновение и содержание физических теорий в той или иной степени связаны с ньютоновской механикой. в курсе физики средней школы. Идеи и положения СТО, кардинально изменившие представления о пространстве, времени и движении, могут быть поняты только в сравнении с соответствующими классическими воззрениями. Рассмотрим особенности ньютоновской модели описания движения
Классическая механика – исторически первая физическая теория. Система ее основных положений была сформулирована И. Ньютоном во второй половине 17 века. Физическое пространство, как идеальный, теоретический объект представлено в классической механике математическим пространством евклида. Оно в абстрактной форме выражает свойства протяженности, конфигурации и относительной расположенности реальных физических макротел. Не следует смешивать его с эмпирическим пространством, т.е. с тем понятием, которое мы вводим и которым пользуемся в процессе измерений при различных опытах и в обыденной жизни. Эмпирическое пространство не тождественно математическому (идеальному, мысленному) пространству. Оно может лишь приближенно описываться евклидовым математическим пространством. Какова степень приближения и возможно ли оно вообще – вопрос эксперимента.
Таким образом евклидово математическое пространство есть теоретическое пространство классической механики. Его фундаментальные свойства таковы:
- евклидово пространство трехмерно – координаты, определяющие местоположение любой его точки относительно избранной системы координат, представляют собой совокупность трех чисел: x, y, z;
- все точки евклидового пространства равноправны и все направления в нем равноценны, т.е. евклидово пространство однородно и изотропно;
- множество точек, образующих евклидово пространство, непрерывно, что в общем понимается, как отсутствие пропусков, недоступных мест, как возможность выбора сколь угодно малых и больших расстояний между точками этого пространства, заполняющих его сплошным образом;
- расстояние между точками евклидового пространства выражается в декартовых координатах соотношением:
(∆r)2= (∆ x)2 + (∆y)2 + (∆z)2, где ∆x = x2 – x1, ∆ y = y2 – y1, ∆z = z2 –z1 –разности координат этих точек.
Свойства евклидового пространства, конечно, имеют опытное обоснование, т.е. они обусловлены объективной действительностью. Этими свойствами в мышлении, т.е. в идеализированной форме, отражаются известные опытные факты, относящиеся, к эмпирическому макропространству, например, в пределах Земли или даже Солнечной системы.
Время в ньютоновской механике определяется как идеальная длительность, которая представляется однородной и непрерывной величиной. Оно аналогично евклидовому пространству «заполнено» сплошным образом моментами времени – точками временной оси. При чем среди последних нет какой либо особой, чем –либо выделенной точки. Так определенное время – это абстракция, мысленная конструкция. К эмпирическому времени, определяемому реальными механическими процессами, оно имеет то отношение, что представляет собой теоретическую идеализацию.
Соответственно рассмотренным выше пространству и времени в классической механике вводится абстрактный физический объект – материальная точка, эмпирическими прообразами которой служат природные тела.
Для определения понятия движения материальной точки вводится особая конструкция – система отсчета. Ее составляют: тело отсчета и связанные с ними – пространственная и временная системы координат.
Посредством трехмерной системы координат, например, декартовой, определяется пространственное положение материальной точки набором из трех чисел (x, y, z).
Временная «система координат» устанавливает временную координату материальной точки. Она представляет собой совокупность идеальных точечных часов, расставленным по всем пространственным точкам и синхронизированных между собой (т. е. одинаково идущих и одинаково поставленных на отсчет времени). В классической механике постулируется мгновенная синхронизация «точного времени».
Согласно классическому определению движение материальной точки представляет собой процесс непрерывного изменения ее пространственных координат с течением времени относительно фиксированной системы отсчета. Среди множества систем отсчета в классической механике выделяется инерциальная система отсчета.
В инерциальной системе отсчета свободная материальная точка либо покоится, либо движется равномерно и прямолинейно (υ = соnst =0 или υ = соnst ≠ 0). Данное утверждение является и определением ИСО и законом (законом инерции).
В классической механике принимается в качестве фундаментального постулата принцип относительности, гласящий, что все ИСО механики равноценны (эквивалентны). Иначе говоря, любые механические явления протекают одинаково при одинаковых начальных условиях.
Из этого принципа, впервые сформулированного в начале 17 в. Г.Галилеем, следуют два важных положения:
1.Любую ИСО можно принять за неподвижную.
- Каждая ИСО движется относительно другой ИСО, принятой за
неподвижную, со скоростью υ = соnst, т. е. равномерно и прямолинейно.
В ньютоновской механике введен постулат абсолютности времени: для всех ИСО существует единое, абсолютное время, совпадающее со временем каждой из них:
t =const или ∆t = τ = inv,
где символ «inv» (инвариант, инвариантный- французское слово - неизменяющийся) используется в том смысле, что величина, к которой он относится, абсолютна – одинакова для всех ИСО, не изменяется при переходе от одной из них к другой. Так, если установлено, что τ = 0, т.е. в какой-либо ИСО два события одновременны, то они будут одновременны и относительно любой другой ИСО.
§2. Законы электродинамики и принцип относительности
После того как во второй половине 19 в. Максвеллом были сформулированы основные законы электродинамики, возникли сомнения в справедливости принципа относительности Галилея применительно к электромагнитным явлениям. Чтобы решить данную проблему, надо было выяснить, меняются ли законы электродинамики (уравнения Максвелла) при переходе от одной системы отсчета к другой, или же, подобно законам Ньютона, они остаются неизменными. Законы электродинамики сложны, и выяснить, инвариантны ли эти законы относительно преобразованиям Галилея или нет, - нелегкая задача. Однако уже простые соображения позволяют найти ответ. В электродинамике скорость распространения электромагнитных волн в вакууме одинакова по всем направлениям с = 3·108 м/с. Однако с другой стороны, в соответствии с законом сложения скоростей, вытекающим из преобразования Галилея, скорость может равняться с только в одной избранной системе отсчета. В любой другой инерциальной системе отсчета, движущей по отношению к этой избранной системе со скоростью υ, скорость света должна равняться с + υ.
Это означает, что если справедлив обычный закон сложения скоростей, то при переходе из одной инерциальной системы отсчета к другой законы электродинамики должны меняться так, что в этой новой системе отсчета скорость света равнялась не с, а с + υ.
Таким образом, обнаружились определенные противоречия между электродинамикой и механикой Ньютона. Возникшие противоречия пытались решить тремя различными способами.
Первый из них состоял в том, что некоторые ученые считали, принцип относительности несостоятелен в применении к электродинамике. На эту точку зрения встал великий голландский физик Х. Лоренц. Вслед за Фарадеем он полагал, что электромагнитные явления протекают в особой среде, заполняющей все пространство, - мировом эфире. Инерциальная система отсчета, покоящаяся относительно эфира, согласно Лоренцу, особая преимущественная система. В ней законы электродинамики справедливы и имеют наиболее простую форму. Только в этой системе отсчета скорость света в вакууме одинакова по всем направлениям.
Второй путь решения проблемы видели в том, чтобы считать неправильными уравнения Максвелла. Была предпринята попытка изменить их так, чтобы при переходе от одной системы к другой не менялись. Такую попытку, например, предпринял Г.Герц. По его мнению, эфир полностью увлекается движущимися телами, и поэтому электромагнитные явления протекают одинаково, независимо от того, покоится ли тело или движется. Принцип относительности, по Герцу, справедлив.
Наконец третья возможность разрешения указанных трудностей состоит в отказе от классических представлений о пространстве и времени, чтобы сохранить как принцип относительности, так и уравнения Максвелла. С данной точки зрения оказались неточными не уравнения электромагнитного поля, а законы механики Ньютона, согласующиеся со старыми представлениями о пространстве и времени, выраженными преобразованиями Галилея. Изменить надо законы механики, а не законы электродинамики.
При попытках Герца изменить законы электродинамики Максвелла выяснилось, что новые уравнения не способны объяснить ряд наблюдаемых фактов. Так, согласно теории Герца, движущаяся вода должна полностью увлекать за собой распространяющийся за собой свет, так как она увлекает эфир, в котором распространяется свет. Опыт показал, что в действительности это не так.
Точка зрения Лоренца, согласно которой должна существовать избранная система отсчета, связанная с мировым эфиром, пребывающем в абсолютном покое, также была опровергнута прямыми опытами.
§ 3. Опыт Майкельсона - Морли
Если бы скорость света была равна 300 000 км/с только в системе отсчета, связанной с эфиром, то, измеряя скорость света в произвольной инерциальной системе отсчета, можно было бы обнаружить движение этой системы по отношению к эфиру и определить скорость этого движения. Или иначе, если, конечно, эфир существует, то должен быть обнаружен «эфирный ветер».
Г.Я.Мякишев предлагает в курсе физики 11-го класса разъяснить эту задачу на примере доступного для учащихся задания.
Выполнение этого задания основано на той идее, что подобно тому как в системе отсчета, движущейся относительно воздуха, возникает ветер, при движении по отношению к эфиру должен быть обнаружен «эфирный ветер».
Задача. Пусть из города А самолет совершает рейс в города В и С (рис. 1). Расстояния между городами одинаковы и равны l = 300 км. Причем трасса АВ перпендикулярна трассе АС. Скорость самолета относительно воздуха с = 200 км/ч. В направлении АВ дует ветер со скоростью υ = 10 км/ч. Какой рейс займет больше время: от А к В и обратно или от А к С и обратно?
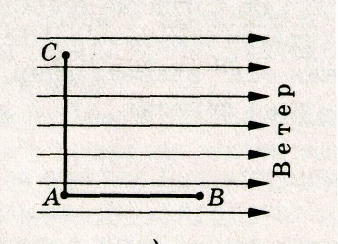
Рис. 1
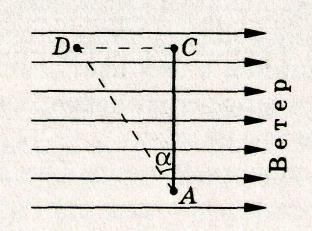
Рис. 2
Р е ш е н и е. В первом случае время полета равно
t1=l/(c + υ) + l/(c - υ) = 3, 00075 ч.
Во втором случае самолет должен держать курс не на сам город С, а на некоторую точку D, лежащую против ветра (рис. б). Относительно воздуха самолет пролетает расстояние АD. Воздушный поток сносит самолет на расстояние DC. Отношение этих расстояний равно отношению скоростей:
DC /AD = υ/с.
Относительно Земли самолет пролетает расстояние AC.
Так как
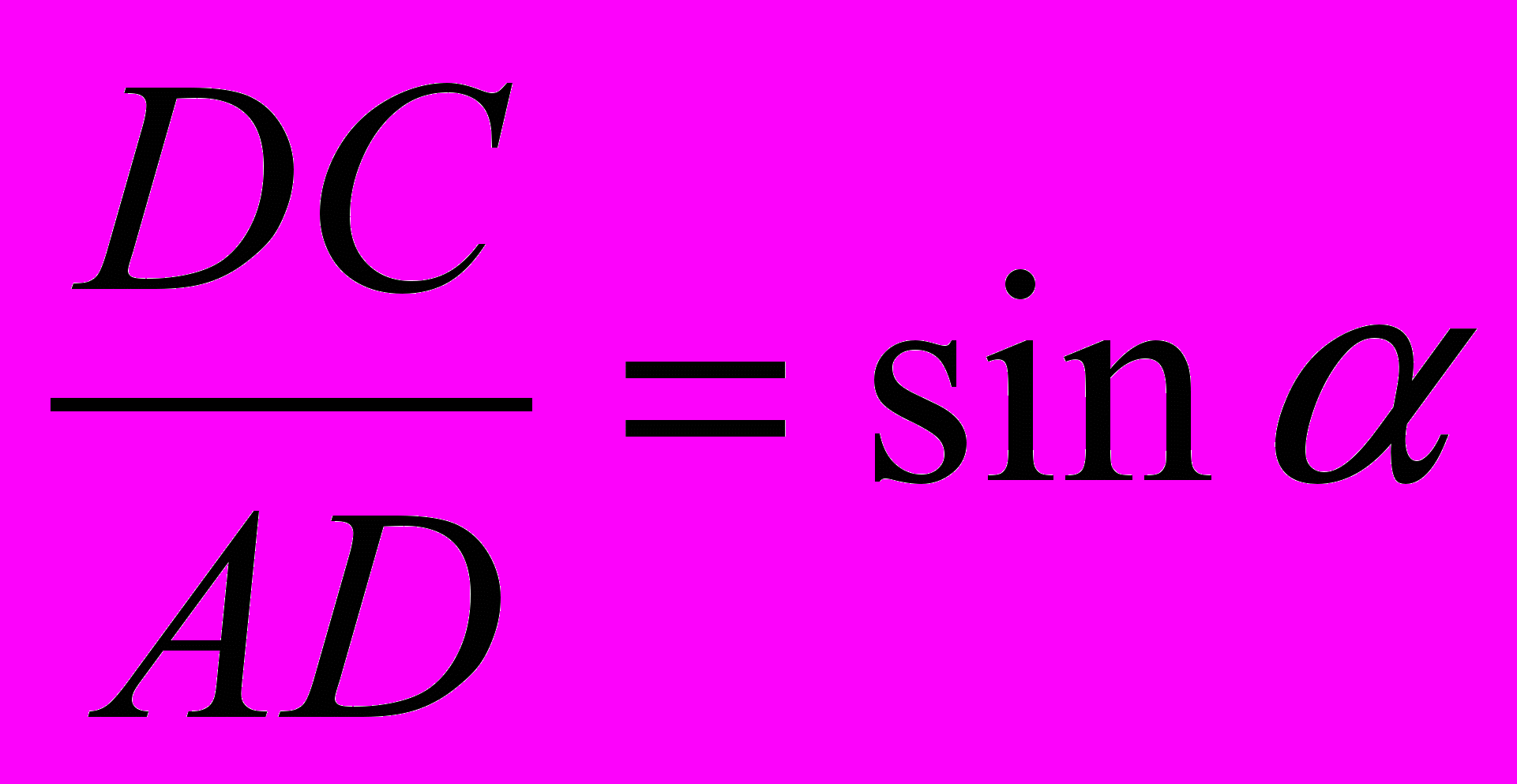 , то
, то 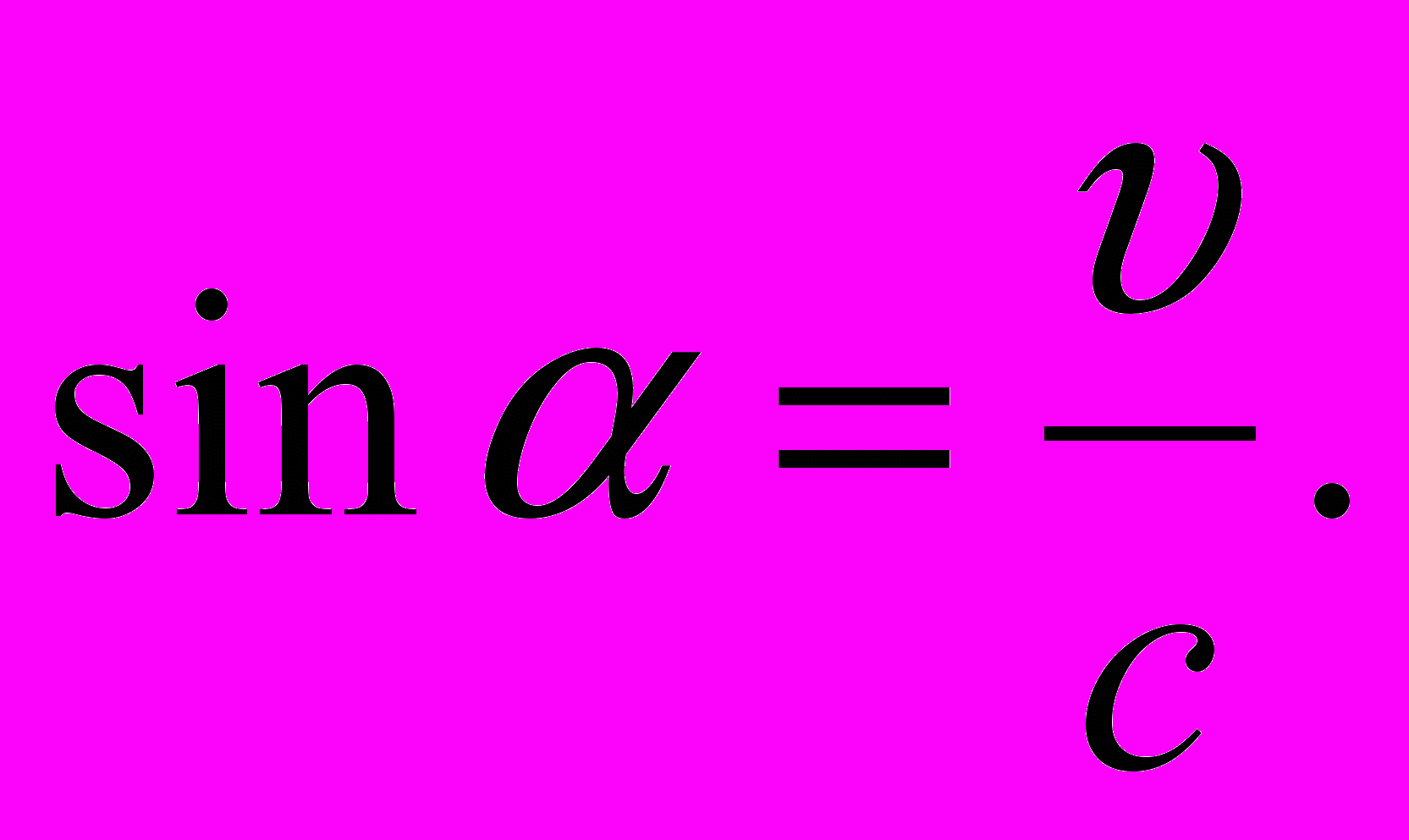 Но AD =
Но AD =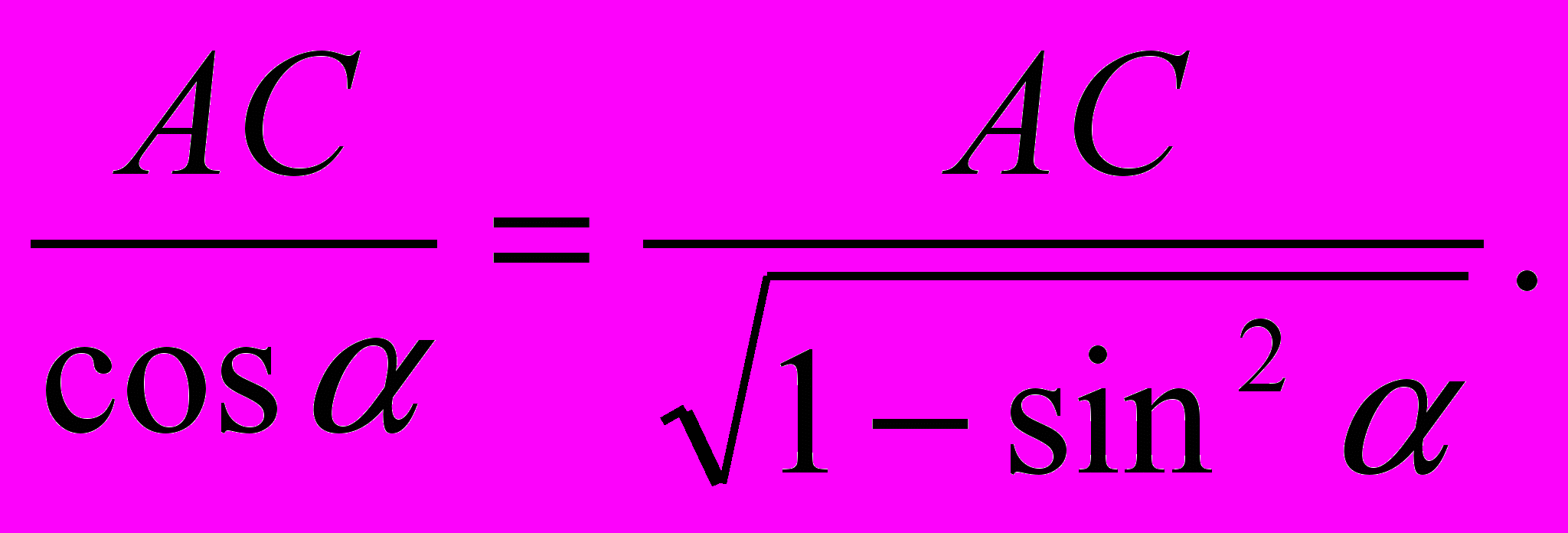 Поэтому
Поэтому 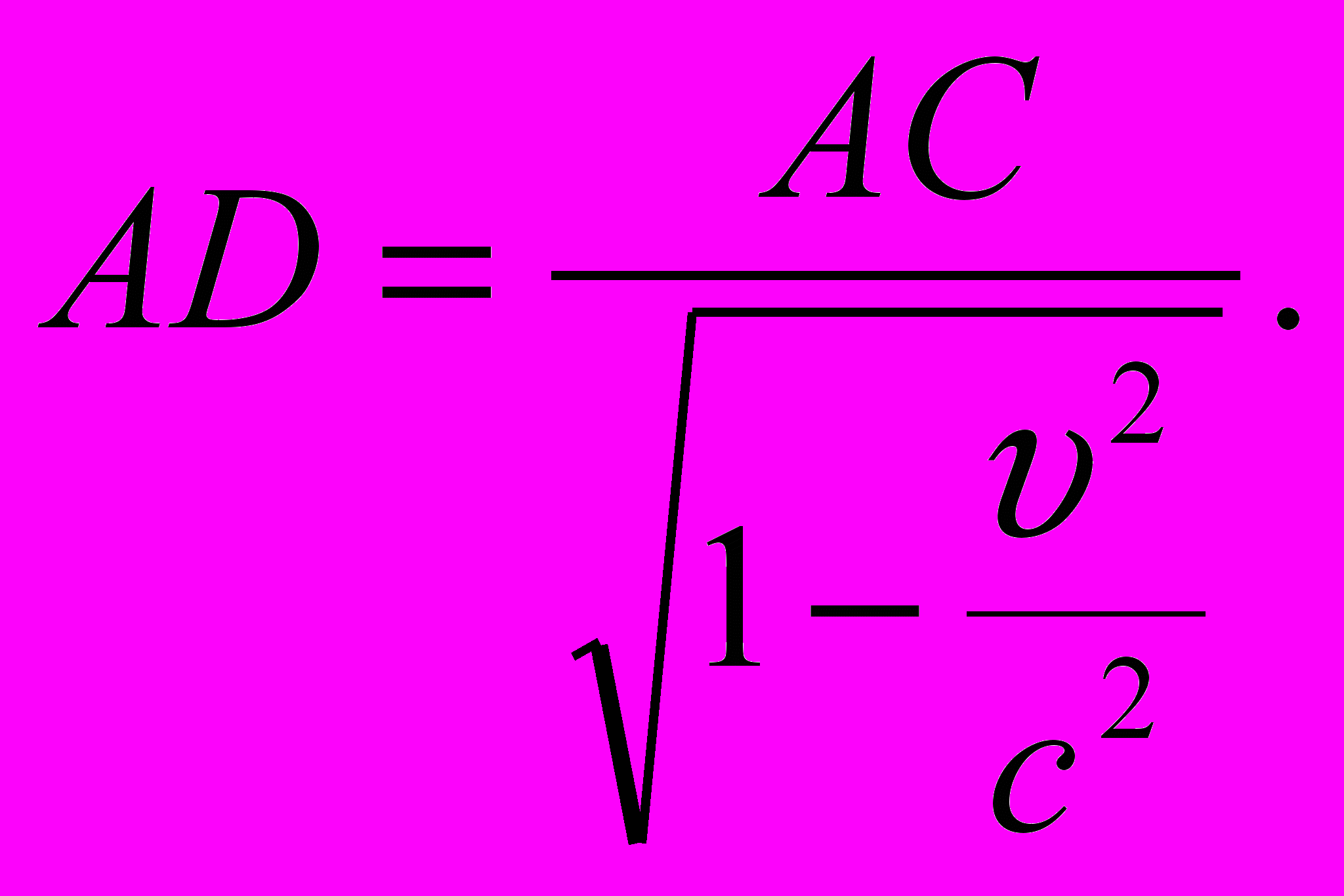
Следовательно, время t2, затраченное самолетом на прохождение этого пути туда и обратно со скоростью с, определяется так:
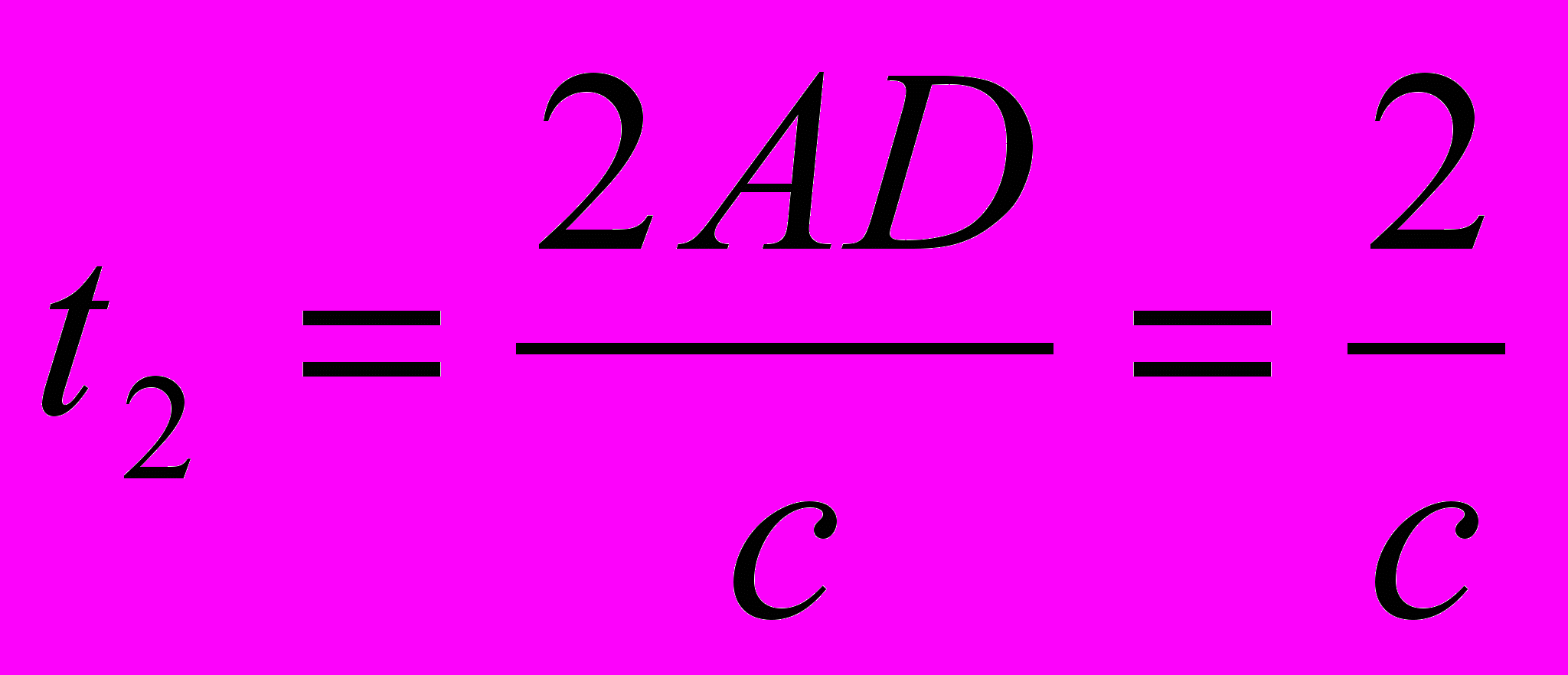
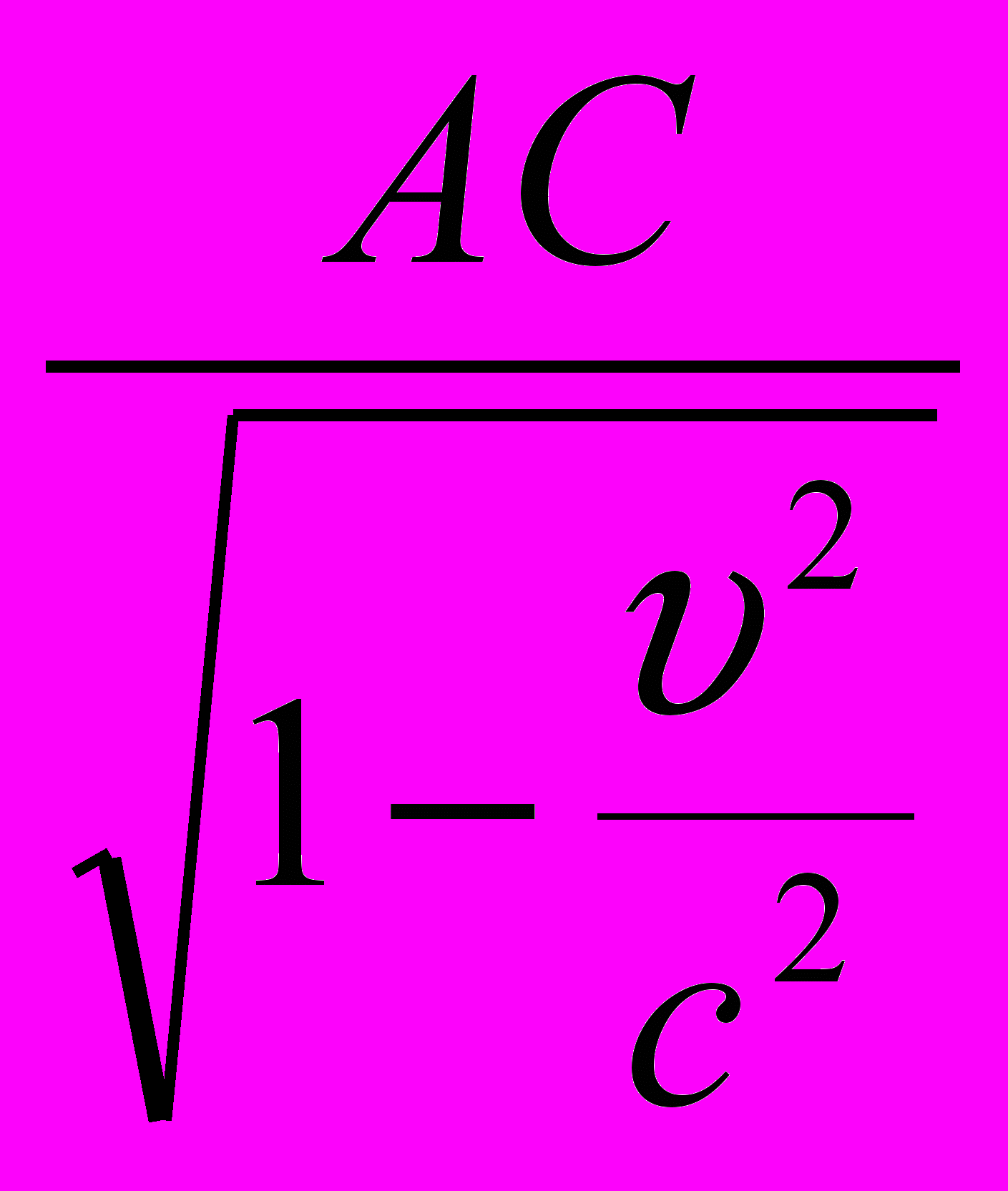 =
=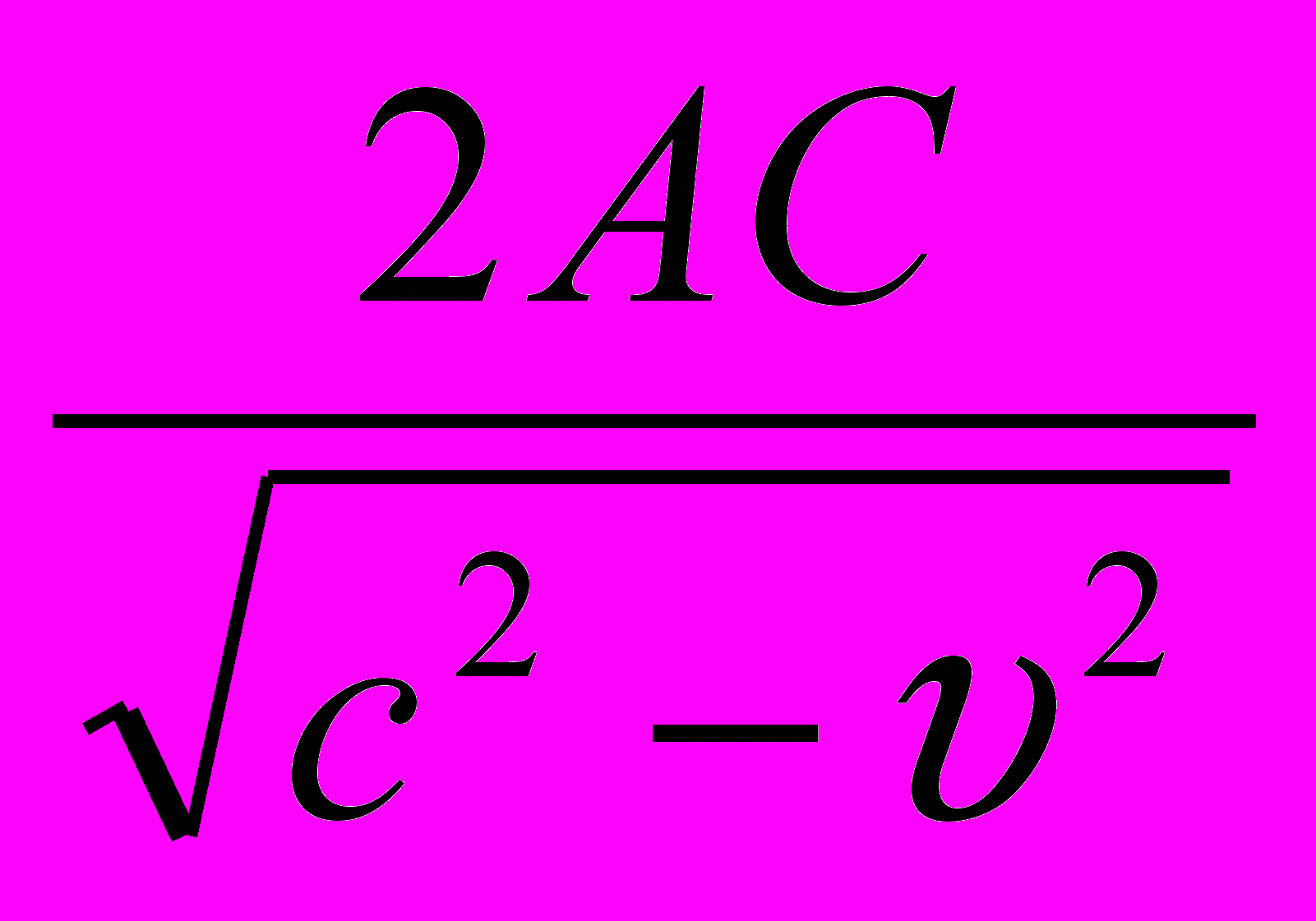 =3,00375 ч.
=3,00375 ч.Разность времени t1 и t2 очевидна. Зная эту разность, а также расстояние АС и скорость с , можно было определить скорость ветра относительно Земли.
Опыт по обнаружению «эфирного ветра» был поставлен в 1881 г. американским ученым А. Майкельсоном и Э. Морли по идее высказанной за 12 лет до этого Максвеллом.
Упрощенная схема опыта Майкельсона приведена на рисунке 3. Если сопоставить решенную задачу на относительность движения, то в опыте роль самолета играет световая волна, имеющая скорость 300 000 км/с относительно эфира. Во время проведения опыта никаких сомнений не было. Роль обычного ветра играл предполагаемый «эфирный ветер», обдувающий Землю. Относительно неподвижного эфира Земля не может покоиться все время, так как она движется вокруг Солнца со скоростью около 30 км/с и эта скорость непрерывно меняет направление. Роль города А играет полупрозрачная пластинка Р, разделяющая поток света от источника S надва взаимно перпендикулярных пучка. Города В и С заменены зеркалами М1 и М2, направляющие световые пучки обратно.
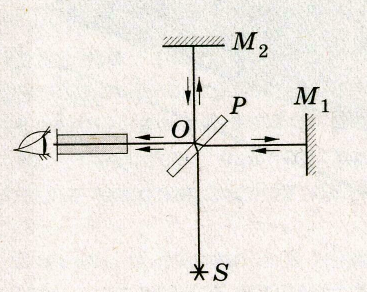
Рис. 3
Далее оба пучка света соединялись и направлялись в объектив зрительной трубы. При этом возникала интерференционная картина, состоящая из чередующих светлых и темных полос (рис. 4 ). Расположение полос зависело от разности времен, затрачиваемых на одном и другом пути.
Прибор был установлен на квадратной каменной плите со сторонами 1,5 м и толщиной более 30 см. Плита плавала в чаше со ртутью, для того чтобы ее можно было поворачивать без сотрясения вокруг вертикальной оси .

Рис. 4
Направление «эфирного ветра» неизвестно. При вращении прибора ориентация световых путей ОМ1 и ОМ2 относительно эфирного ветра должна была изменяться. Следовательно, должна изменяться разность времен прохождения путей ОМ1 и ОМ2, а поэтому должны были смещаться интерференционные полосы в поле зрения трубы. По смещению надеялись определить скорость «эфирного ветра» и ее направление.
Однако, к удивлению ученых, опыт показал, что никакого смещения интерференционных полос при повороте прибора не происходит. Эксперименты ставились в разное время суток и в различные времена года, но всегда с одним и тем же отрицательным результатом. Движение Земли по отношению к эфиру обнаружить не удалось.
Таким образом, идея о существовании преимущественной системы отсчета не выдержала опытной проверки. Это означало, что ь никакой особой среды – «светоносного эфира», - с которой можно было бы связаттакую преимущественную систему отсчета, не существует.
§4. Постулаты теории относительности
В течение длительного времени после опытов Майкельсона и Морли физики стремились определить скорость движения Земли относительно эфира, в котором, как предполагалось, распространяются электромагнитные волны, в частности свет. Однако все такие попытки оказались безуспешными. В связи с этим Х.Лоренц ввел специальную гипотезу о сокращении тел при их движении в эфире. Возникали и другие теории, с помощью которых пытались объяснить отрицательный результат опытов по обнаружению движения Земли относительно эфира.
Французский ученый А.Пуанкаре сформулировал принцип относительности. Согласно этому принципу, никакие опыты не могут решить задачи о движении Земли относительно эфира, ибо, как утверждал Пуанкаре, «законы физических явлений будут одинаковы как для наблюдателя, находящегося в состоянии покоя, так и для наблюдателя, совершающего равномерное поступательное движение, так что мы не имеем и не можем иметь никаких средств, чтобы различать, находимся мы в таком движении или нет».
В 1905 г. вышла работа А. Эйнштейна «К электродинамике движущихся сред». В этой работе А. Эйнштейн подошел к данному вопросу с новой точки зрения. Он показал, что противоречия, которые возникли в оптике движущихся тел, разрешаются, если по-новому взглянуть на понятие пространства и времени.
А.Эйнштейн отмечал, не следует изобретать различные гипотезы для объяснения отрицательных результатов всех опытов обнаружить различие между инерциальными системами. Законом природы является полное равноправие всех систем отчета в отношении не только механических, но и электромагнитных провесов. Нет никакого различия между состояниями покоя и равномерного и прямолинейного движения. Именно это обнаружилось в опыте Майкельсона ( движение Земли по орбите не оказывает влияния на оптические явления на Земле).
Исходя из нового подхода к понятию одновременности, Эйнштейн построил специальную теорию относительности, которая явилась теорией пространства и времени. Специальная теория относительности рассматривает взаимосвязь физических явлений только в инерциальных системах отсчета, т.е. в системах отсчета, движущихся друг относительно друга равномерно и прямолинейно.
После создания специальной теории относительности, А.Эйнштейн создал общую теорию относительности, являющуюся теорией тяготения. В ней представления о пространстве и времени получили дальнейшее развитие. Общая теория относительности описывает физические процессы, происходящие в ускоренно движущихся друг относительно друга (неинерциальных) системах отсчета.
Специальная теория относительности базируется на двух постулатах.
Первый постулат (закон) специальной теории относительности (СТО) является обобщением классического принципа относительности Галилея на любые законы природы. Первый постулат утверждает: все законы природы одинаковы в инерциальных системах отсчета.
Сущность данного закона состоит в том, что все инерциальные системы равноправны. Можно наблюдать только относительное прямолинейное движение. Не существует абсолютного прямолинейного и равномерного движения, иначе имелась бы хотя бы одна инерциальная система отсчета, в которой бы законы природы отличались бы от законов в других системах. Сравнивая эти законы, наблюдатель мог бы установить, в покое или движении находится эта система, что противоречит первому постулату.
Обобщение принципа относительности Галилея на все законы природы состоит в том, что закон сложения скоростей справедлив для описания взаимодействий всех видов, в частности электродинамики. Никакие опыты, как следует из первого постулата, не позволяют выделить предпочтительную систему отсчета.
Второй постулат специальной теории относительности: скорость света в вакууме одинакова во всех инерциальных системах отсчета. Иногда второй постулат называют постулатом абсолютной скорости. Термин «абсолютность» употребляется как синоним термину «инвариантность», означающему неизменность величины при каких-либо преобразованиях. В данном случае – неизменность при переходе от одной инерциальной системы отсчета, к любой другой инерциальной системе отсчета.
Из этого постулата следует, что скорость света в вакууме не зависит от скорости движения источника или приемника света.
Предположим, наблюдатель на Земле с помощью радара видит удаляющийся самолет (рис. 5). Практика показывает, что скорость электромагнитных волн не зависит от скорости υи движения источника и скорости υп движения приемника. Скорость света в воздухе пренебрежимо мало отличается от скорости света в вакууме.
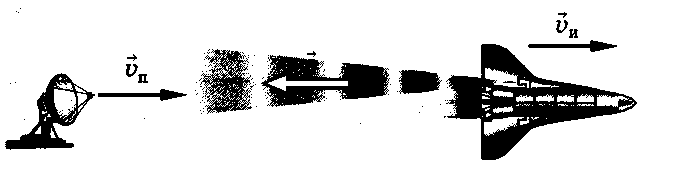
Рис. 5
Независимость скорости света от движения источника неоднократно проверялась на опыте. Так, проводилось измерение скорости света от правого и левого краев Солнца. Известно, что Солнце вращается вокруг оси со скоростью 2,3 км/с относительно Земли. Один край Солнца удаляется со скоростью 2,3 км/с, а другой конец с такой же скоростью приближается. В обоих случаях скорости света совпадают. постоянство скорости света во всех инерциальных системах отсчета – фундаментальное свойство природы. Материальные точки (тела, частицы) не могут иметь скорость в вакууме большую скорости света.
. Известно, что постоянство скорости света во всех инерциальных системах отсчета – фундаментальное свойство природы. Материальные точки (тела, частицы) не могут иметь скорость в вакууме большую скорости света.
Из истории определения постулатов СТО. Выше постулаты специальной теории относительности приведены в современной формулировке. Ниже дан фрагмент из статьи А. Эйнштейна «К электродинамике движущихся тел», в котором сформулированы постулаты самим основателем СТО. «Мы сформулируем оба принципа следующим образом.
1. Законы, по которым изменяются состояния физических систем, не зависят от того, к которой из двух координатных систем, движущихся относительно друг друга равномерно и прямолинейно, эти изменения состояния относятся.
2. Каждый луч света движется в «покоящейся» системе координат с определенной скоростью V, независимо от того, испускается ли этот луч света покоящимся или движущимся телом»
Хотя сущность формулировок не изменилась, но их современные определения показывают, как изменился за истекшие сто лет «язык» науки.
§ 5. «Событие» - одно из основных понятий СТО. Относительность одновременности
В специальной теории относительности событие определяется как физическое явление, происходящее в какой-либо пространственной точке, в данный момент времени в избранной системе отсчета. Событие характеризуется физическим содержанием, местом и временем. Простейшим примером события служит положение тела (материальной точки) в данной точке пространстве в данный момент времени. Допустим, на прямолинейном участке шоссе в данный момент времени, движущийся автомобиль находится от заправочной станции на определенном расстоянии. Это событие характеризуется физическим содержанием: координатой в выбранной системе отсчёта (относительно шоссе), моментом времени.
События, например два или несколько, могут происходить не одновременно, но воспринимаются нашими органами чувств как одновременные. Когда мы смотрим телевизионную передачу, то события на экране даже при прямой трансляции происходят не в момент их наблюдения. Электромагнитное излучение распространяется со скоростью света. Требуется определенное время, чтобы видеосигнал, исходящий от телебашни, доходил до антенны телевизионного приемника. Следовательно, мы наблюдаем на экране событие из близкого прошлого. «Прошлое» – множество событий, которые могли оказать влияние на события в настоящем.
Рассмотрим метод синхронизации часов на примере. Допустим космонавт хочет узнать, одинаково ли идут часы А и В, установленные на противоположных сторонах космического корабля (рис. 6). Для этого с помощью источника, неподвижного относительно корабля и расположенного в его середине, космонавт производит вспышку света. Свет одновременно достигает обоих часов. Если показания часов в этот момент одинаковы, то часы идут синхронно.
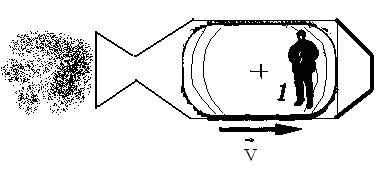
Рис. 6
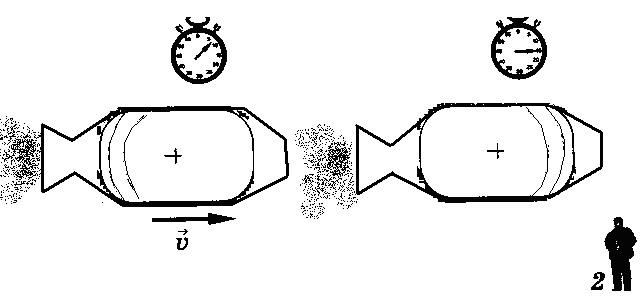
Но так будет лишь относительно системы К´, связанной с кораблем. В системе отсчета К, относительно которой корабль движется, положение будет иное. Часы на носу корабля удаляются от того места, где произошла вспышка света источника, и, чтобы достигнуть часов А, свет должен преодолеть расстояние, больше половины длины корабля (рис. 7, а,б).
а б
Рис. 7
Наоборот , часы на корме приближаются к месту вспышки, и путь светового сигнала меньше половины длины корабля. Поэтому наблюдатель в системе К придет к выводу, что сигналы достигают обоих часов неодновременно. Соответственно часы идут неодинаково.
Два любых события в точках А и В, одновременные в системе координат К´, неодновременны в системе К. Но в силу принципа относительности системы К´ и К совершенно равноправны. Ни одной из этих систем нельзя отдать предпочтение. Поэтому мы вынуждены прийти к заключению, что одновременность разделенных событий относительна. Причиной относительности одновременности является, как мы видим, конечность скорости распространения света.
§ 6. Преобразование Лоренца
Обратимся снова к постулатам теории относительности. С точки зрения классической физики они находятся в противоречии друг с другом. Согласно первому постулату законы механики, как частный случай законов физики, справедливы во всех инерциальных системах отсчета. Следовательно, справедлив и классический закон преобразования скоростей. Однако второй постулат противоречит классическому закону преобразования скоростей, а следовательно, нельзя пользоваться в СТО преобразованиями Галилея, из которых следует этот закон.
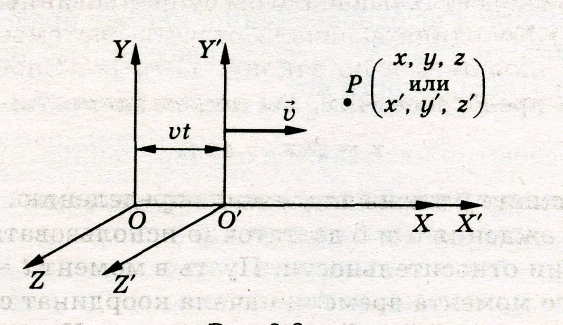
Рис. 8
Эйнштейн заменил преобразования Галилея преобразованиями Лоренца и тем самым устранил кажущееся противоречие между постулатами. Рассмотрим частные преобразования, как это было выполнено при записи преобразований Галилея.
Пусть имеется инерциальная система отсчета К´. Координаты любой точки, например точки Р, в этой системе обозначим через x´, y´, z´. А время через t´ (рис. 8). Инерциальная система К´ движется с постоянной скоростью υ относительно системы К, причем таким образом, что ее ось Х´ совпадает с осью Х системы К, а оси Y´ и Z´ параллельны соответствующим осям Y и Z. (Это означает рассмотрение частных преобразований, а не общих.) Определим координаты x, y, z и времени t некоторого события относительно системы К. Начало отсчета времени выберем таким образом, чтобы в момент t = 0 начала отсчета данных систем (точки О и О´) совпадали.
Так как движение вдоль осей Y и Z отсутствует, то можно ожидать, что y= y´, z= z´.
Начало отсчета системы К´ (точка с координатой x´=0 в этой системе) движется относительно системы К вдоль оси Х со скоростью υ, так как координата точки О´ в системе К изменяется по закону: х = υt. Таким образом, задание условия x´=0 эквивалентно условию х – υt= 0. Учитывая этот факт и линейность преобразований координат, связь между координатами х и х´ для любой точки можно записать в форме:
х´= α(х – υt),
где α- коэффициент, который может зависеть от скорости, но не от координат и времени.
С другой стороны, согласно принципу относительности скорость системы К по отношению к системе К´ должна быть по модулю равна той же скорости υ, но с противоположным знаком. Координата начала отсчета системы К (х=0) в системе К´ изменяется по закону х´ = - υt´. Снова, учитывая линейность преобразований, можно записать:
х= α(х´ + υt´),
где α – коэффициент, зависящий от скорости.
Пусть вспышка света произошла в тот момент, когда начала систем К и К´ совпадали. В этот момент t = t´ = 0. Через промежуток времени t этот сигнал достигает некоторой точки, имеющей координату х в системе К и х´ в системе К´. Так как скорость света с в обоих системах отсчета одинакова, то х = сt и х´ = сt.
Тогда можно записать:
ct = α (c + υ)t´; ct´ = α (c – υ)t.
Подставив значение t´ из второго уравнения в первое, получим
ct = α2 (c2 + υ2)t/c,
откуда
α =
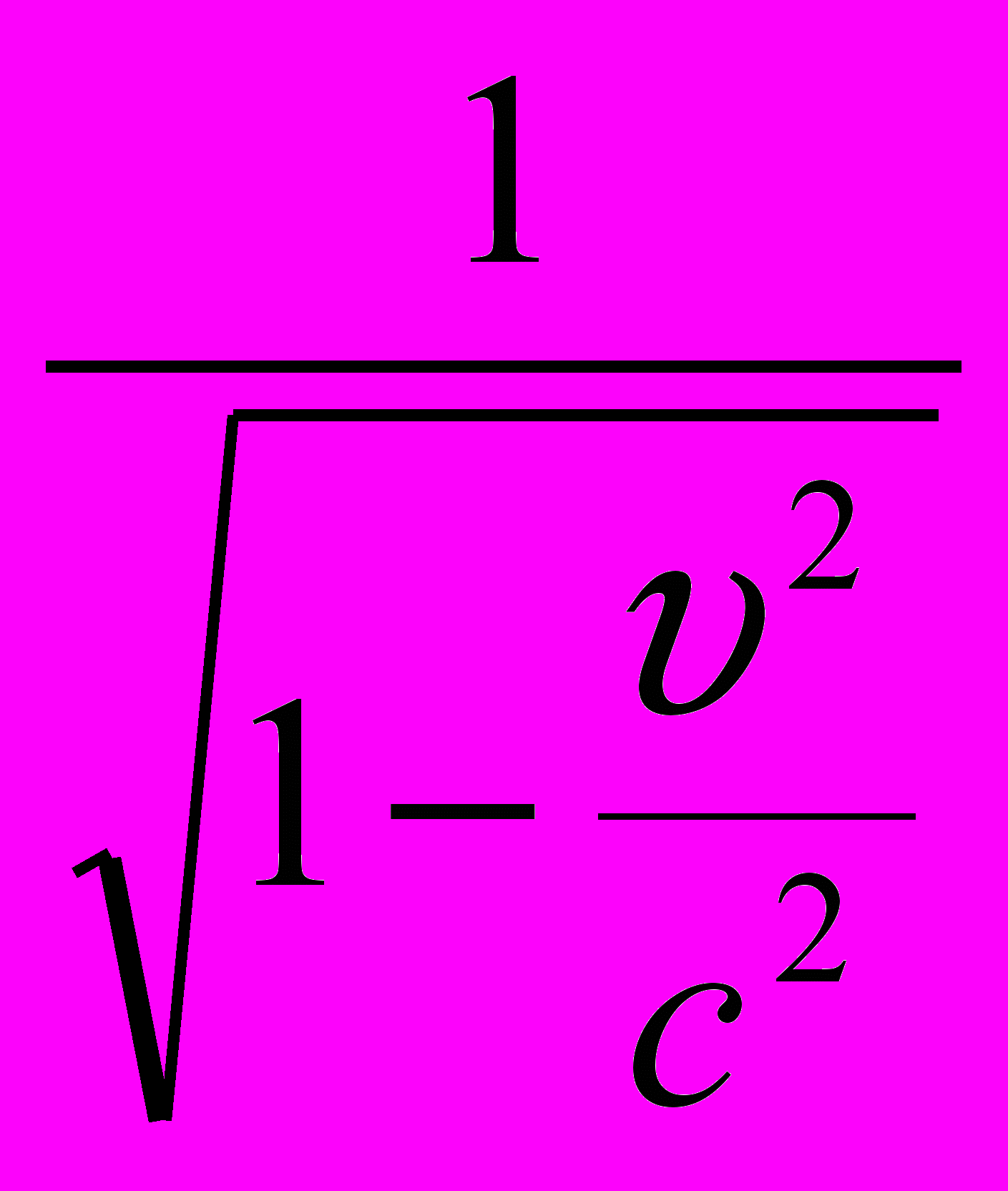
Подставим в формулу х´= α(х – υt) значение α и решим полученное уравнение относительно t. В результате имеем
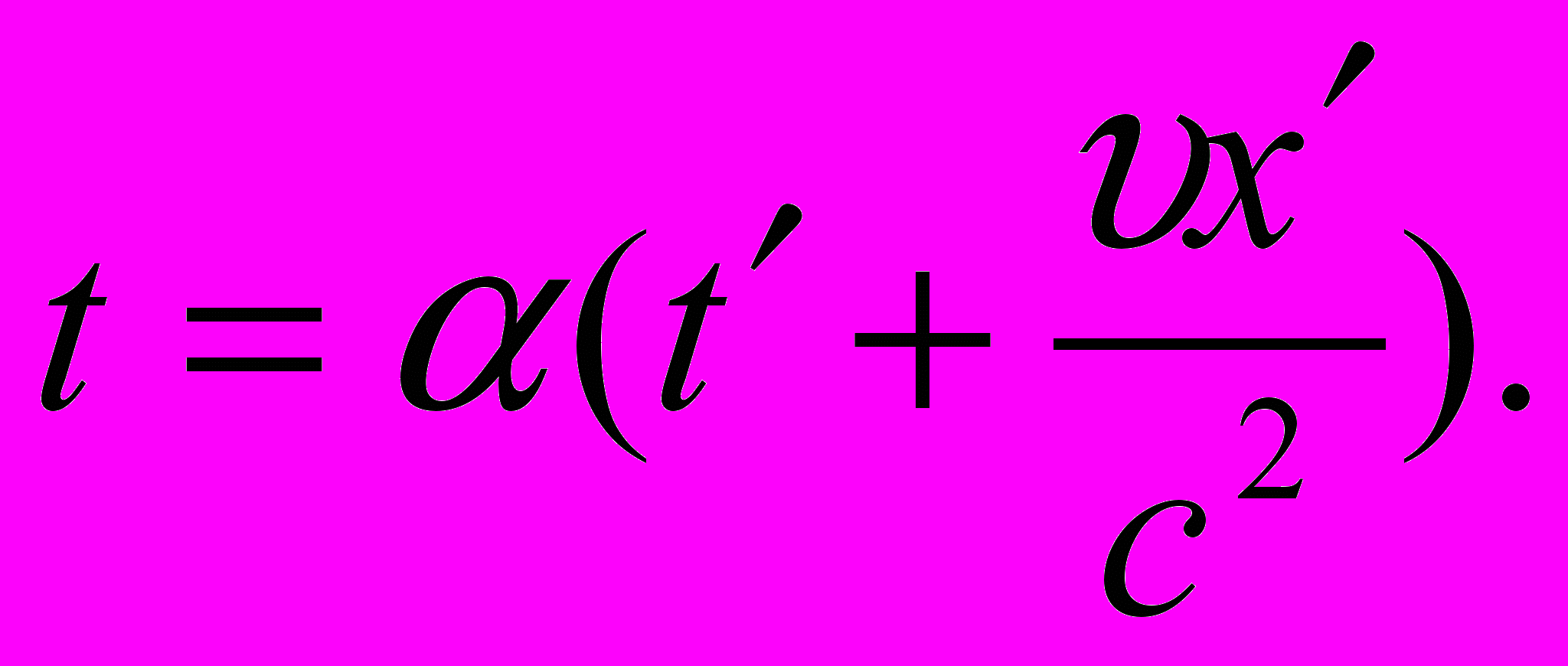
Действительно, преобразования Лоренца имеют вид:
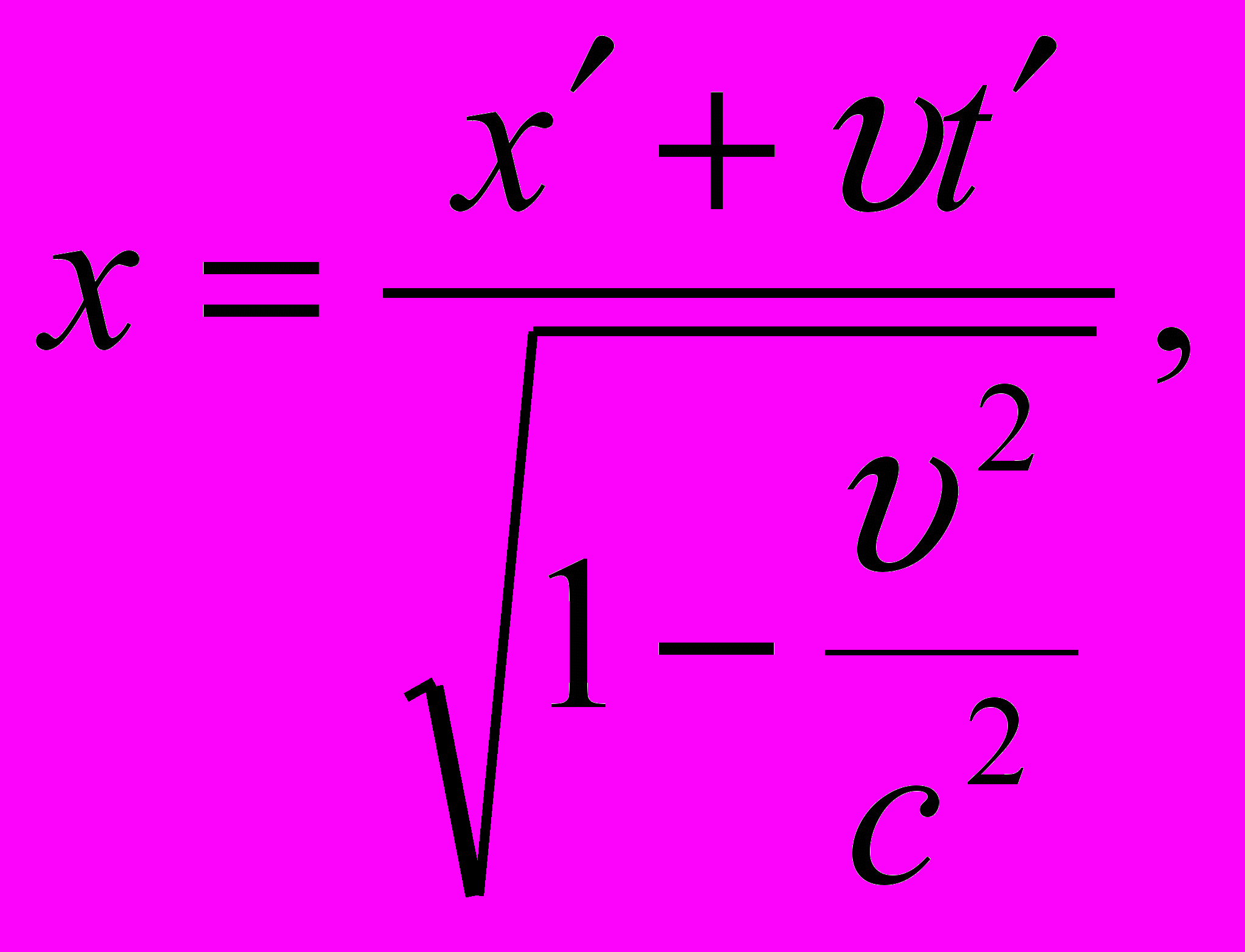
y = y`,
z = z`,
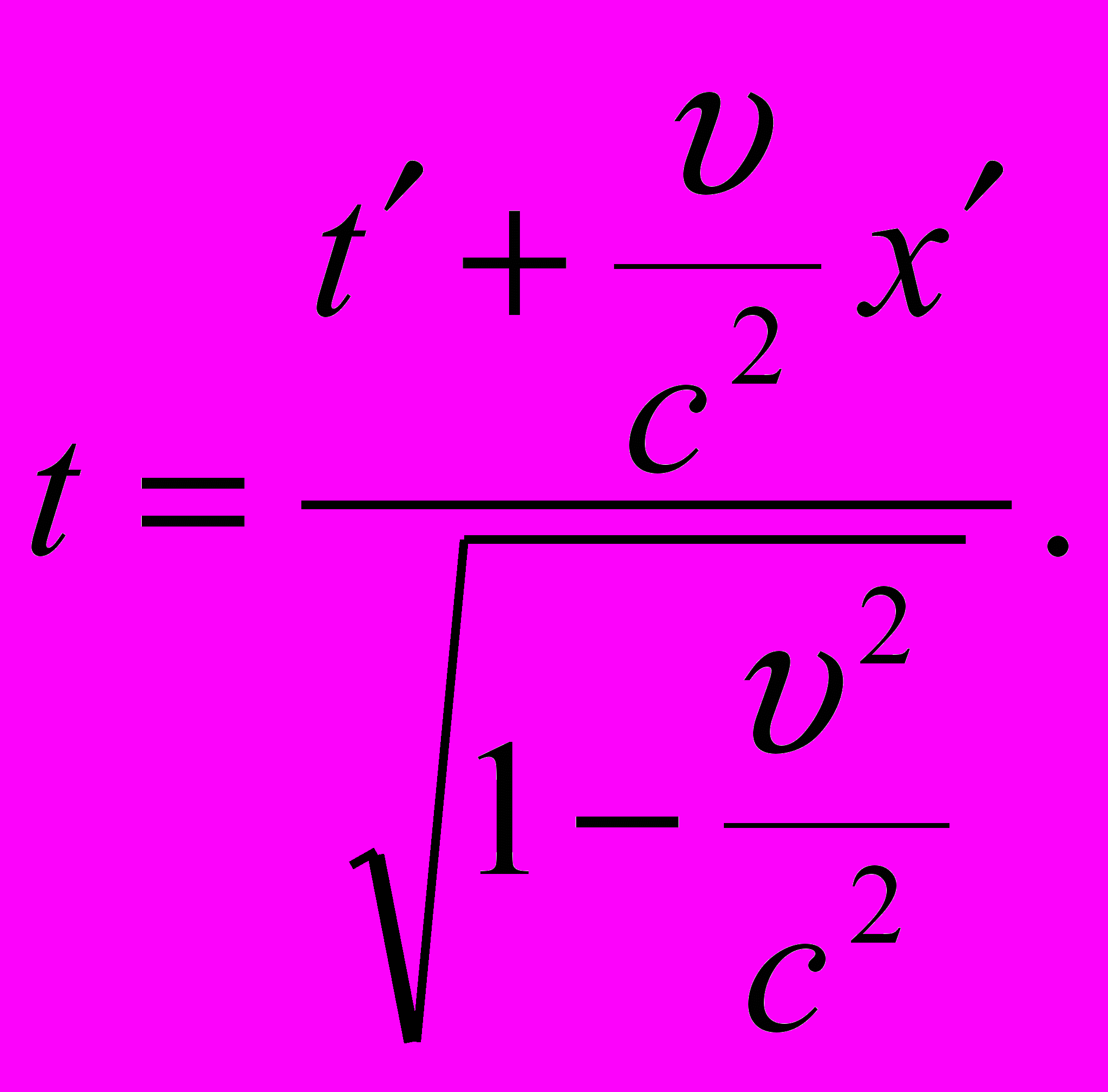
Чтобы выявить особенности формул преобразования Лоренца, обратимся к преобразованиям Галилея. Запишем преобразования Галилея при переходе от инерциальной системы отсчета К` к инерциальной системе отсчета К:
х = х` + υ t,
y = y`
z = z`.
Преобразования Лоренца существенно отличаются от преобразований Галилея.
Из преобразований Лоренца следует, что в них входит скорость света с как постоянная величина (с =соnst). Они показывают, что время в разных системах отсчета зависит от скорости υ одной инерциальной системы отсчета относительно другой, т.е. t не равно t`. Время зависит от координат, что означает, пространство и время связаны между собой.
§ 7. Границы применимости механики Ньютона
Из преобразований Лоренца можно найти условие, при котором преобразования Галилея применимы для пересчёта координаты, скорости тела из одной инерциальной системы в другую инерциальную систему.
Предположим, что скорость υ<<с, то υ2/с2 << 1 и величиной υ2/с2 можно пренебречь. Тогда формулы преобразования Галилея являются частным случаем преобразований Лоренца. Наше предположение о скорости движения тела (υ<<с) означает, что преобразования Галилея применимы в том случае, когда тела движутся с малыми скоростями.
Данный вывод можно интерпретировать так: классическая механика (механика Ньютона) является предельным случаем более общей механики, описывающей процессы в разных ИСО с четом преобразований Лоренца. Данный вывод согласуется с принципом соответствия.
Принцип соответствия – это положение, которое утверждает: любая новая теория, более глубоко отражающая физическую реальность и имеющая более широкую область применимости, чем старая, должна включать последнюю как предельный случай Механика Ньютона является предельным случаем специальной теории относительности.
Тот факт, что специальная теория относительности более общая теория, чем механика Ньютона, убедительно подтверждает эксперимент и практика. Приведем некоторые примеры.
Обнаружено, что время существования (от рождения до распада) движущейся элементарной частицы больше времени жизни такой же покоящейся частицы. Объяснить этот результат с классических позиций нельзя, так как одним из положений механики Ньютона является постулат абсолютности времени. Эксперименты с элементарными частицами явно ему противоречат.
На мощных современных ускорителях никогда не удавалось разогнать частицу (электроны, протоны) до световой скорости. Как объяснить этот факт? Согласно механики Ньютона, для ускорения, например, электрона массы m = 9 . 10-31кг до скорости υ = 3 ∙ 108 м/с достаточно энергии Ек = mυ2/2 = 4 ∙ 10-14 Дж. На некоторых линейных ускорителях электроны получают энергию в 8000 раз больше, но не смогут приобрести скорость света.
Приведем еще один экспериментальный факт, связанный с взаимодействием элементарных частиц. Установлено, что суммарная масса совокупности исходных элементарных частиц не равна суммарной массе совокупности новых частиц, образовавшихся после столкновения первоначальных частиц. Такие процессы нельзя описать в понятиях массы и кинетической энергии механики Ньютона, в которой масса совокупности частиц тождественно равна их суммарной массе.
Экспериментальные факты различных физических явлений электродинамики, ядерной физики и физики элементарных частиц не удается объяснить и описать в рамках механик Ньютона. В этих случаях потребовалось отказаться от представления, будто бы механика Ньютон пригодна для объяснения всех физических явлений. Обнаружилось, что есть границы ее применимости, за пределами которых предсказания механики Ньютона не соответствуют действительности.
§ 7. Собственное время
Под собственным временем частицы понимается промежуток времени для любой пары событий, относящихся к движущейся частице (или телу), определяемый в ее собственной системе отсчета.
Рис.9
С движущимся с постоянной скоростью
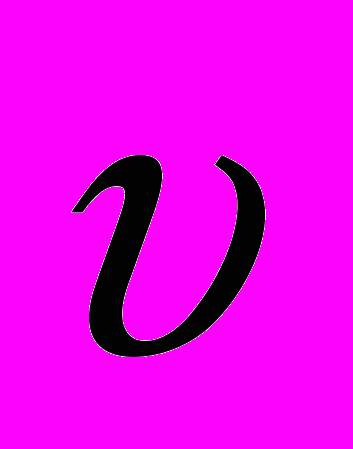 вагоном свяжем систему отсчета К`(рис. 9). Пусть из точки О начинает двигаться частица – одно событие, приход её в точку А – второе событие. Промежуток времени для этой пары событий, относящихся непосредственно к частице, является собственным временем. В этой системе промежуток времени между событиями можно измерить одними часами. Время, отсчитываемое покоящимися в инерциальной системе отсчёта часами, называют собственным временем. Собственное время обозначается буквой
вагоном свяжем систему отсчета К`(рис. 9). Пусть из точки О начинает двигаться частица – одно событие, приход её в точку А – второе событие. Промежуток времени для этой пары событий, относящихся непосредственно к частице, является собственным временем. В этой системе промежуток времени между событиями можно измерить одними часами. Время, отсчитываемое покоящимися в инерциальной системе отсчёта часами, называют собственным временем. Собственное время обозначается буквой  .
.Собственное время – время, измеренное наблюдателем, движущимся вместе с часами.
В системе отсчёта К` указанные события происходят в одной пространственной точке, отмеченной самой частицей. Промежуток времени между событиями в этой системе по определению равен собственному времени частицы для данных событий.
На основании принципа относительности можно сделать вывод, что
 - инвариант, т.е. собственное время частицы абсолютно (инвариантно). Это означает, что при переходе от одной инерциальной системы отсчета к любой другой с частицей ничего физически не происходит. Поэтому течение ее собственного времени при таких переходах не изменяется. Образно говоря, «возраст» частицы (определяемый ее собственным временем) абсолютен, т.е. является инвариантом – величиной, независимой от выбора инерциальной системы отсчёта.
- инвариант, т.е. собственное время частицы абсолютно (инвариантно). Это означает, что при переходе от одной инерциальной системы отсчета к любой другой с частицей ничего физически не происходит. Поэтому течение ее собственного времени при таких переходах не изменяется. Образно говоря, «возраст» частицы (определяемый ее собственным временем) абсолютен, т.е. является инвариантом – величиной, независимой от выбора инерциальной системы отсчёта.§ 9. Замедление времени
Световые часы (одна из разновидностей часов) – два зеркала, установленных на расстоянии l параллельно друг другу (рис. 6).

Рис. 10
Световой импульс, отражаясь от поверхностей зеркал, может перемещаться между ними вверх и вниз за промежуток времени t´=
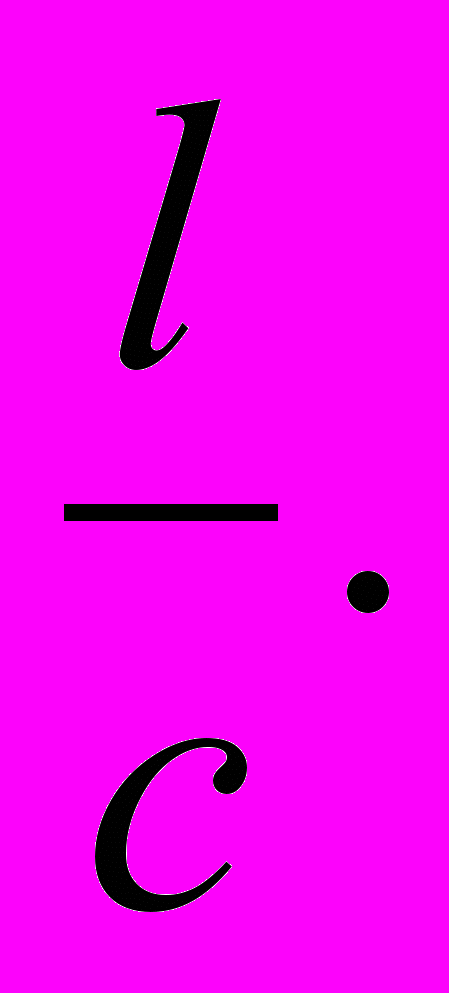 При каждом отражении импульса от зеркала часы тикают. Пилот на борту космического корабля, движущегося со скоростью υ, может измерять время по часам, покоящимся относительно корабля. Время t´- это собственное время
При каждом отражении импульса от зеркала часы тикают. Пилот на борту космического корабля, движущегося со скоростью υ, может измерять время по часам, покоящимся относительно корабля. Время t´- это собственное времяВнешнему наблюдателю путь светового импульса ( при движении часов вместе с ракетой) по диагонали будет казаться более длинным, чем пилоту корабля (рис. 11).
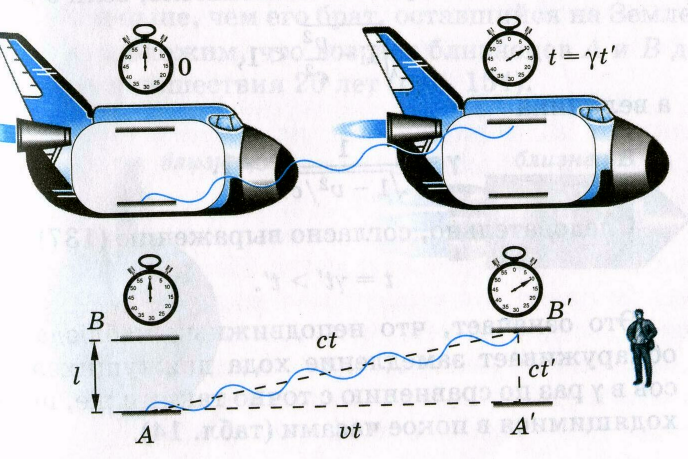
Рис. 11
При этом в соответствии со вторым постулатом СТО движение светового сигнала должно происходить со скоростью с, одинаковой во всех ИСО. Введем промежуток t, за который импульс достигает верхнего зеркала (с точки зрения внешнего наблюдателя). За это время космический корабль пролетает расстояние с t. Применяя теорему Пифагора к треугольнику АВ´ А´, имеем
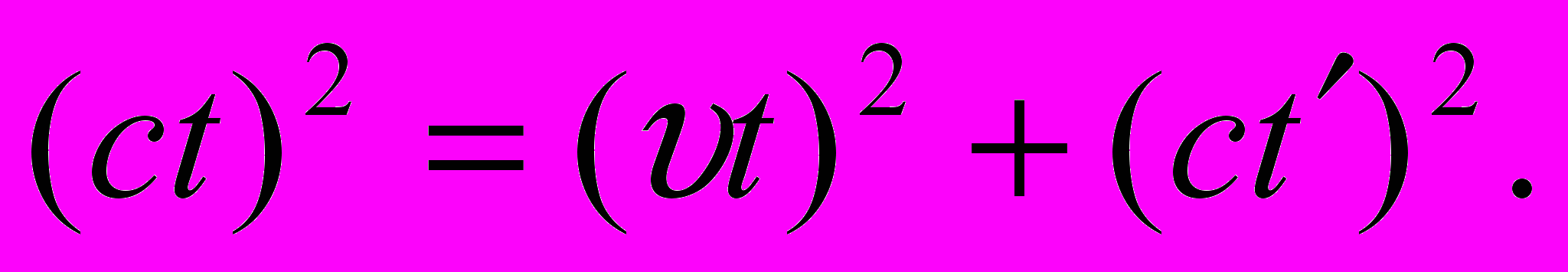 (1)
(1)Предположим, что время в неподвижной и движущейся системах отсчета течет одинаково (t = t´). Тогда
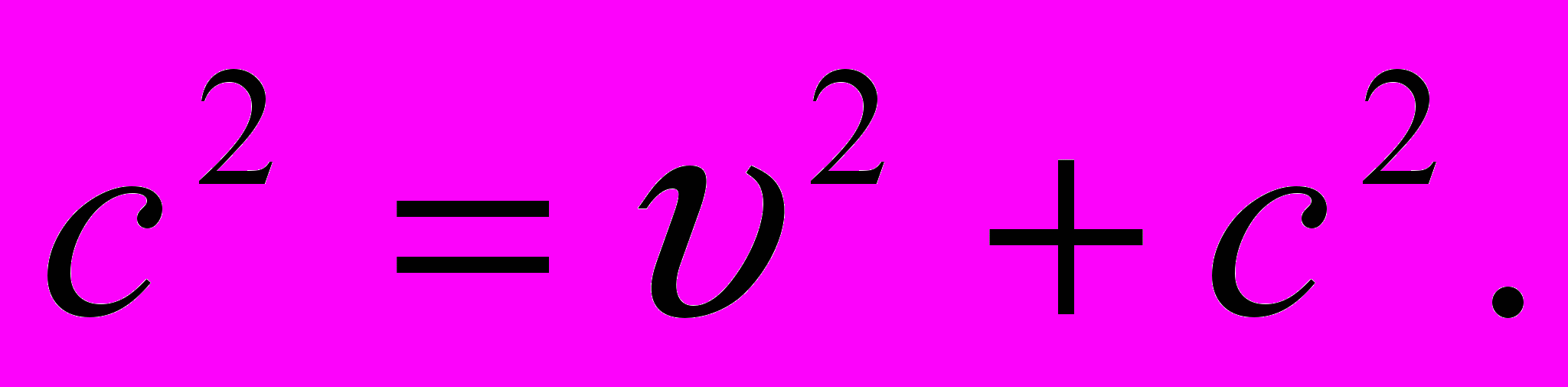
Полученное противоречие означает следующее.
Время в неподвижной системе отсчета и движущейся относительно нее течет с разной скоростью: t ≠ t´.
После перегруппировки слагаемых в (1):
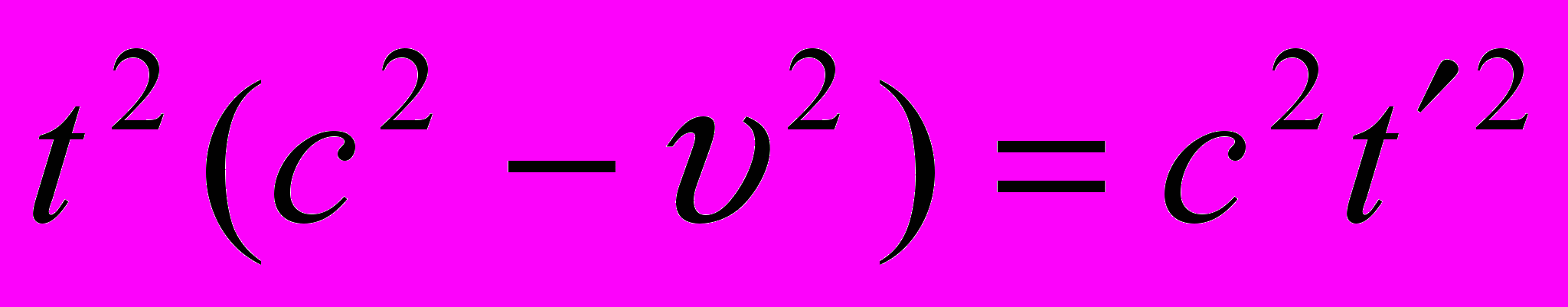
находим время по часам неподвижного наблюдателя
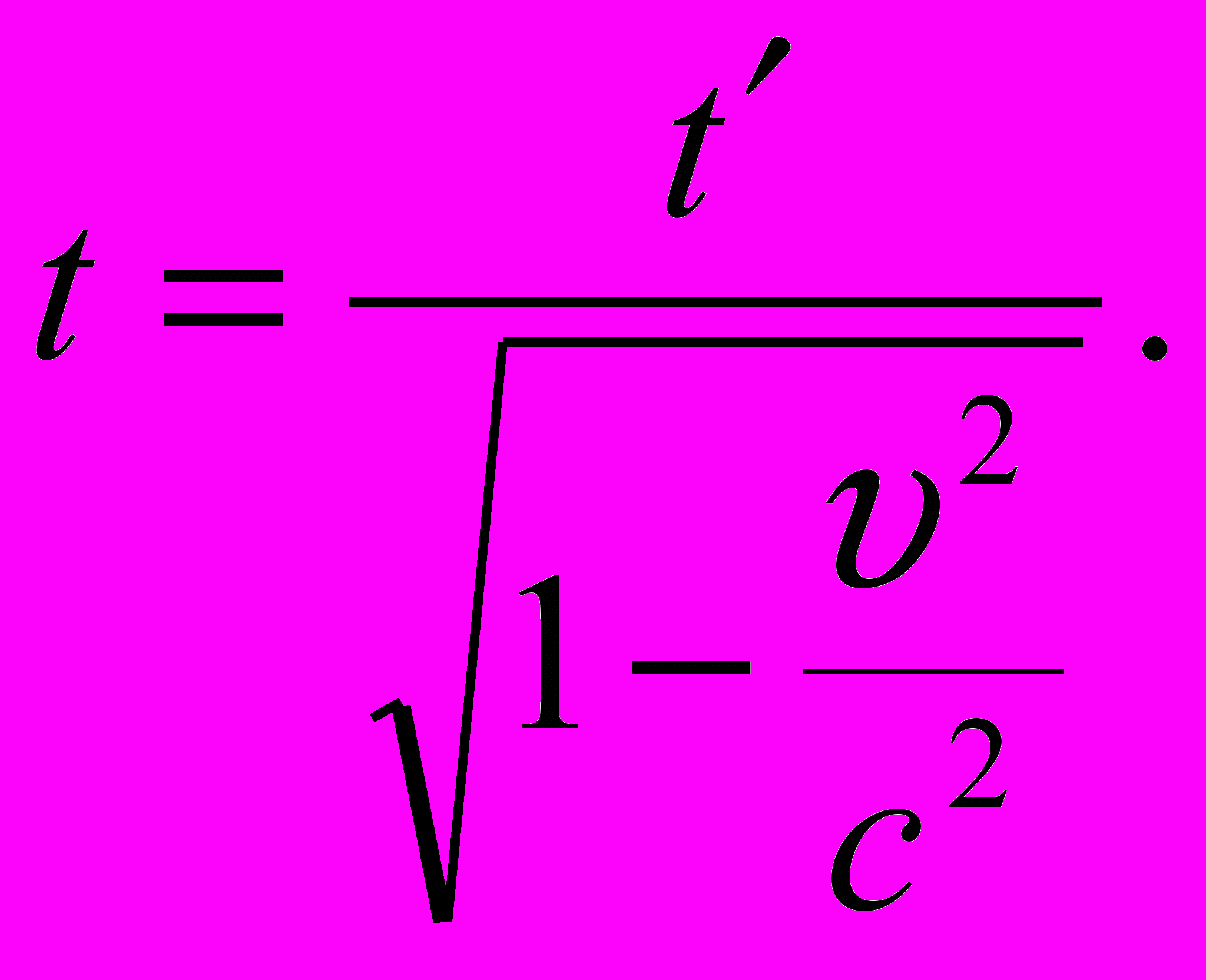
Квадратный корень в знаменателе, если υ≠0,
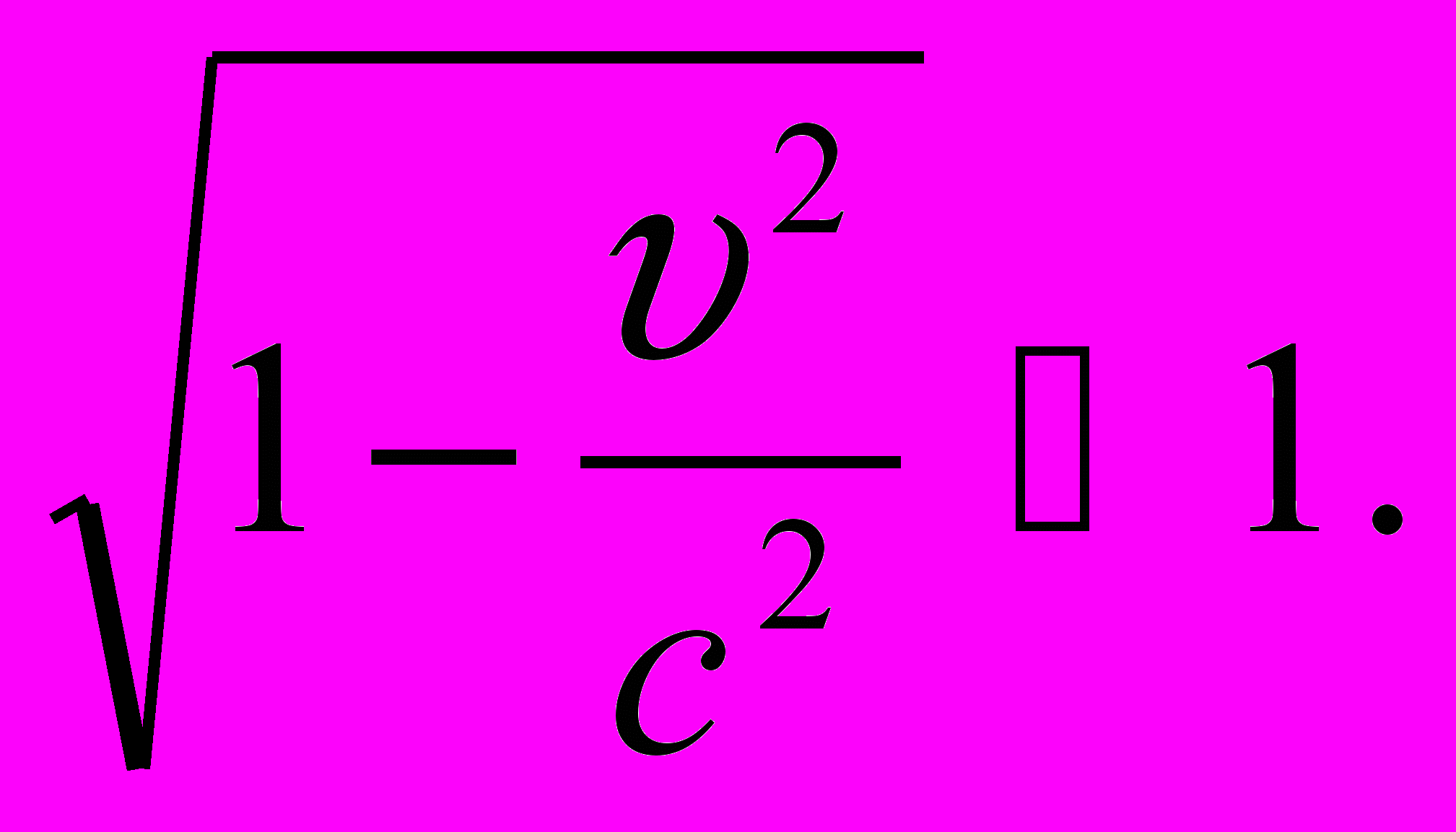
Величина
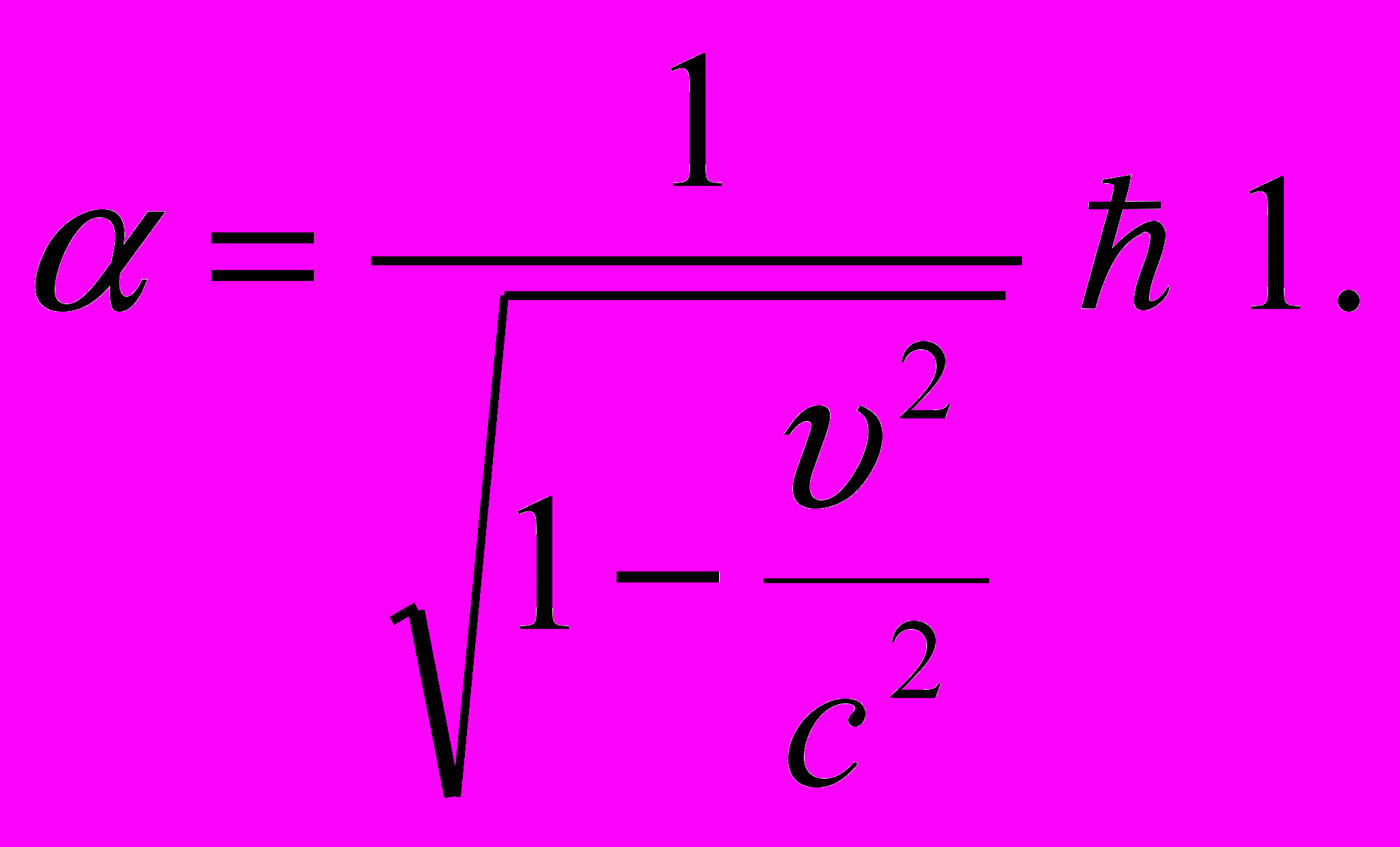
Следовательно,
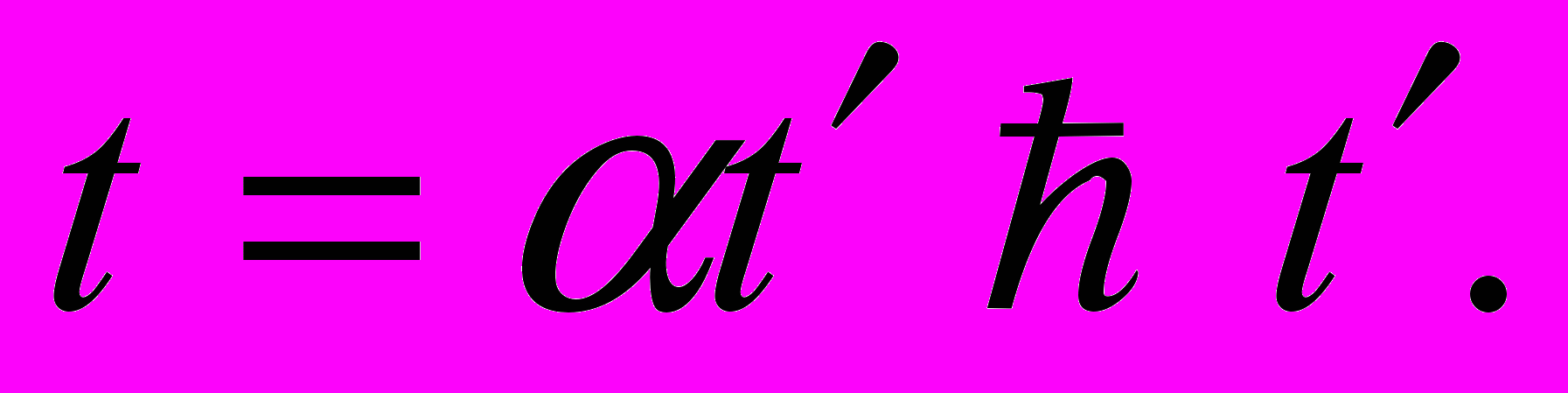
Это означает, что неподвижный наблюдатель обнаруживает замедление хода движущихся часов в α раз по сравнению с точно таким же, но находящимися в покое часами.
Данная формула проверена экспериментально физиками в разных опытах. Приведем один из них. В 1971 г. было проведено сравнение хода цезиевых часов относительно двух систем отсчета. Одни часы находились в полете вокруг Земли на реактивном самолете, а другие оставались в обсерватории на Земле. При приземлении самолета отставание часов, путешествующих вокруг Земли, от покоящихся составляло около 200 нс. На заключительном этапе показания всех часов вновь сравнялись в лаборатории.
§ 10. Относительность расстояний
Рассмотрим стержень, покоящийся относительно инерциальной системы К´и движущейся относительно инерциальной системы К. Возможны следующие два случая.
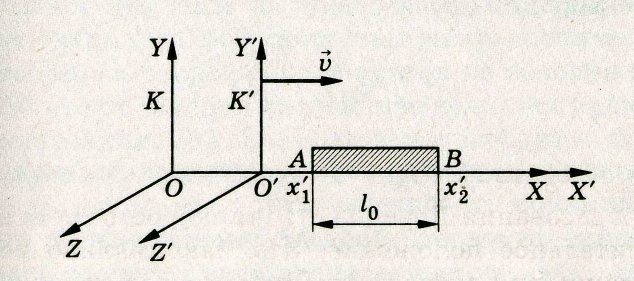
Рис. 12
Оси ОХ и О`Х` систем направлены вдоль одной прямой. Стержень расположен перпендикулярно направлению скорости. Длина стержня в системе К, относительно которой он движется, такова:
L = y2 – y1 (или L = z2 - z1).
В системе К`, относительно которой стержень покоится, его длина будет L` = y2` – y1`.
Оси ОY и OZ перпендикулярны скорости. Поскольку при переходе от одной системы к другой координаты y и z не меняются, то L = L`.Значит, длина стержня, расположенного в направлении, перпендикулярном движению, не меняется при переходе от одной инерциальной системе к другой.
Рассмотрим другой случай, стержень расположен вдоль направления скорости (вдоль оси ОХ). В системе К`, относительно которой стержень покоится, длина стержня
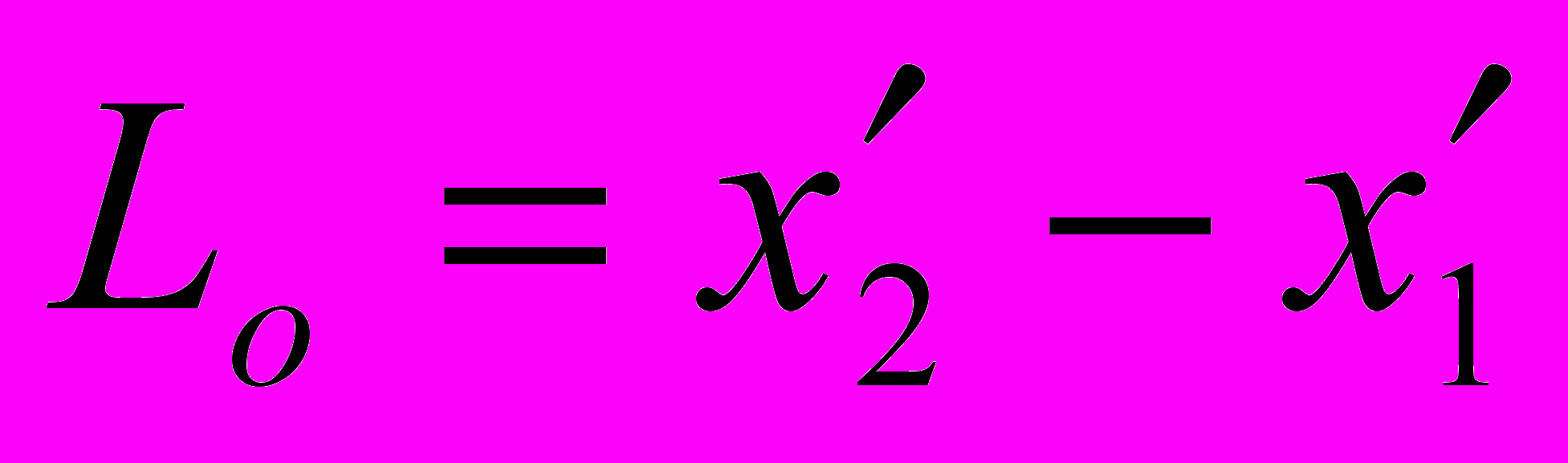 .
. Это длина покоящегося стержня (длина покоя). Какова длина стержня с точки зрения системы К, относительно которой стержень движется со скоростью
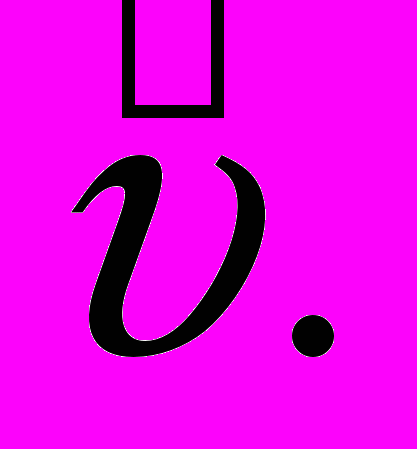 ? Обратимся к определению длины движущегося стержня, предложенное Эйнштейном. Наблюдатель системы К одновременно по своим часам отмечает положение концов стержня в своей системе координат. Длиной стержня L в системе К является разность
? Обратимся к определению длины движущегося стержня, предложенное Эйнштейном. Наблюдатель системы К одновременно по своим часам отмечает положение концов стержня в своей системе координат. Длиной стержня L в системе К является разность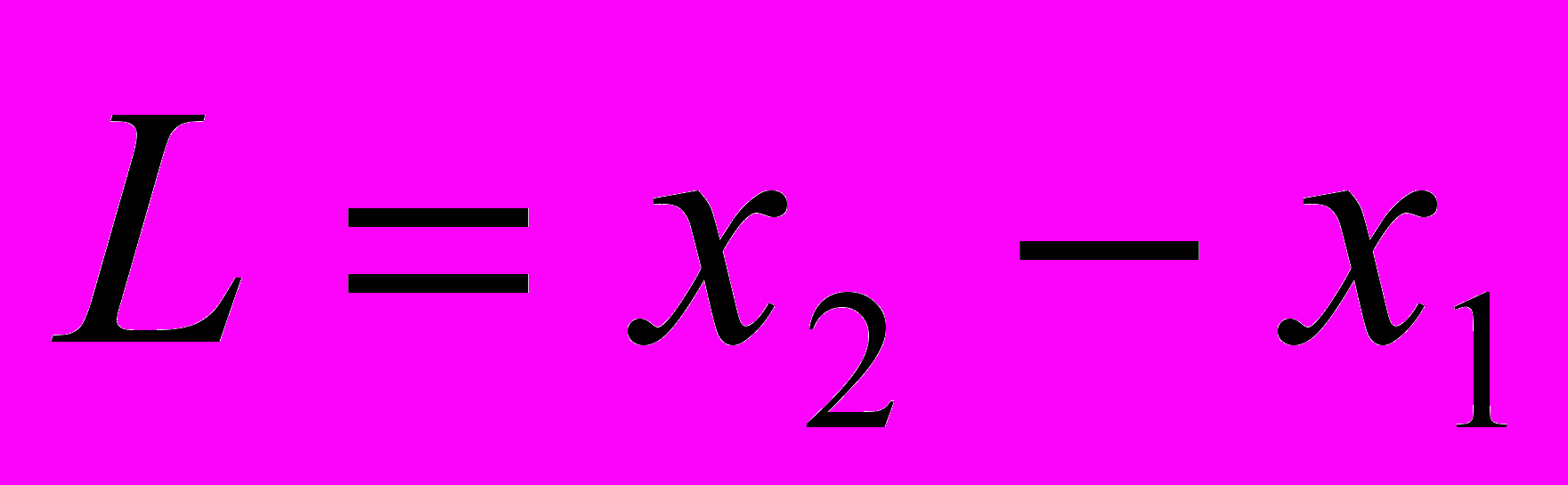 ,
, где х2 и х1 относятся к одному и тому же времени.
Согласно преобразованиям Лоренца для координат

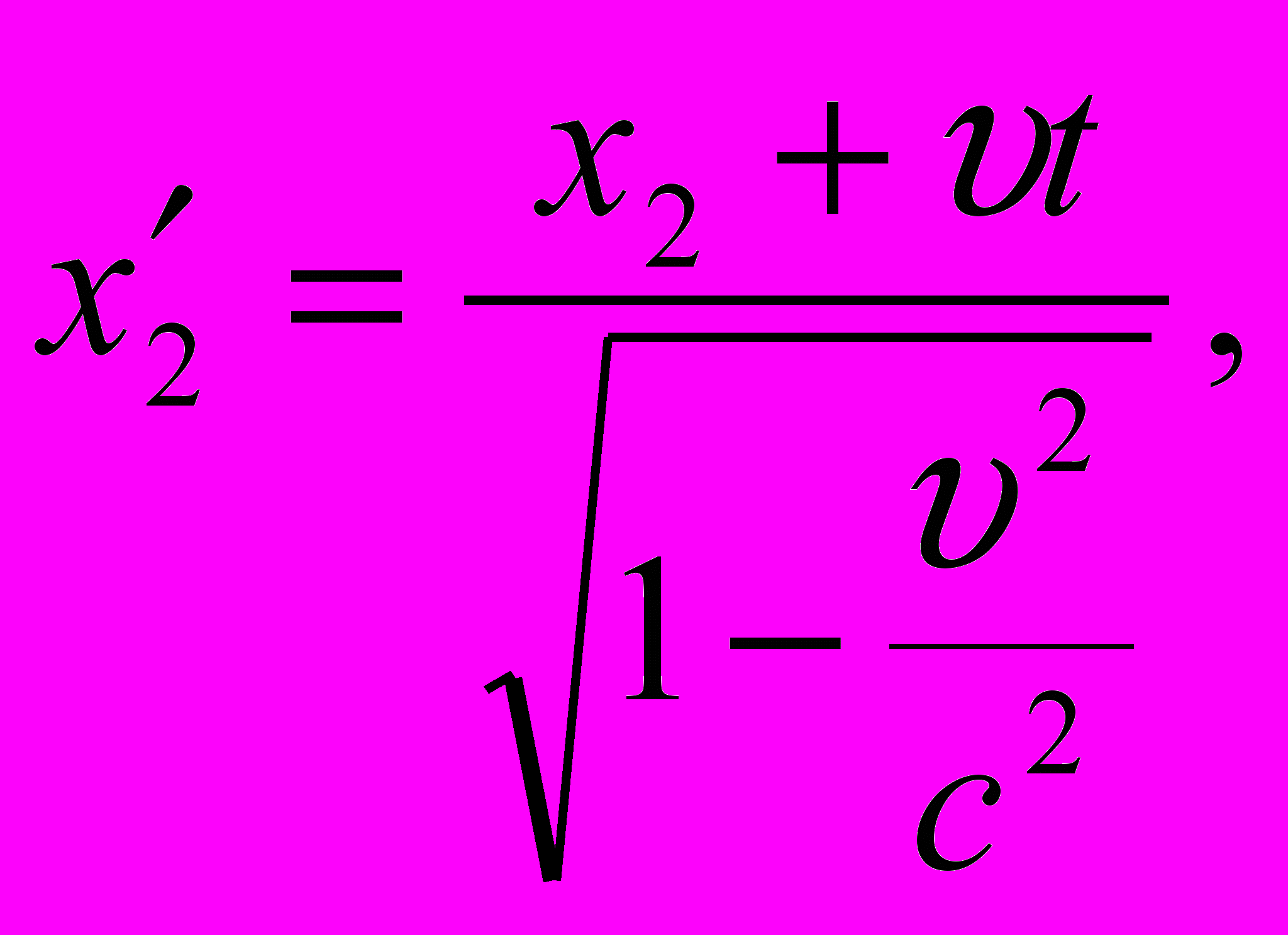
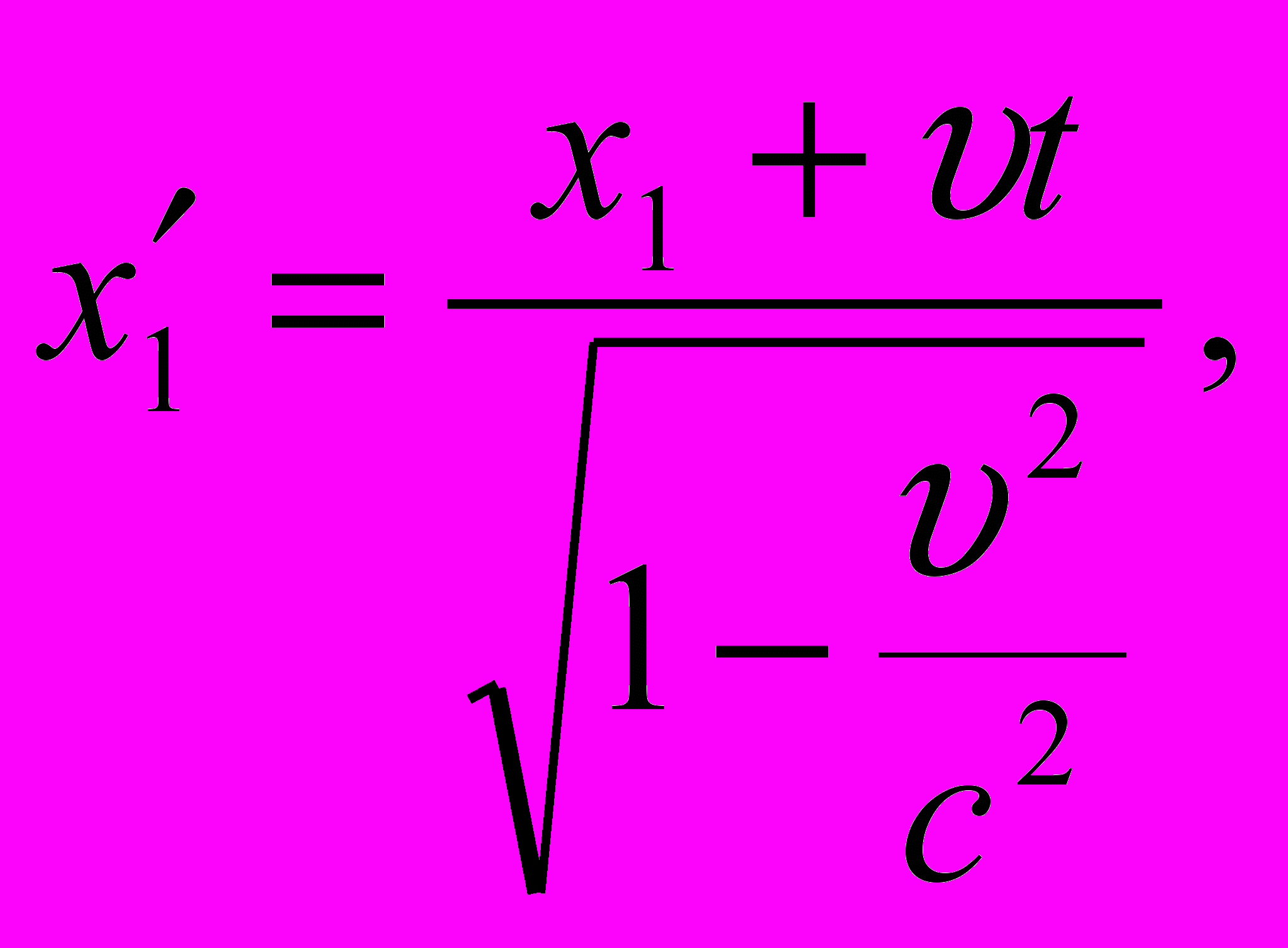
Мы должны использовать именно эти преобразования, содержащие время t, так как концы стержня - х1 и х2 засекаются в один и тот же момент времени t- время в системе К.
Следовательно, L0 = х2` – х1`=
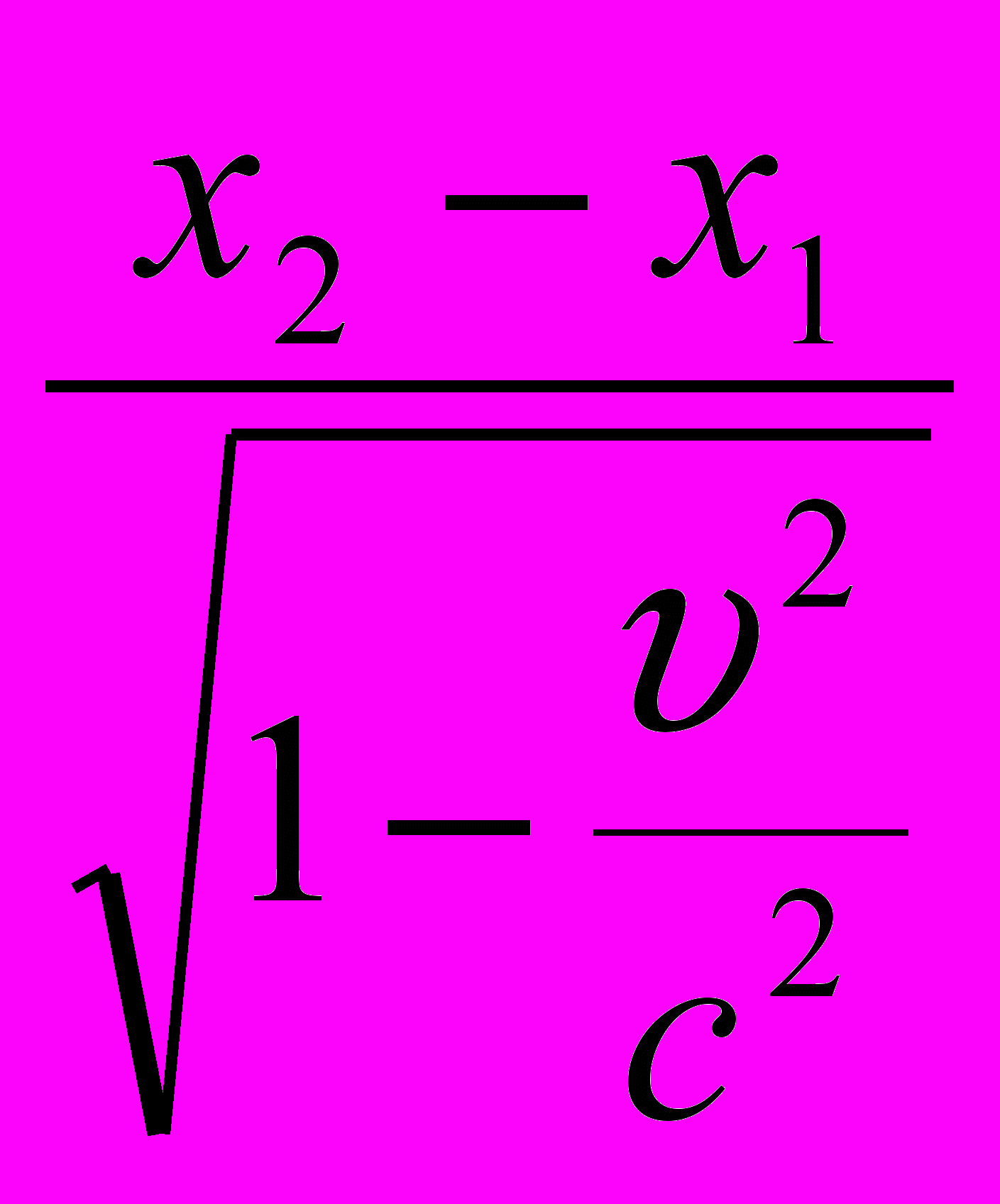 =
=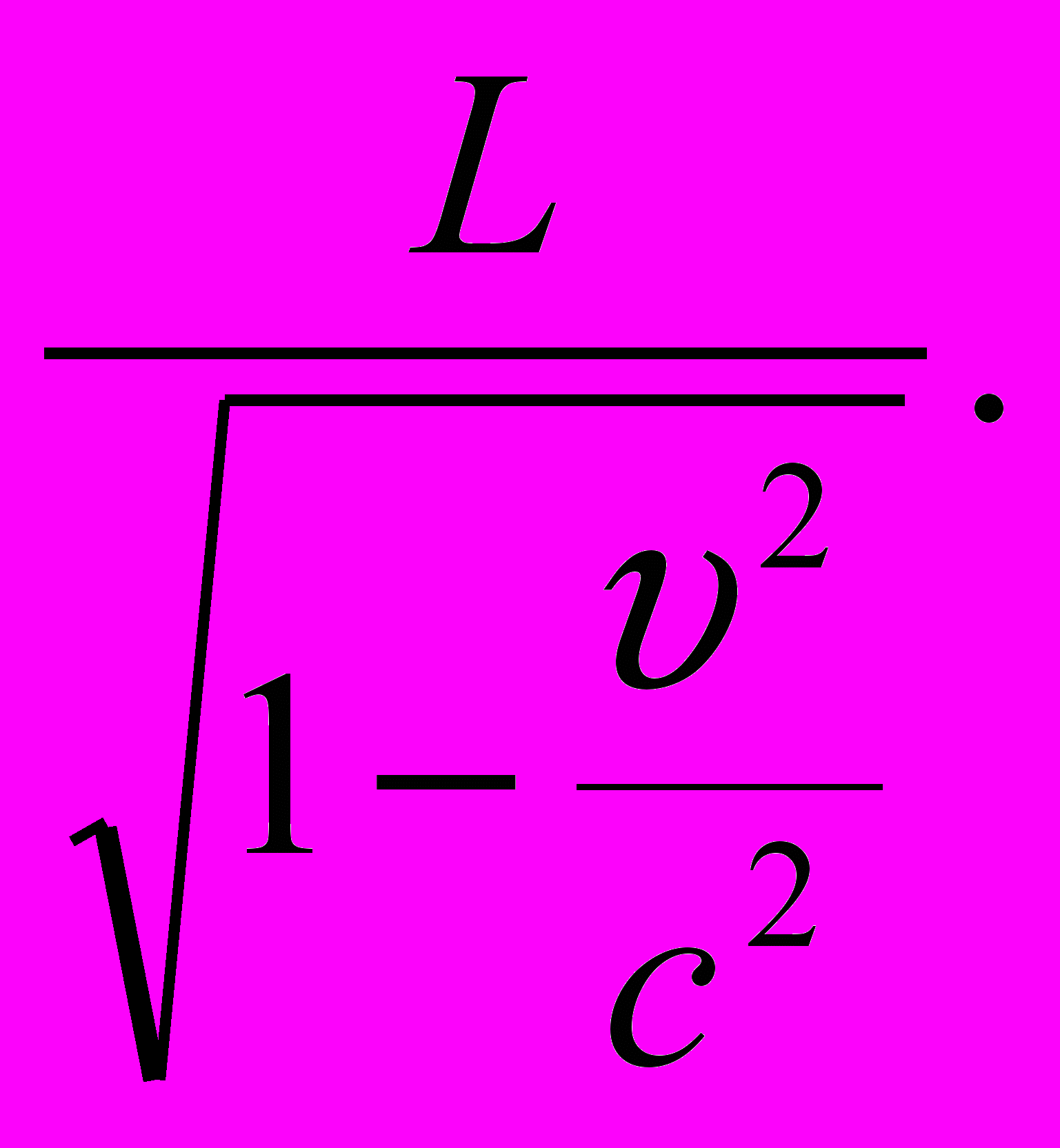
Между величинами L и L0 в специальной теории относительности существует следующая связь:
L = L0
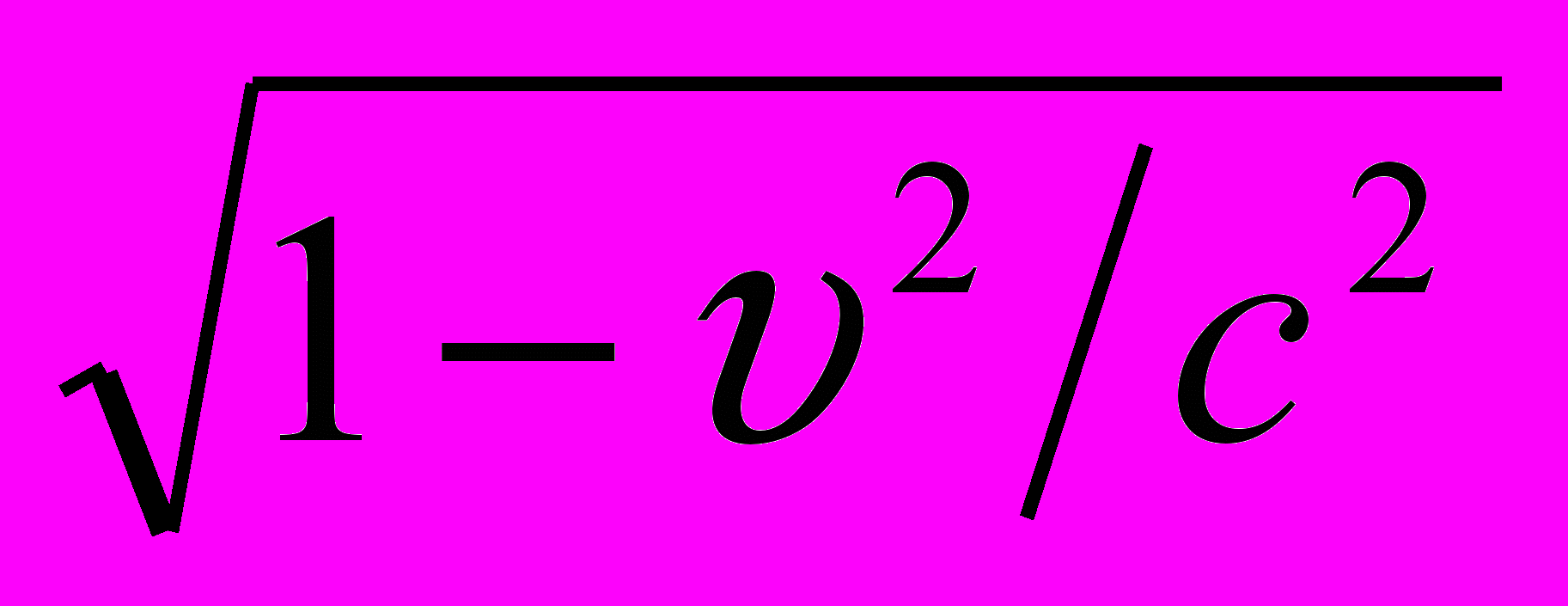 .
.Из формулы следует, что длина стержня, измеренная в системе К, относительно которой он движется, оказывается меньше длины того же стержня, измеренной в системе К`, относительно которой стержень покоится.
Обнаружить сокращение движущегося стержня непосредственно экспериментально не представляется возможным из-за того, что оно может стать заметным лишь при скоростях, близких к скорости света. Измерение длин можно производить только для макроскопических тел, а такие тела практически невозможно разогнать до больших скоростей.
§ 11. Релятивистский закон преобразования скоростей
В классической механике закон преобразования (сложения) скоростей при переходе из одной системы отсчёта в другую выражается соотношением:
υх = υх` + υ0,
где υ0 – модуль скорости инерциальной системы К` относительно системы К (скорость
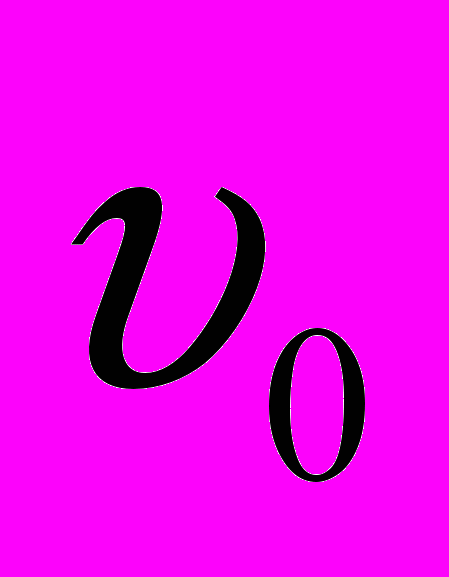 направлена вдоль оси ОХ), υх` = const – проекция на ось ОХ скорости тела в системе К`, υх = const – проекция на ось О`Х` скорости тела в системе К.
направлена вдоль оси ОХ), υх` = const – проекция на ось ОХ скорости тела в системе К`, υх = const – проекция на ось О`Х` скорости тела в системе К.Однако мы убедились, что закон сложения скоростей неприменим при изучении электромагнитных явлений. Если воспользоваться преобразованиями Лоренца, то можно получить релятивистский закон сложения скоростей :
υх = (υх` + υ0)/ (1 + υ0 υх`/ с2).
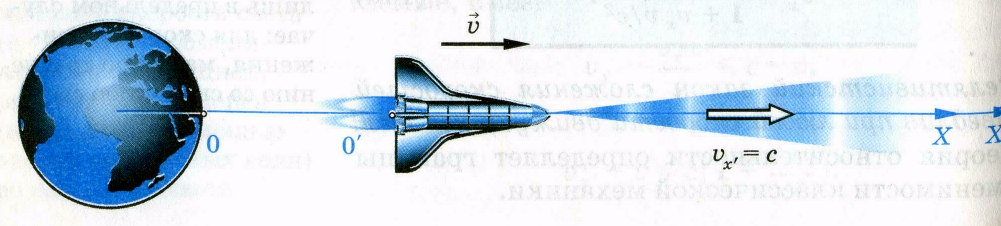
Рис. 13
Сущность этого закона заключается в том, что он выражает постоянство скорости света во всех инерциальных системах отсчета. Поясним это с помощью мысленного эксперимента. Предположим, что ракета движется со скоростью υ0 относительно Земли (рис. 13). И с ракеты на Землю послан радиосигнал. Свяжем с Землей систему К, а с ракетой К`. Скорость радиосигнала в системе К` равна с. Поскольку направление скорости
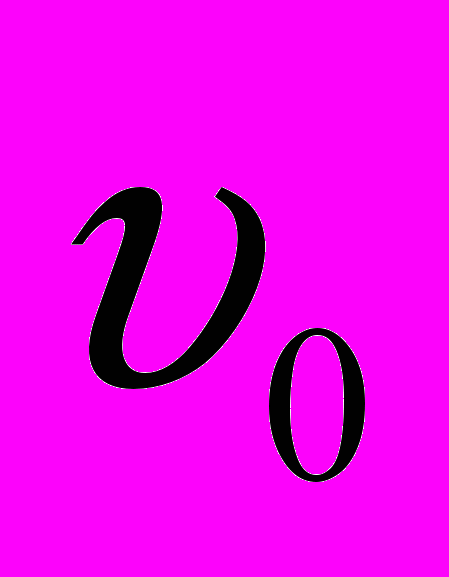 и скорости сигнала совпадают, то υх`= с. Тогда
и скорости сигнала совпадают, то υх`= с. Тогда υх = ( с + υ0)/ (1 + υ0 с/ с2).
После преобразований получим υх = с. Следовательно, формула (закон) сложения скоростей соответствует второму постулату специальной теории относительности.
Данное положение специальной теории относительности подтверждается опытом. Так, в физике частицы условно делят на два класса. К частицам, движущимся со скоростью с, относятся безмассовые частицы – фотоны и нейтрино; к частицам другого класса, скорость которых меньше скорости с - элементарные массовые частицы (электроны, протоны, нейтроны и др.) атомы, молекулы, макроскопические тела. Как показывает опыт, при любых относительных скоростях инерциальных систем отсчета υ0 < с нельзя при переходе от одной из них к другой изменить скорость частицы так, чтобы нарушить принадлежность к ее классу.
§ 12. Интервал
Анализируя содержание специальной теории относительности в форме, данной в 1905 г. А.Энштейном, Г. Минковский в 1908 г. выдвинул идею, которая, обогатила специальную теорию относительности. Подойдем к этой идее следующим образом.
Из соотношения
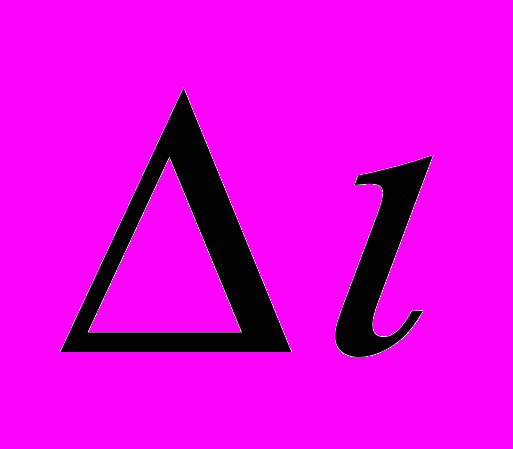 =
=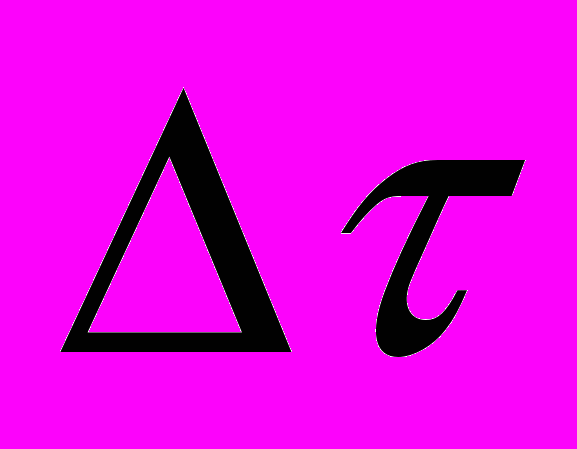 /
/ 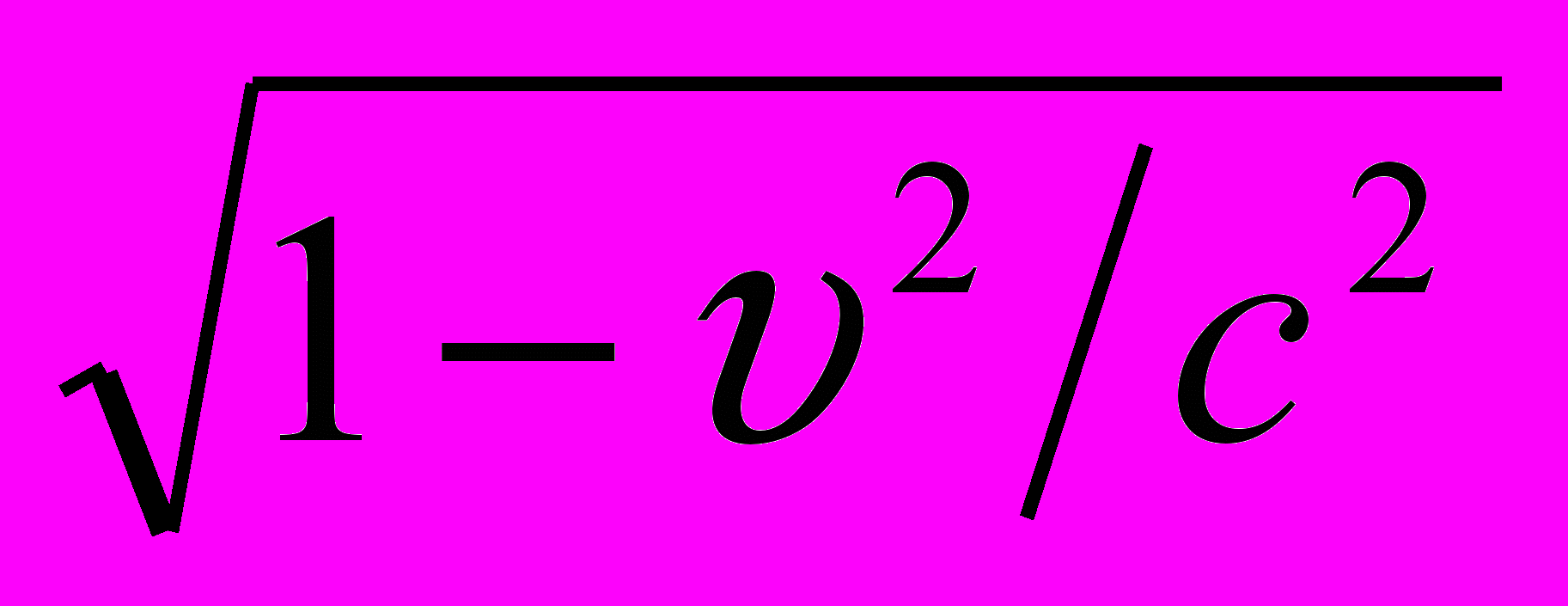 следует:
следует:с2 (
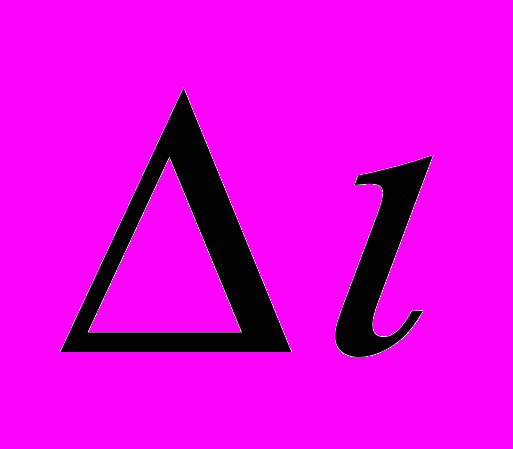 )2 – υ2(
)2 – υ2(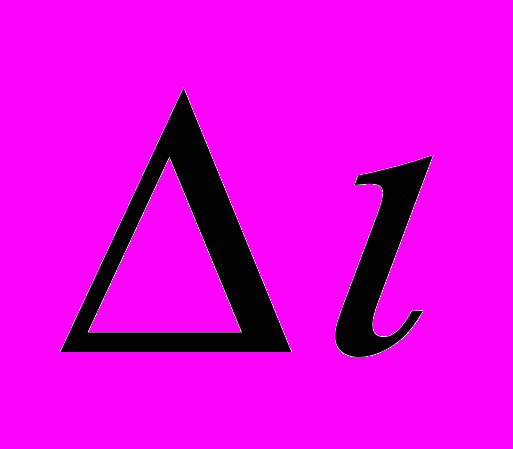 )2 = с2 (
)2 = с2 (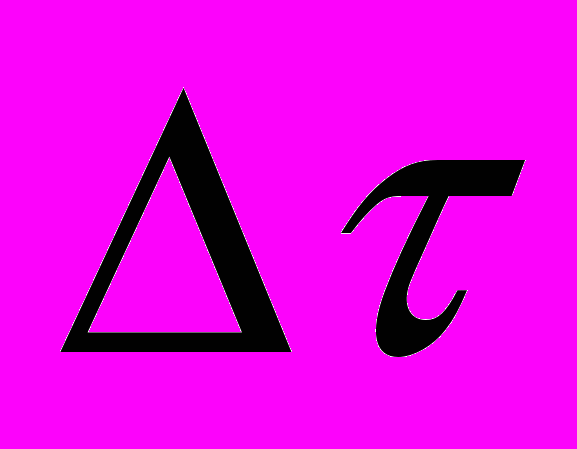 )2.
)2.Перепишем это выражение иначе:
с2 (
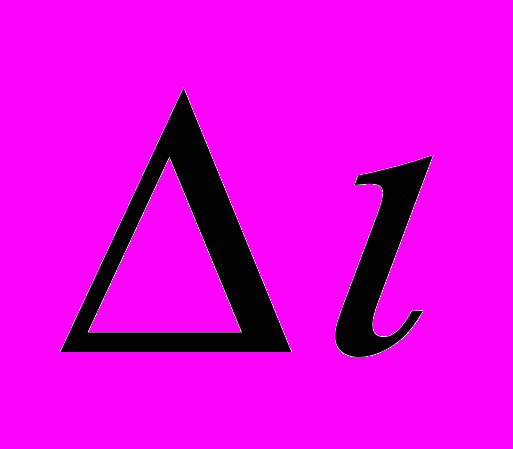 )2 – R2 = с2 (
)2 – R2 = с2 (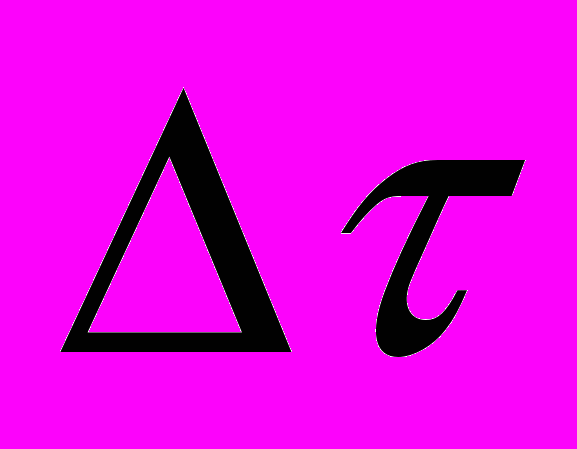 )2,
)2,где R = υ
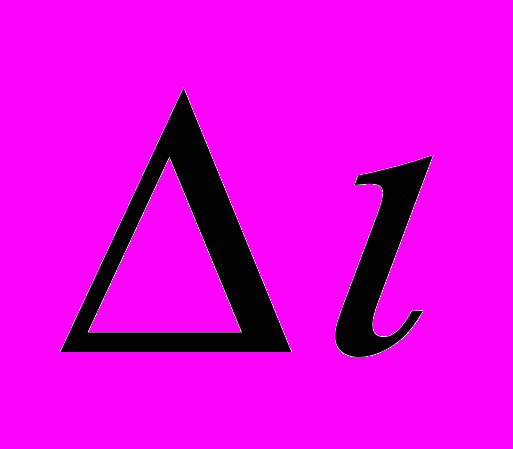 - расстояние, на которое переместится частица при своём движении со скоростью υ в системе отсчета К за время
- расстояние, на которое переместится частица при своём движении со скоростью υ в системе отсчета К за время 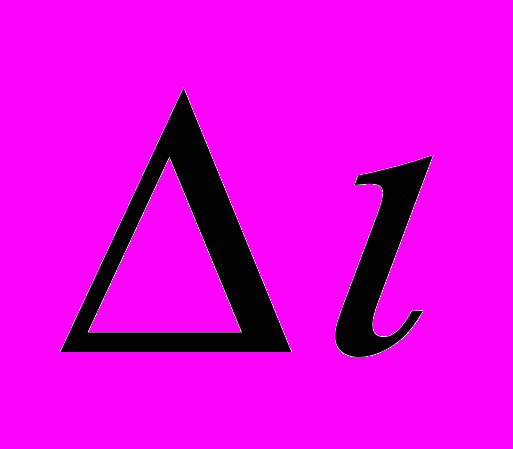 .
. Так как величины с и
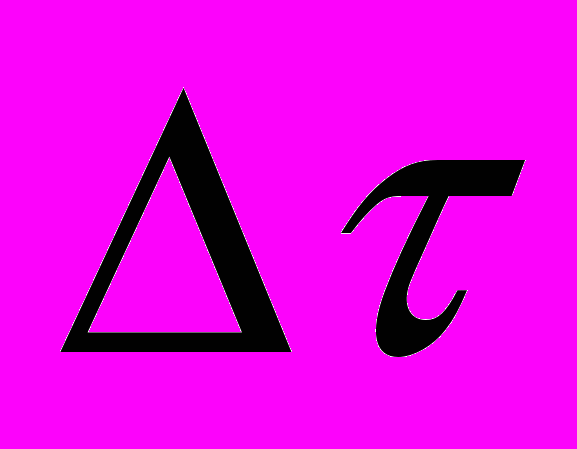 инвариантны в любых инерциальных системах отсчета, то выражение
инвариантны в любых инерциальных системах отсчета, то выражениес2 (
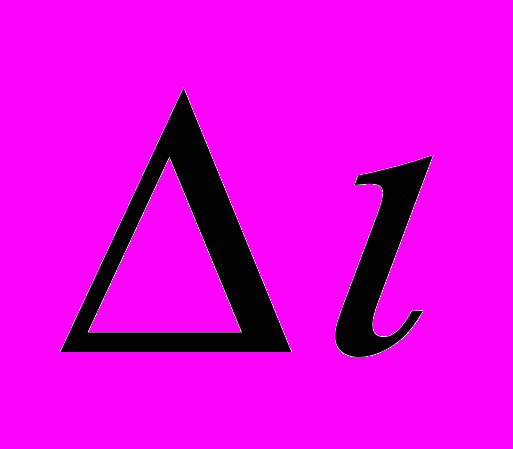 )2 – R = инвариант.
)2 – R = инвариант.Этот инвариант является квадратом очень важной величины, которой назвали интервалом и обозначили буквой s:
с2 (
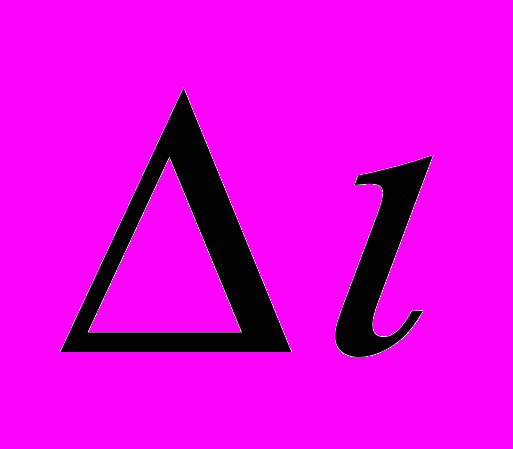 )2 – R = s2.
)2 – R = s2.Г. Минковский показал, что абсолютность пространственно- временного интервала имеет место для любых событий. При этом величины - время и расстояние для определенной пары событий относительны, т.е. их значения зависят от выбора инерциальной системы отсчета. Относительность этих величин является следствием абсолютности составленной из них пространственно-временной величины s, т.е. инвариантности интервала.
Выдвинутая идея Г. Минковским обогатила специальную теорию относительности, которая устанавливает связь пространства и времени. Она состоит в том, что пространство и время объединяются в единое абсолютное пространство – время. Его составляющие – отдельно пространство и отдельно время – относительны в силу абсолютности новой сущности: пространство – время.
§ 13. Энергия, импульс и сила в специальной
теории относительности
Безмассовые частицы. Частицы, движущиеся в вакууме со скоростью света, не могут быть ни замедлены, ни ускорены. Они всегда движутся только по инерции во всех инерциальных системах отсчета. Масса частиц, движущихся с абсолютной скоростью света, равна нулю. Такие частицы называют безмассовыми. Экспериментально такие частицы обнаружены - это фотоны и нейтрино.
Опыты по взаимодействию фотонов и нейтрино с атомами, ядрами и элементарными частицами показывают, что при их взаимодействии выполняются законы сохранения энергии и импульса. Это позволяет сделать вывод, что безмассовые частицы обладают энергией и импульсом.
Частицы с ненулевой массой. Существуют частицы, например, частицы вещества, которые движутся всегда со скоростью, меньшей абсолютной скорости. Скорости этих частиц могут изменяться в широких пределах от нуля до любых значений υ < с. Данное свойство этих частиц определяется наличием у них массы. Называют их массовыми частицами. Масса этих частиц абсолютна, она не зависит от выбора инерциальной системы отсчета, а значит и от скорости частиц.
Если массовая частица в ее собственной системе отсчета имеет импульс равный нулю р = 0, то энергия этой покоящейся частицы отлична от нуля Е ≠ 0.
Закон взаимосвязи массы и энергии. А. Эйнштейном была установлена пропорциональность между энергией и массой:
Е = mc2.
Полученное А. Эйнштейном выражение является фундаментальным законом природы и называется законом взаимосвязи массы и энергии. Согласно данной формуле, всякое тело массой m в состоянии покоя обладает энергией Е, равной произведению массы тела на квадрат скорости света в вакууме. Её иногда называют собственной энергией тела.
Предположим, что покоящаяся частица вещества имеет массу, равную 1 г. Согласно закону взаимосвязи массы и энергии данной массе соответствует энергия 9 ∙ 1013 Дж. Такая энергия выделяется при взрыве атомной бомбы. Её хватило бы для превращения 36 000 т воды (при температуре 00 С и нормальном атмосферном давлении) в пар. Как следует из примеров, энергия Е = mc2 очень велика.
Релятивистская энергия. Из принципа независимости законов физики от инерциальных системах отсчета, следует, что во всех таких системах должен соблюдаться закон сохранения энергии.
Пусть в инерциальной системе отсчета К тело (или частица) движется со скоростью
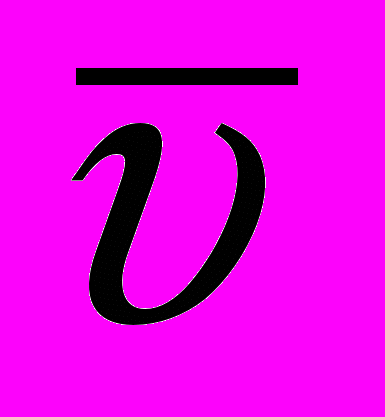 = соnst. Тогда релятивистская энергия Ер, согласно теории относительности, определяется следующим выражением:
= соnst. Тогда релятивистская энергия Ер, согласно теории относительности, определяется следующим выражением:Ер = mc2/
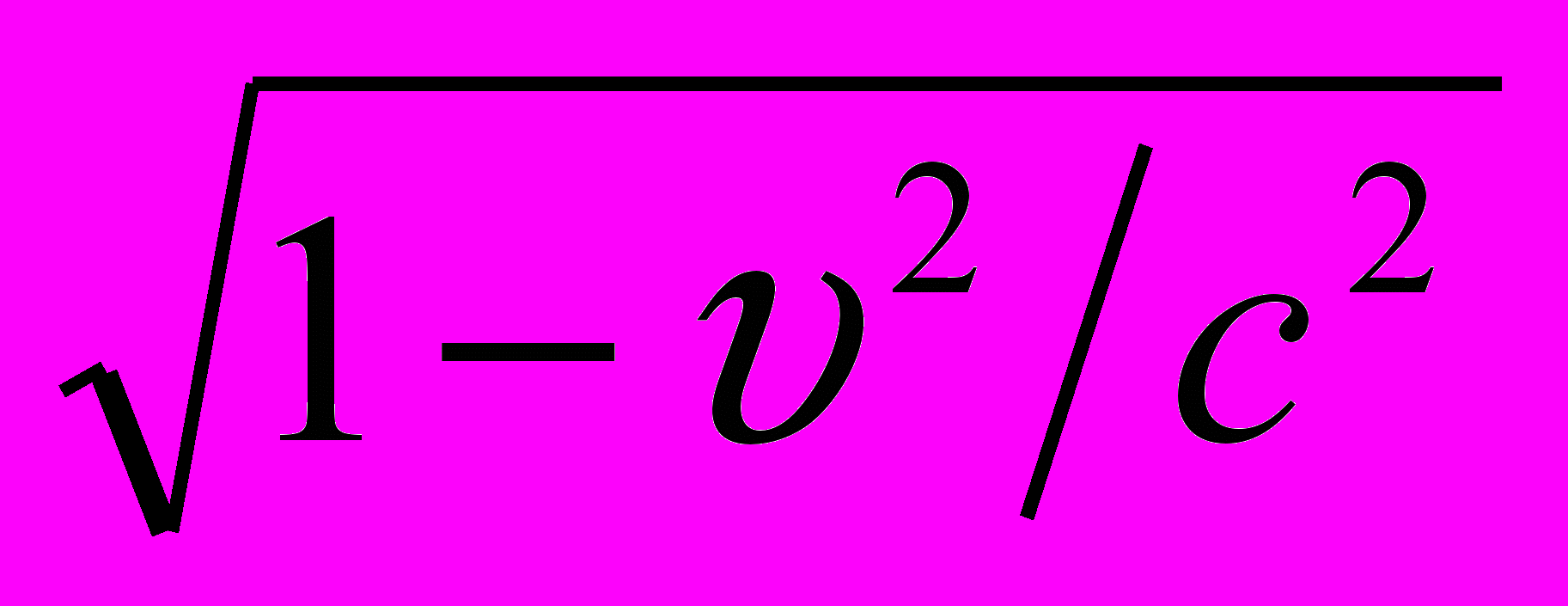 .
.Как следует из формулы, релятивистская энергия больше собственной энергии этого тела, равной Е = mc2. Разность между релятивистской энергией движущегося тела и его собственной энергии равна кинетической энергии Ек тела: Ер – Е = Ек.
Релятивистский импульс. Формула определения релятивистского импульс такова:
р = mυ/
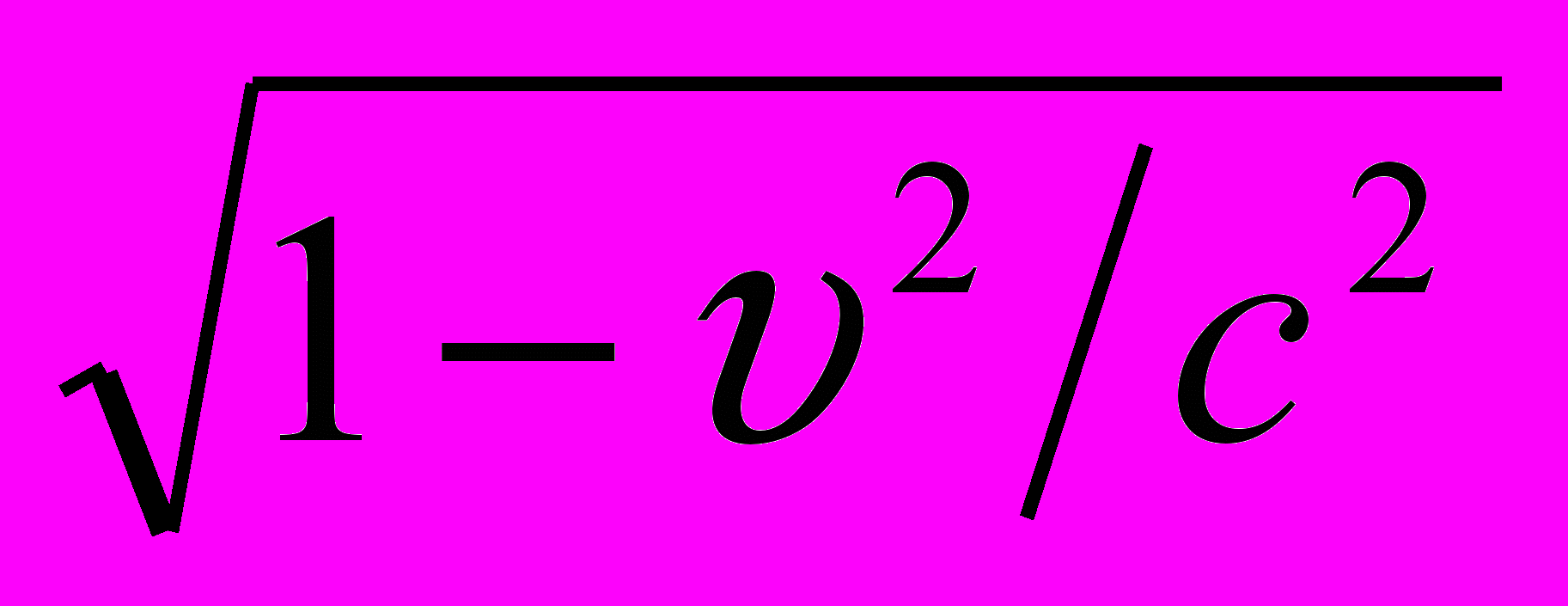 .
.Из формулы видно, что с увеличением скорости υ релятивистский импульс растет быстрее, чем классический рк = mυ. Отметим, что классический импульс может быть получен из формулы релятивистского импульса при υ << с.
Связь между релятивистским импульсом и релятивистской энергией. Иэ формул определения релятивистских импульса и энергии и исключив скорость, после преобразований получим
Е2 = m2c4 + р2 c2. (1)
Это соотношение справедливо не только для массовых, но и для безмассовых частиц. Покажем это. На основании выше указанных формул определения релятивистской энергии и релятивистского импульса можно записать Е = рс2/ υ. Тогда энергия частицы, движущаяся со скоростью υ = с, будет равна Е = рс.
Из уравнения (1) получим m2c4 = Е2 - р2 c2. Но Е = рс, следовательно, m2c4 = 0 или m = 0. Таким образом, мы приходим к выводу, что безмассовые частицы (m = 0) могут двигаться только со скоростью света в вакууме.
Выражение (1) для безмассовой частицы можно записать в виде
Е2 - р2 c2 = m2c4 = 0.
Данное выражение справедливо для любой безмассовой частицы во всех инерциальных системах отсчёта.
§ 14. Методические рекомендации к решению задач
Задача 1. (В уровень, «применение») Частица, называемая мезоном, движущаяся со скоростью 0,99с, пролетела в системе отсчета К от места своего рождения до точки распада расстояние 4,7 км. Найдите собственное время жизни мезона.
Р е ш е н и е. В системе К время движения мезона
 t от точки своего рождения до распада определяется по формуле
t от точки своего рождения до распада определяется по формуле  t = L/υ, (1)
t = L/υ, (1)где L - расстояние, пройденное мезоном, υ – скорость движения. Собственное время
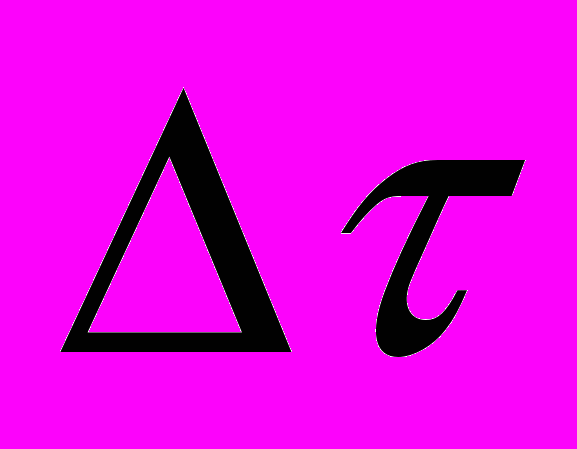 движения частицы в системе координат, связанной с самой частицей, определяется по формуле:
движения частицы в системе координат, связанной с самой частицей, определяется по формуле: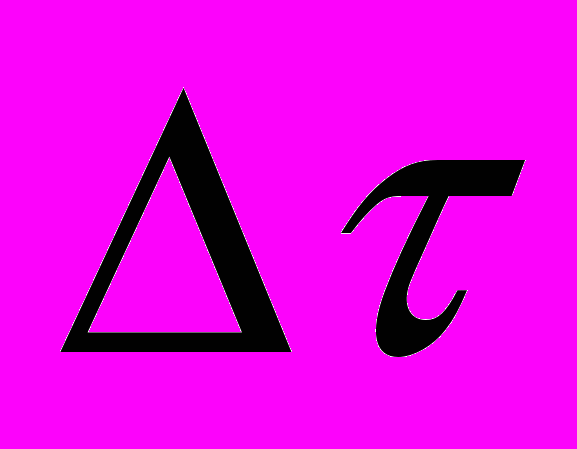 =
=  t
t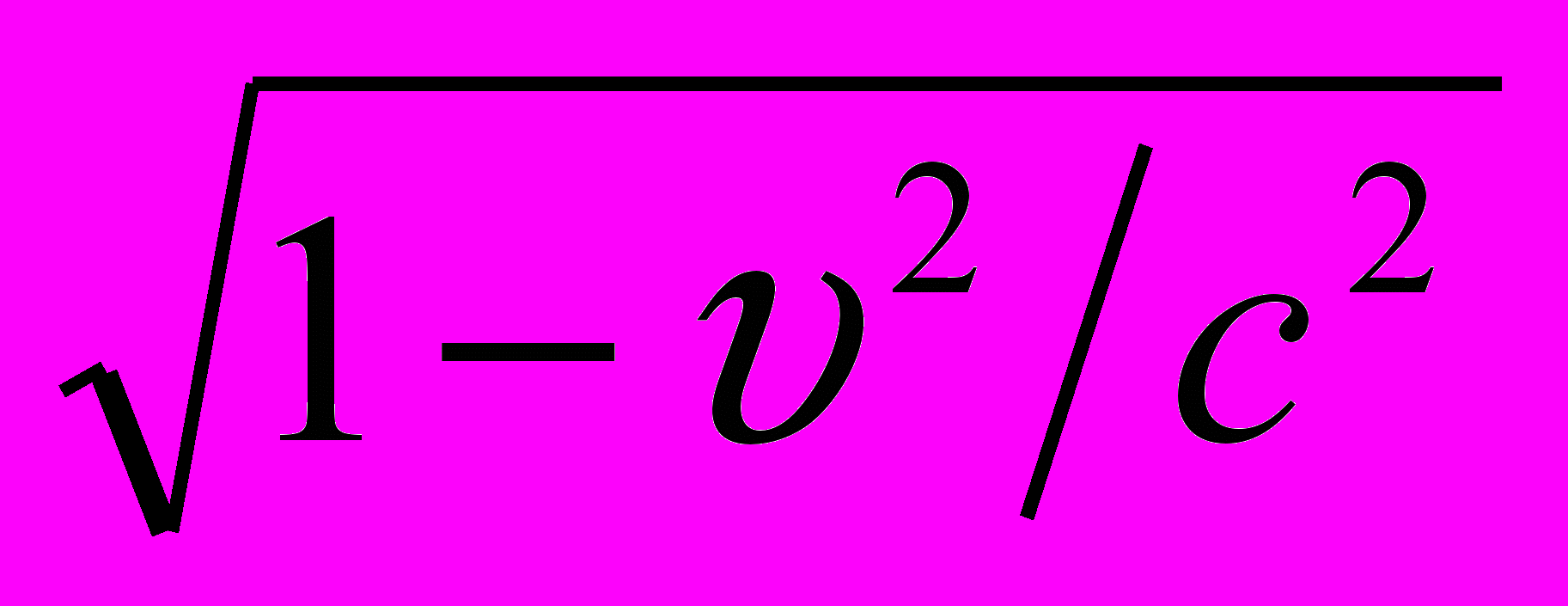 . (2)
. (2)Из уравнений (1) и (2) находим:
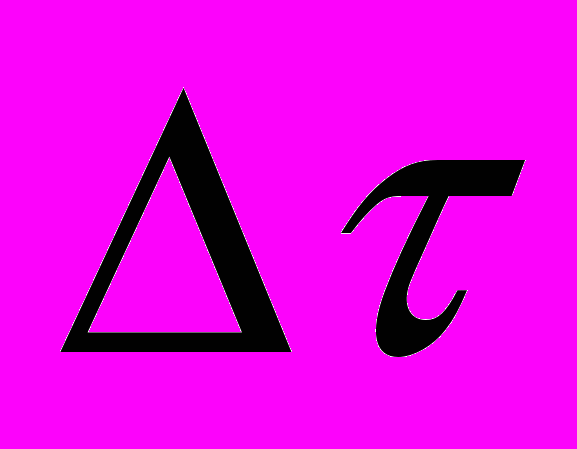 = (L/υ)
= (L/υ) 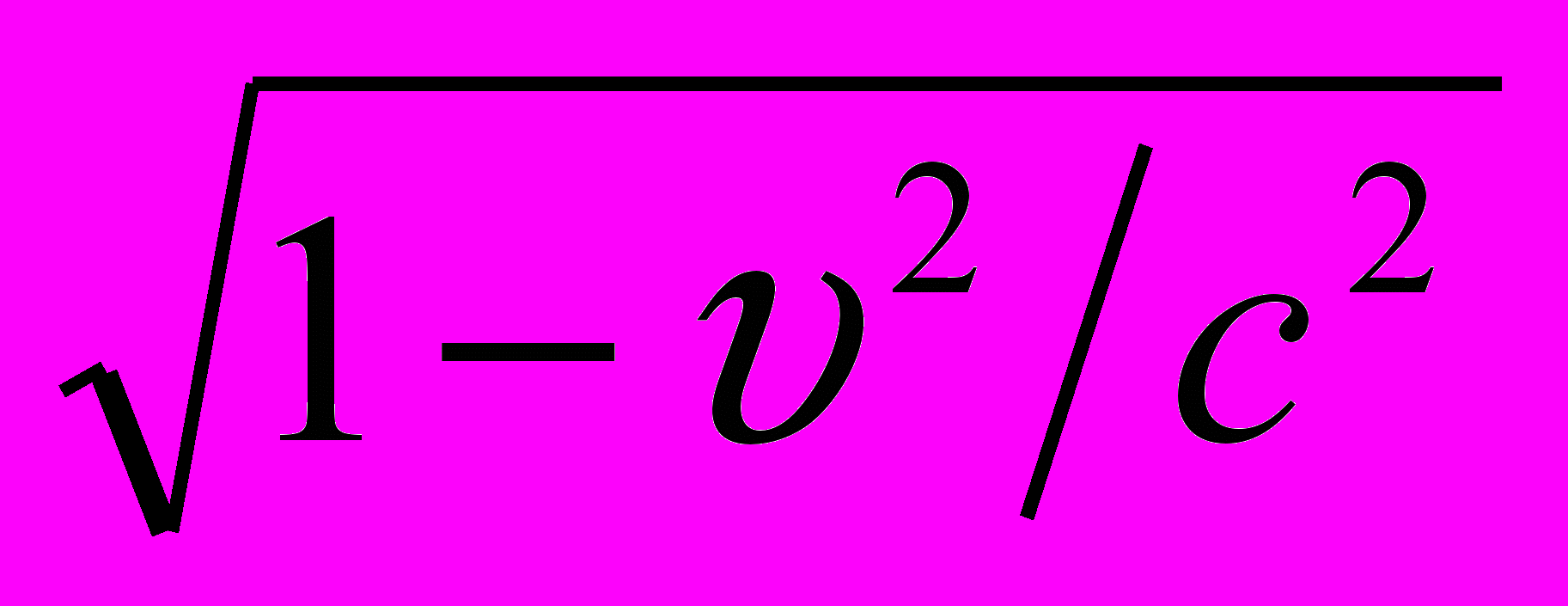 .
.Подставляя числовые значения, получим
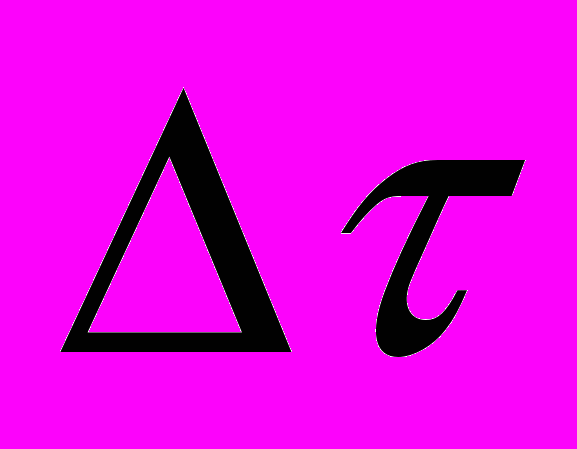 = 2,2 ∙ 10-6 с. Собственное время жизни мезона составляет 2,2 ∙ 10-6 с.
= 2,2 ∙ 10-6 с. Собственное время жизни мезона составляет 2,2 ∙ 10-6 с.Задача 2. (Уровень С, «анализ») Система К` движется относительно К со скоростью 1,50 ∙ 108 м/с. В начале отсчета времени t = 0, t` = 0 начала О и О` систем совпадали. Координаты центра шара, покоящегося в системе К`, x`= 40м, y`= 20 м, z` = 0. Какими будут координаты центра шара в системе К через 2,00 мкс?
Р е ш е н и е. В задаче требуется найти координаты центра шара в системе отсчёта К: x, y, z. Согласно преобразованиям Лоренца имеем
x = (x` + υt`)/
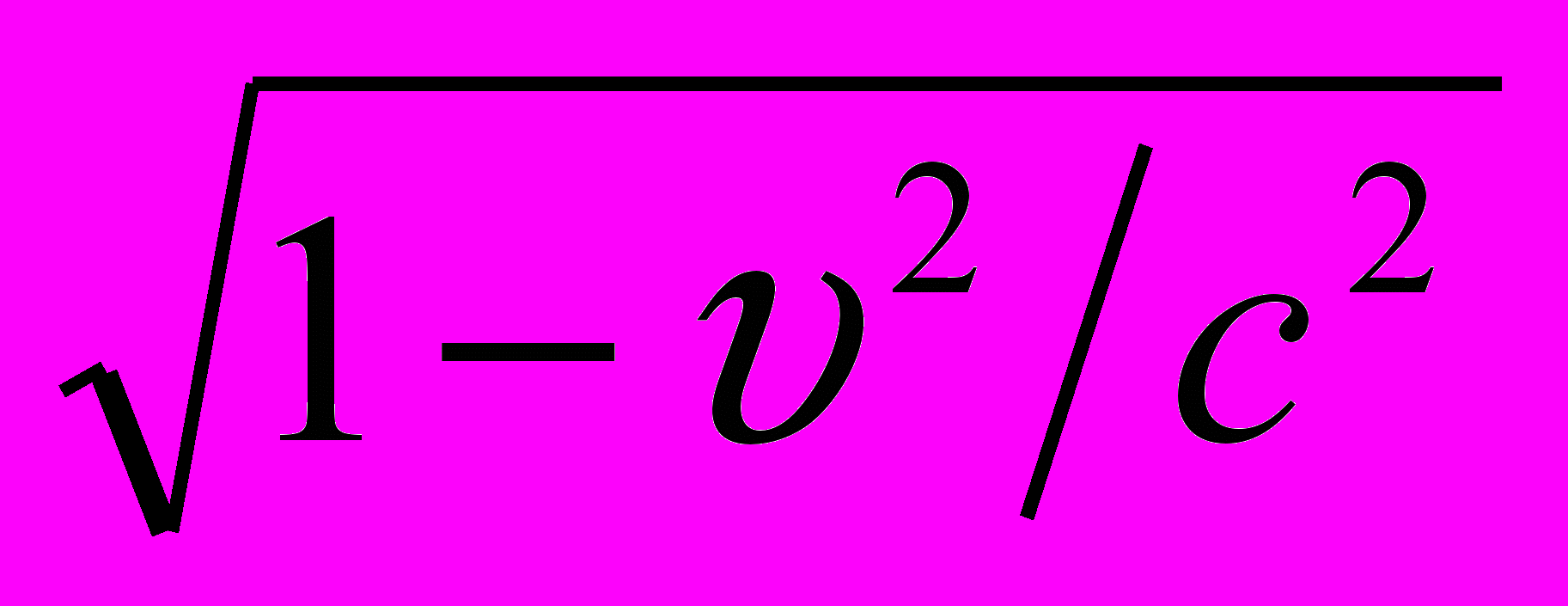 , (1)
, (1)y = y`, (2)
z = z`. (3)
Чтобы определить координату х в системе отсчета К, надо найти собственное время
 между событиями по часам наблюдателя, находящегося в системе К`
между событиями по часам наблюдателя, находящегося в системе К` 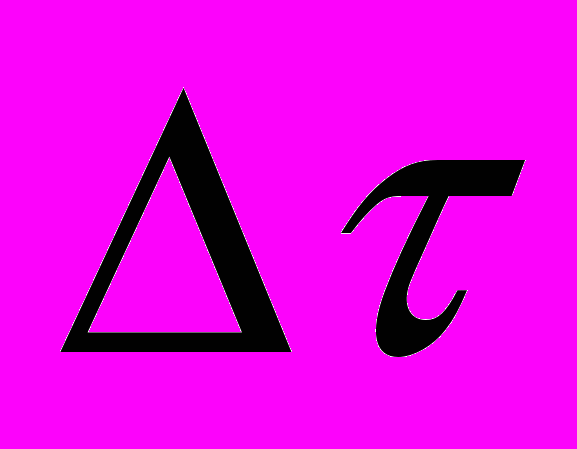 =
=  t
t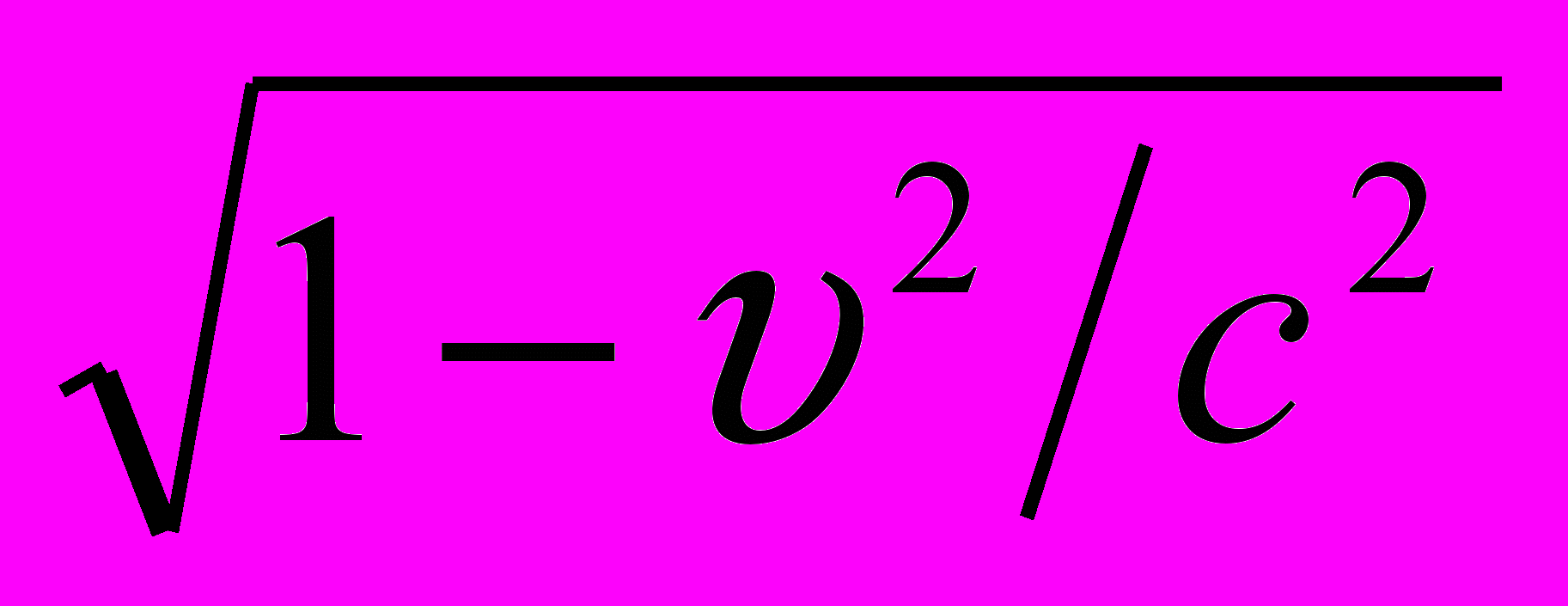 , где
, где  t – промежуток времени между теми же событиями в системе. Подставим в формулу необходимые данные:
t – промежуток времени между теми же событиями в системе. Подставим в формулу необходимые данные: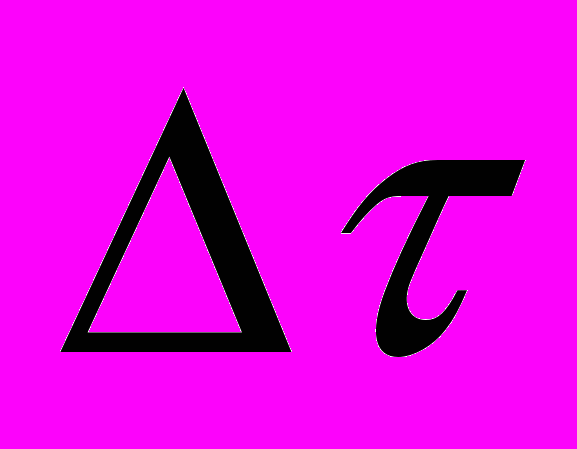 = 2 ∙ 10-6
= 2 ∙ 10-6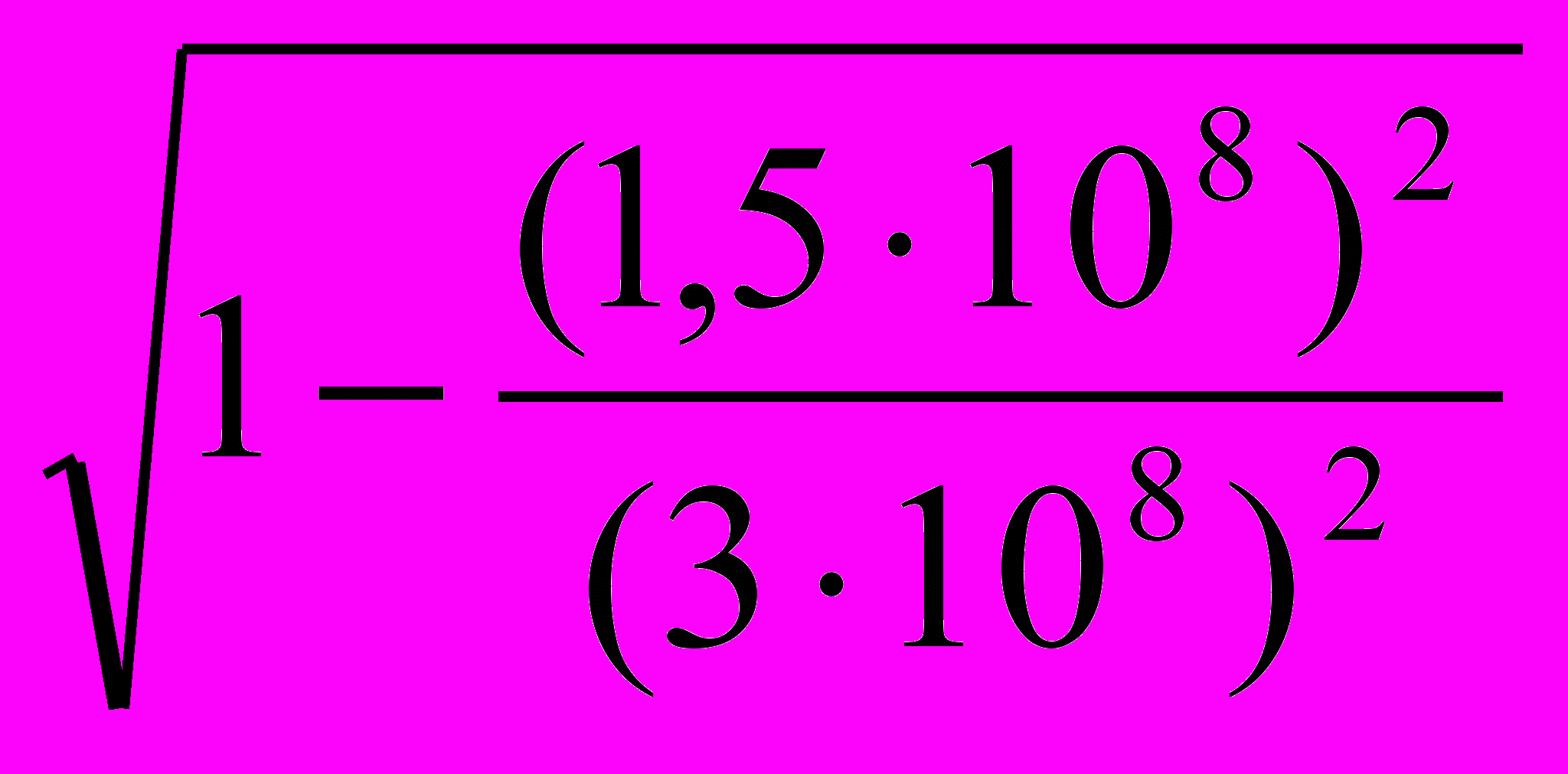 = 1,73 ∙ 10-6 с.
= 1,73 ∙ 10-6 с.Тогда координата х найдем, используя формулу (1):
х = (40 м + 1,50 ∙ 108 м/с ∙ 1,73 ∙ 10-6 с )/ 0,87 ≈344 м.

 Учитывая преобразования Лоренца, имеем y = 20 м , z = 0. Координаты центра шара в системе К такие: х = 344м, y = 20 м , z = 0.
Учитывая преобразования Лоренца, имеем y = 20 м , z = 0. Координаты центра шара в системе К такие: х = 344м, y = 20 м , z = 0. Задача 3. (Уровень С, «анализ») Две галактики разбегаются от центра Вселенной в противоположных направлениях с одинаковой скоростью 0,70 с относительно центра. С какой скоростью они удаляются друг от друга?
Р е ш е н и е. Для определения относительной скорости галактик υ12х воспользуемся релятивистским законом преобразования скоростей:

υ х = ( υ12х` + υ0)/ (1 + υ1х υ0`/ с2). (1)
Учтем, что галактики движутся в разные стороны относительно центра Вселенной, υ1 = υ = 0,70 с и υ2 = - υ = - 070 с. Тогда уравнение (1) примет вид υ = ( υ12` - υ)/ (1 - υ1`υ/ с2). Из данного уравнения находим
υ12` = 2 υ/ (1 – υ2/с2).
Подставим в формулу числовые значения: υ12` = 2 ∙ 0,70с/ (1 – 0,70с ∙ 0,70с /с2) ≈ 0,94с. Две галактики удаляются друг от друга со скоростью 0,94 с.
