В. П. Дьяконов, А. Н. Черничин Новые информационные технологии Часть Основы и аппаратное обеспечение Под общей редакцией проф. В. П. Дьяконова Смоленск 2003
| Вид материала | Документы |
- Высшее образование новые педагогические и информационные технологии в системе образования, 4841.75kb.
- Перевод с норвежского М. П. Дьяконовой Под редакцией М. А. Дьяконова Предисловие проф., 5465.89kb.
- Литература: Калугина Т. А. Новые информационные технологии в сфере образования: методологические, 14.35kb.
- Юрия Михайловича Лахтина, прочитанной на 3-х Лахтинских чтениях 21 сентября 2003 года, 1244.48kb.
- Под общей редакцией проф. Малого В. П., проф. Кратенко И. С. Харьков 2008, 8344.22kb.
- Информационные технологии и управление в технических системах всех форм обучения Под, 793.84kb.
- Леонид Владимирович Дьяконов указатель, 8647.04kb.
- Международный общественный благотворительный, 2426.77kb.
- 2. технические основы информационных технологий в экономике, 988.43kb.
- Учебник под редакцией, 9200.03kb.
1.4. Формы адекватности и объем информации
1.4.1. Формы адекватности информации
Обычно информация должна быть адекватна образу (объекту), который она описывает. Различают три формы адекватности информации:
- синтаксическая, отражающая формально-структурные свойства информации без учета ее смыслового содержания
- семантическая (смысловая), отражающая смысл информации и позволяющая судить о соответствии информационного образа объекта и самим объектом;
- прагматическая (потребительская) ценность информации для тех целей, ради которых она используется.
Ниже мы рассмотрим эти формы и отвечающие им меры информации более подробно.
1.4.2. Синтаксическая мера информации – бит и байт
Синтаксическая форма адекватности информации характеризуется объемом данных и количеством информации. Объем данных чаще всего измеряется числом символов (разрядов) Vd в передаваемом сообщении. В двоичной системе один разряд - это бит (или байт = 8 бит), в десятичной системе - это число, представленное одной арабской цифрой (от 0 до 9).
Единицей двоичной информации является бит. Он имеет всего два значения - логический 0 и 1 (или утверждения «Да» и «Нет» или «True» (Истина) или «False» (Фальшь или неправда). Бит может быть простейшим электрическим сигналом - есть напряжение на проводе, это логическая единица, нет - логический ноль. Точная величина напряжения принципиального значения не имеет.
Двоичные числа могут иметь много разрядов. К примеру, для передачи 16 значений десятичных чисел от 0 до 15 придется использовать минимум четыре разряда двоичного числа (24 = 16). Число 0, к примеру, мы можем записать как двоичное 0000, число 15 как 1111, а число 10 как 1010. В последнем случае имеем 10=18 + 04 + 12 + 01, где 8, 4, 2 и 1 - это веса разрядов двоичного числа.
По мере роста объема передаваемой информации пришлось перейти к более крупным единицам ее измерения. Оказалось, что для кодирования текстов самым приемлемым пакетом двоичных единиц информации стали байты - они содержат восемь двоичных единиц и, соответственно, имеют два в восьмой степени состояний (всего 28 = 256 со значениями от 0 до 255). Итак, информацию можно оценивать ее объемом - байтами, килобайтами (1 Кбайт = 1024 байта), мегабайтами (1 Мбайт = 1024 Кбайт) и т.д.
С идеи двоичного кодирования началось развитие цифровых вычислительных машин. Этому способствовало и то, что были созданы простые электронные схемы с двумя устойчивыми состояниями равновесия - например, электронные триггеры и запоминающие ячейки на основе заряжаемого и разряжаемого конденсатора. Простота этих схем содействовала надежности их работы и возможности миниатюризации.
1.4.3. Числа десятичные и шестнадцатеричные
Цифровая информация основана на применении чисел в той или иной системе исчисления. Числа характеризуются основанием. Выше мы познакомились с числами двоичными (основание 2) и восьмеричными (основание 8). В обиходе такие числа используются редко, хотя пользователям компьютерами они привычны.
А вот десятичные числа более привычны для людей, которых природа наградила 10 пальцами на руках и ногах. Считается, что именно поэтому люди полюбили десятичную систему исчисления, которой широко пользуются и поныне. Конечно же, современные микропроцессоры компьютеров справляются с десятичными числами так же, как и с двоичными - битами или восьмеричными – байтами.
В ряде случаев, например для указания адресов и содержимого ячеек памяти, применяются шестнадцатеричные числа с основанием 16. Каждый p-й разряд такого числа HEX (p = 0, 1, 2,..., 9, A, B, C, D, E, F) дает вклад в десятичное значение адреса A, равный DEC*16p (знак означает возведение в степень), где DEC - десятичное значение числа, определяемое следующим образом:
HEX 0 1 2 3 4 5 6 7 8 9 A B C D E F
DEC 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
Применение шестнадцатеричных чисел требует некоторого навыка, но он приходит очень быстро, если вы всерьез займетесь программированием. К примеру, чему равно значение С7h (h означает принадлежность к шестнадцатеричным числам)? Надо полагать, что вы догадались, что с учетом веса разряда C=12 это дает (16*12)+7=199. Разумеется, преобразовывать числа в уме не стоит – многие простые микрокалькуляторы имеют команды для такого преобразования.
1.4.4. Мера информации по Шеннону
Обычно нам приходится работать в условиях неполных знаний об интересующей нас информационной системе. Поступающая к нам информация носит чаще всего статистический характер. Мы можем, скажем, лишь отчасти знать, какой процент населения поддерживает нашего президента или какую часть новорожденных составляют мальчики. Абсолютно точно этого узнать нельзя из-за ошибок в подсчете и постоянного изменения данных (информационного шума).
Допустим, что до получения информационного сообщения пользователь информационной системой имел предварительные (априорные) сведения о системе – . Его неосведомленность о системе определяется энтропией H(). С получением сообщения неопределенность сведений о системе становится равной H(). Тогда количество информации в сообщении будет равно
I() = H() - H().
Следовательно, количество информации определяется уменьшением неопределенности состояния системы. Если конечная неопределенность H() становится равной 0, то неполное знание о системе H() будет заменено полным знанием, что означает I() = H().
Пусть некоторая информационная система имеет N возможных состояний. Один из крупных специалистов в информатике Шеннон показал, что энтропия системы, как мера недостающей информации о ней, определяется выражением:
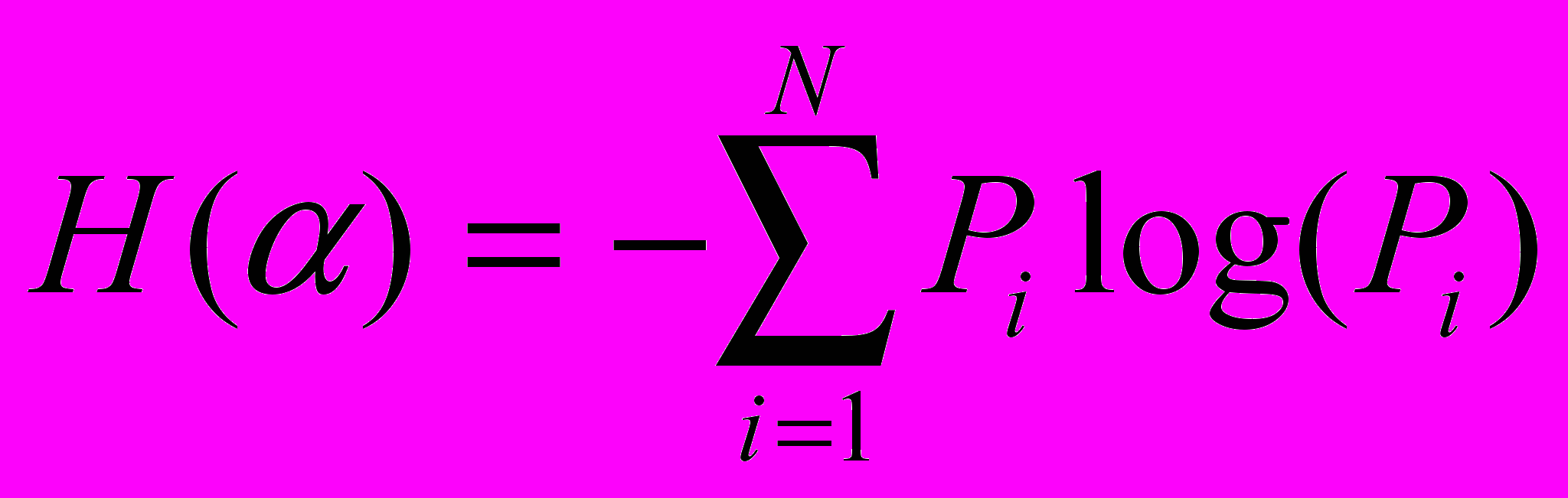 ,
,где Pi – вероятность нахождения системы в i-ом состоянии. Если все состояния системы равновероятны, то имеем:
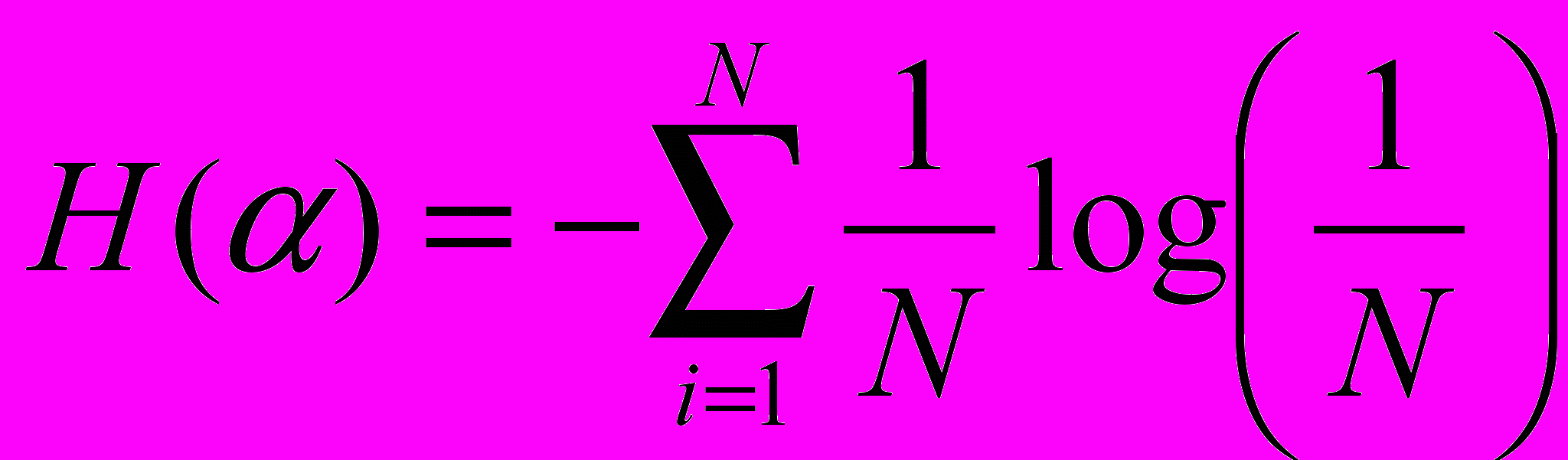 .
.Заметим, что N = mn, где m – основание системы исчисления, n – число разрядов (символов) в сообщении. Коэффициентом или степенью информативности сообщения называют отношение количества информации I к объему данных в сообщении, т. е. величина
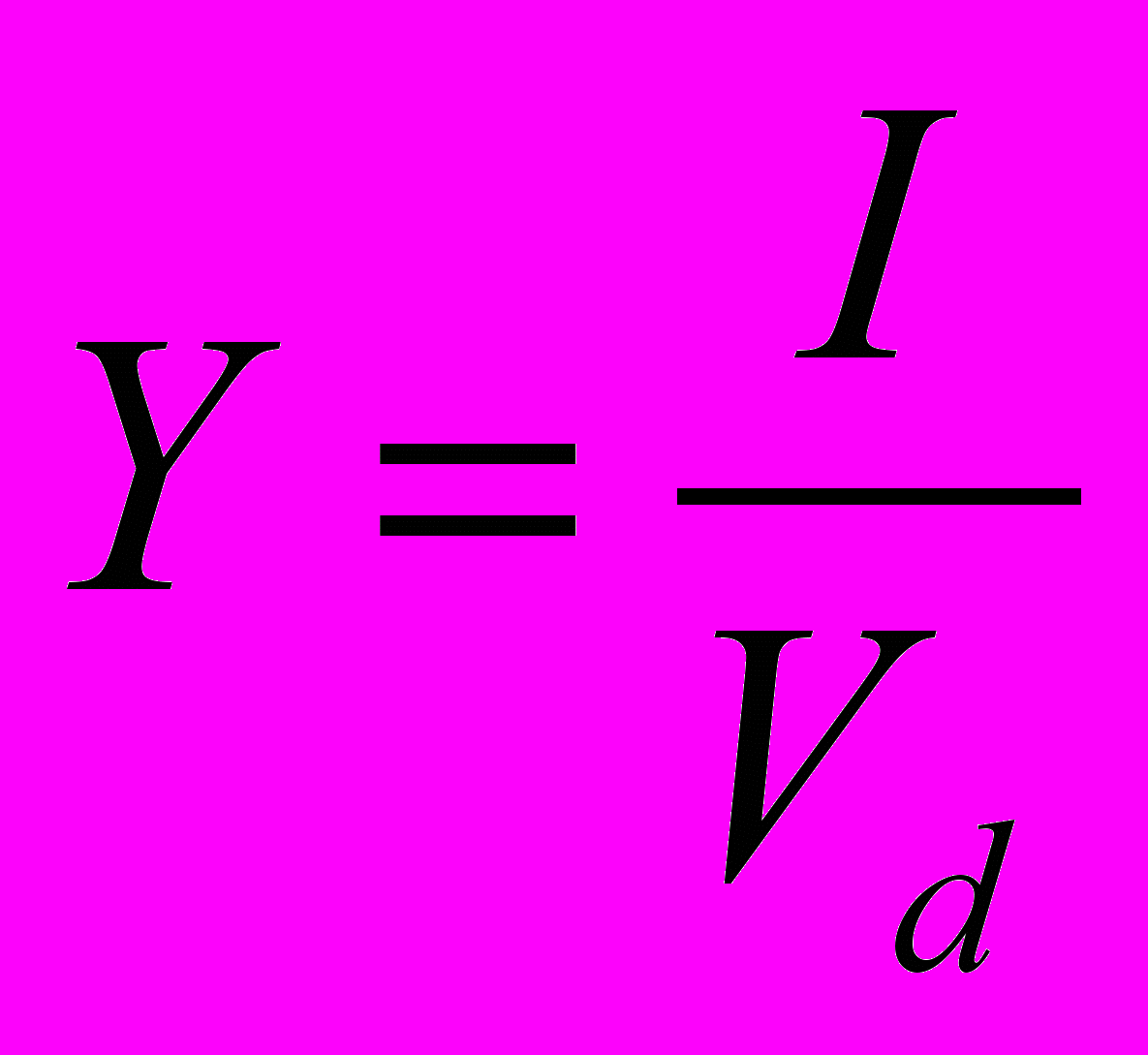 .
.Эта величина лежит в интервале 0
1.4.5. Семантическая и прагматическая меры информации
Для измерения смыслового (семантического) количества информации используется тезаурус – совокупность сведений, которыми располагает пользователь или система распознавания информации. Пусть S – смысловое содержание информации, а Su – тезаурус пользователя. Если Su = 0, то поступающая информация для пользователя (или системы) бесполезна, ибо пользователь не знает, как ее интерпретировать. А если Su , то пользователь уже все знает и поступающая информация для него также бесполезна. Таким образом, можно утверждать, что зависимость количества получаемой семантической информации Is = f(Su) имеет максимум и спадающие участки по обе стороны от него.
Отношение количества семантической информации Is к объему данных Vd принято называть относительной мерой количества семантической информации С = Ic/Vd.
Прагматическая мера информации определяет ее ценность для конкретного пользователя. Например, информация может быть ценной из-за того, что она относится к конкретному лицу или устройству, которое интересует пользователя. Она может быть ценной из-за того, что может размещаться на доступных пользователю накопителях информации и т.д.
