Романова Алла Ивановна учителя физики Научный Бровкин Игорь Борисович методист кафедры естественно-математических дисциплин иро рыбинск, 2006 пояснительная записка
| Вид материала | Пояснительная записка |
- Петрова Светлана Семеновна, учитель математики моу гимназия №1 г. Чебоксары Научный, 47.37kb.
- Пояснительная записка Автор программы: к э. н., доцент Проценко Инга Олеговна. Требования, 113.29kb.
- Воронович Игорь Иванович пояснительная записка Курс Классические аспекты высшей алгебры, 56.33kb.
- Рюмшина Любовь Ивановна, доктор психологических наук, доцент кафедры социальная психология, 400.08kb.
- Московский экономико-правовой институт, 350.39kb.
- Национального Института Образования; М. В. Павлова, методист высшей категории гуо апо;, 998.66kb.
- Рябцева Татьяна Ивановна учитель физики 2011 пояснительная записка, 172.45kb.
- Институт международных экономических связей сборник научных трудов москва 2005 Научный, 2923.4kb.
- Программа Ставрополь 2006 Печатается по решению редакционно издательского Совета, 134.47kb.
- Пояснительная записка Автор программы : д э. н., профессор Дыбская Валентина Владимировна, 101.31kb.
1 2
МОУ средняя общеобразовательная школы №44 г. Рыбинска
Программа элективного курса по физике «Механические свойства вещества»
в профильной школе
Романова Алла Ивановна
учителя физики
Научный руководитель:
Бровкин Игорь Борисович
методист кафедры естественно-математических дисциплин ИРО
Рыбинск, 2006
Пояснительная записка.
Элективный курс «Механические свойства вещества» предназначен для учащихся 10 класса. Курс рассчитан на 16 часов учебного времени.
Содержание курса является дополнением школьной программы и углубляет знания и умения по теме. При его изучении старшеклассники получают дополнительные сведения о видах деформаций и способах их получения, знакомятся с новой физической величиной – модулем Юнга, изучают диаграмму растяжения, способы повышения прочности твердых тел.
Выполнение лабораторных работ позволит учащимся расширить навыки работы с оборудованием, подтвердить теоретические основы практикой.
Данный курс необходим для учащихся, собирающихся поступать после окончания школы в технические ВУЗы.
Цели и задачи курса:
- Развивающие: развитие мышления, познавательных интересов, интеллектуальных и творческих способностей учащихся. Развитие интереса к исследовательской работе, умений наблюдать, анализировать, выдвигать гипотезы, проверять их экспериментом, делать выводы. Ставить проблему и искать пути ее разрешения. Развивать желание самостоятельно добывать знания, использовать различные источники информации.
- Обучающие: расширить кругозор учащихся по данной теме дать дополнительные сведения о видах деформаций и способах их получения. Познакомить с новой физической величиной – модулем Юнга, изучить диаграмму растяжения, способы повышения прочности твердых тел. Показать, как могут применяться и в каких областях знания о механических свойствах веществ, сделать вывод о необходимости учитывать эти свойства на производстве. Научить оформлять и представлять результаты своей деятельности.
- Воспитательные: воспитывать навыки сотрудничества при работе в коллективе, умение принимать решения, брать ответственность на себя. Уважительно относиться к мнению оппонентов в процессе дискуссий. Воспитывать уверенность , убежденность в возможности познания законов природы, разумного использования достижений науки и техники.
Ведущими формами занятий данного курса являются лекции, практические занятия и семинары.
Демонстрации и лабораторный практикум оснащены типовым оборудованием согласно минимальным требованиям к оснащению ученого процесса.
Успешным завершением курса будет выполнение проекта с презентацией или выступление с докладом на школьных научных чтениях.
Учебно – тематический план элективного курса.
| № занятия/№ темы Тема | Кол-во часов | Итого часов по теме | Форма занятия | Контроль знаний | |
| теория | практика | ||||
| 1/1.Виды деформаций. Деформация и напряжение. 2/1.Решение задач | 1ч. 1ч. | 2 | лекция | Р/з | |
| 3/2.Закон Гука. Границы применимости. Жесткость. Модуль Юнга. 4/2.Лабораторная работа «Определение модуля упругости при деформации растяжения» 5/2.Решение задач | 1ч. 1ч. 1ч. | 3 | урок - поиск | Л/р Р/з | |
| 6/3.Диаграмма растяжения. Пределы. Значения прочности на разрыв для некоторых материалов. Твердость. 7/3.Лабораторная работа «Определение твердости металлов» 8/3.Решение задач | 1ч. 1ч. 1ч. | 3 | лекция | Л/р Р/з | |
| 9/4.Анизотропия механических свойств твердых тел. Коэффициент запаса прочности. Необходимость учета в различных областях техники. 10/4.Лабораторная работа «Наблюдение кристаллических и аморфных тел» | 1ч. 1ч. | 2 | круглый стол | Л/р | |
| 11/5.Значение законов деформации. 12/6.Лабораторная работа «Наблюдение упругих и пластических деформаций тел» 13/7.Решение задач | 1ч. 1ч. 1ч. | 3 | семинар | Л/р Р/з | |
| 14/6.Способы повышения прочности твердых тел. Теоретическая оценка предела прочности. Прочность и время действия силы. | 1ч. | 1 | конференция | | |
| 15.Практикум по решению задач | 1ч. | 1 | | Р/з | |
| 16.Заключительное занятие | 1ч. | 1 | | | проверка знаний с использованием компью-тера |
| Итого | 16ч. | 16 | 6 | 9 | 1 |
Содержание программы.(16ч.)
Теоретические основы.(6ч.)
- Виды деформаций. Деформация и напряжение.
- Закон Гука. Границы применимости. Жесткость. Модуль Юнга.
- Диаграмма растяжения. Пределы. Значения прочности на разрыв для некоторых материалов. Твердость.
- Анизотропия механических свойств твердых тел. Коэффициент запаса прочности. Необходимость учета в различных областях техники.
- Значение законов деформации.
- Способы повышения прочности твердых тел. Теоретическая оценка предела прочности. Прочность и время действия силы.
Лабораторный практикум.(4ч.)
- Наблюдение кристаллических и аморфных тел.
- Наблюдение упругих и пластических деформаций тел.
- Определение модуля упругости при деформации растяжения.
- Определение твердости металлов.
Практикум по решению задач.(5ч.)
Заключительное занятие.(1ч.)
Методические рекомендации к проведению занятий элективного курса «Механические свойства вещества».
Тема 1. Виды деформаций. Деформация и напряжение.
На первом занятии учащимся сообщается цель и значение элективного курса, систематизируются знания о видах деформаций: растяжение, сжатие, сдвиг, кручение и изгиб. Изучают физические величины, характеризующие деформацию: абсолютное и относительное удлинения, механическое напряжение.
Полученные знания применяются на практике к решению задач.
Форма занятий – лекция -1ч., решение задач – 1ч. Итого 2ч.
Тема 2. Закон Гука. Границы применимости. Жесткость. Модуль Юнга.
Учащиеся повторяют закон Гука, изученный в 9-ом классе, и анализируют границы его применимости. Выводят формулу коэффициента упругости, находят связь модуля Юнга с напряжением. Объясняют различие модуля упругости для разных кристаллов различием в силах межатомных связей. Выражают коэффициент жесткости через модуль упругости, длину стержня и площадь его поперечного сечения.
Полученные знания применяются на практике к решению задач.
Форма занятий – урок – поиск - 1ч., лабораторная работа «Определение модуля упругости при деформации растяжения»-1ч., решение задач – 1ч. Итого 3ч.
Тема 3. Диаграмма растяжения. Пределы. Значения прочности на разрыв для некоторых материалов. Твердость.
Учащиеся узнают, что графическое изображение зависимости относительного удлинения образца от величины приложенного к нему напряжения называется диаграммой растяжения. Изучая каждый участок диаграммы, приходят к выводу: деформации подразделяются на упругие и остаточные (пластические). Каждой точке на диаграмме соответствует свой предел, характеризующий поведение материала образца от нагрузки: пределы пропорциональности, упругости, текучести, прочности.
Учащиеся должны понять, что не все механические свойства материалов описываются диаграммой растяжения. Важнейшей характеристикой материала является его твердость. Знакомятся с таблицей значений твердости по Моосу.
Полученные знания применяются на практике к решению задач.
Форма занятий – лекция -1ч., лабораторная работа «Определение твердости металлов» –1ч., решение задач – 1ч. Итого 3ч.
Тема 4. Анизотропия механических свойств твердых тел. Коэффициент запаса прочности. Необходимость учета в различных областях техники.
Занятие начинается с постановки проблемных вопросов: рассматривая механические свойства твердых тел, мы не задумывались над тем, влияет ли направление действия силы на величину деформации. Одинаковы или различны в различных направлениях модуль упругости, предел прочности, твердость и другие характеристики? Знакомясь со свойством анизотропия и причинами анизотропии монокристаллов, учащиеся находят самостоятельно ответы на поставленные вопросы. Делают вывод о необходимости учета коэффициента запаса прочности в различных областях техники.
Форма занятий - проблемный урок -1ч., лабораторная работа «Наблюдение кристаллических и аморфных тел» -1ч. Итого 2ч.
Тема 5. Значение законов деформации.
Учащиеся выступают с докладами по данной теме. Занятие носит профориентационный характер, т.к. законы деформации важны во многих производствах (строительство, металлургия, авиация и др.)
Форма занятий – семинар -1ч., лабораторная работа «Наблюдение упругих и пластических деформаций тел» -1ч., решение задач – 1ч. Итого 3ч.
Тема 6. Способы повышения прочности твердых тел. Теоретическая оценка предела прочности. Прочность и время действия силы.
Необходимо познакомить учащихся с методом увеличения прочности А.Ф. Иоффе и другими способами повышения прочности. Учащиеся ищут ответ на чрезвычайно важный в практическом отношении вопрос о том, почему со временем предел прочности различных конструкций понижается.
Форма занятий – конференция -1ч.
Практикум по решению задач.(1ч.)
Заключительное занятие.(1ч.)
Предполагает подведение итогов по изученному курсу. Учащиеся самостоятельно отвечают на вопросы по изученным темам и решают задачи.
Форма занятия – проверка знаний с использованием компьютера –1ч.
Дидактические материалы к элективному курсу «Механические свойства вещества»
Теоретические основы.
Тема 1. Виды деформаций. Атомы и молекулы твердых тел находятся в равновесных положениях, в которых результирующая сила их взаимодействия равна нулю. При сближении атомов преобладает сила отталкивания, а при их удалении от положения равновесия—сила притяжения. Это и обусловливает механическую прочность твердых тел, т. е. их способность противодействовать изменению формы и объема. Растяжению тел препятствуют силы межатомного притяжения, а сжатию - силы отталкивания.
Внешнее механическое воздействие, приложенное к твердому телу, вызывает смещение атомов из равновесных положений и приводит к изменению формы и объема тела, т. е. к его деформации. Абсолютно твердых тел в природе не существует. В то же время часто приходится иметь дело со столь малыми деформациями, что их невозможно обнаружить. Например, если наступить на кирпич, то его высота уменьшится примерно на '/20000 см. При такой деформации соседние атомы сближаются примерно на 2•10-14см!
Но деформации в крупных конструкциях бывают весьма заметными. Так, канаты, на которых висит мост через залив Форт в Шотландии, при длине в 3 км удлинены на 3 м.
Из повседневного опыта известно, что величина деформации тела зависит от материала, из которого оно изготовлено, величины силы и точки ее приложения. В этом легко убедиться, например, на опытах по деформации пластин одинаковых размеров из различных материалов—дерева, стали, алюминия; и пластин из одного и того же материала, но разной длины, толщины и ширины.
С
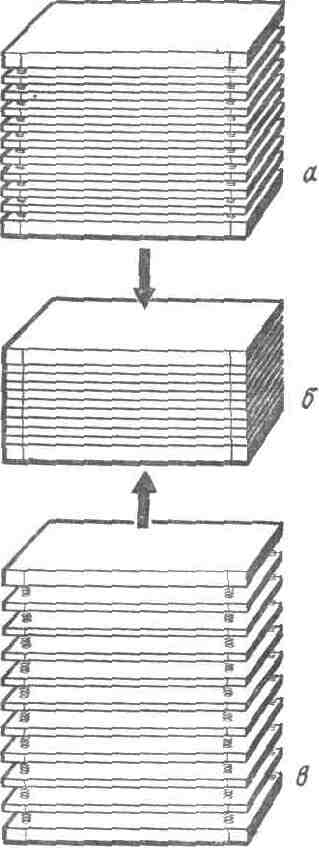 реди деформаций, возникающих в твердых телах, различают пять основных видов: растяжение, сжатие, сдвиг, кручение и изгиб. Для рассмотрения этих видов деформаций воспользуемся моделью твердого тела, состоящей из нескольких деревянных пластинок, скрепленных по углам одинаковыми пружинками (рис.1).
реди деформаций, возникающих в твердых телах, различают пять основных видов: растяжение, сжатие, сдвиг, кручение и изгиб. Для рассмотрения этих видов деформаций воспользуемся моделью твердого тела, состоящей из нескольких деревянных пластинок, скрепленных по углам одинаковыми пружинками (рис.1).При деформации сжатия и растяжения пластинки остаются параллельными друг другу и расстояния между каждой парой соседних пластин изменяются на одну и ту же величину.
На практике растяжение испытывают тросы подъемных кранов, канатных дорог, буксирные тросы, струны музыкальных инструментов. Сжатию подвергаются колонны, стены и фундаменты зданий.
Деформацию сдвига можно получить, смещая верхнюю пластину параллельно самой себе и удерживая нижнюю неподвижной. При этом все пластины сместятся так, что расстояния между ними останутся неизменными. Деформацию сдвига испытывают, например, заклепки и болты, соединяющие металлические конструкции. С очень распространенной деформацией сдвига мы встречаемся при разрезании ножницами бумаги, картона, листового железа.
Деформацию кручения можно наблюдать при повороте верхней пластины модели вокруг вертикальной оси. При этом расстояния между пластинами не меняются, но точки пластин, ранее лежавшие на одной прямой, теперь не укладываются на одну прямую. Деформации кручения возникают при завинчивании гаек, при работе валов машины.
Деформацию изгиба можно наблюдать на бруске, один конец которого закреплен, а к другому подвешен груз (рис.3). Изгиб испытывают балки перекрытий в зданиях, мостах, опирающиеся на опоры двумя концами (рис.2). Наибольшая величина прогиба х называется стрелой прогиба.
Рассмотрим деформацию изгиба на нашей модели. Для этого расположим ее так, как показано на рисунке 2, закрепив одну нижнюю пластину в тисках или в штативе, а к другой подвесив груз. Хорошо видно, что деформация изгиба сводится к деформациям сжатия и растяжения, различным в разных частях тела. В середине бруска существует слой, не подвергающийся ни растяжению, ни сжатию. Этот слой называют нейтральным слоем.
Поскольку слои, близкие к нейтральному, испытывают меньшую деформацию, то детали машин и конструкций, работающие на изгиб, выгодно делать полыми. Замена сплошных стержней и брусков трубами или двутавровыми балками, у которых частично удален средний слой материала, дает экономию материала и значительно снижает массу конструкций без ухудшения их механических свойств (рис. 4).
В результате длительной эволюции кости животных и птиц приобрели рациональное трубчатое строение.
Детали машин и конструкций часто подвергаются сложным деформациям, но их можно рассматривать как различные сочетания деформаций растяжения, сжатия и сдвига. Это значительно облегчает расчет механических свойств конструкций и деталей машин.
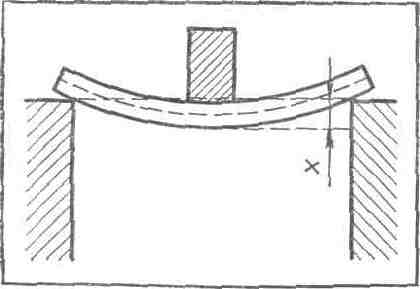
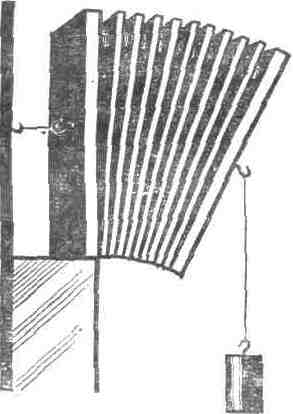

Рис.2 Рис.3 Рис.4
Деформация и напряжение. Качественно деформацию сжатия и растяжения можно характеризовать величиной абсолютного удлинения l , равной разности длин образца до растяжения lо и после него l:
Абсолютное удлинение l при растяжении положительно, при сжатии имеет отрицательное значение.
Как показывает опыт, образцы из одного и того же материала при одинаковом поперечном сечении и одинаковой величине действующей силы получают различные абсолютные удлинения при различной начальной длине образцов.
Но отношение абсолютного удлинения l к длине образцов при этом оказывается одинаковым для всех образцов. Его называют относительным удлинением .
(1)
Относительное удлинение является безразмерной величиной. Например, если стержень длиной lо = 100 см при растяжении удлинился на lo = 1 см, то его относительное удлинение равно 1/100, или 1%. При таком же абсолютном удлинении стержня длиной lo = 1000 см относительное удлинение будет равно 1/1000, или 0,1%.
Опыты с растяжением образцов твердых тел одинаковой длины, но различных сечений показывают, что при одинаковой величине действующей силы абсолютное и относительное удлинения обратно пропорциональны сечениям образцов. Поэтому при расчете деформации удобнее пользоваться не величиной деформирующей силы, а величиной механического напряжения, равной отношению деформирующей силы к сечению образца:
(2)
Механическое напряжение, или просто напряжение, имеет такую же размерность, как и давление. За единицу измерения механического напряжения в системе СИ принята единица давления «паскаль» (Па).
Паскаль—это давление, вызываемое силой 1 Н, равномерно распределенной по поверхности площадью 1 м2.
Напряжение, как и относительное удлинение, не зависит от длины образца.
Тема 2. Закон Гука. Закрепим в тисках стальную пластину, затем согнем ее и отпустим. Мы увидим, что пластина восстановила свою форму. Если повторить опыт со свинцовой, алюминиевой или медной пластинами таких же размеров, то они при тех же деформациях не восстанавливают свою форму полностью. Если после снятия напряжения форма тела восстанавливается, деформация называется упругой. Если же форма тела не восстанавливается, деформация называется пластической.
Нужно отметить, что идеально упругих и идеально пластичных тел не существует. Если свинцовую или алюминиевую пластину подвергнуть кратковременной малой деформации, то и они практически восстанавливают свою форму. С другой стороны, если стальную пластину деформировать достаточно большой силой или малой силой, но длительное время (например, несколько лет), то она после снятия нагрузки полностью свою форму не восстанавливает. Деформация тем ближе к упругой, чем меньше ее величина и чем меньше время действия силы.
Для всех видов упругих деформаций справедлив закон Гука, согласно которому удлинение и укорачивание стержней, пружин, прогибы и сдвиги в различных телах пропорциональны деформирующим силам:
F=k x (3)
где k—коэффициент пропорциональности, называемый коэффициентом жесткости деформируемого тела (стержня, пружины и т. п.); х—величина деформации, равная абсолютному удлинению l при растяжении или сжатии, углу поворота при деформации кручения и т. д. Формулу закона Гука мы записали без знака «минус» потому, что под F понимаем не равнодействующую всех внутренних сил упругости, возникающих в деформируемом теле, а равную, но противоположно направленную им равнодействующую внешних сил.
При действии одинаковой силы F величина деформации х зависит не только от свойств материала, но и от геометрических размеров и формы конструкций. Например, если с одинаковой силой растягивать стальную проволоку, а затем навитую из нее пружину, то результат будет существенно различным — пружина удлинится на гораздо большую величину, чем проволока.
Как показывает эксперимент, величиной, однозначно характеризующей механические свойства материала, независимо от конструкции изготовленных из него деталей, является для деформаций растяжения отношение относительного удлинения растягиваемого стержня к механическому напряжению . Величина этого отношения а, называемого коэффициентом упругости, при малых упругих деформациях ( l lo) одинакова для образцов любой формы и размеров, изготовленных из одного материала:
(4)
Полагая =1 , получим . Следовательно, коэффициент упругости численно равен относительному удлинению при напряжении в 1 .
В технических расчетах обычно пользуются величиной, обратной коэффициенту упругости а, называемой модулем
упругости или модулем Юнга Е:
Е=
(5)
Из выражений (4) и (5) можно установить связь модуля упругости Е с напряжением о и относительным удлинением :
(6)
Полагая =1, получим =Е
Следовательно, модуль упругости Е численно равен напряжению, при котором образец растягивался бы вдвое ( l=lо). Нужно отметить, что все материалы, кроме резины, разрушаются задолго до того, как удвоят свою длину. Модуль Юнга является важнейшей характеристикой материала (но не конструкции).
Значения модуля упругости для некоторых материалов приведены в таблице № 1. Как видно из таблицы, модуль упругости алмаза примерно в 2-Ю5 раз превышает модуль упругости резины. Низкое значение модуля упругости резины объясняется тем, что она образована из длинных и гибких молекулярных цепочек, изогнутых и перепутанных между собой. При растяжении резины молекулярные цепочки распрямляются, что облегчает растяжение. Если бы они были вытянуты в одном направлении, то для того же относительного удлинения потребовалось бы большее напряжение.
Таблица 1
Модуль упругости некоторых материалов
| Наименование материала | Модуль Юнга | |
| Алмаз | 12 ∙10" | |
| Сталь | 2,0-2,2 ∙10" | |
| Чугун белый | 1,15-1,6 ∙10" | |
| Медь прокатная | 1,1 ∙10" | |
| Стекло | 0,56 ∙10" | |
| Алюминий катаный | 0,69 ∙10" | |
| Гранит | 0,49 ∙10" | |
| Свинец | 0,17 ∙10" | |
| Дерево | 0,1∙ 10" | |
| Каучук | 0,00008 ∙10" | |
Различие в величине модуля упругости для разных кристаллов объясняется различием в силах межатомных связей. Преобразовав выражение (6), можно получить:
(7)
или
(8)
Сравнивая полученное выражение с известной формулой закона Гука
F= kх,
мы получаем возможность выразить коэффициент жесткости k через модуль упругости Е, длину растягиваемого стержня lо и площадь его поперечного сечения S:
(9)
Выражение (6) можно рассматривать как другую формулировку закона Гука для деформации растяжения или сжатия, пользуясь которой можно рассчитать относительное изменение образца по заданному напряжению и известному модулю упругости.
Тема 3. Диаграмма растяжения. Зависимость относительного удлинения образца от величины приложенного к нему напряжения является одной из важнейших характеристик механических свойств твердых тел. Графическое изображение этой зависимости называется диаграммой растяжения. По оси ординат обычно откладывается величина механического напряжения , приложенного к образцу, а по оси абсцисс—относительное удлинение . Диаграмма растяжения показана на рисунке 4.
При небольших напряжениях (линейный участок ОА) относительное удлинение прямо пропорционально напряжению, т. е. выполняется закон Гука (6). Это обусловлено тем, что при небольших изменениях межатомных расстояний зависимость смещений атомов из равновесных положений от силы взаимодействия можно считать приблизительно линейной. При снятии напряжения атомы возвращаются в равновесные положения и форма тела практически восстанавливается. При дальнейшем увеличении напряжения деформация еще остается упругой, но ее зависимость от напряжения перестает быть линейной (участок АВ). Наибольшее напряжение Оп, до которого справедлив закон Гука, называют пределом пропорциональности. Предельное напряжение Оу (ордината точки В), при котором деформация еще остается упругой, называется пределом упругости.
Участок АВ невелик, т. е. значения предела упругости Оу и предела пропорциональности Оп настолько близки, что часто их считают совпадающими. Обычно для металлов деформация является упругой, если 0,2%.
При напряжениях, превышающих предел упругости Оу, образец после снятия нагрузки не восстанавливает свою форму (пунктирная кривая). Такие деформации называют остаточными или пластическими. Мерой остаточной деформации служит отрезок ост. Рис.4
В области пластической деформации (участок ВСD) деформация происходит почти без увеличения напряжения. На горизонтальном участке СD материал как бы течет.
Напряжение От (ордината С), при котором материал течет, называют пределом текучести.
М
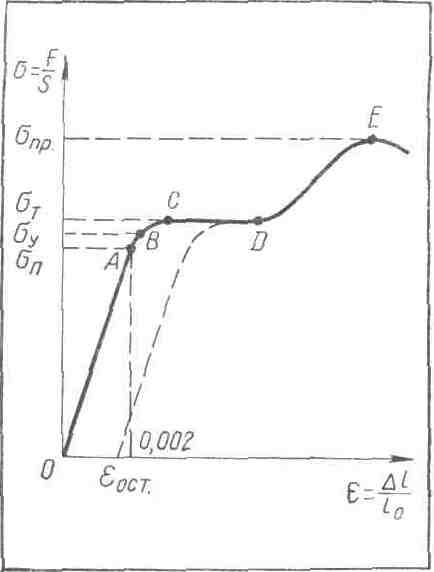 атериалы, у которых область текучести СD значительна, могут без разрушения выдерживать большие деформации. Если же область текучести материала почти отсутствует, он без разрушения сможет выдержать лишь небольшие деформации. Такие материалы называют хрупкими. Примерами хрупких материалов могут служить стекло, кирпич, бетон, чугун.
атериалы, у которых область текучести СD значительна, могут без разрушения выдерживать большие деформации. Если же область текучести материала почти отсутствует, он без разрушения сможет выдержать лишь небольшие деформации. Такие материалы называют хрупкими. Примерами хрупких материалов могут служить стекло, кирпич, бетон, чугун.Из сравнения диаграмм растяжения чугуна и стали, показанных на рисунке 5, видно, что эти материалы примерно одинаково ведут себя в области упругих деформаций, т. е. они в равной мере упруги. Но в противоположность стали, имеющей значительную область пластической деформации, у чугуна эта область чрезвычайно мала. Поэтому
чугун гораздо более хрупок, чем сталь.
Как видно из диаграммы растяжения, для дальнейшего увеличения деформации необходимо снова увеличить напряжение (поднимающийся участок DЕ). В том, что материал в процессе деформации может упрочняться, можно убедиться сгибанием толстого медного прута или пластины. Для того чтобы разогнуть образец, требуются заметно большие усилия, чем для его сгибания. Объяснение этому явлению будет дано далее.
После точки Е кривая идет вниз и дальнейшая деформация вплоть до разрыва происходит при все меньшем напряжении. Наибольшее напряжение Опр, которое способен выдержать образец без разрушения, называют пределом прочности.
В таблице № 2 приведены значения прочности на разрыв для некоторых материалов.
Таблица 2 Значения прочности на разрыв для некоторых материалов
190 •107
20-30 ∙107 7-15 • 107 7 107
15-60•10 12-40 •107 20-24• 107
10 - 107 0,3∙ 107
3-20 • 107 0,5 • 107 35 ∙107 70 • 107
Сталь высокопрочная
Сталь прокатная низкоуглеродистая
Чугун
Алюминий чистый
Алюминиевые сплавы
Латунь
Медь
Дерево (ель)
вдоль волокон
поперек волокон Стекло оконное Кирпич
Шелк
Льняное волокно
Твердость. Не все механические свойства материалов описываются диаграммой растяжения. Важной характеристикой материала является его твердость. Твердость характеризует способность материала оказывать сопротивление проникновению в него другого тела, т. е. способность противодействовать вдавливанию или царапанью. При измерении твердости методом вдавливания преодолеваются силы, препятствующие скольжению частиц, а в методе царапанья—силы сопротивления отрыву частиц. Поэтому результаты измерения твердости различными методами не всегда дают совпадающие результаты.
При определении твердости методом вдавливания в испытуемый образец с помощью гидравлического пресса вдавливается стальной закаленный шарик, который после снятия нагрузки оставляет на образце отпечаток в виде лунки. Чем тверже материал, тем на меньшую глубину проникает шарик и тем меньшую площадь поверхности 5 имеет лунка. Твердость при одном и том же радиусе шарика определяется отношением:
,
где F—сила, действующая на шарик. Твердость измеряется в .
В другом методе измерения твердости из двух материалов более твердым считается тот, который оставляет царапину на другом. Проведя краем стеклянного осколка по медной пластинке, мы получим царапину. В то же время с помощью медной пластины нельзя получить царапину на стекле. Значит, стекло тверже меди.
Моос предложил условную шкалу, в которой твердость оценивается царапаньем минералами, которые приняты за эталонные (табл.3).
Таблица 3
Эталонные материалы и соответствующие им значения твердости в единицах шкалы Мооса
| Минерал | Алмаз | Корунд | Топаз | Кварц | Полевой шпат | Апатит | Флюорит | Кальций | Гипс | Тальк |
| | | | | | | | | | | |
| Твердость по Моосу | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
Тема 4. Анизотропия механических свойств твердых тел. Рассматривая механические свойства твердых тел, мы не задумывались над тем, влияет ли направление действия силы на величину деформации. Одинаковы или различны в различных направлениях модуль упругости, предел прочности, твердость и другие характеристики?
Опыт показывает, что у многих материалов, широко применяемых в технике, механические свойства во всех направлениях одинаковы.
С другой стороны, у ряда твердых тел механические свойства и соответствующие им характеристики — модуль упругости, предел прочности и другие—зависят от направления действия силы.
Тела, физические свойства которых во всех направлениях одинаковы, называют изотропными. Тела, обладающие различными свойствами в разных направлениях, называют анизотропными
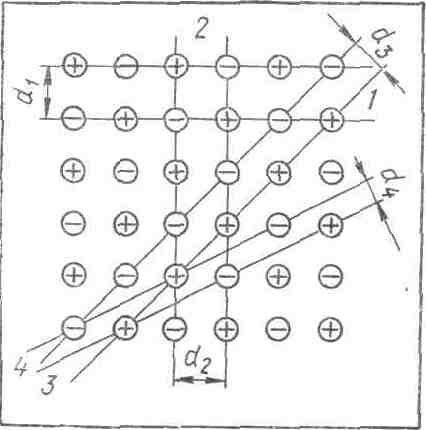
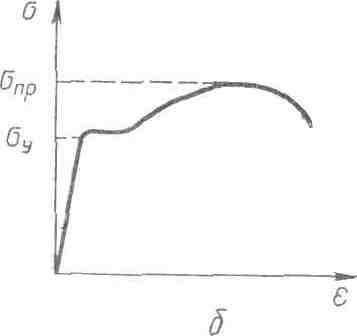
Диаграмма растяжения стали Рис.6
Анизотропия характерна для монокристаллов. Все монокристаллы в той или иной мере анизотропны. В зависимости от направления, выбранного для измерений, монокристалл обладает различной упругостью, прочностью и другими физическими параметрами.
В чем же причина анизотропии монокристаллов? На рисунке 6 условно изображено расположение атомов
в одной из плоскостей монокристалла. Через узлы этой плоской решетки проведены различно ориентированные параллельные прямые. Видно, что на единицу длины прямых, принадлежащих к различным семействам, приходится неодинаковое количество атомов. Но механические свойства кристалла зависят от плотности размещения образующих его частиц. Из сказанного можно сделать вывод, что анизотропия механических свойств является следствием правильного чередования атомов в монокристаллах.
Наименее анизотропны монокристаллы с кубической, наиболее симметричной решеткой. Но анизотропия и в этом случае значительна. Так, предел прочности монокристалла меди. обладающего кубической гранецентрированной решеткой, при растяжении вдоль ребра куба равен 1,5∙108 н/м2, а при растяжении вдоль диагонали куба —3,5∙108 н/м2.
Физические свойства монокристаллов зависят от направления, а не от места: они одинаковы в различных местах, но различны в различных направлениях. В этом нетрудно убедиться, если, например, на поверхность пластинки слюды поставить острие иглы и нанести по ней легкий удар молотком. При рассматривании поврежденной поверхности в лупу хорошо видны так называемые фигуры удара—совокупность трещин, расположенных в направлениях минимальной прочности кристалла. Фигуры удара на слюде всегда имеют вид шестилучевых звездочек, соответствующие лучи-трещины которых параллельны. Фигуры удара на гипсе имеют вид четырехлучевых звезд. Аналогичные опыты с изотропными телами, например со стеклом, всегда дают случайные, невоспроизводимые фигуры удара. Вид фигур удара на слюде, гипсе и стекле представлен на фотографии.
Ярко выраженной анизотропией механических свойств обладают монокристаллы асбеста, графита и слюды, решетки которых имеют слоистую структуру. Слюда легко расслаивается на лепестки. Опытные экспериментаторы получают листочки слюды толщиной 10-5 см. Но слюду трудно разрезать ножом в перпендикулярном слою направлении. Это обусловлено тем, что силы связи между атомами внутри слоев больше, чем силы связи между слоями. В монокристаллах асбеста имеется всего одно направление повышенной прочности. Поэтому асбест легко расчленяется на нити. Из нитей асбеста делают несгораемые веревочные пожарные лестницы, несгораемые ткани, из которых шьют спецодежду для работы в горячих цехах.
В противоположность монокристаллам поликристаллические тела изотропны, хотя и состоят из анизотропных кристаллитов. В большинстве случаев кристаллиты ориентированы хаотично, дальний порядок не распространяется на весь поликристалл и анизотропия не наблюдается. Свойства отдельных кристаллитов усредняются по всем направлениям и в среднем оказываются одинаковыми. Поэтому поликристаллические тела, к которым принадлежит большинство применяемых в технике металлов, обычно изотропны. Но при некоторых видах обработок (волочение и др.) может произойти преимущественная ориентация кристаллитов в определенном направлении. Тогда свойства отдельных кристаллитов не усредняются по всем направлениям и поликристаллическое тело оказывается анизотропным.
Тема 5. Значение законов деформаций. Знание законов деформаций имеет огромное значение для техники. В наше время учение о прочности - это большая отрасль науки, позволяющая рассчитывать конструкции зданий, мостов, корпусов кораблей, фюзеляжей самолетов и других сооружений и деталей.
Выдающимся достижением инженерной и строительной техники является Останкинская телевизионная башня в Москве - самое высокое сооружение в мире. Вершина башни отстоит от ее основания на 540 м. Более чем полукилометровое тело башни и ее фундамент должны быть устойчивыми и обладать большим запасом прочности, для того чтобы веками противостоять ураганным ветрам, изменениям температуры и другим воздействиям. Главный конструктор башни лауреат Ленинской премии Н. В. Никитин рассчитал ее на ураган со скоростью ветра 43 м/сек. Статистика показывает, что в Московской области такой ураган можно ожидать один раз в 2200 лет. Основная часть башни построена из железобетона. Точный расчет позволил поставить ее на очень маленьком по сравнению с высотой фундаменте - железобетонной шайбе диаметром 70 м, шириной 8 м и толщиной 3,5 м.
Железобетонный конус низа башни разрезан арками на десять лап. Это не архитектурные украшения. Расчеты показали, что сочленения сплошного конуса основания башни, изменяющего
свои размеры при колебаниях температуры, с фундаментом, находящимся почти при постоянной температуре, привело бы к его растрескиванию. Лапы и арки нужны для того, чтобы повысить способность основания башни к упругим деформациям.
В трубчатое бетонное тело башни заложено в натянутом состоянии 150 стальных канатов диаметром 38 мм с разрывным усилием 1120 кН каждый. Эти стальные струны сжимают бетон верхней части башни с усилием 95 000 кН, а нижней части — с усилием 38 000 кН. Такой железобетон называют предварительно напряженным.
Обычный бетон обладает значительно меньшей прочностью на растяжение, чем на сжатие, а у стальных тросов прочность на растяжение велика, зато отсутствует прочность на сжатие. Предварительно напряженный железобетон лишен обоих этих недостатков. Он обладает прочностью на сжатие обычного бетона и имеет гораздо большую по сравнению с ним прочность на растяжение.
За счет того, что обращенная к Солнцу сторона башни днем нагревается, происходит удлинение освещенной ее стороны и изгиб башни в теневую сторону. При этом отклонение вершины башни от вертикали составляет 2,5 м, а иногда при совместном действии разности температур и ветра оно достигает 5 м. Только ночью в безветренную погоду башня стоит вертикально.
Упругие свойства материалов используются не только в строительном деле, но и в машиностроении, приборостроении и других областях техники. Особенно высокие требования предъявляются к материалам, идущим на изготовление деталей, подвергающихся многократным знакопеременным нагрузкам. Ясно, что в таких деталях совершенно нельзя допускать даже малых остаточных деформаций. Это достигается не только выбором материала, но и конструкцией детали. Наглядным примером является пружина балансира в часах, совершающая 1800 изгибов в час, или рессора автомобиля, испытывающая значительные переменные деформации при движении автомобиля по неровной дороге (рис. 7).
Рессора состоит из отдельных листов специальной стали, обладающей высоким значением предела упругости. Длина листов различна. Пирамидальная и пластинчатая конструкция обеспечивает рессоре переменный коэффициент жесткости, возрастающий при увеличении нагрузки. По мере увеличения нагрузки в работу вступает все большее число листов.
Все детали машин и механизмов изготавливаются со значительным, но разумным запасом прочности, для того чтобы случайные перенапряжения, возникающие при эксплуатации, не разрушали машину или конструкцию. Без знания величин пределов упругости и прочности используемых материалов инженеры-конструкторы не могли бы рационально сочетать наименьшую массу (а значит, расход материала) с необходимой надежностью конструкций и машин.
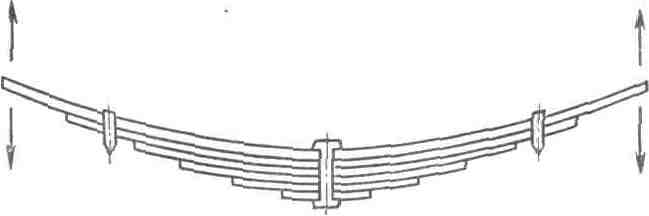
Рис. 7. Схема устройства рессоры.
Отношение предела прочности материала Опр (или предела текучести для пластичных тел) к фактически действующему напряжению о называют коэффициентом запаса прочности: k=
Например, в строительном деле коэффициент запаса прочности стальных балок установлен не менее 2,5—2,6, а для балок из хрупких материалов (чугун, бетон) не менее 3—9. Значения коэффициента запаса прочности для некоторых материалов приведены в таблице № 4.
Таблица 4
Коэффициент запаса прочности некоторых материалов
| Характер нагрузки | Материал, подвергающийся нагрузке | Коэффициент запаса |
| | | прочности |
| Статическая длительная на | Стальные конструкции из про | |
| грузка | катного металла | 2,4-2,6 |
| Статическая длительная на | Чугун, бетон | 3,0-9,0 |
| грузка | | |
| Ударные нагрузки | Сталь | 2,8-5,0 |
| Переменные нагрузки | Сталь | 5,0-15 |
Не менее важно уметь управлять пластическими свойствами материалов. Многие методы обработки — прокатка, ковка, волочение, прессование металлов основаны на использовании их пластичности. Для изготовления методом штамповки многометровых деталей подводных лодок, таких самолетов-гигантов, как «Антей», созданы уникальные прессы, способные развивать усилия в 750000 кн. Однако и такой пресс (размером в двенадцатиэтажный дом) не удовлетворяет всех запросов современной техники. Алюминий в авиации заменяется более прочными материалами — титаном и специальными сталями, для штамповки которых требуются в 5—6 раз большие усилия. Сейчас проектируются прессы на усилие в 2∙106 кн.
Контрольные вопросы
1. Что называют пределом упругости и пределом прочности материала?
2 Что такое анизотропия?
3 Приведите примеры анизотропии физических свойств кристаллов.
4. Почему монокристаллы анизотропны?
5 Почему предел прочности на растяжение у предварительно напряженного железобетона выше, чем у обычного железобетона?
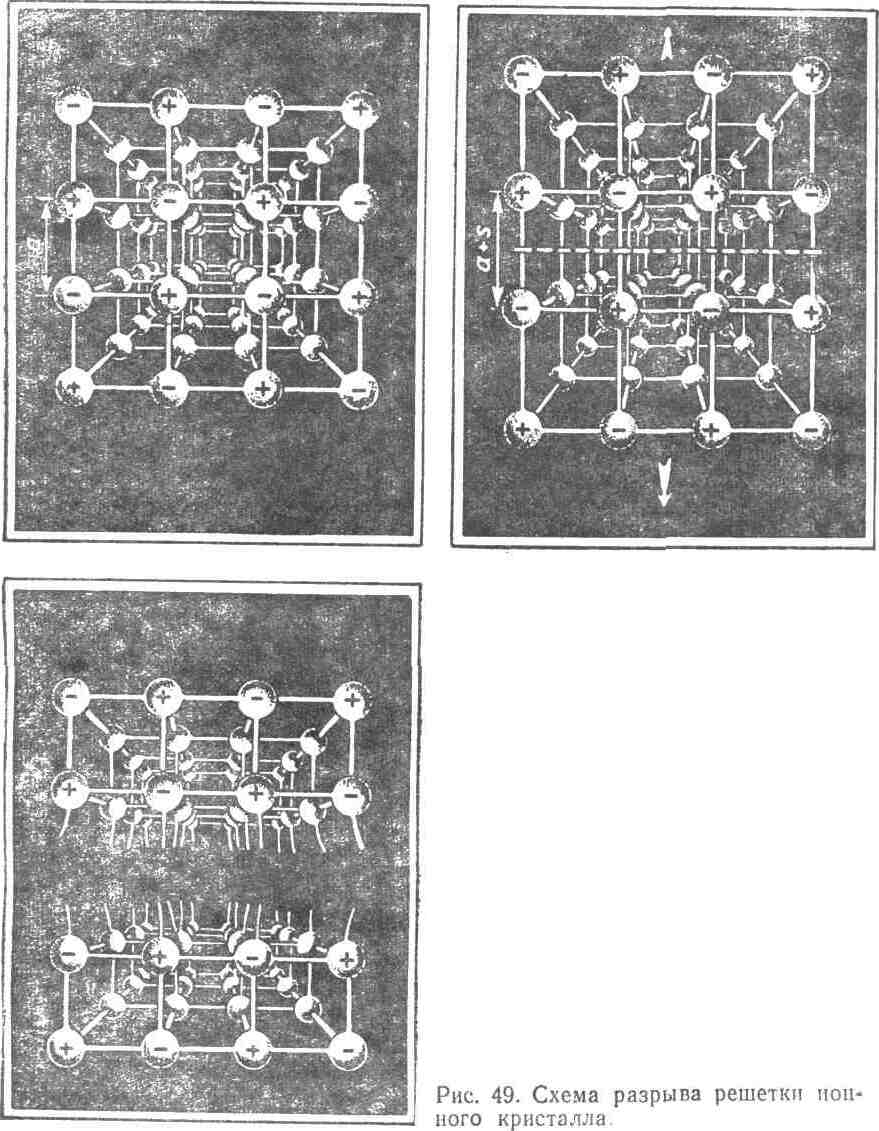
Тема 6. Способы повышения прочности твердых тел
Теоретическая оценка предела прочности твердого тела. При растяжении образца его прочность определяется величиной сил межатомного притяжения, рассчитанных на 1 кв.м поверхности разрыва.
Оценим предел прочности на растяжение ионного кристалла каменной соли. Для простоты будем учитывать только взаимо¬действие между ближайшими противоположно заряженными ионами натрия Nа+ и хлора С1-, расположенными по обе стороны предполагаемой поверхности разрыва.
Согласно примерным оценкам расстояние между атомами в твердом теле составляет 3 10 м.
Считая ионы точечными зарядами, удаленными на расстояние d==3∙ 10 м друг от друга, вычислим силу притяжения между двумя разноименными нонами:
На каждый ион, расположенный на поверхности разрыва, в среднем приходится площадь поперечного сечения
Отсюда число ионов на одном квадратном метре поверхности разрыва
Тогда предел прочности каменной соли равен:
Сравнение результатов более точных расчетов предела прочности некоторых материалов, приведенных в таблице с их реальной прочностью показывает, что эти данные различаются на 1—2 порядка величины.
Способы повышения прочности твердых тел. Физикам и инженерам очень важно было узнать, по какой причине реальная прочность твердых тел
оказывается в десятки и сотни раз меньше величин, рассчитанных для идеальной модели. Оказалось, что причина расхождения теории и эксперимента—наличие внутренних и поверхностных дефектов кристаллов.

В 1924 г. академик А. Ф. Иоффе показал, что прочность кристаллов каменной соли на разрыв увеличивается в 400 раз, если измерения проводить с кристаллами, погруженными в раствор каменной соли. Из-за процессов растворения и кристаллизации различного рода дефекты поверхности кристалла - трещины, дислокации - исчезают, поэтому прочность его возрастает почти до теоретического значения 150∙107 н/м2.
Около десяти лет тому назад было достигнуто огромное упрочнение промышленного листового стекла. Его прочность была доведена до 500∙107 н/м2 путем применения метода А. Ф. Иоффе, заключающегося в уменьшении дефектов на поверхности путем специальной обработки.
Внутренние дефекты иногда положительно влияют на механические свойства твердых тел. При наличии дислокации для осуществления пластической деформации нет необходимости в одновременном разрыве всех связей между двумя плоскостями. Достаточно разорвать небольшое число связей и переместить дислокацию на расстояние порядка постоянной решетки, как это показано на рисунке 8. Таким образом, дислокации позволяют осуществлять поочередной разрыв небольшого числа связей и этим облегчают пластическую деформацию.
Для получения материалов с высокой прочностью на разрыв и сдвиг, т. е. с большим сопротивлением пластической деформации, необходимо либо уменьшить в них число дислокации, либо создать условия, затрудняющие перемещение дислокации. Препятствием перемещению дислокации может служить другая дислокация, встретившаяся на ее пути. Поэтому при увеличении числа дислокации в единице объема прочность кристалла сначала уменьшается, а затем начинает возрастать. Это обстоятельство иллюстрируется на графике зависимости предела прочности от числа дефектов в единице объема кристалла р. Кривая имеет U-образный вид.
При некоторой плотности дислокации рм кристалл обладает минимальным сопротивлением деформации. Уменьшение р по сравнению с рм сопровождается увеличением прочности, так как приближает структуру к идеальной.
Полученные в лабораторных условиях методом выращивания из паров бездислокационные кристаллы металлов в виде тонких нитей толщиной несколько нанометров, как видно из таблицы № 9, имеют прочность, близкую к теоретической. Например, «усы» железа выдерживают нагрузку 1,3 ∙1010 н/м2. Нитевидные кристаллы сапфира являются рекордсменами прочности. У них она достигает 2,8∙1010 н/м2.
Таблица 9
Теоретическое значение прочности некоторых материалов и прочности их монокристаллов в виде „усов"
-
Материал
Окись алюминия (сапфир)
Железо
Медь
Теоретическая прочность в н/м2 Прочность «усов» в н/м2
3 • 10ю
2,8 ∙ 10ю
2,2∙ 1010
1,3 • 1010
1,2 • 10'°
0,4 • 1010
Способ повышения прочности твердых тел путем получения кристаллов с очень малым количеством дислокации пока еще не используется в промышленности. Большинство современных методов упрочнения материалов основано на противоположном •способе, состоящем в искажении кристаллической структуры путем создания в ней различного рода дефектов — введение атомов посторонних включений, создание дислокации. Например, при легировании стали - введении в расплав небольших добавок хрома, вольфрама и других элементов - ее прочность увеличивается примерно втрое.
При протяжке, дробеструйной обработке металлов и т. п. происходит так называемый наклеп, приводящий к увеличению плотности дислокации. В результате, например, после протяжки бруска углеродистой стали предел прочности возрастает вдвое.
Обработка металлов давлением приводит к уменьшению размеров кристаллитов и увеличению дефектов структуры внутри самих зерен. И то, и другое мешает передвижению дислокации и приводит к значительному повышению прочности.
Следует отметить, что при чрезмерной концентрации дефектов структуры кристаллическая решетка становится неустойчивой, поэтому увеличение дефектов с целью повышения прочности должно производиться в разумных пределах.
Ни один из известных сейчас материалов не может соперничать со сталью, сочетающей такие свойства, как прочность и низкая стоимость. Не удивительно, что 93% используемых во всем мире металлов составляют стали и сплавы на основе железа.
По ориентировочным прогнозам специалистов, предел прочности на разрыв обыкновенной конструкционной стали, т. е. той, что используется при сооружении мостов, каркасов зданий и т. п., к 1984 г. достигнет 7∙108 н/м2, тогда как сейчас предел прочности стального проката составляет (2—3) • 10" н/м2.
Прочность и время действия силы. Давно было замечено, что в ряде случаев, когда тело длительное время находится под напряжением меньше предела прочности, оно все же разрушается. Время, в течение которого тело еще способно противодействовать внешней силе, уменьшается с повышением температуры и по мере приближения нагрузки к пределу прочности. Довольно долго таким фактам не придавали особого значения, считая, что предел прочности снижается, например, за счет коррозии материала. Но изучение деформаций в условиях глубокого вакуума и тщательной очистки поверхности от загрязнений показало, что, строго говоря, предел прочности и другие количественные характеристики механических свойств твердого тела не являются константами материала. Все они зависят от времени действия нагрузки.
Ответ на чрезвычайно важный в практическом отношении вопрос о том, почему со временем предел прочности различных конструкций понижается, был найден в 60-х годах в Ленинградском физико-техническом институте. Упрощенно его можно изложить следующим образом.
В силу неравномерного распределения энергии тепловых колебаний атомов твердого тела в данный момент некоторые атомы приобретают энергию больше средней энергии при данной температуре. Попросту говоря, несколько соседей атома могут совершенно случайно одновременно «толкнуть» его в одну сторону и он «выпадет» из узла решетки и внедрится в междоузлие. На месте, ранее занимаемом этим атомом, образуется вакансия.
При данной температуре и в отсутствие нагрузки число выпадающих атомов равно числу «захваченных» вакансиями, поэтому кристалл не разрушается. С увеличением температуры это равенство соблюдается, но общее число выпавших и захваченных атомов резко возрастает.
Если же к кристаллу приложена внешняя сила, то на хаотические перемещения атомов накладываются направленные перемещения в сторону действия силы; одновременно затрудняются перемещения в обратном направлении. Постепенно число разорванных связей под нагрузкой увеличивается и происходит разрушение тела путем поочередного разрыва связей.
Необходимо подчеркнуть, что не внешняя сила непосредственно осуществляет разрыв атомных связей. Она только облегчает отрыв атомов и обеспечивает направленность процесса разрушения. Разъединение же атомов происходит за счет тепловых флуктуации. В то же время без внешней силы разрушение одним только тепловым движением из-за его хаотичности невозможно при всех температурах ниже точки плавления. На рисунке 52 показаны результаты испытаний алюминия, подвергавшегося действию разрушающих напряжений. По горизонтальной оси отложено напряжение о, а по вертикальной — время, в течение которого образец выдержал нагрузку с момента ее приложения до разрушения (так называемое «время жизни» под нагрузкой). Обратите внимание на масштаб по вертикали!
Из рисунка видно, как сильно зависит «время жизни» образца под нагрузкой от приложенных напряжений и температуры. Например, при изменении напряжений от 2∙107 до 4 ∙107 н/м2 при температуре 200°С оно изменяется более чем в 105 раз.
Изучение законов зависимости прочности твердых тел от температуры и времени действия нагрузки имеет большое практическое значение, позволяя предсказывать научно обоснованные пути повышения долговечности деталей и конструкций, находить оптимальные условия использования материалов в условиях длительно действующих вибрационных и статических нагрузок.
Контрольные вопросы
1. Почему предел прочности реальных тел значительно ниже его теоретического значения?
2. Каковы способы повышения прочности твердых тел?
3. Какова роль внешней силы и теплового движения в процессе разрушения тел?
Лабораторный практикум.
Лабораторная работа № 1.
ОПРЕДЕЛЕНИЕ МОДУЛЯ УПРУГОСТИ ПРИ ДЕФОРМАЦИИ РАСТЯЖЕНИЯ
Оборудование: резиновый шнур длиной 25—30 см и сечением 4— 10 мм2, набор грузов по 0,1 кг, штатив, линейка, штангенциркуль или микрометр.
Цель работы определение модуля упругости резины при растяжении.
При установившейся упругой деформации равнодействующая всех внутренних сил упругости, возникающих в теле в любом его сечении, уравновешивает внешние силы, действующие на тело.
Согласно закону Гука, напряжение о и вызванное им относительное удлинение е пропорциональны: а==Ее, где Е— модуль упругости.
После преобразования этого выражения получим:
Для экспериментального определения модуля упругости нужно измерить все величины, стоящие в правой части выражения: деформирующую силу F, сечение образца S, его первоначальную длину lо и абсолютное удлинение l.
Образец—резиновый шнур— укреплен в штативе. Шнур растягивают грузами, масса которых известна. Отсчет первоначальной длины образца lо и абсолютного удлинения l делается по линейке, укрепленной на том же штативе.
Порядок выполнения работы
1. Укрепите резиновый шнур в штативе и, подвесив к его концу один груз mо==0,1 кг, измерьте первоначальную длину шнура lo.
2. Измерьте с помощью штангенциркуля или микрометра тол¬щину шнура и вычислите площадь его поперечного сечения S.
3. Подвешивая к шнуру грузы массой 0,1 кг, 0,2 кг, 0,3 кг, измерьте соответствующие абсолютные удлинения шнура: и вычислите относительные удлинения шнура.
4. По результатам измерений вычислите модуль упругости резины Е и оцените погрешности эксперимента.
5. Результаты опытов занесите в отчетную таблицу.
