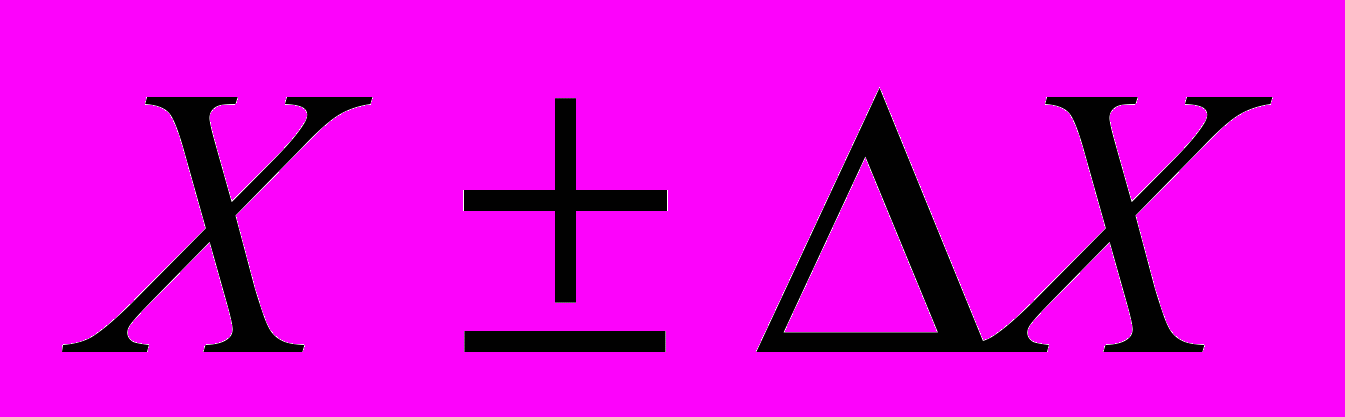Методические указания по определению погрешностей при измерениях в лабораторном практикуме по физике

Вид материала

Методические указания

Содержание Физические измерения Погрешности измерений Систематической погрешностью Оценка погрешностей при прямых измерениях Погрешности приборов Максимальное значение погрешности равно при этом

Подобный материал:

• Образовательные электронные издания и ресурсы в лабораторном практикуме, 354.5kb.
• Методические указания по нормированию топливно-энергетических ресурсов при производстве, 3182.98kb.
• Программа вступительного экзамена в магистратуру элементы теории погрешностей, 51.03kb.
• Методические указания по нормированию топливно-энергетических ресурсов при производстве, 1982.9kb.
• Изучение полупроводникового диода Методические указания к лабораторной работе, 269.79kb.
• Использование программы electronics workbench в лабораторном практикуме по дисциплинам,, 34.69kb.
• Методические указания к практическим занятиям и индивидуальные домашние задачи по физике, 635.57kb.
• При измерении размеров объектов по изображениям важным вопросом является точность получаемых, 8.51kb.
• Методические указания по определению величины накладных расходов в строительстве, 1125.86kb.
• Методические указания по определению величины накладных расходов в строительстве, (мдс, 1587.24kb.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ ПО ОПРЕДЕЛЕНИЮ ПОГРЕШНОСТЕЙ ПРИ ИЗМЕРЕНИЯХ В ЛАБОРАТОРНОМ ПРАКТИКУМЕ ПО ФИЗИКЕ

При выполнении лабораторных работ по всем разделам курса общей физики студенты осуществляют постановку тех или иных физических экспериментов. Целью указанных экспери­ментов является определение некоторых физических величин с помощью измерений. При этом существенное значение имеет точность проводимых измерений. Оценка погрешностей получен­ных результатов является, таким образом, неотъемлемой частью практически каждой экспериментальной работы. Поэтому в задачу лабораторного практикума по физике входит не только знакомство с методами и средствами измерений, но и обучение методам определения ошибок, возникающих в процессе проведе­ния измерений различными измерительными приборами.

Настоящие методические указания содержат в себе основ­ные принципы оценки погрешностей в ходе обработки результа­тов лабораторных работ, выполняемых при изучении всех трех частей курса общей физики. При этом исключительно важно привить студентам навыки правильной обработки экспериментальных данных с первого их появления в лаборатории.

Физические измерения

Физические измерения делятся на прямые и косвенные. Примерами прямых измерений могут служить измерения линей­ных размеров предметов различными измерительными инстру­ментами : линейкой, штангенциркулем, микрометром, измерения времени секундомером, измерения электрических величин (тока, напряжения) соответствующими электроизмерительными приборами.

В большинстве случаев, однако, искомую величину нель­зя получить непосредственно прямым измерением. Тогда изме­ряют некоторые другие величины, связанные с искомыми определенными соотношениями. При таких измерениях, называемых кос­венными, экспериментатор должен вычислить нужную величину, используя известные физические законы и математические фор­мулы. К косвенным относятся, например, проводимые в учебных лабораториях измерения плотности тел (работа 1.01), измере­ния ускорения движения тел (работа 1.12 ), измерения индук­ции магнитных полей (работы 2.26, 2.27, 2.28 ) и т.д.

Погрешности измерений

Любое измерение производится с какой-то степенью точ­ности. Это связано с несовершенством измерительных приборов, методики измерений, несовершенством органов человеческих чувств и т.п. При этом измеренная величина всегда отличается от ее истинного значения. Другими словами, всякое измерение характеризуется наличием ошибок - погрешностей. Во многих случаях погрешности оказываются весьма значительными. Поэто­му в задачу экспериментатора помимо измерения искомой вели­чины в обязательном порядке входит оценка погрешности полу­ченного результата. Без такой оценки результат опыта не имеет, как правило, практической ценности.

Обычно значение измеренной величины X записывают в следующем виде :

где ΔХ - абсолютная погрешность измерения, характеризую­щая отклонение измеренного значения данной величины от ее истинного значения. При этом, поскольку истинное значение остается неизвестным (т.к. в принципе нельзя осуществить абсолютно точное измерение ), можно дать лить приближенную оценку абсолютной погрешности.

Поскольку причины возникновения ошибок могут быть са­мыми разными, необходимо классифицировать погрешности, возни­кающие в ходе экспериментов. Только в этом случае возможна правильная опенка погрешности полученного результата, так как от типа погрешностей зависит и способ их вычисления.

Погрешности подразделяются на случайные и систематичес­кие.

Систематической погрешностью называют составляющую погреш­ности измерения, остающуюся постоянной или закономерно из­меняющуюся при повторных измерениях одной и той же величины. Случайной погрешностью называют составляющую погрешности из­мерения, изменяющуюся случайным образом при повторных изме­рениях одной и той же величины. Выделяют также погрешности приборов, которые могут иметь как систематический, так и случайный характер.

Рассмотрим некоторые причины, вызывающие появление сис­тематических и случайных погрешностей. Систематическая пог­решность может быть связана с неисправностями измерительных приборов, неточностью их регулировки, несоблюдением условий их эксплуатации и т.п. Такие погрешности возникают, например, при не совсем горизонтальном положении некоторых приборов или при использовании стрелочного прибора, у которого стрелка до начала измерений не была установлена на нуль. Заметим, что указанные погрешности не относятся к разряду приборных, кото­рые характеризуют вполне исправные и правильно эксплуатируе­мые инструменты.

Причина возникновения систематической погрешности может заключаться и в самой методике измерений. Так, например, оп­ределяя плотность твердого тела по измерениям его массы и объема, можно допустить ошибку, если внутри исследуемого тела имеются пустоты в виде пузырьков воздуха. В этом случае ус­транить ошибку можно только изменив метод измерений.

Случайные погрешности связаны с некоторыми случайными факторами, влияющими на точность измерений. Они могут зависеть от условий, в которых производится эксперимент. Например, обычный сквозняк в лабораторном помещении может случайным об­разом сказаться на измерениях температуры. Измерения проме­жутков времени запускаемым вручную секундомером также приво­дит к возникновению случайных погрешностей, связанных со слу­чайным изменением времени реакции экспериментатора.

Появление случайных погрешностей может быть связано со спецификой измеряемой величины. Если, например, измерять штангенциркулем размеры неточно изготовленной детали, то по­лученные результаты будут случайным образом зависеть от положения измерительного прибора. Еще один пример – неточность отсчета по шкале стрелочного прибора, связанная со случайным Мнением положения глаз экспериментатора относительно прибора.

Основным способом уменьшения случайных погрешностей является многократное измерение одной и той же физической ве­личины. Заметим, однако, что максимально возможная точность измерения определяется теми приборами, которые используются в эксперименте. Поэтому уменьшение случайной погрешности пу­тем увеличения числа опытов имеет смысл до тех пор, пока ее величина не станет явно меньше величины погрешности прибора. Погрешности приборов связаны с несовершенством любого измерительного инструмента. Если значение измеряемой величины определяется по шкале инструмента, абсолютная погрешность прибора считается, как правило, равной половине цены деления шкалы (например, линейки) или цене деления шкалы, если стрелка прибора перемещается скачком (секундомер) приборов, снабженных нониусом, погрешность можно считать равной точности нониуса. Погрешности электроизмерительных приборов определяют по их классу точности, который указывается на шкале.

Оценка погрешностей при прямых измерениях

Для повышения точности измерений (если, конечно, этом есть необходимость ) следует по возможности устранить математические погрешности. Это можно сделать различными способами. Если известна природа такой ошибки, и может быть определена ее величина, достаточно ввести соответствующую поправку. Это возможно, например, для исключения влияния на результат измерения таких факторов, как температура и давление воздуха, или факторов, связанных с известным недостатком измерительного инструмента (неравноплечностые рычажных весов обитым нулем прибора и т.п.). Разумеется, что вносить такого рода поправки есть смысл только в том случае, когда их величина соизмерима с величиной других ошибок, сопровождающих данные измерения.

Можно также исключить некоторые виды систематических погрешностей, используя спецальные методы измерений. Так, влияние уже упомянутой неравноплечности весов можно устранить, взвесив исследуемое тело дважды - сначала на одной чаше весов, а затем на другой. Есть и другие способы исключения системати­ческих погрешностей. Однако, как было отмечено выше, всегда остается ошибка; связанная с погрешностью используемого при­бора, а также случайные погрешности, которые заранее учесть нельзя.

В том случае, если погрешность прибора заведомо больше величины случайных погрешностей, присущих данному методу при данных условиях эксперимента, достаточно выполнить измерение один раз (например, при измерении обычной масштабной линей­кой длины, точно изготовленной детали ). Тогда абсолютная пог­решность измерения будет равна погрешности прибора. Если, наоборот, определяющей является случайная погрешность, надо уменьшить ее величину с помощью многократных измерений. Рас­смотрим методику оценки случайной погрешности в этом случае.

Предположим, что мы произвели n прямых измерений величины Х . Обозначим через Х₁ , Х₂, ... Х_n резуль­таты отдельных измерений, которые вследствие наличия случай­ных погрешностей будут в общем случае неодинаковыми. В теории вероятностей доказывается, что истинное значение измеряемой величины (при отсутствии систематических погрешностей ) равно ее среднему значению, получаемому при бесконечно большом числе измерений, т.е.

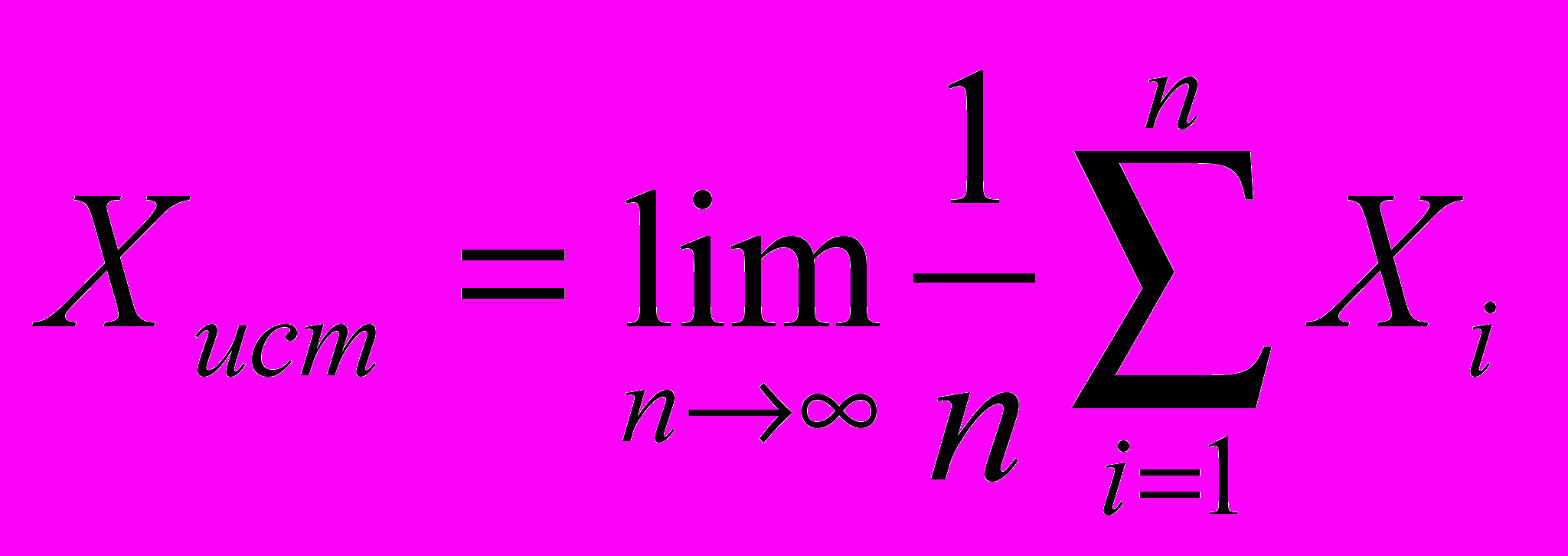(1)

Поэтому наиболее близким Х истинному будет для данной серии измерений среднее арифметическое значение, а именно:

(2)

Отклонения измеренных значении Х_n от X_ср носят слу­чайный характер и называются абсолютными ошибками отдельных намерений :

(3)

В элементарной теории ошибок, разработанной Гауссом мерой случайной погрешности отдельного измерения является так называемая средняя квадратичная погрешность, вычисляем по формуле

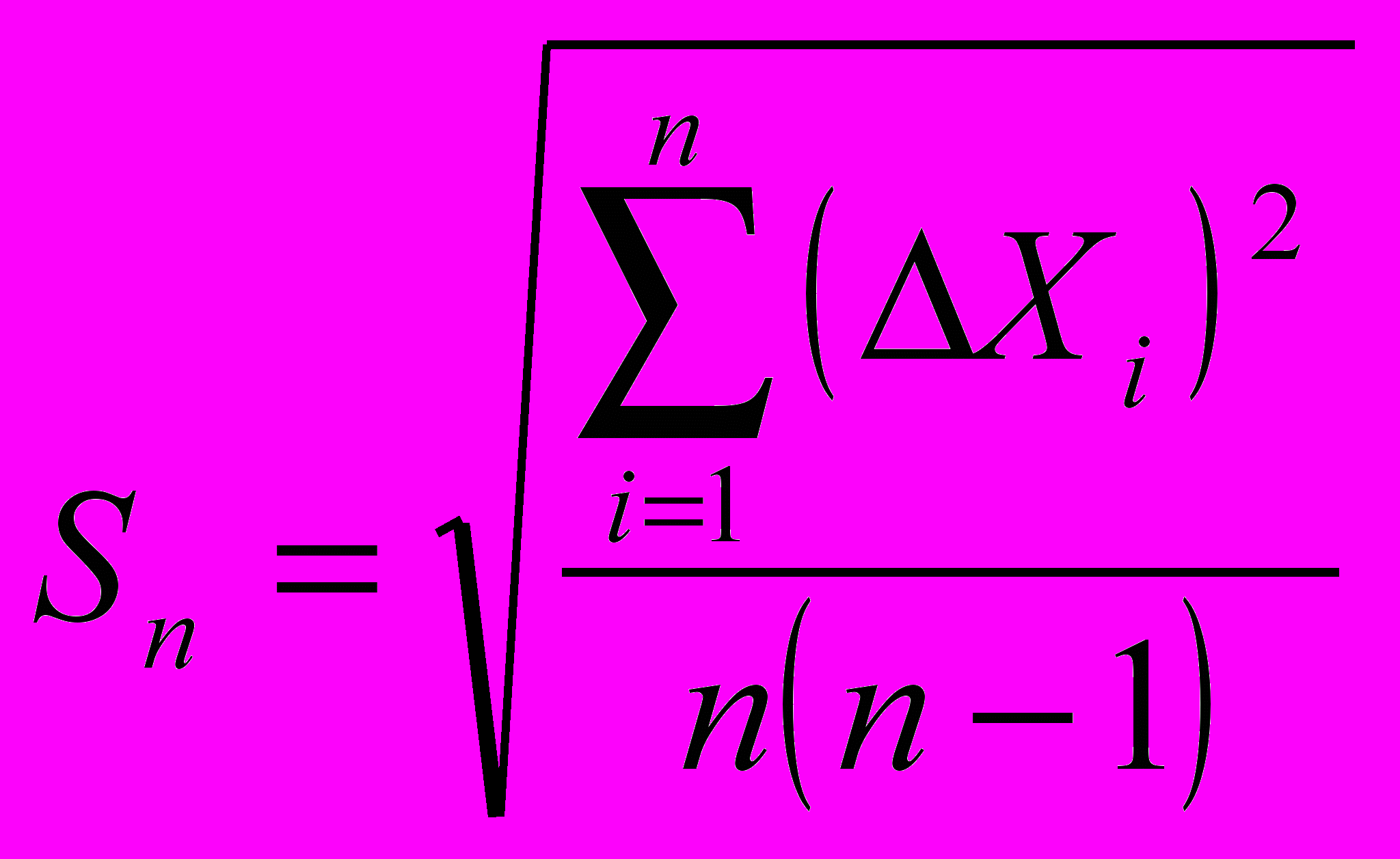(4)

При большом числе измерений величина S_n стремится к некото­рому пределу σ, т.е.



Строго говоря, именно этот предел называется средней квадра­тичной погрешностью, а квадрат этой величины - дисперсией измерений.

Однако средняя квадратичная погрешность отдельного из­мерения Sn полезна лишь для оценки точности применяемого способа измерений. Нас же, главным образом, интересует погреш­ность результата всей серии измерений. Для этого надо найти среднюю квадратичную погрешность среднего арифметического, характеризующую отклонение Х_ср от истинного значения искомой величины. Из закона сложения ошибок вытекает, что сред­няя квадратичная погрешность среднего арифметического равна

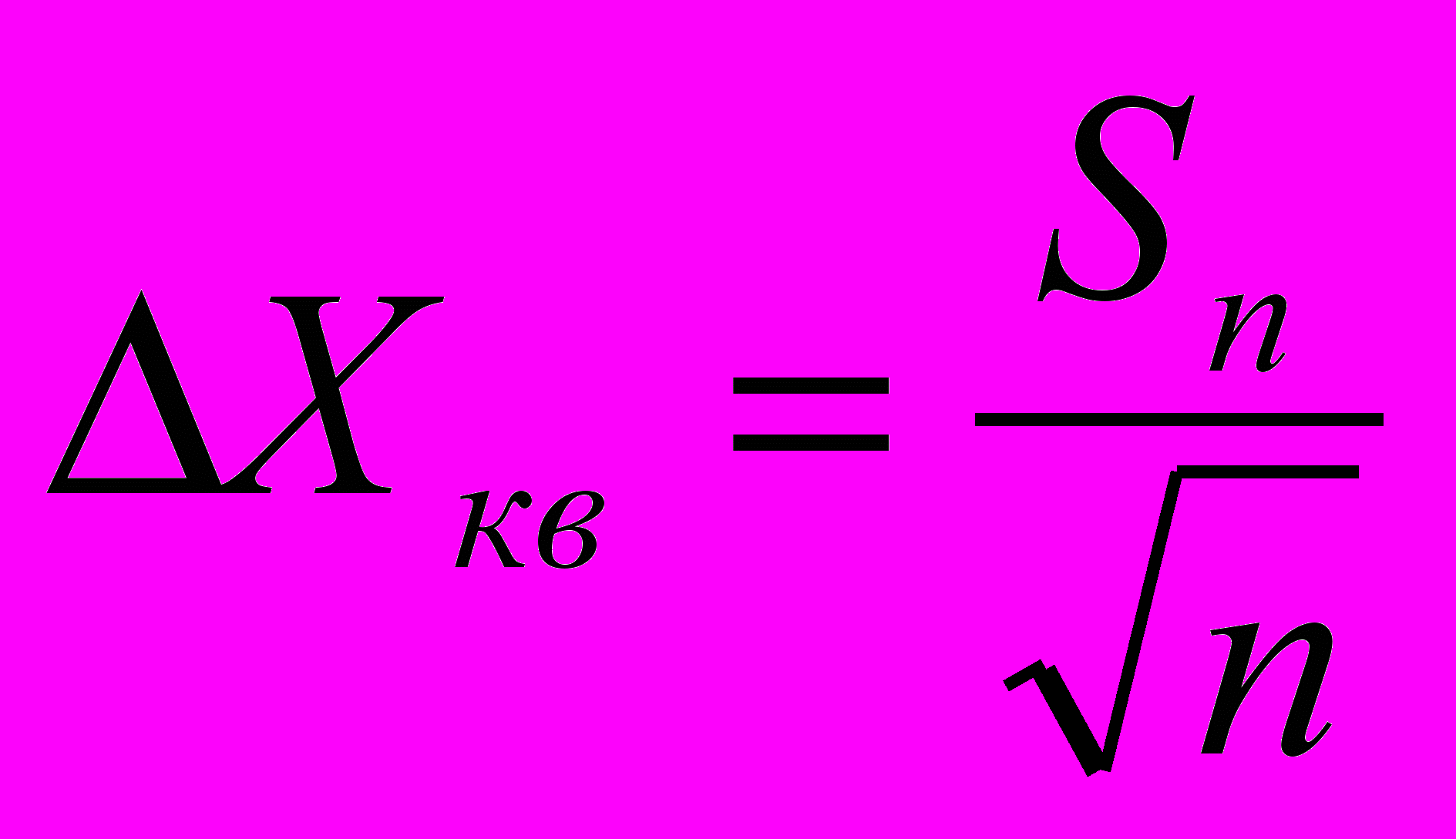(5)

Отсюда следует, что чем больше проделано измерений одной и той же величины, тем меньше случайная погрешность результата. Это вполне понятно, т.к. согласно (1) и (2), чем больше число опытов, тем ближе Х_ср к Х_ист

Используя соотношения (4) и (5) , можно записать сле­дующее окончательное выражение для средней квадратичной пог­решности результата серии измерений

(6)

Это не означает, однако, что истинное значение измеря­емой величины обязательно будет заключено в интервале от X_ср - ΔX_кв до Х_ср + ΔX_кв. Оказывается, что паже при очень большом числе измерений вероятность того, что истинное значение попадет в указанный интервал, не превышает 0,7. Другими словами, надежность полученного резуль­тата в данном случае составляет около 70 %. При малом числе измерений (n < 10) она будет еде меньше.

Вероятность того, что истинное значение измеряемой величины попадет в заданный интервал, называется доверитель­ной вероятностью, или коэффициентом доверия Р , а соответствующий интервал, определяемый величиной абсолютной погреш­ности – доверительным интервалом. Достоверность результата при данном количестве измерений можно увеличить, уменьшая его точность, т.е. расширяя доверительный интервал.

Обычно случайную погрешность рассчитывают по формуле:

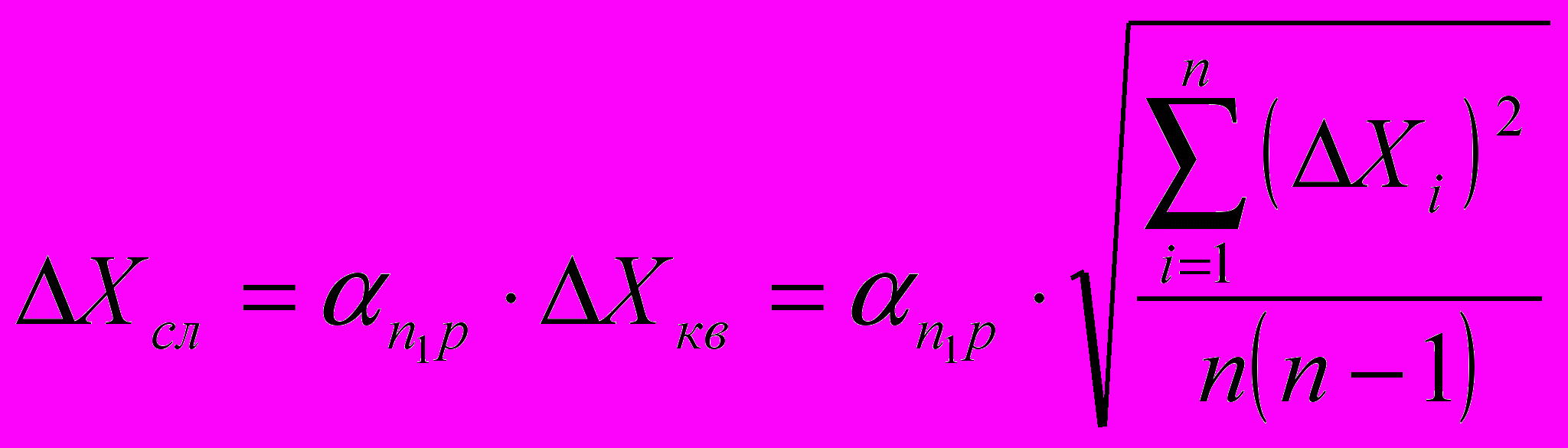(7)

где α_n,p — коэффициент Стьюдента, зависящий от числа из­мерений П. и выбранного значения доверительной вероятнос­ти P. Значения α_n,p для ряда случаев приведены в таблице I.

Таблица I.

	3	4	5	6	7	8	9	10	…	100
0,5	0,82	0,77	0,74	0,73	0,72	0,71	0,71	0,70		0,68
0,7	1,3	1,3	1,2	1,2	1,1	1,1	1,1	1,1		1,0
0,95	4,3	3,2	2,8	2,6	2,4	2,4	2,3	2,3		2,0

Как видно из таблиц, увеличение числа опытов позво­ляет при заданной доверительной вероятности существенно уменьшить случайную погрешность. Здесь следует учесть, что помимо коэффициента α_n,p с ростом n уменьшается и значение Х_кв.

Таким образом, для характеристики величины случайной погрешности в принципе необходимо задать два числа : саму погрешность X_кв и доверительную вероятность P, позво­ляющую оценить степень надежности полученного результата. Необходимая степень надежности определяется спецификой производимых измерений. Доверительная вероятность должна быть, например, очень высокой при контроле размеров дета­лей самолетов и достаточно низкой при аналогичном контроле деталей ручной тележки. В условиях учебной лаборатории достаточно брать P = 0,7.

Для окончательной оценки величины абсолютной погреш­ности ΔХ следует теперь сравнить полученную случайную погрешность с погрешностями других видов. Если путем много­кратных измерений удалось сделать случайную ошибку заметно меньше приборной ( при незначительных систематических ошиб­ках ), то в качестве ΔХ можно взять погрешность использо­вавшегося прибора. В противном случае в качестве ΔX берут значение X_сл .

Таким образом, для оценки абсолютной погрешности при прямых измерениях следует :

1) произвести серию измерений искомой величины и вы­числить среднее значение по формуле (2);

2) вычислить абсолютные ошибки отдельных опытов сог­ласно (3);

3) рассчитать ΔХ_кв по формуле (б);

4) определить случайную погрешность, пользуясь форму­лой (7) и таблицей 1 (или формулой Стъюдента);

5) сравнить ΔХ_ср погрешность прибора, выбирая в качестве абсолютной погрешности наибольшую из этих погрешностей;

6) записать результат измерений в виде X = Х_ср ± ΔХ (8)

Заметим, что если величины случайной и приборной пог­решностей близки друг к другу, то обе они влияют на точность результата, примерно в одинаковой степени. Поэтов иногда в мчестве максимального значения абсолютной ошибки берут сумму указанных погрешностей.

Следует обратить внимание на то обстоятельство, что величина абсолютной погрешности сама по себе дает мало ин­формации о действительной точности измерения, если не сопос­тавлять ее со значением измеряемой величины. Действительно, пусть погрешность, полученная при измерении линейных раз­меров, равна 0,5 см. или при этом идет речь о длине, на­пример, спичечной коробки, то точность будет очень плохой, а если с такой же погрешностью измерена длина заводского корена, то точность измерения следует считать даже излиш­не высокой.

Поэтому помимо абсолютной погрешности часто исполь­зуется так называемая относительная погрешность измерения Р. Она равна отношению абсолютной погрешности измерения к среднему значению измеряемой величины :

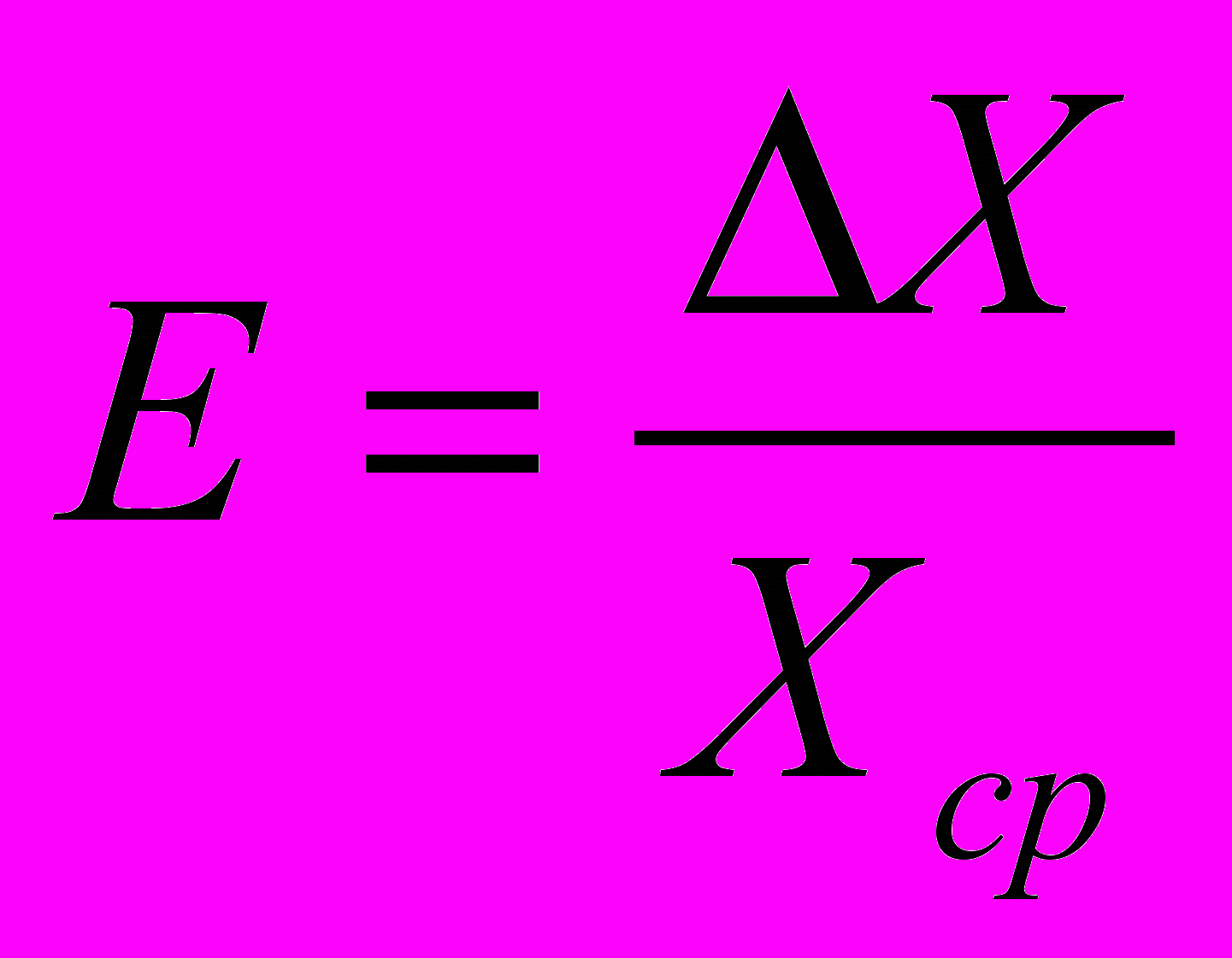(9)

Относительную погрешность иногда выражают в процентах. Тог­да:



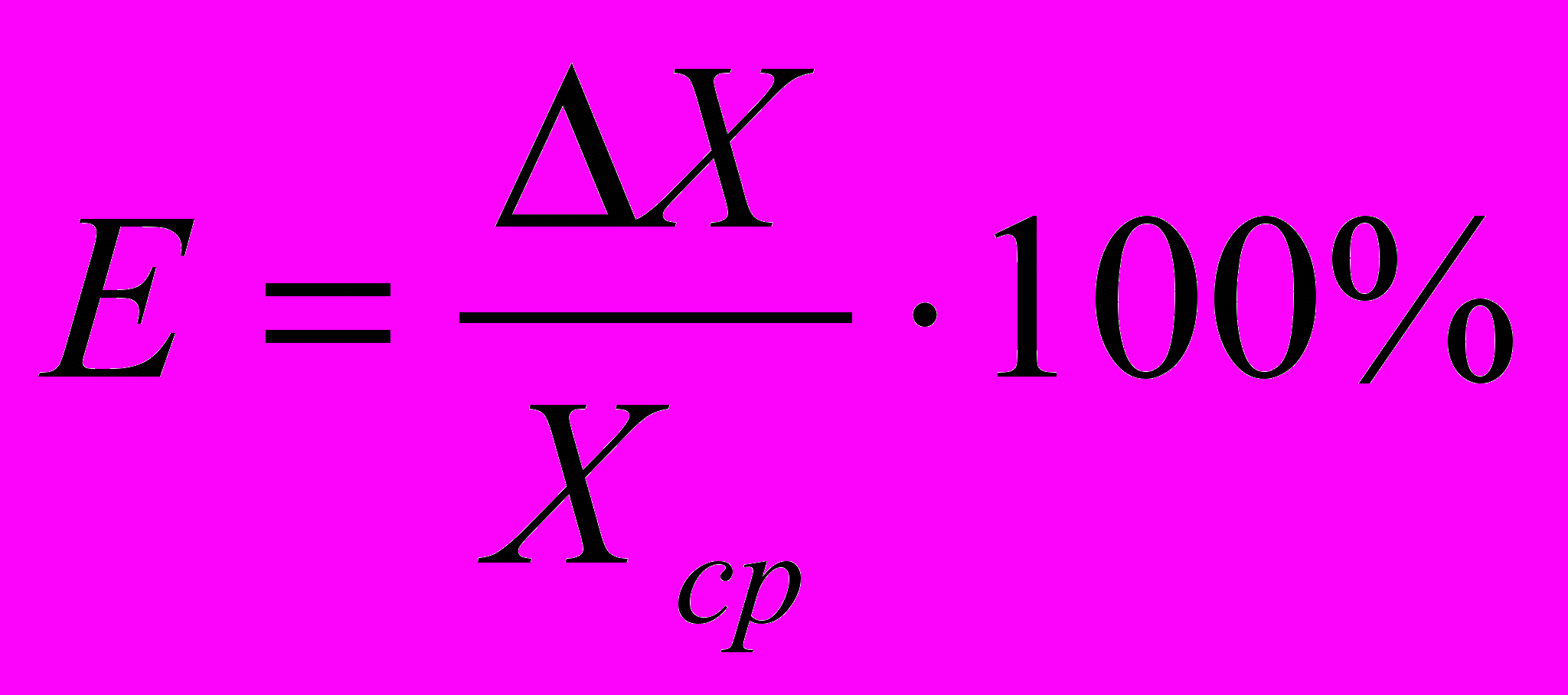
Особенно удобно использовать относительную погрешность при сравнении точности измерений разнородных физических величин.

Погрешности приборов

Основной частью большинства измерительных приборов является икала с нанесенными на ней делениями. Погрешность таких приборов составляет, как уже отмечалось, величину порядка половины цены деления шкалы в той ее части, где производится отсчет (шкала может быть и неравномерной). Поэтому, как правило, не следует стараться при измерениях оценивать на глаз малые доли деления, тем более, что при изготовлении прибора шкала обычно наносится в соответствии с его классом точности (см. ниже).

Для существенного повышения точности измерений в ряде приборов помимо основной имеется дополнительная шкала, на­зываемая нониусом. Обычно это маленькая линейка с делениями, скользящая вдоль основной шкалы. Деления на нониусе наносят таким образом, что одно деление нониуса составляет 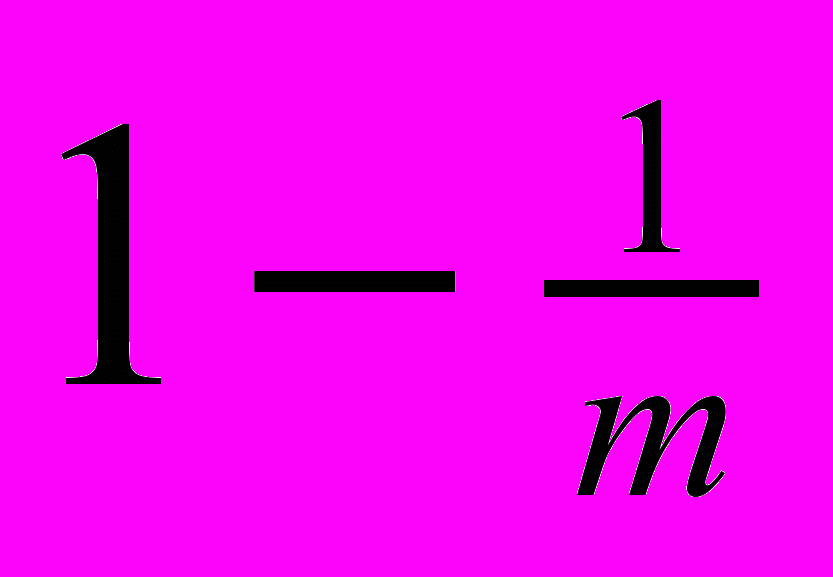деления основной шкалы, где m — число делений нониуса. Если масштаб мелкий, то деления нониуса делают более крупны­ми, равными 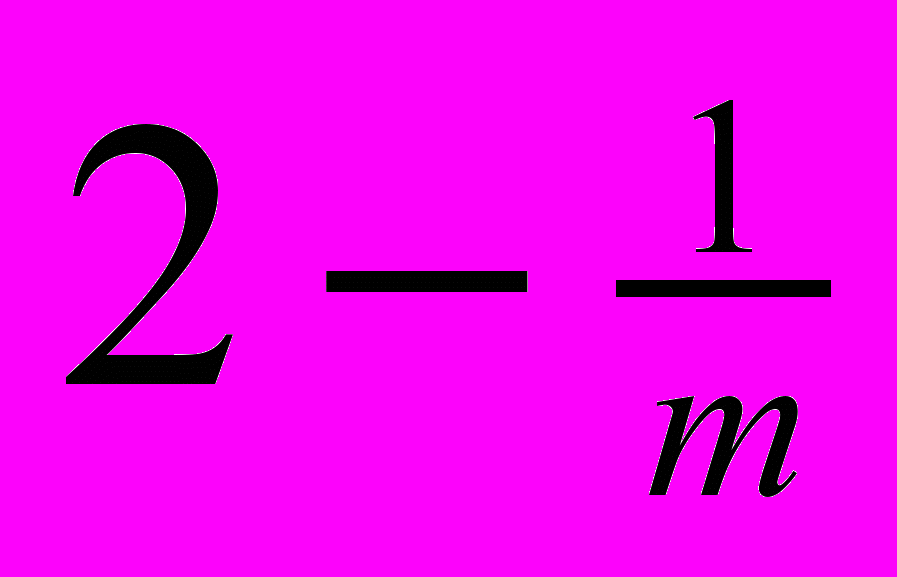делений основной шкалы. И в том, и в другом случае оказывается, что при любом положении нониу­са один из его штрихов совпадает с каким-либо штрихом ос­новной шкалы. Отсчет по нониусу основан на способности глаза достаточно точно фиксировать это совпадение. Поэтому, пользуясь нониусом, можно производить отсчеты с точностью до 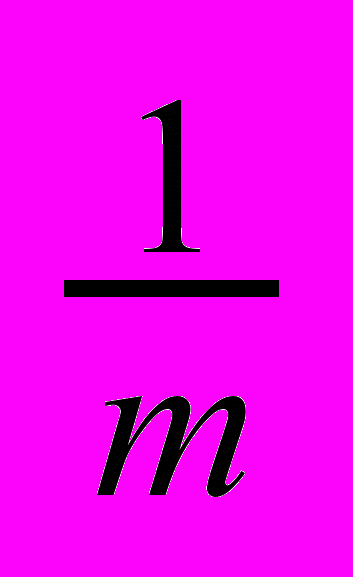части наименьшего деления основной шкалы.

Рассмотрим процессе измерений простейшим приборок, снабженным нониусом, - штангенциркулем. В исходном положе­нии (рис. 1а) нулевой штрих нониуса совпадает о нулем ос­новной шкалы, цена деления которой 1 мм. Число делений но­ниуса m в нашем примере равно 20. а его точность 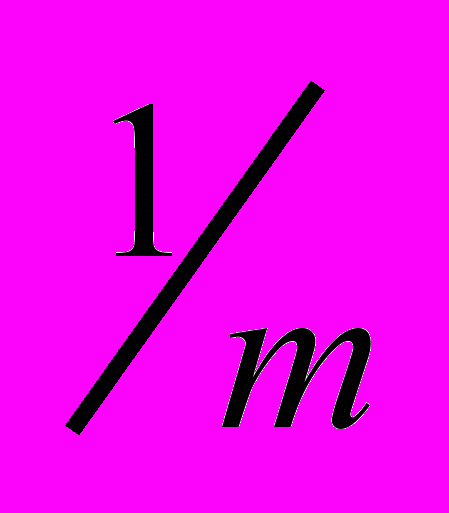= 0,05 мм. Одно деление нониуса составляет 2 -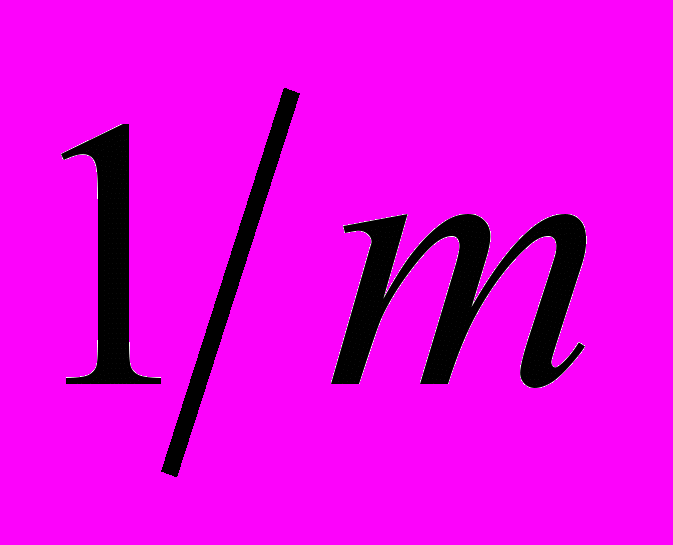. = 1,95 мм. Это означает, что первый (после нуле­вого) штрих нониуса смещен относительно второго штриха основной шкалы на 0,05 мм. Соответственно штрих с номером К смещен относительно ближайшего к нему справа штриха ос­новной шкалы на К' 0,05 мм. Поэтому, сдвигая нониус на эту величину, мы получим совпадение К-го штриха с одним из делений основной шкалы. Сдвинув нониус еще на 0,5 мм, мы обнаружим совпадение со штрихом основной шкалы К + 1 -го штриха нониуса и т.д. Аналогичная картина будет наблюдаться при смещении нулевого штриха нониуса вправо от любого из де­лений основной шкалы. Таким образом, с помощью изображенного на рисунке штангенциркуля можно оценивать размеры предметов с точностью до 0,05 мм.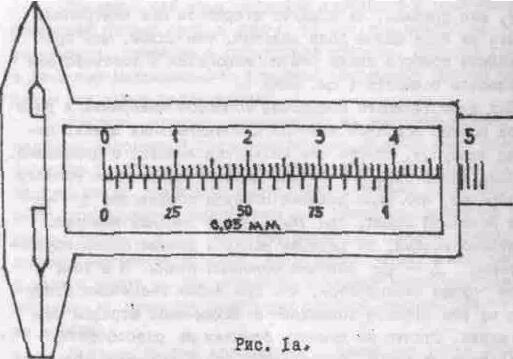







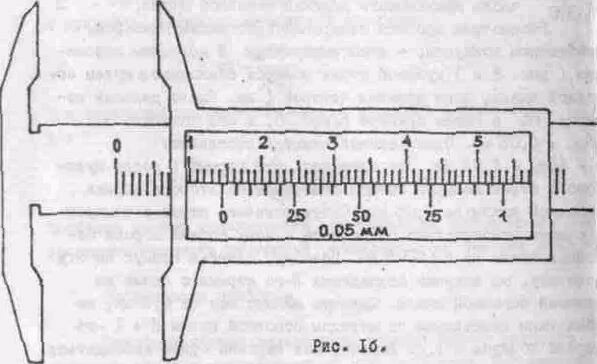
Действительно, при измерении (см. рис. 1б) нулевой штрих нониуса, расположенного на подвижной части прибора, сдвигается как раз на величину, равную размеру предмета. Следовательно, отсчет надо произвести по основной шкале напротив нулевого штриха нониуса, который в общем случае будет находится между двумя соседними штрихами основной шкалы. При этом искомый размер будет равен целому числу делений основной шкалы плюс точность нониуса 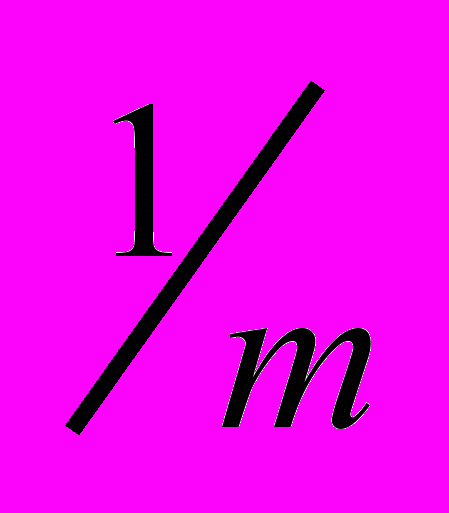(в нашем случае 0,05 мм.), умноженная на номер штриха нониуса, сов­павшего е некоторым штрихом основной шкалы. В примере на рис. 1б отечет должен быть равен 14,35 мм.

Погрешность штангенциркуля обуславливается неточностью совпадения штрихов, и не может быть, очевидно, больше точ­ности нониуса (иногда берут погрешность, равную половине точности нониуса ). Точность нониуса 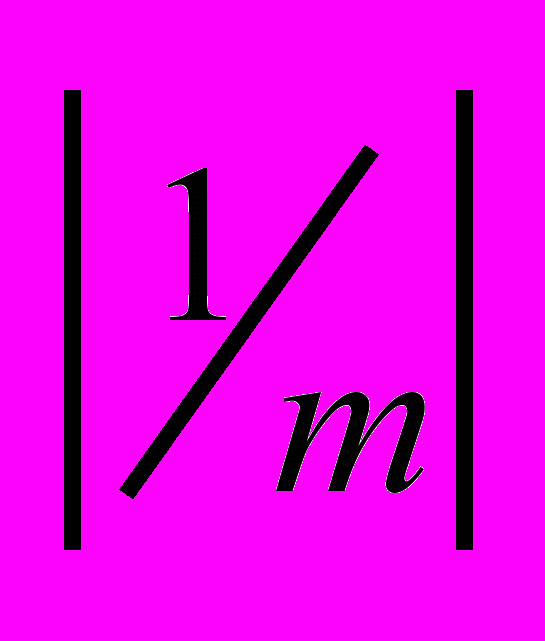указывается, как правило, на самом приборе. Для штангенциркуля она обычно составляет 0,05 (иногда 0,1 мм).

Аналогично устроены и так называемые круговые нониусы, использующиеся в приборах с изогнутой шкалой. служащих глав­ным образом для измерения углов.

Особую роль играет оценка погрешностей, возникающих при использовании электроизмерительных приборов. В этом случае измерение каждой величины проводится, как правило, только один раз, и точность его определяется погрешностью используемого прибора. При электрических измерениях помимо абсолютной погрешности ΔX, равной разности между по­казанием прибора и действительным (истинным) значением измеряемой величины, и относительной погрешности 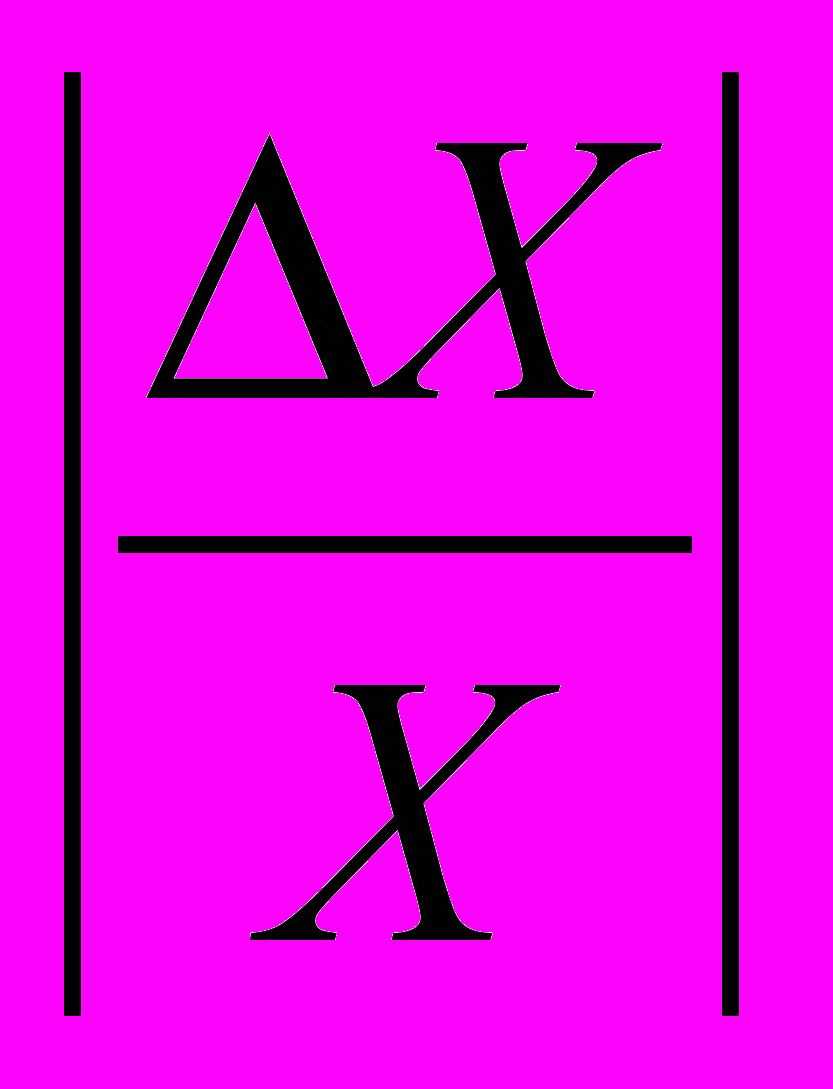оценивается также приведенная погрешность. Она равна отно­шению абсолютной погрешности к предельному значению вели­чины, т.е. наибольшему ее значении, которое можно измерить по шкале прибора |ΔX_m| . Наибольшее значение приведенной погрешности, соответствующее максимально абсолютной пог­решности, допускаемой данным прибором, называется классом точности:

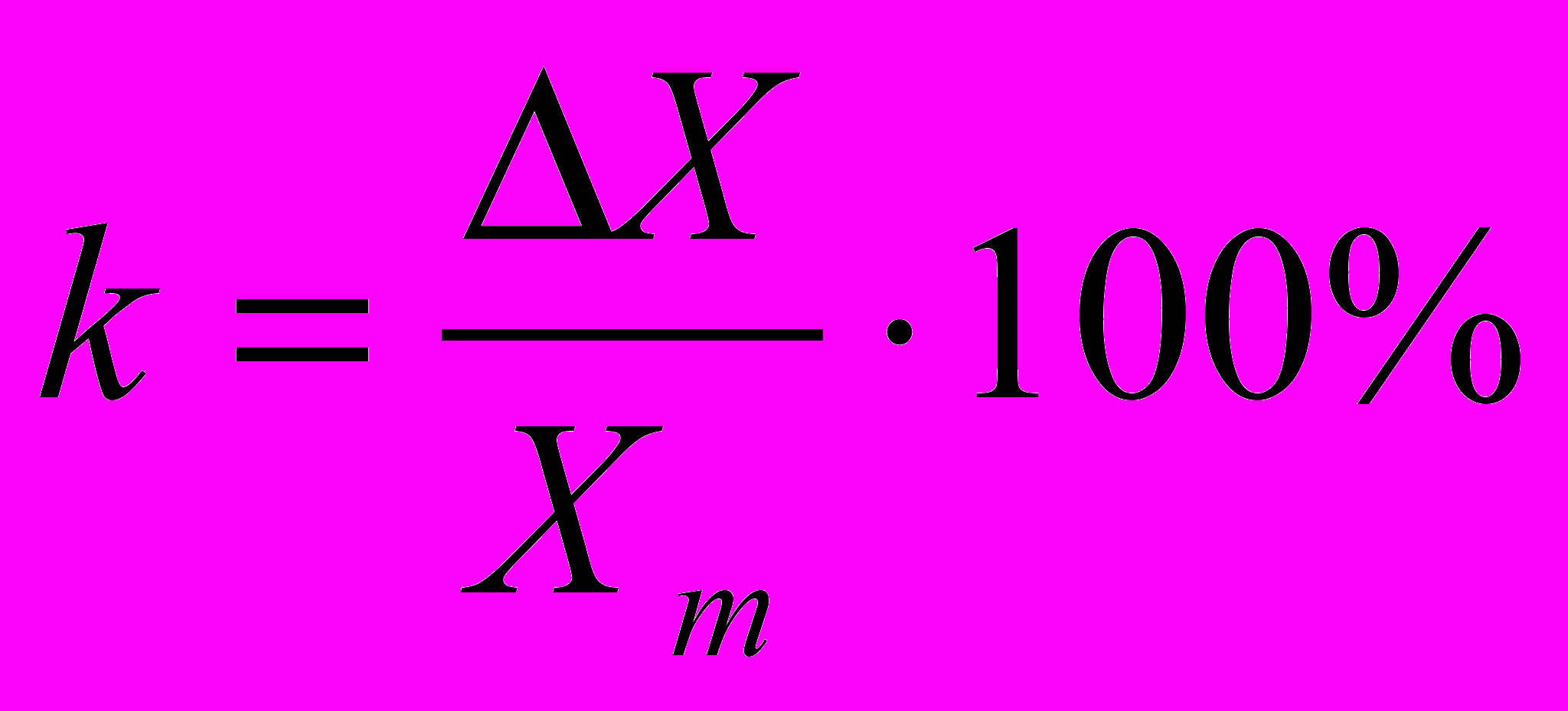(10)

Согласно ГОСТ 1845-52, электроизмерительные приборы делятся на семь классов точности : 0,1; 0,2; 0,5; 1,0; 1.8;

2,5; 4,0. Значение класса точности помещается на лицевой стороне прибора. Зная К, можно найти наибольшую абсолютную погрешность :

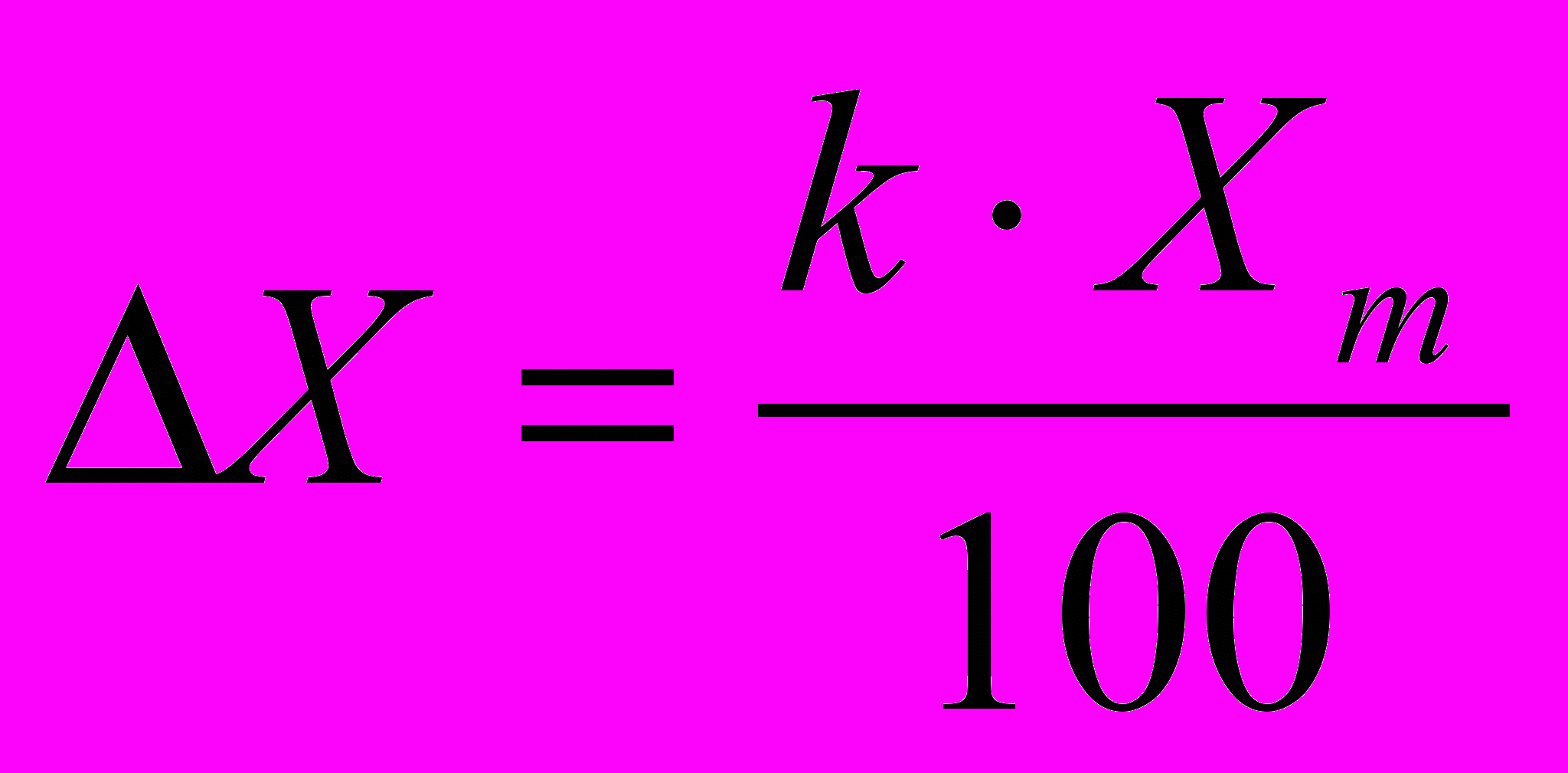(11)

При измерениях электрических величин могут быть ис­пользованы приборы различных систем. Наиболее употребитель­ны приборы магнитоэлектрической системы, электромагнитные, электродинамические и тепловые приборы. У приборов магнито­электрической системы, основанных на действии магнитного поля постоянного магнита на рамку с током, угол поворота рамки пропорционален протекающему по ней току. Поэтому Чувствительность таких приборов постоянна, а измерительная шкала равномерна. Приборы других систем характеризуются не­равномерной шкалой. Однако абсолютная погрешность остается постоянной во всём диапазоне измерений.

Что касается относительной погрешности, то она будет тем больше, чем меньше измеряемая величина. Следовательно, нужно избегать таких измерений, при которых измеряемая ве­личина намного меньше ее предельного значения Х_m . Иными словами, желательно, чтобы при измерении стрелка прибора от­клонялась по возможности на больший угол. Если же искомое значение приходится отсчитывать в самом начале шкалы, сле­дует воспользоваться более чувствительным прибором. Особенно удобны приборы с несколькими пределами измерений, позволяю­щее производить измерения в различных диапазонах с наиболь­шей точностью.

Оценка погрешностей при косвенных измерениях При косвенных измерениях искомая физическая величина А является функцией величин Х , У , Z ...., которые мо­гут быть получены с помощью прямых измерений. Результат кос­венного измерения записывается в виде :

А ± ΔА (12)

где A = ƒ(X, Y, Z, …) - значение искомой величины, рассчитанное по средним значениям параметров X , Y, Z, ..., каждый из которых измеряется, как правило, по несколько раз. ΔА - абсолютная погрешность косвенного измерения. зависящая от погрешностей параметров X , Y , Z, ... ( т.е. от ΔХ , ΔY , ΔZ , ...).

В простейших случаях абсолютную и относительную пог­решность косвенных измерений подсчитать нетрудно. Рассмот­рим несколько примеров.

Пусть А = Х + У . Если известны погрешности ΔX и ΔY , то

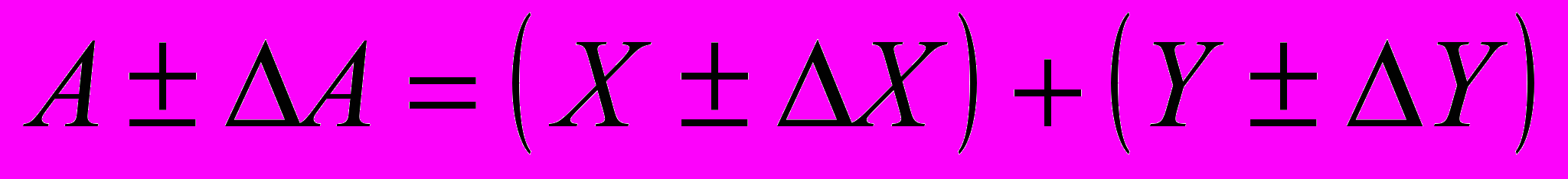
Максимальное значение погрешности равно при этом

ΔА = ΔX + ΔY. (13)

Такова ие будет максимальная абсолютная погрешность при

А = X – Y. Таким образом, относительные погрешности величин, являющихся суммой или разностью двут! параметров, равны соответственно :

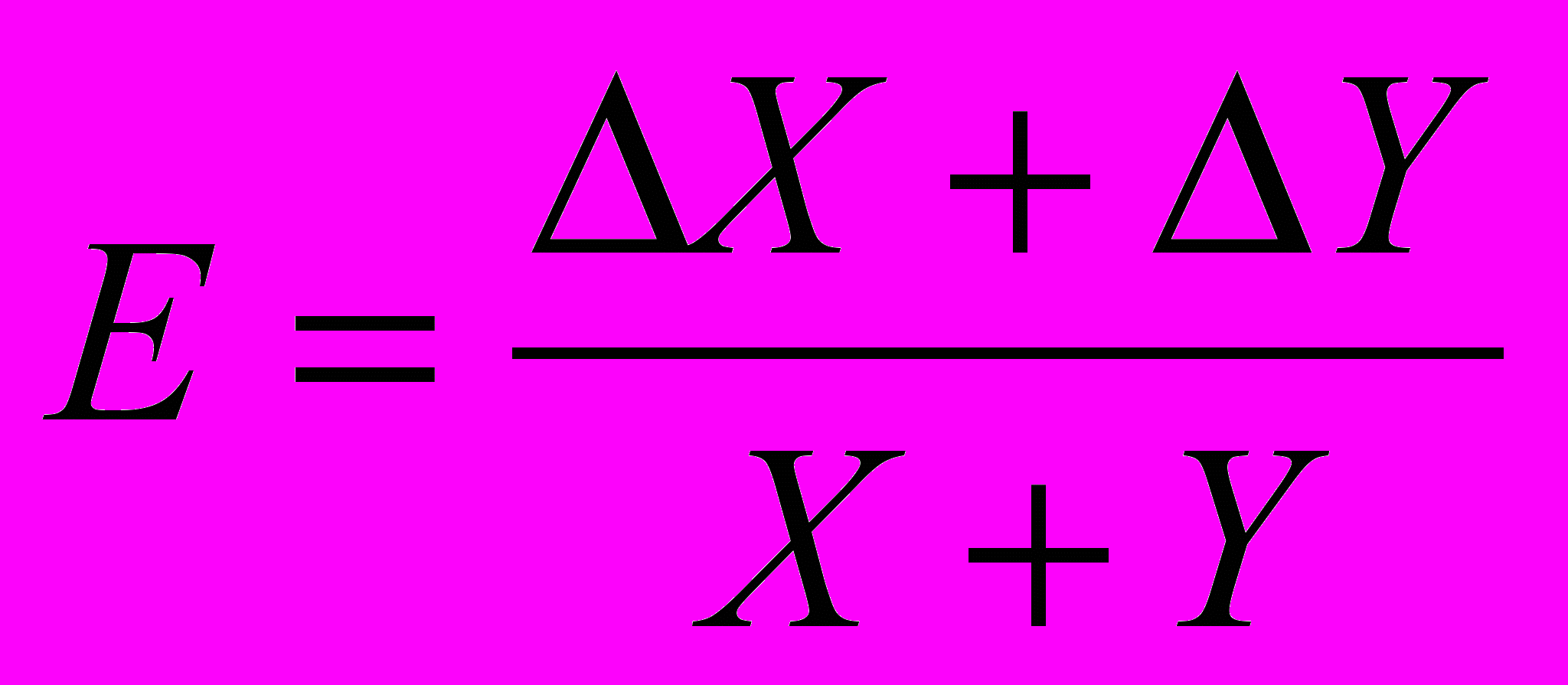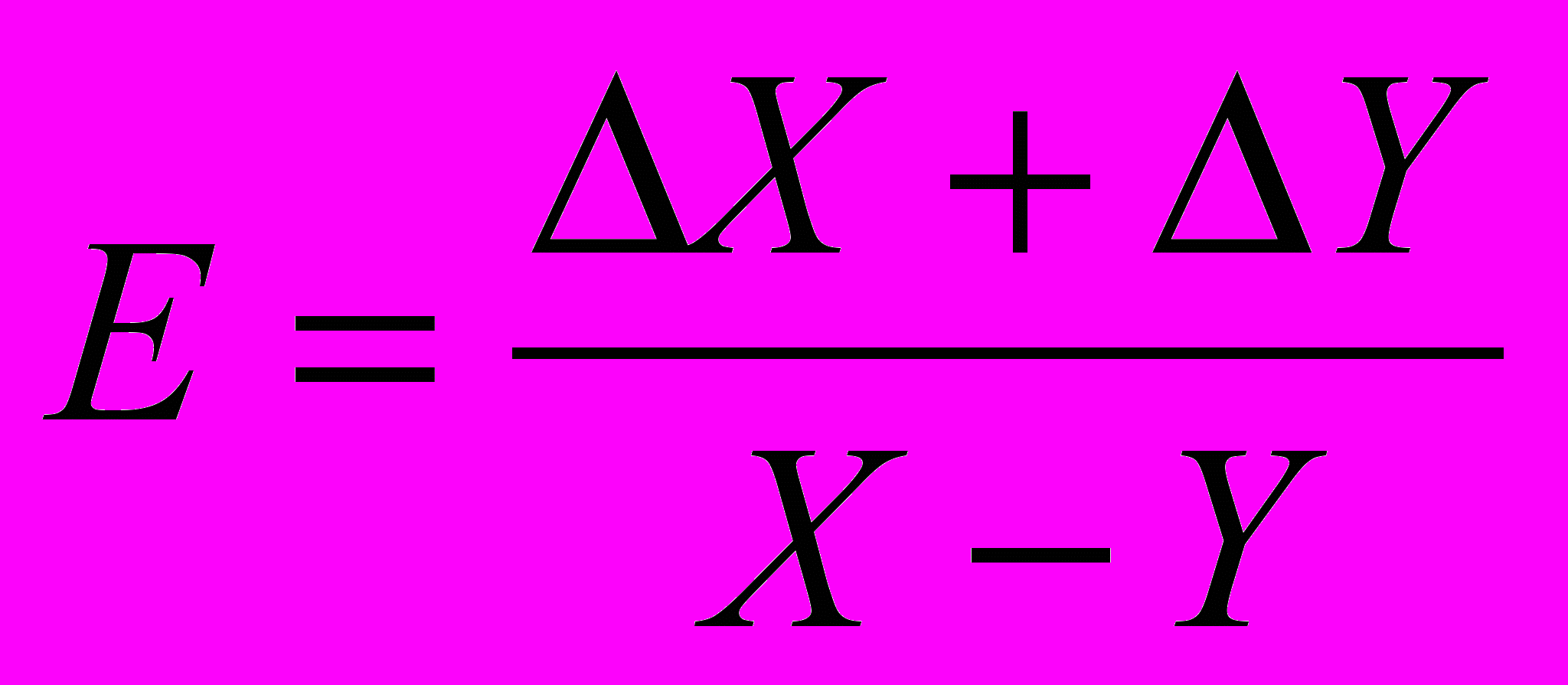и (14)

Пусть теперь A = X^.Y - тогда



Пренебрегая слагаемым второго порядка малости |ΔX^. ΔY| имеем :

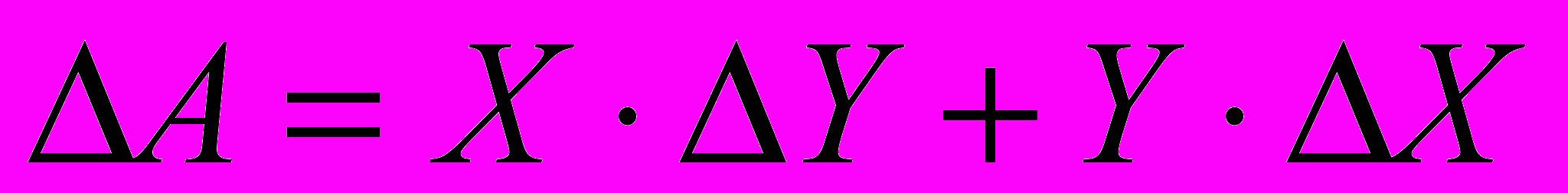(15)

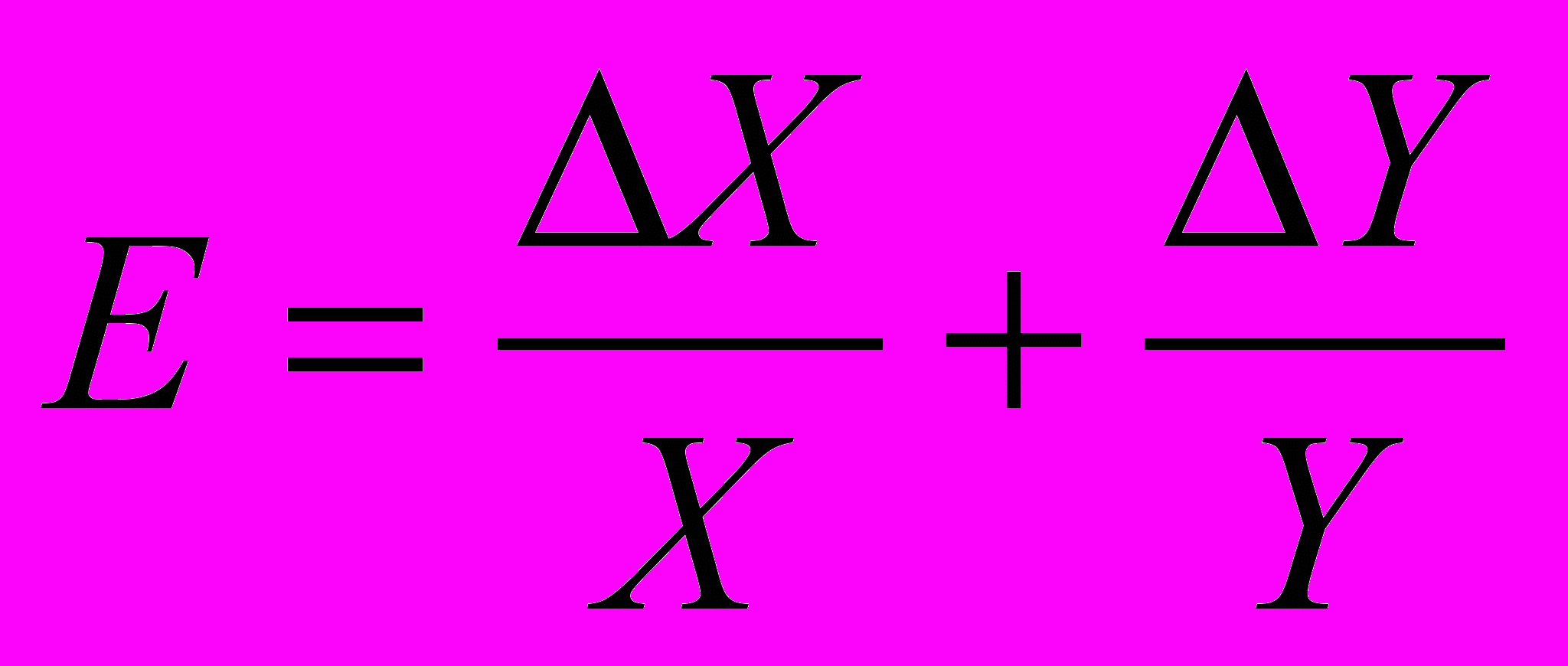или (16)

Если 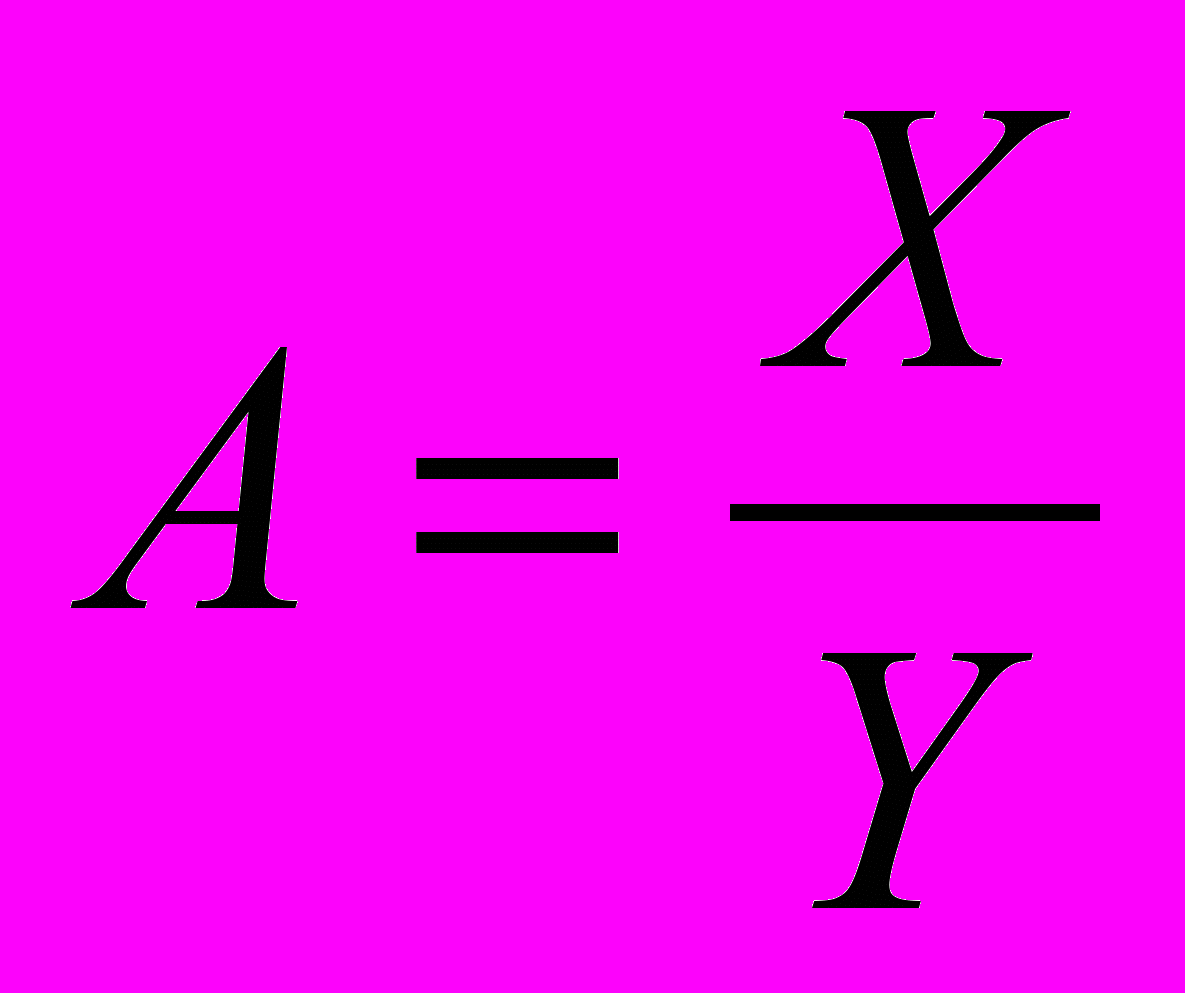, то

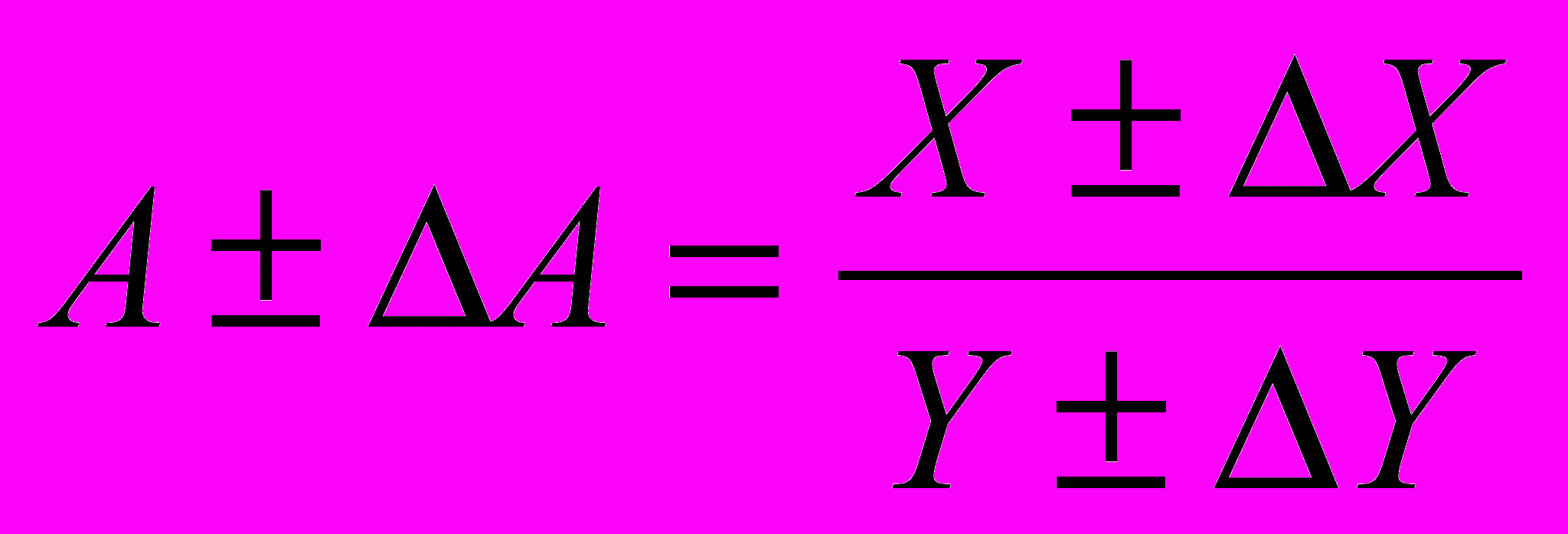
Максимальное значение погрешности ΔА получится в случае, если погрешности в числителе и в знаменателе данного выражения взять с разными знаками. Тогда можно записать :



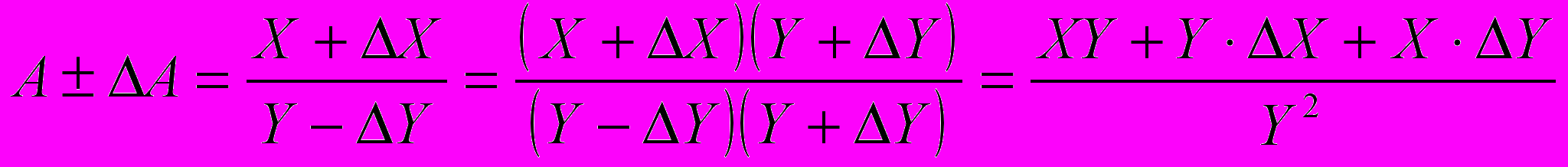
Здесь мы пренебрегли членами (ΔY)² и ΔX^. ΔY . Максимальная абсолютная погрешность равна в этом случае

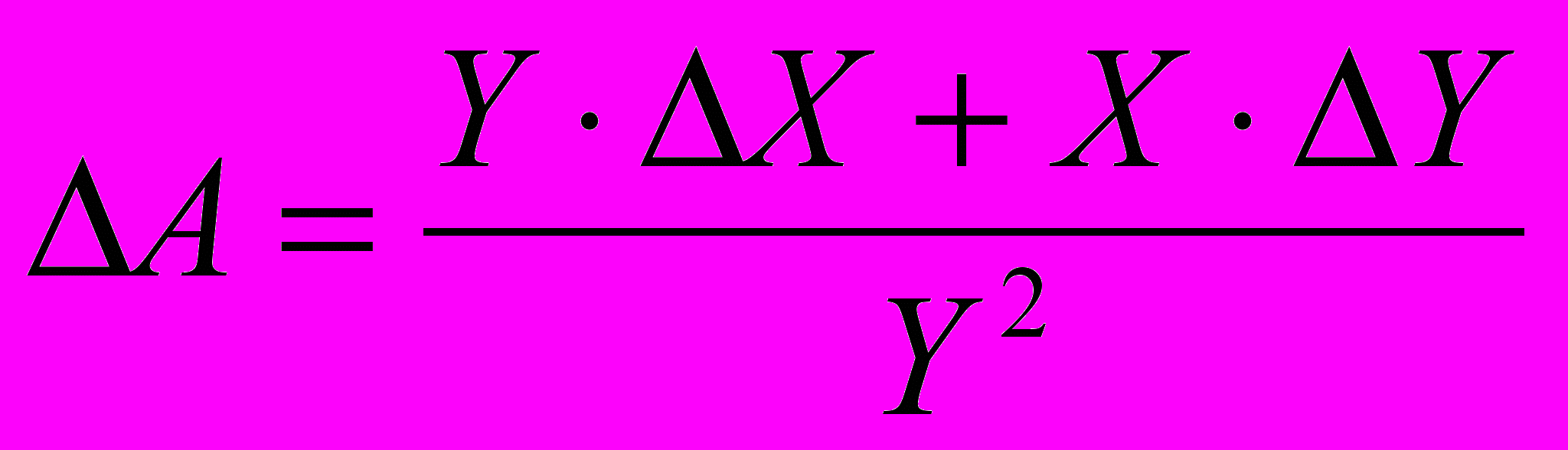, (17)

а относитедьная погрешностс, как и в (16), равна



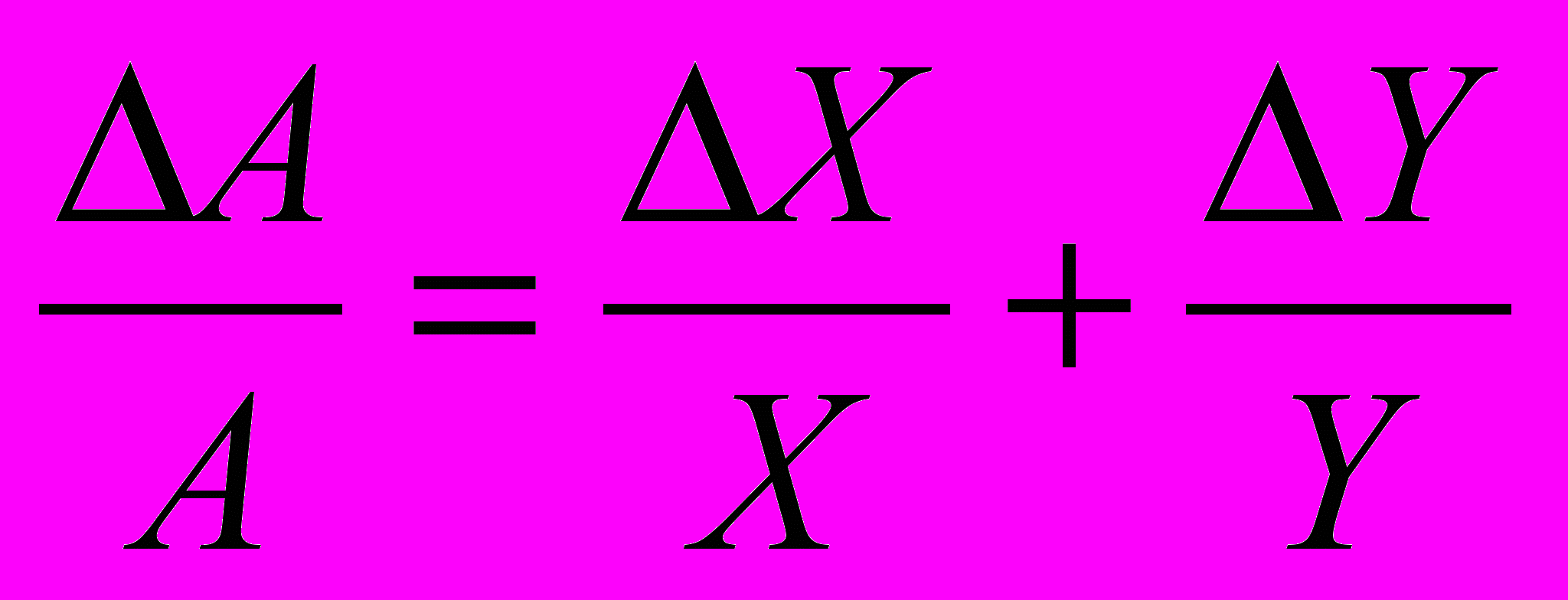
Полученные результаты легко обобщаются на произвольное количество сомножителей. Если в самом общем случае

,

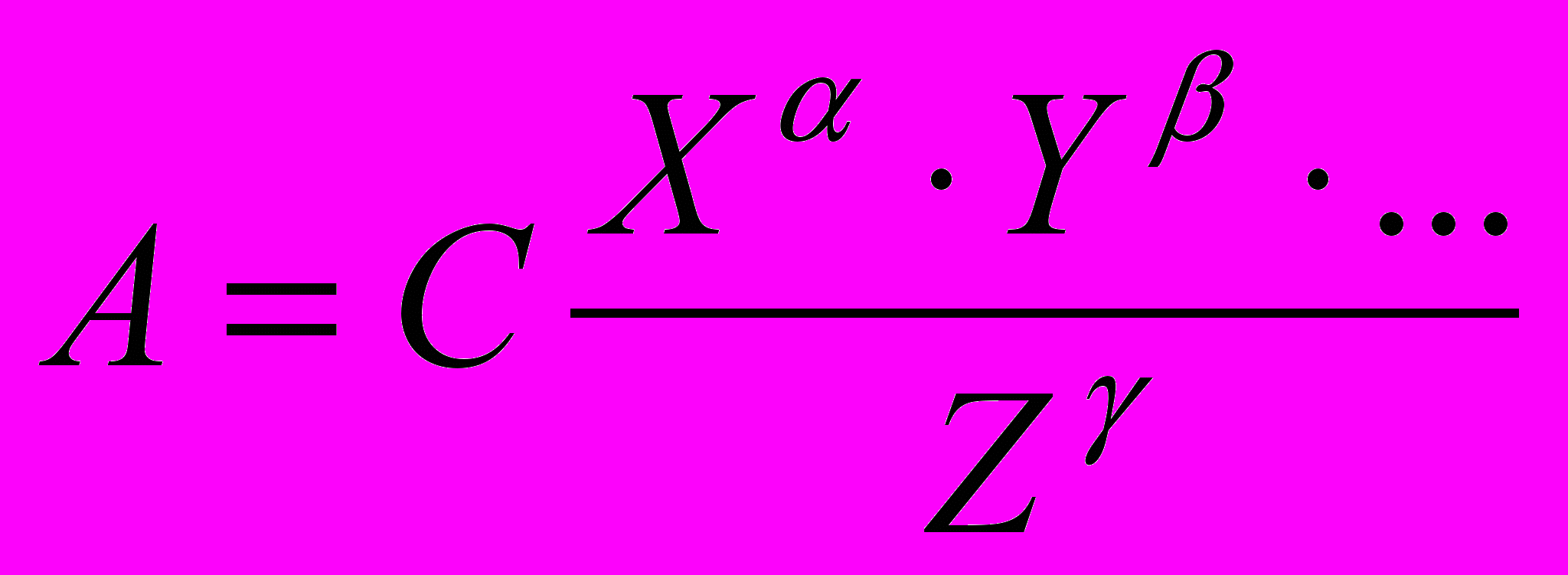где С — постоянный коэффициент, а α, β, γ, ... — любые целые или дробные числа, то относительную погрешность косвенного измерения величины А можно эаплеать в виде :

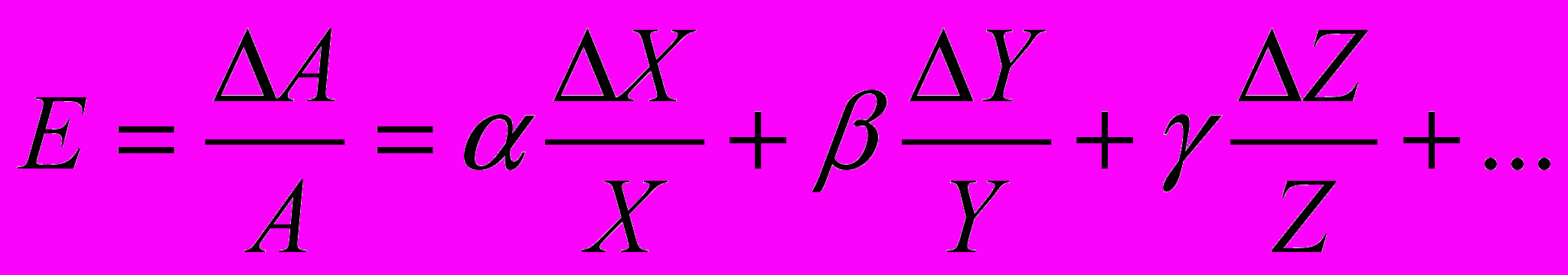(18)

Простота последнего выражения указывает на то, что в большинстве случаев удобно оценить сначала относительную погрешность косвенного измерения, а потом уже найти его абсолютную погрешность. Следует, однако, обратить внимание на то обстоятельство, что приведенные формулы применимы только в том случае, если параметры X , Y , Z , .... не зависят друг от друга. Если же, к примеру, 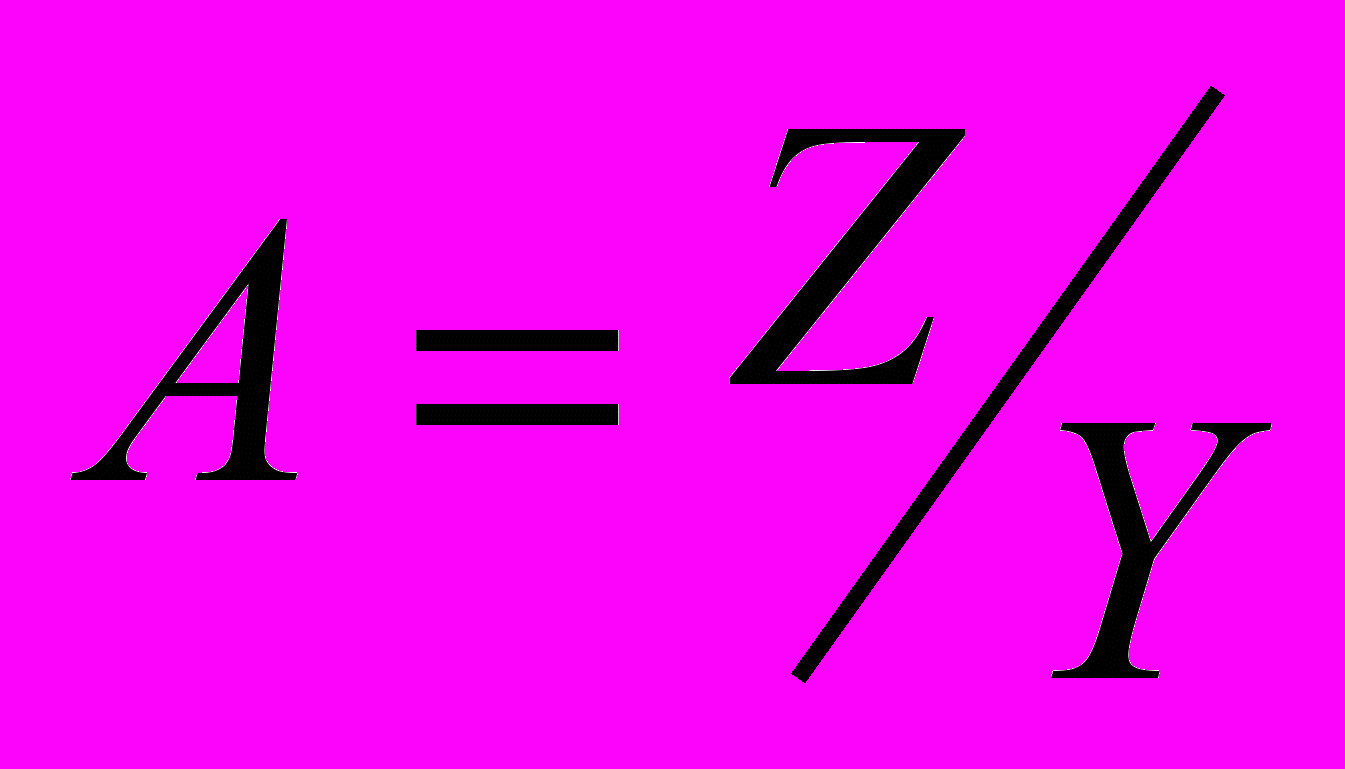, где Z = X + Y расчет по формуле (18) приведет к неправиль­ному результату, т.к. погрешности одной и той же величины Y будут приписаны различные знаки, поскольку указанная величина фигурирует как в числителе, так и в знаменателе исходного выражения.

Более общие правила вычисления погрешностей, позво­ляющие избежать подобных ошибок, можно получить, исполь­зуя дифференциальное исчисление.

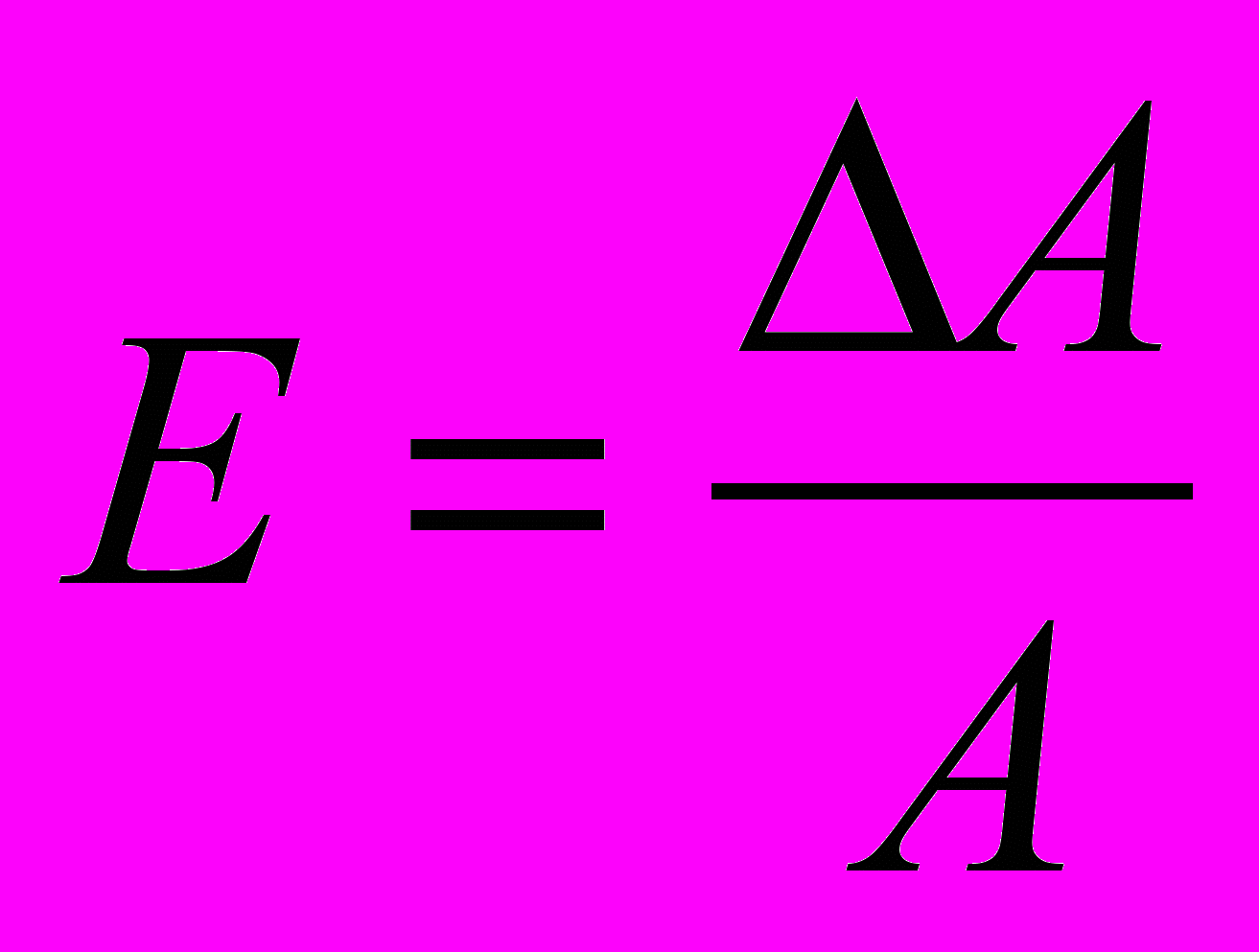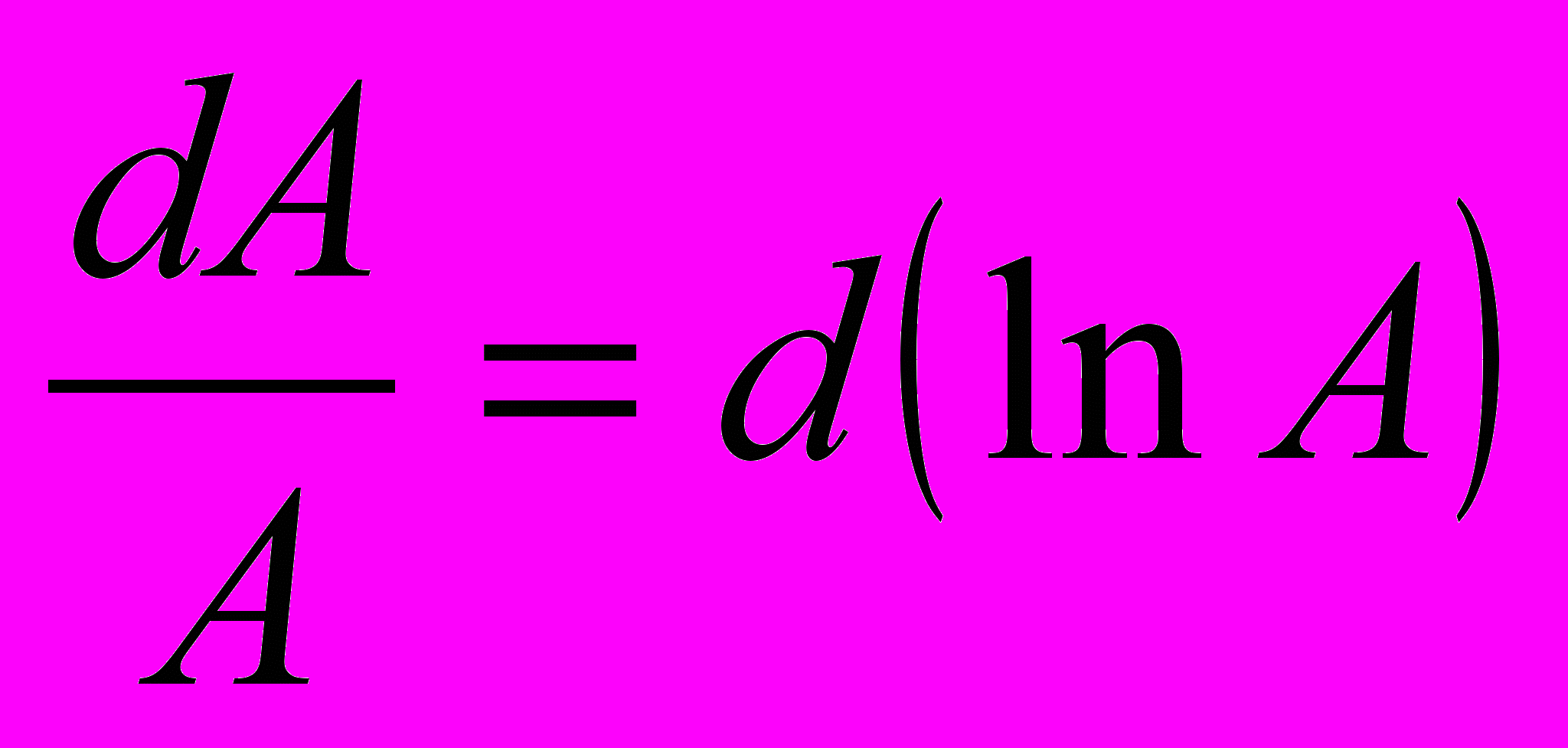Пусть по-прежнему A = ƒ(X, Y, Z, …) . Тогда отно­сительную погрешность косвенного измерения можно записать в виде. С другой стороны, Таким образом, относительая погрешность величины А равна полному дифференциалу на­турального логарифма функции, определяющей зависимость данной величины от измеряемых, т.е.

Таким образом, для нахождения 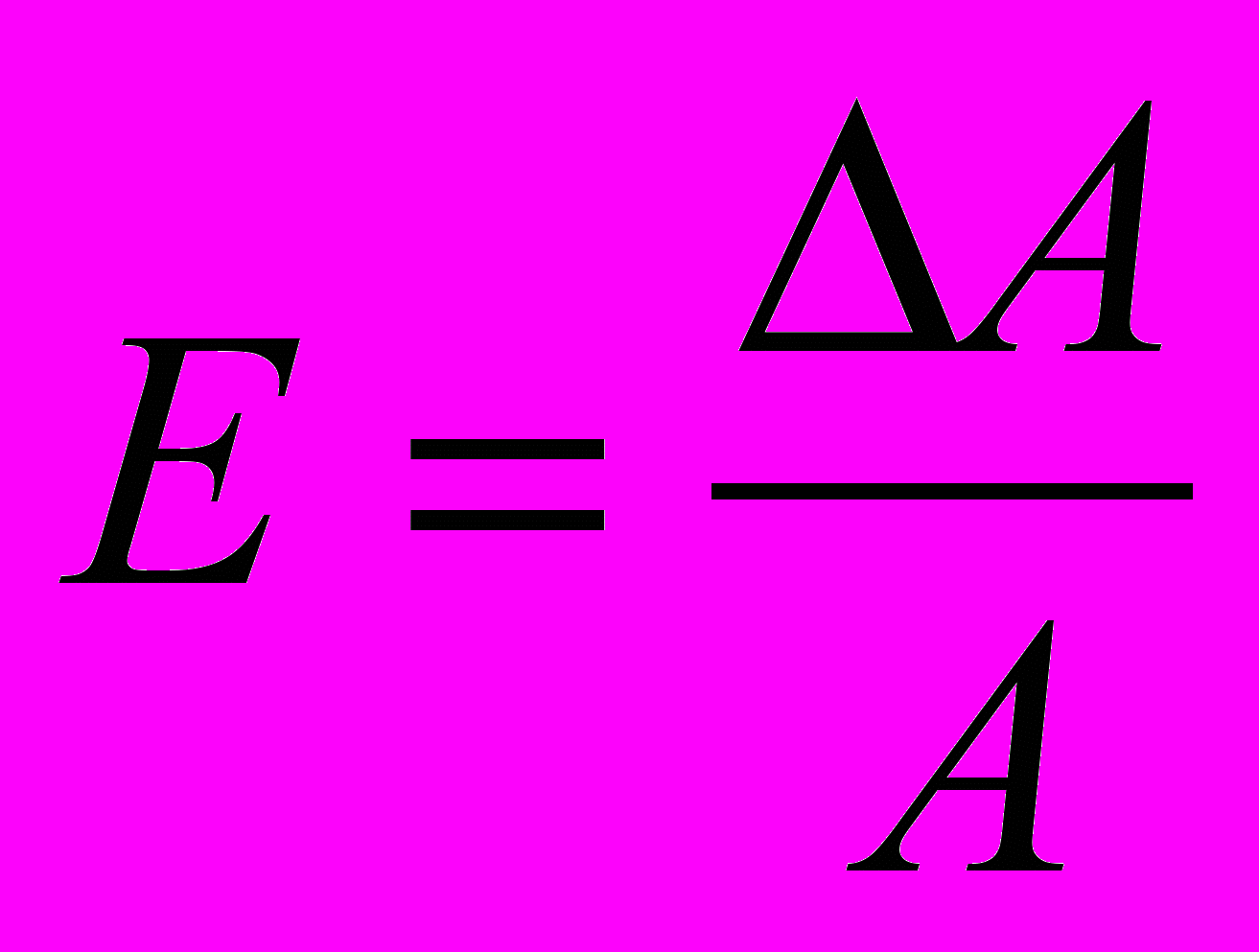необходимо:

1. прологарифмирэвать исходную формулу ln A = ln ƒ(X, Y, Z, …)
   

2) продифференцировать полученное уравнение, заменив затем дифференциалы dA , dX , dY ... погрешностями ΔA , ΔX , ΔY , ... ;

3) сгруппировать члены, содержащие одни и те же погрешности, вынести эти погрешности за скобки, а выражения в скобках взять по модулю;

4) заменить знаки “-” перед коэффициентами при погрешностях на знак “+” (для нахождения максимального значения Е).

Общая формула для расчета относительной погрешности будет при этом выглядеть следующим образом:

, (19)

В качества примера приведем оценку относительной погрешности величины γ, вычисляемой по формуле , где средние значения параметров, полученные после проведения серии измерений (отсчеты по шкале мано­метра в работе 1.65 ).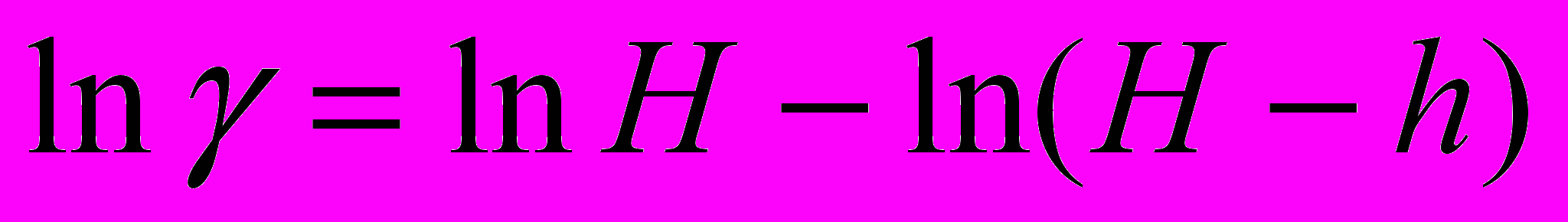







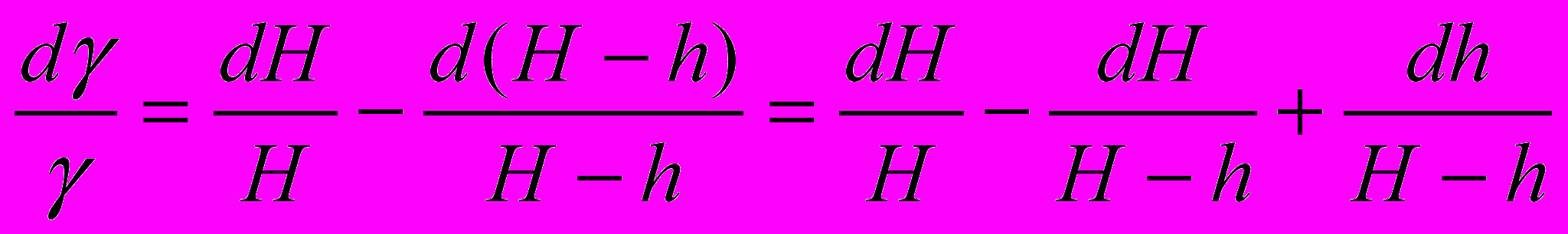
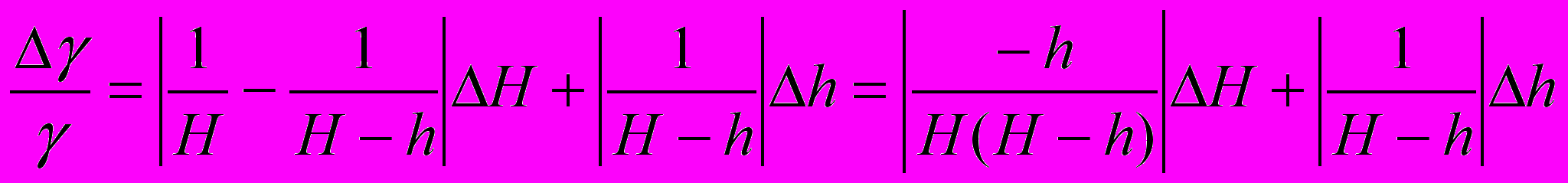
Надо сказать, что расчет по формуле (20) приводит, как правило, к завышению погрешности результата косвенных измере­ний. Причем это завышение зависит от числа параметров Х , Y , Z , ... Если, например, имеется пять таких параметров, то вероятность того, что все ошибки будут иметь заданный знак равна 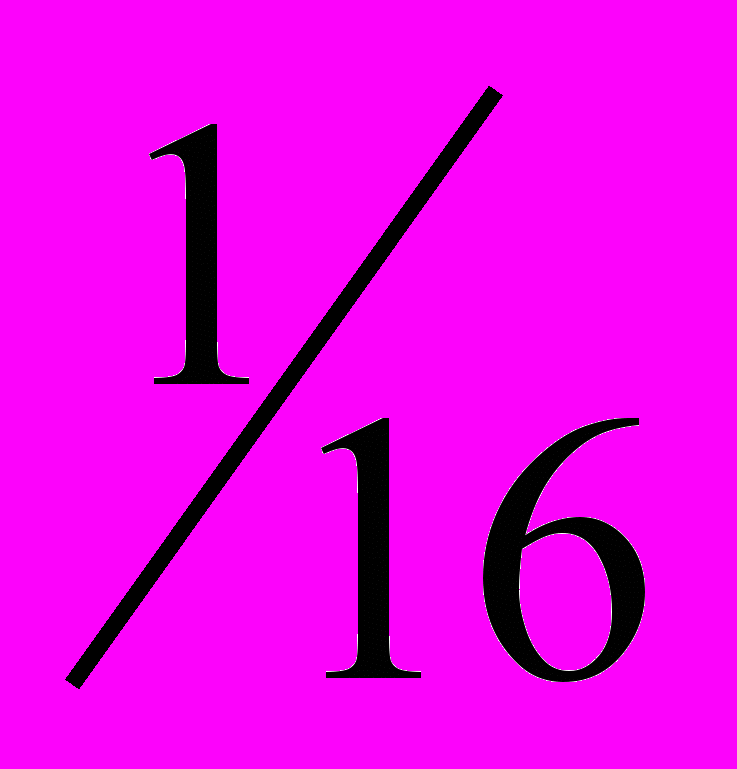. При большем их числе указанная вероятность будет еще меньше. Таким образом, понятно, что максимально возможное значение относительной погрешности, даваемое выра­жением (20), во многих случаях значительно больше реальной погрешности результата.

Теория вероятностей дает более правильные формулы для оценки погрешностей косвенных измерений. Если при пря­мых измерениях параметров X , Y , Z ... доминирующей является случайная погрешность, то погрешность косвенного измерения также является случайной величиной. Это означает, что следует искать среднюю квадратичную погрешность резуль­тата. Так, если A = X + У , то вместо выражений (13) и (14) будем иметь :

и (21)

Общая формула для расчета относительной погрешности будет в этом случае иметь следующий вид :


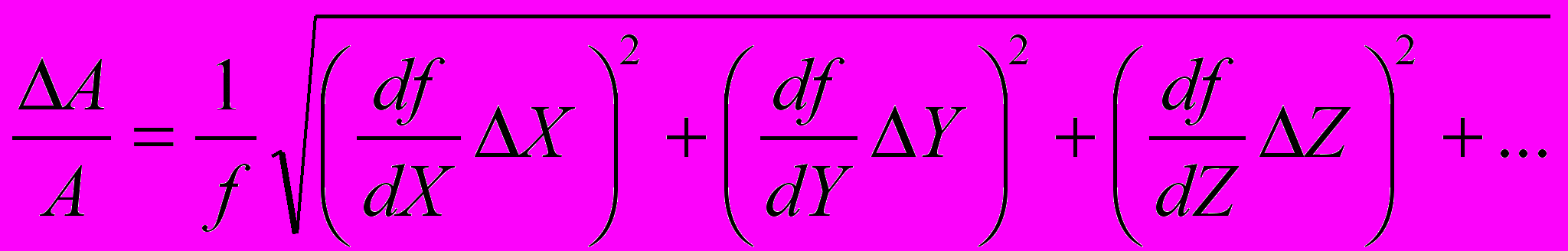(22)

или

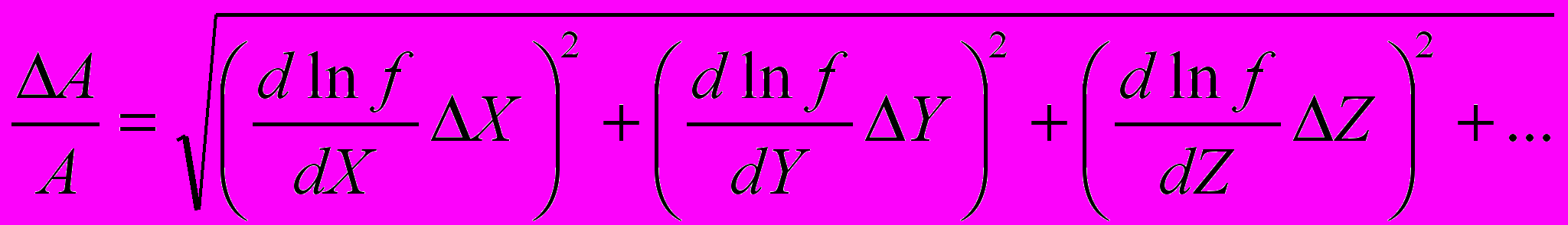(23)

В частности, при 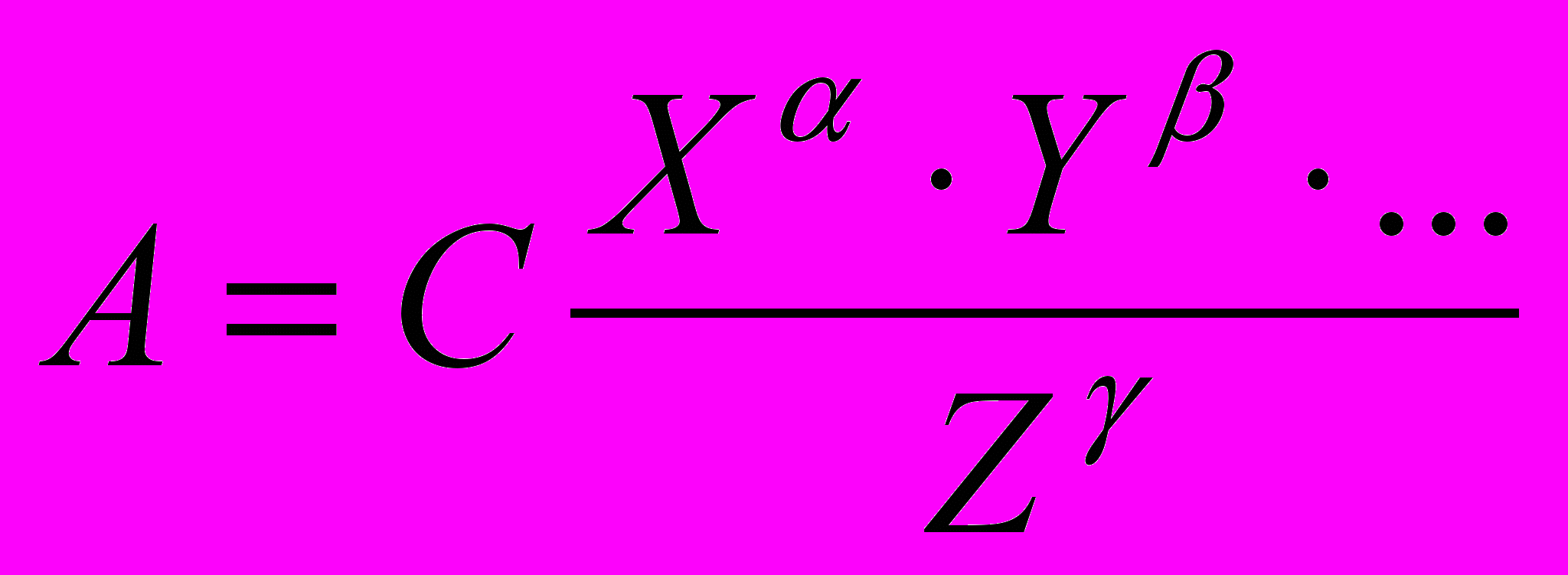имеем:

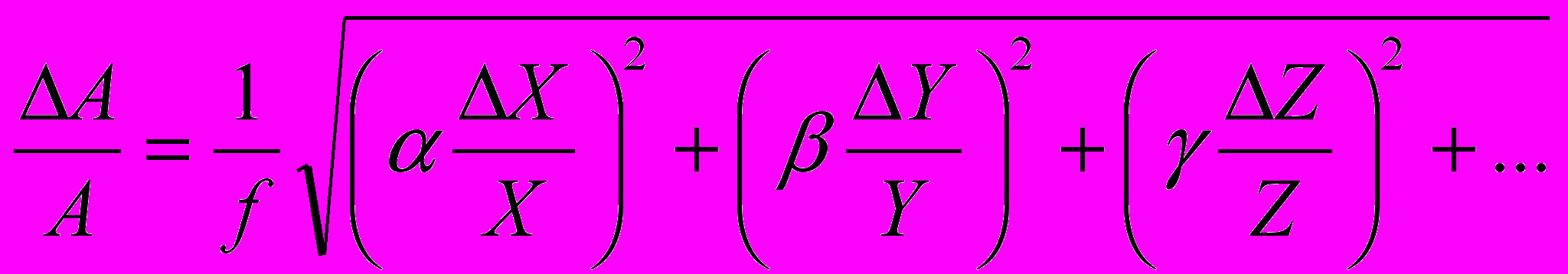(24)


Следует подчеркнуть, что расчет погрешностей по формулах (22) - (24) желательно производить в тех случаях, ког­да погрешности измеряемых параметров имеют, в основном, слу­чайный характер. В условиях же, например, учебной лаборато­рии. ввиду несовершенства измерительных приборов приходится главным образом иметь дело с приборными погрешностями. При этом большинство величин, входящих в расчетную формулу, изме­ряются только один раз. К тому же общее число параметров обычно невелико. Поэтому можно рекомендовать для оценки погрешностей косвенных измерений более простые формулы (13) – (20).

Очень часто в выражении, используемом для определения искомой величины, встречаются параметры, которые в данном эксперименте непосредственно не измеряются. Это могут быть табличные величины (π , g , и т.п.), либо величины, определенные кем-либо заранее и представленные в виде готового результата (например, масса гири или диаметр катушки, заклю­ченной внутри установки). Поскольку указанное величины не являются абсолютно точным, следует учесть вклад соответствующих погрешностей в погрешность вычисляемого результата (см. работы 1.01, 1.25).,

Для оценки погрешности в этих случаях (если, конечно, последняя не задана в явном виде) может быть рекомендовано следующее общее правило: абсолютная погрешность берется равной половине единицы наименьшего разряда, представленного в числе. Так, если задана плотность жидкости

ρ = 4,0380·10³ кг/м³, то погрешность следует взять рав­ной 0,00003 кг/м³

Указанный способ оценки погрешностей вытекает из того факта, что последняя цифра в числе уже не является в боль­шинстве случаев точной (смотри ниже правила округления). Что касается табличных величин, то они при необходимости мо­гут быть взяты с очень большой точностью. Тогда связанными с ними ошибками пренебрегают. При значительном же округлении этих величин погрешности возрастают и, в принципе, должны быть учтены. Их расчет обычно ведется по общему правилу, т.е. если используется значение π = 3,14, то Δπ = 0,005.

Рассчитав окончательно относительную погрешность Е , находят затем абсолютную погрешность косвенного измерения ΔА = Е·А. (25)

Обработка результатов измерений

Все экспериментальные данные, получаемые в результате прямых измерений, должны быть занесены в специальную табли­цу ( или таблицы). Для величин, значения которых измерялись по нескольку раз, необходимо подсчитать среднее арифмети­ческое серии измерений. При этом следует пенить, что точ­ность обработки числового материала должна быть согласована с точностью самих измерений. Обычно при вычислении средних значений рекомендуется оставлять на одну значащую цифру больше, чем содержится в непосредственно измеренных значе­ниях.

Затем необходимо произвести оценку случайной погреш­ности. Используемые для расчетов средней квадратичной ошиб­ки значения ΔX_i и (ΔХ_i)² удобно поместить в ту же таблицу, где находятся результаты опытов (т.е. значения X_i). Для сравнения там же обычно указывают и погрешности использовавшихся приборов.

Расчет конечного результата измерений, которые являют­ся в большинстве случаев косвенными, производится один раз. При этом в расчетную формулу подставляются средние значения измеренных параметров. Дальнейшая обработка сводится к вы­числению относительной и абсолютной погрешностей по изло­женной методике.

Для правильной записи конечного результата в виде (12) необходимо округлить значение абсолютной погрешности и сам результат измерений. Как правило, точность оценки погрешности оказывается очень небольшой, особенно в тех случаях, когда число входящих в расчетную формулу парамет­ров велико. Поэтому абсолютная погрешность округляется, как правило, до одной значащей цифры. Если, однако, эта цифра оказалась единицей, следует оставить две значащие цифры.

Округление самой измеренной величины следует проводить, учитывая ее абсолютную погрешность. При этом последняя значащая цифра в приводимом результате должна быть того же по­рядка величины (находиться в той же десятичной позиции), что и погрешность. Все более мелкие разряды не несут ника­кой информации и должны быть отброшены (или заменены ну­лями). Особенно строго следует придерживаться этого пра­вила в тех случаях, когда погрешность не указывается в яв­ном виде, так как именно последний разряд числа, дающего значение физической величины, показывает точность ее оп­ределения. Или, например, в результате расчетов получено, что J = 0,1428 кг·м³, ΔJ = 0,00791 кг·м³, то правиль­ная запись конечного результата будет выглядеть так :

J = 0,014 ± 0,008 кг·м³.

В некоторых случаях при обработке результатов измере­ний удобно пользоваться графическим методом. Этот метод позволяет проследить зависимость одной физической величины от другой (например, зависимость периода колебаний физи­ческого маятника от расстояния между его центром масс и осью вращения ). Иногда построение графиков необходимо для определения усредненных значений тех или иных параметров. ( Можно, к примеру, найти ускорение тела по графику зависи­мости пути от квадрата времени).

При построении графиков обычно используется прямоуголь­ная систем координат с равномерным масштабом по осям Х и Y. Значения аргумента следует откладывать по оси X , а значение функции - по оси Y. Масштаб может быть произ­вольным, но при его выборе рекомендуем руководствоваться следующими указаниями.

Проводимая кривая должна занимать весь лист используе­мой миллиметровой бумаги. При этом следует иметь в виду, что пересечение координатных осей совсем необязательно должно совпадать с нулевыми значениями аргумента и функции. Важную роль играет также удобство построения и использова­ния графиком. Надо поэтому выбирать такой масштаб, чтобы координаты любой точки графика могли быть быстро и легко определены. Это условие всегда выполняется, если в единице масштаба (например, в 1 см) заключается 10ⁿ , 2·10ⁿ или 5·10ⁿ единиц измерения физических величин, откладываемых по осям координат (n - любое целое число).

После того, как масштаб выбран, следует начертить коор­динатные оси, отметив на них деления масштаба. и указать буквенные обозначения и размерность откладываемых величин. Если эти величины очень малы (или очень велики) при нане­сении масштаба удобно использовать рационализированную фор­му записи, указывая порядок величины рядом с ее буквенным обозначением. При этом допускается два вида записи. Пусть, например, индукция магнитного поля катушки с током меняется в пределах (2÷8) 10^-5 Тл. На графике зависимости В(I) около делений масштаба надо проставить числа 2, 3, 4 и т.д., а сверху написать либо В, 10^-5 Тл, либо Вx10^-5, Тл.

Полученные экспериментальные данные наносятся в виде графика Y = Y(Х), где точки имеют координаты Х_n , Y_n , окруженные эллипсами с главными полуосями ΔX_n , ΔY_n . Эллипсы отражают погрешности измерения. Часто вместо эллип­сов рисуют крестики, точки, кружочки и пр. Затем строится кривая, демонстрирующая вид изучаемой функции. Кривая должна быть плавной и может проходить как через эксперимен­тальные точки, так и в непосредственной близости от них. Желательно, чтобы указанные точки оказались па обе стороны кривой, приблизительно на одинаковых от нее расстояниях.

Для наиболее точного построения искомой кривой ис­пользуют так называемый метод наименьших квадратов (см. Дополнение). Следует подчеркнуть, что указанный ме­тод не дает ответа на вопрос, какого вида функция наилучшие образом аппроксимирует данные точки, а позволяет лишь выбрать наиболее подходящую кривую определенного вида (пара­болу, прямую, экспоненту и т.д.).

Как правило, отклонение точек от кривой не должно превышать абсолютную погрешность проведенных измерений. Эти погрешности, как уже говорилось, могут быть указаны на гра­фике в виде эллипсов или отрезков, отложенных от каждой точки (рис. 2). Сильное отклонение отдельных точек от аппроксимирующей кривой связано в основном с ошибками, до­пущенными при восполнении опытов. Поэтов желательно строите графики в процессе измерений или сразу же после них, чтобы иметь возможность выявить подобные ошибки, называемые про­махами, и при необходимости, провести дополнительные изме­рения.

Построение графика в ходе эксперимента позволяет также осуществить наиболее рациональное количество измерений. В тех областях, где ход кривой монотонный, можно ограничиться небольшим числом измерений. Вблизи максимумов, минимумов и точек перегибов кривой измерения надо производить значитель­но чаще.

Пользуясь полученной кривой, можно оценить значения изучаемой функции для тех значений аргумента, которые не­посредственно не наблюдались (интерполяция). Для этого из любой точки на оси абсцисс (в пределах диапазона изменения аргумента) надо провести перпендикуляр до пересечения с кри­вой. Его длина с учетом масштаба даст значение искомой функции, соответствующее выбранному значению аргумента. Пример­ный вид графика, построенного по экспериментально получен­ной зависимости напряжения на конденсаторе колебательного контура от частоты генератора (вынужденные колебания), показан на рисунке 2 (см. работу 2.39).


Электронная версия лабораторных работ по физике

© Otl. Company Ltd. 2000г.

Сканировал (очень плохо – лучше бы не сканировал) Комаров Н., распознавали и редактировали Смирнов К. и Молоков В.