Строение атмосферы Земли. Метеорологические наблюдения и основные метеорологические величины

Вид материала

Документы

Содержание Основные метеорологические величины. Давление и плотность воздуха. Метеорологическими величинами Влажность воздуха Абсолютная влажность воздуха (а) Направление ветра Метеорологическая дальность видимости Солнечная радиация Ослабление солнечной радиации при ее прохождении через атмосферу. Отражение и поглощение солнечной радиации деятельным слоем. Излучение деятельного слоя. Встречное излучение. Эффективное излучение и радиационный баланс деятельного слоя. Тепловой режим почвы и водоемов. Изменение температуры почвы и водоемов во времени и в пространстве. Теплофизические характерист Теплоемкостью (с) называется величина, равная количеству теплоты(Q), необходимой Удельная теплоемкость с Объемная теплоемкость Температуропровдность а 1-ый закон Фурье 3-ий закон Фурье ... Полное содержание

Подобный материал:

• Погодные условия в жизни че­ловека играют огромную роль, по­этому очень важно заранее, 273.99kb.
• Метеорологические элементы и явления погоды, определяющие условия полета, 551.75kb.
• Государственный стандарт союза сср охрана природы. Атмосфера источники и метеорологические, 206.3kb.
• Эксплуатация и техника пилотирования серийных планеров, 1357.71kb.
• Тематическое планирование по дисциплине «Медицинская география», 60.27kb.
• 3 Радиационная обстановка в Кировской области, 109.09kb.
• Программа 8-11 июня 2010 г. Южно-сахалинск Организаторы: Институт морской геологии, 223.95kb.
• Краткое содержание курса, 84.97kb.
• Конспект урока по природоведению 5 класс тема: «внутреннее строение земли. Горные породы», 68.31kb.
• Погода и климат земли погода и климат земли, 193.32kb.

Строение атмосферы Земли. Метеорологические наблюдения и

основные метеорологические величины.

Атмосферой называется газовая оболочка Земли с содержащимися в ней аэрозольными частицами, движущаяся вместе с Землей в мировом пространстве как единое целое и одновременно принимающая участие во вращении Земли.

Воздух, в отличие от воды, сжимаем, поэтому с высотой плотность его убывает и атмосфера постепенно сходит на нет (переходит в космическое пространство). Половина всей массы атмосферы сосредоточена в нижних 5 км, три четверти - в нижних 10 км, девять десятых - в нижних 20 км. Атмосфера отчетливо расслаивается на концентрические сферы, отличающиеся друг от друга по своим характеристикам. По составу воздуха она подразделяется на гомосферу и гетеросферу. Первая характеризуется однородностью вещественного состава, связанной с постоянным перемешиванием воздуха, вторая - дифференциацией газов по удельному весу и поэтому является неоднородной по вещественному составу.

В зависимости от распределения температуры, атмосфера также подразделяется на несколько концентрических сфер: тропосферу, стратосферу, мезосферу и экзосферу и разделяющих их тропопаузу, стратопаузу и мезопаузу.

Основные метеорологические величины.

Основными величинами, характеризующими физическое состояние газа, в том числе и воздуха, являются его давление, температура и плотность.

Температура (t, T)

Воздух, как и всякое физическое тело, имеет температуру, отличную от абсолютного нуля. В большинстве стран мира температуру воздуха, а также почвы и воды в метеорологии измеряют в единицах СИ, т.е. в градусах Международной температурной шкалы, или шкалы Цельсия (⁰С)

Нуль этой шкалы приходится на температуру, при которой тает лед, а 100 ⁰С - на температуру кипения воды. Наряду со шкалой Цельсия широко распространена, особенно в теоретических расчетах, шкала Кельвина. Нуль этой шкалы соответствует полному прекращению теплового хаотического движения молекул. В формулах температура по абсолютной шкале обозначается обычно ТК, а температура по Цельсию – t С .

В США, Англии и некоторых странах бывшей Британской империи используют также шкалу Фаренгейта (⁰F). За нуль этой шкалы принята температура смеси снега и нашатыря, а за 100⁰ - нормальная температура человеческого тела. Ранее использовалась также температурная шкала Реомюра (⁰ R ).

Температуру воздуха при стандартных сетевых наблюдениях определяют с точностью до0,1 ⁰, исключение составляет измерение температуры с помощью дистанционной метеорологической станции (ДМС) и регистрация термографом, где точность измерения составляет 1⁰С.

Давление и плотность воздуха.

Атмосферное давление (р) в Международной системе единиц (СИ) измеряется в паскалях (Па). За единицу давления принимается такое равномерно распределенное давление, при котором на единицу поверхности приходится единица силы. Один паскаль - это давление силой в 1 ньютон (н), приходящееся на площадь в 1 м². В метеорологии до недавнего времени использовалась единица давления, называющаяся миллибаром (мбар), которая представляет давление силой в 10³ дин, приходящееся на 1 см² . Точность измерения давления составляет 0,1 гПа.

На практике часто применяется внесистемная единица давления - 1 мм рт. ст. Давление в 1 мм рт. ст. - это вес столба ртути высотой в 1мм, приходящийся на 1 м² на уровне моря и на широте в 45⁰ . Нормальное давление на этой широта на уровне моря составляет 760 мм рт. ст.

1 мбар = 100 Па =1 гПа, 1 мм рт.ст. = 1, 33 гПа.

Газы сжимаемы, поэтому их плотность меняется в широких пределах в зависимости от давления и температуры. Связь между давлением, температурой и плотностью для идеальных газов устанавливается уравнением состояния газов, известным из физики. Для единицы массы газов его можно записать:

pv = RT (1)

p - давление, v - удельный объем, т.е. объем единицы массы газов, R - удельная газовая постоянная, зависящая от природы газа, T - температура по абсолютной шкале.

При температурах и давлениях, встречающихся в атмосфере, основные газы, составляющие воздух ведут себя как идеальные. Поэтому уравнение состояния газов с достаточным приближением применимо к сухому воздуху, к водяному пару и к влажному воздуху. В каждом случае будет свое значение удельной газовой постоянной. Так как удельная газовая постоянная смеси газов, которой является воздух, равна средневзвешенной величине удельных газовых постоянных составляющих смесь газов, удельную газовую постоянную сухого воздуха принимают равной R_d 287,05 джоуль/кг*К.

Плотность - это масса в единице объема. В метеорологии плотность воздуха не измеряется, она вычисляется с помощью уравнения состояния газов по измеренным значениям давления р и температуры Т.

Учитывая, что плотность единичной массы газа составляет  = 1/v, уравнение (1) для единицы объема можно записать как:

= p/RT

Зная удельную постоянную сухого воздуха R_d = 287,05 м²/с²*К (или джоуль/кг*К), плотность сухого воздуха определяется:

_d= p/R _dT

Уравнение состояния водяного пара можно представить в следующем виде:

еv=R_nT,

где е – парциальное давление, v –удельный объем, R_n - удельная газовая постоянная водяного пара.

Уравнение состояния газов для влажного воздуха имеет вид

 = р/R_dT_v

т.е. плотность влажного воздуха описывается уравнением состояния сухого воздуха, но только с заменой истинной температуры на виртуальную. Виртуальная температура Т_v ( температура влажного воздуха) - это температура, которую должен был бы иметь сухой воздух, чтобы его плотность равнялась плотности данного влажного воздуха с температурой Т, давлением р и давлением водяного пара е.

Т_v = Т(1 + 0,378 е/р)

Виртуальная температура всегда несколько выше истинной температуры, а плотность влажного воздуха всегда меньше плотности сухого. Последнее может служить дополнительным фактором, способствующим развитию свободной конвекции в атмосфере.

Метеорологическими величинами, определяемыми на метеостанциях, являются влажность воздуха, скорость ветра, направление ветра, осадки, количество облаков, метеорологическую дальность видимости и продолжительность солнечного сияния. Они характеризуют состояние воздуха, атмосферных процессов и радиационного режима. Точность их измерений определяется наименьшим значением, которое можно определить с уверенностью в правильности получаемых значений (т.е. на основе оценки погрешностей)

Влажность воздуха характеризуемая парциальным давлением водяного пара (е), и выражаемая в тех же единицах, что и атмосферное с точностью до 0,1 гПа.

Относительная влажность воздуха (f) – отношение фактической влажности к влажности насыщения при той же температуре. Вычисляется до целых процентов

Абсолютная влажность воздуха (а) - определяется с точностью до 01г/м³.

Скорость ветра (u) – измеряется с помощью анемометра или анеморумбометра с точностью до 1 м/с и до 0,1 м/с с помощью ручных анемометров.

Направление ветра определяется по анеморубометру в углах геодезического азимута с точностью до 5^0., по флюгеру – с точностью до румба.

Осадки измеряются с точностью до 0,1 мм слоя воды.

Количество облаков определяется в баллах с точностью 1 балла, а в долях единицы – до 0,1.

Метеорологическая дальность видимости оценивается в баллах или километрах (до 0,1 км).

Продолжительность солнечного сияния по гелиографу или иным самописцам определяется с точностью до целых минут.

Солнечная радиация распространяется по всем направлениям в виде электромагнитных волн, характеризующихся длиной волны () и частотой колебаний. Приходящая к земной поверхности солнечная радиация, которую изучает метеорология, имеет длины волн в интервале от сотен микрометров до тысячных долей микрометра (1 мкм = 10^-6 м). Количественной мерой солнечной радиации, поступающей на некоторую поверхность, служит энергетическая освещенность или плотность потока радиации, т.е. количество лучистой энергии, падающей на единицу площади в единицу времени. Энергетическая освещенность измеряется в Вт/м² . Это означает, что на 1м² в секунду поступает 1 дж лучистой энергии.

Общая характеристика солнечной радиации. Солнечная радиация у земной поверхности. Отражение и поглощение радиации деятельным слоем. Радиационный баланс деятельного слоя.


Солнечная радиация, которая является основным источником энергии для всех процессов на Земле, в том числе и в атмосфере распространяется по всем направлениям в виде электромагнитных волн. Общий поток солнечной энергии вне атмосферы при среднем расстоянии между Землей и Солнцем (149,6х10⁶ км) считают постоянной величиной. Энергетическую освещенность солнечной радиации, падающей на площадку единичной площади, перпендикулярную солнечным лучам в единицу времени на верхней границе атмосферы при среднем расстоянии от Земли до Солнца называют солнечной постоянной Sо.

Ослабление солнечной радиации при ее прохождении через атмосферу.

Ослабление прямой солнечной радиации при ее прохождении от верхней границы атмосферы до земной поверхности определяется формулой Бугера

S = S₀ p^m (1),

где S - энергетическая освещенность солнечной радиацией площадки у земной поверхности, перпендикулярной к солнечным лучам;

S₀ - солнечная постоянная;

p - интегральный коэффициент прозрачности атмосферы;

m - оптическая масса атмосферы, пройденной солнечными лучами.

При m = 1, т.е. при Солнце в зените,

S = S₀p, а p = S/S₀.

Следовательно, коэффициент прозрачности показывает, какая доля солнечной радиации доходит до земной поверхности при отвесном падении солнечных лучей.

При h_c = 0, т.е. при Солнце на горизонте, m равна не бесконечности, а 35.

Ослабление радиации путем поглощения и рассеяния можно разделить на две части: ослабление постоянными газами (идеальной атмосферой) и ослабление водяным паром и аэрозольными примесями.

Соотношение коэффициента прозрачности идеальной атмосферы (р_i) к коэффициенту прозрачности реальной атмосферы (р) называется фактором мутности (К_м). Он показывает, какое число идеальных атмосфер нужно взять, чтобы получить такое же ослабление радиации, какое производит реальная атмосфера.

К_м = lg р/ lg р_i

Значения К_м определяются с точностью до сотых.

Приход солнечной радиации на земную поверхность.

Энергетическая освещенность прямой солнечной радиацией горизонтальной поверхности (S^ инсоляция) вычисляется по формуле:

S = S sin h_c,

где S - прямая радиация на перпендикулярную поверхность;

h_c - высота Солнца в момент, когда вычисляется S.

Энергетическая освещенность суммарной солнечной радиации вычисляется по формуле:

Q = S + D,

где S - энергетическая освещенность прямой радиации на горизонтальную поверхность;

D - энергетическая освещенность рассеянной солнечной радиации.

Эти мгновенные (правильнее - секундные) значения выражаются в кВт/м² с точностью до сотых.

Действительные часовые, суточные, месячные и годовые энергетические экспозиции солнечной радиации на горизонтальную поверхность определяются путем численного интегрирования функций, выражающих зависимость радиации от времени. Энергетические экспозиции за определенный интервал времени называют часовыми, суточными, месячными и годовыми суммами соответствующей (прямой, рассеянной, суммарной) радиации и обозначают _чS, _сутD. Все эти суммы выражаются в МДж/м², часовые и суточные с точностью до сотых, месячные - до единиц, годовые до десятков.

Отражение и поглощение солнечной радиации деятельным слоем.

Коэффициент отражения солнечной радиации деятельным слоем - A (альбедо) - определяется как отношение:

A = Q_отр / Q,

где Q _{отр -} отраженная радиация, т.е. отразившаяся часть суммарной радиации (кВт/м²).

Q - суммарная солнечная радиация (кВт/м²).

Альбедо выражается в долях единицы с точностью до сотых или в процентах. Часть суммарной радиации (кВт/м²), поглощенная деятельным слоем, составляет:

Q _п= Q (1 – A)

Эту величину (Q_п) называют поглощенной радиацией или коротковолновым радиационным балансом. В последнем случае ее обозначают В_к


Излучение деятельного слоя.

Энергетическая светимость деятельного слоя (Е_с) вычисляется по формуле:

E_с = T₀⁴,

где  - коэффициент теплового излучения, называемый также коэффициентом черноты,

 - постоянная Стефана-Больцмана, 5, 67 х10 ^-8 вт/ м² х К

Т₀ - температура деятельного слоя (К).

Произведение Т₀⁴ при разных температурах затабулировано (приложение 1).

Эти же значения характеризуют поглощательные свойства деятельного слоя по отношению к падающей на него длинноволновой радиации.

Излучение деятельного слоя называют также собственным излучением. Мгновенные (секундные) значения Е_с и энергетические экспозиции этого излучения за различные интервалы (суммы) выражаются в тех же единицах и с тем же округлением, что и соответствующие характеристики коротковолновой радиации.

Встречное излучение.

Энергетическая освещенность деятельного слоя встречным излучением при ясном небе определяется по формуле Брента:

Е_А = Т_А ⁴ (D + G)

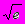где -Т_А - температура воздуха (К) на высоте 2 м над земной поверхностью, е -парциальное давление водяного пара (гПа) на той же высоте, D и G - постоянные (D =0,61, G =0,05).

Поглощенная (Е_{А п}) и отраженная (Е _{А отр}) деятельным слоем части встречного излучения определяются соотношениями:

Е_{А п} = Е_А , Е_{А отр} = (1- ) Е_А

где Е_А, Е_{А п} и Е_{А отр} выражаются в тех же единицах, что и Е_с.

Эффективное излучение и радиационный баланс деятельного слоя.

Эффективное излучение деятельного слоя (Е _эф) при ясном небе определяется соотношением:

E_эф = E_с - E_в ,

где Е _с - собственное излучение;

Е _в - встречное излучение.

 - коэффициент черноты.

Эффективное излучение, взятое со знаком минус, представляет собой длинноволновый радиационный баланс

В_д =E_в - E_с


Эффективное излучение при наличии облачности характеризуется соотношением:

Е_{эф о} = Е_{эф я} (1-С_н n_н -С_сn_с -С_вn_в ),

где Е_{эф о} - эффективное излучение при облачности разного яруса,

Е_{эф я} - эффективное излучение при ясном небе,

С- эмпирические облачные коэффициенты для облачности разного яруса ( С_н- нижнего, равный 0,076, С_с - среднего, равный 0,052, и С_в - верхнего -0,022).

n_н , n_с, n_в - количество облаков в баллах по ярусам

Радиационный баланс деятельного слоя характеризуется соотношением:

R = (S + D ) (1-A) - E_эф

Мгновенные значения радиационного баланса деятельного слоя и его суммы выражаются в тех же единицах и с таким же округлением, как и все остальные потоки радиации.

Тепловой режим почвы и водоемов. Изменение температуры почвы и водоемов во времени и в пространстве. Теплофизические характеристики почвы и водоемов.

Изменения температуры земной поверхности (деятельного слоя) определяют тепловой режим нижних слоев атмосферы. Земная поверхность (поверхность почвы или воды, а также растительного, снежного или ледяного покрова) непрерывно и разными способами получает и теряет тепло. Через земную поверхность тепло передается вверх - в атмосферу и вниз - в почву или воду.

Режимы нагревания и охлаждения поверхностных слоев почвы и водных бассейнов существенно различаются. Эти различия связаны с разными теплофизическими характеристиками почвы и воды.

Основными теплофизическими характеристиками деятельного слоя являются теплопроводность, теплоемкость, удельная и объемная теплоемкость и температуропроводность.

Теплопроводность как один из видов теплообмена, при котором перенос энергии в форме теплоты в неравномерно нагретой среде имеет атомно-молекулярный характер, характеризуется коэффициентом теплопроводности () и выражается в Вт/(мград К) с точностью до десятых, а при очень маленьких значениях - с точностью до тысячных.

Теплоемкостью (с) называется величина, равная количеству теплоты(Q), необходимой для нагревания тела на один градус.

Q= Ct

Теплоемкость выражается в Дж/град.К.

Удельная теплоемкость с_уд выражается в Дж/(кгград. К) с точностью до сотых, и характеризует теплоту, необходимую для нагревания на 1 градус вещества единичной массы.

Объемная теплоемкость с выражается в Дж/(м³град. К) с точностью до сотых, характеризует теплоту, необходимую для нагревания на 1 градус вещества единичного объема и равна:

для сухой почвы

с_с= с_{уд с} ,

где  - плотность вещества;

для влажной почвы

с_в =(с_{уд с} + с_{уд в} w) ,

где w - влажность почвы, (отношение массы воды в некотором объеме почвы к массе сухой ее части в том же объеме, выражается в долях единицы).

Влажность почвы и плотность сухой части почвы определяется соответственно:

w = (F₁ -F₂)/F₂ ,  = F₂/Vg ,

где F₁ и F₂ - вес почвы объемом V до и после просушивания.

Температуропровдность а характеризует скорость выравнивания температуры в среде и выражается в м²/с (или чаще в см²/ч) с точностью до сотых (1см²/ч. = 2,8 10^-8 м²/с).

Распространение колебаний температуры в почвах теоретически рассчитывается в соответствии с законами Фурье. Если почва однородна по вертикали, то ее температура t на глубине z в момент времени  определяется из уравнения теплопроводности (уравнение Фурье)

dt/d = a d² t/dz²,

где а – температуропроводность.

Распространение температурных колебаний в почве описывается следующими законами.

1-ый закон Фурье - закон неизменности периода колебаний с глубиной. Независимо от типа почвы период колебаний температуры не изменяется с глубиной:



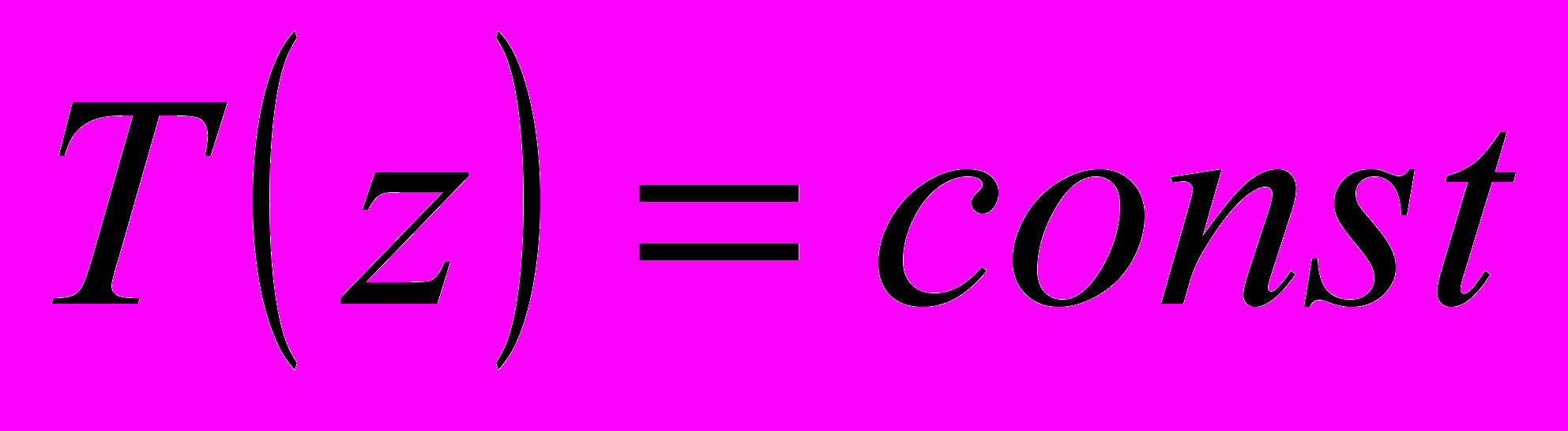
2-ой закон Фурье – закон уменьшения амплитуды колебаний с глубиной. Возрастание глубины в арифметической прогрессии приводит к уменьшению амплитуды в геометрической прогрессии

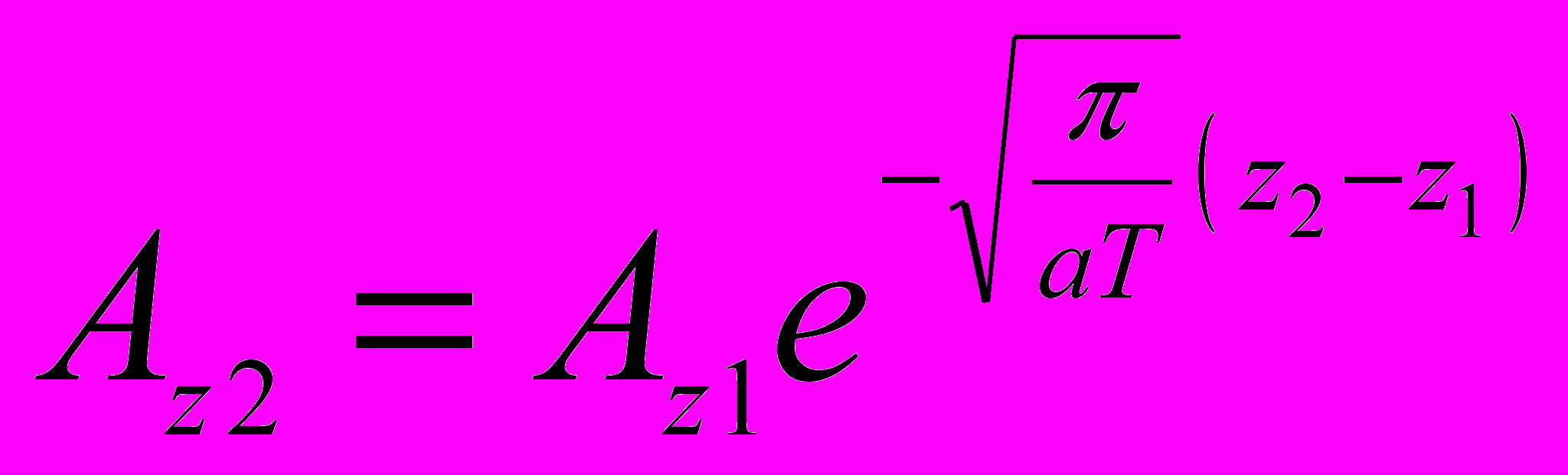(1)

где А_z2 и А_z1 - амплитуды на глубинах z₁ и z₂ (z₂>z₁), а - температуропроводность слоя почвы, лежащего между глубинами z₁ и z₂;

Из формулы (1) вытекают следующие следствия:

• глубины, на которых в разных почвах амплитуды температурных колебаний с одинаковым периодом уменьшаются в одинаковое число раз, относятся между собой как корни квадратные из температуропроводности этих почв:
  

;

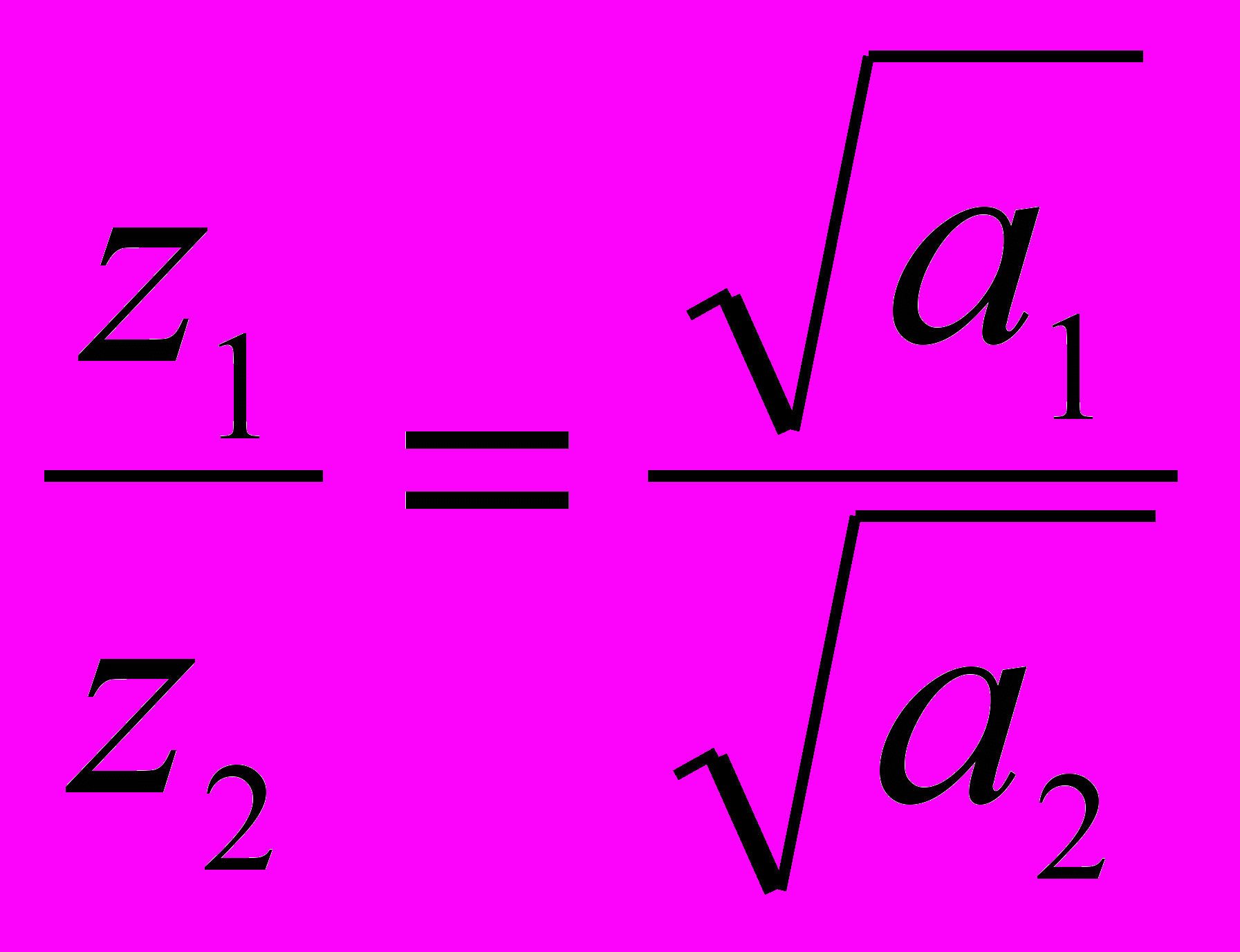• убывание амплитуды до нуля приводит к возникновению на некоторой глубине слоев постоянной суточной или постоянной годовой температуры.
  

3-ий закон Фурье - закон запаздывания. Сроки наступления максимальных и минимальных температур, как в суточном, так и в годовом ходе запаздывают с глубиной пропорционально увеличению глубины:



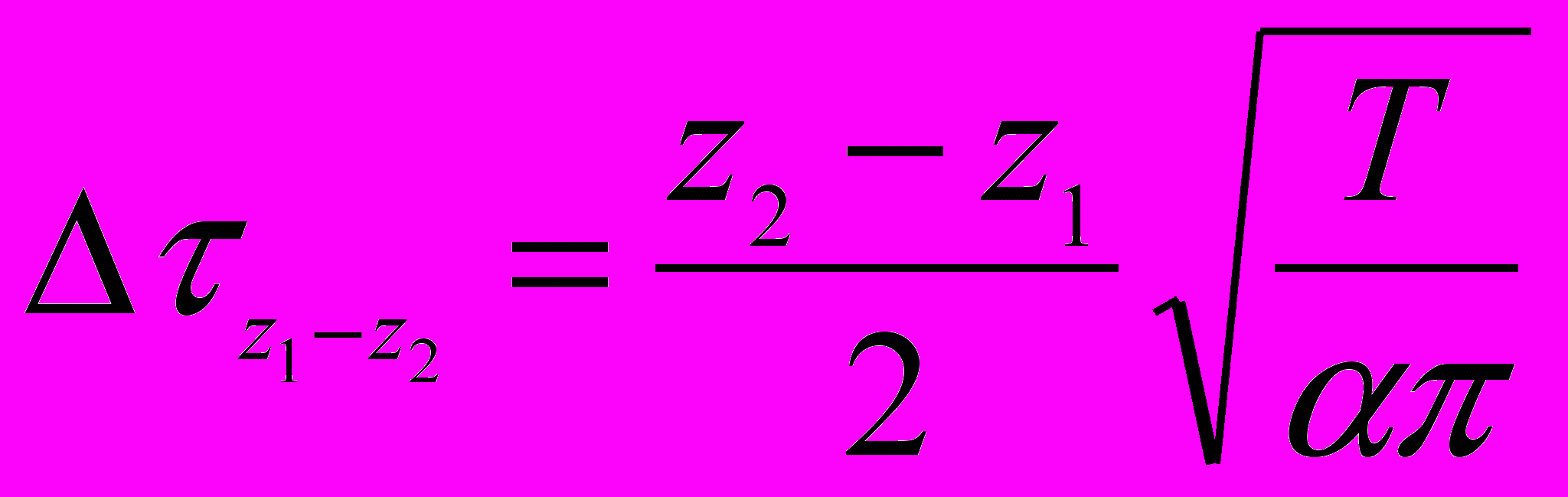
где _z1-z2 - запаздывание, т.е. разность между моментами наступления одинаковой фазы колебаний на глубинах z₁ и z₂.

Колебания температуры проникают в почву до глубины Zпр, определяемой соотношение

Zпр = 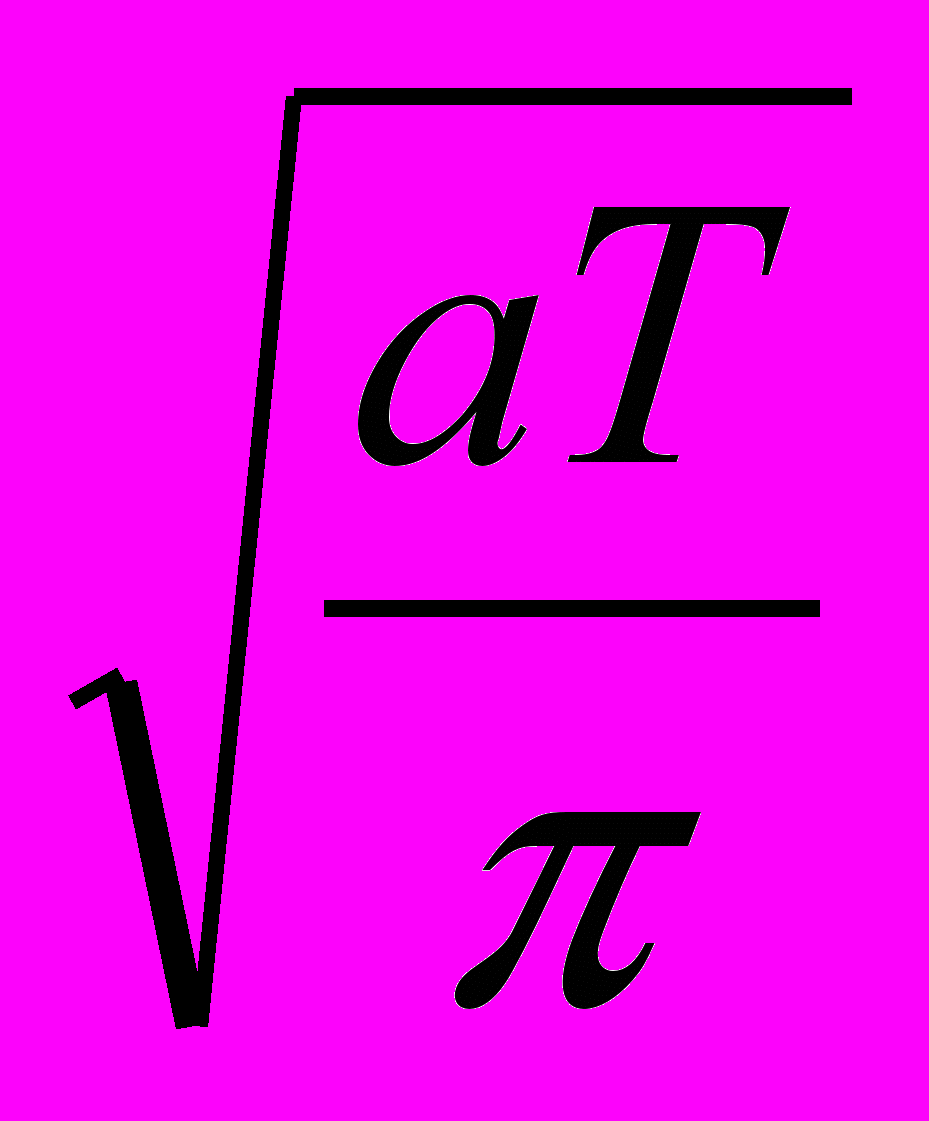**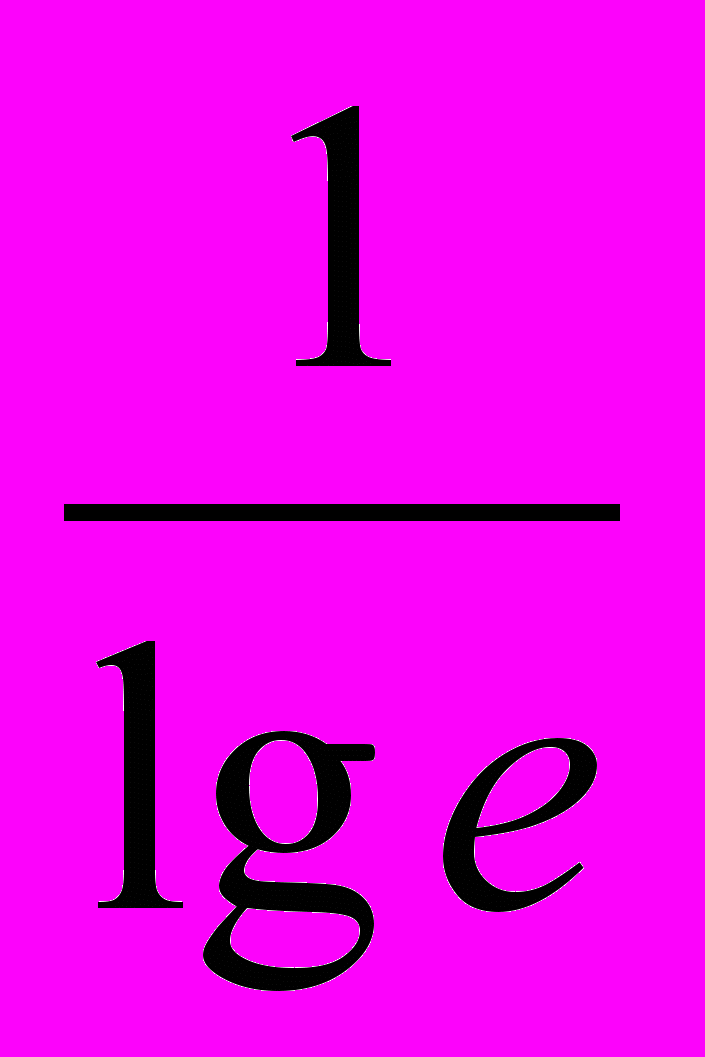lg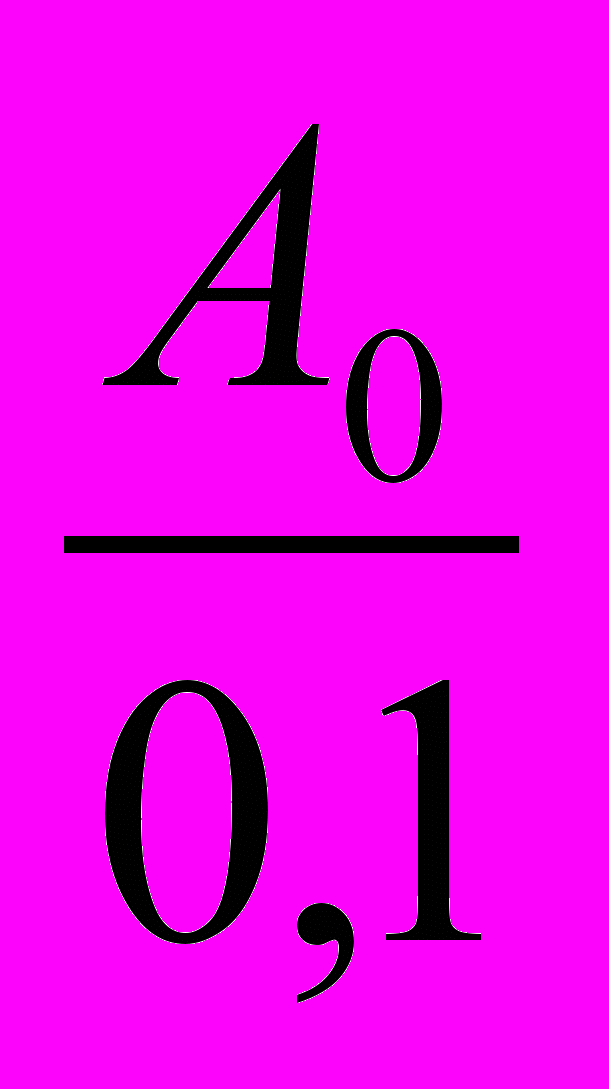

4-ый закон Фурье. Глубины, на которых в одной и той же почве амплитуды температурных колебаний с разными периодами уменьшаются в одинаковое число раз, относятся между собой как корни квадратные из периодов колебаний:



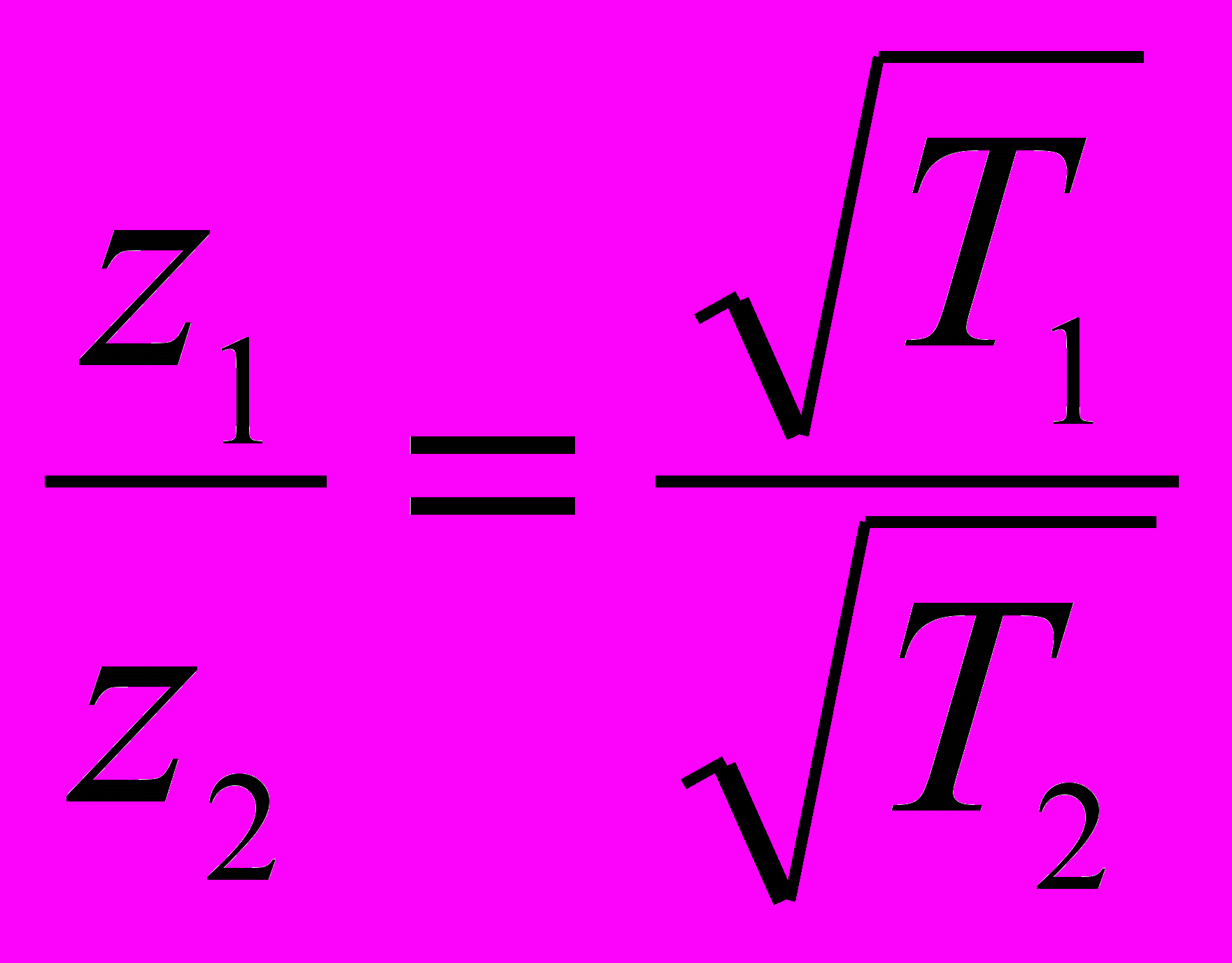
Из этого уравнения следует, что глубины слоев постоянной суточной и годовой температур относятся между собой как корни квадратные из периодов колебаний, т.е. как 1:

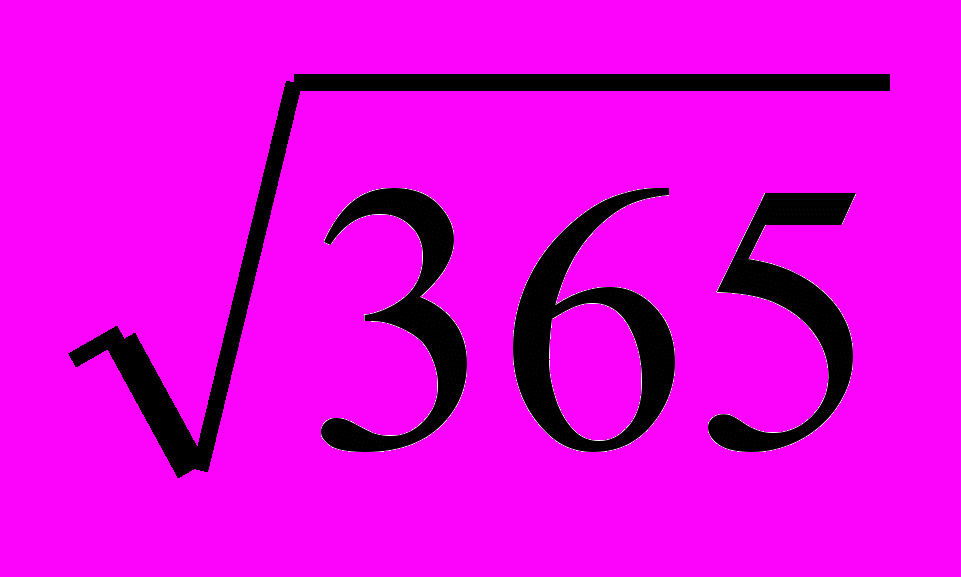
Вертикальный температурный градиент – изменение температуры на единицу глубин. Для почвы рассчитывается как изменение температуры на каждый метр глубины.


Тепловой режим нижнего слоя атмосферы. Изменения температуры воздуха во времени и пространстве. Вертикальный и горизонтальный температурный градиент.

Воздух, как и всякое тело, всегда имеет температуру, отличную от абсолютного нуля. Температура воздуха в каждой точке атмосферы непрерывно меняется с изменением времени. Кроме того, в разных местах Земли и на разной высоте в одно и то же время она также различна.

В вертикальном атмосферном столбе температура может распределяться по высоте различным образом, отражая тепловое влияние самых разнообразных процессов, происходящих во всей толще атмосферы, поэтому кривая фактического распределения температуры в более или менее толстом слое атмосферы, в общем случае является сложной кривой. Кривая фактического распределения температуры с высотой в данный момент времени называется кривой стратификации («кривой расслоения»).

Изменения температуры с высотой характеризуют с помощью вертикального градиента температуры

 = -(dt_a/dz),

где  - вертикальный градиент температуры, dt_а - разница в температуре воздуха (t₂ –t₁) между высотами z₂ и z₁, dz =z₂-z₁ - изменение высоты. Таким образом, вертикальный градиент температуры характеризует изменение температуры воздуха на единицу высоты. Обычно характеризуют изменения температуры на 100м высоты. Так как перед производной ставится знак минус, то в случае падения температуры с высотой, т.е. при отрицательном dt_a и положительном dz градиент положителен (0). При увеличении температуры с высотой (dt_a 0, dz 0), градиент отрицателен (0).

В реальной атмосфере вертикальный температурный градиент может меняться в широких пределах. В нижних 10-11 км в умеренных широтах и в нижних 15-17 км в тропиках он в среднем равен 0,65⁰С/100 м. В атмосфере над тропическими пустынями он может возрастать до 0,9⁰С/100 м. Вертикальный температурный градиент приземного слоя составляет десятки, а иногда и сотни градусов на 100 м.

В тропосфере, при нормальном распределении температуры, она с высотой падает (вертикальный градиент положительный). Но в ряде случаев возможны ситуации повышения температуры с высотой в пределах отдельных слоев. В этом случае вертикальный градиент будет отрицательным, и такое распределение температуры с высотой называют инверсией. Условие постоянства температуры в отдельном слое (при вертикальном градиенте равном нулю) называют изотермией.

Кроме вертикальных изменений температуры, часто определяют изменение температуры по горизонтали - горизонтальный температурный градиент, который отражает изменение температуры на единицу расстояния.

Распределение температуры на обширных пространствах показывают с помощью карт изотерм - линий равных значений температур. Изотермы можно проводит как по данным регулярных наблюдений (изотермы на тот или иной срок наблюдений), так и по значениям средних температур (среднелетних, среднезимних, средних самого теплого или самого холодного месяца, среднегодовых температур или годовых амплитуд). В каждом конкретном случае интервал температур между соседними изотермами определяется размахом крайних значений, требуемой точностью и масштабом карты.

Для климатической характеристики используют значения суточной амплитуды (разности максимальной и минимальной температур за сутки) и годовой амплитуды (разности средних месячных температур самого теплого и самого холодного месяцев). Годовые и суточные амплитуды температуры зависят от широты местности. Годовые амплитуды являются также характеристикой степени континентальности климата.

Адиабатические изменения состояния воздуха. Стратификация слоев атмосферы.

Адиабатические изменения состояния воздуха ненасыщенного паром (сухоадиабатические процессы) характеризуются уравнением Пуассона

Т₂/Т₁= (р₂/р₁)^0,286,

где р₁ Т₁ давление и температура воздуха в начальном состоянии, а р₂ и Т₂ –давление и температура в конечном состоянии.

Если воздух с ненасыщенным паром, имевший на начальном уровне z₁ (м) температуру Т₁, адиабатически переместится на уровень z₂ (м), то его температура станет равной

Т₂ = Т₁ –_a(z₂-z₁),

где _a – сухоадиабатический градиент, равный 1⁰/100м.

Если температура единичного объема воздуха Т_i, содержащего ненасыщенный пар, отличается от температуры окружающей атмосферы Т_е, то этот объем воздуха перемещается по вертикали с ускорением а_i

а_i = g

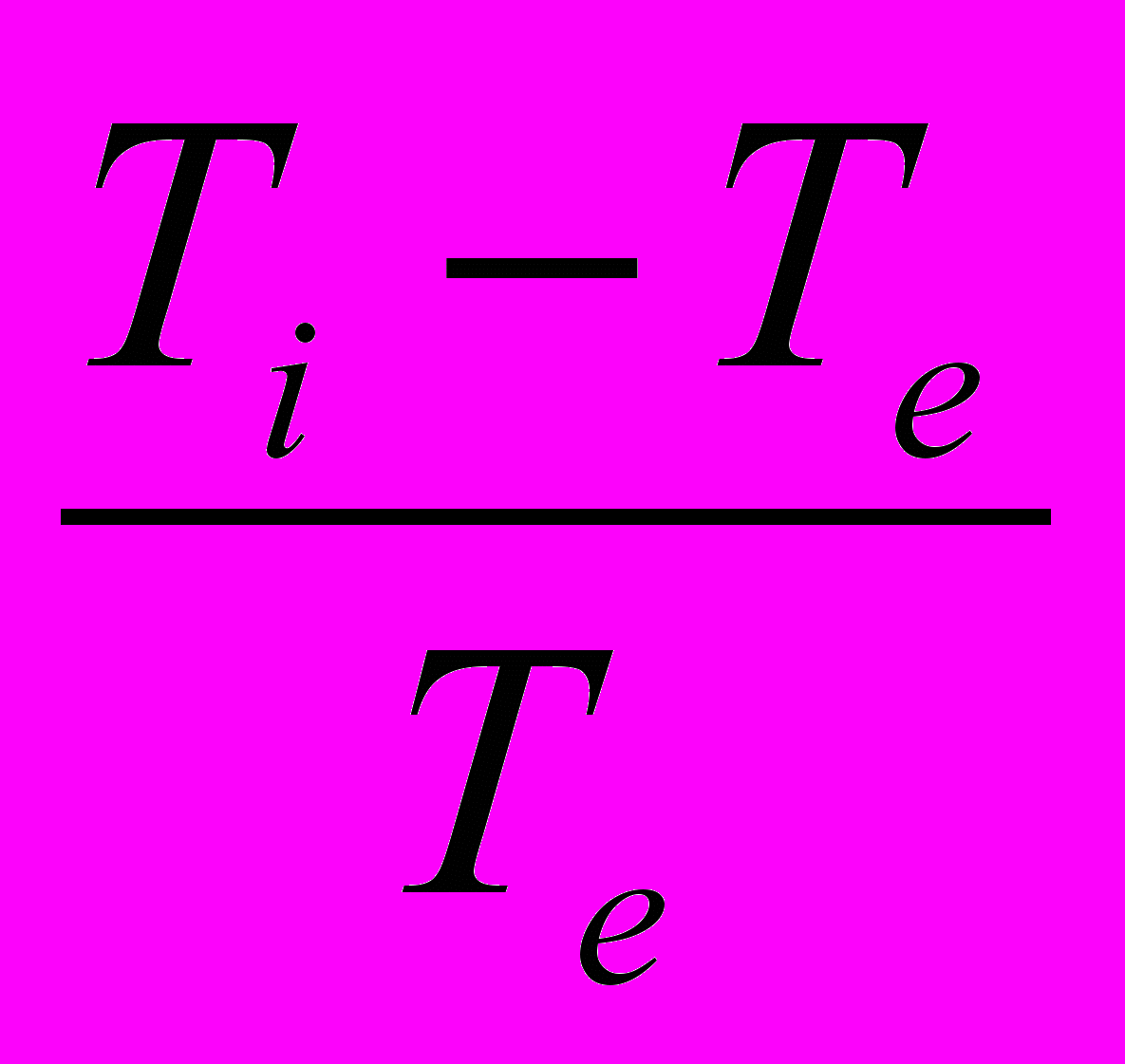
где g – ускорение свободного падения.

Уровень, на котором температура вертикально перемещающегося воздуха станет равной температуре окружающей атмосферы, называют уровнем выравнивания температур (z_выр), его высота определяется по формуле:

z_выр= (Т_i0 – Т_е )/(_a - ),

где Т_i0 – температура перемещающегося объема воздуха на начальном уровне, Т_e0 – температура окружающей атмосферы на том же уровне, _a сухоадиабатический градиент,  - вертикальный температурный градиент.

Стратификация слоев атмосферы (т.е. «расслоение» атмосферы по температурным условиям) определяется по соотношениям вертикальных градиентов температуры фактическому  и сухоадиабатическому _а в ненасыщенном воздухе:

при _а - слой сухоустойчив,

при  = _а - сухобезразличен,

при _а - сухонеустойчив.

Фактическому и влажноадиабатическому _ва в воздухе насыщенном водяными парами:

при _ва – влажноустойчив,

при =_ва – влажнобезразличен,

при _ва – влажнонейстойчив.


Водяной пар в атмосфере. Основные характеристики влажности.

Cуточный и годовой ход влажности

.


Выполните следующие задания.

1.Температуре воздуха 16,7 ⁰С, парциальное давление водяного пара 12,1 гПа. Найти дефицит насыщения. Как и почему он изменится, если при данной температуре увеличится (уменьшится) парциальное давление водяного пара? Если при данном парциальном давлении повысится (понизится) температура воздуха? В каких пределах может изменяться дефицит насыщения? Может ли он быть отрицательным?

2.Вычислить относительную влажность, если при температуре 14,4⁰С парциальное давление водяного пара равно 0,0; 4,1; 8,2; 12,3; 16,4 гПа. Первое или последнее из найденных значений чаще встречается в природе?

3.Температура воздуха -8,6⁰С, относительная влажность 74%. Найти давление насыщенного водяного пара, парциальное давление водяного пара, находящегося в воздухе, и дефицит насыщения.

4.До какой температуры должен изобарически охладится воздух, чтобы содержащийся в нем пар стал насыщенным, если начальная температура воздуха 13,4⁰С и дефицит насыщения 4,2 гПа?

Как и почему изменится ответ, если при той же начальной температуре дефицит насыщения будет больше (меньше) заданного? Если при данном дефиците насыщения повысится (понизится) начальная температура воздуха?

5.Температура воздуха 7,2⁰С, парциальное давление водяного пара 4,7 гПа. Вычислить абсолютную влажность.

Как и почему она изменится, если при данном парциальном давлении водяного пара температура повысится (понизится)? Если при данной температуре парциальное давление пара увеличится (уменьшится)? При изменении какой величины - температуры воздуха или парциального давления пара - абсолютная влажность изменится больше?

6.Температура воздуха -7,1⁰С, давление 993,9 гПа, массовая доля водяного пара 0,2 промилле. Найти парциальное давление водяного пара, дефицит насыщения, относительную влажность, точку росы и абсолютную влажность.

7..По данным таблицы 6.1 построить и проанализировать кривые суточного хода температуры воздуха t, парциального давления водяного пара е, относительной влажности f и дефицита точки росы t_d в ясный и пасмурный дни (n - количество облаков) по данным станции , находящейся в Ленинградской области за 2 летних и 2 зимних дня.

Указать время наступления и значения максимума и минимума рассматриваемых метеорологических элементов и привести объяснения. Сопоставить суточный ход характеристик влажности с суточным ходом температуры. Объяснить различие суточного хода характеристик влажности в ясные и пасмурные дни. Какие факторы определяют суточный ход парциального давления водяного пара, относительной влажности и температуры точки росы? Определить, чем отличается суточный ход характеристик влажности воздуха в холодный и теплый сезоны?

8.Какой процесс (испарение или конденсация) будет происходить над водоемом или увлажненной поверхностью суши при относительной влажности 100%, если температура их поверхности равна 2,5; 10,3, 12,5⁰С; а температура воздуха - соответственно 0,0; 7,3; 15,8⁰С?

Какое атмосферное явление при условии данной задачи может наблюдаться над водоемом (увлажненной сушей)?

9.Температура воздуха 10,0⁰С, температура испаряющей поверхности 4,0⁰С. При какой относительной влажности прекратится испарение? При каком соотношении температур испаряющей среды и воздуха испарение прекратится?

10.Вечером температура воздуха в почвы составляла 10.0⁰С относительная влажность воздуха 80%. В течение ночи парциальное давление водяного пара, находящегося в воздухе, не менялось, но температура почвы и воздуха понизилась до 8,0⁰С. Наблюдатель зафиксировал появление росы. Верна ли запись?


Конденсация и сублимации. Облака. Снежный покров.

Конденсация – это переход воды из газообразного состояния в жидкое. При конденсации в атмосфере образуются мельчайшие капельки воды диаметром в несколько микрометров. Конденсация начинается тогда, когда воздух достигает насыщения, что чаще всего связано с его охлаждением. При температуре точки росы и достижении состояния насыщения, дальнейшее понижение температуры приводит к тому, что избыток водяного пара переходит в жидкое состояние. Охлаждение воздуха чаще всего происходит адиабатически, что связано с подъемом воздуха. Пока воздух не насыщен, он охлаждается на 1⁰С на каждые 100 метров подъема. Поэтому если воздух не очень далек от насыщения, ему достаточно подняться на несколько сот метров, чтобы в нем началась конденсация. Для определения возможной высоты уровня конденсации при подъеме в горах приблизительные расчеты проводят с учетом сухоадиабитического градиента.

В свободной атмосфере механизмы подъема воздуха различны – это могут быть турбулентные движения в виде неупорядоченных вихрей или восходящие токи конвекции. Подъем воздуха может происходить в гребнях атмосферных волн или вдоль атмосферных фронтов. В зависимости от механизма подъема в результате конденсации образуются различные типы облаков, высота нижней границы которых рассчитывается по следующим эмпирическим формулам:

• для слоистообразных облаков нижнего яруса (St, Ns)
  

H = 215 (t-t_d), H= 25 (102-f),

• для облаков вертикального развития:
  

H = 121 (t-t_d),

где t – температура воздуха, t_d – точка росы, f – относительная влажность воздуха.

Степень неравномерности в годовом распределении осадков можно охарактеризовать числовым индексом – показателем неравномерности (или показателем периодичности):


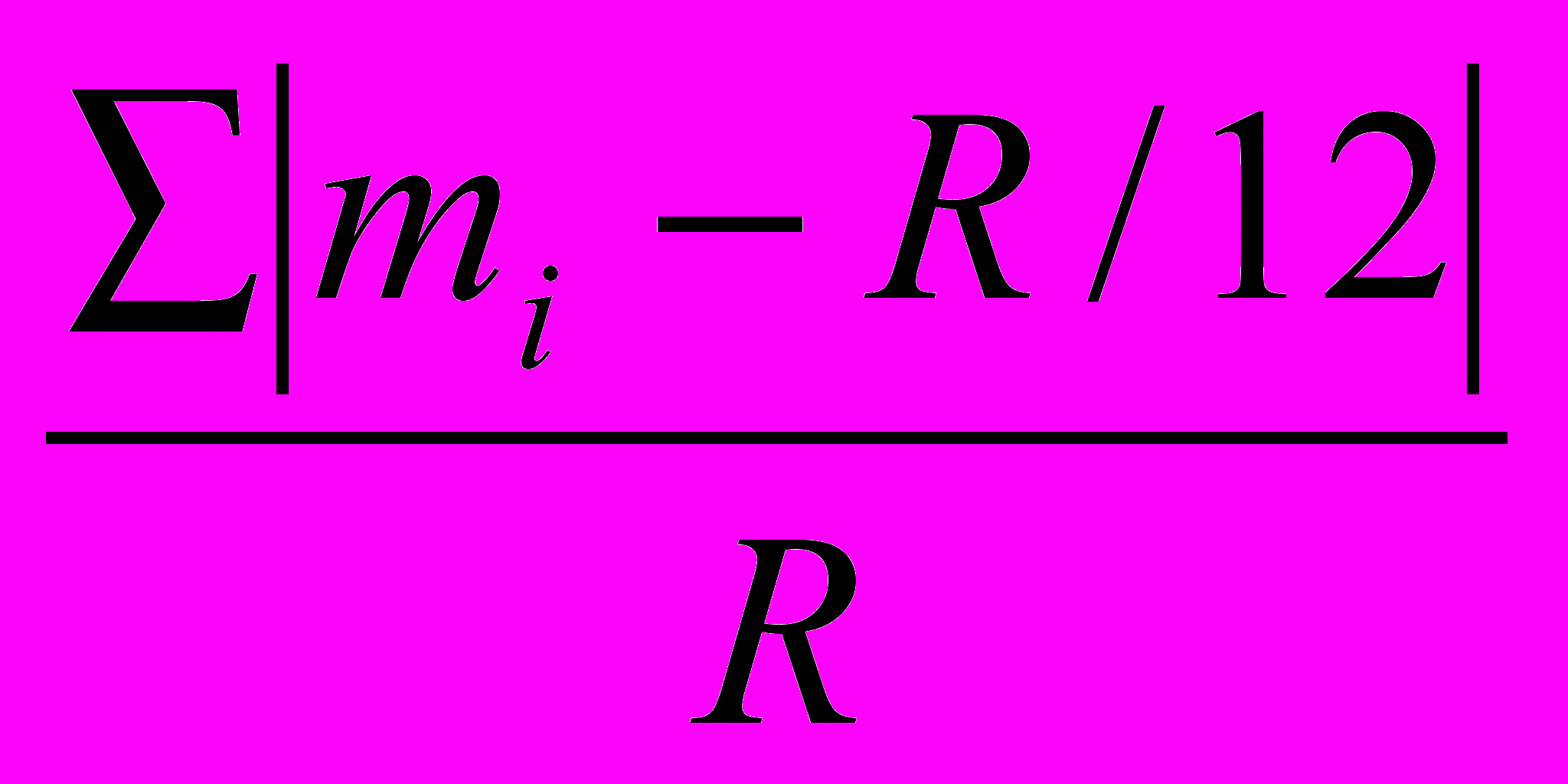 = *100%,

где R – годовая сумма осадков, m_i - R/12 - сумма абсолютных величин разностей между количеством осадков каждого месяца и 1/12 частью годовой суммы осадков. При равномерном выпадении осадков по месяцам (морской, экваториальный тип годового хода осадков) показатель  минимален. Чем больше отличаются одна от другой месячные суммы осадков, тем больше должен быть . В муссонных областях и тропических пустынях он достигает 125%, В экваториальных областях  ниже 50%. В умеренной зоне по мере роста континентальности он возрастает от 25% до 100% и выше.

При конденсации водяного пара у поверхности земли образуются туманы. Для образования туманов необходимо охлаждение воздуха ниже точки росы настолько, чтобы сконденсировалось достаточное количество водяного пара, необходимое для создания определенной водности. При формировании туманов главной причиной охлаждения воздуха является не адиабатический подъем воздуха, а отдача тепла из воздуха земной поверхности.

Понижение температуры, необходимое для образования тумана рассчитывается по формуле:

= ₁+₂,

где ₁ – понижение температуры до точки росы, ₂- понижение температуры ниже точки росы, необходимое для создания тумана определенной водности.

₁ и ₂можно определить по формулам

₁ = 0,115Т(2-lg f), ₂= 19/е,

где  - водность тумана (г/м³), е – парциальное давление водяного пара (гПа) в вечерний срок.

Основными величинами, характеризующими снежный покров, являются его высота и плотность. Располагая данными о высоте и плотности снежного покрова, можно вычислить запасы воды в снежном покров. Для определения этих характеристик снежного покрова используют весовой снегомер, размеченный на сантиметровые деления. Плотность снега (d) определяется по формуле:

d = m/10h (г/см³),

где m - число делений по линейке, h -высота снeжного покрова.

Запасы влаги в снежном покрове (мм) вычисляются по формуле

a = dh 10,

где d - плотность снега, h -высота пробы снега, 10 - множитель для перевода сантиметров в миллиметры.

Измерение высоты снежного покрова осуществляется с помощью снегомерной рейки. Постоянная снегомерная рейка представляет собой деревянный брусок высотой до 2 м и шириной не менее 5 см, размеченный и раскрашенный на сантиметровые деления. При ежедневных наблюдениях в утренние часы берется отсчет по рейке с точностью до 1 см, всегда с одного и того же места на расстоянии не ближе чем 2 м от рейки.

Определение плотности снежного покрова с помощью весового снегомера состоит в измерении высоты снежного покрова и веса взятой пробы. Затем по полученным данным вычисляют плотность снега. Весовой снегомер состоит из полого металлического цилиндра высотой 60 см и площадью сечения 50 см² и весов типа безмен. Цилиндр погружают в снег заточенным краем до соприкосновения с почвой и отсчитывают высоту снежного покрова по шкале, нанесенной на цилиндре. Затем измеряют вес взятой пробы снега и рассчитывают его плотность.

Барическое поле и барический градиент. Ветровой режим.

Атмосферный воздух, как и всякий газ, действует на ограничивающие его стенки с какой-то силой, т.е. в каждой точке атмосферы имеется определенная величина давления воздуха или атмосферного давления. На уровне моря атмосферное давление близко к одному килограмму на квадратный сантиметр. В метеорологии давление воздуха выражают в миллиметрах ртутного столба, в миллибарах или гектопаскалях. За нормальное давление атмосферного воздуха принято давление на уровне моря на широте 45⁰ и оно составляет 760 мм рт. ст. или 1013 мб.

Атмосферное давление изменяется как в вертикальном, так и в горизонтальном направлениях и образует поле, которое называют барическим полем. Такое поле наглядно представляют в трехмерном пространстве системой поверхностей равных значений давления - изобарическими поверхностями. Количественной характеристикой барического поля является барический градиент – вектор, направленный перпендикулярно к изобарической поверхности в сторону уменьшения давления и равный изменению давления на единицу расстояния. Вертикальную составляющую барического градиента называют вертикальный барический градиент. Горизонтальную – горизонтальный барический градиент.

Вертикальный барический градиент характеризует величину падения давления на единицу прироста высоты. Вертикальный барический градиент измеряется обычно в гПа/100 м с точностью до десятых.

G = 3,42 p/T,

где р выражается в гПа, Т – в К.

Кроме барического градиента, важную роль для понимания процессов, происходящих в атмосфере, имеет барическая ступень - прирост высоты, при которой атмосферное давление меняется на единицу. Барическая ступень (h) выражается в м/гПа с точностью до десятых и вычисляется по формулам:

h = 100/G, или h = 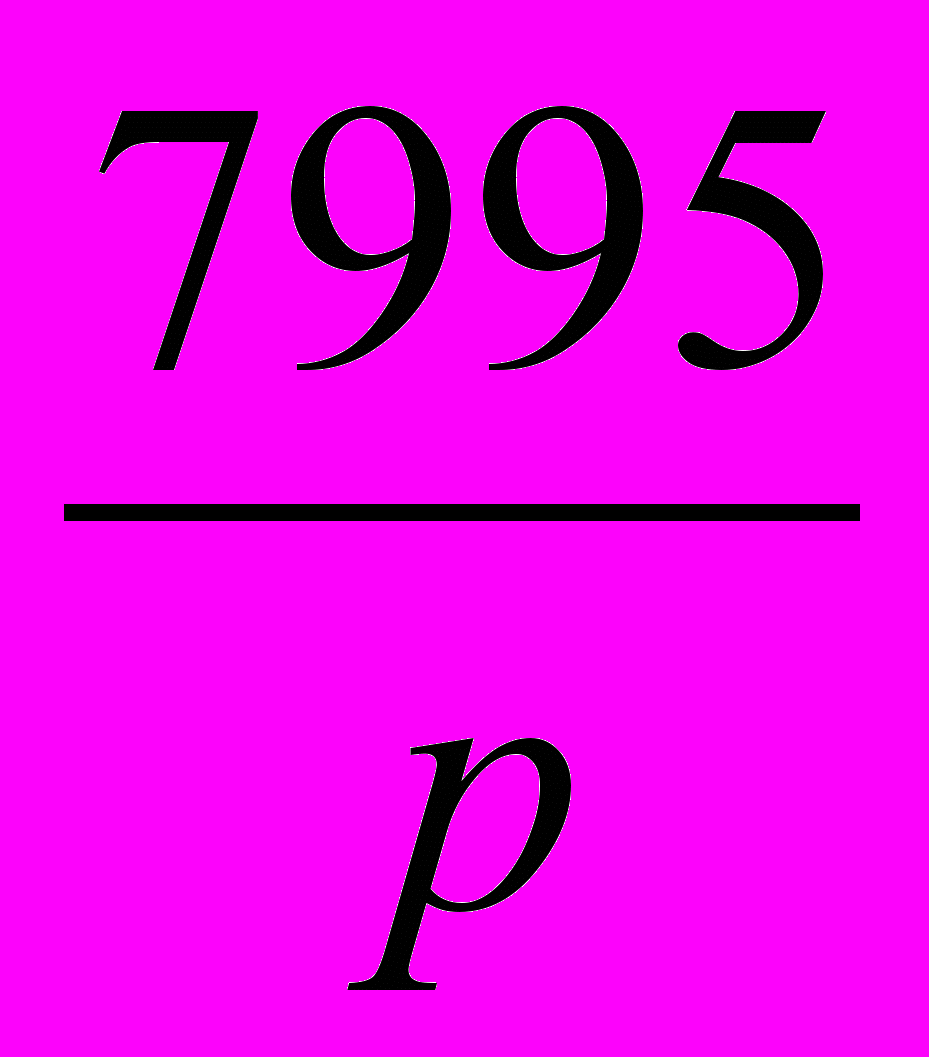(1+ t),

где р – атмосферное давление, выраженное в гПа, a – коэффициент объемного расширения газов (a = 1/273,15 = 3,66*10^-3 (С^о)^-1).

Барическая ступень прямо пропорциональна температуре воздуха, причем при одном и том же давлении барическая ступень больше при более высокой температуре, чем при более низкой. Это определяет более быстрое падение давления в холодном воздухе, чем в теплом. В результате этого на определенной высоте давление в холодном и теплом воздухе становится неодинаковым, и теплые области в атмосфере являются областями высокого давления, а холодные - областями низкого давления.

Изменение атмосферного давления в горизонтальном направлении выражается с помощью горизонтального барического градиента. Горизонтальным градиентом называют вектор, который направлен по нормали к изобаре, в сторону низкого давления и по величине равный производной давления по нормали. Горизонтальный барический градиент представляет собой изменение давления на единицу расстояния в горизонтальной плоскости и обычно выражается в гПа/111 км.

Линии пересечения изобарических поверхностей с горизонтальной плоскостью называют изобарами - линиями равных значений давления. Изобары строятся обычно на уровень моря. Для построения карты изобар на географическую основу наносят точки, соответствующие метеостанциям, со значениями атмосферного давления, измеренными на этих станциях и приведенными на уровень моря, затем через равные интервалы значений давления проводят изолинии. При необходимости производится интерполяция значений давления между станциями. На этих картах замкнутыми изобарами изображаются циклоны области с пониженным давлением в центре, и антициклоны - области с повышенным давлением в центре. Кроме того, выделяют также незамкнутые барические системы – ложбины, седловины и гребни. Ложбинами называют полосы пониженного давления между двумя областями повышенного, гребнями наоборот, полосы относительно повышенного давления между областями пониженного. Между двумя ложбинами или гребнями выделяют седловину.

Изменение атмосферного давления с высотой используют для барометрического нивелирования, т.е. определение превышения одного пункта над другим с помощью измерения давления. Наиболее точной формулой барометрического нивелирования является формула Лапласа. Она получена для влажного воздуха с учетом изменения ускорения свободного падения с широтой и высотой. В метеорологии используют барометрическую формулу реальной атмосферы. Но в практике полевых работ для определения небольшого перепада высот используют формулу Бабине:

h = z₂-z₁ = 8000 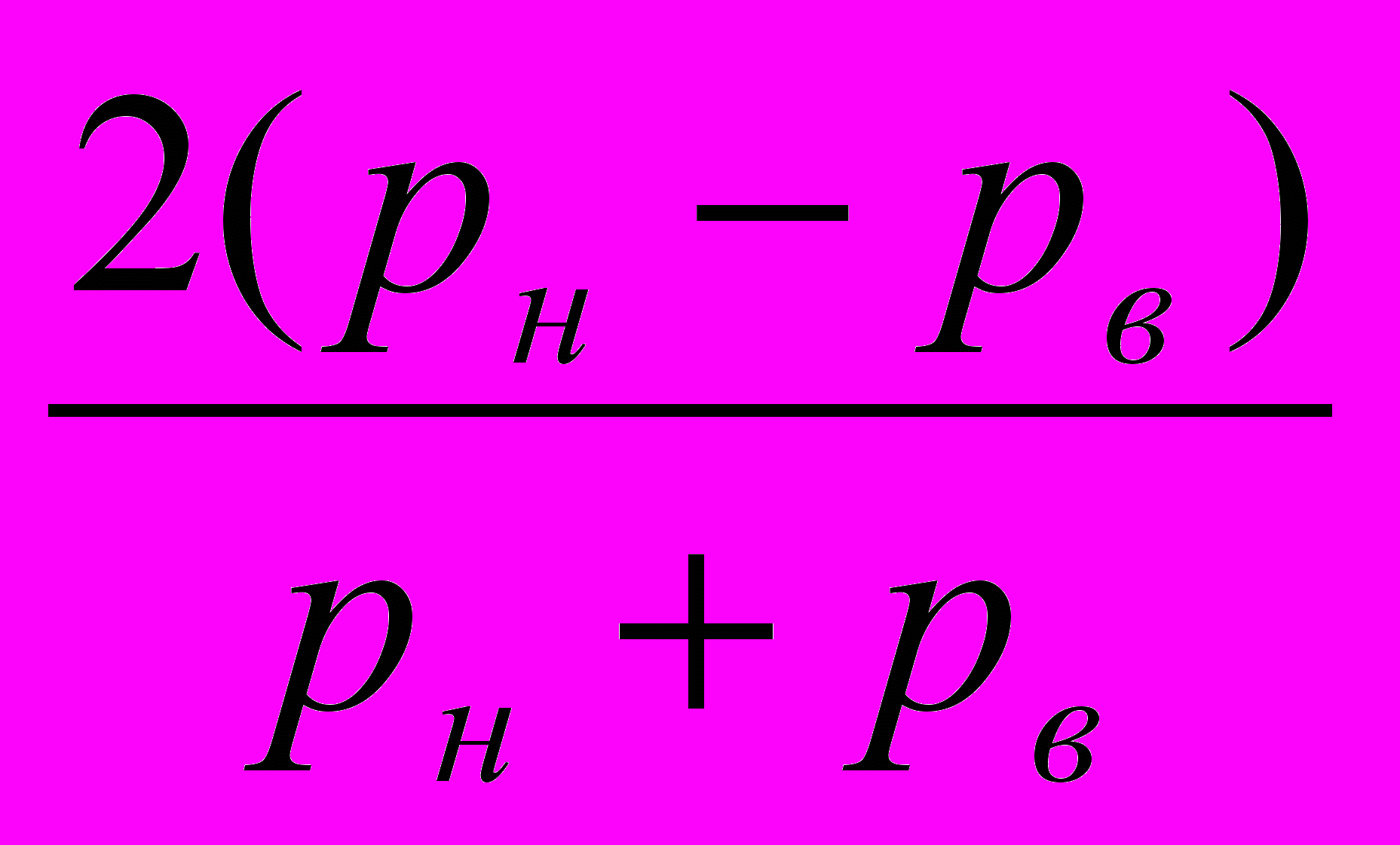(1+t_m),

где р_н - давление на нижнем уровне z_1, а р_в – давление на верхнем уровне z₂,  - коэффициент объемного расширения газов.

Кроме ветров общей циркуляции атмосферы, выделяют местные ветры. Под местными ветрами понимают ветры, характерные для определенных географических районов. Такими ветрами являются бриз, бора, горно-долинный ветер, фён.

Климат города Изучение влияния городской агломерации на основные климатические характеристики на примере Москвы


В работе используются данные по нескольким метеостанциям, расположенным в черте города Москвы.

Метеостанция Балчуг (Б) организована 20 сентября 1946 г. С момента организации работает без перерыва. Станция расположена в центре Москвы. Рельеф местности равнинно-увалистый с абсолютными высотами 100-150 м, изрезан сетью оврагов и рек. Леса находятся на расстоянии более 10 км от метеостанции, река Москва протекает в 300 м к северу от метеостанции. С востока и запада и юга метеостанцию окружают двухэтажные дома высотой 8-10 м, с севера проходит асфальтовое шоссе, за ним водоотводный канал шириной около 60 м, далее многоэтажные дома и на расстоянии 200 м - ТЭЦ.

Обсерватория им. В.А.Михельсона (Т) организована в конце 1878 года и наблюдения ведутся непрерывно с 1 января 1879 года. Обсерватория расположена на территории Сельскохозяйственной академии им. К.А.Тимирязева. Станция расположена на северо-северо-западной окраине Москвы в 8-9 км от центра. К западу, на расстоянии 3 км от метеостанции находится Химкинское водохранилище шириной 0,5 км, длиной 4-5 км, вытянутое с северо-северо-запада на юго-юго-восток. К югу и юго-западу в 7 км течет река Москва, в 3,5 км к восток-северо-востоку с севера на юг течет р.Яуза, с западной стороны находится пруд размером 0,2х0,8 км. Естественных лесов в районе нет, но имеются значительные по площади парковые зоны. Застройка прилегающих районов началось в конце 60-70-ые годы 20 века, но наиболее интенсивное многоэтажное строительство происходит с конца 70-ых годов.

Агрометеостанция ВДНХ (В) открыта 1 августа 1939 года и, после временного закрытия, продолжила работу с 1948 года. Станция расположена на территории Всероссийского выставочного фонда (бывш.ВДНХ) в северной части Москвы. Территория ВДНХ граничит на севере с Леоновским лесом площадью 25 га, на северо-западе и западе с главным ботаническим садом площадью 400 га и на юго западе с ПКиО им. Дзержинского площадью 75 га. К южной и юго-восточной границе примыкает жилой район Останкино. Рельеф окружающей местности волнистый с незначительными повышениями и понижениями. С запада, севера и востока к метеостанции примыкают выставочные павильоны, на юго-востоке – жилые массивы. На прилегающей территории встречаются насаждения декоративных и плодовых деревьев.

Метеостанция Ленино-Дачное (ЛД) организована и работает с 30 сентября 1951 года. Расположена она на юго-юго-восточной окраине Москвы, на восточных отрогах Смоленско-Московской возвышенности с абсолютными высотами 160-200 м. Рельеф местности слегка всхолмленный, пересечен небольшими оврагами. Леса расположены с востока и запада на расстоянии 2-6 км. Река Битца протекает в 800 -1200 м к востоку. Многоэтажная застройка прилегающих районов началась в 70-ые годы.

Метеостанция Немчиновка (Н) расположена на юго-западной окраине Москвы, в центре питомника Всесоюзного института лекарственно-ароматических растений (ВИЛАР), на пологом северо-западном склоне. С северо-запада, на расстоянии 80-100 м проходит шоссе, с юго-востока в 50 м - полотно железной дороги. К северу и северо-востоку, на расстоянии 100-150 м, расположены жилые двухэтажные дома и служебные постройки высотой 10-12 м, окруженные деревьями и кустарниками.


Выполнить следующие задания:

1.Радиационный режим города Москвы. Для анализа радиационного режима использованы данные Метеорологической обсерватории МГУ

По данным таблицы 8.1 определить:

суммарную радиацию в городе Москве и долю прямой и рассеянной радиации в суммарной по месяцам. Указать причину изменений соотношения прямой и рассеянной радиации по месяцам; поглощенную радиацию по месяцам и эффективное излучение

2. Анализ годового хода температуры воздуха в городе.

По приведенным ниже данным (таблица 8.2) построить графики годового хода температуры на метеостанциях Москвы. Определить:

1.годовую амплитуду температуры на каждой станции,

2.среднегодовую амплитуду температуры по Москве,

3.относительные отклонения годовой амплитуды для каждой метеостанции.

Проанализировать различия годового хода температуры на каждой метеостанции и сделать выводы о влиянии города на температуру воздуха.

3.Характеристика относительной влажности воздуха.

По приведенным ниже данным (таблица 8.3):

1.определить средние сезонные значения относительной влажности по метеостанциям;

2.определить относительные отклонения значений относительной влажности для каждой станции по сезонам от среднего городского значения.

3.проанализировать особенности годового хода относительной влажности в разных районах города;

4.оценить влияние города на годовой ход влажности.

4.Характерстика годового хода осадков.

По данным таблицы 8.4. определить:

1. среднегодовое количество осадков для каждой метеостанции и для города в целом;
   
2. относительные отклонения среднегодового количества осадков для каждой метеостанции от среднегородского значения;
   
3. долю каждого вида осадков (общих (О), твердых (Т), жидких (Ж) и смешанных (С)) в годовом ходе по станциям.
   

Проанализировать особенности годового хода осадков на каждой станции.

5.Характеристика ветрового режима в городе.

Построить розы ветров для каждой станции по приведенным ниже данным (таблицы:8.5, 8.6)

по средним за сезон скоростям ветра (м/с),

повторяемости ветров определенного направления (число случаев) в различные сезоны за два срока наблюдений (1-1966-70 гг. и 2 -1983-87гг).

Определить, что произошло с ветровым режимом в различных частях города за период интенсивного строительства многоэтажных домов в окраинных районах города.

6. Анализ режима облачности в городе.

По данным таблицы 8.7 построить графики среднемесячной общей и нижней облачности;

выявить сезонные особенности облачности в городе и различия между нижней и общей облачностью на разных метеостанциях.

Важным показателем режима облачности является соотношение ясных и пасмурных дней. По данным таблицы 8.8 определите соотношение (разность) ясных и пасмурных дней в разные сезоны годы и в среднегодовом ходе для двух метеостанций

7.Туманы.

В таблице 8.9 содержатся данные о процентном соотношении туманов в разные сезоны годы для центра города и периферийной зоны за 40 лет (1950-1989 гг.)

Сопоставить повторяемость туманов по разным сезонам, разному времени суток на этих метеостанциях.

8. Загрязнение атмосферы г. Москвы.

По данным таблицы 8.10 определить в какие годы и на сколько процентов были превышены в Москве санитарные нормы (ПДК_сс - среднесуточные предельно допустимые концентрации этих веществ в атмосфере) концентрации основных загрязнителей атмосферы.

9. Годовой ход рН осадков в Москве.

Фоновые значения рН осадков составляют в зоне умеренного климата в среднем 5.6. В городах, как правило, кислотность осадков повышается и составляет в среднем (для Москвы) 4.6-5.2. Но, как показали исследования, в течение года в зависимости от агрегатного состояния выпадающих осадков кислотность осадков меняется.

Осредненные данные по кислотности осадков за 10 лет наблюдений приведены в таблице 8.11.

Построить кривую годового хода кислотности осадков и определить как меняется она по сезонам.

10. Макрокомпоненты осадков.

Основными ионами, содержащимися в осадков являются HCO₃^- , SO^-₄, Cl^-, NH₄⁺. Степень очищения атмосферы осадками в значительной степени зависит от интенсивности и продолжительности дождя. В таблицах приведены данные анализов двух дождей разной интенсивности, но примерно с равным количеством осадков. При исследованиях отбирались равные по количеству пробы дождя и фиксировалось время выпадения данного объема. Затем в каждой пробе определялась концентрация основных ионов. Предлагается проанализировать влияние интенсивности осадков на степень очищения атмосферы (таблица 8.12 и 8.13).