И. М. Гонсалес Ортис. Конспект лекций по научному прогнозированию
| Вид материала | Конспект |
- И. М. Гонсалес Ортис. Конспект лекций по научному прогнозированию, 230.88kb.
- Конспект лекций 2010 г. Батычко Вл. Т. Муниципальное право. Конспект лекций. 2010, 2365.6kb.
- Конспект лекций 2008 г. Батычко В. Т. Административное право. Конспект лекций. 2008, 1389.57kb.
- Конспект лекций 2011 г. Батычко В. Т. Семейное право. Конспект лекций. 2011, 1718.16kb.
- Конспект лекций 2011 г. Батычко Вл. Т. Конституционное право зарубежных стран. Конспект, 2667.54kb.
- Конспект лекций 2010 г. Батычко В. Т. Уголовное право. Общая часть. Конспект лекций., 3144.81kb.
- Конспект лекций для студентов по специальностям 190302 «Вагоны», 783.17kb.
- Конспект лекций бурлачков в. К., д э. н., проф. Москва, 1213.67kb.
- Конспект лекций для студентов специальности 080504 Государственное и муниципальное, 962.37kb.
- Конспект лекций по курсу "Начертательная геометрия и инженерная графика" Кемерово 2002, 786.75kb.
И. М. Гонсалес – Ортис. Конспект лекций по научному прогнозированию. ISMA. Рига, 2010 г.
Динамические ряды
- Понятие о динамических рядах
- Условия правильного построения динамических рядов
- Виды динамических рядов. Вычисление средней динамического ряда
- Важнейшие математические показатели анализа рядов динамики
- Приемы преобразования временных рядов
- Понятие о динамических рядах
Все происходящие явления находятся в развитии. Изучение происходящих при этом изменений является одним из необходимых условий познания закономерностей их динамики. Динамизм социально – экономических явлений есть результат взаимодействия разнообразных причин и условий.
Основная цель статистического изучения динамики коммерческой деятельности состоит в выявлении и измерении закономерностей их развития во времени. Это достигается посредством построения и анализа статистических рядов динамики.
| Рядами динамики называются статистические данные, отображающие развитие изучаемого явления во времени. |
В каждом ряду динамики имеются два основных элемента:
1) показатель времени t;
2) соответствующие им уровни развития изучаемого явления y.
| Уровни ряда y | y1 | y2 | y3 | y4 | … | yn |
| Время (периоды или моменты) t | t1 | t2 | t3 | t4 | … | tn |
В качестве показаний времени в рядах динамики выступают либо определенные даты (моменты) времени, либо отдельные периоды (годы, кварталы, месяцы, сутки)
Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами.
В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим ряды динамики подразделяются на:
- моментные;
- интервальные.
Примером моментного ряда динамики является следующая информация о списочной численности студентов экономического факультета за 1990 ÷ 1991 гг.
| Дата | 1.09.1990 | 1.01.1991 | 1.06.1991 | 1.09.1991 |
| Численность студентов ЭФ, чел. | 538 | 473 | 450 | 675 |
Особенностью моментного ряда динамики является то, что в его уровни могут входить одни и те же единицы изучаемой совокупности.
Так, основная часть студентов, составляющая списочную численность студентов на 1.09.1990 г., продолжающая учиться в течение года, отображена в уровнях последующих периодов. Поэтому при суммировании уровней моментного ряда динамики может возникнуть повторный счет.
Интервальные ряды динамики отображают итоги развития изучаемых явлений за отдельные периоды (интервалы) времени.
Примером интервального ряда динамики могут служить данные о численности населения Латвии за 2003 ÷ 2009 гг. (чел.)
-
2003
2 331 480
2004
2 319 203
2005
2 306 434
2006
2 294 590
2007
2 281 305
2008
2 270 894
2009
2 261 294
Особенностью интервального ряда динамики является то, что каждый его уровень складывается из данных за более короткие интервалы (субпериоды) времени.
Например, суммируя товарооборот за первые три месяца года, получают его объем за 1 квартал, а сумма товарооборота 4 – х кварталов дает объем товарооборота за год.
Свойство суммирования уровней за последующие интервалы времени позволяет получать ряды динамики более укрупненных периодов.
С помощью рядов динамики изучение закономерностей развития социально – экономических явлений осуществляется в следующих основных направлениях:
- характеристика уровней развития изучаемых явлений во времени;
- измерение динамики изучаемых явлений посредством статистических показателей;
- выявление и количественная оценка основной тенденции развития (тренда);
- изучение периодических колебаний;
- экстраполяция и прогнозирование.
II. Условия правильного построения динамических рядов
Основным условием для получения правильных выводов при анализе рядов динамики является сопоставимость его элементов.
Сопоставимость проявляется в том, что показатели должны относиться к одной и той же территории, к одному кругу объектов, быть исчисленными по одной методологии, находиться в тех же единицах измерения.
Причина несопоставимости:
- Несопоставимость возникает в результате административно – территориальных изменений, т. е. изменение отдельных границ районов;
- Несопоставимость по кругу охватываемых объектов, возникающая в результате различных реорганизаций, когда предприятия переходят из одного ведомства в другое;
- Применение различных методов расчета статистических данных;
- Несопоставимость может возникнуть в результате изменения единиц измерения;
- Проблема сопоставимости возникает в связи с применением в статистической информации различных по экономическому значению денежных измерителей.
Пример: Так, для денежной оценки объема поставки (оптовой продажи) товаров применяются оптовые цены промышленности, а для оценки объема продажи населению – розничные цены.
К разновидностям розничных цен относятся кооперативные и договорные цены, цены базарной торговли, закупочные и сдаточные цены на сельскохозяйственную продукцию.
Уровни цен изменяются во времени, то для стоимостной оценки товарооборота используются цены соответствующих периодов. Но для изучения динамики физического объема продажи товаров денежная оценка товарооборота в ценах соответствующих периодов не подходит. На объем товарооборота влияет не только фактор реализованной товарной массы, но и фактор изменения цен.
Для устранения влияния изменения цен товарооборот пересчитывается в неизменные (базисные) цены. В результате получают ряды динамики объема товарооборота в сопоставимых ценах.
- Виды динамических рядов. Вычисление средней динамического ряда.
Динамические ряды подразделяются по способу выравнивания данных на ряды абсолютных, относительных и средних величин.
По времени подразделяются на:
- моментные;
- интервальные.
Для характеристики какого – то явления за период времени исчисляется средний уровень ряда.
Средний уровень ряда динамики характеризует типичную величину абсолютных уровней.
Способы расчета зависят от вида динамических рядов.
- Интервальный ряд.
а) при условии равных интервалов формула среднего уровня ряда находится по формуле простой средней арифметической:
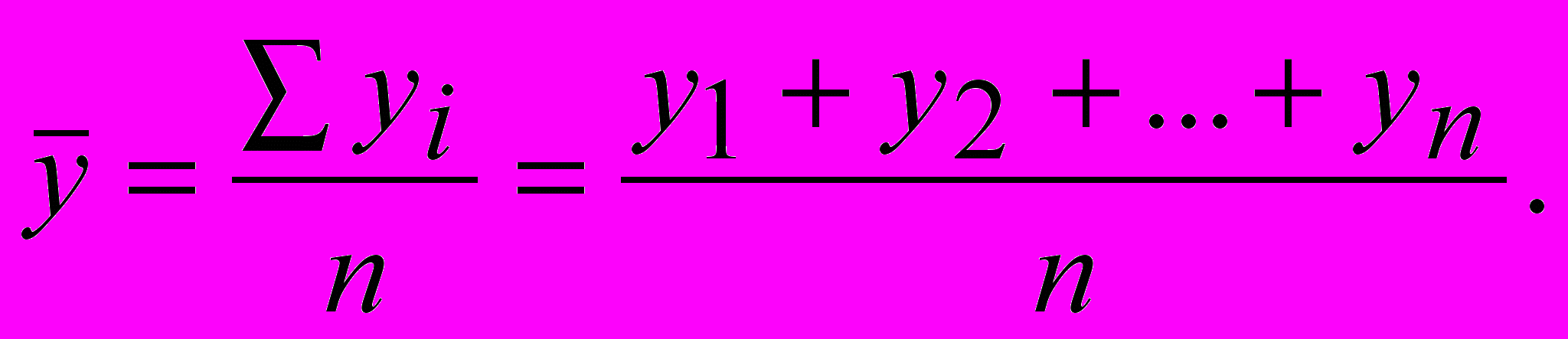
Применение формулы проиллюстрируем на данных интервального ряда динамики численности населения Латвии за 2003 ÷ 2009 гг.
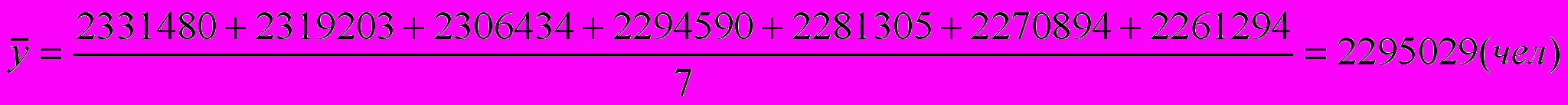
б) при условии неравных интервалов применяется формула средней арифметической взвешенной, весами служат промежутки времени
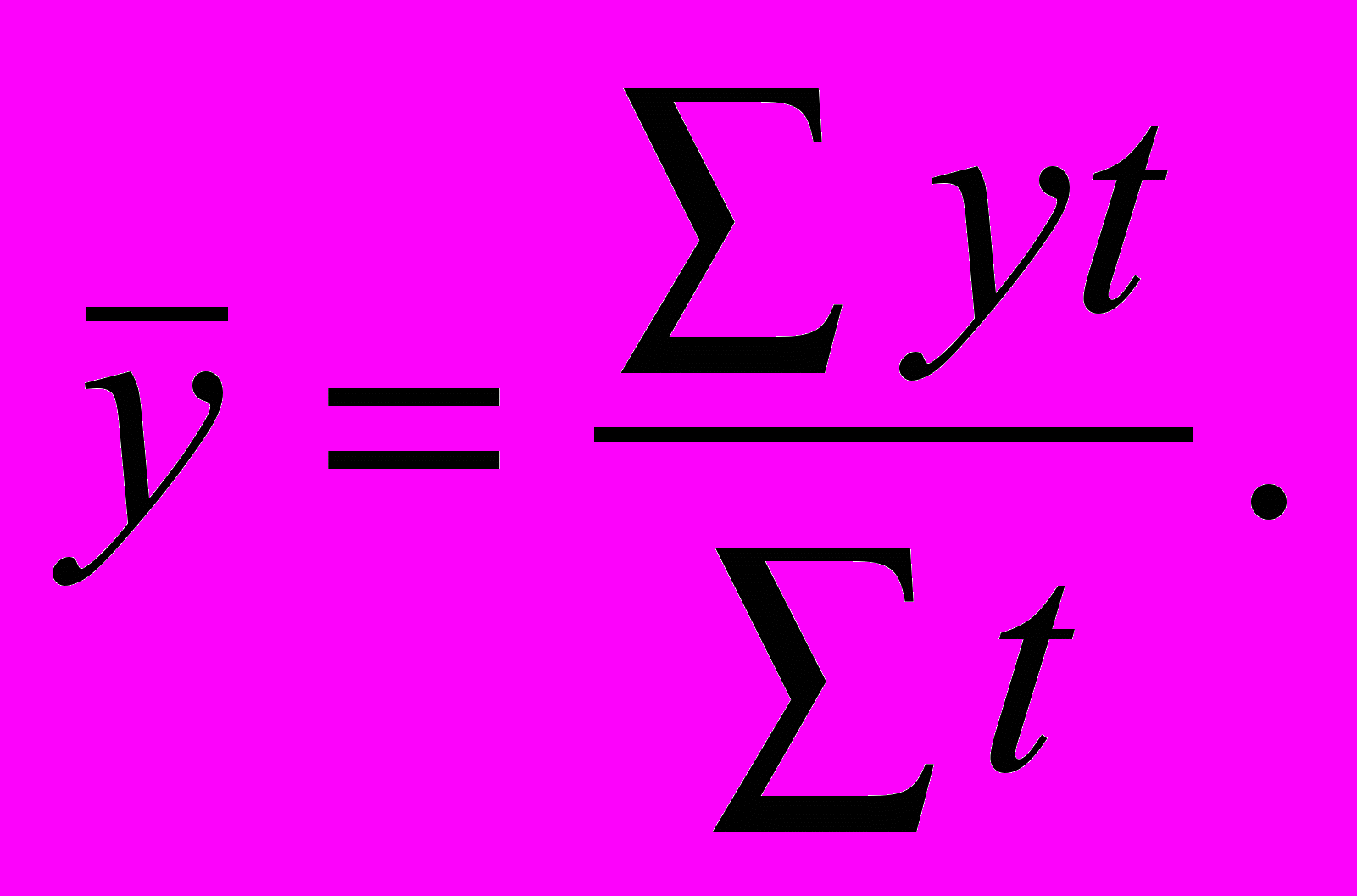
- Моментный ряд
а) моментный ряд динамики с равностоящими датами времени
Средний уровень ряда определяется по формуле средней хронологической
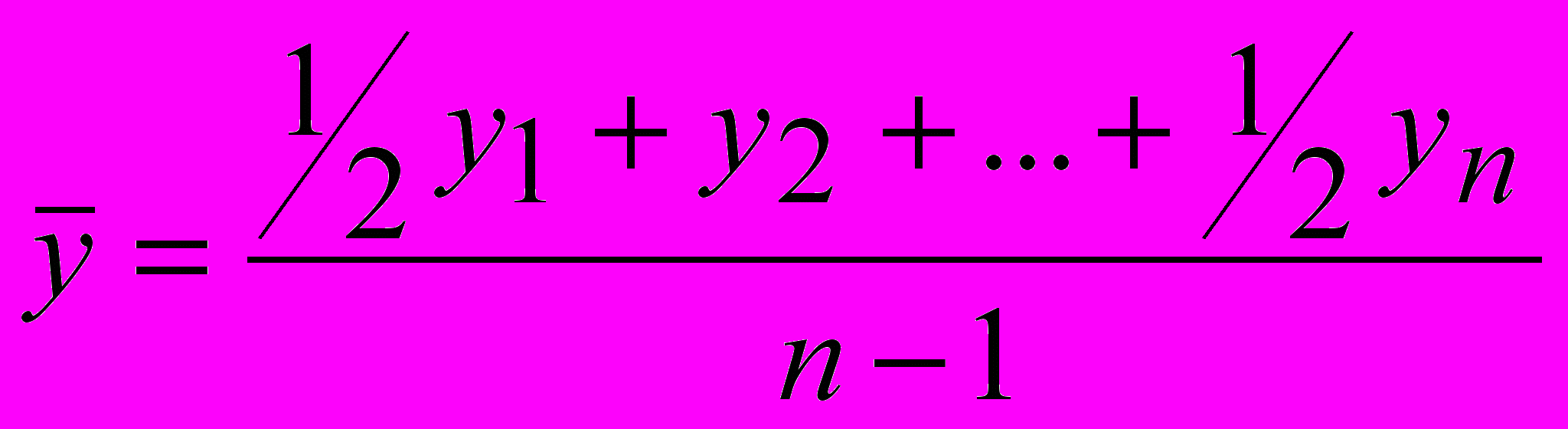
Пример. Найти среднемесячную численность работников магазина за квартал.
| 1.01 | 1.02 | 1.03 | 1.04 |
| 150 | 138 | 140 | 146 |
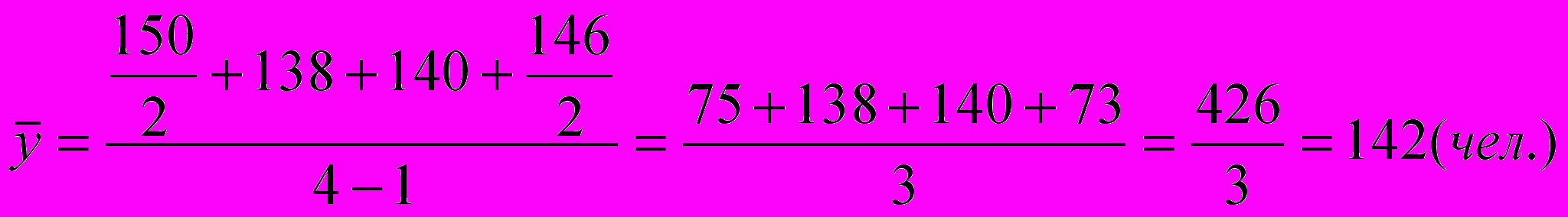
б) в моментном ряду динамики с неравностоящими датами средний уровень определяется по формуле:
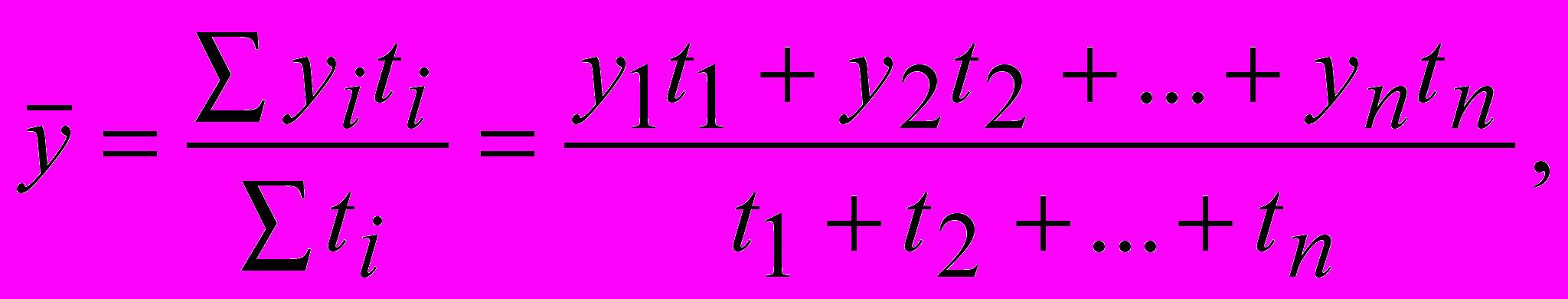
где yi – уровни ряда динамики, сохранившиеся без изменения в течение промежутка времени ti,
ti – отрезки времени между датами.
IV. Важнейшие математические показатели анализа рядов динамики
Для количественной оценки динамики социально – экономических явлений применяются статистические показатели:
- Абсолютный прирост (Δy)
- Темп роста (Тр)
- Темп прироста (Тпр)
- Абсолютное значение 1% прироста (А%)
- Средний абсолютный прирост (
)
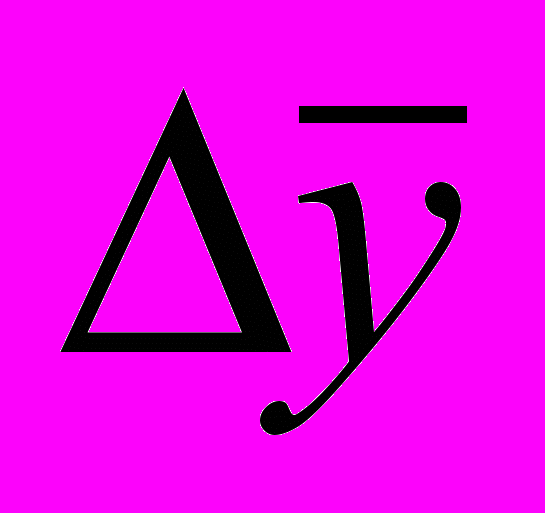- Средний темп роста
)
- Средний темп прироста
)
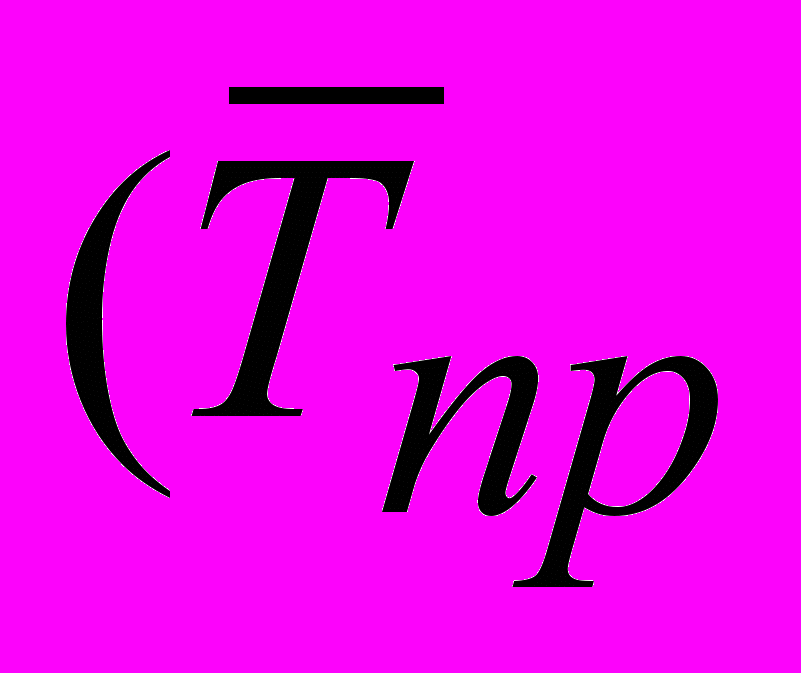- Среднегодовое значения 1% прироста (
)
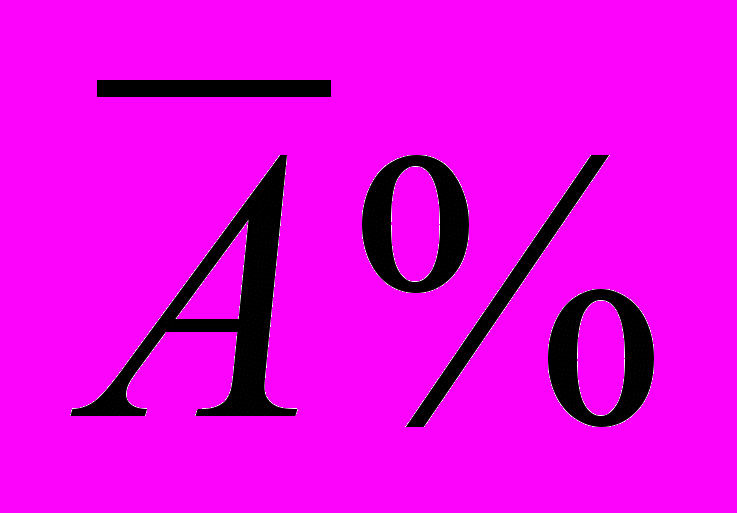В основе расчета показателей рядов динамики лежит сравнение его уровней. В зависимости от применяемого способа сопоставления показатели динамики могут вычисляться на постоянной и переменной базах сравнения.
1. Абсолютный прирост характеризует размер увеличения или уменьшения изучаемого явления за определенный период времени.
Исчисляется как разность между сравниваемым уровнем (yi) и уровнем, принятым за базу сравнения (y0i) или уровнем, который ему предшествует (yi-1)
-
Δyб = yi – y0
– базисный абсолютный прирост
Δyц = yi – yi-1
- цепной абсолютный прирост
- Распространенным статистическим показателем динамики является темп роста, который исчисляется отношением сравниваемого уровня yi на уровень принятый за постоянную базу сравнения y0 – базисный темп роста или на предыдущий уровень yi-1 – цепной темп роста.
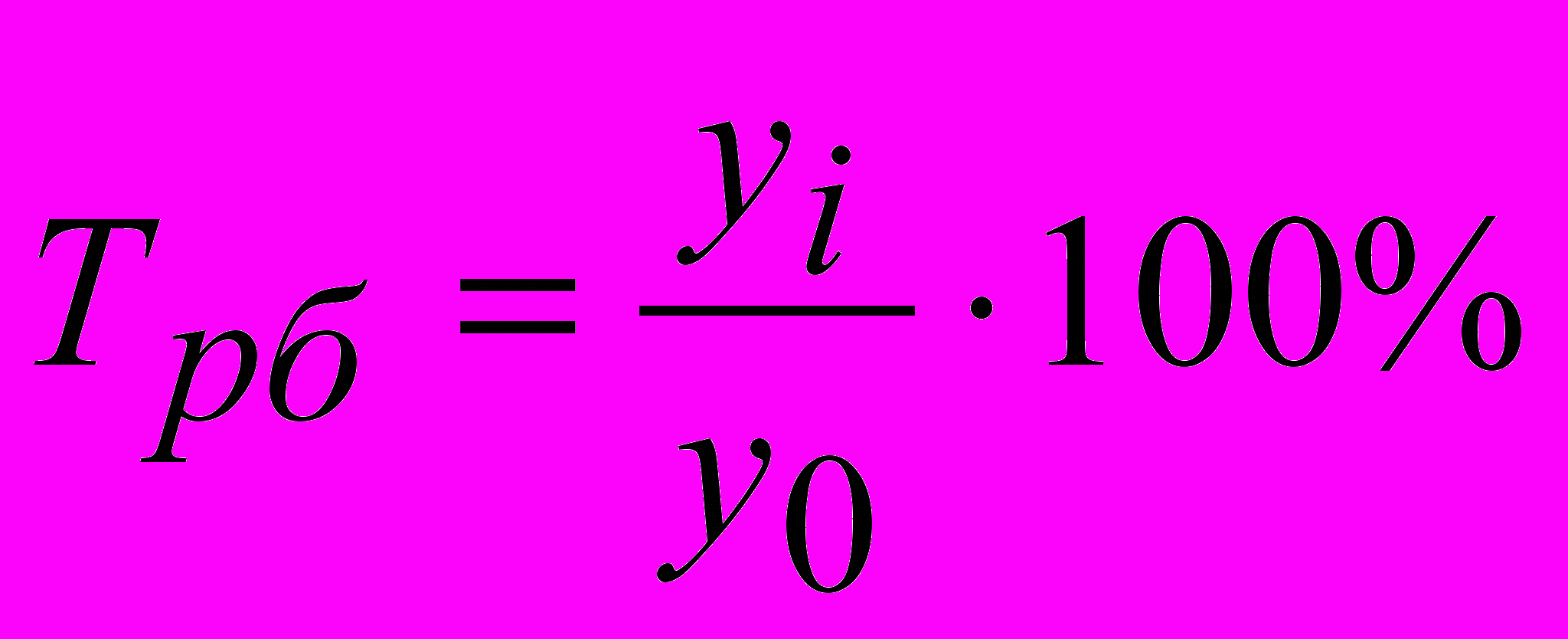
- базисный темп роста
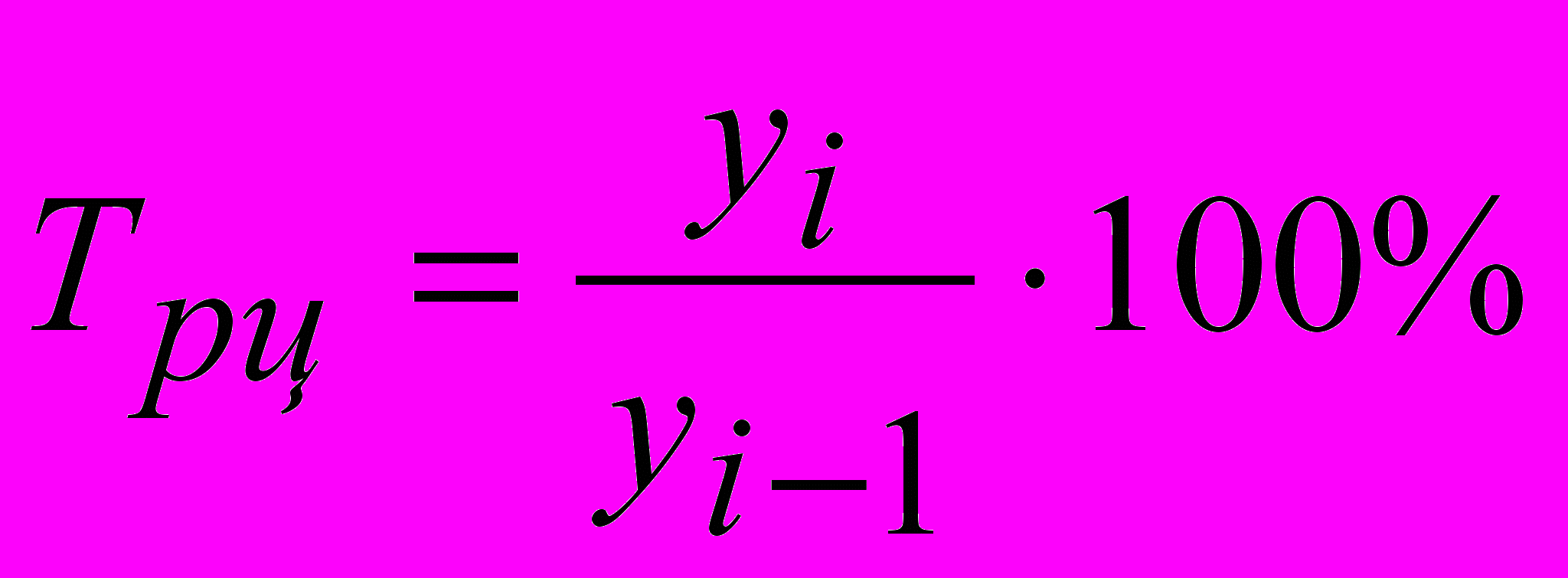
- цепной темп роста
- Темп прироста – характеризует абсолютный прирост в относительных величинах. Исчисленный в процентах темп прироста показывает на сколько процентов изменился сравниваемый уровень с уровнем, принятым за базу сравнения.
Вычисляется отношением базисного абсолютного прироста Δyб на уровень, принятый за постоянную базу сравнения y0 – базисный темп прироста или отношением сравниваемого цепного абсолютного прироста Δyц к предыдущему уровню yi-1.
-
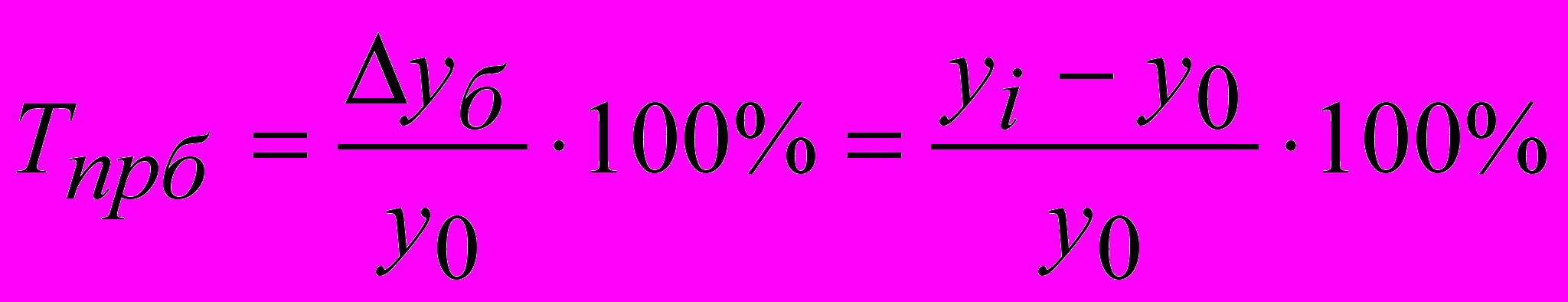
- базисный темп прироста
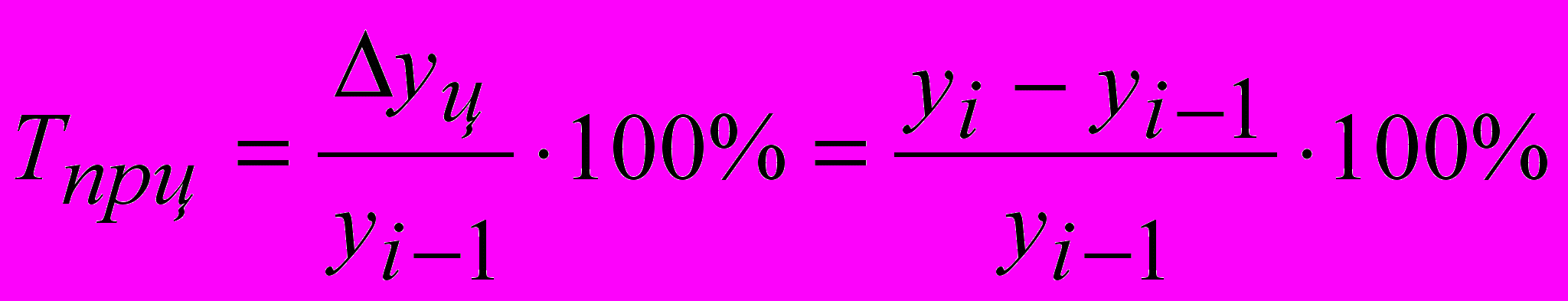
- цепной темп прироста
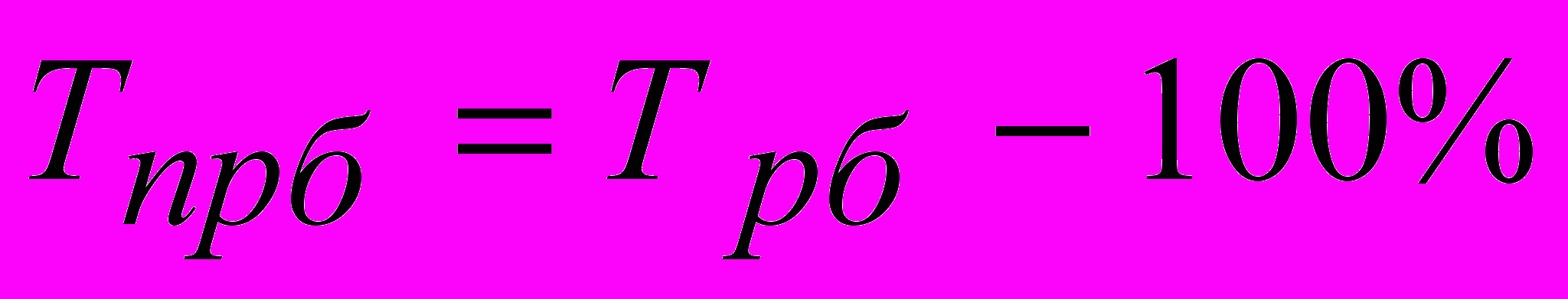
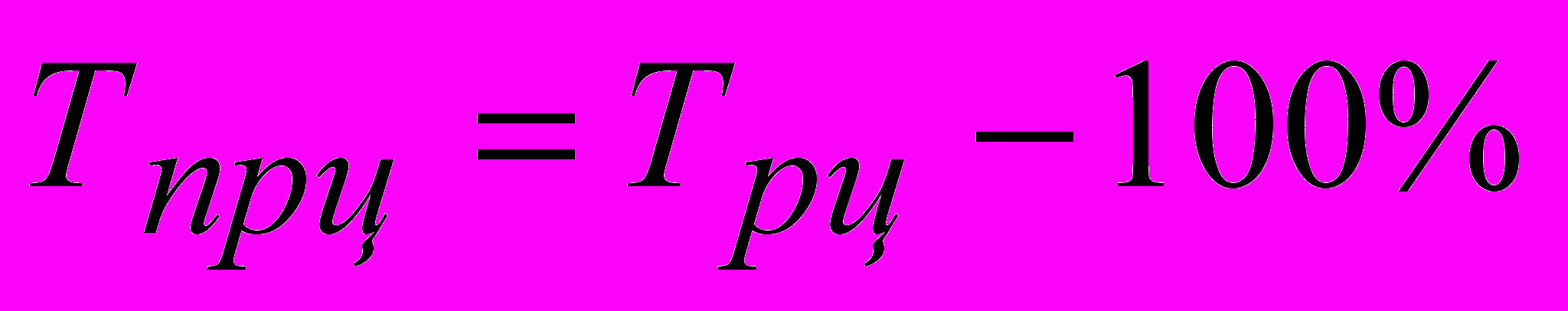
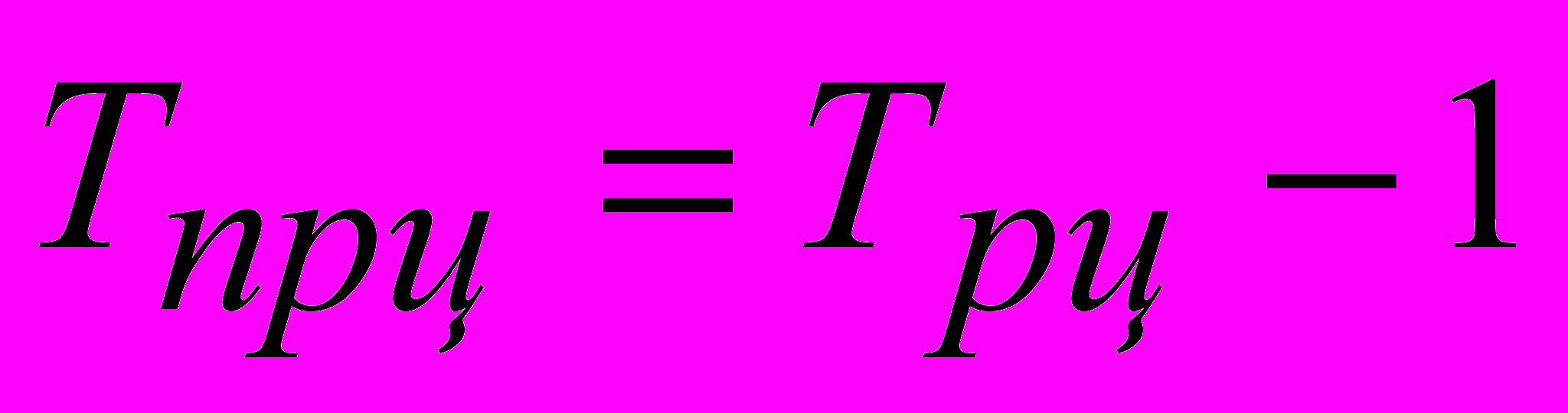
Важным статистическим показателем динамики явления темп наращивания, который в условиях интенсификации экономики измеряет наращивание во времени экономического потенциала.
Вычисляются темпы наращивания Тн делением цепных абсолютных приростов Δyц на уровень, принятый за постоянную базу сравнения y0.
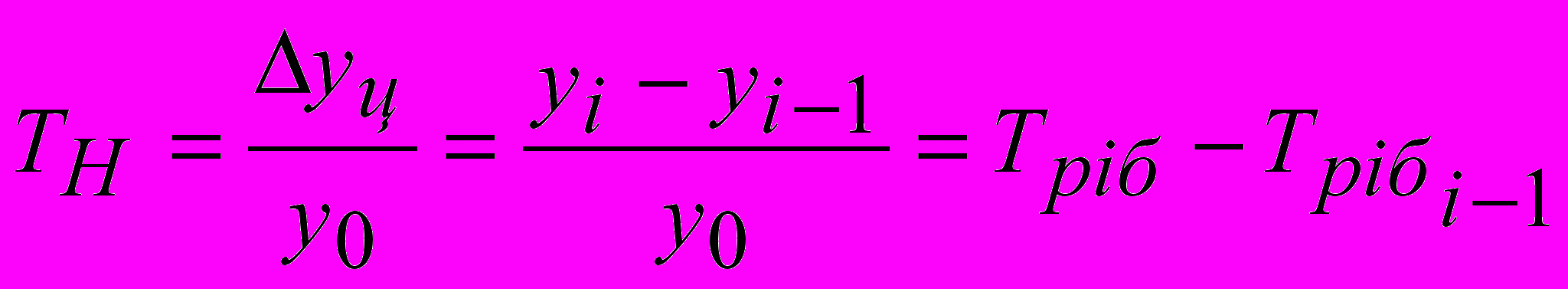
- Абсолютное значение 1% прироста
Представляет собой отношение абсолютного прироста к темпу прироста. Смысл имеет на цепной основе.
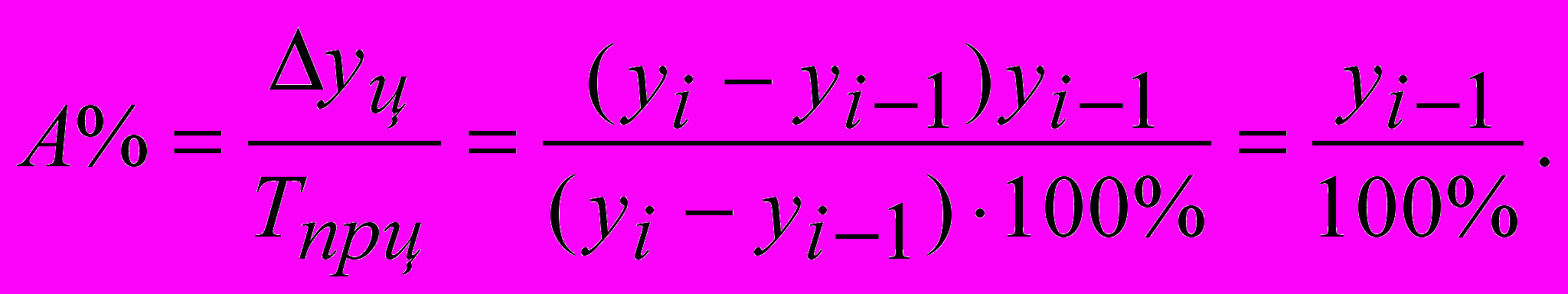
- Если имеются абсолютные приросты по годам, то вычисляется средний абсолютный прирост:
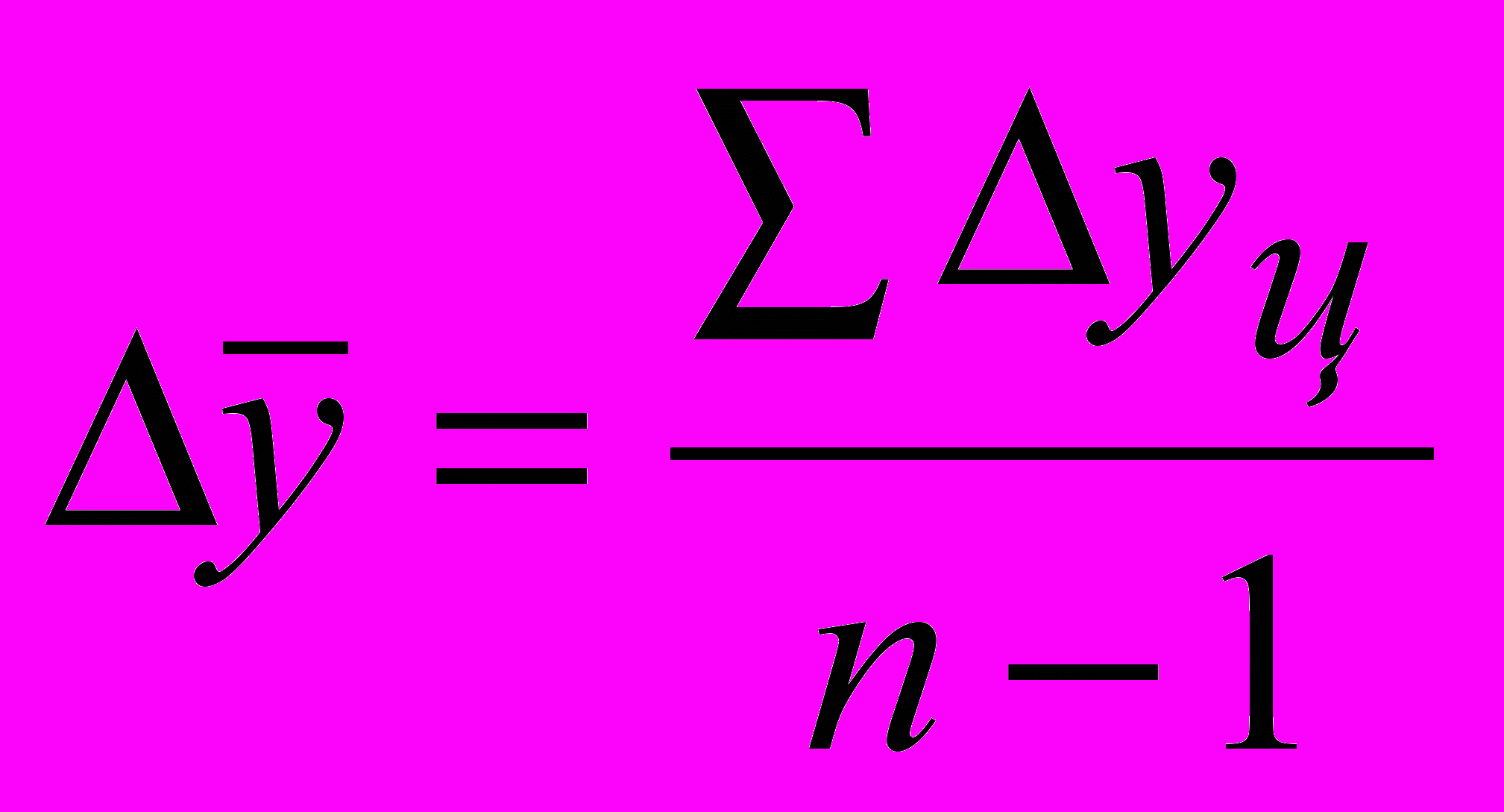 | средняя арифметическая простая годовых (цепных приростов) |
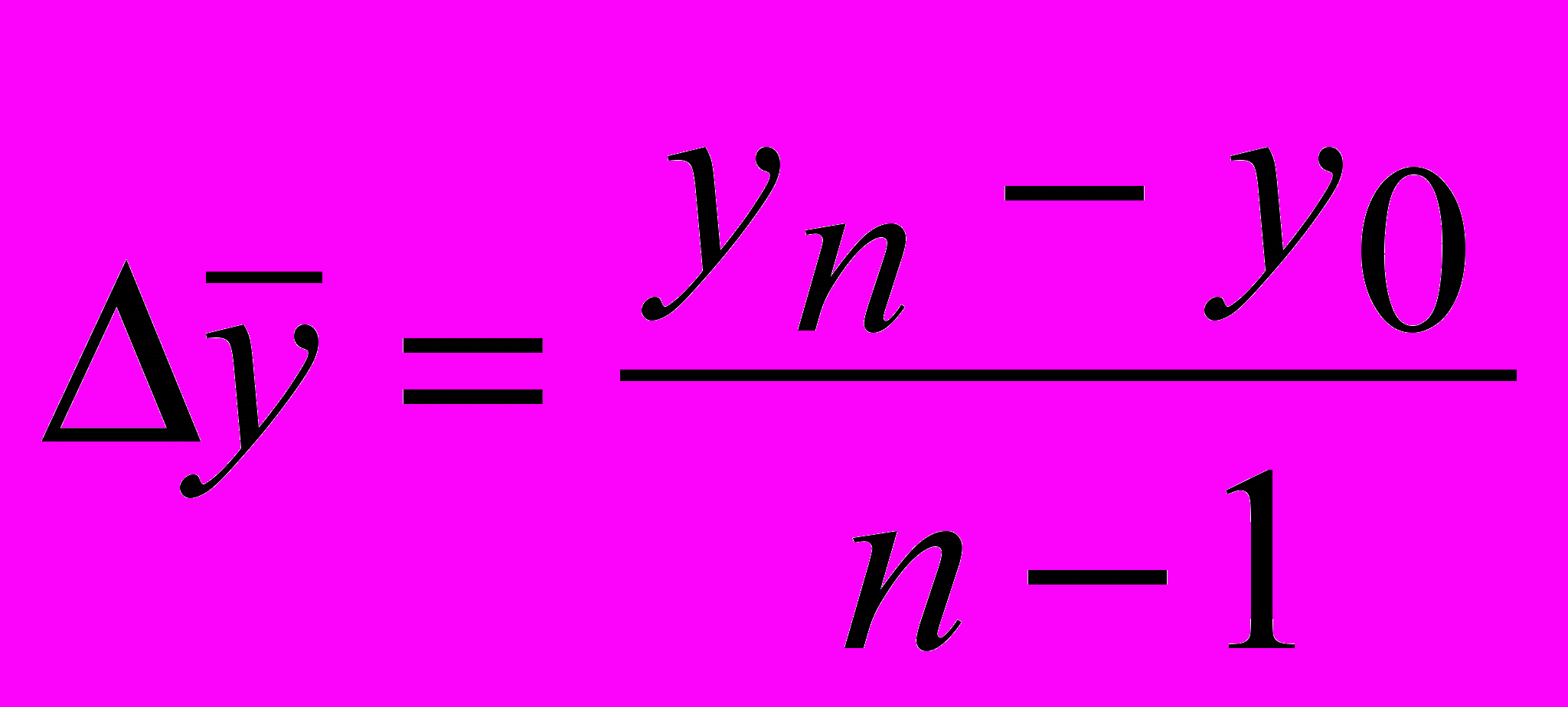 | отношение базисного прироста к числу периодов |
Представляет собой обобщенную характеристику индивидуальных абсолютных приростов ряда динамики.
- Средний темп роста – обобщенная характеристика индивидуальных темпов роста ряда динамики. Вычисляется по формуле:
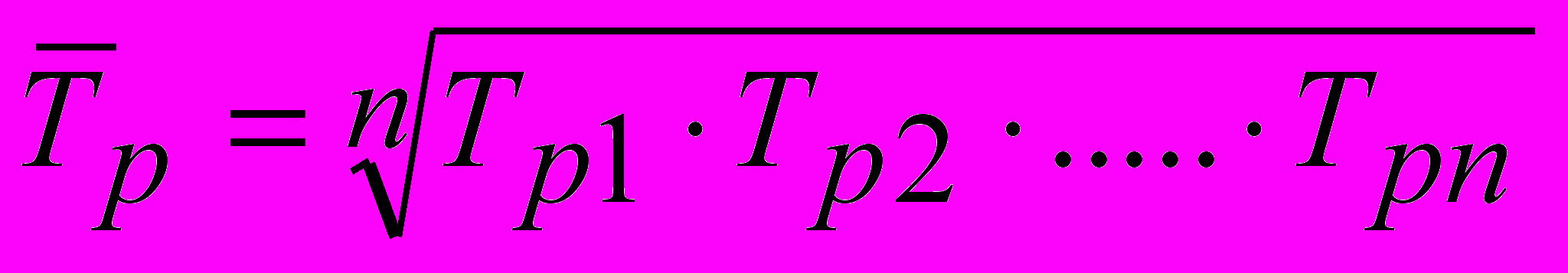,где Tp1, Tp2, Tpn – индивидуальные темпы роста (в коэффициентах) (цепные), n – число индивидуальных темпов роста.
Если средний темп роста определяется по абсолютным уровням ряда динамики, то в этом случае применяется формула
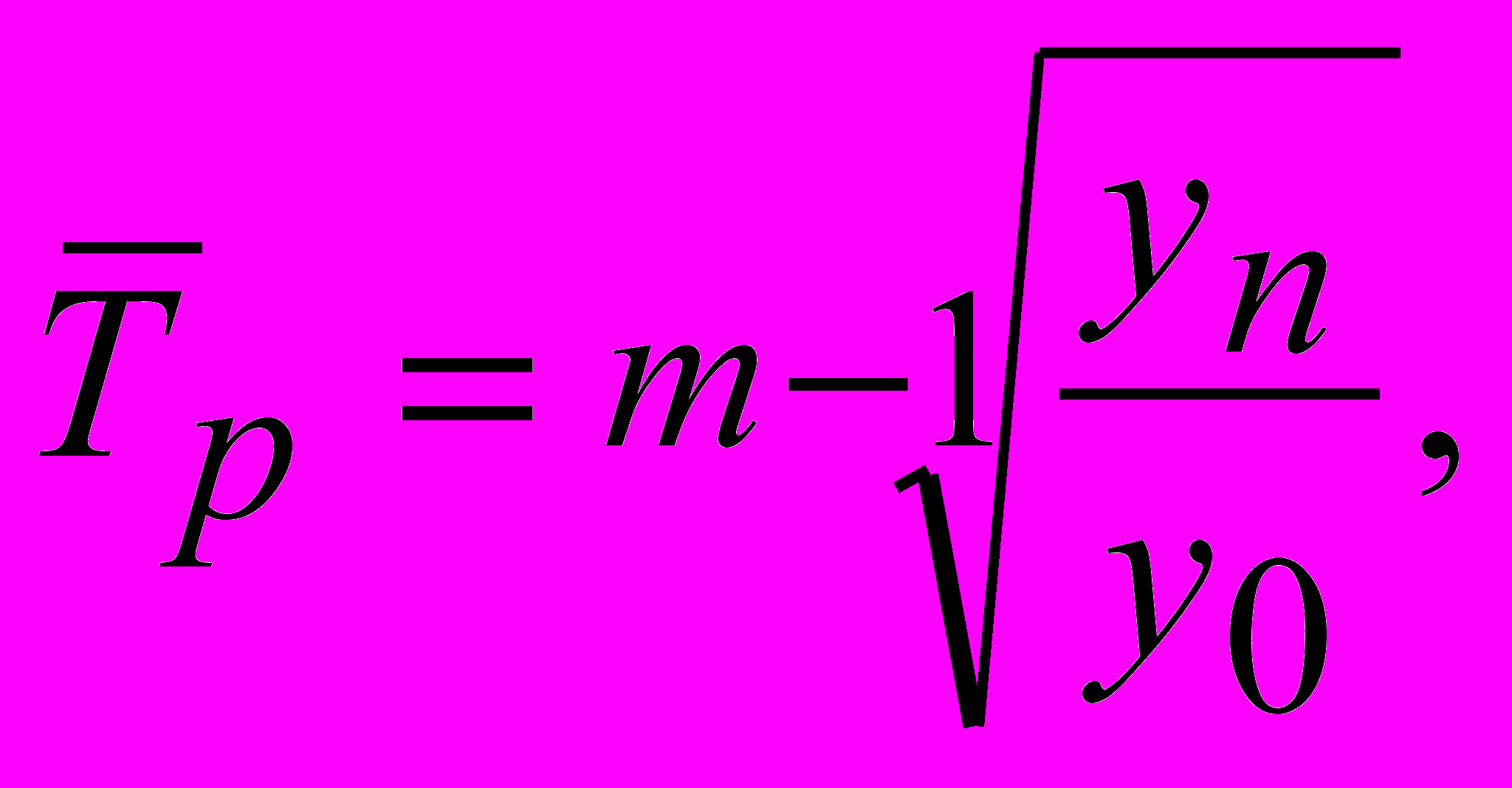
где m – число членов динамического ряда.
- Средний темп прироста
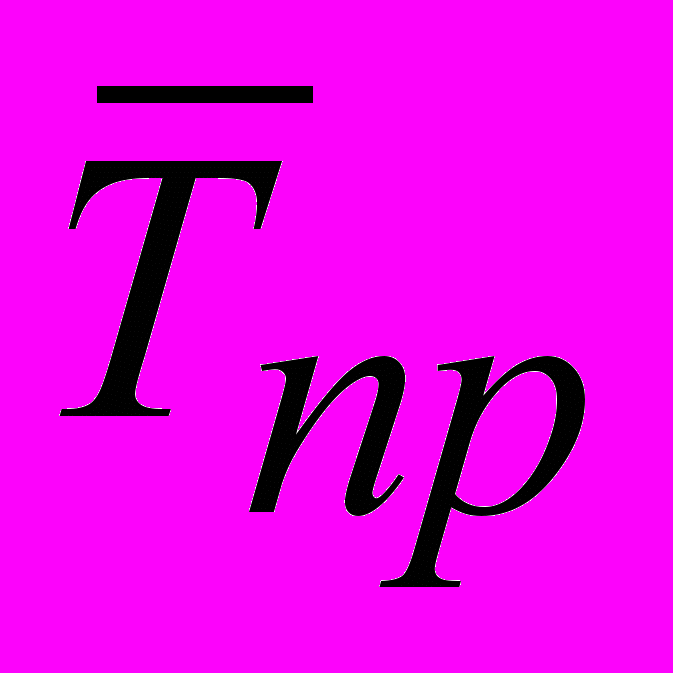можно определить на основе взаимосвязи между темпами роста и прироста:
 |
 |
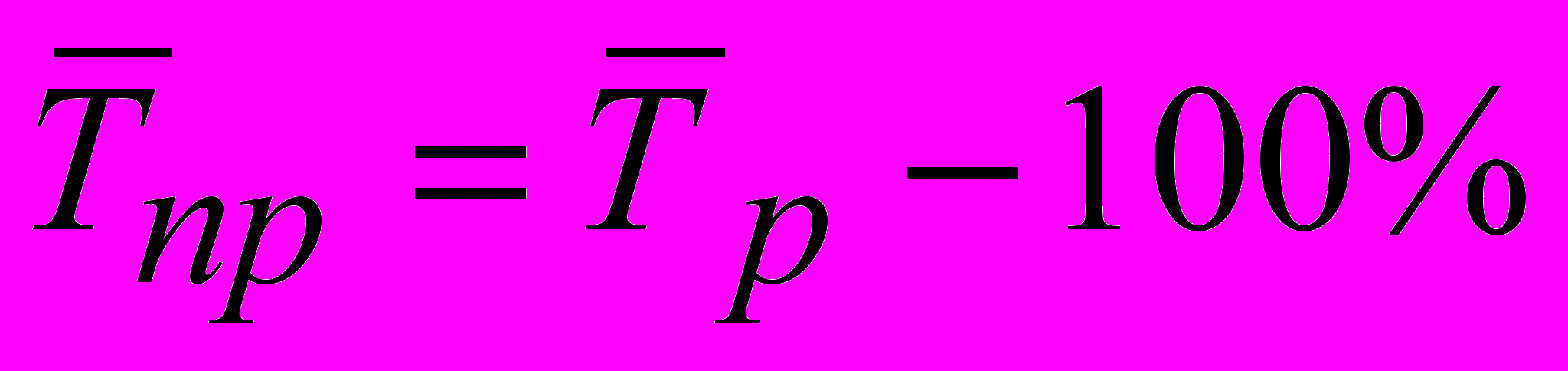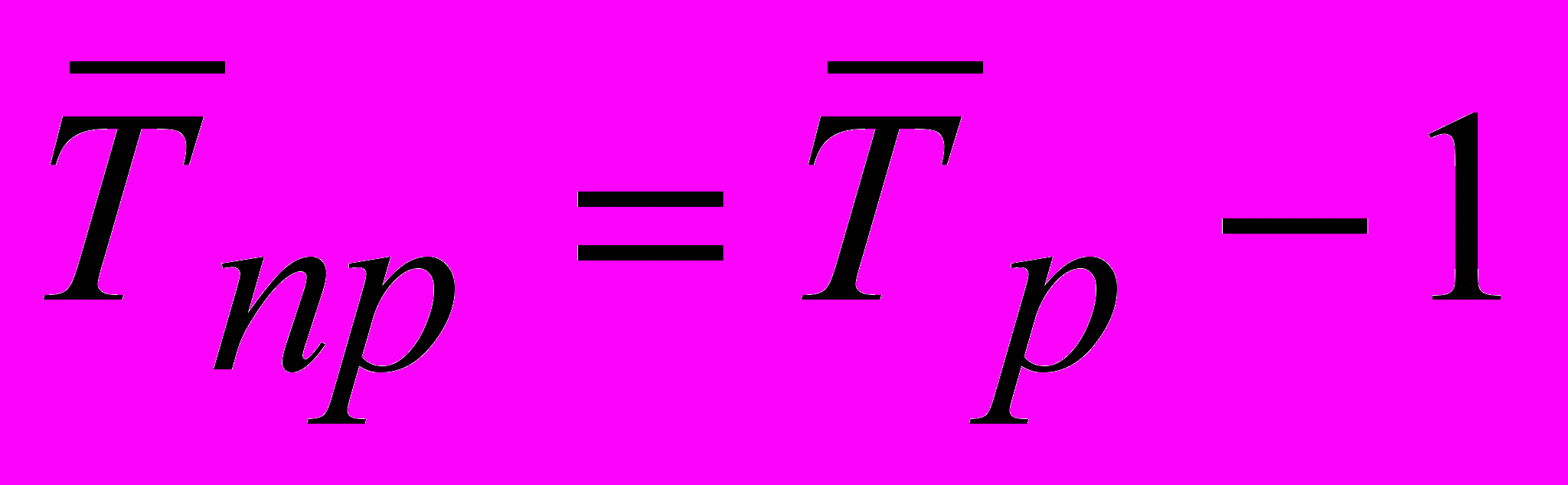8. Среднегодовое значения 1% прироста
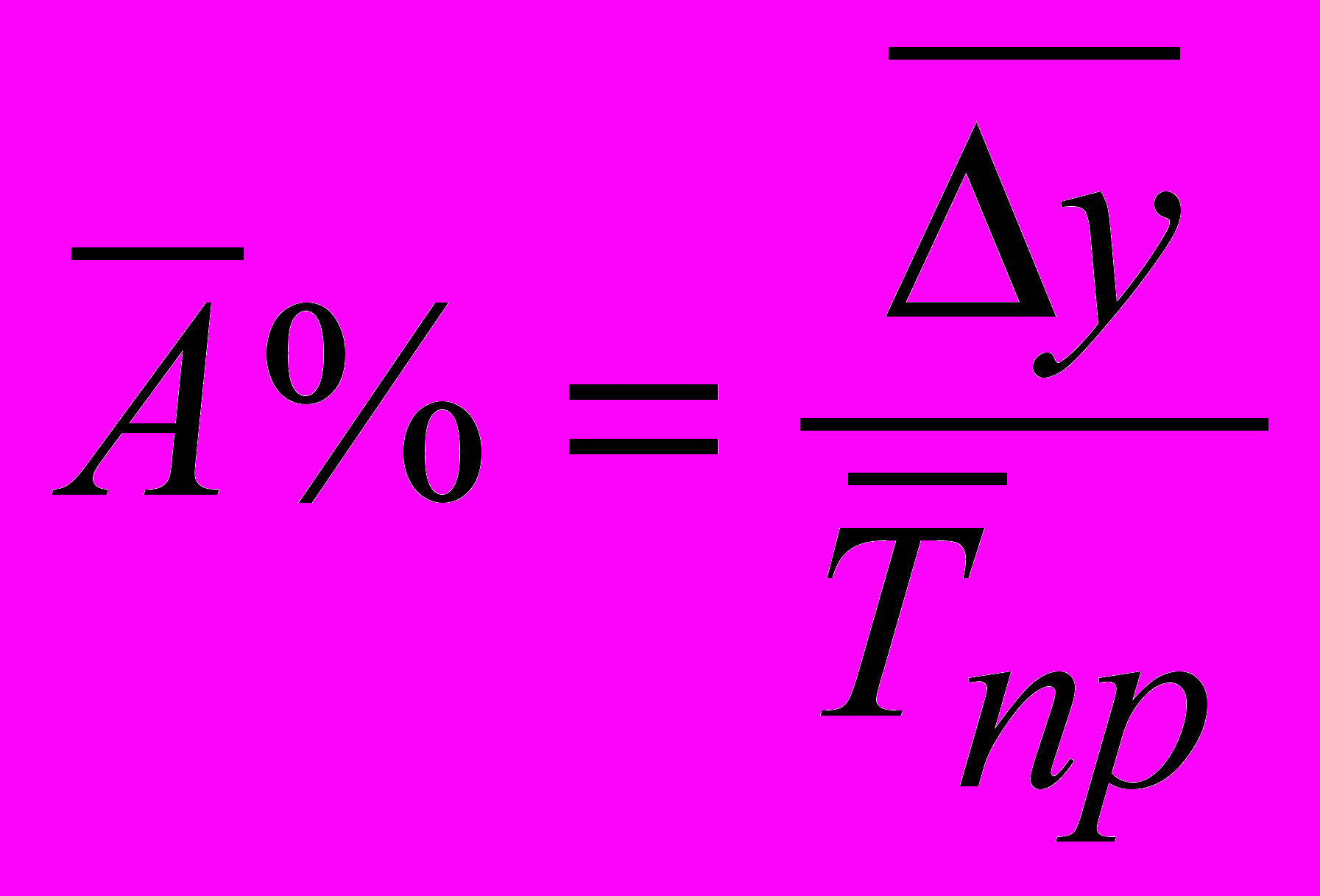
Статистика выделяет следующие виды рядов динамики:
- Падающие абсолютные приросты;
- Стабильные абсолютные приросты;
- Стабильные темпы роста;
- Увеличивающие темпы роста.
- Приемы преобразования временных рядов
Преобразование временных рядов включает в себя приемы, позволяющие сделать ряды более удобными для анализа. В частности, оно включает в себя приведение рядов к одному основанию и их смыкание.
Приведение рядов к одному основанию приходится использовать тогда, когда временные ряды имеют различия, затрудняющие их непосредственное сравнение (разные начальные периоды, разную валюту и др.). При приведении рядов к одному основанию выбирается один, общий для всех рядов, период, который принимается у них за 100%. От выбора упомянутого периода подчас зависит ответ на вопрос, какой ряд растет быстрее. Приведем в подтверждение пример.
Пример 1.
Имеются следующие данные о численности населения на территории Латвии 1959 – 2009 гг., тыс. чел.
| Население | 1959 | 1970 | 1979 | 1989 | 1990 | 1991 | 1995 | 2000 | 2003 | 2005 | 2007 | 2009 |
| Городское | 1076 | 1435 | 1664 | 1851 | 1848 | 1842 | 1721 | 1618 | 1580 | 1567 | 1550 | 1532 |
| Сельское | 1004 | 917 | 839 | 815 | 821 | 816 | 780 | 760 | 751 | 739 | 731 | 729 |
Если возьмем за базу 1959, то получим таблицу, по которой увидим рост численности городского населения и убыли населения в сельских районах.
Динамика численности населения на территории Латвии 1959 – 2009 гг., в процентах
| Население | 1959 | 1970 | 1979 | 1989 | 1990 | 1991 | 1995 | 2000 | 2003 | 2005 | 2007 | 2009 |
| Городское | 100 | 133,3 | 154,6 | 172,0 | 171,7 | 171,1 | 159,9 | 150,4 | 146,8 | 145,6 | 144,1 | 142,4 |
| Сельское | 100 | 91,2 | 83,5 | 81,2 | 81,8 | 81,2 | 77,7 | 75,7 | 74,8 | 73,6 | 72,8 | 72,6 |
Картина получится иной, если за базу взять 1989 г.. Уменьшается как городское, так и сельское население, но более быстрыми темпами городское.
Динамика численности населения на территории Латвии в процентах к 1989 г.
| Население | 1989 | 1990 | 1991 | 1995 | 2000 | 2003 | 2005 | 2007 | 2009 |
| Городское | 100 | 99,8 | 99,5 | 92,9 | 87,4 | 85,4 | 84,7 | 83,7 | 82,8 |
| Сельское | 100 | 100,7 | 100,1 | 95,7 | 93,3 | 92,1 | 90,7 | 89,7 | 89,4 |
Твердого правила для выбора общего основания сравниваемых рядов нет. Это позволяет недобросовестным исследователям манипулировать данными.
Смыкание временных рядов используются тогда, когда надо создать один длинный, сквозной ряд из нескольких коротких рядов, отличающихся либо методологией расчета показателей, либо границами территории, либо ценами, что не позволяет их соединить вместе без всяких пересчетов. Смыкание рядов может быть осуществлено только в том случае, если ряды имеют хотя бы один общий период.
Пример 2.
По одному из районов имеются данные о численности населения с 1970 г. По 1990 г. в старых границах, а с 1990 г. по 2000 г. – в новых. Эти данные приведены ниже:
Численность населения района на начало года, тыс. чел.
| Население | 1970 | 1985 | 1990 | 1995 | 2000 |
| В старых границах | 200 | 230 | 240 | - | - |
| В новых границах | - | - | 300 | 330 | 340 |
Поскольку у двух рядов имеется один общий год, то их смыкание возможно. По данным этого общего года исчисляем коэффициент пересчета данных из старых границ в новые:
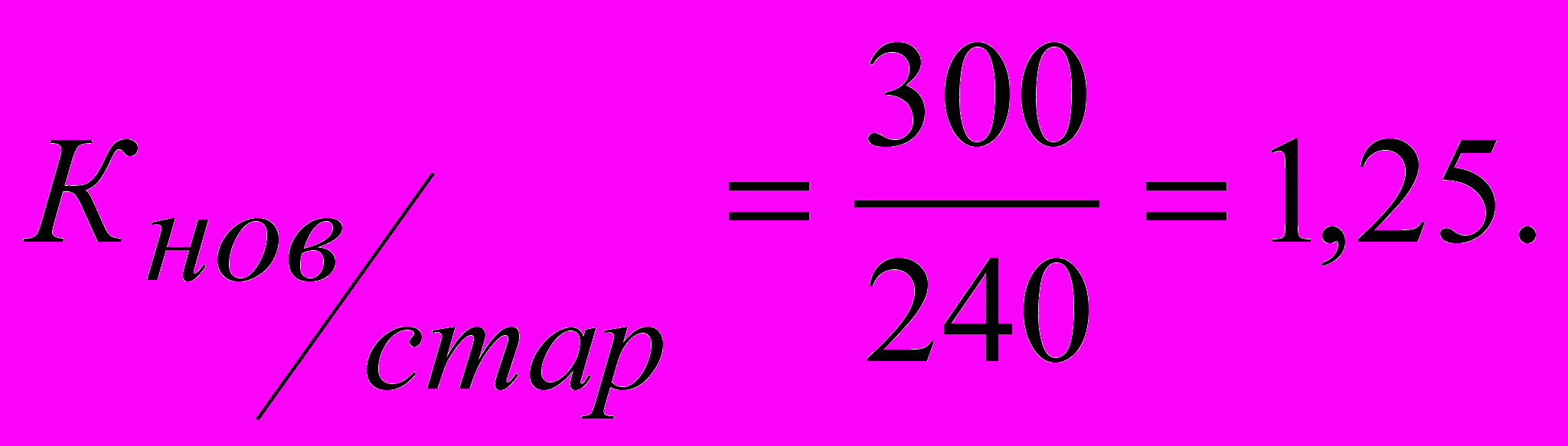
С помощью этого коэффициента делаем пересчет численности населения:
для 1970 г. 200·1,25 = 250;
для 1985 г. 230·1,25 = 287,5
Можно сделать и обратный пересчет – из новых границ в старые:
для 1995 г. 330:1.25 = 264;
для 2000 г. 340:1,25 = 272.
В результате этих пересчетов получим таблицу.
Численность населения района на начало года, тыс. чел.
| Население | 1970 | 1985 | 1990 | 1995 | 2000 |
| В старых границах | 200 | 230 | 240 | 264 | 272 |
| В новых границах | 250 | 287,5 | 300 | 330 | 340 |