Направление 2 Разработка, исследование и совершенствование методов расчета конструкций и сооружений
| Вид материала | Исследование |
- Задачи конференции: обсуждение аналитических методов расчета зданий, сооружений, 31.66kb.
- Iii международный симпозиум актуальные проблемы компьютерного моделирования конструкций, 77.34kb.
- Актуальные проблемы компьютерного моделирования конструкций и сооружений, 53.18kb.
- Аннотация Дисциплины «Программные комплексы расчёта конструкций на эвм», 14.73kb.
- Заярный Виктор Вильевич разработка и исследование, 473.46kb.
- Удк 504. 056: 574 разработка и исследование методов технического мониторинга химически, 331.8kb.
- Совершенствование методов и технических средств тепловой диагностики ограждающих конструкций, 233.66kb.
- Иванов Петр Алексеевич ввт-406 тудент группа т исследование, 71.44kb.
- Моделирование и разработка методов расчета процессов теплопередачи в кристаллизаторе, 251.19kb.
- Свод правил по проектированию и строительству сп 13-102-2003 "Правила обследования, 1033.77kb.
ВТОРОЕ ЗАСЕДАНИЕ
12 апреля, 9.30.00, ауд. 4–209
1. Н.М. Якупов, Р.Р. Гиниятуллин, С.Н. Якупов. (Институт механики и машиностроения КазНЦ РАН). Влияние характера деформирования поверхности элементов конструкций на коррозионный износ.
Из электрохимической теории коррозионного износа известно, что на поверхности металла, находящегося в агрессивной среде, образуется тонкая пленка – защитная пленка, разрушение которой приводит к интенсивному коррозионному износу. Среди факторов, способствующих разрушению защитной пленки, можно отметить наличие деформации. Для ответа на вопрос, «Какие деформации как влияют на состояние защитной пленки?» рассмотрены три цикла исследований. Для анализа используется экспериментально-теоретический метод. В первом цикле исследований растягивающие и сжимающие деформации на поверхностях образцов создавались приложением магнитного поля. Во втором и третьем циклах исследований, для исключения влияния магнитного поля на сам процесс коррозионного износа, растягивающие и сжимающие деформации на поверхностях создавались путем механического изгибания исследуемых металлических образцов путем стягивания через уголки противоположных кромок. Стягивание производилось в пределах упругих деформаций. Анализ полученных результатов показывает, что коррозионный износ на растянутых поверхностях идет быстрее, чем на сжатых поверхностях.
2. Н.М. Якупов, Х.Г. Киямов. Новый вариант конструктивно-силовой схемы крупногабаритного отстойника.
Одним из важных составных элементов очистных сооружений являются отстойники, которые представляют собой круговые бассейны диаметром сорок метров, в центральной части которых имеются агрегаты, обеспечивающие движение радиальной щетки по кругу. С ужесточением экологических норм и под давлением общественности возникла проблема снижения вредных газообразных выбросов в атмосферу. При этом форма конструкции должна обеспечивать отсос газов из воздушного пространства бассейна. Ранее были рассмотрены некоторые возможные конструктивно-силовые схемы покрытия отстойника (см. например, Якупов Н.М. Механика: проблема – идея – практика. Казан. гос. ун-т, 2010. 161 с.). Каждая из этих схем имела преимущества и недостатки. В данной работе представлена новая схема покрытия отстойника, состоящая из трех слоев: двух гладких сферических оболочек, между которыми располагается гофрированная оболочка. Такая схема: значительно увеличивает жесткость и несущую способность всей конструкции; увеличивает число продувочных каналов, обеспечивая вынос влажной среды (конденсата) от металлических поверхностей и охлаждение поверхности, что позволяет существенно снизить коррозионную активность. Для расчета напряженно-деформированного состояния используется сплайновый вариант метода конечных элементов.
3. Н.М. Якупов, А.А. Абдюшев (ИММ КазНЦ РАН). Численное исследование панели с трещиной с системой накладок.
В патентах на изобретения №2310797 и №2380585 описан эффективный способ и крепежный элемент для «лечения» дефектов в виде трещин (щелей). Методом конечных элементов проведены численные исследования влияния активных и пассивных «лечащих» накладок на напряженно - деформированное состояние панели с дефектом (см., например, статьи: Абдюшев А.А., Якупов Н.М. Исследование влияния активных и пассивных лечащих накладок на напряженно-деформированное состояние панели с трещиной // Вестник КГТУ им. А.Н.Туполева. №4, 2010. С.5-9; Якупов Н.М., Абдюшев А.А., Якупов С.Н. Механика дефектных панелей с активными и пассивными накладками // Пленки и покрытия - 2011: Тр.10 Межд. конф. СПб: Изд-во Политехн. ун-а, 2011. С.96-99). Отмечена эффективность использования активных «лечащих» накладок, а также возможность рационального размещения таких накладок. Идея этих работ развита для случая лечения дефекта в виде трещины путем использования группы накладок. Выполнены численные эксперименты, проверяющие влияния величин заданных деформаций в группе одинаковых накладок на центральной трещине. Рассмотрен линейный закон распределения деформации по накладкам с целью определения наиболее рационального закона распределения заданных деформаций. Результаты представлены в виде графиков, также из полученных результатов составлен фильм.
4 . Н.М. Якупов, Р.Н. Якупова (ИММ КазНЦ РАН). Экспериментальный способ параметризации трехмерных тел сложной геометрии.
Задача параметризации сложной области на единичный куб или прямоугольный параллелепипед – самостоятельная сложная задача. В патенте РФ на изобретение №2374697 изложен способ параметризации сложной двумерной пространственно искривленной области параметрами единичного квадрата. По аналогии идея работы развита для трехмерных областей. Разработан подход параметризации, включающий изготовление пространственного каркаса с двенадцатью ребрами из криволинейных формообразующих элементов. Контурный каркас с сетью фиксируют относительно опорных плоскостей и замеряют координаты узловых точек деформированной (преобразованной) сети в трехмерной системе координат относительно опорных плоскостей оснований. Исходно кубическую или прямоугольную трехмерную сеть из эластичного материала в виде параметрического куба или параметрического параллелепипеда с назначенным типом разбивки на ячейки в виде параллелепипедов натягивают на контуры каркаса. Замеряют координаты узловых точек и данные представляются в виде таблиц. Далее выполняют обработку полученных результатов с определением компонент метрики рассматриваемой области.
5. Н.М. Якупов, Л.У. Султанов (ИММ КазНЦ РАН). К определению напряжений в сферических оболочках с дефектами трехмерными конечными элементами.
Оболочки, сочетающие в себе легкость с высокой прочностью, находят широкое применение в строительстве и машиностроении. Это – покрытия зданий и сооружений, корпуса летательных аппаратов и судов, резервуары и трубопроводы, подводные аппараты и корпуса автомобилей и т.д. В процессе эксплуатации на поверхностях оболочек могут появиться различные дефекты. Для относительно достоверной оценки уровня напряжений в таких областях необходимо использовать трехмерные конечные элементы. В двумерной постановке в принципе невозможно оценить уровень концентрации напряжений по толщине. В работе рассматриваются сферические оболочки с локальными утонениями. Для оценки напряженно-деформированного состояния таких оболочек используются конечные элементы на базе 8-узловой трехмерной изопараметрической аппроксимации. Рассмотрены сферические оболочки с дефектами канонической геометрии. Выполнен анализ напряженно-деформированного состояния, в том числе, в дефектной области.
6. А.Р.Нургалиев (ИММ КазНЦ РАН), Н.М. Якупов. Анализ напряженно-деформированного состояния конструкции градирни с учетом коррозионного износа и рекомендации по их усилению.
Отмечаются результаты обследования состояния строительных конструкций крупногабаритной градирни СК-1200. Отмечены наиболее критические изношенные области сооружения. На базе сплайнового варианта МКЭ выполнен анализ напряженно - деформированного состояния ее металлической части с учетом изменения механических характеристик в области коррозионных дефектов. Для оценки модуля упругости, подверженных коррозионному износу, используется экспериментально-теоретический метод (патент №2296976). Максимальный коррозионный износ наблюдается в областях максимальных напряжений. Дано объяснение влияния деформации на ускорение коррозионного процесса вследствие разрушения пассивирующего слоя. Для предотвращения разрушения градирни разработана опорная система для усиления стоек (патент №2196209). Для предотвращения разрушения области опоры конфузора на железобетонную часть разработаны устройства, которые имеют консоли (патенты №№2239033 и 2326218). Для усиления цилиндрической железобетонной части рекомендована схема усиления по патенту №2343256, а для области горловины металлической части – схема по патенту №2186182. Разработки предотвращают аварийное разрушение, повышают сейсмостойкость и устойчивость сооружений и обеспечивают безопасность эксплуатации.
7. З.Р.Низамиев (гр. 1СМ101, н. рук. Н.М. Якупов). Исследования изменения механических характеристик кровли при контакте с водой или воздействия солнечного излучения.
Кровля является одним из ответственных элементов строительных конструкций: крупных жилых, производственных и общественных зданий. В последнее время все большее распространение получают так называемые мембранные кровли, в частности, мембраны поливинилхлоридные (ПВХ), мембраны ТПО, мембраны на основе синтетического каучука (ЭПДМ). К мембранным кровлям предъявляются высокие требования к надежности и сроку службы. В связи с этим представляет интерес исследования по изучению влияния сред и полей на механические характеристики мембранной кровли.
В данной работе рассмотрена мембранная кровля «Техноэласт СОЛО РП1 ЭКЭ». Были проведены два цикла исследований влияния на механические характеристики мембранной кровли: 1) длительность контакта с водой; 2) длительность воздействия солнечного излучения. Были подготовлены образцы диаметром 120 мм. Подготовленные образцы выдерживались в воде в течение 2, 4, 6 и 8 недель соответственно. Во 2-ом цикле исследований подвергались воздействию солнечного излучения также в течение 2, 4, 6 и 8 недель. Затем для оценки влияния того или иного фактора образцы исследовались экспериментально-теоретическим методом, разработанным в лаборатории НМО ИММ КазНЦ РАН. Результаты обработки представлены в виде графиков.
8. И.А. Ситдиков (гр. 1СМ102, н. рук. Н.М. Якупов). Исследование распределения напряженно-деформированного состояния для балки-стенки в области заделки.
В строительной механике при рассмотрении конкретной конструкции выбирают схемы расчета: одномерные, двумерные и трехмерные. При расчете стержневых конструкций (рамы, фермы, стержневые и балочные системы, арочные системы) обычно используются одномерные схемы. Для определения внутренних усилий в стержнях составляются уравнения равновесия участка стержня и получают систему уравнений с неизвестными внутренними усилиями. При этом предполагается простейший закон изменения напряжений по сечению. Такие предположения относительно неплохо отражают распределение внутренних усилий вдали от: заделок, от точек приложения сосредоточенных нагрузок и областей со скачкообразным изменением жесткостей. Однако для отмеченных выше особых областей для уточнения решения необходимо увеличить мерность схемы, то есть перейти к двумерной или к трехмерной схеме расчета. В данной работе на примере балки - стенки иллюстрируется этот эффект. Рассматривается конечно - элементная разбивка балки - стенки в области заделки и анализируется распределение напряжений в различных сечениях от заделки.
9. Р.Р. Рамазанов (гр. 1СМ101, н. рук. Н.М. Якупов). Исторические аспекты и некоторые проблемы сооружения высотных зданий.
В строительном деле пройден путь от примитивных глиняных домов до высотных жилых комплексов, от каменных менгиров до ажурных телебашен, покоривших пятисотметровую высоту. Каждая эпоха оставляла после себя различные уникальные сооружения: пирамида Хеопса (147 м), дагоба Абхаягиры (150 м), Александрийский маяк (120 м), Вавилонская башня и т.д. Развитие мореходства потребовало строительство различных маяков, потребность в передаче различных звуковых сигналов предупреждения, опасности, призыва к молитве и т.д. привело к необходимости сооружения колоколен и минаретов. Отмечаются падающие башни. Современные небоскребы появились в XX веке. Хотя следует вспомнить и о, возможно, первом городе небоскребов, построенном из глины несколько сот лет назад в далеких горах Южной Аравии. Историю развития небоскребов исследовали Харт Ф., Хакстебл Л., Масловская О.В. и др. Экологические и энергосберегающие аспекты рассматривали Фостер Н., Пиано Р., Табунщиков Ю.А., Шилкин Н.В. и др. Отмечаются вопросы определения ветровых воздействий испытанием макетов в аэродинамической трубе. Пример увеличения сейсмостойкости здания рассматривается на примере небоскреба Тайбэй 101 с уникальной системой амортизации. Отмечаются некоторые характеристики здания рекордсмена – Башня “Халифа” 828 м.
10. Д.Н. Яковкин (гр. 1СМ101, н. рук. Н.М. Якупов). Этапы становления строительной механики.
Строительство - одно из древнейших и важнейших занятий человечества. С началом строительного дела появились и первые понятия строительной механики. Решая проблемы сооружения строительных объектов, проблемы создания машин и механизмов, шаг за шагом механика крепла и росла. Отмечаются этапы рождения и развития строительной науки в зависимости от используемых материалов, конструктивных элементов, энергии, от уровня оснащенности техникой, от применения математического аппарата и т.д. Более подробно отмечаются моменты развития строительной механики. В частности, упоминаются Л. да Винчи, Г. Галилей и Э.Мариотт (испытания балки на изгиб), Я. и И. Бернулли (уравнения равновесия гибких нитей), Р. Гук (соотношение между силой и деформацией), Л. Эйлер (теории упругих кривых, вариационное исчисление), Ш. Кулон (растяжение и кручение стержней), Т. Юнг (связь продольных и поперечных деформаций), Ж. Лагранж (аналитическая механика, понятия: обобщенные силы и координаты), О. Коши (в теорию упругости введено понятие напряжения), С. Пуассон (уравнение поперечного прогиба пластинки), Л. Навье (изгиб пластинок, основные уравнения теории упругости, метод решения статически неопределимых задач) и др. Отмечаются основоположники нелинейной теории оболочек (Х. Муштари, К. Галимов).
11. А.В. Торбина (гр. 1СМ106, н. рук. Н.М. Якупов). Подходы к защите зданий и сооружений в сейсмоопасных областях.
При землетрясении в очаге частицы горных пород толкают, колеблют соседние частицы, которые передают колебания еще дальше в виде волны. Характер распространения волн определяется геологическими условиями района. Точно определить величины сейсмических сил и направления их действия на сооружение не представляется возможным. Существенную роль в сохранности здания или сооружения играет состояние грунта, фундамента и прочность самой конструкции здания или сооружения. Отмечаются каноны, подтвержденные опытом многих веков. Сейсмостойкость сооружения в сейсмоопасных областях обеспечивается разработкой рациональных конструктивных схем зданий и сооружения, а также специальными конструктивными мероприятиями. Для снижения сейсмических нагрузок разрабатываются пружинные, маятниковые, резинометаллические и другие сейсмоизоляторы. Появляются также сейсмоизоляторы с использованием трения качения с использованием шаров и эллипсоидов и др. Разрабатываются перестраиваемые конструкции здания в направлении снижения сейсмической нагрузки. Больший эффект дает комбинация способов и приемов сейсмозащиты, например, для повышения сейсмостойкости разработан способ, который описан в патенте №2214491. Также для повышения сейсмостойкости предложена древообразная схема фундаментной опоры.
12. Л.М. Звонова (гр. 1СМ106, н. рук. Н.М. Якупов). Арки и арочные композиции – первые криволинейные строительные элементы.
Уже во времена Древнего Египта начали интуитивно осознавать роль криволинейных форм. Очевидно, природные арки и мосты подсказали им эту уникальную идею. Изобретение бетона в Древнем Риме способствовало широкому распространению круглых арочных структур. Примером использования арочных конструкций являются акведуки древних римлян. Симфонией арочных композиций в древнеримской эпохе можно назвать уникальное сооружение Колизей. В Исламской архитектуре в начальный период использовали полукруглые арки, впоследствии их конфигурация была видоизменена – вместо плавной, круглой кривой внутренний контур арок в вершине был заострен и их контур принял дугообразную форму. Несколько позже эта идея была использована и в Западной Европе – появились стрельчатые арки и полуарки. Наличие угла на вершине арки “рассекал” поток весовой нагрузки, исключая возникновение зоны растяжения, уменьшал боковые нагрузки и увеличивал надежность конструкции при землетрясениях, благодаря возможности возникновения шарнирного механизма в вершине арки. Методом конечных элементов анализируются напряженно-деформированные состояния арок различной конфигурации, подчеркивая естественность и необходимость пройденных этапов развития арок и арочных композиций.
Кафедра теоретической механики
| Председатель | Ф.Г. Шигабутдинов |
| Зам. председателя | А.З. Камалов |
| Секретарь | А.М. Тартыгашева |
Первое ЗАСЕДАНИЕ
5 апреля, 9.00, ауд. 4 –111
1. Ф.Г. Шигабутдинов. О реализации новых учебных планов по теоретической механике в условиях «перехода на бакалавриат».
Образовательные стандарты третьего поколения, которые будут действовать минимум пять следующих лет, определяют три главные компоненты образования: требования к результатам освоения ООП (основных образовательных программ), требования к структуре ООП и требования к условиям реализации ООП. Все эти требования надо внимательно изучить. Если два последних требования достаточно просто могут быть реализованы, то в отношении требований к результатам освоения ООП (они сформулированы в виде «компетенций») будут, видимо, разночтения. Особенно сильно сокращается время на руководство самостоятельной работой студентов на первых курсах, хотя это и не вытекает из содержания и идей, заложенных в образовательные стандарты. Это, несомненно, ставит под удар овладение, пожалуй, главными компетенциями ПК-1 и ПК-2 (направление 27800-Строительство) и углубляет разрыв между привычной для первокурсников школьной и вузовской системами образования. Нужно так организовать самостоятельную работу, чтобы на начальных этапах своей учебы в университете студент не чувствовал своей оторванности от университета. Встречаться со студентами надо не реже одного раза в неделю. Это нужно понимать и руководителям образовательных структур, и преподавателям, ведущим соответствующую дисциплину.
2. Ф.Г. Шигабутдинов, Р.З. Муртазин, Р.Ф. Мухутдинов. Выпучивание упругих ортотропных и изотропных цилиндрических оболочек со шпангоутами при продольном ударе.
Рассматривается влияние шпангоутов на картины волнообразования цилиндрических оболочек при продольных ударах абсолютно твердым телом. Геометрически нелинейные дифференциальные уравнения продольно-поперечных движений тонкой ортотропной оболочки типа Тимошенко, учитывающие сдвиг и инерцию вращения, получены из уравнений Галимова К.З. (Теория оболочек с учетом поперечного сдвига, 1977).
По длине оболочки принимается от одного до пяти шпангоутов, которые располагаются как симметрично, так и произвольно. Исследуется влияние количества и расположения на характер волнообразования, смещение максимальных прогибов и изменение их величины. Начальные условия для перемещений и деформаций приняты нулевыми. Срединная поверхность выбиралась в форме круговой цилиндрической оболочки. Граничные условия принимались в виде подвижной шарнирной опорой на торце, воспринимающем удар, и неподвижной шарнирной опорой на другом конце. Результаты решения показаны в виде двухмерных и трехмерных картин форм изгиба срединной поверхности оболочек в различные моменты времени. Получены формы поперечного волнообразования (прогибы по всей длине оболочки) для двадцати четырех пробегов продольной волны вдоль оболочек.
3. А.З. Камалов. О собственных колебаниях арочного сооружения.
В работе исследуются собственные колебания арочного сооружения, представляющего тонкое незамкнутое цилиндрическое покрытие с равномерно распределенными подкрепляющими арками и находящегося под действием ветровой нагрузки. В дальнейшем нас будет интересовать свободные колебания только арочного сооружения и здесь не ставиться задача об исследовании поведения самой среды. Поэтому будем пренебрегать потенциалом рассеянных волн, порождаемых колеблющимся упругим покрытием сооружения по сравнению с потенциалом волн для абсолютно жесткого покрытия. А уравнения движения составим для деформированного элемента конструкции, тогда внутренние усилия будут дополнительными, возникающими в оболочке при отклонении ее от начальной формы равновесия. При таких допущениях составлены уравнения собственных колебаний системы. Из условия нетривиальности решения системы уравнений, получено уравнение для определения частот свободных колебаний оболочечной конструкции в виде определителя для различного числа волн в окружном и в продольном направлениях. Получены аналитические формулы для определения спектора собственных частот данной конструкции. Рассмотрены частные задачи.
4. Т.К. Хамитов, Ф.Г. Шигабутдинов. Исследование потери устойчивости упруго-пластических стержней конечной длины при продольном ударе.
В работе приводятся результаты решения задач о потере устойчивости упругопластических идеально прямых стержней конечной длины при продольном ударе. На ударяемом торце стержня мгновенно прикладывается постоянное во времени напряжение, превышающее предел текучести материала. Учитываются эффекты, связанные с конечностью скорости распространения продольной волны вдоль элемента. Для материала стержня принимается схема с линейным упрочнением.
Для решения уравнения движения задачи применяются методы разложения искомых функций в ряды Фурье и Бубнова-Галеркина, а также для сравнения результатов приводится «точное» решение. Всего рассмотрено восемь вариантов граничных условий на концах стержня. Результаты решения задач представлены в виде зависимости «критическое напряжение – возмущенная длина» при первом прохождении продольной волны вдоль стержня. Под критическим напряжением понимается напряжение, обращающее частоту свободных колебаний стержня в ноль в момент потери устойчивости (статический критерий). Исследовано влияние неоднородности напряженного состояния по длине стержня, вызванное конечностью скоростей распространения продольных упругих и пластических волн на критические напряжения.
5. Е.Р. Газизов. Безволновое докритическое обтекание двух вихрей тяжелой жидкостью.
Рассматривается стационарное потенциальное течение слоя идеальной несжимаемой весомой жидкости. В поток помещены два вихря заданной интенсивности. Одним из параметров, которые характеризуют такие течения является число Фруда:
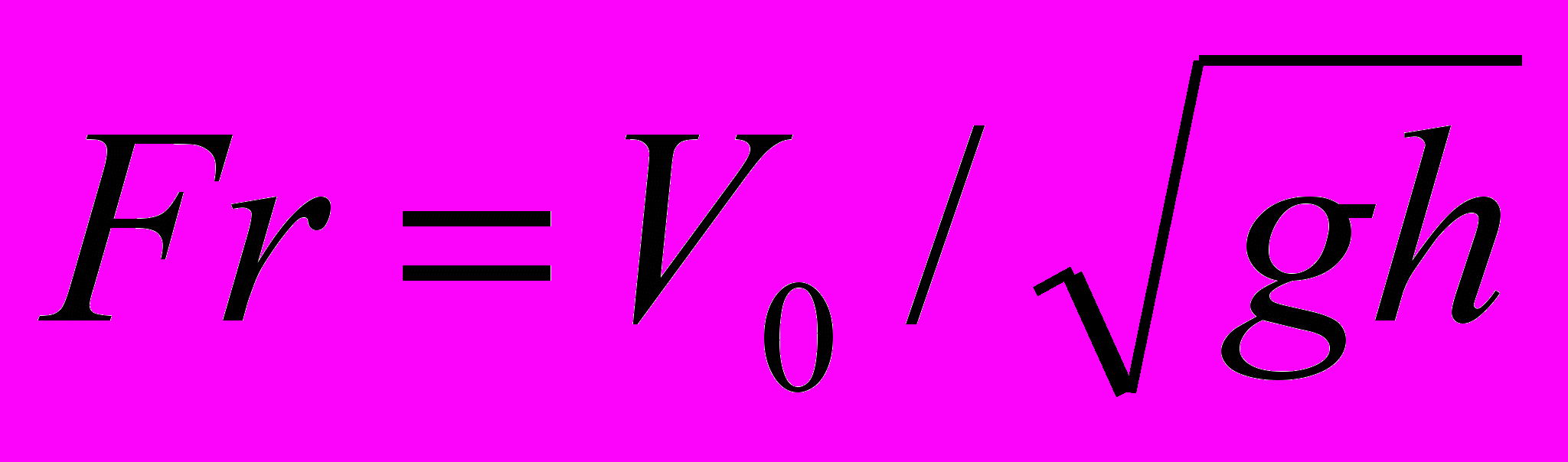, где h и v0 - ширина слоя жидкости и скорость невозмущенного потока слева на бесконечности, g - ускорение силы тяжести. Изучается случай докритического режима обтекания. При этом считается, что докритическое течение слева (
) переходит в сверхкритическое справа (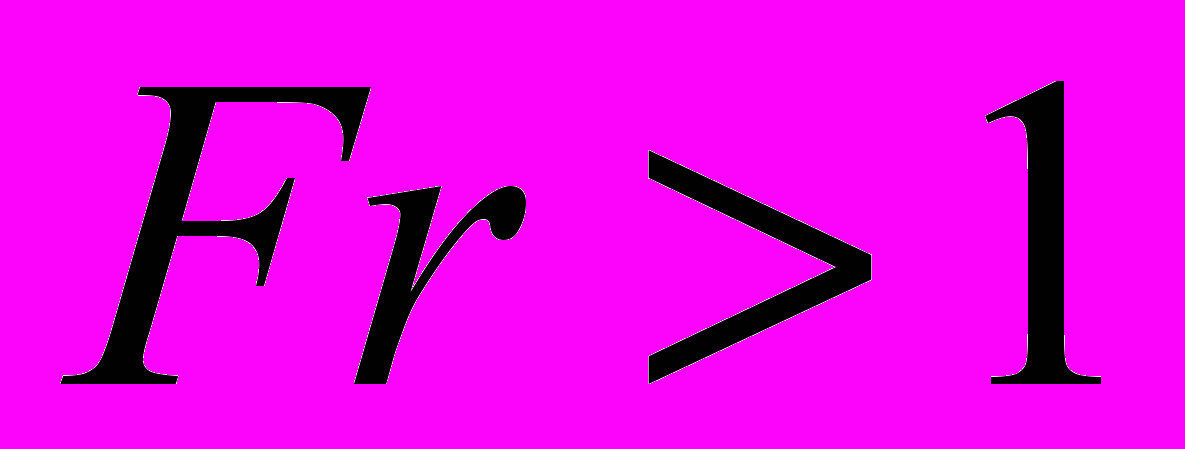
). Исходная задача сводится к краевой задаче отыскания аналитической в канонической области функции 
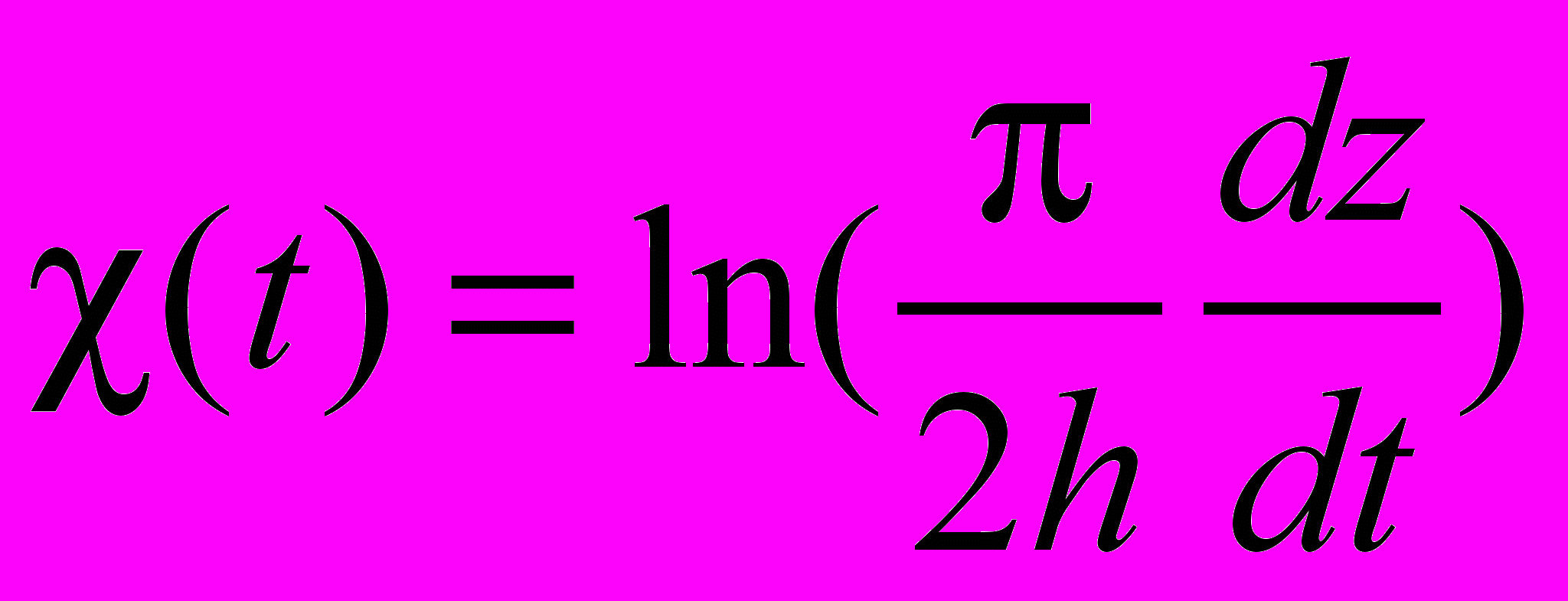. В качестве канонической области выбирается полоса ширины 2 в параметрической плоскости t. В результате решения смешанной краевой задачи в канонической области получаются условия, связывающие действительные и мнимые части функции 
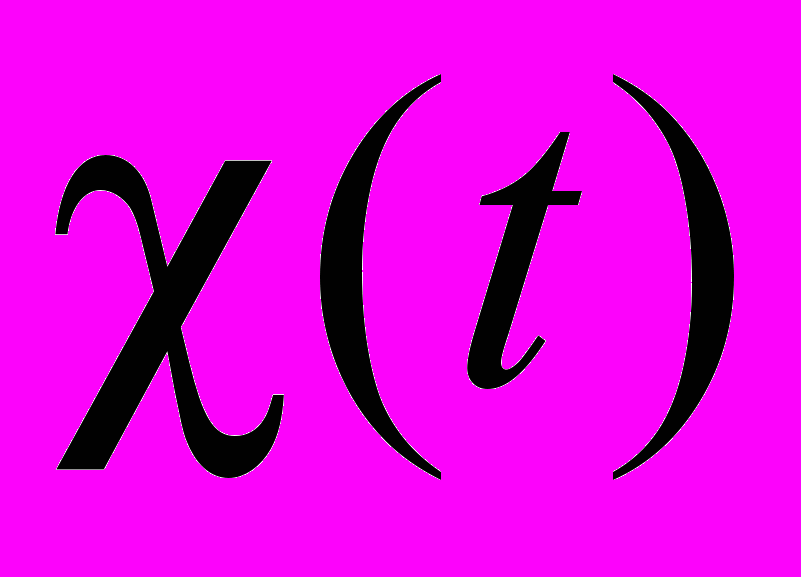на границах полосы. Слева на бесконечности Fr<1, и там могут возникнуть волны. Используя то, что на свободной поверхности давление постоянно, выводится условие отсутствия волн слева на бесконечности. Решение сводится к решению системы нелинейных интегро-дифференциальных уравнений для отыскания параметров, определяющих конформное отображение канонической области на физическую. Система уравнений решается методом Ньютона. 6. А.М. Тартыгашева, О.В. Клейдман, К.Е. Камаева. Анализ НДС нелинейной области сдвиговой трещины в трубопроводах.
Работа посвящена численному исследованию влияния сил трения между берегами сдвиговой трещины (трещины типа II) на напряженно-деформированное состояние (НДС) в ее вершине. Для обоснованного выбора варианта расчетной схемы проведен анализ типов образцов, применяемых при экспериментальном исследовании роста трещин при смешанных типах деформирования. В расчетах использованы два типа расчетных схем. Расчет выполнен в контактной постановке с учетом трения берегов трещины и физически нелинейного поведения материала в ее вершине. Проведенные численные исследования показали влияние коэффициента трения на параметры механики разрушения – коэффициент интенсивности напряжений KII и J-интеграл для двух случаев нагружения пластины с трещиной - чистым сдвигом и смешанным нагружением сдвиг-сжатие. Установлено, что в условиях чистого сдвига влияние коэффициента трения на исследуемые параметры механики разрушения незначительно. Дополнение сдвига компонентой сжатия приводит к тому, что коэффициент трения начинает оказывать значительное влияние на коэффициент интенсивности напряжений KII. Значение KII уменьшается с увеличением коэффициента трения, а также зависит от соотношения сжимающей и сдвиговой нагрузки.
7. А.В. Гумеров. Расчет движения вихря вокруг эллипса методом конформного отображения.
Рассматривается задача по определению траектории движения вихря постоянной интенсивности вокруг эллипса в идеальной несжимаемой жидкости. Пусть на плоскости z вне эллипса имеется вихрь, интенсивности Г. Комплексный потенциал течения в плоскости круга равен сумме потенциалов вихря и инверсионного вихря внутри круга радиуса R. Интегрируя комплексно-сопряженную скорость вихря, находим траекторию движения этого вихря вокруг круга. В процессе интегрирования конформным отображением по формуле Жуковского находим положение вихря в плоскости эллипса, в каждый момент времени. Траектория вихря в плоскости эллипса также определялась интегрированием скорости вихря в этой плоскости с учетом поправки Рауса. Третья траектория находилась интегрированием скорости вихря в плоскости круга с поправкой Рауса и дальнейшим отображением в плоскость z. Данная траектория оказалась не правдоподобной и была исключена из рассмотрения. Были проведены расчеты с варьированием положения вихря и формы эллипса. Согласно результатам расчетов, при положении вихря на расстоянии 3R и более от поверхности цилиндра, траектории вихрей на плоскости эллипса практически совпадают. При меньшем расстоянии траектория движения вихря полученная интегрированием в плоскости z с учетом поправки Рауса проходит несколько ближе к эллипсу.