«смещение потенциала нейтрали в четырехпроводной трехфазной электрической цепи»

Вид материала

Лабораторная работа

Содержание Узловое напряжение в цепи постоянного тока и четырехпроводной трехфазной цепи Таблица 14.3. Результаты вычислений

Подобный материал:

• Электрические цепи постоянного тока, 1039.6kb.
• Математики и программирования пояснительная записка к курсовой работе по курсу «Введение, 151.91kb.
• Экзаменационная программа Электротехника и электроника Раздел Цепи постоянного тока, 19.14kb.
• 1 Расчет линейной электрической цепи постоянного тока Задание, 93.15kb.
• Ei al republicii moldova universitatea Liberă Internaţională din Moldova, 51.82kb.
• Программа вступительных экзаменов в магистратуру по специальности 6М071800 «Электроэнергетика», 590.06kb.
• Методика ми5 проверки цепи фаза нуль в электроустановках до 1 кВ с глухим заземлением, 53.81kb.
• Задача № расчет линейной электрической цепи постоянного тока по заданной обобщенной, 87.8kb.
• Закон Ома для участка электрической цепи. Закон Ома для замкнутой цепи, 59.73kb.
• Закон Ома для участка электрической цепи. Закон Ома для замкнутой цепи, 46.75kb.

Лабораторная работа EW-14

«СМЕЩЕНИЕ ПОТЕНЦИАЛА НЕЙТРАЛИ

В ЧЕТЫРЕХПРОВОДНОЙ ТРЕХФАЗНОЙ

ЭЛЕКТРИЧЕСКОЙ ЦЕПИ»

Цель работы

Определить, используя графическое построение, смещение потенциала нейтрали в четырехпроводной трехфазной цепи; сравнить полученный результат с измеренным значением.


Краткие теоретические сведения

Особенности рассматриваемой цепи

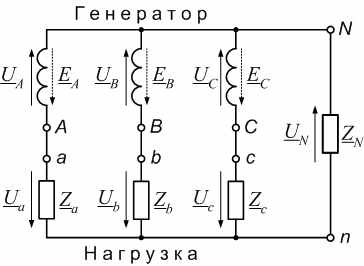
В настоящей работе исследуется трехфазная цепь с нулевым (нейтральным) проводом, обладающим сопротивлением Z_N, не равным нулю (рис. 14.1, а).

а	б
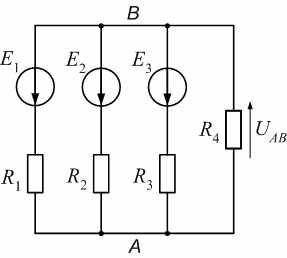
Рис. 14.1. Цепи, рассчитываемые методом узлового напряжения: а − четырехпроводная трехфазная цепь с учетом сопротивления нулевого провода; б − цепь постоянного тока с двумя узлами

Частный случай исследуемой цепи  трехфазная трехпроводная цепь при соединении однофазных приемников звездой, в которой величина Z_N стремится к бесконечности. (Этот случай рассматривался в лабораторной работе EW-13.)

В четырехпроводной цепи, при неодинаковых сопротивлениях однофазных приемников, по нулевому проводу проходит ток I_N; при этом между нейтралью сети N и нейтралью нагрузки n возникает разность потенциалов, называемая смещением потенциала нейтрали U_N (или просто смещением нейтрали). При этом справедливо следующее комплексное равенство:

U_N = I_NZ_N. (14.1)

Если сопротивлением линейных проводов можно пренебречь, то напряжения фаз нагрузки (т.е. напряжения на отдельных однофазных приемниках) равны разностям соответствующих фазных напряжений сети и смещения потенциала нейтрали:

U_a = U_A  U_N; U_b = U_B  U_N; U_c = U_C  U_N. (14.2)

Данные выражения записаны с учетом условных направлений напряжений, показанных на рис. 14.1, а. Необходимо иметь в виду, что эти разности вычисляются по правилам действий с комплексными числами. Поскольку комплексные числа изображаются на комплексной плоскости с помощью векторов, аналитический расчет можно заменить действиями с векторами.

П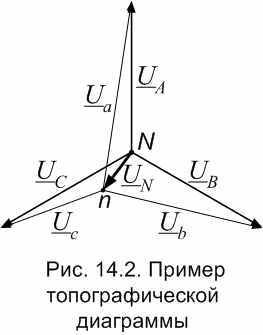ример топографической диаграммы четырехпроводной цепи с учетом сопротивления нулевого провода показан на рис. 14.2 (см. также рис. 13.4).

Если нельзя пренебречь сопротивлениями линейных проводов, то их учитывают как слагаемые сопротивлений однофазных приемников.

Смещение потенциала нейтрали можно найти методом узлового напряжения, который заимствуется из методов расчета цепей постоянного тока, поскольку известно, что уравнения, описывающие цепи постоянного тока, можно использовать при анализе цепей синусоидального тока, если при этом пользоваться комплексным представлением соответствующих величин.

Узловое напряжение в цепи постоянного тока

и четырехпроводной трехфазной цепи

Сначала выпишем выражение узлового напряжения U_AB (напряжения между узлами цепи), которое получается в результате анализа цепи постоянного тока, имеющей два узла А и В (такая цепь показана на рис. 14.1, б):

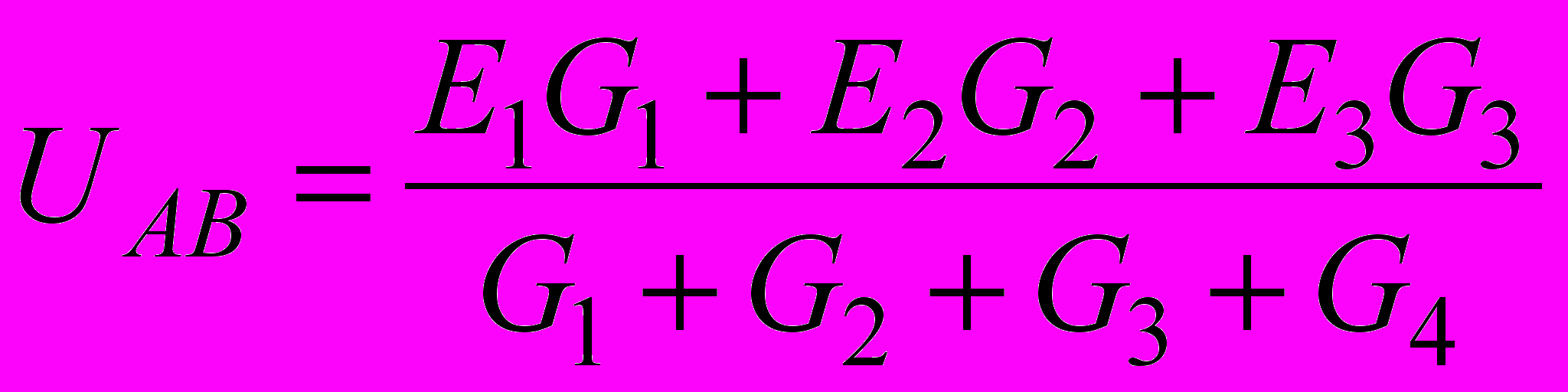, (14.3)

где Е_­1, Е_­2, Е_­3  ЭДС источников энергии; G_­1, G_­2, G_­3, G_­4  проводимости ветвей цепи:

, , , .

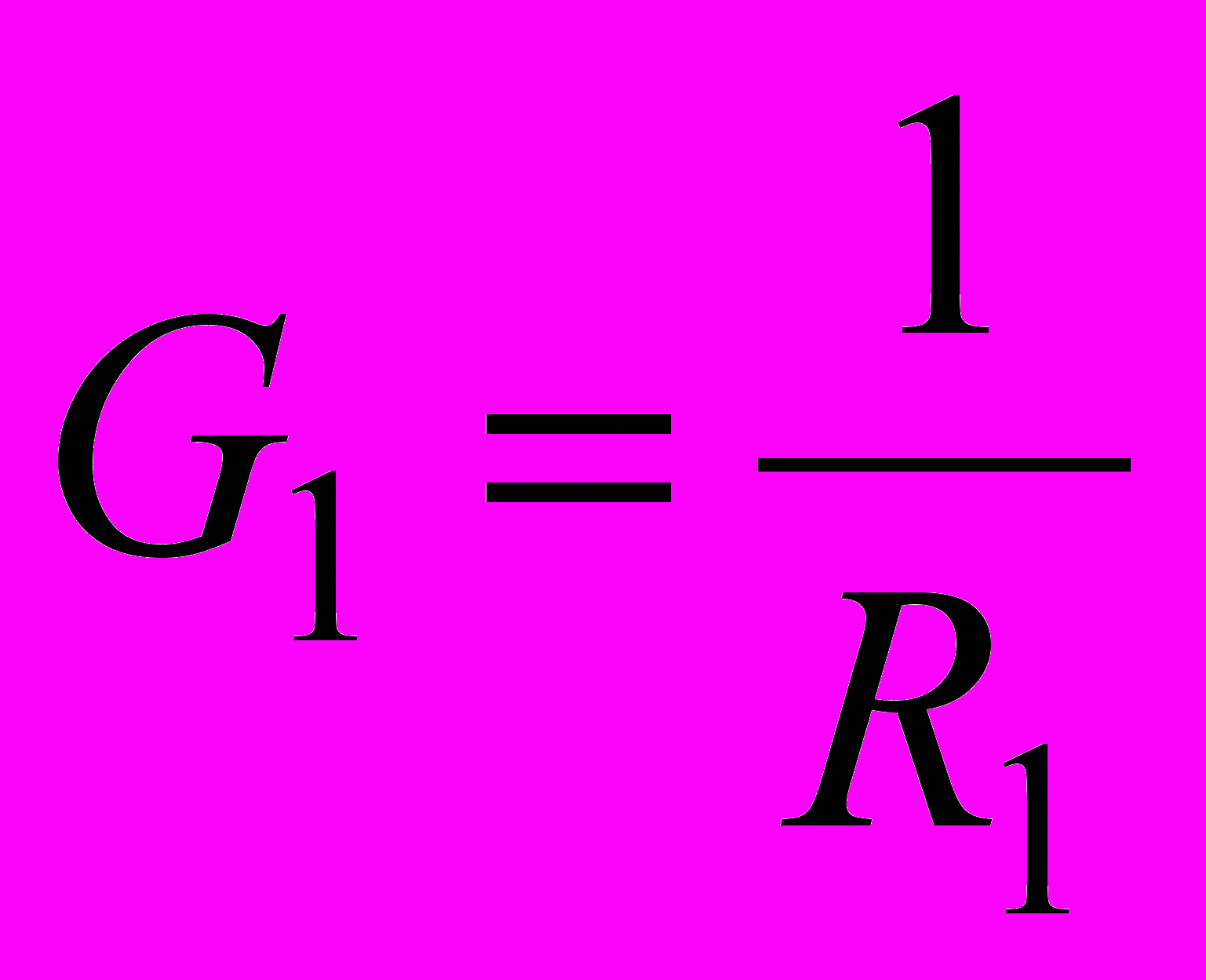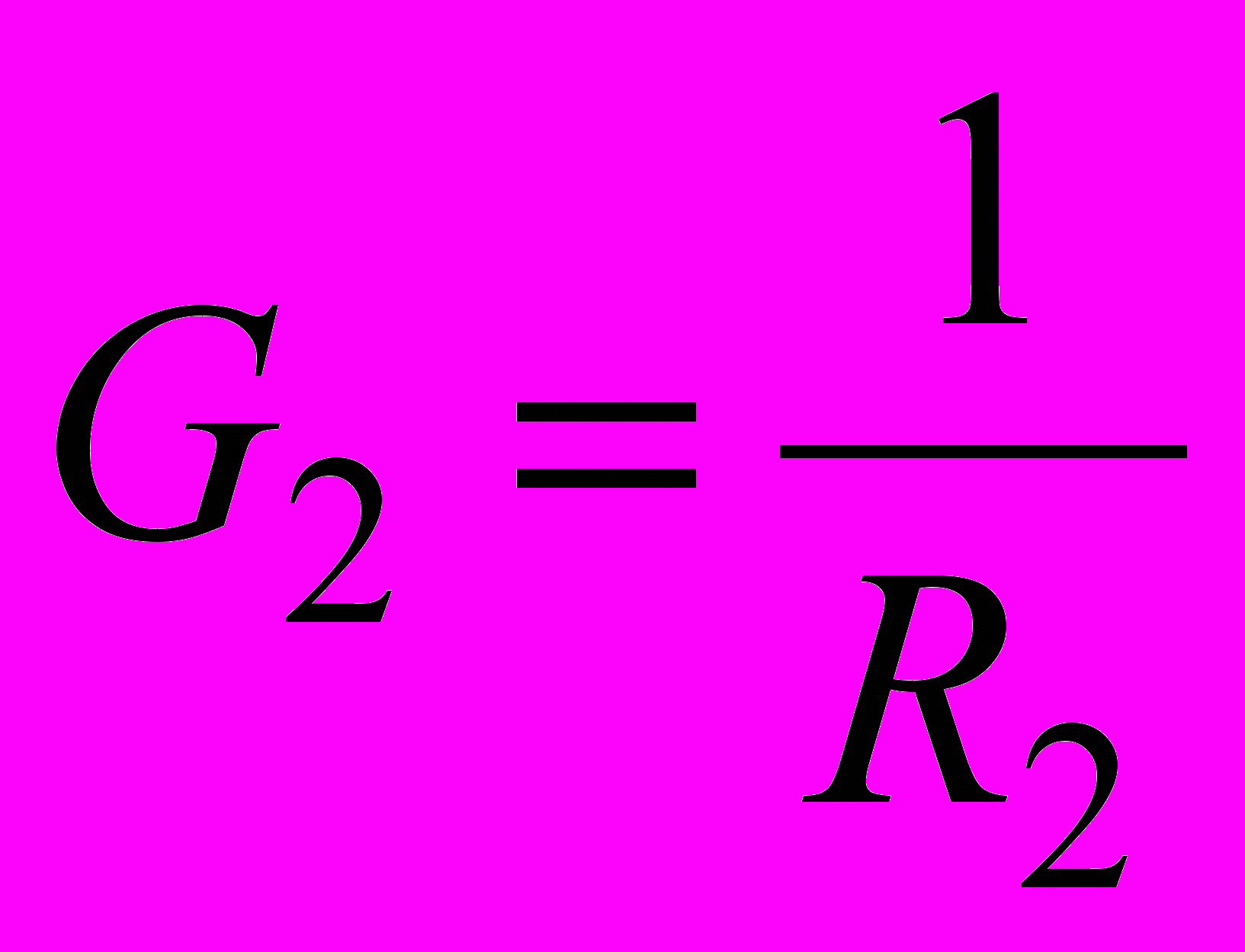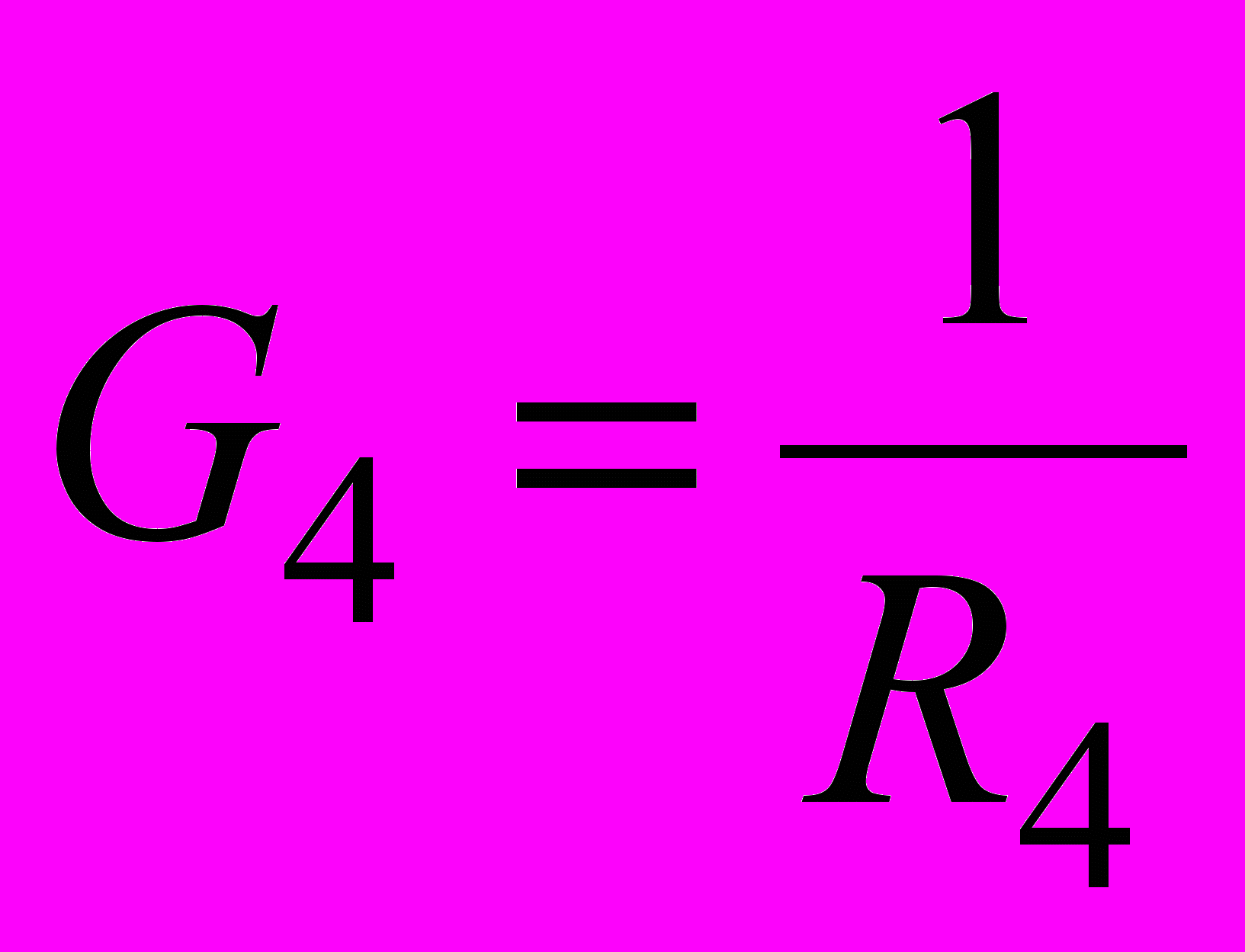Если нельзя пренебречь внутренними сопротивлениями источников, то они учитываются в значениях R_­1, R_­2, R_­3.

Для четырехпроводной трехфазной цепи (рис. 14.1, а) справедливо аналогичное выражение, записанное для комплексных величин (используем аналогию двух схем):

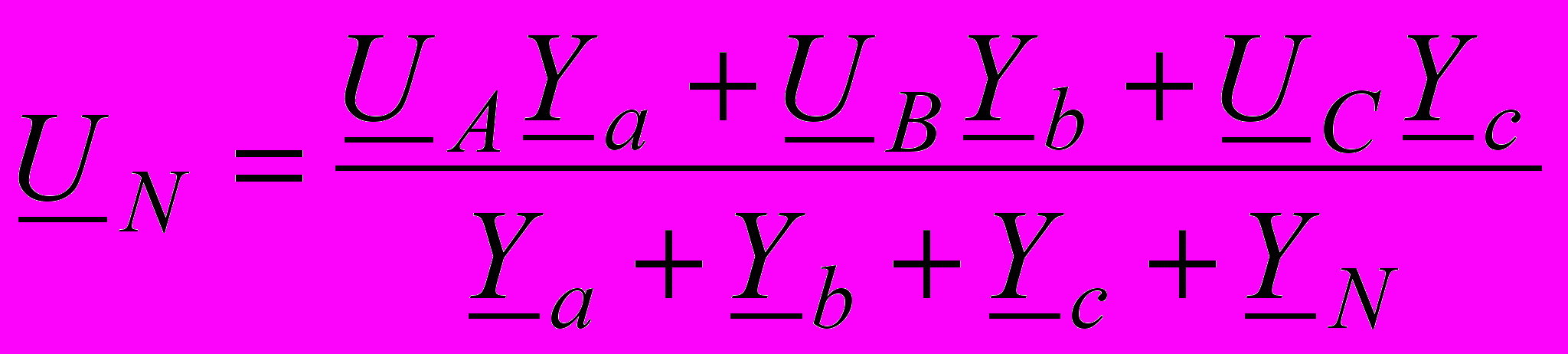, (14.4)

где U­_N  смещение потенциала нейтрали;

U_A, U_B, U_C  фазные напряжения сети (эти напряжения равны соответствующим ЭДС, если внутренние сопротивления фаз сети пренебрежимо малы);

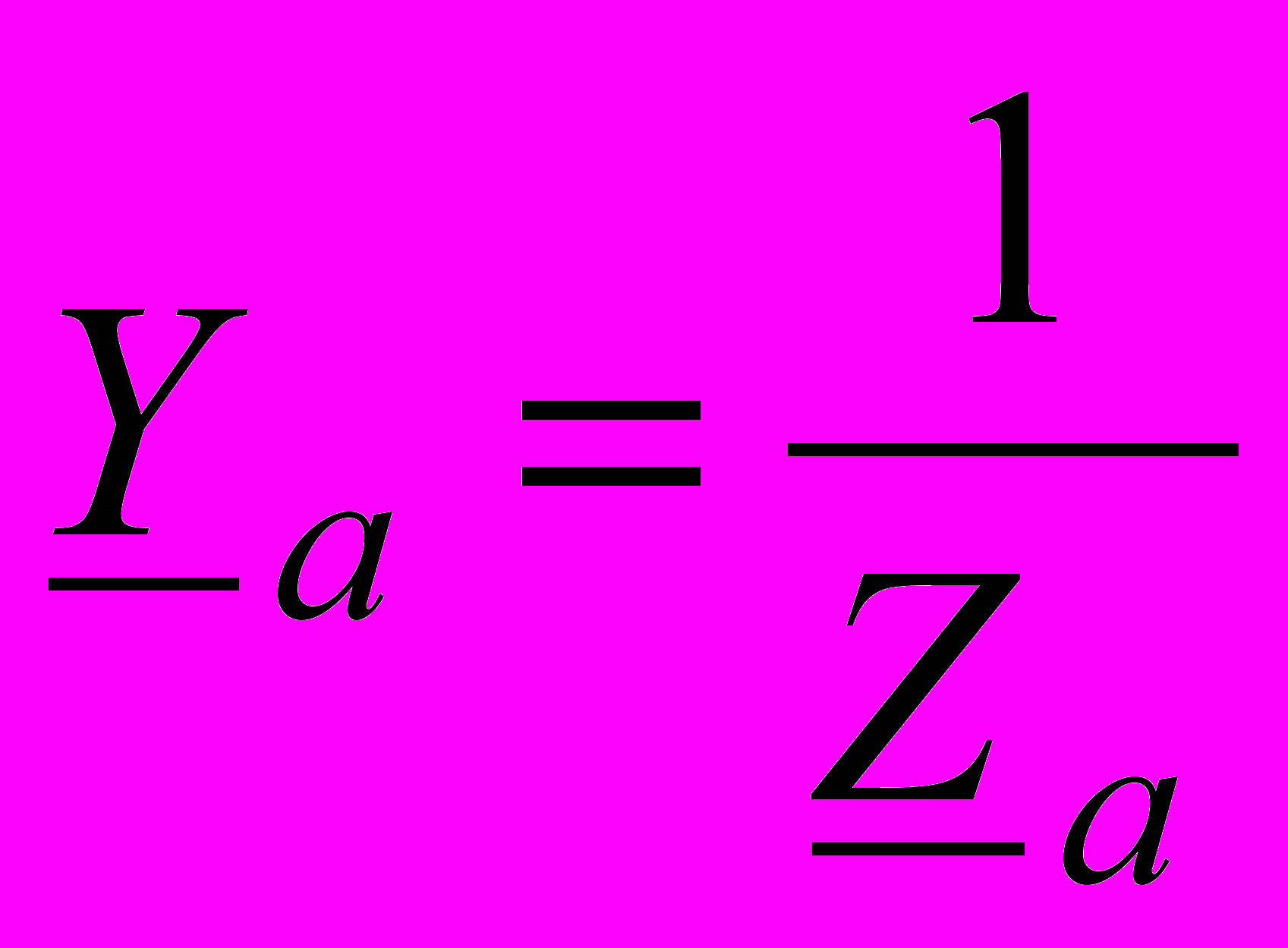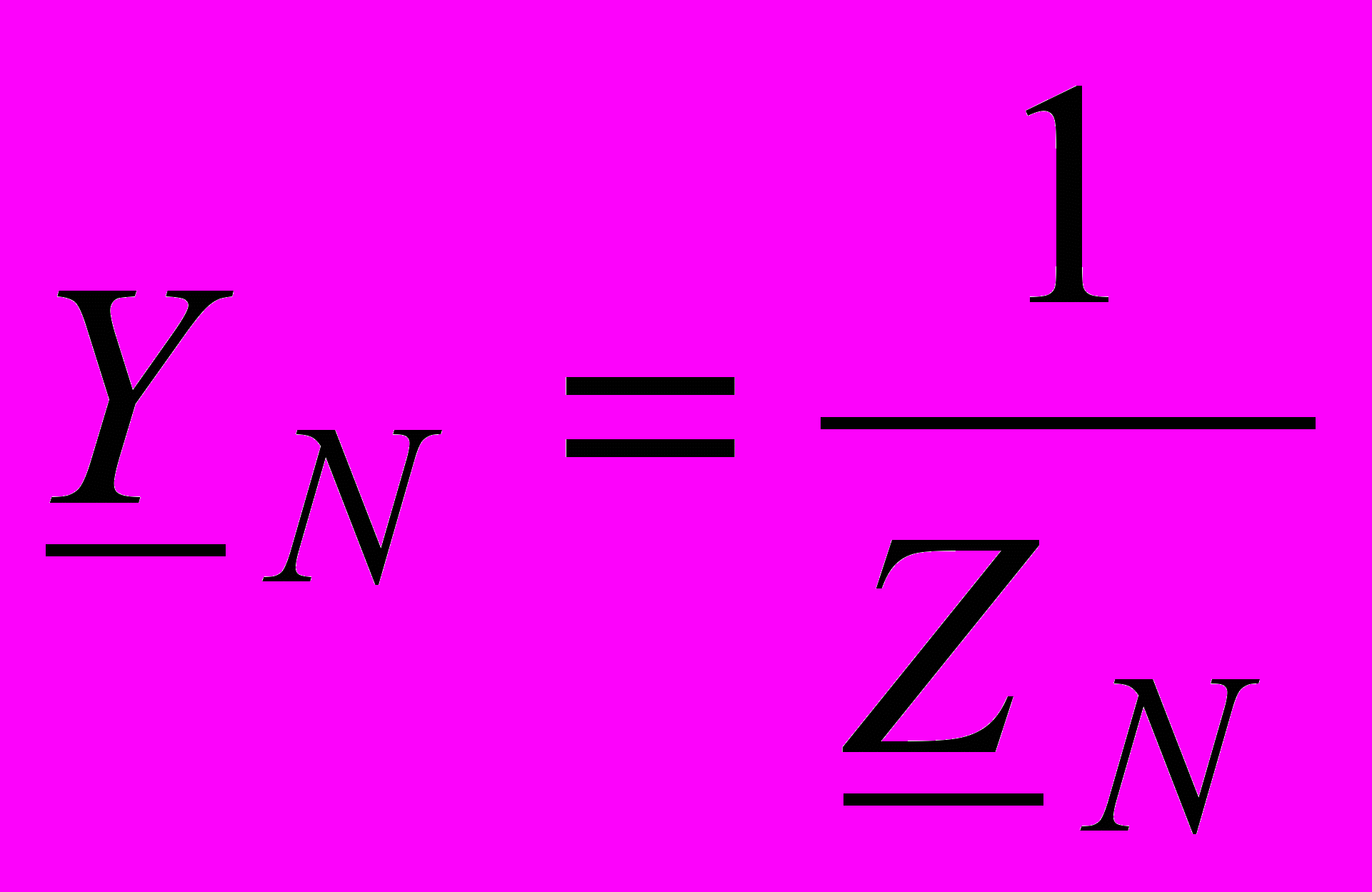, … ,  комплексные проводимости фаз приемника и нулевого провода.


Порядок выполнения работы

Этап 1. Экспериментальная часть

1. 
   Начертите в отчете о работе схему, показанную на рис. 14.3, применяя стандартные графические обозначения.
   

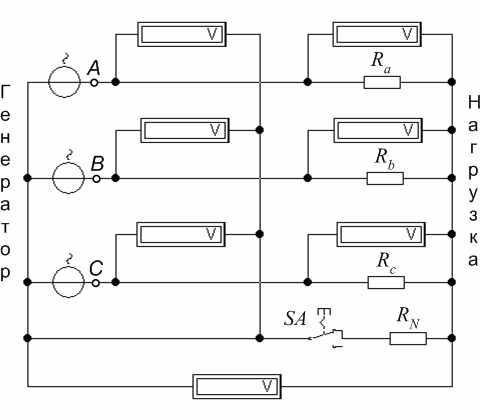Рис. 14.3.  Исследуемая схема

2. Откройте файл Wewb32. Установите использование английского языка.
   
3. Соберите исследуемую схему на монтажном поле виртуального стенда и выполните следующие действия:
   

• Измерительные приборы установите в режим переменного тока (АС).
  
• Выберите и задайте параметры источников однофазного синусоидального напряжения, входящих в схему генератора трехфазного напряжения. При этом действующие значения напряжения, а также значения частоты напряжения всех однофазных источников должны быть одинаковыми (можно оставить их установленными по умолчанию либо задать собственные значения). Значения фаз (в градусах) установите так, чтобы получилась симметричная трехфазная система ЭДС. Запишите под схемой установленные Вами параметры источников.
  
• Задайте различные значения сопротивлений R_a, … R_N (R_N имитирует сопротивление нулевого провода). Эти значения не должны отличаться друг от друга слишком сильно, иначе будет неудобно строить векторные диаграммы, и они не будут наглядными. Заданные значения занесите в таблицу 14.1.
  

Таблица 14.1. Заданные значения сопротивлений

	№ опыта	Ra, …	Rb, …	Rc, …	RN, …
	1
	2

4. Опыт № 1. Включите питание лабораторного стенда, измерьте и занесите в таблицу 14.2 значения фазных напряжений генератора, напряжений фаз нагрузки и смещения потенциала нейтрали.
   
5. Опыт № 2. Разомкните нулевой провод с помощью выключателя SA и заполните соответствующие строки таблиц 14.1 и 14.2.
   

Таблица 14.2. Результаты измерений и построений

№	UA, В	UВ, В	UС, В	Ua, В		Ub, В		Uc, В		UN, В
	изм.	изм.	изм.	изм.	топ.д.	изм.	топ.д	изм.	топ.д	изм.	выч.
1
2

Этап 2. Обработка результатов измерений

6. Выполните вычисления и заполните таблицу 14.3, в которой буквой G обозначены активные проводимости фаз нагрузки и нулевого провода ( 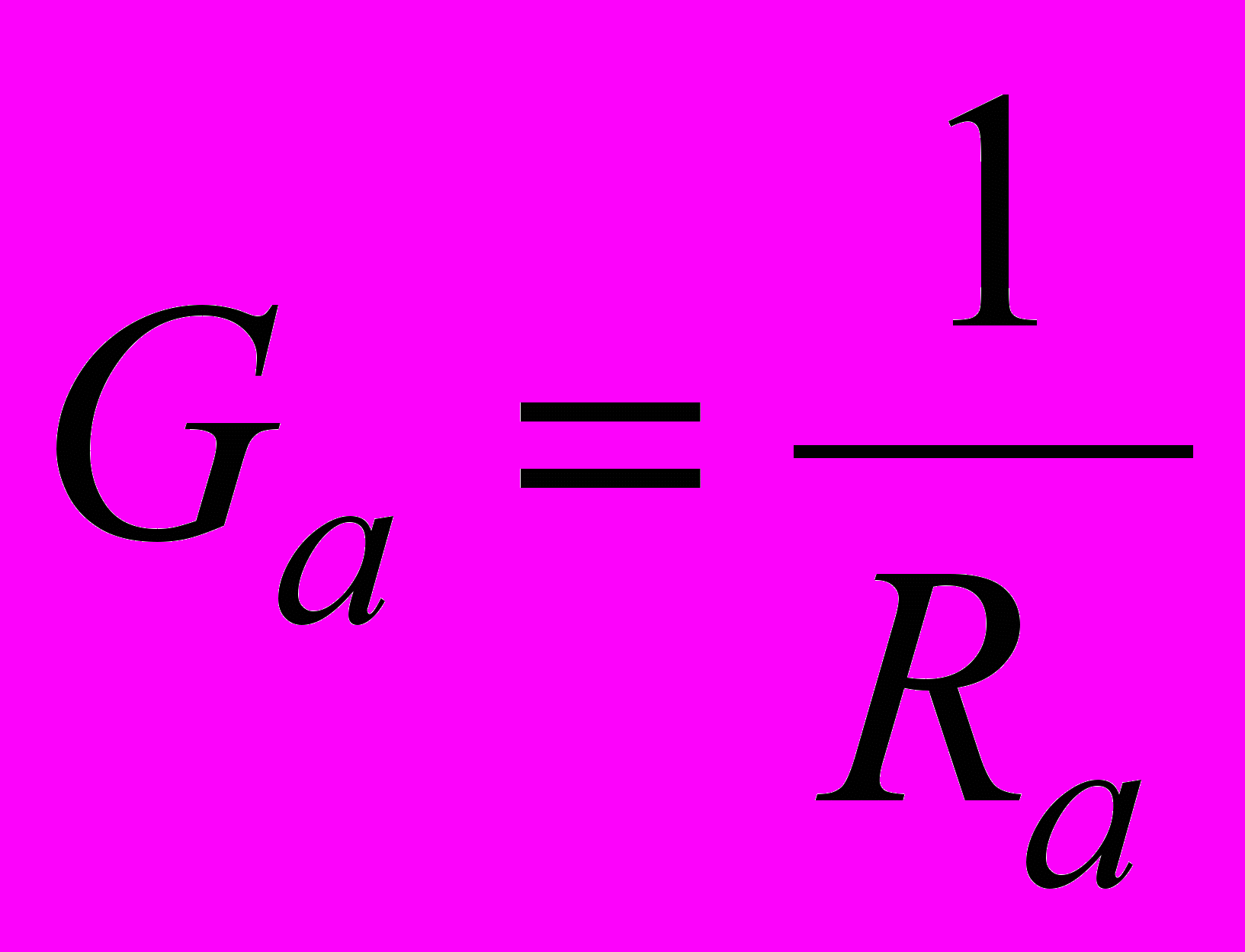и т.д.). Обратите внимание, что в выражении U_AG_a стоит фазное напряжение генератора, а не нагрузки.
   

Таблица 14.3. Результаты вычислений

№	Ga, …	Gb, …	Gc, …	GN, …	UAGa, …	UBGb, …	UCGc, …	Ga+Gb+Gc+GN, …
1
2

Приемники энергии R_a … R_N обладают чисто активным сопротивлением. В этом случае выражение (14.4) можно записать в следующем виде:

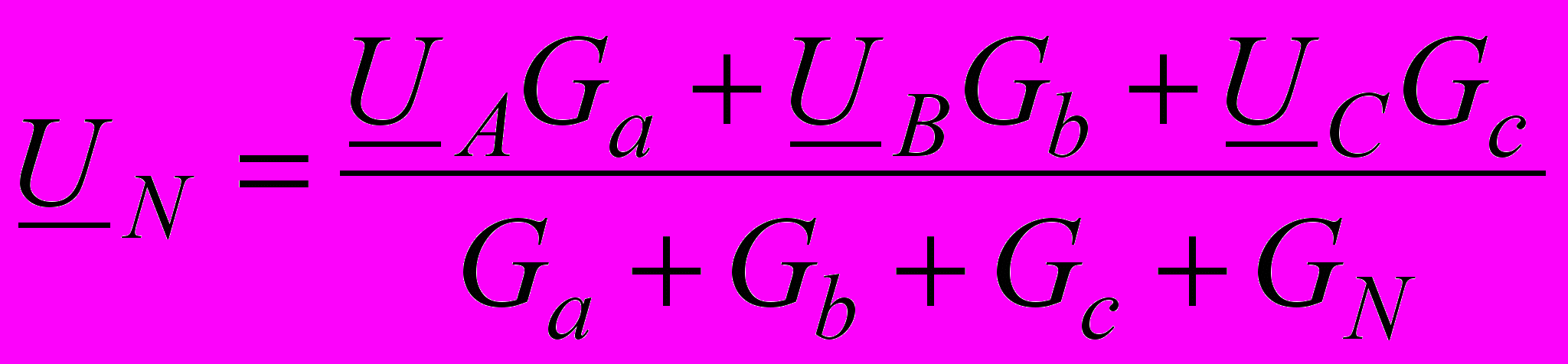. (14.5)

Выполните пункты 7 ... 11 сначала по результатам опыта № 1, затем по результатам опыта № 2. Рядом с построенными векторными и топографическими диаграммами должны быть указаны номера опытов.

7. П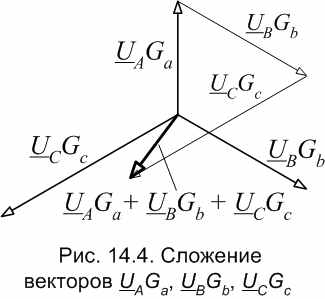остройте три луча, исходящие из одной точки и повернутые один относительно другого на 120. Пользуясь данными таблицы 14.3 и выбрав подходящий масштаб, отложите вдоль этих лучей векторы U_AG_a, U_BG_b, U_CG_c. Выполните геометрическое сложение этих векторов (пример показан на рис. 14.4).
   
8. Измерьте длину полученного вектора-суммы (U_AG_a + U_BG_b + U_CG_c) и, зная масштаб, найдите абсолютное значение этого вектора в единицах тока. Запишите полученный результат рядом с векторной диаграммой.
   
9. В знаменателе выражения (14.5) стоит действительное число. Поэтому полученный вектор-сумма сонаправлен с вектором U_N, а абсолютная величина вектора равна:
   

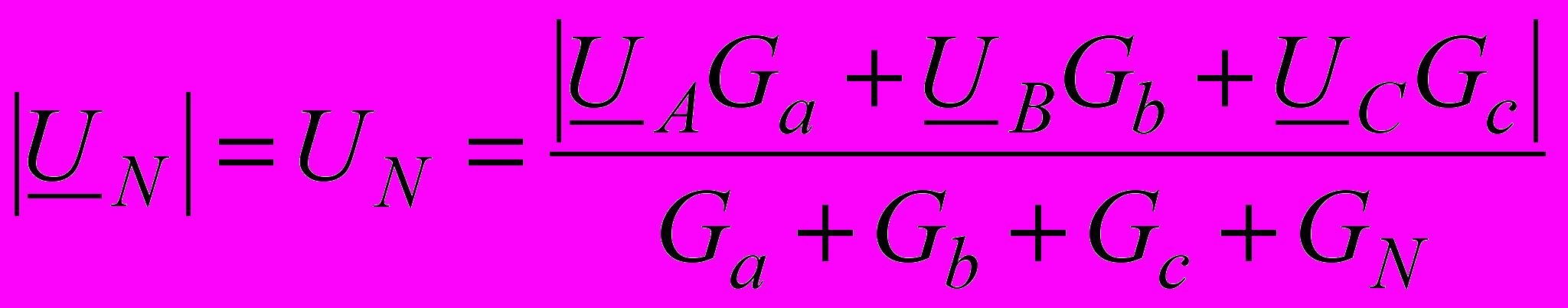, (14.6)

где в числителе стоит абсолютное значение вектора-суммы, найденное при выполнении предыдущего пункта, а в знаменателе  сумма проводимостей, занесенная в таблицу 14.3. Вычислите значение U_N по формуле (14.6) и занесите его в таблицу 14.2 (в ячейку, предназначенную для значения, полученного вычислением).

10. Постройте топографическую диаграмму напряжений (см. пример на рис. 14.2), отложив от одной точки векторы фазных напряжений генератора U_A, U_B, U_C, а также вектор смещения потенциала нейтрали U_N. В соответствии со сказанным в начале пункта 9, вектор U_N необходимо отложить в направлении вектора-суммы (U_AG_a + U_BG_b + U_CG_c), т.е. следует выполнить параллельный перенос луча, вдоль которого направлен вектор-сумма, совместив его начало с началом координат топографической диаграммы напряжений, а затем отметить на перенесенном луче значение U_N в выбранном масштабе напряжений. На топографической диаграмме укажите точку N (нейтраль генератора) и точку n (нейтраль нагрузки).
    
11. Соедините точку n с концами векторов U_A, U_B, U_C, получив, таким образом, векторы U_a, U_b, U_c (см. рис. 14.2). Измерьте длины этих векторов и, зная масштаб, найдите действующие значения напряжений U_a, U_b, U_c (в вольтах). Результаты занесите в таблицу 14.2 (в ячейки, предназначенные для значений, полученных с помощью топографической диаграммы).
    

Контрольные вопросы

1. В каком случае в четырехпроводной трехфазной цепи имеет место смещение потенциала нейтрали?
   
2. Что представляет собой каждая из величин, входящих в формулу (14.4)?
   
3. В чем заключается разница между формулами (14.4) и (14.5)? При каком условии для определения смещения потенциала нейтрали можно пользоваться формулой (14.5)?
   
4. Являются ли векторы U_AG_a, U_BG_b, U_CG_c векторами токов в фазах нагрузки?
   
5. Объясните построение вектора U_N и векторов напряжений фаз нагрузки на топографической диаграмме.