Sherman Riemenschneider, Bao Liu, Yuesheng Xu and Norden E
| Вид материала | Документы |
СодержаниеИллюстрация 2.10: Гильбертов спектр третьего к шестому IMFs, показанному в рис. |
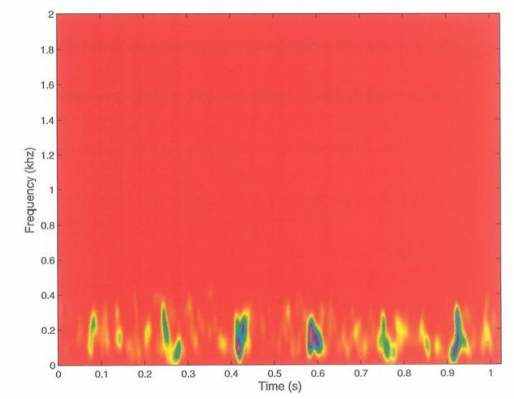
Иллюстрация 2.10: Гильбертов спектр третьего к шестому IMFs, показанному в рис. 2.9.
то, что переходные процессы распространяются по частотному диапазону этих четырех IMFs. Гильбертов спектр, полученный из Гильбертовой трансформанты этих четырех IMFs, дается в рис. 2.10, где более яркие исправления показывают частотные характеристики времени переходных процессов. Для лучшей идентификации показанных компонентов приглаженное представление Гильбертова спектра используется в этом разделе (см. Хуэнг и др. 1998). От Рис. 2.9 и 2.10 мы можем получить следующую информацию. Во-первых, среднее время, оставляя промежутки между соседними переходными процессами является приблизительно 0.17 s, соответствуя 5.9 Гц в частоте - частота вращения поврежденного механизма. Во-вторых, частота импульсов колеблется от 0 приблизительно до 300 Гц и покрывает боковые полосы частоты ловли в сети последней пары механизма в пути передачи. Эта частота петли составляет приблизительно 88.4 Гц. Наконец, пятый IMF показывает, что фазовая задержка происходит в некоторых из импульсов. Основанный на общем знании диагноза коробки передач (Брон 1986), мы знаем, что эти особенности указывают существование локализованного дефекта на ведущем зубчатом колесе последней пары механизма.
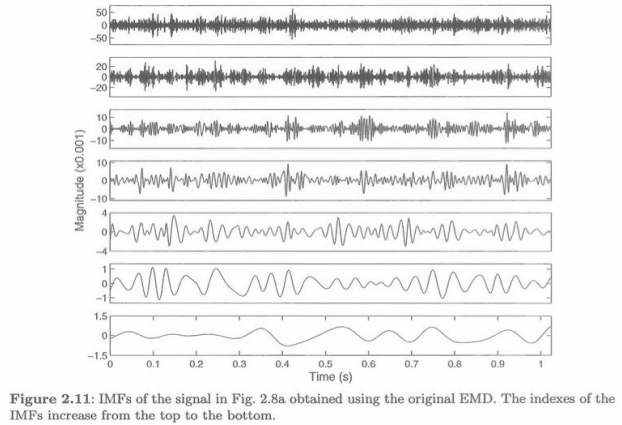
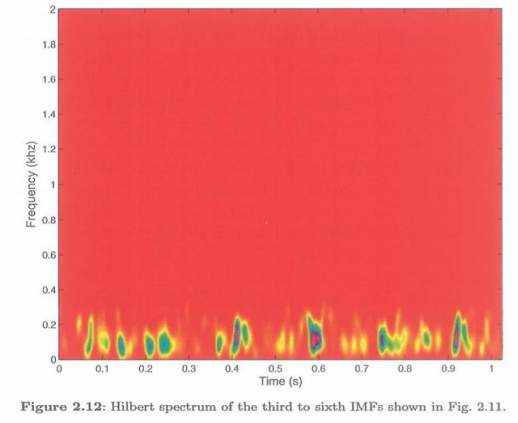
Иллюстрации 2.11 и 2.12 показывают первые семь IMFs и Гильбертов спектр IMFs 3-6 полученный при использовании первоначального EMD. Для этого удельного сигнала IMFs и Гильбертов спектр, полученный при использовании BS-EMD, кажется, открывают импульсы лучше чем полученные при использовании первоначального EMD.
Задача, которую возводит в степень второй пример, является локализованным диагнозом отказа прокручивающегося отношения образующей через кратковременное выпрямление. Спецификации поведения в испытании были аз, следует: номер прокручивающихся элементов, 8; диаметр прокручивающихся образующих, 15 MMS; средний диаметр, 65 MMS; и войдите в контакт с углом, 0 °. Поведение
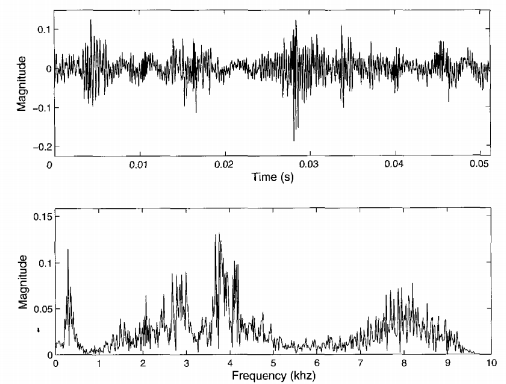
Иллюстрация 2.13: (a, вершина), сигнал вибрации собрался от отношения(поведения), и (b, основа) ее Преобразование Фурье. Сигнал был нормализован как энергия модуля.
несший дефект на его внутренней гонке стимулировал в форме впадины измерительное приблизительно 0.1 MMS подробно и 1 MMS в диаметре, чтобы моделировать зарождающееся поверхностное расщепление. Сигналы вибрации были приняты на постоянной внутренней скорости вращения гонки 1900 оборотов в минуту. Они были lowpass-фильтрованы в 9 кГц и оцифрованы в частоте дискретизации 20 кГц. Внутренний дефект гонки мог генерировать последовательность высокочастотных переходных процессов вибрации. В этих переходных процессах одновременно оставляют промежутки вовремя, но обычно имеют различные амплитуды и частотные диапазоны, если внутренняя гонка вращается. При существующих испытательных условиях это может быть вычислено, что среднее время, оставляя промежутки между соседними переходными процессами является 6.4 ms (Брон 1986).
Иллюстрация 2.13 показывает типичный отчет вибрации от поведения и его трансформанты Фурье. Сигнал содержит немного ударов(импульсов) и высокочастотных компонентов. Эти особенности более или менее показывают присутствие локализованного(ограниченного) дефекта в отношении(поведении). IMFs, полученные при использовании BS-EMD, представляются в рис. 2.14, которого первые три IMFs лучше открывают существование переходных процессов чем форма волны первоначального сигнала.
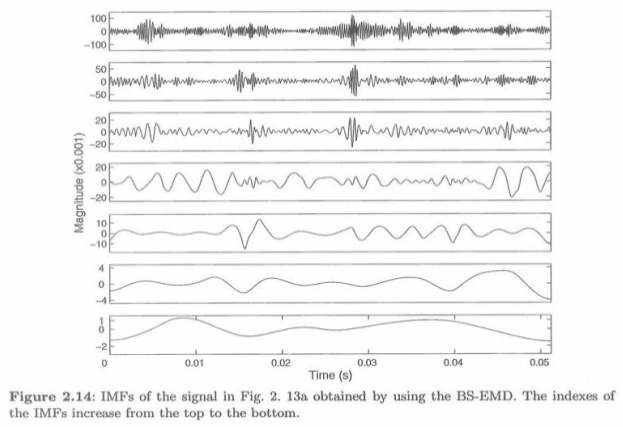
Иллюстрация 2.15 показывает соответствующий Гильбертов спектр. Это открывает соответствующий частотный диапазон каждого переходного процесса. Некоторые переходные процессы, которые являются трудными идентифицировать от форм волны IMFs, становятся более чистыми(более ясными) в Гильбертовом спектре, таком как переходный процесс, представленный ярким исправлением близко к моменту времени 0.01 s и в полосе частот от 7 кГц до 9 кГц. Иллюстрации 2.14 и 2.15 также открывают, что среднее время, оставляя промежутки между соседними переходными процессами является приблизительно 6 ms или его множественным. Это значение близко к вычисленному упомянутому выше. Основанный на этих особенностях, обнаружение, что поведение несло локализованный внутренний дефект гонки, убедительно.

Иллюстрация 2.15: Гильбертов спектр первого, к тирХ ТМФС показанный в рис. 2 14
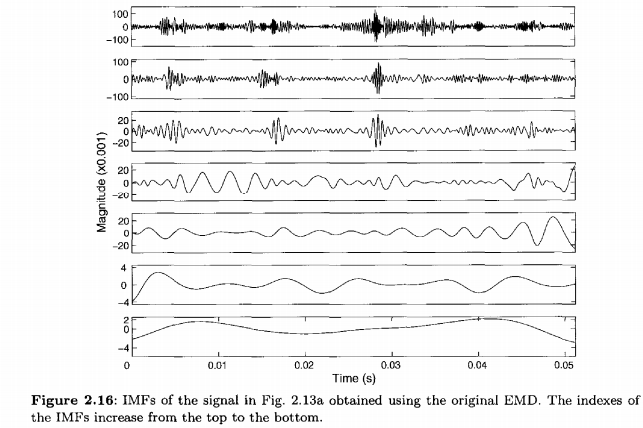
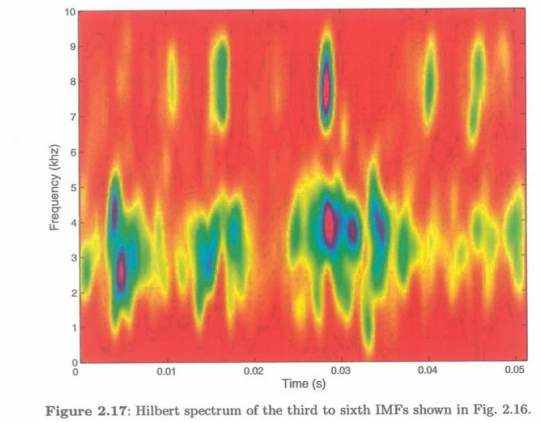
Иллюстрации 2.16 и 2.17 показывают IMFs, полученный при использовании первоначального EMD и Гильбертова спектра, вычисленного от первых трех IMFs. Они предоставляют подобную информацию к этому в Рис. 2.14 и 2.15. Мы разложили больше сигналов. Результаты показывают, что действия этих двух методов вообще сопоставимы.
2.6. Заключение и будущее исследуют темы
Эмпирическая модовая декомпозиция и Гильбертов спектральный анализ, включая трансформанту Гильберта-Huangа, были применены с большим успехом для нелинейного и неустановившегося анализа сигнала в различных областях. Однако, большинство основных математических задач оставили невылеченными. Учитывая быстрые успехи, сделанные в методологии и применениях, мы срочно должны разработать твердую математическую основу для трансформанты Гильберта-Huangа. Эта работа рассматривала работу в том направлении, основанном на Чен и др. (2004), Лиу и др. (2004), и Ксу и Ян (2004). Мы описали алгоритм нашего B-сплайна, базировал EMD и представил результаты некоторых связанных математических изучений. Моделируемые и практические прикладные примеры, данные в бумаге, показали, что у BS-EMD есть сопоставимая производительность к тому из первоначальных EMD. Чтобы облегчить будущее продвижение, мы идентифицировали выдающиеся математические задачи в Чен и др. (2004). Мы теперь суммируем те задачи, близко связанные с B-сплайном EMD.
На частотном анализе времени традиционные методы часто проводятся с априорным базисом, созданным на определенных общих критериях. Для нелинейных и неустановившихся сигналов, у которых есть переменные локальные характеристики, невозможно ожидать фиксированный базис, чтобы приспособить все сигналы, не вызывая поддельных гармоник. Прорыв в улучшении технологии является разработкой адаптивных методов представления(изображения), используя сверхзаконченную библиотеку базиса, например, Койфман и др. (1992), Маллэт и Жэнг (1993), Чен и Донохо (1995). Они выбирают от библиотеки базис, который "адаптируется" к разложенному сигналу. Эти методы имеют хорошие математические основания, но не полностью адаптивны, поскольку сама библиотека будет априорной, и увеличение размера библиотеки будет следовать вычислительными трудностями. В случае подхода EMD представление обще и достаточно адаптивно, но не математически строго. Фундаментальная причина для последнего то, что встроенное отсутствие функций режима математически строгое определение. К этой задаче можно обратиться в пределах B-сплайна метод EMD, поскольку все встроенные функции режима, кроме первого, получили или из оригинала или из B-сплайна, EMD может быть представлен как суммы кривых B-сплайна.
По той же самой упомянутой выше причине B-сплайн EMD мог также использоваться, чтобы обратиться к задаче сходимости EMD. "Конвергенцией(Сходимостью)" мы подразумеваем, что EMD произведет только конечное множество компонентов IMF. Хотя все интуитивное рассуждение и численные эксперименты предлагают, чтобы процедура EMD была сходящейся, общее и законченное доказательство все еще желает. Вообще, кубическая сплайновая средняя огибающая могла создать дополнительное пространство экстремума отдельно. Эта возможность представляет больше трудностей для попыток доказать конвергенцию(сходимость). Ожидаемая прибыль от использования B-сплайнов - то, что сходимость могла бы прибыть в результате хороших уменьшающих разновидность свойств прогрессии B-сплайна. Конечно, там все еще существуют запросы, например, как иметь дело со скрытыми масштабами, вызванными точками перегиба в данных.
Несколько проблем реализации должны уладиться для подхода B-сплайна, так же, как они делают для подхода огибающей. Во-первых, B-сплайн EMD также зависит от критерия остановки. Так как различные критерии остановки приводят к различным множествам IMFs, оптимальный естественно желателен. Во-вторых, хотя у нас есть интуитивная причина, как упомянуто в разделе 2.4, выбрать кубический B-сплайн для BS-EMD, точный выбор порядка все еще остается вопросом. Наконец, так как мы имеем дело с конечными данными, наш алгоритм должен также быть откорректирован, чтобы использовать некоторую форму граничных условий. Хотя можно вызвать "зафиксированную" конечную опцию точки, чтобы установить концы, как выбрать фиксированный конец все еще задача. Даже если локальное свойство изменения B-сплайна ограничит влияние до конца области, область влияния станет большей и большей, поскольку масштаб режима IMF становится большим, и влияние концов распространится в низкочастотные компоненты данных. Ясно, если подход B-сплайна должен стать жизнеспособным вариантом к подходу огибающей, детальное исследование этих задач срочно необходимо.
Хотя у подхода B-сплайна есть те же самые задачи как первоначальный подход относительно вышеупомянутых проблем, с аналитическим выражением, подход B-сплайна, однако, является более подсудным к математическому анализу. Уменьшающие изменение свойства и разбиение свойств единицы прогрессии B-сплайна могут быть особенно полезными. С этими преимуществами подход B-сплайна действительно заслуживает более детального исследования(расследования).
Благодарности.
Эта работа была поддержана частично Национальным управлением по аэронавтике и исследованию космического пространства (НАСА) под грантом NAG5-5364, и Национальный научный фонд под грантами NSF0314742 и NSF0312113.
Ссылки




Шермэн Рименшнеидер
Отдел Математики, Университет Западной Вирджинии, Моргэнтаун, Западная Вирджиния 26506, США. sherm@math.wvu. edu Bao Liu
Отдел Математики, Университет Западной Вирджинии, Моргэнтаун, Западная Вирджиния 26506, США. bliu@math. вву. edu Yuesheng Ксу
Отдел Математики, Сиракузский Университет, Сиракузы, Нью-Йорк 13244, США yxu06@syr.edu
Норден E. Хуэнг. Институт Годдард Анализа данных, Кода 614-2, Зелёной зоны Центра Космического полета НЭЗЭ/ГОДДАРД, Мэриленд 20771, США норден. e.huang@nasa.gov
