Упорядоченное (направленное) движение заряженных частиц
| Вид материала | Документы |
- Тс сила тока. Напряжение. Сопротивление. Закон Ома для участка цепи, 64.04kb.
- Самостоятельная работа Кредитная стоимость Лекции 36 Число недель, 154.88kb.
- Лабораторная работа №2 Моделирование движения небесных тел и заряженных частиц, 91.57kb.
- Изирующее излучение любое излучение, взаимодействие которого со средой приводит к образованию, 33.08kb.
- Молекулярная физика основы мкт изменение агрегатного состояния, 505.21kb.
- 01. 04. 20 – физика пучков заряженных частиц и ускорительная техника, 445.01kb.
- Фатихова Дания Ахтямовна, 249.42kb.
- «Проблемы теоретической и прикладной электронной и ионной оптики», 238.99kb.
- Спецификация темы «Тепловые явления» и примеры заданий к ней, 23.63kb.
- А. Н. Алмалиев, И. С. Баткин, М. А. Долгополов, И. В. Копытин, П. В. Лукин,, 70.09kb.
и хода лучей при преломлении света
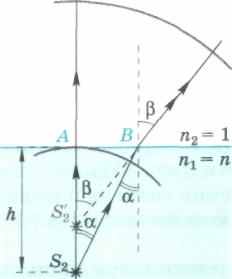
Изображение точечного источника. Построение изображений при преломлении света основано на использовании закона преломления волн.
Рассмотрим сначала точечный источник света Sx (рис. 180, а), находящийся в воздухе (п1 = 1) на расстоянии StA = h от границы оптически более плотной среды п2 = п. Сферический фронт волны, распространяющейся из точки Sv определяется лучами SXA и S. Углы падения этих лучей равны 0 и а, а углы преломления 0 и (3 соответственно. Продолжения лучей (определяющих положение сферического фронта преломленной волны) расходящегося пучка пересекаются в точке S[, являющейся мнимым изображением точки Sx. Найдем расстояние SA от мнимого изображения до границы раздела:
S[A =
АВ
tgP'
а)
б)
< 180
Изображение точечного источника:
а) находящегося
в оптически менее плотной среде;
б) находящегося
в оптически более плотной среде
218 Электромагнитное излучение
Так как АВ = htg а, то S{A = h.
При малых углах аир можно считать, что tg а ~ sin а и tg Р ~ sin р.
Тогда
с л , sin а , S-,A = h—— = nh.
1 sin Р
При наблюдении точечного источника из более плотной среды наблюдателю будет казаться, что источник расположен от границы раздела в п раз дальше, чем он находится на самом деле.
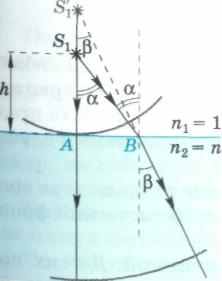
Рассмотрим теперь точечный источник света S2, находящийся в жидкости с показателем преломления пх = п на глубине h (рис. 180, б). Найдем изображение источника при наблюдении его из менее плотной среды (например, из воздуха (п2 = 1)).
Сферический фронт волны, распространяющейся из точки >S2, определяется лучами SgA и S2B. Углы падения этих лучей равны 0 и а, а углы преломления 0 и Р соответственно. Продолжения лучей (определяющих положение сферического фронта преломленной волны) расходящегося пучка пересекаются в точке S2, являющейся мнимым изображением точки
НОСТИ ЖИДКОСТИ, S2A = -—jt .
Учитывая, что АВ = htg ос, получаем SA = h-~ .
/-, sin а 1
Согласно закону преломления ——х = - .
sin р п
Тогда при малых а и р tg а ~ sin а, a tg р ~ sin p.
Следовательно, S!A. = - .
с п
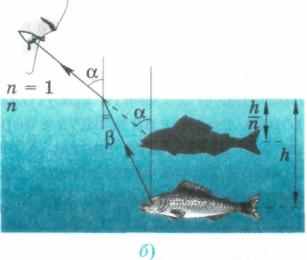
При наблюдении точечного источника из менее плотной среды наблюдателю будет казаться, что источник расположен в п раз ближе к границе раздела, чем он находится на самом деле. Вследствие этого эффекта предметы, находящиеся в воде, кажутся расположенными на меньшей глубине, чем в действительности (рис. 181).
В целом при преломлении света на плоской границе раздела двух сред сферический фронт падающей волны преобразуется в сферический фронт преломленной волны.
Преломление света плоскопараллельной пластинкой. До сих пор аы рассматривали преломление света на одной поверхности раздела не-)граниченных сред. Изучим теперь особенности последовательного пре-
Геометрическая оптика
219
181
Преломление света в жидкости:
а) кажущаяся форма
предмета;
б) мнимое изображение
рыбы
ломления света на нескольких границах раздела прозрачных ограниченных сред.
Предположим, что луч света падает из воздуха (п1 = 1) под углом а на прозрачную плоскопараллельную пластину (п2 = п) толщиной d (рис. 182). Найдем, под каким углом (р луч выйдет в воздух после преломления в пластинке. Воспользуемся законом преломления (см. формулу (166)) на верхней границе пластинки:
sin ос sin Р
= п.
| | | а |
| п1 = 1 | \ог | |
| п2= п | d | |
sin|3 = 1 sin (р п '
Перемножая левые и правые части законов преломления на обеих границах, получаем sin а
а.
О,
sin ф
«!= 1
= 1, т. е. ф
Луч, прошедший плоскопараллельную пластину, выходит из нее параллельно направлению падения.
Боковое смещение луча h пропорционально толщине пластинки d.
То, что угол выхода луча равен углу падения на пластину, можно было доказать и по принципу обратимости лучей. Если луч падает из пер-
|ф= а
А 182
Преломление света
плоскопараллельной
пластиной
220
Электромагнитное излучение
ВЬ \с
А 183
Преломление света призмой с малым преломляющим углом (а < а0)
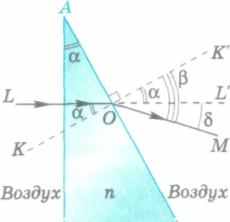
вой среды под углом а и преломляется во второй под углом (3, то, падая из второй среды под углом Р, луч будет преломляться в первой под углом а. Преломление света призмой. Рассмотрим преломление света треугольной призмой, на которую падает из воздуха перпендикулярно одной из ее граней луч света. Абсолютный показатель преломления материала призмы п, ее преломляющий угол а (рис. 183).
Преломляющий угол призмы — угол между гранями призмы, на которых происходит преломление света.
Предположим сначала, что преломляющий угол призмы меньше угла полного внутреннего отражения:
а < а0.
Найдем угол отклонения 8 луча от первоначального направления падения после преломления луча призмой.
При нормальном падении на грань АВ призмы луч не преломляется, падая на вторую преломляющую грань АС под углом а (/. LOK = Z. ВАС = ос как углы с соответственно перпендикулярными сторонами). Угол преломления (3 = /.КОМ на грани АС найдем из закона преломления:
sin а _ 1 sin р п '
При малом преломляющем угле призмы а можно считать, что sin а = а, sin Р « р, поэтому Р ~ па.
• Как показано на рисунке 183, треугольная призма отклоняет луч, падающий на нее из воздуха к основанию. Угол отклонения луча б = Р - а-
Тогда
5 = а(/1-1). (167)
Чем больше преломляющий угол призмы и абсолютный показатель преломления вещества, из которого она сделана, тем больше она отклоняет луч от первоначального направления.
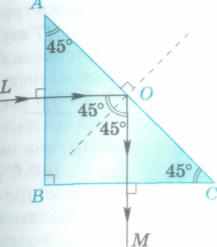
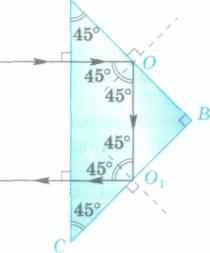
Рассмотрим теперь преломление света треугольной призмой с преломляющим углом, большим угла полного внутреннего отражения а > ао'
Геометрическая оптика 221
А
< 184
Призма полного внутреннего отражения:
а) поворот луча на 90°;
а)
о)
б) отражение луча
{поворот на 180°)
Пусть для определенности призма стеклянная (а0 = 42°), а а = 45° (рис. 184, а). Луч, нормально падающий на грань АВ, не преломляется на ней. Его угол падения на грань АС равен 45° > ос0, поэтому в точке О он испытывает полное внутреннее отражение. На грань ВС отраженный луч падает перпендикулярно и не преломляется, выходя из призмы под углом 90° к направлению падения. Такую призму называют поворотной, так как она поворачивает луч на угол 90°.
При падении луча на грань поворотной призмы, проектирующуюся в сечении в гипотенузу АС, падающий луч в результате двух отражений от граней АВ и ВС изменяет направление на противоположное (рис. 184, б). Возникает обращение светового луча.
ВОПРОСЫ
- Где находится изображение точечного источника, наблюдаемого из оптически более плотной среды?
- Где находится изображение точечного источника, наблюдаемого из оптически менее плотной среды?
- В чем особенность преломления света плоскопараллельной пластинкой?
- Какой угол призмы называют преломляющим? Как угол отклонения луча, падающего на призму, зависит от ее преломляющего угла и коэффициента преломления?
5- Как используется призма полного внутреннего отражения для поворота и обращения луча?
ЗАДАЧ И
■ Толщина стекла зеркала (п = 1,5) d = 1 см. Задняя часть зеркала посеребрена. На ка
ком расстоянии от наружной части зеркала будет находиться изображение предме
та, удаленного от нее на 50 см. [51,3 см]
222
Электромагнитное излучение
В сосуд вначале наливают воду (я, = 1,33) до высоты h: = 4см, а поверх нее
доверху — бензин (п2 = 1,5) с высотой столба h2 = 6 см. Чему равна кажущаяся глу
бина сосуда? [7 см]
Луч света падает на плоскопараллельную стеклянную пластинку (п = 1,5) толщиной
d- 10 см под углом а = 60°. Найдите боковое смещение луча на выходе из плас
тинки. [dsina(1 -cosa/Vw2 - sin2a ) = 5,1 см]
Луч света выходит из стеклянной призмы (п = 1,5) под тем же углом, под которым
падает на нее. Преломляющий угол призмы 60°. Найдите угол падения луча на
призму. [48,6°]
На одну из граней стеклянной призмы, сечением которой является правильный тре
угольник, падает параллельно основанию луч света определенной частоты. На какой
угол относительно первоначального направления падения он отклоняется после
преломления призмой? , лР [60°]

§ 58. Линзы
Геометрические характеристики. Преломление света на плоских границах пространственно ограниченных прозрачных сред (плоскопараллельная пластинка, призма) приводит к смещению изображений относительно самих предметов. При этом размер изображения остается равным размеру предмета. Отличие размера изображения Н от размера предмета h наблюдается лишь при преломлении света на криволинейных прозрачных поверхностях и характеризуется линейным увеличением оптической системы.
Линейное увеличение оптической системы — физическая величина, равная отношению размера изображения к размеру предмета:
Г0-|. (168)
Для увеличенного изображения (Н > h) Г0 > 1, при уменьшенном изображении (Н < К) Г0 < 1. В случае совпадения размера изображения с размером предмета (Н = h) Г0 = 1.
Важнейшим элементом многочисленных оптических приборов и систем, начиная от очков и кончая гигантскими телескопами, является линза.
Дадим определение геометрических характеристик линзы.
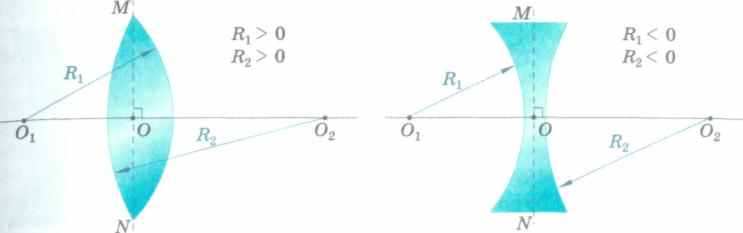
Главная оптическая ось — прямая, на которой лежат центры сферических поверхностей, ограничивающих линзу (рис. 185).
Главная оптическая ось Ох02 является осью симметрии линзы.
Геометрическая оптика
223
а) б)
А 185
Геометрические характеристики линзы:
а) двояковыпуклая линза; б) двояковогнутая линза
Линза — прозрачное тело, ограниченное двумя сферическими по верхностями.
Главная плоскость линзы — плоскость, проходящая через центр линзы (точку О) перпендикулярно главной оптической оси.
Типы линз. На рисунке 185, а главная плоскость MN проходит через линию пересечения сферических поверхностей с радиусами Rt и R2, называемыми радиусами кривизны. Будем считать, что для сферической поверхности, выпуклой относительно главной плоскости, радиус кривизны положителен.
Для сферической поверхности, вогнутой относительно главной плоскости, радиус кривизны отрицателен (рис. 185, б).
Одна из ограничивающих поверхностей линзы может быть плоской. Плоскую поверхность можно рассматривать как частный случай сферической, радиус кривизны которой стремится к бесконечности.
По форме ограничивающих поверхностей различают шесть типов
линз (рис. 186):
• Двояковыпуклая; • двояковогнутая;
плоско-выпуклая; • плоско-вогнутая;
вогнуто-выпуклая; • выпукло-вогнутая.
Выпуклые линзы являются собирающими (мы покажем это далее).
Собирающие линзы — линзы, преобразующие параллельный пучок световых лучей в сходящийся.
24
Электромагнитное излучение
Собирающие линзы
Рассеивающие линзы
ях> о
Д,ос
%
; у*г

/ 1
| i?!< 0 | Лх< 0 | J*j-> °° | flj> 0 |
| R2> 0 | Д2< 0 | Д2< 0 | Д2< 0 |
| 1 Rt 1 > R2 | | | Дх> |Д2 |
| 3 | 4 | 5 | 6 |
4 186
Гипы линз: двояковыпуклая 1; плоско-выпуклая 2; вогнуто-выпуклая 3; двояковогнутая 4; плоско-вогнутая 5; выпукло-вогнутая 6
Вогнутые линзы являются рассеивающими.
Рассеивающие линзы — линзы, преобразующие параллельный пучок световых лучей в расходящийся.
В дальнейшем для простоты мы будем рассматривать преломление ветовых лучей тонкими линзами.
Тонкая линза — линза, толщина которой пренебрежимо мала по сравнению с радиусами кривизны ее поверхности (1 <& Rv R2).
ВОПРОСЫ
. Дайте определение линейного увеличения оптической системы. Что оно характеризует?
!. Дайте определение главной оптической оси и главной плоскости линзы.
I. Охарактеризуйте шесть типов линз, отличающихся формой ограничивающих поверхностей. Как определяется знак радиуса кривизны этих поверхностей?
■. В чем отличие собирающих и рассеивающих линз?
'. Какая линза называется тонкой?
Геометрическая оптика
225
§ 59. Собирающие линзы
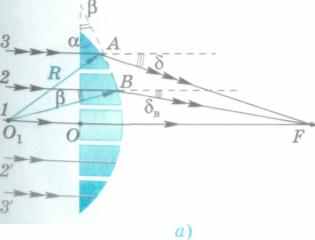
фокусное расстояние, оптическая сила. Рассмотрим, как преломляется пучок лучей, параллельных главной оптической оси (рис. 187, а), при падении на плоско-выпуклую линзу (с показателем преломления п и радиусом кривизны R). Условно линзу можно представить как совокупность призм с различными углами преломления, поэтому будет различным и преломление луча, попадающего на каждую из призм. Луч 1, направленный вдоль главной оси, не преломляется, так как падает практически на плоскопараллельную пластинку.
Преломляющий угол призмы 2 равен р\ поэтому после прохождения призмы луч 2 отклоняется от первоначального направления на угол Ъв = р(я - 1) (см. формулу (169)). Преломленный луч 2 пересекает главную оптическую ось в точке F.
Луч 3 падает на призму 3, имеющую преломляющий угол а. После ее прохождения преломленный луч 3 отклоняется от горизонтали на угол 8 = ос(п - 1).
При этом 5 > Ъв. Можно показать, что и луч 3 пересекает главную оптическую ось в точке F, называемой главным фокусом линзы.
Главный фокус собирающей линзы — точка на главной оптической оси, в которой собираются лучи, падающие параллельно главной оптической оси, после преломления их в линзе.
Фокусное расстояние (обозначаемое как и главный фокус F) — расстояние от главного фокуса до центра линзы.
| 1 | 00 к/ | i *! \ | ML | | J} | |
| hL- | Ог | о\ \ | | F | | *•'"- |
| a~~ | 1 / | | | | i |
б)
А 187
Преломление собирающей линзой лучей, параллельных главной °птической оси: я) главный фокус линзы;
> связь фокусного расстояния с радиусом кривизны линзы
о
°- А. Касьянов, 11 кл.
226
Электромагнитное излучение
Покажем, что фокусное расстояние линзы связано с ее радиусом кривизны (рис. 187, б). Для этого рассмотрим преломление луча 3 на части линзы — призме с преломляющим углом а. Луч падает в точке А под углом а и отклоняется от горизонтали (первоначального направления его падения) на угол 8, равный ZAFO, как накрест лежащие углы при параллельных прямых. Радиус кривизны линзы ОхА =йв точке А совпадает по направлению с перпендикуляром к преломляющей грани призмы и составляет с оптической осью ОхО угол а.
Угол 8 можно найти из AAOF: tg 8 = h/F, а угол а из ААОгО: sin а = h/R.
Для тонкой линзы углы преломления а (и соответственно 8) столь малы, что можно считать sin ос ~ а = h/R, a tg 8 « 8 = h/F.
Тогда, учитывая связь 8 и а, находим
= (п-1)
h F Сокращая на А, получаем
(169)
<*~1>!
1 F
Фокусное расстояние плоско-выпуклой линзы, в вакууме определяется радиусом кривизны ее поверхности и абсолютным показателем преломления материала линзы.
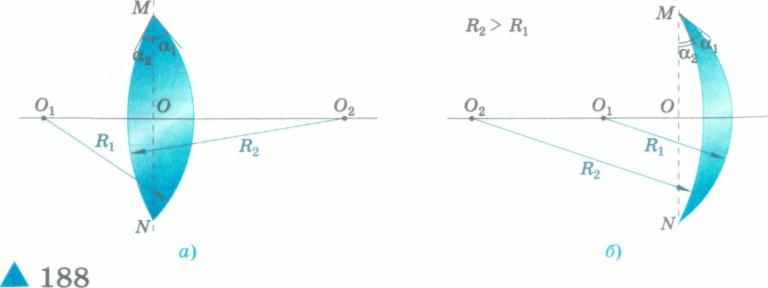
Любую выпуклую линзу можно рассматривать как совокупность двух плоско-выпуклых линз. Для двояковыпуклой линзы полный преломляющий угол а складывается из преломляющих углов ах и а2 двух плоско-выпуклых линз (рис. 188, а). Для вогнуто-выпуклой линзы прелом-
Собирающие линзы как совокупность двух плоско-выпуклых линз: а) двояковыпуклая линза; б) вогнуто-выпуклая линза
Геометрическая оптика
227
ляющий угол определяется разностью преломляющих углов ах - а2 двух плоско-выпуклых линз (рис. 188, б).
Для двояковыпуклой тонкой линзы луч, параллельный главной оптической оси, вблизи точки М отклоняется от оси на угол
8 = (п - 1)(аг + а2), (170)
а для вогнуто-выпуклой тонкой линзы
en-lXo-Oj,). (171)
Считая так же, как и для одной плоско-выпуклой линзы, 8 = h/F, ttl = h/Rlt а2 = h/R2, находим: для двояковыпуклой тонкой линзы
?-<я-Чк+к) (172)
для выгнуто-выпуклой тонкой линзы
F=-4i-i\ (173>
Наличие в формулах (169), (172), (173) величины 1/F привело к введению оптической силы линзы.
Оптическая сила — величина, обратная фокусному расстоянию линзы:
Ь-у. (174)
Чем сильнее линза собирает параллельный пучок лучей, т. е. чем меньше ее фокусное расстояние, тем больше оптическая сила линзы.
Единица оптической силы — диоптрия (дптр).
Диоптрия — оптическая сила линзы с фокусным расстоянием 1 м.
Оптическая сила для любой собирающей линзы может быть представлена формулой:
» = '»-"(s; + |l <1Г5>
Формула (175) является обобщением выражений (169), (172), (173). Действительно, для плоско-выпуклой линзы R2 -> оо (1/J?1 = 0), а для вогнуто-выпуклой линзы можно считать, что радиус кривизны вогнутой поверхности отрицателен, т. е. R2 < 0 (|Д2| > Rlt поэтому j- - - > 0 J.
Для собирающих линз оптическая сила положительна: D > 0.
8*
228
Электромагнитное излучение
Основные лучи для собирающей линзы. Рассмотрение преломления световых лучей собирающей тонкой линзой позволяет выделить важнейшие характерные лучи, достаточные для построения хода любого луча, падающего на линзу, а также для получения изображения предмета в линзе.
- Луч, параллельный главной оптической оси, преломляясь в линзе, проходит через ее главный фокус.
- Луч, проходящий через главный фокус (по принципу обратимости лучей), после преломления в линзе идет параллельно главной оптической оси.
- Луч, идущий через оптический центр тонкой линзы, проходит через нее, не преломляясь. Это объясняется тем, что такой луч падает практически на плоскопараллельную пластинку. Ввиду того что линза тонкая, незначительным параллельным отклонением преломленного луча можно пренебречь.
На рисунке 189, а приведен ход характерных лучей для собирающей линзы и использовано ее условное обозначение.
Как мы установили ранее, лучи, параллельные главной оптической оси, падающие на линзу, преломляясь, пересекаются в главном фокусе.
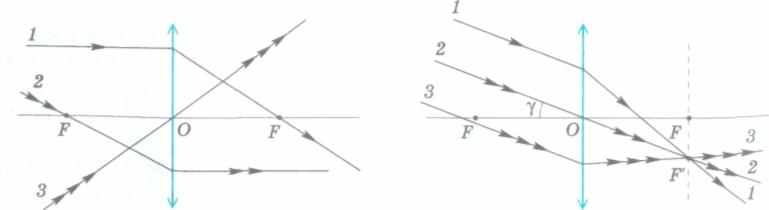
Если пучок параллельных лучей падает на собирающую линзу под небольшим углом у к главной оптической оси, то преломленные лучи пересекаются в одной точке F' фокальной плоскости линзы, называемой побочным фокусом (рис. 189, б). (Доказательство этого утверждения, подобное выводу формулы (169), мы для краткости не приводим.)
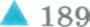
Основные лучи для собирающей линзы:
а) характерные лучи; б) параллельные лучи
Фокальная плоскость линзы — плоскость, проходящая через главный фокус линзы перпендикулярно главной оптической оси.
Геометрическая оптика
229
а)
б)
О
О

< 190
Построение хода лучей в собирающей линзе:
а) построение прелом
ленного луча;
б) построение падаю
щего луча
Положение побочного фокуса определяется пересечением луча 2, проходящего через оптический центр О линзы с фокальной плоскостью, находящейся за линзой.
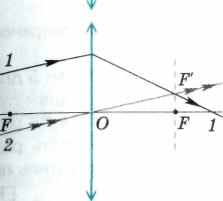
Известные свойства характерных и параллельных лучей позволяют построить ход произвольного луча 1, падающего на собирающую линзу с фокусным расстоянием jF (рис. 190, а). Для определения направления преломленного луча воспользуемся лучом 2, проходящим через оптический центр О параллельно падающему лучу 1. Луч 2 проходит линзу, не преломляясь, пересекая фокальную плоскость в побочном фокусе F'.
Согласно свойству параллельных лучей после преломления луч 1 также пройдет через этот побочный фокус.
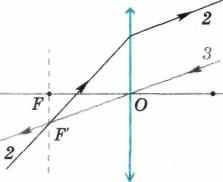
Найдем теперь направление падающего луча, если известен ход преломленного луча 2 (рис. 190, б). По принципу обратимости лучей данную задачу можно свести к предыдущей, считая, что известно направление падающего на линзу луча. Тогда, повторяя предыдущее построение с помощью луча 3, проходящего через оптический центр О линзы параллельно лучу 2, получим побочный фокус F', через который проходит искомый падающий луч 2.
1.
2.
ВОПРОСЫ
Объясните, как преломляются лучи, параллельные главной оптической оси, плоско-выпуклой линзой. Дайте определение главного фокуса и фокусного расстояния линзы. Как связано фокусное расстояние плоско-выпуклой линзы с радиусом кривизны ее поверхности и абсолютным коэффициентом преломления материала линзы?
230
Электромагнитное излучение
Какая величина называется оптической силой? В каких единицах она измеряется? Как зависит оптическая сила линзы от ее абсолютного коэффициента преломления и радиусов кривизны ограничивающих ее поверхностей?
Перечислите и нарисуйте основные характерные лучи в собирающей линзе. Сфор
мулируйте свойство параллельных лучей, падающих на собирающую линзу под уг
лом к главной оптической оси. j
ЗАДАЧИ
1. Плоско-выпуклая линза из пластика (и = 1,58) имеет радиус кривизны поверхности
11,6 см. Найдите фокусное расстояние линзы и ее оптическую силу.
[20 см; 5 дптр]
2. Найдите оптическую силу стеклянной (п = 1,5) плоско-выпуклой линзы диаметром
d = 4 см, имеющей в центральной части толщину Н = 2 мм. [4,95 дптр]
3. Плоско-выпуклая линза имеет ограничивающую сферическую поверхность ради
усом 12 см. Фокусное расстояние линзы 24 см. Найдите абсолютный показатель пре
ломления материала, из которого сделана линза. [1,5]
4. Двояковыпуклая линза сделана из стекла (п, = 1,5)
с радиусами кривизны (R =R2 = 0,2 м). Найдите ее оп
тическую силу в воздухе и в воде (п2 = 1,33).
[5 дптр; 1,28 дптр]
191
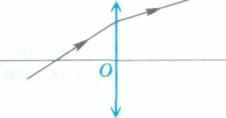
5. Известен ход падающего и преломленного собираю
щей линзой лучей (рис.191). Найдите построением
главный фокус линзы слева и справа от нее.
