Упорядоченное (направленное) движение заряженных частиц
| Вид материала | Документы |
- Тс сила тока. Напряжение. Сопротивление. Закон Ома для участка цепи, 64.04kb.
- Самостоятельная работа Кредитная стоимость Лекции 36 Число недель, 154.88kb.
- Лабораторная работа №2 Моделирование движения небесных тел и заряженных частиц, 91.57kb.
- Изирующее излучение любое излучение, взаимодействие которого со средой приводит к образованию, 33.08kb.
- Молекулярная физика основы мкт изменение агрегатного состояния, 505.21kb.
- 01. 04. 20 – физика пучков заряженных частиц и ускорительная техника, 445.01kb.
- Фатихова Дания Ахтямовна, 249.42kb.
- «Проблемы теоретической и прикладной электронной и ионной оптики», 238.99kb.
- Спецификация темы «Тепловые явления» и примеры заданий к ней, 23.63kb.
- А. Н. Алмалиев, И. С. Баткин, М. А. Долгополов, И. В. Копытин, П. В. Лукин,, 70.09kb.
§39. Конденсатор в цепи переменного тока
Разрядка конденсатора. В цепи, содержащей конденсатор, постоянный ток протекать не может, так как цепь оказывается разомкнутой. Между пластинами конденсатора нет свободных носителей зарядов ни в воздухе, ни в диэлектрике, так что конденсатор является разрывом цепи для постоянного тока. Зазор между пластинами конденсатора аналогичен пробке в водопроводной системе, которая не позволяет воде постоянно циркулировать, т. е. работать в стационарном (не зависящем от времени) режиме. В то же время пробка не мешает жидкости заполнять систему, а также сливать жидкость, т- е. работать в нестационарном (зависящем от времени) режиме.
Аналогичными режимами в электрической цепи является зарядка и Разрядка конденсатора, при которых заряженные частицы перемещают-
Разрядка конденсатора. В цепи, содержащей конденсатор, постоянный ток протекать не может, так как цепь оказывается разомкнутой. Между пластинами конденсатора нет свободных носителей зарядов ни в воздухе, ни в диэлектрике, так что конденсатор является разрывом цепи для постоянного тока. Зазор между пластинами конденсатора аналогичен пробке в водопроводной системе, которая не позволяет воде постоянно циркулировать, т. е. работать в стационарном (не зависящем от времени) режиме. В то же время пробка не мешает жидкости заполнять систему, а также сливать жидкость, т- е. работать в нестационарном (зависящем от времени) режиме.
Аналогичными режимами в электрической цепи является зарядка и Разрядка конденсатора, при которых заряженные частицы перемещают-
136
Электродинамика
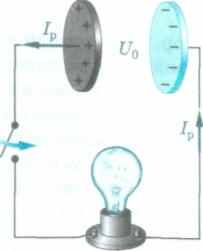
ся по проводникам, соединяющим пластины конденсатора, но не перемещаются в зазоре между ними. Если заряженный до напряжения конденсатор отключить от источника постоянного тока и соединить его обкладки с клеммами лампы накаливания, наблюдается кратковременная вспышка лампы (рис. 127, а). Ток 1р, протекающий через лампу от положительной обкладки к отрицательной, приводит к разрядке конденсатора. Попадающие на отрицательную пластину положительные заряды быстро нейтрализуют ее.
Время релаксации R—С-цепи. Оценим время разрядки конденсатора емкостью С через сопротивление R. В отсутствие внешней ЭДС суммарная разность потенциалов в контуре на сопротивлении и конденсаторе равна нулю:
uR + uc = o,
или
LR+17C = 0.
Так как
/ = q' = СЩ,
то изменение напряжения на конденсаторе в единицу времени равно
(-Uc) (-Uc)
U с
RC
(102)
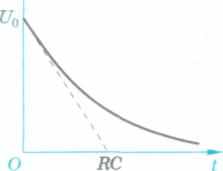
Величина (-Uc) в числителе формулы (102) характеризует полное изменение напряжения на конденсаторе при его разрядке. Следовательно, величина хс = RC в знаменателе формулы (102) определяет по порядку величины время разрядки конденсатора, или время релаксации R—Сцепи.
Геометрически производная U'c в формуле (102) характеризуется тангенсом угла наклона касательной к кривой Uc(t). При t = 0 касательная к
 а)
а) С/Ги
б)
127
Разрядка конденсатора:
а) через лампу;
б) зависимость напря
жения на конден
саторе от времени
Электромагнетизм
137
зависимости Uc(t) (рис. 127, б) пересекает ось t в точке хс = RC. Так можно найти графически время релаксации R—Сцепи.
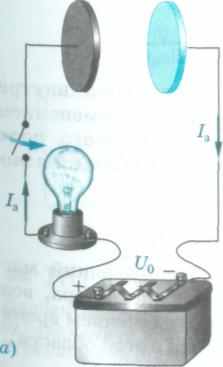
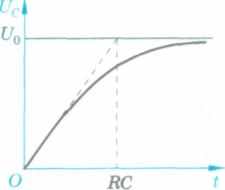
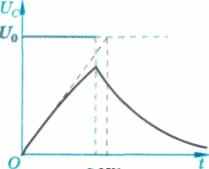
Зарядка конденсатора. Ток смещения. При подключении конденсатора к источнику постоянного напряжения U0 в цепи возникает кратковременный импульс тока 1а, который заряжает конденсатор до напряжения источника (рис. 128, а). После зарядки конденсатора ток прекращается. Время релаксации хс = RC характеризует как время разрядки, так и время зарядки конденсатора (рис. 128, б).
При подключении к конденсатору генератора прямоугольных импульсов длительностью Т с амплитудой напряжения U0 (рис. 129, а) зависимость от времени напряжения на конденсаторе повторяет кривые зарядки и разрядки при постоянном напряжении (рис. 129, б).
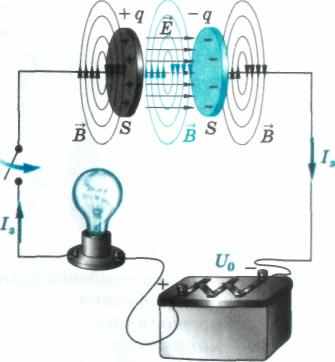
В процессе зарядки ток, протекающий по подводящим проводам, или ток проводимости, создает вокруг себя переменное магнитное поле. Линиями индукции этого поля являются концентрические окружности (рис. 130). Так как подводящие проводники располагаются снаружи от конденсатора, то, казалось бы, только снаружи от него должно существовать и магнитное поле. Однако из замкнутости линий индукции магнитного поля следует постоянство его потока через любую поверхность. Поэтому, если существует магнитная индукция вне конденсатора, она должна существовать и внутри него, где ток проводимости отсутствует. Магнитное поле возникает при наличии тока. По определению
dt'
б)
<ф28
Зарядка конденсатора от источника постоянного напряжения:
а) схема зарядки;
б) изменение со време
нем напряжения на
конденсаторе
138
Электродинамика

б)
где
<ф29
Зарядка конденсатора импульсным напряжением:
а) схема зарядки;
б) зависимость
напряжения на кон
денсаторе от времени
т
 . е. сила тока равна изменению заряда в единицу времени. При зарядке плоского конденсатора изменение заряда на его пластинах приводит к изменению напряженности электрического поля внутри конденсатора. Напряженность электрического поля внутри плоского конденсатора (см. Ф-10, § 81) равна:
. е. сила тока равна изменению заряда в единицу времени. При зарядке плоского конденсатора изменение заряда на его пластинах приводит к изменению напряженности электрического поля внутри конденсатора. Напряженность электрического поля внутри плоского конденсатора (см. Ф-10, § 81) равна:Е
= _£_ Se0e
Следовательно, сила тока внутри конденсатора связана с изменением напряженности электрического поля со временем. Такой ток называется током смещения:
Т =CFf см -Ь£0е df ■
А130
Ток смещения при зарядке конденсатора от аккумулятора
Ток смещения, порождающий магнитное поле внутри конденсатора, возникает при изменении с течением времени электрического поля в этой области.
Электромагнетизм
139
Изменяющееся во времени электрическое поле (согласно гипотезе Д. Максвелла) является (наряду с движущимися свободными зарядами) источником магнитного поля.
Магнитоэлектрическая индукция — явление возникновения магнитного поля в переменном по времени электрическом поле.
Между электрическим и магнитным полями существует взаимосвязь и прослеживается симметрия: переменное магнитное поле порождает вихревое электрическое поле (электромагнитная индукция), а переменное электрическое поле порождает вихревое магнитное (магнитоэлектрическая индукция). Эти поля образуют единое электромагнитное поле.
Емкостное сопротивление. Предположим, что в качестве нагрузки генератора переменного тока используется конденсатор электроемкостью С (рис. 131, а). Переменное напряжение на обкладках конденсатора изменяется по закону:
и = Umcos со*.
В результате периодически повторяющихся процессов зарядки и разрядки конденсатора в цепи возникает переменный ток (ток проводимости в подводящих проводах и равный ему ток смещения между обкладками конденсатора).
Установим связь между амплитудами переменного напряжения и тока в цепи. Электрический ток в цепи возникает в результате изменения заряда конденсатора: i = q'.
Заряд на его обкладках изменяется по закону:
q = Cu = CUmcos wt. (103)
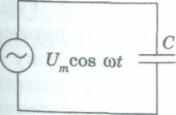
и I
о
-и.
| л | Т= 27С/СО | ■1 | |
| | \/г/у | г\ | Г |
| | | | |
YL
и_
A i3i
а)
б)
в)
 Конденсатор в цепи переменного тока: а) схема включения; ) переменное напряжение и сила тока в цепи конденсатора; в) векторная диаграмма
Конденсатор в цепи переменного тока: а) схема включения; ) переменное напряжение и сила тока в цепи конденсатора; в) векторная диаграмма140
Электродинамика
Следовательно, сила тока
1 = d? = ~ImSin Ю*' (104)
где Im = (uCUm — амплитуда силы тока.
Графиком зависимости силы тока от времени является отраженная от оси t синусоида (рис. 131, б). Для изображения силы тока на векторной диаграмме удобно представить выражение (105) в виде:
i = /mcos (со* + я/2). (105)
Начальная фаза колебаний напряжения равна нулю, а тока — л/2 (рис. 133, в).
Колебания силы тока в цепи конденсатора опережают по фазе колебания напряжения на его обкладках на л/2.
Мгновенная мощность переменного тока на конденсаторе определяется выражением
p = iu = -0,5ImUmsin 2at. (106)
Из графика зависимости мгновенной мощности на конденсаторе от времени (рис. 132) следует, что среднее значение мощности переменного тока на конденсаторе за период Т равно нулю. Принято говорить, что элементы цепи, для которых средняя мощность переменного тока равна нулю, обладают реактивным сопротивлением. Для этих элементов разность фаз колебаний силы тока и напряжения составляет л/2. Реактивное сопротивление конденсатора называется емкостным сопротивлением. Найдем сопротивление конденсатора переменному току, или емкостное сопротивление, с помощью закона Ома как отношение амплитуды переменного напряжения к амплитуде силы тока:
**-!;-&■ 1 (107>
Емкостное сопротивление обратно пропорционально частоте переменного тока. Конденсатор оказывает значительное сопротивление току ма-
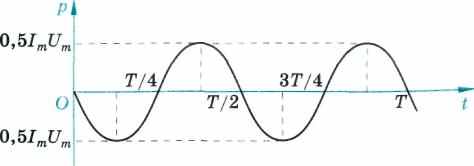
132 ►
Зависимость мгновенной мощности на конденсаторе от времени
142
Электродинамика
<Эи-
cos art
| uii | Т = | = 2п/ю | | | |
| Um | | | | | |
| 'т | У | | \т/г/ | i \*~ | |
| 0 | | | | /т | t |
| -1т | | - -\ | - - У*.— | | |
| -ит | | | | | |
YL
Т
и_
б)
а)
А133
Катушка индуктивности в цепи переменного тока: а) схема включения;
б) переменное напряжение и сила тока в катушке индуктивности;
в) векторная диаграмма
В любой момент времени ЭДС самоиндукции равна по модулю и противоположна по знаку напряжению на концах катушки, созданному внешним генератором:
Т dt
Ifcos (dt.
(108)
Будем искать решение уравнения (108) в виде:
i = /msin (at. Подстановка решения (109) в уравнение (108) дает:
(109)
(oLImcos (Ot = Umcos oat.
Следовательно, амплитуда силы тока 1т в катушке связана с амплитудой переменного напряжения Um законом Ома:
1я-%*, (НО)
XL
где xL = coL — индуктивное сопротивление катушки.
Индуктивное сопротивление прямо пропорционально частоте переменного тока. При увеличении частоты тока вихревое электрическое поле заметно препятствует тем изменениям тока, которые его вызвали.
Разность фаз между силой тока в катушке и напряжением на ней. Графиком зависимости (109) силы тока от времени является синусоида (рис. 133, б). Для изображения силы тока на векторной диаграмме удобно представить выражение (109) в виде:
Электромагнетизм
143
J =/mcos (cot - ! ). (Ill)
Начальная фаза колебаний напряжения равна нулю, а тока л/2
(рис. 133, в).
Колебания силы тока в катушке индуктивности отстают по фазе на к/2 от колебаний напряжения на ней.
Мгновенная мощность переменного тока в катушке определяется выражением
р = ш = 0,5ImUmsin 2ю*. (112]
Из графика зависимости мгновенной мощности в катушке от времени (рис. 134) следует, что среднее значение мощности переменного тока е катушке индуктивности за период Т равно нулю. Индуктивное сопро тивление является реактивным сопротивлением.
ВОПРОСЫ
- Почему при изменении силы тока в катушке в ней возникает ЭДС самоиндукции?
- Чему равно индуктивное сопротивление катушки?
- Как соотносятся фазы силы тока, протекающего через катушку индуктивности, и напряжения на ней?
- Чему равно среднее значение мощности переменного тока в катушке за период?
- Почему индуктивное сопротивление катушки называют реактивным сопротивлением?
ЗАДАЧИ
- Рассчитайте величину индуктивного сопротивления катушки индуктивностью L = = 20 мГн на частоте 50 Гц. [6,28 Ом
- Постройте график зависимости индуктивного сопротивления катушки от частоть переменного тока. Как изменится индуктивное сопротивление при увеличении час тоты в 3 раза?
- Катушка индуктивностью L = 10 мГн обладает активным сопротивлением 10 Ом. Прь каком значении частоты переменного тока индуктивное сопротивление катушки бу дет в 10 раз больше ее активного сопротивления? [1590 Гц
 | / ' \ | Т/2/ | | Т/ |
| О | г/А | 1 / 1 / | ЗГ/4\ | |
134
Зависимость мгновенной мощности в катушке от времени
144
Электродинамика
- Катушка индуктивностью L = 0,35 Гн включена в сеть с действующим значением напряжения [/д = 220 В и частотой v = 50 Гц. Найдите действующее значение силы тока, протекающего через катушку. Изобразите напряжение и силу тока на векторной диаграмме. [2 А]
- К катушке приложено напряжение, изменяющееся с течением времени по закону u = 311cos (ЮОяг). Найдите индуктивность катушки, если действующее значение силы тока, протекающего через нее, равно 7 А. [0,1 Гн]
§ 41. Свободные гармонические электромагнитные колебания в колебательном контуре
Энергообмен между электрическим и магнитным полями. Колебания силы тока в нагрузке генератора переменного тока являются вынужденными колебаниями, возникающими под действием приложенного переменного напряжения. Такими колебаниями являются, например, колебания силы тока в резисторе, конденсаторе, катушке индуктивности.
Однако существует также замкнутая электрическая цепь — колебательный контур, в котором могут возникать свободные электромагнитные колебания.
Колебательный контур — цепь, состоящая из последовательно включенных катушки индуктивностью L и конденсатора емкостью С.
Обычно активное сопротивление проводов катушки пренебрежимо мало (R ~ 0).
Электромагнитные колебания заряда и силы тока в колебательном контуре сопровождаются взаимными превращениями электрического и магнитного полей.
Рассмотрим последовательные стадии колебательного процесса в L—С-контуре.
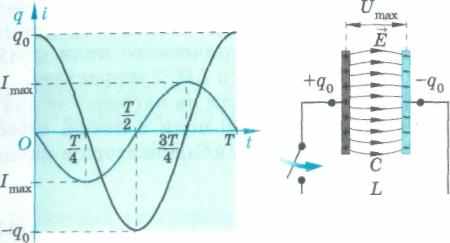
Для возбуждения колебаний в контуре конденсатор предварительно заряжают, сообщая его обкладкам заряды ±q0. Тогда в начальный момент времени (t = 0) (рис. 135) между обкладками конденсатора возникает электрическое поле. Полная энергия в контуре определяется энергией электрического поля конденсатора:
W=W = — . р 1С
Электромагнетизм
145
1ШИ
q = q0,i = 0,W = Wp-
LI2
9-0, i-J ,W = Wm =
-u
max
н—
; £ '
A—-4
+%
-%
Gbrr
с
L
ЧМИ
P 2C
q--q0,l-0,W-W
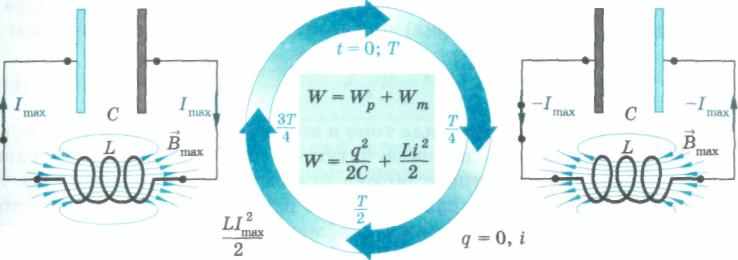
A 135
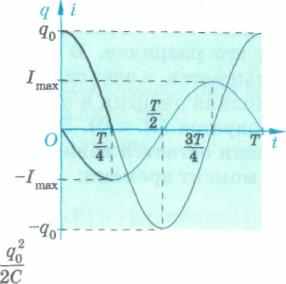
Энергообмен между электрическим и магнитным полями в колебательном контуре
146
Электродинамика
При замыкании ключа в контуре возникает возрастающий со временем ток. Этот ток нейтрализует заряд на пластинах конденсатора, приводя к его разрядке. В результате энергия электрического поля q2/(2C) уменьшается, а энергия магнитного поля катушки LI2/2 возрастает.
Полная энергия в контуре сохраняется, так как на нагревание она не эасходуется (R ~ 0). Энергия электромагнитного поля в любой момент зремени остается равной электрической энергии конденсатора в начальный момент времени:
В момент времени t = Т/4, когда конденсатор полностью разрядится, •нергия электрического поля обращается в нуль, а энергия магнитного по-1я (а следовательно, и сила тока) достигает максимального значения:
= т = - (П4)
Начиная с этого момента сила тока в контуре убывает; следовательно, гменьшается магнитный поток в катушке (Ф= Ы). Согласно правилу 1енца, изменению магнитного потока препятствует индукционный ток, [ротекающий в том же направлении, что и ток разрядки конденсатора. Конденсатор начинает перезаряжаться, между его обкладками возникает лектрическое поле, стремящееся ослабить ток, который в момент време-:и t = Т/2 обращается в нуль. В этот момент времени заряд +qQ на обклад-:ах достигнет первоначального значения, при этом знак заряда окажется ротивоположным первоначальному. Далее те же процессы начнут про-екать в обратном направлении и через такой же промежуток времени Т/2, . е. в момент времени t = Т, система вернется в первоначальное состоя-ие. После этого начнется самопроизвольное повторение рассмотренного икла. В отсутствие потерь на нагревание проводов в контуре совершают-я гармонические незатухающие колебания заряда на обкладках конден-атора и силы тока в катушке индуктивности.
Частота и период собственных гармонических колебаний. Найдем равнение этих колебаний с помощью закона Ома для колебательного онтура. ЭДС самоиндукции катушки равна разности потенциалов Uc на ластинах конденсатора:
-Li' = Uc. (115)
Учитывая, что i = q',Uc=%, получаем
С
Lq" = -\q. (Пб)
Электромагнетизм
147
Проверим подстановкой, что решением уравнения (116) является функция
q = q0cos(j)0t, (117)
для которой при t = О, q = q0. При вычислении второй производной от q по времени отметим, что ее первая производная равна силе тока:
i = g'=-g0w0sin со0* =-/„sin co0i; Im = q0®0, (118)
q" = -g0cogcos co0£. (119)
Подставим выражения для g из (117) и q" из (119) в уравнение (118):
9о
„ cos co0t.
-Lg0cogcos ш0£ =
Сокращая на g0cos со0£, получаем круговую частоту собственных колебаний в контуре:
(Оп =
1
(120)
Период собственных колебаний заряда на конденсаторе и силу тока в катушке индуктивности позволяет определить следующая формула, впервые полученная в 1853 г. английским ученым Уильямом Томсоном:
m 2л
(121)
= 2nJLC
Юп
У.
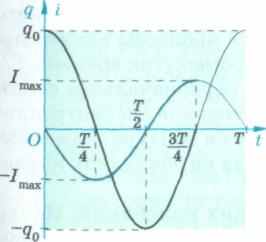
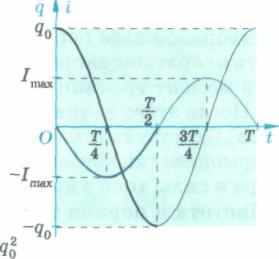
На векторной диаграмме видно, что колебания силы тока, изменяющейся по закону i = Imcos ((o0t + л/2) (сравните с формулой (118)), опережают колебания заряда на л/2 (рис. 136).
В реальном колебательном контуре свободные электромагнитные колебания являются затухающими из-за выделения джоулева тепла в проводнике катушки (R Ф 0) (а также из-за излучения электромагнитных волн). Однако на протяжении небольших интервалов времени собственные электромагнитные колебания в контуре можно считать гармоническими, происходящими по законам (117), (118).
Щ
о
V
Q0
А 136
Сила тока и заряд в колебательном контуре
ВОПРОСЫ
1 ■ Какую электрическую цепь называют колебательным контуром?
2. Почему сохраняется полная энергия электромагнитного поля в колебательном контуре?
148 Электродинамика
- Объясните, почему в контуре возникают гармонические незатухающие колебания заряда и силы тока.
- По какому закону изменяют со временем заряд на конденсаторе и силу тока в катушке индуктивности?
- Как зависит период собственных колебаний в колебательном контуре от величины электроемкости конденсатора и индуктивности катушки?
ЗАДАЧ И
1. Конденсатор электроемкостью 1 мкФ, заряженный до напряжения 225 В, подключи
ли к катушке с индуктивностью 10 мГн. Найдите максимальную силу тока в контуре.
[2,25 А]
- Колебательный контур состоит из катушки индуктивностью L = 4 мГн и плоского воздушного конденсатора. Площадь пластин конденсатора S = 10 см2, расстояние между ними d= 1 мм. Найдите период собственных колебаний в контуре. [1,18 мкс]
- Найдите диапазон частот v,— v2 колебаний в контуре с катушкой, индуктивность которой L = 1 мГн, и конденсатором, емкость которого может изменяться в пределах от С1 = 40 пФ до С2 = 90 пф. [530—800 кГц]
- Колебательный контур состоит из двух одинаковых конденсаторов, включенных последовательно, и катушки индуктивности. Период собственных колебаний контура Т = 50 мкс. Чему равен период колебаний контура, если конденсаторы включить параллельно? [ 100 мкс]
- Напряжение на конденсаторе емкостью С = 0,1 мкФ, включенном в колебательный контур, изменяется по закону ис = 200cos(103t). Найдите индуктивность контура и максимальную силу тока в нем. [0,1 Гн;0,2А]
