В. М. Кафидов На основании результатов постоянного мониторинга внутренней и внешней среды фирмы разрабатывают математические модели, позволяющие с применением пк гибко корректировать политику ценообразования в соот

Вид материала

Документы

Содержание Методы исследования Результаты исследования Список использованных литературных источников

Подобный материал:

• Методика экспертизы программ основных и специальных курсов 6 Аналитическая справка, 1551.87kb.
• Облачные услуги различного уровня, ведущие мировые фирмы по ит-технологиями разрабатывают, 127.18kb.
• 52. Анализ макроэкономических условий, внешней среды и учет его результатов в управлении, 33.16kb.
• Отчет Ивгу по разделу «Система контроля качества подготовки специалистов» 44 Из опыта, 750.82kb.
• Темы курсовых работ особенности внутренней и внешней среды предприятия (организации), 41.06kb.
• Маркетинговая среда фирмы. Курсовая работа, 316.13kb.
• Воздействие факторов внешней среды на результаты деятельности предприятий водопроводно-канализационного, 166.19kb.
• Методика получения математических моделей элементов. Математические модели, используемые, 28.81kb.
• Регистрация цен и ассортимента усилится ли ценовая конкуренция в условиях кризиса?, 163.52kb.
• Анализ внутренней среды фирмы, 13.56kb.

УДК 338.5(075)


РЫНОЧНЫЕ МЕТОДЫ ЦЕНООБРАЗОВАНИЯ ИННОВАЦИЙ


В.М. Кафидов


На основании результатов постоянного мониторинга внутренней и внешней среды фирмы разрабатывают математические модели, позволяющие с применением ПК гибко корректировать политику ценообразования в соответствии с динамикой конъюнктуры рынка.


мониторинг рынка, цена, политика ценообразования


ВВЕДЕНИЕ

С учетом конъюнктуры рынка, устанавливаемой на основании постоянного мониторинга внутренней и внешней среды фирмы, корректируются математические модели рыночного спроса (кривая С_n) и предложения (кривая Пр) с применение ЭВМ.

В зависимости от политики ценообразования фирмы возможны различные подходы к формированию рыночной цены. Если фирма устанавливает максимально возможные цену и объем реализации (Ц_м и V_м), в этом случае, следуя методике разомкнутого цикла, формирует рыночную цену по принципу "закручивающейся спирали", т.е. перемещаясь соответственно к точке рыночного равновесия Р (пересечение функций Vc = f₁(Ц) и Vп = f₂(Ц), которые корректируются в соответствии с динамикой конъюнктуры рынка) [1, 2].

Следует отметить, что в данном случае "продвижение" возможно к конечной точке рыночного равновесия (Р), а также "остановка" на любой из точек от точки Ц_м до Р, т.е. возможно фиксирование цены (Ц_i) и объема реализации (V_i) на любом из этапов на период времени, обусловленный конкретной рыночной ситуацией.


МЕТОДЫ ИССЛЕДОВАНИЯ

Методика с использованием разомкнутого цикла формирования цены может использоваться в более широком диапазоне, практически в любых заданных интервалах контролируемых параметров (цены и объемов реализации продукции, финансовых и производственных возможностей фирмы и т.п.). При этом графически процесс формирования цены имеет вид (форму) спирали. Установив основные параметры процесса реализации товара и математические модели кривых спроса (С_n) и предложения (Пр), для определения динамики цен (и объемов) при планировании можно предусмотреть соответствующую форму (математическую модель) разомкнутого цикла, отвечающую принятой политике ценообразования фирмы.

В процессе исследования использовались методы, основанные на выявлении и обобщении мнений опытных специалистов-экспертов (в том числе SWOT-анализ); методы формализованного представления систем управления, основанные на использовании экономико-математических методов и моделей, в том числе дифференциальных, вариационных исчислений и др.; статистические, использующие стохастические представления процессов; графические и логические. Логистическое моделирование, опираясь на решение системы уравнений, позволяет проследить характер взаимосвязей между объёмом предложения (Vп) и спроса (Vc) на рынке инновационной продукции, влияние интенсивности удовлетворения потребности в расчёте на единицу продукции (k_и) и других факторов. Коэффициент k_и характеризует полезность единицы новшества, обеспечивая удовлетворение потребности меньшим количеством продукции, соответственно повышая конкурентоспособность продукции (при той же цене), однако обуславливает снижение объёма спроса, соответственно и объёма производства. Логистическое уравнение эффективности внедрения инноваций на рынке может быть представлено в виде:

dVп/dt = k_pVп(Vc - k_иVп) - k_фVп,

где k_p – темп (коэффициент) роста производства инноваций; k_ф - коэффициент фактического использования инноваций (потерь, отбраковки и пр.).

При определении коэффициента k_p используются методы исследования, основанные на соответствующих расчётных алгоритмах производственного процесса; на мнении специалистов-экспертов (в том числе SWOT-анализ) и статистические, использующие вероятностное представление производственных процессов.

Коэффициент k_ф характеризует фактическое распространение новаций: его увеличение обуславливает снижение себестоимости продукции и соответственно увеличение прибыли фирмы. При определении коэффициентов k_и и k_ф используются социологические методы исследования (и другие методы, используемые при мониторинге рынка), основанные на результатах анкетирования реальных и потенциальных потребителей продукции.

Конкретный объём спроса на новшество (Vс) зависит от многих факторов и в первую очередь от его цены (Цн), а также от качества и количества предлагаемого товара (услуг) [3, 4]. В связи с этим целью исследования является разработка динамических методов формирования рыночной цены на инновации, позволяющие гибко корректировать политику ценообразования фирмы, ориентированную на конъюнктуру рынка [5, 6].


РЕЗУЛЬТАТЫ ИССЛЕДОВАНИЯ

Для анализа динамики цен в любом заданном интервале предлагается использовать, например, модели архимедовых спиралей (рис.1). Кривая (спираль) представляет собой путь, описываемый некоторой точкой, движущейся с постоянной скоростью v по лучу, вращающемуся около полюса (точки Р) с постоянной угловой скоростью . В качестве полюса принимается точка пересечения С_n и Пр (точка рыночного равновесия Р), через которую проходит ось х.

Уравнение кривой (математическая модель) в полярных координатах:  = а  , где а = v / 0, -  <  < . Величина  определяет количество циклов (витков спирали) [7], программно (для ЭВМ) ее можно задать через величины Ц и V. Например: 0,6Ц_р  Ц_i < 2Ц_р или 0,5 V_p  V_i < 2,5V_p соответственно определит диапазон анализа (при планировании). Кривая Ф1: 0   < + ; Ф2: -  <   0. Для обеспечения условий, предусмотренных в примере (Ц_i и V_i), производим перенос исходной системы координат Ц0V для совмещения точки 0 с точкой Р, а оси х с осью V. После выполнения всех расчетов производится перенос системы координат в исходное положение.





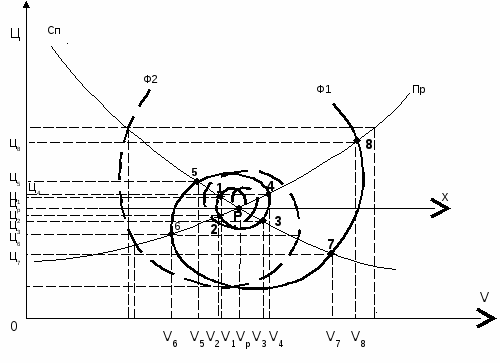
Рис.1. Формирование цены по спирали Архимеда


Кривая Ф1 пересекается с С_n в точках 1, 5, ..., n и в точках 3, 7, ..., m, а с Пр в точках 2, 6, ..., t и в точках 4, 8, ..., q, находящихся друг от друга на расстоянии l: l_1-5 = l_2-6 = l_i = 2a. Задавая параметры v через величины V_i и Ц_i, а  через интервалы времени этапов цикла (или суммы реализации товара между точками 1-2, 2-3, 3-4 и т.д.), тем самым устанавливаем величину а и соответственно радиус кривизны:

R() = a(³ + 1)^3/2/(² + 2).

Задавая различные значения исходным параметрам с помощью ЭВМ, определяем гамму динамики цен Ц_i (соответственно и объема реализации V_i). На основании анализа полученных данных с учетом политики ценообразования фирмы устанавливаются плановые показатели.

Если при планировании необходимо учесть какие-либо ограничения (квоты, объем производства, предельную величину цены товара и т.п.), то при планировании целесообразно использовать модель гиперболические спирали (рис. 2).

Уравнения (математические модели) в параметрическом виде: 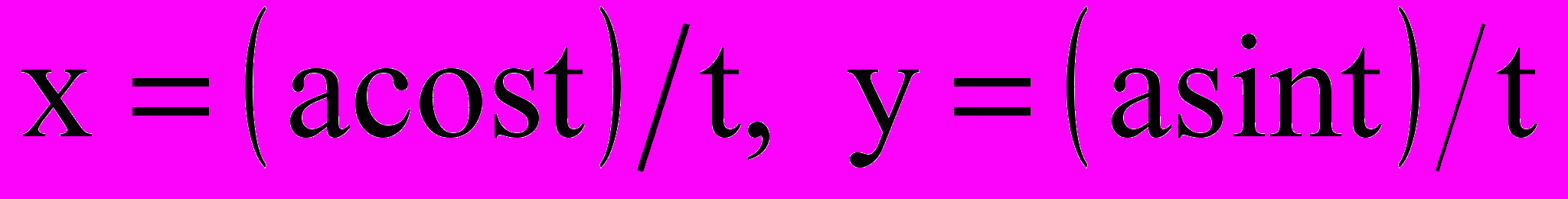. Кривая Ф₁: 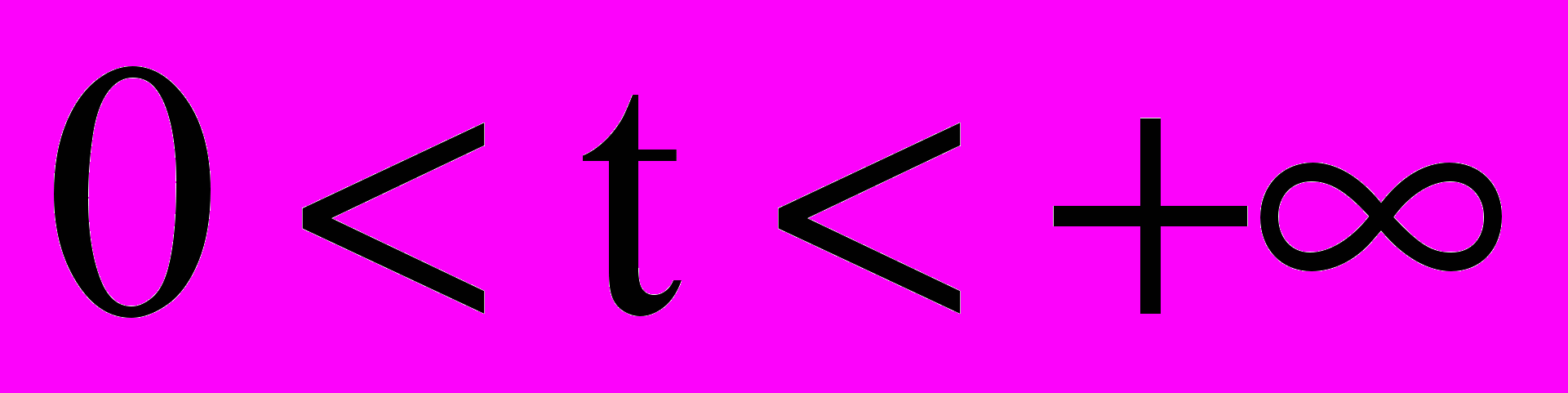, а Ф₂: 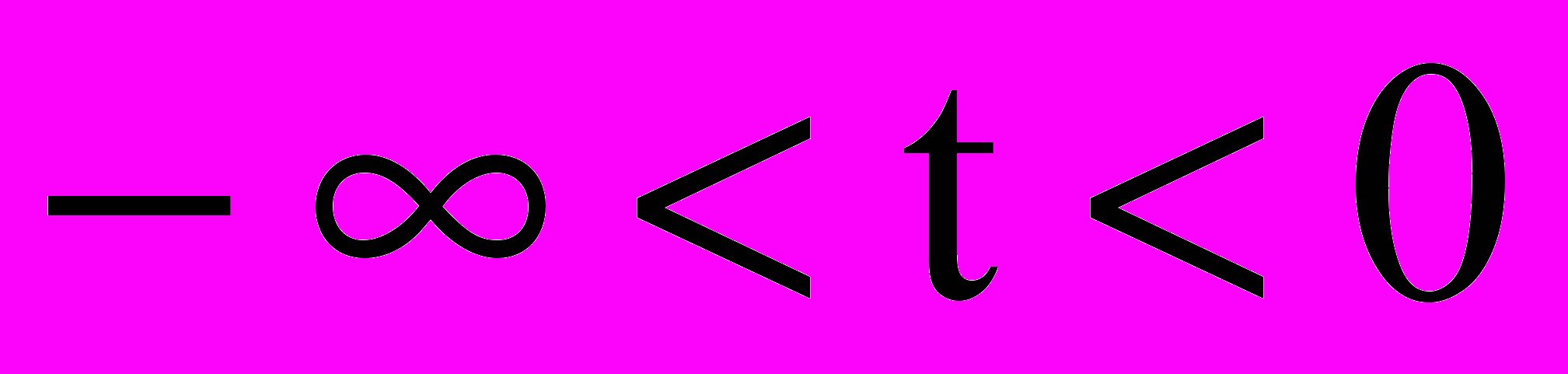. Кривые Ф₁ и Ф₂ расположены симметрично относительно оси у. В процессе анализа производится соответствующий перенос системы координат ЦОV [7].

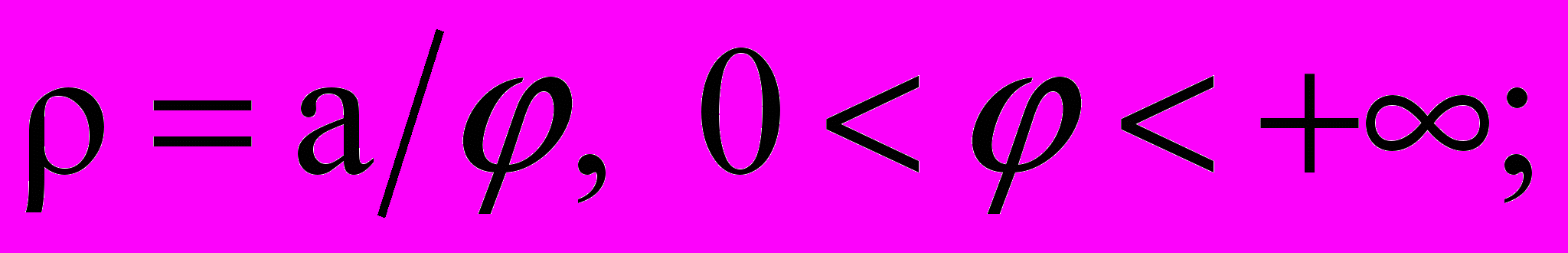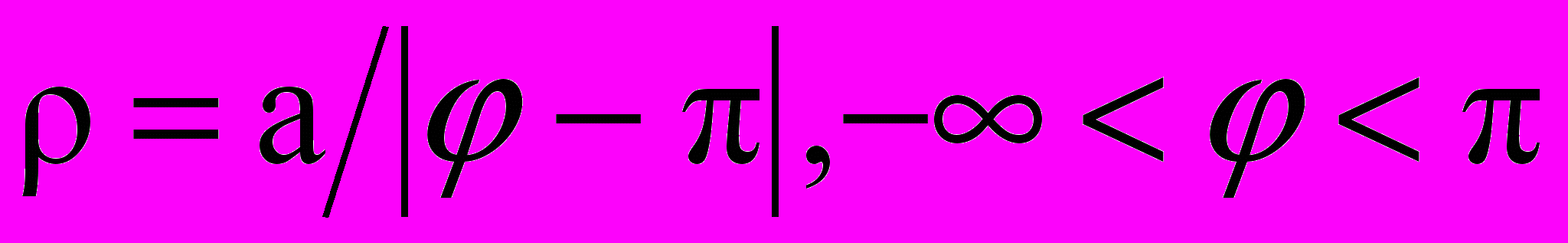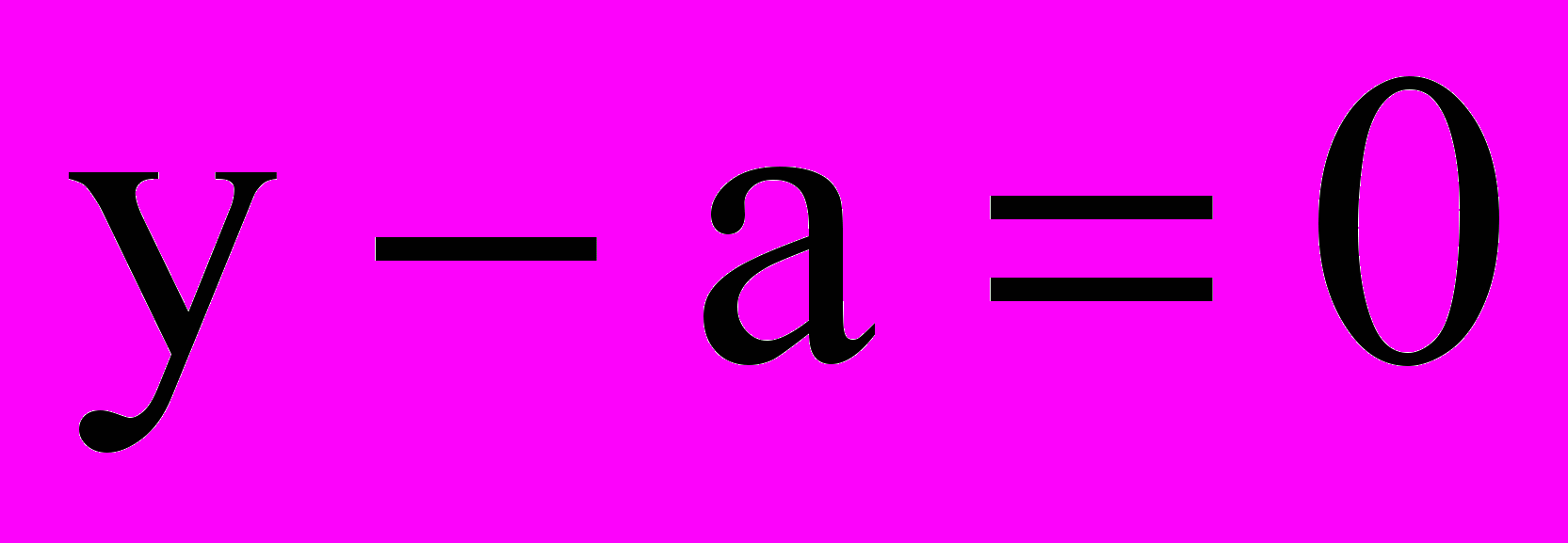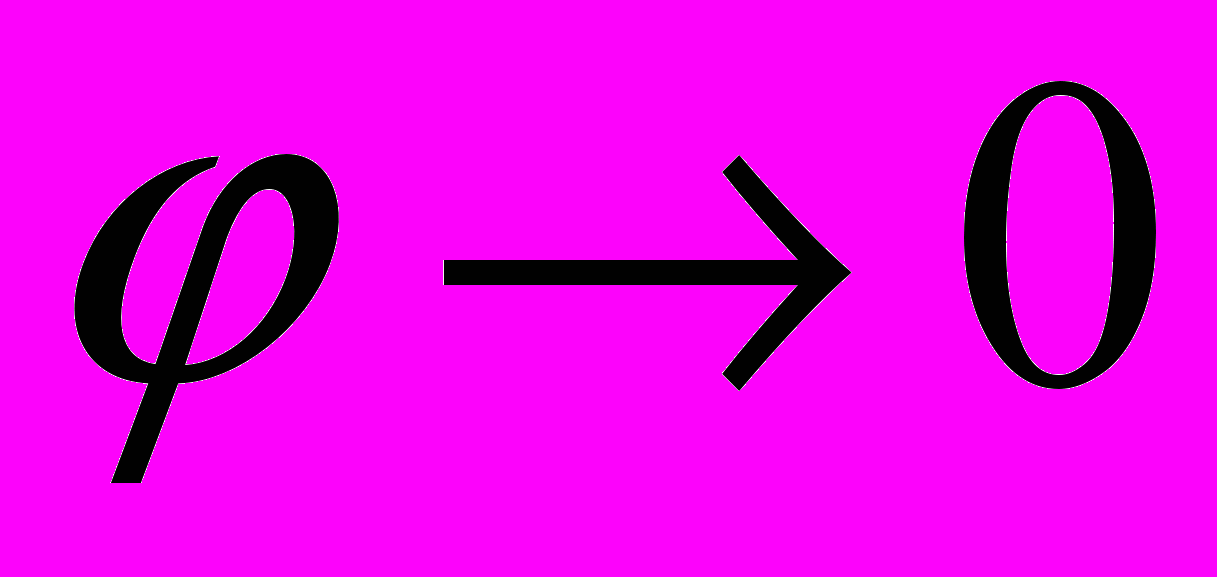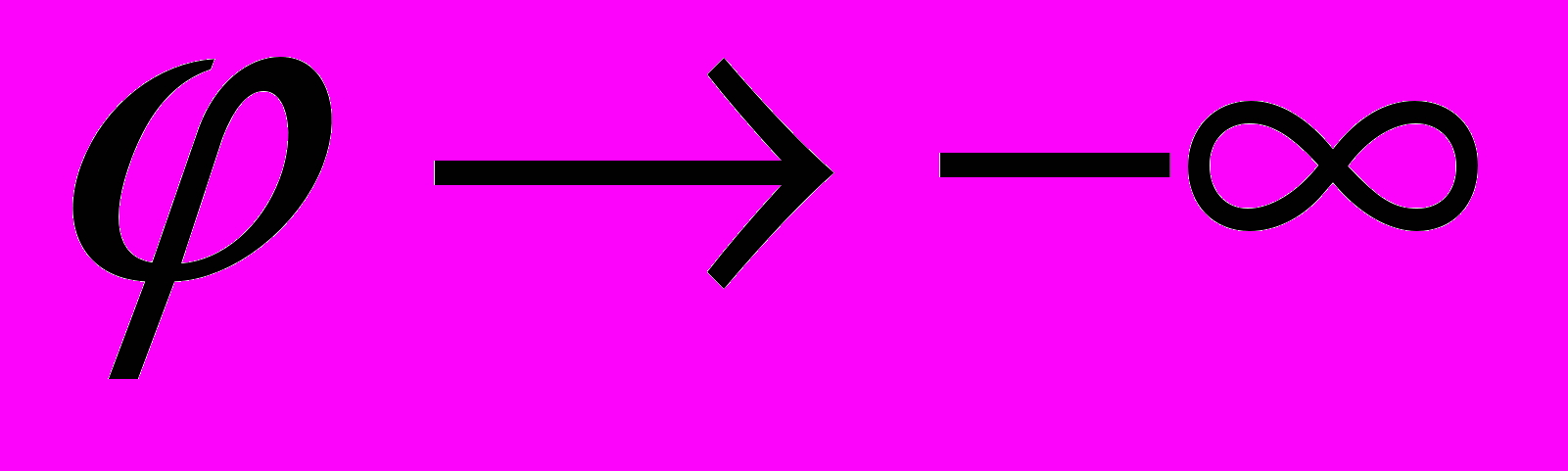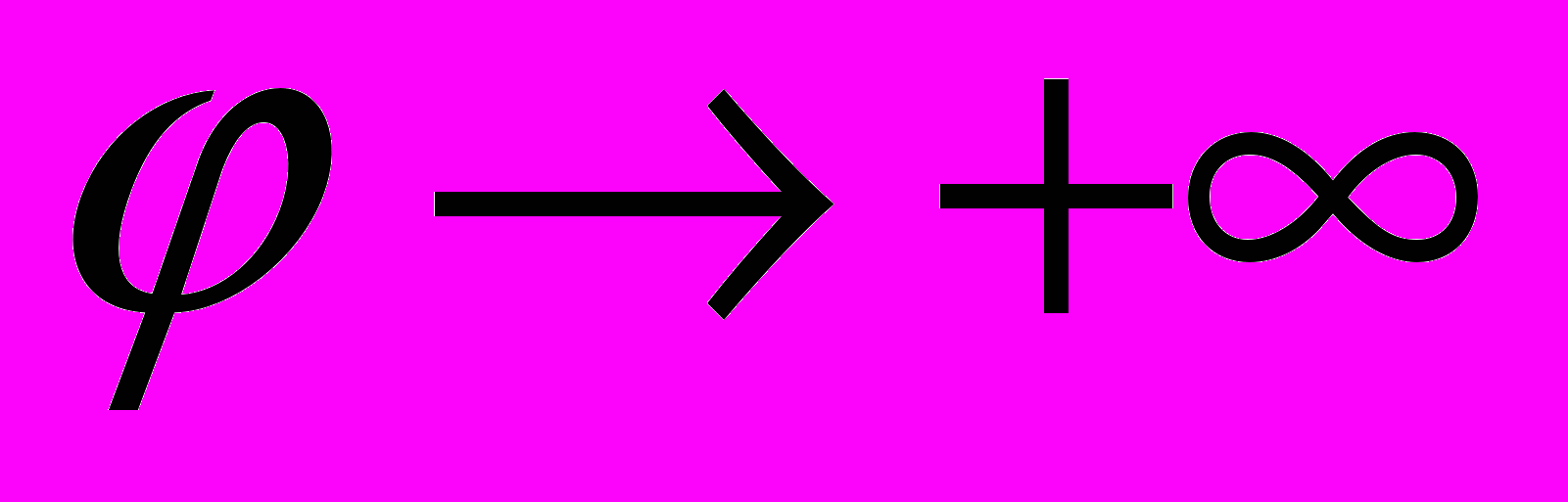Уравнение в полярных координатах: кривая Ф₁: а Ф₂: . Для обеих кривых (Ф₁ и Ф₂) прямая – асимптота ( и ), а точка Р – асимптотическая точка ( и). Радиус кривизны (Ф₁):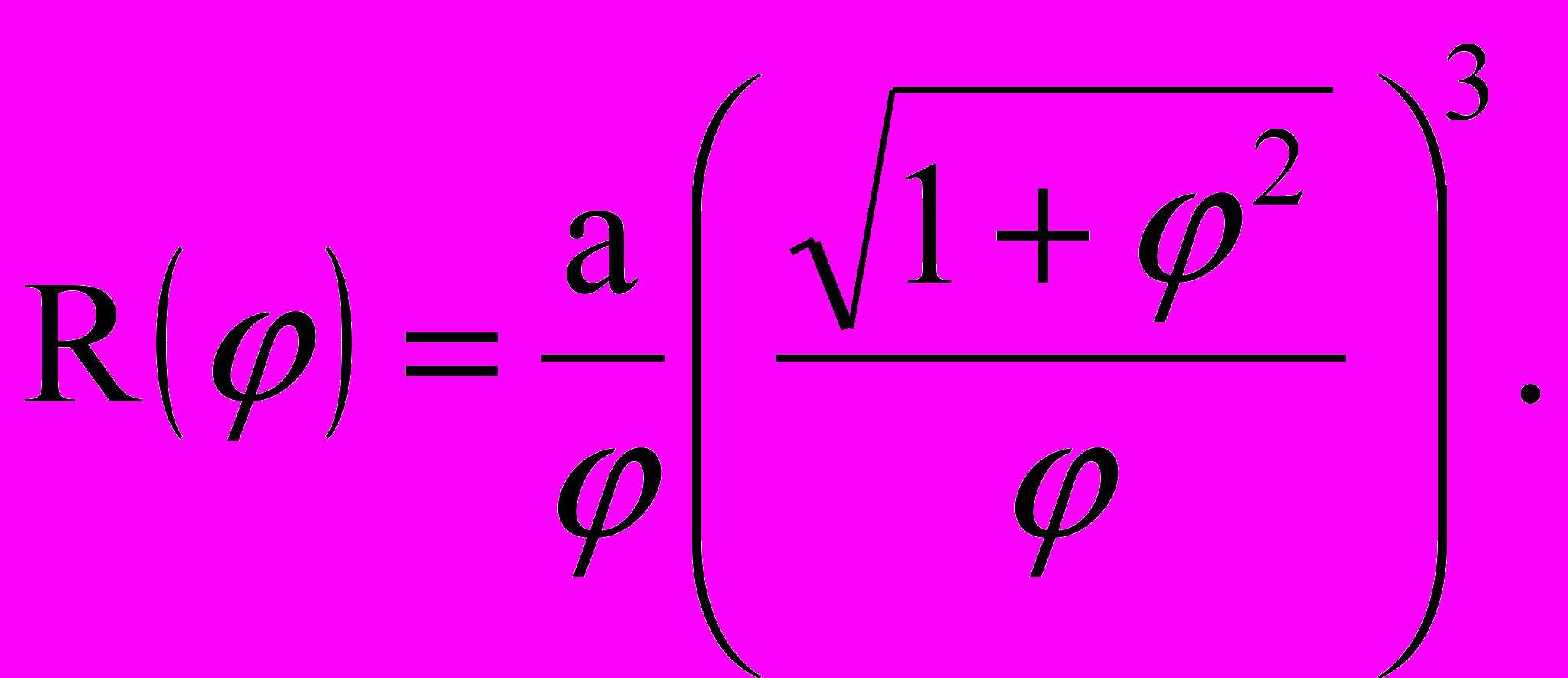







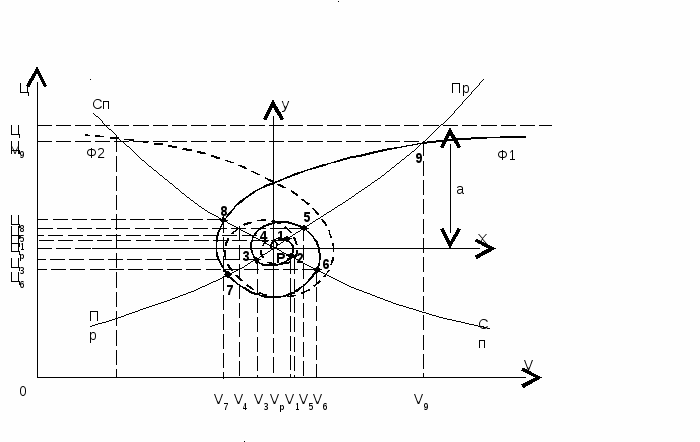
Рис. 2. Формирование цены по гиперболической спирали


Значение а определяется ограничивающим параметром (например, Ц_m или др.).

Задавая различные значения анализируемым параметрам, определяем соответствующую динамику цены Ц_i (и объема V_i) по мере достижения ограничивающего параметра заданной величины (а).

На основании полученных данных фирма устанавливает плановые показатели с учетом конкретных ограничивающих факторов.

При определенных условиях при планировании могут быть использованы и логарифмические спирали для описания процесса формирования рыночной цены.

Уравнение (математическая модель) в полярных координатах:  = ае^k, a  0, -  <  < + . Кривая пересекает линии спроса и предложения под одним и тем же углом . При этом k = ctg . При  = /2, т.е. k = 0, кривая превращается в окружность (получаем замкнутый цикл формирования рыночной цены).

Различные значения  определяются соответствующими величинами Ц (или V).

Данная методика позволяет производить анализ в достаточно широком диапазоне с возможным переходом от разомкнутого к замкнутому (и наоборот) циклу формирования рыночной цены.

Полюс (рыночная точка равновесия) Р – асимптотическая точка кривой. Радиус кривизны 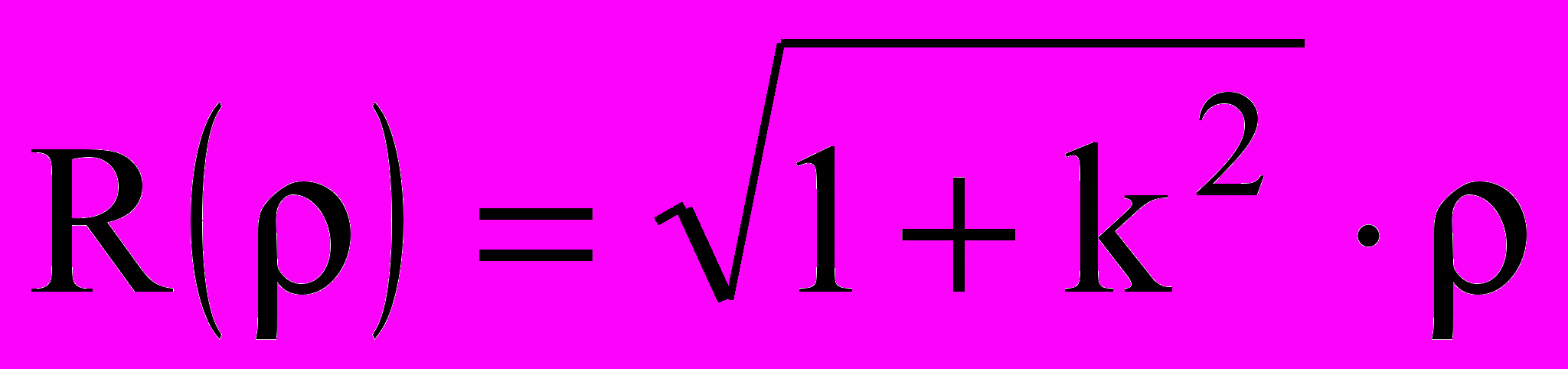количественно характеризует планируемую динамику цен.

Плановые показатели фирма устанавливает на основании анализа результатов расчета.

В зависимости от финансового положения, производственных условий, политики ценообразования и других внутренних и внешних факторов фирма выбирает соответствующую методику анализа динамики цен на этапе планирования вывода товара на рынок. Может быть использована одна из рассмотренных математических моделей (спиралей) формирования рыночной цены, а также и другие. Кроме того, в процессе планирования в качестве альтернативных вариантов возможно использование двух (и более) математических моделей.

Если при планировании устанавливаются определенные параметры и в соответствии с ними рассчитывается рыночная динамика (планируемая) цен, то в реальных условиях рынка (после вывода товара на рынок) изменение величин параметров носит вероятностный характер, т.е. имеет неизвестные функциональные зависимости. Поэтому для анализа параметров рыночных ситуаций необходимо использовать соответствующие математические модели. Этим условиям наиболее соответствуют дифференциальные уравнения.

Дифференциальное уравнение – уравнение, содержащее неизвестную функцию одного или нескольких переменных (параметров ценообразования), независимые переменные (параметры) и производные неизвестной функции по независимым переменным. Проанализировать рыночную ситуацию, т.е. решить дифференциальное уравнение – это значит, найти все неизвестные функции, обращающие уравнение в тождество. В общем случае неизвестные функции определяются дифференциальным уравнением неоднозначно (решения может вообще не существовать), поэтому на искомые функции необходимо «наложение» дополнительных условий в соответствии с политикой ценообразования фирмы и другими факторами реально складывающейся рыночной ситуации. Интегрирование уравнения – это нахождение функции у(х), которая удовлетворяет этому уравнению, т.е. функция у(х) - решение дифференциального уравнения. Общее решение обыкновенного дифференциального уравнения порядка n имеет вид:

у = у (х; С₁, ..., С_n),

где C₁, ..., С_n – постоянные, характеризующие соответствующие параметры рыночной ситуации.

При любом наборе конкретных постоянных получаются частные решения. Графическое изображение частного решения - интегральная кривая. Общее решение дифференциального уравнения n-го порядка определяет n-параметри-ческое семейство интегральных кривых. Таким образом, дифференциальное уравнение описывает семейство кривых.

Например, семейство окружностей (замкнутых циклов формирования цены) содержит три параметра: (х – С₁)² + (у – С₂)² = С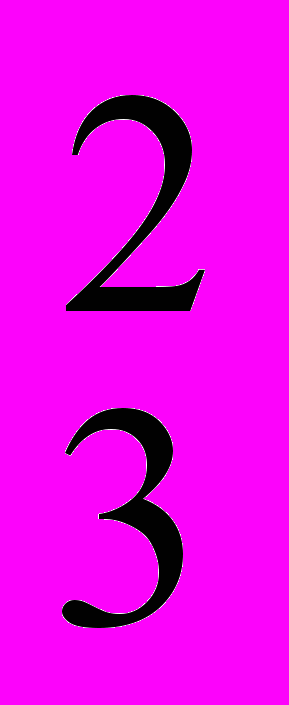, где С₁ и С₃ характеризуют величины Ц и V. Трехкратное дифференцирование приводит к уравнениям (х – С₁) + (у – С₂) у= 0; 1 + (у - С₂) у+ (у)² = 0; (у – С₂)у+3у(у)² = 0. Исключая С₂ из двух последних уравнений, получаем: у(1 + (у)²)–3у(у)³ = 0.

Динамика цен практически характеризуется несколькими неизвестными функциями: у₁(х), у₂(х), ..., у_n(x), поэтому для анализа может понадобиться система уравнений. Система обыкновенных дифференциальных уравнений имеет вид:

F_i x, y₁, y₂, ..., y_n, y₁, ..., у_n, y₁^(r), ..., y_n⁽ⁿ⁾  = 0. (i = 1, ..., n).

Решением системы обыкновенных дифференциальных уравнений является любая упорядоченная совокупность функций у₁(х), ..., у_n(x), обращающих каждое уравнение в тождество.

Для анализа динамики цен целесообразно в качестве математических моделей использовать дифференциальные уравнения 1-го порядка, в явном виде имеющие вид [7]:

у = f(x, y).

При анализе динамики цен практический интерес представляют особые точки дифференциального уравнения. Пусть

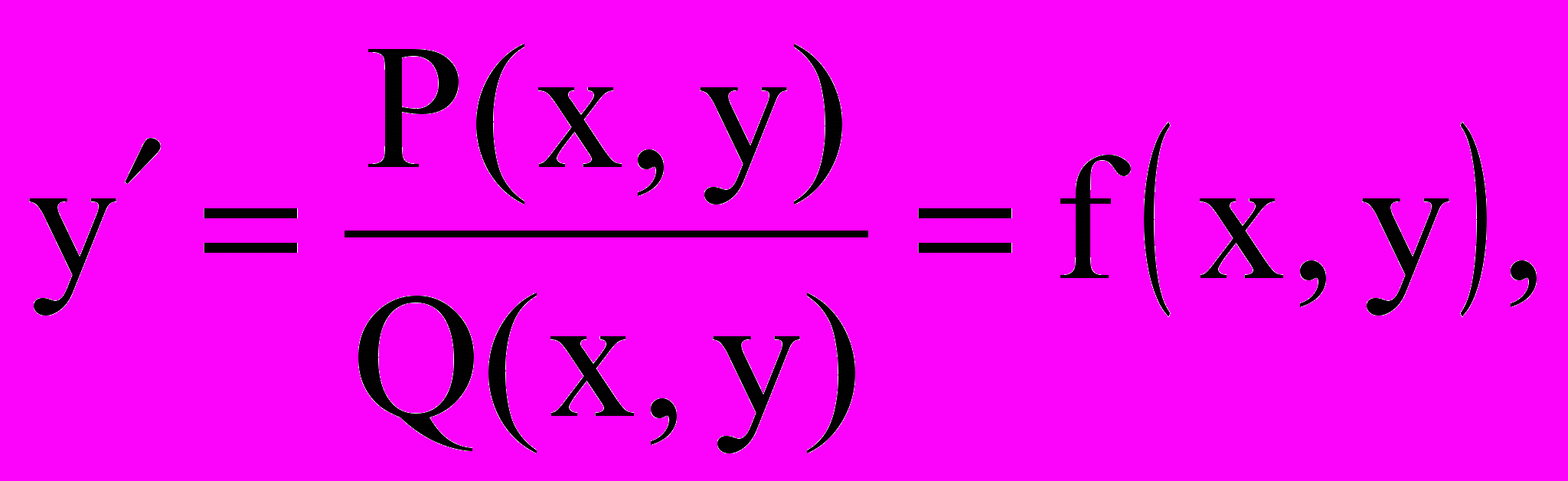(1)

где Р и Q – многочлены (характеризующие величины V и Ц) по х и у без общего множителя: производная 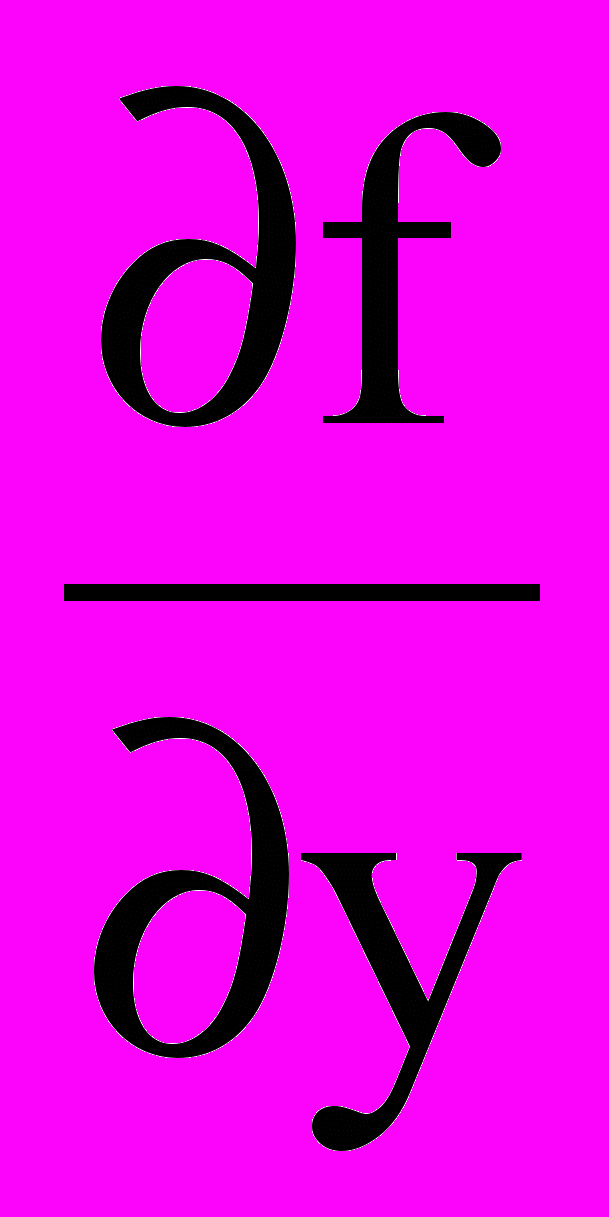обращается в бесконечность в тех точках (х₀, у₀), в которых Q(x₀, y₀) = 0.

В этих точках как правая часть уравнения 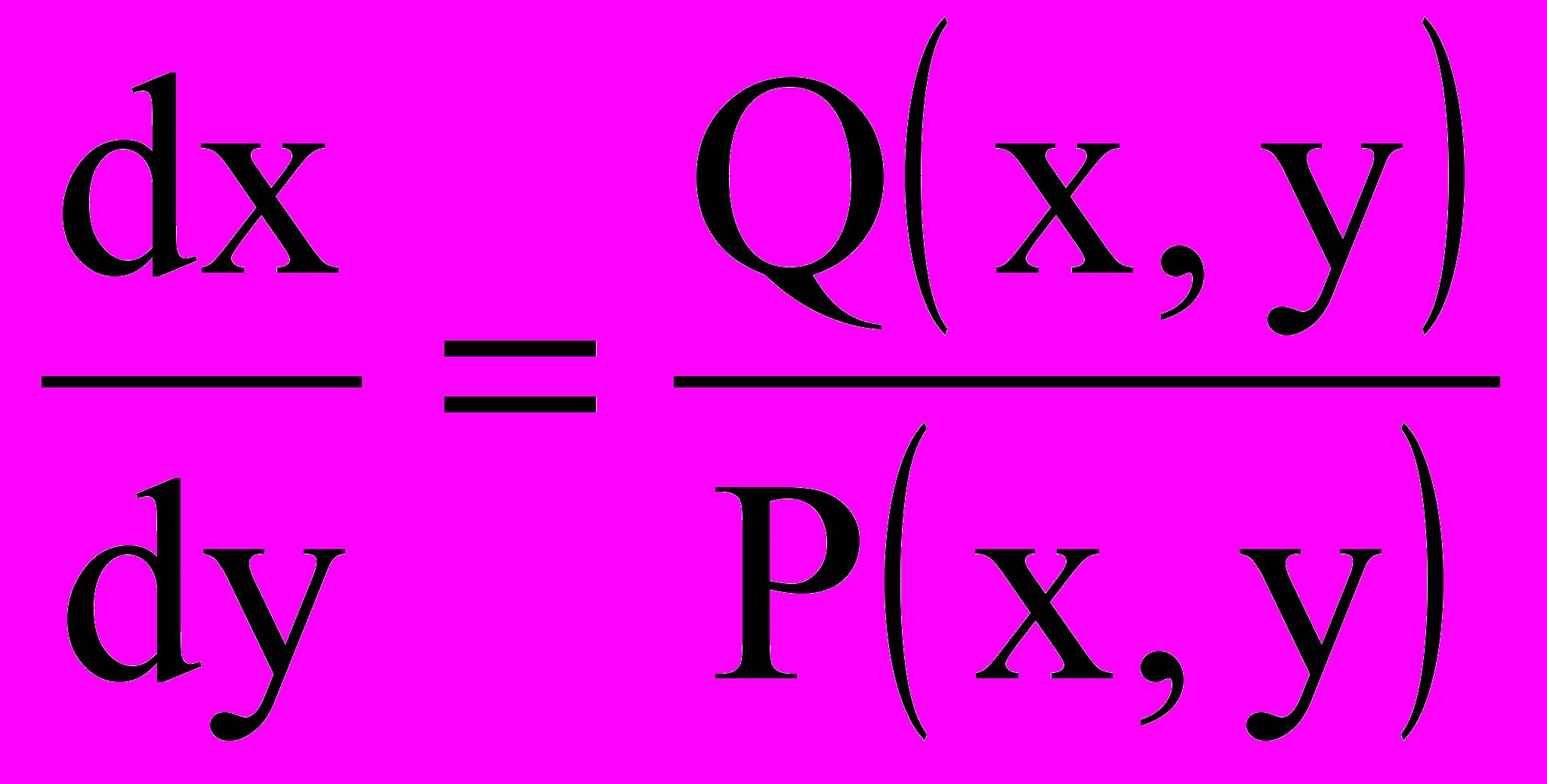(если Р(х₀,у₀)0), так и ее производная по х непрерывны. По теореме существования и единственности через такую точку проходит единственная интегральная кривая x = (y). Если Р(х₀, у₀) = Q(x₀, y₀) = 0 (при данных предположениях это может быть только в изолированных точках), то (х₀, у₀) называется особой точкой дифференциального уравнения (1). В нашем случае это точка Р рыночного равновесия. Особых решений для такого уравнения не существует.

Практический интерес для анализа динамики цен представляет дифференциальное уравнение вида [7]:


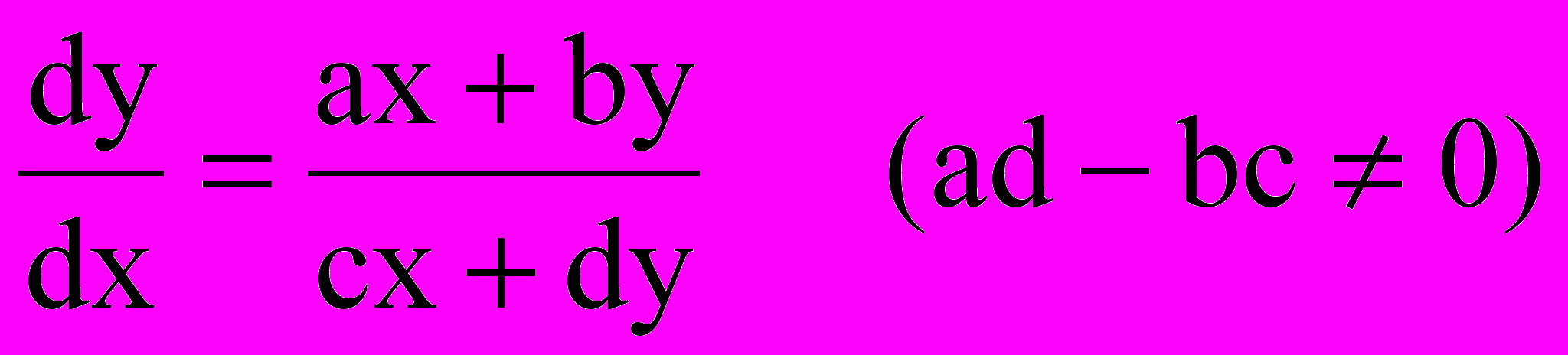(2)

(а, b, c, d – постоянные), имеет особую изолированную точку (0, 0), в нашем примере рыночного равновесия (Р). Через каждую другую точку, достаточно близкую к Р, проходит единственная интегральная кривая (характеризующая динамику цен). Каждая из интегральных кривых будет характеризовать соответствующую динамику цен, на которую также влияет и форма кривой, обусловленная постоянными (а, b, c, d), характеризующими соответствующие факторы ценообразования.

Рассмотрим корни z₁ и z₂ характеристического уравнения:



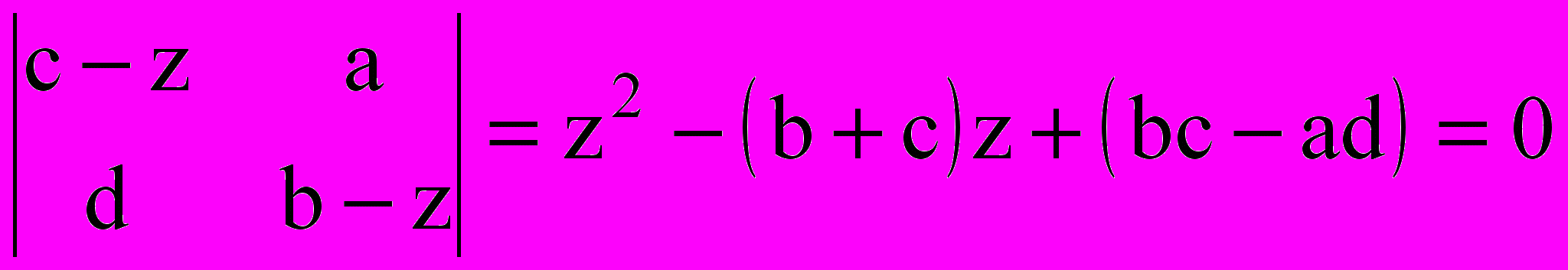
и приведем уравнение (2) при z₁  z₂ посредством замены переменных 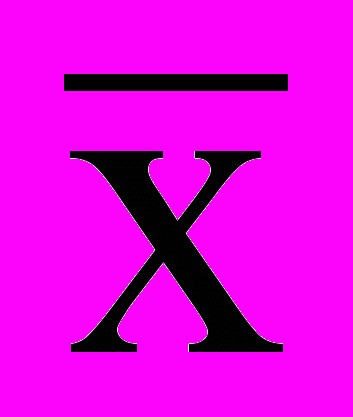= Ах + By, 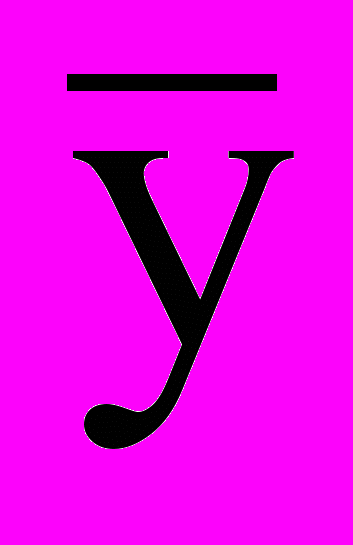= Cx +Dy, где А, В, С, D можно найти из систем



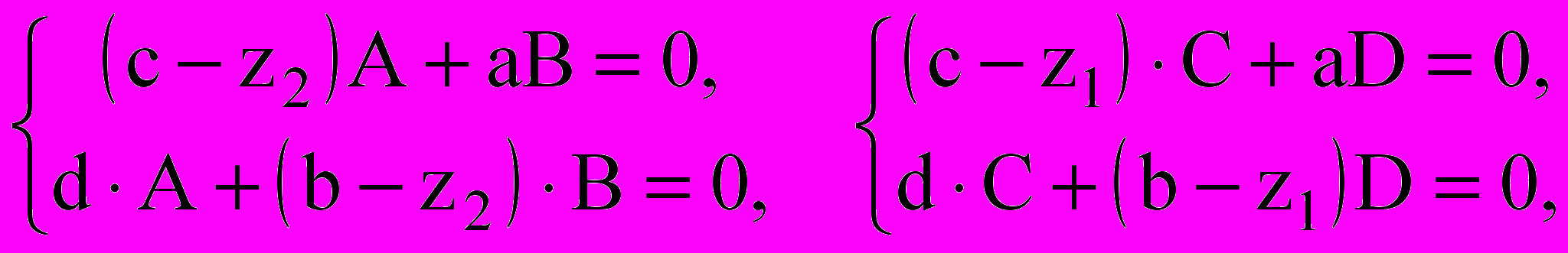
к дифференциальному уравнению:

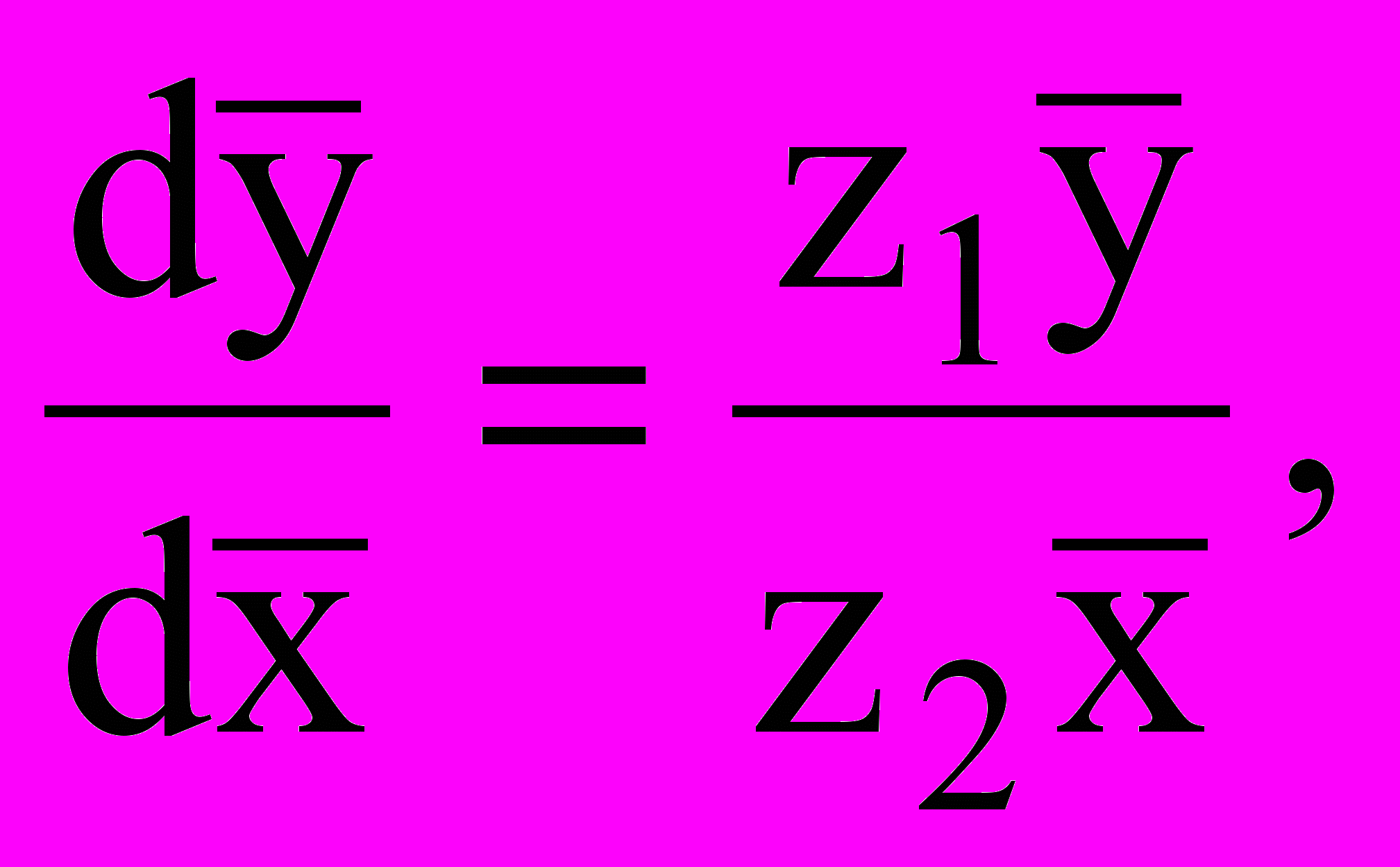(3)

его решение имеет вид: 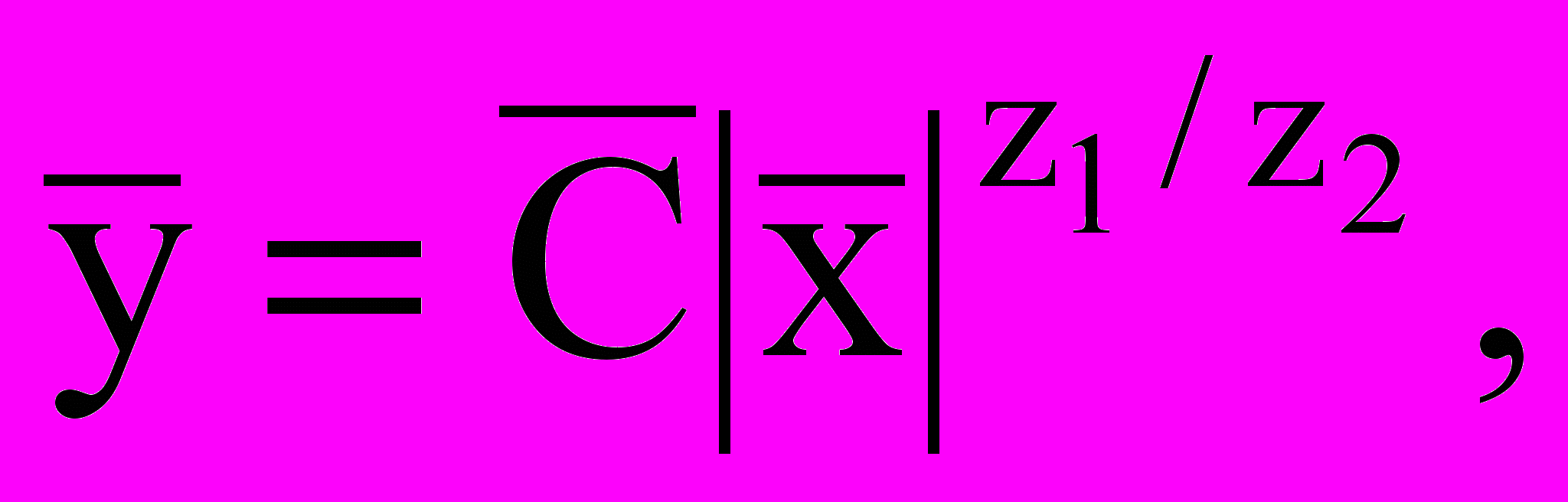а при z₀ = z₁ = z₂ посредством замены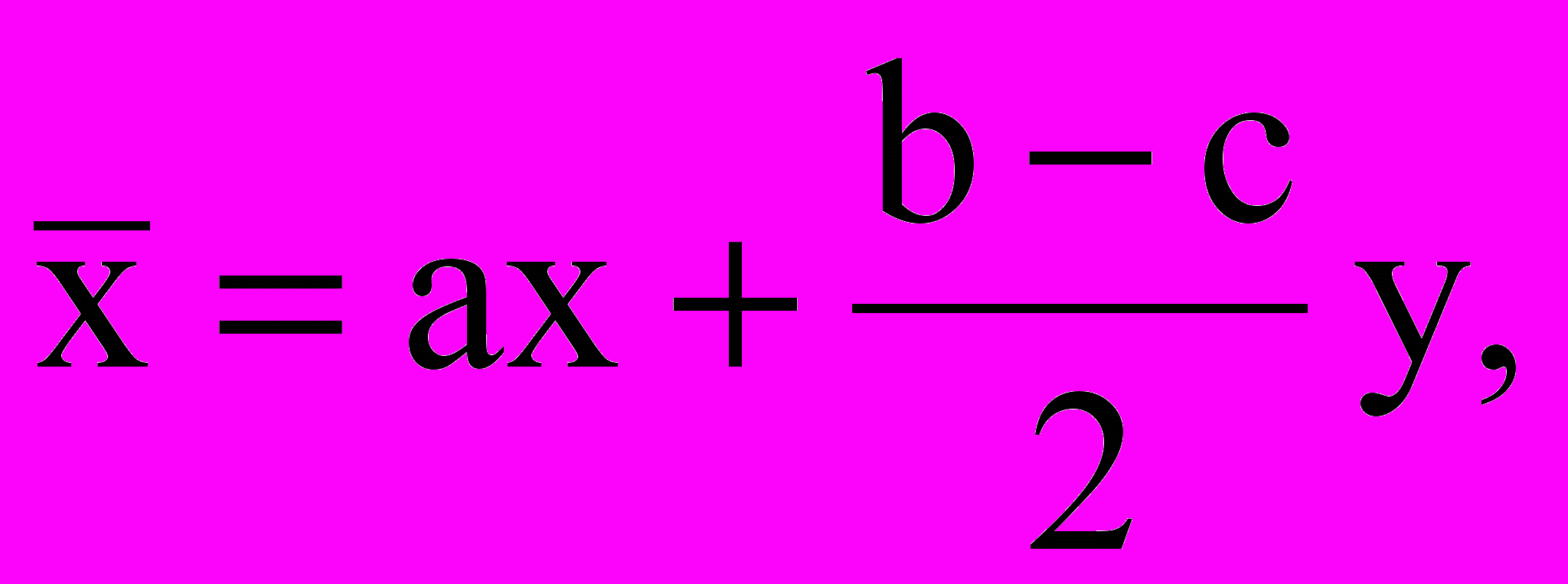 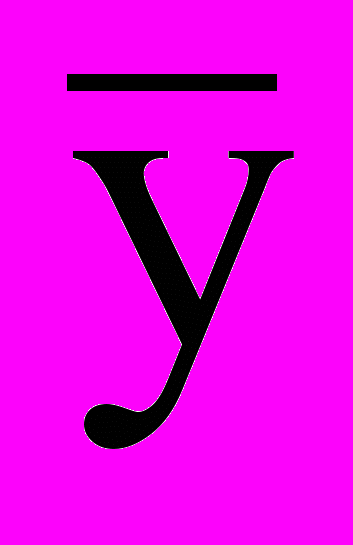= у – к уравнению:

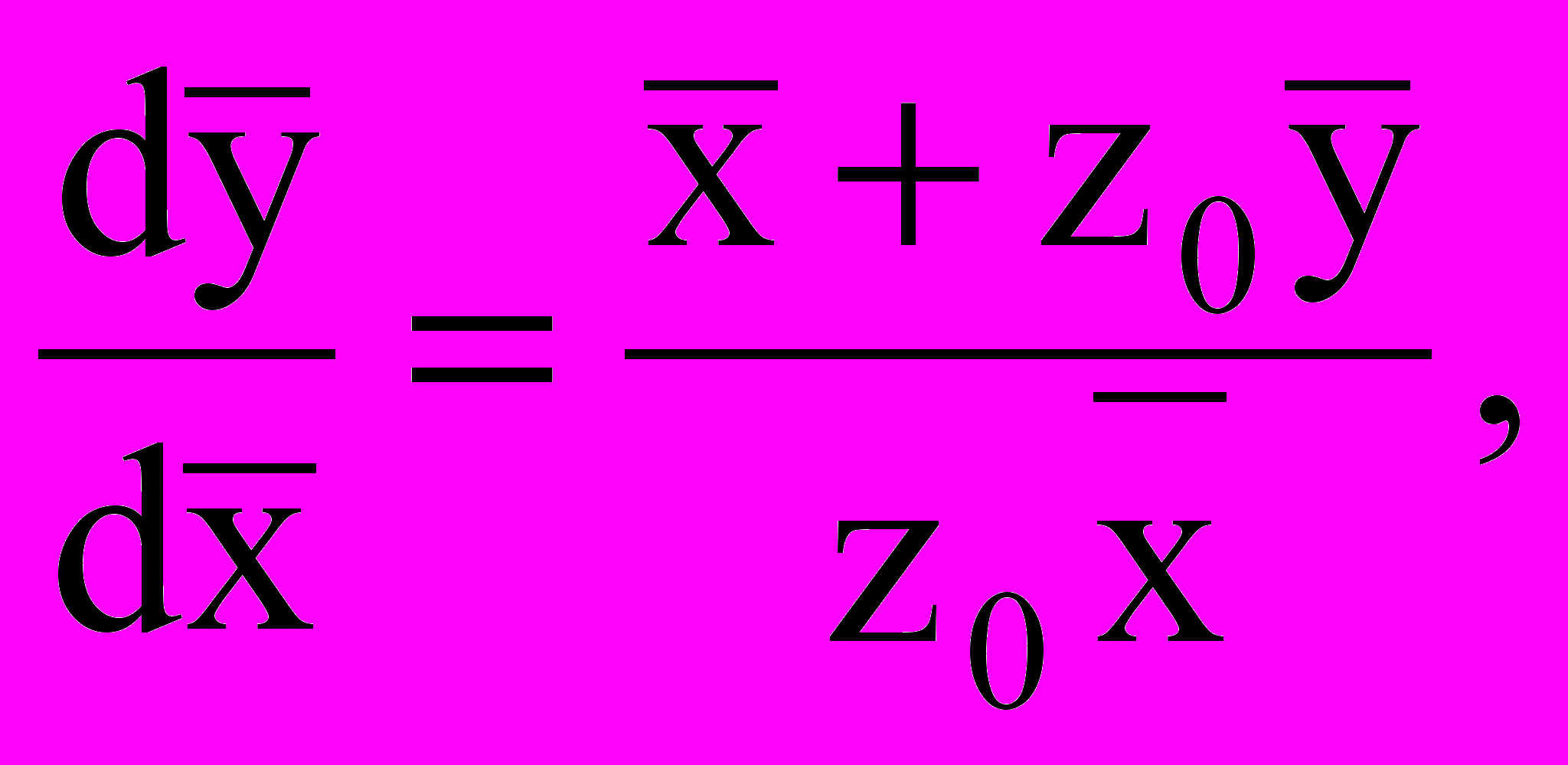(4)

его решение имеет вид:

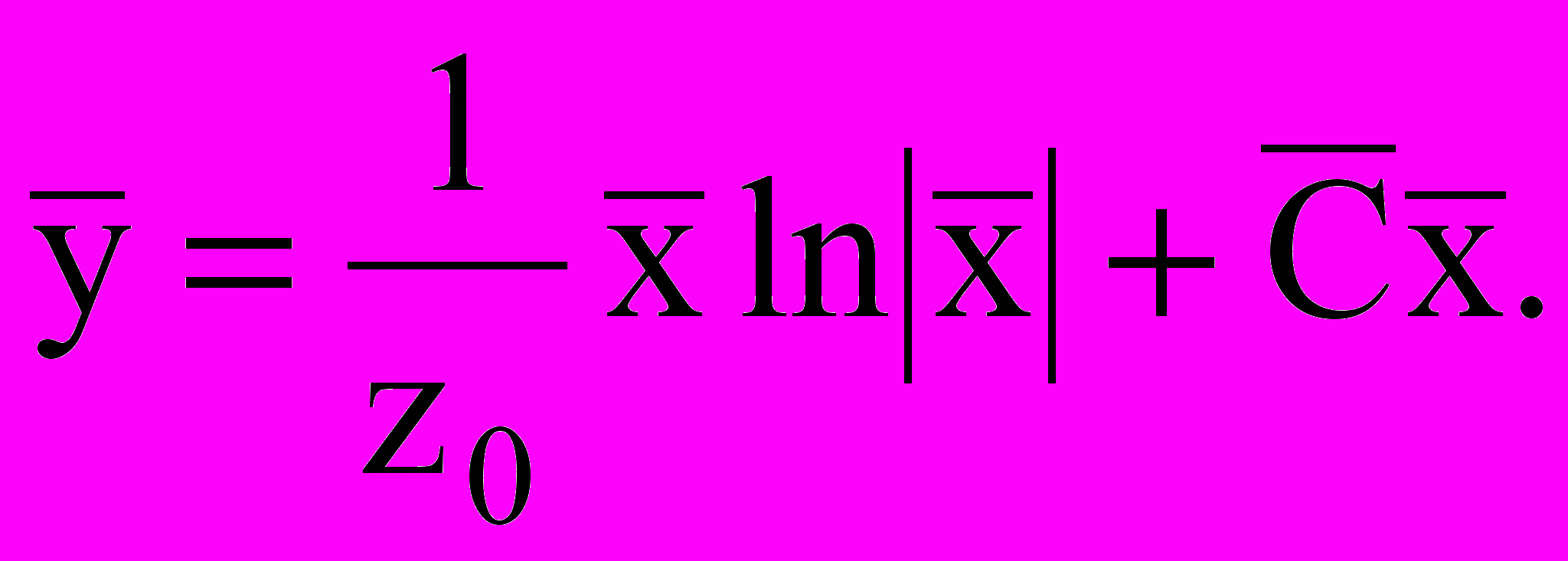
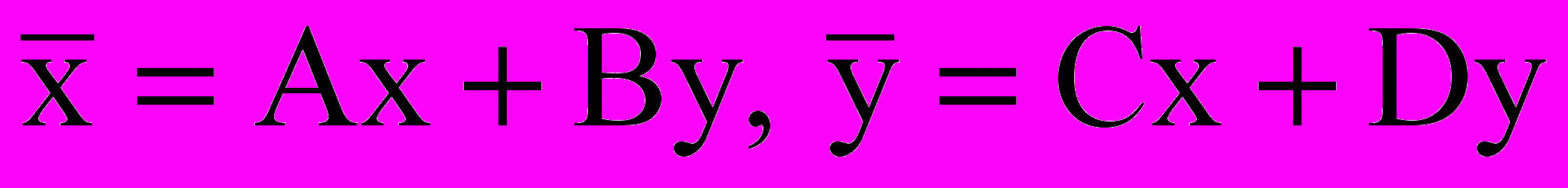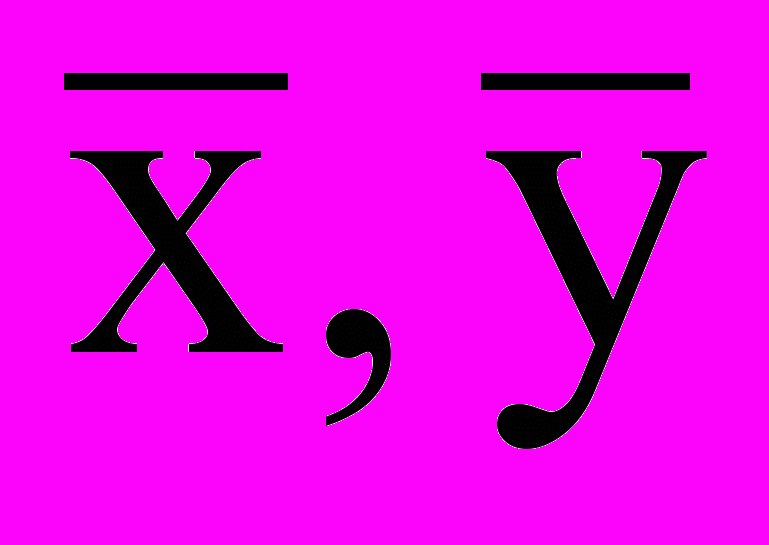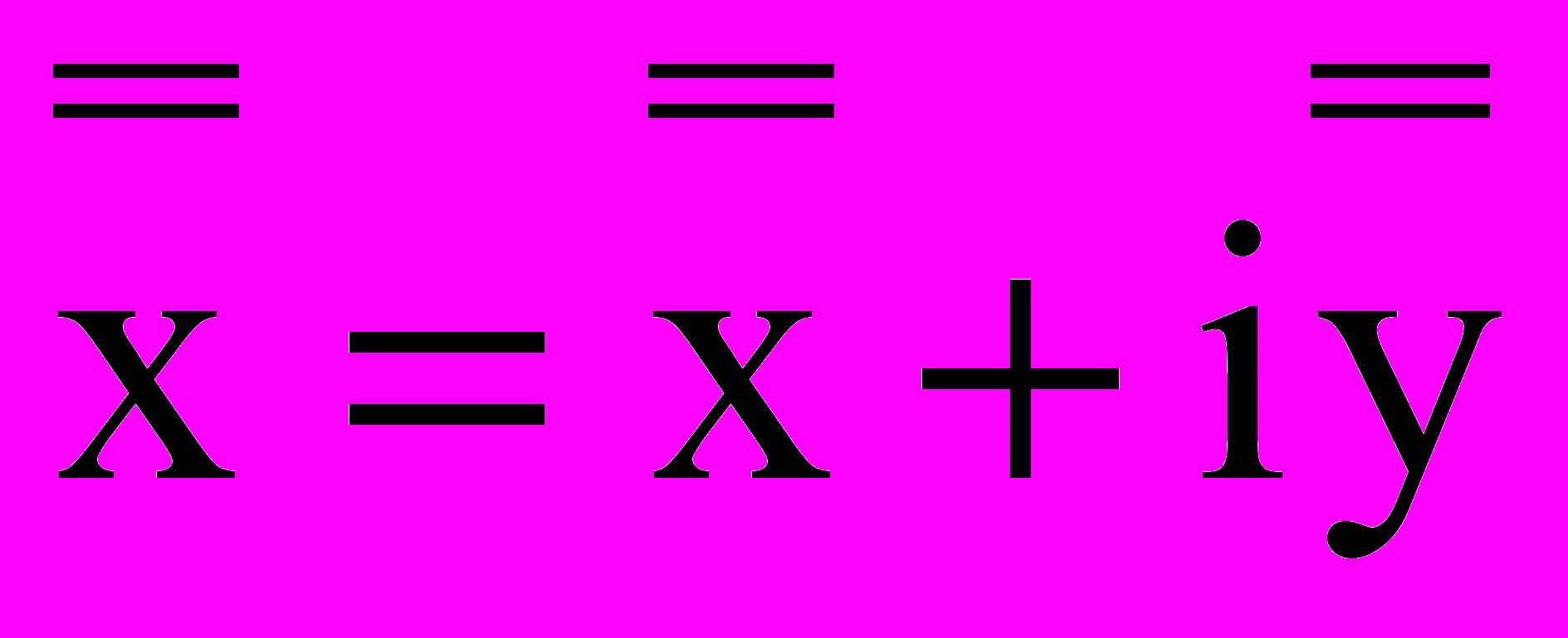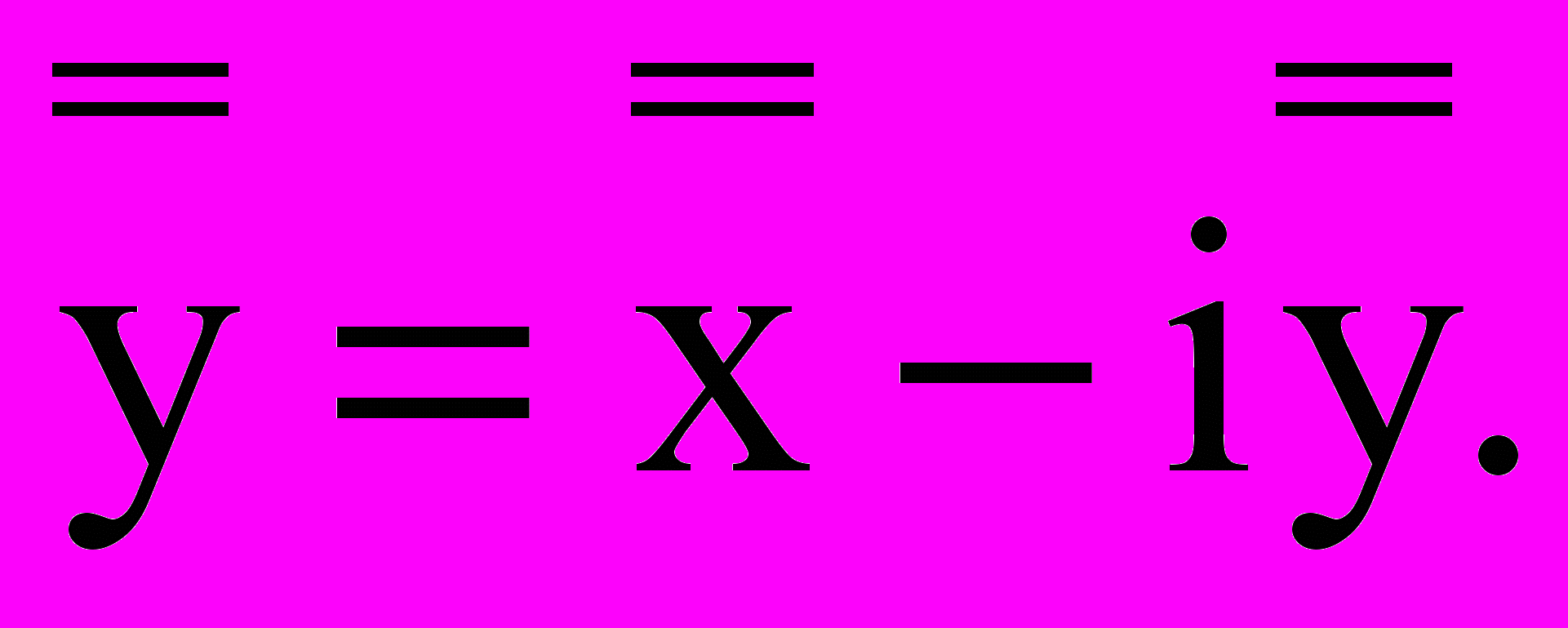В случае, когда корни z₁ и z₂ – комплексно сопряженные (но не чисто мнимые), особая точка называется фокусом. При замене переменных коэффициенты А и В можно определить так, чтобы они были комплексно сопряжены по отношению к коэффициентам С и D. Так как в общем случае для действительных х и у будут комплексными, то вводят новые переменные , полагая и Характер особой точки при такой замене не меняется. Общее решение уравнения (2) в координатах 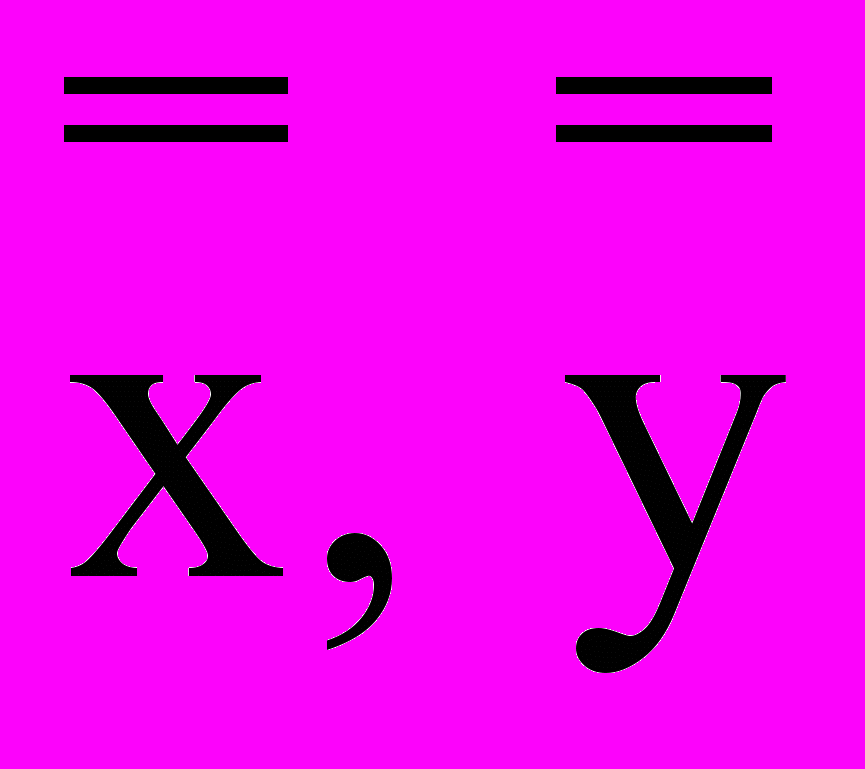имеет вид 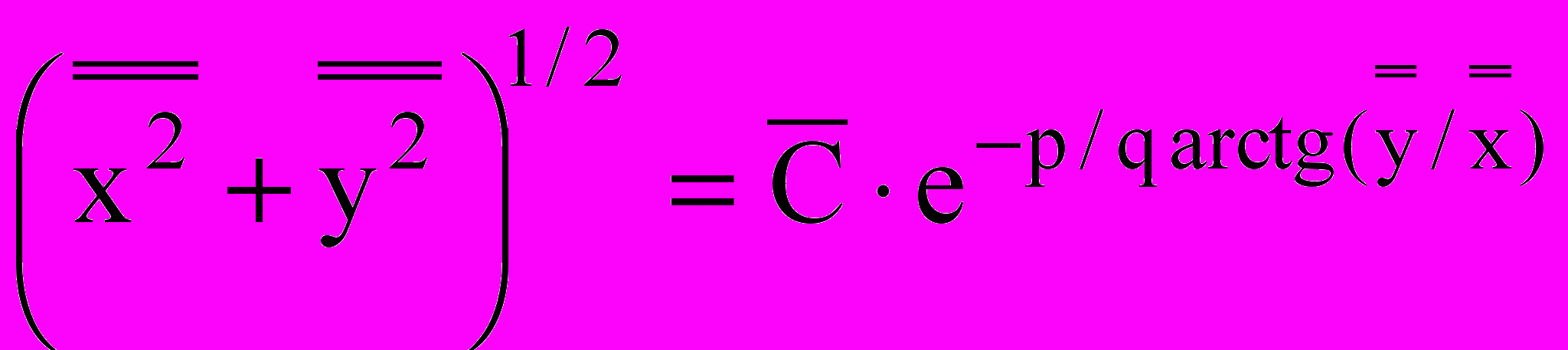где z₁ = p + iq, z₂ = p – iq, или в полярных координатах: 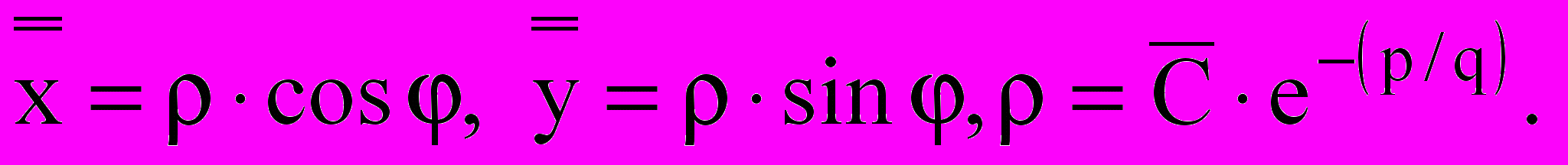Это – семейство логарифмических спиралей в плоскости 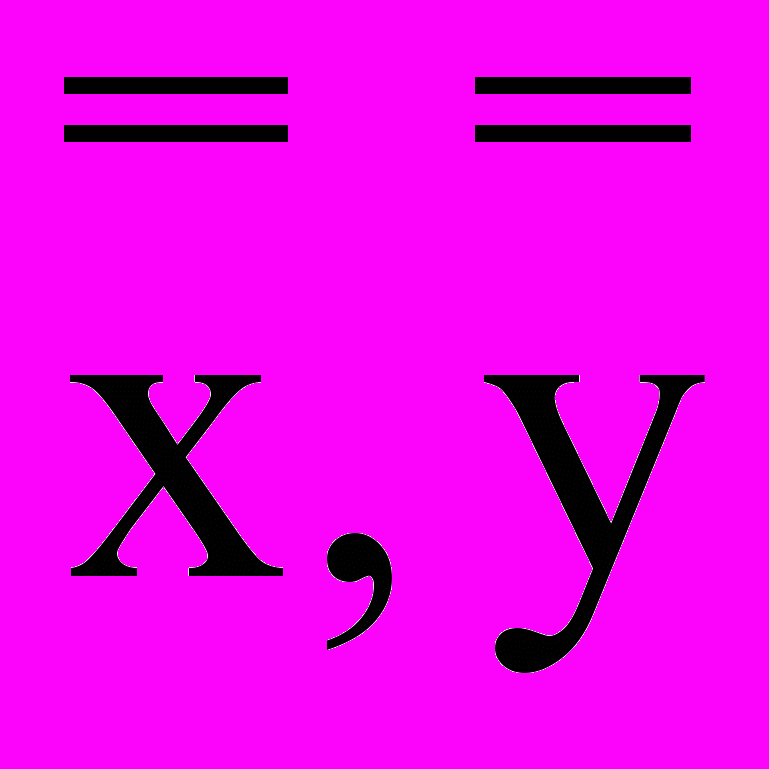с асимптотической особой точкой. Все кривые (которые могут быть использованы для анализа динамики цен) входят в особую точку (равновесную Р). С математической точки зрения они (кривые) не имеют в точке Р определенной производной и совершают бесконечное множество оборотов вокруг нее, что можно интерпретировать как функционирование в режиме рыночного равновесия.

Например, спираль разомкнутого цикла формирования рыночной цены имеет математическую модель (описывается уравнением):



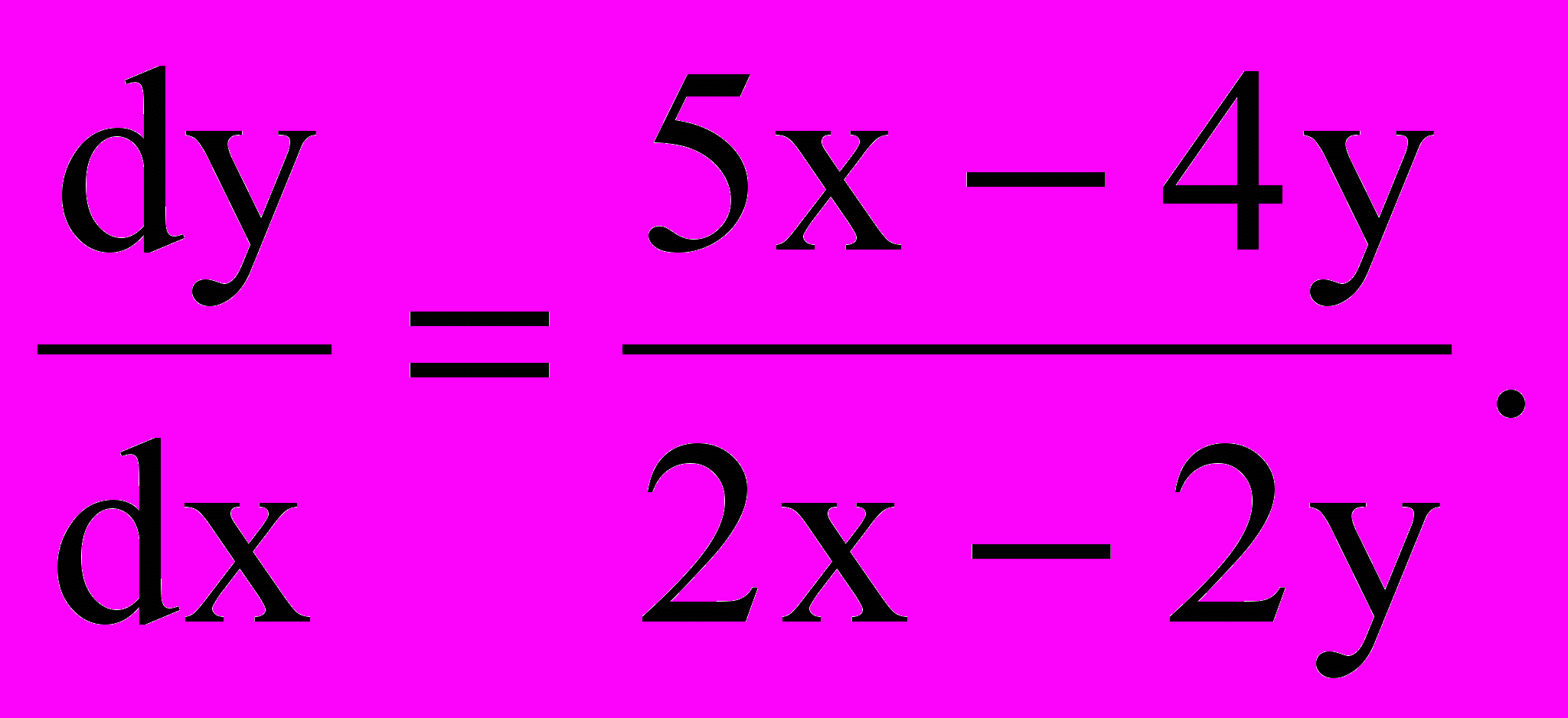
Характеристическое уравнение имеет корни z₁ = -1 + i, z₂ = -1 – i, и замена 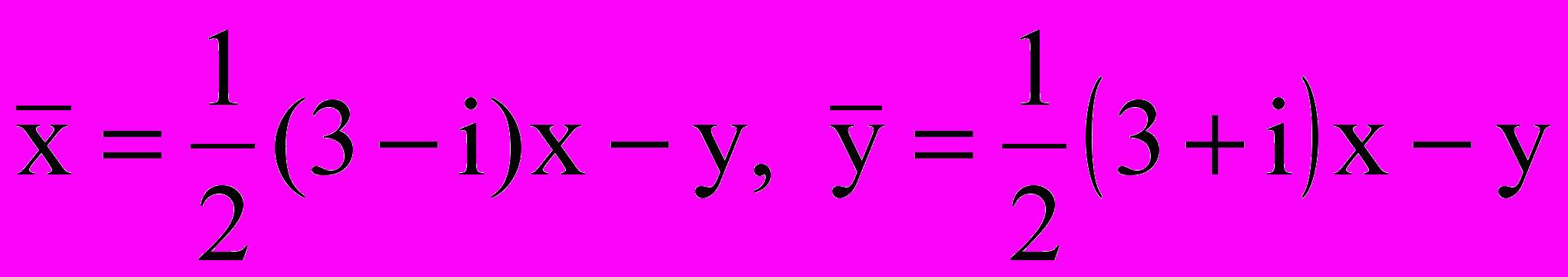приводит к уравнению: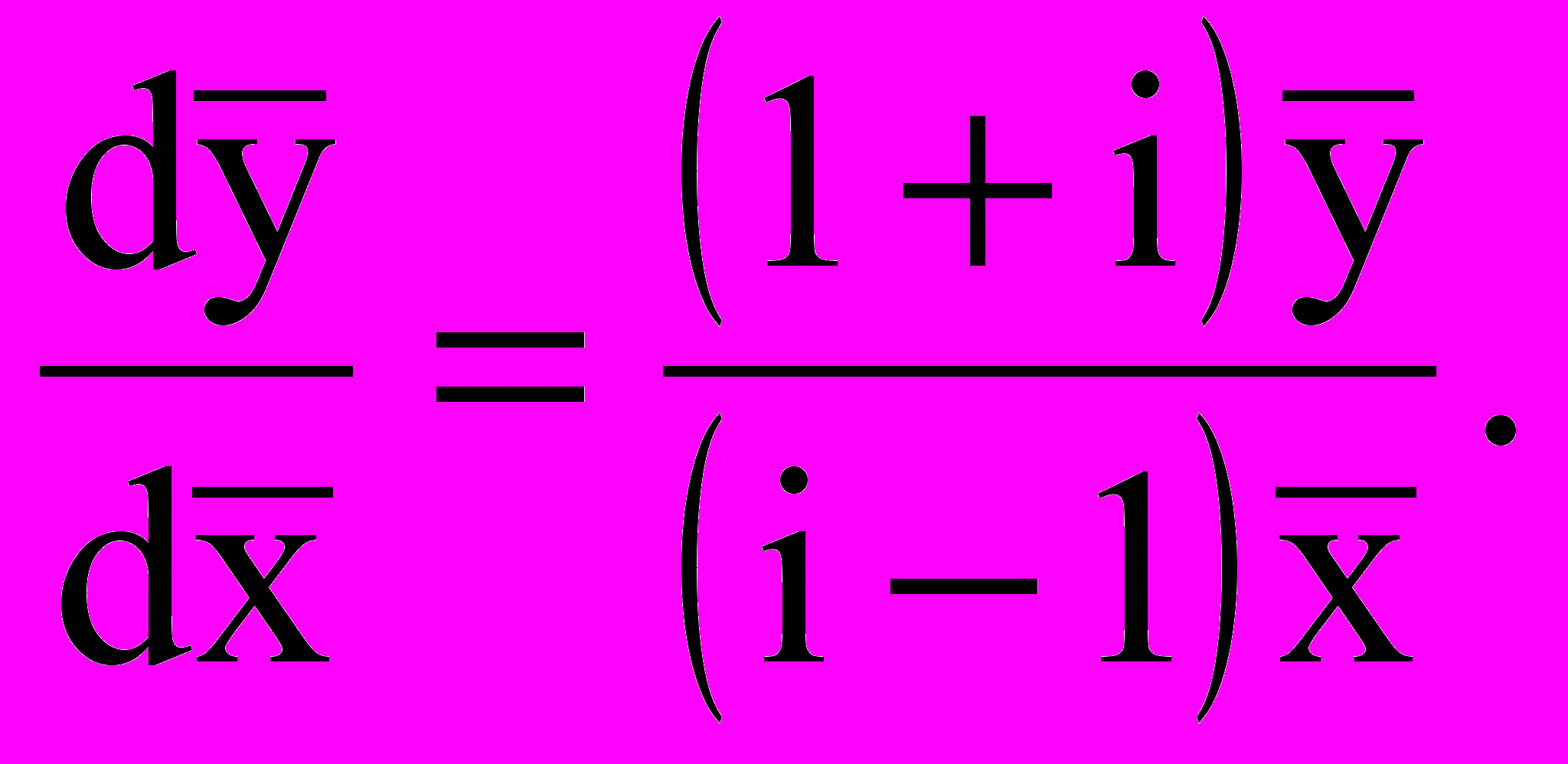



Замена 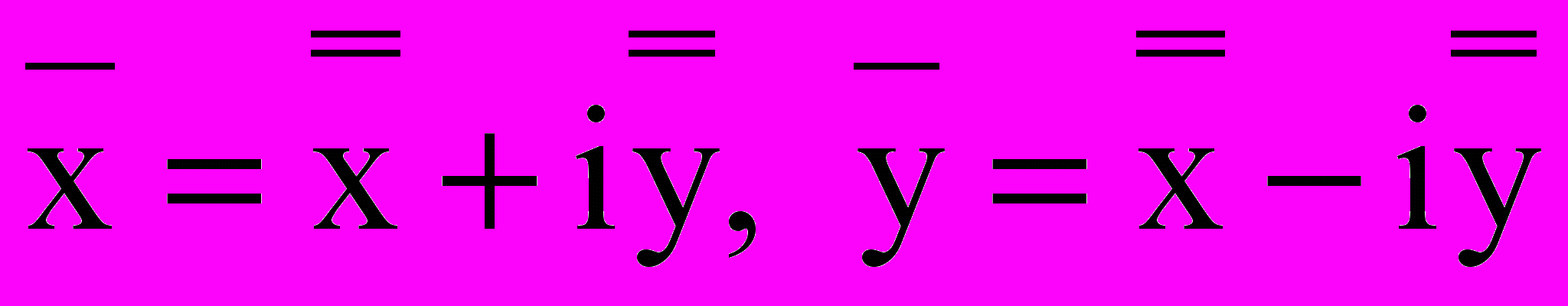приводит к уравнению: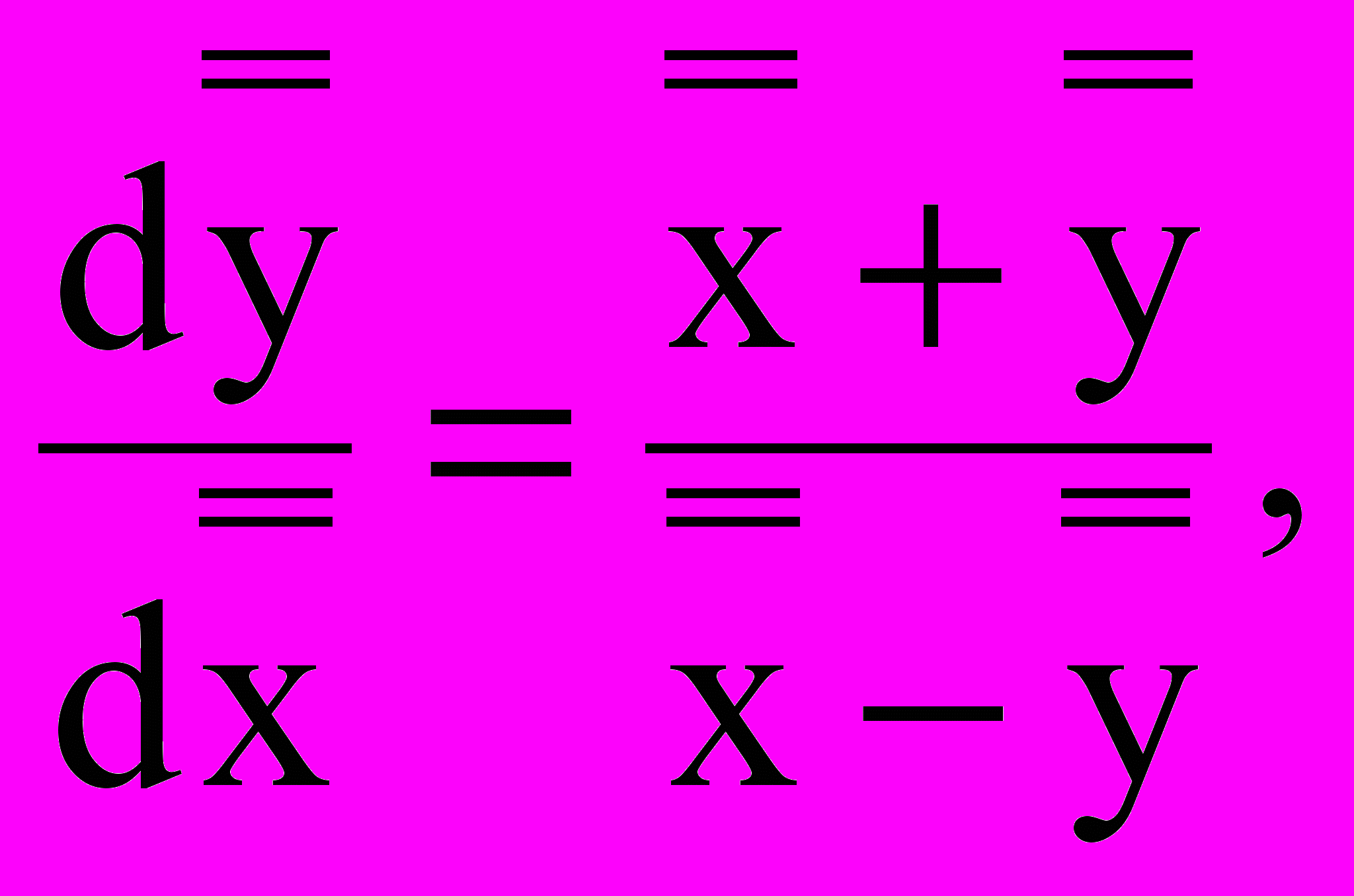



решение которого имеет вид:

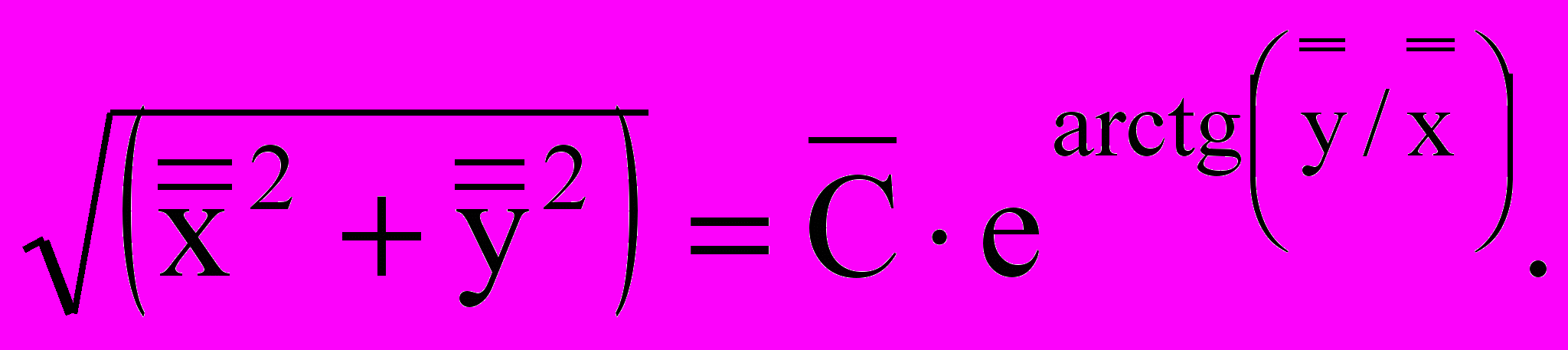(5)


Уравнение (5) описывает семейство кривых, имеющих форму спирали, с общим центром (фокусом), которым может быть точка Р (рыночного равновесия), а его совместное решение с уравнениями кривых С_n и Пр позволит оценить динамику цен и принять соответствующее решение.

В случае, когда корни z₁ и z₂ - чисто мнимые сопряженные, особая точка называется центром. Переменные 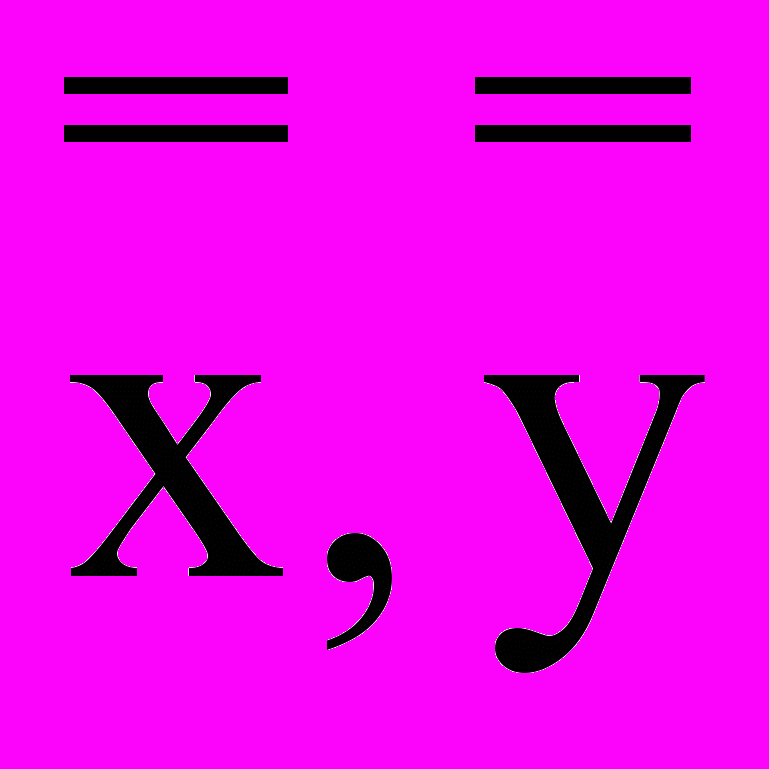(выбранные аналогично вышерассмотренному примеру) дают интегральные кривые 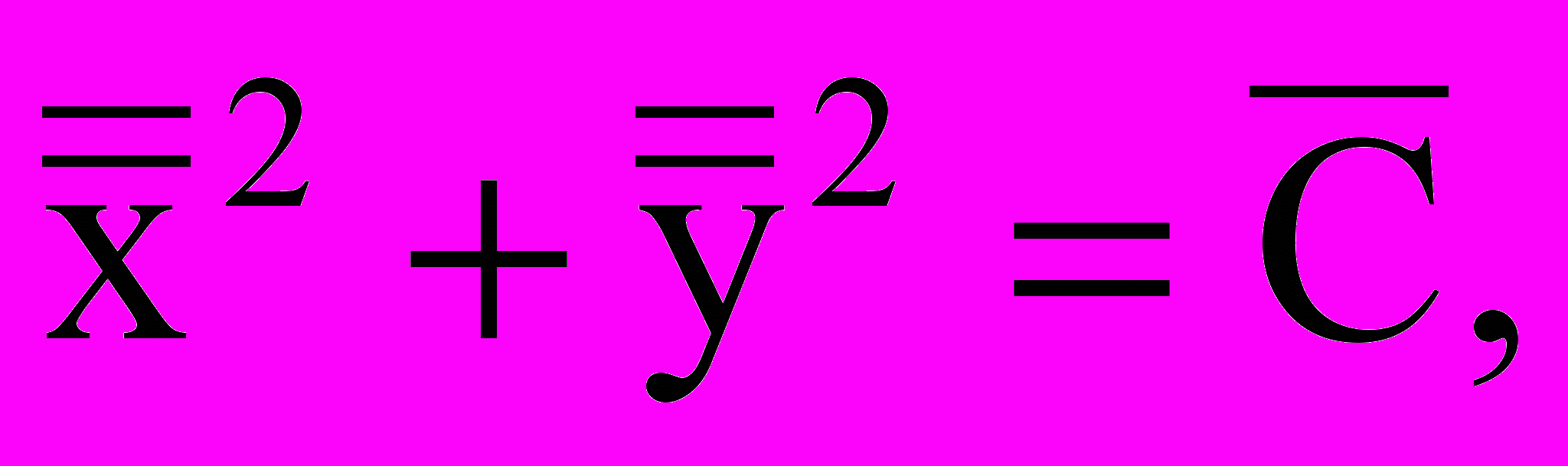т.е. семейство замкнутых кривых (можно рассматривать как замкнутые циклы формирования рыночной цены), окружающих особую точку (центр), которой может быть точка рыночного равновесия (Р).

Например, замкнутый цикл формирования рыночной цены описывается уравнением:



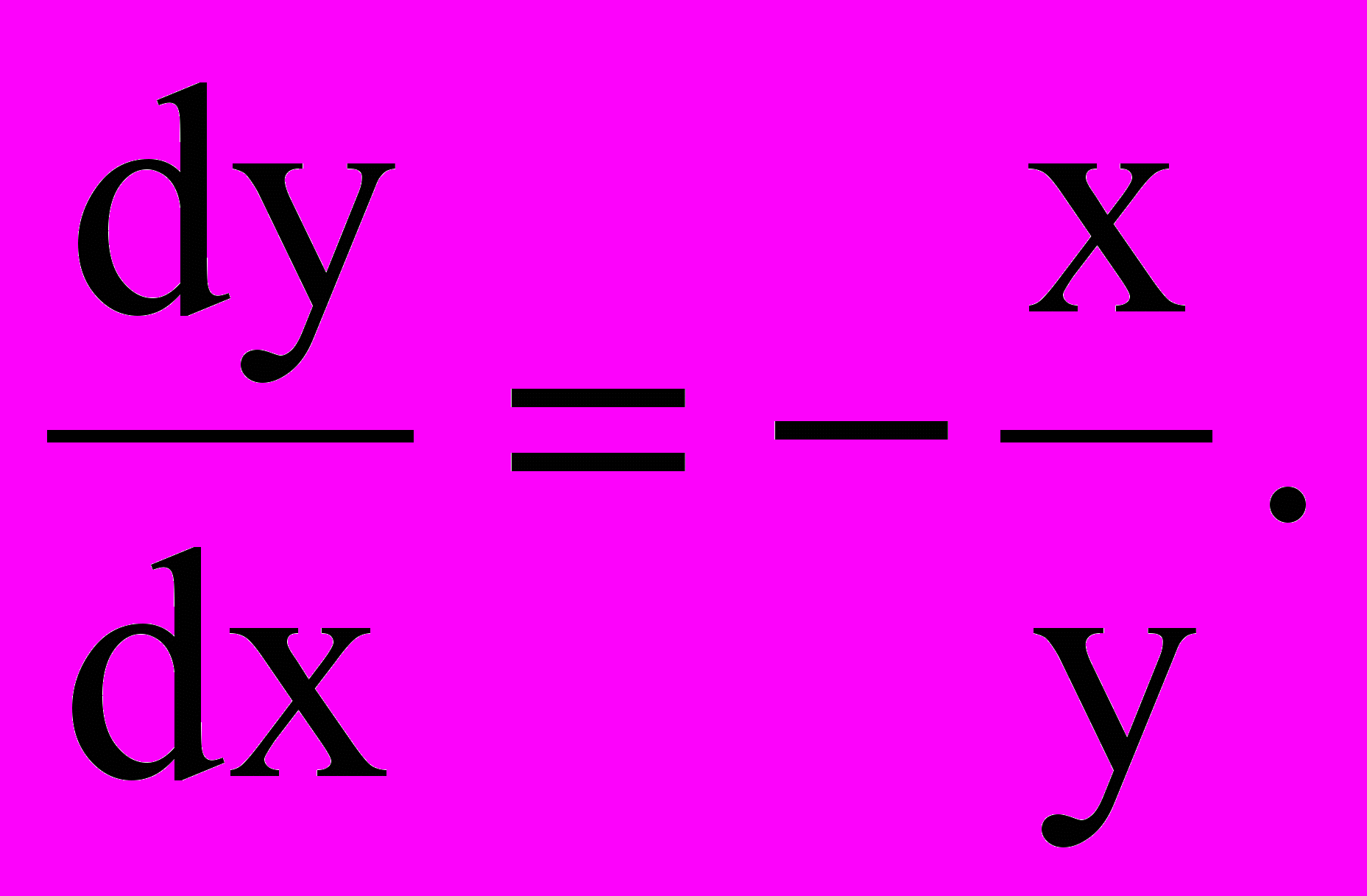
Корни характеристического уравнения z² + 1 = 0 равны z₁ = i и z₂ = -i. Уравнения интегральных кривых: х² + у² = 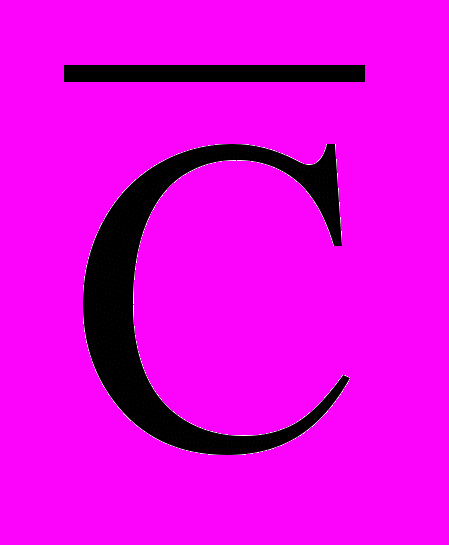описывают окружности с центром в точке Р. Кривые могут иметь и отличную от окружностей форму (соответственно другая математическая модель).

При различных значениях 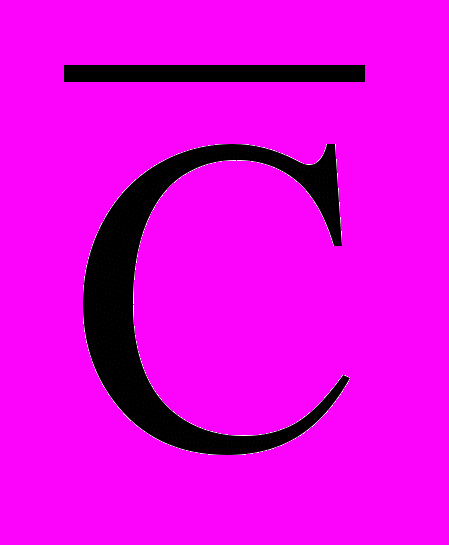, что будет соответствовать различным значениям изменения цены Ц_i, можно проанализировать динамику цен не только в течение одного замкнутого цикла, но и между несколькими, количество которых определяется методикой исследования в зависимости от политики ценообразования фирмы и других факторов.

Если необходимо оценить не только динамику рыночной цены на продукцию, но и одновременное влияние изменения объема реализации товара, необходимо составить систему из двух дифференциальных уравнений.


ВЫВОДЫ

1. Ориентируясь на конъюнктуру рынка, фирмы должны использовать гибкие методы ценообразования.

2. Объём спроса на продукцию, обуславливая прибыль фирмы, зависит от многих факторов и прежде всего от цены и качества продукции.

3. Динамические методы формирования цены на продукцию позволяют с помощью ЭВМ гибко корректировать политику ценообразования фирмы в зависимости от изменения конъюнктуры рынка.

4. Предложенные методы ценообразования позволяют оценивать не только динамику рыночной цены, но и учитывать изменение объёма реализации продукции.


СПИСОК ИСПОЛЬЗОВАННЫХ ЛИТЕРАТУРНЫХ ИСТОЧНИКОВ

1. Кафидов В.М. Управление качеством продукции: учеб. пособие: в 2-х ч. / В.М. Кафидов. – Калининград: КГТУ, 2009. – Ч.1. – 269 с.

2. Кафидов В.М. Управление качеством продукции: учеб. пособие: в 2-х ч. / В.М. Кафидов. – Калининград: КГТУ, 2010. – Ч.2. – 332 с.

3. Цацулин А.Н. Цены и ценообразование в системе маркетинга: учеб. пособие / А.Н. Цацулин. – М., 1998. – 442 с.

4. Цены и ценообразование: ученик для вузов / под ред. В.Е. Есипова. – М., 2004. – 560 с.

5. Кафидов В.М. Оценка инвестиций: учеб. пособие: в 3-х ч. / В.М. Кафидов. – Калининград: КГТУ, 2007. – Ч.1. – 255 с.; ч.2. – 242 с.

6. Кафидов В.М. Оценка инвестиций: учеб. пособие: в 3-х ч. / В.М. Кафидов. – Калининград: КГТУ, 2008. – Ч.3. – 194 с.

7. Выгодский М.Я. Справочник по высшей математике / М.Я. Выгодский. – М., 1963. – 870 с.


MARKET PRICING TECHNIKQUES INNOVATION


V.M. Kafidov


Based on continuous monitoring of internal and external environment company developed a mathematical model, allowing the use of a PC flexible to adjust pricing policies in accordance with the dynamics of market conditions.