Моделирование элементов систем применения смазочно-охлаждающих жидкостей на этапах их проектирования, создания и эксплуатации

Вид материала

Автореферат

Содержание Полянсков Юрий Вячеславович Смагин Алексей Аркадьевич Общая характеристика работы Объектом исследований Цель и задачи диссертации Методы исследования Научная новизна Основные положения, выносимые на защиту Практическая значимость научных исследований Достоверность результатов исследования Апробация работы Личный вклад Структура и объем работы Содержание работы P – давление СОЖ;  – динамическая вязкость жидкости; F Q – расход очистителя; V В заключении Список публикаций по теме диссертации

Подобный материал:

• А. Г. Тюрганов уфимский государственный авиационный технический университет семантическое, 25.57kb.
• Программа-минимум кандидатского экзамена по специальности 05. 13. 12 «Системы автоматизации, 99.32kb.
• Правила создания и эксплуатации подземных хранилищ газа в пористых пластах I. Область, 575.4kb.
• Рабочая программа учебной дисциплины «насосы и насосные установки». Цикл, 149.3kb.
• Концепция баз данных уже давно стала определяющим фактором при создании эффективных, 293.58kb.
• Программный комплекс для проектирования экспертных систем «ExSys». Д. П. Ветров,, 38.38kb.
• Рэа им. Г. В. Плеханова Основные направления автоматизации проектирования информационных, 54.51kb.
• Программа спецкурса "Компьютерное моделирование нелинейных волновых процессов" Специальность, 27.11kb.
• 2 Имитационное моделирование систем массового обслуживания, 29.08kb.
• Е. В. Чепин московский инженерно-физический институт (государственный университет), 30.11kb.

На правах рукописи


Емелин Сергей Валерьевич


МОДЕЛИРОВАНИЕ ЭЛЕМЕНТОВ СИСТЕМ ПРИМЕНЕНИЯ
СМАЗОЧНО-ОХЛАЖДАЮЩИХ ЖИДКОСТЕЙ НА ЭТАПАХ

ИХ ПРОЕКТИРОВАНИЯ, СОЗДАНИЯ И ЭКСПЛУАТАЦИИ


Специальность 05.13.18 – математическое моделирование,
численные методы и комплексы программ


АВТОРЕФЕРАТ

диссертации на соискание учёной степени

кандидата технических наук


Ульяновск – 2012

Работа выполнена на кафедре математического моделирования технических систем в ФГБОУ ВПО «Ульяновский государственный университет».


Научный руководитель: доктор технических наук,

профессор

Полянсков Юрий Вячеславович


Официальные оппоненты: доктор технических наук,

профессор, лауреат Премии Правительства РФ,

Булыжёв Евгений Михайлович


доктор технических наук,

профессор

Смагин Алексей Аркадьевич


Ведущая организация: ФГБОУ ВПО МГТУ «Станкин»


Защита диссертации состоится «15» февраля 2012 г. в 11³⁰ часов на заседании диссертационного совета Д 212.278.02 при ФГБОУ ВПО «Ульяновский государственный университет» по адресу: г. Ульяновск, ул. Набережная реки Свияги, 106, корп. 1, ауд. 703.


С диссертацией можно ознакомиться в библиотеке Ульяновского государственного университета, с авторефератом – на сайте вуза ссылка скрыта и на сайте Высшей аттестационной комиссии при Министерстве образования и науки Российской Федерации.


Отзыв на автореферат присылать по адресу: 432017, г. Ульяновск,
ул. Л. Толстого, д. 42, УлГУ, Отдел послевузовского и профессионального образования.


Автореферат разослан «13» января 2012 года


Ученый секретарь

диссертационного совета Волков М.А.


Общая характеристика работы


Актуальность исследования

Исследование и моделирование состояния жидких сред с последующей оптимизацией их параметров часто применяются в различных областях науки и техники. Немаловажное значение имеет исследование поведения составляющих компонентов жидких сред (примесей): при механической обработке с использованием смазочно-охлаждающих (технологических) жидкостей (СОЖ), в физических, химических, биологических и геологических исследованиях и др. Контролирование уровня (концентрации) примесей в жидких средах важно как для достижения заданной чистоты жидкости (механообработка, применение топлива и т.п.), так и, наоборот, при обогащении полезных ископаемых примесями. Рассмотрим более подробно процессы механической обработки материалов¹.

Механическая обработка материалов используется во многих производственных процессах в различных областях промышленности. Эффективность процесса механообработки зависит от множества элементов технологической системы, одним из которых, наряду со станком, приспособлением, режущим инструментом, является СОЖ. Применение СОЖ при технологическом процессе подразумевает использование системы применения СОЖ, в которую входит оборудование для подачи СОЖ в зону механообработки и поддержание ее в работоспособном состоянии в течение длительного времени.

В большинстве случаев получение высокой производительности и качества механообработки достигается за счет техники применения СОЖ, а именно рациональной организацией систем ее эксплуатации вспомогательными службами цехов и заводов машиностроительных отраслей. Широкое внедрение новых СОЖ предъявило к системам их применения широкий диапазон требований², которые непрерывно ужесточаются.

Описание поведения СОЖ в системах ее применения с помощью математических моделей позволяет максимально точно определить состояние СОЖ и ее компонентов в любой момент времени в любой точке системы применения СОЖ. Математические модели дают возможность выявить зависимости основных параметров СОЖ (таких как концентрация механических примесей, концентрация эмульсола) от других параметров жидкости (давление, температура, скорость движения жидкости, граничные и начальные условия). Анализ данных зависимостей позволяет более эффективно влиять на процесс механической обработки с использованием СОЖ: контролировать концентрацию механических примесей, регулировать уровень основного компонента, влиять на качество обрабатываемых изделий. Развитие программных средств и численных методов позволяет на ранних этапах спрогнозировать работу систем применения, смоделировать поведение СОЖ, и в частности наиболее значимых ее параметров (концентрации примесей и основного компонента), в определенный момент времени.


Объектом исследований в диссертационной работе являются элементы систем применения СОЖ³.


Предметом исследований является математическая модель концентрации механических примесей и основного компонента⁴ как параметров, оказывающих значительное влияние на свойства СОЖ в системе ее применения.


Цель и задачи диссертации

Цель диссертации состоит в разработке математической модели поведения значимых параметров СОЖ в системе ее применения, позволяющей создавать и прогнозировать работу элементов систем применения, а также осуществлять управляющее воздействие для эффективного использования СОЖ.

Для достижения поставленной цели в работе решаются следующие задачи:

1. Разработать математическую модель поведения механических примесей и основного компонента СОЖ для элементов системы применения.
   
2. Определить начальные и граничные условия для решения полученной математической модели.
   
3. Разработать алгоритм решения математической задачи поведения механических примесей и основного компонента СОЖ в элементах системы применения.
   
4. Создать комплекс программных средств автоматизации процесса проектирования и эксплуатации элементов систем применения СОЖ на основе разработанной математической модели.
   
5. Провести экспериментальные исследования для оценки адекватности полученной математической модели поведения механических примесей и основного компонента.
   
6. Провести опытно-промышленные испытания созданного комплекса программного обеспечения.
   
7. Внедрить результаты работы в промышленность.
   

Методы исследования

Для решения поставленных задач в работе использовалось математическое моделирование, численное моделирование, метод конечных элементов, экспериментальное исследование течения жидкости в системе ее циркуляции.


Научная новизна:

1. Предложена методика проектирования, прогнозирования и оказания управляющего воздействия для элементов систем применения СОЖ с использованием математической модели поведения концентрации механических примесей и основного компонента, с возможностью оценки изменения во времени.
   
2. Разработана математическая модель поведения механических примесей и основного компонента СОЖ при ее движении в элементах системы применения.
   
3. Создан комплекс программ, использующий численные методы, для автоматизации процесса проектирования и прогнозирования работы элементов систем применения СОЖ, на основе анализа поведения концентрации механических примесей СОЖ, интегрированный с программным обеспечением ANSYS.
   

Основные положения, выносимые на защиту:

1. Методика проектирования, прогнозирования работы и оказания управляющего воздействия для элементов систем применения СОЖ с использованием математической модели поведения механических примесей и основного компонента, с возможностью оценки изменения во времени.
   
2. Математическая модель поведения механических примесей и основного компонента СОЖ при ее движении в элементах системы применения.
   
3. Комплекс программ автоматизации процесса проектирования и эксплуатации элементов систем применения СОЖ.
   

Практическая значимость научных исследований:

Применение предложенной методики проектирования, прогнозирования работы и оказания управляющего воздействия для элементов систем применения СОЖ и разработанной модели поведения концентрации механических примесей и основного компонента позволяет оптимизировать процесс моделирования и эксплуатации элементов систем применения, а также получать представление о поведении механических примесей и основного компонента в любой точке элемента систем применения в любой момент времени.

Более точные математические разработки и автоматизация процесса проектирования и прогнозирования значительно снижают затраты на разработку и эксплуатацию элементов систем применения, уменьшают процент ошибок при расчетах, дают возможность достаточно быстро и эффективно внести изменения в элементы систем применения СОЖ, наглядно моделируют работу будущих элементов систем применения, позволяя определить критичные режимы и области.

Предложенный метод при разработке математической модели поведения концентрации механических примесей и основного компонента может быть использован для подобных исследований других жидких сред (оценка биодобавок, синтетических присадок и т.п.).

Результаты диссертационный работы использовались в практике проектирования систем применения СОЖ на предприятиях г. Ульяновска (ОАО «Строймаш», ГП «СТАНКОСЕРВИС», ФГУП ПО «Ульяновский машиностроительный завод «Завод «Каркас»). Предложенные рекомендации позволили повысить эффективность работы систем применения СОЖ, сократить расходы на проектирование и эксплуатацию и более рационально использовать ресурсы предприятий.


Достоверность результатов исследования

Достоверность результатов исследования подтверждается следующим:

1. Математические зависимости не противоречат фундаментальным положениям теоретической механики.
   
2. Экспериментальные исследования подтверждают адекватность полученной математической модели.
   
3. Разработанный на основе полученной математической модели комплекс программ успешно прошел внедрение на производстве.
   

Апробация работы

Основные положения исследования докладывались и обсуждались на следующих конференциях:

1. III научная конференция «Математическое моделирование физических, экономических, социальных систем и процессов», г. Ульяновск, 2000;
   
2. IV научная конференция «Математическое моделирование физических, экономических, социальных систем и процессов», г. Ульяновск, 2001;
   
3. V Международная конференция «Математическое моделирование физических, экономических, технических, социальных систем и процессов», г. Ульяновск, 2003;
   
4. VI Международная конференция «Математическое моделирование физических, технических, экономических, социальных систем и процессов», г. Ульяновск, 2005.
   

Личный вклад

Разработка математической модели, проведение экспериментальных исследований, анализ результатов и обоснование выводов выполнено автором самостоятельно.


Публикации

Основные материалы диссертации отражены в 9 публикациях, в том числе 2 статьи в журналах из списка ВАК.


Структура и объем работы

Диссертационная работа состоит из введения, четырех глав, заключения, приложений и содержит 153 страницы текста, 38 рисунков, 20 таблиц, а также список литературы из 161 наименования.


Содержание работы


Во введении диссертации изложена актуальность выполняемых работ, описаны цель, задачи и положения, выносимые на защиту.

В главе 1 производится обзор элементов систем применения, анализ параметров работы элементов системы, рассмотрены параметры СОЖ, влияющие на эффективность ее работы.

При проектировании и эксплуатации систем применения СОЖ следует учитывать, что системы применения выполняют функцию поддержания работоспособности СОЖ как можно более длительное время⁵. Многократное использование СОЖ сказывается на затратах, которые необходимы при использовании дорогостоящих эмульсолов. Ключевым вопросом синтеза систем применения СОЖ при автоматизированном проектировании является выбор параметров работ, влияющих на эффективность функционирования технологических систем. В результате анализа литературных источников по определению наиболее значимых функциональных параметров элементов систем применения СОЖ, а также произведенного детального обзора различных систем применения СОЖ (индивидуальных, централизованных, групповых) выяснено, что большинство элементов систем применения характеризуются расходом протекающей через них жидкости и степенью влияния элемента системы на очистку СОЖ от механических примесей. Поэтому в качестве значимых параметров поведения СОЖ в процессе ее эксплуатации выбраны концентрация механических примесей и концентрация основного компонента как параметры, оказывающие наибольшее влияние на свойства СОЖ.

В качестве значимых элементов систем применения СОЖ выбраны следующие:

• зона резания как элемент, привносящий в систему циркуляции СОЖ механические примеси и влияющий на концентрацию основного компонента;
  
• очистители (фильтры) как элементы, влияющие на уровень концентрации механических примесей;
  
• баки-отстойники как элементы, влияющие на седиментацию механических примесей и испарение основного компонента;
  
• насосы как элементы, влияющие на физические свойства течения СОЖ;
  
• система трубопроводов как элемент, влияющий на течение СОЖ и концентрацию механических примесей.
  

В качестве вспомогательного инструмента для моделирования движения СОЖ в системе ее применения, на основании детального обзора разнообразных CAD/CAM/CAE-систем, выбран программный комплекс ANSYS как самый распространенный и надежный на мировом рынке, позволяющий решать различные задачи течения жидкостей и интегрироваться с другими программными продуктами.

В главе 2 на примере изменения концентрации механических примесей и основных компонентов СОЖ производится моделирование элементов систем применения СОЖ. Для этого разрабатывается модель концентрации примесей и поведения основных компонентов жидкости, зависящая от параметров системы применения и от параметров движения СОЖ. Разработка математической модели поведения концентрации механических примесей и основного компонента СОЖ производится с использованием уравнений Навье-Стокса для турбулентного движения жидкости. Для полученной модели параметров поведения СОЖ определяются граничные и начальные условия.

СОЖ рассмотрена как многокомпонентная среда, состав которой меняется внутри объема. Состав одного из компонентов СОЖ (механических примесей) описан концентрацией C, которая определяется в некотором объеме V₀ как отношение массы примесей M к полной массе жидкости в данном объеме⁶ M_жV:

.

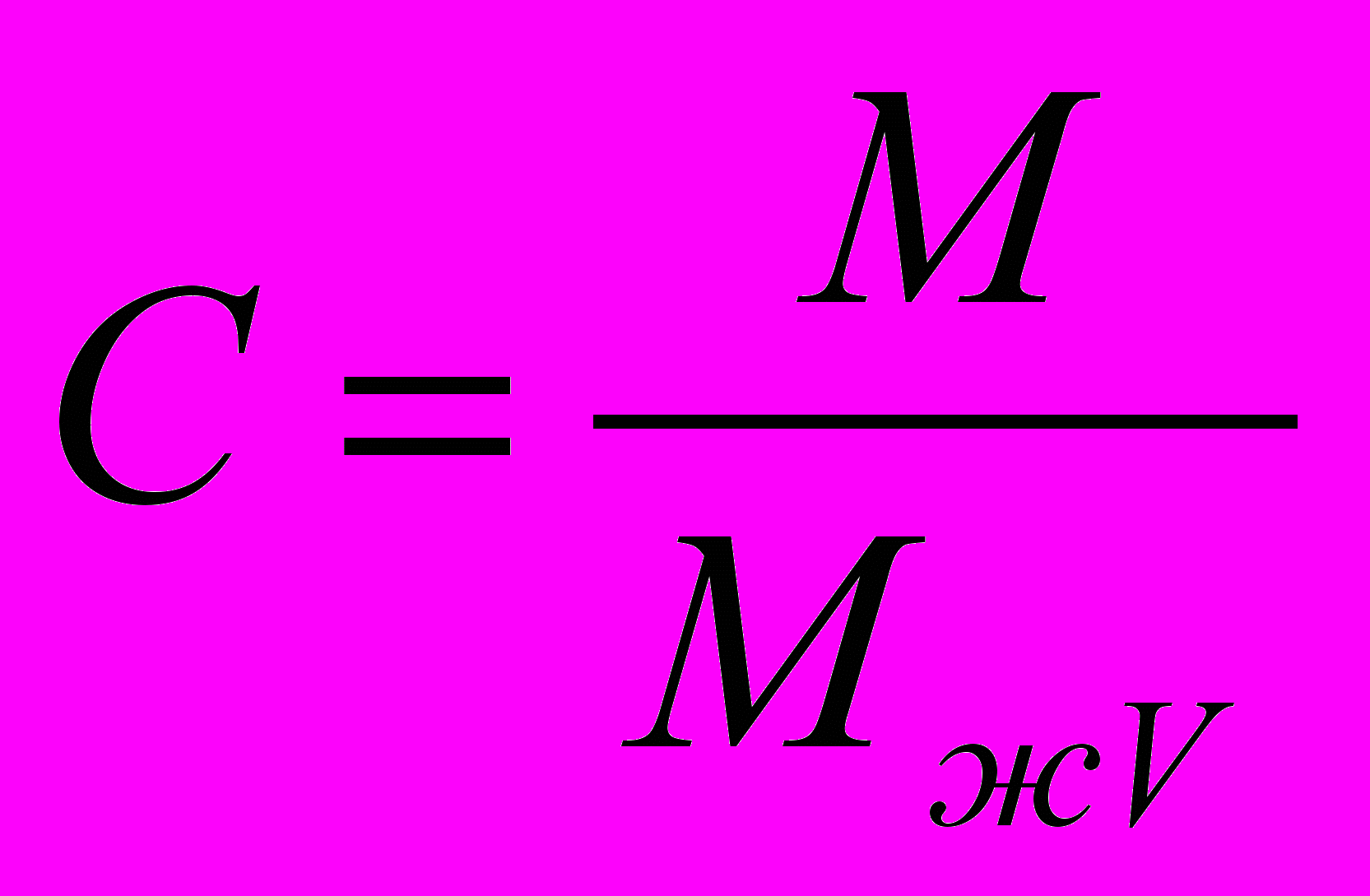В диссертационной работе на примере плоского шлифования получена зависимость, позволяющая определить объем снимаемого материала в единицу работы режущим инструментом. Ниже приведен краткий вывод данной зависимости.

Зона контакта обрабатываемой детали и шлифовального круга представлена в виде тонкой элементарной пластины (рис. 1), двигающейся по радиусу к центру шлифовального круга со скоростью .

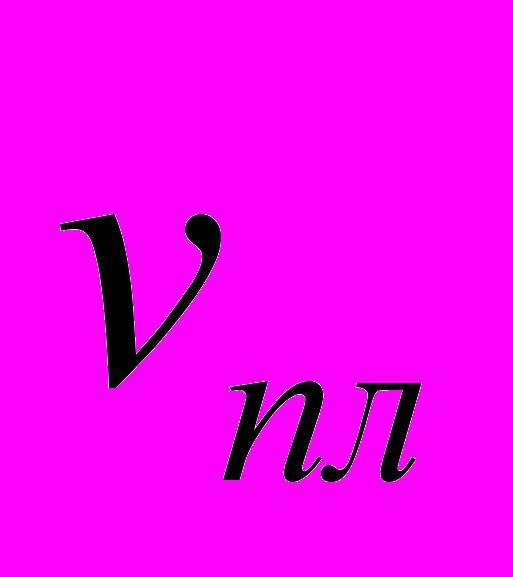Представив рабочую поверхность круга в виде множества элементарных слоев бесконечно малой толщины dy_S, содержащих одинаковое число вершин зерен, а зону контакта обрабатываемой детали и круга – в виде тонкой элементарной пластины толщиной dl, получаем элементарный объем стружки, срезаемой в единицу времени зернами шлифовального круга 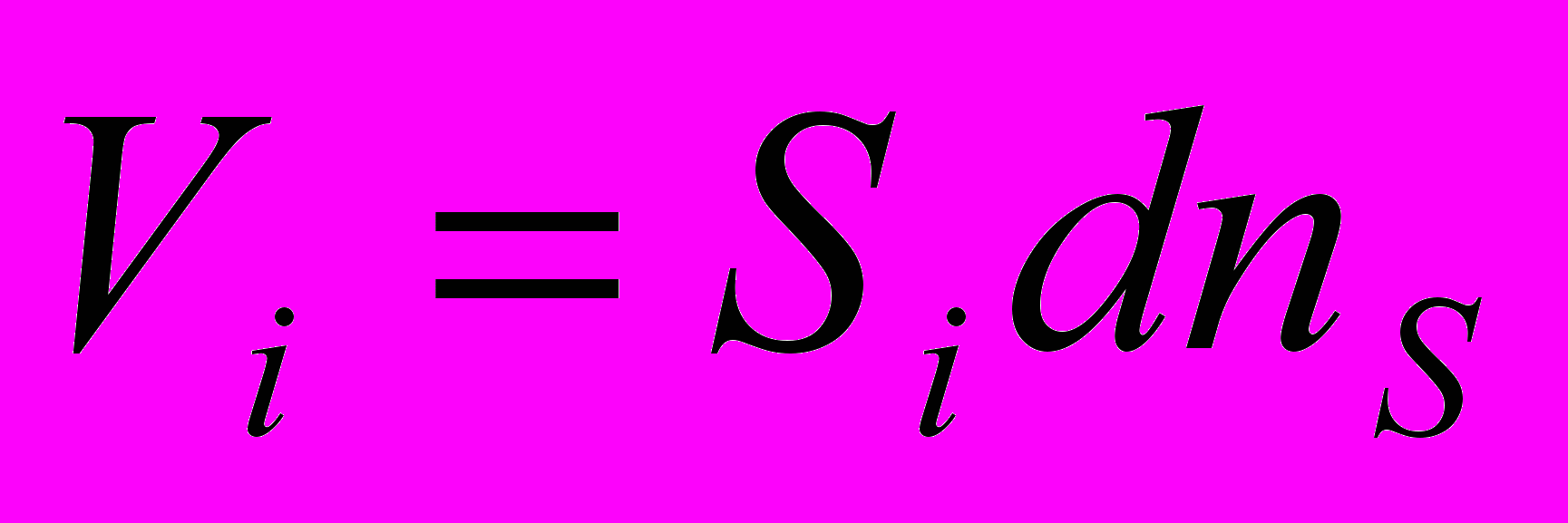, где S_i – площадь поперечного сечения единичного среза; dn_S – толщина слоя, срезаемого одновременно работающими зернами. Проделав выкладки и интегрируя объемы всех элементарных горизонтальных слоев зерен шлифовального круга, получаем выражение для объема снимаемой стружки в единицу времени в зависимости от параметров шлифования: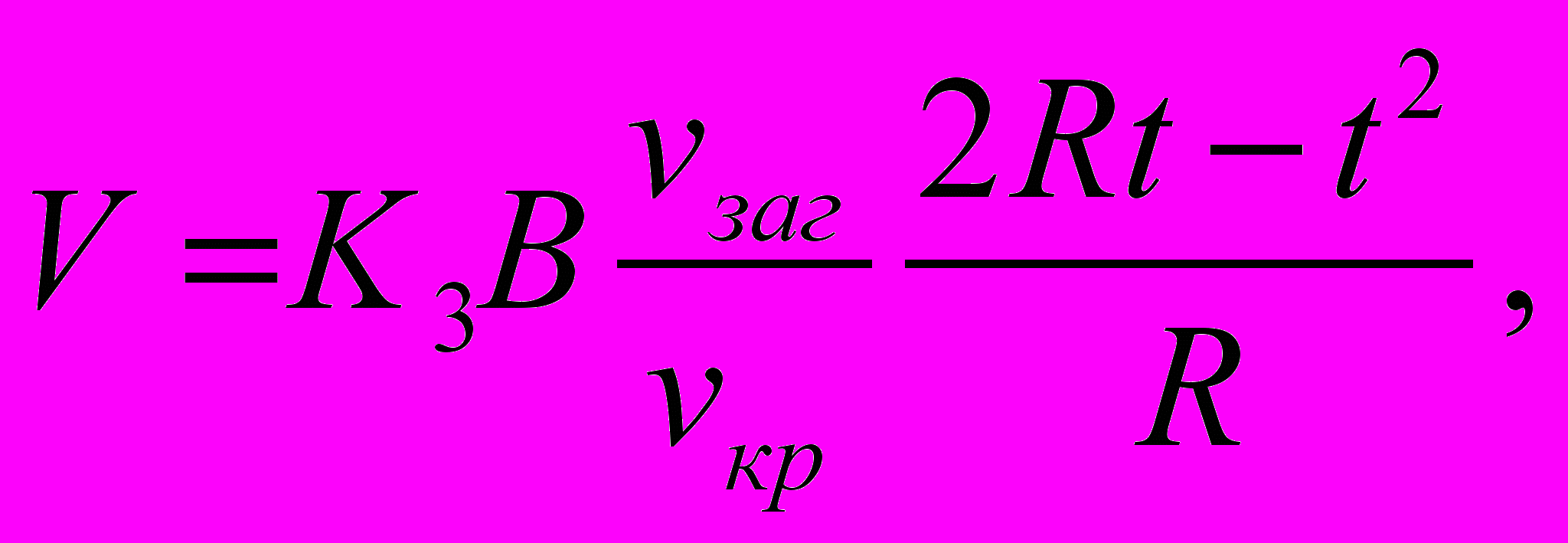



где R – радиус шлифовального круга;
t – глубина шлифования; 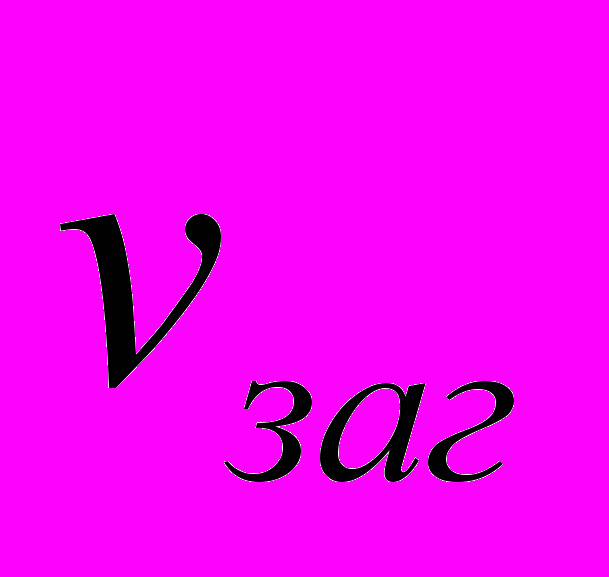– скорость заготовки при плоском шлифовании; – скорость вращения шлифовального круга; B – ширина шлифования; К₃ – коэффициент, зависящий от характеристик процесса резания (для плоского шлифования он равен 0,506).

Рассматривая некоторый объем СОЖ V₀ с плотностью жидкости , определяем количество (массу) примесей в этом объеме как интеграл произведения плотности и концентрации. Далее с помощью интегрирования по поверхности рассматриваемого объема СОЖ определяем количество «втекающих» и «вытекающих» в данный объем примесей в единицу времени.

Анализируя движение СОЖ в трубопроводе, продемонстрируем алгоритм получения математических моделей. В процессе движения СОЖ учитывалось, что примеси осаждаются на стенках трубопровода. Плотность распределения осаждающихся примесей задается выражением μ'C, где
μ' = μ' (x,y,z,t) – заданная функция (линейное приближение к более сложному закону, справедливое при достаточно малых С). Функция μ' задается для всех трубопроводов, входящих в систему применения. Следовательно, уменьшение количества примесей, которые осаждаются в рассматриваемом объеме V₀, определяется интегрированием по объему V₀ произведения плотности  и μ'C. Считая, что изменение количества в объеме V₀ вещества равно количеству этого вещества, перенесенному жидкостью через поверхность объема V₀, и используя формулу Остроградского, получаем уравнение поведения концентрации механических примесей в СОЖ при ее движении в трубопроводе:

,

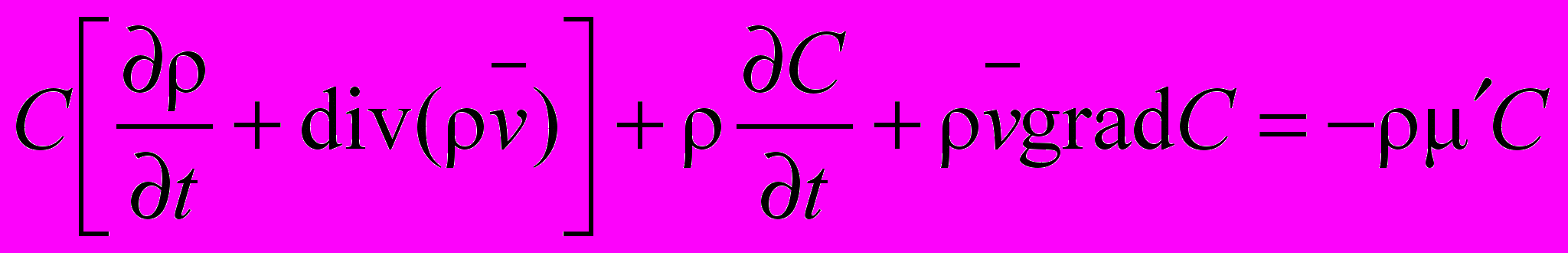которое после преобразований приводится к следующему виду:



Аналогичным способом, анализируя движение СОЖ в различных элементах системы применения, получаем математические модели поведения концентрации механических примесей в баке-отстойнике:



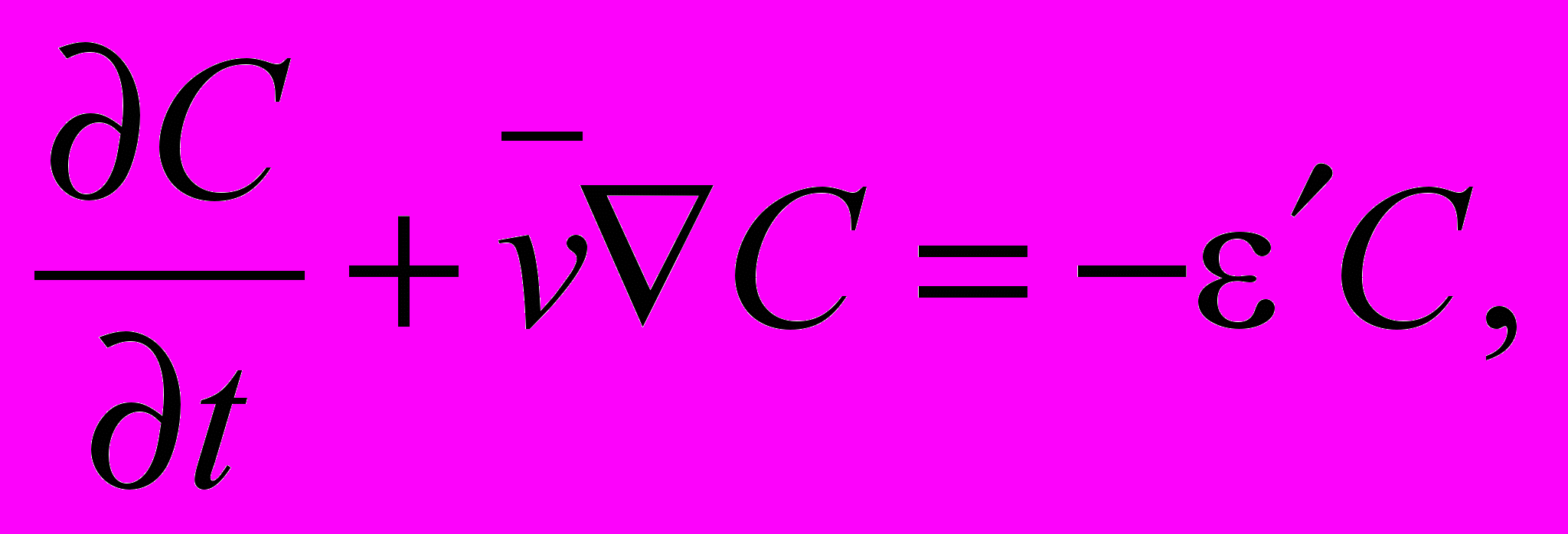
в очистителе:



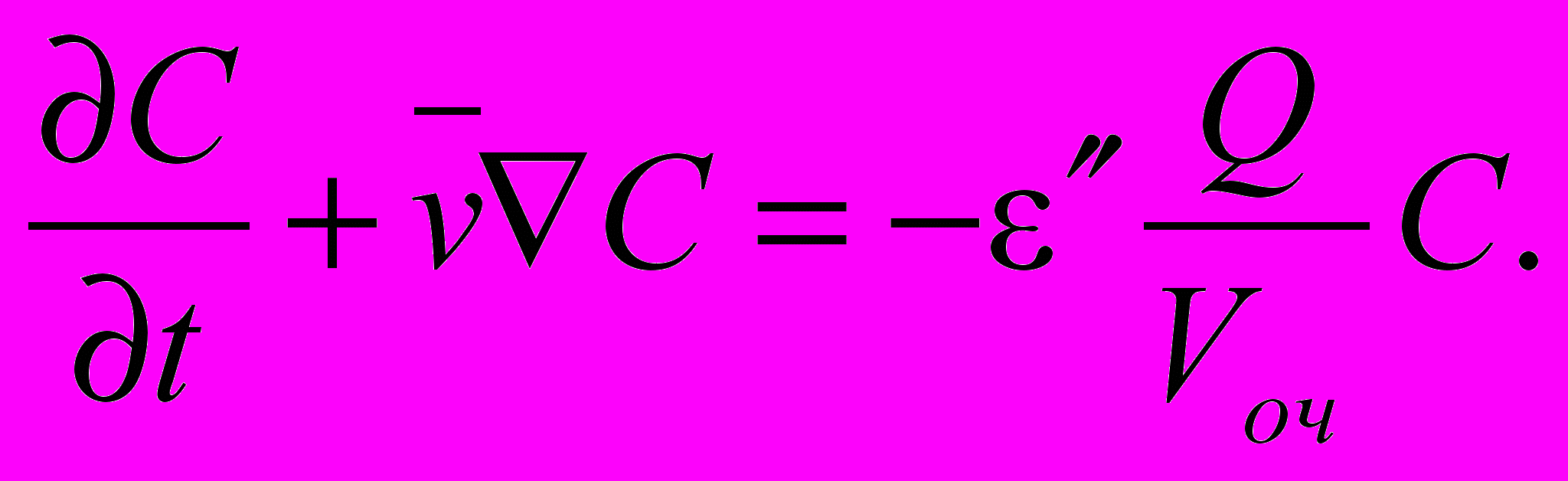
Рассмотрим систему применения, состоящую из: трубопроводов, занимающих область пространства E; емкостей, количество которых равно n, и занимающих области пространства Θ_i (i=1,...,n); очистителей в количестве, равном m, и ограниченных областями пространства Ψ_j (j=1,...,m); а также включающую в себя p зон резания. Используя параметры, характеризующие поведение жидкости в каждом элементе системы (коэффициент седиментации, степень очистки, расход, скорость поступления механических примесей), уравнения турбулентного движения жидкости (Навье-Стокса) и проделав математические выкладки по анализу движения жидкости в различных элементах системы применения, получаем систему уравнений (1), описывающую поведение концентрации механических примесей СОЖ (далее – модель поведения СОЖ).



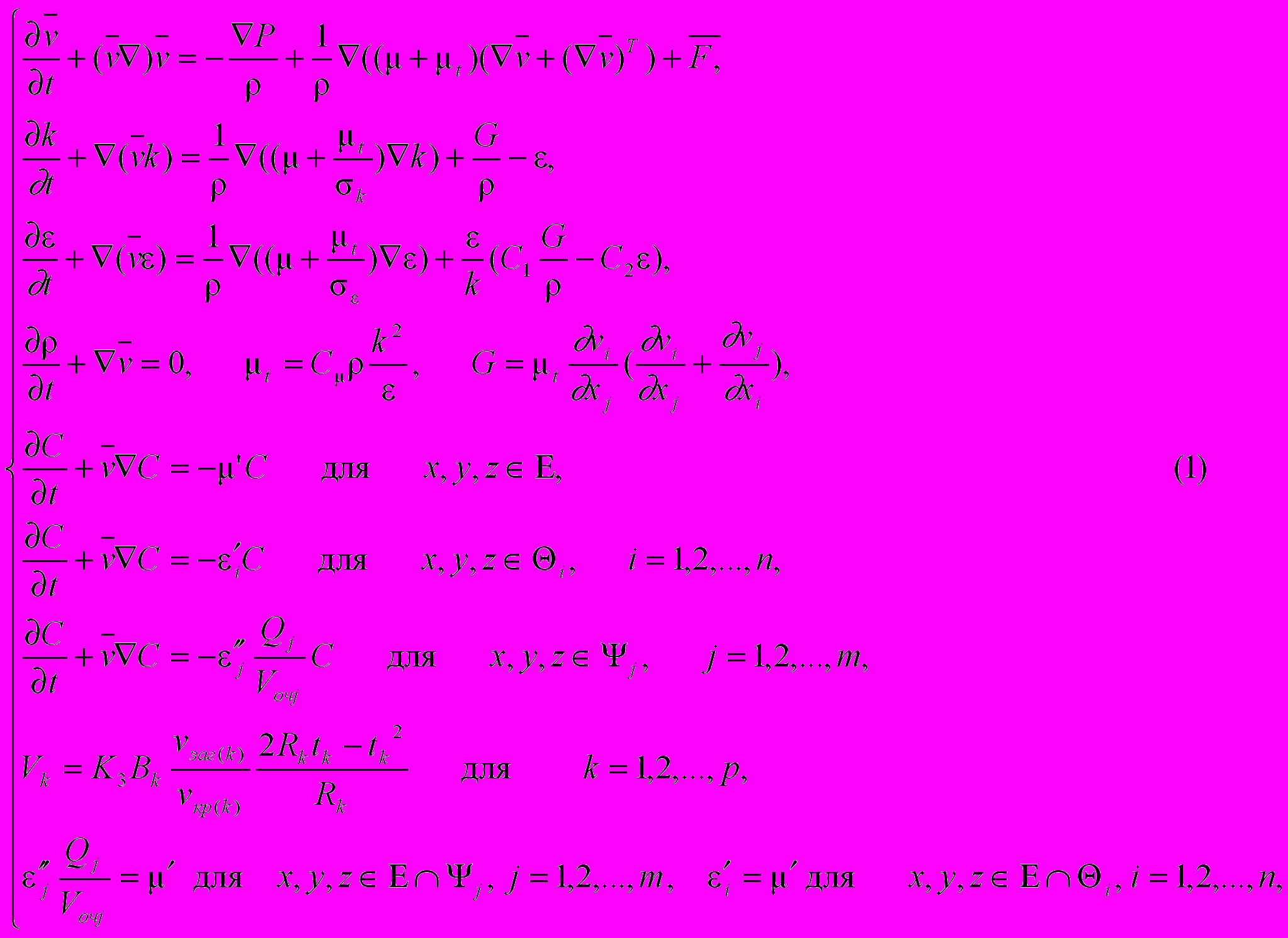
где первые шесть уравнений (уравнения Навье-Стокса, неразрывности, коэффициента турбулентной вязкости, турбулентной энергии, скорости диссипации) описывают турбулентное движение СОЖ;  – плотность жидкости; 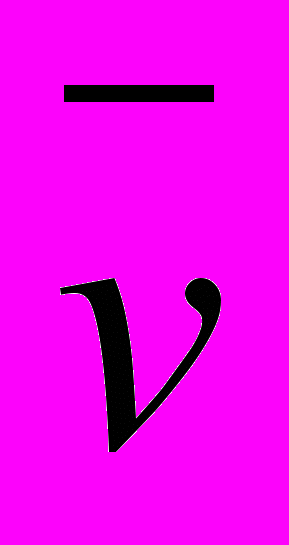– скорость течения жидкости; P – давление СОЖ;  – динамическая вязкость жидкости; F – вектор внешних сил (например, тяжести); _t – коэффициент турбулентной вязкости; k – турбулентная энергия;  – скорость диссипации турбулентной энергии; следующие четыре уравнения описывают поведение концентрации механических примесей в трубопроводах, баках, очистителях и зонах резания соответственно; следующие два уравнения накладывают условия сопряженности соседних элементов системы применения для модели концентрации механических примесей; 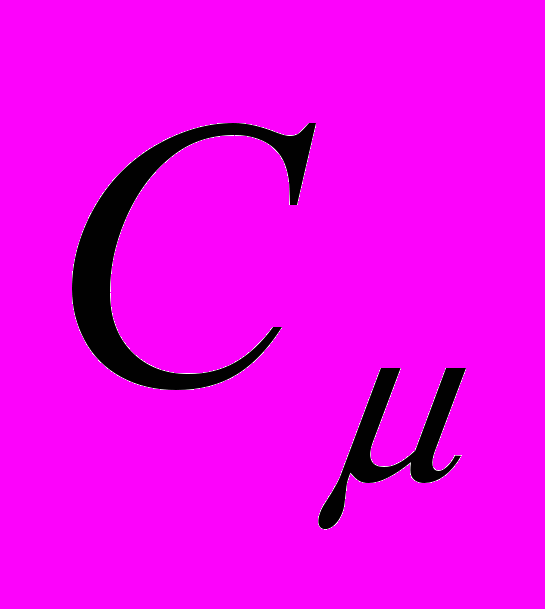= 0,09; 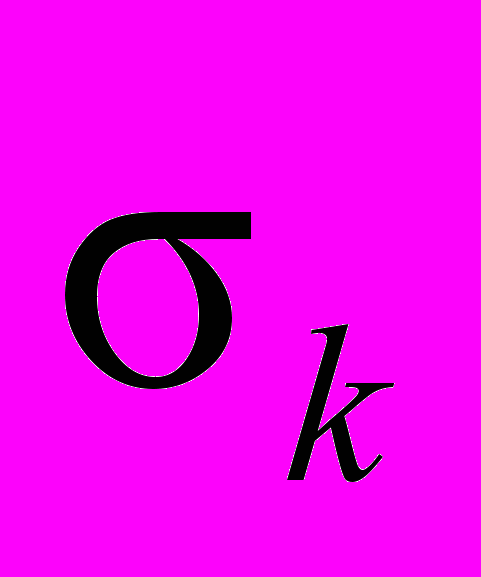= 1,0;
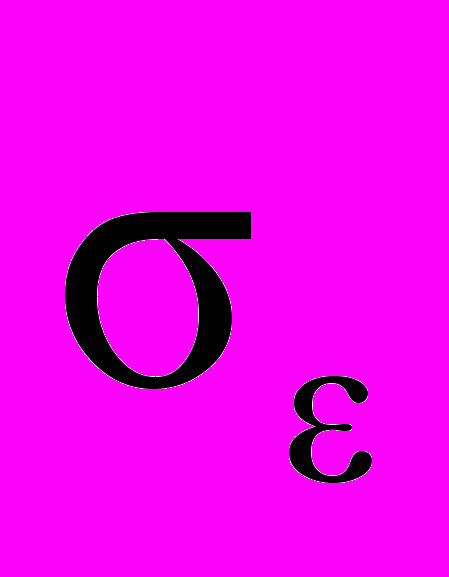= 1,3; С₁ = 1,44; С₂ = 1,92; E – область пространства, ограниченная трубопроводами; μ' = μ' (x,y,z,t) – заданная функция, характеризующая седиментацию примесей в трубопроводе;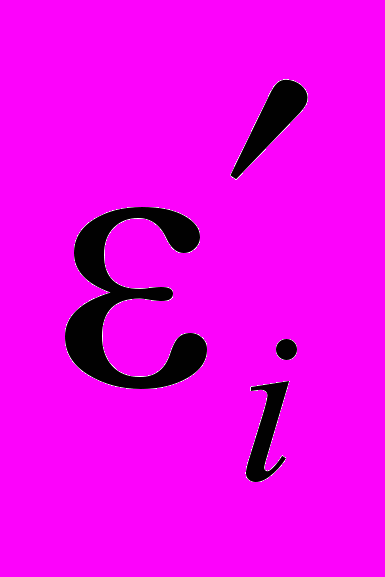– коэффициент седиментации в i-м баке;
Θ_i – область пространства, ограниченная i-м баком; 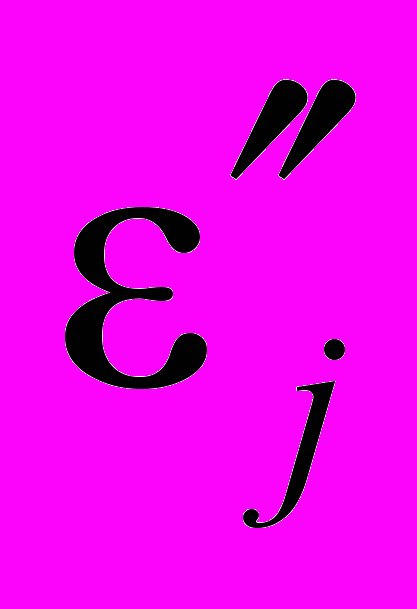– степень очистки
j-го очистителя; Q_j – расход j-го очистителя; V_очj – объем j-го очистителя;
Ψ_j – область пространства, ограниченная j-м очистителем; v_заг(k) – скорость заготовки в k-й зоне резания; v_кр(k) – скорость вращения шлифовального круга в k-й зоне резания; R_k – радиус шлифовального круга в k-й зоне резания;
t_k – глубина шлифования в k-й зоне резания; B_k – ширина шлифования в k-й зоне резания; K₃ – коэффициент, зависящий от характеристик процесса резания (для плоского шлифования он равен 0,506); V_k – объем снимаемой стружки в k-й зоне резания.

Аналогичным образом получены математические модели поведения концентрации основного компонента (на примере эмульсола) в системе применения СОЖ (табл. 1).


Таблица 1.Модели концентрации основного компонента (на примере эмульсола)
для различных элементов системы применения

Элемент системы применения	Модель
Трубопровод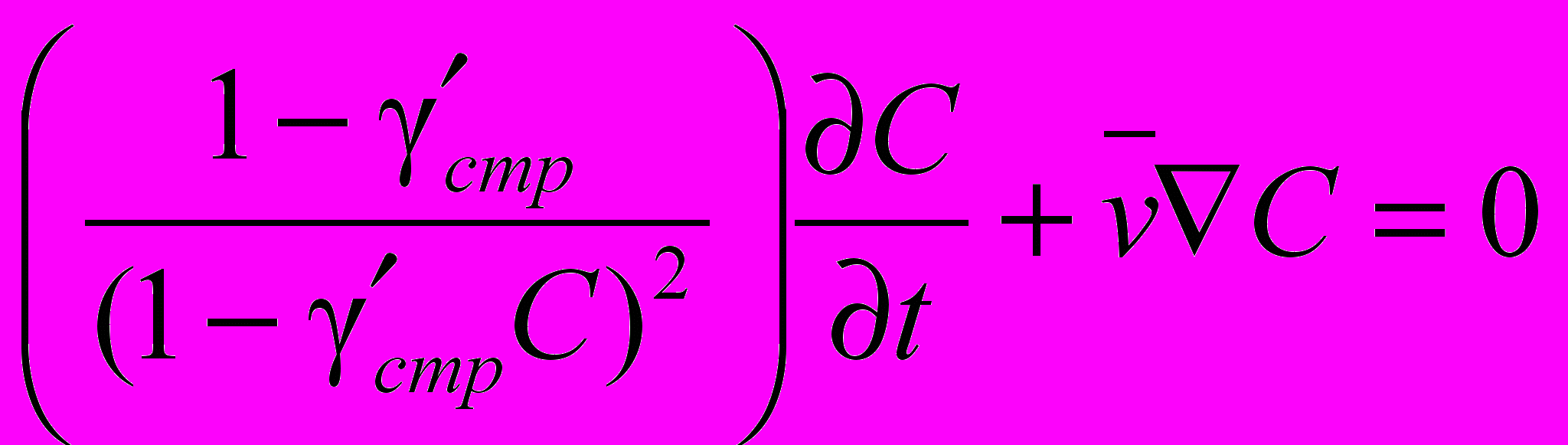
Бак-отстойник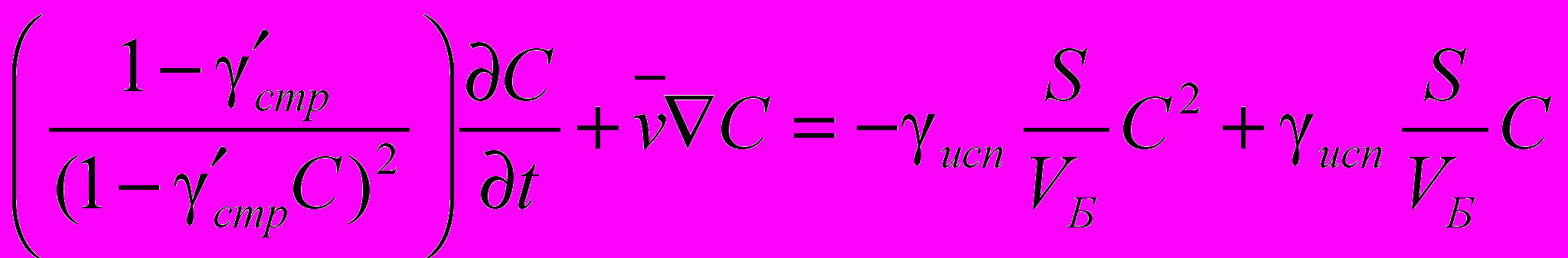
Очиститель
Зона резания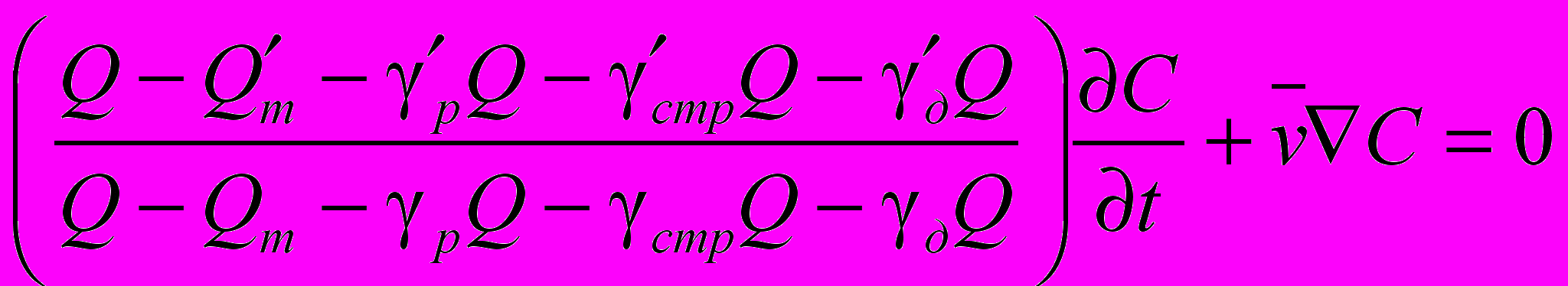

На основании модели поведения СОЖ (1) рассмотрена и решена задача о распределении концентрации механических примесей при движении СОЖ в трубопроводе большого сечения (для ламинарного течения). На рис. 2 в графическом виде приведено распределение концентрации механических примесей в продольном сечении трубопровода в различные моменты времени и в различных сечениях трубопровода.




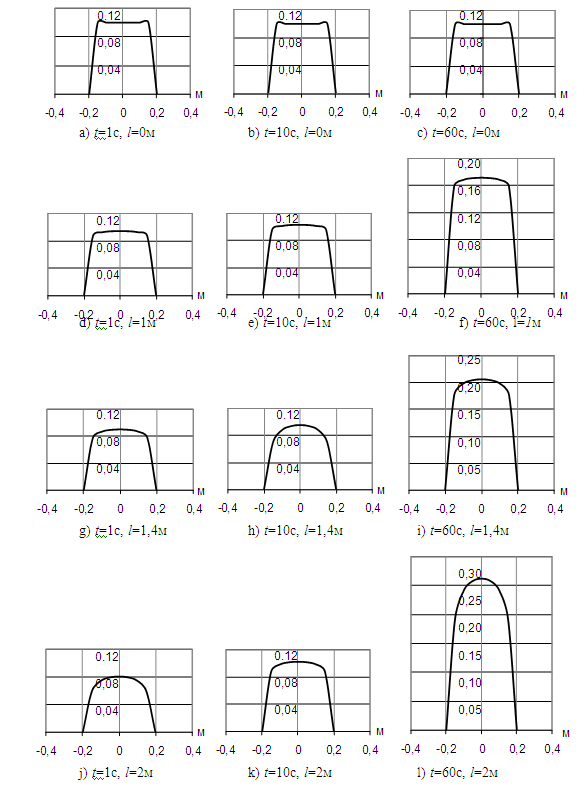
Рис. 2. Распределение концентрации механических примесей в продольном сечении
трубопровода в различные моменты времени (t) и в различных сечениях трубопровода (l). По оси абсцисс отображается сечение трубопровода диаметром d = 400 мм; по оси
ординат – значение концентрации механических примесей в СОЖ в долях по отношению к общей массе

Для разработанной модели поведения СОЖ (1) в диссертационной работе были приведены основные граничные и начальные условия, позволяющие ставить задачу о движении СОЖ с учетом механических примесей при ламинарном и турбулентном ее течении. В диссертационной работе также предложено описание систем применения СОЖ в виде ориентированных графов для облегчения работы при моделировании на ЭВМ. Пример некой обобщенной системы применения СОЖ и ее описание в виде графа приведены на рис. 3 и 4.




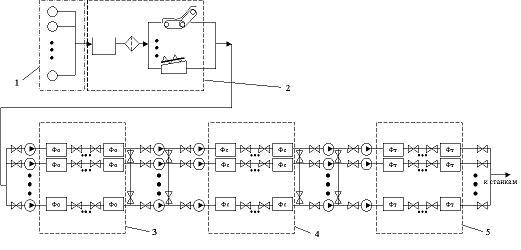
Рис. 3. Схема обобщенной системы применения СОЖ: 1 – блок зоны резания; 2 – блок грубой очистки (фильтры грубой очистки, баки-отстойники, транспортеры); 3 – блок
очистки (магнитные сепараторы, центрифуги, баки-отстойники, патроны, уловители);
4 – блок средней очистки (флотаторы, гидроциклоны, центрифуги); 5 – блок тонкой очистки (намывные фильтры, баки для чистой СОЖ)


Оптимизация параметров работы систем применения СОЖ, а также их отдельных элементов на основе полученной математической модели поведения концентрации механических примесей и основного компонента производится методом наименьших квадратов, с учетом наложенных ограничений на элементы систем применения.




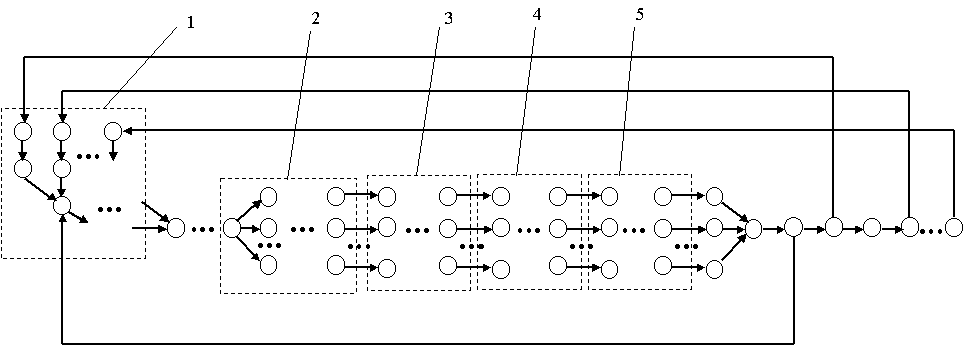
Рис. 4. Граф обобщенной системы применения СОЖ: 1 – блок зоны резания; 2 – блок
грубой очистки; 3 – блок очистки; 4 – блок средней очистки; 5 – блок тонкой очистки


В главе 3 проведено исследование модели поведения СОЖ (1). Показана корректность математической формулировки модели (1) путем сведения модели для частного случая к модели, полученной ранее⁷.

Описан алгоритм решения модели концентрации при помощи метода конечных элементов, программной среды ANSYS и разработанного программного обеспечения «Автоматизированная Информационная Система расчета движения СОЖ (АИС СОЖ)».

Для решения модели поведения СОЖ (1) применяется метод конечных элементов, который сводится к решению системы k уравнений:

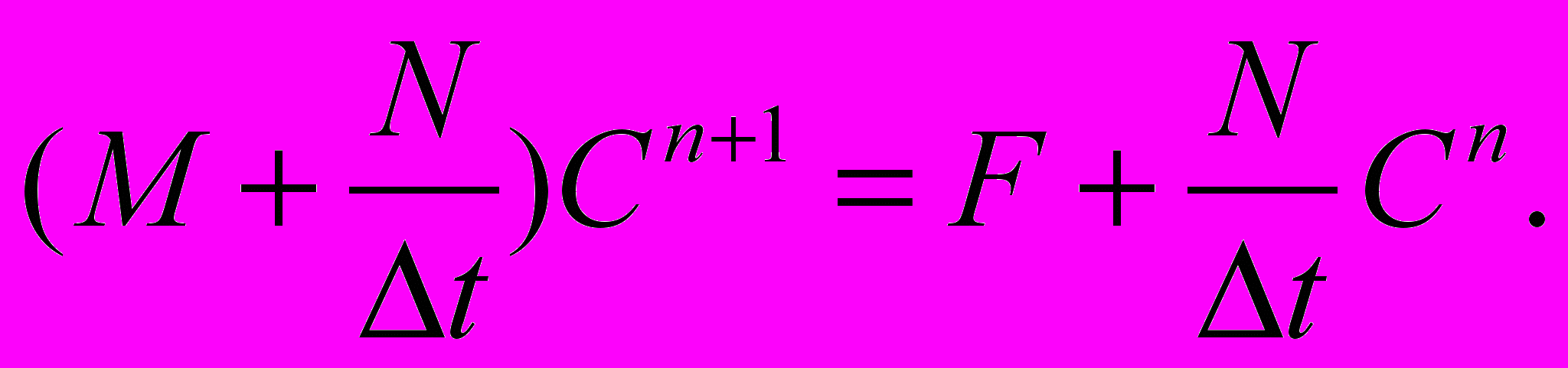(2)

Считая вектор скорости 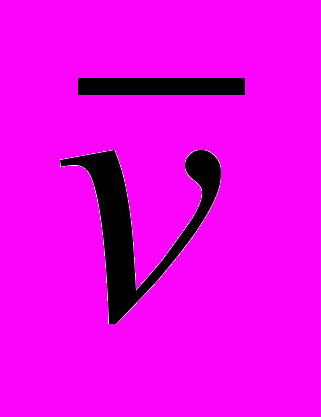известной величиной, получена линейная система (2) из k уравнений для k неизвестных С_i(t) с постоянными коэффициентами. Решение таких систем упрощается, поскольку матрицы М и N постоянны, а трудоемкие матричные преобразования выполняются только один раз.

Выбрав в качестве конечного элемента тетраэдр и произведя дальнейшие преобразования, система уравнений (2) сведена к линейным системам вида

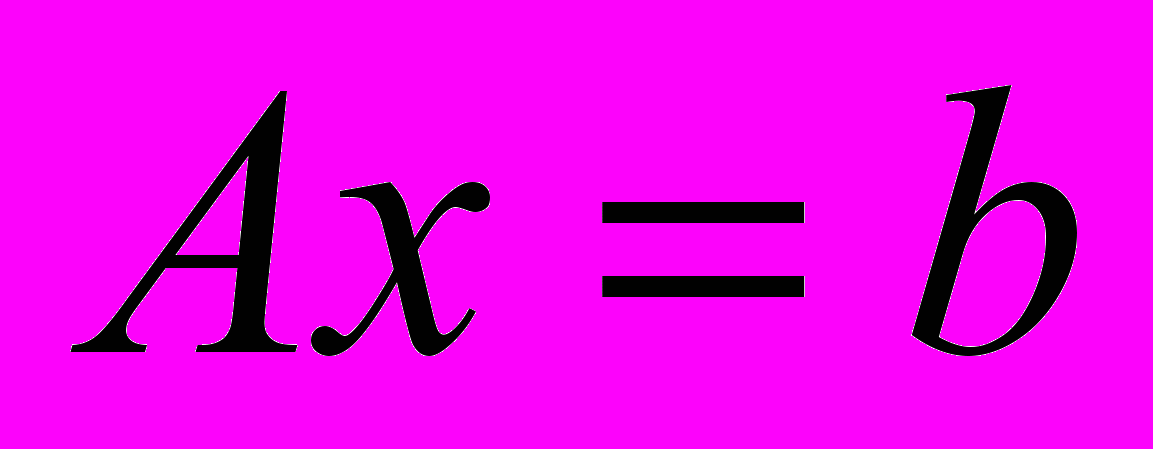, (3)

где

, , .

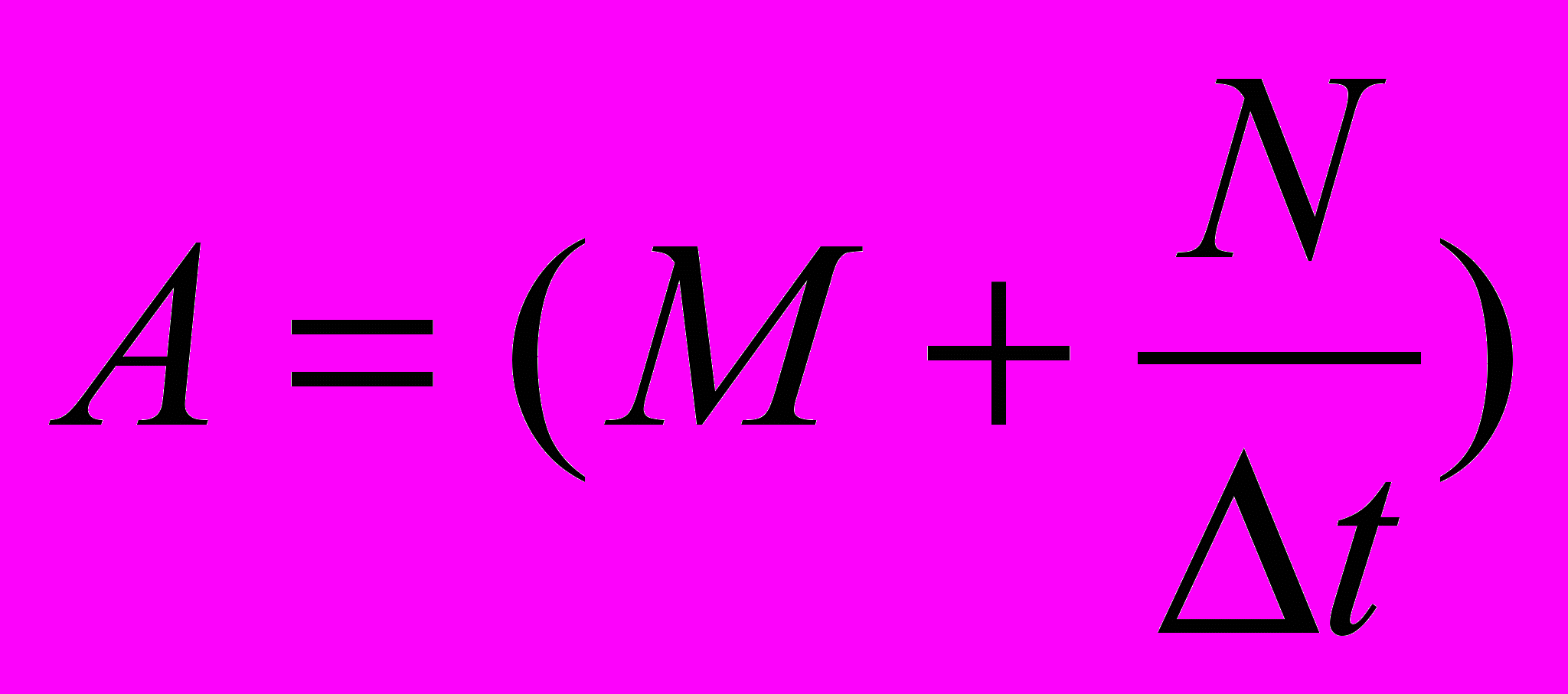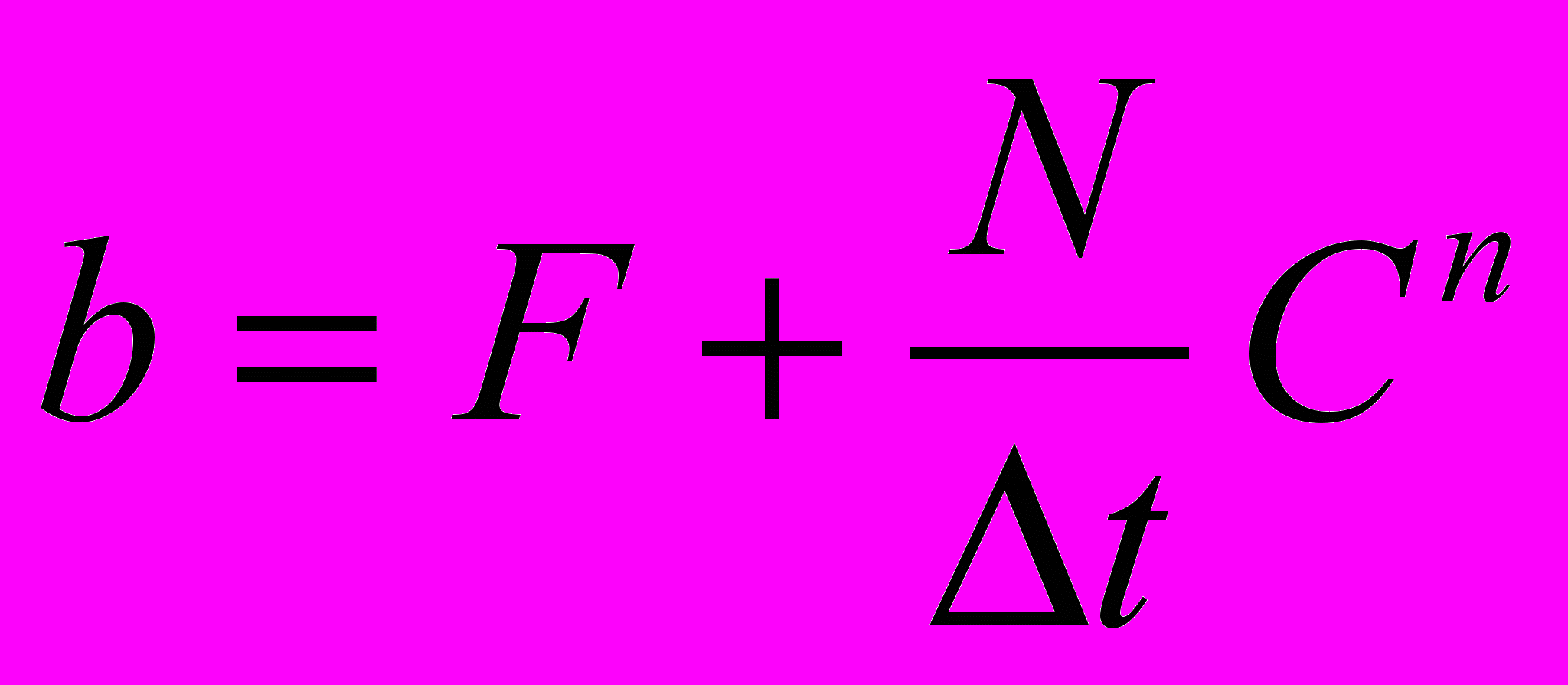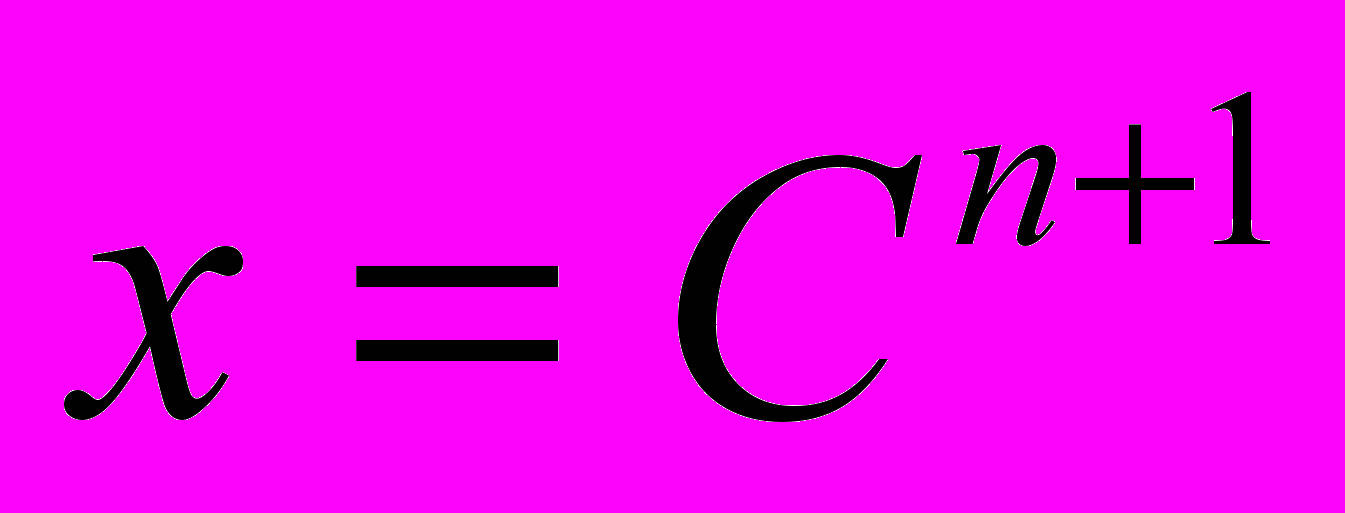При этом матрица А, в силу своего построения, является разреженной и симметричной. Решение (3) ищется либо прямым методом Гаусса, либо итерационным методом сопряженных градиентов. При использовании итерационного метода вычисления производятся до тех пор, пока выдерживается заданная точность.

Модифицированы параметры численного метода. При решение модели (1) получены для каждого конечного элемента е (табл. 2).


Таблица 2. Измененные матрицы М, N, F для каждого конечного элемента е

Элемент системы применения	Значения матриц
Трубопровод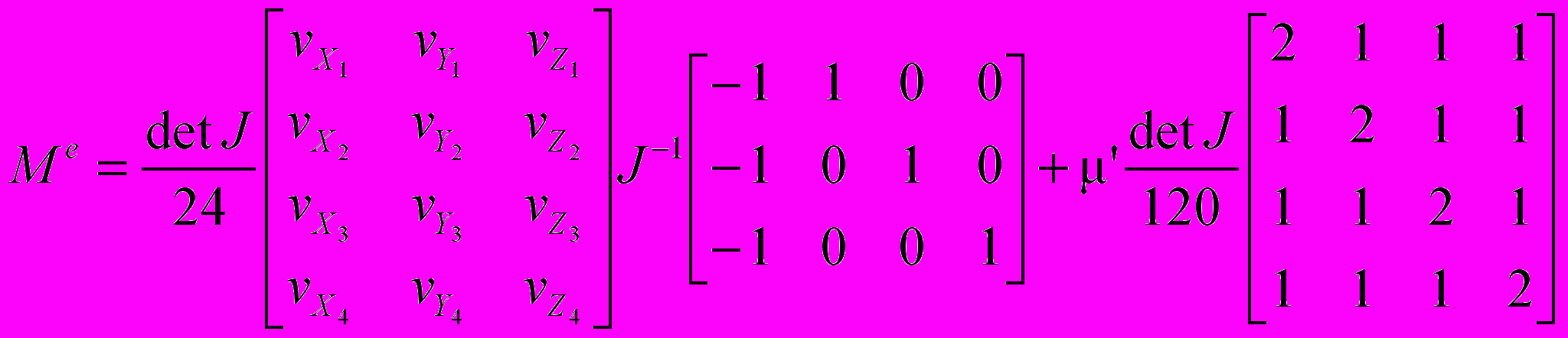
Бак-отстойник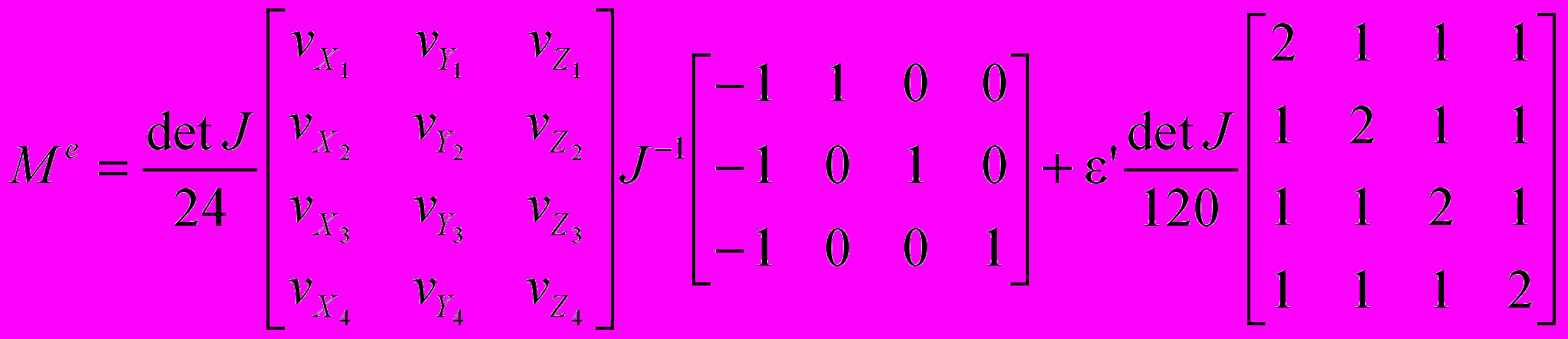
Очиститель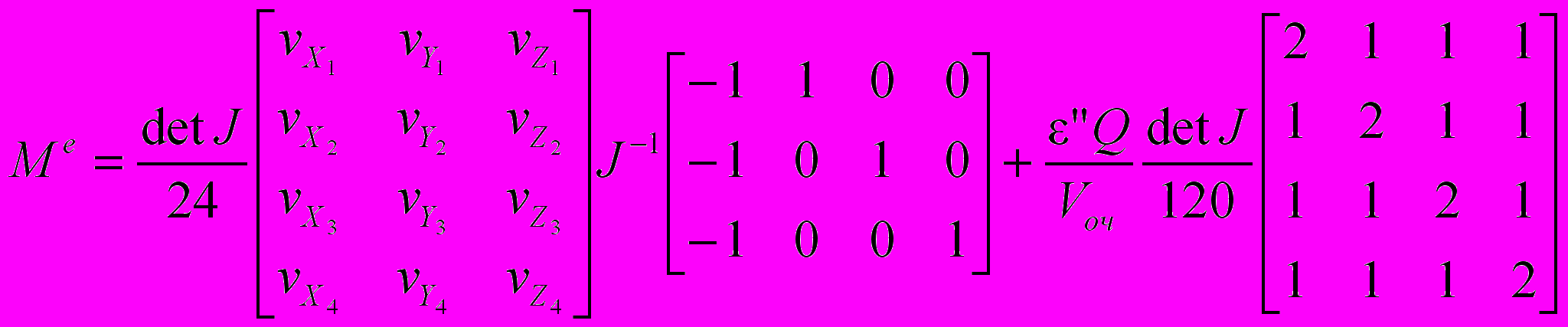
Для всех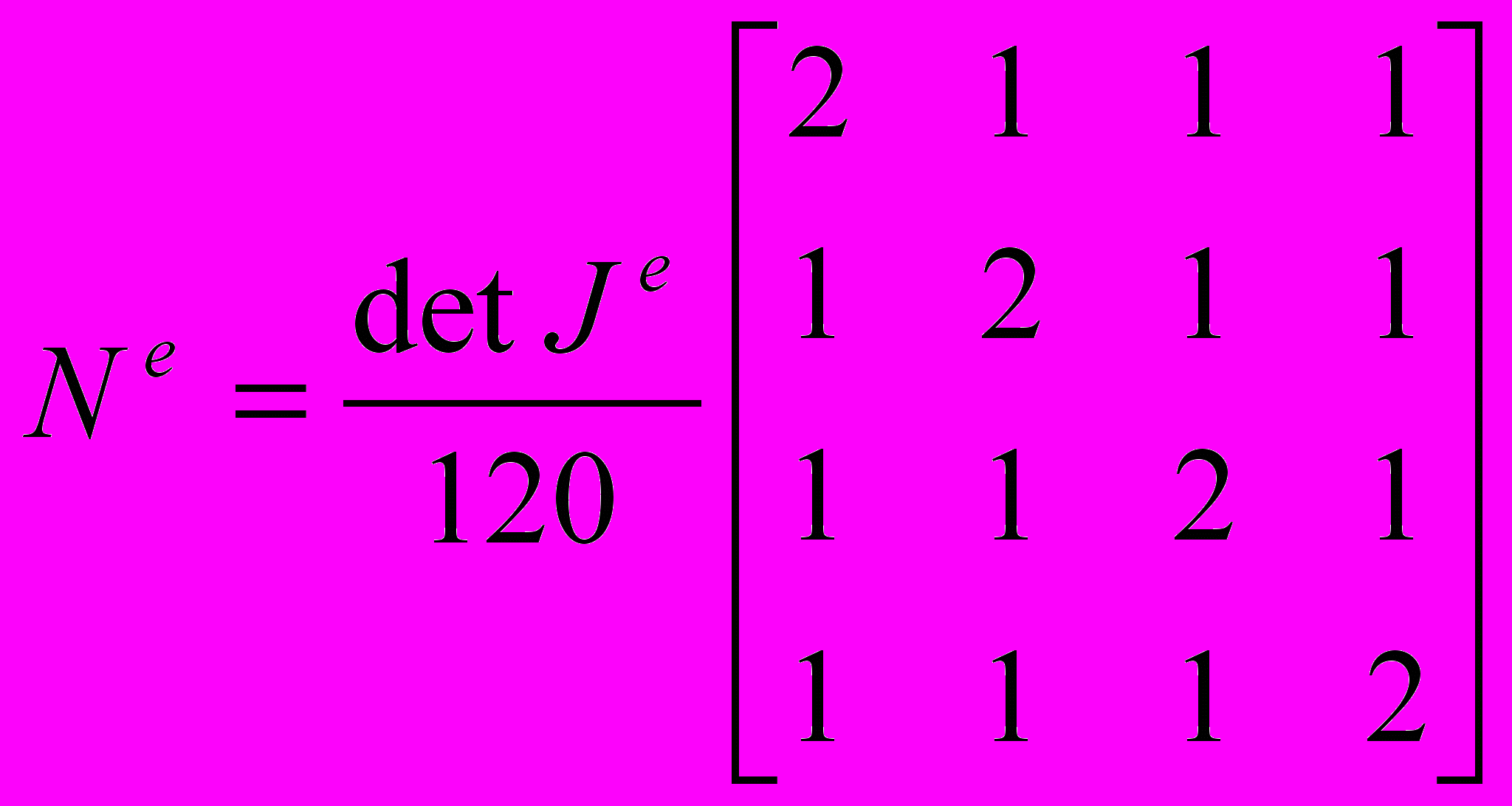
Для всех	Fе= 0

Примечание. 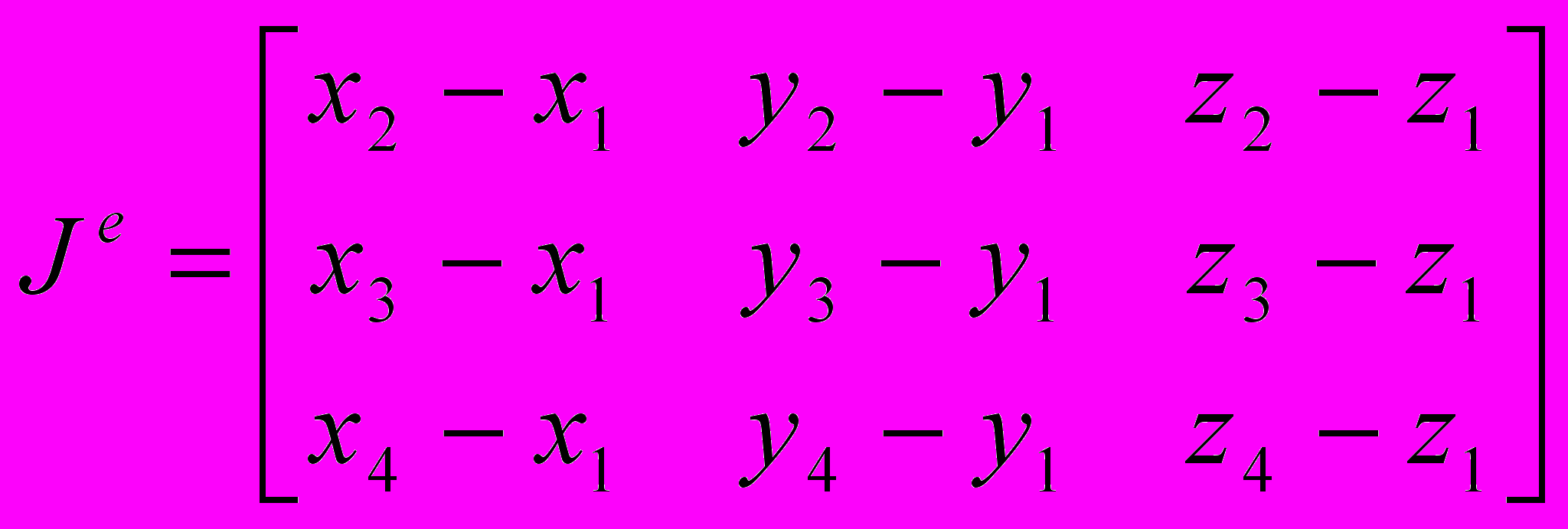– матрица преобразования конечного элемента е; x₁,y₁,z₁,x₂,y₂,z₂,x₃,y₃,z₃,x₄,y₄,z₄ – координаты узлов конечного элемента е; 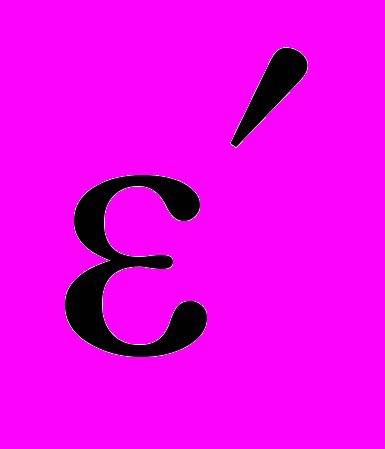– коэффициент седиментации в баке; 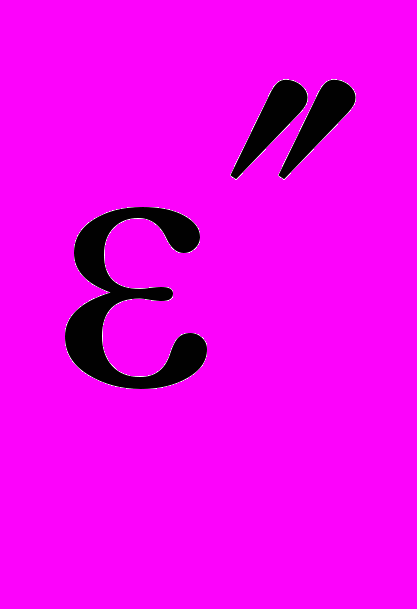– степень очистки очистителя; Q – расход очистителя; V_оч – объем очистителя;
μ' = μ' (x,y,z,t) – заданная функция, характеризующая седиментацию примесей в трубопроводе; 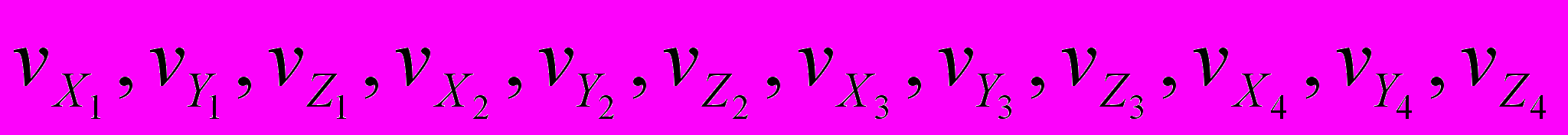– значения вектора скорости в соответствующих узлах конечного элемента е.


Схема процесса автоматизированного проектирования элементов систем применения СОЖ представлена на рис. 5. Процесс проектирования начинается с выбора предварительной геометрической модели, начальных и граничных условий. Выбранные данные являются входными параметрами для моделирования элементов систем применения в ANSYS. Программный продукт ANSYS используется как инструмент для решения задачи течения жидкости (СОЖ) в геометрической модели. На выходе из ANSYS получаем разбиение геометрической модели на конечные элементы и значение поля скоростей в каждом узле конечного элемента.





Рис. 5. Схема процесса автоматизированного проектирования элементов
систем применения СОЖ с использованием ANSYS и АИС СОЖ

На этапе получения решения в ANSYS, производится анализ решения. Если расчетная модель не удовлетворяет первоначальным требованиям к моделируемому элементу системы применения, то начальные данные подвергаются корректировке и оптимизации. В противном случае выходные данные из ANSYS являются входными для расчета движения СОЖ, загрязненной примесями. Дальнейший расчет производится в разработанном специально для этой цели программном продукте АИС СОЖ. В АИС СОЖ решается задача распределения концентрации механических примесей в СОЖ в системе ее применения на основании модели поведения СОЖ (1). На выходе из АИС СОЖ полученное решение (распределение концентрации механических примесей) подвергается повторной проверке на удовлетворение первоначальным требованиям.

В главе 4 описано проведение экспериментальных исследований с целью оценки адекватности разработанной модели поведения СОЖ (1). Под адекватностью подразумевается степень соответствия полученных моделей реальному поведению концентрации механических примесей в системах применения на операциях механообработки. Для этого сравнивались значения концентрации механических примесей, полученные при экспериментальных исследованиях, с соответствующими значениями концентраций механических примесей, полученными расчетным путем. Расчет модели поведения концентрации механических примесей производился численным методом с использованием программных продуктов ANSYS 5.5 и АИС СОЖ. Исходные данные для численного расчета полностью соответствуют реальной опытной модели.

С целью проведения экспериментальных исследований был разработан и создан в заводских условиях опытный образец для моделирования движения и очистки СОЖ (далее – установка). Схема установки приведена на
рис. 6.

Для анализа концентрации механических примесей в пробах СОЖ использовалось устройство для фотометрического анализа концентрации механических примесей в СОЖ (ПКП СОЖ-2)⁸ как один из наиболее точных и удобных на данный момент приборов по контролю концентрации примесей в СОЖ. Прибор отвечает требованиям для использования его в системах прогнозирующего контроля и в качестве датчика в системах управления параметрами СОЖ. Данный прибор позволяет производить массовое измерение гранулометрического состава в различных СОЖ, используя методику фотоседиментационного анализа.





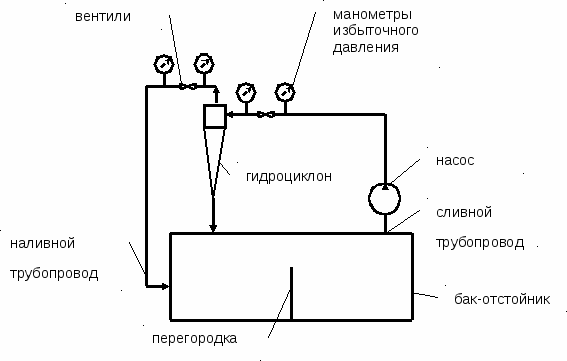
Рис. 6. Схема опытного образца установки для моделирования движения СОЖ
и оценки адекватности математической модели


Параметры жидкости (плотность и вязкость), граничные условия скорости и давления при моделировании в ANSYS были заданы в точности с параметрами экспериментальных исследований СОЖ на установке. В результате было получено распределение поля скоростей течения СОЖ в исследуемых элементах установки (бак и гидроциклон).

С целью получения объективных результатов экспериментальных исследований производилось несколько замеров с различными характеристиками движения СОЖ в установке. При каждом пуске при помощи вентилей изменялось давление на входе и выходе гидроциклона. Перед каждым пуском установки механические примеси, выведенные из предыдущего пуска установки посредством очистки СОЖ в гидроциклоне и через заборы проб СОЖ, возвращались в СОЖ. Тем самым перед каждым экспериментом начальная концентрация механических примесей в СОЖ была постоянной и близкой к 1%, или 10 г/дм³. Параметры пусков установки приведены в
табл. 3.

На рис. 7 представлен графический результат моделирования бака-отстойника установки в ANSYS. На рис. 8 в графическом виде представлены одновременно результаты экспериментальных и расчетных исследований поведения концентрации механических примесей при движении СОЖ в установке. В центральном сечении бака цветными областями указано распределение концентрации механических примесей (г/л) на основании расчетных данных, а числовыми значениями – концентрация механических примесей (г/л) на основании экспериментальных данных.


Таблица 3. Параметры экспериментов (пусков установки)

№ пуска	Давление на входе, МПа	Давление на выходе, МПа	Длина заборных трубок, мм	Начальная концентрация механических примесей, г/дм3	Продолжительность эксперимента, мин
1	0,05	0,010	100	10	60
2	0,10	0,015	100	10	60
3	0,15	0,020	100	10	60
4	0,20	0,025	200	10	60
5	0,25	0,030	200	10	60
6	0,30	0,035	200	10	60
7	0,35	0,040	300	10	60
8	0,40	0,045	300	10	60
9	0,45	0,050	300	10	60
10	0,50	0,055	300	10	60

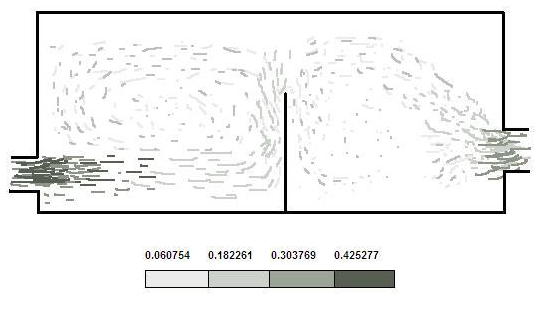
Рис. 7. Графическая модель поля скоростей СОЖ в центральном сечении
бака установки на основании моделирования в ANSYS


Для подтверждения адекватности разработанной модели поведения СОЖ (1) использовалась гипотеза о близости среднего значения концентраций механических примесей расчетных данных среднему значению концентраций механических примесей экспериментальных данных. Основой для проверки гипотезы является t-статистика (распределение Стьюдента). Анализ по критерию Стьюдента определил степень адекватности модели поведения СОЖ (1) не менее 90%.




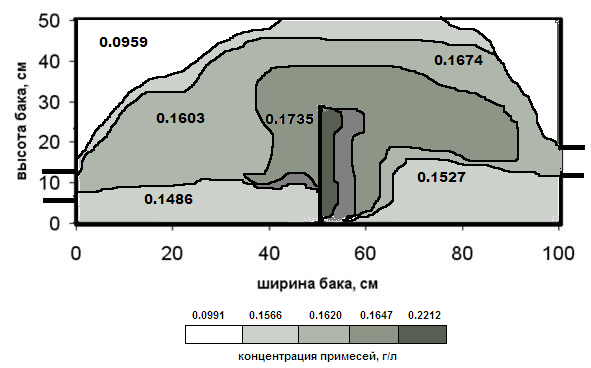
Рис. 8. Распределение концентрации механических примесей в центральном сечении
бака установки на основании расчетных (нижняя шкала) и экспериментальных
(числовые значения) данных


В табл. 4 приведены значения относительных отклонений концентрации механических примесей СОЖ, полученные экспериментальным путем, от соответствующих значений концентрации примесей, полученных расчетным путем, при движении СОЖ в установке.


Таблица 4. Относительные отклонения концентрации механических примесей СОЖ

№ точки	№ расчета
	1	2	3	4	5	6	7	8	9	10
1	-0,1111	-0,1818	-0,2460	0,0352	-0,1014	-0,1498	0,0853	-0,2363	-0,3602	-0,3037
2	-0,1250	-0,1590	-0,1522	-0,2966	-0,1594	-0,3820	-0,4005	-0,2152	-0,1557	-0,0761
3	-0,2551	-0,1944	-0,1558	-0,2176	-0,2196	-0,0997	-0,0736	-0,2862	-0,0873	-0,1260
4	0,1315	0,1278	0,1563	0,1372	0,2315	0,1149	0,1798	0,1887	0,2287	0,1627
5	0,0527	0,1103	0,1227	-0,0805	-0,1324	-0,1857	0,0410	0,1248	0,2043	0,2268
6	0,1700	0,0847	0,0872	0,1202	0,1176	0,1685	0,1232	0,1626	0,0507	0,1510
7	0,2036	-0,1784	-0,1969	-0,1709	-0,1923	-0,2676	-0,1691	-0,2697	-0,1434	-0,1751
8	-0,2192	-0,1222	-0,2698	-0,2160	-0,1993	-0,2071	-0,2118	-0,2852	-0,1888	-0,1633
9	0,2295	0,1564	0,2701	0,1578	0,2269	0,1808	0,2767	0,2479	0,2246	0,3357

В заключении приведены следующие основные результаты диссертационной работы.

Основные результаты и выводы

1. Для элементов системы применения СОЖ (зона резания, трубопроводы, очистители, баки-отстойники) разработана математическая модель поведения СОЖ при ее ламинарном и турбулентном движении в элементах системы применения на примере поведения концентрации механических примесей и основного компонента.
   
2. Для разработанной математической модели определены начальные и граничные условия, позволяющие поставить и решить сложные математические задачи. На основании современных численных методов разработан алгоритм решения поставленных математических задач.
   
3. На основании разработанной математической модели поведения концентрации механических примесей создан комплекс программ, интегрированный с программным обеспечением ANSYS («Автоматизированная Информационная Система расчета движения СОЖ (АИС СОЖ)»), позволяющий автоматизировать процесс проектирования и прогнозирования работы элементов систем применения СОЖ.
   
4. Разработана методика проектирования и прогнозирования работы элементов систем применения СОЖ методом компьютерного моделирования с использованием разработанного комплекса программ АИС СОЖ.
   
5. Разработанная методика прошла лабораторные испытания на модели системы применения СОЖ, загрязненной механическими примесями в системе применения, состоящей из бака-отстойника, гидроциклона, системы трубопроводов и насоса. По результатам лабораторных исследований доказана адекватность полученной математической модели поведения концентрации механических примесей СОЖ в системе применения.
   
6. Комплекс программ АИС СОЖ успешно прошел опытные испытания на ряде промышленных предприятий г. Ульяновска и внедрен на ФГУП ПО «Ульяновский машиностроительный завод «Завод «Каркас», ГП «СТАНКОСЕРВИС», ЗАО НПИ «Волга-ЭКОПРОМ».
   

Автор выражает искреннюю благодарность за ценные советы и помощь в работе доценту кандидату технических наук Евсееву Александру Николаевичу и профессору доктору физико-математических наук Леонтьеву Виктору Леонтьевичу.


Список публикаций по теме диссертации


Публикации в журналах, входящих в список ВАК:


1. Емелин С. В. Модель поведения концентрации механических примесей при движении смазочно-охлаждающей жидкости / Ю. В. Полянсков, А. Н. Евсеев, С. В. Емелин // Автоматизация и современные технологии. – 2010. – № 11. – С. 32–34.

2. Емелин С. В. Оптимизация систем применения смазочно-охлаждающих жидкостей на основе модели концентрации механических примесей / Ю. В. Полянсков, А. Н. Евсеев, С. В. Емелин // Известия вузов. Машиностроение. – 2002. – № 7. – С. 56–60.


Другие публикации:


3. Емелин С. В. Моделирование и оптимизация параметров систем применения СОЖ на операциях механообработки / А. Н. Евсеев, А. Р. Гисметулин, С. В. Емелин // Математическое моделирование физических, экономических, социальных систем и процессов : труды III научной конференции. – Ульяновск, 2000. – С. 64.

4. Емелин С. В. Моделирование турбулентного движения СОЖ с механическими примесями в системах применения / Ю. В. Полянсков, А. Н. Евсеев, С. В. Емелин // Ученые записки Ульяновского государственного университета. Фундаментальные проблемы математики и механики. – Ульяновск, 2000. – Вып. 1, Т. 8. – С. 108–111.

5. Емелин С. В. Модель движения смазочно-охлаждающей жидкости в системе ее применения / Ю. В. Полянсков, А. Н. Евсеев, С. В. Емелин // Математическое моделирование физических, экономических, технических, социальных систем и процессов : труды IV научной конференции. – Ульяновск, 2001. – С. 126–128.

6. Емелин С. В. Методика оптимизации систем применения СОЖ с использованием ориентированного графа // Машиностроитель. – 2002. –
№ 4. – С. 37.

7. Емелин С. В. Модель движения СОЖ, содержащей механические примеси, в системе ее применения / Ю. В. Полянсков, А. Н. Евсеев,
С. В. Емелин // Математическое моделирование физических, технических, экономических, социальных систем и процессов : труды V Международной конференции. – Ульяновск, 2003. – С. 138–140.

8. Емелин С. В. Математическое моделирование распределения примесей СОЖ в центробежных устройствах / А. Н. Евсеев, С. В. Емелин,
Л. А. Бодрова // Математическое моделирование физических, технических, экономических, социальных систем и процессов : труды VI Международной конференции. – Ульяновск, 2005. – С. 40–41.

9. Емелин С. В. Моделирование процесса очистки СОЖ в гравитационном устройстве / А. Н. Евсеев, С. В. Емелин, О. С. Золотова // Математическое моделирование физических, технических, экономических, социальных систем и процессов : труды VI Международной конференции. – Ульяновск, 2005. – С. 42–43.


Подписано в печать 10.01.12.

Формат 60х84/16. Усл. печ. л. 1.

Тираж 120 экз. Заказ 3 /


Отпечатано в Издательском центре

Ульяновского государственного университета

432000, г. Ульяновск, ул. Л. Толстого, 42