Программный комплекс для проектирования экспертных систем «ExSys». Д. П. Ветров, Д. А. Кропотов

Вид материала

Документы

Содержание Структура системы. Возможности системы.

Подобный материал:

• Рабочая программа учебной дисциплины (модуля) Программная реализация экспертных систем, 94.38kb.
• 6. Лекция: Методология построения экспертных систем, 291.07kb.
• Программный комплекс автоматизированного динамического анализа многокомпонентных механических, 10.27kb.
• Ния инструментальной среды приобретения знаний для прикладных экспертных систем, сделаны, 112.06kb.
• О. А. Щербина University of Vienna,\\, 120.29kb.
• Применение экспертных систем на геотехнологическом предприятии атомной отросли, 94.06kb.
• В. В. Пивоваров московский инженерно-физический институт (государственный университет), 27.99kb.
• Встатье рассмотрены вопросы применения экспертных систем в экономике и бизнесе, экспертные, 20kb.
• M. 13. O. программный Комплекс для исследования статистических характеристик шумовых, 126.35kb.
• Ульяновск, tv afanaseva@mail, 52.83kb.

Программный комплекс для проектирования экспертных систем «ExSys».

Д.П. Ветров, Д.А. Кропотов

(Москва)

Введение.

В различных областях человеческой деятельности, таких как медицина, экономика, социология, физика, биология для решения задач интеллектуального анализа данных и обработки информации часто используют экспертные системы. Основной отличительной особенностью таких систем является наличие некоторой априорной информации об исследуемом процессе, получаемой от экспертов. В теории логического управления эта информация получила название базы знаний. Исследования в области экспертных систем ведутся с середины 50-х годов прошлого столетия, и за это время был реализован целый ряд успешных проектов по созданию подобных систем, работающих на практике [1]. Большинство из них следует отнести к области систем, построенных на принципах нечеткой логики. Однако каждый раз такие проекты требовали специальных трудозатрат и денежных вливаний. Эксперты прикладных областей знаний, которые сами не являются специалистами в теории распознавания образов, предпочитают пользоваться готовыми программными продуктами, реализующими общие и достаточно простые механизмы проектирования экспертных систем. Среди подобных программных продуктов общего пользования стоит выделить, прежде всего, пакет fuzzy logic toolbox системы MatLab [2]. Среди его недостатков можно отметить его склонность к переобучению и низкие результаты прогнозирования в реальных задачах [5], длительное время работы и высокие требования к производительности вычислительной системы, требование специальной подготовки пользователей, а также отсутствие гибкости и простоты использования системы, связанное с консервативностью выбора теоретических основ обработки нечеткой информации. К числу последних стоит отнести в первую очередь необходимость задания формы и размеров нечетких множеств, используемых в системе, а также так называемый нейро-нечеткий подход к генерации нечетких правил, при котором у эксперта не остается возможности внести какие-либо изменения в базу знаний системы.

В виду указанных проблем появилась идея создания универсального программного комплекса для проектирования экспертной системы, позволяющего исследователям проходить все этапы создания системы в интерактивном режиме. Кроме того, он должен обходить недостатки, указанные для случая системы MatLab.

Структура системы.

В основе экспертной системы «ExSys» («EXpert SYStem») лежит общая теория построения нечетких экспертных систем [1], [3], а также ряд специальных методов автоматического формирования структуры нечетких множеств и генерации нечетких правил, развиваемых в работах [4], [5]. Общая структура программного комплекса представлена на рисунке 1.

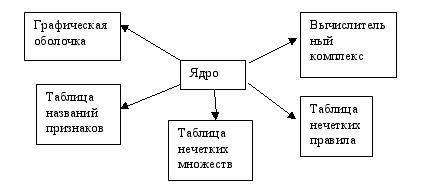Рис 1. Общая схема программы.

Система состоит из нескольких модулей, каждый из которых осуществляет свою функцию. Ядро является основным модулем, который осуществляет связь всех модулей и обмен данных между ними. Таблицы названий признаков, нечетких множеств и нечетких правил представляют собой стандартные таблицы базы данных типа Paradox и хранят в себе информацию о названиях признаков, регулярных разбиениях признаков и названиях нечетких множеств, список нечетких правил соответственно. Посредством графической оболочки эксперт контролирует все этапы проектирования системы.

Возможности системы.



Рис. 2. Возможности системы.

В зависимости от того, на что способен эксперт, данная система может работать в нескольких режимах (рис. 2). В том случае, когда отсутствует какая-либо априорная информация об исследуемой области, все необходимые шаги могут быть проведены в автоматическом режиме. Пользователь должен лишь указать число нечетких множеств для каждого признака и, быть может, дать им названия. В случае необходимости, эксперт может определить примерные границы между множествами вручную. Совокупность нечетких правил вывода (база знаний) генерируется автоматически с использованием таблицы прецедентов или/и вводится экспертом. Он также в случае необходимости может изменить посылки или веса некоторых правил. Форма нечетких множеств определяется путем процедуры оптимизации. Различные режимы работы системы представляются от полностью автономного режима до случая, когда все нечеткие множества и правила вывода задаются экспертом. В последнем случае система функционирует как классический нечеткий контроллер [3].

Нечеткая экспертная система «ExSys» позволяет:

• Задавать регулярное разбиение признакового пространства в интерактивном режиме либо генерировать его автоматически
  
• Определять форму нечетких множеств вручную либо путем оптимизации по прецедентам
  
• Создавать базу знаний системы через интерактивный интерфейс, а также путем генерации методом эффективных сужений с различным набором параметров
  
• Отображать все данные внутри системы через стандартные таблицы базы данных типа Paradox.
  

В созданном программном продукте реализованы все изначально поставленные цели. Он является удобным инструментом для разработки и тестирования нечетких экспертных систем.

Литература

1. Тэрано Т., Асаи К., Сугено М. Прикладные нечеткие системы. Мир, Москва, 1993.
   
2. Дьяконов В., Круглов В. Математические пакеты расширения MATLAB. Специальный справочник. Питер, Москва, 2001.
   
3. Перфильева И. Приложения теории нечетких множеств // Итоги науки и техники. Том 29. Серия Теория вероятностей. Математическая статистика. Теоретическая кибернетика. ВИНИТИ, Москва, 1990, с.83-151.
   
4. Ветров Д., Кропотов Д. Об использовании прецедентной информации в нечетких экспертных системах // Труды 6-ой международной конференции «Распознавании образов и анализ изображений: новые информационные технологии» (РОАИ-6-2002). НовГУ им. Ярослава Мудрого, Великий Новгород, 2002, с. 100-104.
   
5. Kropotov D., Vetrov D. One Approach To Fuzzy Expert System Construction // Proceedings of fifth International Conference On Enterprise Information Systems (ICEIS-2003). Escola Superior de Techologia do Instituto Politecnico de Setubal, Setubal, 2003, pp 566-570.